高数第三章一元函数的导数和微分
高等数学 第三章 一元函数微积分学及其应用

存在且相等.
现在,我们可回答函数 y | x | 在 x 0 处不可导的原因: f0 f0
27
四、左、右导数
第三章 一元函数微分学及其应用
例10
已知
f
x
sin
x
x
x0
x 0 ,求 f0, f0 及 f 0 .
9
二、导数的定义
第三章 一元函数微分学及其应用
定义
设函数 y f x 在 x0 的某个邻域内有定义,当 x 在 x0 处增量为 x ( x0 x 在该邻域内)时,相应地, 函数有增量 y f x0 x f x0 .
如果
lim y lim f x0 x f x0 lim f (x) f (x0)
例6 求 f x x2 的导数.
解 x2 lim x+x2 x lim x 2x 2x
x0
x
x0
一般地,当 x 0 , y x 有定义时,
x lim x x x x1
x0
x
当 x 0 时, y x 有定义时也有上式成立.
例如,取 1 ,则有 2
x
8
一、 割线与切线
练习
第三章 一元函数微分学及其应用
1.求单位圆 x2 y2 1上过点 (1, 0) 的切线方程. 2. 求抛物线 y x2 上过点 (1,1) 和 (2, 4) 的割线方程. 3.求抛物线 y x2 上过点 (1,1) 的切线方程.
4.求函数 y ex 在点 x 1处的切线斜率.
30
五、切线与法线方程
第三章 一元函数微分学及其应用
例11
求曲线
y1 x
一元函数的导数与微分

h→0
h2
解答:
(D) lim f (2h) − f (h) 存在
h→0
h
首先,若 f (x) 在 x = 0 可导,则 f ′(0) = lim f (x) − f (0) = lim f (x) 存在。从这一点
x→0
x
x→0 x
来看,只要 f (x) 在 x =0 处可导,则 A,B,C,D 四个极限都是存在的。事实上,
B 选项,若 lim f (x) + f (−x) 存在,同上面,可知 lim[ f (x) + f (−x)] = 0 。由 f (x) 在
x→0
x
x→0
认识自我,准确定位,重新设计你的人生
5
x = 0 的连续性, lim[ f (x) + f (−x)] = 2 f (0) = 0 ,即 f (0) = 0 。 x→0
C 选项,若 lim f (x) 存在,同前面,我们得到 f (0) = lim f (x) = 0 。于是,
x→0 x
x→0
f ′(0) = lim f (x) − f (0) = lim f (x) 存在。
x→0 x − 0
x→0 x
D 选项,若 lim f (x) − f (−x) 存在,却无法说明 f ′(0) 存在。如果 f ′(0) 存在,那么
(A) f (x) 在 (0, δ) 内单调增加
ห้องสมุดไป่ตู้
(B) f (x) 在 (−δ ,0) 内单调减少
(C) 对任意的 x ∈ (0,δ ) 有 f (x) > f (0)
(D) 对任意的 x ∈ (−δ ,0) 有 f (x) > f (0)
解答:f ′(0) = lim f (x) − f (0) > 0 ,由极限的保号性,存在一个 δ > 0 ,当 0 < x < δ ,
高等数学 第三章 一元函数微积分学及其应用

x x0
x0
x
xx0
x x0
存在,则称该极限为 y f x 在点 x0 处的导数,记为
dy
df (x)
f x0 , y xx0 , dx xx0 或
dx xx0
10
二、导数的定义
第三章 一元函数微分学及其应用
这时也称函数 y f x 在点 x0 处可导.
如果该极限不存在,称函数 y f x 在点 x0处不可导 .
例1 求函数 y ln x 在点 x e 处的切线斜率.
解
k lim f (x) f (x0 ) = lim ln x ln e
x x0
x x0
xe x e
ln x = lim e
xe x e
lim
ln 1
xe e
xe
xe
所以
xe lim e 1
xe x e e
第三章 一元函数微分学及其应用
y
此刻切线的斜率即为 k lim y y0 lim f (x) f (x0 )
x x xx0
0
x x0
x x0
y f x
N Δy T
从上面的例子可以看出, 在求切线斜率的过
程中, 需要用到极限
lim f (x) f (x0 )
x x0
x x0
M C
α
Δx
O
x0
xx
7
二、导数的定义
故 y x2
在 x=0处导数为零,即
dy dx
x x0
0.
O
x
图 3-7
12
二、导数的定义
第三章 一元函数微分学及其应用
例3 求函数 y | x |,在点 x 0 处(见图2-8)的导数.
高等数学微积分第三章一元函数导数与微分

法线方程为:
1 y y0 f ( x0 ) ( x x0 ).
定义 2(单侧导数,左右导数)
f( x0 )
lim
x0
y x
lim x0
f ( x0 x) x
f ( x0 )
(令
x
x0
x)
lim
x x0
f (x) f (x0 ) x x0
存在,
则称
f (x) 在
x0
处
右 左
可导,
x 0
x
注意:
f ( x0 )
f ( x)
,但
x x0
f ( x0 )
f ( x0 ) .
二. 函数不可导的情况
函数 f ( x) 在 x0 不可导,有以下三种情况:
1. 若 f ( x) 在 x0 不连续, 则 f ( x) 在 x0 不可导.
2. 由定理1,知
( 定理 2 )
( i ) 若 f( x0 ) 与 f( x0 ) 都存在但值不相等,
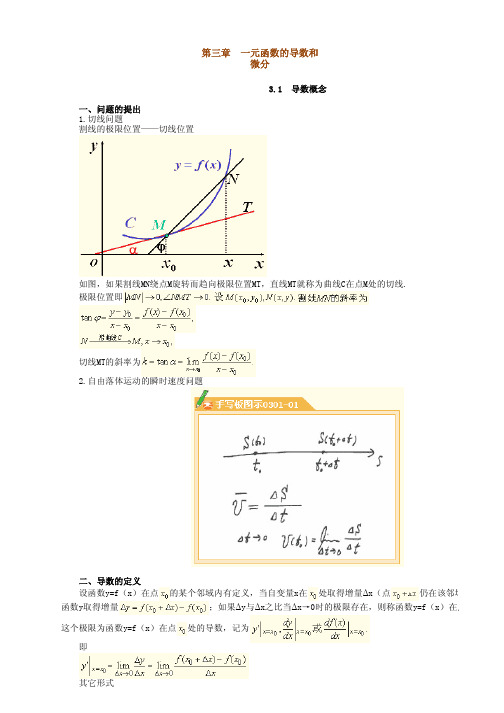
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1.切线问题 割线的极限位置——切线位置
1. 给 x 一增量 x,求 y f ( x x) f ( x);
2. 计算 y f ( x x) f ( x);
x
x
3. 计算极限 :
lim y lim f ( x x) f ( x)(存在) f ( x)
一元函数的导数公式和微分

一、一元函数微分学一元函数微分学由导数和微分组成。
导数:样本量随自变量的变化而变化的快慢程度;微分:曲线的切线上的纵坐标的增量。
二、常数和基本初等函数求导公式 (1) 0)(='C(2) 1)(-='μμμx x (3) x x cos )(sin ='(4) x x sin )(cos -='(5) x x 2sec )(tan =' (6) x x 2csc )(cot -=' (7) x x x tan sec )(sec ='(8) x x x cot csc )(csc -=' (9) a a a x x ln )(='(10) (e )e x x '=(11) a x x a ln 1)(log ='(12) x x 1)(ln =',(13) 211)(arcsin x x -='(14) 211)(arccos x x --='(15)21(arctan )1x x '=+(16)21(arccot )1x x '=-+三、函数的和、差、积、商的求导法则 设)(x u u =,)(x v v =都可导,则 (1) v u v u '±'='±)( (2) u C Cu '=')((C 是常数)(3)v u v u uv '+'=')((4)2v v u v u v u '-'='⎪⎭⎫ ⎝⎛四、反函数求导法则若函数)(y x ϕ=在某区间y I 内可导、单调且0)(≠'y ϕ,则它的反函数)(x f y =在对应区间x I 内也可导,且)(1)(y x f ϕ'='或dydxdx dy 1=五、复合函数求导法则 设)(u f y =,而)(x u ϕ=且)(u f 及)(x ϕ都可导,则复合函数)]([x f y ϕ=的导数为dy dy du dx du dx =或()()y f u x ϕ'''=六、高阶导数的莱布尼兹公式七、隐函数的导数一般地,如果变量x ,y 之间的函数关系是由某一个方程()0,=y x F 所确定,那么这种函数就叫做由方程所确定的隐函数. 对数求导法根据隐函数的求导法,我们还可以得到一个简化求导运算的方法.它适合由几个因子通过乘、除、乘方、开方所构成的比较复杂的函数(包括幂指函数)的求导.这个方法是先取对数,化乘、除为加、减,化乘方、开方为乘积,然后利用隐函数求导法求导,因此称为对数求导法.幂指函数的一般形式为()0v y u u =>,其中,u v 是x 的函数. 八、由参数方程所确定的函数的导数22234241433339t t t t t ed dte e e dx dt dx e dt--⎛⎫=-⋅=-== ⎪-⎝⎭22223t d y d dy d e dx dx dx dx ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭一般地,如果参数方程()()x t y t ϕψ=⎧⎪⎨=⎪⎩,(t 为参数) 确定y 与x 之间的函数关系,则称此函数关系所表示的函数为由参数方程所确定的函数.如果函数()t x ϕ=,()t y ψ=都可导,且()0≠'t ϕ,又()t x ϕ=具有单调连续的反函数()x t 1-=ϕ,则由参数方程所确定的函数可以看成()t y ψ=与()x t 1-=ϕ复合而成的函数()[]x y 1-=ϕψ,根据复合函数与反函数的求导法则,有()()t t dtdx dt dy dx dt dt dy dx dy ϕψ''=⋅=⋅=1,即()()t t dx dy ϕψ''= ,也可写成 dtdxdtdy dx dy=.求方程32ttx ey e-⎧=⎪⎨=⎪⎩所确定的函数的二阶导数22d ydx.解 ()()tt t t t e ee e e dx dy 2323232-=-=''=--,注意二阶导的求法。
一元函数的导数与微分

一元函数的导数与微分导数和微分是微积分的重要概念,它们描述了一元函数的变化率和局部线性逼近,对于函数的研究和应用具有重要的意义。
本文将介绍一元函数的导数和微分的概念、性质以及应用。
一、导数的概念对于给定的一元函数f(x),在某一点x=a处,函数的导数表示函数在该点的变化率。
导数用符号f'(a)或df(a)/dx表示。
导数的定义为:f'(a) = lim_(x→a) (f(x)-f(a))/(x-a)其中lim表示极限运算。
这个定义可以解释为函数曲线在点(a,f(a))处的切线的斜率。
二、导数的性质1. 可导性:如果函数f(x)在某一点x=a处可导,则该点为可导点。
2. 连续性:如果函数f(x)在某一点x=a处可导,则该点也是函数f(x)在该点处连续的必要条件。
3. 导数的代数运算:导数具有线性性质,即对于常数c,以及可导函数f(x)和g(x),有以下性质:a) (cf(x))' = cf'(x)b) (f(x) + g(x))' = f'(x) + g'(x)c) (f(x)g(x))' = f'(x)g(x) + f(x)g'(x)d) (f(x)/g(x))' = (f'(x)g(x) - f(x)g'(x))/g^2(x) (其中g(x)≠0)三、微分的概念微分是导数的一个重要应用,它表示函数在某一点附近的线性逼近。
给定函数f(x)和点x=a,函数在该点附近的微分表示为:df(a) = f'(a)dx其中df(a)表示函数f(x)在点x=a处的微分,dx表示自变量的一个微小增量。
四、微分与导数的关系微分与导数是密切相关的概念。
对于函数f(x),如果它在点x=a处可导,则在该点附近的微分可以表示为:df(a) = f'(a)dx通过微分,可以得到函数在某一点附近的局部线性逼近。
一元函数导数

一元函数导数在微积分中,导数是一个非常重要的概念。
导数可以用来描述函数在某一点的变化率,也可以用来求函数的最值、最小值等。
在本文中,我们将介绍一元函数导数的概念、性质和应用。
一、导数的定义设函数y=f(x),在点x0处有定义,若极限lim(f(x)-f(x0))/(x-x0)存在,则称函数f(x)在点x0处可导,其导数为f'(x0)=lim(f(x)-f(x0))/(x-x0)x→x0二、导数的性质1. 可导必连续,连续不一定可导。
2. 导数具有可加性,即(f+g)'(x)=f'(x)+g'(x)。
3. 导数具有可乘性,即(fg)'(x)=f'(x)g(x)+f(x)g'(x)。
4. 导数具有链式法则,即(f(g(x))')=f'(g(x))g'(x)。
三、导数的应用1. 求函数的最值若函数f(x)在[a,b]上连续,在(a,b)内可导,则f(x)在[a,b]上的最大值和最小值必定出现在f'(x)=0或f'(x)不存在的点上。
2. 求函数的单调性若函数f(x)在[a,b]上连续,在(a,b)内可导,则f(x)在[a,b]上单调递增的条件是f'(x)>0,单调递减的条件是f'(x)<0。
3. 求函数的凹凸性若函数f(x)在[a,b]上连续,在(a,b)内可导,则f(x)在[a,b]上凹的条件是f''(x)>0,凸的条件是f''(x)<0。
4. 求函数的极值若函数f(x)在x0处可导,且f'(x0)=0或f'(x0)不存在,则x0为f(x)的极值点。
导数是微积分中的一个重要概念,它可以用来描述函数的变化率、求函数的最值、单调性、凹凸性和极值等。
在实际应用中,导数也有着广泛的应用,如物理学中的速度、加速度等概念都与导数有关。
高等数学导数微分学习辅导及公式总结

高等数学(1)学习辅导(三)第三章 导数与微分导数与微分这一章是我们课程的学习重点之一。
在学习的时候要侧重以下几点:⒈理解导数的概念;了解导数的几何意义;会求曲线的切线和法线;会用定义计算简单函数的导数;知道可导与连续的关系。
)(x f 在点0x x =处可导是指极限xx f x x f x ∆-∆+→∆)()(lim000存在,且该点处的导数就是这个极限的值。
导数的定义式还可写成极限0)()(limx x x f x f x x --→函数)(x f 在点0x x =处的导数)(0x f '的几何意义是曲线)(x f y =上点))(,(00x f x 处切线的斜率。
曲线)(x f y =在点))(,(00x f x 处的切线方程为)())((000x f x x x f y +-'=函数)(x f y =在0x 点可导,则在0x 点连续。
反之则不然,函数)(x f y =在0x 点连续,在0x 点不一定可导。
⒉了解微分的概念;知道一阶微分形式不变性。
⒊熟记导数基本公式,熟练掌握下列求导方法 (1)导数的四则运算法则 (2)复合函数求导法则 (3)隐函数求导方法 (4)对数求导方法(5)参数表示的函数的求导法正确的采用求导方法有助于我们的导数计算,如一般当函数表达式中有乘除关系或根式时,求导时采用取对数求导法, 例如函数xx y 2)1(-=,求y '。
在求导时直接用导数的除法法则是可以的,但是计算时会麻烦一些,而且容易出错。
如果我们把函数先进行变形,即21212322212)1(-+-=+-=-=xx x xx x xx y再用导数的加法法则计算其导数,于是有2321212123----='x x x y这样计算不但简单而且不易出错。
又例如函数321-+=x x y ,求y '。
显然直接求导比较麻烦,可采用取对数求导法,将上式两端取对数得)2ln(31)1ln(21ln --+=x x y 两端求导得)2(31)1(21--+='x x y y 整理后便可得)2(682123---⋅-+='x x x x x y若函数由参数方程⎩⎨⎧==)()(t y t x ϕψ 的形式给出,则有导数公式)()(d d t t x y ϕψ''=能够熟练地利用导数基本公式和导数的四则运算法则、复合函数的求导法则计算函数的导数,能够利用隐函数求导法,取对数求导法,参数表示的函数的求函数的导数。
§3一元函数微积分解读

§3 一元函数微积分3.1 微分一元函数可记为)(x y y = 或 )(x F y =在它的连续区域内,如图附-20所示,自变量若从x 增加到x x ∆+,便称x ∆为自变量x 的增量。
相应地,自变量从)(x y 增加到)(x x y ∆+,称)()(x y x x y y -∆+=∆为函数增量。
y x ∆∆、既可以是正的,也可以是负的。
几个函数的y x ∆∆、间关系如下:B Ax y += []x A B Ax B x x A y ∆=+-+∆+=∆)()( 2Ax y = 222)(2)(x A x Ax Ax x x A y ∆+∆=-∆+=∆x y sin = x x x x x x x y ∆+-∆=-∆+=∆sin cos )1(cos sin sin )sin( x e y = )1(-=-=∆∆∆+x x x x x e e e e y 例中B A ,均是常量。
自变量增量0→∆x 时,称为自变量微分,改记成dx 。
dx 是无穷小量,但不是零。
在连续区域内,自变量增量取微分dx 时,函数增量0→∆y ,称为函数微分,记成dy ,它也是无穷小量,可正,可负。
dy 与dx 间关系为)()(x y dx x y dy -+= 几个实例如下:B Ax y += Adx dy =2Ax y = dx dx x A dy )2(+=x y s i n= dx x dx x dy sin cos )1(cos sin +-= xe y = )1(-=dxxee dy数学中可以证明,对无穷小量dx ,有Ax Bdx Ax →+ 简书为 Ax Bdx Ax =+ 1cos →dx 简书为 1cos =dx dx dx →sin 简书为 dx dx =sin dx dx →tan 简书为 dx dx =tan e dx dx→+1)1( 简书为 ...718281828.2)1(1==+e dx dx例题6. 试证 dx dx dx ==tan sin 。
一元函数导数

一元函数导数一元函数导数的作用在于描述函数在某一点的变化率。
通过求导可以得到函数的切线斜率,从而帮助我们理解函数在不同点的趋势和性质。
在本文中,我们将从不同角度探讨一元函数导数的相关内容。
一、导数的定义和基本概念导数的定义是函数在某一点的极限值,表示函数在该点的瞬时变化率。
导数可以通过函数的极限运算来求得,一般用符号f'(x)或dy/dx表示。
导数的存在性保证了函数在该点的光滑程度,也决定了函数的单调性和凸凹性。
二、导数的几何意义导数可以理解为函数曲线在某一点的切线斜率。
切线斜率为正表示曲线在该点上升,为负表示曲线下降。
当导数为零时,表示函数在该点达到极值,可以帮助我们找到函数的极值点和拐点。
三、导数的运算法则1.常数乘法法则:导数与常数的乘积等于常数乘以导数。
2.和差法则:导数与函数的和(差)的导数等于函数的导数的和(差)。
3.积的求导法则:导数与函数的积的导数等于函数的导数乘以另一个函数,再加上另一个函数的导数乘以该函数。
4.商的求导法则:导数与函数的商的导数等于分子函数的导数乘以分母函数,减去分子函数乘以分母函数的导数,再除以分母函数的平方。
5.复合函数的求导法则:导数与复合函数的导数等于外函数的导数乘以内函数的导数。
四、导数的应用1.切线问题:通过求导可以得到函数曲线在某一点的切线方程,进而求出曲线在该点的切线。
2.极值问题:通过求导可以找到函数的极值点,从而确定函数的最大值和最小值。
3.凸凹性和拐点:通过求导可以判断函数的凸凹性和拐点的位置,进而分析函数的变化趋势。
4.速度和加速度问题:导数可以描述物体的速度和加速度,帮助我们理解物体的运动规律。
5.最优化问题:通过求导可以求解最优化问题,例如求解函数的最大值、最小值或最优解。
五、导数与原函数的关系导数与原函数之间存在一个重要的关系,即导数是原函数的斜率函数。
如果函数的导数存在,则函数在某一点的导数等于该点的切线斜率。
反过来,如果函数在某一区间内连续且可导,则函数在该区间内的导数是唯一的。
《高等数学课件-一元函数微积分》

3
应用
极限可用于求斜率、判断函数的收敛性等。
4. 连续性与间断点的概念及分类讨论
连续性
连续函数的图像没有断裂或跳跃。
间断点
间断点将连续函数的图像切割成不同的部分。
5. 导数的定义、基本性质及其求解方 法
1 定义
2 基本性质
导数描述了函数在某一点的变化速率。
导数可用于求切线、判断函数的平滑 性等。
2. 函数的基本概念及其符号表示法
定义
函数描述了两个变量之间 的关系,每个输入值都有 唯一的输出值。
符号表示法
函数可以用公式、图像或 表格形式表示。
常用函数类型
包括线性函数、指数函数、 对数函数等。
3. 极限的定义、常用极限法则与应用
1
定义
极限描述了函数在某一点附近的行为。
2
常用极限法则
包括极限的四则运算法则、夹逼定理等。
2 判定条件
凸曲线的二阶导数大于等于零,凹曲 线的二阶导数小于等于零。
3 性质
凸曲线整体向上弯曲,凹曲线整体向下弯曲。
12. 函数的最大极值、最小极值及其求解 方法
最大极值
最大极值函数取得的最小值。
3 求解方法
包括使用导数公式和求极限的方法。
6. 中值定理及利用中值定理证明函数的 性质
1
中值定理简介
中值定理建立了导数与函数性质之间
罗尔定理
2
的关系。
如果一个函数在两个点上取得相同的
函数值,那么在两点之间,函数的导
数为零。
3
拉格朗日中值定理
如果一个函数在一个闭区间上连续, 在该区间内可导,那么在该区间内至 少存在一个点,使得导数等于函数在 该区间的平均变化率。
7.第三章一元函数微分学(导数的概念)

0
0
f x在点 x x 处的函数值,即 0
f (x ) f (x) .
0
x x0
2. 左、右导数 左可导 如果极限lim y 存在,则这个极限称为函数 y f (x)在
x x0
点 x 处的左导数,并且说 f (x)在点 x 处左可导,记作 f (x ).
0
0
0
右可导 如果极限lim y 存在,则这个极限称为函数 y f (x)在 x x0
x 处的导数 f (x ) 在几何上表示曲线 y f (x) 在点 M (x , y )
0
0
00 0
处的切线的斜率.
过切点M (x , y )且垂直于切线的直线叫做曲线 y f (x) 00 0
在点M (x , y )处的法线. 00 0
求导举例
由导数的定义可知,求 y f (x)的导数 y的一般步骤如下:
点 x 处的右导数,并且说 f (x)在点 x 处右可导,记作 f (x ).
0
0
0
根据极限存在的充要条件,我们有下面的定理:
定理 函数 f (x)在点 x 处的左、右导数存在且相等是 f (x) 在 0
点 x 处可导的充要条件. 0
3. 导数的几何意义
由切线问题的讨论和导数的定义知,函数 y f (x)在点
s f t在t 0 处对时间 t 的导数,即
vt ds .
0
dt tt0
(2)曲线 y f (x)在点M x , y 处的切线斜率,就是函数 y f (x) 00 0
在点 x 处对自变量 x 的导数,即 0
k y | 。 x x0
例 1 设 f (x) x2,求 f 1, f x . 0
第三章 一元函数微分学
高等数学课件:专题三 一元函数微分法

,
x
0
,问:a和b为何值时,f (x)
a bx, x 0
在x 0处可导?
例5.设f
(
x)
aex
,
x
0
,若f (x)在x 0处可导,
b ln(1 x), x 0
则a _______,b _________
例6. f (x) (x | sin x |) cosx,则f (x)在x 0是否可导?
三.对数求导法
例14.求 (sin x)x _______
例15.y xtgx,则dy _______
四.隐函数求导 例16.y y(x)由方程x sin y yex 0所确定的隐函数,
2 则y(0) _______
例17.求方程sin y xey 0所确定曲线y y(x)在(0,0)点 的切线和法线方程
f f
(t) ,求
(e3t 1)
yt0及yt0
六.微分,切线方程
dy
f (x)dx, dy x x0
f (x0 )dx
例26.已知y arctgex x 1 ln(e2x 1),则dy ______
2
x1
例27.y log x e(x 0, x 1),则微分dy ______
例36. f (x) x2 cos2 x,求f (n) (x)(n 3)
思考:
1.函数f (x) lim ln(en xn ) (x 0),讨论f (x)连续性
n
n
和可导性
2.隐函数y f (x y),其中f二阶可导, f 1,则y ______
3.已知y 3 2x 1,求y(n) _______
例28.当x _______时,y arcsin 的切线与y x2的
微积分讲义_第三章-一元函数的导数和微分
3.6 导数和微分在经济学中的简单应用,由于知识体系的关联性,我们把本节放到第四章后面讲。
例11.求
的导数
【答疑编号11030311:针对该题提问】
例12.求
的导数
【答疑编号11030312:针对该题提问】
例13.求
的导数
【答疑编号11030313:针对该题提问】
例14.求
的导数
【答疑编号11030314:针对该题提问】
例15.(教材习题3.2,8题)已知 【答疑编号11030315:针对该题提问】
切线方程为 法线方程为
例8、求双曲线
处的切线的斜率,并写出在该点处的切线方程和法线方程。
【答疑编号11030108:针对该题提问】
解 由导数的几何意义, 得切线斜率为
所求切线方程为
法线方程为
六、可导与连续的关系 1.定理 凡可导函数都是连续函数. 注意:该定理的逆定理不成立,即:连续函数不一定可导。 我们有:不连续一定不可导 极限存在、连续、可导之间的关系。
2.连续函数不存在导数举例
例9、讨论函数
在x=0处的连续性与可导性。
【答疑编号11030109:针对该题提问】
解:
例10、 P115第10题
设
,α在什么条件下可使f(x)在点x=0处。
(1)连续;(2)可导。 【答疑编号11030110:针对该题提问】 解:(1)
(2)
七、小结 1.导数的实质:增量比的极限; 2.导数的几何意义:切线的斜率; 3.函数可导一定连续,但连续不一定可导;
第三章 一元函数的导数和 微分
一、问题的提出 1.切线问题 割线的极限位置——切线位置
3.1 导数概念
如图,如果割线MN绕点M旋转而趋向极限位置MT,直线MT就称为曲线C在点M处的切线. 极限位置即
电子教案-高等数学(工科类)(魏寒柏 骈俊生)ppt-第三章一元函数微分学及其应用-电子课件

分析:运动员跳水过程可以视为自由落体
运动,该案例实际上一个求变速直线运动
第
的瞬时速度问题。
一
节
运动跳下的距离和时间的关系为:s 1 gt 2 4.9t 2
2
导 数 的
如果运动员起跳时间记为 t 0 ,则入水时间为t 28 2.4(s)
4.9
概
我们用一些持续缩短的时间间隔 [2.4,2.4 t]上的平均速度
导
特别地,若
lim
x0
y x
,
也称函数
y
f
(x) 在
数 的 概
点 x0 的导数为无穷大,其属于导数不存在 的情形。
念
导数定义的 等价形式
前面两个案例中的导数:
第
v(t0
)
s(t0
)
lim
t 0
s(t0
t) t
s(t0
)
一
节 导
k
f (x0 )
lim
x0
f
( x0
x) x
f
(x0 )
数
的
概
念
y
y 1 3(x 1) , 3x y 2 0
法线方程:
y 1 1 (x 1) , 3
x 3y 4 0
可导与连续的关系 可导必定连续,反之则不成立。
第
一 节
例如函数 f (x) x 在点 x 0处连续但不可导,
导
因为
数 的 概
f
(0)
lim
x0
f (0 x) f (0)
x
lim x0
导
增量的比值的极限,即平均变化率的极限。
数
的
概
类似问题还有:
一元函数微分学总结

例5. 设 y
( x 1)3 4 2 x
5
( x 3)
2
求y' .
1 2 解 取对数 ln y 3ln x 1 ln(2 x) ln x 3 4 5
1 3 1 2 等式两边对 x 求导数: y' y x 1 4(2 x ) 5(x 3)
sinx ). 则有: y' x (cosxlnx x 解法2: 作指数对数恒等变形:
y x e = esinxlnx , y = (esinxlnx ) = esinxlnx (sinx lnx)
sinx
ln( xsinx )
=x
sin x
1 (cosx lnx sinx ). x
则曲线 y = f (x) 在
是曲线y = f (x) 的拐点.
机动
目录
上页
下页
返回
结束
二﹑典型例题分析与解答
例6. 已知 解: 应填−1. 注释: 本题考查导数的定义. 则
机动
目录
上页
下页
返回
结束
e , x 1 例7. 设 f ( x) 在 x 1处可导,求 a, b. ax b, x 1 解: x 1 处连续且可导,即 f ( x) 在
由
例8. 设f (x)可导, F ( x) f ( x)(1 | sinx |) 则 f (0) 0 是F (x)在x=0可导的( A ). (A) 充分必要条件 ; (B) 充分条件但非必要条件; (C) 必要条件但非充分条件; (D) 既非充分条件又非必要条件. 解: 直接计算解此题. 由于F ( x) f ( x)(1 | sinx |)= f ( x) + f ( x) | sinx |, 而f (x)可导, 所以F (x)的可导性与 f ( x) | sinx | 的可导性相同.
一元函数导数与微分(数三)考研真题

[]
(D) 0
二、填空题
1、(03,4 分)已知曲线 y x3 3a 2 x b 与 x 轴相切,则 b2 可以通过 a 表示
为 b2 ________.
2、(06,4 分)设函数 f (x)在x 2 的某领域内可导,且 f x e f x , f 2 1 ,
[]
3.(05,4 分)当 a 取下列哪个值时,函数 f (x) 2x3 9x 2 12x a 恰好
有两个不同的零点.
(A) 2. (B) 4. (C) 6.
(D) 8.
[
]
4. (06,4 分)设函数 y f x 具有二阶导数,且 f x 0, f x 0, x 为
(C) f (x) g(x) h(x)
(D) g(x) f (x) h(x)
9、(11,4 分)已知 f (x) 在 x 0 处可导,且 f (0) 0 ,则
lim x2 f (x) 2 f (x3)
x0
x3
(A). 2 f (0)
(B) f (0)
(C) f (0)
自变量 x 在点 x0 处的增量, y与dy 分别为 f x 在点 x0 处对应的增量与
微分,若 x 0 ,则
[
]
(A) 0 dy v
(B) 0 y dy
(C) y dy 0
(D) dy y 0
5.
(06,4 分)设函数
f
x 在 x=0 处连续,且 lim n0
一元函数导数与微分(数三)考研真题
一、 选择题(将最佳答案的序号填写在括号内)
1.(03,4 分)设 f(x)为不恒等于零的奇函数,且 f (0) 存在,则函数 g(x) f (x) x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章一元函数的导数和微分【字体:大中小】【打印】3.1 导数概念一、问题的提出1.切线问题割线的极限位置——切线位置如图,如果割线MN绕点M旋转而趋向极限位置MT,直线MT就称为曲线C在点M处的切线.极限位置即切线MT的斜率为2.自由落体运动的瞬时速度问题二、导数的定义设函数y=f(x)在点的某个邻域内有定义,当自变量x在处取得增量Δx(点仍在该邻域内)时,相应地函数y取得增量;如果Δy与Δx之比当Δx→0时的极限存在,则称函数y=f(x)在点处可导,并称这个极限为函数y=f(x)在点处的导数,记为即其它形式关于导数的说明:在点处的导数是因变量在点处的变化率,它反映了因变量随自变量的变化而变化的快慢程度。
如果函数y=f(x)在开区间I内的每点处都可导,就称函数f(x)在开区间I内可导。
对于任一,都对应着f(x)的一个确定的导数值,这个函数叫做原来函数f(x)的导函数,记作注意:2.导函数(瞬时变化率)是函数平均变化率的逼近函数.导数定义例题:例1、115页8设函数f(x)在点x=a可导,求:(1)【答疑编号11030101:针对该题提问】(2)【答疑编号11030102:针对该题提问】三、单侧导数1.左导数:2.右导数:函数f(x)在点处可导左导数和右导数都存在且相等. 例2、讨论函数f(x)=|x|在x=0处的可导性。
【答疑编号11030103:针对该题提问】解闭区间上可导的定义:如果f(x)在开区间(a,b)内可导,且及都存在,就说f(x)在闭区间[a,b]上可导.由定义求导数步骤:例3、求函数f(x)=C(C为常数)的导数。
【答疑编号11030104:针对该题提问】解例4、设函数【答疑编号11030105:针对该题提问】解同理可以得到例5、求例6、求函数的导数。
【答疑编号11030106:针对该题提问】解例7、求函数的导数。
【答疑编号11030107:针对该题提问】解四、常数和基本初等函数的导数公式五、导数的几何意义表示曲线y=f(x)在点处的切线的斜率,即切线方程为法线方程为例8、求双曲线处的切线的斜率,并写出在该点处的切线方程和法线方程。
【答疑编号11030108:针对该题提问】解由导数的几何意义, 得切线斜率为所求切线方程为法线方程为六、可导与连续的关系1.定理凡可导函数都是连续函数.注意:该定理的逆定理不成立,即:连续函数不一定可导。
我们有:不连续一定不可导极限存在、连续、可导之间的关系。
2.连续函数不存在导数举例例9、讨论函数在x=0处的连续性与可导性。
【答疑编号11030109:针对该题提问】解:例10、 P115第10题设,α在什么条件下可使f(x)在点x=0处。
(1)连续;(2)可导。
【答疑编号11030110:针对该题提问】解:(1)(2)七、小结1.导数的实质:增量比的极限;2.导数的几何意义:切线的斜率;3.函数可导一定连续,但连续不一定可导;4.5.求导数最基本的方法:由定义求导数.6.判断可导性3.2 求导法则3.3 基本求导公式一、和、差、积、商的求导法则1.定理:如果函数在点x处可导,则它们的和、差、积、商(分母不为零)在点x 处也可导,并且推论2.例题分析例1、求的导数。
【答疑编号11030201:针对该题提问】解例2、求的导数。
【答疑编号11030202:针对该题提问】解例3、求y=tanx的导数。
【答疑编号11030203:针对该题提问】解同理可得例4、求y=secx的导数。
【答疑编号11030204:针对该题提问】解同理可得例5、131页例2设,求.【答疑编号11030205:针对该题提问】二、反函数的导数1.定理:如果函数在某区间内单调、可导且,那么它的反函数在对应区间内也可导,且有即反函数的导数等于直接函数导数的倒数.2.例题分析例6、求函数y=arcsinx的导数【答疑编号11030206:针对该题提问】解同理可得例7、求函数的导数。
【答疑编号11030207:针对该题提问】解特别地三、小结:初等函数的求导问题1.常数和基本初等函数的导数公式2.函数的和、差、积、商的求导法则设u=u(x),v=v(x)可导,则例8、127页1题(6)(14)(15)(1)1题(6)小题【答疑编号11030208:针对该题提问】解:(2)1题(14)小题【答疑编号11030209:针对该题提问】解:(3)1题(15)小题【答疑编号11030210:针对该题提问】解:例9、115页3若一直线运动的运动方程为,求在t=3时运动的瞬时速度。
【答疑编号11030211:针对该题提问】解:例10、115页5求曲线的与直线y=5x的平行的切线。
【答疑编号11030212:针对该题提问】另一条求出来是四、分段函数的求导问题1.114页定理:设(1)如果函数在上连续,在上可导,且当时,则(2)如果函数在上连续,在上可导,且当时,则2.分段函数的求导问题举例例11、 116页11 求下列分段函数f(x)的:(1)【答疑编号11030213:针对该题提问】解:五、复合函数的求导法则1.复合函数的求导法则定理如果函数在点x0可导,而y=f(u)在点可导,则复合函数在点x0可导,且其导数为即因变量对自变量求导,等于因变量对中间变量求导,乘以中间变量对自变量求导。
(链式法则)推广设,则复合函数的导数为2.例题分析例1.求函数y=lnsinx的导数。
【答疑编号11030301:针对该题提问】解∵y=lnu,u=sinx.例2.已知y=(2x2-3x+5)100,求。
【答疑编号11030302:针对该题提问】例3.求y=sin5x的导数【答疑编号11030303:针对该题提问】例4.求函数的导数【答疑编号11030304:针对该题提问】解例5.(教材133页习题3.3,1题(2)小题)求的导数【答疑编号11030305:针对该题提问】例6.求的导数【答疑编号11030306:针对该题提问】例7.求的导数(a>0)【答疑编号11030307:针对该题提问】例8.求函数的导数【答疑编号11030308:针对该题提问】解例9.(教材128页习题3.2,3题(5)小题)求的导数【答疑编号11030309:针对该题提问】例10.(教材128页习题3.2,3题(7)小题)求y=(sinnx)(cos n x)的导数【答疑编号11030310:针对该题提问】例11.求的导数【答疑编号11030311:针对该题提问】例12.求的导数【答疑编号11030312:针对该题提问】例13.求的导数【答疑编号11030313:针对该题提问】例14.求的导数【答疑编号11030314:针对该题提问】例15.(教材习题3.2,8题)已知在点x=1可导,求a,b。
【答疑编号11030315:针对该题提问】幂指函数、抽象的复合函数的求导例题一、幂指函数求导例1: x x【答疑编号11030401:针对该题提问】例2: y=(sinx)cosx求y'【答疑编号11030402:针对该题提问】二、抽象的复合函数求导例3:设f(u)可导,求下列函数的导数(1)f(lnx)+lnf(x)【答疑编号11030403:针对该题提问】解:(2)y=f(e-x)【答疑编号11030404:针对该题提问】解:(3)y= e f(x)【答疑编号11030405:针对该题提问】(4)【答疑编号11030406:针对该题提问】(5)【答疑编号11030407:针对该题提问】3.4 高阶导数一、高阶导数的定义问题:变速直线运动的加速度。
设s=f(t),则瞬时速度为v(t)=f'(t)∵加速度α是速度v对时间t的变化率∴a(t)=v'(t)=[f'(t)]'定义如果函数f(x)的导数f'(x)在点x处可导,即存在,则称(f'(x))'为在点x处的二阶导数。
记作。
二阶导数的导数称为三阶导数,。
三阶导数的导数称为四阶导数,。
例4:y=3x2+sinx【答疑编号11030408:针对该题提问】一般地,函数f(x)的n-1阶导数的导数称为函数f(x)的n阶导数,记作相应地,f(x)称为零阶导数;f'(x)称为一阶导数。
例5:求下列函数的二阶导数:(1)y=ax+b【答疑编号11030409:针对该题提问】(2)y=cos nx;【答疑编号11030410:针对该题提问】(3)y=e sinx【答疑编号11030411:针对该题提问】二、对于某些特殊的导数的高阶导数是有规律的。
例6:求下列函数的n阶导数(1)y=e x【答疑编号11030412:针对该题提问】(2)y=x5【答疑编号11030413:针对该题提问】例7:设y=xμ求y(n)解:用数学归纳法可以证明:特别,当μ=n时,即y=xn,其n阶导数y(n)= (x n)(n)=n!【答疑编号11030414:针对该题提问】例8:【答疑编号11030415:针对该题提问】例9:设y=(x2+1)10(x9+x3+1),求y(30)【答疑编号11030416:针对该题提问】例10:设y=sinx,求y(n)。
【答疑编号11030417:针对该题提问】解……同理可得注意:求n阶导数时,求出1——3或4阶后,不要急于合并,分析结果的规律性,写出n 阶导数.(数学归纳法证明)例11:设f(x)的n-2阶导数,求f(n)(x)。
【答疑编号11030418:针对该题提问】3.5 函数的微分问题的提出实例:正方形金属薄片受热后面积的改变量.设边长由x0变到x0+△x,∵正方形面积∴是△x的线性函数且为△A的主要部分,是△x的高阶无穷小,当|△x|很小时可忽略。
微分的定义定义:设函数y=f(x)在某区间内有定义,x0及x0+△x在这区间内,如果成立(其中A是与△x无关的常数),则称函数y=f(x)在点x0可微,并且称A·△x为函数y=f(x)在点x0相应于自变量增量△x的微分,记作微分dy叫做函数增量△y的线性主部。
(微分的实质)可微的条件定理:函数f(x)在点x0可微的充要条件是函数f(x)在点x0处可导,且通常把自变量x的增量△x称为自变量的微分,记作dx,即dx=△x即函数的微分dy与自变量的微分dx之商等于该函数的导数,导数也叫“微商”。
微分的几何意义几何意义:(如图)当△y是曲线的纵坐标增量时,dy就是切线纵坐标对应的增量,当|△x |很小时,在点M的附近,切线段MP可近似代替曲线段MN。
微分的求法求法: 计算函数的导数, 乘以自变量的微分。
1.基本初等函数的微分公式2.函数和、差、积、商的微分法则例1:设,求dy。
【答疑编号11030501:针对该题提问】例2:,求dy。
【答疑编号11030502:针对该题提问】例3:,求dy。
【答疑编号11030503:针对该题提问】微分形式的不变性设函数y=f(x)有导数f'(x)(1)若x是自变量时,dy= f'(x)dx(2)若x是中间变量时,同样有结论:无论x是自变量还是中间变量,函数y=f(x)的微分形式总是,这就是微分形式的不变性例4:设y=sin(2x+1),求dy。
