结晶学基础第八章习题答案
晶体学基础与晶体结构习题与答案

晶体学基础与晶体结构习题与答案1. 由标准的(001)极射赤面投影图指出在立方晶体中属于[110]晶带轴的晶带,除了已在图2-1中标出晶面外,在下列晶面中哪些属于[110]晶带?(1-12),(0-12),(-113),(1-32),(-221)。
图2-12. 试证明四方晶系中只有简单立方和体心立方两种点阵类型。
3. 为什么密排六方结构不能称作为一种空间点阵?4. 标出面心立方晶胞中(111)面上各点的坐标。
5. 标出具有下列密勒指数的晶面和晶向:a)立方晶系(421),(-123),(130),[2-1-1],[311];b)六方晶系(2-1-11),(1-101),(3-2-12),[2-1-11],[1-213]。
6. 在体心立方晶系中画出{111}晶面族的所有晶面。
7. 在立方晶系中画出以[001]为晶带轴的所有晶面。
8. 已知纯钛有两种同素异构体,密排六方结构的低温稳定的α-Ti和体心立方结构的高温稳定的β-Ti,其同素异构转变温度为882.5℃,使计算纯钛在室温(20℃)和900℃时晶体中(112)和(001)的晶面间距(已知aα20℃=0.29506nm,cα20℃=0.46788nm,aα900℃=0.33065nm)。
9. 试计算面心立方晶体的(100),(110),(111),等晶面的面间距和面致密度,并指出面间距最大的面。
10.平面A在极射赤平面投影图中为通过NS及核电0°N,20°E的大圆,平面B的极点在30°N,50°W处,a)求极射投影图上两极点A、B间的夹角;b)求出A绕B顺时针转过40°的位置。
11. a)说明在fcc的(001)标准极射赤面投影图的外圆上,赤道线上和0°经线上的极点的指数各有何特点,b)在上述极图上标出(-110),(011),(112)极点。
12. 图2-2为α-Fe的x射线衍射谱,所用x光波长λ=0.1542nm,试计算每个峰线所对应晶面间距,并确定其晶格常数。
《结构化学》(7-10章)习题答案
《结晶学基础》习题答案目录第7章答案----------------------------------------------------------------------1第8章答案---------------------------------------------------------------------12第9章答案---------------------------------------------------------------------20第10章答案------------------------------------------------------------------251《结晶学基础》第七章习题答案7001 单晶:一个晶体能基本上被一个空间点阵的单位矢量所贯穿。
多晶:包含许多颗晶粒,这些晶粒可能为同一品种,也可能不同品种,由于各晶粒在空间取向可能不同,不能被同一点阵的单位矢量贯穿。
7002 (D) 7004 简单立方; Cs +和Cl -; 4C 37005 (1) 立方F (2) A 和 B (3) 4 个 (4) 4 组 (5) 3a (6) a /2 7007 4n 个 A, 8n 个 B, n 为自然数。
7010 d 111= 249 pm ; d 211= 176 pm ; d 100= 432 pm 7011 六方; D 3h 70127013 依次为立方,四方,四方,正交,六方。
7014 立方 P ,立方 I ,立方 F ; 四方 P ,四方 I 。
7015 旋转轴,镜面,对称中心,反轴; 旋转轴,镜面,对称中心,反轴,点阵,螺旋轴,滑移面;n =1,2,3,4,6; 32个; 七个晶系; 14种空间点阵型式; 230个空间群。
7016 (1) 四方晶系 (2) 四方 I (3) D 4 (4) a =b ≠c , α=β=γ=90° 7017 (1) 单斜晶系,单斜 P (2) C 2h (3) C 2, m , i 7018 (2a ,3b ,c ):(326); (a ,b ,c ):(111); (6a ,3b ,3c ):(122); (2a ,-3b ,-3c ):(322)。
结晶学试题及答案

结晶学试题及答案一、选择题(每题2分,共20分)1. 下列哪种物质属于晶体?A. 玻璃B. 珍珠C. 橡胶D. 食盐答案:D2. 结晶学中,晶体的对称性由什么决定?A. 原子大小B. 原子间距离C. 晶体的晶格结构D. 晶体的颜色答案:C3. 下列哪项不是晶体的基本性质?A. 各向异性B. 自范性C. 均匀性D. 可塑性答案:D4. 晶体生长的驱动力是什么?A. 温度升高B. 压力增大C. 化学势梯度D. 重力作用答案:C5. 晶体的晶面间距与晶面指数之间的关系是什么?A. 正比关系B. 反比关系C. 没有关系D. 指数关系答案:B6. 下列哪种晶体结构不属于七大晶系?A. 立方晶系B. 四方晶系C. 三方晶系D. 十二面体晶系答案:D7. 布拉格定律适用于哪种类型的晶体?A. 单晶B. 多晶C. 非晶D. 纳米晶答案:A8. X射线衍射分析中,布拉格定律的公式是什么?A. nλ = 2d sinθB. nλ = d sinθC. nλ = d cosθD. nλ = 2d cosθ答案:A9. 下列哪种物质不具有晶体结构?A. 金刚石B. 石墨C. 沥青D. 石英答案:C10. 晶体的熔点与其对称性有什么关系?A. 熔点随对称性增加而升高B. 熔点随对称性增加而降低C. 没有关系D. 熔点与对称性成指数关系答案:B二、填空题(每题2分,共20分)11. 结晶学中的“晶格”指的是_____________________。
答案:晶体内部的三维结构排列12. 晶体的三个基本特征包括____________、____________和____________。
答案:自范性、均一性和各向异性13. 晶体生长过程中,晶核的形成是____________的结果。
答案:过饱和溶液或过冷液体14. 晶体的晶面指数通常用____________表示。
答案:米勒指数15. 在晶体中,晶格常数是指晶格中相邻原子间的平均距离。
无机材料物理化学课后习题及答案

第一章几何结晶学基础1-1.晶体、晶胞的定义;空间格子构造的特点;晶体的基本性质。
1-2.参网页上的模型,运用对称要素组合定律,写出四方柱、六方柱、四方四面体、斜方双锥、六八面体、三方柱、复三方三角面体、四六面体的点群符号,并写出其所属的晶系和晶族。
1-3.参阅网页上的模型,请确定单型中的六八面体、复三方偏三角面体、复六方双锥、和聚型中2、3、4号模型在晶体定向中,各晶体的晶轴分别与哪些对称轴重或晶棱方向平行?1-4.请写出单型三方柱、四方柱、四方双锥、六方柱、菱面体、斜方双锥各晶面的主要晶面符号。
1-5.请写出下列聚型模型各晶面的晶面符号:1、2、3、4。
两个对称面相互成1)60°、2)90°、3)45°、4)30°,可组合成什么点群?1-6.由两根相交的二次轴互成1)90°、2)60°、3)45°、4)30°,可以组合成什么点群?试在面心立方格子中画出菱面体格子1-7.一晶面在X、Y、Z轴分别截得2、4、6个轴单位,请写出此晶面符号。
1-8.作图表示立方晶体的(123)、(012)、(421)晶面。
1-9.在六方晶体中标出晶面(0001)、(2110)、(1010)、(1120)、(1210)的位臵。
1. 答:晶体最本质的特点是其内部的原子、离子、或原子集团在三维空间以一定周期性重复排列而成 , 晶体的空间格子构造有如下特点:结点空间格子中的点,在实际晶体中它们可以代表同种质点占有的位臵,因此也称为晶体结构中的等同点位臵。
行列结点在一维方向上的排列 . 空间格子中任意两个结点连接的方向就是一个行列方向。
面网结点在平面上的分布构成面网。
空间格子中,不在同一行列上的任意三个结点就可联成一个面网。
平行六面体空间格子中的最小单位。
它由六个两两平行且大小相等的面组成。
晶体的基本性质是指一切晶体所共有的性质,这些性质完全来源于晶体的空间格子构造。
《结构化学》(7-10章)习题答案全解
《结晶学基础》习题答案目录第7章答案----------------------------------------------------------------------1第8章答案---------------------------------------------------------------------12第9章答案---------------------------------------------------------------------20第10章答案------------------------------------------------------------------251《结晶学基础》第七章习题答案7001 单晶:一个晶体能基本上被一个空间点阵的单位矢量所贯穿。
多晶:包含许多颗晶粒,这些晶粒可能为同一品种,也可能不同品种,由于各晶粒在空间取向可能不同,不能被同一点阵的单位矢量贯穿。
7002 (D) 7004 简单立方; Cs +和Cl -; 4C 37005 (1) 立方F (2) A 和 B (3) 4 个 (4) 4 组 (5) 3a (6) a /2 7007 4n 个 A, 8n 个 B, n 为自然数。
7010 d 111= 249 pm ; d 211= 176 pm ; d 100= 432 pm 7011 六方; D 3h 70127013 依次为立方,四方,四方,正交,六方。
7014 立方 P ,立方 I ,立方 F ; 四方 P ,四方 I 。
7015 旋转轴,镜面,对称中心,反轴; 旋转轴,镜面,对称中心,反轴,点阵,螺旋轴,滑移面;n =1,2,3,4,6; 32个; 七个晶系; 14种空间点阵型式; 230个空间群。
7016 (1) 四方晶系 (2) 四方 I (3) D 4 (4) a =b ≠c , α=β=γ=90° 7017 (1) 单斜晶系,单斜 P (2) C 2h (3) C 2, m , i 7018 (2a ,3b ,c ):(326); (a ,b ,c ):(111); (6a ,3b ,3c ):(122); (2a ,-3b ,-3c ):(322)。
(完整word版)结晶化学习题答案

第一章·习题与答题1.晶体的两个最显著且重要的特点是什么?★答:(1)化学元素是质点,和(2)质点在三维空间的周期重复。
或者(1)一定的化学成分,和(2)一定的晶体结构。
2.晶体一定是固态的吗?答:是。
因为它的内部质点在三维空间做周期性重复排列。
3.简述晶体结构和晶体结构要素。
答:晶体结构:反映晶体结构中全部基元之间关联特征的整体。
四种晶体结构要素:(1)质点,即构成晶体的离子、原子、离子团或分子;(2)行列,是质点在一维方向上周期重复排列构成的直线;(3)面网,是质点在二维方向上周期重复排列形成的平面;(4)晶胞,晶体结构的最小重复单位。
将晶胞在三维空间无间隙平移就可建立起整个晶体结构。
4.综合说明各晶体结构要素之间的关系。
答:(1)构成晶体结构的质点在一维空间按一定规律周期重复排列可以建立行列;在二维空间按一定规律周期重复排列可以建立面网,在三维空间按一定规律周期重复排列可以建立晶体结构。
(2)在晶体结构的任一行列上总可找出一单位行列,即质点在该行列方向上的最小周期重复单位;沿该行列方向无间隙平移其单位行列即可建立该行列。
找出晶体结构中互相平行、但不同的行列,将它们沿另二维方向按一定的周期平移,整个晶体结构即可建立.(3)在晶体结构的任一面网上总可以找出一个单位面网,将这个单位面网在该二维方向无间隙平移,可推导出该二维的整个面网.找出晶体结构中平行、但不同的面网,将它们按一定周期在另一维方向平移,可以建立整个晶体结构。
(4)将上述的中在晶体结构中一定、也只能找到一个最小重复单位,晶胞,将晶胞在三维方向无间隙平移,可以获得整个晶体结构。
晶胞里可以找到所有的质点、单位行列和单位面网(有些行列和面网需要拓展结构以后才能看出).5.简述晶体结构要素分别与晶面、晶棱和角顶的关系.★答:晶体结构最外的那层面网就是晶面,最外的两面网相交的一条行列即是晶棱,最外的三个面网或三根行列的交点处的质点就是角顶.6.指出晶体、准晶体和玻璃体的异同,解释为什么它们有此区别。
《结晶学基础》第八章习题 8001 在A1型等径圆球密堆积中,密置层 ...

《结晶学基础》第八章习题8001在A 1型等径圆球密堆积中,密置层为:----------------------------------- ( )(A) (100)面 (B) (110)面 (C) (111)面 (D) (210)面8002在A 1型堆积中,可取出一立方面心晶胞,金刚石晶体可抽出立方面心点阵,所 以C 原子是按A 1型堆积的,对否?8003从A 3型堆积中可取出一个六方晶胞,晶胞中含有两个球,坐标分别为(0,0,0)和(1/3,2/3,1/2),故为六方体心点阵,对否? 8004在A 1型堆积中,球数:正四面体空隙数:正八面体空隙数=________。
8005等径圆球作A 2型堆积,其密置列方向为:----------------------------------- ( )(A) a (B) b (C) c (D) a +b (E) a +b +c8006原子按六方最密堆积排列,原子在六方晶胞中的坐标为_______。
8007已知 Mg 的原子半径为 160 pm ,属 hcp(六方最密堆积)结构。
(1) 晶体有什么微观特征对称元素?属什么空间点阵型式?(2) 原子分数坐标;(3) 若原子符合硬球堆积规律,求金属镁的摩尔体积; (4) 求d 002值。
8008等径圆球六方最密堆积,中最近两个相邻八面体空隙公用的几何元素为_____;最近两个相邻四面体空隙公用的几何元素为____________。
8009等径圆球的六方最密堆积可划分出六方晶胞,晶胞中两个原子的分数坐标分别为(0,0,0)和(1/3,2/3,1/2)。
(1)八面体空隙中心的分数坐标为____________,_____________。
(2)四面体空隙中心的分数坐标为____________,____________,___________ ____________。
8010由直圆柱形分子堆积,最高的空间利用率为____________。
《晶体学》各章练习题及答案解析

《晶体学》各章练习题及答案解析第一章复习题答案一、是非题:1、在物体诸态中,晶体是最稳定的。
(√)2、空间群包含了宏观晶体中全部要素的总和以及它们相互间的结合关系。
(×)3、离子晶体的结构取决于其正负离子半径之比。
(×)4、空间点阵中按平行六面体选取原则所得到的空间格子的基本单位称为晶胞。
(×)5、六方紧密堆积的原子密排面是晶体中的(001)面。
(×)6、在单质晶体中,原子作等大球体的紧密堆积,不论是六方还是立方其每个原子的配位数CN=12。
(√)7、阳离子在配位数相同的情况下,其配位多面体形状都是完全相同的。
(×)8、八面体空隙的空间小于四面体空隙的空间。
(×)9、立方晶系的单位平行六面体参数为a0≠b0≠c0,α=β=900,γ=1200。
(×)二、选择题1、下列性质中 B 不是晶体的基本性质。
A、对称性B、有限性C、均一性D、各向异性2、点群L6PC属 C 晶族 C 晶系。
A、高级等轴B、高级六方C、中级六方D、低级正交3、在Si—O四面体中,一般采用 A 方式相连。
A、共顶B、共面C、共棱D、不确定4、晶体结构中一切对称要素的集合称为 D 。
A、对称性B、点群C、微观对称要素的集合D、空间群5、晶体在三结晶轴上的截距分别为2a、3b、6c。
该晶面的晶面指数为 C 。
A 、(236)B 、(326)C 、(321)D 、(123)6、依据等径球体的堆积原理得出,六方密堆积的堆积系数 C 面心立方堆积的堆积系数。
A 、大于 B 、小于 C 、等于 D 、不确定7、晶体中具有方向性的化学键为 A 。
A 、共价键 B 、离子键 C 、金属键 D 、分子键8、某晶体AB ,A —的电荷数为1,A —B 键的S=1/6,则A +的配位数为 B 。
(n/CN=1/6) A 、4 B 、6 C 、8 D 、129、在单位晶胞的NaCl 晶体中,其八面体空隙和四面体空隙的数量分别为 A 。
结晶学基础习题答案

结晶学基础习题答案结晶学基础习题答案结晶学是研究晶体的形成和生长过程的学科,是材料科学中的重要分支。
通过理解结晶学的基础知识和习题的解答,我们可以更好地理解晶体的形成规律和性质。
下面是一些结晶学基础习题的答案,希望对大家的学习有所帮助。
1. 什么是晶体?答:晶体是由原子、分子或离子按照一定的空间排列规律而形成的固态物质。
晶体具有有序的结构和规则的外形,拥有特定的物理和化学性质。
2. 什么是晶体的晶格?答:晶体的晶格是指晶体中原子、分子或离子的周期性排列方式。
晶格可以看作是一个无限延伸的周期性结构,由晶胞和晶胞间隙组成。
3. 什么是晶胞?答:晶胞是晶体中的最小重复单元,它可以代表整个晶体的结构。
晶胞通常由一组原子、分子或离子构成,且具有特定的几何形状。
4. 什么是晶体的晶系?答:晶体的晶系是指晶体的晶格几何形状和对称性。
根据晶胞的几何形状和对称性,晶体可以分为七个晶系:立方晶系、四方晶系、正交晶系、单斜晶系、菱面晶系、三斜晶系和六方晶系。
5. 什么是晶体的晶面?答:晶体的晶面是指晶体表面上的平坦区域,它是晶体晶格的截面。
晶面的性质和排列方式对晶体的形态和性质具有重要影响。
6. 什么是晶体的晶体学指标?答:晶体的晶体学指标是用来描述晶体晶面的一组数值。
晶体学指标由三个整数(hkl)表示,分别代表了晶面与晶轴的交点数目。
7. 什么是晶体的晶体学方向?答:晶体的晶体学方向是指晶体内的某个方向,它由一组整数(uvw)表示。
晶体学方向可以用来描述晶体的生长方向和晶体的物理性质。
8. 什么是晶体的晶体学点阵?答:晶体的晶体学点阵是指晶体中的原子、分子或离子的周期性排列方式。
晶体学点阵可以通过晶胞的重复堆积来描述晶体的结构。
9. 什么是晶体的晶体学缺陷?答:晶体的晶体学缺陷是指晶体中存在的非理想结构或非周期性排列的部分。
晶体学缺陷可以影响晶体的物理性质和力学性能。
10. 什么是晶体的晶体学生长?答:晶体的晶体学生长是指晶体从溶液或气相中生长出来的过程。
结晶学(山东联盟)智慧树知到答案章节测试2023年齐鲁工业大学

第一章测试1.晶体是具有格子构造的固体。
A:对B:错答案:A2.晶体与非晶体在一定条件下是可以互相转化的。
A:对B:错答案:A3.准晶体的内部质点排列具有远程规律,但没有近程规律,也没有平移周期,所以不具有格子构造。
A:对B:错答案:B4.非晶体只有近程规律,而没有远程规律。
A:对B:错答案:A5.晶体能够发育成几何多面体外形仅仅是晶体内部本质的一种外在表现形式。
A:对B:错答案:A6.面网密度越大的面网,其面网间距也越大。
A:对B:错答案:A7.互不平行的面网,面网密度及面网间距一般不同。
A:对B:错答案:A8.在相互平行的行列上,结点间距必定相等。
A:错B:对答案:B9.相当点的原始点可以选择晶体结构中某种质点的中心,也可以选择晶体结构中的任一几何点。
A:错B:对答案:B10.实际晶体中的同种质点,一定只占据在相应空间格子的同一套结点上。
A:对B:错答案:B11.晶体结构可视为晶胞在三维空间平行地、毫无间隙地重复累叠而成。
A:错B:对答案:B12.晶体的稳定性是晶体具有最小内能性的必然结果。
A:错B:对答案:B13.下列物质中,属于非晶体的有哪些?A:石墨B:琥珀C:玻璃D:蛋白石E:石英答案:BCD14.以下哪种性质反映不出晶体结构的异向性?A:折射率B:导热率C:硬度D:密度E:解理答案:D15.下面说法中不正确的是哪项?A:准晶体具有远程规律B:非晶体具有近程规律C:晶体具有近程和远程规律D:非晶体具有远程规律E:准晶体具有近程规律答案:D16.除了对称性以外,晶体的基本性质还包括哪些?A:最小内能B:自限性C:均一性D:稳定性E:各向异性答案:ABCDE17.金红石中的Ti4+分属几套相当点?A:3B:2C:5D:4E:1答案:B18.空间格子中的最小重复单位是什么?A:面网B:结点C:晶胞D:行列E:平行六面体答案:E19.空间格子的平行六面体中含有几个结点?A:8B:4C:6D:10E:2答案:A20.可以用来比较内能大小的是哪项?A:电能B:势能C:动能D:热能答案:B第二章测试1.六方晶系的最高对称型是L66L26PC。
结晶学期末总结答案

结晶学期末总结答案(总7页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章晶体的特性1.什么是晶体?答:内部微粒(分子、原子或离子)按一定规则周期性排列而构成的固体、或具有格子构造的固体称为晶体2.晶体的基本性质?(1)自范性:晶体具有自发生长成一个结晶多面体的可能性,即晶体常以平面作为与周围介质的分界面,拉晶过程中,在放肩部位出现平整的晶面,在等径部位出现的棱线是自范性的表现。
通常暴露在表面的晶面是具有最低表面能的微粒平面。
(2)均匀性和各向异性:均匀性是指晶体的各个部位表现出的各种宏观性质是完全相同的。
各向异性是指从不同方向上看,晶体内部的微粒排列情况的不同,导致在晶体内沿不同方向上的性质又有所差异。
(3)对称性:所有的晶体在外型上和各种性质上都或多或少地具有对称性。
(4)最小内能和固定熔点:从气体,液体,和非晶体转变成晶体时要放热,相反地,从晶体转变为非晶体、液体和气体时都要吸热。
这说明在一定的热力学条件(T,P)下,晶态的内能最小。
3.晶体的类型和结合力?1) 离子键和离子晶体如果组成晶体的两种元素的电负性之差比较大,一般ΔX>时,则两者相互作用时价电子将几乎全部被电负性较大的原子所占有将形成正、负离子和离子键。
离子晶体一般具有硬度较大,熔点较高,熔融后能导电及许多离子晶体能溶于极性溶剂(如溶于水)等特点。
离子键的特点是没有饱合性和方向性。
2)共价健和共价晶体同种元素原子之间,或夺取电子能力相近的两种元素的原子之间相互作用时,ΔX=0 或ΔX<,原子通过共用电子对的方式相结合。
ΔX=0, 属于非极性共价键,或称典型的共价键;ΔX< 属于极性共价键极性共价键与典型的共价键结合的晶体有所差别。
公用电子对将偏向电负性大的原子一边。
即共价键中含有一定程度的离子键成份。
共价键的特点: 有方向性、饱和性,硬度和熔点一般比较高在常温下纯净的共价晶体一般不导电。
结晶学课后习题资料

影响因素为:光的频率、两种物质的成分与界面平坦度。
光的折射是光从一种透亮介质斜射入另一种透亮介质时,或者在同一种介质中折射率不 同的局部传播时,由于波速的差异,而使光的传播方向转变的现象;折射与折射率有关。
折射率:光在真空中的速度与光在该材料中的速度之比率。
n=sinr/sinβ,n 为折射率,r 为入射角,β 为折射角。
其数值随介质的性质、密度、光的波长、温度变化而变化。
传播的速度 v 越大,折射率 n 越小。
依据光学公式可推得折射率与波 长关系如下: λ”=λ/n(λ” 为光在介质中的波长 ) 依据 n=sinr/sin ,β当光入射角大于或等于全反射临界角时,不存在折射现象。
习题 11.1 偏振光和自然光的区分与联系,光进入非均质体时有什么特征?答:自然光:直接由光源发出的光,其在垂直光传播方向的平面内,各方向上都有相等振幅的光波振动。
偏振光:在垂直传播方向的某个固定方向上振动的光波。
自然光或偏振光射入非均质体后将产生双折射现象,分解成两束传播速度不同,振动方向相互垂直的偏光。
2、晶轴、光学主轴、光轴、对称轴有什么不同?答:晶轴是晶体元胞的三个基矢,反映晶体构造。
光学主轴,简称主轴。
即二轴晶光率体的三个相互垂直而不等长的轴;其长度代表相应的三个主折射率,分别用 Ng 、Nm 、Np 表示。
光轴:当光线从某个特别的方向通过非均质体时,不发生双折射现象,这个特别的方向称为光轴。
对称轴:晶体构造的对称要素之一,是一假想的直线,物体绕该直线旋转肯定角度后, 可使一样局部重复。
3、简述光的反射、折射与折射率及其影响因素。
答:光的反射是指光在两种物质的界面上转变传播方向后又返回原来物质中的现象;其4、折射率与光波传播速度、波长、全反射临界角之间有什么关系?答:折射率:光在真空中的速度与光在该材料中的速度之比率,即 n = c/v 。
其在介质中5、什么叫光率体?它有几种类型?各有几种切面类型及其特点?答:光率体是表示光波在晶体中传播时,光波振动方向与相应折射率值之间关系的一种光性指示体。
结晶学及矿物学习题答案

第一章习题1.晶体与非晶体本质的区别是什么?准晶体是一种什么物态?答:晶体和非晶体均为固体,但它们之间有着本质的区别。
晶体是具有格子构造的固体,即晶体的内部质点在三维空间做周期性重复排列。
而非晶体不具有格子构造。
晶体具有远程规律和近程规律,非晶体只有近程规律。
准晶态也不具有格子构造,即内部质点也没有平移周期,但其内部质点排列具有远程规律。
因此,这种物态介于晶体和非晶体之间。
2.在某一晶体结构中,同种质点都是相当点吗?为什么?答:晶体结构中的同种质点并不一定都是相当点。
因为相当点是满足以下两个条件的点:a.点的内容相同;b.点的周围环境相同。
同种质点只满足了第一个条件,并不一定能够满足第二个条件。
因此,晶体结构中的同种质点并不一定都是相当点。
3.从格子构造观点出发,说明晶体的基本性质。
答:晶体具有六个宏观的基本性质,这些性质是受其微观世界特点,即格子构造所决定的。
现分别叙述:a.自限性晶体的多面体外形是其格子构造在外形上的直接反映。
晶面、晶棱与角顶分别与格子构造中的面网、行列和结点相对应。
从而导致了晶体在适当的条件下往往自发地形成几何多面体外形的性质。
b.均一性因为晶体是具有格子构造的固体,在同一晶体的各个不同部分,化学成分与晶体结构都是相同的,所以晶体的各个部分的物理性质与化学性质也是相同的。
c.异向性同一晶体中,由于内部质点在不同方向上的排布一般是不同的。
因此,晶体的性质也随方向的不同有所差异。
d.对称性晶体的格子构造本身就是质点周期性重复排列,这本身就是一种对称性;体现在宏观上就是晶体相同的外形和物理性质在不同的方向上能够有规律地重复出现。
e.小内能性晶体的格子构造使得其内部质点的排布是质点间引力和斥力达到平衡的结果。
无论质点间的距离增大或缩小,都将导致质点的相对势能增加。
因此,在相同的温度条件下,晶体比非晶体的内能要小;相对于气体和液体来说,晶体的内能更小。
f.稳定性内能越小越稳定,晶体的稳定性是小内能性的必然结果。
结晶学习题答案
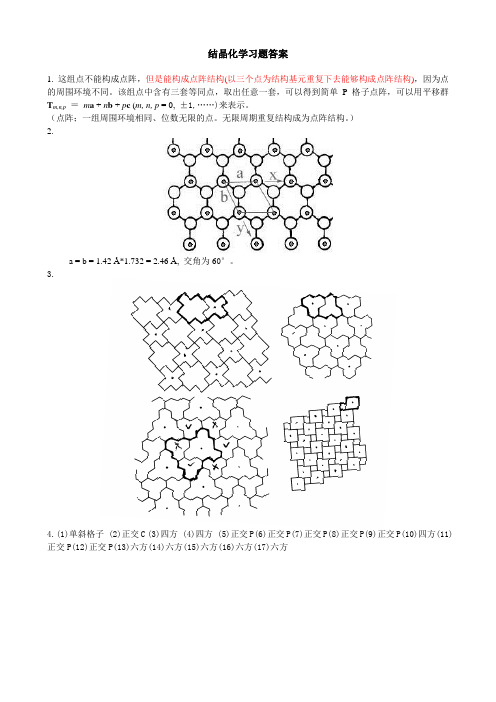
结晶化学习题答案1. 这组点不能构成点阵,但是能构成点阵结构(以三个点为结构基元重复下去能够构成点阵结构),因为点的周围环境不同。
该组点中含有三套等同点,取出任意一套,可以得到简单P格子点阵,可以用平移群T m,n,p=m a + n b + p c (m, n, p = 0,±1,……)来表示。
(点阵;一组周围环境相同、位数无限的点。
无限周期重复结构成为点阵结构。
)2.a =b = 1.42 Å*1.732 = 2.46 Å, 交角为60°。
3.4.(1)单斜格子 (2)正交C (3)四方 (4)四方 (5)正交P(6)正交P(7)正交P(8)正交P(9)正交P(10)四方(11)正交P(12)正交P(13)六方(14)六方(15)六方(16)六方(17)六方5. 设a,b,c的交点为O,反向延长A交立方体的顶点为M点,b和c交顶点分别为N,P点,所以:(1)A = 1/2(-a+b+c),同理,也可以得到B = 1/2(a-b+c), C = 1/2(a+b-c)。
(2)6.若在B面加心,可以在不减少直角数目,不影响对称性C2h的前提下划出一个体积小一倍的P格子,即单斜B = 单斜P,如图1所示;若在A面上加心,得到的是和在C面上加心同样的格子,即单斜A = 单斜C;若加上体心时,在直角数,对称性不变的前提下,可以划出一个C格子,如图2所示,即单斜I = 单斜C;若在各面上加心,在直角数,对称性不变的前提下,可以划出一个C格子,如图3所示,即单斜F = 单斜C。
因此单斜只有P和C两种格子,7. 六方P格子中可以取出一个三方R定向的三重复格子,三方R格子中可以取出具有六方定向的三重复格子,三方晶体允许占有六方P格子,但是六方晶体不会占有三方R格子,因为三方R格子不可能有6次轴的对称性。
8. 因为旋转轴之间的组合不会产生反映面,而反映面间的组合却会产生旋转轴,所以在32个点群中,有些点群有很多旋转轴而没有反映面,但是却找不到只有反映面而无旋转轴的点群。
无机材料物理化学课后习题及答案

第一章几何结晶学基础1-1.晶体、晶胞的定义;空间格子构造的特点;晶体的基本性质。
1-2.参网页上的模型,运用对称要素组合定律,写出四方柱、六方柱、四方四面体、斜方双锥、六八面体、三方柱、复三方三角面体、四六面体的点群符号,并写出其所属的晶系和晶族。
1-3.参阅网页上的模型,请确定单型中的六八面体、复三方偏三角面体、复六方双锥、和聚型中2、3、4号模型在晶体定向中,各晶体的晶轴分别与哪些对称轴重或晶棱方向平行1-4.请写出单型三方柱、四方柱、四方双锥、六方柱、菱面体、斜方双锥各晶面的主要晶面符号。
1-5.请写出下列聚型模型各晶面的晶面符号:1、2、3、4。
两个对称面相互成1)60°、2)90°、3)45°、4)30°,可组合成什么点群1-6.由两根相交的二次轴互成1)90°、2)60°、3)45°、4)30°,可以组合成什么点群试在面心立方格子中画出菱面体格子1-7.一晶面在X、Y、Z轴分别截得2、4、6个轴单位,请写出此晶面符号。
1-8.作图表示立方晶体的(123)、(012)、(421)晶面。
1-9.在六方晶体中标出晶面(0001)、(2110)、(1010)、(1120)、(1210)的位置。
1. 答:晶体最本质的特点是其内部的原子、离子、或原子集团在三维空间以一定周期性重复排列而成, 晶体的空间格子构造有如下特点:结点空间格子中的点,在实际晶体中它们可以代表同种质点占有的位置,因此也称为晶体结构中的等同点位置。
行列结点在一维方向上的排列. 空间格子中任意两个结点连接的方向就是一个行列方向。
面网结点在平面上的分布构成面网。
空间格子中,不在同一行列上的任意三个结点就可联成一个面网。
平行六面体空间格子中的最小单位。
它由六个两两平行且大小相等的面组成。
晶体的基本性质是指一切晶体所共有的性质,这些性质完全来源于晶体的空间格子构造。
晶体化学基础复习题答案

晶体化学基础复习题答案1. 晶体的三种基本对称操作是什么?答案:晶体的三种基本对称操作是旋转、反射和反演。
2. 简述晶体的七大晶系及其对应的对称特点。
答案:晶体的七大晶系包括三斜晶系、单斜晶系、正交晶系、四方晶系、三方晶系、六方晶系和立方晶系。
三斜晶系没有高次对称轴;单斜晶系有一个二次对称轴;正交晶系有三个互相垂直的二次对称轴;四方晶系有一个四次对称轴和三个互相垂直的二次对称轴;三方晶系有一个三次对称轴和三个互相垂直的二次对称轴;六方晶系有一个六次对称轴和三个互相垂直的二次对称轴;立方晶系有四个三次对称轴和三个互相垂直的二次对称轴。
3. 描述晶体中原子的配位数是如何确定的?答案:晶体中原子的配位数是通过考虑原子周围最近邻原子的数量来确定的,通常与原子半径、键角和晶体结构类型有关。
4. 什么是晶格能?晶格能的大小受哪些因素影响?答案:晶格能是指晶体中所有离子之间的静电作用能。
晶格能的大小受离子电荷、离子半径、离子间距离以及晶体结构的影响。
5. 简述X射线衍射的基本原理。
答案:X射线衍射的基本原理是当X射线照射到晶体时,晶体中原子排列的周期性结构会导致X射线发生衍射,通过测量衍射角和强度,可以确定晶体结构。
6. 晶体缺陷有哪几种类型?答案:晶体缺陷主要有三种类型:点缺陷、线缺陷和面缺陷。
点缺陷包括空位、间隙原子和替代原子;线缺陷主要是位错;面缺陷包括晶界和堆垛层错。
7. 什么是布拉格定律?其公式是什么?答案:布拉格定律描述了X射线在晶体中的衍射条件,其公式为:nλ = 2d sinθ,其中n是衍射级数,λ是X射线波长,d是晶面间距,θ是入射角。
8. 晶体的各向异性和各向同性有何区别?答案:晶体的各向异性指的是晶体的物理性质随方向不同而变化,而各向同性则是指晶体的物理性质在各个方向上都相同。
9. 什么是晶体的熔点?影响晶体熔点的因素有哪些?答案:晶体的熔点是指晶体从固态转变为液态的温度。
影响晶体熔点的因素包括晶体的化学组成、晶体结构、原子间的键合力等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《结晶学基础》第八章习题答案8001(C)8002非。
8003非。
六方晶系只有简单六方一种点阵型式,六方晶胞中所含的两个球,均属一个结构基元。
80041:2:18005(E)80060,0,0; 1/3,2/3,1/2 (或 0,0,0; 2/3,1/3,1/2)8007(1) 63,6 简单六方。
(2) 0,0,0; 1/3,2/3,1/2。
(3) (N A ·34r 3)/0.7405 = 13.95 cm 3(4) d 002= 2×1.633×160/2 pm = 522.6/2 pm = 261.3 pm8008面; 面8009(1) (1/3,2/3,1/4); (1/3,2/3,3/4);(2) (2/3,1/3,1/8); (2/3,1/3,7/8); (0,0,3/8); (0,0,5/8)8010分子占据面积πr 2; 平行四边形面积 2r ×2r ×sin60°r r r 22866.02⨯⨯π = 0.9078011布拉格角: 34.27°; 40.56°; 66.83°;指标: 111; 200; 220 。
8012(1) a = 352.4 pm(2) d =V N nM A/=2432310524.31002.6/70.584-⨯⨯⨯ g▪cm -3 = 8.906 g▪cm -3(3) 略8013A 1型堆积为立方面心结构,第一对谱线的衍射指标为111a = 362.0 pmr = 128.0 pm立方面心,每个晶胞中有4个Cu 原子, d = 8.89 g ·cm -38014r = 143 pm; θ= 19.3°8015a = 400.4 pmr = 141.6 pmA 1堆积每个晶胞中有4个Al 原子, d = 2.793 g ·cm -38016(1) r = 138.4 pm(2) 最多能得到(100)的4级衍射8017体心点阵8018r =41(3×4292)1/2= 185.8 pm8019d (110)=330×sin45°pm = 233.3 pmsin θ=0.660, θ=41.3°8020d = 21.45 g ·cm -3r = 138.7 pm8021a = 405.0 pm8021r =41(2×405.02)1/2 pm = 143.2 pm8022a =b =2×146 pm = 292 pmc =292×1.633 pm = 477 pm8023对于体心立方,只能出现h +k +l =偶数之衍射线,即只出现(110),(200), (211),(220), (310),(222),(231),(004)等。
sin θ hkl = a 2λ(h 2+k 2+l 2)1/2=0.2674(h 2+k 2+l 2)1/2 由于h 2+k 2+l 2≥14, sin θhkl >1, 所以只能得到下列6条衍射线:(110),(200),(211),(220),(310),(222)。
其衍射角分别为: θ110= 22.2°; θ200= 32.3°;θ211= 40.9°; θ220= 49.1°;θ310= 57.7°; θ222= 67.9°。
8024(1) 点阵型式:简单立方; 结构基元:1Cu,1Zn; r = 138 pm;(2) 点阵型式:体心立方; 结构基元: 21Cu, 21Zn; r = 133 pm 。
8025(1) Cu 的摩尔分数为x ,Zn 为1-x ;63.5x :65.4(1-x )=75%:25%x=0.755,即Cu 的原子百分数为75.5 1-x =0.245, 即Zn 的原子百分数为24.5(2) 4.25×10-22g(3) V =0.5×10-22cm 3(4) a = 368 pm; r = 130 pm 。
8026(1) a = 320.9 pm, c = 524.0 pm(2) 1.727 g ·cm -38028(1) 185.8 pm; (2) 0.967 g ·cm -3; (3) 303.3 pm8029(1)白锡变灰锡,体积膨胀;(2)增大26%。
8030减少8031(1) a = 200 pm, c = 326.6 pm(2) 22.5 pm(3) (0,0,0.375); (0,0,0.625); (1/3,2/3, 0.125); (1/3,2/3, 0.875)。
80331,1,280341,1,280351,18036ABCABC...8037ABAB...8038(0,0,0); (1/3,2/3,1/2)。
或 (0,0,0); (2/3,1/3,1/2)8039禁带宽度不同 (半导体 E g < 3eV )8040> 74.05%8041V =A dN ZM=5.00×10-23cm 3a =367.7pm 统计原子半径: r =(2/4)a =130.0pm8042Mo 的原子半径: r =(3/4)a =136.26pm d 100=314.70pmd 110=222.56pm8043a =(8/3)r =648.96pmV = a 3=2.73×108pm 3 d =A VN ZM =5.78g ·cm -38044111; sin θ=[(λ/2a )2(h 2+k 2+l 2)]1/2=0.3469θ=20.30︒8045参看周公度《结构化学基础》图8.3.1(c) 四方P 结构基元:2Au,2Cu8046参看周公度《结构化学基础》图8.3.1(a) 立方F 结构基元:一个统计原子8047M =130.288048白锡: d =7.31g ·cm -3 灰锡: d =5.78g ·cm -3 白锡密度大,灰锡密度小,白锡转变为灰锡,由于体积骤然膨胀,使锡器碎裂8049∇2ψ+228h mπE ψ=08050参看周公度《结构化学基础》p.36780516,3,2N,2 。
8052异: (1)A1: ABC|ABC|...堆积A3: AB|ABC|...堆积(2)A1: 可取出面心立方晶胞A3:可取出六方晶胞(3)A1: 密置层为(111)A3:密置层为(001)同: (1)每一层都是密置层,由密置层作最密堆积(2)配位数都为12(3)堆积系数都为74.05%(4)晶胞中球数、八面体空隙数、四面体空隙数的比值都为1∶1∶28053a=2rc=正四面体高×2=1.633×2rc/a=1.63380544r=3aV=a3=[(4/3)r]3堆积系数为68.02%805541/482805661/66180572d sin θhkl =[2a /(h 2+k 2+l 2)1/2]sin θhkl =λ∵sin θhkl ≤1∴ h 2+k 2+l 2≤12根据面心立方的消光规律,衍射图中将出现五条谱线: 111, 200, 220, 311, 222 29.11︒, 34.18︒, 52.60︒, 68.69︒, 76.67︒8058a =408.57pm Z =4 根据消光条件,Ag 晶体属面心立方点阵,Ag 原子的分数坐标应为: (0,0,0), (1/2,0,1/2), (1/2,1/2,0), (0,1/2,1/2)8059a =286.64pm Z =M dVNA =2根据消光条件,α-Fe 属体心立方点阵,Fe 原子的分数坐标应为: (0, 0, 0), (21,21,21)8060∵sin θhkl ≤1∴ h 2+k 2+l 2≤19根据面心立方的消光规律,衍射图上有9条衍射线,前三条为: 110, 200, 211 18.81︒,27.13︒,33.96︒8061d =8.86g ·cm -3Co 原子半径为:a /2=125.35pm8062Z=8由sin2θ=(λ/2)2(h2/a2+k2/b2+l2/c2)得θ=31.47︒8063Pd晶胞体积V=a3=5.89×107pm31cm3 Pd含有的晶胞数为:(1×1030pm3)/(5.89×107pm3)=1.70×1022 Pd晶胞中有4个八面体空隙和8个四面体空隙.1cm3 Pd中含有的空隙数为:12×1.70×1022=2.04×1023700 cm3H2即为0.03125 molH2,含H2分子数为:0.0315×6.023×1023=1.88×1022H原子数为:2×1.88×1022=3.76×1022H原子所占空间的百分数为18.4%8064(4r)2=2a2r=a/(22)=137.5pmPd原子之间最短距离为:2r=275.0pmd=12.00g·cm-380651284垂直于三次轴方向8066a=2×158.3 pm =316.6pmc=1.633×316.6 pm =517.0pmd=5.85g·cm-38067a=4r/2=405.1pmd=2.70g·cm-38068Z =2 体心立方点阵 (0,0,0); (1/2,1/2,1/2)8069a =4r /3=570.0pm 相对原子质量为85.298070V =A dN ZM=1.51×10-22cm 3a =(1.51×10-22)1/3 pm =532.1pm r =230.4pm d (110)=376.2pm8071(1) 六方(2) 六方P(hp)(3) 2个,(0,0,0), (1/3,2/3,1/2)(4) 128072一晶胞中共有四个A 原子,另外三个坐标是 (1/4,3/4,3/4),(3/4,1/4,3/4),(3/4,3/4,1/4)8073θ111=21.7°θ200=25.3° θ220=37.1° θ311=45.0°d =8.97g ·cm -38074(1) 8.61 eV (2) 7.01 eV(3) 1.36:1 (4) 0.368075E F (0)= (h 2/8m *)(3n /π)2/3=4.72 eV80762d hkl sin θhkl =λd hkl =a /(h 2+k 2+l 2)1/2a =hkl θλsin 2 (h 2+k 2+l 2)1/2='1781sin 22.154︒⨯ × 33pm=404.9 pm8077(1) 0.816R(2) 2.45R8078(1)224h mLπ d E(2)224mL N h π8079(1)由布拉格方程 2d sin θ=λ 得 d =λ/(2sin θ)=80/(2×0.133) pm =300 pm 对立方体心结构, (200)面间距d 200是晶胞边长的一半a =2d =600pm(2) 晶体密度为 d = 2.0 g/cm 3 d =2M /(N A V )=2M /(6.023×1023×63×10-24)∴ M =130(3) 立方体心晶胞的原子分数坐标: (0,0,0),(1/2,1/2,1/2)原子的半径 r =21·(3/2)a =3a /4=259.8pm(4) 空间利用率: 晶胞中有两个原子 2(4π/3)(3a /4)3/a 3=68.02%8080波矢空间 E =E F 的等能面称为费米面。
