龙格-库塔实习题

合集下载

工业设计心理学题目(新整理有答案参考)

填空1.格式塔心理学又称为。

2.认知心理学用计算机来验证心理学的假设。

3.认知的各个方面都具有因素。

设计者必须考虑这些因素，通过人机界面设计，减少或避免非理性因素造成的负面后果。

4.人机界面设计要解决的关键问题是：行动-操作转换。

这应该由机器完成，而不应该推给操作者。

5.用户操作使用任何东西时，他们都要组织自己的知觉和操作动作，使其组合成为完成的和谐的行动。

了解这些组织结构，才能设计出比较符合用户操作的人机界面。

1.知觉与动作形成自动链，达到“”，不需要明显的反馈控制。

2.知觉会产生错觉，视觉的错觉叫视错。

3.出现认知心理学后，人们把归为它的一个部分。

认知包含了知觉、记忆、思维、判断、推理、发现问题和解决问题、决断、学习、概念形成、知识表达、语言使用等方面。

4.操作越难，越需要用户付出意志。

减少操作意志是改进人机界面设计的主要思考点之一。

5.从1970年代人们开始深入研究用户出错，建立了若干理论方法。

其中比较有影响的是Reason（1990）的方法，他分析了各种行为中的出错类型。

1.工程心理学主要目的是研究军事设备操作员的。

2.控制动作的两种主要方法中动作编程方法强调动作的中央神经控制。

3.探索发现式思维被用于。

这种思维方式可能导致创新。

迄今，人们已经发现了若干探索发现式思维方法：尝试法、means-ends法、减少差别法、回溯法（又被称为逆向思维法或反求法）、模拟求解法、机会计划法、对比法、反常法等。

4.人们把各种感知到的分别表示各种符号，主要包括：图形、象征、索引、信号和比喻等。

设计师必须了解人们把什么信息表示为什么符号，并把人们熟知的表示用于设计，不应该生造符号给用户造成理解困难。

5.思维模型描述了用户操作中的思维过程。

1.科学研究主要考虑三方面：目的对象、怎样认识、。

2.弗洛伊德早期的心理学把意识分为三种功能层次：有意识、和无意识3.短期记忆可以保持个信息块。

设计人机界面提供的信息应该符合这个特性。

（完整版）KUKA试题5

（完整版）KUKA试题5⼀、单项选择题（本⼤题共20 ⼩题。

每⼩题1分，共20 分）1、下列外部⾃动输出端RK9的含义（ D ）A、编程运⾏B、单步运⾏。

C、语句吻合D、⾃动运⾏2、机器⼈TP⾯板中R绿灯表⽰什么意思？（B ）A、运⾏⾄⼯作程序的最后⼀条B、⼯作程序正在运⾏C、运⾏⾄⼯作程序的第⼀条D、没有选定⼯作程序3、机器⼈零点丢失后会有什么后果？（ A ）A、仅能单轴运⾏B、仅能在规定路径上运⾏C、仅能⽤专⽤装置驱动D、机器⼈不能运动4、机器⼈⾯板上的提⽰符号是什么意思？（ B ）A、状态性提⽰B、说明性提⽰C、确认性提⽰D、对话信息5、标准KRC2控制柜（不增加控制柜的情况下）可扩展到⼏轴？（ B ）A、2轴B、8轴C、10轴D、12轴6、经常会被调⽤的信号序列我们通常将它编⼊到什么程序⾥（ B ）A、FLOGEB、MACROC、UPD、MACROSPS7、菲利克斯模块IBS RL 24 DIO 8-8-8 LK中的“24”表⽰什么意思（ D ）A、模块占24位B、模块出⼚ID号为24C、模块有24个接⼝D、模块电压为24V8、SAK指的是什么意思？（ C ）A、机器⼈在原位B、机器⼈在运⾏C、机器⼈在运动轨迹上D、机器⼈暂停运动9、正常情况下机器⼈六轴可以运⾏多少度？（ C ）A、180°B、360°C、⼤于360°D、90°10、KUKA机器⼈操作⾯板⼜叫做什么？（A）A 、KCPB 、TPC 、MPD 、PHG11、OUTB22=5中“5“表⽰什么含义？（ C ）A、⽹络中的第5个设备B、⽹络中的第5个⽹段C、设备在⽹络中的第5个字节D、设备在⽹络中的第5个字12、程序被修改后你需要做什么？（ D ）A、程序需再次进⼊B、控制系统需再次被引导C、重新命名D、降低速度，测试程序13、下列哪⼀个操作⾯板的按键可以实现窗⼝的选择切换（ A ）A、B、C、D、14、更改语⾔需要在哪个菜单下操作（A ）A、编辑-设置B、配置-设置C、⽂件-更改D、显⽰-窗⼝15、出⼚情况下机器⼈⼯具坐标系原点在哪⼉？（D ）A、机器⼈底座中⼼B、机器⼈外部某⼀个点C、机器⼈六轴关节处D、机器⼈六轴法兰盘中⼼16、笛卡尔坐标系中与XYZ对应的旋转运动是_____？（C ）A、A-B-CB、B-C-AC、C-B-AD、C-A-B17、机器⼈电机的旋转变压器旋转⼀圈发出多少个脉冲？（C ）A、1024B、2048C、4096D、51218、机器⼈控制SCA涂胶设备，涂胶量由机器⼈发出的什么控制？（B ）A、数字量B、模拟量C、⼆进制数D、M位19、强制数字量输出信号，需要在下列哪项操作中进⾏？（C ）A、显⽰-输⼊输出端B、配置-输⼊输出端C、显⽰-诊断D、显⽰-修改变量20、指令“Ana konst”是什么意思？（ C ）A、⽅形波模拟电压B、同速度成正⽐的模拟电压C、恒定的模拟电压D、同速度成反⽐的模拟电压⼆、多项选择题（本⼤题共5⼩题，每题2分，共10分）21、在进⾏机器⼈保养时，为防⽌未经许可的重新开机可采取下列哪些措施（ABE_A、挂安全锁B、贴警⽰标签C、保持⾃动状态D、移动机器⼈到安全区域E、按下机器⼈急停开关22、下列哪⼏项在“显⽰”菜单下( ABD ）A、计数器B、变量C、杂项D、诊断E、开关/选项23、机器⼈⼯艺移动⽅式（BD ）A、PTPB、KLINC、CIRCD、KCIRCE、CALL24、下列哪些选项属于操作符（ABCD ）A、+B、>C、关D、&E、BIN125、KRC2系统的机器⼈在ESC诊断中可以监控以下哪⼏部分的运⾏情况（BCE ）A、KSDB、ESC板C、RDW卡D、KPS-600E、KCP三、填空题（本⼤题共10道⼩题，每空1分，共10分）26、在做保养和修理⼯作之前必须_______，以防⽌机器⼈被未经允许的误动作。

数值分析计算实习题答案

数值分析计算实习题答案数值分析计算实习题答案数值分析是一门研究如何利用计算机对数学问题进行近似求解的学科。

在数值分析的学习过程中，实习题是一种重要的学习方式，通过实践来巩固理论知识，并培养解决实际问题的能力。

本文将为大家提供一些数值分析计算实习题的答案，希望能够帮助大家更好地理解和掌握数值分析的相关知识。

一、插值与拟合1. 已知一组数据点，要求通过这些数据点构造一个一次插值多项式，并求出在某一特定点的函数值。

答案：首先，我们可以根据给定的数据点构造一个一次插值多项式。

假设给定的数据点为(x0, y0), (x1, y1)，我们可以构造一个一次多项式p(x) = a0 + a1x，其中a0和a1为待定系数。

根据插值条件，我们有p(x0) = y0，p(x1) = y1。

将这两个条件代入多项式中，可以得到一个方程组，通过求解这个方程组，我们就可以确定a0和a1的值。

最后，将求得的多项式代入到某一特定点，就可以得到该点的函数值。

2. 已知一组数据点，要求通过这些数据点进行最小二乘拟合，并求出拟合曲线的表达式。

答案：最小二乘拟合是一种通过最小化误差平方和来找到最佳拟合曲线的方法。

假设给定的数据点为(x0, y0), (x1, y1)，我们可以构造一个拟合曲线的表达式y =a0 + a1x + a2x^2 + ... + anx^n，其中a0, a1, ..., an为待定系数。

根据最小二乘拟合原理，我们需要最小化误差平方和E = Σ(yi - f(xi))^2，其中yi为实际数据点的y值，f(xi)为拟合曲线在xi处的函数值。

通过求解这个最小化问题，我们就可以确定拟合曲线的表达式。

二、数值积分1. 已知一个函数的表达式，要求通过数值积分的方法计算函数在某一区间上的定积分值。

答案：数值积分是一种通过将定积分转化为数值求和来近似计算的方法。

假设给定的函数表达式为f(x)，我们可以将定积分∫[a, b]f(x)dx近似为Σwi * f(xi)，其中wi为权重系数，xi为待定节点。

数值分析第五版_李庆扬

数值分析第五版_李庆扬数值分析第五版_李庆扬一、课程基本信息课程中文名称：数值分析课程英文名称：Numerical Analysis课程类别：专业基础课开课学期：秋适用专业：信息与计算科学；应用数学总学时：86学时（其中理论课56学时，上机实习30学时）总学分：5（理论课3学分；上机实习2学分）预修课程（编号）：数学分析，高等代数，常微分方程课程简介：本课程是大学本科信息与计算科学和应用数学专业的一门基础课，也是工科研究生的必修课。

本课程的主要内容是研究各种数学问题的数值计算方法的设计、计算误差分析以及有关理论和具体实现的一门数学课程。

是应用数学的重要分支之一。

建议教材：《计算方法》（二版）（邓建中、刘之行），西安，西安交通大学出版社，2001 参考书：[1]数值分析学习指导，关治编，出版社：清华大学出版社，出版时间：2008年；[2]数值分析，何汉林，梅家斌，科学出版社，2007年；[3]《数值计算引论》白峰杉高等教育出版社 2005年[4]《数值分析》（第五版）李庆扬易大义等清华大学出版社2008年[5]Numerical Analysis，R.Kress，世界图书出版公司20036、数值分析学习辅导习题解析，李宏、徐长发编，华中科技大学出版社，2001年。

二、理论课程教育目标通过本课程的教学使学生能了解现代科学计算中常用的数值计算方法及其基本理论，系统掌握数值分析的基本概念和分析问题、解决问题的基本方法，为运用数值分析的理论知识并为掌握更复杂的现代计算方法打好。

三、理论教学内容与要求（含学时）第一章：计算方法的一般概念（4学时）本章教学内容：理解计算方法的意义、研究内容与方法，理解并掌握误差的概念（包括误差的来源、绝对误差、相对误差），掌握有效数字及舍入误差对计算的影响。

第二章：解线性方程组的直接法（8学时）本章教学内容：1、高斯消去法；选主元的高斯消去法；2、矩阵的LR分解；解三对角方程组的追赶法；解方程组的平方根法；矩阵的求逆；3、方程组的数；病态方程组的判断。

实习面试参考题汇总

汽车生产工艺实习面试参考题—基础篇—✧实习要求：通过理论学习和参观实践，了解机械制造工艺学的基本概念、原理和方法，并能结合具体的汽车与发动机零部件的加工工艺进行运用和分析。

✧参考题：1.名词解释根据已学知识，查找相关资料，了解和掌握以下基本概念。

1）生产过程、工艺过程、工序，安装；2）钻、扩、铰、车、铣、磨；3）内铣、外铣及刀具；4）定位与夹紧的概念，有何不同，各起什么作用？5）六点定位原理，过定位，欠定位；6）机械加工工艺中的定位、夹紧符号是什么？7）加工精度：尺寸精度、形状精度、位置精度；8）设计基准、工艺基准；9）基准选择：1）粗基准选择原则，2）精基准选择原则；；—典型工艺篇—✧实习要求：通过参观实践与深入探究，了解汽车与发动机主要部件（曲轴、连杆、凸轮轴、缸体、转向节等）的加工工艺，掌握典型的工艺过程特点，理解其工序安排、定位基准、定位方式和精度控制，并能运用基本的机械制造工艺学原理进行分析和应用。

✧参考题：2.曲轴1)简述曲轴技术要求（此内容可根据已学发动机知识并查找相关资料）；2)曲轴在加工过程中的主要基准是什么？3)如何理解质量中心孔和几何中心孔？那么各自的作用与区别？4)曲轴毛坯的第一道加工工序是什么？加工端面和中心孔时的基准是什么？5)简述曲柄销（连杆轴颈）的加工工艺过程（重点关注定位及加工方式）；6)曲轴加工的精基准是什么？7)曲轴的热处理工序安排在什么时候？有何作用？8)曲轴表面喷丸的目的是什么？9)曲轴抛光的目的是什么？10)曲轴加工工序中有两道热压加工工艺分别是什么？有何区别，能否加以组合？11)曲轴内铣加工的铣刀盘如何运动？12)曲轴在使用中的主要失效方式有什么？在加工中如何应对采取措施。

13)曲轴的钻油孔安排在热处理之前还是之后，为什么？14)为什么要修磨中心孔？简述主轴颈和曲柄销最后一道工序；15)曲轴和凸轮轴的加工有哪些相似之处？16)简述曲轴上油道加工的加工工艺过程。

龙格库塔法

2019/12/21
17
类似于前面的讨论，把K2、K3、K4分别在xi点展成h的幂级数，代
入线性组合式中，将得到的公式与y(xi+1)在xi点上的泰勒展开式比较，使其两式右端直到h4的系数相等，经过较复杂的解方程过程便可得到关于ci，ai ，bij的一组特解
a2=a3=b21=b32=1/2 b31=b41=b42=0 a4=b43=1 c1=c4=1/6 c2=c3=1/3
或称为线性组合)来求取平均斜率k*的近似值K，即
K c1K1 c2K2
式中:K1为xi点处的切线斜率值 K1 =hf(xi, yi)=hy'(xi) K2为xi +a2h点处的切线斜率值,比照改进的欧拉法,将xi+a2视为xi+1，即可得
K2 hf (xi a2h, yi b21K1)

yi 1

yi1Biblioteka 6(K14K2

K3)
K1
K
2

hf (xi , yi ) h
hf (xi 2
,
yi

1 2
K1 )
K3 hf (xi h, yi K1 2K 2 )
2019/12/21
15
9.4.4 四阶(经典)龙格—库塔法
如果需要再提高精度，用类似上述的处理方法，只需在区间[xi,xi+1] 上用四个点处的斜率加权平均作为平均斜率K*的近似值，构成一系列四阶龙格—库塔公式。具有四阶精度，即局部截断误差是O(h5)。
y y(x)
间[xi , xi1]上平均斜率的近似值 K
K
就可得到相应的Runge-Kutta方法

《数值计算方法》复习资料

实用文档《数值计算方法》复习资料第一章数值计算方法与误差分析第二章非线性方程的数值解法第三章线性方程组的数值解法第四章插值与曲线拟合第五章数值积分与数值微分第六章常微分方程的数值解法自测题课程的性质与任务数值计算方法是一门应用性很强的基础课，在学习高等数学，线性代数和算法语言的基础上，通过本课程的学习及上机实习、使学生正确理解有关的基本概念和理论，掌握常用的基本数值方法，培养应用计算机从事科学与工程计算的能力，为以后的学习及应用打下良好基础。

第一章数值计算方法与误差分析一考核知识点误差的来源类型；绝对误差和绝对误差限，相对误差和相对误差限，有效数字；绝对误差的传播。

二复习要求1.知道产生误差的主要来源。

2.了解绝对误差和绝对误差限、相对误差和相对误差限和有效数字等概念以及它们之间的关系。

3.知道四则运算中的误差传播公式。

实用文档三例题例 1 设x*= =3.1415926⋯近似值 x=3.14 ＝ 0.314× 101,即 m=1，它的绝对误差是－ 0.001 592 6 ，⋯有即 n=3，故 x=3.14 有 3 位有效数字 .x=3.14准确到小数点后第 2 位 .又近似值 x=3.1416，它的绝对误差是0.0000074 ⋯，有即 m=1,n＝ 5， x=3.1416 有 5 位有效数字 .而近似值x=3.1415，它的绝对误差是0.0000926 ⋯，有即 m=1,n＝ 4， x=3.1415 有 4 位有效数字 .这就是说某数有s 位数，若末位数字是四舍五入得到的，那么该数有s 位有效数字；例 2指出下列各数具有几位有效数字，及其绝对误差限和相对误差限：2.000 4－0.002 009 0009 000.00解因为 x1=2.000 4＝ 0.200 04× 101, 它的绝对误差限 0.000 05=0.5 × 10 1―5，即m=1,n=5, 故 x=2.000 4 有 5 位有效数字 . a1=2，相对误差限x2=－ 0.002 00，绝对误差限0.000 005，因为 m=－2，n=3 ，x2=－ 0.002 00 有 3 位有效数字 . a1=2 ，相对误差限r ==0.002 5实用文档x3=9 000 ，绝对误差限为0.5× 100，因为 m=4, n=4, x3=9 000 有 4 位有效数字， a=9 ，相对误差限r＝＝ 0.000 056x4=9 000.00 ，绝对误差限0.005，因为 m=4， n=6， x4=9 000.00 有 6 位有效数字，相对误差限为r＝＝ 0.000 000 56由 x3与 x4可以看到小数点之后的0，不是可有可无的，它是有实际意义的.例 3 ln2=0.69314718⋯，精确到10－3的近似值是多少？解精确到 10－3＝ 0.001，意旨两个近似值x1,x2满足，由于近似值都是四舍五入得到的，要求满足，近似值的绝对误差限应是＝0.0005,故至少要保留小数点后三位才可以。

龙格库塔法例题

四阶龙格一库塔法通常所说的龙格一库塔法是指四阶而言的．我们可以仿二阶、三阶的情形推导出常用的标准四阶龙格一库塔公式(9.22)公式(9.22)的局部截断误差的阶为．龙格一库塔法具有精度高，收敛，稳定(在一定的条件下)，计算过程中可以改变步长，不需要计算高阶导数值等优点．但仍需计算在一些点上的值，如四阶龙格－库塔法每计算一步需要算四次的值，这给实际计算带来一定的复杂性，因此，多用来计算“表头”．(即开始几点的近似值)．例3.用标准龙格一库塔法求初值问题在处的解．解因与．若应用标准龙格一库塔方法公式(9.22)计算，对于n=0时，则有于是得这个值与准确解在处的值已十分接近．再对n=1，2，3，4应用式(9.22)计算，具体计算结果如表3所示：例3写出用四阶龙格――库塔法求解初值问题的计算公式，取步长h＝0.2计算y(0.4)的近似值。

至少保留四位小数。

解此处f(x，y)＝8－3y，四阶龙格――库塔法公式为其中κ1＝f(x k，y k)；κ2＝f(x k+0.5h，y k+0.5hκ1)；κ3＝f(x k+0.5h，y k+0.5hκ2)；κ4＝f(x k+h，y k+hκ3)本例计算公式为：＝8－3y k；κ2＝5.6－2.1y k；其中κ1κ3＝6.32－2.37y k；κ4＝4.208－1.578y k＝1.2016＋0.5494y k (k＝0，1，2，…)当x0＝0，y0＝2，y(0.2)≈y＝1.2016＋0.5494y0＝1.2016＋0.5494×2＝2.30041y(0.4)≈y＝1.2016＋0.5494y1＝1.2016＋0.5494×2.3004＝2.46542。

4月见习工业工程师考试试题(含答案)资料

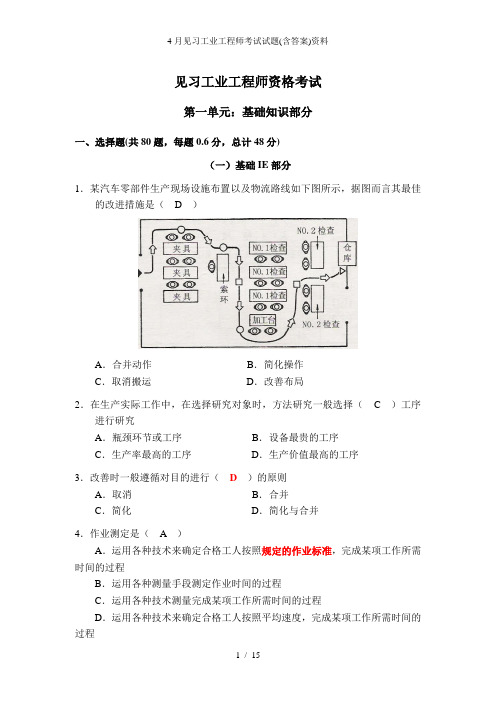
见习工业工程师资格考试第一单元：基础知识部分一、选择题(共80题，每题0.6分，总计48分)（一）基础IE部分1．某汽车零部件生产现场设施布置以及物流路线如下图所示，据图而言其最佳的改进措施是（ D ）A．合并动作B．简化操作C．取消搬运D．改善布局2．在生产实际工作中，在选择研究对象时，方法研究一般选择（ C ）工序进行研究A．瓶颈环节或工序B．设备最贵的工序C．生产率最高的工序D．生产价值最高的工序3．改善时一般遵循对目的进行（D）的原则A．取消B．合并C．简化D．简化与合并4．作业测定是（ A ）A．运用各种技术来确定合格工人按照规定的作业标准，完成某项工作所需时间的过程B．运用各种测量手段测定作业时间的过程C．运用各种技术测量完成某项工作所需时间的过程D．运用各种技术来确定合格工人按照平均速度，完成某项工作所需时间的过程5．程序分析方法中的5个方面主要是指（ A ）。

A．操作分析、搬运分析、等待分析、储存分析和检验分析B．取消分析、简化分析、重排分析、合并分析和改善分析C．动素分析、动作分析、操作分析、工序分析和工艺过程分析D．5W1H6．工艺程序分析的工具是（ A ）A．工艺程序图B．流程程序图C．线路布置图D．工艺程序图与线路布置图7．流程程序分析的对象是产品或零件（ A ）A．加工制造全过程B．工序全过程C．操作全过程D．动作全过程8．流程程序分析对（ D ）进行分析A．“加工”、“检查”B．“加工”、“检查”、“搬运”C．“加工”、“检查”、“搬运”、“储存”D．“加工”、“检查”、“搬运”、“储存”、“等待”9．作业分析的基本类型有（ A ）A．人—机作业分析、联合作业分析、双手作业分析B．程序分析、流程分析、工序分析C．操作系统、动作分析、程序分析D．单机作业分析、双机作业分析、多机作业分析10．联合作业分析的含义是指（ A ）A．几个作业人员共同作业于一项工作时，对作业人员时间上的关系的分析以及排除作业人员作业过程中存在的不经济、不均衡、不合理和浪费等现象的一种分析方法。

工业机器人实训考试试题2 - 含参考程序

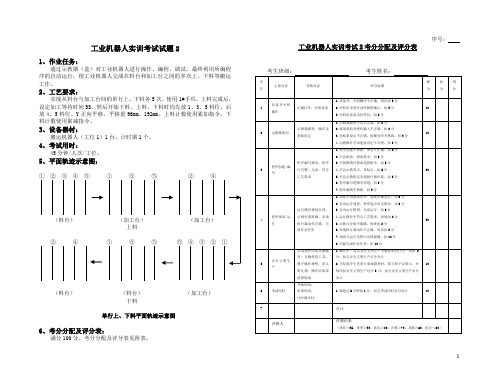
工业机器人实训考试试题21、作业任务：通过示教器（盒）对工业机器人进行操作、编程、调试，最终利用所编程序的自动运行，使工业机器人完成在料台和加工台之间的多次上、下料等搬运工作。

2、工艺要求：实现从料台与加工台间的单行上、下料各5次，使用1#手爪。

上料完成后，设定加工等待时间5S，然后开始下料。

上料、下料时均先放1、3、5料位，后放4、5料位。

Y正向平移，平移量96mm、192mm。

上料计数使用累加指令，下料计数使用累减指令。

3、设备器材：搬运机器人（工位1）1台、计时器1个。

4、考试用时：45分钟/人次/工位。

5、平面轨迹示意图：①②③④⑤①③⑤②④（料台）（加工台）（加工台）上料②④①③⑤⑤④③②（料台）（料台）（加工台）下料单行上、下料平面轨迹示意图6、考分分配及评分表：满分100分。

考分分配及评分表见附表。

序号：工业机器人实训考试2考分分配及评分表7、参考程序（示例程序16）：—主/子程序—P000=-2.794532,-2.354631,2.188341,0.003075,90.157050,0.001526,0.000000,0.000000;P001=-63.710039,25.299595,-7.861327,4.556348,23.249510,125.626166,0.000000,0.000000;P002=41.545406,3.321531,18.073557,45.076682,45.993369,16.956343,0.000000,0.000000;P003=-63.710039,26.567787,-24.203067,2.900811,38.293129,127.536598,0.000000,0.000000;P004=-58.026860,-16.387816,16.735965,-25.931263,54.361455,131.271836,0.000000,0.000000;P005=-7.803018,5.567475,-5.638086,43.137545,94.729901,-7.908513,0.000000,0.000000;P006=58.646248,-16.083230,24.034333,27.601415,46.612482,47.158405,0.000000,0.000000;P007=41.545406,2.731131,12.660845,41.393473,50.371408,22.474144,0.000000,0.000000;0001 MAIN; //程序头0002 MOVJ P0 ,V20 ,Z0 ; //零点0003 SET R0 ,0 ; //给R0变量赋值为00004 SET R1 ,5 ; //给R1变量赋值为50005 SETE PX0 (0) ,0 ; //给PX0变量在各方向均赋值为00006 SETE PX1 (0) ,0 ; //给PX1变量在各方向均赋值为00007 SETE PX1 (2) ,96 ; //给PX1变量在Y方向正方向赋值为96 0008 SETE PX2 (0) ,0 ; //给PX2变量在各方向均赋值为00009 SETE PX3 (0) ,0 ; //给PX3变量在各方向均赋值为00010 SETE PX3 (2) ,192 ; //给PX3变量在Y方向正方向赋值为192 0011 SETE PX4 (0) ,0 ; //给PX4变量在各方向均赋值为00012 SETE PX5 (0) ,0 ; //给PX5变量在各方向均赋值为00013 SETE PX5 (2) ,384 ; //给PX5变量在Y方向正方向赋值为384 0014 SETE PX6 (0) ,0 ; //给PX6变量在各方向均赋值为00015 SETE PX6 (2) ,384 ; //给PX6变量在Y方向正方向赋值为384 0016 SETE PX7 (0) ,0 ; //给PX7变量在各方向均赋值为00017 SETE PX7 (2) ,384 ; //给PX7变量在Y方向正方向赋值为384 0018 DOUT OT9 ,OFF ; //抓取输出信号关闭0019 DOUT OT8 ,ON ; //松开输出信号打开0020 WAIT IN8 ,ON ,T0 ; //松开到位输入信号延时-无限延长0021 DELAY T0.5 ; //延时0.5S0022 LAB0: //程序段标签00023 INC R0; //R0加10024 MOVJ P4 ,V20 ,Z0 ; //过渡点0025 SHIFTON PX0; //平移打开，平移量PX00026 MOVJ P3 ,V20 ,Z0 ; //过渡点0027 MOVL P1 ,V100 ,Z0 ; //料台抓取点0028 DOUT OT8 ,OFF ; //松开输出信号关闭0029 DOUT OT9 ,ON ; //抓取输出信号打开0030 WAIT IN9 ,ON ,T0 ; //抓取到位输入信号延时-无限延时0031 DELAY T0.5 ; //延时0.5S0032 MOVL P3 ,V100 ,Z0 ; //过渡点0033 SHIFTOFF; //平移关闭0034 MOVJ P4 ,V20 ,Z0 //过渡点; 0035 MOVJ P5 ,V20 ,Z0 ; //安全点、延时点、判断点0036 PX0 = PX0 + PX1 ; //PX0在Y方向正方向加96，实现向右偏移0037 JUMP LAB1 ,IF R0 <= 3 ; //如果R0值<=3时，转到LAB1，否则执行下一行指令0038 JUMP LAB2 ,IF R0 <= 5 ; //如果R0值<=5时，转到LAB2，否则执行下一行指令0039 LAB1 : //程序段标签10040 MOVJ P6 ,V20 ,Z0 ; //过渡点0041 SHIFTON PX2 ; //平移打开，平移量PX20042 MOVJ P7 ,V20 ,Z0 ; //过渡点0043 MOVL P2 ,V100 ,Z0 ; //加工台放置点（料位1、3、5）0044 DOUT OT9 ,OFF ; //抓取输出信号关闭0045 DOUT OT8 ,ON ; //松开输出信号打开0046 WAIT IN8 ,ON ,T0 ; //松开到我输入信号延时-无限延时0047 DELAY T0.5 ; //延时0.5S0048 MOVL P7 ,V100 ,Z0 ; //过渡点0049 SHIFTOFF; //平移关闭0050 MOVJ P6 ,V20 ,Z0 ; //过渡点0051 MOVJ P5 ,V20 ,Z0 ; //安全点、延时点、判断点0052 PX2 = PX2 + PX3 ; //PX2在Y方向正方向加192，实现向右偏移0053 JUMP LAB0 ,IF R0 < 5 ; //R0值<5时，转到LAB0，否则执行下一行指令0054 LAB2 : //程序段标签20055 PX4 = PX4 + PX1 ; //PX3在Y方向正方向加96，实现向右偏移0056 MOVJ P6 ,V20 ,Z0 ; //过渡点0057 SHIFTON PX4 ; //平移打开0058 MOVJ P7 ,V20 ,Z0 ; //过渡点0059 MOVL P2 ,V100 ,Z0 ; //加工台放置点（料位2、4）0060 DOUT OT9 ,OFF ; //抓取输出信号关闭0061 DOUT OT8 ,ON ; //松开输出信号打开0062 WAIT IN8 ,ON ,T0; //松开到位输入信号延时-无限延时0063 DELAY T0.5 ; //延时0.5S0064 MOVL P7 ,V100 ,Z0 //过渡点0065 SHIFTOFF; //平移关闭0066 MOVJ P6 ,V20 ,Z0 ; //过渡点0067 MOVJ P5 ,V20 ,Z0 ; //安全点、延时点、判断点0068 PX4 = PX4 + PX1 ; //PX3在Y方向正方向加96，实现向右偏移0069 JUMP LAB0 ,IF R0 < 5 ; //R0值<5时，转到LAB0，否则执行下一行指令0070 DELAY T5 ; //延时5S（等待加工完成）0071 LAB3 : //程序段标签30072 DEC R1 ; //R1减10073 MOVJ P6 ,V20 ,Z0 ; //过渡点0074 SHIFTON PX5 ; //平移打开，平移量PX50075 MOVJ P7 ,V20 ,Z0 ; //过渡点0076 MOVL P2 ,V100 ,Z0 ; //加工台抓取点0077 DOUT OT8 ,OFF ; //松开输出信号关闭0078 DOUT OT9 ,ON ; //抓取输出信号打开0079 WAIT IN9 ,ON ,T0 //抓取到位输入信号延时-无限延时0080 DELAY T0.5 ; //延时0.5S0081 MOVL P7 ,V100 ,Z0 ; //过渡点0082 SHIFTOFF; //平移关闭0083 MOVJ P6 ,V20 ,Z0 ; //过渡点0084 MOVJ P5 ,V20 ,Z0 ; //安全点、延时点、判断点0085 PX5 = PX5 - PX1 ; //PX5在Y方向正方向减96，否则执行下一行指令0086 JUMP LAB4 ,IF R1 >= 2 ; //如果R0值>=2时，转到LAB4,否则执行下一行指令0087 JUMP LAB5 ,IF R1 >= 0 ; //如果R0值>=0时，转到LAB5，否则执行下一行指令0088 LAB4 : //程序段标签40089 MOVJ P4 ,V20 ,Z0 ; //过渡点0090 SHIFTON PX6 ; //平移打开，平移量PX60091 MOVJ P3 ,V20 ,Z0 ; //过渡点0092 MOVL P1 ,V100 ,Z0 ; //料台放置点（料位1、3、5）0093 DOUT OT9 ,OFF ; //抓取输出信号关闭0094 DOUT OT8 ,ON ; //松开输出信号打开0095 WAIT IN8 ,ON ,T0 ; //松开到位输入信号延时-无限延时0096 DELAY T0.5 ; //延时0.5S0097 MOVL P3 ,V100 ,Z0 ; //过渡点0098 SHIFTOFF; //平移关闭0099 MOVJ P4 ,V20 ,Z0 ; //过渡点0100 MOVJ P5 ,V20 ,Z0 ; //安全点、延时点、判断点0101 PX6 = PX6 - PX3 ; //PX6在Y方向正方向减192，实现向左偏移0102 JUMP LAB3 ,IF R1 > 0 ; //P1值>0时，转到LAB3,否则执行下一行指令0103 LAB5 : //程序段标签50104 PX7 = PX7 - PX1 ; //PX7在Y方向正方向减96，实现向左偏移0105 MOVJ P4 ,V20 ,Z0 ; //过渡点0106 SHIFTON PX8 ; //平移打开，平移量PX70107 MOVJ P3 ,V20 ,Z0 ; //过渡点0108 MOVL P1 ,V100 ,Z0 ; //料台放置点（料位2、4）0109 DOUT OT9 ,OFF ; //抓取输出信号关闭0110 DOUT OT8 ,ON ; //松开输出信号打开0111 WAIT IN8 ,ON ,T0 ; //松开到位输入信号延时-无限延时0112 DELAY T0.5 ; //延时0.5S0113 MOVL P3 ,V100 ,Z0 ; //过渡点0114 SHIFTOFF; //平移关闭0115 MOVJ P4 ,V20 ,Z0 ; //过渡点0116 MOVJ P5 ,V20 ,Z0 ; //安全点、延时点、判断点0117 PX7 = PX7 - PX1 ; //PX7在Y方向正方向减96，实现向左偏移0118 JUMP LAB3 ,IF R1 > 0; //R1值>0时，否则执行下一行指令0119 MOVJ P0 ,V20 ,Z0 ; //回零0120 # RET; //返回调用此程序的主程序0121 END; //程序结束0122 MOVJ P0 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0123 MOVJ P1 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0124 MOVJ P2 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0125 MOVJ P3 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0126 MOVJ P4 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0127 MOVJ P5 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0128 MOVJ P6 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0129 MOVJ P7 ,V20 ,Z0 ; //记录点位，便于重新获取示教点0130 END; //程序结束①②③④⑤①③⑤②④（料台）（加工台）（加工台）上料②④①③⑤⑤④③②①（料台）（料台）（加工台）下料单行上、下料平面轨迹示意图。

第一章数值分析(误差分析)

*
* e x x * e r * * x x x x* er 则称η 为 x* 的相对误差限。 x
如果
这时 x=10,
x*=10±1;
2019/3/13
第一章绪论与误差分析
2
本章内容安排
1. 目的意义：了解计算数学的背景知识；掌握误差的基本知识 2.重点：误差来源、误差表示、误差传播及算法设计原则 3.难点：有效数字 4.内容分配：第 1 次：§1 计算数学研究的对象和内容第
§2 误差的来源和分类 2 次：§3 误差的表示 §4 误差的传播 §5 算法设计的若干原则
由于计算机的字长有限，参加运算的数据以及计算结果在计算机上存放时，计算机会按舍入原则舍去每个数据字长之外的数字，从而产生误差，这种误差称为舍入误差或计算误差。例如，在十进制十位的限制下，会出现 (1.000002)2-1.000004=0
这个结果是不准确的，准确的结果应是 (1.000002)2-1.000004 =1.000004000004-1.000004=4×10-12 这里所产生的误差就是计算舍入误差。在数值分析中，一般总假定数学模型是准确的，因而不考虑模型误差和观测误差，主要研究截断误差和舍入误差对计算结果的影响。
则有误差限 |x-x*|≤1= εx ,
虽然εy是εx 的3倍，但在1000内差3显然比10内差1更精确些。这说明一个近似值的精确程度除了与绝对误差有关外，还与精确值的大小有关，所以这时可以用相对误差来比较这两个近似数的准确度。
2019/3/13 19
第一章绪论与误差分析
e x x 定义1 .2 记 er x x 则称其为近似值 x *的相对误差。由于 x 未知，实际使用时总是将 x * 的相对误差取为

龙格库塔法-原理及程序实现

龙格库塔法一、基本原理：“龙格-库塔(Runge-Kutta)方法”是一种在工程上应用广泛的“高精度单步算法”。

由于此算法精度高，采取措施对误差进行抑制，可以得出四阶龙格－库塔公式，也就是在工程中应用广泛的经典龙格－库塔算法，即：yi＋１＝yi＋h*( K1+ 2*K2 +2*K3+ K4)/6K1=f(xi,yi)K2=f(xi+h/2,yi+h*K1/2)K3=f(xi+h/2,yi+h*K2/2)K4=f(xi+h,yi+h*K3)通常所说的龙格-库塔法就是指四阶——龙格库塔法，我们可以仿二阶、三阶的情形推导出常用的标准四阶龙格-库塔法公式。

（1）计算公式（1）的局部截断误差是。

龙格-库塔法具有精度高，收敛，稳定（在一定条件下），计算过程中可以改变步长，不需要计算高阶导数等优点，但仍需计算在一些点上的值，如四阶龙格-库塔法每计算一步需要计算四次的值，这给实际计算带来一定的复杂性，因此，多用来计算“表头”。

二、小程序#include<stdio.h>#include<math.h>#define f(x,y) (-1*(x)*(y)*(y))void main(void){double a,b,x0,y0,k1,k2,k3,k4,h;int n,i;printf("input a,b,x0,y0,n:");scanf("%lf%lf%lf%lf%d",&a,&b,&x0,&y0,&n); printf("x0\ty0\tk1\tk2\tk3\tk4\n");for(h=(b-a)/n,i=0;i!=n;i++){k1=f(x0,y0);k2=f(x0+h/2,y0+k1*h/2);k3=f(x0+h/2,y0+k2*h/2);k4=f(x0+h,y0+h*k3);printf("%lf\t%lf\t",x0,y0);printf("%lf\t%lf\t",k1,k2);printf("%lf\t%lf\n",k3,k4);y0+=h*(k1+2*k2+2*k3+k4)/6;x0+=h;}printf("xn=%lf\tyn=%lf\n",x0,y0);}运行结果：input a,b,x0,y0,n:0 5 0 2 20x0y0k1k2k3 k40.000000 2.000000-0.000000-0.500000-0.469238-0.8861310.250000 1.882308-0.885771-1.176945-1.129082-1.2800600.500000 1.599896-1.279834-1.295851-1.292250-1.2227280.750000 1.279948-1.228700-1.110102-1.139515-0.9901621.000000 1.000027-1.000054-0.861368-0.895837-0.7528521.2500000.780556-0.761584-0.645858-0.673410-0.5621891.5000000.615459-0.568185-0.481668-0.500993-0.4205371.7500000.492374-0.424257-0.361915-0.374868-0.3178552.0000000.400054-0.320087-0.275466-0.284067-0.2435982.2500000.329940-0.244935-0.212786-0.218538-0.1894822.5000000.275895-0.190295-0.166841-0.170744-0.1495632.7500000.233602-0.150068-0.132704-0.135399-0.1197033.0000000.200020-0.120024-0.106973-0.108868-0.0970483.2500000.172989-0.097256-0.087300-0.088657-0.0796183.5000000.150956-0.079757-0.072054-0.073042-0.0660303.7500000.132790-0.066124-0.060087-0.060818-0.0553054.0000000.117655-0.055371-0.050580-0.051129-0.0467434.2500000.104924-0.046789-0.042945-0.043363-0.0398334.5000000.094123-0.039866-0.036750-0.037072-0.0342024.7500000.084885-0.034226-0.031675-0.031926-0.029571xn=5.000000yn=0.076927。

弹道计算与飞行仿真

第五章弹道计算与飞行仿真目的要求：1、掌握弹道计算的建模方法；2、掌握弹道数字仿真的方法；3、了解弹道飞行视景仿真的方法；4、了解飞行器设计与试验的虚拟样机技术。

重点、难点：1、具有使用方便、清晰的界面和结果显示，且计算速度块的编程方法；2、飞行视景仿真的设计方法和总体框架。

教学方法：1、课堂教学讲解一般的程序设计步骤、框架和方法；2、实例介绍；3、上机实际编程设计、计算、调试程序，给出仿真结果。

教学时数：课堂教学：6学时；上机实习：10学时。

§5-1 仿真的基本概念一、仿真的定义雷诺对仿真的定义：“仿真是在数字计算机上进行试验的数字化技术，它包括数字与逻辑模型的某些模式，这些模型描述某一事件或经济系统(或者它们的某些部分)在若干周期内的特征。

”系统仿真实质上应该包括三个基本因素：系统、系统模型和计算机。

联系这三项要素的基本活动则是：模型建立、仿真模型建立和仿真试验。

5]综合国内外仿真界对仿真的定义，可对系统仿真作如下定义[1：仿真是建立在控制理论、计算技术、信息处理技术和计算技术等理论基础之上的，以计算机和其它专业物理效应设备为工具，利用系统模型对真实或假想的系统进行试验，并借助于专家经验知识、统计数据和信息资料对试验结果进行分析研究，进而做出决策的一门综合性和试验性的科学。

上述定义中的计算技术，除了包含通常意义下的计算理论和技术，还应包括现代运筹学的绝大部分内容。

定义中的模型可以是定量的，也可以是定性的；可以是物理的，也可以是数学的，或二者兼而有之。

二、仿真的分类依据不同的分类标准，可将仿真进行不同的分类。

(1)根据被研究系统的特征可分为两大类：连续系统仿真和离散事件系统仿真。

(2)按仿真实验过程中的时间t与自然时钟T之间的比例关系，分为实时仿真和非实时100仿真。

(3) 按照参与仿真的模型种类，分为物理仿真、数学仿真和物理－数学仿真(又称半物理仿真或半实物仿真)§5-2 弹道仿真的基本方法一、飞行弹道的仿真模型在前几章，我们已经建立了弹道计算的理论模型(theoretical model)，但这样的模型还不能直接用于计算机仿真。

大连生产实习考试题

大连生产实习考试题第一篇：大连生产实习考试题大连生产实习考试题目1.什么是生产过程？什么是工艺过程？（5分）2.产品的开发流程包括哪几类？（5分）3.激光刻字的原理（5分）4.什么是胎具？与通用夹具有什么区别与联系？（5分）5.常用涡轮加工的方法，优缺点是什么？（10分）6.简述加工柴油机厂用的钻头种类，怎么区分？（10分）7.船用阀门厂加工阀门的种类，蝶阀的分类？（10分）8.什么是炉号？有什么作用？（10分）9.什么是假叶型？作用及原理（10分）10.柴油机的工作原理？有几个流程？（10分）11.柴油机连杆加工过程？画出草图，标示加工连杆的主要尺寸及采用的机床。

（20分）第二篇：大连东软生产实习日记软件工程专业教学单位软件学院班级10-6班学生姓名萧翎学号1020010615实习时间2013-6-17至2013-7-5 指导教师邱云飞辽宁工程技术大学教务处制软件项目实践（生产实习）日志日期： 2013年6月30 日学生：萧翎东软印象今天早晨六点半，伴随着同学的欢声笑语，我们踏上了通往大连的火车。

下午两点半，我们来到了期盼已久的实训基地——大连东软软件园区。

之后，交了押金，领了行李和工牌，整理完床铺后，我便和同学们怀揣着好奇和激动的心情游玩了东软软件园。

东软园区给我的第一感觉就是大气、神秘。

因为园区建在群山之上，走在园区内有一种“曲尽通幽处”的感觉，而且建筑和别的地方的建筑有很大的不同，算是欧式风格的吧。

像是古堡似的建筑群高耸入云，类似于好莱坞的logo的东软logo——“NEWSOFT”在夕阳的映衬下更是显得恢弘大气，特别是整个园区有大山环绕着的，满眼绿色，处处都有吸引我眼球的景色。

痴迷于此间山水的我，不由的拿起手机想要记录下这里的一切。

参观完园区后，我们去了餐厅，餐厅的食物真可谓让大家馋涎欲滴，大饱口福。

晚餐过后，我们也渐感疲惫，打道回府——回寝休息。

日期： 2013年7月2日学生：萧翎学校人与企业人今天上午，于晓飞老师和我们分享了“从学校人到企业人的转变”的话题。

仿真技术实验程序及思考题解答(仅供参考)

实验一连续系统的数字仿真一、实验目的1．熟悉Matlab 中m 文件的编写；2．掌握龙格－库塔法的基本原理。

二、实验设备计算机、MATLAB 软件三、实验内容假设单变量系统如图所示。

试根据四阶龙格－库塔法，求系统输出y 的动态响应。

1．首先把原系统转化为状态空间表达式：⎪⎩⎪⎨⎧=+=•CXy bu AX X ，根据四阶龙格－库塔公式，可得到： ⎪⎩⎪⎨⎧=++++=+++1143211)22(6k k k k CX y K K K K h X X （1）其中： ⎪⎪⎪⎩⎪⎪⎪⎨⎧+++=+++=+++=+=)()()2()2()2()2()(3423121h t bu hK X A K h t bu K h X A K h t bu K h X A K t bu AX K k k k k k k k k （2）根据（1）、（2）式编写仿真程序。

2．在Simulink 环境下重新对上述系统进行仿真，并和1中结果进行比较。

四、实验结果及分析要求给出系统输出响应曲线，并分析计算步长对龙格－库塔法的影响。

计算步长对龙格－库塔法的影响：单从每一步看，步长越小，截断误差就越小，但随着步长的缩小，在一定求解范围内所要完成的步数就增加，不但引起计算量的增大，而且可能导致舍入误差严重积累，因此同积分的数值计算一样，微分方程的解法也有选择步长的问题。

源程序：r=5;numo=[1];deno=[1 4 8 5];numh=1;denh=1;[num,den]=feedback(numo,deno,numh,denh);[A,b,C,d]=tf2ss(num,den);Tf=input('仿真时间 Tf= ');h=input('计算步长 h=');x=[zeros(length(A),1)];y=0;t=0;for i=1:Tf/h;K2=A*(x+h*K1/2)+b*r;K3=A*(x+h*K2/2)+b*r;K4=A*(x+h*K3)+b*r;x=x+h*(K1+2*K2+2*K3+K4)/6;y=[y;C*x];t=[t;t(i)+h];endplot(t,y)Tf=5 h=0.02五、思考题1．试说明四阶龙格－库塔法与计算步长关系，它与欧拉法有何区别。