第三章 机械零件的强度
合集下载
第三章 机械零件的强度

• 变应力的应力比保持不变,即:r = C
• 变应力的平均应力保持不变,即:sm = C • 变应力的最小应力保持不变,即:smin = C
1.变应力的应力比保持不变,即 r C (如转轴)
s a s max s min 1 r C s m s max s min 1 r
一、疲劳破坏 机械零件在变应力作用下,即使变应力的 smax < sb ,而应
力的每次循环也仍然会对零件造成轻微的损伤。随应力循环次数的 增加,当损伤累积到一定程度时,在零件的表面或内部将出现(萌 生)裂纹。之后,裂纹又逐渐扩展直到发生完全断裂。这种缓慢形 成的破坏称为 “疲劳破坏”。
“疲劳破坏” 是循环应力作用下零件的主 要失效形式。
直线CG方程:
s ae s m e s s
三、单向稳定变应力时机械零件的疲劳强度计算
一般步骤:
1)由外载荷smax 、smin sm 、sa——工作应力;
2)将工作应力sm、sa标在零件极
限应力图上,得工作应力点:
M( sm,sa )
M s m e,s ae M s m,s a
在零件极限应力图上表示 为:平行 纵坐标 的一条 直线。
M s m e,s ae M s m,s a
1)如果此线与AG线交于M( sme ,sae ),则有:
s m e s m
,
s ae
s 1
ss m
Ks
s lim s m ax s ae s m e s 1
M s m e,s ae
s a Cs m
显然,直线OM上任一点的应力
比均相同,M 就是零件的极限
应力点。
M s m,s a
• 变应力的平均应力保持不变,即:sm = C • 变应力的最小应力保持不变,即:smin = C
1.变应力的应力比保持不变,即 r C (如转轴)
s a s max s min 1 r C s m s max s min 1 r
一、疲劳破坏 机械零件在变应力作用下,即使变应力的 smax < sb ,而应
力的每次循环也仍然会对零件造成轻微的损伤。随应力循环次数的 增加,当损伤累积到一定程度时,在零件的表面或内部将出现(萌 生)裂纹。之后,裂纹又逐渐扩展直到发生完全断裂。这种缓慢形 成的破坏称为 “疲劳破坏”。
“疲劳破坏” 是循环应力作用下零件的主 要失效形式。
直线CG方程:
s ae s m e s s
三、单向稳定变应力时机械零件的疲劳强度计算
一般步骤:
1)由外载荷smax 、smin sm 、sa——工作应力;
2)将工作应力sm、sa标在零件极
限应力图上,得工作应力点:
M( sm,sa )
M s m e,s ae M s m,s a
在零件极限应力图上表示 为:平行 纵坐标 的一条 直线。
M s m e,s ae M s m,s a
1)如果此线与AG线交于M( sme ,sae ),则有:
s m e s m
,
s ae
s 1
ss m
Ks
s lim s m ax s ae s m e s 1
M s m e,s ae
s a Cs m
显然,直线OM上任一点的应力
比均相同,M 就是零件的极限
应力点。
M s m,s a
03机械零件的强度

§3-2 机械零件的疲劳强度 1. 由于零件的几何形状的变化、尺寸大小、加工质量及强化 由于零件的几何形状的变化、尺寸大小、 因素等影响,使零件的疲劳极限要小于材料试件的疲劳极限。 因素等影响,使零件的疲劳极限要小于材料试件的疲劳极限。 综合影响系数K 2. 若以弯曲疲劳极限的综合影响系数 σ 若以弯曲疲劳极限的综合影响系数 表示材料r 及零件r 的疲劳极限值之比, 表示材料 = -1及零件 = -1的疲劳极限值之比,即: 及零件 的疲劳极限值之比
§3-4 机械零件的接触强度
1、接触应力 、 两圆柱体接触——线接触 两圆柱体接触——线接触 ——
F 1 1 ( ± ) B ρ1 ρ2 σH = 2 2 1− µ1 1− µ2 π( + ) E1 E2
F:作用于接触面上的总压力
(3-36) )
B:初始接触线长度
零件1和零件2初始接触处的曲率半径。 ρ1和ρ2:零件1和零件2初始接触处的曲率半径。 公式中, 号为外接触, 为内接触。 公式中,+号为外接触,- 为内接触。 μ和 E:分别为材料的泊松比和弹性模量
3.零件的极限应力图 3.零件的极限应力图
有影响, 无影响, 由于 k 只对 有影响,而对 σ 无影响,∴在材料 m σ 的极限应力图 A´D´G´C上几个特殊点的坐标计入 影响 σ 零件对称循环疲劳点
k
(一)、单向稳定变应力时的疲劳强度计算 )、单向稳定变应力时的疲劳强度计算 1、 r = σ
σ−1 Kσ = σ−1e
若r≠-1时 , - 时
(3-7) )
则
σ−1e =
σ−1
Kσ
3-8) (3-8)
′ σa Kσ = ′ σ ae
因此将零件材料的极限应力线图按比值下移, 因此将零件材料的极限应力线图按比值下移,则折线 ADGCO 即为零件的极限应力线图。 即为零件的极限应力线图 零件的极限应力线图。
第3章 机械零件的强度(用)
变载荷:随时间作周期性或非周期性变化的载荷.如
汽车的齿轮和轴所承受的动载荷。
注意:在设计计算中,载荷又可分为名义载荷和计 算载荷,计算载荷等于载荷系数乘以名义载荷。
名义载荷: 根据机器在稳定和理想工作条件下的工作阻力,
按力学公式求出的载荷称为名义载荷. 计算载荷:
考虑机器在工作中载荷的变化和载荷在零件上
s
m rN
N
C (NC
N
ND)
D点以后(无限寿命区间):
s rN s r (N ND )
用N0及其相对应的疲劳极限σr来近
似代表ND和 σr∞,有:
s
m rN
N
s
m r
N0
C
s-N疲劳曲线
§3-1 材料的疲劳特性 疲劳曲线
2、 s-N疲劳曲线
有限寿命区间内循环次数N与
疲劳极限srN的关系为:
CG'直线的方程为:
s a s m s s
σ为试件受循环弯曲 应力时的材料常数,其值 由试验及下式决定:
s
2s 1 s 0 s0
对于碳钢,σ≈0.1~0.2,对于合金钢,σ≈0.2~0.3。
§3-2 机械零件的疲劳强度计算
1、零件的极限应力线图
如设弯曲疲劳极限的综合影响系数 Kσ ,且 s 1 ―材料对称循环弯曲疲劳极限
s rN s r
m
N0 N
KNsr
式中, N0为循环基数;
sr为与N0相对应的疲劳极限
s-N疲劳曲线
m为材料常数,值由材料试验确定。
疲劳曲线的意义
s rN
sr m
N0 N
KNsr
汽车的齿轮和轴所承受的动载荷。
注意:在设计计算中,载荷又可分为名义载荷和计 算载荷,计算载荷等于载荷系数乘以名义载荷。
名义载荷: 根据机器在稳定和理想工作条件下的工作阻力,
按力学公式求出的载荷称为名义载荷. 计算载荷:
考虑机器在工作中载荷的变化和载荷在零件上
s
m rN
N
C (NC
N
ND)
D点以后(无限寿命区间):
s rN s r (N ND )
用N0及其相对应的疲劳极限σr来近
似代表ND和 σr∞,有:
s
m rN
N
s
m r
N0
C
s-N疲劳曲线
§3-1 材料的疲劳特性 疲劳曲线
2、 s-N疲劳曲线
有限寿命区间内循环次数N与
疲劳极限srN的关系为:
CG'直线的方程为:
s a s m s s
σ为试件受循环弯曲 应力时的材料常数,其值 由试验及下式决定:
s
2s 1 s 0 s0
对于碳钢,σ≈0.1~0.2,对于合金钢,σ≈0.2~0.3。
§3-2 机械零件的疲劳强度计算
1、零件的极限应力线图
如设弯曲疲劳极限的综合影响系数 Kσ ,且 s 1 ―材料对称循环弯曲疲劳极限
s rN s r
m
N0 N
KNsr
式中, N0为循环基数;
sr为与N0相对应的疲劳极限
s-N疲劳曲线
m为材料常数,值由材料试验确定。
疲劳曲线的意义
s rN
sr m
N0 N
KNsr
第三章机械零件的强度

22
σa A' D' G' σ−1 σ0/2
45° O σ0/2 σs
45° C σm
曲线上的点对应着不同应力循环特性下的材料疲劳极限 σ γ A′——对称疲劳极限点 对称疲劳极限点 A′ C —— 屈服极限点 D′——脉动疲劳极限点 脉动疲劳极限点 D′
23
§3-2 机械零件的疲劳强度计算
前边提到的各疲劳极限 ,实际上是材料的力学性能指标,是用试件通过 试验测出的。 而实际中的各机械零件与标准试件,在形体,表面质量以及绝对尺寸等 方面往往是有差异的。因此实际机械零件的疲劳强度与用试件测出的必然 有所不同。 疲劳强度设计的主要目的是计算危险剖面处的安全系数,以 判断零件的安 全程度。安全条件是:S ≥ [S] 。
1
2
3
4
第三章 机械零件的强度
复习基本概念 一、 复习基本概念 1、载荷(load) 、载荷( )
作用在零件 上的外力 按理论力学 考虑动力参数、 考虑动力参数、 公称载荷( 公称载荷(nominal load) 方法计算出 工作阻力的变动 ) 来的载荷 而计算出的载荷 用Fn、Mn、Tn表示 计算载荷( 计算载荷(calculated load) ) 用Fca、Mca、Tca表示 Fca=KFn K——载荷系数(工况系数) 载荷系数(工况系数) 载荷系数
11
复合应力计算安全系数为: 复合应力计算安全系数为:
σs sca = ≤ [ s] σs 2 2 2 σ +( ) τ τs
s ca =
sσ sτ
2 sσ + sτ2
≤ [s]
三、脆性材料与低塑性材料 脆性材料与低塑性材料 材料与低塑性
失效形式:断裂 失效形式: 脆性材料极限应力: σ B (强度极限) 脆性材料极限应力: 强度极限) 1、单向应力状态 σB σB sσ = ≥ [s]σ 强度条件: σ ca ≤ [σ ] = 强度条件: 或 [ s]σ σ ca
机械设计 第03章 强度

m rN
N
C ( N C
N
ND)
疲劳曲线2
D点以后——无限寿命疲劳阶段
rN r (N N D )
σr∞ 称为持久疲劳
-N疲劳曲线
由于ND很大,所以在作疲劳试验时,常规定一个循环次数 N0(称为循环基数),用N0及其相对应的疲劳极限σr来近似代表ND
和 σr∞ ,于是有:
有限寿命区间内循环次数N与疲劳极限rN的关系为:
D′点: σm = σa = σ0/2,为脉动循环点。
σa A'(0, 1 )
D'(20
,
0
2
)
G
' m
' a
r
2
0
2
45° O
45°
σm
C( S , 0) B
则A′D′G′C即为简化极限应力图。
返回目录
前一页
后一页
退出
3、材料极限应力图的画法
已知: σ-1,σ0, σs;
σa A'(0, 1) D'( 0 , 0 )
即 σa=cσm 同理σa′=cσm ′
C值取决于应力比r
所以,极限应力点为经过坐标原点O点和工作点M的直线上。
σa
A
计算安全系数:
M'( m e , ae )
Sca lim
' max
' ae
' me
max
max
a m
极限应力点M′的坐标值可以用图解
M( m , a )
G 和解析两种方法求解。 解析法:联立AG和OM两条直线的方
M(σm,σa)
2)如果工作点M在AB范围外,则工作点处于不安全工作 区,材料在该应力作用下会发生破坏。
第三章 机械零件的强度

应力幅: σ a =
σ max − σ min
2
平均应力: σ m =
σ max + σ min
2
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
强度计算
静应力强度 变应力强度
2、静应力时的机械零件的强度 σ lim σ ≤ [σ ] = S
—— AG 的方程 ′ ′ 2. CG方程:
' ' σ ae + σ me = σ s
σ +σ =σs
' a ' m
—— CG′的方程
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
1. 单向稳定变应力时机械零件的疲劳强度计算 机械零件应力的变化规律: ①变应力的循环特性不变 ②变应力的平均应力不变 ③变应力的最小应力不变
′ ′ AG 的方程:
' ' σ−1 =σa +ϕσσm
其中:
ϕσ =
2 −1 −σ0 σ
σ0
CG′ 的方程:
材料的极限应力线图
' ' σa +σm =σs
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
§3-2 机械零件的疲劳强度计算
机械设计
Design of Machinery
第三章 机械零件的强度
1.载荷和应力的分类 静载荷、变载荷 静应力、变应力
静载荷:大小和方向不随时间变化或变化缓慢的载荷。 变载荷:随时间周期性变化或非周期性变化的载荷。 静应力:不随时间变化或变化缓慢的应力。 (只在静载荷作用下产生) 变应力:随时间变化的应力。 (可由变载荷产生,也可由静载荷产生) σ
σ max − σ min
2
平均应力: σ m =
σ max + σ min
2
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
强度计算
静应力强度 变应力强度
2、静应力时的机械零件的强度 σ lim σ ≤ [σ ] = S
—— AG 的方程 ′ ′ 2. CG方程:
' ' σ ae + σ me = σ s
σ +σ =σs
' a ' m
—— CG′的方程
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
1. 单向稳定变应力时机械零件的疲劳强度计算 机械零件应力的变化规律: ①变应力的循环特性不变 ②变应力的平均应力不变 ③变应力的最小应力不变
′ ′ AG 的方程:
' ' σ−1 =σa +ϕσσm
其中:
ϕσ =
2 −1 −σ0 σ
σ0
CG′ 的方程:
材料的极限应力线图
' ' σa +σm =σs
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
§3-2 机械零件的疲劳强度计算
机械设计
Design of Machinery
第三章 机械零件的强度
1.载荷和应力的分类 静载荷、变载荷 静应力、变应力
静载荷:大小和方向不随时间变化或变化缓慢的载荷。 变载荷:随时间周期性变化或非周期性变化的载荷。 静应力:不随时间变化或变化缓慢的应力。 (只在静载荷作用下产生) 变应力:随时间变化的应力。 (可由变载荷产生,也可由静载荷产生) σ
机械设计-第三章 机械零件的强度(疲劳)

AB(103前):最大应力值变化很小,相当于静强度状况; BC(103-104):N增加,σmax减小,有塑性变形特征—应变疲
劳,低周疲劳,不讨论; CD(>104):有限寿命疲劳阶段 ,任意点的疲劳极限--有限寿
命疲劳极限σrN ,该曲线近似双曲线。
公式描述:
c,m—材料常数 D点后:材料不发生疲劳破坏,无限寿命疲劳阶段,
件的疲劳极限,用综合影响系数Kσ 表示。 如:对称循环弯曲疲劳极限的综合影响系数Kσ。 则:
σ -1试件的对称循环弯曲疲劳极限; σ -1e零件的对称循环弯曲疲劳极限。
不对称时:Kσ 是试件与零件的极限应力幅的比值。
零件的极限应力线图—ADGC 试件线图A’ D’ G’C—综合修正系数Kσ—零件线图ADGC
机械设计
第三章:机械零件的强度(疲劳强度)
主讲老师:吴克勤
第三章 机械零件的强度(疲劳)
一、材料的疲劳特性 1、 σ - N曲线 ①疲劳断裂:变应力下的零件损坏形式,与循环次数有关。 ②特征: σmax< σlim; 脆性材料和塑性材料都突然断裂; 损伤的积累。 ③疲劳极限:循环特征r一定时,应力循环N次后,材料不 发生破坏的最大应力σrN ; ④疲劳曲线:r一定的条件下,表示N与σrN 关系的曲线。
零件的极限应力曲线:
φσe-零件受循环弯曲应力时的材料常数; σ’ae -零件受循环弯曲应力时的极限应力幅; σ’me-零件受循环弯曲应力时的极限平均应力。
Kσ 为弯曲疲劳极限的综合影响系数
kσ-零件的有效应力集中系数(σ 表示在正应力条 件下);
εσ - 零件的尺寸系数; βσ -零件的表面质量系数; βq -零件的强化系数。 上面所有的计算公式,同样适用于剪切应力。
第3章机械零件的强度hm

∴过工作应力点M(N)作与横坐标成45°的直线,则这直线任一
点的最小应力 min m 均a 相同,∴直线与极限应力线图交
点 M 3 (N3即) 为所求极限应力点。
a) 工 作 应 力 点 位 于 OJGI区域内
极限应力为疲劳极限, 按疲劳强度计算
求AG与MM3´的交点:
1e
1
k
ae
e
等寿命曲线或极限应力线图(σ- N 曲线)
在特定寿命条件下,最大应力σmax =σm +σa与应力比
m a 的关系。
m a
(二)等寿命疲劳曲线(疲劳极限应力线图)
材料试验一般只给出r=-1及r=0时的疲劳极限,即σ-1、σ0。为获得各 种不同循环特性r时的疲劳极限,常借助简化的疲劳极限应力图。
•曲线CD段代表有限寿命疲劳阶段,有限寿命疲劳极限用符号 rN 表示。
•D点以后称为无限寿命疲劳阶段,无限寿命疲劳极限用 r 表示。
m rN
N
C
NC N ND
rN r
N ND
ND 106 ~ 25107
在做疲劳试验时,常规定一个循环次数 N0 (称为循环基数)。
用N0和与N0相对应的疲劳极限 rN(0 简写脉动循环) 1 r (1 非对称循环)
r = -1 对称循环应力
r=0 脉动循环应力
r=1 静应力
m
max
min
2
a
max
min
2
r min max
几种典型变应力的循环特征和应力特点
循环名称 循环特性
应力特点
对称循环 r=-1 脉动循环 r=0 非对称循环 -1<r<1
q — —强化系数
注:求K时,将式中换成
点的最小应力 min m 均a 相同,∴直线与极限应力线图交
点 M 3 (N3即) 为所求极限应力点。
a) 工 作 应 力 点 位 于 OJGI区域内
极限应力为疲劳极限, 按疲劳强度计算
求AG与MM3´的交点:
1e
1
k
ae
e
等寿命曲线或极限应力线图(σ- N 曲线)
在特定寿命条件下,最大应力σmax =σm +σa与应力比
m a 的关系。
m a
(二)等寿命疲劳曲线(疲劳极限应力线图)
材料试验一般只给出r=-1及r=0时的疲劳极限,即σ-1、σ0。为获得各 种不同循环特性r时的疲劳极限,常借助简化的疲劳极限应力图。
•曲线CD段代表有限寿命疲劳阶段,有限寿命疲劳极限用符号 rN 表示。
•D点以后称为无限寿命疲劳阶段,无限寿命疲劳极限用 r 表示。
m rN
N
C
NC N ND
rN r
N ND
ND 106 ~ 25107
在做疲劳试验时,常规定一个循环次数 N0 (称为循环基数)。
用N0和与N0相对应的疲劳极限 rN(0 简写脉动循环) 1 r (1 非对称循环)
r = -1 对称循环应力
r=0 脉动循环应力
r=1 静应力
m
max
min
2
a
max
min
2
r min max
几种典型变应力的循环特征和应力特点
循环名称 循环特性
应力特点
对称循环 r=-1 脉动循环 r=0 非对称循环 -1<r<1
q — —强化系数
注:求K时,将式中换成
机械设计-第三章 机械零件的强度
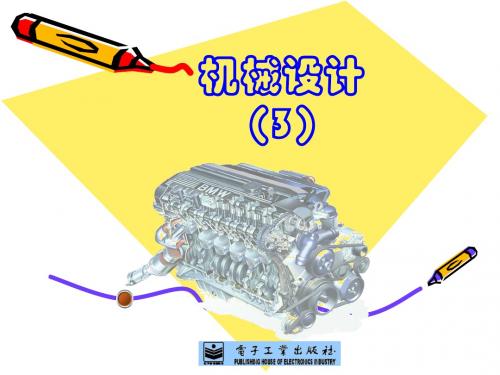
接触失效形式——疲劳点蚀
引起振动、噪声 使温度升高、磨损加快
ρ1
F F
O1
对于线接触的情况,其最大接触应力可用赫兹 应力公式计算: b
1 1 F 1 2 sH 2 1 12 1 2 b E1 E2
ρ22 ρ
sH
2a O22
F
§3.2 机械零件的疲劳强度计算
三、单向稳定变应力时的疲劳强度计算
机械零件疲劳强度计算的步骤: 根据零件危险截面上的σmax 及 σmin,确定平 均应力σm与应力幅σa; 在极限应力线图中标出相应工作应力点M或N ( σm, σa ); 找出该点对应的位于曲线AGC上的极限应力 点M’或N’(σ’m,σ’a ) ; 计算安全系数及疲劳强度条件为: ca S
s-N疲劳曲线
低周疲劳(BC段):N↑→ σmax↓。C点对应的循环次数约为104。 有限寿命疲劳阶段(CD段):实践证明大多数机械零件的疲劳发生在CD段,可用 下式描述: m σrN—有限寿命疲劳极限; s rN N C C N N D ) C—试验常数;m —材料常数。 (N 无限寿命阶段(D点以后的水平线): D点代表材料的无限寿命疲劳极限,用符号 σr∞表示,只要σmax<σr∞ ,无论N为多大,材料都不会破坏。可用下式描述:
σa
A’ M D’ G’ N O σm
σa
σs
C
σm
s max s m s a [S ] s max s m s a
M’或N’的位置与循环应力的变化规律有关。 可能发生的应力 变化规律: 1. 应力比为常数:r=C 2. 平均应力为常数σm=C 3. 最小应力为常数σmin=C
P O
第3章机械零件的强度

压应力远远大于拉伸应力,取最大应力
ca max
杜永平 机械零件的强度
b、双向应力
x y x y 2 2 ca ( ) xy 2 2
② 最大剪应力理论(第三强度理论)
ca 2 4 2
③ 最大形变能理论(第四强度理论)
ca 3
杜永平 机械零件的强度
lim S 极限应力与许 [ ]
二、静应力(static stress)的强度计算
1. 单向应力状态 应力变化次数小于10 3
危险剖面的最大应力即为计算应力
ca max
2. 双向理论)
a、脆性材料
静强度条件
s lim s Sca S max a m
杜永平
机械零件的强度
3. 变应力的最小应力保持不变 ( min C ) 情况
受轴向变载荷螺栓联接的应力状态
杜永平
机械零件的强度
min m a C
M点的极限应力为
杜永平
' max
第三章 机械零件的强度
一、 基本概念 作用在零件 1. 载荷(load) 上的外力 按理论力学 考虑动力参数、 公称载荷(nominal load) 方法计算出 工作阻力的变动 来的载荷 而计算出的载荷 用F 、M 、T 表示
n n n
计算载荷(calculated load)
用Fca、Mca、Tca表示
N D不大时, N 0= N D
N D很大时, N 0< N D
任意循环N次的疲劳极限:
rN r
m
N0 r KN N
式中:K N——寿命系数
杜永平
机械设计第三章机械零件强度
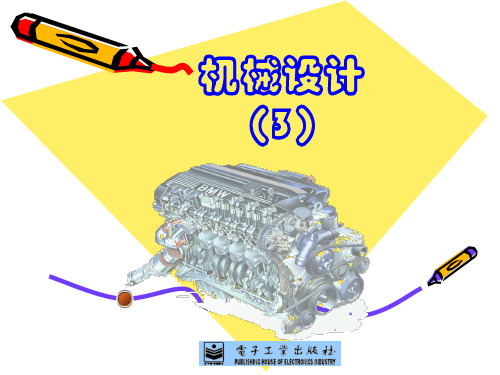
45° B
C
σm
σS σB
AG直线上任意点代表了一定循环特性时的疲劳极限。
已知C点坐标:(σS , 0) CG直线的斜率: k=tan135°=-1
CG直线的方程:
a m s
CG直线上任意点的最大应力达到了屈服极限应力。
§3.1 材料的疲劳特性
疲劳破坏的判据:
1. 当循环应力参数( σm,σa )
静应力只能由静载荷产生。 注意: 静载荷和变载荷均可能产生变应力。
绝大多数机械零件都是处于变应力状态下工作的。
§3.1 材料的疲劳特性
四、 变应力的描述
平均应力:
m
max
min
2
应力幅值:
a
max
min
2
-1,对称循环应力
应力比 (循环特性):
r
min max
=
0,脉冲循环应力 描述规律性的变应力有5个参数,但
由于实际零件的几何形状、尺寸大小、加工质量及强化因素等与材料 标准试件有区别,使得零件的疲劳极限要小于材料标准试件的疲劳极限。
1. 应力集中
由于零件形状突然变化而引起的局部应力增大现象。 应力集中的存在会降低零件的疲劳极限。
2. 零件尺寸
其他条件相同的情况下,零件的绝对尺寸越大,其疲劳强度 越低。
零件的表面状态包括表面粗糙度和表面处理。
二、名义载荷与计算载荷
➢名义载荷Fn :根据额定功率用力学公式计算出作用在零件上的载荷。 ➢计算载荷Fca:考虑载荷的时间不均匀性、分布的不均匀性以及其它
影 响因素对名义载荷进行修正得到的载荷。
Fca K Fn
K—— 载荷系数
§3.1 材料的疲劳特性
三、应力
机械设计第三章机械零件的强度

第三章 机械零件的强度
学习要求:
1. 了解疲劳曲线及极限应力曲线的来源,意义及用途, 能从材料的几个基本机械性能及零件的几何特性,绘 制零件的极限应力简化线图
2. 学会单向变应力时的强度计算方法 3. 了解疲劳损伤累积假说的意义及其应用
4. 学会双向变应力时的强度校核方法
学习重点:
极限应力线图的绘制及含义
强度准则是设计机械零件的最基本准则。
通用机械零件的强度分为静应力强度和变应力 强度两个范畴。
在机械零件整个工作寿命期间应力变化次数小 于103的通用零件,均按静应力强度进行设计。
即使是承受变应力的零件,在按疲劳强度进行 设计的同时,还有不少情况需要根据受载过程 中作用次数很少而数值很大的峰值载荷作静应 力强度校核。本章以下只讨论零件在变应力下的疲劳、低应力下 的脆断和接触强度等问题。
根据零件载荷的变化规律以及零件与相邻零件互相约 束情况的不同,可能发生的典型的应力变化规律通常 有下述三种:
a)变应力的应力比保持不变,即r=C(例如绝大 多数转轴中的应力状态);
b)变应力的平均应力保持不变,即σm=C(例如 振动着的受载弹簧中的应力状态);
c)变应力的最小应力保持不变, σmin=C(例如 紧螺栓联接中螺栓受轴向变载荷时的应力状 态)。以下分别讨论这三种情况。
e 可用下式计算
e
K
1 K
2 1 0 0
(3 11)
Kσ——弯曲疲劳极限的综合影响系数
K
k
1
1
1
q
(3 12)
式中:kσ——零件的有效应力集中系数 εσ——零件的尺寸系数; βσ——零件的表面质量系数; βq——零件的强化系数。
(一)单向稳定变应力时机械零件的疲劳强度计算
学习要求:
1. 了解疲劳曲线及极限应力曲线的来源,意义及用途, 能从材料的几个基本机械性能及零件的几何特性,绘 制零件的极限应力简化线图
2. 学会单向变应力时的强度计算方法 3. 了解疲劳损伤累积假说的意义及其应用
4. 学会双向变应力时的强度校核方法
学习重点:
极限应力线图的绘制及含义
强度准则是设计机械零件的最基本准则。
通用机械零件的强度分为静应力强度和变应力 强度两个范畴。
在机械零件整个工作寿命期间应力变化次数小 于103的通用零件,均按静应力强度进行设计。
即使是承受变应力的零件,在按疲劳强度进行 设计的同时,还有不少情况需要根据受载过程 中作用次数很少而数值很大的峰值载荷作静应 力强度校核。本章以下只讨论零件在变应力下的疲劳、低应力下 的脆断和接触强度等问题。
根据零件载荷的变化规律以及零件与相邻零件互相约 束情况的不同,可能发生的典型的应力变化规律通常 有下述三种:
a)变应力的应力比保持不变,即r=C(例如绝大 多数转轴中的应力状态);
b)变应力的平均应力保持不变,即σm=C(例如 振动着的受载弹簧中的应力状态);
c)变应力的最小应力保持不变, σmin=C(例如 紧螺栓联接中螺栓受轴向变载荷时的应力状 态)。以下分别讨论这三种情况。
e 可用下式计算
e
K
1 K
2 1 0 0
(3 11)
Kσ——弯曲疲劳极限的综合影响系数
K
k
1
1
1
q
(3 12)
式中:kσ——零件的有效应力集中系数 εσ——零件的尺寸系数; βσ——零件的表面质量系数; βq——零件的强化系数。
(一)单向稳定变应力时机械零件的疲劳强度计算
机械设计第3章机械零件的强度

根据零件载荷的变化规律以及零件与相邻零件互相约 束情况的不同,可能发生的典型的应力变化规律通常 有下述三种:
a)变应力的应力比保持不变,即r=C(例如绝大 多数转轴中的应力状态);
b)变应力的平均应力保持不变,即σm=C(例如 振动着的受载弹簧中的应力状态);
c)变应力的最小应力保持不变, σmin=C(例如 紧螺栓联接中螺栓受轴向变载荷时的应力状 态)。以下分别讨论这三种情况。
(3—9)
直线CG的方程为
σa'+σm'=σs
(3—10)
式中:σae'——零件受循环弯曲应力时的极限应力幅; σme'——零件受循环弯曲应力时的极限平均应力; e ——零件受循环弯曲应力时的材料常数。
e 可用下式计算
e
K
1 K
2 1 0 0
(3 11)
Kσ——弯曲疲劳极限的综合影响系数
S a
ae a
1 m K a
对应于N点的极限应力由N2'点表示,它位于直线CG上,故 仍只按式(3—18)进行静强度计算,分析图3—7可知,凡是工 作应力点位于CGH区域内时,在σm=C的条件下,极限应力 统为屈服极限,也是只进行静强度计算。
3.σmin=C的情况
当σmin=C时,需找到一个其最小应力与零件工 作应力的最小应力相同的极限应力。因为
分别是: 1 K ae m e
1 K ae m
ae
1
m
K
m ax
ae
m e
1
m
K
m
1
K
K
m
Sca
lim
m ax max
1 (K ) m
K
也有文献上建议,在σm=C的情况下,按照应力幅来 校核零件的疲劳强度,即按应力幅求得安全系数计算 值为
第3章机械零件的强度第3章

3、发动机连杆横截面上的应力变化规律如图所示,则该变应力的应力比r
为 2。
(1)0.24;(2)-0.24;(3)-4.17;(4)4.17。
0
31.2N/mm2 t
-130N/mm2
4、发动机连杆横截面上的应力变化规律如题3图所示,则其应力幅a和平
均应力m分别为 2 。
(1)a = -80.6Mpa,m = 49.4Mpa;(2)a = 80.6Mpa,m = -49.4Mpa; (3)a = 49.4Mpa,m = -80.6Mpa;(4)a = -49.4Mpa,m = - 80.6Mpa。
200 100 2
150
200
a
50 0 min
-100
max
m
t
例2 已知:a= 80N/mm2,m=-40N/mm2 求:max、min、r、绘图。
解:
max m a 40 (80) 120
min m a 40 (80) 40 r min 40 1 max 120 3
a m s
说明CG‘直 线上任意点的最大应力达到了屈服极限应力。
当循环应力参数( σm,σa )落在OA’G’C以内时,
表示不会发生疲劳破坏。
σa
当应力点落在OA’G’C以外 时,一定会发生疲劳破坏。
A’
D’ G’
σ-1 σ0 /2
而正好落在A’G’C折线上 时,表示应力状况达到疲 劳破坏的极限值。
(1)专用零件和部件;(2)在高速、高压、环境温度过高或过低 等特殊条件下工作的以及尺寸特大或特小的通用零件和部件;(3) 在普通工作条件下工作的一般参数的通用零件和部件;(4)标准化 的零件和部件。
机械设计第03章 机械零件的强度

的受载弹簧应力状态) 的受载弹簧应力状态)
• • •
• •
当σm =C时,需找到一个其平均应力与零件工作应力的平均 时 应力相同的极限应力。 应力相同的极限应力。 在图3- 中 作平行线MM’2(或NN’2),则该 ),则该 在图 -7中,过M(或N)点,作平行线 或 ) 线上的任何点所代表的应力循环都具有相同的平均应力值。 线上的任何点所代表的应力循环都具有相同的平均应力值。 σ 联解MM’2和AG两直线方程,求出 2的坐标的: me 、 σ ′ 两直线方程, 联解 两直线方程 求出M’ 的坐标的: ′ ae 点的疲劳极限应力: 则M点的疲劳极限应力: 点的疲劳极限应力 ψσ σ −1 + ( K σ − ψ σ )σ m ′ ′ ′ σ max = σ ae + σ me = σ −1e + σ m (1 − )= Kσ Kσ σ −ψ σ ′ σ ae = −1 σ m 零件的极限应力幅: 零件的极限应力幅: Kσ 计算安全系数: 计算安全系数:
•
E1、E2--为零件1、零件2材料的弹性模量。
在接触点、线连续改变位置时,显然 对于零件上任一点处的接触应力只能在 0~σH之间变化。 • 接触应力是脉动循环变应力。 • 在作接触疲劳计算时,极限应力也应 是脉动循环的极限接触应力。 •
总结: 1.材料的极限应力线图帮助我们了解零件的失 效的可能形式,要记住三个区域的意义,它是 讨论其它线图的基础。 σ−1 2.Sca = ≥ S 适用于各种循环特性的疲劳破坏。
§3-1 材料的疲劳特性
• 材料疲劳特性描述:最大应力 σ max • 应力循环次数 N σ min • 应力比(循环特性) r = σ • 其它符号:极限平均应力 • 极限应力幅值 • • 材料屈服极限
• • •
• •
当σm =C时,需找到一个其平均应力与零件工作应力的平均 时 应力相同的极限应力。 应力相同的极限应力。 在图3- 中 作平行线MM’2(或NN’2),则该 ),则该 在图 -7中,过M(或N)点,作平行线 或 ) 线上的任何点所代表的应力循环都具有相同的平均应力值。 线上的任何点所代表的应力循环都具有相同的平均应力值。 σ 联解MM’2和AG两直线方程,求出 2的坐标的: me 、 σ ′ 两直线方程, 联解 两直线方程 求出M’ 的坐标的: ′ ae 点的疲劳极限应力: 则M点的疲劳极限应力: 点的疲劳极限应力 ψσ σ −1 + ( K σ − ψ σ )σ m ′ ′ ′ σ max = σ ae + σ me = σ −1e + σ m (1 − )= Kσ Kσ σ −ψ σ ′ σ ae = −1 σ m 零件的极限应力幅: 零件的极限应力幅: Kσ 计算安全系数: 计算安全系数:
•
E1、E2--为零件1、零件2材料的弹性模量。
在接触点、线连续改变位置时,显然 对于零件上任一点处的接触应力只能在 0~σH之间变化。 • 接触应力是脉动循环变应力。 • 在作接触疲劳计算时,极限应力也应 是脉动循环的极限接触应力。 •
总结: 1.材料的极限应力线图帮助我们了解零件的失 效的可能形式,要记住三个区域的意义,它是 讨论其它线图的基础。 σ−1 2.Sca = ≥ S 适用于各种循环特性的疲劳破坏。
§3-1 材料的疲劳特性
• 材料疲劳特性描述:最大应力 σ max • 应力循环次数 N σ min • 应力比(循环特性) r = σ • 其它符号:极限平均应力 • 极限应力幅值 • • 材料屈服极限
第三章机械零件的强度

lim rN
第三章 机械零件的强度
CD段代表有限寿命疲劳阶段,CD曲线上任何一点所
代表的疲劳极限,称为有限寿命疲劳极限,用 rN 表
示,脚标r表示该变应力的应力比,N表示应力循环次 数。
CD段可用下式来描述:
m rN
N
C
(NC N ND)
σmax
σB A
B C
N=1/4 103 104
m
max
2
a
、
r
0
σ r =-1
σ
σmax
r =0 σa
σmax σmin
σa σa
σa σm
o
to
σmin
t
3) 非对称循环变应力:
4)静应力:
r =+1 σ
σ =常数
o
t
m
min
min max m 、 r 1
第三章 机械零件的强度
二、材料的疲劳特性
变应力下,零件的损坏形式是疲劳断裂。
r m ax m a
试件的试验条件: 1)光滑、无应力集中源; 2)标准尺寸。
第三章 机械零件的强度
在作材料试验时,求出对称循环和脉动循环时的疲劳极限
1和 0 ,把这两个极限应力标在 m a 图上。在对称循环 中:
σa
对称循环疲劳极限可以
用纵坐标上的A’点表示。
疲劳断裂过程:
很多机械零件受变应力作用。即使变应力的 max b 或 s 。而变应力的每次循环也仍然会对零件造成轻微的损
伤。随应力循环次数的增加,当损伤累积到一定程度时, 零件表层产生微小裂纹;随着循环次数增加,微裂纹逐 渐扩展;当剩余材料不足以承受载荷时,突然脆性断裂。
第三章 机械零件的强度
CD段代表有限寿命疲劳阶段,CD曲线上任何一点所
代表的疲劳极限,称为有限寿命疲劳极限,用 rN 表
示,脚标r表示该变应力的应力比,N表示应力循环次 数。
CD段可用下式来描述:
m rN
N
C
(NC N ND)
σmax
σB A
B C
N=1/4 103 104
m
max
2
a
、
r
0
σ r =-1
σ
σmax
r =0 σa
σmax σmin
σa σa
σa σm
o
to
σmin
t
3) 非对称循环变应力:
4)静应力:
r =+1 σ
σ =常数
o
t
m
min
min max m 、 r 1
第三章 机械零件的强度
二、材料的疲劳特性
变应力下,零件的损坏形式是疲劳断裂。
r m ax m a
试件的试验条件: 1)光滑、无应力集中源; 2)标准尺寸。
第三章 机械零件的强度
在作材料试验时,求出对称循环和脉动循环时的疲劳极限
1和 0 ,把这两个极限应力标在 m a 图上。在对称循环 中:
σa
对称循环疲劳极限可以
用纵坐标上的A’点表示。
疲劳断裂过程:
很多机械零件受变应力作用。即使变应力的 max b 或 s 。而变应力的每次循环也仍然会对零件造成轻微的损
伤。随应力循环次数的增加,当损伤累积到一定程度时, 零件表层产生微小裂纹;随着循环次数增加,微裂纹逐 渐扩展;当剩余材料不足以承受载荷时,突然脆性断裂。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、应力(stress)
工作应力(working stress) 材料某个机械 性能极限值 计算应力( calculated stress) 按材料力学公式 用σca表示 求出的作用在零 极限应力( ultimate stress ) 按一定的强度 计算应力允许 件剖面上的应力 理论求出的与 达到的最大值 用σlim 表示 单向拉伸同等 强度极限σB,屈服极限σS,疲劳极限σr 作用的应力 许用应力(allowable stress) 用[σ]表示
i 1 z i
应力由小到大作用
ni 1 i 1 N i
机械零件的强度
m rN N rm N0
1 m N1 N 0 ( ) , 1
1 N 0
m 1
1 m N 2 N0 ( ) , 2
z
N3
代入累计损伤公式得:
m (n1 1m n2 2 )
τa '和σa ' —同时作 1、对称循环稳定变应力 用的切向和法向应 A 零件上同时作用的法向及切 力幅的极限值 C'
向变应力σa和τa时,试验得 到的源自限应力关系式为:C1e
M'
M
2 2 ( ) ( ) 1 1e 1e
' a ' a
机械零件的强度
a 1e
lgσr C
N C
m rN
lgN
机械零件的强度
D
lgN0
lgND
lgN
循环基数N 0 对应的疲劳极限 rN 简写为σr 0 N D不大时, N 0= N D N D很大时, N 0< N D
σmax B C
任意循环N次的疲劳极限为:
rN r
m
D
N0 rKN N
103
104
3、零件的极限应力图
机械零件的强度
四、单向稳定变应力的机 械零件疲劳强度
1 、变应力的循环特性保持 不变(r=C)的情况 绝大多数转轴中的应力 状态。
1 r a max min C' 1 r m max min
A
σa
M1΄(σ ΄me、 σ ΄ae)
• 利用疲劳损伤累计假说进行计算。
机械零件的强度
每一次循环的损伤率:1/N n次循环的损伤率:n/N
ni i 1 N i
z
累计损伤率为:
各应力幅无大的差别 z ni 1 及强烈的短时过载 累计损伤率100%时, i 1 N i 材料发生疲劳破坏 z n i 为什么? N 1 应力由大到小作用
机械零件的强度
1 S K a m
机械零件的强度
七、提高机械零件疲劳强度的措施
在设计阶段就应考虑采取设计措施来提高 机械零件的疲劳强度: ①、尽可能降低应力集中; ②、选用疲劳强度高的材料; ③、选用能提高疲劳强度的热处理方法和强化 工艺;
④、提高机械零件表面的质量;
⑤、尽可能减小或消除零件表面可能发生的初 始裂纹尺寸。
N0 ND
N
式中:K N——寿命系数
机械零件的强度
对称循环变应力 : 脉动循环变应力 : 2、材料的极限应力图 平均应力σm平均应力 =0 σm=0.5σ0 最大应力σmax =σσ = σ + σ = σ a` 应力幅 σ = 0.5 σ max m a S ` 0 A G Ca折线为疲劳极限 OA的变应力 ´G´C 区域为安全区 静应力 : ' ' 1 平均应力 K ae σ = σ m me s 应力幅σa=0 ' ' s ae me
机械零件的强度
即σ—N给定的循环特性条 曲线 件下,应力循环次 AB段:静应力区间,B点 数 N 与疲劳极限 σ rN 对应的的应力循环次 之间的关 σ 系 曲 线 B 数大约为10 3; 疲劳曲线
max
C
BC段:随N的增大,σ max
下降,C点所对应的 N值大约为10 4,这种 破坏为应变疲劳,或 低周疲劳。
' max
1 ( K ) m 1e m (1 ) K K
安全系数计算值及强度条件
' 1 ( K ) m lim max S ca S max K ( a m )
静强度条件
m n i i i 1
N 0
m 1
1
不破坏的条件:
令计算应力为:
m m n N i i 0 1
ca m
机械零件的强度
1 z m n i i N 0 i 1
则
ca 1
1 Sca S ca
a
安全系数
六、双向稳定变应力时的疲劳强度
机械零件的强度 103 104 D
N0 ND
N
CD段:随N的增大,σmax下降较快,这阶段称为 有限寿命阶段,也称为高周疲劳。
D点以后:D点以后的曲线趋于水平,说明随N的 增多, σmax不再下降,即到无限寿命阶段,一 般工程材料的D点约为10 6~2510 7。 双对数坐标表示 m—与材料有关的常数 的疲劳曲线CD C—常数 段方程:
1 S K a m
静强度条件
s lim s S ca S max a m
a
A
M2’ D G M H O N2‘ N C σm
2 、变应力的平均应力保持 不变(σm=C)的情况 振动着的受载弹簧的应 力状态
机械零件的强度
M点的极限应力为
机械零件的强度
3、安全系数(safety factor)
安全系数
lim 极限应力与许 S [ ] 用应力的比值
lim 极限应力与计 安全系数计算值 S ca ca 算应力的比值 引入安全系数的原因:
① 应力计算时的载荷不精确性; ② 力学模型与实际状况的差异; ③ 材料机械性能的不均匀性; ④ 零件使用场合的重要性。
机械零件的强度
1e 又因为 S a
1e S a
Sca 2 Sca 2 S S 所以( ) ( ) 1 Sca 2 2 S S S S
2、非对称循环稳定变应力 先求出Sσ和Sτ,再求出计算安全系数Sca
1 S K a m
O
D
D'
B
M点的计算安全系数为:
OM ' OC ' OD' Sca OM OC OD
' OC' a 1e
a OC 1e
OD 1e
' ' a
a OD 1e
' 代入整理得: a Sca a
Sca a
' a
Sca a 2 Sca a 2 ( ) ( ) 1 1e 1e
b) 稳定循环变应力种类: γ = –1 ——对称循环变应力 -1< γ<+1——不对称循环变应力 γ =+1 —— 静应力
γ = 0 —— 脉动循环变应力
机械零件的强度
注意:静应力只能由静载荷产生,而变应力可能由变载荷产生, 也可能由静载荷产生
a O O t
a
t
3)名义应力和计算应力 名义应力——由名义载荷产生的应力
s s lim S ca S max a m
机械零件的强度
3 、变应力的最小应力保持 不变(min=C)情况 受轴向变载荷螺栓联接 的应力状态
σminM A
σa
M3’
M
J
G N N3‘
C
σm
σminN
σmin=σm-σa=C
M点的极限应力为
2 1 ( K ) min K
机械零件的强度
二、载荷的分类
静载荷
变载荷: 1)循环变载荷 a) 稳定循环变载荷 b) 不稳定循环变载荷 2)随机变载荷
载荷:1)名义载荷 P 2)计算载荷 PC
机械零件的强度
三、应力的分类
1、应力种类 静应力 变应力: 稳定循环变应力 不稳定变应力:
一个循环
O
t
O
t
规律性不稳定变应力
机械零件的强度
M1’ M N D G N1‘ C σm
M点的极限应力为
' max
' ae
' me
1 ( m a ) 1 max K a m K a m
机械零件的强度
安全系数计算值及强度条件
' max lim S ca max
机械零件的强度
( )
计算应力——由计算载荷产生的应力 ca ( ca )
四、变应力(variable stress)的强度计算
1、疲劳极限
衡量变应力的参数有
最大应力σmax( max) 循环特性 r 一定 最小应力 σmin ( min) 时, 力 循 环 平均应力 σ应 ( ) m N次后 ,m 材料 应力幅 σ发 a疲 )劳 破 不 生 a( 坏时的最 应 /σ 应力循环特性 r大 =σ min max 力 疲劳极限 用σrN 表示
随机变应力
2、稳定循环变应力的基本参数和种类 a) 基本参数 最大应力 最小应力 平均应力 应力幅 应力比(循环特 性)
max m a min m a
m max m
2 m a max 2
min max
1 1
对称循环弯曲疲劳极限 S 工作应力幅 应力幅的综合影响系数
机械零件的强度
工作应力(working stress) 材料某个机械 性能极限值 计算应力( calculated stress) 按材料力学公式 用σca表示 求出的作用在零 极限应力( ultimate stress ) 按一定的强度 计算应力允许 件剖面上的应力 理论求出的与 达到的最大值 用σlim 表示 单向拉伸同等 强度极限σB,屈服极限σS,疲劳极限σr 作用的应力 许用应力(allowable stress) 用[σ]表示
i 1 z i
应力由小到大作用
ni 1 i 1 N i
机械零件的强度
m rN N rm N0
1 m N1 N 0 ( ) , 1
1 N 0
m 1
1 m N 2 N0 ( ) , 2
z
N3
代入累计损伤公式得:
m (n1 1m n2 2 )
τa '和σa ' —同时作 1、对称循环稳定变应力 用的切向和法向应 A 零件上同时作用的法向及切 力幅的极限值 C'
向变应力σa和τa时,试验得 到的源自限应力关系式为:C1e
M'
M
2 2 ( ) ( ) 1 1e 1e
' a ' a
机械零件的强度
a 1e
lgσr C
N C
m rN
lgN
机械零件的强度
D
lgN0
lgND
lgN
循环基数N 0 对应的疲劳极限 rN 简写为σr 0 N D不大时, N 0= N D N D很大时, N 0< N D
σmax B C
任意循环N次的疲劳极限为:
rN r
m
D
N0 rKN N
103
104
3、零件的极限应力图
机械零件的强度
四、单向稳定变应力的机 械零件疲劳强度
1 、变应力的循环特性保持 不变(r=C)的情况 绝大多数转轴中的应力 状态。
1 r a max min C' 1 r m max min
A
σa
M1΄(σ ΄me、 σ ΄ae)
• 利用疲劳损伤累计假说进行计算。
机械零件的强度
每一次循环的损伤率:1/N n次循环的损伤率:n/N
ni i 1 N i
z
累计损伤率为:
各应力幅无大的差别 z ni 1 及强烈的短时过载 累计损伤率100%时, i 1 N i 材料发生疲劳破坏 z n i 为什么? N 1 应力由大到小作用
机械零件的强度
1 S K a m
机械零件的强度
七、提高机械零件疲劳强度的措施
在设计阶段就应考虑采取设计措施来提高 机械零件的疲劳强度: ①、尽可能降低应力集中; ②、选用疲劳强度高的材料; ③、选用能提高疲劳强度的热处理方法和强化 工艺;
④、提高机械零件表面的质量;
⑤、尽可能减小或消除零件表面可能发生的初 始裂纹尺寸。
N0 ND
N
式中:K N——寿命系数
机械零件的强度
对称循环变应力 : 脉动循环变应力 : 2、材料的极限应力图 平均应力σm平均应力 =0 σm=0.5σ0 最大应力σmax =σσ = σ + σ = σ a` 应力幅 σ = 0.5 σ max m a S ` 0 A G Ca折线为疲劳极限 OA的变应力 ´G´C 区域为安全区 静应力 : ' ' 1 平均应力 K ae σ = σ m me s 应力幅σa=0 ' ' s ae me
机械零件的强度
即σ—N给定的循环特性条 曲线 件下,应力循环次 AB段:静应力区间,B点 数 N 与疲劳极限 σ rN 对应的的应力循环次 之间的关 σ 系 曲 线 B 数大约为10 3; 疲劳曲线
max
C
BC段:随N的增大,σ max
下降,C点所对应的 N值大约为10 4,这种 破坏为应变疲劳,或 低周疲劳。
' max
1 ( K ) m 1e m (1 ) K K
安全系数计算值及强度条件
' 1 ( K ) m lim max S ca S max K ( a m )
静强度条件
m n i i i 1
N 0
m 1
1
不破坏的条件:
令计算应力为:
m m n N i i 0 1
ca m
机械零件的强度
1 z m n i i N 0 i 1
则
ca 1
1 Sca S ca
a
安全系数
六、双向稳定变应力时的疲劳强度
机械零件的强度 103 104 D
N0 ND
N
CD段:随N的增大,σmax下降较快,这阶段称为 有限寿命阶段,也称为高周疲劳。
D点以后:D点以后的曲线趋于水平,说明随N的 增多, σmax不再下降,即到无限寿命阶段,一 般工程材料的D点约为10 6~2510 7。 双对数坐标表示 m—与材料有关的常数 的疲劳曲线CD C—常数 段方程:
1 S K a m
静强度条件
s lim s S ca S max a m
a
A
M2’ D G M H O N2‘ N C σm
2 、变应力的平均应力保持 不变(σm=C)的情况 振动着的受载弹簧的应 力状态
机械零件的强度
M点的极限应力为
机械零件的强度
3、安全系数(safety factor)
安全系数
lim 极限应力与许 S [ ] 用应力的比值
lim 极限应力与计 安全系数计算值 S ca ca 算应力的比值 引入安全系数的原因:
① 应力计算时的载荷不精确性; ② 力学模型与实际状况的差异; ③ 材料机械性能的不均匀性; ④ 零件使用场合的重要性。
机械零件的强度
1e 又因为 S a
1e S a
Sca 2 Sca 2 S S 所以( ) ( ) 1 Sca 2 2 S S S S
2、非对称循环稳定变应力 先求出Sσ和Sτ,再求出计算安全系数Sca
1 S K a m
O
D
D'
B
M点的计算安全系数为:
OM ' OC ' OD' Sca OM OC OD
' OC' a 1e
a OC 1e
OD 1e
' ' a
a OD 1e
' 代入整理得: a Sca a
Sca a
' a
Sca a 2 Sca a 2 ( ) ( ) 1 1e 1e
b) 稳定循环变应力种类: γ = –1 ——对称循环变应力 -1< γ<+1——不对称循环变应力 γ =+1 —— 静应力
γ = 0 —— 脉动循环变应力
机械零件的强度
注意:静应力只能由静载荷产生,而变应力可能由变载荷产生, 也可能由静载荷产生
a O O t
a
t
3)名义应力和计算应力 名义应力——由名义载荷产生的应力
s s lim S ca S max a m
机械零件的强度
3 、变应力的最小应力保持 不变(min=C)情况 受轴向变载荷螺栓联接 的应力状态
σminM A
σa
M3’
M
J
G N N3‘
C
σm
σminN
σmin=σm-σa=C
M点的极限应力为
2 1 ( K ) min K
机械零件的强度
二、载荷的分类
静载荷
变载荷: 1)循环变载荷 a) 稳定循环变载荷 b) 不稳定循环变载荷 2)随机变载荷
载荷:1)名义载荷 P 2)计算载荷 PC
机械零件的强度
三、应力的分类
1、应力种类 静应力 变应力: 稳定循环变应力 不稳定变应力:
一个循环
O
t
O
t
规律性不稳定变应力
机械零件的强度
M1’ M N D G N1‘ C σm
M点的极限应力为
' max
' ae
' me
1 ( m a ) 1 max K a m K a m
机械零件的强度
安全系数计算值及强度条件
' max lim S ca max
机械零件的强度
( )
计算应力——由计算载荷产生的应力 ca ( ca )
四、变应力(variable stress)的强度计算
1、疲劳极限
衡量变应力的参数有
最大应力σmax( max) 循环特性 r 一定 最小应力 σmin ( min) 时, 力 循 环 平均应力 σ应 ( ) m N次后 ,m 材料 应力幅 σ发 a疲 )劳 破 不 生 a( 坏时的最 应 /σ 应力循环特性 r大 =σ min max 力 疲劳极限 用σrN 表示
随机变应力
2、稳定循环变应力的基本参数和种类 a) 基本参数 最大应力 最小应力 平均应力 应力幅 应力比(循环特 性)
max m a min m a
m max m
2 m a max 2
min max
1 1
对称循环弯曲疲劳极限 S 工作应力幅 应力幅的综合影响系数
机械零件的强度
