正弦余弦函数诱导公式

合集下载

正弦余弦的诱导公式

正弦余弦的诱导公式正弦和余弦的诱导公式是三角函数中非常重要的两个公式，它们描述了两个角的正弦和余弦之间的关系。

通过这些公式，我们可以使用已知角的正弦或余弦来求解其他角度的正弦和余弦值，从而在三角函数中起到了非常关键的作用。

首先，我们先来看正弦的诱导公式。

对于一个角度为θ的三角形，假设角θ的对边长度为b，斜边长度为c。

根据三角形的定义可以知道：sin(θ) = b/c接下来我们使用勾股定理，即c²=a²+b²，其中a表示角度为θ的三角形的邻边长度。

将c²=a²+b²代入上式，可以得到：sin(θ)= b/√(a² + b²)我们知道，正弦函数是一个周期性函数，且满足-sin(θ) = sin(180° + θ)。

因此，对于角度大于90°的情况，可以通过此公式来计算正弦值。

根据逆三角函数的定义，我们还可以推导出：sin(180° - θ) = sin(θ)这就是正弦的诱导公式，它描述了正弦函数的周期性和对称性。

接下来，我们来看余弦的诱导公式。

同样考虑一个角度为θ的三角形，对于角度大于90°的情况，我们可以使用余弦函数来表示。

余弦函数定义为：cos(θ) = a/c假设角θ的邻边长度为a，斜边长度为c。

利用勾股定理可以得到：cos(θ) = a/√(a² + b²)由余弦函数的周期性和对称性，我们可以推导出：cos(-θ) = cos(θ)cos(180° - θ) = -cos(θ)cos(180° + θ) = -cos(θ)这些公式描述了余弦函数的周期性和对称性。

通过正弦和余弦的诱导公式，我们可以求解其他角度的正弦和余弦值。

例如，对于sin(30°)，我们可以使用sin(90° - 30°) = sin(60°) = √3/2来求解。

三角函数诱导公式大全

三角函数诱导公式大全1.正弦函数诱导公式：正弦函数的诱导公式是通过余弦函数定义和平方性质得到的。

sin^2A + cos^2A = 1根据这个公式，我们可以得到以下诱导公式：sin(-A) = -sinAsin(A ± B) = sinA cosB ± cosA sinBsin2A = 2sinAcosAsin3A = 3sinA - 4sin^3A2.余弦函数诱导公式：余弦函数的诱导公式是通过正弦函数定义和平方性质得到的。

sin^2A + cos^2A = 1根据这个公式，我们可以得到以下诱导公式：cos(-A) = cosAcos(A ± B) = cosA cosB - sinA sinBcos2A = cos^2A - sin^2A = 2cos^2A - 1 = 1 - 2sin^2Acos3A = 4cos^3A - 3cosA3.正切函数诱导公式：正切函数的诱导公式是通过正弦函数和余弦函数诱导公式得到的。

tanA = sinA / cosA根据正弦函数和余弦函数诱导公式，我们可以得到以下诱导公式：tan(-A) = -tanAta n(A ± B) = (tanA ± tanB) / (1 ∓ tanA tanB)tan2A = 2tanA / (1 - tan^2A)tan3A = (3tanA - tan^3A) / (1 - 3tan^2A)4.余切函数诱导公式：余切函数的诱导公式是通过正切函数的诱导公式得到的。

cotA = 1 / tanA根据正切函数的诱导公式，我们可以得到以下诱导公式：cot(-A) = -cotAcot(A ± B) = (cotA cotB ∓ 1) / (cotB ± cotA)cot2A = (1 - tan^2A) / 2tanAcot3A = (3cotA - cot^3A) / (cot^2A - 3)5.正割函数诱导公式：正割函数的诱导公式是通过余弦函数的诱导公式得到的。

正弦余弦公式总结

正弦余弦公式总结正弦余弦公式总结1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(2π-a)=cos(a)cos(2π-a)=sin(a)sin(2π+a)=cos(a)cos(2π+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)tgA=tanA=sinAcosA2.两角和与差的三角函数sin(a+b)=sin(a)cos(b)+cos(α)sin(b)cos(a+b)=cos(a)cos(b)-sin(a)sin(b)sin(a-b)=sin(a)cos(b)-cos(a)sin(b)cos(a-b)=cos(a)cos(b)+sin(a)sin(b)tan(a+b)=[tan(a)+tan(b)]/[1-tan(a)tan(b)] tan(a-b)=[tan(a)-tan(b)]/[1+tan(a)tan(b)]3.和差化积公式sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)4.积化和差公式(上面公式反过来就得到了)sin(a)sin(b)=-1/2* [cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2* [cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2* [sin(a+b)+sin(a-b)]cos(a)sin(b)=1/2* [sin(a+b)-sin(a-b)]5.二倍角公式sin(2a)=2sin(a)cos(a)cos(2a)=cos2(a)-sin2(a)=2cos2(a)-1=1-2sin2(a) 6.半角公式2sin2(a/2)=1-cos(a)2cos2(a/2)=1+cos(a)tan(a/2)=[1-cos(a)]/sin(a)=sina/[1+cos(a)] tan2(a/2)= [1-cos(a)]/[1+cos(a)]7.万能公式sin(a)=2tan(a/2)/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=2tan(a/2)/[1-tan2(a/2)]8.其它公式(推导出来的)a*sin(a)+b*cos(a)=sin(a+c) 其中tan(c)=b/a a*sin(a)-b*cos(a)=cos(a-c) 其中tan(c)=a/b 1+sin(a)=(sin(a/2)+cos(a/2))21-sin(a)=(sin(a/2)-cos(a/2))2三、正弦定理:a/sinA=b/sinB=c/sinC=2R其中R是三角形外接圆半径正弦定理可以解决下列三角问题：①已知两角和任一边，求其它两边和一角。

三角函数的诱导公式

三角函数的诱导公式1.正弦函数和余弦函数的诱导公式：正弦函数和余弦函数是最基本的三角函数，它们之间存在一个非常重要的诱导公式：sin(π/2 - θ) = cos(θ)这个公式告诉我们，如果将一个角的余角代入正弦函数，得到的结果是对应角的余弦函数。

通过这个公式，我们可以推导出一些其他的三角函数的诱导公式。

2.正切函数的诱导公式：正切函数是正弦函数和余弦函数的商：tan(θ) = sin(θ) / cos(θ)通过将正弦函数和余弦函数的诱导公式代入，我们可以得到正切函数的诱导公式：tan(θ) = sin(θ) / cos(θ) = cos(π/2 - θ) / sin(π/2 - θ)这个公式告诉我们，如果将一个角的余角代入正切函数，得到的结果是对应角的余切函数的倒数。

3.余切函数的诱导公式：余切函数是正切函数的倒数：cot(θ) = 1 / tan(θ) = cos(θ) / sin(θ)通过将正弦函数和余弦函数的诱导公式代入，我们可以得到余切函数的诱导公式：cot(θ) = 1 / tan(θ) = 1 / [cos(π/2 - θ) / sin(π/2 - θ)] = sin(π/2 - θ) / cos(π/2 - θ)这个公式告诉我们，如果将一个角的余角代入余切函数，得到的结果是对应角的正切函数的倒数。

4.正弦函数和余弦函数的平方和差公式：sin(θ ± ϕ) = sin(θ)cos(ϕ) ± cos(θ)sin(ϕ)cos(θ ± ϕ) = cos(θ)cos(ϕ) ∓ sin(θ)sin(ϕ)这两个公式称为正弦函数和余弦函数的平方和差公式，它们揭示了正弦函数和余弦函数的和角和差角的关系。

通过这两个公式，我们可以将任意两个角的和、差转化为正弦函数和余弦函数的乘积，从而进行更复杂的运算。

这里的正弦函数和余弦函数的平方和差公式可以通过三角函数的诱导公式和欧拉公式来证明。

正弦和余弦的诱导公式

①sin(180°+α)=sinαcos(180°+α)=cosα②sin(-α) = -sinα cos(-α) = cosα1,利用单位圆表示任意角α的正弦值和余弦值xyoP(x,y)(1,0)．α的终边．yxoP(x,y)(1,0)．α的终边．xyoP(x,y)(1,0)．α的终边．xyoP(x,y)(1,0)．α的终边．如左图，由定义，都有：sinα= y cosα= x1,利用单位圆表示任意角α的正弦值和余弦值xyoP(x,y)(1,0)．α的终边．yxoP(x,y)(1,0)．α的终边．如左图，由定义，都有：sinα= y cosα= x2,诱导公式一及其用途sin(α+k·360°) = sinαcos(α+k·360°) = cosαtan(α+k·360°) = tanα 其中k ∈Z任意角的三角函数值公式一的用途0 °~ 360 °角的三角函数值本单元的内容0 °~ 90 °角的三角函数值（1）0 °~ 90 °角的正弦值、余弦值用何法可求得？（2）90 °~ 360 °的角β能否与锐角α相联系？设0°≤α≤90 °，那么，对于90°~ 180 °间的角，可表示成：180 °-α;180°~ 270 °间的角，可表示成：180 °+α;270°~ 360 °间的角，可表示成：360 °-α;（1）锐角α的终边与180 °+α角的终边，位置关系如何？（2）任意角α与180 °+α呢？yxoP(x,y)(1,0)．α的终边．xyoP(x,y)(1,0)．α的终边．α180 °+α的终边180 °+α的终边．P’．P’由分析可得：角α180 °+α终边关系关于原点对称点的关系P(x,y)P’(-x,-y)函数关系sinα= ycosα= xsin(180 °+α)= -ycos(180 °+α)= -x因此，可得：sin(180 °+α) = -sinαcos(180 °+α) = -cosα公式二2，同理可研究-α与α的三角函数值的关系yxoP(x,y)(1,0)．α的终边．-α的终边．P’角α-α终边关系关于X 轴对称点的关系P(x,y)P’(x,-y)函数关系sinα= y cosα= xsin(-α) = -y cos(-α) = x因此，可得：sin(-α) = -sinαcos(-α) = cosα公式三sin(180 °+α) = -sinαcos(180 °+α) = -cosα公式二：公式二与公式三的成立条件，以及它们的特点，用途。

三角函数的诱导公式知识点

三角函数的诱导公式知识点三角函数的诱导公式是数学中关于三角函数之间的一组等式，通过这组等式可以在不依赖计算器或表格的情况下直接计算出一些角度的三角函数值，从而简化计算。

诱导公式的基本思想是通过将一个角度的三角函数转化为另一个角度的三角函数来求解。

一、正弦和余弦的诱导公式：根据正弦函数和余弦函数的定义，对于任意角度θ，有：sin θ = y/rcos θ = x/r其中，x，y，r代表直角三角形中的边长。

利用勾股定理可以得到x²+y²=r²。

现在考虑角度θ+90°，即sin(θ+90°)和cos(θ+90°)的值。

根据正弦函数和余弦函数的定义，有：sin(θ+90°) = y’/rcos(θ+90°) = x’/r其中，x’，y’，r由右边角相等可知。

然后考虑直角三角形中的边长关系：y’=xx’=-y(由右边角相等，即90°+(-θ))代入sin(θ+90°)和cos(θ+90°)，得到：sin(θ+90°) = x/r，即sin(θ+90°) = cosθcos(θ+90°) = -y/r，即cos(θ+90°) = -si nθ得到正弦的诱导公式：sin(θ+90°) = cosθ；得到余弦的诱导公式：cos(θ+90°) = -sinθ。

利用这两个诱导公式，我们可以在计算中互相转化正弦和余弦的值。

二、正切和余切的诱导公式：正切和余切的定义是：tan θ = sin θ / cos θcot θ = cos θ / sin θ。

根据正弦和余弦的诱导公式，我们可以得到：sin(θ+90°) = cosθcos(θ+90°) = -sinθ。

将这两个式子带入正切和余切的定义，有：tan(θ+90°) = sin(θ+90°) / cos(θ+90°) = cosθ / (-sinθ) = -cotθcot(θ+90°) = cos(θ+90°) / sin(θ+90°) = (-sinθ) /cosθ = -tanθ。

三角函数的诱导公式

三角函数的诱导公式三角函数的诱导公式是指通过一些基本的三角函数值，推导出其他三角函数的值的公式。

这些基本的三角函数包括正弦函数、余弦函数和正切函数。

在证明三角函数的诱导公式时，可以运用几何图形、代数运算以及三角函数的定义等方法。

首先，我们来讨论正弦函数和余弦函数的诱导公式。

假设在单位圆上，角A对应的弧度为θ，其坐标为(x,y)，则可以得到以下关系式：x = cosθy = sinθ我们可以通过单位圆的对称性，得到以下诱导公式：1. sin(-θ) = -sinθ证明：设角B为-A，对应的弧度为-θ，其坐标为(-x,y)。

由对称性可知，-x = cos(-θ) = cosθ，y=sin(-θ)。

所以，sin(-θ) = -sinθ。

2. sin(π-θ) = sinθ证明：设角C为π-A，对应的弧度为π-θ，其坐标为(-x,-y)。

由对称性可知，-x = cos(π-θ) = cosθ，-y = sin(π-θ)。

所以，sin(π-θ) = sinθ。

3. sin(θ+π) = -sinθ证明：设角D为A+π，对应的弧度为θ+π，其坐标为(-x,-y)。

由对称性可知，-x = cos(θ+π) = -cosθ，-y = sin(θ+π)。

所以，sin(θ+π) = -sinθ。

通过这些诱导公式，我们可以计算任意角度的正弦函数值，而不仅仅局限于0到π的范围。

接下来，我们来讨论正弦函数和余弦函数的平方和公式和差公式。

1. sin²θ + cos²θ = 1证明：根据单位圆上坐标的定义，可以得到(x,y)² = x² + y² = cos²θ + sin²θ = 1、所以，sin²θ + cos²θ = 12. cos(θ±φ) = cosθcosφ - sinθsinφ证明：设角A对应的弧度为θ，角B对应的弧度为φ。

正弦余弦公式总结

1.诱导公式sin(-a）=—sin(a)cos（-a)=cos（a）sin(2π-a）=cos（a）cos（2π-a)=sin(a)sin(2π+a)=cos（a）cos(2π+a)=—sin(a)sin（π-a)=sin(a)cos(π—a）=—cos(a)sin(π+a)=—sin（a)cos(π+a)=-cos(a)tgA=tanA=sinAcosA2.两角和与差的三角函数sin(a+b）=sin（a）cos（b)+cos(α)sin（b）cos(a+b)=cos（a)cos（b）-sin（a）sin（b）sin（a-b)=sin(a)cos（b)-cos(a）sin(b)cos(a-b）=cos（a)cos(b)+sin（a）sin(b)tan（a+b）=[tan(a)+tan(b)］/[1—tan(a)tan(b）] tan（a—b)=［tan(a）—tan（b)]/［1+tan(a)tan(b)］3。

和差化积公式sin(a)+sin(b）=2sin((a+b）/2）cos（（a-b)/2)sin（a)−sin（b）=2cos（（a+b）/2)sin((a-b）/2)cos(a)+cos(b）=2cos（(a+b)/2）cos((a—b）/2）cos(a)-cos(b）=—2sin（(a+b）/2)sin(（a-b)/2）4。

积化和差公式(上面公式反过来就得到了）sin(a)sin(b)=-1/2＊[cos（a+b)-cos(a-b)]cos（a)cos（b)=1/2* ［cos（a+b)+cos(a-b）]sin(a）cos（b)=1/2＊［sin(a+b)+sin(a-b）］cos（a）sin(b）=1/2* [sin（a+b)—sin(a-b)］5.二倍角公式sin（2a)=2sin(a)cos(a)cos（2a）=cos2(a）-sin2(a）=2cos2(a）—1=1—2sin2（a)6.半角公式2sin2（a/2）=1-cos(a）2cos2(a/2)=1+cos（a）tan(a/2）=［1-cos（a)]/sin(a)=sina/[1+cos（a)]tan2(a/2）= ［1-cos(a）］/[1+cos（a）］7。

三角函数的8个诱导公式(汇总)

三角函数的8个诱导公式（汇总）三角函数的8个诱导公式1. 正弦函数的诱导公式sin(-x) = -sin(x)这个公式表明，正弦函数的值在x轴上是关于原点对称的。

也就是说，如果一个角度的正弦值为a，那么它的相反数的正弦值就是-a。

这个公式在解三角形问题时非常有用，为它可以帮助我们计算负角度的正弦值。

2. 余弦函数的诱导公式cos(-x) = cos(x)这个公式表明，余弦函数的值在y轴上是关于原点对称的。

也就是说，如果一个角度的余弦值为a，那么它的相反数的余弦值也是a。

这个公式同样也可以帮助我们计算负角的余弦值。

3. 正切函数的诱导公式tan(-x) = -tan(x)这个公式表明，正切函数的值在原点上是关于y轴对称的。

也就是说，如果一个角的正切值为a，那么它的相反数的正切值就是-a。

这个公式在计算负角的正切值时非常有用。

4. 余切函数的诱导公式cot(-x) = -cot(x)这个公式表明，余切函数的值在原点上是关于x轴对称的。

也就是说，如果一个角的余切值为a，那么它的相反数的余切值就是-a。

这个公式同样也可以帮助我们计算负角的余切值。

5. 正弦函数的平方的诱导公式sin^2(x) + cos^2(x) = 1这个公式是三角函数中最著名的公式之一，它表明正弦函数的平方加上余弦函数的平方等于1。

这个公式在解三角形问题时非常有用，为它可以帮助我们计算三角形中的未知边长。

6. 正切函数的平方的诱导公式tan^2(x) + 1 = sec^2(x)这个公式表明，正切函数的平方加1等于其对应的正割函数的平方。

这个公式在计算三角形中的未知边长时非常有用。

7. 余切函数的平方的诱导公式cot^2(x) + 1 = csc^2(x)这个公式表明，余切函数的平方加1等于其对应的余割函数的平方。

这个公式同样也可以帮助我们计算三角形中的未知边长。

8. 正弦函数和余弦函数的诱导公式sin(x + π/2) = cos(x)cos(x + π/2) = -sin(x)这两个公式表明，正弦函数和余弦函数之间存在一种特殊的关系，即它们的相位差为π/2。

数学三角函数诱导公式

数学三角函数诱导公式三角函数诱导公式是指通过已知的三角函数关系，推导出其他三角函数之间的关系的公式。

它们在解决三角函数相关问题时非常重要，可以简化计算，并扩展了三角函数的应用。

下面介绍常见的三角函数诱导公式。

一、正弦函数与余弦函数的诱导公式1.1诱导公式1：根据勾股定理，我们可以得到sin^2(x) + cos^2(x) = 1从上面的公式可以推导出以下诱导公式：sin^2(x) = 1 - cos^2(x)cos^2(x) = 1 - sin^2(x)1.2诱导公式2：根据正弦和余弦的定义，可得到以下诱导公式：sin(π/2 - x) = cos(x)cos(π/2 - x) = sin(x)1.3诱导公式3：利用双曲线法，可以得到以下诱导公式：sin(ix) = i*sinh(x)cos(ix) = cosh(x)二、正切函数的诱导公式2.1诱导公式4：利用正弦和余弦的定义，可得到以下诱导公式：tan(x) = sin(x)/cos(x)2.2诱导公式5：利用诱导公式1和诱导公式4，可以得到以下诱导公式：tan^2(x) = 1 - cos^2(x)/sin^2(x)2.3诱导公式6：利用诱导公式2和诱导公式4，可以得到以下诱导公式：tan(π/2 - x) = 1/tan(x)三、余切函数的诱导公式根据正切的定义，我们可以得到以下诱导公式：cot(x) = 1/tan(x)四、割函数和余割函数的诱导公式根据正弦、余弦和正切的定义sec(x) = 1/cos(x)csc(x) = 1/sin(x)诱导公式的应用：1.在三角函数的计算中，利用诱导公式可以简化计算步骤，提高计算的速度和准确性。

2.在三角函数的图像分析中，利用诱导公式可以推导出其他函数的图像，帮助理解和描述函数的性质。

3.在解决三角函数相关问题中，利用诱导公式可以将问题转化为更简单的形式，从而得到更方便的解法。

综上所述，三角函数诱导公式是数学中重要的工具，它们扩展了三角函数的应用领域，帮助我们更好地理解和应用三角函数。

三角函数诱导公式正弦定理余弦定理基本公式

三角函数诱导公式正弦定理余弦定理基本公式1.三角函数诱导公式：正弦诱导公式：sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)余弦诱导公式：cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)正切诱导公式：tan(a ± b) = (tan(a) ± tan(b))/(1 ∓ tan(a)tan(b))这些诱导公式可以用来简化计算，将三角函数的运算转化为其他三角函数的运算，从而简化复杂的计算过程。

2.正弦定理：正弦定理用于求解具有三个边的三角形的角度。

根据正弦定理，三角形的三个边的比例等于其对应角度的正弦值的比例。

正弦定理的公式如下：a/sin(A) = b/sin(B) = c/sin(C)其中，a、b、c为三角形的三个边的长度，A、B、C为对应的三个角的度数。

正弦定理可以通过三边求角、两边一角求边等问题中使用。

3.余弦定理：余弦定理用于求解具有三个边或两边一角的三角形的边长。

根据余弦定理，三角形的一个边的平方等于另外两边的平方的和减去这两边长度的乘积与这两边所夹角的余弦值的两倍的乘积。

余弦定理的公式如下：c² = a² + b² - 2abcos(C)其中，a、b、c为三角形的三个边的长度，C为夹在a、b之间的角的度数。

余弦定理可以通过三边求角、两边一角求边等问题中使用。

4.基本三角函数公式：基本三角函数公式包括正弦、余弦、正切的定义和性质。

正弦公式：sin(a) = opposite/hypotenuse = a/c余弦公式：cos(a) = adjacent/hypotenuse = b/c正切公式：tan(a) = opposite/adjacent = a/b其中，a、b为直角三角形的两个直角边的长度，c为斜边的长度。

这些基本公式在解决直角三角形问题中非常常用。

三角公式总结正弦定理余弦定理诱导公式二倍角公式半角公式积化和差公式和差化积公式

三角公式总结正弦定理余弦定理诱导公式二倍角公式半角公式积化和差公式和差化积公式三角公式是解决三角形问题的基本工具，包括正弦定理、余弦定理、诱导公式、二倍角公式、半角公式、积化和差公式和和差化积公式等。

下面我们详细介绍这些公式。

1. 正弦定理（Sine Rule）：在一个三角形ABC中，边长a、b、c与其对应的角A、B、C满足如下关系：a/sinA = b/sinB = c/sinC这个公式可以用于求解已知三角形任意两边及其夹角，求解三角形内外角和的问题。

2. 余弦定理（Cosine Rule）：在一个三角形ABC中，边长a、b、c 与其对应的角A、B、C满足如下关系：a^2 = b^2 + c^2 - 2bc*cosAb^2 = a^2 + c^2 - 2ac*cosBc^2 = a^2 + b^2 - 2ab*cosC这个公式可以用于求解已知三角形两边及其夹角，求解三角形内外角和的问题。

3. 诱导公式（Tangent Addition Formula）：对于角A和角B，有如下关系：tan(A+B) = (tanA + tanB) / (1 - tanA*tanB)tan(A-B) = (tanA - tanB) / (1 + tanA*tanB)这个公式可以用于求解角的和与差的正切值。

4. 二倍角公式（Double Angle Formula）：对于角A，有如下关系：sin(2A) = 2*sinA*cosAcos(2A) = cos^2(A) - sin^2(A)tan(2A) = 2*tanA / (1 - tan^2(A))这个公式可以用于求解角的两倍角的正弦、余弦和正切值。

5. 半角公式（Half Angle Formula）：对于角A，有如下关系：sin(A/2) = ±√[(1 - cosA) / 2]cos(A/2) = ±√[(1 + cosA) / 2]tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]这个公式可以用于求解角的半角的正弦、余弦和正切值。

三角函数诱导公式总结

三角函数诱导公式总结三角函数诱导公式是指将一个三角函数的一个角度用另外一个角度的三角函数表示的公式。

它们是三角函数的基本性质，可以用于简化计算和推导其他三角函数的性质。

在这篇文章中，我们将总结常见的三角函数诱导公式，并给出相关推导和示例。

一、正弦函数的诱导公式正弦函数的诱导公式是：sin(A + B) = sinAcosB + cosAsinB这个公式可以通过将A角和B角的正弦函数展开，然后利用三角函数的加法关系来推导得到。

例1：证明sin(A + B) = sinAcosB + cosAsinB解：我们知道sin(A + B)是一个由A和B两个角度组成的三角函数，我们要将它转化为一个由单个角度表示的三角函数。

首先，我们展开sin(A + B)的定义：sin(A + B) = sinAcosB + cosAsinB这样，我们就得到了sin(A + B)的诱导公式。

二、余弦函数的诱导公式余弦函数的诱导公式是：cos(A + B) = cosAcosB - sinAsinB这个公式可以通过将A角和B角的余弦函数展开，然后利用三角函数的加法关系来推导得到。

例2：证明cos(A + B) = cosAcosB - sinAsinB解：我们知道cos(A + B)是一个由A和B两个角度组成的三角函数，我们要将它转化为一个由单个角度表示的三角函数。

首先，我们展开cos(A + B)的定义：cos(A + B) = cosAcosB - sinAsinB这样，我们就得到了cos(A + B)的诱导公式。

三、正切函数的诱导公式正切函数的诱导公式是：tan(A + B) = (tanA + tanB) / (1 - tanAtanB)这个公式可以通过将A角和B角的正切函数展开，然后利用三角函数的加法关系来推导得到。

例3：证明tan(A + B) = (tanA + tanB) / (1 - tanAtanB)解：我们知道tan(A + B)是一个由A和B两个角度组成的三角函数，我们要将它转化为一个由单个角度表示的三角函数。

三角函数诱导公式大全

三角函数诱导公式大全(1).正弦定理：a²=b²+c²–2bc·cosAb²=a²+c²–2ac·cosBc²=a²+b²–2ab·cosC(2).余弦定理：a/cosA=b/cosB=c/cosC(3).正切定理：a·tanA=b·tanB=c·tanC(4).正弦函数诱导公式：sin(A+B)=sinA·cosB+cosA·sinBsin(A-B)=sinA·cosB-cosA·sinBsin(2A)=2sinA·cosAsin(-A)=-sinAcos(A+B)=cosA·cosB-sinA·sinBcos(A-B)=cosA·cosB+sinA·sinBcos(2A)=cos²A-sin²Acos(-A)=cosA(5).余弦函数诱导公式：cos(A+B)=cosA·cosB-sinA·sinBcos(A-B)=cosA·cosB+sinA·sinBcos(2A)=cos²A-sin²Acos(-A)=cosAsin(A+B)=sinA·cosB+cosA·sinBsin(A-B)=sinA·cosB-cosA·sinBsi n(2A)=2sinA·cosAsin(-A)=-sinA(6).正切函数诱导公式：tan(A+B)= (tanA+tanB)(1–tanA·tanB) tan(A-B)= (tanA–tanB)(1+tanA·tanB) tan(2A)=2tanA/(1–tan²A)tan(-A)=-tanA(7).反正弦函数诱导公式：arcsinX=arcsinpx+2nπarccosX=π/2+arcsinpx+2nπarctanX=arctanpx+2nπ(8).反余弦函数诱导公式：arcsinX=π/2-arccosXarccosX=arccospx+2nπarctanX=π/2+arccospx+2nπ(9).反正切函数诱导公式：arcsinX=arctanX+2nπarccosX=π/2-arctanX+2nπarctanX=arctanpx+2nπ(10).双曲正弦函数诱导公式：sinhA=sinhpA+2nπcoshA=coshpA+2nπtanhA=tanhpA+2nπ(11).反双曲正弦函数诱导公式：arcsinhX=arcsinhpX+2nπarccoshX=arccoshpX+2nπ。

三角函数的诱导公式与应用

三角函数的诱导公式与应用三角函数是数学中非常重要的概念，广泛应用于物理、工程等领域。

为了推导和简化三角函数之间的关系，人们发现了许多有用的公式，称之为三角函数的诱导公式。

本文将介绍三角函数的诱导公式以及其应用。

一、正弦函数与余弦函数的诱导公式1. 正弦函数的诱导公式正弦函数的诱导公式是通过将一个角的正弦函数表示成另一个角的正弦函数来简化计算。

假设有两个角A和B，它们满足以下关系：A = π/2 - B。

则有以下诱导公式：sin(A) = sin(π/2 - B) = cos(B)通过正弦函数的诱导公式，我们可以将一个角的正弦函数转化为另一个角的余弦函数。

这在计算中十分有用。

2. 余弦函数的诱导公式余弦函数的诱导公式是通过将一个角的余弦函数表示成另一个角的余弦函数来简化计算。

同样假设有两个角A和B，它们满足以下关系：A = π/2 - B。

则有以下诱导公式：cos(A) = cos(π/2 - B) = sin(B)通过余弦函数的诱导公式，我们可以将一个角的余弦函数转化为另一个角的正弦函数。

这在解决问题时非常有用。

二、正切函数的诱导公式与倒数公式1. 正切函数的诱导公式正切函数的诱导公式是通过将一个角的正切函数表示成其他两个角的正切函数之商来简化计算。

假设有两个角A和B，它们满足以下关系：A = π/2 - B。

则有以下诱导公式：tan(A) = tan(π/2 - B) = 1/tan(B)通过正切函数的诱导公式，我们可以将一个角的正切函数表示成其他两个角的正切函数之商。

这在解决实际问题时非常有用。

2. 正切函数的倒数公式正切函数的倒数公式是通过将一个角的正切函数的倒数表示成该角的余切函数来简化计算。

假设有一个角A，那么有以下倒数公式：1/tan(A) = cot(A)通过正切函数的倒数公式，我们可以将正切函数的倒数转化为余切函数，进一步简化计算。

三、三角函数的应用三角函数的诱导公式在物理、工程等领域有着广泛的应用。

正弦余弦的诱导公式

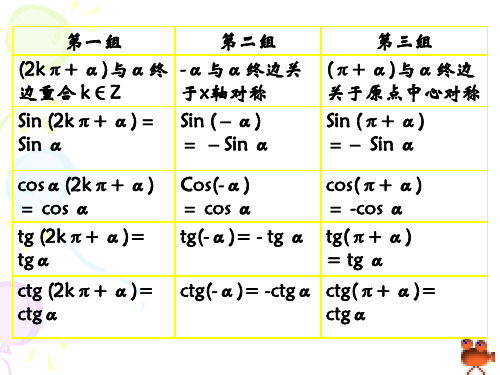
解:原式
( sin )( cos )
( cos ) sin( )[ sin( )]

sin cos
( cos ) sin [( sin )]
1
s in
例4 填写下表

2 4 5 7
33 3
33
sin 3 2
3 2
=-
Sin
π 4
Cos
3π 19
∵
π 4
，319π 都是第一象限角。
∴原式值为负。
（3） ∵11弧度≈11×57.30= 630.30
5弧度≈5×57.30= 286.50
Sin11 -Cos5≈ Sin 630.30 -Cos286.50 = Sin 89.70 -Cos73.50
89.70 ＞450 ∴ Sin89.70 ＞ Sin450 = 2
另一类诱导公式
第一组
第二组
sin(π/2－α)=cosα sin(π/2+α)=cosα
cos(π/2-α)=sinα cos(π/2+α)=- sinα
tg (π/2-α) =ctgα tg (π/2+α) =- ctgα
ctg(π/2-α) =tg α ctg (π/2+α)=- tg α
另一类诱导公式
例1 求下列三角函数值
1) cos 225 o
2) sin 11
10
解： 1）cos225o cos(180o 45o )
cos45o 2
2
2) sin 11 sin( 1 )
10
10
sin 1 0.31
10
例2 求下列三角函数值

三角函数的诱导公式

三角函数的诱导公式三角函数在数学中是一类基础重要的函数，其中正弦函数、余弦函数和正切函数是最为常见和常用的三角函数。

在学习三角函数时，我们经常会遇到需要化简和推导三角函数的表达式的情况。

而三角函数的诱导公式则是帮助我们简化和推导这些表达式的重要工具。

一、正弦和余弦的诱导公式正弦函数和余弦函数是最为基础的三角函数之一，在数学中具有广泛的应用。

它们之间通过诱导公式可以相互转化和推导出一些简化的表达式。

1. 正弦的诱导公式：sin(A ± B) = sinA·cosB ± cosA·sinB这个诱导公式是我们最常用的，通过它我们可以将两个正弦函数的和差转换为两个三角函数的乘积或差积。

2. 余弦的诱导公式：cos(A ± B) = cosA·cosB ∓ sinA·sinB与正弦的诱导公式类似，余弦的诱导公式可以将两个余弦函数的和差转换为两个三角函数的乘积或差积。

二、正切的诱导公式正切函数是另一个常见的三角函数，它表示一个角的正弦值与余弦值的商。

正切函数的化简和推导也可以借助诱导公式来完成。

正切的诱导公式可以表示为：tan(A ± B) = (tanA ± tanB) / (1 ∓ tanA·tanB)该诱导公式可以将正切函数的和差转换为两个正切函数的商或差商，帮助我们简化三角函数的表达式。

三、其他除了正弦、余弦和正切之外，还有一些其他的三角函数，如余割、正割和余切等。

这些三角函数同样可以通过诱导公式进行化简和推导。

具体的诱导公式可以表述如下：1. 余割的诱导公式：csc(A ± B) = 1 / (sinA·cosB ± cosA·sinB)2. 正割的诱导公式：sec(A ± B) = 1 / (cosA·cosB ∓ sinA·sinB)3. 余切的诱导公式：cot(A ± B) = (cotA·cotB ∓ 1) / (cotB ± cotA)以上是几个常见三角函数的诱导公式，它们对于化简和推导三角函数表达式时起着至关重要的作用。