杠杆滑轮计算题练习(打印版)
杠杆与滑轮练习题

杠杆与滑轮练习题杠杆与滑轮练习题杠杆与滑轮是物理学中常见的两种简单机械。
它们在日常生活中的应用广泛,不仅在工程领域中发挥着重要作用,也在我们的日常活动中起到了便利和辅助的作用。
本文将通过一些练习题来帮助读者更好地理解和应用杠杆与滑轮的原理。
一、杠杆练习题1. 一个杠杆的长度为2米,杠杆的一端放置了一个质量为10千克的物体,另一端放置了一个质量为5千克的物体。
如果杠杆平衡,求两个物体之间的距离。
解析:根据杠杆平衡条件,杠杆两端所受的力矩相等。
设两个物体之间的距离为x,则有10 * (2 - x) = 5 * x。
解得x = 1.33米。
2. 一个杠杆的长度为3米,杠杆的一端放置了一个质量为20千克的物体,另一端放置了一个质量为15千克的物体。
如果杠杆平衡,求两个物体之间的距离。
解析:同样根据杠杆平衡条件,设两个物体之间的距离为x,则有20 * (3 - x) = 15 * x。
解得x = 1.8米。
以上两个练习题展示了杠杆平衡的基本原理,即力矩相等。
通过解方程可以求得两个物体之间的距离,这对于平衡杠杆的设计和应用有着重要意义。
二、滑轮练习题1. 一个滑轮组由两个滑轮组成,滑轮A的半径为10厘米,滑轮B的半径为20厘米。
如果滑轮A的线速度为2米/秒,求滑轮B的线速度。
解析:滑轮的线速度与滑轮半径之间成反比关系。
设滑轮B的线速度为v,则有2 * 10 = v * 20。
解得v = 1米/秒。
2. 一个滑轮组由三个滑轮组成,滑轮A的半径为5厘米,滑轮B的半径为10厘米,滑轮C的半径为15厘米。
如果滑轮A的线速度为3米/秒,求滑轮C的线速度。
解析:同样根据滑轮的线速度与滑轮半径之间的关系,设滑轮C的线速度为v,则有3 * 5 = v * 15。
解得v = 1米/秒。
通过以上滑轮练习题,我们可以看到滑轮的线速度与滑轮半径之间成反比关系。
这个关系在实际应用中非常重要,例如在起重机的设计中,通过合理选择滑轮的半径可以实现不同的力比。
杠杆与滑轮练习题

杠杆与滑轮练习题一、选择题1. 杠杆的五要素包括:A. 支点、力臂、动力、阻力、杠杆B. 支点、力臂、动力、阻力、平衡C. 支点、力臂、动力、阻力、作用点D. 支点、力臂、动力、阻力、力矩2. 以下哪种情况,杠杆处于平衡状态?A. 动力臂大于阻力臂B. 动力小于阻力C. 动力臂等于阻力臂D. 动力等于阻力3. 滑轮组中,动滑轮的作用是:A. 改变力的方向B. 改变力的大小C. 同时改变力的方向和大小D. 增加摩擦力4. 使用定滑轮时,以下说法正确的是:A. 可以省力B. 可以改变力的方向C. 不能省力,但可以改变力的方向D. 不能省力,也不能改变力的方向5. 以下哪种滑轮是省力杠杆?A. 定滑轮B. 动滑轮C. 滑轮组D. 以上都不是二、填空题6. 杠杆的平衡条件是_________。
7. 一个杠杆的动力臂是阻力臂的两倍,那么动力是阻力的_________。
8. 滑轮组由_________和_________组成。
9. 使用动滑轮可以省力,但需要_________。
10. 定滑轮实质上是一个等臂杠杆,它的作用是_________。
三、判断题11. 动力臂大于阻力臂的杠杆是省力杠杆。
()12. 滑轮组的省力情况取决于动滑轮的数量。
()13. 定滑轮不能省力,但可以改变力的方向。
()14. 动滑轮的实质是一个动力臂是阻力臂两倍的省力杠杆。
()15. 杠杆的分类是根据动力臂和阻力臂的相对大小来划分的。
()四、简答题16. 简述杠杆的分类及其特点。
17. 解释为什么使用滑轮组可以省力。
18. 描述定滑轮和动滑轮在实际应用中的区别。
五、计算题19. 假设有一个杠杆,其动力臂是阻力臂的3倍,动力是200N,求阻力的大小。
20. 如果使用一个动滑轮,已知施加的力是100N,物体的重力是500N,计算物体被提升的高度。
六、应用题21. 某工厂需要提升一个重1000N的货物,使用一个由两个动滑轮和一个定滑轮组成的滑轮组,求需要施加的最小力是多少?22. 描述在建筑工地上,如何利用杠杆原理来移动一块重物。
初三物理杠杆滑轮练习题

初三物理杠杆滑轮练习题在初三物理学习中,杠杆和滑轮是非常重要的两个概念。
它们在解决物理问题中起到了至关重要的作用。
下面将提供一些物理杠杆和滑轮的练习题,以帮助学生深入理解这两个概念并提高解决问题的能力。
练习题1:杠杆问题1. 在一个平衡杠杆上,两个物体分别位于杠杆的两端。
左端的质量为2kg,距离支点的距离为4m。
右端的质量为5kg,距离支点的距离为x米。
求x的值。
解析:根据杠杆的平衡条件,左端的力矩等于右端的力矩,即2kg* 4m = 5kg * x。
解得x = 1.6m。
练习题2:滑轮问题2. 在一个滑轮系统中,两个物体分别悬挂在两个滑轮的两端。
左侧滑轮的半径为0.5m,右侧滑轮的半径为1m。
左侧物体的质量为4kg,左右两侧绳子不可伸长或收缩。
求右侧物体的质量。
解析:根据滑轮的性质,相连的物体悬挂在不可伸长或收缩的绳子上,左右两侧的拉力相等。
由于左侧滑轮的半径是右侧滑轮的二倍,根据力矩平衡条件,可得4kg * g * 0.5m = M * g * 1m,解得右侧物体的质量M为2kg。
练习题3:杠杆和滑轮混合问题3. 在一个杠杆和滑轮组成的复杂系统中,左端悬挂着一个重锤,右端悬挂着一个物体。
左端重锤的质量为8kg,右端物体的质量为4kg。
左杠杆臂的长度为2m,右杠杆臂的长度为4m。
右侧滑轮的半径为0.5m。
系统处于平衡状态,求右侧滑轮的拉力。
解析:首先根据杠杆的平衡条件,左边的力矩等于右边的力矩。
即8kg * g * 2m = 4kg * g * 4m + T * 0.5m,其中T表示右侧滑轮的拉力。
解得T = 48N。
通过以上这些练习题,我们可以看到杠杆和滑轮在物理学习中的重要性。
掌握了杠杆和滑轮的原理和运用,不仅能够很好地解决物理问题,还可以通过它们来解释和理解自然界中的现象。
然而,这些习题只是一部分,初三物理杠杆和滑轮的知识还远远不止于此。
在未来的学习中,同学们还需要进一步学习相关的公式和定律,并进行更加复杂的问题解析和应用。
物理杠杆滑轮练习题含答案-打印 (科组教研精品 低碳排版)

6.(佛山市)如图所示的简单机械,在使用中属于费力杠杆的是()解析:判断一个杠杆是什么类型的杠杆,通常采用比较杠杆动力臂和阻力臂长短。
动力臂比阻力臂长的是省力杠杆,反之是费力杠杆。
镊子是费力杠杆,羊角锤、瓶起子是省力杠杆,托盘天平是等臂杠杆。
答案:B25.(佛山市)如图所示,甲是我们常使用的指甲钳,乙是它的示意图。
请细心观察,此钳哪些部位分别应用了哪些物理知识及原理,请你写出二个应用不同原理的例子。
答案:钳口D很锋利——压力一定时,减小受力面积可增加压强;钳柄(AC)上有粗糙的刻纹——增大摩擦;指甲钳的CBA部分——省力杠杆17.(广州)在图中用线代表绳子,将两个滑轮连成省力的滑轮组,要求人用力往下拉绳使重物升起.解析:理论上吊起动滑轮绳子股数越多,越省力,但由于人站在地面上向下拉,有两股绳子吊起动滑轮,根据“奇动偶定”的方法,绳子起点定在定滑轮上。
所以画出如图所示的绕线。
答案:如图所示。
5.(成都)如图所示的简单工具在使用过程中,不能省力的是()解析:定滑轮不能省力,但能改变施力的方向。
答案:D5.( 成都)在抗震救灾中,为了从垮塌的建筑中尽快地实施救援,营救生命,使用到了大量的汽车起重机。
正在家中复习的小陈同学看到救灾现场的救援画面后,在感动之余,找来了一台玩具汽车起重机,进行了探究。
小陈要探究的问题是,起重机吊起的重物静止在空中时:①支撑臂对起重臂的作用力大小;②水平地面受到的起重机的压强。
为此,小陈除起重机外,还准备了以下器材:重物、弹簧测力计、棉线、面积足够大的坐标纸、墨水、毛笔、复写纸。
(1)要完成他的探究,上述器材中还应该增加的是_________________________________。
(2)为完成问题①的探究,需要测量力臂。
请你在图18中作出支撑臂CD 对起重臂AB 的作用力F的力臂,其中O 点是支点。
(3)在问题②的探究中,针对接触面积的测量中遇到的困难,小陈设计了两套实验方案。
杠杆滑轮练习44题

《杠杆和滑轮》练习班级姓名家长签字______________一、知识点:(必须要熟记)1.杠杆:在力的作用下绕固定点转动的硬棒,杠杆可直可弯。
2.力臂:是支点到力的作用线的垂直距离。
3.杠杆的平衡条件:杠杆处于静止或缓慢匀速转动状态,平衡条件是F1×L1=F2×L2。
4.杠杆的应用:省力杠杆,L1<L2;费力杠杆,L1>L2;等臂杠杆,L1=L2;5.滑轮和滑轮组:定滑轮相当于等臂杠杆,不省力但可改变力的方向;动滑轮相当于动力臂为阻力臂二倍的杠杆,可省一半力,但不能改变力的方向。
滑轮组即可以省力又可以改变力的方向,但却不能同时省距离。
6.对于滑轮或滑轮组,S= h;若不计摩擦绳重和动滑轮重有F= ;若不计摩擦绳重有F=二、巩固题1.如图1所示,轻质杠杆支点为O,在已调平的杠杆两端分别挂上一些钩码,每一个钩码的质量相等,杠杆恰好在水平位置平衡,如果两边各拿走一个钩码,杠杆将 ( ) A.仍保持平衡并静止B.不平衡,向顺时针方向转动C.不平衡,向逆时针方向转动D.仍保持平衡,但要转动2.图2中属费力杠杆的是()3.下列说法正确的是()A.杠杆一定能够省力B.定滑轮既能省力又能改变力的方向C.动滑轮既能省力又能改变力的方向D.滑轮组既能省力又能改变力的方向4.家用的手摇晾衣架如图所示,它实际是由定滑轮和动滑轮组成的滑轮组。
假设衣服和晾衣架的总重为100N,则静止时绳子自由端的拉力为(不计动滑轮重及摩擦)()A、100NB、50NC、25ND、20N5.用如图所示的装置提升同一物体,在滑轮重及摩擦不计的情况下最省力的是()6.一辆汽车不小心陷进泥潭后,司机按图所示的甲、乙两种方法安装滑轮,均可将汽车从泥潭中匀速拉出。
比较这两个装置,下列说法正确的是()A.甲、乙安装的都是动滑轮,都能省力 B.甲、乙安装的都是定滑轮,都不能省力C.甲安装的是动滑轮,能省力 D.乙安装的是动滑轮,能省力7.如图所示,一名同学在做俯卧撑,如果把人的躯干看作一个杠杆,这是一个________(填“省力”或“费力”)杠杆,该杠杆的支点是________(填图中字母)。
杠杆、滑轮作图专题训练word版

一、杠杆作图1、如图所示,一杠杆在力F1的作用下处于静止状态,请画出它的力臂L1。
2、杠杆在我国古代就有了许多巧妙的应用,护城河上安装的吊桥(如图)就是一个杠杆,它的支点是C 点,画出绳对吊桥的拉力及拉力的力臂。
3、如图,画出人对杠杆作用力F的力臂L和物体A所受重力G的示意图。
4、如图所示,请画出动力的力臂L。
5、如图所示的组合机械,请在图中画出杠杆OA的动力臂L和所挂重物G的重力示意图.6、请作出图中:①物体A所受重力G的示意图;②力F的力臂L。
7、杠杆OA可绕O点转动,受力情况如图所示。
请作出力F的力臂L。
8、曲杆可绕固定点O转动,在一个最小的拉力F的作用下,在图所示位置保持静止,请在图乙中画出:①拉力F的力臂和拉力F的示意图;②所挂物体受到重力的示意图。
9、在图中,O是杠杆的支点,请在图中画出能使杠杆平衡的最小的力F1的示意图及其力臂L1。
10、如图所示,轻质杠杆可绕O转动,杠杆上吊一重物G,在动力F1作用下杠杆静止在水平位置,l为动力F1的力臂,请在图中作出动力F1和阻力F2的示意图。
11、如图所示杠杆OA处于静止状态,L2是力F2的力臂.请在图中画出力F1的力臂L1和力F2的示意图.12、如图所示,轻质杠杆AOB处于静止状态,作出作用在A点的最小力F和力臂l。
二、滑轮作图1、按要求连接滑轮组2、画出右图中最省力的绳子的绕线方法3、小红借助滑轮组提升重物,请画出最省力的绕线方法。
4、图中的定滑轮和动轮绕制滑组,要能够改变力的方向。
5、如图,站在地面上的人通过滑轮组提升物体,请画出滑轮组的绕线。
6、如图所示,某人站在A处通过一根绳和两个滑轮匀速提起物体B,所用的拉力F=100N,物体B重300N,(不计滑轮重、绳重及摩擦力),画出滑轮组的绕线。
7、建筑工地上,工人师傅将如图丙所示的滑轮装配成最省力的滑轮组,利用它站在地面上向下拉绳提升重物,请在图中画出滑轮组的绕线。
9、根据题中所给出的滑轮组,请在图中画出省力的绕法(要求所给的滑轮都利用)。
杠杆、滑轮及机械效率练习题

杠杆、滑轮及机械效率练习题(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--杠杆专项练习一、下列杠杆中,O是支点,在图上画出F1、F2的力臂,并且用L1、L2表示它们:二、应用杠杆原理F1l1=F2l2解决杠杆问题:1、在均匀铁条的中点O处用线将其悬挂起来,铁条水平平衡,如图5(a)所示。
若将OB弯折,如图(b)所示,则铁条将[ ]A.A端下降,C端上升 B.A端上升,C端下降C.仍然平衡 D.无法判断2、在图2中,能够平衡的杠杆是图[ ]3、一根不均匀木棒长1米,当用力F1=6牛竖直向上作用在它的A端时,刚能抬起A端,当用力F2=12牛竖直向上作用在它的B端,刚能抬起它的B端,求此棒的重力和重心距A端的距离。
4、一根扁担长,前后两筐内分别装有300N和400N的货物。
问:人肩挑处离前筐多远才能平衡(不计扁担及筐的质量)5、一根杠杆长1米,支点O在它的最左端,现将一G为90牛顿的重物放在距O点20厘米处,若使杠杆处于水平静止状态,则动力作用在杠杆最右端时,应向____时(左,中,右),动力最小,且动力的大小是______牛顿。
6、杠杆两端各挂有重力不相等的两块同种材料做成的实心金属块A、B,已知G A<G B,此时杠杆平衡,如图4所示。
当把A、B金属块都浸没在水中时,杠杆将 [ ]A.失去平衡,A端向下倾斜 B.失去平衡,B端向下倾斜C.仍然保持平衡 D.条件不足,无法判断7、一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g。
用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡若秤杆长60cm,则这把秤最大能称量多少千克的物体8、身高几乎相同的兄弟二人,用长米的扁担抬一桶水,水桶挂在距哥哥肩米处的扁担上,桶和水共重300牛,问兄弟二人肩上各负担多大的力(不计扁担重)9、一根轻质杠杆AB 长,当A 点挂质量为的实心铝块,B 端挂重物P 为9N 时,杠杆能平衡。
杠杆滑轮计算题练习(打印版)
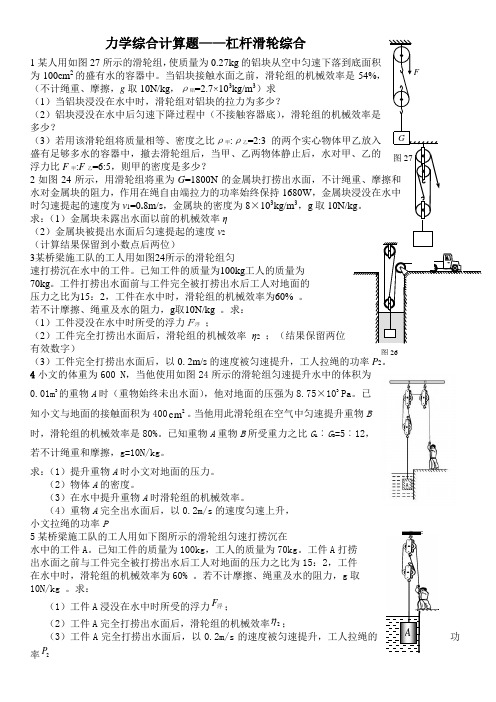
力学综合计算题——杠杆滑轮综合1某人用如图27所示的滑轮组,使质量为0.27kg 的铝块从空中匀速下落到底面积为100cm 2的盛有水的容器中。
当铝块接触水面之前,滑轮组的机械效率是54%,(不计绳重、摩擦,g 取10N/kg ,ρ铝=2.7×103kg/m 3)求(1)当铝块浸没在水中时,滑轮组对铝块的拉力为多少?(2)铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率是多少?(3)若用该滑轮组将质量相等、密度之比ρ甲:ρ乙=2:3的两个实心物体甲乙放入盛有足够多水的容器中,撤去滑轮组后,当甲、乙两物体静止后,水对甲、乙的浮力比F 甲:F 乙=6:5,则甲的密度是多少?2如图24所示,用滑轮组将重为G =1800N 的金属块打捞出水面,不计绳重、摩擦和水对金属块的阻力,作用在绳自由端拉力的功率始终保持1680W ,金属块浸没在水中时匀速提起的速度为v 1=0.8m/s ,金属块的密度为8×103kg/m 3,g 取10N/kg 。
求:(1)金属块未露出水面以前的机械效率η(2)金属块被提出水面后匀速提起的速度v 2(计算结果保留到小数点后两位)3某桥梁施工队的工人用如图24所示的滑轮组匀速打捞沉在水中的工件。
已知工件的质量为100kg 工人的质量为70kg 。
工件打捞出水面前与工件完全被打捞出水后工人对地面的压力之比为15:2,工件在水中时,滑轮组的机械效率为60% 。
若不计摩擦、绳重及水的阻力,g 取10N/kg 。
求:(1)工件浸没在水中时所受的浮力F浮 ;(2)工件完全打捞出水面后,滑轮组的机械效率η2 ;(结果保留两位有效数字) (3)工件完全打捞出水面后,以0.2m/s 的速度被匀速提升,工人拉绳的功率P 2。
4小文的体重为600 N ,当他使用如图24所示的滑轮组匀速提升水中的体积为0.01m 3的重物A 时(重物始终未出水面),他对地面的压强为8.75×103 Pa 。
(完整版)杠杆滑轮测试题

(完整版)杠杆滑轮测试题杠杆的B点悬挂一个质量为500克的钩码,当杠杆在水平位置上平衡时,线的拉力为_______。
12、如下图所示,重力不计的杠杆OA,O为支点,在拉力F和重力为20N的重物P的作用下,恰在水平位置平衡。
已知OA=60cm,AB=30cm,杠杆与转动轴间的摩擦忽略不计。
那么拉力F的力臂L=________cm,拉力的大小F=_________N。
13、如下图所示,AB为一根质量不计的细棒,用绳在O处吊起,当A、B两端分别挂两个重物1. 下图展示了一件名为“龙虾网与鱼尾巴”的活动雕塑作品,其中O是支点。
作者将艺术天赋与物理学中的平衡原理相结合,创造出一种新的艺术形式,带给人们美感。
我们在日常生活中也可以看到应用这一原理的例子,请举出一例。
2. 某人用甲、乙两种方法分别挑着同一个物体赶路。
在甲图中,肩膀受到的压力大于乙图中肩膀受到的压力;在甲图中,手施加的动力小于乙图中手施加的动力。
3. 如上图所示,AOB为一轻质杠杆(杠杆自重忽略不计),O为支点,OA=OB,在杠杆的B端挂一重20N的重物,要使杠杆平衡,则在A端施加的力F至少为10N。
4. 如上图所示,重力不计的杠杆OA,O为支点,在拉力F和重力为30N的重物P的作用下,恰在水平位置平衡。
已知OA=80cm,AB=20cm,杠杆与转动轴间的摩擦忽略不计。
那么拉力F的力臂L=20cm,拉力的大小F=60N。
5. 如下图所示,AB是一根质量不计的细棒,用绳在O处吊起。
当甲、乙两个重物分别挂在AB的两端时,杠杆恰好平衡。
若OA=0.8m,OB=0.4m,甲的质量为10kg,则乙的质量为5kg。
6. 如下图所示,若拉力F=900牛顿,物体A重1500牛顿,不计滑轮重和绳与滑轮间摩擦。
当绳子自由端移动3米,则沿水平方向匀速拉动物体A前进时,物体A与地面间摩擦力是600牛顿,物体A移动3米。
7. 如下图所示,在水平面桌面上放一个200N重的物体,物体与桌面的摩擦力为40N。
杠杆 滑轮 练习题

杠杆滑轮练习题在物理学中,杠杆和滑轮是两个常见的机械原理。
它们的应用广泛,不仅在实际生活中,还在工程领域中发挥着重要作用。
为了更好地理解和应用杠杆和滑轮原理,下面将给出一些练习题,帮助读者巩固相关知识。
一、杠杆练习题1. 一个杠杆的长度为2m,物体A位于杠杆的一侧,距离杠杆支点的距离为0.5m;物体B位于杠杆的另一侧,距离杠杆支点的距离为1.5m。
如果物体A的质量为10kg,物体B的质量为15kg,求杠杆平衡时物体A与物体B之间的力的大小。
解析:根据杠杆平衡的条件,物体A产生的力矩应该等于物体B产生的力矩。
力矩的计算公式为力乘以力臂。
设物体A的力为F,物体B的力为5,则有0.5F=1.5×5。
解方程可得F=15N。
因此,物体A与物体B之间的力的大小为15N。
2. 一个杠杆的长度为3m,杠杆的支点离物体A的距离为1m,杠杆的支点离物体B的距离为2m。
已知物体A的质量为20kg,物体B的质量为15kg。
求杠杆平衡时物体A与物体B之间的力的大小。
解析:根据杠杆平衡的条件,物体A产生的力矩应该等于物体B产生的力矩。
力矩的计算公式为力乘以力臂。
设物体A的力为F,物体B的力为5,则有F×1=5×2。
解方程可得F=10N。
因此,物体A与物体B之间的力的大小为10N。
二、滑轮练习题1. 一个滑轮系统由两个滑轮组成,滑轮的半径分别为1m和0.5m。
已知下滑轮承受的重力为200N,求上滑轮需要承受的力大小。
解析:根据滑轮原理可知,滑轮系统的各滑轮所受的力大小相等。
因此,上滑轮需要承受的力大小也为200N。
2. 一个滑轮系统由三个滑轮组成,滑轮的半径分别为2m、1m和0.5m。
已知下滑轮承受的重力为300N,求上滑轮需要承受的力大小。
解析:根据滑轮原理可知,滑轮系统的各滑轮所受的力大小相等。
设上滑轮需要承受的力为F,则下滑轮承受的力为3F。
根据等式关系可知,3F=300N,解得F=100N。
初三物理杠杆与滑轮练习题

初三物理杠杆与滑轮练习题杠杆和滑轮是物理学中重要的力学工具,在解决力学问题时经常会遇到。
掌握了杠杆和滑轮的原理和应用,可以帮助我们更好地理解和解决相关问题。
下面,我们将通过一些练习题来加深对杠杆和滑轮的理解。
1. 杠杆练习题(1) 若杠杆两端的力臂分别为5cm和10cm,力臂较长的一端受到的力为20N,求力臂较短一端的力是多少?解析:根据杠杆原理,在平衡条件下,杠杆两端受到的力的乘积相等。
即力臂1乘以力1等于力臂2乘以力2。
设力臂2的力为F2,则可得到以下方程:5cm × 20N = 10cm × F2400N·cm = 10cm × F2F2 = 40N因此,力臂较短一端的力为40N。
(2) 一根杠杆上有两个力F1和F2,力F1作用在杠杆的左边,力F2作用在杠杆的右边。
如果力F1为100N,力F2为50N,杠杆长度为2m,力F1的位置离杠杆左端0.5m,求力F2的位置离杠杆左端多远?解析:根据杠杆原理,在平衡条件下,杠杆两端受到的力的乘积相等。
即力臂1乘以力1等于力臂2乘以力2。
设力臂2的长度为x,可得以下方程:0.5m × 100N = x × 50N50N·m = 50N・xx = 1m因此,力F2的位置离杠杆左端1m。
2. 滑轮练习题(1) 若滑轮组有3个滑轮,要提升一个重物,一端用力F,另一端挂重物,求所需施加的力F是多少?已知滑轮组的机械优势为6。
解析:滑轮组的机械优势等于所施加的力F与挂重物的比值。
设所需施加的力F为x,则可得以下方程:x/重物的重力 = 6重物的重力 = 重物的质量 ×重力加速度代入数值并整理方程,得到:x/(m × g) = 6x = 6m × g因此,所需施加的力F为6倍重力。
(2) 若滑轮组由2个滑轮组成,要提升一个重物,一端用力F,另一端挂重物,已知所需施加的力F为200N,滑轮组的机械优势为4,求挂重物的重力是多少?解析:滑轮组的机械优势等于所施加的力F与挂重物的比值。
初三杠杆滑轮练习题

初三杠杆滑轮练习题一、杠杆的原理及计算杠杆是一种简单机械装置,由一个固定支点和两个力臂组成。
其中,支点位置固定不动,作为杠杆的转动中心。
力臂是指从支点到力的作用点的距离。
根据杠杆原理,当力臂和力矩相等时,杠杆保持平衡。
例如,如果一个杠杆的支点距离力臂的左侧为1米,支点距离力臂的右侧为3米,左侧施加的力为10牛顿,右侧施加的力为30牛顿。
我们可以用力矩来计算杠杆的平衡情况。
力矩等于施加力乘以力臂的长度。
左侧力矩 = 10N × 1m = 10Nm右侧力矩 = 30N × 3m = 90Nm由于右侧力矩大于左侧力矩,杠杆向右侧转动。
为了使杠杆保持平衡,我们可以增加左侧力的大小,或者减小右侧力的大小。
二、滑轮的原理及计算滑轮是一种简单机械装置,用于改变力的方向和大小。
滑轮由一个轮轴和一个块轮组件组成。
当力通过滑轮传递时,方向会改变,但大小保持不变。
例如,如果我们有一个滑轮系统,由一个绳子绕过两个滑轮组成,上部滑轮固定在支架上,下部滑轮可以移动。
通过上部滑轮施加的力为20牛顿,我们可以计算下部滑轮承受的力。
由于滑轮上的绳子拉力相等,所以上部滑轮承受的力等于下部滑轮承受的力。
因此,下部滑轮承受的力也为20牛顿。
三、杠杆和滑轮的综合练习题现在,我们将结合杠杆和滑轮的原理来解决以下练习题。
练习题一:有一个平衡杆,左侧长度为2米,右侧长度为4米。
左侧施加的力为15牛顿,该杠杆保持平衡的情况下,右侧施加的力是多少?解答:根据杠杆的原理,左侧力矩等于右侧力矩。
左侧力矩 = 15N × 2m = 30Nm右侧力矩 = 右侧施加的力 × 4m由于左侧力矩等于右侧力矩,我们可以得到以下等式:30Nm = 右侧施加的力 × 4m解方程,我们得到右侧施加的力为:右侧施加的力 = 30Nm ÷ 4m = 7.5牛顿练习题二:有一个滑轮系统,上部滑轮固定在支架上,下部滑轮可以移动。
杠杆与滑轮练习题

杠杆与滑轮练习题在物理学中,杠杆和滑轮是两个经常使用的力学工具。
它们可以通过习题来加深我们对它们的理解。
下面是一些与杠杆和滑轮有关的练习题,帮助我们更好地掌握这些概念。
练习题一:杠杆平衡有一根均质杠杆,长度为L,重量为W。
假设杠杆是质量均匀分布的,重心在离支点的距离为a处。
如果杠杆保持平衡,求支力F和支点的距离x之间的关系。
解答:根据杠杆平衡的条件,可以得到以下的方程:F(a-x) = W(x)通过展开方程,可以得到:Fa - Fx = Wx整理上述方程,可以得到:(F+W)x = Fa因此,支力F和支点的距离x之间的关系为:F = (Wx) / (a-x)练习题二:滑轮组一个滑轮组由两个固定在一起的滑轮组成。
一个绳子绕过滑轮组,并连接着一个重物。
假设滑轮组的半径分别为r1和r2,重物的质量为m。
求支持重物的力F和绳子两端所受的力T1和T2之间的关系。
解答:根据滑轮组的原理,可以得到以下的方程:T1 = 2FT2 = F+r2*m*g其中,g为重力加速度。
由于在滑轮中没有动摩擦力,绳子的张力在整个系统中保持不变,即T1=T2。
将上述两个方程相等,可以得到:2F = F+r2*m*g整理上述方程,可以得到:F = (r2*m*g) / (2-r2)练习题三:杠杆与滑轮的联合应用一个杠杆的长度为L,重力作用在离支点的距离为a的地方。
一个绳子连接着杠杆的一端,另一端连接着一个滑轮,并悬挂着一个重物。
滑轮的半径为r。
求滑轮所支持的重物的质量m和杠杆的重力W之间的关系。
根据杠杆与滑轮的联合应用,在平衡状态下,可以得到以下的方程:m*g = W其中,g为重力加速度。
根据滑轮的原理,可以得到以下的方程:T = 2FT = r*m*g由于在滑轮中没有动摩擦力,绳子的张力在整个系统中保持不变,即T=W。
将上述两个方程相等,可以得到:2F = r*m*g整理上述方程,可以得到:m = (2F) / (r*g)代入杠杆平衡的条件,可以得到:m = (2W) / (L*r)练习题四:力矩平衡一个均匀的杠杆在两个支点之间有质量为m1和m2的两个物体。
完整版功杠杆滑轮练习题及其答案zqx全解

功杠杆滑轮练习题一、选择题用手直;c.沿光滑斜面将重物提高a.用不计摩擦的定滑轮将重物提高h ;b.h1、用三种方法来提升同一个重物:( )h.其中做功大小是:接将重物提高 .b方式做功最少BA.a方式做功最少三种方式做功一样多. DC.c方式做功最少2)、汽车在平直道路上做匀速直线运动,下列说法中正确的是( B.汽车所受的摩擦力为零A.汽车的牵引力为零 D.汽车所受的合力为零C.汽车牵引力所做的功为零3。
设他每跳次,每次跳离地面的高度为5cm2005年中考体能测试中,某同学选择跳绳。
他在1min 内跳了120、在( ) 一次所用的时间相等,则他跳绳时的功率最接近D.5000WA.5WB.50WC.500W4内吊10s,又在5s内沿水平方向将货物移送了10m,则、一吊车在2s内将1500N的货物提高2m 后,在空中停留了3s )车的功率为(1500W..18000W C.1800W D300W BA.5( ) 则甲、乙两台机器的在相同的时间内通过的路程之比为3∶1,、甲、乙两台机器的功率相等,1 ∶∶1,受到的牵引力之比为1∶1,受到的牵引力之比为3∶1 B. 做功之比为1A. 做功之比为11 3,受到的牵引力之比为3∶1,受到的牵引力之比为1∶3 D. 做功之比为1∶C. 做功之比为1∶6( ) 、分别用定滑轮、动滑轮、滑轮组把同一物体匀速提升到同一高度,其中机械效率最高的是D. 无法确定定滑轮 B.动滑轮 C.滑轮组A.7( )、用同一个滑轮组来测挂不同钩码时的机械效率,下述结论正确的是 .钩码较轻的一次机械效率较高A.钩码较重的一次机械效率较高B .机械效率与提升高度有关C.两次机械效率是一样的D8)滑轮组机械效率时提出了下列假设(1、同学们在探究影响滑轮组机械效率高低的因素)滑轮组机械效3高低可能与动滑轮重有关(2)滑轮组机械效率高低可能与被物重有关(然率高低可能与物体提升高度有关(4)滑轮组机械效率高低可能与与承重绳子段数有关进行对比实验来验证提出的假设,则该实验验证后一位同学设计了如图所示的两个滑轮组,)的假设是() D.)(4A.(1) B.(2) C.(3GG9,用它们分别将重相同的甲、小于物重)、如图(不计绳重与摩擦,且动滑轮重动FF它们的机械效率分别为、,乙两物体匀速提升相同的高度,所用的拉力分别为乙甲F甲ηη( )。
杠杆滑轮单元测试题及答案

杠杆滑轮单元测试题及答案一、选择题(每题2分,共20分)1. 杠杆的五要素包括:A. 支点、力臂、力B. 支点、力臂、力、阻力臂C. 支点、力臂、力、阻力臂、阻力D. 支点、力臂、力、阻力、阻力臂2. 以下哪种情况的杠杆是省力杠杆?A. 阻力臂大于力臂B. 力臂大于阻力臂C. 力臂等于阻力臂D. 力臂小于阻力臂3. 滑轮的类型包括:A. 定滑轮和动滑轮B. 单滑轮和复滑轮C. 定滑轮、动滑轮和复滑轮D. 单滑轮、双滑轮和复滑轮4. 使用定滑轮时,以下说法正确的是:A. 可以省力B. 不能省力,但可以改变力的方向C. 可以省力,但不能改变力的方向D. 既不能省力,也不能改变力的方向5. 使用动滑轮时,以下说法正确的是:A. 可以省力,但不能改变力的方向B. 不能省力,但可以改变力的方向C. 既不能省力,也不能改变力的方向D. 可以省力,也可以改变力的方向6. 以下哪种情况下,使用滑轮组可以省力?A. 滑轮组的绳索端固定不动B. 滑轮组的绳索端与重物相连C. 滑轮组的绳索端与动滑轮相连D. 滑轮组的绳索端与定滑轮相连7. 滑轮组的省力效果与以下哪个因素有关?A. 滑轮组中定滑轮的数量B. 滑轮组中动滑轮的数量C. 滑轮组中绳索的段数D. 滑轮组中重物的重量8. 以下哪种情况下,使用杠杆可以省距离?A. 力臂大于阻力臂B. 力臂小于阻力臂C. 力臂等于阻力臂D. 力臂与阻力臂成一定角度9. 杠杆的平衡条件是:A. 力×力臂=阻力×阻力臂B. 力=阻力C. 力臂=阻力臂D. 力+阻力=阻力臂+力臂10. 滑轮组的效率与以下哪个因素无关?A. 滑轮的摩擦力B. 滑轮的重量C. 滑轮组的省力效果D. 滑轮组的绳索长度二、填空题(每空2分,共20分)11. 杠杆的五要素包括支点、力臂、力、阻力臂和________。
12. 省力杠杆的特点是________大于阻力臂。
13. 定滑轮实质上是一个等臂杠杆,它的作用是________。
12.2杠杆、滑轮(练习题)

第十二章
简单机械
第1-2节杠杆、滑轮
5.按要求画出滑轮组的绕绳方法:
F F F
第十二章
简单机械
第1-2节杠杆、滑轮
6.如图所示,一辆汽车陷入泥坑,现用一 滑轮组把它拉出来,请画出最省力的绕法。
F
第十二章
简单机械
第1-2节杠杆、滑轮
7.如图所示,物体A重为100N,挂重物的钩 100 。人匀速拉绳子的 子承受的拉力是______N 50 力是_________N (动滑轮自重不计)。
第十二章
简单机械
第1-2节杠杆、滑轮
3.工人们为了搬运一个笨重的机器进入 厂房,他们设计了如图所示的四种方案(机 器下方的小圆表示并排放置的圆形钢管的横 截面)。其中最省力的方案是( C )
第十二章
简单机械
第1-2节杠杆、滑轮
1.如图所示,甲、乙不计滑轮重和摩擦, 丙动滑轮重为50N,求出拉力大小。 50N 100N 75N
第十二章
简单机械
第1-2节杠杆、滑轮
[练一练] 1.下列工具在正常使用中,属于费力杠杆的 是 C ( )
A.启瓶器 B.切纸铡刀 C.食品夹 D.羊角锤
第十二章
简单机械
第1-2节杠杆、滑轮
2.小阳同学在做“探究杠杆平衡条件”的实验时, 他把杠杆挂在支架上,发现左端向下倾斜。 (1 )若使杠杆在 水平 位置平衡,需把平衡螺母 向 右 端调节。 (2)如果在杠杆的A处挂三个相同的钩码,则在B 处要挂 2 个同样的钩码,杠杆才能重新位置平衡。 (3 )若在C 处挂 6 N 的钩码,用弹簧测力计作用 在B点,要使杠杆在水平位置平衡,最小拉力的方 向应该竖直向上 ,此时弹簧测力计的示数为2 N 。
第十二章
杠杆滑轮练习题

杠杆滑轮练习题在物理学中,杠杆和滑轮是两个重要的力学概念。
它们分别通过杠杆原理和滑轮原理来解释力的传递和乘积的变化。
本文将为您介绍一些杠杆滑轮练习题,帮助您更好地理解和应用这些原理。
练习题1:杠杆原理问题描述:有一个杠杆,其中心支点P距离两端A和B的距离分别为10cm和30cm。
在杠杆上有两个力F1和F2作用,F1 = 20N,F2 =30N。
求杠杆的平衡条件下,力F1和F2的距离。
解题思路:根据杠杆平衡的条件,力矩的和为0。
力矩可以通过力乘以力臂得到。
设F1与P的距离为x,F2与P的距离为y,则有20x + 30y = 0。
同时,F1与P的距离等于AP的长度减去x,F2与P的距离等于BP的长度减去y。
由此可以得到两个方程:10 - x = 0 和 30 - y = 0。
解这个方程组可以得到x = 10cm,y = 30cm。
练习题2:滑轮原理问题描述:有一台滑轮组,由固定滑轮和可移动滑轮组成。
固定滑轮上挂着一个质量为5kg的物体A,通过绳子与可移动滑轮相连,可移动滑轮上另一端挂着一个质量为2kg的物体B。
如果忽略滑轮的质量,求物体B的加速度。
解题思路:根据滑轮原理,可移动滑轮上的张力为绳子两端力的平均值。
设物体A的重力为F1,物体B的重力为F2,绳子的张力为T,则有F1 = 5g,F2 = 2g,其中g为重力加速度。
由于物体A和物体B相互连接,所以它们的加速度相同。
根据牛顿第二定律,物体A的受力为F1 - T = m1a,物体B的受力为T - F2 = m2a。
联立这两个方程可以解得a = (F1 - F2) / (m1 + m2) = (5g - 2g) / (5 + 2) = 3g / 7。
练习题3:杠杆与滑轮组合问题描述:有一个杠杆和一个滑轮组合体。
杠杆的长度为4m,滑轮的半径为0.5m。
在杠杆的一端挂着一个质量为800kg的物体C,在滑轮上挂着一个质量为200kg的物体D,两者用绳子相连。
杠杆滑轮专题练习(含答案)
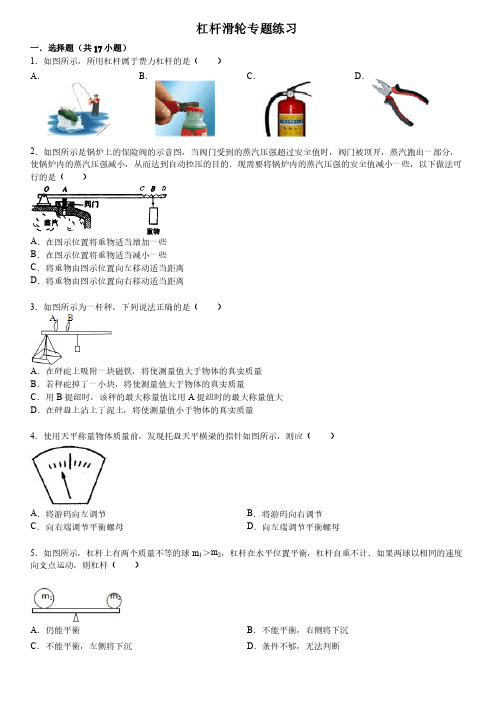
杠杆滑轮专题练习一.选择题(共17小题)1.如图所示,所用杠杆属于费力杠杆的是()A.B.C.D.2.如图所示是锅炉上的保险阀的示意图,当阀门受到的蒸汽压强超过安全值时,阀门被顶开,蒸汽跑出一部分,使锅炉内的蒸汽压强减小,从而达到自动控压的目的.现需要将锅炉内的蒸汽压强的安全值减小一些,以下做法可行的是()A.在图示位置将重物适当增加一些B.在图示位置将重物适当减小一些C.将重物由图示位置向左移动适当距离D.将重物由图示位置向右移动适当距离3.如图所示为一杆秤,下列说法正确的是()A.在砰砣上吸附一块磁铁,将使测量值大于物体的真实质量B.若秤砣掉了一小块,将使测量值大于物体的真实质量C.用B提纽时,该秤的最大称量值比用A提纽时的最大称量值大D.在砰盘上沾上了泥土,将使测量值小于物体的真实质量4.使用天平称量物体质量前,发现托盘天平横梁的指针如图所示,则应()A.将游码向左调节B.将游码向右调节C.向右端调节平衡螺母D.向左端调节平衡螺母5.如图所示,杠杆上有两个质量不等的球m1>m2,杠杆在水平位置平衡,杠杆自重不计.如果两球以相同的速度向支点运动,则杠杆()A.仍能平衡B.不能平衡,右侧将下沉C.不能平衡,左侧将下沉D.条件不够,无法判断6.如图所示,在均匀的杠杆两端分别放上A 、B 两支大小相同、长度不等的蜡烛,这时杠杆平衡.若蜡烛燃烧速度相同,过一段时间后[蜡烛未燃完]杠杆将(杠杆将( )A . 左端下沉端下沉B . 右端下沉端下沉C . 仍平衡平衡D . 无法确定法确定7.如图所示,杠杆OA 可绕支点O 转动,B 处挂一重物G ,在A 处用一竖直向上的力F 拉杠杆.当杠杆和竖直墙之间夹角逐渐增大时,为了使杠杆平衡,则(之间夹角逐渐增大时,为了使杠杆平衡,则( )A . F 逐渐增大,但F <G B . F 大小不变,但F >G C . F 逐渐减小,但F >G D . F 大小不变,但F<G 8.如图所示,有一固定在墙壁上的可绕支点O 转动杠杆,在杠杆上A 点悬挂一装有水的敞口水杯,在B 点施加竖直向上的拉力F 使杠杆在水平位置保持平衡.则拔下水杯底部的塞子后,拉力F 随时间t 变化的图象是(变化的图象是( )A .B .C .D .9.利用一个滑轮组提升物体,不计摩擦阻力,则用这个滑轮组(.利用一个滑轮组提升物体,不计摩擦阻力,则用这个滑轮组( )A . 提升的物体重力越小,机械效率越高升的物体重力越小,机械效率越高B . 提升的物体重力越大,机械效率越高升的物体重力越大,机械效率越高C . 把物体提的越高,机械效率越高物体提的越高,机械效率越高D . 自由端拉力越大,机械效率越高由端拉力越大,机械效率越高10.如图所示,三个滑轮下悬挂的重物的质量相等,若滑轮、绳的重力及滑轮与轴的摩擦忽略不计,则F 1、F 2、F 3的关系为(的关系为( )A .F 1=F 2=F 3 B . F 1>F 2>F 3 C . F 2>F 3>F 1 D . F 3>F 1>F 211.如图所示,三个滑轮拉同一物体在水平面作匀速直线运动,所用拉力分别为F1、F2、F3,不计滑轮重和绳子与滑轮之间的摩擦,那么有( )滑轮之间的摩擦,那么有(A.F1>F2>F3B.F1<F2<F3C.F3>F1>F2D.F2<F3<F1,若不计摩擦力和滑轮重,则( )12.如图所示,分别用滑轮和滑轮组提起重物,其中G1=G2=G3,若不计摩擦力和滑轮重,则(A.F1>F2>F3B.F1<F2<F3C.F1=F2=F3D.F1=F2>F3 13.(2014•无锡模拟)甲乙两个滑轮组如图所示,其中的每一个滑轮都相同,用它们分别将重物G1、G2提高相同的高度,不计滑轮组的摩擦,下列说法中正确的是( )的高度,不计滑轮组的摩擦,下列说法中正确的是(A.若G1=G2,拉力做的额外功相同,拉力做的额外功相同B.若G1=G2,甲的机械效率大于乙的机械效率,甲的机械效率大于乙的机械效率C.若G1=G2,拉力做的总功相同,拉力做的总功相同D.用甲乙其中的任何一个滑轮组提起不同的重物,机械效率不变甲乙其中的任何一个滑轮组提起不同的重物,机械效率不变14.如图所示,G=80N,在力F的作用下,滑轮以0.4m/s的速度匀速上升,不计摩擦及滑轮重,则物体的速度和力F的大小分别是(的大小分别是( )A.0.8m/s,160N B.0.8m/s,40N C.0.4m/s,160N D.0.2m/s,40N 15.如图所示,滑轮沿水平方向匀速拉动物体A,若拉力F=180N,则物体A与水平桌面的摩擦力为(滑轮重及轮和绳的摩擦不计)()A.180 N B.360 N C.90 N D.无法确定法确定16.如图所示,滑轮重及滑轮摩擦不计,物体A和B都处于静止状态.下列几种说法中正确的是(都处于静止状态.下列几种说法中正确的是( )A . 两物体重力的大小关系是G 1=2G 2B . A 物体受到的摩擦力的大小f A =2G 2C . A 物体所受的合力的方向是向右的物体所受的合力的方向是向右的D . A 物体受到三个力的作用,B 物体受到两个力的作用物体受到两个力的作用17.(2014•黄石)如图所示,小王在探究“力和运动的关系”的实验中,他将物体M 放在水平桌面上,两边用细线通过滑轮与吊盘相连.若在左盘中放重为G 的砝码,右盘中放重为2G 的砝码时,物体M 能以速度v 向右作匀速直线运动.如果左、右盘中的砝码不变,要让物体M 能在水平桌面上以2v 的速度向左作匀速直线运动,则应在左盘中再加上砝码,所加砝码的重为(吊盘重、滑轮与细线间和滑轮与轴间摩擦不计)( )A .G B . 2G C . 3G D . 4G 二.填空题(共5小题)18.如图是一种拉杆式旅行箱的示意图,使用时相当于一个.如图是一种拉杆式旅行箱的示意图,使用时相当于一个 _________ (填“省力”或“费力”)杠杆,而且把手处做的比较宽大,这是为了做的比较宽大,这是为了 _________ 手受到的压强(填“增大”或“减小”).19.杆秤加一些小配件就可以设计制造出一杆能测出液体密度的杆秤.杆秤加一些小配件就可以设计制造出一杆能测出液体密度的杆秤.在秤盘中放一个容积为在秤盘中放一个容积为500mL 、质量为200g 的玻璃容器,然后在杆秤的某些刻度上标上密度值,就制成了一杆简单而实用的液体密度秤(如图所示).只要在玻璃容器中加500mL 的待测液体,就可以直接“称”出该液体的密度.在这杆秤上,密度为“0”刻度应标在原刻度刻度应标在原刻度 _________ kg 处;请通过计算,确定杆秤上“0.6kg ”刻度处对应的密度值刻度处对应的密度值 _________ g/cm 3.20.(2014•鄂州模拟)如图,长为3米的质地均匀平板的中点能绕固定的支点转动,平板与水平地面的夹角为30°,在板上站两个小孩.已知30千克的甲小孩位于板的左端,20千克的乙小孩位于板的右端.现甲小孩以0.1米/秒的速度向右慢慢移动,速度向右慢慢移动, _________ 秒时间后平板开始转动;甲小孩在平板转动前的过程中,克服自身重力做功的功率为功率为 _________ 瓦.(g=10牛/千克)千克)21.请完成如图所示杠杆的示意图..请完成如图所示杠杆的示意图.22.如图中的水平桌面足够长,不计托盘质量和滑轮与绳的摩擦.物体A 重10N ,当物体B 重为2N 时,物体A 保持静止,这时A 物体受到的摩擦力为物体受到的摩擦力为 _________ N ;当物体B 重为3N 时,物体A 向右做匀速直线运动,运动一段时间托盘着地,此后物体继续运动一段时间,此时物体A 受到的摩擦力是受到的摩擦力是 _________ N .方向是.方向是 _________ .三.解答题(共8小题)23.如图所示是一个指甲刀的示意图,它由三个杠杆ABC 、OBD 和OED 组成,用指甲刀剪指甲时,下面说法正确的是的是 _________A .三个杠杆都是省力杠杆.三个杠杆都是省力杠杆B .三个杠杆都是费力杠杆.三个杠杆都是费力杠杆C .ABC 是省力杠杆,OBD 、OED 是费力杠杆是费力杠杆D .ABC 是费力杠杆,OBD 、OED 是省力杠杆.是省力杠杆.24.杠杆OBA 平衡,画出动力的力臂.平衡,画出动力的力臂.25.图是锅炉上的保险阀,当阀门受到的蒸气压强超过安全值时,阀门就会被顶开,让蒸气跑出一部分,使锅炉内的蒸气压强减小,阀门面积为3厘米2,杠杆重不计.,杠杆重不计. (1)用毫米刻度尺从图上量出并记录杠杆的动力臂和阻力臂.)用毫米刻度尺从图上量出并记录杠杆的动力臂和阻力臂. (2)要保持锅炉内蒸气的压强为1.2×105帕,应在B 处挂多重的物体?处挂多重的物体?(3)锅炉用久了耐压能力会降低,怎样调节能使锅炉内蒸气的最大压强小于1.2×105帕?帕?26.在“研究杠杆的平衡条件”实验中:实验中:(1)实验前,发现杠杆处于如图(a )所示的状态,为了使杠杆在水平位置平衡,应将杠杆右端的平衡螺母向)所示的状态,为了使杠杆在水平位置平衡,应将杠杆右端的平衡螺母向 _________ (选填“左”或“右”)移动.)移动.(2)左右两端添加钩码后,此时杠杆的状态如图(b )所示,可以将右端钩码的位置向)所示,可以将右端钩码的位置向 _________ (选填“左”或“右”),使杠杆重新平衡在水平位置.,使杠杆重新平衡在水平位置.(3)上面两次操作都要使杠杆平衡在水平位置,这样做的目的是)上面两次操作都要使杠杆平衡在水平位置,这样做的目的是 _________ .(4)某实验小组进行正确的实验操作后,得到的数据为F 1=6N ,L 1=20cm ,F 2=4N 和L 2=30cm .该实验小组根据这些数据能否得出探究结论?些数据能否得出探究结论? _________ 理由是理由是 _________ .(5)另一小组的同学获得的数据如右表所示:)另一小组的同学获得的数据如右表所示:他们得出的结论是:“动力+动力臂=阻力+阻力臂.”你认为这个结论是你认为这个结论是 _________ (选填“正确的”或“错误的”).理由是由是 _________ .27.(2013•丰台区二模)某提升装置中,杠杆AB 能绕固定点O 在竖直平面内转动,水平地面上的配重乙通过细绳竖直拉着杠杆B 端.已知AO :OB=2:5,配重乙与地面的接触面积为S 且S=200cm 2.当用动滑轮速提升重1000N 的物体甲时(甲未浸入水中),竖直向下拉绳子自由端的力为T 1,杠杆在水平位置平衡,此时配重乙对地面的压强为P 1且P 1=3.5×104Pa ;如果在动滑轮下挂一个质量为动滑轮质量5倍的实心物体丙,并把物体丙浸没在水中匀速提升时,如图甲所示,竖直向下拉绳子自由端的力为T 2,T 2的功率随速度变化的关系图象如图乙所示,杠杆始终保持水平平衡.此时配重乙对地面的压强为P 2且P 2=5.6×104Pa .如果不计杠杆重、绳重和滑轮轴间摩擦,图中两个滑轮所质量相同,取g=10N/kg .求:.求:(1)提升物体甲时滑轮组的机械效率;(保留一位小数)(保留一位小数)(2)实心物体丙的密度.)实心物体丙的密度.28.如图所示,重16kg 的金属圆柱体放在圆筒形容器中,细绳AD 系于圆柱体上底面中央并沿竖直方向,杠杆AB 可绕O 点在竖直平面内转动.当把小球P 先后挂在B 点与C 点时,圆柱体对水平容器底面的压强变化了2500p a .当需将小球P悬挂于距支点O1.4m的地为使圆柱体对容器底面的压力恰好为零,需将小球向容器中注水,使圆柱体没入水中,为使圆柱体对容器底面的压力恰好为零,方.已知杠杆在以上的各个状态中,杠杆均在水平位置上平衡,AO=0.5m,CB=0.5m,圆柱体高h=0.1m.(g取10N/km,杠杆的质量、悬挂圆柱体和小球P的细绳的质量均忽略不计)求:金属圆柱体的密度.的细绳的质量均忽略不计)求:金属圆柱体的密度.29.某人用长1.5m的扁担挑重物的情景如图所示,前面物体质量为20kg,后面物体质量为30kg,若要保持扁担平衡,则人的肩应在距扁担前端多远处?(扁担的自重可以不计,g取10N/kg)30.如图甲是用汽车打捞水下重物的示意图.汽车通过定滑轮牵引水下一圆柱形重物,在整个打捞过程中,汽车以恒定的速度V=0.2m/s向右运动.图乙是此过程中汽车拉动重物的功率P随时间t变化的图象.设t=0汽车开始提升,求:重物,忽略水的阻力和滑轮的摩擦,g取10N/kg,求:)画出汽车的重力示意图;(1)画出汽车的重力示意图;)圆柱形重物的密度.(2)圆柱形重物的密度.时,圆柱形重物上表面受到水的压力多大?(3)t=30s时,圆柱形重物上表面受到水的压力多大?一.选择题(共17小题)1.如图所示,所用杠杆属于费力杠杆的是(.如图所示,所用杠杆属于费力杠杆的是( )A.B.C.D.考点:杠杆的分类.简单机械.专题:简单机械.分析:结合图片和生活经验,判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.杠杆.解:解答:解:A、钓鱼竿在使用过程中,动力臂小于阻力臂,是费力杠杆;、钓鱼竿在使用过程中,动力臂小于阻力臂,是费力杠杆;B、瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;、瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;C、灭火启动夹在使用过程中,动力臂大于阻力臂,是省力杠杆;、灭火启动夹在使用过程中,动力臂大于阻力臂,是省力杠杆;D、钳子在使用过程中,动力臂大于阻力臂,是省力杠杆.、钳子在使用过程中,动力臂大于阻力臂,是省力杠杆.故选A.点评:此题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于等臂杠杆,动力臂等于阻力臂.阻力臂;③等臂杠杆,动力臂等于阻力臂.2.如图所示是锅炉上的保险阀的示意图,当阀门受到的蒸汽压强超过安全值时,阀门被顶开,蒸汽跑出一部分,使锅炉内的蒸汽压强减小,从而达到自动控压的目的.现需要将锅炉内的蒸汽压强的安全值减小一些,以下做法可行的是( )行的是(A.在图示位置将重物适当增加一些图示位置将重物适当增加一些B.在图示位置将重物适当减小一些图示位置将重物适当减小一些C.将重物由图示位置向左移动适当距离重物由图示位置向左移动适当距离D.将重物由图示位置向右移动适当距离重物由图示位置向右移动适当距离考点:杠杆的动态平衡分析.简单机械.专题:简单机械.分析:要解决此题,需要掌握杠杆的平衡条件:F1L1=F2L2.根据选项中物理量的变化及平衡条件公式来判断安全值的变化情况,便可得到答案.值的变化情况,便可得到答案.解答:解:A、根据杠杆的平衡条件,若将重物的重力增大,则蒸汽压强的安全值也会增大,所以A不符合要求.B、将重物适当减小一些,根据杠杆的平衡条件,则蒸汽压强的安全值减小,所以B符合题意.符合题意.C、若将重物向左移动,则其力臂变短,根据杠杆的平衡条件,阀门的安全值减小,所以C符合题意.符合题意.D、若将重物向右移动,则其力臂变长,根据杠杆的平衡条件,阀门的安全值变大,所以D不符合题意.不符合题意. 故选BC.点评:此题主要考查了有关杠杆平衡条件的应用,首先要掌握杠杆的平衡条件,注意题目中力臂或力的变化情况,从而做出正确判断.从而做出正确判断.3.如图所示为一杆秤,下列说法正确的是(.如图所示为一杆秤,下列说法正确的是( )A.在砰砣上吸附一块磁铁,将使测量值大于物体的真实质量砰砣上吸附一块磁铁,将使测量值大于物体的真实质量B.若秤砣掉了一小块,将使测量值大于物体的真实质量秤砣掉了一小块,将使测量值大于物体的真实质量C.用B提纽时,该秤的最大称量值比用A提纽时的最大称量值大提纽时的最大称量值大D.在砰盘上沾上了泥土,将使测量值小于物体的真实质量砰盘上沾上了泥土,将使测量值小于物体的真实质量考点:杠杆的平衡分析法及其应用.专题:简单机械.简单机械.分析:根据杠杆平衡条件来分析,在物体质量不变,力臂不变的情况下,在秤砣上吸附一块磁铁相当于改变了秤砣的重力,重力变大,力臂变小,将使测量值小于物体的真实质量.用B提纽时,改变了支点位置,相当于物体的力臂变大,该秤的最大秤量值比用A提纽时的最大秤量值小.提纽时的最大秤量值小.解答:解:A、在秤砣上吸附一块磁铁相当于改变了秤砣的重力,重力变大,力臂变小,从秤砣读取的数变小,将错误;使测量值小于物体的真实质量,故A错误;B、若秤砣掉了一小块,相当于改变了秤砣的重力,秤砣重力变小,力臂变大,从秤砣读取的数变大,将使正确;测量值大于物体的真实质量,故B正确;C、用B提纽时,改变了支点位置,相当于物体的力臂变大,该秤的最大秤量值比用A提纽时的最大秤量错误;值小,故C错误;D、在砰盘上沾上了泥土,相当于增大了物体的质量,杆秤平衡时,杆秤读数变大,将使测量值大于物体的错误;真实质量,故D错误;故选B.点评:本题是一道关于杠杆平衡的应用题,知道杆秤的工作原理,确定支点、动力、动力臂、阻力与阻力臂后,应用杠杆平衡条件认真分析即可正确解题.本题考查学生对杠杆平衡条件的理解并会分析实际问题.4.使用天平称量物体质量前,发现托盘天平横梁的指针如图所示,则应(.使用天平称量物体质量前,发现托盘天平横梁的指针如图所示,则应( )A.将游码向左调节游码向右调节游码向左调节 B.将游码向右调节C.向右端调节平衡螺母左端调节平衡螺母右端调节平衡螺母 D.向左端调节平衡螺母考点:天平的使用.应用题;图析法.专题:应用题;图析法.天平使用之前首先要进行调平,方法是:分析:天平使用之前首先要进行调平,方法是:(1)天平放在水平台上,将游码移动到标尺左端的零刻度线上;)天平放在水平台上,将游码移动到标尺左端的零刻度线上;)调节横梁右侧的平衡螺母,当指针指到分度盘的中央位置时,天平平衡;(2)调节横梁右侧的平衡螺母,当指针指到分度盘的中央位置时,天平平衡;(3)如指针往左偏,应向右调节平衡螺母;如向右偏,应向左调节平衡螺母,简记为“左偏右旋、右偏左旋”.解答:解:题干图中,指针指在分度盘的左侧,说明左盘比较重,因此调节平衡螺母向右移动,直到指针指在分读盘的中央为止.读盘的中央为止.故选C.点评:天平平衡的标志有两个,一是指针左右摆动的幅度一样大;二是横梁静止时,指针指在分度盘的中线处,调平时通过调节平衡螺母实现,称量时通过增减砝码和移动游码实现的.调平时通过调节平衡螺母实现,称量时通过增减砝码和移动游码实现的.5.如图所示,杠杆上有两个质量不等的球m 1>m 2,杠杆在水平位置平衡,杠杆自重不计.如果两球以相同的速度向支点运动,则杠杆(向支点运动,则杠杆( )A . 仍能平衡能平衡B . 不能平衡,右侧将下沉能平衡,右侧将下沉C . 不能平衡,左侧将下沉能平衡,左侧将下沉D . 条件不够,无法判断件不够,无法判断考点: 杠杆的平衡分析法及其应用.专题: 应用题;图析法.应用题;图析法.分析: 两球以相同的速度向支点运动,即相等的时间内运动的路程相等,那么质量大的球其力×力臂减小的快,根据杠杆原理可分析知道杠杆向小球(质量小)那边倾斜,最终导致小球反向滑落.解答: 解:∵m 1>m 2, 两球以相同的速度向支点运动,即相等的时间内运动的路程相等,即△L 1=△L 2,∴△m 1gl 1>△m 2gl 2即质量大的那边:重力×力臂减小的快,力臂减小的快,∴根据杠杆原理可分析知道杠杆向小球(质量小)那边倾斜,最终导致小球反向滑落.故选B .点评: 注意:一开始杠杆在水平位置平衡,一开始杠杆在水平位置平衡,说明重球离支点近,说明重球离支点近,如果依旧平衡,当重球到达支点后当重球到达支点后 轻球还没到达,这时杠杆往质量轻的那边倾斜.这时杠杆往质量轻的那边倾斜.6.如图所示,在均匀的杠杆两端分别放上A 、B 两支大小相同、长度不等的蜡烛,这时杠杆平衡.若蜡烛燃烧速度相同,过一段时间后[蜡烛未燃完]杠杆将(杠杆将( )A . 左端下沉端下沉B . 右端下沉端下沉C . 仍平衡平衡D . 无法确定法确定考点: 杠杆的平衡条件.专题: 应用题;简单机械.应用题;简单机械.分析: (1)根据杠杆平衡条件先分析出两力臂的大小;)根据杠杆平衡条件先分析出两力臂的大小;(2)蜡烛燃烧速度相同,经过一段时间后,蜡烛燃烧的质量相同、重力相同,求出蜡烛燃烧后左右两边力与力臂的乘积,然后比较它们的大小,根据左右两边力与力臂乘积的大小,判断杠杆的状态.解答: 解:解:(1)由图可知,m A >m B ,G=mg ,所以G A >G B ,开始,杠杆平衡,,开始,杠杆平衡,由杠杆平衡条件可得:G A L A =G B L B ,∵G A >G B , ∴L A <L B ; (2)蜡烛燃烧速度相同,过一段时间后,蜡烛减少的质量△m 相同,相同,减少的重力△G 相同,左边(G A ﹣△G )L A ,右边(G B ﹣△G )L B , ∵G A L A =G B L B , ∴(G A ﹣△G )L A ﹣(G B ﹣△G )L B =G A L A ﹣G B L B ﹣△GL A +△GL B =△GL B ﹣△GL A , ∵L A <L B , ∴△GL B ﹣△GL A >0, (G A ﹣△G )L A ﹣(G B ﹣△G )L B >0, 即:左边力与力臂的乘积大于右边力与力臂的乘积,杠杆不再平衡,左端下沉.即:左边力与力臂的乘积大于右边力与力臂的乘积,杠杆不再平衡,左端下沉. 故选A .点评: 本题考查了杠杆平衡条件的应用,有一定难度,根据题意判断出哪边力与力臂的乘积大,是解题的关键.7.如图所示,杠杆OA 可绕支点O 转动,B 处挂一重物G ,在A 处用一竖直向上的力F 拉杠杆.当杠杆和竖直墙之间夹角逐渐增大时,为了使杠杆平衡,则(之间夹角逐渐增大时,为了使杠杆平衡,则( )A . F 逐渐增大,但F <G B . F 大小不变,但F >G C . F 逐渐减小,但F >G D . F 大小不变,但F <G 考点: 杠杆的动态平衡分析.专题: 压轴题;简单机械.压轴题;简单机械.分析: 从支点向力的作用线作垂线,垂线段的长度即力臂.根据杠杆平衡条件动力×动力力臂=阻力×阻力力臂分析力臂变化可知力的变化.力臂变化可知力的变化.解答: 解:如图所示,根据相似三角形知识可知,L G 与L F 的比值不变,并且L G <L F ;由杠杆平衡条件得:GL G =FL F ,则:F==G ,由于G 和L G 与L F 的比值都不变,则力F 大小不变;大小不变;因为L G <L F ,所以G >F .故选D .点评: 本题考查学生对杠杆平衡条件的理解和运用,是一道难题.本题考查学生对杠杆平衡条件的理解和运用,是一道难题.8.如图所示,有一固定在墙壁上的可绕支点O 转动杠杆,在杠杆上A 点悬挂一装有水的敞口水杯,在B 点施加竖直向上的拉力F 使杠杆在水平位置保持平衡.则拔下水杯底部的塞子后,拉力F 随时间t 变化的图象是(变化的图象是( )A .B .C .D .考点: 杠杆的平衡条件.专题: 压轴题;简单机械.压轴题;简单机械.分析: 随着水不断流出,水杯及水的重力不断减小,当杯子中的水完全流出时,杯子的重力不再改变,应用杠杆平衡条件分析答题.平衡条件分析答题.解答: 解:拉力F 是动力,杯子及杯子中水的重力是阻力,是动力,杯子及杯子中水的重力是阻力,由杠杆平衡条件得:F ×OB=G ×0A ,则F=,拔下水杯底部的塞子后,OA、OB不变,随着水不断流出,不变,随着水不断流出,G减小,因此F减小,当杯子中的水全部流出后,G不再改变,不再改变,正确.力F不再改变,由图示可知C符合的F变化情况,故C正确.故选C.如何变化,是正确解题的关键.点评:本题考查了杠杆平衡条件的应用,根据杠杆平衡条件,判断出力F如何变化,是正确解题的关键.9.利用一个滑轮组提升物体,不计摩擦阻力,则用这个滑轮组(.利用一个滑轮组提升物体,不计摩擦阻力,则用这个滑轮组( )A.提升的物体重力越小,机械效率越高升的物体重力越小,机械效率越高B.提升的物体重力越大,机械效率越高升的物体重力越大,机械效率越高C.把物体提的越高,机械效率越高物体提的越高,机械效率越高D.自由端拉力越大,机械效率越高由端拉力越大,机械效率越高考点:增大或减小机械效率的方法.要解答本题需掌握:增大和减小滑轮组机械效率的方法有哪些.分析:要解答本题需掌握:增大和减小滑轮组机械效率的方法有哪些.解答:解:对同一滑轮组来说,提高机械效率的方法是:增加提升的物重或者减轻动滑轮的重力.而物体提升的高度和绳子自由端的拉力,都不能影响到滑轮组的重力.而物体提升的高度和绳子自由端的拉力,都不能影响到滑轮组的重力.故选B.本题主要考查学生对:改变滑轮组机械效率的方法的了解和掌握.点评:本题主要考查学生对:改变滑轮组机械效率的方法的了解和掌握.10.如图所示,三个滑轮下悬挂的重物的质量相等,若滑轮、绳的重力及滑轮与轴的摩擦忽略不计,则F1、F2、F3的关系为( )的关系为(A.F1=F2=F3B.F1>F2>F3C.F2>F3>F1D.F3>F1>F2考点:定滑轮及其工作特点;动滑轮拉力的计算.应用题.专题:应用题.分析:使用滑轮组时,有几段绳子承担动滑轮和物体的重,拉力就是重力的几分之一,因此承担动滑轮和物体的重的绳子段数越多越省力.重的绳子段数越多越省力.解答:解:三个滑轮下悬挂的重物的质量相等,所以左边的滑轮为动滑轮,则F1=G;中间的滑轮使用时,则F2=2G;右边的滑轮为定滑轮,则F3=G;由此可知:F2>F3>F1.故选C.本题解答时可以利用物体受力平衡,根据合力为零分析解答.点评:本题解答时可以利用物体受力平衡,根据合力为零分析解答.11.如图所示,三个滑轮拉同一物体在水平面作匀速直线运动,所用拉力分别为F1、F2、F3,不计滑轮重和绳子与滑轮之间的摩擦,那么有( )滑轮之间的摩擦,那么有(A.F1>F2>F3B.F1<F2<F3C.F3>F1>F2D.F2<F3<F1考点:滑轮组绳子拉力的计算;摩擦力的大小.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力学综合计算题——杠杆滑轮综合08年丰台区二模:某人用如图27所示的滑轮组,使质量为0.27kg的铝块从空中匀速下落到底面积为100cm2的盛有水的容器中。
当铝块接触水面之前,滑轮组的机械效率是54%,(不计绳重、摩擦,g取10N/kg,ρ铝=2.7×103kg/m3)求(1)当铝块浸没在水中时,滑轮组对铝块的拉力为多少?(2)铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率是多少?(3)若用该滑轮组将质量相等、密度之比ρ甲:ρ乙=2:3的两个实心物体甲乙放入盛有足够多水的容器中,撤去滑轮组后,当甲、乙两物体静止后,水对甲、乙的浮力比F甲:F乙=6:5,则甲的密度是多少?08年石景山区一模:如图24所示,用滑轮组将重为G=1800N的金属块打捞出水面,不计绳重、摩擦和水对金属块的阻力,作用在绳自由端拉力的功率始终保持1680W,金属块浸没在水中时匀速提起的速度为v1=0.8m/s,金属块的密度为8×103kg/m3,g取10N/kg。
求:(1)金属块未露出水面以前的机械效率η(2)金属块被提出水面后匀速提起的速度v2(计算结果保留到小数点后两位)08年怀柔区二模:某桥梁施工队的工人用如图24所示的滑轮组匀速打捞沉在水中的工件。
已知工件的质量为100kg工人的质量为70kg。
工件打捞出水面前与工件完全被打捞出水后工人对地面的压力之比为15:2,工件在水中时,滑轮组的机械效率为60% 。
若不计摩擦、绳重及水的阻力,g取10N/kg 。
求:(1)工件浸没在水中时所受的浮力F浮;(2)工件完全打捞出水面后,滑轮组的机械效率η2;(结果保留两位有效数字)(3)工件完全打捞出水面后,以0.2m/s的速度被匀速提升,工人拉绳的功率P2。
图26图27F09年崇文区一模:小文的体重为600 N ,当他使用如图24所示的滑轮组匀速提升水中的体积为0.01m 3的重物A 时(重物始终未出水面),他对地面的压强为8.75×103 Pa 。
已知小文与地面的接触面积为4002cm 。
当他用此滑轮组在空气中匀速提升重物B 时,滑轮组的机械效率是80%。
已知重物A 重物B 所受重力之比G A ︰G B =5︰12,若不计绳重和摩擦,g=10N/kg 。
求:(1)提升重物A 时小文对地面的压力。
(2)物体A 的密度。
(3)在水中提升重物A 时滑轮组的机械效率。
(4)重物A 完全出水面后,以0.2m/s 的速度匀速上升,小文拉绳的功率P 。
09年顺义区一模:某桥梁施工队的工人用如下图所示的滑轮组匀速打捞沉在 水中的工件A 。
已知工件的质量为100kg ,工人的质量为70kg 。
工件A 打捞出水面之前与工件完全被打捞出水后工人对地面的压力之比为15:2,工件在水中时,滑轮组的机械效率为60% 。
若不计摩擦、绳重及水的阻力,g 取10N/kg 。
求:(1)工件A 浸没在水中时所受的浮力浮F ;(2)工件A 完全打捞出水面后,滑轮组的机械效率2 ;(3)工件A 完全打捞出水面后,以0.2m/s 的速度被匀速提升,工人拉绳的功率2P 。
09海淀区一模:如图23所示,质量为70kg 的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的石材,3.09年海淀区一模:该滑轮组中动滑轮质量为5kg 。
当工人用120N 的力拉滑轮组的绳端时,石材仍沉在水底不动。
工人继续增大拉力将石材拉起,在整个提升过程中,石材始终以0.2m/s 的速度匀速上升。
在石材还没有露出水面之前滑轮组的机械效率为η1,当石材完全露出水面之后滑轮组的机械效率为η2。
在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比为29:21。
绳重及滑轮的摩擦均可忽略不计,石材的密度ρ石=2.5×103kg/m 3,取g =10N/kg ,求:(1)与打捞前相比,当人用120N 的力拉绳端时,水池底部对石材的支持力变化了多少;(2)η1与η2的比值;(3)当石材完全露出水面以后,人拉绳子的功率。
图2309年怀柔区一模:如图21所示,某工地用固定在水平工作台上的卷扬机(其内部有电动机提供动力)通过滑轮组匀速提升货物,已知卷扬机的总质量为120kg ,工作时拉动绳子的功率恒为400W 。
第一次提升质量为320kg 的货物时,卷扬机对绳子的拉力为F 1,对工作台的压力为N 1;第二次提升质量为240kg 的货物时,卷扬机对绳子的拉力为F 2,对工作台的压力为N 2。
已知N 1与N 2之比为25:23,取g=10N/kg ,绳重及滑轮的摩擦均可忽略不计。
求:(1)卷扬机对绳子的拉力F 1的大小; (2)第一次提升货物过程中滑轮组的机械效率;(3)前后两次提升货物过程中货物竖直向上运动的速度之比。
09年平谷一模:体重为510N 的人,站在水平地面上对地面的压强为p 1, .如图3所示,用滑轮组拉物体A 沿水平方向做匀速运动,此时人对地面的压强为p 2,压强变化了2750pa 。
已知人一只脚的面积是200cm 2,滑轮组的机械效率为80%。
(不计绳重和摩擦,地面上的定滑轮与物体A 相连的绳子沿水平方向,地面上的定滑轮与动滑轮相连的绳子沿竖直方向,人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,)。
求:(1)绳对人的拉力; (2)物体A 与地面的摩擦力;(3)若在物体A 上再放一个物体B,滑动摩擦力增大了30N,此时该装置的机械效率是多少?(7分)09年西城区二模:工人利用滑轮组按照图25所示的方式提升货箱。
工人的体重为G 人=800N 。
提升第一个货箱时,工人用F 0=500N 的竖直向下的力拉绳时,没有提起货箱。
工人用F 1=600N 的竖直向下的力拉绳时,货箱恰能以0.2m/s 的速度匀速上升。
此时工人提升货箱的效率为62.5%。
第二个货箱比第一个货箱重500N ,工人仍能提起第二个货箱并使第二个货箱以0.1m/s的速度匀速上升。
求:⑴第一个货箱未被拉动时,水平地面对货箱的支持力;⑵工人提升第一个货箱和第二个货箱做功功率变化量的大小。
09年丰台区二模:如图18所示,金鹏同学为他的妈妈设计了一款颈椎拉伸器,左边滑轮下端是由密度为3×103kg/m 3的圆柱体合金块充当配重,它的底面积为5dm 2,高为4dm 。
右边自由端安放颈圈套在患者的颈部。
当颈部承受拉力为55N 时,配重对地面的压强为p 1,当颈部承受的拉力为105N 时,配重对地面的压强为p ’1,已知p 1:p ’1‘=2:1,妈妈重600N ,忽略绳重和摩擦,g =10N/kg ,求:(1)配重单独放置时对地面的压强;(2)动滑轮自重;(3)当配重与地面的压强为零时,妈妈对地面的压力为多少。
图 3 图2109年宣武区一模:如图25所示,是一个上肢力量健身器示意图。
配重A受到的重力为350N,其底面积为5×10-2m2。
B、C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE=3OH。
小明受到的重力为500N,当他通过细绳在H点分别施加竖直向下的拉力T1、T2时,杠杆两次都在水平位置平衡,小明对地面的压力分别为F1、F2,配重A受到的拉力分别为F A1、F A2,配重A对地面的压强分别为p1、p2,且两次A对地面的压强相差2×103Pa。
已知F1∶F2=4∶3,p1∶p2=3∶2 。
杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计。
求:(1) 拉力F A2与F A1之差;(2) 小明对地面的压力F1;(3)当小明通过细绳在H点施加竖直向下的拉力T 3时,配重A匀速上升2cm,此时滑轮组的机械效率η。
(请画出相关..受力分析图.....)09年怀柔区二模:某校科技小组的同学设计了一个从水中打捞物体的模型,如图22所示其中D、E、G、H都是定滑轮,M是动滑轮,杠杆BC可绕O点在竖直平面内转动,OC∶OB=3∶4。
杠杆BC和细绳的质量均忽略不计。
人站在地面上通过拉绳子提升水中的物体A,容器的底面积为300 cm2,人的质量是70 kg,通过细绳施加竖直向下的拉力时, A始终以0.6m/s的速度匀速上升。
当杠杆到达水平位置时物体A总体积的五分之三露出液面,液面下降了50cm,此时的拉力为F1 ,它的功率为P1,地面对他的支持力是N1;当物体A完全离开液面时,此时通过细绳施加竖直向下的拉力为F2 ,它的功率为P2,地面对人的支持力是N2。
已知A的质量为75kg,N1∶N2=2∶1,忽略细绳与滑轮的摩擦以及水对物体的阻力,g取10N/kg。
求:⑴当物体露出液面为总体积的五分之三时,物体所受的浮力;⑵动滑轮M受到的重力;⑶P1∶P2的值。
09年西城区一模:在图23所示装置中,甲物重G甲=10N,乙物重G乙是动滑轮重G轮的8倍。
物体乙跟地面的接触面积为1.5×10-2m2。
轻杆AB可以绕O点转动,且OA∶OB=2∶1。
不计轴摩擦,装置如图所示处于平衡状态时,乙对水平地面的压强P=2×103Pa。
求:此时动滑轮对物体乙的拉力F拉;若在物体甲下面再加挂物体丙,恰使物体乙对地面的压强为零。
求:丙的物重G丙。
图25图2309年门头沟二模:火车道口处设置人工控制的栏杆,图25是栏杆的示意图。
密度和粗细均匀的栏杆全长6m ,质量为40kg 。
栏杆的重心位于P 点,栏杆可绕O 点在竖直平面内无摩擦转动。
栏杆的H 端通过滑轮组来提升栏杆,其中A 、B 、D 、E 、都是定滑轮,C 是动滑轮,T 为固定在水平地面上的挂钩。
当火车通过岔道口后, 管理人员用力F 1竖直向下拉绳子, 栏杆恰好在水平位置平衡。
管理人员为了减轻自己的工作强度,他在H 端下方的绳子上加挂了一个质量为10kg 的重物,用力F 2以0.2m/s 的速度匀速拉动绳子使栏杆逆时针转动45°角时车辆放行。
此时管理人员将绳端固定在挂钩T 上。
已知:F 1∶F 2=17∶15;OH=1m, 忽略细绳与滑轮的摩擦。
g 取10N/kg 。
求:⑴动滑轮C 的重力; ⑵F 1的大小; ⑶F 2的功率;08年中考题:如图是一个上肢力量健身器示意图。
配重A 受到的重力为1200N ,其底面积为5×10-2m2. B 、C 都是定滑轮,D 是动滑轮;杠杆EH 可绕O 点在竖直平面内转动,OE :0H =2:5。
小成受到的重力为600N ,他通过细绳在H 点施加竖直向下的拉力为T1时,杠杆在水平位置平衡,小成对地面的压力为F1,配重A 受到的拉力为FA1,配重A 对地面的P1为6×103pa 。
小成在H 点施加竖直向下的拉力为T2时,杠杆仍在水平位置平衡,小成对地面的压力为F2,配重A 受到的拉力为FA2,配重A 对地面的压强P2为4×103pa 。
