最新人教版高中数学选修1-1 3.1.1变化率与导数优质课件
高中数学选修1-1精品课件2:3.1.1 变化率问题

[点评] 瞬时速度是平均速度在 Δt→0 时的极限值.因此, 要求瞬时速度,应先求出平均速度.
(2012~2013 学年度山东潍坊高二期末测试)已知物体的运
动方程是 S=-4t2+16t(S 的单位为 m;t 的单位为 s),则该物
体在 t=2s 时的瞬时速度为( )
A.3m/s
B.2m/s
C.1m/s
题目类型二、瞬时变化率
[例 2] 以初速度 v0(v0>0)垂直上抛的物体,t 秒时的高 度为 s(t)=v0t-12gt2,求物体在时刻 t0 处的瞬时速度.
[解析] ∵Δs=v0(t0+Δt)-12g(t0+Δt)2-(v0t0-12gt02)=(v0 -gt0)Δt-12g(Δt)2,
∴ΔΔst=v0-gt0-12gΔt,当 Δt→0 时,ΔΔst→v0-gt0. 故物体在时刻 t0 的瞬时速度为 v0-gt0.
题目类型一 平均变化率
[例 1] 求函数 y=x3 在 x0 到 x0+Δx 之间的平均变化率,并 计算当 x0=1,Δx=12时平均变化率的值.
[分析] 直接利用概念求平均变化率,先求出表达式,再 直接代入数据就可以得出相应的平均变化率.
[解析] 当自变量从 x0 变化到 x0+Δx 时,函数的平均变化 率为fx0Δ+xΔx=x0+ΔΔxx3-x03=3x20+3x0Δx+(Δx)2.
3.瞬时变化率、瞬时速度
物体在某一时刻的速度称为瞬时速度.
4.一般地,如果物体的运动规律是 s=s(t),那么物体在
时刻 t 的瞬时速度 v,就是物体在 t 到 t+Δt 这段时间内,当 Δt→0
时平均速度的极限,即 v=lim Δt→0
ΔΔst为 t 时刻的瞬时速度.
1.在高台跳水运动中,运动员在 t1≤t≤t2 这段时间里的位
人教A版高中数学选修1-1《三章 导数及其应用 3.1 变化率与导数 3.1.2 导数的概念》赛课课件_2

问题二:请大家继续思考,当Δt取不同值时,尝试
计算 v 4.9t 13.1 的 值 ,同时观察讨论,表格中
的数据有着怎样的规律?
Δt
-0.1 -0.01 -0.001 -0.0001 -0.00001
……….
3.1.2导数的概念
1
在高台跳水运动中,运动员相对水面的高度h
(单位:m)与起跳后的时间t(单位:s)存
在函数关系
计算运动员
在 0 t 65 这段时间里的平均速度,并
49
思考下面的问题:
(1)运动员在这段时间里是静止的吗?
(2)你认为用平均速度描述运动员的运动状态 有什么问题吗?
2
平均速度不一定能反映运动员在某一时 刻的运动状态,可以看出,平均速度只 能粗略地描述物体在某段时间内的运动 状态,为了能更精确地刻画物体运动, 我们有必研究某个时刻的速度即
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或
,即
14
由导数的定义可知, 求函数 y = f (x)在x=x0的导数的一般方法:
1.求平均变化率 2. 取极限求值 一平、二极 同学们可以这么记求导数的方法:“一贫而急”
瞬时速度。
3
什么是瞬时速度呢? 如何求瞬时速度呢?
4
3.1.2导数的概念
5
我们把物体在某一时刻的速度称为
瞬时速度.
又如何求 瞬时速度呢?
6
问题一:请大家思考如何求运动员的瞬时速度, 如t=2时刻的瞬时速度?
平均变化率
高中数学选修1-1优质课件9:3.1.1变化率问题

课前热身
1.函数 y=f(x)在区间[x1,x2]上的变化率可用f(xx2)2--fx(1x1),我
们把这个式子称为函数 y=f(x)从 x1 到 x2 的_平__均__变__化__率_.习惯上 用 Δx 表示___x__2-_x_1___,Δy 表示__f(_x_2_)_-f_(_x_1_) .
自测自评
1.已知函数 f(x)=2x2-4 的图象上一点(1,f(1))及附近一点
(1+Δx,f(1)+Δy),则ΔΔyx等于( )
A.4
B.4x
C.4+2Δx
D.4+2(Δx)2
【解析】ΔΔyx=f(1(1++ΔΔxx)-)-f(11)
2(1+Δx)2-4-2×12+4
=
Δx
=4+2Δx.
【答案】C
(3)ΔS=S(0.5)-S(0) =3×0.5-0.52-0=1.25, Δt=0.5-0=0.5. ∴-v =ΔΔSt =10.2.55=2.5. ∴从 t=0 到 t=0.5 的平均速度为 2.5.
规律技巧 物体在 t=0 时的瞬时速度也叫做物体的初速 度,当 t=0 时,初速度 v0 不一定为 0.
当 x0=2,Δx=12时,函数在[2,2.5]上的平均变化率为 k2=6×2 +3×0.5=13.5;
当 x0=3,Δx=12时,函数在[3,3.5]上的平均变化率为 k3=6×3 +3×0.5=19.5,
所以 k1<k2<k3.
2.设物体的运动方程为 S=S(t),如果一个物体在时刻 t0 时位于 S(t0),到时刻 t0+Δt 这段时间内,物体的位置增量是 ΔS =S(t0+Δt)-S(t0).那么位置增量 ΔS 与时间增量 Δt 的比,就是
(人教)高中数学选修1-1(课件):3.1变化率与导数3.1.1变化率问题3.1.2导数的概念

问範精说7想_想(1)在经营某商品中,甲挣到10万元,乙挣到2万元,如何比较和评价甲,乙两人的经营成果?(2)在经营某商品中,甲用5年时间挣到10万元,乙用5个月时间挣到2万元,如何比较和评价甲,乙两人的经营成果?痒龜说师t 屮仅比怨一金養的安祂是水经过虹吸管从容器甲中流向容器乙,fs 后容器甲中水的体积(单位: cm3)f计算第一个ios内砌如纯化。
现有宿迁市某年3月和4月某天日最高气温记载.时间3月18日4月18日4月20日日最高气温 3.5°C18.6°C33・4°C温差15・1°C温差14.8 °C问龜精境“衣济昌衬枪过山车是一项富有刺激性的娱乐工具也风驰电掣、有惊无险的快感令不少人r 卜B>-x c -x B该比值近似量化BQ 间 这一段曲线的陡哨程度.称该比值为曲线在B.C 之 间这一段年谢麦祀半・容易看出点B.C 之间的曲线较* A.B 之间的曲线更加"陡哨〃・ 如何量化陡哨程度呢? OAy建构數修鰹捡4均变化率的定义: 一般地,函数介莊区间[Xp%2]±的平均变化率为说明:⑴平均变化率的实质就是:两点(引, 佩現⑥)连线的斜率.(皿吏代曲思您丿(2)平均变化率是曲线陡峭程度的“数量化”,或者说曲线陡峭程度是平均变化率“视觉化”(救形箱合思越丿AyAx /(兀2)- /(兀1)例1、已知函数f(x)=2x+l, g{x) =-2x ,分另!J 计算在区间[-3, T], [0, 5]上f(x)及g{x)的平均变化率•思考:一次函数y二kx+b在区间[m, n]上的平均变化率有什么特点?例2、已知函数/(x)=x1 2,分别计算/匕)在下列区间上的平均变化率:⑴[1, 3];弋(2)[1, 2];3\(3)[1, 1.1];2.1\(4)[1, 1.001]・2.001变题:(5) [0.9, 1]; 1.9 \1 3 x 篠后思考:为什么趋近于2呢?2的几何意义是什么?救摩宗用(6)[0.99, 1];1.99(7)[0.999, 1].] 999仁平均变化率的定义:学/g —/g) Ax 兀 _x. 2. 平均变化率的意义:大量生活中的实例 建立数学模型数学应用 3. 求平均变化率的步骤: 这节篠我的收获是什么? ㈢救摩宗用4. 思想方法:。
最新-人教A版高中数学选修11 311 变化率和导数的概念 课件 共28张 精品

Δx
Δx
(3)求极限li m Δy. Δx→0 Δx
2.瞬时变化率的变形形式
li m
Δx→0
fx0+Δx-fx0=li m
Δx
Δx →0
f
x
0-Δx-fx -Δx
0=li m Δx→0
fx0+nΔx-fx0 nΔx
=li m Δx→0
f
x0+Δx
-f 2Δx
x
0-Δx
=f′(x
0).
学以致用
3、求函数 y=x-1在 x=1 处的导数. x
(3)求平均变化率Δy=f Δx
x1-fx x1-x0
0.
学以致用
1、求函数 y=x3 从 x0 到 x0+Δx 之间的平均变化率,并计算 当 x0=1,Δx=12时平均变化率的值.
解:当自变量从 x0 变化到 x0+Δx 时,函数的平均变化率为
Δy=fx0+Δx-fx0=x0+Δx3-x30
Δx
1+1 Δx-1 Δx
= lim Δx→0
-1 1+Δx1+
1+Δx=-12.
课堂小结
1.体会数学的博大精深以及学习数学的意义. 2.平均变化率、瞬时变化率和导数的数学背景.
作业
生活中没有什么可怕的东西,只有需 要理解的东西.
——居里夫人
谢谢观看
下课
(D )
2.函数
f(x)在
x0
处可导,则lim h→0
fx0+h-fx0 h
A.与 x0、h 都有关
B.仅与 x0 有关,而与 h 无关
C.仅与 h 有关,而与 x0 无关
D.与 x0、h 均无关
( B)
3.已知函数 f(x)=2x2-1 的图象上一点(1,1)及邻近一点(1+
人教版高中数学选修1-1-3.1 变化率与导数 3.1.3ppt课件

知识点2 导函数的概念 观察图形,回答下列问题:
问题:导函数f′(x)与f′(x0)有何区别与联系?
【总结提升】
导函数的相关概念
(1)函数在一点处的导数f′(x0),就是在该点处函数值的改变量与自 变量的改变量之比的极限值,它是一个常数,不是变数.
(2)函数的导数是对某一区间内任意点x而言的,就是函数f(x)的导函
(4)根据斜率相等求得x0,然后求得斜率k. (5)根据点斜式写出切线方程. (6)将切线方程化为一般式.
【变式训练】求曲线f(x)= 2 在点(-2,-1)处的切线的方程.
x 【解析】由于点(-2,-1)恰好在曲线f(x)= 上2 ,所以曲线在点(-2,-1)
处的切线的斜率就等于函数f(x)= Nhomakorabea 在点(-2x ,-1)处的导数.
【补偿训练】如果曲线y=x3+x-10的一条切线与直线y=4x+3平行,那么 曲线与切线相切的切点坐标为 ( ) A.(1,-8) B.(-1,-12) C.(1,-8)或(-1,-12) D.(1,-12)或(-1,-8)
【解析】选C.设切点坐标为P(x0,y0), 则y0=x03+x0-10的切线斜率为k=
1 2
【解析】(1)选A.因为y′|x=1= lima(1x)2a12
x0
x
= lim2axa((2xa)2+= alΔim x)=2a,
所以x 20a=2,所x以a=1.x 0
(2)由导数的几何意义可知k1,k2分别为曲线在A,B处切线的斜率,而
k3=f(2)-f(1)= f 2 f为(1直)线AB的斜率,
所以切线的方程为y=x-1.
即x-y-1=0.
【方法技巧】过曲线上一点求切线方程的三个步骤
人教A版高中数学选修1-1《三章 导数及其应用 3.1 变化率与导数 3.1.1 变化率问题》赛课课件_2
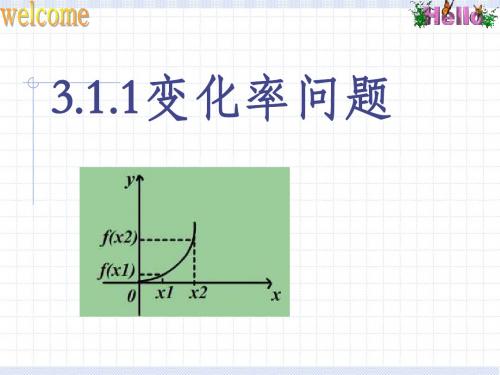
x2 x1
平均速度
思考:求t1到t2时的平均速度.
v S (t2 ) S(t1) t2 t1
课时小结
1.理解平均变化率的含义和表示; 2.应用平均变化率解决一些问题的方法; 3.体会由实际生活问题到数学模型的归纳思想。
课后作业
1.习题3.1A组第1题,B组第2题; 2.预习下一节内容。
动状态, 那么:
在0 ≤ t ≤0.5这段时间里,
在1≤ t ≤2这段时间里,
探究讨论:
计算运动员在0 t 65 这段时间的平均速度,思考 49
下面的问题:(1)运动员在这段时间里静止吗? (2)你认为用平均速度描述运动员的
运动状态有什么问题吗?
平均变化率
平均变化率:式子
f
(x2 ) x2
3
由气球体积V(r) 4 r3 r (V) 3V .
3
4
当v由0 1时,气球的平均变化率:r (1) r (0) 0.62(dm/L), 10
当v由1 2时,气球的品均变化率:r (2) r (1) 0.16(dm/L) 2 1
结论:随着气球体积逐渐变大,它的平均膨胀率逐渐变小.
3.1.1变化率问题
目标分析
[自学目标]: 了解导数概念的实际背景 [重点]:气球膨胀率和高台跳水问题的理解 [难点]:计算平均变化率的方法
平均变化率
问题1 气球膨胀率
在吹气球的过程中, 可发现,随着气球内空气容量的 增加, 气球的半径增加得越来越慢. 从数学的角度, 如何 描述这种现象呢?
f (x1) x1
称为f
x1 到f
x2
的
平均变化率
令Δ x = x2 – x1 , Δ f = f (x2) – f (x1) ,
高中数学选修1-1第3章3.1.1-3.1.2变化率与导数课件人教A版

到������2 的平均变化率.
习惯上用Δx表示x2-x1,即Δx=x2-x1,可把Δx看作是相对于x1的一个 “增量”,可用x1+Δx代替x2.类似地,Δy=f(x2)-f(x1).于是,平均变化率可 Δ������ 表示为 .
������
名师点拨 1.变化率问题来源于现实生活中的实际问题.平均变化 率是一个比值,它是表示一个量随另一个量变化快慢的重要指标, 如物体运动的平均速度、气球的平均膨胀率等.函数的平均变化率 就是从这些实际问题中抽象出来的一个重要数学概念. 2.Δx≠0,但可正可负;要注意Δx是一个整体符号,而不是Δ与x相乘. 3.改变量的对应:若Δx=x2-x1,则Δy=f(x2)-f(x1),而不是Δy=f(x1)-f(x2).
2.瞬时变化率
函数 y=f(x)在 x=x0 处的瞬时变化率是函数 f(x)从 x0 到 x0+Δx 的 平均变化率在 Δx→0 时的极限,即 lim
f(x0 +������x)-f(x0 ) ������x Δ������ →0
= ������������������ Δ������. ������x →0
������
名师点拨 瞬时变化率是当自变量的改变量趋近于0时,平均变化 率趋近的值,它刻画了函数在某一点处变化的快慢.瞬时变化率可 反映运动物体的瞬时速度、切线的斜率等.
-9-
3.1.1 变化率问题 3.1.2 导数的概念
1 2 3
M 目标导航
UBIAODAOHANG
Z 知识梳理
HISHI SHULI
-7-
3.1.1 变化率问题 3.1.2 导数的概念
1 2 3
M 目标导航
UBIAODAOHANG
人教A版高中数学选修1-1第三章3.1.1变化率问题教学课件

我们都吹过气球,回忆一下吹气球的过程, 可以发现,随着气球内空气容量的增加,气 球的半径增加越来越慢.
从数学角度,如何描述这种现象呢?
问题一:气球膨胀率 气球的体积V(单位:L)与半径r(单
位:dm)之间的函数关系是:
V (r) 4 r3
3
用V 表示r得:
r(V ) 3 3V
4
问题一:气球膨胀率
我们称它为函数 y f (x)在x x0处的导数;
例1将原油精练为汽油、柴油、塑胶等各种
不同产品,需要对原由进行冷却和加热。如
果第 x(h)时,原油的温度(单位:0C)
为 y f (x) x2 7x 15(0 x 8).计算第2(h)和第 6(h)时,原油温度的瞬时变化率,并说明它
们的意义。 关键是求出:
则平均变化率为:y 20 5x x
探 究
计算:运动员在 0 t 65
49
这段时间内的平均速度,
并思考下面的问题: P73
(1)运动员在这段 时间里是静止的吗?
(2)你认为用平均速度描述运动员的运动状态有 什么问题吗?
平均速度只是粗略地描述这段时间内运动员 运动的快慢,不能反应他在这段时间里运动状态, 需要用瞬时速度描述运动状态。
x1 x2 x
平均变化率表示函数图像上两点连线的斜
率,即割线的斜率。
随堂练习
1.函数 f (x) x2 在区间 1,3上的平均变化率( )
A. 4 B. 2
C. 1
4
D. 3
4
2.求函数y=5x2+6在区间[2,2+△x]内的平均变化
率。
解:y 5(2 x)2 6 (5 22 6) 20x 5x2
它说明在第2(h)附近,原 油温度大约以3 0C/H的速 度降落;在第6(h)附近, 原油温度大约以5 0C/H的
数学:选修1-1人教版精品课件3.1.1变化率与导数

解析:分别写出 x=x0 和 x=x0+Δx 对应的函数值 f(x0) 和 f(x0+Δx),两式相减,就得到了函数值的改变量 Δy=f(x0 +Δx)-f(x0),故应选 D.
答案:D
8
2.若一质点按规律 s=8+t2 运动,则在时间段 2~2.1 中,平均速度是( ) A.4 B.4.1 C.0.41 D.-1.1
答案:3-Δx
12
5.求函数 y=x2 在点 x=1 处的导数.
解:Δy=(1+Δx) -1=2Δx+(Δx) , Δy ∴ =2+Δx.y′|x=1= lim (2+Δx)=2. Δx Δx→0
2
2
13
14
1.函数的平均变化率的理解 定义中的 x1,x2 是指其定义域内不同的两个数,记 Δx fx2-fx1 Δy =x2-x1,Δy=f(x2)-f(x1),则当 Δx≠0 时, = Δx x2-x1 称作函数 y=f(x)从 x1 到 x2 的平均变化率,理解平均变化率 应注意以下几点:
24
练 1 求函数 y=2x2+5 在区间[2,2+Δx]上的平均变化 1 率;并计算当 Δx= 时,平均变化率的值. 2
[ 解 ] 因为 Δy= 2×(2 + Δx) + 5 - (2×2 + 5)= 8Δx + Δy 2 2(Δx) ,所以平均变化率为 =8+2Δx. Δx 1 1 当 Δx= 时,平均变化率的值为 8+2× =9. 2 2
18
注意:令 x=x0+Δx,得 Δx=x-x0, fx-fx0 于是 f′(x0)= lim x x0 x-x0 fx0+Δx-fx0 与定义中的 f′(x0)= lim 意义相同. Δx Δx→0
19
函数的平均变化率 2 例 1 已知函数 f(x)=2x +3x-5. Δy (1)求当 x1=4,且 Δx=1 时,函数增量 Δy 和平均变化率Δx; Δy (2)求当 x1=4,且 Δx=0.1 时,函数增量 Δy 和平均变化率Δx; (3)若设 x2=x1+Δx.分析(1)(2)题中的平均变化率的几何意义.
人教A版高中数学选修1-1《三章 导数及其应用 3.1 变化率与导数 3.1.3 导数的几何意义》赛课课件_11

1. 已知y=f(x)的图象如图所示,则f′(xA)与f′(xB)的
大小关系是
()
A. f′(xA)>f′(xB) C.f′(xA)=f′(xB)
B.f′(xA)<f′(xB) D.不能确定
2.若曲线y=f(x)在点P(x0,f(x0))处的切线方程为 2x+y+1=0,那么( )
A.f′(x0)=0 C.f′(x0)>0
例1 求曲线y=f(x)=x2+1在点P(1,2)处的切线方 程并画出曲线在该点出的切线.
yQ
y = x 2 +1
y
P
M
x
1j
-1 O 1
【变式练习】 曲线y=f(x)=x2+1上
哪一点的切线平行于
直线4x-y-2=0?
x
例2:已知曲线y= x3上一点P(1, ), 求过点P的切线的方程.
平均速度
y=f(x) x
探究点2 导数的几何意义
在上面的研究过程中,某点的割线斜率和切线 斜率与某点附近的平均变化率和某点的瞬时变化率 有何联系?
回答
割线→切线
已知曲线y=f(x)上两点,
y
P(x0, f (x0 )), Pn (x0 x, f (x0 x))
⑴(1) yy割表线示什的么斜?率
建构新知:
当 Pn P,割线趋近于确定的位置,这个确定位置上的直线就是
曲线在点 P 处的切线
切线的定义:
y
当点Pn 沿着曲线趋近于
点 P ,即 x 0 时,割线 PPn
趋近于一个确定的位置,
这个确定位置的直线PT
o
称为点P处的切线。
注:曲线的切线,并不一定与曲线只有一 个交点, 可以有多个,甚至可以有无穷多个.
人教高中数学选修1-1课件:3.1.1 变化率问题 3.1.2 导数的概念

D.f′(x0)=b
【解析】选C. y f (x0 x) f (x0) a bgx,
x
x
f′(x0)= lim y lim (a bgx) a.
x x0
x0
3.已知函数f(x)= 1, 则 f ( 2 ) =
.
x
2
【解析】 f (
2 ) lim f (
2 x) f ( 2 )
或 y |x=x0
lim f (x0 x) f (x0)=lim y
x0
x
x0 x
【对点训练】
1.已知函数f(x)=20x-19,则表达式 lim f (3 x) f (3)
的值为 ( )
x0
x
A.3
B.Δx
C.3+Δx D.20
【解析】选D.因为 lim f (3 x) f (3)
【对点训练】
1.函数y=x3在 [0,1] 上的变化率为A,在[1,2]上的变化 率为B,则 A 的值2 为 ( )
B
A.28 B. 1
C. 7 D. 4
28
4
7
【解析】选B.因为
A
(1)3 2
0
1,B
23
1
7,
所以 A 1 .
10 4
2 1
2
B 28
2.质点运动规律s=t2+3,则在时间[3,3+Δt]中,相应的
v h(0.5) h(0) 4.05(m / s).
在1≤t0≤.52这0 段时间里的平均速度是
=-8.2(m/s).
v h(2) h(1) 2 1
结论:平均变化率概念
我们把式子__f(_x_2 )__f_(_x1_)_称为函数y=f(x)从__到__的平
人教A版高中数学选修1-1《三章 导数及其应用 3.1 变化率与导数 3.1.3 导数的几何意义》赛课课件_3

教材P77:观察 当点Pn(xn, f (xn))(n=1,2,3,4)沿着曲线 f(x)趋近于 点P(x0, f (x0)) 时,割线 PPn的变化趋势是什么?
动画演示
当点Pn趋近于点P时,割线PPn趋近于确定的位置,这个确 定位置的直线PT称为点P处的切线.
割线PPn的斜率与切线PT的斜率k有什么关系呢?
l1
l2
l1比l2的倾斜程度小 h(t)在t1比在t2的下降慢
练习
描述函数h(t)在t3和t4附近增(减)以及增(减)快慢的情况.
(1)当t=t3时,曲线h(t)在t3处的 切线l3的斜率h(t3)>0.所以,在 t=t3附近曲线上升,即函数h(t) 在t=t3附近单调递增.
l3
l4
(2)当t=t4时,曲线h(t)在t4处的 切线l4的斜率h(t4)>0.所以,在 t=t4附近曲线上升,即函数h(t) 在t=t4附近单调递增. l3比l4的倾斜度大,h(t) 在t3比在t4的上升快
当x=x0时,f (x0)是一个确定的数. 当x变化时, f (x)便是一个函数,称它为f (x)的导函数(简称 导数)(也就是说函数f (x)的导数f (x)也是一个函数)
y=f (x)的导数有时也记作y
f 'x y' lim f x x f x
x0
x
例 1:(1)求曲线 y=f(x)=x2+1 在点 P(1,2)处的切线方程.
(2)求函数 y=3x2 在点
处的导数.
例 2、已知曲线 y=13x3 上一点 P2,83,求:
(1)求在点P处的切线方程; (2)求过点P的曲线的切线方程.
练习 1、求双曲线 y=1x在点12,2处的切线的斜率, 并写出切线方程.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数的概念 例 3 求函数 y=x42在 x=2 处的导数.
[分析] 通常以某一具体函数为载体,利用求导的“三 步曲”,进行计算.
[解] 解法一:(导数定义法) ∵Δy=Δx+4 22-242=Δx+4 22-1=-ΔΔxx2++24Δ2x, ∴ΔΔxy=-ΔΔxx++242. ∴Δlixm→0ΔΔxy=-Δlixm→0ΔΔxx++242=-1.
(1)求当 x1=4,且 Δx=1 时,函数增量 Δy 和平均变化率ΔΔxy; (2)求当 x1=4,且 Δx=0.1 时,函数增量 Δy 和平均变化率ΔΔxy; (3)若设 x2=x1+Δx.分析(1)(2)题中的平均变化率的几何意义.
[解] f(x)=2x2+3x-5,
∴Δy=f(x1+Δx)-f(x1) =2(x1+Δx)2+3(x1+Δx)-5-(2·x21+3·x1-5) =2[(Δx)2+2x1Δx]+3Δx =2(Δx)2+(4x1+3)Δx.
答案:A
4.已知函数 y=f(x)=-x2+x 的图象上一点(-1,-2) 及邻近一点(-1+Δx,-2+Δy),则ΔΔxy=______.
解析:Δy=f(-1+Δx)-f(-1)=-(-1+Δx)2+(-1+ Δx)-(-2)=-(Δx)2+3Δx,所以ΔΔxy=-ΔxΔ2x+3Δx=3-Δx, 故应填 3-Δx.
A.f(x0+Δx) B.f(x0)+Δx C.f(x0)·Δx D.f(x0+Δx)-f(x0)
解析:分别写出 x=x0 和 x=x0+Δx 对应的函数值 f(x0) 和 f(x0+Δx),两式相减,就得到了函数值的改变量 Δy=f(x0 +Δx)-f(x0),故应选 D.
答案:D
2.若一质点按规律 s=8+t2 运动,则在时间段 2~2.1
3.函数 f(x)在 x=x0 处的导数 函数 y=f(x)在 x=x0 处的③__瞬__时__变__化__率___称为函数 y=
fΔΔ(xyx=)在④x_=_Δlix_xm→_00_处f_x_的0_+_导_Δ_数Δx_x_,-_记_f_作x_0_f.′(x0)或 y′|x=x0 ,即 f′(x0)=Δlixm→0
练 4 如下图,函数 f(x)的图象是折线段 ABC,其中 A, B,C 的坐标分别为(0,4),(2,0),(6,4),则 f[f(0)]=____2____; Δlixm→0f1+ΔΔxx-f1=__-__2__.(用数字作答)
[解析] 由图及题中已知可得折线的方程为 f(x)=-x-22x,-22<x,≤06≤. x≤2, f(0)=4,f[f(0)]=f(4)=2, ∵直线 AB 和 BC 的斜率分别为-2 和 1, ∴Δlixm→0f1+ΔΔxx-f1=-2.
法二:f′(x)=Δlixm→02x+Δx2+4xΔ+xΔx-2x2+4x =Δlixm→04x·Δx+2ΔΔxx2+4Δx =lim(4x+2Δx+4)=4x+4,
Δx→0
∴y′|x=3=f′(3)=4×3+4=16.
导数的简单应用
例 4 设函数 f(x)在点 x0 处可导,试求下列各极限的值. (1) Δlixm→0fx0-ΔΔxx-fx0; (2) lhi→m0fx0+h2-hfx0-h.
=12[f′(x0)+f′(x0)]=f′(x0).
[点拨] 在导数的定义中,增量 Δx 的形式是多种多样 的,但不论 Δx 选择哪种形式,Δy 也必须选择与之相对应的 形式.利用函数 f(x)在 x=x0 处可导的条件,可以将已给定 的极限式恒等变形为导数定义的形式.概念是解决问题的重
要依据,只有熟练掌握概念的本质属性,把握其内涵与外延, 才能灵活地应用概念进行解题.
练 2 以初速度 v0(v0>0)竖直上抛物体,t 秒时的高度为 s(t)=v0t-12gt2,求物体在时刻 t0 的瞬时速度.
[解] 因为 Δs=v0(t0+Δt)-12g(t0+Δt)2-(v0t0-21gt20)= (v0-gt0)Δt-12g(Δt)2,所以ΔΔst=v0-gt0-12gΔt,当 Δt 趋近于
[分析] 给出某抽象函数在某点 x0 处可导的条件,求另 一抽象函数在某点 x0 处的导数,或求另一抽象函数在某点 x0 处的极限.
[解] (1)原式=Δlixm→0fx0--Δ-xΔ-xfx0 =--lΔixm→0fx0--ΔxΔ-x fx0(Δx→0 时,-Δx→0) =-f′(x0).
(2)原式=lhi→m0 fx0+h-fx02+hfx0-fx0-h =12[lhi→m0 fx0+hh-fx0+lhi→m0 fx0--hh-fx0] =12[f′(x0)+l-him→0 fx0--hh-fx0]
练 3 求函数 y=2x2+4x 在 x=3 处的导数.
[解] 法一:Δy=2(3+Δx)2+4(3+Δx)-(2×32+4×3) =12Δx+2(Δx)2+4Δx =2(Δx)2+16Δx, ∴ΔΔxy=2Δx2Δ+x 16Δx=2Δx+16. y′|x=3=Δlixm→0ΔΔxy=Δlixm→0(2Δx+16)=16.
§3.1变化率与导数 3.1.1~3.1.2变化率问题 导数的概念
1.通过实例,领悟由平均变化率到瞬时变化率刻画现实 的过程.
2.了解导数概念的实际背景,知道瞬时变化率就是导数. 3.体会导数的思想及其内涵,并能运用.
1.平均变化率
fx2-fx1
函数 y=f(x)从 x1 到 x2 的平均变化率为①____x_2_-__x_1___,
简记作:ΔΔxy.
2.瞬时变化率
函数 f(x)在 x=x0 处的瞬时变化率是
lim
Δx→0
ΔΔxy=②__Δli_xm→_0_f_x_0_+__Δ_Δx_x_-__f_.x0
思考探究 1. 物体在运动过程中,不论从哪一时刻起,当 Δt 相同 时,平均变化率一定相同吗?
提示:不一定.平均变化率等于在时间段内速度的变化 除以时间的变化,所以在匀速运动中,当 Δt 相同时,ΔΔvt 一 定相同,但在变速运动中却不一定,因为 Δt 相同,Δv 不一 定相同.
解法二:(导函数的函数值法) ∵Δy=x+4Δx2-x42=-4xΔ2xx2+x+ΔxΔx2 , ∴ΔΔxy=-x422xx++ΔΔxx2. ∴y′=Δlixm→0ΔΔxy=-Δlixm→0x422xx++ΔΔxx2=-x83. ∴f′(2)=y′|x=2=-1. [点拨] 根据导数的定义求导数是求函数的导数的基本 方法.
(1)函数 f(x)在 x1,x2 处有定义; (2)x2 是 x1 附近的任意一点,即 Δx=x2-x1≠0,但 Δx 可正可负;
(3)注意变量的对应,若 Δx=x2-x1,则 Δy=f(x2)-f(x1), 而不是 Δy=f(x1)-f(x2);
(4)平均变化率可正可负,也可为零.
2.根据导数的定义,求函数 y=f(x)在 x0 处的导数的步 骤
[解] (1)质点在[1,1+Δt]这段时间内的平均速度为 ΔΔst=8-31+ΔtΔ2t-8+3×12=-6-3Δt. (2)由(1)知ΔΔst=-6-3Δt,当 Δt 无限趋近于 0 时, lΔitm→0ΔΔst=-6,所以质点在 t=1 时的瞬时速度为-6.
[点拨] 本例引导学生理解瞬时速度是物体在 t 到 t+Δt 这段时间内的平均速度ΔΔst当 Δt 趋近于 0 时的极限,即为 s 对 t 的导数.对于作匀变速运动的物体来说,其位移对时间 的函数的导数就是其运动的速度对时间的函数,速度对时间 的函数的导数就是其运动的加速度对时间的函数,这是导数 的物理意义,利用导数的物理意义可以解决一些相关的物理 问题.
(1)当 x1=4,Δx=1 时,Δy=2+(4×4+3)×1=21, ∴ΔΔxy=211=21; (2)当 x1=4,Δx=0.1 时, Δy=2×0.12+(4×4+3)×0.1=0.02+1.9=1.92,
∴ΔΔxy=10.9.12=19.2;
(3)在(1)题中ΔΔxy=fxx22--xf1x1=f55--4f4,它表示抛物线 上 P0(4,39)与点 P1(5,60)连线的斜率.
Δx→0
C.f′(x0)=f(x0+Δx)-f(x0) D.f′(x0)=fx0+ΔΔxx-fx0
解析:考查导数的定义,B 中 f′(x0)=Δlixm→0[f(x0+Δx)- f(x0)],右边的式子表示函数值的变化量的极限.C 中 f′(x0) =f(x0+Δx)-f(x0),右边的式子表示函数值的变化量;D 中 f′(x0)=fx0+ΔΔxx-fx0,右边的式子表示函数的平均变化 率.故应选 A.
(1)求函数的增量 Δy=f(x0+Δx)-f(x0); (2)求平均变化率ΔΔxy=fx0+ΔΔxx-fx0;
(3)取极限,得导数 f′(x0)=Δlixm→0ΔΔxy.
3.对导数概念的理解 某点导数即为函数在这点的瞬时变化率,含着两层含 义:
(1) Δlixm→0ΔΔxy存在,则称 f(x)在 x=x0 处可导并且导数即为 极限值;
答案:3-Δx
5.求函数 y=x2 在点 x=1 处的导数.
解:Δy=(1+Δx)2-1=2Δx+(Δx)2, ∴ΔΔxy=2+Δx.y′|x=1=Δlixm→0(2+Δx)=2.
1.函数的平均变化率的理解
定义中的 x1,x2 是指其定义域内不同的两个数,记 Δx =x2-x1,Δy=f(x2)-f(x1),则当 Δx≠0 时,fxx22--xf1x1=ΔΔxy 称作函数 y=f(x)从 x1 到 x2 的平均变化率,理解平均变化率 应注意以下几点:
在(2)题中,ΔΔxy=fxx22--xf1x1=f44.1.1--4f4,它表示抛物 线上点 P0(4,39)与点 P2(4.1,40.92)连线的斜率.
[点拨] 求函数 f(x)的平均变化率的步骤是: (1)根据 x1 和 x2 值写出自变量的增量 Δx; (2)由 Δy=f(x2)-f(x1)=f(x1+Δx)-f(x1)计算函数增量;
