高一物理万有引力定律的应用
高中物理必修二 第三章 第三节 万有引力定律的应用

二、预测未知天体
海王 星的发现,以及英国天文学家 哈雷 根据万有引力定律预言的哈 雷彗星“按时回归”,确立了万有引力定律的地位,充分显示了科学 理论对实践的巨大指导作用.
三、估算天体的质量 一般求中心天体质量的两种方法: (1)知道卫星或行星绕中心天体运动的 周期 及两者之间的 距离 . (2)知道天体半径及其 表面重力加速度 .
1 2 3 4 5 6 7 8 9 10 11 12 13
3.2020年11月24日,我国嫦娥五号探测器成功发射,在探测器“奔向”
月球的过程中,用h表示探测器与地球表面的距离,g表示探测器所受
地球引力产生的加速度,g随h的变化关系如图所示,将地球看成质量
均匀分布的球体,当h=3R(R是地球的半径)时g为
由Gmr地2m太=m
4π2 地 T2 r
知
m
太=4GπT2r23,可以求出太阳的质量.
导学探究
(2)如果求太阳的密度,还需要已知什么条件?
答案
4π2r3 还需要已知太阳的半径 R,此时 ρ 太=mV太=34GπTR23=G3Tπ2rR33
(3)当卫星绕天体表面运动时,运动周期为T,引力常量为G,则天
=GMRm2 .
知识深化
2.重力与高度的关系 若距离地面的高度为 h,则 mg′=GRM+mh2(R 为地球半径,g′为 离地面 h 高度处的重力加速度).在同一纬度,距地面越高,重力加速 度越小.
例1 地球可近似看成球形,由于地球表面上物体都随地球自转,所以有
√A.物体在赤道处受到的地球引力等于两极处,而重力小于两极处
知识深化
(3) 从 赤 道 到 两 极 : 随 着 纬 度 增 加 , 向 心 力 F′ =
mω2R′减小,F′与F引夹角增大,所以重力mg在 增大,重力加速度增大.
高一物理必修三知识点总结

三一文库()/高一〔高一物理必修三知识点总结〕【万有引力定律及其应用】1.万有引力定律:引力常量G=6.67×N#m2/kg22.适用条件:可作质点的两个物体间的相互作用;若是两个均匀的球体,r应是两球心间距.(物体的尺寸比两物体的距离r小得多时,可以看成质点)3.万有引力定律的应用:(中心天体质量M,天体半径R,天体表面重力加速度g)(1)万有引力=向心力(一个天体绕另一个天体作圆周运动时)(2)重力=万有引力地面物体的重力加速度:mg=Gg=G≈9.8m/s2高空物体的重力加速度:mg=Gg=G 4.第一宇宙速度----在地球表面附近(轨道半径可视为地球半径)绕地球作圆周运动的卫星的线速度,在所有圆周运动的卫星中线速度是最大的。
由mg=mv2/R或由==7.9km/s5.开普勒三大定律6.利用万有引力定律计算天体质量7.通过万有引力定律和向心力公式计算环绕速度8.大于环绕速度的两个特殊发射速度:第二宇宙速度、第三宇宙速度(含义)功、功率、机械能和能源1.做功两要素:力和物体在力的方向上发生位移2.功:功是标量,只有大小,没有方向,但有正功和负功之分,单位为焦耳(J)3.物体做正功负功问题(将α理解为F与V所成的角,更为简单)(1)当α=90度时,W=0.这表示力F的方向跟位移的方向垂直时,力F不做功,如小球在水平桌面上滚动,桌面对球的支持力不做功。
(2)当α0,W>0.这表示力F对物体做正功。
如人用力推车前进时,人的推力F对车做正功。
(3)当α大于90度小于等于180度时,cosα如人用力阻碍车前进时,人的推力F对车做负功。
一个力对物体做负功,经常说成物体克服这个力做功(取绝对值)。
例如,竖直向上抛出的球,在向上运动的过程中,重力对球做了-6J的功,可以说成球克服重力做了6J的功。
说了“克服”,就不能再说做了负功4.动能是标量,只有大小,没有方向。
表达式5.重力势能是标量,表达式(1)重力势能具有相对性,是相对于选取的参考面而言的。
万有引力高一物理知识点

万有引力高一物理知识点万有引力是高一物理学习中的重要知识点,它是描述物体之间相互作用的力。
在这篇文章中,我们将深入探讨万有引力的定义、公式、特点以及与其他力的比较等内容。
一、万有引力的定义万有引力是由英国科学家牛顿提出的,它指的是地球或其他物体对其他物体产生的吸引力。
根据牛顿的万有引力定律,任意两个物体之间的引力大小与它们的质量有关,并与它们之间的距离平方成反比。
二、万有引力的公式根据牛顿的定律,万有引力的计算公式可以表示为:F =G * (m1 * m2) / r^2其中,F代表引力的大小,G代表万有引力常数,m1和m2分别代表两个物体的质量,r代表它们之间的距离。
万有引力常数G 是一个恒定值,约等于6.67430 × 10^-11 N·(m/kg)^2。
三、万有引力的特点1. 无论物体的质量大小,万有引力对所有物体都起作用,大小相等。
2. 引力的大小与物体的质量成正比,质量越大,引力越大。
3. 引力的大小与物体之间的距离的平方成反比,距离越近,引力越大。
4. 引力是一个吸引力,即两个物体之间的引力是相互的。
四、万有引力与其他力的比较与其他力相比,万有引力具有以下几点特点:1. 万有引力是唯一一个不需要接触的力,即两个物体之间无需直接接触,也可以产生引力。
2. 与电场力和磁场力相比,万有引力作用的范围更广,包括宏观物体之间的相互作用。
3. 万有引力是人们日常生活中常见的力之一,如地球对物体的吸引力、月球对地球的引力等。
4. 万有引力是地球上物体受力情况的基础,它影响着行星运动、悬挂物体的稳定性等现象。
五、总结万有引力是高一物理学习中的重要知识点,它描述了物体之间相互作用的力。
这篇文章介绍了万有引力的定义、公式、特点以及与其他力的比较。
通过学习万有引力,我们可以更好地理解宇宙中物体之间的相互作用,并应用到实际生活中。
希望本文对你理解万有引力有所帮助。
万有引力定律高中物理

有关高中物理“万有引力定律”的概念
有关高中物理“万有引力定律”的概念如下:
万有引力定律是描述物体之间相互引力的定律,由艾萨克·牛顿在1687年提出。
它表明任何两个物体之间都存在引力,且这个引力与它们质量的乘积成正比,与它们距离的平方成反比。
在高中物理中,万有引力定律通常表示为:F = G * (m1 * m2) / r^2,其中F 是两个物体之间的引力,m1 和m2 分别是两个物体的质量,r 是它们之间的距离,G 是引力常量,其值约为6.67430 × 10^-11 m^3 kg^-1 s^-2。
万有引力定律在天文学中有着重要的应用,它解释了行星轨道运动和天体运动的规律。
此外,万有引力定律也是研究宇宙学和天体物理学等领域的基础。
在高中物理中,学生通常会学习如何使用万有引力定律计算两个物体之间的引力,以及如何使用它来解释一些天体运动的规律。
同时,学生也会学习到万有引力定律的一些特殊情况,例如在地球表面的物体所受的重力可以看作是地球对该物体的万有引力。
总之,万有引力定律是高中物理中的一个重要概念,它描述了物体之间的引力规律,为我们理解天体运动和宇宙结构提供了基础。
高一物理万有引力定律和天体运动

-R,因G、M、ω、R均为定值,因此h一定为定值,故
B对; 因同步卫星周期T同=24小时,月球绕地球转动周期T月=30 天,即T同<T月,由公式ω=
2019/1/26
得,ω同>ω月,故C对;
同步卫星与静止在赤道上的物体具有共同的角速度, 由公式a向=rω2,可得: 其向心加速度不同,D错误. 因轨道半径不同,故
②若已知天体的半径R,则天体的密度
ρ=
2019/1/26
③若天体的卫星在天体表面附近环绕天体运动,可认为
其轨道半径r等于天体半径R,则天体密度ρ=
可见,
只要测出卫星环绕天体表面运动的周期T,就可估测出中 心天体的密度.
2019/1/26
不考虑天体自转,对任何天体表面都可以认为mg =G 从而得出GM=gR2(通常称为黄金代换),其中M为
(3)其他轨道:除以上两种轨道外的卫星轨道.
一切卫星的轨道的圆心与地心重合.
2019/1/26
据报道,我国数据中继卫星“天链一号01 星”于2008年4月25日在西昌卫星发射中心发射升空,经过4 次变轨控制后,于5月1日成功定点在东经77°赤道上空的同 步轨道.关于成功定点后的“天链一号01星”, 下列说法正确的是 ( )
判断.
(12分)土星周围有许多大小不等的岩石颗粒,
其绕土星的运动可视为圆周运动.其中有两个岩石颗粒A和B
与土星中心的距离分别为rA=8.0×104 km和rB=1.2×105 km. 忽略所有岩石颗粒间的相互作用.(结果可用根式表示)
2019/1/26
(1)求岩石颗粒A和B的线速度之比. (2)求岩石颗粒A和B的周期之比. (3)土星探测器上有一物体,在地球上重为10 N,推算出 它在距土星中心3.2×105 km处受到土星的引力为0.38 N.已知 地球半径为6.4×103 km,请估算土星质量是地球质量的多少 倍?
高一物理下册万有引力基本规律及应用拓展

万有引力基本规律及运用拓展1.开普勒行星运动定律 ⑴ 开普勒第一定律(轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
⑵ 开普勒第二定律(面积定律):对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积。
⑶ 开普勒第三定律(周期定律):所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等。
若用a 代表椭圆轨道的半长轴,T 代表公转周期,则32a k T =。
其中k 是对所有行星都相同的常量。
开普勒三大定律不仅适用于行星绕太阳的运动,也适用于卫星绕行星运动等其它天体运动,只不过在这些问题中,开普勒第三定律写成32a k'T=,其中k'是与环绕天体无关,只与被环绕的中心天体有关的常量。
2.万有引力定律⑴ 内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量1m 和2m 的乘积成正比,与它们之间距离r 的二次方成反比。
⑵ 公式:122m mF G r=,G 是比例系数,叫做引力常量,适用于任何两个物体,通常取11226.6710N m /kg G -=⨯⋅。
G 值由卡文迪许首先精确测出。
⑶ 万有引力定律的适用条件① 当两个物体间的距离远远大于每个物体的尺寸时,物体可以看成质点,它们之间的引力可直接使用万有引力定律公式计算。
② 通过严格的理论分析得到,质量分布均匀的球体,它们之间的引力也可直接使用公式计算,这时r 是两球心间的距离。
3.三种宇宙速度⑴ 第一宇宙速度(环绕速度):v =7.9km/s ;第一宇宙速度是使卫星能环绕地球运行所需的最小发射速度。
⑵ 第二宇宙速度(脱离速度):v =11.2km/s ;在地面附近发射人造卫星,如果发射速度大于7.9km/s ,而小于11.2km/s ,那么它绕地球运行的轨迹将是椭圆。
当发射速度等于或大于11.2km/s 时,卫星会克服地球的引力而永远离开地球。
⑵ 第三宇宙速度(逃逸速度):v =16.7km/s 。
重难点14万有引力定律之一专题高一物理题组法突破重难点(人教版2019必修第二册)(解析版)

人教版新教材高中物理必修第二册 第七章 万有引力与宇宙航行万有引力定律专题(题组分类训练)题组特训 特训内容题组一 开普勒三定律的理解与应用 题组二 万有引力定律的理解及简单应用 题组三万有引力与重力的关系开普勒定律的理解1. 在相等的时间内,面积S A =S B ,这说明离太阳越近,行星在相等时间内经过的弧长越长,即行星的速率越大.开普勒第二定律又叫面积定律.(在这里面积相等指同一颗行星面积相等,不同行星相等时间内面积是不相等的)。
微元法解读开普勒第二定律:行星在近日点、远日点时的速度方向与两点连线垂直,若行星在近日点、远日点到太阳的距离分别为a 、b ,取足够短的时间Δt ,则行星在Δt 时间内的运动可看作匀速直线运动,由S a =S b 知12v a ·Δt ·a =12v b ·Δt ·b ,可得v a =v b b a 。
行星到太阳的距离越大,行星的速率越小,反之越大。
2.行星绕太阳的运动通常按匀速圆周运动处理。
3.开普勒行星运动定律也适用于其他天体,例如月球、卫星绕地球的运动。
4.开普勒第三定律a 3T2=k 中,k 值只与中心天体的质量有关,不同的中心天体k 值不同,故该定律只能用在同一中心天体的两星体之间。
题组特训一:开普勒三定律的理解与应用1.(多选)关于开普勒行星运动定律,下列说法正确的是( )A .地球绕太阳在椭圆轨道上运行,在近日点速率小于远日点运行的速率B .所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上基础知识清单C.表达式椭圆半长轴的a与公转周期T,32aT比值为常数D.若图中两阴影部分行星运动时间相等,则右侧面积大于左侧面积【答案】BC【解析】A.地球绕太阳在椭圆轨道上运行,从近日点到远日点,太阳对地球的引力做负功,则速度减小,即在近日点速率大于远日点运行的速率,选项A错误;B.根据开普勒第一定律可知,所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上,选项B正确;C.根据开普勒第三定律可知,表达式椭圆半长轴的a与公转周期T,32aT比值为常数,选项C正确;D.根据开普勒第二定律可知,若图中两阴影部分行星运动时间相等,则右侧面积等于左侧面积,选项D错误。
新人教版 年 高一物理必修2 第六章 专题:万有引力定律应用-课件

例1.关于万有引力定律和引力常量的发现,下面
说法中哪个是正确的 ( D )
A.万有引力定律是由开普勒发现的,而引 力常量是由伽利略测定的
B.万有引力定律是由开普勒发现的,而引 力常量是由卡文迪许测定的
C.万有引力定律是由牛顿发现的,而引力 常量是由胡克测定的
D.万有引力定律是由牛顿发现的,而引力 常量是由卡文迪许测定的
例2.关于第一宇宙速度,下面说法正确的有( B C ) A. 它是人造卫星绕地球飞行的最小速度 B. 它是发射人造卫星进入近地圆轨道的最小速度 C.它是人造卫星绕地球飞行的最大速度 D. 它是发射人造卫星进入近地圆轨道的最大速度。
(提示:注意发射速度和环绕速度的区别)
练习.已知金星绕太阳公转的周期小于地球绕太阳 公转的周期,它们绕太阳的公转均可看做匀速圆周 运动,则可判定 ( C )
法正确的是 ( B D ) A.卫星的轨道半径越大,它的 运行速度越大 B.卫星的轨道半径越大,它的 运行速度越小 C.卫星的质量一定时,轨道半径越大,它需要的
向心力越大 D.卫星的质量一定时,轨道半径越大,它需要的
向心力越小
例5.一宇宙飞船在离地面h的轨道上做匀速圆周运
动,质量为m的物块用弹簧秤挂起,相对于飞船静
练习.一颗人造地球卫星在离地面高度等于地球半
径的圆形轨道上运行,其运行速度是地球第一宇宙
速度的
2 2
倍.
此处的重力加速度g'= 0.25 g0 .(已知地球表面
处重力加速度为g0)
练习、 从地球上发射的两颗人造地球卫星A和B, 绕地球做匀速圆周运动的半径之比为RA∶RB=4∶1, 求它们的线速度之比和运动周期之比。
n= T1/(T2-T1), ∴ t1 =T1T2/(T2-T1) ,
高一物理万有引力定律

思考与讨论
◆ 我们人与人之间也一样存在万有引力,可是为 什么我们感受不到呢?
假设质量均为60千克的两位同学,相距1米, 他们之间的相互作用的万有引力多大?
F=Gm1m2/r2 =6.67×10-11×60×60/12 =2.4×10-7(N)
2.4×10-7N是一粒芝麻重的几千分之一, 这么小的力人根本无法察觉到。
万有引力定律:
1.内容:自然界中任何两个物体都是相互吸引的,引
力的大小跟这两个物体的质量的乘积成正比,跟它们
的距离的二次方成反比。
2.公式:
F=
Gm1m2r23源自G:是引力常数,适用于任何两个物体。
其标准值为G=6.67259×10-11N·m2/kg2
通常情况下取G=6.67×10-11N·m2/kg2
F引= F向=mw2r=mv2/r 因为: w=2π/T ; v=2πr/T 得:F引=m(2πr/T)2/r= 4π2mr/T2
怎么办 呢??
根据开普勒第三定律:r3/T2是常数k
F引=4π2mr/T2= 4π2(r3/T2) m/r2 有:F引=4π2km/r2
所以可以得出结论:太阳对行星的引力跟行星的
F引 ∝ Mm/r2
写成等式:F引= GMm/r2
行星绕太阳运动遵守这个规律,那么 在其他物体之间是否适用这个规律呢??
牛顿还研究了月球绕地球的运动,发现它们间的 引力跟太阳与行星间的引力遵循同样规律。
牛顿在研究了许多物体间遵循规律的引力之后, 进一步把这个规律推广到自然界中任何两个物体之间, 于1687年正式发表了万有引力定律:
4.距离r的确定 a.若两物体可看作质点,则为两质点间距; b.对于均匀的球体,应是两球心间距。
高一物理必修二万有引力的成就

引
质量为1kg的物体静止在赤道上时的 ①如果以水星绕太阳做匀速圆周运动为研究对象,需要知道哪些量才能求得太阳的质量?
M 海王星发现之后,人们发现它的轨道也与理论计算的不一致。
向心加速度。(已知地球半径R=6.×10 m) R 此后,“九大行星”成为家喻户晓的说法。
6
了解发现未知天体的基本思路
是一样的,根据开普勒第三定律,对于同一中心天体,所有环绕天体
从(此当以 卫后星,在这天门体自表然面科做学近成地了飞巨行大呢的?精)神工国……”牛顿还用月球和太阳的万有引力解释了潮汐现象、用万有引力定律和其他力学定律,推测地球呈赤道处略m为g隆起的扁平形状。
试求: 67×10-11 N·m2/kg2,试估算地球的质量. θF A.求出“嫦娥三号”探月卫星的质量
许多人感到不解,为什么从儿时起就一直熟知的太阳系“九大行星”概念如今要被重新定义,而冥王星又因何被“降级”?
“行星”这个说法起源于希腊语,原意指太阳系中的“漫游者”。
因此一般粗略计算中不考虑(或忽略)地球自转的影响。
近千年来,人们一直认为水星、金星、地球、火星、木星和土星是太阳系中的标准行星。
一、天体质量和密度的计算
mg
G
Mm R2
gR2 M
G
GM=gR2
黄金代换式
例1:设地面附近的重力加速度g=9.8 m/s2,地球半径R=6.4×106 m,引力常量G=6.67×10-11 N·m2/kg2,试估算地球的质量.
答案 ME= gGR2=9.86×.676×.41×0-110162 kg≈6.0×1024 kg
是一样的,根据开普勒第三定律,对于同一中心天体,所有环绕天体
r3
的值是 一样的。所以 r 3 r 3
专题03 万有引力与宇宙航行-2022-2023学年高一物理下学期期中期末考点大串讲(原卷版)
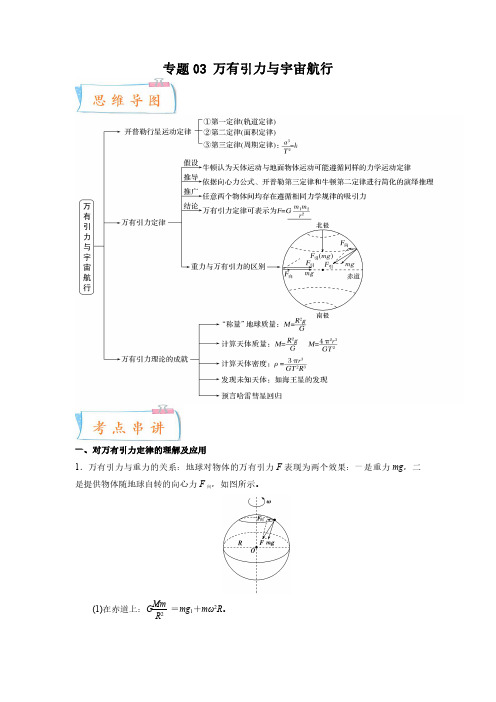
专题03万有引力与宇宙航行一、对万有引力定律的理解及应用1.万有引力与重力的关系:地球对物体的万有引力F表现为两个效果:一是重力mg,二,如图所示。
是提供物体随地球自转的向心力F向+mω2R。
(1)在赤道上:G MmR2=mg1(2)在两极上:GMmR 2=mg 2。
(3)在一般位置:万有引力GMmR 2等于重力mg 与向心力F 向的矢量和。
越靠近南北两极g 值越大。
由于物体随地球自转所需的向心力较小,常认为万有引力近似等于重力,即GMmR 2=mg 。
2.重力加速度(1)在地球表面附近的重力加速度g (不考虑地球自转):mg =GMm R 2,得g =GMR 2。
(2)在地球上空距离地心r =R +h 处的重力加速度g ′:mg ′=GMm (R +h )2,得g ′=GM(R +h )2。
3.万有引力的“两个推论”推论1:在匀质球壳空腔内的任意位置处,质点受到球壳的万有引力的合力为零,即∑F引=0。
推论2:在匀质球体内部距离球心r 处的质点(m )受到的万有引力等于球体内半径为r的同心球体(M ′)对其的万有引力,即F =GM ′mr 2。
【例1】由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同。
已知地球表面两极处的重力加速度大小为g 0,在赤道处的重力加速度大小为g ,地球自转的周期为T ,引力常量为G 。
假设地球可视为质量均匀分布的球体,下列说法正确的是()A .质量为m 的物体在地球北极受到的重力大小为mgB .质量为m 的物体在地球赤道上受到的万有引力大小为mg 0C .地球的半径202()4g g T π-D .地球的密度为23GT π二、天体质量(密度)的估算1.重力加速度法利用天体表面的重力加速度g 和天体半径R 求解。
(1)由G Mm R 2=mg 得天体质量M =gR 2G 。
(2)天体密度ρ=M V =M 43πR 3=3g4πGR 。
2.天体环绕法利用卫星绕天体做匀速圆周运动的周期T 和半径r 求解。
高一物理必修二第六章 2 3 太阳与行星间的引力 万有引力定律---学生版

2 太阳与行星间的引力--学生版3 万有引力定律[学习目标] 1.知道太阳与行星间存在引力.2.能利用开普勒定律和牛顿运动定律推导出太阳与行星之间的引力表达式.3.理解万有引力定律的内容、含义及适用条件.4.认识万有引力定律的普遍性,能应用万有引力定律解决实际问题.一、太阳与行星间的引力1.太阳对行星的引力:太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间距离的二次方成反比,即F ∝mr2.2.行星对太阳的引力:太阳与行星的地位相同,因此行星对太阳的引力和太阳对行星的引力规律相同,即F ′∝Mr2.3.太阳与行星间的引力:根据牛顿第三定律F =F ′,所以有F ∝Mm r 2,写成等式就是F =G Mmr 2.二、月—地检验1.猜想:维持月球绕地球运动的力与使得苹果下落的力是同一种力,同样遵从“平方反比”的规律.2.推理:根据牛顿第二定律,物体在月球轨道上运动时的加速度大约是它在地面附近下落时的加速度的1602.3.结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同(填“相同”或“不同”)的规律. 三、万有引力定律1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比.2.表达式:F =G m 1m 2r2.3.引力常量G :由英国物理学家卡文迪许测量得出,常取G =6.67×10-11N·m 2/kg 2.1.判断下列说法的正误.(1)万有引力不仅存在于天体之间,也存在于普通物体之间.()(2)质量一定的两个物体,若距离无限小,它们间的万有引力趋于无限大.()(3)把物体放在地球中心处,物体受到的引力无穷大.()(4)由于太阳质量大,太阳对行星的引力大于行星对太阳的引力.()(5)牛顿发现了万有引力定律,并测出了引力常量.()2.两个质量都是1 kg的物体(可看成质点),相距1 m时,两物体间的万有引力F=________ N,一个物体的重力F′=________ N,万有引力F与重力F′的比值为________.(已知引力常量G=6.67×10-11 N·m2/kg2,取重力加速度g=10 m/s2)一、对太阳与行星间引力的理解1.是什么原因使行星绕太阳运动?2.在推导太阳与行星的引力时,我们对行星的运动怎么简化处理的?用了哪些知识?太阳与行星间引力关系的得出过程例1 (多选)根据开普勒关于行星运动的规律和圆周运动的知识知:太阳对行星的引力F ∝m r 2,行星对太阳的引力F ′∝Mr 2,其中M 、m 、r 分别为太阳质量、行星质量和太阳与行星间的距离,下列说法正确的是( ) A.由F ′∝M r 2和F ∝mr 2,得F ∶F ′=m ∶MB.F 和F ′大小相等,是作用力与反作用力C.F 和F ′大小相等,是同一个力D.太阳对行星的引力提供行星绕太阳做圆周运动的向心力二、万有引力定律(1)通过月—地检验结果表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同的规律.一切物体之间都存在这样的引力,那么,为什么通常两个人(如图1)间的万有引力我们却感受不到?图1(2)地球对人的万有引力与人对地球的万有引力大小相等吗?1.万有引力定律表达式F =G m 1m 2r 2,G =6.67×10-11 N·m 2/kg 2.2.万有引力定律公式适用的条件(1)万有引力定律适用于两个质点间的相互作用.(2)一个均匀球体与球外一个质点,r 为球心到质点的距离. (3)两个质量均匀的球体,r 为两球心间的距离.例2 关于万有引力和万有引力定律的理解正确的是( ) A.不能看做质点的两物体间不存在相互作用的引力 B.只有能看做质点的两物体间的引力才能用F =Gm 1m 2r2计算C.由F =Gm 1m 2r 2知,两物体间距离r 减小时(没有无限靠近),它们之间的引力增大D.引力常量的大小是牛顿首先测出来的,且约等于6.67×10-11N·m 2/kg 2例3 如图2所示,两球间的距离为r 0,两球的质量分布均匀,质量分别为m 1、m 2,半径分别为r 1、r 2,则两球间的万有引力大小为( )图2A.Gm 1m 2r 02B.Gm 1m 2r 12C.Gm 1m 2(r 1+r 2)2D.Gm 1m 2(r 1+r 2+r 0)2例4 (2019·江川二中高一期末)一个质量均匀分布的球体,半径为2r ,在其内部挖去一个半径为r 的球形空穴,其表面与球面相切,如图3所示.已知挖去小球的质量为m ,在球心和空穴中心连线上,距球心d =6r 处有一质量为m ′的质点,求:图3(1)被挖去的小球挖去前对m ′的万有引力为多大? (2)剩余部分对m ′的万有引力为多大?三、重力和万有引力的关系1.物体在地球表面上所受引力与重力的关系图4除两极以外,地面上其他点的物体,都围绕地轴做圆周运动,这就需要一个垂直于地轴的向心力.由地球对物体引力的一个分力F ′提供向心力,另一个分力为重力G ,如图4所示. (1)当物体在两极时:G =F 引,重力达到最大值G max =G MmR 2.(2)当物体在赤道上时:F ′=mω2R 最大,此时重力最小G min =GMmR 2-mω2R (3)从赤道到两极:随着纬度增加,向心力F ′=mω2R ′减小,F ′与F 引夹角增大,所以重力G 在增大,重力加速度增大.因为F ′、F 引、G 不在一条直线上,重力G 与万有引力F 引方向有偏差,重力大小mg <G MmR 2.2.重力与高度的关系若距离地面的高度为h ,则mg ′=G Mm(R +h )2(R 为地球半径,g ′为离地面h 高度处的重力加速度).在同一纬度,距地面越高,重力加速度越小. 3.特别说明(1)重力是物体由于地球吸引产生的,但重力并不是地球对物体的引力.(2)只有在两极,mg =G Mm R 2,其他地方mg <G MmR 2,但相差不大,在忽略地球自转的情况下,认为mg =G MmR2.(3)在两极、赤道,两个力的方向相同,其他地方二者方向不同,略有偏差.引力的方向指向地心,重力的方向竖直向下.例5 (多选)万有引力定律能够很好地将天体运行规律与地球上物体运动规律具有的内在一致性统一起来.用弹簧测力计称量一个相对于地球静止的质量为m 的小物体的重力,随称量位置的变化可能会有不同的结果.已知地球质量为M ,引力常量为G .将地球视为半径为R 、质量均匀分布的球体.下列说法正确的是( )A.在北极地面称量时,弹簧测力计读数为F 0=G Mm R 2B.在赤道地面称量时,弹簧测力计读数为F 1=G MmR2C.在北极上空高出地面h 处称量时,弹簧测力计读数为F 2=G Mm(R +h )2D.在赤道上空高出地面h 处称量时,弹簧测力计读数为F 3=G Mm(R +h )2例6 火星半径是地球半径的12,火星质量大约是地球质量的19,那么地球表面上质量为50 kg的宇航员(地球表面的重力加速度g 取10 m/s 2) (1)在火星表面上受到的重力是多少?(2)若宇航员在地球表面能跳1.5 m 高,那他在火星表面能跳多高?1.(对万有引力定律的理解)(2019·武威第十八中学高一期末)对于万有引力定律的表达式F =G m 1m 2r2,下列说法正确的是( ) A.公式中G 为引力常量,它是由实验测得的,而不是人为规定的 B.当r 趋近于零时,万有引力趋于无穷大C.对于m 1与m 2间的万有引力,质量大的受到的引力大D.m 1与m 2受到的引力是一对平衡力2.(月—地检验)(2018·北京卷)若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律,在已知月地距离约为地球半径60倍的情况下,需要验证( ) A.地球吸引月球的力约为地球吸引苹果的力的1602B.月球公转的加速度约为苹果落向地面加速度的1602C.自由落体在月球表面的加速度约为地球表面的16D.苹果在月球表面受到的引力约为在地球表面的1603.(万有引力定律的简单应用)两个完全相同的实心均质小铁球紧靠在一起,它们之间的万有引力为F .若将两个用同种材料制成的半径是小铁球2倍的实心大铁球紧靠在一起,则两个大铁球之间的万有引力为( ) A.2F B.4F C.8F D.16F4.(重力加速度的计算)据报道,在太阳系外发现了首颗“宜居”行星,设其质量为地球质量的k 倍,其半径为地球半径的p 倍,由此可推知该行星表面的重力加速度与地球表面重力加速度之比为( ) A.k p B.k p 2 C.k 2p D.k 2p2[基础对点练]考点一 万有引力定律的理解1.(2019·肥东高级中学高一下期末)下列关于行星对太阳的引力的说法中正确的是( ) A.行星对太阳的引力与太阳对行星的引力是同一种性质的力 B.行星对太阳的引力与太阳的质量成正比,与行星的质量无关 C.太阳对行星的引力大于行星对太阳的引力D.行星对太阳的引力与太阳的质量成正比,与行星距太阳的距离成反比2.(多选)关于引力常量G ,下列说法中正确的是( ) A.在国际单位制中引力常量G 的单位是N·m 2/kg 2B.引力常量G 的大小与两物体质量的乘积成反比,与两物体间距离的平方成正比C.引力常量G 在数值上等于两个质量都是1 kg 的可视为质点的物体相距1 m 时的相互吸引力D.引力常量G 是不变的,其数值大小由卡文迪许测出,与单位制的选择无关3.(2019·北京牛栏山一中期中)图1(a)是用来“显示桌(或支持)面的微小形变”的演示实验;图(b)是用来“测量万有引力常量”的实验.由图可知,两个实验共同的物理思想方法是( )图1A.极限的思想方法B.放大的思想方法C.控制变量的方法D.猜想的思想方法考点二 万有引力定律的简单应用4.(2019·永春县第一中学高一期末)要使两物体间的万有引力减小到原来的14,下列办法不正确的是( )A.使两物体的质量各减小一半,距离不变B.使其中一个物体的质量减小到原来的14,距离不变C.使两物体间的距离增大到原来的2倍,质量不变D.使两物体的质量和距离都减小到原来的145.某物体在地面上受到地球对它的万有引力为F .若此物体受到的引力减小到F4,则此物体距离地面的高度应为(R 为地球半径)( ) A.2R B.4R C.R D.8R6.地球半径为R ,地球表面的重力加速度为g ,若高空中某处的重力加速度为g2,则该处距地球表面的高度为( )A.(2-1)RB.RC.2RD.2R7.(多选)如图2所示,三颗质量均为m 的地球同步卫星等间隔分布在半径为r 的圆轨道上,设地球质量为M ,半径为R ,下列说法正确的是( )图2A.地球对一颗卫星的引力大小为GMm(r -R )2B.一颗卫星对地球的引力大小为GMmr 2C.两颗卫星之间的引力大小为Gm 23r2D.三颗卫星对地球引力的合力大小为3GMmr28.地球质量大约是月球质量的81倍,一飞行器位于地球与月球之间,当地球对它的引力和月球对它的引力大小相等时,飞行器距月球球心的距离与月球球心距地球球心的距离之比为( )A.1∶9B.9∶1C.1∶10D.10∶1[能力综合练]9.如图3所示,一个质量均匀分布的半径为R 的球体对球外质点P (图中未画出)的万有引力为F .如果在球体中央挖去半径为r 的一部分球体,且r =R2,则原球体剩余部分对质点P 的万有引力变为( )图3A.F 2B.F 8C.7F 8D.F 410.(多选)宇宙中存在着由四颗星组成的孤立星系.如图4所示,一颗母星处在正三角形的中心,三角形的顶点各有一颗质量相等的小星围绕母星做圆周运动.如果两颗小星间的万有引力为F ,母星与任意一颗小星间的万有引力为9F .则( )图4A.每颗小星受到的万有引力为(32+9)F B.每颗小星受到的万有引力为(3+9)F C.母星的质量是每颗小星质量的3倍 D.母星的质量是每颗小星质量的33倍11.若地球半径为R ,把地球看做质量分布均匀的球体.“蛟龙”号下潜深度为d ,“天宫一号”轨道距离地面高度为h ,“蛟龙”号所在处与“天宫一号”所在处的重力加速度之比为[在匀质球体内部距离球心r 处的质点(m )受到的万有引力等于球体内半径为r 的同心球体(M ′)对它的万有引力]( ) A.R -d R +h B.(R -d )2(R +h )2 C.(R -d )(R +h )2R 3D.(R -d )(R +h )R 212.某地区的地下发现了天然气资源,如图5所示,在水平地面P 点的正下方有一球形空腔区域内储藏有天然气.假设该地区岩石均匀分布且密度为ρ,天然气的密度远小于ρ,可忽略不计.如果没有该空腔,地球表面正常的重力加速度大小为g ;由于空腔的存在,现测得P 点处的重力加速度大小为kg (k <1).已知引力常量为G ,球形空腔的球心深度为d ,则此球形空腔的体积是( )图5A.kgd GρB.kgd 2GρC.(1-k )gd GρD.(1-k )gd 2Gρ13.已知太阳的质量为M ,地球的质量为m 1,月球的质量为m 2,当发生日全食时,太阳、月球、地球几乎在同一直线上,且月球位于太阳与地球之间,如图6所示.设月球到太阳的距离为a ,地球到月球的距离为b ,则太阳对地球的引力F 1和对月球的引力F 2的大小之比为多少?图614.某物体在地面上受到的重力为160 N ,将它放置在卫星中,在卫星以a =12g 的加速度随火箭向上加速升空的过程中,当物体与卫星中支持物的相互挤压的力为90 N 时,卫星距地球表面有多远?(地球半径R 地=6.4×103 km ,g 表示地面处重力加速度,g 取10 m/s 2)[拓展提升练]15.(2019·安徽师大附中高一下学期期中)地球可视为质量均匀分布的球体.某物体在地球北极点静止时对水平地面的压力为F N0,物体在地球赤道上静止时对水平地面的压力为F N ;地球自转周期为T ,万有引力常量为G ,地球密度的表达式为( )A.3πF N0GT 2(F N0-F N )B.3π(F N0-F N )GT 2F N0C.3πF N0GT 2D.3πF N0GT 2F N。
高一物理必修二第六章 2 3 太阳与行星间的引力 万有引力定律---教师版

2 太阳与行星间的引力3 万有引力定律[学习目标] 1.知道太阳与行星间存在引力.2.能利用开普勒定律和牛顿运动定律推导出太阳与行星之间的引力表达式.3.理解万有引力定律的内容、含义及适用条件.4.认识万有引力定律的普遍性,能应用万有引力定律解决实际问题.一、太阳与行星间的引力1.太阳对行星的引力:太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间距离的二次方成反比,即F ∝mr2.2.行星对太阳的引力:太阳与行星的地位相同,因此行星对太阳的引力和太阳对行星的引力规律相同,即F ′∝Mr2.3.太阳与行星间的引力:根据牛顿第三定律F =F ′,所以有F ∝Mm r 2,写成等式就是F =G Mmr 2.二、月—地检验1.猜想:维持月球绕地球运动的力与使得苹果下落的力是同一种力,同样遵从“平方反比”的规律.2.推理:根据牛顿第二定律,物体在月球轨道上运动时的加速度大约是它在地面附近下落时的加速度的1602.3.结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同(填“相同”或“不同”)的规律. 三、万有引力定律1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比.2.表达式:F =G m 1m 2r2.3.引力常量G :由英国物理学家卡文迪许测量得出,常取G =6.67×10-11N·m 2/kg 2.1.判断下列说法的正误.(1)万有引力不仅存在于天体之间,也存在于普通物体之间.(√)(2)质量一定的两个物体,若距离无限小,它们间的万有引力趋于无限大.(×)(3)把物体放在地球中心处,物体受到的引力无穷大.(×)(4)由于太阳质量大,太阳对行星的引力大于行星对太阳的引力.(×)(5)牛顿发现了万有引力定律,并测出了引力常量.(×)2.两个质量都是1 kg的物体(可看成质点),相距1 m时,两物体间的万有引力F=________ N,一个物体的重力F′=________ N,万有引力F与重力F′的比值为________.(已知引力常量G=6.67×10-11 N·m2/kg2,取重力加速度g=10 m/s2)答案 6.67×10-1110 6.67×10-12一、对太阳与行星间引力的理解1.是什么原因使行星绕太阳运动?答案太阳对行星的引力使行星绕太阳运动.2.在推导太阳与行星的引力时,我们对行星的运动怎么简化处理的?用了哪些知识?答案将行星绕太阳的椭圆运动看成匀速圆周运动.在推导过程中,用到了向心力公式、开普勒第三定律及牛顿运动定律.太阳与行星间引力关系的得出过程例1 (多选)根据开普勒关于行星运动的规律和圆周运动的知识知:太阳对行星的引力F ∝m r 2,行星对太阳的引力F ′∝Mr 2,其中M 、m 、r 分别为太阳质量、行星质量和太阳与行星间的距离,下列说法正确的是( ) A.由F ′∝M r 2和F ∝mr 2,得F ∶F ′=m ∶MB.F 和F ′大小相等,是作用力与反作用力C.F 和F ′大小相等,是同一个力D.太阳对行星的引力提供行星绕太阳做圆周运动的向心力 答案 BD解析 F ′和F 大小相等、方向相反,是作用力和反作用力,太阳对行星的引力提供行星绕太阳做圆周运动的向心力,故正确答案为B 、D. 二、万有引力定律(1)通过月—地检验结果表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同的规律.一切物体之间都存在这样的引力,那么,为什么通常两个人(如图1)间的万有引力我们却感受不到?图1(2)地球对人的万有引力与人对地球的万有引力大小相等吗?答案 (1)任意两个物体间都存在着万有引力.但由于地球上物体的质量一般很小(与天体质量相比),地球上两个物体间的万有引力远小于地面对物体的摩擦力,通常感受不到,但天体质量很大,天体间的引力很大,对天体的运动起决定作用. (2)相等.它们是一对相互作用力.1.万有引力定律表达式F =G m 1m 2r 2,G =6.67×10-11 N·m 2/kg 2.2.万有引力定律公式适用的条件(1)万有引力定律适用于两个质点间的相互作用.(2)一个均匀球体与球外一个质点,r 为球心到质点的距离. (3)两个质量均匀的球体,r 为两球心间的距离.例2 关于万有引力和万有引力定律的理解正确的是( ) A.不能看做质点的两物体间不存在相互作用的引力 B.只有能看做质点的两物体间的引力才能用F =Gm 1m 2r2计算C.由F =Gm 1m 2r 2知,两物体间距离r 减小时(没有无限靠近),它们之间的引力增大D.引力常量的大小是牛顿首先测出来的,且约等于6.67×10-11N·m 2/kg 2答案 C解析 任何物体间都存在相互作用的引力,故称万有引力,A 错;两个质量分布均匀的球体间的万有引力也能用F =Gm 1m 2r 2来计算,B 错;物体间的万有引力与它们间距离r 的二次方成反比,故r 减小,它们间的引力增大,C 对;引力常量G 是由卡文迪许首先精确测出的,D 错.例3 如图2所示,两球间的距离为r 0,两球的质量分布均匀,质量分别为m 1、m 2,半径分别为r 1、r 2,则两球间的万有引力大小为( )图2A.Gm 1m 2r 02B.Gm 1m 2r 12C.Gm 1m 2(r 1+r 2)2D.Gm 1m 2(r 1+r 2+r 0)2答案 D解析 两个匀质球体间的万有引力F =Gm 1m 2r2,r 是两球心间的距离,选D.例4 (2019·江川二中高一期末)一个质量均匀分布的球体,半径为2r ,在其内部挖去一个半径为r 的球形空穴,其表面与球面相切,如图3所示.已知挖去小球的质量为m ,在球心和空穴中心连线上,距球心d =6r 处有一质量为m ′的质点,求:图3(1)被挖去的小球挖去前对m ′的万有引力为多大? (2)剩余部分对m ′的万有引力为多大? 答案 (1)G mm ′25r 2 (2)G 41mm ′225r 2解析 (1)被挖去的小球挖去前对m ′的万有引力为 F 2=G mm ′(5r )2=G mm ′25r 2 (2)将挖去的小球填入空穴中,由V =43πr 3可知,大球的质量为8m ,大球对m ′的万有引力为F 1=G 8m ·m ′(6r )2=G 2mm ′9r 2m ′所受剩余部分的万有引力为F =F 1-F 2=G 41mm ′225r 2.三、重力和万有引力的关系1.物体在地球表面上所受引力与重力的关系图4除两极以外,地面上其他点的物体,都围绕地轴做圆周运动,这就需要一个垂直于地轴的向心力.由地球对物体引力的一个分力F ′提供向心力,另一个分力为重力G ,如图4所示. (1)当物体在两极时:G =F 引,重力达到最大值G max =G MmR 2.(2)当物体在赤道上时:F ′=mω2R 最大,此时重力最小G min =GMmR 2-mω2R (3)从赤道到两极:随着纬度增加,向心力F ′=mω2R ′减小,F ′与F 引夹角增大,所以重力G 在增大,重力加速度增大.因为F ′、F 引、G 不在一条直线上,重力G 与万有引力F 引方向有偏差,重力大小mg <G MmR 2.2.重力与高度的关系若距离地面的高度为h ,则mg ′=G Mm(R +h )2(R 为地球半径,g ′为离地面h 高度处的重力加速度).在同一纬度,距地面越高,重力加速度越小. 3.特别说明(1)重力是物体由于地球吸引产生的,但重力并不是地球对物体的引力.(2)只有在两极,mg =G Mm R 2,其他地方mg <G MmR 2,但相差不大,在忽略地球自转的情况下,认为mg =G MmR2.(3)在两极、赤道,两个力的方向相同,其他地方二者方向不同,略有偏差.引力的方向指向地心,重力的方向竖直向下.例5 (多选)万有引力定律能够很好地将天体运行规律与地球上物体运动规律具有的内在一致性统一起来.用弹簧测力计称量一个相对于地球静止的质量为m 的小物体的重力,随称量位置的变化可能会有不同的结果.已知地球质量为M ,引力常量为G .将地球视为半径为R 、质量均匀分布的球体.下列说法正确的是( )A.在北极地面称量时,弹簧测力计读数为F 0=G Mm R 2B.在赤道地面称量时,弹簧测力计读数为F 1=G MmR2C.在北极上空高出地面h 处称量时,弹簧测力计读数为F 2=G Mm(R +h )2D.在赤道上空高出地面h 处称量时,弹簧测力计读数为F 3=G Mm(R +h )2答案 AC解析 物体在两极时,万有引力等于重力,则有F 0=G MmR 2,故A 正确;在赤道地面称量时,万有引力等于重力加上随地球一起自转所需要的向心力,则有F 1<G MmR2,故B 错误;在北极上空高出地面h 处称量时,万有引力等于重力,则有F 2=G Mm(R +h )2,故C 正确;在赤道上空高出地面h 处称量时,万有引力大于重力,则有F 3<G Mm(R +h )2,故D 错误.例6 火星半径是地球半径的12,火星质量大约是地球质量的19,那么地球表面上质量为50 kg的宇航员(地球表面的重力加速度g 取10 m/s 2) (1)在火星表面上受到的重力是多少?(2)若宇航员在地球表面能跳1.5 m 高,那他在火星表面能跳多高? 答案 (1)222.2 N (2)3.375 m 解析 (1)在地球表面有mg =G MmR 2在火星表面上有mg ′=G M ′mR ′2联立解得g ′=409 m/s 2宇航员在火星表面上受到的重力 G ′=mg ′=50×409 N ≈222.2 N.(2)在地球表面宇航员跳起的高度H =v 022g在火星表面宇航员跳起的高度h =v 022g ′综上可知,h =g g ′H =10409×1.5 m =3.375 m.1.(对万有引力定律的理解)(2019·武威第十八中学高一期末)对于万有引力定律的表达式F =G m 1m 2r2,下列说法正确的是( ) A.公式中G 为引力常量,它是由实验测得的,而不是人为规定的 B.当r 趋近于零时,万有引力趋于无穷大C.对于m 1与m 2间的万有引力,质量大的受到的引力大D.m 1与m 2受到的引力是一对平衡力 答案 A解析 万有引力定律的表达式F =G m 1m 2r2,公式中G 为引力常量,它是由实验测得的,而不是人为规定的,选项A 正确;当r 趋近于零时,万有引力定律不再适用,选项B 错误;m 1与m 2间的万有引力是相互作用力,两物体受到的万有引力是等大反向的,与质量大小无关,选项C 错误;m 1与m 2受到的引力是一对相互作用力,因作用在两个物体上,故不是平衡力,选项D 错误.2.(月—地检验)(2018·北京卷)若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律,在已知月地距离约为地球半径60倍的情况下,需要验证( ) A.地球吸引月球的力约为地球吸引苹果的力的1602B.月球公转的加速度约为苹果落向地面加速度的1602C.自由落体在月球表面的加速度约为地球表面的16D.苹果在月球表面受到的引力约为在地球表面的160答案 B解析 若想检验“使月球绕地球运动的力”与“使苹果落地的力”遵循同样的规律——万有引力定律,则应满足G Mmr2=ma ,因此加速度a 与距离r 的二次方成反比.3.(万有引力定律的简单应用)两个完全相同的实心均质小铁球紧靠在一起,它们之间的万有引力为F .若将两个用同种材料制成的半径是小铁球2倍的实心大铁球紧靠在一起,则两个大铁球之间的万有引力为( ) A.2F B.4F C.8F D.16F 答案 D解析 两个小铁球之间的万有引力为F =G mm (2r )2=G m 24r 2.实心小铁球的质量为m =ρV =ρ·43πr 3,大铁球的半径是小铁球的2倍,则大铁球的质量m ′与小铁球的质量m 之比为m ′m =r ′3r 3=8,故两个大铁球间的万有引力为F ′=G m ′m ′4r ′2=16F .故选D.4.(重力加速度的计算)据报道,在太阳系外发现了首颗“宜居”行星,设其质量为地球质量的k 倍,其半径为地球半径的p 倍,由此可推知该行星表面的重力加速度与地球表面重力加速度之比为( )A.k pB.k p 2C.k 2pD.k 2p 2 答案 B解析 由mg =G MmR 2可知:g 地=G M 地 R 地2,g 星=G M 星R 星2,g 星g 地=M 星M 地·R 地2R 星2=k p2,所以选项B 正确.[基础对点练]考点一 万有引力定律的理解1.(2019·肥东高级中学高一下期末)下列关于行星对太阳的引力的说法中正确的是( ) A.行星对太阳的引力与太阳对行星的引力是同一种性质的力 B.行星对太阳的引力与太阳的质量成正比,与行星的质量无关 C.太阳对行星的引力大于行星对太阳的引力D.行星对太阳的引力与太阳的质量成正比,与行星距太阳的距离成反比 答案 A解析 行星对太阳的引力和太阳对行星的引力都是万有引力,性质相同,故A 正确;根据万有引力定律分析可知:行星对太阳的引力与行星和太阳的质量的乘积成正比,与两者的质量都有关,故B 错误;由牛顿第三定律分析得知,太阳对行星的引力等于行星对太阳的引力,故C 错误;根据万有引力定律分析可知:行星对太阳的引力与行星和太阳的质量的乘积成正比,与行星距太阳的距离的平方成反比,故D 错误. 2.(多选)关于引力常量G ,下列说法中正确的是( ) A.在国际单位制中引力常量G 的单位是N·m 2/kg 2B.引力常量G 的大小与两物体质量的乘积成反比,与两物体间距离的平方成正比C.引力常量G 在数值上等于两个质量都是1 kg 的可视为质点的物体相距1 m 时的相互吸引力D.引力常量G 是不变的,其数值大小由卡文迪许测出,与单位制的选择无关 答案 AC解析 由F =G m 1m 2r 2得G =F ·r 2m 1m 2,所以在国际单位制中单位为N·m 2/kg 2,选项A 正确;引力常量是一个常数,其大小与质量以及两物体间的距离无关,选项B 错误;根据万有引力定律可知,引力常量G 在数值上等于两个质量都是1 kg 的可视为质点的物体相距1 m 时的相互吸引力,选项C 正确;引力常量是定值,其数值大小由卡文迪许测出,但其大小与单位制的选择有关,选项D 错误.3.(2019·北京牛栏山一中期中)图1(a)是用来“显示桌(或支持)面的微小形变”的演示实验;图(b)是用来“测量万有引力常量”的实验.由图可知,两个实验共同的物理思想方法是( )图1A.极限的思想方法B.放大的思想方法C.控制变量的方法D.猜想的思想方法答案 B考点二 万有引力定律的简单应用4.(2019·永春县第一中学高一期末)要使两物体间的万有引力减小到原来的14,下列办法不正确的是( )A.使两物体的质量各减小一半,距离不变B.使其中一个物体的质量减小到原来的14,距离不变C.使两物体间的距离增大到原来的2倍,质量不变D.使两物体的质量和距离都减小到原来的14答案 D解析 万有引力定律的表达式为F =G Mmr 2,根据该公式可知,使两物体的质量各减小一半,距离不变,则万有引力变为原来的14,A 正确;使其中一个物体的质量减小到原来的14,距离不变,则万有引力变为原来的14,B 正确;使两物体间的距离增大到原来的2倍,质量不变,则万有引力变为原来的14,C 正确;使两物体的质量和距离都减小到原来的14,则万有引力大小不变,D 错误.5.某物体在地面上受到地球对它的万有引力为F .若此物体受到的引力减小到F4,则此物体距离地面的高度应为(R 为地球半径)( ) A.2R B.4R C.R D.8R 答案 C解析 根据万有引力定律有F =G Mm R 2,14F =G Mm(R +h )2,解得h =R ,选项C 正确.6.地球半径为R ,地球表面的重力加速度为g ,若高空中某处的重力加速度为g2,则该处距地球表面的高度为( )A.(2-1)RB.RC.2RD.2R 答案 A解析 万有引力近似等于重力,设地球的质量为M ,物体质量为m ,物体距地面的高度为h ,则有GMm R 2=mg ,G Mm (R +h )2=m g 2,联立得2R 2=(R +h )2,解得h =(2-1)R ,选项A 正确. 7.(多选)如图2所示,三颗质量均为m 的地球同步卫星等间隔分布在半径为r 的圆轨道上,设地球质量为M ,半径为R ,下列说法正确的是( )图2A.地球对一颗卫星的引力大小为GMm (r -R )2B.一颗卫星对地球的引力大小为GMmr 2C.两颗卫星之间的引力大小为Gm 23r2D.三颗卫星对地球引力的合力大小为3GMmr 2答案 BC解析 地球与一颗卫星间的引力大小为GMmr 2,A 错误,B 正确.由几何关系可知两卫星之间的距离为3r ,两卫星之间的引力为Gmm (3r )2=Gm 23r 2,C 正确.三颗卫星对地球引力的合力大小为零,D 错误.8.地球质量大约是月球质量的81倍,一飞行器位于地球与月球之间,当地球对它的引力和月球对它的引力大小相等时,飞行器距月球球心的距离与月球球心距地球球心的距离之比为( )A.1∶9B.9∶1C.1∶10D.10∶1 答案 C解析 设月球质量为m ,则地球质量为81m ,月球球心距地球球心的距离为r ,飞行器质量为m 0,当飞行器距月球球心的距离为r ′时,地球对它的引力等于月球对它的引力,则G mm 0r ′2=G 81mm 0(r -r ′)2,所以r -r ′r ′=9,r =10r ′,r ′∶r =1∶10,故选项C 正确.[能力综合练]9.如图3所示,一个质量均匀分布的半径为R 的球体对球外质点P (图中未画出)的万有引力为F .如果在球体中央挖去半径为r 的一部分球体,且r =R2,则原球体剩余部分对质点P 的万有引力变为( )图3A.F 2B.F 8C.7F 8D.F 4 答案 C解析 利用填补法来分析此题.原来物体间的万有引力为F ,挖去的半径为R2的球体的质量为原来球体质量的18,其他条件不变,故剩余部分对质点P 的万有引力为F -F 8=78F .10.(多选)宇宙中存在着由四颗星组成的孤立星系.如图4所示,一颗母星处在正三角形的中心,三角形的顶点各有一颗质量相等的小星围绕母星做圆周运动.如果两颗小星间的万有引力为F ,母星与任意一颗小星间的万有引力为9F .则( )图4A.每颗小星受到的万有引力为(32+9)F B.每颗小星受到的万有引力为(3+9)F C.母星的质量是每颗小星质量的3倍 D.母星的质量是每颗小星质量的33倍 答案 BC解析 假设每颗小星的质量为m ,母星的质量为M ,正三角形的边长为a ,则小星绕母星运动的轨道半径为r =33a . 根据万有引力定律,两颗小星间的万有引力为F =G mma 2,母星与任意一颗小星间的万有引力为9F =G Mmr 2,联立解得M =3m ,故C 正确,D 错误.任意一颗小星受到的万有引力F ′=9F+2F ·cos 30°=(3+9)F ,故A 错误,B 正确.11.若地球半径为R ,把地球看做质量分布均匀的球体.“蛟龙”号下潜深度为d ,“天宫一号”轨道距离地面高度为h ,“蛟龙”号所在处与“天宫一号”所在处的重力加速度之比为[在匀质球体内部距离球心r 处的质点(m )受到的万有引力等于球体内半径为r 的同心球体(M ′)对它的万有引力]( ) A.R -d R +hB.(R -d )2(R +h )2 C.(R -d )(R +h )2R 3D.(R -d )(R +h )R 2答案 C解析 设地球的密度为ρ,则在地球表面,重力和地球的万有引力大小相等,有:g =G MR 2.由于地球的质量为:M =ρ·43πR 3,所以重力加速度的表达式可写成:g =GM R 2=ρG 43πR 3R 2=43πGρR .根据题意有,质量分布均匀的球壳对壳内物体的引力为零,故在深度为d 的地球内部,受到地球的万有引力即为半径等于(R -d )的球体在其表面产生的万有引力,故“蛟龙”号的重力加速度g ′=43πGρ(R -d ),所以有g ′g =R -d R .根据万有引力提供向心力G Mm(R +h )2=ma ,“天宫一号”所在处的重力加速度为a =GM (R +h )2,所以a g =R 2(R +h )2,g ′a =(R -d )(R +h )2R 3,故C 正确,A 、B 、D 错误.12.某地区的地下发现了天然气资源,如图5所示,在水平地面P 点的正下方有一球形空腔区域内储藏有天然气.假设该地区岩石均匀分布且密度为ρ,天然气的密度远小于ρ,可忽略不计.如果没有该空腔,地球表面正常的重力加速度大小为g ;由于空腔的存在,现测得P 点处的重力加速度大小为kg (k <1).已知引力常量为G ,球形空腔的球心深度为d ,则此球形空腔的体积是( )图5A.kgd GρB.kgd 2GρC.(1-k )gd GρD.(1-k )gd 2Gρ答案 D解析 如果将近地表的球形空腔填满密度为ρ的岩石,则该地区重力加速度便回到正常值,因此,如果将空腔填满密度为ρ的岩石,地面质量为m 的物体的重力为mg ,没有填满时重力是kmg ,故空腔填满的岩石所引起的引力为(1-k )mg ,根据万有引力定律有(1-k )mg =G ρVmd 2,解得V =(1-k )gd 2Gρ,故选D. 13.已知太阳的质量为M ,地球的质量为m 1,月球的质量为m 2,当发生日全食时,太阳、月球、地球几乎在同一直线上,且月球位于太阳与地球之间,如图6所示.设月球到太阳的距离为a ,地球到月球的距离为b ,则太阳对地球的引力F 1和对月球的引力F 2的大小之比为多少?图6答案 m 1a 2m 2(a +b )2解析 由太阳与行星间的引力公式F =G Mmr2得太阳对地球的引力F 1=G Mm 1(a +b )2太阳对月球的引力F 2=G Mm 2a2联立可得F 1F 2=m 1a 2m 2(a +b )2.14.某物体在地面上受到的重力为160 N ,将它放置在卫星中,在卫星以a =12g 的加速度随火箭向上加速升空的过程中,当物体与卫星中支持物的相互挤压的力为90 N 时,卫星距地球表面有多远?(地球半径R 地=6.4×103 km ,g 表示地面处重力加速度,g 取10 m/s 2) 答案 1.92×104 km解析 卫星的升空过程可以认为是竖直向上的匀加速直线运动,设卫星离地面的距离为h ,这时受到地球的万有引力为F =G Mm (R 地+h )2. 在地球表面G MmR 地2=mg在上升至离地面h 时,F N -F =ma . 联立解得(R 地+h )2R 地2=mgF N -ma ,则h =(mgF N -ma-1)R 地.代入数值解得h =1.92×104 km.[拓展提升练]15.(2019·安徽师大附中高一下学期期中)地球可视为质量均匀分布的球体.某物体在地球北极点静止时对水平地面的压力为F N0,物体在地球赤道上静止时对水平地面的压力为F N ;地球自转周期为T ,万有引力常量为G ,地球密度的表达式为( ) A.3πF N0GT 2(F N0-F N ) B.3π(F N0-F N )GT 2F N0C.3πF N0GT 2D.3πF N0GT 2F N答案 A解析 地球自转周期为T ,物体在北极水平地面上静止时所受到的支持力:F N0=GMmR2;同一物体在赤道上静止时所受到的支持力:F N =GMm R 2-m (2πT )2R ;地球的质量:M =43πR 3·ρ,联立解得:ρ=3πF N0GT 2(F N0-F N ),故A 正确,B 、C 、D 错误.。
万有引力综合应用——原卷版高一物理同步讲义(人教版2019必修第二册)

第8讲 万有引力综合应用模块一:天体运动的一般规律1.卫星变轨问题 (1)圆轨道上的稳定运行圆周运动:万有引力提供圆周运动向心力(球心间距等于轨道半径)2221222π===ω⎛⎫ ⎪⎝⎭m m v G m mr m r r r T(2)变轨运行分析椭圆运动:万有引力提供椭圆运动向心力(球心间距不等于轨道半径)①当v 增大时,所需向心力2v m r增大,即万有引力不足以提供向心力,卫星将做离心运动,脱离原来的圆轨道,轨道半径变大,但卫星一旦进入新的轨道运行,由GMv r=速度要减小,但重力势能、机械能均增加.②当卫星的速度突然减小时,向心力2v m r 减小,即万有引力大于卫星所需的向心力,因此卫星将做向心运动,同样会脱离原来的圆轨道,轨道半径变小,进入新轨道运行时由2v mr知运行速度将增大,但重力势能、机械能均减少. 规律总结:(1)稳定在新轨道上的运行速度由GMv r=(2)卫星绕过不同轨道上的同一点(切点)时,其加速度大小关系可用2=GMmF ma r=比较得出. (3)卫星在不同轨道上的运行周期大小可以借助开普勒第三定律再结合半长轴比较得出. 2.卫星的追及和相遇问题两天体(行星、卫星或探测器)相遇,实际上是指两天体相距最近.若两环绕天体的运动轨道知识点碎片难度卫星变轨及追及问题★★★☆☆ 宇宙速度 ★★★☆☆ 同步卫星与近地卫星 ★★★☆☆ 计算中心天体的质量和密度★★★☆☆在同一平面内,则两环绕天体与中心体在同一直线上,且位于中心天体的同侧时相距最近.两环绕天体与中心天体在同一直线上,且位于中心天体的异侧时相距最远.设卫星1(离地球近些)与卫星2某时刻相距最近,如果经过时间t ,两卫星与地心连线半径转过的角度相差2π的整数倍,则两卫星又相距最近,即:()112221,2,3,t t n n ωωπ-==⋅⋅⋅;如果经过时间't ,两卫星与地心连线半径转过的角度相差π的奇数倍,则两卫星相距最远,即:()()112221π1,2,3,ωω-=-=⋅⋅⋅t t n n .例1.★★☆☆☆2013年12月2日凌晨1时30分,嫦娥三号月球探测器搭载长征三号乙火箭发射升空.这是继07年嫦娥一号、10年嫦娥二号之后,我国发射的第3颗月球探测器,也是首颗月球软着陆探测器.嫦娥三号携带有一台无人月球车,重3吨多,是我国设计最复杂的航天器.如图所示为其飞行轨道示意图,则下列说法正确的是( )A .嫦娥三号的发射速度应该大于11.2 km/sB .嫦娥三号在环月轨道1上P 点的加速度大于在环月轨道2上P 点的加速度C .嫦娥三号在环月轨道2上运行周期比在环月轨道1上运行周期小D .嫦娥三号在下降段中一直处于完全失重状态 练1-1.★★☆☆☆发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3,轨道1、2相切于Q 点,轨道2、3相切于P 点,如图所示.则以下说法不正确的是( )A .要将卫星由圆轨道1送入圆轨道3,需要在椭圆轨道2的近地点Q 和远地点P 分别点火加速一次B .由于卫星由圆轨道l 送入圆轨道3被点火加速两次,则卫星在圆轨道3上正常运行速度要大于在圆轨道l 上正常运行的速度C .卫星在椭圆轨道2上的近地点Q 的速度一定大于7.9 km/s ,而在远地点P 的速度一定小于7.9 km/sD .卫星在椭圆轨道2上经过P 点时的加速度等于它在圆轨道3上经过P 点时的加速度练1-2.★★★☆☆如图所示,搭载着“嫦娥二号”卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100 km 、周期为118 min 的工作轨道,开始对月球进行探测,则( ) A .卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度大B .卫星在轨道Ⅲ上经过P 点的加速度速度与在轨道 II 上经过P 点时的加速度相等C .卫星在轨道Ⅲ上运行周期比在轨道Ⅰ上大D .卫星在轨道Ⅲ上经过P 点的速度比在轨道Ⅰ上经过P 点时的大例2.★★★☆☆如图所示,A 为太阳系中的天王星,它绕太阳O 运行可视为做轨道半径为R 0,周期为T 0的匀速圆周运动.天文学家经长期观测发现,天王星实际运动的轨道与圆轨道总有一些偏离,且每隔t 0时间发生一次最大偏离,形成这种现象的原因是天王星外侧还存在着另一颗行星B ,假设行星B 与A 在同一平面内,且与A 的绕行方向相同,绕O 作匀速圆周运动,它对天王星的万有引力导致了天王星轨道的偏离,由此可推测行星B 的运动轨道半径是( ) A .R 000t t T - B .R 03000()t t T - C .R 020030()t T t - D .R 020300()t t T -练2-1.★★★☆☆甲,乙两颗人造卫星在同一平面内沿同一方向做匀速圆周运动,甲卫星距离地面的高度是地球半径的12,乙卫星距离地面的高度是地球半径的5倍.某时刻两卫星相距最近,问:经过多少个乙卫星做圆周运动的周期,两卫星第一次相距最远? 练2-2.★★★☆☆“行星冲日”是指当地球恰好运行到某地外行星和太阳之间且三者排成一条直线的天文现象.2014年4月9日发生了火星冲日的现象.已知火星和地球绕太阳公转的方向相同,轨迹都可近似为圆,公转轨道半径为地球的1.5倍,以下说法正确的是()A.火星的公转周期比地球大B.火星的运行速度比地球大C.每年都会出现火星冲日现象D.2015年一定会出现火星冲日现象模块二:双星及多星问题1.双星模型在天体运动中,将两颗彼此相距较近且在相互之间万有引力作用下,绕两者连线上的某点做周期相同的匀速圆周运动的行星称为双星. 模型特点如图所示为质量分别是m 1和m 2的两颗相距较近的恒星。
专题-物理-万有引力计算天体质量和密度

R2
3
得 3g . 4 GR
巩固练习1:宇航员在某星球表面,将一小球从离地面为h高处以初速度v0水平抛出,测出小球落地点 与抛出点间的水平位移为s,若该星球的半径为R,万有引力恒量为G,求该星球的质量多大?
巩固练习2:地球绕太阳公转的轨道半径为1.49 ×1011m,公转的周期是3.16×107s,太阳的质量是多 少?
(3)若已知月球运行的线速度v和运行周期T,由于地球对月球的引力等于月球做匀速圆周运 动的向心力,根据牛顿第二定律,得
G
=m月·v·
以上两式消去r,解得
G
=m月.
M地=v3T/(2πG).
(4)若已知地球的半径R和地球表面的重力加速度g,根据物体的重力近为M地= .
本课小结
动力学分析
计算方法
典型例题
一、计算天体的质量
1.地球质量的计算
利用地球表面的物体,若不考虑地球自转,质量为m的物体的重力等于地球对物体的万有引
力,即mg=GRM2m
,则M=
gR2,由于g、R已经测出,因此可计算出地球的质量. G
2.太阳质量的计算 利用某一行星:由于行星绕太阳的运动,可看做匀速圆周运动,行星与太阳间的万有引力 充当向心力,即G =mω2r,而ω= ,则可以通过测出行星绕太阳运转的周期和轨道 半径,得到太阳质量M= . 3.其他行星质量的计算 利用绕行星运转的卫星,测出该卫星绕行星运转的周期和轨道半径同样可得出行星的质量.
一、天体质量的估算(以地球质量的计算为例) 1.已知卫星绕地球做匀速圆周运动的周期为T,半径为r,
二、天体密度的估算
1.密度公式
4
M
R3
,只要先得出天体的质量和半径就可代入此式计算天体的密度.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测一测,你学会了吗?
(主题资源/实战演练) 时间:5min
“神六”是怎样飞上天空的呢? 它又为何不掉下来?
讨论与交流: 当它抛到多大速度的时候就不会落回地球,而 围绕地球旋转?
卫星环绕地球做匀速圆周运动,由万有引力提供向心力,即F万=F向 设地球质量为M,卫星质量为m,两者中心的距离为r,
所以G
第一宇宙速度(环绕速度): 7.9km/s 第二宇宙速度(脱离速度):11.2km/s 第三宇宙速度(逃逸速度):16 .7km/s
扬帆应用知识的海洋!
作业:P54 4、5
;温州乐清包船捕鱼 温州乐清包船捕鱼 ;
材的多样化,非要把闲情雅致、风花雪月从散文主题上驱逐出去不可,而是指一个“比例”问题。我和散文家刘烨园先生在谈话中,他提出一个“比例”说,问题点得很到位:评价一种事物和现象,关键看它所包含的各项的比例。纠正一个偏颇,其实即对一种比例作调整,而非彻底颠覆或灭杀 什么。现在的情况是:散文中赋闲成分太大,精神比例过小。对我们这样一个远不轻松的时代更是如此。除了过去所赋予散文的那些品质以外,散文应融入更多的思想和良知的品质,除了生命美学和感性元素,更应融入理性揭批功能,应在问题上更贴近当代生存,应放扩关怀力,让更多更严峻 的事物进入视野……尤其眼下是这样一个“问题”和“隐患”威胁到人类生存的时代,散文应适度地选择承担,选择发言,而非冷漠与旁观。 过去有一句话:“民族的,就是世界的。”套用一下,也可以说:“当代的,就是永恒的”,如果对当代最重大和最急峻的现实命题都回避,如果连 当代生活都不感兴趣的话,那所谓“藏之名山”的想法无疑是可笑的,一种虚妄的幻觉与自欺罢了。其实,西方的优秀作家和作品,本质上无时无刻不是在为当代人而作,也是为未来而作——因为未来者对先人生存历史和精神困境的了解,无不是通过这些作品实现的。 当代叙事的不足,也 表现在所谓的“文化大散文”上,它们更多地扮演了一种“棕子”,一种“裹脚”的叙事角色,更多的停滞在对史事片段的重复叙述和揣摩上(我一点不否定它的价值,只是觉得它应该而且能够承担更多的东西)。文化不应只是“过去时”的,更应有“现在时”和“进行时”,应把精神触角延 伸至当下的国民生态,应在时间过渡的表面下,找到“根”和“枝叶”的血脉递承与母子关系,否则,文化散文就成了彻头彻尾的“历史散文”。说到底,这取决于作者的内里和品格,尤其在中国,这甚至不是才华、能力和技术问题,而是一个写作信仰问题,是对作家生命关怀力的考验,对其 精神诉求和承担能力的考验! 所以我觉得,其实有一个比“写得好坏”更重大的问题我们没解决好:“为什么写作?”在这样一个职业选择日益多样化的时代,是什么样的绝对理由和终极信仰使一个人选择了孤独的写作生涯而没有去干别的?这个问题在西方作家身上可以说是一个永恒的终 身命题,从他开始写作的那天起,就要面对,就要选择,就要确立一种生存立场和写作姿势,就要为自己一生的作品命名,一直到死。但在很多中国作家这儿,你很可能找不到这样一个“基因”,或者未曾遇到,或者根本不当回事。也就是说,我们的文学深处,很有可能缺乏一个结实的“奠 基”,缺乏一种“根”。 最后,我还想说明的一点是:当前散文的“热闹”很大程度上是由杂文、思想或文化随笔——由作者队伍的结构和角色改变所带来的,散文从业人员的成分复杂和丰富了,它不再是传统文学作者的专利,诗人、人文学者、自然科学家、批评型知识分子、小说家的 “另类散文”都给人耳目一新的感觉。虽然表面上看,涉及社会民生、历史文化、自然生态的文本如今比任何一个时期显得都多,但实际质量不容乐观,除了刚才提到的“文化散文”的缺陷外,还要警惕一点:在给散文松绑、融入理性品质的同时,要防止文学美质和艺术性的流失!我注意到很 多理性散文和思想性随笔在文本上的机械、粗糙与僵硬,其美学含量是严重不足的——不仅仅反映在语言表层,更多还体现于思维、思路的粗糙和欠精准上。 总之,散文现在面临的不再是它能承载什么——允许什么进入的问题?而关键看我们能够赋予散文什么?散文应从传统的那种松垮、 慵散、懈怠的过于休闲状态中解脱出来,应该更多针承担人文精神与良知功能,应该有更多对社会和当代的思考……在生命诚实、精神关怀力社会良知和道义承担上下工夫!应该端正身子,以直视生命的态度写散文,而非懒洋洋地画散文,描散文。 散文不该沦为文学的剩饭、闲饭、馊饭。 而文学,更不应被稀释成一个时代的胃酸和呕吐物。 向一个人的死因致敬 王开岭 一 一个人精神毁容了,被自己或别人的硫酸,如何是好,如何是好…… 面皮移植?铸一铁面具?归隐山泉与雀兽为伴? 卢武铉先是对观众说了声对不起,然后散步,迎着日出,迎着故里的崖。 山脚下的小村子 很美,无论地理还是气质,卢武铉回忆得也很美,说那是个“连乌鸦都会因找不到食物哭着飞走”的地方,他的话深情而充满感恩。在乌鸦身上,他用了个哭字。 想当年,他就是因找不到食物而哭着飞走的。去了大田,去了汉城,去了青瓦台。 每次出发,他都空空荡荡,除了一个贫民之子的 誓言、一个清卷书生的豪气,别无行李。 坑坑洼洼的故乡,那些含辛茹苦、蓬蓬勃勃的野草,似乎给了他最生动的精神注脚,也预支了最有力的人格担保。 怎么看,此人的变节风险都是最小的。他有着淳朴的起点和奋斗史。 坎坷身世、卑微学历、民权斗士、草根总统……卢武铉像一个童话。 全世界,包括我这个外国人都对这个童话喜爱不已,也觉得和自己隐隐有关。 这世界需要童话,需要一次童话的胜利,就像需要一场雪。 最近一场雪是奥巴马带来的,他的肤色照亮了星条旗,也鼓舞了地球仪。只是他离得远了点,不如卢武铉这般近,像亲戚。 有时,我觉得卢武铉酷似中国史 书上的那些前辈,很儒家,很士林。你看他说过的—— 大选获胜后,他用噙泪的语调承诺:“我知道大家对我的期望是什么,那是一个没有腐败、没有特权、没有违规的社会,一个用自己双手生活的诚实的社会。” 面对反腐的重重险碍,他说:“没有一个农民,会因土地贫瘠而放弃劳作。” 住青瓦台后,他与友人私下谈心,称执政关键有三:一将改革进行到底,二让总统府远离金钱,三管好自己亲属。 凡此种种,都让我想起先人那句话:“富贵不能淫,贫贱不能移,威武不能屈。” 做好这几条,孟子说,你就是大丈夫了。其实,也就是最好的公仆。 还有啊,论面相,卢武铉的 东方脸孔上有一种让人特放心的东西,温绵、敦厚、亲蔼,处处散发着安全感,完全符合中国人推崇的“方正”。 然而,童话终究是童话。事实明,贫穷和廉洁并无直接关系,监督权力和坐拥权力是截然不同的两份差事。 当他和故乡不再为食物发愁的时候,其家人被怀疑偷拿了别人的东西。 终于,一名英勇的律师站在了审判席上,一位历史的原告变成了现实的被告。某种意义上,卢武铉成了自己信仰的敌人。至少客观上,他互换了位置。 二 为什么会这样,怎么会这样呢? 对此我不感兴趣,我只留意到了那天,他最后一次攀登。 他选择了故乡的崖。崖,本身就意味着高度,是 尊严的象征,是清高者的去处。 可以想象,这曾是他少年立志和理想出发的地方。 清晨的草木,带露水,很干净。 一个人在做自由落体前,心真的会安宁吗? 世间很美,他远远看见山脚下活动的人影。同胞的生活又开始了,接下来,将是忙碌而幸福的一天。 对他来说,今天只意味着一个早 晨。 这一天,卢武铉将成为全世界的新闻头条。他料到了,但他已从看客中划掉了自己。 这是个脸皮薄的男人。性情如铅笔,直、细、脆,又爱哭鼻子。有人说,流泪是孱弱的表现,他不具职业政治家应有的坚韧。何谓坚韧呢?我不太懂。稍后,似乎也懂了,就是脸皮厚实且富弹性吧。 不错, 论政治体格,此人是弱了点,可谓弱不禁风。和城府深沉、世故圆滑的同行相比,他似乎太嫩,像书生,不像政客,甚至还有孩子的茸毛。 “我已丧失了再讲民主、进步与正义的资格……各位不能和我一起陷入这个泥淖,请大家舍弃我卢武铉吧。” 他没有狡辩,他说他无颜家乡父老,无颜全 体国民。其歉意之巨大,甚至连肇事的家人,他都表示了歉意。他觉得是自己,让最爱的人不幸沾染了权力,是自己的事业把亲属带到了危险地带。 非得纵身一跳?别无选择吗? 世间那么多毁容者,不都活得好好的? 这大概和一个人的精神体质有关。该体质决定了一个人的生命意义和存在依 据,决定了他遇事妥协的程度、忍受之底限。比如逆境之下的抉择,“好死不如赖活着”是一种,“留得青山在”是一种,“宁玉碎不瓦全”是一种,“万念俱灰唯死一途”是一种…… 卢武铉属哪种呢?我说不太清。 但有一点能确认:他死于面子,死于廉耻和羞愧,死于精神毁容后的照镜子。 “我现在没有脸正对你们的眼睛……我现在完全可以被抛弃了,现在我完全不足代表任何道德进步。” 这是个爱照镜子的政治家,是一个道德自尊心极强、自珍甚至自恋的人。他并非死于惊恐和畏惧,而是死于意境的破灭,死于内心的狂风,死于肖像的被毁,死于一个理想主义者和完美主义者 的失败感。还有,就是对清静、安宁和独处的渴望。 这种死因,包括死法,确不像现代政客所为。对许许多多政客来说,精神毁容、身败名裂,不过是轻若稻草的一件事,审判席上,磕头捣蒜乞饶求生者多如蝼蚁,贪生即怕死。但于一个自我器重惯了、把尊严和仪容视若性命之人,这事故就如 泰山压顶,漆黑一片。 所以,当有人说他死于一根道德稻草时,我不同意,我说他死于泰山。 不是说他死得重于泰山。 三 这种死因,多少让我想起了古人,想起了士林之风。我觉得精神气质上,卢武铉很有点前辈风度,像从竹林里走出来的,士大夫的腰板,昂首挺胸,纤尘不染。 古人是把 “知耻”当头等大事的,礼义廉耻被看作国之四维。 “无羞恶之心,非人也”“羞耻之心,义之端也”“五刑不如一耻”“士皆知有耻,则国家无耻矣”。 如果说古代士子是吃“素”的,一日三省谋求肺腑洁净,衣冠楚楚力图众口皆碑;那现代政客则少然,他们更崇尚丛林法则和蔽人耳目, 内心多“荤腥”之物。逻辑和尺度变了,精神体质也就变了,政治品格也就变了。丑事当前,拼命遮挡;铁如山,又死乞白赖。 古人惜名,今人惜命。古人自责,今人诿责。 谁脸上没个疮?在今人看来,卢武铉在道德反应上显然过度了,但古时候,这绝对算一个正常的“均值”,算一个合理 的脸皮厚度。 由此我涌生敬意。我向一个人的死因致敬。向他骨子里的那份“古意”致敬。 古意,让生命葱茏如竹。 我还想起了另一位自杀者,一个小得不能再小的小人物。三年前,南方一家小煤矿爆出档新闻,纸媒标题是,《倔犟矿工打赌嫖娼后服毒自杀“谢罪”》。事情大致如此:端午 节,矿上发了点酒,歇工后,矿友们围一起打牙祭,不能喝酒的张某很快有了醉意,后和人打起了赌,对方说如果你敢去“耍小姐”
