1 c○1997 American Mathematical Society
数学最吃香的十大专业数学杂志

数学最吃香的十大专业数学杂志在数学领域,专业的学术期刊扮演着至关重要的角色,它们汇集了最新的研究成果、批判性分析和前沿思想,为数学界的学者们提供了学术交流的平台。
而在众多的数学期刊中,哪些被认为是最吃香的呢?本文将为您介绍数学领域最受欢迎的十大专业数学杂志。
1. Journal of the American Mathematical Society美国数学协会杂志是一个备受尊敬的数学期刊,它涵盖了各个数学领域的前沿研究成果,具有很高的影响力和学术地位。
2. Annals of Mathematics《数学年刊》是一本历史悠久且声誉卓著的数学期刊,其刊载的文章常常代表了数学研究领域的最前沿。
3. Inventiones Mathematicae《数学发明》杂志是一个在数学领域备受赞誉的期刊,其刊载的论文通常包含了具有创新性和深度的数学研究成果。
4. Journal of Differential Geometry微分几何杂志致力于在微分几何领域发布高质量的论文,被认为是研究微分几何的顶尖杂志之一。
5. SIAM Journal on Applied Mathematics应用数学学会杂志关注应用数学的最新发展,提供了应用数学研究领域的精彩论文和成果。
6. Journal of Algebra代数学杂志专注于代数结构和代数学理论,它是代数学领域的一个重要刊物,被广泛认可。
7. Advances in Mathematics《数学进展》杂志发布具有极高水平和启发性的数学研究论文,被视为数学界的重要平台。
8. Communications in Mathematical Physics数学物理通讯杂志专注于数学物理学领域,刊载了许多关于数学物理交叉领域的创新性研究成果。
9. Journal of Number Theory数论杂志是一个关注数论研究的重要期刊,它介绍了数论领域的重要成果和方法。
10. Topology拓扑学杂志关注拓扑学领域的发展,刊载了许多有关拓扑空间和结构的研究成果,被视为拓扑学领域的重要期刊之一。
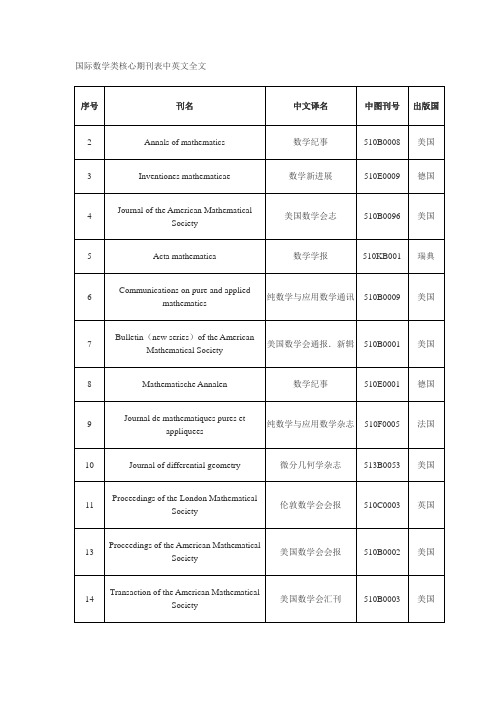
国际数学类核心期刊表中英文全文
519B0012
加拿大
73
The Bulletin of theLondonMathemetical Society
伦敦数学会通报
510C0056
美国
74
Mathematische Zeitschrift
数学杂志
510E0002
英国
75
Commentarii mathematici Helvetici
513LB006
英国
67
Differential equations
微分方程
513LB027
荷兰
68
IndianaUniversitymathematics Journal
印第安纳大学数学杂志
519B0003
荷兰
69
Communications in statistics.Theory and methods
国际数学类核心期刊表中英文全文
序号
刊名
中文译名
中图刊号
出版国
2
Annals of mathematics
数学纪事
510B0008
美国
3
Inventiones mathematicae
数学新进展
510E0009
德国
4
Journal of the American Mathematical Society
35
The American mathematical monthly
美国数学月刊
510B0007
美国
36
Discrete mathematics
离散数学
513LB005
美国
40
American Mathematical Society, 7, 844--851.

Aagaard, M. and Leeser, M. (1994) Verifying a logic synthesis tool in Nuprl: A case study in software veri cation. In v. Bochmann, G. and Probst, D. K. (eds.), Computer Aided Veri cation: Proceedings of the Fourth International Workshop, CAV'92, Volume 663 of Lecture Notes in Computer Science, Montreal, Canada, pp. 69{81. Springer Verlag.
Lagarias, J. (1985) The 3x + 1 problem and its generalizations. The
American Mathematical Monthly, 92, 3{23. Available on the Web as . http://www.cecm.sfu.ca/organics/papers/lagarias/index.html Landin, P. J. (1966) The next 700 programming languages. Communications of the ACM , 9, 157{166. Lindemann, F. (1882) Uber die Zahl . Mathematische Annalen, 120, 213{225. Mairson, H. G. (1990) Deciding ML typability is complete for deterministic exponential time. In Conference Record of the Seventeenth Annual ACM Symposium on Principles of Programming Languages (POPL), San Francisco, pp. 382{401. Association for Computing Machinery. Mairson, H. G. (1991) Outline of a proof theory of parametricity. In Hughes, J. (ed.), 1991 ACM Symposium on Functional Programming and Computer Architecture, Volume 523 of Lecture Notes in Computer Science, Harvard University, pp. 313{327. Martelli, A. and Montanari, U. (1982) An e cient uni cation algorithm. ACM Transactions on Programming Languages and Syst
ams学科分类

ams学科分类
AMS(American Mathematical Society)学科分类是指美国数
学学会关于数学研究领域的分类体系。
根据AMS学科分类,
数学被划分为63个主要领域,并进一步细分为更具体的子领域。
以下是AMS学科分类的一些主要领域:
1. 代数:包括了代数学、组合学和数论等领域;
2. 分析:包括了实分析、复分析、调和分析和泛函分析等领域;
3. 几何:包括了几何学和拓扑学等领域;
4. 拓扑:包括了拓扑学、几何拓扑学和代数拓扑学等领域;
5. 数学物理:包括了数学物理方程、动力系统和统计力学等领域;
6. 应用数学:包括了数学建模、计算数学和优化等领域;
7. 运筹学与管理科学:包括了线性规划、整数规划和排队论等领域;
8. 统计学:包括了统计推断、实验设计和数据分析等领域。
除了上述主要领域外,AMS学科分类还包括了许多其他重要
的数学研究领域,如微分方程、数学教育、概率论和数学逻辑等。
每个主要领域下还有更具体的子领域,使得学者可以在特定的数学研究领域进行深入研究。
数学领域的重要奖项与荣誉介绍

数学领域的重要奖项与荣誉介绍在数学领域,重要的奖项和荣誉广泛鼓励和认可了对数学的杰出贡献。
这些奖项旨在表彰数学家们的创新思维、卓越成就和对学术界的影响。
本文将介绍数学领域的一些重要奖项和荣誉,以展示数学界的追求卓越的精神和成就。
1. 菲尔兹奖(Fields Medal)菲尔兹奖是数学领域最高荣誉之一,历史悠久且备受崇敬。
该奖项每四年颁发一次,旨在表彰不超过40岁的数学家在数学领域做出的重要贡献。
菲尔兹奖得主不仅因其卓越的数学成就而获得奖项,同时也因其对数学领域的潜力和影响力而备受赞誉。
2. 阿贝尔奖(Abel Prize)阿贝尔奖是另一个备受推崇的数学奖项,由挪威政府设立,旨在表彰对数学做出卓越贡献的个人或团队。
该奖项每年颁发一次,该奖项也允许不限年龄。
阿贝尔奖颁发给那些在纯数学和应用数学领域中有深刻影响且作出突出贡献的人。
3. 克雷数学奖(Clay Mathematics Institute Millennium Prize)克雷数学奖是由克雷数学研究所设立的一系列数学奖项,包括黎曼猜想、黎曼假设、庞加莱猜想、Poincaré猜想等共7个问题。
成功解决其中任何一个问题的数学家将获得一百万美元的奖励。
该奖项旨在鼓励和推动数学的重要研究和发展。
4. 图灵奖(ACM A.M. Turing Award)图灵奖是计算机领域的最高奖项,有时也被认为是数学和计算机科学之间的桥梁。
每年由计算机学会(ACM)颁发,旨在表彰对计算机科学作出卓越贡献的个人或群体。
该奖项以图灵机的概念命名,是计算机领域最具声誉和影响力的奖项之一。
除了以上提到的奖项,还有一些其他重要奖项和荣誉,如数学学会颁发的高等研究学者(Fellow of the American Mathematical Society)称号,国际数学联合会颁发的数学家荣誉(The ICM Emmy Noether Lecture)等。
这些奖项和荣誉的共同目标是鼓励数学家们在创新研究和教学方面取得突破,推动数学领域的发展。
MathSciNet

(10)“Journal ”:可连到该刊的网站;
(11)“Article ”:链接的是该文献的全文, 若拥护已购买刊登该文献期刊的电子版, 则可直接打开全文。
(12)页面左上角的下拉菜单可以选择题 录或评论的显示格式。
3篇引用文献
通过合作者之间的关系,揭示权威和相关文献Erdos系数: Paul Erdö s是二十世纪一个著名美籍匈牙利裔的数学家。他最大 的特点就是多产,而且涉及的数学领域非常之广,也都有不错的贡 献。他一生和无数同时代的数学家 (大概500个左右)在不同的领 域内进行过合作,发表了大约1,500篇论文。 因为他的合作者很多,于是在数学界内,就流行起了一个Erdos Number的说法,意思是: Erdos自己的Erdos Number就是0, 那么直接和Erdos一起写过paper的co-author的Erdos Number就是1。 那么Erdos的co-author的co-author的Erdos Number就是2, 以此类推。 Erdos Number越小,说明此人和Erdos的学术关系越近。 据说,当今世界90%的还活跃的数学家的Erdos Number小于8。
作者检索:全拼,姓在前,名在后,用逗 号隔开 ,不区分大小写 。例如:hua,luo*
期刊检索:可输入刊物的全称、缩写、一 部分或ISSN号 引文检索:包括作者被引用的信息检索和 杂志被引用的信息检索
题录信息有MR或CMP记录顺序号、作者姓 名、题名、刊名及年、卷、期、页码等 (1)MR或CMP记录顺序号:该记录的详 细信息; (2)作者姓名:该作者写的所有文章; (3)刊名:该刊的基本信息; (4)期号:该期的文章题录;
数据来源:美国数学会(Amarican Mathematical Socicty,AMS)将其著名 的评论期刊《Mathematiቤተ መጻሕፍቲ ባይዱal Reviews》(MR)及检索期刊《Current Mathematical Publications》(CMP)制作成网络电子版数据库 收录范围:1940年至今,内容包括数学及数学在统计学、工程学、物理学、 经济学、生物学、运筹学、计算机科学中的应用等文献信息。
数学专业的学术出版社推荐

数学专业的学术出版社推荐数学是一门深奥而广泛应用的学科,它在各个领域都扮演着重要的角色。
随着科技的发展和学术研究的深入,对于数学专业的学术出版物的需求也越来越大。
在这篇文章中,我们将介绍一些数学专业的学术出版社,帮助读者更好地获取与数学相关的学术信息和研究成果。
1. Springer 数学出版社Springer 数学出版社是全球最大的学术出版社之一,也是数学领域出版物的主要提供商。
该出版社涵盖了广泛的数学领域,包括纯数学、应用数学、数理统计等。
其出版物以高质量和国际性知名度而闻名,涵盖的内容不仅对于学术研究人员有价值,也对于学生和教师提供了丰富的教学资源。
2. American Mathematical Society (AMS)作为美国最具权威性的数学学术组织,美国数学学会 (AMS) 也是一家重要的数学学术出版社。
AMS出版的期刊、图书和会议记录涵盖了纯数学以及与其他学科的交叉研究领域,如计算数学和统计学等。
其出版物具有高度学术性和严谨性,被广大数学专业人士认可。
3. Institute of Mathematical Statistics (IMS)数学统计学是数学专业中一个重要的分支领域,而IMS则是从事数学统计学研究的重要学术组织之一。
它出版了高质量的统计学期刊和丛书,囊括了统计学理论、数据分析、概率论等领域的前沿研究成果。
对于专注于统计学研究的学者和研究人员来说,IMS的出版物是必不可少的学术资料。
4. Cambridge University Press (CUP)剑桥大学出版社(CUP) 出版了许多具有权威性的数学学术刊物和图书,以其学术严谨性和国际化影响力而受到广泛关注。
数学专业的学术出版物涉及了各个数学领域,如代数学、几何学、数论等。
展示了最新的研究成果和数学理论的发展动态。
5. Elsevier ScienceElsevier Science 是另一家在学术出版领域具有广泛影响力的出版社。
mathematical reviews 管理

mathematical reviews 管理《数学评论》(Mathematical Reviews)是一个由美国数学学会(American Mathematical Society)编纂、出版的数学学术期刊,也是一份对数学领域内的出版物进行综述和评论的参考工具。
该期刊的内容主要包括数学领域的最新研究成果、论文摘要和评论。
作为全球数学界最重要、最权威的数学文摘期刊之一,《数学评论》在国内外学术界具有广泛的影响力。
它的主要目标是为数学研究人员提供一个便捷的资源,帮助他们追踪和了解最新的数学进展,以及评估各种数学研究成果的质量和重要性。
同时,这个期刊也为数学教师、学生和其他对数学领域感兴趣的人提供了一个学习和了解数学的重要工具。
《数学评论》的编纂工作对于数学研究的发展和推动起着重要的作用。
因为数学研究的速度和广度都在不断增加,研究者们很难仅仅依靠个人的努力来追踪和了解全球范围内的数学研究成果。
《数学评论》通过将全球各地的数学文献进行综述和分类,为数学研究人员提供了一个系统化的信息检索和学习平台。
研究者们可以根据《数学评论》中的分类体系,快速找到自己感兴趣领域内的最新研究成果,并通过评论和摘要了解这些成果的关键点和主要结论。
这样,研究者们就可以更好地把握前沿学术动态,与同行保持紧密的交流,并在自己的研究工作中积极应用和推广新的数学理论和方法。
《数学评论》还提供了一个评估数学研究成果的重要参考。
对于一个数学研究成果的质量和重要性,研究者们通常需要参考多个方面的因素,如研究方法和结果、证明的严密性和深度、研究领域的前沿性等。
《数学评论》的评论内容往往会涉及这些方面的评估,对读者来说,可以通过阅读这些评论来了解一个研究成果的优缺点和意义,为他们的研究工作提供参考和启示。
除了对数学研究成果进行评论和综述,《数学评论》还为数学领域内的重要学术活动提供了广告和宣传的机会。
例如,研究者们可以在《数学评论》中发布他们组织的会议、研讨会或工作坊等学术活动的通知和信息,以吸引更多的同行参与并促进学术界的交流与合作。
数学期刊发表有哪些

数学期刊发表有哪些数学期刊是数学领域内学术交流的重要平台,对于数学研究人员来说,发表在权威的数学期刊上是展示研究成果、提升学术声誉的重要途径。
那么,数学期刊都有哪些呢?接下来,我们将对数学期刊进行分类介绍。
首先,我们来看看国际上著名的数学期刊。
在国际上,有一些数学期刊享有很高的声誉,如《数学评论》(Mathematical Reviews)、《数学年刊》(Annals of Mathematics)、《数学杂志》(Journal of the American Mathematical Society)等。
这些期刊在数学界具有很高的影响力,发表在这些期刊上的论文往往能够获得更多的关注和引用。
其次,我们来看看国内的数学期刊。
中国数学界也有一些具有一定影响力的期刊,如《数学学报》、《中国科学》(数学)、《数学进展》等。
这些期刊在国内数学领域内具有一定的影响力,是中国数学研究人员发表研究成果的重要选择。
除了上述的一些著名期刊外,还有一些专业性较强的数学期刊,如《离散数学》、《数学物理学报》等。
这些期刊针对特定的数学领域或者交叉学科领域,为研究人员提供了一个专业性的交流平台。
另外,近年来,随着开放获取期刊的发展,越来越多的数学期刊开始采用开放获取的出版模式,如《Public Library of Science》(PLoS)的一些数学相关期刊。
这些期刊为广大的研究人员提供了一个更加开放、公平的发表平台。
除了以上介绍的一些数学期刊外,还有很多其他的数学期刊,涵盖了数学的各个领域和方向。
研究人员在选择发表期刊时,应该根据自己的研究方向和研究成果的特点,选择合适的期刊进行投稿。
总的来说,数学期刊是数学研究人员重要的学术交流平台,选择合适的期刊发表论文对于提升学术声誉、促进学术交流具有重要意义。
希望本文对于数学期刊的选择有所帮助,谢谢阅读。
数学杂志期刊

数学杂志是数学家交流学术的主要阵地.一切数学成果可以在学术会上报告,通过新闻报导和信件交流得以传播,但是最终必须在专业杂志上发表才算正式得到确认。
即使现在已经出现了一些电子杂志,如美国数学会出版的《电子研究公报》(Electronic Research Announcements),不过人们还是觉得白纸黑字的印刷方式最具权威性.19世纪能够发表数学论文的杂志有950种,但专门的数学杂志术过几十种,真正重要的就更少.大多集中在欧洲,尤以英、德、法、意诸国的数学杂志较为著名,一个国家也就是一两份.进入20世纪,职业数学家的人数大为增加,分工日益精细,除统一的数学杂志以外,还出版几何、代数、微分方程、逻辑、泛函分析、组合数学等许多专业性更强的杂志.到20世纪末年,世界数学杂志的数目已经无法精确统计.美国《数学评论》评论的数学杂志数目达到4000余种.日本的《岩波数学辞典》(中译名为《数学百科辞典》,科学出版社出版)是目前国际通用的数学辞典,其中收录的名家著作,出自254种数学杂志和丛书.数学家把自己认为重要的数学论文投寄一些国际上最著名的数学杂志.哪些杂志是“著名”的,或者“高质量”的呢?这没有明确的界定.依通常的印象,也许以下几种有特殊的重要性:《数学学报》(Acta Mathematica)(瑞典乌普萨拉),1882年创刊。
《纯粹数学与应用数学杂志》(Journal fur die Reine und Angwandte Mathematik)(柏林),由克雷尔(August leopold Crelle,1780~1855)于1826年创办,俗称克雷尔杂志。
《数学年刊》(Mathematische Annalen) (柏林-格丁根-海得尔贝格)。
《伦敦数学会杂志》(The Journal of Lundon Mathematical Society)(伦敦),1865年创刊。
《剑桥哲学会进展》(Proceedings of the Cambridge PhilosophicalSociety)(英国剑桥)。
数学研究期刊评介

数学研究期刊评介数学是一门博大精深的学科,其中包含了众多的分支和领域。
为了促进学术交流和学科发展,许多数学研究期刊涌现出来。
本文将对几本重要的数学研究期刊进行评介,介绍它们的背景、特点和对学术界的影响。
一、Annals of Mathematics (《数学年刊》)《数学年刊》是一本拥有百年历史的顶级数学研究期刊,由普林斯顿大学出版,创办于1884年。
这本期刊以发表重要的原创数学研究成果而闻名于世。
它涵盖了广泛的数学领域,包括代数、几何、数论、拓扑等。
《数学年刊》以其高质量的论文和严格的审稿流程而广受数学界的认可和推崇。
在数学学术界,一篇发表在《数学年刊》上的论文往往具有较高的学术价值和影响力。
二、Journal of the American Mathematical Society (《美国数学学会杂志》)《美国数学学会杂志》是美国数学学会(AMS)旗下的一本重要期刊,创办于1988年。
该期刊在数学学术界具有很高的声誉和影响力,涵盖了数学的各个领域。
《美国数学学会杂志》每期都会发表一些重要的原创性研究论文,这些论文在学界引起广泛关注,对数学研究的发展起到了积极的推动作用。
此外,该期刊还会发表一些综述性的文章,为读者提供对某一领域的全面了解和综合把握。
三、Inventiones Mathematicae (《发明数学》)《发明数学》是一本在纯数学研究领域有很高声誉的期刊,由斯普林格出版,创办于1966年。
该期刊主要发表在代数、几何、拓扑和数论等领域的重要研究成果。
《发明数学》以其高度创新的研究内容和深入的数学思考而闻名于世。
许多该期刊上发表的论文在学界引起了广泛的讨论和关注,在数学研究中具有重要的地位和贡献。
四、Acta Mathematica (《数学学报》)《数学学报》是一本由斯德哥尔摩数学研究所出版的数学期刊,创办于1882年。
该期刊主要发表在纯数学领域的高水平论文,涉及的领域广泛,包括代数、几何、数论、拓扑等。
amc评分标准

amc评分标准摘要:一、AMC评分标准的简介1.AMC评分标准的发展历程2.AMC评分标准的重要性二、AMC评分标准的具体内容1.评分标准概述2.评分细则详解a.内容准确性b.内容完整性c.语言质量d.创意与创新性三、AMC评分标准在我国的应用1.我国对AMC评分标准的接受程度2.我国在实际应用中的经验与教训四、AMC评分标准对我国知识类写作的启示1.对提高内容质量的指导意义2.对提升写作创意的帮助3.对培养专业写作人才的推动作用正文:AMC评分标准,即美国数学竞赛(American MathematicsCompetitions)评分标准,是由美国数学及其应用联合会(American Mathematical Society, AMS)制定并实施的一套针对数学竞赛的评分体系。
该体系自上世纪60年代起逐渐发展完善,现已成为全球最具权威性的数学竞赛评分标准之一。
AMC评分标准的重要性在于,它为参赛者提供了一个公平、公正、公开的竞争平台。
无论是学生、教师还是家长,都可以通过这套标准来了解参赛者的真实水平,以便为他们的未来发展提供更好的指导。
在具体内容方面,AMC评分标准包括四个方面:内容准确性、内容完整性、语言质量以及创意与创新性。
其中,内容准确性是指参赛者在解决问题时,需要正确理解题目要求,准确运用数学知识;内容完整性则要求参赛者对问题进行全面分析,给出完整的解题过程;语言质量则评价参赛者在表达过程中的语法、用词、表达是否清晰、准确;创意与创新性则考察参赛者在解决问题时,能否提出新颖的思路或方法。
AMC评分标准在我国的应用已逐渐被广泛接受。
我国许多数学竞赛都参照这套标准进行评分,旨在提高竞赛的公平性和专业性。
在实际应用过程中,我国积累了丰富的经验,也从中吸取了一些教训。
例如,在评分过程中,要注重对参赛者创新思维的鼓励,同时也要保证评分的公正性和客观性。
总的来说,AMC评分标准对我国知识类写作有着重要的启示作用。
密码学报latex模板

密码学(Cryptography)领域的学术论文通常需要遵循严格的格式和结构。
如果你正在寻找密码学的LaTeX模板,你可以考虑使用一些通用的学术LaTeX模板,然后根据密码学领域的特点进行适当的调整。
以下是一些流行的LaTeX模板包,它们可以作为撰写密码学论文的起点:1.IEEEtran - 对于准备提交给IEEE会议或期刊的文章,IEEEtran模板是非常合适的选择。
它提供了符合IEEE出版要求的文章格式。
2.amsart - 这是美国数学学会(American Mathematical Society)提供的一个模板,适合用于数学和理论密集型的文章,包括密码学。
3.elsarticle - 这个模板是为Elsevier期刊定制的,如果你的目标是将你的工作发表在Elsevier出版的密码学期刊上,这个模板会很有用。
4.springer - Springer出版社也提供了自己的LaTeX模板,适用于多种学科,包括密码学。
5.ieeeconf - 如果你的工作是为了某个IEEE会议准备的,那么这个模板会非常有用。
6.cryptocode 和eprint - 这些是专门为密码学社区设计的LaTeX模板,它们包含了格式化密码学论文所需的特定命令和环境。
为了使用这些模板,你需要在你的LaTeX发行版中安装它们,或者从相应的网站上下载。
一旦安装完毕,你可以在你的LaTeX编辑器中创建一个新的项目,并选择适当的模板作为起点。
请注意,即使你使用了模板,你仍然需要仔细阅读目标期刊或会议的作者指南,以确保你的论文格式完全符合要求。
这可能包括字体大小、边距、引用样式、图表和公式的格式等。
如果模板不完全符合要求,你可能需要手动调整模板的某些部分。
普特南数学竞赛试题

普特南数学竞赛试题摘要:一、普特南数学竞赛背景介绍1.普特南数学竞赛的起源2.竞赛的组织机构3.竞赛的规模和影响力二、普特南数学竞赛试题特点1.试题难度和范围2.试题的原创性3.试题的区分度三、普特南数学竞赛对我国学生的启示1.提高学生的数学素养2.培养学生的创新思维3.激发学生对数学的兴趣四、我国学生参加普特南数学竞赛的意义1.提升国际竞争力2.扩大国际交流与合作3.为我国数学教育发展提供借鉴正文:普特南数学竞赛(Putnam Mathematical Competition)是由美国数学及其应用联合会(American Mathematical Society,AMS)和美国数学竞赛委员会(Mathematical Association of America,MAA)共同组织的一年一度的国际性数学竞赛。
竞赛始于1938 年,以纪念美国数学家、教育家、哲学家普特南(Joseph Henry Putnam)而命名。
该竞赛旨在选拔和培养全球优秀的数学人才,激发青少年对数学的兴趣和热情,提高数学教育水平。
普特南数学竞赛试题以严谨、创新、挑战性强而著称。
竞赛试题分为两部分,共计12 道题,难度逐渐提高。
试题涵盖了代数、几何、组合、数论、概率等广泛的数学领域,要求参赛者在规定时间内完成。
竞赛试题的原创性极高,往往需要参赛者运用创新思维和灵活解题技巧。
此外,普特南数学竞赛试题具有良好的区分度,能够有效地选拔出具有潜力和天赋的数学人才。
我国学生参加普特南数学竞赛有着重要的意义。
首先,参加普特南数学竞赛有助于提高学生的数学素养,拓宽数学视野,培养逻辑思维能力。
其次,竞赛过程中,学生可以锻炼创新思维,学会在看似复杂的问题中寻找规律,提升解决问题的能力。
最后,普特南数学竞赛能够激发学生对数学的兴趣,培养学生的学术热情,为我国数学教育发展提供源源不断的人才。
总之,普特南数学竞赛作为一项具有国际影响力的数学竞赛,对我国学生具有重要的启示作用。
数学领域的重要学术期刊介绍

数学领域的重要学术期刊介绍在学术研究领域,期刊发表是学者们交流和展示研究成果的重要方式之一。
特别是在数学领域,学术期刊扮演着极为重要的角色,是推动数学研究和学术进展的重要平台。
本文将介绍一些数学领域的重要学术期刊,以帮助读者更好地了解当前数学研究的前沿动态。
1. Annals of Mathematics(《数学年刊》)《数学年刊》是世界上最古老、最权威的数学期刊之一,创办于1884年。
该期刊发布了许多重要的数学成果和重大研究,被广泛认为是数学领域最顶尖的期刊之一。
它涵盖了广泛的数学领域,包括代数、几何、数论、拓扑学等。
《数学年刊》的严谨性和深度使得它成为数学界最为受重视的期刊之一。
2. Journal of the American Mathematical Society(《美国数学学会期刊》)《美国数学学会期刊》是美国数学学会旗下的一本重要期刊,创办于1988年。
它发表了许多有影响力的数学研究,涵盖了许多数学领域,如代数学、数论、几何、应用数学等。
该期刊被广泛认为是数学研究的世界权威,每年发布的论文吸引了许多数学家的关注和引用。
3. Inventiones Mathematicae(《数学发明》)《数学发明》是一本国际性的高水平数学期刊,成立于1966年。
该期刊以发表高质量、具有创新性的数学论文为特点,涵盖了许多数学领域,如代数、几何、数论、动力系统等。
《数学发明》在数学界享有很高的声誉,其中发表的论文常常成为后续研究的重要基础。
4. Journal of Differential Geometry(《微分几何学期刊》)《微分几何学期刊》是专注于微分几何领域的重要期刊之一。
该期刊涵盖了从流形的基础理论到微分几何的最新发展。
发表在《微分几何学期刊》上的论文通常对于微分几何专业的研究者具有重要的参考价值,并对相关学科的发展起到推动作用。
5. Acta Mathematica(《数学学报》)《数学学报》是瑞典皇家科学院主办的著名学术期刊,创办于1882年。
amc数学竞赛成绩划分

amc数学竞赛成绩划分摘要:1.AMC 数学竞赛简介2.AMC 数学竞赛成绩划分标准3.AMC 数学竞赛成绩等级对应能力分析4.AMC 数学竞赛成绩对学生发展的影响正文:一、AMC 数学竞赛简介AMC(American Mathematics Competitions)是美国数学竞赛的简称,是由美国数学及其应用联合会(American Mathematical Society and Mathematical Association of America)主办的一项面向全球中学生的数学竞赛活动。
AMC 数学竞赛旨在激发学生学习数学的兴趣,培养学生的数学思维能力和解决问题的能力,选拔优秀的数学人才。
二、AMC 数学竞赛成绩划分标准AMC 数学竞赛成绩的划分主要依据参赛选手的得分情况,通常分为以下几个等级:1.杰出奖(Outstanding):得分位于全球前1% 的学生2.优秀奖(Distinguished):得分位于全球前2.5% 的学生3.良好奖(Meritorious):得分位于全球前5% 的学生4.合格奖(Pass):得分位于全球前25% 的学生5.不及格(Fail):得分位于全球后25% 的学生三、AMC 数学竞赛成绩等级对应能力分析1.杰出奖:获得杰出奖的学生通常具备极高的数学天赋和扎实的数学基础,能够在短时间内迅速解答出高难度的数学问题。
2.优秀奖:获得优秀奖的学生在数学方面具有较强的竞争力,能够较好地应对各种复杂的数学问题。
3.良好奖:获得良好奖的学生在数学能力方面较为稳定,能够在一定程度上解决数学问题。
4.合格奖:获得合格奖的学生具备一定的数学基础,能够在简单的数学问题上取得较好的成绩。
5.不及格:获得不及格的学生在数学方面尚需加强学习和训练,提高自己的数学能力。
四、AMC 数学竞赛成绩对学生发展的影响AMC 数学竞赛成绩对学生的发展具有一定的影响。
首先,竞赛成绩可以作为学生申请国外高校的加分项,提高申请成功率;其次,通过参加AMC 数学竞赛,学生可以锻炼自己的数学思维和解题能力,为以后的学习和职业发展奠定基础;最后,AMC 数学竞赛成绩也是衡量学生数学能力和选拔优秀数学人才的重要依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p(z ) ± z n+1 − z 2n+2 p(−1/z )
ak z k ,
with each ak ∈ {+1, −1} (thus a Littlewood polynomial), is a polynomial where each a cyclic autocorrelation coefficient satisfies |cj | ≤ K, j = 1, 2, . . . , n.
= (n + 1)2 + n
,
while if p(z ) is a Barker polynomial of odd degree n then p
4
= (n + 1)2 + n + 1
1/4
.
If p(z ) is a Barker polynomial of even degree n then p
s s
t−r ( p t ) t−r . ≤( p r r) t t−s s−r
So with r := 1, s := 2 and t := 4 we deduce, with the above, the following. p
2
≤ p ≥
1/3 1
p
2/3 4
and if p(z ) is a Barker polynomial of even degree n then p
4 4
j = 1, 2, . . . , n.
n − k odd n − k even.
n
=
k=−n
c2 k
we have that if p(z ) is a Barker polynomial of even degree n then p
4
= (n + 1)2 + n
1/4
,
while if p(z ) is a Barker polynomial of odd degree n then p
2 1
(n + 1)3 (n + 1)2 + n
and if p(z ) is a Barker polynomial of odd degree n then p
2 1
≥
(n + 1)3 . (n + 1)2 + n + 1
For any Littlewood polynomial of degree n 1 pn 4 4 −1= 2 (n + 1) 2π
MATHEMATICS OF COMPUTATION Volume 00, Number 0, Pages 000–000 S 0025-5718(XX)0000-0
K-BARKER POLYNOMIALS AND SEQUENCES
P. B. BORWEIN
Abstract. A Barker sequence is a binary sequence with all non–trivial acyclic autocorrelation coefficients of size at most 1. It is widely believed (and confirmed up to size 1022 ) that none exist of length greater than 13. A Barker polynomial is a polynomial whose coefficients form a Barker sequence. This problem has been around for at least 40 years. A K-Barker sequence is a binary sequence with all non–trivial acyclic autocorrelation coefficients of size at most K. It is widely believed that for eack K there are only finitely many such sequences (though this appears very hard and has been open for decades even for k:=1). A K-Barker polynomial is a polynomial whose coefficients form a Barker sequence.
4
P. B. BORWEIN
Proof. A Barker polynomial
n
p(z ) :=
k=0
ak z k ,
with each ak ∈ {+1, −1} (thus a Littlewood polynomial), is a polynomial where each acyclic autocorrelation coefficient satisfies |cj | ≤ 1, Thus, c0 = n + 1, and by parity ck = 0, and Since |ck | = 1, p(z )
K-BARKER POLYNOMIALS
3
are both skewsymmetric. While, if n is even and p is of degree n, then are both skewsymmetric. All skewsymmetric Littlewood polynomials are of the above form. 2. Basic Theorems on Barker Polynomials A K-Barker polynomial p(z ) :=
A real polynomial is skewsymmetric if p(z ) = ±z d p(−1/z ), where d is the degree of p. If n is odd and p is of degree n, then p(z ) ± z n+1 + z 2n+2 p(−1/z )
4
= (n + 1)2 + n + 1
1/4
.
Thus, when a Barker polynomial of degree n exists, it minimizes the L4 norm (and maximizes the so-called merit factor) of polynomials from the class L n . Note that the sequence of coefficients of a Barker polynomial of degree n forms a Barker sequence of length n +1. We prefer to deal with polynomials and care must be taken in the conversion from length to degree when going from sequences to polynomials (the count is out by 1). Also, if 0 < r < s < t then, the norms satisfy p
2π 0
2 log(|pn (eiθ )|) − log(n + 1)
2
dθ ≤
c−2 (n + 1)
2π √ 1 d log(|pn (eiθ )|) dθ = log n + 1 + √ 2π 0 n+1 where |d| ≤ c−1 /2 ≤ 3/2. And the Mahler measure, M of a sequence of Barker polynomials satisfies √ M (pn ) = (1 + n ) n + 1 where √ 0 ≤ n ≤ c2 / n + 1 and c2 ≤ 2.
2π 1 α dθ p eiθ . 2π 0 and for a polynomial p(z ) := an z n + · · · + a1 z + a0 , the L2 norm on D is also given by p 2 = |an |2 + · · · + |a1 |2 + |a0 |2 . 1/α
p
α
:=
In the limiting case
α→0
lim p
α
= exp
1 2π
2π
log p eiθ
0
dθ
=: p 0 .
This is called the Mahler measure and is denoted by M (p). For a polynomial Jensen’s theorem gives pn (z ) := a(z − α1 )(z − α2 ) · · · (z − αn ) M (pn ) = |a| Let Ln :=
c 1997 American Mathematical Society
பைடு நூலகம்
1
2
P. B. BORWEIN
1. Introduction For any polynomial with real coefficients
n
p(z ) :=
k=0
ak z k ,
the k th acyclic autocorrelation coefficient is defined, for −n ≤ k ≤ n, by
n−k j =0
(1.1) So
