全等三角形专项训练2
专项12-2 三角形全等的判定(SSS)(解析版)

2020—2021八年级上学期专项冲刺卷(人教版)专项12.2 三角形全等的判定(SSS )姓名:___________考号:___________分数:___________(考试时间:100分钟 满分:120分)一、 选择题(本大题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,工人师傅常用角尺平分一个任意角.做法如下:如图,AOB ∠是一个任意角,在边,OA OB 上分别取OM ON =,移动角尺,使角尺两边相同的刻度分别与,M N 重合.则过角尺顶点C 的射线OC 便是AOB ∠的平分线,其依据是( )A .SSSB .SASC .ASAD .AAS【答案】A【分析】 利用全等三角形判定定理AAS 、SAS 、ASA 、SSS 对△MOC 和△NOC 进行分析,即可作出正确选择.【详解】解:∵OM =ON ,CM =CN ,OC 为公共边,∴△MOC ≌△NOC (SSS ).∴∠MOC =∠NOC故选:A .【点睛】此题主要考查学生对全等三角形判定定理的理解和掌握,此题难度不大,属于基础题.2.如图,已知AOB ∠,观察图中尺规作图的痕迹,可以判定111COD C O D ≌,其判定的依据是( )A .SSSB .SASC .ASAD .AAS【答案】A【分析】 由作法易得OD =O 1D 1,OC =O 1C 1,CD =C 1D 1,根据SSS 得到三角形全等.【详解】解:在△COD 和△C 1O 1D 1中,111111CO C O DO D O CD C D =⎧⎪=⎨⎪=⎩,∴111COD C O D ≌(SSS ).故选:A .【点睛】本题考查了全等三角形的判定方法SSS 的运用,熟练掌握三角形全等的判定是正确解答本题的关键.3.如图,在ABD △和ACD △中,AB AC =,BD CD =,则ABD ACD △≌△的依据是( )A .SASB .ASAC .AASD .SSS【答案】D【分析】 由SSS 判定△ABD ≌△ACD ,即可得出结论.【详解】解:在△ABD 和△ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,∴△ABD 和△ACD (SSS );故选:D .【点睛】本题考查了全等三角形的判定方法;熟记全等三角形的判定方法是解决问题的关键.4.如图,2AB =,6BC AE ==,7CE CF ==,8BF =,则四边形ABDE 与CDF 面积的比值是( )A .1B .34C .23D .12【答案】A【分析】 由题意得AC=CB+BA=8,可得AC=BF ,利用SSS 可证得△AEC ≌△BCF ,从而可得S △AEC =S △BCF ,也就得出S △CDF +S △CDB =S ABDE +S △CDB ,这样可求出四边形ABDE 与△CDF 面积的比值.【详解】解:由题意得AC=CB+BA=8,∴AC=BF ,在△AEC 和△BCF 中AC BF CE CF AE BC ⎧⎪⎨⎪⎩===∴△AEC ≌△BCF ,∴S △AEC =S △BCF ,故可得S △CDF +S △CDB =S ABDE +S △CDB ⇒S ABDE =S △CDF ,∴四边形ABDE 与△CDF 面积的比值是1.故选:A .【点睛】本题考查了三角形的面积及等积变换的知识,证明△AEC ≌△BCF 是解答本题的关键. 5.如图,已知AC =AD ,BC =BD ,能确定△ACB ≌△ADB 的理由是( )A .SASB .AASC .ASAD .SSS【答案】D【分析】 因为AC=AD ,BC=BD ,AB 共边,所以可根据SSS 判定△ACB ≌△ADB .【详解】∵AC=AD ,BC=BD ,AB=AB ,∴△ABC ≌△ABD (SSS ),A 、B 、C 都不是全等的原因.故选D .【点睛】本题考查了全等三角形的判定定理的应用,能熟练地掌握全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有:SAS ,ASA ,AAS ,SSS .6.如图,点D 在线段BC 上,若1802ACE ABC x ∠=︒-∠-︒,且BC DE =,AC DC =,AB EC =,则下列角中,大小为x ︒的角是( )A .EFC ∠B .ABC ∠ C .FDC ∠D .DFC ∠【答案】C先证明()ABC CED SSS ∆≅∆得到B E ∠=∠、FCD FDC ∠=∠,再根据1802ACE ABC x ∠=︒-∠-︒可得2CFE x ∠=︒;然后根据外角的性质可得2EFC FDC FCD FDC ∠=∠+∠=∠即可解答.【详解】解:在ABC ∆和CED ∆中,AC CD AB CE BC ED =⎧⎪=⎨⎪=⎩,()ABC CED SSS ∴∆≅∆,B E ∴∠=∠,FCD FDC ∠=∠1802180ACE ABC x E CFE ∠=︒-∠-︒=︒-∠-∠,2CFE x ∴∠=︒,2EFC FDC FCD FDC ∠=∠+∠=∠=2x ︒,FDC x ∴∠=︒.故答案为C .【点睛】本题主要考查全等三角形的判定和性质、三角形的外角的性质等知识,弄清题意、理清角之间的关系是解答本题的关键.7.平面上有△ACD 与△BCE ,其中AD 与BE 相交于P 点,如图.若AC=BC ,AD=BE ,CD=CE ,∠ACE=55°,∠BCD=155°,则∠BPD 的度数为( )A .110°B .125°C .130°D .135°【答案】C【分析】 易证△ACD ≌△BCE ,由全等三角形的性质可知:∠A=∠B ,再根据已知条件和四边形的内角和为360°,即可求出∠BPD 的度数.解:在△ACD 和△BCE 中,AC BC CD CE AD BE =⎧⎪=⎨⎪=⎩,∴△ACD ≌△BCE (SSS ),∴∠A=∠B ,∠BCE=∠ACD ,∴∠BCA=∠ECD ,∵∠ACE=55°,∠BCD=155°,∴∠BCA+∠ECD=100°,∴∠BCA=∠ECD=50°,∵∠ACE=55°,∴∠ACD=105°∴∠A+∠D=75°,∴∠B+∠D=75°,∵∠BCD=155°,∴∠BPD=360°-75°-155°=130°,故选:C .【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出∠B+∠D=75°.8.如图,在ABC ∆中,,,,AB AC BD CD E F ==是AD 上的任意两点.若8,6BC AD ==,则图中阴影部分的面积为( )A .12B .20C .24D .48【答案】A【分析】利用SSS 证明△ADC ≌△ADB ,可得S △ADC =S △ADB ,通过拼接可得S 阴影=S △ADB ,再利用三角形的面积公式可求解.【详解】∵AB=AC ,BD=CD ,AD=AD ,∴△ADC ≌△ADB (SSS ),AD ⊥BC∴S △ADC =S △ADB ,BD=12BC , ∵BC=8,∴BD=4,∵S △BEF =S △CEF ,AD=6,∴S 阴影=S △ADB =12BD•AD 12=×4×6=12. 故选:A .【点睛】本题主要考查了全等三角形的性质与判定,三角形的面积,理解S 阴影=S △ADB 是解题的关键. 9.用直尺和圆规作一个角等于已知角的示意图如图所示,则说明A O B AOB '''∠=∠的依据是( )A .SSSB .SASC .SSAD .ASA【答案】A【分析】 OC O C ='',OD O D ='',CD C D ='',从而可以利用SSS 判定DOC △≌△D O C ''',即可得到结论.【详解】1 、以O 为圆心, 任意长为半径用圆规画弧, 分别交OA 、OB 于点C 、D ;2 、任意画一点O ',画射线O A '',以O '为圆心,OC 长为半径画弧C E ',交O A ''于点C ';3 、以C '为圆心,CD 长为半径画弧, 交弧C E '于点D ;4 、过点D 画射线O B '',A O B '''∠就是与AOB ∠相等的角 .则通过作图我们可以得到OC O C ='',OD O D ='',CD C D ='',从而可以利用SSS 判定DOC △≌△D O C ''',所以A O B AOB '''∠=∠,【点睛】此题考查了学生对常用的作图方法及全等三角形的判定方法的掌握情况.由作法找已知条件,结合判定方法进行思考是解题关键.10.如图,四边形ABCD 的对角线AC ,BD 相交于点O ,ABO ADO △≌△,下列结论:①AC BD ⊥;②CB CD =;③ABC ADC △≌△;④DA DC =.其中所有正确结论的序号是( )A .①②③④B .①②③C .①②④D .①②【答案】B【分析】 根据全等三角形的性质得出∠AOB=∠AOD=90°,OB=OD ,AB=AD ,再根据全等三角形的判定定理得出△ABC ≌△ADC ,进而得出其它结论.【详解】∵△ABO ≌△ADO ,∴∠AOB=∠AOD=90°,OB=OD ,AB=AD ,∴AC ⊥BD ,故①正确;∵四边形ABCD 的对角线AC 、BD 相交于点O ,OB=OD ,AC ⊥BD ,∴BC=DC ,②正确;在△ABC 和△ADC 中,AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩,∴△ABC ≌△ADC (SSS ),故③正确;AB=AD ,BC=DC ,没有条件得出DA=DC ,④不正确;综上,①②③正确,故选:B .本题考查了全等三角形的判定和性质、等腰三角形的性质,掌握全等三角形的判定方法是解题的关键.11.如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )A.1:1 B.2:1 C.1:2 D.2:3【答案】A【解析】【分析】由题意得AC=CB+BA=8,可得AC=BF,利用SSS可证得△AEC≌△BCF,从而可得S△AEC=S△BCF,也就得出S△CDF+S△CDB=S四边形ABDE+S△CDB,这样可求出四边形ABDE与△CDF面积的比值.【详解】解:∵AB=2,BF=8,BC=AE=6,∴AC=CB+BA=8,∴AC=BF,在△AEC和△BCF中,AC BF CE CF BC AE=⎧⎪⎨⎪⎩==∴△AEC≌△BCF(SSS),∴S△AEC=S△BCF,∴S△CDF+S△CDB=S四边形ABDE+S△CDB∴S四边形ABDE=S△CDF,∴四边形ABDE与△CDF面积的比值是1:1.故选A.【点睛】本题考查了面积及等积变换的知识,难度一般,根据题意证明△AEC≌△BCF是解答本题的关键,另外要注意等量代换在解答数学题目中的运用.12.如图,已知AE=AD ,AB=AC ,EC=DB ,下列结论:①∠C=∠B ;②∠D=∠E ;③∠EAD=∠BAC ;④∠B=∠E ;其中错误的是( )A .①②B .②③C .③④D .只有④【答案】D【详解】解:因为AE =AD ,AB =AC ,EC =DB ;所以△ABD ≌△ACE(SSS);所以∠C =∠B ,∠D =∠E ,∠EAC=∠DAB ;所以 ∠EAC-∠DAC=∠DAB-∠DAC ;得∠EAD=∠CAB .所以错误的结论是④,故选D .【点睛】此题考查了全等三角形的判定方法,根据已知条件利用SSS 证明两个三角形全等,还考查了全等三角形的性质:全等三角形的对应角相等,全等三角形的对应边相等.二、 填空题(本大题共6小题,每小题3分,共18分)13.如图,在ABC ∆和ADC ∆中,AB AD =,BC DC =,80DAB ∠=︒,则DAC ∠=_______.【答案】40︒【分析】根据全等三角形的判定定理得出△ABC ≌△ADC ,根据全等三角形的性质得出∠DAC=∠BAC ,即可求出结果.【详解】解:在△ABC 和△ADC 中,AB AD AC AC BC DC ⎧⎪⎨⎪⎩===,∴△ABC ≌△ADC (SSS ),∴∠DAC=∠BAC∵∠DAB=80°,∴∠DAC=40°,故答案为:40°.【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定定理是解此题的关键.14.如图,已知AB =AC ,AD =AE ,BD =CE ,B ,D ,E 三点在同一直线上︒︒∠=∠=125,355,则2∠=________.【答案】30°【分析】先根据SSS 证明△ABD ≌△ACE ,然后根据全等三角形的性质可得∠ABD=∠2,再利用三角形的外角性质求解即可.【详解】解:∵AB =AC ,AD =AE ,BD =CE ,∴△ABD ≌△ACE (SSS ),∴∠ABD=∠2,∵B ,D ,E 三点在同一直线上,∴∠ABD=∠3-∠1=55°-25°=30°,即∠2=30°.故答案为:30°.【点睛】本题考查了全等三角形的判定和性质以及三角形的外角性质,属于基础题型,熟练掌握全等三角形的判定和性质是解题的关键.15.如图,AB =AC ,BD =CD ,AD =AE ,∠EDC =16°,则∠BAD =_____度.【答案】32【分析】证明△ABD ≌△ACD (SSS ),得出∠BAD =∠CAD ,∠ADB =∠ADC =90°,求出∠ADE =90°﹣∠EDC =74°,由等腰三角形的性质得出∠AED =∠ADE =74°,由三角形内角和定理即可得出答案.【详解】解:在△ABD 和△ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,∴△ABD ≌△ACD (SSS ),∴∠BAD =∠CAD ,∠ADB =∠ADC =90°,∴∠ADE =90°﹣∠EDC =90°﹣16°=74°,∵AD =AE ,∴∠AED =∠ADE =74°,∴∠BAD =∠CAD =180°﹣2×74°=32°;故答案为:32.【点睛】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握等腰三角形的性质,证明三角形全等是解题的关键.16.如图所示,AB AC =,BD DC =,若35B ∠=︒,则C ∠=_________.【答案】35︒【分析】连接AD ,根据SSS 证明△ABD ≌△ACD ,再根据全等三角形的性质得出C ∠=35B ∠=︒.【详解】如图所示:连接AD ,在△ABD 和△ACD 中,AB AC AD AD BD CD =⎧⎪=⎨⎪=⎩,∴△ABD ≌△ACD (SSS ),∴C ∠=B ,又∵35B ∠=︒,∴C ∠=35︒.故答案为:35︒.【点睛】考查了全等三角形的判定和性质,解题关键是正确添加辅助线,构成全等三角形.17.如图,AB=AC ,BE=CD ,要使ABE ACD ≅,依据SSS ,则还需添加条件_______________.(填一个即可)【答案】AE AD =或CE BD =(填其中任一个均可)【分析】根据SSS 定理、线段的和差即可得.【详解】由题意,有以下两种情况:(1)当AE AD =时,由SSS 定理可证得ABE ACD ≅;(2)当CE BD =时,AB AC =,AC CE AB BD ∴-=-,即AE AD =,则当CE BD =时,也可利用SSS 定理证得ABE ACD ≅;故答案为:AE AD =或CE BD =(填其中任一个均可).【点睛】本题考查了SSS 定理,熟练掌握SSS 定理是解题关键.18.如图,点E ,F 在线段AD 上,且AE DF =,//AB DC ,AB DC =,连接BE ,BF ,CE ,CF ,则图中共有_____对全等三角形.【答案】3【分析】易证△ABE ≌△DCF,从而可得出△ABF ≌△DCE,进而可得出△BEF ≌△CFE .【详解】∵AB ∥DC∴∠A=∠D∵AB=CD,AE=DF∴△ABE ≌△DCF(SAS)∴AE=DF ,BE=CF∴AF=ED∴△ABF ≌△DCE(SAS)∴BF=EC∵EF=EF∴△BEF ≌△CFE(SSS)故答案为:3.【点睛】本题考查三角形全等的证明,需要注意SSA 是不能证明全等的.三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程) 19.已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,求证:BC ∥EF .【答案】见解析【分析】先根据AF =DC ,可推得AF -CF =DC -CF ,即AC =DF ;再根据已知AB =DE ,BC =EF ,根据全等三角形全等的判定定理SSS ,即可证明△ABC ≌△DEF ,然后利用全等三角形的性质求解.【详解】证明:∵AF =DC ,∴AF ﹣CF =DC ﹣CF ,即AC =DF ;在△ABC 和△DEF 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩∴△ABC ≌△DEF (SSS ).∴∠ACB =∠DFE又∵∠ACB +∠BCD =180°;∠DFE +∠EF A =180° ∴∠BCD =∠EF A∴BC ∥EF【点睛】本题考查了全等三角形全等的判定和性质,熟练掌握各判定定理正确推理论证是解题的关键. 20.已知:如图,,,AB CD DE BF AE CF ===.(1)求证:ABE CDF △≌△;(2)请直接判断AE 与CF 的位置关系.【答案】(1)见详解;(2)AE ∥CF ,理由见详解【分析】(1)证得DF =BE ,可证明△ABE ≌△CDF (SSS ).(2)由全等三角形的性质得出∠AEB =∠DFC ,得出∠AEF =∠EFC ,则可得出结论.【详解】(1)证明:∵DE =BF ,∴DE −EF =BF −EF .即DF =BE ,在△ABE 和△CDF 中,AB CD BE DF AE CF ⎧⎪⎨⎪⎩===,∴△ABE ≌△CDF (SSS ).(2)解:AE ∥CF .理由:∵△ABE ≌△CDF ,∴∠AEB =∠DFC ,∵∠AEB +∠AEF =∠DFC +∠EFC =180°,∴∠AEF =∠EFC ,∴AE ∥CF .【点睛】本题考查了全等三角形的判定和性质,平行线的判定,熟练掌握全等三角形的判定与性质是解题的关键.21.如图,点E 在线段BD 上,已知,,AB AC AD AE BE CD ===.(1)求证:BAC EAD ∠=∠.(2)写出123∠∠∠、、之间的数量关系,并予以证明.【答案】(1)证明见解析;(2)312∠=∠+∠,证明见解析.【分析】(1)根据SSS 证BAE CAD ≅,推出 1BAE ∠=∠即可;(2)根据全等三角形性质推出1BAE ∠=∠,2ABE ∠=∠,代入 3BAE ABE ∠=∠+∠求出即可.【详解】证明:(1)∵在BAE △和CAD 中AE AD AB AC BE DC =⎧⎪=⎨⎪=⎩,∴()BAE CAD SSS ≌,∴1BAE ∠=∠,∴1BAE EAC EAC ∠+∠=∠+∠,∴BAC EAD ∠=∠.(2)312∠=∠+∠,证明:∵BAE CAD △≌△,∴1BAE ∠=∠,2ABE ∠=∠,∵3BAE ABE ∠=∠+∠,∴312∠=∠+∠.【点睛】本题考查了全等三角形的性质和判定和三角形外角性质的应用,注意:全等三角形的对应角相等. 22.如图,点B ,E ,C ,F 在一条直线上,AB=DE ,AC=DF ,BE=CF .试说明:(1)ABC DEF ≅;(2)A EGC ∠=∠.【答案】(1)见解析;(2)见解析【分析】(1)根据等式性质,由BE=CF 得BC=EF ,再根据SSS 定理得△ABC ≌△DEF 即可;(2)由全等三角形得∠B=∠DEF ,由平行线的判定定理得AB ∥DE ,再根据平行线的性质得∠A=∠EGC .【详解】(1)∵BE CF =,∴BE EC CF EC +=+,即BC EF =,在△ABC 与△DEF 中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,∴(SSS)ABC DEF ≅△△;(2)∵△ABC ≌△DEF ,∴∠B=∠DEF ,∴AB ∥DE ,∴∠A=∠EGC .【点睛】本题考查了全等三角形的判定和性质,平行线的性质与判定,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.23.如图,点A D C F 、、、在同一条直线上,,,AD CF AB DE BC EF ===.(1)请说明ABC DEF △≌△;(2)BC 与EF 平行吗?为什么?【答案】(1)详见解析;(2)//BC EF ,理由详见解析.【分析】(1)根据线段的和差关系可得AC=DF ,利用SSS 即可证明△ABC ≌△DEF ;(2)根据全等三角形的性质可得∠ACB=∠F ,即可证明BC//EF .【详解】(1)∵AD=CF ,∴AD+CD=CF+CD ,即AC=DF ,在△ABC 和△DEF 中, AB CD BC CF AC DF=⎧⎪=⎨⎪=⎩,∴△ABC ≌△DEF .(2)//BC EF ,理由如下:由(1)可知,ABC DEF △≌△,∴F ACB ∠=∠,∴//BC EF .【点睛】本题考查全等三角形的判定与性质及平行线的判定,熟练掌握判定定理是解题关键.24.已知:如图,AB DC =,AD CB =,在DA 、BC 的延长线上各任取一点E ,F ,连接EF .求证:(1)//AB CD ;(2)E F ∠=∠.【答案】(1)见解析;(2)见解析【解析】【分析】(1)连接BD ,证明ABD CDB ∆≅∆,根据全等三角形的性质得到∠3=∠4,由平行线的判定即可得到结论;(2)根据全等三角形的性质得到∠1=∠2,根据平行线的判定和性质即可得到结论.【详解】证明:(1)连接BD ,在ABD ∆和CDB ∆中,AB DC BD DB AD BC =⎧⎪=⎨⎪=⎩,∴ABD CDB ∆≅∆,∴34∠=∠,∴//AB CD ;(2)∵ABD CDB ∆≅∆,∴12∠=∠,∴//AD BC ,∴E F ∠=∠.【点睛】本题考查了全等三角形的判定和性质,平行线的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.。
全等三角形二次全等训练习题
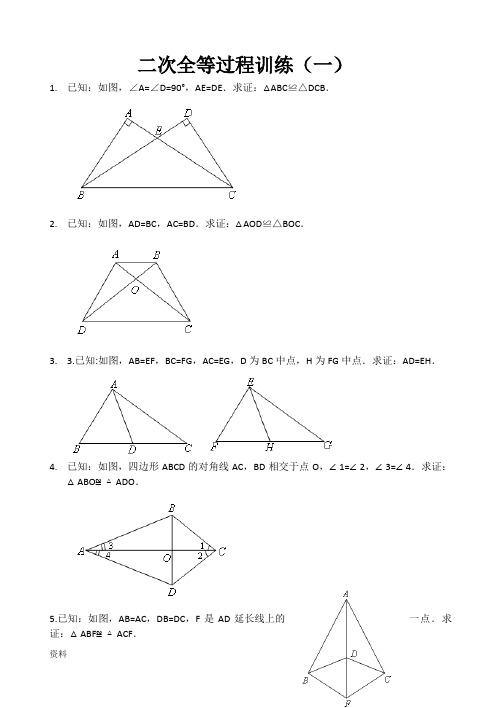
二次全等过程训练(一)1.已知:如图,∠A=∠D=90°,AE=DE.求证:△ABC≌△DCB.2.已知:如图,AD=BC,AC=BD.求证:△AOD≌△BOC.3. 3.已知:如图,AB=EF,BC=FG,AC=EG,D为BC中点,H为FG中点.求证:AD=EH.4.已知:如图,四边形ABCD的对角线AC,BD相交于点O,∠1=∠2,∠3=∠4.求证:△ABO≌△ADO.5.已知:如图,AB=AC,DB=DC,F是AD延长线上的一点.求证:△ABF≌△ACF.6.已知:如图,∠E=∠D,AM=CN,ME=ND.求证:△ABE≌△CBD.二次全等过程训练(二)一、单选题1.已知:如图,AD∥BC,AB,CD相交于点O,AO=BO,过点O作EF交AD于点E,交CB 于点F.求证:△EOD≌△FOC.2.已知:如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且BD=CD.求证:Rt△DEB≌Rt△DFC.3.已知:如图,在四边形ABCD中,AB=CD,AB∥CD,E,F分别是DA,BC延长线上的点,且AE=CF,连接EF交BD于点O.求证:△EOD≌△FOB.4.已知:如图,点C,D在线段BE上,且BD=EC,CA⊥AB于A,DF⊥EF于F,且AB=EF.求证:△ABD≌△FEC.5.如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,AB=AC.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.求证:△EAM≌△FAN.二次全等过程训练(三)1.已知:如图,在△ABC中,AD平分∠BAC,点D是BC的中点,DF⊥AB于F,DE⊥AC于E.求证:△BDF≌△CDE.2.已知:如图,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,连接AB,CD,BD,BD交AC于点G,AB=CD.求证:△DEG≌△BFG.3.已知:如图,在Rt△ACD中,∠ADC=90°,BE⊥AC于E,交CD于点F,AE=AD.求证:△CEF≌△BDF.4.已知:如图,在四边形ABCD中,AB=BC=CD=AD,BD平分∠ABC,E为BD上任意一点,连接AE,CE.求证:△ADE≌△CDE.55..已知:如图,在△ABC中,∠ACB=∠ABC=60°,∠EDF=60°,BD=CD,∠DBC=∠DCB=30°,∠BDC=120°,延长AC到点G,使CG=BE.求证:△EFD≌△GFD.二次全等过程训练(四)1.已知:如图,点A,C在直线EF上,BC=AD,AB=CD,AE=CF.求证:∠E=∠F.2.已知,如图,AE=BF,AD=BC,CE=DF.求证:AO=BO.已知:如图,∠D=∠E,AM=ME=CN=DN.试猜想AB和BC的数量关系,并证明你的猜想.4.已知:如图,在△ABC中,点D是BC的中点,DF⊥AB于F,DE⊥AC于E,DF=DE.求证:AB=AC.5.如图,在正方形ABCD中,∠ABC=∠BCD=90°,AB=BC=CD=AD.E为BC边上一点,且AE=DE,AE与对角线BD交于点F,∠ABF=∠CBF,连接CF交DE于点G.求证:DE⊥CF.。
初中数学《全等三角形》基本模型训练含解析

全等三角形基本模型专项训练一、单选题1如图,在Rt△ABC中,AB=AC,∠BAC=90°,点D,E分别在边BC及其延长线上,BD2+CE2=DE2,F为△ABC外一点,且FB⊥BC,FA⊥AE,则结论:①FA=AE;②∠DAE=45°;③S△ADE=14AD⋅EF;④CE2+BE2=2AE2,其中正确的是()A.①②③④B.①②④C.①③④D.①②【答案】A【分析】根据全等三角形的性质,证明△ABF和△ACE全等,即可得到FA=AE;连接DF如图见解析,证明△ADE和△ADF全等,即可得到∠DAE=45°;延长AD交EF于H如图见解析,利用等腰直角△AFE三线合一的性质,∠FAE=90°,∠DAE=45°∠DAE=45°,可知AH⊥EF,S△ADE=12AD⋅EH,HE=HF=12EF,即可判断③;在Rt△EBF和Rt△EAF中,利用勾股定理以及等式的性质,即可判断④.【详解】解:∵AB=AC,∠BAC=90°∴∠ABC=∠ACB=45°∴∠ACE=180°-∠ACB=135°∵FB⊥BC∴∠FBE=90°∴∠ABF=∠ABC+∠FBE=135°∴∠ABF=∠ACE∵FA⊥AE∴∠FAE=90°=∠BAC∴∠FAE-∠FAC=∠BAC-∠FAC即∠CAE=∠BAF在△ABF和△ACE中,∠ACE=∠ABF AC=AB∠CAE=∠BAF∴△ACE≌△ABF ASA∴FA=EA,故①正确;连接DF,如图:∵△ACE≌△ABF∴BF=CE在Rt△BDF中,BD2+BF2=DF2∴BD2+CE2=DF2∵BD2+CE2=DE2∴DE=DF∵AE=AF,AD=AD∴△ADE≌△ADF SSS∴∠DAE=∠DAF∴∠DAE=12∠EAF=45°,故②正确;延长AD交EF于H,如图:∵AE=AF,∠EAD=∠FAD∴AH⊥EF,HE=HF=12EF∴S△ADE=12AD⋅EH=12AD⋅12EF=14AD⋅EF,故③正确;在Rt△EBF中,BE2+BF2=EF2∵CE=BF∴BE2+CE2=EF2∵AE=AF,∠FAE=90°∴EF2=AE2+AF2=2AE2∴BE2+CE2=2AE2,故④正确,综上所述,正确的有①②③④,故选:A.【点睛】本题考查了全等三角形的判定与性质、勾股定理、等腰直角三角形性质等知识,解题的关键是灵活运用所学知识.2如图所示,△ABC中,AC=BC,M、N分别为BC、AC上动点,且BM=CN,连AM、CN,当AM +BN最小时,CMCN=( ).A.2B.32C.54D.1【答案】D 【分析】过B 点在BC 下方作BH ∥AC ,且BH =AC ,链接BH ,AH ,先证明△BCN ≌△HBM ,即有BN =HM ,则AM +BN =AM +MH ,当A 、M 、H 三点共线时,AM +MH 值最小,再证明△ACM ≌△HBM ,问题随之得解.【详解】如图,过B 点在BC 下方作BH ∥AC ,且BH =AC ,链接BH ,AH ,∵BH ∥AC ,∴∠C =∠CBH ,∵BH =AC ,BM =CN ,∴△BCN ≌△HBM ,∴BN =HM ,∴AM +BN =AM +MH ,当A 、M 、H 三点共线时,AM +MH 值最小,如图,此时∵BH ∥AC ,∴∠C =∠CBH ,∠CAM =∠BHM ,∵AC =BC ,∴△ACM ≌△HBM ,∴CM =BM ,∵BM =CN ,∴CM CN=CM BM =1,故选:D .【点睛】本题主要考查了全等三角形的判定与性质,作出辅助线,构造全等三角形是解答本题的关键.3如图,正五边形ABCDE 中,点F 是边CD 的中点,AF ,BC 的延长线交于点N ,点P 是AN 上一个动点,点M 是BN 上一个动点,当PB +PM 的值最小时,∠BPN =()A.72°B.90°C.108°D.120°【答案】C【分析】本题考查了正多边形的定义,全等三角形的判定与性质等知识.连接BF ,EF ,PE ,EM ,根据全等三角形的判定与性质可得EP =BP ,则当E 、P 、M 三点共线,且EM ⊥BC 时,PB +PM 的值最小,过点E 作EH ⊥BC 于H ,交AF 于P ,分别求出∠BAP 和∠ABP 的度数,然后利用三角形外角的性质求解即可.【详解】解:连接BF ,EF ,PE ,EM ,∵正五边形ABCDE ,∴AE =AB =BC =ED ,∠BAE =∠AED =∠BCD =∠EDC =5-2 ×180°5=108°,∵点F 是边CD 的中点,∴CF =DF ,∴△BCF ≌△EDF SAS ,∴BF =EF ,又AE =AB ,AF =AF ,∴△AEF ≌△ABF SSS ,∴∠EAF =∠BAF =12∠BAE =54°,∴△AEP ≌△ABP SAS∴EP =BP ,∴PB +PM =EP +PM ≥EM ,∴当E 、P 、M 三点共线,且EM ⊥BC 时,PB +PM 的值最小,过点E 作EH ⊥BC 于H ,交AF 于P ,同理可求∠ABP =∠AEP =12∠AED =54°,∴∠BP N =∠BAP +∠ABP =108°,即当PB +PM 的值最小时,∠BPN =108°.故选:C .4如图,在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形ABEF ,正方形BCGH 和正方形ACMN ,给出下列结论:①AB =MG ;②S △ABC =S △AFN ;③过点B 作BI ⊥EH 于点I ,延长B 交AC 于点J ,则AJ =CJ .④若AB =1,则EH 2+FN 2=5.其中正确的结论个数是()A.1个B.2个C.3个D.4个【答案】D 【分析】本题考查勾股定理,全等三角形的性质和判定,解题的关键是正确作出辅助线.首先根据题意证明出△ACB ≌△MCG SAS ,进而得到AB =MG ,即可判断①;过点F 作FO ⊥NA 交NA 延长线于点O ,证明出△AFO ≌△ABC AAS ,得到OF =BC ,然后利用三角形面积公式即可得到S △ABC =S △AFN ,即可判断②;过点A 作AP ⊥BJ 交BJ 的延长线于点P ,过点C 作CQ ⊥BJ ,证明出△ABP ≌△BEI AAS ,得到AP =BI ,同理得到CQ =BI ,得到CQ =AP ,然后证明出△AJP ≌△CJQ AAS ,得到AJ =CJ ,即可判断③;根据全等三角形的性质得到EH =2BJ ,然后利用勾股定理证明出EH 2=AC 2+4BC 2,同理得到NF 2=4AC 2+BC 2,然后得到EH 2+NF 2=5AB 2=5,即可判断④.【详解】∵在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向外作正方形ABEF ,正方形BCGH 和正方形ACMN ,∴AC =MC ,BC =GC ,∠MCA =∠GCB =90°∵∠ACB =90°∴∠MCG =∠ACB =90°∴△ACB ≌△MCG SAS∴AB =MG ,故①正确;如图所示,过点F 作FO ⊥NA 交NA 延长线于点O ,∵∠FAO +∠BAO =∠CAB +∠BAO =90°∴∠FAO =∠CAB又∵∠O =∠ACB =90°,AF =AB∴△AFO ≌△ABC AAS∴OF =BC∵AN =AC∵S △ANB =12AN ⋅OF ,S △ACB =12AC ⋅BC ∴S △ABC =S △AFN ,故②正确;如图所示,过点A 作AP ⊥BJ 交BJ 的延长线于点P ,过点C 作CQ ⊥BJ∵∠ABP +∠BEI =90°,∠EBI +∠BEI =90°∴∠ABP =∠BEI又∵∠P =∠BIE =90°,AB =BE∴△ABP ≌△BEI AAS∴AP =BI同理可证,△BCQ ≌△HBI AAS ∴CQ =BI∴CQ =AP∵∠P=∠CQJ=90°,∠AJP=∠CJQ∴△AJP≌△CJQ AAS∴AJ=CJ,故③正确;∵△ABP≌△BEI AAS∴BP=EI∵△BCQ≌△HBI AAS∴BQ=HI∵△AJP≌△CJQ AAS∴PJ=QJ∵EH=EI+HI=PB+BQ=PJ+QJ+BQ+BQ=2BJ ∵AJ=CJ∴BJ2=CJ2+BC2=14AC2+BC2∴EH2=2BJ2=4BJ2=414AC2+BC2=AC2+4BC2同理可证,NF2=4AC2+BC2∴EH2+NF2=AC2+4BC2+4AC2+BC2=5AC2+BC2=5AB2=5×12=5,故④正确.综上所述,正确的结论个数是4.故选:D.5如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠E=∠F=90 °,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE= CF;④△ACN≅△ABM.其中正确的结论是()A.①③④B.①②③④C.①②③D.①②④【答案】A【分析】本题考查了两个全等三角形的判定及性质,根据已知条件判定两个三角形全等,可得到对应边及对应角相等,据此可判断①③,再结合条件证明两个三角形全等,可得到④,即可求得结果,灵活运用两个全等三角形的条件及性质是解题的关键.【详解】解:∵∠EAC=∠FAB,∴∠EAB=∠FAC,在△EAB 和△FAC 中,∠E =∠F =90 °AE =AF ∠EAB =∠FAC,∴△EAB ≌△FAC ASA ,∴∠B =∠C ,BE =CF ,AB =AC ,∴①③都正确,在△ACN 和△ABM 中,∠B =∠CAB =AC ∠CAN =∠BAM,∴△ACN ≌△ABM ASA ,故④正确,根据已知条件无法证明②是否正确,故①③④正确,故选:A .二、填空题6如图,在△ABC 中,AH 是高,AE ⎳BC ,AB =AE ,在AB 边上取点D ,连接DE ,DE =AC ,若S △ABC =5S △ADE ,BH =1,则BC =.【答案】2.5【分析】过点E 作EF ⊥AB ,交BA 的延长线于点F ,先分别证明△ABH ≌△EAF ,Rt △ACH ≌Rt △EDF ,由此可得S △ABH =S △EAF ,S △ACH =S △EDF =S △EAF +S △ADE ,再结合S △ABC =S △ABH +S △ACH =5S △ADE 可得S △ACH S △ABH =32,由此可得CH BH=32,进而即可求得答案.【详解】解:如图,过点E 作EF ⊥AB ,交BA 的延长线于点F ,∵EF ⊥AB ,AH ⊥BC ,∴∠EFA =∠AHB =∠AHC =90°,∵AE⎳BC ,∴∠EAF =∠B ,在△ABH 与△EAF 中,∠AHB =∠EFA∠B =∠EAFAB =EA∴△ABH ≌△EAF (AAS ),∴AH =EF ,S △ABH =S △EAF ,在Rt△ACH与Rt△EDF中,AH=EF AC=DE∴Rt△ACH≌Rt△EDF(HL),∴S△ACH=S△EDF=S△EAF+S△ADE,∵S△ABC=S△ABH+S△ACH=5S△ADE,∴S△ABH+S△EAF+S△ADE=5S△ADE,∴2S△ABH+S△ADE=5S△ADE,解得:S△ABH=2S△ADE,∴S△ACH=5S△ADE-S△ABH=3S△ADE,∴S△ACHS△ABH=3S△ADE2S△ADE=32,∴12CH⋅AH12BH⋅AH=32,即CHBH=32,又∵BH=1,∴CH=1.5,∴BC=BH+CH=2.5,故答案为:2.5.【点睛】本题考查了全等三角形的判定与性质以及三角形的面积公式,作出正确的辅助线并能灵活运用全等三角形的判定与性质是解决本题的关键.7如图,在△ADE和△ABC中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE,垂足为F,DE交CB的延长线于点G,连接AG.四边形DGBA的面积为12,AF=4,则FG的长是.【答案】3【分析】过点A作AH⊥BC于H,证△ABC≌△AED,得AF=AH,再证Rt△AFG≌Rt△AHG,同理Rt△ADF≌Rt△ABH,得S四边形DGBA=6,进而得到FG的长.【详解】解:过点A作AH⊥BC于H,如图所示:在△ABC 和△ADE 中,BC =DE∠C =∠E CA =EA,∴△ABC ≌△AED SAS∴AD =AB ,S △ABC =S △AED ,又∵AF ⊥DE ,∴12×DE ×AF =12×BC ×AH ,∴AF =AH ,∵AF ⊥DE ,AH ⊥BC ,∴∠AFG =∠AHG =90°,在Rt △AFG 和Rt △AHG 中,AG =AG AF =AH ,∴Rt △AFG ≌Rt △AHG HL ,同理:Rt △ADF ≌Rt △ABH HL ,∴S 四边形DGBA =S 四边形AFGH =12,∵Rt △AFG ≌Rt △AHG ,∴S Rt △AFG =6,∵AF =4,∴12×FG ×4=6,解得:FG =3;故答案为:3.【点睛】本题考查了全等三角形的判定与性质以及三角形面积等知识,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.8如图,动点C 与线段AB 构成△ABC ,其边长满足AB =9,CA=2a +2,CB =2a -3.点D 在∠ACB 的平分线上,且∠ADC =90°,则a 的取值范围是,△ABD 的面积的最大值为.【答案】a >52454【分析】在△ABC 中,由三角形三边关系“在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边”可知AC +BC >AB ,代入数值即可确定a 的取值范围;延长AD 、CB交于点E ,首先利用“ASA ”证明△ACD ≌△ECD ,由全等三角形的性质可得AC =EC =2a +2,AD =ED ,进而可求得BE =5,结合三角形中线的性质易知S △ABD :S △ABE =1:2,确定△ABE 面积的最大值,即可获得答案.【详解】解:∵在△ABC 中,AC +BC >AB ,∴2a +2+2a -3>9,解得a >52;如下图,延长AD 、CB 交于点E ,∵CD 为∠ACB 的平分线,∴∠ACD =∠ECD ,在△ACD 和△ECD 中,∠ACD =∠ECDCD =CD ∠ADC =∠EDC =90°,∴△ACD ≌△ECD (ASA ),∴AC =EC =2a +2,AD =ED ,∵CB =2a -3,∴BE =2a +2-(2a -3)=5,∵AD =ED ,∴S △ABD :S △ABE =1:2,当BE ⊥AB 时,△ABE 的面积取最大值,即S △ABE max =12×9×5=452,∴S △ABD max =454.故答案为:a >52,454.【点睛】本题主要考查了三角形三边关系、解一元一次不等式、角平分线、全等三角形的判定与性质、三角形中线的性质等知识,熟练掌握相关知识,正确作出辅助线是解题关键.9如图,AB =AC ,AD=AE ,∠BAC =∠DAE =40°,BD 与CE 交于点F ,连接AF ,则∠AFB 的度数为.【答案】70°/70度【分析】本题考查了全等三角形的判定与性质,三角形内角和定理,构造全等三角形是解答本题的关键.过点A作AM⊥BD于点M,AN⊥CE于点N,根据手拉手模型证明△BAD≌△CAE,得到∠ADM=∠AEN,然后证明△AMD≌△ANE,得到∠DAM=∠EAN,AM=AN,进一步推得∠MAN=∠DAE= 40°,再证明△AMF≌△ANF,可得∠FAM=20°,最后根据三角形内角和定理即得答案.【详解】过点A作AM⊥BD于点M,AN⊥CE于点N,∵∠BAC=∠DAE=40°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE SAS,∴∠ADM=∠AEN,∵∠AMD=∠ANE=90°,AD=AE,∴△AMD≌△ANE AAS,∴∠DAM=∠EAN,AM=AN,∴∠DAM+∠DAN=∠EAN+∠DAN,即∠MAN=∠DAE=40°,∵∠AMF=∠ANF=90°,AM=AN,AF=AF,∴△AMF≌△ANF HL,∴∠FAM=∠FAN=1∠MAN=20°,2∴∠AFB=180°-90°-∠FAM=70°.故答案为:70°.10如图所示,已知△ABC,∠BAC=90°,AB=AC,点D和点E分别是AB和AC边上的动点,满足AD=CE,连接DE,点F是DE的中点,则CDAF的最大值为.【答案】5+1/1+5【分析】作EM⊥ED,且EM=ED,连DM,MC,取ME中点N,连ND、NC、NF,可根据“SAS”证明△ADE≌△CEM,可得∠ECM=90°,再设AF=1,并表示DE,EM,及CN,然后根据勾股定理求出DN,最后根据三角形的三边关系ND+NC≥DC,求出CD最大值,可得答案.【详解】解:过E作EM⊥ED,且EM=ED,连DM,MC.取ME中点N,连ND、NC、NF.∵∠ADE+∠AED=90°,∠AED+∠MEC=90°,∴∠ADE=∠MEC.∵AD=CE,DE=EM,∴△ADE≌△CEM,∴∠ECM=∠DAE=90°.设AF=1,∵F为DE中点,∴DE=2AF=2,∴EM=2.∵N为EM中点,∴CN=EN=1.∴DN=DE2+EN2= 5.∵ND+NC≥DC,∴CD最大值5+1,=5+1.∴CDAF故答案为:5+1.【点睛】本题主要考查了全等三角形的性质和判定,勾股定理,根据三角形的三边关系求最大值,作出辅助线是解题的关键.三、解答题11数学兴趣小组在活动时,老师提出了这样,一个问题:如图1:在△ABC中,AB=3,AC=5,D是BC的中点,求BC边上的中线AD的取值范围.【问题初探】:第一小组经过合作交流,得到如下解决方法:如图2延长AD至E.使得DE=AD,连接BE.利用三角形全等将线段AC转移到线段BE,这样就把线段AB,AC,2AD集中到△ABE中.利用三角形三边的关系即可得到中线AD的取值范围,第二小组经过合作交流,得到另一种解决方法:如图3过点B作AC的平行线交AD的延长线于点F,利用三角形全等将线段AC转移到BF,同样就把线段AB,AC,2AD集中到△ABF中,利用三角形三边的关系即可得到中线AD的取值范围.(1)请你选择一个小组的解题思路.写出证明过程【方法感悟】当条件中出现“中点”“中线”等条件时,可考虑将中线延长一倍或者作一条边的平行线.构造出“平行八字型”全等三角形;这样就把分散的已知条件和所证的结论集中到一个三角形中,顺利解决问题【类比分析】(2)如图4:在△ABC中,∠B=90°,AB=6,AD是△ABC的中线,CE⊥BC,CE=10且∠ADE=90°.求AE的长度.【思维拓展】(3)如图5:在△ABC中,AF⊥BC于点F在AB右侧作AD⊥AB,且AD=AB,在AC的左侧作AE⊥AC,且AE=AC,连接DE,延长AF交DE于点O,证明O为DE中点.【答案】(1)见解析(2)16(3)见解析【分析】(1)选择第一个小组的解题思路:延长AD到点E,使DE=AD,证明△ADC≌△EDB(SAS),得到BE=AC=10,再根据在△ABE中,5-3<AE<5+3,即2<2AD<8,求解即可;选择第二个小组的解题思路:过点B作AC的平行线交AD的延长线于点F,先证明△BDF≌△CDA (AAS),得到DF=AD,BF=AC=5,则2AD=AF,再根据在△ABF中,5-3<AF<5+3,即2<2AD<8,求解即可;(2)延长AD到点F,使DF=AD,连接CF,先证明△ABD≌△FCD SAS,得到∠FCD=∠ABD=90°,CF=AB=6,再证明E、C、F三点共线,得到EF=EC+CF=10+6=16,然后证明△ADE≌△FDE SAS,得到AE=EF=16解决问题;(3)过点E作EM∥AD交AD延长线于M,先证明△AEM≌△CAB AAS,得到EM=AB,再证明△AOD≌△MOE AAS,得到OD=OE,即可得出结论.【详解】解:(1)选择第一个小组的解题思路:如图2,延长AD到点E,使DE=AD,∵D是BC的中点,∴BD=CD,∵∠ADC=∠EDB,∴△ADC≌△EDB(SAS),∴BE=AC=10,△ABE中,5-3<AE<5+3,∴2<2AD<8,∴1<AD<4;选择第二个小组的解题思路:如图3,过点B作AC的平行线交AD的延长线于点F,∵D是BC的中点,∴BD=CD,∵BF∥AC,∴∠FBD=∠C,∠F=∠CAD,∴△BDF≌△CDA(AAS),∴DF=AD,BF=AC=5,∴2AD=AF,在△ABF中,5-3<AF<5+3,∴2<2AD<8,(2)延长AD到点F,使DF=AD,连接CF,如图4,∵D是BC的中点,∴BD=CD,∵∠ADB=∠FDC,DF=AD,∴△ABD≌△FCD SAS,∴∠FCD=∠ABD=90°,CF=AB=6,∵CE⊥BC,∴∠BCD=90°,∴∠FCD+∠ECD=180°,∴E、C、F三点共线,∴EF=EC+CF=10+6=16,∵∠ADE=90°,∴∠FDE=∠ADE=90°,∵DE=DE,AD=DF,∴△ADE≌△FDE SAS,∴AE=EF=16;(3)证明:过点E作EM∥AD交AD延长线于M,如图4,∵AD⊥AB,AE⊥AC,∴∠3+∠2+∠CAD=∠3+∠2+∠BAE=90°,∴∠CAD=∠BAE,又∵AF⊥BC,∴∠3+∠2+∠CAD=∠3+∠BAE+∠B=90°,∴∠2=∠B,∵EM∥AD,∴∠2=∠M,∴∠B=∠M,∵AE⊥AC,AF⊥BC,∴∠3+∠CAM=∠C+∠CAM=90°,∴∠3=∠C,∵AE=AC,∴△AEM≌△CAB AAS,∵AB =AD ,∴EM =AD ,∵∠2=∠M ,∠AOD =∠EOM ,∴△AOD ≌△MOE AAS ,∴OD =OE ,∴O 为DE 中点.【点睛】本题考查三角形三边的关系,全等三角形的判定与性质,余角的性质,平行线的性质,熟练掌握倍长中线,构造出“平行八字型”全等三角形是解题的关键.12已知,在等腰直角三角形ABC 中,AB =AC ,∠BAC =90°,∠ABC =∠ACB =45°,点D 是线段BC 上一点,点D 不与点B ,点C 重合,连接AD ,以AD 为一边作△ADE ,AD =AE ,∠DAE =90°,且点E 与点D 在直线AC 两侧,DE 与AC 交于点H ,连接CE .(1)如图1,求证:△ABD ≌△ACE .(2)如图2,在CE 的延长线上取一点F ,当∠AEF =∠AFE 时,求证:CD =CF .(3)过点A 作直线CE 的垂线,垂足为G ,当CD =6EG 时,直接写出△CDH 与△CEH 的面积比.【答案】(1)见详解(2)见详解(3)32或34【分析】本题主要考查了全等三角形的判定与性质,涉及SAS 、AAS 以及HL 等判定方法,(1)利用“SAS ”证明△ABD ≌△ACE 即可作答;(2)结合(1)的结论,再利用“AAS ”证明△ACD ≌△ACF 即可作答;(3)分类讨论,第一种情况:点G 在点E 的下方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,先证明△AOC ≌△AGC ,即有AO =AG ,CO =CG ,同理可证明:MH =NH ,再证明Rt △AOD ≌Rt △AGE HL ,可得OD =GE ,问题即可作答;第二种情况:点G 在点E 的上方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,按照第一种情况作答即可.【详解】(1)∵∠DAE =90°,∠BAC =90°,∴∠DAE -∠DAH =∠BAC -∠DAH ,∴∠CAE =∠BAD ,又∵AB =AC ,AD =AE ,∴△ABD ≌△ACE SAS ;(2)∵△ABD ≌△ACE SAS ,∴∠ADB =∠AEC ,∠ABD =∠ACE =45°,∴180°-∠ADB =180°-∠AEC ,∠ACB =∠ACE =45°,∴∠ADC =∠AEF ,∵∠AEF =∠AFE ,∴∠ADC =∠AFE ,在△ACD 和△ACF 中,∴∠ACD =∠ACF∠ADC =∠AFC AC =AC,∴△ACD ≌△ACF AAS ,∴CD =CF ;(3)分类讨论:第一种情况:点G 在点E 的下方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,如图,∵AO ⊥BC ,AG ⊥CE∴∠AOC =∠AGC =90°,又∵∠ACB =∠ACE =45°,AC =AC ,∴△AOC ≌△AGC ,∴AO =AG ,CO =CG ,同理可证明:MH =NH ,又∵AD =AE ,∴Rt △AOD ≌Rt △AGE HL ,∴OD =GE ,∵CD =6EG ,∴CO =CD -OD =5EG ,∴CG =CO =5EG ,∴CE =CG -EG =4EG ,∵S △CHD =12×CD ×MH ,S△CHE =12×CE ×NH ,MH =NH ,∴S △CHD S △CHE =12×CD ×MH 12×CE ×NH =CD ×MH CE ×NH ,∵CD =6EG ,CE =4EG ,MH =NH ,∴S △CHD S △CHE =CD ×MH CE ×NH=32;第二种情况:点G 在点E 的上方,过点A 作AO ⊥BC 于点O ,点H 作HM ⊥BC 于点M ,点H 作HN ⊥CG 于点N ,如图,同理可得:OD =GE ,OC =CG ,MH =NH ,∵CD =6EG ,∴CO =CD +OD =7EG ,∴CG =CO =7EG ,∴CE =CG +EG =8EG ,∴S △CHD S △CHE =CD ×MH CE ×NH=34;综上:△CDH 与△CEH 的面积比为32或者34.13如图,在平面直角坐标系中,O 为坐标原点,△ABC 的边BC 在x 轴上,A 、C 两点的坐标分别为A (0,m ),C (n ,0),B (-5,0),且m ,n 满足方程组m +2n =103m -n =9 ,点P 从点B 出发,以每秒2个单位长度的速度沿射线BO 匀速运动,设点P 运动时间为t 秒.(1)求A 、C 两点的坐标;(2)连接P A ,用含t 的代数式表示△AOP 的面积,并直接写出t 的取值范围;(3)当点P 在线段BO 上运动时,在y 轴上是否存在点Q ,使△POQ 与△AOC 全等?若存在,请求出t 的值并直接写出Q 点标;若不存在,请说明理由.【答案】(1)A (0,4),C (3,0);(2)0≤t <52,S △AOP =10-4t ;t >52,S △AOP =4t -10.(3)存在,Q (0,3)或(0,-3)或Q (0,4)或(0,-4).【分析】本题考查了全等三角形的性质和判定,二元一次方程组的解法,坐标与图形性质等知识点的综合运用,关键是利用分类讨论求出符合条件的所有情况.(1)解二元一次方程组求出m ,n 的值即可;(2)分为两种情况:当0≤t <52时,P 在线段OB 上,②当t >52时,P 在射线OC 上,求出OP 和OA ,根据三角形的面积公式求出即可;(3)分为四种情况:①当BP =1,OQ =3时,②当BP =2,OQ =4时,③④利用图形的对称性直接写出其余的点的坐标即可.【详解】(1)解方程组m +2n =103m -n =9 得m =4n =3 ,∴ A 的坐标是0,4 ,C 的坐标是3,0 ;(2)由已知,BP =2t ,OB =5.①0≤t <52,P 在线段OB 上.OP =OB -BP =5-2tS △AOP =12×OP ×OA 2=12×(5-2t )×4=10-4t .②t >52,P 在射线OC 上,OP =BP -OP =2t -5S △AOP =12×OA ×OP =12×4×(2t -5)=4t -10(3)在y 轴上存在点Q ,使△AOC 与△POQ 全等.①△POQ ≌△AOC 时,OQ =OC =3.OP =OA =4.t =5-42=12,Q (0,3)或Q (0,-3)②△POQ ≌△COA 时,OQ =OA =4,OP =OC =3.t =5-32=1 Q (0,4)或(0,-4)t =12,Q (0,3)或(0,-3);t =1,Q (0,4)或(0,-4);综上所述,t =12,Q (0,3)或(0,-3);t =1,Q (0,4)或(0,-4).14某校课后延时兴趣小组尝试用尺规来“作一条线段的三等分点”,请认真阅读下面的操作过程并完成相应的学习任务.如图1,①分别以点A ,B 为圆心,大于12AB 的长为半径在AB 两侧画弧,四段弧分别交于点C ,点D ;②连接AC ,BC ,AD ,作射线BD ;③以D 为圆心,BD 的长为半径画弧,交射线BD 于点E ;④连接CE ,交于AB 点F .点F 即为AB 的一个三等分点(即AF =13AB ).学习任务:(1)填空:四边形ADBC的形状是,你的依据是;(2)证明:AF=13AB;(3)如图2,若CE交AD于点H,∠CAD=60°,AC=6,将CH绕着点C旋转,当点H的对应点H 落在直线FD上时,求DH 的长.【答案】(1)菱形;四条边相等的四边形为菱形(2)见解析(3)DH′的长为33+32或33-32【分析】本题考查了菱形的判定与性质、相似三角形的判定与性质、等边三角形的判定与性质、全等三角形的判定与性质、勾股定理,善于利用特殊叫以及直角三角形中的关系是解题的关键.(1)根据菱形的性质判定即可.(2)证明△AFC∽△BFE,得出AFFB =ACBE,再根据线段关系即可求出.(3)利用菱形及已知条件推出相关信息,证明△ACD为等边三角形,再根据AAS证明△AHC≌△DHE,求得CH ;然后证明△AKF∽△BDF,根据相似三角形的性质得出AK、CK;最后用勾股定理解三角形即可.CH绕着点C旋转,点H的对应点H 需要分情况讨论.【详解】(1)解:由图的作法可知:AC=AD=BC=BD,∴四边形ADBC的形状是菱形,依据是:四条边相等的四边形为菱形.故答案为:菱形;四条边相等的四边形为菱形;(2)证明:∵四边形ADBC的形状是菱形,∴AC∥BE,∴△AFC∽△BFE,∴AF FB =ACBE.∵AC=BD,BD=DE,∴BE=2AC,∴AF FB =12,∴FB=2AF,∴AB=3AF.∴AF=13AB.(3)解:①当点H 在线段FD上时,连接CD,如图,∵AC=AD,∠CAD=60°,∴△ACD为等边三角形,∴CD=AD=6,∠ADC=60°.∵AC∥BE∴∠ACF =∠DEC .在△AHC 和△DHE 中,∠AHC =∠DHE∠ACE =∠DEC AC =DE,∴△AHC ≌△DHE AAS ,∴AH =HD =3,∵△ACD 为等边三角形,∴CH ⊥AD ,∠ACH =∠DCH =30°,∴CH =33.∴CH =CH =33.设FD 与AC 交于点K ,∵AC ∥BE ,∴△AKF ∽△BDF ,∴AK BD =AF FB=12.同理:CK ED =AF FB=12,∴AK BD =CK ED.∵BD =ED ,∴AK =CK =3,∴HK ⊥AC ,∠CDK =12∠ADC =30°.∴H K =CH 2-CK 2=32,DK =33.∴DH =DK -H K =33-32.②当点H 在射线FD 上时,连接CD ,如图,由①知CH =CH =33,HK ⊥AC ,AK =KC =3,∴DK =AD 2-AK 2=33,∴H K =CH 2-CK 2=32.∴DH =H K +DK =33+32.综上,DH 的长为33+32或33-32.15(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC 中,∠BAC =90°,AB =AC ,直线l 经过点A ,BD ⊥直线l ,CE ⊥直线l ,垂足分别为点D 、E .证明:DE =BD +CE .(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线l 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.【答案】(1)见解析;(2)DE =BD +CE ,见解析;(3)见解析【分析】本题主要考查全等三角形的判定和性质,由条件证明三角形全等得到BD =AE 、CE =AD 是解题的关键.(1)由条件可证明△ABD ≌△CAE ,可得DA =CE ,AE =BD ,可得DE =BD +CE ;(2)由条件可知∠BAD +∠CAE =180°-α,且∠DBA +∠BAD =180°-α,可得∠DBA =∠CAE ,结合条件可证明△ABD ≌△CAE ,可得出结论;(3)由条件可知EM =AH =GN ,可得EM =GN ,结合条件可证明△EMI ≌△GNI ,可得出结论I 是EG 的中点.【详解】解:(1)如图1,∵BD ⊥直线l ,CE ⊥直线l ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD ,在△ABD 和△CAE 中,∠ABD =∠CAE∠BDA =∠CEA AB =AC,∴△ABD ≌△CAE AAS ,∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(2)成立,理由如下:如图,证明如下:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°-α,∴∠DBA =∠CAE ,在△ABD 和△CAE 中.∠BDA =∠AEC∠DBA =∠CAE AB =AC.∴△ABD ≌△CAE AAS∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(3)如图3,过E 作EM ⊥HI 于M ,GN ⊥HI 的延长线于N .∴∠EMI =∠EMA =∠GNA =90°,∠BAE =90°,∴∠EAM +BAH =90°,∵AH 是BC 边上的高,∴∠AHB =90°,∴∠BAH +∠ABH =90°,∴∠ABH =EAM ,∵AE =AB ,∴△ABH ≌△EAM ,∴EM =AH ,同理△ACH ≌△GAN ,∴AH =GN ,∴EM =GN ,在△EMI 和△GNI 中,∠EIM =∠GIN∠EMI =∠GNI EM =GN,∴△EMI ≌△GNI AAS ,∴EI =GI ,∴I 是EG 的中点.16如图,在△ABC 中,BC =5,高AD 、BE 相交于点O ,BD =2,且AE =BE.(1)请说明△AOE ≌△BCE 的理由;(2)动点P 从点O 出发,沿线段OA 以每秒1个单位长度的速度向终点A 运动,动点Q 从点B 出发沿射线BC 以每秒4个单位长度的速度运动,P 、Q 两点同时出发,当点P 到达A 点时,P 、Q 两点同时停止运动.设点P 的运动时间为t 秒,求当t 为何值时,△AOQ 的面积为3.(3)在(2)的条件下,点F 是直线AC 上的一点且CF =BO .当t 为何值时,以点B 、O 、P 为顶点的三角形与以点F 、C 、Q 为顶点的三角形全等?(请直接写出符合条件的t 值).【答案】(1)见解析(2)当t 为15或45时,△AOQ 的面积为3(3)t =1或53s 时,△BOP 与△FCQ 全等【分析】本题考查三角形综合题、全等三角形的判定和性质、三角形的面积等知识,(1)首先推导出∠EAO =∠EBC ,通过ASA 即可证明△AOE ≌△BCE ;(2)分两种情形讨论求解即可①当点Q 在线段BD 上时,QD =2-4t ,②当点Q 在射线DC 上时,DQ =4t -2时;依据三角形面积计算公式解答即可;(3)分两种情形求解即可①如图2中,当OP =CQ 时,BOP ≌△FCQ .②如图3中,当OP =CQ 时,△BOP ≌△FCQ .【详解】(1)如图1中,∵AD 是高,∴∠ADC =90°,∵BE 是高,∴∠AEB =∠BEC =90°,∴∠EAO +∠ACD =90°,∠EBC +∠ECB =90°,∴∠EAO =∠EBC ,在△AOE 和△BCE 中,∠EAO =∠EBCAE =BE ∠AEO=∠BEC,∴△AOE ≌△BCE ASA ,(2)解:由(1)知△AOE ≌△BCE ,∴OA =BC =5,∵BD =2,∴CD =3,由题意OP =t ,BQ =4t ,①当点Q 在线段BD 上时,QD =2-4t ,∴S △AOQ =12OA ⋅QD =12×5×2-4t =3,解得:t =15;②当点Q 在BD 延长线上时,DQ =4t -2,∴S △AOQ =12OA ⋅DQ =12×5×4t -2 =3,解得:t =45,综上,当t 为15或45时,△AOQ 的面积为3;(3)存在.①如图2中,当OP =CQ 时,∵OB =CF ,∠POB =∠FCQ ,∴△BOP ≌△FCQ .∴CQ =OP ,∴5-4t =t ,解得t =1,②如图3中,当OP =CQ 时,∵OB =CF ,∠POB =∠FCQ ,∴△BOP ≌△FCQ .∴CQ =OP ,∴4t -5=t ,解得t =53.综上所述,t =1或53s 时,△BOP 与△FCQ 全等.17如图1,在△ABC 中,BD 为AC 边上的高,BF 是∠ABD 的角平分线,点E 为AF 上一点,连接AE ,∠AEF =45°.(1)求证:AE平分∠BAF(2)如图2,连接CE交BD于点G,若△BAE与△CAE的面积相等,求证:BG=CF【答案】(1)见解析;(2)见解析【分析】本题主要考查了全等三角形的证明以及性质运用,角平分线的判定以及基本性质,熟练掌握全等三角形的几种判定方法以及角平分线的判定是解答该题的关键.(1)根据BF是∠ABD的角平分线和,BD为AC边上的高,可得12∠BAD=45°-12∠ABD,由∠AEF=45°得∠BAE=45°-∠ABE=45°-12∠ABD,即可证明∠BAE=12∠BAD;(2)过点E作EM⊥AB于点M,EN⊥AC于点N,由角平分线性质可以得EM=EN,由△BAE与△CAE的面积相等可得AB=AC,证明△ABE≌△ACE(SAS),得出∠AEB=∠CEB=135°,BE=EC,即可得出∠BEG=∠CEF=360°-∠AEB-∠AEC=90°,再根据垂直模型证明△BEG≌△CEF(ASA),即可得出结论.【详解】(1)证明:∵BD为AC边上的高,即∠ADB=90°,∴∠ABD+∠BAD=90°,∴12(∠ABD+∠BAD)=45°,∴1 2∠BAD=45°-12∠ABD∵∠AEF=∠ABF+∠BAE=45°,∴∠BAE=45°-∠ABF,∵∠ABF=12∠ABD,∴∠BAE=45°-12∠ABD,∴∠BAE=12∠BAF,即:AE平分∠BAF.(2)过点E作EM⊥AB于点M,EN⊥AC于点N,∵AE平分∠BAC,且EM⊥AB,EN⊥AC,∴EM=EN.∵S△ABE=S△ACE,∴AB=AC,∵AE平分∠BAC,∴∠BAE=∠CAE,在△ABE和△ACE中,AB=BC∠BAE=∠CAE AE=AE∴△ABE≌△ACE(SAS),∴∠AEB=∠CEB,BE=EC,∵∠AEF=45°,∴∠AEB=∠AEC=135°,∴∠BEG=∠CEF=360°-∠AEB-∠AEC=90°,∵BD为AC边上的高,∴∠ADB=90°,∴∠FBD+∠BFC=∠BFC+∠FCE,∴∠EBG=∠ECF.在△BEG和△CEF中,∠BEG=∠CEF BE=CE∠EBG=∠ECF∴△BEG≌△CEF(ASA).∴BG=CF .18如图,已知A a,0,B0,b,AB=AC且AB⊥AC,AC交y轴于E点.(1)如图1,若a2+b2-4a-8b+20=0,求C点坐标;(2)如图2,A,B两点分别在x轴,y轴正半轴上,E为AC的中点,BC交x轴于G点,连EG,若a=3,求G点的坐标;(3)如图3,A在x轴的负半轴上,以BC为边在BC的右侧作等边△BCD,连OD,当∠BOD=60°时,请探究线段OA、OB、OD之间的数量关系,并证明.【答案】(1)(-2,-2)(2)(-2,0)(3)OD=OB+2OA【分析】(1)利用完全平方公式将等式变形为两个数平方和的形式,即可求出a=2,b=4,如图1中,过点C作CH ⊥x轴于点H,证明△AHC≌△BOA,可得CH=OA=2,AH=OB=4,即可得到点C坐标.(2)根据(1)可得CH=OA=a,AH=OB=b,再由a=3,E为AC的中点,可得点C(-3,-3),AH=OB=6,再利用面积法求出AG =5,即可解题;(3)过点C 作CH ⊥x 轴于点H ,在OD 上取一点M ,使得OM =OB ,证明△OBM 是等边三角形,进而证明△MBD ≌△OBC ,得∠BMD =∠BOC =120°,MD =OC ,再证明∠COH =30°,得OC =2CH =2OA ,即可得出OD =OB +2OA .【详解】(1)解:∵a 2+b 2-4a -8b +20=0,∴(a 2-4a +4)+(b 2-8b +16)=0,即(a -2)2+(b -4)2=0,∴a =2,b =4,∴A 2,0 ,B 0,4如图1中,过点C 作CH ⊥x 轴于点H ,∵∠AHC =∠BOA =∠BAC =90°,∴∠CAH +∠BAO =90°,∠BAO +∠ABO =90°,∴∠CAH =∠ABO ,在△AHC 和△BOA 中,∠AHC =∠BOA∠CAH =∠ABO AC =BA,∴△AHC ≌△BOA (AAS ),∴CH =OA =2,AH =OB =4,∴OH =AH -OA =4-2=2∴点C 坐标为(-2,-2);(2)如图2,同理(1)可证明:CH =OA =a ,AH =OB =b ,∵a =3,E 为AC 的中点,OE 平行于CH ,∴OA =OH =3,CH =3,∴点C (-3,-3),AH =OB =6,AB =AC =OA 2+OB 2=62+32=35,∵S △ABC =S △AGC +S △AGB ,即12×35×35=12×3⋅AG +12×6⋅AG ,∴AG =5,∴GO =AG -OA =5-3=2,∴点G 坐标为(-2,0);(3)结论:OD =OB +2OA ,如图3,过点C 作CH⊥x轴于点H ,同理可得:CH =OA ,AH =OB ,在OD 上取一点M ,使得OM =OB ,∵OM =OB ,∠BOD =60°,∴△OBM 是等边三角形,∴BO =BM ,∠OMB =60°,∴∠BMD =120°,∵△BCD 是等边三角形,∴BC =BD ,∠CBD =∠OBM =60°,∴∠DBM =∠CBO ,在△MBD 和△OBC 中,BM =OB∠DBM =∠CBO BD =BC,∴△MBD ≌△OBC (SAS ),∴∠BMD =∠BOC =120°,MD =OC ,∴∠COH =120°-90°=30°,∵CH ⊥x 轴,∴OC =2CH =2OA ,∵OD =OM +MD ,∴OD =OB +OC =OB +2OA【点睛】本题考查了等腰直角三角形的性质,等边三角形的判定和性质,全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.19已知△ABC 为等边三角形,D 是边AC 上的一点,连接BD ,E 为BD 上的一点,连接CE.(1)如图1,延长CE 交AB 于点G .若∠DCG =15°,BG =2,求BC 的长;(2)如图2,将△BEC 绕点B 逆时针旋转60°至△BFA ,延长CB 至点M ,使得BM =DC ,连接AM 交BF 于点N ,探究线段FN ,DE ,BE 之间的数量关系,并说明理由;(3)如图3,在(2)问的条件下,过点A 作AH ⊥BC 于点H ,过点B 作BK ∥AH 且BK =AH ,连接HK ,NK ,NH ,NC .若BC =4,当12BD +NK 的值最小时,请直接写出CD NH的值.【答案】(1)1+3(2)2FN +DE =BE .理由见解析(3)277【分析】(1)作CF⊥BC,解直角三角形BFG求得BF和FG,进而解直角三角形CFG求得CF,从而得出结果;(2)延长BF至G,使FG=DE,连接AG,作BH∥AF,交BF于H,证明△ABG≌△CBD,进而证明△ANG≌ΔMNB,△AFN≌△MHN,△BMH≌△DCE,进一步得出结论;BD+NK最小,此时BG⊥AG,即BD⊥AC,进一步得出(3)可得出当K、N、G共线且与AG垂直时,12结果.【详解】(1)解:如图1,作CF⊥BC于F,∴∠CFG=∠BFG=90°,∵△ABC是等边三角形,∴∠ACB=∠ABC=60°,在Rt△BFG中,BG=2,∠ABC=60°,=1,∴BF=2cos60°=2×12=3,FG=2⋅sin60°=2×32在Rt△CFG中,FG=3,∠FCG=∠ACB-∠ACG=60°-15°=45°,∴CF=FG=3,tan∠FCG∴BC=BF+FC=1+3;(2)证明:如图2,延长BF至G,使FG=DE,连接AG,作BH∥AF,交BF于H,∴∠MHN=∠AFN,∠NMH=∠FAN,∴∠MHB=∠AFG∵△BEC绕点B逆时针旋转60°至△BFA,∴BF=BE,∠ABF=∠CBE,AB=BC,∴BG=BD,∴△ABG≌△CBD,∴AG=CD=BM,∠G=∠BDC=180°-∠CBE-∠ACB=120°-∠CBE,∵∠MBN=180°-∠ABC-∠ABF=120°-∠CBE,∴∠G=∠MBN,∴△ANG≌△MNB,∴AN=MN,∴△AFN≌△MHN,∴FN=NH,∵△ANG ≌△MNB ,∴NG =BN ,∵FN =NH ,∴BH =FG ,∵FG =DE∴BH =DE ,∵旋转,∴CE =AF ,∵△AFN ≌△MHN ,∴AF =MH ,∴MH =CE ,∵CD =BM ,∴△BMH ≌△DCE ,∴BH =DE ,∵FN +NH +BH =BF ,∴2FN +DE =BE ;(3)解:如图3,由(2)知:BD =BG =2BN ,∴12BD +NK =GN +NK ,∴当K 、N 、G 共线且与AG 垂直时,12BD +NK 最小,此时BG ⊥AG ,即BD ⊥AC ,如图4,连接NH ,∵AC =BC =4,∴CD =BH =2,BD =32BC =23,BN =GN =12BG =12BD =3,∵NH =BH 2+BN 2=2+(3)2=7,∴CD NH=277.【点睛】本题考查了等边三角形的性质,全等三角形的判定和性质,解直角三角形等知识,解决问题的关键是作辅助线,构造全等三角形.。
专题训练(二) 全等三角形判定方法的灵活选用

专题训练(二)全等三角形判定方法的灵活选用►类型一已知两边对应相等Ⅰ.已知两边对应相等找第三边对应相等,应用“SSS”证明三角形全等1.如图2-ZT-1所示,BC=DE,BE=DC.求证:(1)BCⅠDE;(2)ⅠA=ⅠADE.图2-ZT-1Ⅱ.已知两边对应相等找两边的夹角对应相等,应用“SAS”证明三角形全等2.如图2-ZT-2,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:ⅠA=ⅠE.图2-ZT-23.如图2-ZT-3,DC⊥CA,EA⊥CA,CD=AB,CB=AE.求证:ⅠBCDⅠⅠEAB.图2-ZT-3►类型二已知一边一角对应相等Ⅰ.已知一边一角对应相等找另一角对应相等,应用“ASA”或“AAS”证明三角形全等4.如图2-ZT-4,在Rt△ABC中,∠ABC=90°,点D在边AB上,使DB=BC,过点D作EFⅠAC,分别交AC,CB的延长线于点E,F.求证:AB=BF.图2-ZT-4Ⅱ.已知一边一角对应相等找已知角的另一边对应相等,应用“SAS”证明三角形全等5.2019·武汉如图2-ZT-5,点C,F,E,B在一条直线上,∠CFD=ⅠBEA,CE=BF,DF=AE.写出CD与AB之间的关系,并证明你的结论.图2-ZT-56.如图2-ZT-6,AC=AD,∠BAC=ⅠBAD,点E在AB上.(1)你能找出________对全等的三角形;(2)请写出一对全等三角形,并证明.图2-ZT-6►类型三已知两角对应相等Ⅰ.已知两角对应相等找夹边对应相等,应用“ASA”证明三角形全等7. 如图2-ZT-7,已知Ⅰ1=Ⅰ2,∠3=Ⅰ4.求证:AD=AC.图2-ZT-7Ⅱ.已知两角对应相等找一角的对边对应相等,应用“AAS”证明三角形全等8.如图2-ZT-8,点E,F在BC上,BE=CF,∠A=ⅠD,∠B=ⅠC.求证:AB=DC.图2-ZT-8►类型四全等基本图形归纳(平移、旋转)9.如图2-ZT-9,在图Ⅰ中,点A,E,F,C在一条直线上,AE=CF,过点E,F 分别作DEⅠAC,BF⊥AC,BD与AC交于点G,且ABⅠCD.图2-ZT-9(1)求证:BD平分EF;(2)若将图Ⅰ变成图Ⅰ,其余条件不变,(1)中的结论是否仍成立?请说明理由.10.如图2-ZT-10,在ⅠABC和△ADE中,AB=AC,AD=AE,∠BAC=ⅠDAE=90°.(1)当点D在AC上时,如图Ⅰ,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;(2)将图Ⅰ中的ⅠADE绕点A顺时针旋转角α(0°<α<90°),如图Ⅰ,线段BD,CE有怎样的数量关系和位置关系?图2-ZT-10详解详析1.[解析] 连接BD,可以得到两个三角形,并且是全等的三角形,利用全等我们就可以证明题目中的问题了.证明:(1)连接BD.在ⅠBCD 和ⅠDEB 中,⎩⎨⎧BC =DE ,BD =DB ,DC =BE ,∴△BCD ≌△DEB ,∴∠CBD =ⅠEDB ,∴BC ∥DE.(2)ⅠBCⅠDE ,∴∠A =ⅠADE.2.证明:ⅠBCⅠDE ,∴∠ABC =ⅠBDE.在ⅠABC 与ⅠEDB 中,⎩⎨⎧AB =ED ,∠ABC =ⅠBDE ,BC =DB ,∴△ABC ≌△EDB(SAS),∴∠A =ⅠE.3.证明:ⅠDCⅠCA ,EA ⊥CA ,∴ ∠C =ⅠA =90°.在ⅠBCD 和ⅠEAB 中,⎩⎨⎧ CD =AB ,∠C =ⅠA ,CB =AE ,∴△BCD ≌△EAB.4.证明:ⅠEFⅠAC ,∴∠F +ⅠC =90°.∵∠A +ⅠC =90°,∴∠A =ⅠF.又ⅠⅠABC =ⅠFBD ,BC =DB ,∴△ABC ≌△FBD ,∴AB =BF.5.解:CD =AB ,CD ∥AB.证明:ⅠCE =BF ,∴CF =BE在ⅠCDF 和ⅠBAE 中,∵⎩⎨⎧CF =BE ,∠CFD =ⅠBEA ,DF =AE ,∴△CDF ≌△BAE ,∴CD =AB ,∠C =ⅠB ,∴CD ∥AB.6.[解析] 由已知AC =AD ,∠BAC =ⅠBAD ,只需再满足一个条件就可得全等三角形.由题图可知,AB 是公共边,可得到3对全等三角形,分别是ⅠABCⅠⅠABD ,△AEC ≌△AED ,△BEC ≌△BED ,3对全等三角形均可用SAS 证明.解:(1)3(2)答案不唯一,如ⅠABCⅠⅠABD.证明:在ⅠABC 和ⅠABD 中, ∵⎩⎨⎧AC =AD ,∠BAC =ⅠBAD ,AB =AB ,∴△ABC ≌△ABD(SAS).7.证明:因为Ⅰ3=Ⅰ4,所以ⅠABD =ⅠABC.在ⅠABD 和ⅠABC 中,因为⎩⎨⎧Ⅰ1=Ⅰ2,AB =AB ,∠ABD =ⅠABC ,所以ⅠABDⅠⅠABC(ASA),所以AD =AC.8.证明:ⅠBE =CF ,∴BE +EF =CF +EF ,即BF =CE.在ⅠABF 与ⅠDCE 中,∵⎩⎨⎧ⅠA =ⅠD ,∠B =ⅠC ,BF =CE ,∴△ABF ≌△DCE ,∴AB =DC.9.解:(1)证明:ⅠBFⅠAC ,DE ⊥AC , ∴∠AFB =ⅠCED =90°.∵AF =AE +EF ,CE =CF +EF ,AE =CF , ∴AF =CE.∵AB ∥CD ,∴∠A =ⅠC ,∴△ABF ≌△CDE(ASA),∴BF =DE.又ⅠⅠCGB =ⅠAGD ,∠BGF =ⅠDGE , ∴△BGF ≌△DGE(AAS),∴FG =EG ,∴BD 平分EF.(2)成立.理由如下:∵BF ⊥AC ,DE ⊥AC ,∴∠AFB =ⅠCED =90°.∵AF =AE -EF ,CE =CF -EF ,AE =CF , ∴AF =CE.∵AB ∥CD ,∴∠A =ⅠC ,∴△ABF ≌△CDE(ASA),∴BF =DE.又ⅠⅠAGB =ⅠCGD ,∠BFG =ⅠDEG , ∴△DGE ≌△BGF(AAS),∴EG =FG ,∴BD 平分EF.10.解:(1)BD =CE ,BD ⊥CE.证明:延长BD 交CE 于点M.在ⅠABD 和ⅠACE 中,∵⎩⎨⎧AB =AC ,∠BAD =ⅠCAE ,AD =AE ,∴ⅠABDⅠⅠACE(SAS),∴BD =CE ,∠ABD =ⅠACE.∵∠ADB =ⅠMDC ,∴∠DMC =ⅠBAC =90°,∴BD ⊥CE.(2)BD=CE,BD⊥CE.。
全等三角形基本模型综合训练(二)(解析版)(北师大版)

全等三角形基本模型综合训练(二)1.如图,将△ABC 沿DE ,EF 翻折,顶点A ,B 均落在点O 处,且EA 与EB 重合于线段EO ,若△CDO +△CFO =98︒,则△C 的度数为( )A .40°B .41°C .42°D .43°【答案】B 【详解】解:如图,连接AO 、BO .由折叠的性质可得EA =EB =EO ,△△AOB =90°,△OAB +△OBA =90°,△DO =DA ,FO =FB ,△△DAO =△DOA ,△FOB =△FBO ,△△CDO =2△DAO ,△CFO =2△FBO ,又△△CDO +△CFO =98°,△2△DAO +2△FBO =98°,△△DAO +△FBO =49°,△△CAB +△CBA =△DAO +△OAB +△OBA +△FBO =139°,△△C =180°﹣(△CAB +△CBA )=180°﹣139°=41°,故选B .2.如图,已知正方形ABCD 的边长为3,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接,DF CF ,则当DF CF +之和取最小值时,DCF 的周长为( )A.353B.433C.523D.133【答案】A【详解】解:连接BF,过点F作FG△AB交AB延长线于点G,△将ED绕点E顺时针旋转90°到EF,△EF△DE,且EF=DE,△△AED△△GFE(AAS),△FG=AE,△F点在BF的射线上运动,作点C关于BF的对称点C',△EG=DA,FG=AE,△AE=BG,△BG=FG,△△FBG=45°,△△CBF=45°,△BF是△CBC′的角平分线,即F点在△CBC′的角平分线上运动,△C'点在AB的延长线上,当D、F、C'三点共线时,DF+CF=DC'最小,在Rt△ADC'中,AD=3,AC'=6,△DC5△DF+CF的最小值为5△此时DCF的周长为353.故选:A.3.如图,△ABC 中,△A =30°,BC =3,△ABC 的面积9,点D 、E 、F 分别是三边AB 、BC 、CA 上的动点,则△DEF周长的最小值为( )A .5B .6C .8D .10【答案】B 【详解】解:作E 点关于AB 的对称点G ,作E 点关于AC 的对称点H ,连接GH ,交AB 于D 点,交AC 于F 点,连接AG ,AH ,AE ,如图所示:∴由对称性可知GD DE =,EF FH =,AG AE AH ==,DEF ∴∆的周长DE DF EF GD DF FH GH =++=++=,GAD DAE ∠=∠,EAC HAC ∠=∠,2GAH BAC ∴∠=∠,30BAC ∠=︒,60GAH ∴∠=︒,GH AE ∴=,∴当AE BC ⊥时,GH 最短,此时DEF ∆的周长最小,3BC =,ABC ∆的面积9,6AE ∴=,DEF ∴∆的周长最小值为6,故选:B .4.如图,等边三角形ABC的边长为4,点D是AB边的中点,点E是BC边上的一个动点,以DE为边作等边三角形DEF,连接AF,则AF的最小值为()A.2B3C.2D.3【答案】B【详解】解:当AF△AB时,AF的值最小,过D作DG△BC,△DG△BC,AF△AB△△DGB=△DGE=△DAF=90°△△B+△BDG=90°,△GDE+△DEG=90°△△ABC和△DEF都是等边三角形△DF=EF,△B=△FDE=60°,△BDG=30°△△ADF+△GDE=180°-△BDG-△FDE=180°-60°-30°=90°△△ADF=△DEG又△△DGE=△DAF=90°,DE=DF△△DEG△△FDA(AAS)△AF=DG331BD43 222故选:B.5.如图,P为等边△ABC内一点,△APC=150°,且△APD=30°,AP=6,CP=3,DP=7,则BD的长为______.【答案】34【详解】将△CP A绕点C逆时针旋转60°得到△CEB,连接EP,△CE=CP,△ECB=△PCA,△CEB=△CP A=150°,BE=AP=6,△等边△ABC,△△ACP+△PCB=60°,△△ECB+△PCB=60°,即△ECP=60°,△△ECP为等边三角形,△△CPE=△CEP=60°,PE=6,△△DEB=90°,△△APC=150°,△APD=30°,△△DPC=120°,△△DPE=180°,即D、P、E三点共线,△ED=3+7=10,△BD22DE BE34故答案为346.如图,以Rt△ABC的斜边AB为一边在△ABC同侧作正方形ABEF.点O为AE与BF的交点,连接CO.若CA=2,CO=3CB的长为________.【答案】26【详解】如图,在BC上截取BD=AC=2,连接OD,△四边形AFEB 是正方形,△AO =BO ,△AOB =△ACB =90°,△△CAO =90°-△ACH ,△DBO =90°-△BHO ,△△ACH =△BHO ,△△CAO =△DBO ,△△ACO △△BDO ,△DO =CO =23△AOC =△BOD ,△△BOD +△AOD =90°,△△AOD +△AOC =90°,即△COD =90°,△CD 22(23)(23)26+△BC =BD +CD =26+故答案为:26+7.已知:如图,BD 为△ABC 的角平分线,且BD=BC ,E 为BD 延长线上的一点,BE=BA ,过E 作EF△AB ,F 为垂足,下列结论:①△ABD△△EBC ;②△BCE+△BCD=180°;③AD=EF=EC ;④BA+BC=2BF ,其中正确的结论有________(填序号).【答案】①②④【详解】解:①△BD 为△ABC 的角平分线,△△ABD=△CBD ,在△ABD 和△EBC 中,BD BC ABD CBD BE BA =⎧⎪∠=∠⎨⎪=⎩,△△ABD△△EBC (SAS ), △①正确;②△BD 为△ABC的角平分线,BD=BC ,BE=BA ,△△BCD=△BDC=△BAE=△BEA ,△△ABD△△EBC,△△BCE=△BDA,△△BCE+△BCD=△BDA+△BDC=180°,△②正确;③△△BCE=△BDA,△BCE=△BCD+△DCE,△BDA=△DAE+△BEA,△BCD=△BEA,△△DCE=△DAE,△△ACE为等腰三角形,△AE=EC,△△ABD△△EBC,△AD=EC,△AD=AE=EC,△BD为△ABC的角平分线,EF△AB,而EC不垂直与BC,△EF≠EC,△③错误;④过E作EG△BC于G点,△E是BD上的点,△EF=EG,在Rt△BEG和Rt△BEF中,BE BEBE EG=⎧⎨=⎩,△Rt△BEG△Rt△BEF(HL),△BG=BF,在Rt△CEG和Rt△AFE中,EF FG AE CE=⎧⎨=⎩,△Rt△CEG△Rt△AFE(HL),△AF=CG,△BA+BC=BF+FA+BG-CG=BF+BG=2BF,△④正确.故答案为①②④.8.如图,已知四边形ABCD中,AC平分△BAD,CE△AB于点E,且AE=12(AB+AD),若△D=115°,则△B=________.【答案】65°【详解】试题分析:如图,在AB上截取AF=AD,连接CF,△AC平分△BAD,AC为公共边,△△AFC△△ADC,△△ADC=△AFC,△AE=12(AB+AD),AF=AD,△AF+EF=12(AF+BF+AF),△EF=12BF,△EF=BE,△CE△AB,△△ABC=△BFC,△△ADC+△ABC=180°,△△D=115°,△△B=65°.9.已知在Rt ABC 中,90C ∠=︒,75ABC ∠=︒,5AB =.点E 为边AC 上的动点,点F 为边AB 上的动点,则线段FE EB +的最小值是__________.【答案】52【详解】解:如图作F 点关于AC 的对称点F ',连接A F '并延长交BC 延长线于点B ′,作BD △AB ′于点D ,由对称性可得EF =E F ',由垂线段的性质可得B 到AB ′的最短距离为BD ,△EF +EB =E F '+EB =B F '≥BD ,Rt △ABC 中,△BAC =90°-△ABC =15°,△△BAD =2△BAC =30°,Rt △ABD 中,AB =5,△BDA =90°,△BAD =30°,△BD =52,△线段FE EB +的最小值是52, 故答案为:52; 10.在矩形ABCD 中,AD ,CD 边的中点分别为E ,F ,连接BF ,CE 交于点G ,若2AB =,CG CF =,则BG 的长为______.410 【详解】解:如图,延长AD 交BF 的延长线于M .△AD ,CD 边的中点分别为E ,F ,2AB =,△11122CF DF AB CD ====,AE DE =. △CG CF =,△1CG =.△四边形ABCD 是矩形,△BC AM ∥,BC AD =,△CBF DMF ∠=∠,90BCF MDF ∠=∠=︒. 在BCF △与MDF △中90CBF DMF BCF MDF CF DF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,△()BCF MDF AAS ≌,△=BC DM AD =. 设AE DE x ==,则2AD DM BC x ===.△BC EM ,△CBG M ∠=∠,BCG GEM ∠=, △BCG MEG ∽,△CG BC BG EG EM GM==. △1CG =,AE DE x ==,2AD DM BC x ===,△122x EG x x =+,△32EG =, △35122CE EG CG =+=+=,△222253222ED CE CD ⎛⎫=--= ⎪⎝⎭, △23AD BC DM ===,39322EM =+=,△3462AM AE DE DM =++=⨯=, △222226210BM AB AM++△210GM BM BG BG =-=.△BC BG EM GM =,△392102BG -,△410BG = 410 11.如图,已知△AED =△ACB =90°,AC =BC =3,AE =DE =1,点D 在AB 上,连接CE ,点M ,点N 分别为BD ,CE 的中点,则MN 的长为_____.10【详解】解:连接DN 并延长DN 交AC 于F ,连接BF ,如图,△△AED =△ACB =90°,AC =BC =3,AE =DE =1,45EAD EDA BAC ∴∠=∠=∠=︒,DE AC ∴∥,DEN FCN ∴∠=∠,△点N 为CE 的中点,EN NC ∴=,在DEN 和FCN △中,DNE FNC EN NCDEN FCN ∠=∠⎧⎪=⎨⎪∠=∠⎩()DEN FCN ASA ∴△≌△,DE FC DN NF ∴==,,AE FC ∴=,△点M 为BD 的中点,MN ∴是BDF 的中位线,12MN BF ∴=, 45EAD BAC ∠=∠=︒,90EACFCB ∴∠=∠=︒,在CAE 和BCF △中,EAC FCB AE FC ⎪∠=∠⎨⎪=⎩()CAE BCF SAS ∴△≌△,BF CE ∴=,22221111013222MN CE AE AC ∴==++=. 12.如图,已知△ABC 中,AB=AC ,△BAC=90°,分别过B ,C 向经过点A 的直线EF 作垂线,垂足为E ,F .(1)如图1,当EF 与斜边BC 不相交时,请证明EF=BE+CF ;(2)如图2,当EF 与斜边BC 相交时,其他条件不变,写出EF 、BE 、CF 之间的数量关系,并说明理由; (3)如图3,猜想EF 、BE 、CF 之间又存在怎样的数量关系,写出猜想,不必说明理由.【答案】(1)证明见解析;(2) EF= BE -CF ,理由见解析;(3)EF=CF -BE ,理由见解析.【详解】(1)证明:△BE△EA ,CF△AF ,△△BAC=△BEA=△CFE=90°,△△EAB+△CAF=90°,△EBA+△EAB=90°,△△CAF=△EBA ,在△ABE 和△CAF 中,BEA AFC EBA FAC AB AC ===∠∠⎧⎪∠∠⎨⎪⎩△△BEA△△AFC (AAS ), △EA=FC ,BE=AF ,△EF=EA+AF=BE+CF .(2)证明:△BE△EA ,CF△AF ,△△BAC=△BEA=△CFE=90°,△△EAB+△CAF=90°,△ABE+△EAB=90°,△△CAF=△ABE ,在△ABE 和△ACF 中,EBA FAC BEA CFA AB AC ∠∠⎧⎪∠∠⎨⎪⎩===,△△BEA△△AFC (AAS ),△EA=FC ,BE=AF ,△EF=AF -AE ,△EF=BE -CF .(3)EF=CF -BE ,理由是:△BE△EA ,CF△AF ,△△BAC=△BEA=△CFA=90°,△△EAB+△CAF=90°,△ABE+△EAB=90°,△△CAF=△ABE ,在△ABE 和△ACF 中,BEA CFA AB AC ⎪∠∠⎨⎪⎩==,△△BEA△△AFC (AAS ),△EA=FC ,BE=CF ,△EF=EA -AF ,△EF=CF -BE .13.如图①,在四边形ABCD 中,5AB AD ==,53BC CD ==,90B ∠=︒.点M 在边AD 上,2AM =,点N 是边BC 上一动点.以MN 为斜边作Rt MNP △,若点P 在四边形ABCD 的边上,则称点P 是线段MN 的“勾股点”.(1)如图①,线段MN 的中点O 到BC 的距离是______.A 3B .52C .3D .23(2)如图②,当2AP =时,求BN 的长度.(3)是否存在点N ,使线段MN 恰好有两个“勾股点”?若存在,请直接写出BN 的长度或取值范围;若不存在,请说明理由.【答案】(1)C ;(2)33(3)33318【解析】(1)如图1,过点M 作 MQ △AB 交BA 的延长线于点Q ,过点O 作 OE △BC ,垂足为E ,过点M 作MF △BC ,垂足为F ,连接AC ,△AB =AD ,CB =CD ,AC =AC ,5AB AD ==,53BC CD ==90B ∠=︒,AM =2,△△ABC △△ADC ,△△D =△B =90°,AC 225(53)10+=,△△DAC =△BAC =△QAM =60°,△DCA =BCA =△QMA =30°,△△DAC =△BAC =60°,△DCA =BCA =30°,△QA =1,QM 3△MQ △AB ,OE △BC ,90B ∠=︒,△四边形MQBF 是矩形,△MF =QB =AB +QA =5+1=6,,△MF △CB ,OE △BC ,△OE ∥MF ,△NO NE OM EF =, △OM =ON ,△NE =EF ,△OE =12MF =3,故选C .(2)过点M 作MQ △AB 交BA 的延长线于点Q ,△点P 是线段MN 的“勾股点”.△△MPN =90°,△△QPM =△BNP ,△△QPM △△BNP ,△QP QM BN BP =, △33BN =△BN =33 (3)根据(2)得,BN =33P 是线段MN 的“勾股点”.过点N 作NG △DC ,垂足为G ,当DM =DP =3时, 点P 是线段MN 的“勾股点”.△点P 是线段MN 的“勾股点”.△△MPN =90°,△PG =GN ,设BN =x ,则NC =(53x ),根据(2),得△NCG =60°,△PG =GN 3(53)x ,GC =1(53)2x ,3(53)x +1(53)2x =(533),解得x =318, 故当BN =318或33MN 恰好有两个“勾股点”.14.已知ABC ,90,6cm ACB AC BC ∠==︒=,点P 从点A 出发,沿AB 2cm 的速度向终点B 运动,同时,动点Q 从点B 出发沿BC 方向以每秒1cm 的速度向终点C 运动,设运动的时间为t 秒.(1)如上左图,若PQ BC ⊥,求t 的值;(2)如上中图,若PQ PC =,求t 的值;(3)如上右图,将PQC △沿BC 翻折至P QC '处,当t 为何值时,四边形QPCP '为菱形?【答案】(1)3t =;(2)2t =;(3)2t = 【解析】(1)解:由题意可得:2AP t =,226662AB +cm BQ t =, 则(622)cm BP AB AP t =-=,△90,ACB PQ BC ︒∠=⊥,△PQ AC ∥, △PQB ACB ∽,△BP BQ BA BC=, 622662t t -=, △3t =.(2)过点P 作PE BC ⊥交BC 于E 点,如图,BQ t =,6CQ t =-, △PQ PC =,△622CQ t QE EC -===, △PE AC ∥,△PEB ACB ∽,△BP BE AB BC=, 66222662t t t -+-=,解得:2t =.(3)如图,连接PP '交CQ 于D ,△四边形QPCP '为菱形,△PP CQ '⊥,CD DQ =,△点Q 的速度是每秒1cm ,△11(8)cm 22CD CQ t ==-, 过点P 作PO AC ⊥于O ,则四边形CDPO 是矩形,△CD OP =,△90,C AC BC ∠=︒=,△ABC 是等腰直角三角形,△45A ∠=︒,△点P 2cm , △22cm PO t t ==, △1(6)2t t -=,解得:2t =.15.图1是边长分别为a 和()b a b >的两个等边三角形纸片ABC 和CDE △叠放在一起(C 与C '重合)的图形.(1)操作:固定ABC ,将CDE △绕点C 按顺时针方向旋转20°,连结AD ,BE ,如图2,则ECA ∠=______度,并直接写出线段BE 与AD 的数量关系____.(2)操作:若将图1中的CDE △,绕点C 按顺时针方向旋转120°,使点B 、C 、D 在同一条直线上,连结AD 、BE ,如图3.①线段BE 与AD 之间是否仍存在(1)中的结论?若是,请证明;若不是,请直接写出BE 与AD 之间的数量关系;②求APB ∠的度数.(3)若将图1中的CDE △,绕点C 按逆时针方向旋转一个角()0360αα<<︒,当α等于多少度时,BCD △的面积最大?请直接写出答案.【答案】(1)40,BE =AD ;(2)①存在,理由见详解;②60°(3)当α=150°或330°时,BCD △的面积最大【解析】(1)△△ABC 和△CDE 是等边三角形,△BC =AC ,CE =CD ,△BCA =60°,△旋转20°△△BCE =△ACD =20°,△△CBE △△CAD (SAS ),△BE =AD (全等三角形的对应边相等),△ECA ∠=△BCA -△BCE△ECA ∠=60°-20°=40°故答案为:40,BE =AD(2)如图1,①(1)中结论仍然成立,理由如下:△△ABC和△CDE是等边三角形,BC=AC,CE=CD,△△BCE=△ACD=120°,△△CBE△△CAD(SAS),△BE=AD;②△△CBE△△CAD,△△CBE=△CAD,又△AOP=△BOC,△△APB=△ACB=60°;(3)如图2,当D运动到D1或D2,即BC△D1D2S△BCD最大12BC CD=⋅12=ab,此时旋转角是60°+90°=150°,或360°﹣30°=330°,△当α=150°或330°.16.知识再现:已知,如图1,四边形ABCD 是正方形,点M 、N 分别在边BC 、CD 上,连接AM 、AN 、MN ,且45MAN ∠=︒,延长CB 至G 使BG DN =,连接AG ,根据三角形全等的知识,我们可以证明MN BM DN =+.(1)知识探究:如图1中,作AH MN ⊥,垂足为点H ,猜想AH 与AB 有什么数量关系?并进行证明.(2)知识运用:如图2,四边形ABCD 是正方形,E 是边BC 的中点,F 为边CD 上一点,2FEC BAE ∠=∠,24AB =,求DF 的长.(3)知识拓展:已知45BAC ∠=︒,AD BC ⊥于点D ,且2BD =,6AD =,求CD 的长.【答案】(1)=AH AB ,证明见解析;(2)8;(3)3CD =【解析】(1)解:=AH AB ,理由如下:△四边形ABCD 是正方形,△AD AB =,=90ABG ADN ∠∠=︒,在ADN △和ABG 中,AD AB ADN ABG DN BG =⎧⎪∠=∠⎨⎪=⎩△()ADN ABG SAS ≌△△,△AG AN =,GAB NAD ∠=∠,△45MAN ∠=︒,90DAB ∠=︒,△45BAM NAD ∠+∠=︒,△45BAM GAB ∠+∠=︒,即45GAM MAN ∠=∠=︒,在GAM △和NAM △中,AG NG GAM MAN AM AM =⎧⎪∠=∠⎨⎪=⎩△()GAM NAM SAS ≌△△,△MN GM =,△GAM NAM =S △△S ,即1122AB GM AH MN =, △=AH AB ,(2)解:作AM EF ⊥交EF 与点M ,连接EF ,如图,设=BAE α∠,则2FEC α∠=,△=90B ∠︒,△=90BEA α∠︒-,△2FEC α∠=,△=90AEM α∠︒-,在ABE △和AME △中,ABE AME AEB AEM AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩△()ABE AME AAS ≌△△,△=BE ME ,=A AB M ,△24AB =,ABCD 为正方形,E 为BC 中点, △==12BE M E ,在Rt AMF △和Rt ADF 中,AD AM AF AF =⎧⎨=⎩△()AMF ADF HL ≌△△,△DF MF =,设DF x =,则24CF x =-,12EF x =+,△222EF CF EC =+,即()()222122412x x +=-+,解之得:8x =, △8DF =,(3)方法1、解:由题意可知:22210AB AD BD =+=作CE AB ⊥交AB 于点E ,如图,设CD a =,则236AC a =+△45BAC ∠=︒,236AC a =+△2362a AE EC += △()2113662=210222a a +⨯⨯+=12a -(舍去),=3a ,△3CD = 方法2、解:对比图1和图3可以发现当6AH AD ==,2BD MH ==,45BAC MAN ∠=∠=︒,CD NH =, 由(1)可知:AH AB =, 在Rt ABM 和Rt AHM 中,AM AM AB AH =⎧⎨=⎩△()ABM AHM HL △≌△, △2BM MH ==,△624MC =-=,同理可得:()AHN ADN HL △≌△, △DN HN =,设=DN HN x =,则6NC x =-,2MN x =+,△222NC MC MN +=,即()()222642x x -+=+,解之得3x =△=3CD NH。
2022年人教版初中数学8年级上册全等三角形判定二(SSS,AAS)(基础)巩固练习及答案

2022年人教版初中数学8年级上册【巩固练习】一、选择题1.(2020•奉贤区二模)如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是()A.∠B=45° B.∠BAC=90° C.BD=AC D.AB=AC2.如图,已知AB=CD,AD=BC,则下列结论中错误的是()A.AB∥DCB.∠B=∠DC.∠A=∠CD.AB=BC3.下列判断正确的是()A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4.如图,AB、CD、EF相交于O,且被O点平分,DF=CE,BF=AE,则图中全等三角形的对数共有()A.1对B.2对C.3对D.4对5.如图,∠1=∠2,∠3=∠4,下面结论中错误的是()A.△ADC≌△BCD B.△ABD≌△BACC.△ABO≌△CDO D.△AOD≌△BOC6.如图,已知AB⊥BD于B,ED⊥BD于D,AB=CD,BC=ED,以下结论不正确的是()A.EC⊥ACB.EC=ACC.ED+AB=DBD.DC=CB二、填空题7.如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=_________.8.如图,已知:∠1=∠2,∠3=∠4,要证BD=CD,需先证△AEB≌△AEC,根据是,再证△BDE≌△,根据是.9.(2020秋•大同期末)如下图∠1=∠2,由AAS判定△ABD≌△ACD,则需添加的条件是.10.如图,AC=AD,CB=DB,∠2=30°,∠3=26°,则∠CBE=_______.11.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC,若∠B=20°,则∠C=_______.12.已知,如图,AB=CD,AC=BD,则△ABC≌,△ADC≌.三、解答题13.(2020•通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.14.如图,已知D、E、B三点共线,AE=CE,AE⊥CE,∠D=∠B=90°.求证:CD+AB=DB.15.如图,已知AB=DC,AC=DB,BE=CE求证:AE=DE.【答案与解析】一.选择题1.【答案】D;【解析】解:当AB=AC时,△ABD≌△ACD,∵AD是△ABC的边BC上的高,AB=AC,∴BD=CD,∵在△ABD 和△ADC 中,∴△ABD≌△ACD(SSS).2.【答案】D;【解析】连接AC 或BD 证全等.3.【答案】D;4.【答案】C;【解析】△DOF≌△COE,△BOF≌△AOE,△DOB≌△COA.5.【答案】A;【解析】将两根钢条'AA ,'BB 的中点O 连在一起,说明OA='OA ,OB='OB ,再由对顶角相等可证.6.【答案】D;【解析】△ABC≌△EDC,∠ECD+∠ACB=∠CAB+∠ACB=90°,所以EC⊥AC,ED +AB =BC+CD=DB.二.填空题7.【答案】66°;【解析】可由SSS 证明△ABC≌△DCB,∠OBC=∠OCB=82412︒=︒,所以∠DCB=∠ABC=25°+41°=66°.8.【答案】ASA,CDE,SAS;【解析】△AEB ≌△AEC 后可得BE=CE.9.【答案】∠B=∠C.【解析】解:由图可知,只能是∠B=∠C,才能组成“AAS”.故填∠B=∠C.10.【答案】56°;【解析】∠CBE=26°+30°=56°.11.【答案】20°;【解析】△ABE≌△ACD(SAS).12.【答案】△DCB,△DAB;【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】解:∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,在△ACD 中,∠ACD=90°,∴∠2+∠D=90°,∵∠BAE=∠1+∠2=90°,∴∠1=∠D,在△ABC 和△DEC 中,,∴△ABC≌△DEC(AAS).14.【解析】证明:∵AE⊥CE,∴∠AEB+∠CED=90°,又∵∠B=90°∴∠A+∠AEB=90°,∴∠A=∠CED,在△AEB 与△ECD 中,A CEDB DAE CE ∠=∠∠=∠=⎧⎪⎨⎪⎩∴△AEB≌△ECD(AAS)∴AB=DE ,BE=CD∵DE+BE=DB∴CD+AB=DB15.【解析】证明:在△ABC 和△DCB 中AB DC AC DB BC =CB ⎧⎪⎨⎪⎩==∴△ABC≌△DCB(SSS)∴∠ABC=∠DCB,在△ABE 和△DCE 中ABC DCB AB DC BE CE =∠=∠=⎧⎪⎨⎪⎩∴△ABE≌△DCE(SAS)∴AE=DE.全等三角形的判定二(SSS,AAS)(基础)【学习目标】1.理解和掌握全等三角形判定方法3——“边边边”,和判定方法4——“角角边”;2.能把证明角相等或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释:如图,如果''A B =AB,''A C =AC,''B C =BC,则△ABC≌△'''A B C .要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等SAS SSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.【典型例题】类型一、全等三角形的判定3——“边边边”1、已知:如图,△RPQ 中,RP=RQ,M 为PQ 的中点.求证:RM平分∠PRQ.【思路点拨】由中点的定义得PM=QM,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM=QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边∴△RPM≌△RQM(SSS).∴∠PRM=∠QRM(全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中.把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.举一反三:【变式】已知:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC.【答案】证明:连接DC,在△ACD 与△BDC 中()AD BC AC BD CD DC ⎧=⎪=⎨⎪=⎩公共边∴△ACD≌△BDC(SSS)∴∠CAD=∠DBC(全等三角形对应角相等)类型二、全等三角形的判定4——“角角边”2、已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC 和△EAD 中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC≌△EAD(AAS)∴AC=AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.举一反三:【变式】如图,AD 是△ABC 的中线,过C、B 分别作AD 及AD 的延长线的垂线CF、BE.求证:BE=CF.【答案】证明:∵AD 为△ABC 的中线∴BD=CD∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°,在△BED 和△CFD 中BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩(对顶角相等)∴△BED≌△CFD(AAS)∴BE=CF3、(2020春•雅安期末)如图:AB=A′B′,∠A=∠A′,若△ABC≌△A′B′C′,则还需添加的一个条件有()种.A.1B.2C.3D.4【思路点拨】本题要证明△ABC≌△A′B′C′,已知了AB=A′B′,∠A=∠A′,可用的判别方法有ASA,AAS,及SAS,所以可添加一对角∠B=∠B′,或∠C=∠C′,或一对边AC=A′C′,分别由已知与所添的条件即可得证.【答案与解析】解:添加的条件可以为:∠B=∠B′;∠C=∠C′;AC=A′C′,共3种.若添加∠B=∠B′,证明:在△ABC 和△A′B′C′中,,∴△ABC≌△A′B′C′(ASA);若添加∠C=∠C′,证明:在△ABC 和△A′B′C′中,,∴△ABC≌△A′B′C′(AAS);若添加AC=A′C′,证明:在△ABC 和△A′B′C′中,,∴△ABC≌△A′B′C′(SAS).故选C.【总结升华】此题考查了全等三角形的判定,是一道条件开放型问题,需要由因索果,逆向推理,逐步探求使结论成立的条件,解决这类问题要注意挖掘隐含的条件,如公共角、公共边、对顶角相等,这类问题的答案往往不唯一,只有合理即可.熟练掌握全等三角形的判定方法是解本题的关键.类型三、全等三角形判定的实际应用4、“三月三,放风筝”.下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学的知识证明.【答案与解析】证明:在△DEH 和△DFH 中,DE DF EH FH DH DH ⎧⎪⎨⎪=⎩==∴△DEH≌△DFH(SSS)∴∠DEH=∠DFH.【总结升华】证明△DEH≌△DFH,就可以得到∠DEH=∠DFH,我们要善于从实际问题中抽离出来数学模型,这道题用“SSS”定理就能解决问题.举一反三:【变式】(2020秋•紫阳县期末)雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=AB,AF=AC,当O 沿AD 滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD 与∠CAD 有何关系?说明理由.【答案】解:雨伞开闭过程中二者关系始终是:∠BAD=∠CAD,理由如下:∵AB=AC,AE=AB,AF=AC,∴AE=AF,在△AOE 与△AOF 中,,∴△AOE≌△AOF(SSS),∴∠BAD=∠CAD.【巩固练习】一、选择题1.如图,∠A=∠D,∠B=∠E,BF=CE,下列结论错误的是()A.△ABC≌△DEFB.BF=ECC.AC∥DED.AC=DF2.如图,AB∥EF,DE∥AC,BD=CF,则图中不是全等三角形的是()A.△BAC≌FEDB.△BDA≌FCEC.△DEC≌CADD.△BAC≌FCE3.如图,AB=BD,∠1=∠2,要用AAS判定△ABC≌△DBE,则添加的条件是()A.AE=ECB.∠D=∠AC.BE=BCD.∠DEB=∠C4.下列判断中错误的是()A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5.(2020•滕州市校级模拟)如图,在下列条件中,不能证明△ABD≌△ACD的是()A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC6.如图,点A在DE上,AC=CE,∠1=∠2=∠3,则DE的长等于()A.DC B.BC C.AB D.AE+AC二、填空题7.(2020春•鹤岗校级期末)如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件________________时,就可得到△ABC≌△FED.(只需填写一个即可)8.如图,点D在AB上,点E在AC上,且∠B=∠C,在条件①AB=AC,②AD=AE,③BE=CD,④∠AEB=∠ADC中,不能使△ABE≌△ACD的是_______.(填序号)9.已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.10.如图,AB∥CD,AD∥BC,OE=OF,图中全等三角形共有______对.11.如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是1和2,则EF的长是___________.12.在△ABC 和△DEF 中(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F 从这六个条件中选取三个条件可判定△ABC 与△DEF 全等的方法共有________种.三、解答题13.(2020秋•景洪市校级期中)如图,O 为码头,A,B 两个灯塔与码头的距离相等,OA,OB 为海岸线,一轮船离开码头,计划沿∠AOB 的平分线航行,在航行途中,测得轮船与灯塔A 和灯塔B 的距离相等,试问轮船航行时是否偏离预定航线,请说明理由.14.已知:如图,ABC △中,45ABC ∠=°,CD AB ⊥于D ,BE AC ⊥于E ,BE 与CD 相交于点F .求证:BF AC =.15.如图,DC∥AB,∠BAD 和∠ADC 的角平分线相交于E,过E 的直线分别交DC、AB 于C、B 两点.求证:AD=AB+DC.【答案与解析】一、选择题1.【答案】C;2.【答案】D;3.【答案】D;【解析】满足判定定理AAS的只有D选项.4.【答案】B;【解析】C选项和D选项都可以由SSS定理证全等.5.【答案】D;【解析】解:A、∵在△ABD和△ACD中,∴△ABD≌△ACD(SSS),故本选项错误;B、∵在△ABD和△ACD中,∴△ABD≌△ACD(SAS),故本选项错误;C、∵在△ABD和△ACD中,∴△ABD≌△ACD(AAS),故本选项错误;D、不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项正确;故选D.6.【答案】C;【解析】可证∠BAC=∠E,∠BCA=∠DCE,所以△ABC≌△EDC,DE=AB.二、填空题7.【答案】BC=ED.8.【答案】④【解析】三个角对应相等不能判定三角形全等.9.【答案】6;【解析】△ABF≌△CDE,BE=CF=2,EF=10-2-2=6.10.【答案】6;【解析】△ABO≌△CDO,△AFO≌△CEO,△DFO≌△BEO,△AOD≌△COB,△ABD≌△CDB,△ABC≌△CDA.11.【答案】3;【解析】由AAS证△ABF≌△CBE,EF=FB+BE=CE+AF=2+1=3.12.【答案】13;【解析】ASA类型3种,AAS类型6种,SAS类型3种,SSS类型一种,共13种.三、解答题13.【解析】解:此时轮船没有偏离航线.理由:由题意知:假设轮船在D处,则DA=DB,AO=BO,在△ADC和△BDC中,,∴△ADO≌△BDO(SSS),∴∠AOD=∠BOD,即DO 为∠AOB 的角平分线,∴此时轮船没有偏离航线.14.【解析】证明:∵CD AB⊥∴90BDC CDA ∠=∠=︒∵45ABC ∠=︒∴45DCB ABC ∠=∠=︒∴DB DC=∵BE AC⊥∴90AEB ∠=︒∴90A ABE ∠+∠=︒∵90CDA ∠=︒∴90A ACD ∠+∠=︒∴ABE ACD∠=∠在BDF ∆和CDA ∆中BDC CDADB DC ABE ACD∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆(AAS)∴BF AC =.15.【解析】证明:延长DE 交AB 的延长线于F∴∠CDE=∠F,∠CDA+∠BAD=180º∵DE 平分∠CDA,AE 平分∠DAB ∴∠CDE=∠ADE=21∠CDA,∠DAE=∠EAF=21∠BAD∴∠ADE=∠F,∠EDA+∠DAE=90º∴∠AED=∠AEF=90º在△ADE 与△AFE 中⎪⎩⎪⎨⎧=∠=∠∠=∠AE AE FEA DEA F ADE ∴△ADE≌△AFE (AAS)∴DE=EF,AD=AF在△DCE 与△FBE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠FEB DEC FE DE F CDE ∴△DCE≌△FBE(ASA)∴DC=BF,∴AD=AB+DC.全等三角形的判定二(SSS,AAS)(提高)【学习目标】1.理解和掌握全等三角形判定方法3——“边边边”,和判定方法4——“角角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释:如图,如果''A B =AB,''A C =AC,''B C =BC,则△ABC≌△'''A B C.要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等SASSSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.【典型例题】类型一、全等三角形的判定3——“边边边”1、如图,在△ABC 和△ADE 中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD≌△ACE(SSS)∴∠BAD=∠CAE(全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质.要证∠BAD=∠CAE,先找出这两个角所在的三角形分别是△BDA 和△CAE,然后证这两个三角形全等.【变式】(2020•静海县模拟)已知点A、D、C、F 在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需添加一个条件是.【答案】AC=DF.解:理由是:∵在△ABC 和△DEF中,∴△ABC≌△DEF(SSS),故答案为:AC=DF.类型二、全等三角形的判定4——“角角边”2、已知:如图,∠ACB=90°,AC=BC,CD 是经过点C 的一条直线,过点A、B 分别作AE⊥CD、BF⊥CD,垂足为E、F.求证:CE=BF【答案与解析】证明:∵AE⊥CD、BF⊥CD,∴∠AEC=∠BFC=90°∴∠BCF+∠B=90°∵∠ACB=90°,∴∠BCF+∠ACF=90°∴∠ACF=∠B在△BCF 和△CAE 中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC ∴△BCF≌△CAE(AAS)∴CE=BF.【总结升华】要证CE=BF,只需证含有这两个线段的△BCF≌△CAE.同角的余角相等是找角3、平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C 作CE⊥MN 于点E,过点B 作BF⊥MN 于点F.当点E 与点A 重合时(如图1),易证:AF+BF=2CE.当三角板绕点A 顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.【思路点拨】过B 作BH⊥CE 与点H,易证△ACE≌△CBH,根据全等三角形的对应边相等,即可证得AF+BF=2CE.【答案与解析】解:图2,AF+BF=2CE 仍成立,证明:过B 作BH⊥CE 于点H,∵∠CBH+∠BCH=∠ACE+∠BCH=90°∴∠CBH=∠ACE在△ACE 与△CBH 中,90ACH CBH AEC CHB AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ACE≌△CBH.(AAS)∴CH=AE,BF=HE,CE=EF,∴AF+BF=AE+EF+BF=CH+EF+HE=CE+EF=2EC.【总结升华】正确作出垂线,构造全等三角形是解决本题的关键.举一反三:【变式】已知Rt△ABC 中,AC=BC,∠C=90°,D 为AB 边的中点,∠EDF=90°,∠EDF 绕D 点旋转,它的两边分别交AC、CB 于E、F.当∠EDF 绕D 点旋转到DE⊥AC 于E 时(如图1),易证12DEF CEF ABC S S S +=△△△;当∠EDF 绕D 点旋转到DE 和AC 不垂直时,在图2情况下,上述结论是否成立?若成立,请给予证明;若不成立,请写出你的猜想,不需证明.图2ADBC E M N F 【答案】解:图2成立;证明图2:过点D 作DM AC DN BC⊥⊥,则90DME DNF MDN ∠=∠=∠=°在△AMD 和△DNB 中,AMD=DNB=90A B AD BD ∠∠︒⎧⎪∠=∠⎨⎪=⎩∴△AMD≌△DNB(AAS)∴DM=DN∵∠MDE+∠EDN=∠NDF+∠EDN=90°,∴∠MDE=∠NDF在△DME 与△DNF 中,90EMD FDN DM DN MDE NDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△DME≌△DNF(ASA)∴DME DNFS S =△△∴DEF CEF DMCN DECF S =S =S S .+△△四边形四边形可知ABC DMCN 1S =S 2△四边形,∴12DEF CEF ABC S S S +=△△△.类型三、全等三角形判定的实际应用4、(2020秋•内丘县期中)如图,AD 是一段斜坡,AB 是水平线,现为了测斜坡上一点D 的竖直高度DB 的长度,欢欢在D 处立上一竹竿CD,并保证CD⊥AD,然后在竿顶C 处垂下一根绳CE,与斜坡的交点为点E,他调整好绳子CE 的长度,使得CE=AD,此时他测得DE=2米,求DB 的长度.【思路点拨】延长CE交AB于F,根据等角的余角相等求出∠A=∠C,再利用“角角边”证明△ABD和△CDE全等,根据全等三角形对应边相等可得DB=DE.【答案与解析】解:如图,延长CE交AB于F,则∠A+∠1=90°,∠C+∠2=90°,∵∠1=∠2(对顶角相等),∴∠A=∠C,在△ABD和△CDE中,,∴△ABD≌△CDE(AAS),∴DB=DE,∵DE=2米,∴DB的长度是2米.【总结升华】本题考查了全等三角形的应用,仔细观察图形求出∠A=∠C是解题的关键.。
全等三角形综合练习
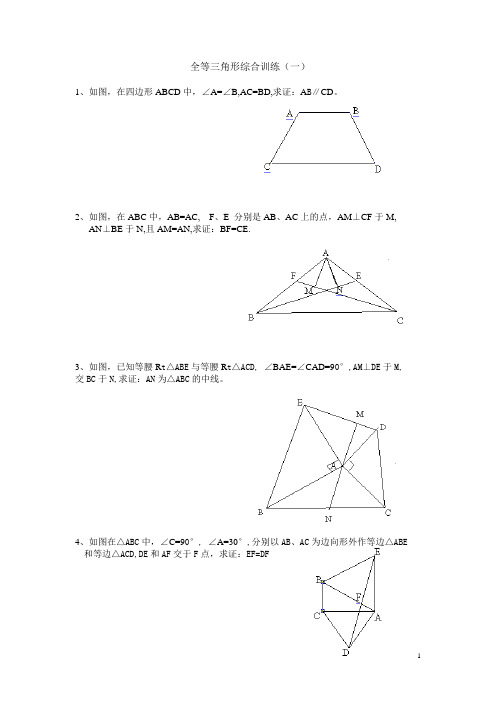
全等三角形综合训练(一)1、如图,在四边形ABCD中,∠A=∠B,AC=BD,求证:A B∥CD。
2、如图,在ABC中,AB=AC, F、E 分别是AB、AC上的点,AM⊥CF于M,AN⊥BE于N,且AM=AN,求证:BF=CE.3、如图,已知等腰R t△ABE与等腰R t△ACD,∠BAE=∠CAD=90°,AM⊥DE于M, 交BC于N,求证:AN为△ABC的中线。
4、如图在△ABC中,∠C=90°,∠A=30°,分别以AB、AC为边向形外作等边△ABE和等边△ACD,DE和AF交于F点,求证:EF=DF5、如图、已知等边△ABC和等边△BDE,点A、B、D在一条直线上,连AE、CD交于点P.(1)AE=CD;(2)求∠DPE的度数;(3)若△BDE绕B点旋转任意角度,其它条件不变,则(1)、(2)的结论是否仍成立?试证明。
6、如图、已知等腰Rt△ABC和等腰Rt△CDE,AC=BC,CD=CE,M、N分别为AE、BD的中点,连CM、CN.(1)判断CM与CN的位置关系和数量关系;(2)若Rt△CDE绕C点旋转任意角度,其它条件不变,则(1)的结论是否仍成立?试证明。
7、如图,已知等腰Rt△ABC的直角顶点C在X轴上,B在Y轴上。
(1)若点C的坐标为(2,0),A的坐标为(-2,-2),求点B的坐标;(2)在(1)的条件下,AB交X轴于F,边AC交Y轴于E,连EF,①求证:CE=AE;②求证:∠CEB=∠AEF。
(3)如图,直角边BC在坐标轴上运动,使点A在第四象限内,过点A作AD⊥y轴y于点D,求的值。
8、如图,在平面直角坐标系中,点B的坐标是(-1,0),点C的坐标是(1, 0),点D 为y轴上一点,点A为第二象限内一动点,且∠BAC=2∠BDO;过D作DM⊥AC于M.(1)求证:∠ABD=∠ACD;(2)若点E在BA的延长线上,求证:AD平分∠CAE;(3)当A点运动时,的值是否发生变化?若不变,求其值,若变化,请说明理由。
全等三角形的判定练习

全等三角形的判定专项练习一.填空题(每题4分,共24分)1.如图,△ABD ≌△ACE,对应角是_______________________,对应边是__________________.2. 已知:如图,△ABC ≌△FED,且BC=DE.则∠A=__________,A D=_______.3. 如图,△ABD ≌△ACE,则AB 的对应边是_________,∠BAD 的对应角是______. 4.如图,∠1=∠2,由AAS 判定△ABD ≌△ACD ,则需添加的条件是____________.1 2 3 45.如图, 已知:∠1=∠2 , ∠3=∠4 , 要证BD=CD , 需先证△AEB ≌△A EC , 根据是_________再证△BDE ≌△______ , 根据是__________.6.如图,ABC △中,∠B =∠C ,D ,E ,F 分别在AB ,BC ,AC 上,且BD CE ,=DEF B ∠∠ 求证:=ED EF .证明:∵∠DEC =∠B +∠BDE ( ),又∵∠DEF =∠B (已知),∴∠______=∠______(等式性质).在△EBD 与△FCE 中,∠______=∠______(已证), ______=______(已知),∠B =∠C (已知), ∴EBD FCE △≌△( ).∴ED =EF ( ). 5 6 二.选择题(每题5分,共40分)7. 下列各条件中,不能作出惟一三角形的是( )A .已知两边和夹角B .已知两角和夹边C .已知两边和其中一边的对角D .已知三边8. 如图,已知:△ABE ≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是 ( )A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE8 99. 图中全等的三角形是 ( )A.Ⅰ和ⅡB.Ⅱ和ⅣC.Ⅱ和ⅢD.Ⅰ和Ⅲ10. AD=AE , AB=AC , BE 、CD 交于F , 则图中相等的角共有(除去∠DFE=∠BFC )A.5对B.4对C.3对D.2对 ( ) 11.如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED 的度数是 ( )A.70°B. 85°C. 65°D. 以上都不对A B CD12AD EC B F 4321E D C BA12. 已知:如图,△ABC ≌△DEF,AC ∥DF,BC ∥EF.则不正确的等式是 ( )A.AC=DFB.AD=BEC.DF=EFD.BC=EF10 11 12 13 14 13.如图 , ∠A=∠D , OA=OD , ∠DOC=50°, 求∠DBC 的度数为 ( )A.50°B.30°C.45°D.25° 14. 如图 , ∠ABC=∠DCB=70°, ∠ABD=40°, AB=DC , 则∠BAC= ( )A.70°B.80°C.100°D.90° 三.解答题(每题9分,共36分)15. 已知:如图 , 四边形ABCD 中 , AB ∥CD , AD ∥BC .求证:△ABD ≌△CDB.16. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .17.如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF .18.如图,工人师傅要检查人字梁的∠B 和∠C 是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:①分别在BA 和CA 上取BE CG =; ②在BC 上取BD CF =;③量出DE 的长a 米,FG 的长b 米.如果a b =,则说明∠B 和∠C 是相等的.他的这种做法合理吗?为什么?七年级全等三角形判定专题训练 (查找隐含着的三角形全等的条件)(一)公共边1、已知:如图,AD ∥BC ,AD =CB ,你能说明△ADC ≌△CBA 吗? 证明:FG E D C B A AD E CBFG CEDBO A∵AD ∥BC (已知)∴∠=∠(两直线平行,内错角相等)在 中⎪⎪⎩⎪⎪⎨⎧∠=∠(公共边)=(已证)(已知)= ∴ ≌ ( )2、如图,∠B =∠C ,AD 平分∠BAC ,求证:△ABD ≌△ACD 证明: ∵AD 平分∠BAC ( )∴∠ =∠ (角平分线的定义) 在△ABD 和△ACD 中⎪⎪⎩⎪⎪⎨⎧∠∠∠=∠(公共边)=(已证)=(已知) ∴△ABD △ACD ( )3、如图,已知AB =AC ,AD 是BC 边上的中线,求证:AD 是角平分线吗 证明:∵AD 是BC 边上的中线(已知)∴ = (中线的定义) 在 中∴ ≌ ( ).∴ = (全等三角形的对应角相等) ∴AD 是角平分线( )4、如图,已知21∠=∠,AD=AB ,求证:ADC ABC ∆≅∆。
中考全程演练(第02期)第18课时:全等三角形(含答案)

三角形第18课时全等三角形基础达标训练1. (2021合肥长丰县模拟)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A. 带①去B. 带②去C. 带③去D. 带①和②去第1题图2. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是()第2题图A. 75°B. 70°C. 65°D. 60°3. (8分)(2021合肥期末)如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.第3题图4. (8分)(2021泸州) 如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF.求证:AB=DE.第4题图5. (8分)(2021广安)如图,四边形ABCD是正方形,E、F分别是AB、AD上的一点,且BF⊥CE,垂足为G.求证:AF=BE.第5题图6. (8分)(2021恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.第6题图7. (10分)(2021温州)如图,在五边形ABCDE中,∠BCD=∠EDC =90°,BC=ED,AC=AD.(1)求证:△ABC≌△AED;(2)当∠B=140°时,求∠BAE的度数.第7题图8. (10分)(2021常州)如图,已知在四边形ABCD中,点E在AD 上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.第8题图9. (10分)(2021连云港)如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD交于点F.(1)判断∠ABE 与∠ACD 的数量关系,并说明理由; (2)求证:过点A 、F 的直线垂直平分线段BC .第9题图能力提升拓展1. (10分)(2021合肥肥城三模)已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F .(1)求证:BF =AC ; (2)求证:CE =12BF .第1题图2. (12分)(2021合肥模拟)已知,△ABC 中,AB =AC ,∠BAC =90°,E 为边AC 任意一点,连接BE .(1)如图①,若∠ABE =15°,O 为BE 中点,连接AO ,且AO =1,求BC 的长;(2)如图②,F 也为AC 上一点,且满足AE =CF ,过A 作AD ⊥BE 交BE 于点H ,交BC 于点D ,连接DF 交BE 于点G ,连接AG .若AG 平分∠CAD ,求证:AH=12AC.第2题图教材改编题1. (沪科八上P95习题14.1第2题改编)如图,已知CE⊥AB于E,BD⊥AC于D,AC=AB=6,BE=2,则AD的长为()第1题图A. 2B. 3C. 4D. 52.教材母题(沪科八上P150A组复习题第10题)已知:如图,AD⊥DE,BE⊥DE,AC,BC分别平分∠DAB,∠ABE,点C在线段DE上.求证:AB=AD+BE.第2题图变式1:(8分)如图,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E,求证:DE=BD+CE;变式1题图拓展变式:(8分)将直线m绕点A旋转,使其与BC边相交,则结论DE=BD+CE是否还成立?如果成立,请你给出证明;若不成立,请写出所有可能的结论,并在图中画出相应的图形.拓展变式题图变式2:(8分)如图,已知△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,请问结论DE=BD+CE是否成立?请说明理由;变式2题图变式3:(8分)如图,D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF 和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.变式3题图拓展变式:(8分)如图,过△ABC 的边AB 、AC 向外作正方形ABDE 和正方形ACFG ,AH 是BC 边上的高,延长HA 交EG 于点I ,求证:I 是EG 的中点.拓展变式题图答案基础达标训练 1. C2. C 【解析】∵AB =AC ,∴∠B =∠C ,在△DBE 和△ECF 中,⎪⎩⎪⎨⎧=∠=∠=CF EB C B EC BD ∴△DBE ≌△ECF (SAS),∴∠EFC =∠DEB ,∵∠A =50°,∴∠C =(180°-50°)÷2=65°,∴∠CFE +∠FEC =180°-65°=115°,∴∠BED +∠FEC =115°,∴∠DEF =180°-115°=65°.3. 证明:∵∠1=∠2, ∴∠1+∠EAC =∠2+∠EAC , ∴∠BAC =∠DAE , 又∵∠C =∠E ,∴在△ABC 和△ADE 中,⎩⎪⎨⎪⎧∠C =∠E ∠BAC =∠DAE AC =AE, ∴△ABC ≌△ADE (ASA). 4. 证明:∵BC ∥EF , ∴∠ACB =∠DFE , 又∵AF =DC , ∴AF +FC =DC +FC , 即AC =DF .在△ABC 与△DEF 中,⎪⎩⎪⎨⎧∠=∠=∠=∠DFE ACB DFAC D A ∴△A B C ≌△DEF (ASA), ∴AB =DE .5. 证明:∵四边形ABCD 是正方形, ∴AB =BC ,∠A =∠ABC =90°, ∴∠AFB +∠ABF =90°, ∵BF ⊥CE ,垂足为G , ∴∠BEC +∠A B F =90°, ∴∠AFB =∠BEC , 在△AFB 和△BEC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠BC AB BEC AFB ABC A , ∴△AFB ≌△BEC (AAS), ∴AF =BE.6. 证明:∵△ABC 、△CDE 为等边三角形, ∴∠ACB =∠ECD =60°, ∴∠ACE =∠BCD , 在△ACE 与△BCD 中,⎪⎩⎪⎨⎧=∠=∠=CD CE BCD ACE BC AC , ∴△ACE ≌△BCD (SAS), ∴∠CAE =∠CBD ,∵∠AOB +∠CBD +∠BPO =180°, ∠BCA +∠C A E +∠A PC =180°, 且∠BPO =∠APC , ∴∠AOB =∠BCA =60°. 7. (1)证明:∵AC =AD , ∴∠ACD =∠ADC , ∵∠BCD =∠EDC =90°,∴∠BCD -∠ACD =∠EDC -∠ADC , 即∠BCA =∠ADE , 在△ABC 与△AED 中,⎪⎩⎪⎨⎧=∠=∠=AD AC ADE BCA ED BC , ∴△ABC ≌△AED (SAS); (2)解:∵△ABC ≌△AED , ∴∠E =∠B =140°,∵五边形ABCDE 内角和为(5-2)×180°=540°, ∴∠BAE =540°-2×90°-2×140°=80°.8. (1)证明:∵∠BCE =∠ACD =90°,∠BCE =∠ACB +∠ACE , ∠ACD =∠ACE +∠DCE , ∴∠ACB =∠DCE , 在△ABC 和△DEC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠CE BC DCE ACB D BAC , ∴△ABC ≌△DEC (AAS),∴AC =CD ;(2)解:由(1)知AC =CD , ∵∠ACD =90°, ∴∠CAD =45°, ∵AC =AE ,∴∠ACE =∠AEC =12(180°-45°)=67.5°, ∴∠DEC =180°-67.5°=112.5°. 9. (1)解:∠ABE =∠ACD.理由:∵AB =AC ,∠BAE =∠CAD ,AE =AD ,∴△ABE ≌△ACD (SAS),∴∠ABE =∠ACD ;(2)证明:∵AB =AC ,∴∠ABC =∠ACB.由(1)可知∠ABE =∠ACD ,∴∠FBC =∠FCB ,∴FB =FC.又∵AB =AC ,∴点A 、F 均在线段BC 的垂直平分线上,即过点A 、F 的直线垂直平分线段BC.能力提升拓展1. (1)证明:∵CD ⊥AB ,∠ABC =45°,∴△BCD 是等腰直角三角形.∴BD =CD.∵∠DBF =90°-∠BFD ,∠DCA =90°-∠EFC ,且∠BFD =∠EFC ,∴∠DBF =∠DCA .在Rt △DFB 和Rt △DAC 中,⎪⎩⎪⎨⎧=∠=∠∠=∠DC BD DFBA CDA BDF , ∴Rt △DFB ≌Rt △DAC (AAS),∴BF =AC.(2)证明:∵BE 平分∠ABC ,∴∠ABE =∠CBE.在Rt △BEA 和Rt △BEC 中,⎪⎩⎪⎨⎧∠=∠=∠=∠CBE ABE BEBE CEB AEB , ∴Rt △BEA ≌Rt △BEC (ASA).∴CE =AE =12AC ,又∵BF =AC,∴CE =12BF .2. (1)解:如解图①,在AB 上取一点M ,使得BM =ME ,连接ME .第2题解图①在Rt △ABE 中,∵OB =OE ,∴BE =2OA =2,∵MB =ME ,∴∠MBE =∠MEB =15°,∴∠AME =∠MBE +∠MEB =30°,设AE =x ,则ME =BM =2x ,AM =3x , ∵AB 2+AE2=BE 2,∴(2x +3x )2+x 2=22,∴x =2-3(负根已经舍弃),∴AB =AC =(2+3)·2-3=2+3,∴BC =2AB =4+23=(3+1)2=3+1.第2题解图②(2)证明:如解图②中,作CP ⊥AC ,交AD 的延长线于P ,GM ⊥AC 于点M .∵BE ⊥AP , ∴∠AHB =90°,∴∠ABH +∠BAH =90°,∵∠BAH +∠P AC =90°,∴∠ABE =∠P AC ,在△ABE 和△CAP 中,⎪⎩⎪⎨⎧∠=∠=∠=∠ACP BAE ACAB PAC ABE , ∴△ABE ≌△CAP (ASA),∴AE =CP =CF ,∠AEB =∠P ,在△DCF 和△DCP 中,⎪⎩⎪⎨⎧=∠=∠=CP CF DCP DCF CD CD ,∴△DCF ≌△DCP (SAS),∴∠DFC =∠P ,∴∠GFE =∠GEF ,∴GE =GF ,∵GM ⊥EF ,∴FM =ME ,∵AE =CF ,∴AF =CE ,∴AM =CM , 在△GAH 和△GAM 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AG AG AMG AHG GAM GAH ,∴△AGH ≌△AGM (AAS),∴AH =AM =CM =12AC .教材改编题1. C 【解析】∵CE ⊥AB 于E ,BD ⊥AC 于D ,∴∠AEC =∠ADB =90°,∵AC =AB ,∠A =∠A ,∴△ADB ≌△AEC (AAS),∴AD =AE ,∵AB =6,BE =2,∴AE =4,∴AD =4.2.变式1 :证明:∵BD ⊥直线m ,CE ⊥直线m ,∴∠BDA =∠CEA =90°.∵∠BAC =90°,∴∠BAD +∠CAE =90°.∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD.∵∠CAE =∠ABD ,∠ADB =∠CEA =90°,AB =AC ,∴ △ADB ≌△CEA (AAS),∴ AE =BD ,AD =CE ,∴ DE =AE +AD =BD +CE .拓展变式解::当m ⊥BC 时,根据D 和E 重合,则DE =0,BD =CE ;当m 与AC 的夹角小于45°时,如解图,拓展变式题解图∵∠BAD +∠CAE =90°,在Rt △ADB 中,∠ABD +∠BAD =90°, ∴∠CAE =∠ABD ,∴△ABD 和△CAE 中,⎪⎩⎪⎨⎧=∠=∠︒=∠=∠AC AB CAEABD AEC BDA 90, ∴△ABD ≌△CAE (AAS),∴BD =AE ,EC =DA ,又∵DE =AE -AD ,∴DE =BD -CE ;同理,当m与AC的夹角大于45°小于90°时,DE=CE-BD. 变式2:解:成立,理由如下:∵∠BDA=∠BAC=α,∴∠DBA+∠BDA=∠BAC+∠CAE,∴∠DBA=∠CAE.∵∠BDA=∠AEC=α,∠ABD=∠CAE,AB=AC,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.变式3:解:△DEF为等边三角形,理由如下:由(2)知,△ADB≌△CEA,∴BD=AE,∠BDA=∠CEA.∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠F AE.∵B F=AF,∠DBF=∠F AE,BD=AE,∴△DBF≌△EAF(SAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DF A+∠AFE=∠DF A+∠BFD=60°,∴△DEF为等边三角形.拓展变式:证明:如解图,过E作EM⊥HI于M,GN⊥HI的延长线于N.拓展变式解题图∴∠EMI =∠GNI =90°,由(1)和(2)的结论可以知道EM =AH =GN , ∴EM =GN ,在△EMI 和△GNI 中,⎪⎩⎪⎨⎧∠=∠=∠=∠GNI EMI GNEM GIN EIM , ∴△EMI ≌△GNI (AAS),∴EI =GI ,∴I 是EG 的中点.。
全等三角形专项练习及答案
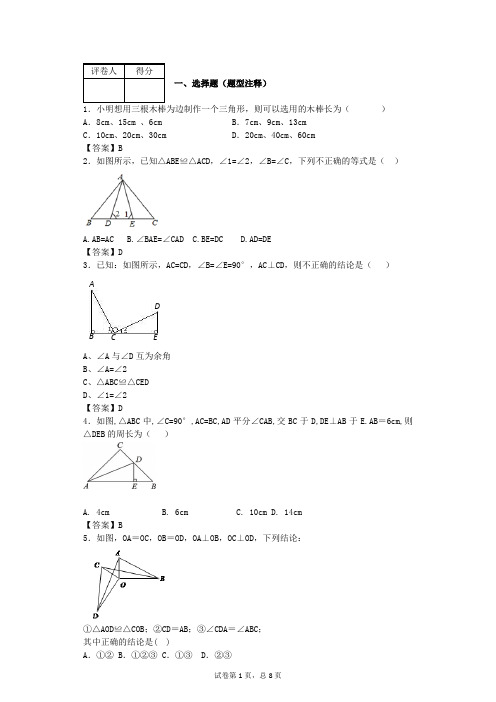
评卷人得分 一、选择题(题型注释)1.小明想用三根木棒为边制作一个三角形,则可以选用的木棒长为( )A .8cm 、15cm 、6cmB .7cm 、9cm 、13cmC .10cm 、20cm 、30cmD .20cm 、40cm 、60cm【答案】B2.如图所示,已知△ABE ≌△ACD ,∠1=∠2,∠B=∠C ,下列不正确的等式是( )A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE【答案】D3.已知:如图所示,AC=CD ,∠B=∠E=90°,AC ⊥CD ,则不正确的结论是( )A 、∠A 与∠D 互为余角B 、∠A=∠2C 、△ABC≌△CEDD 、∠1=∠2【答案】D4.如图,△ABC 中,∠C=90°,AC=BC,AD 平分∠CAB,交BC 于D,DE ⊥AB 于E.AB =6cm,则△DEB 的周长为( )A. 4cmB. 6cmC. 10cmD. 14cm【答案】B5.如图,OA =OC ,OB =OD ,OA ⊥OB ,OC ⊥OD ,下列结论:①△AOD ≌△COB ;②CD =AB ;③∠CDA =∠ABC ;其中正确的结论是( )A .①②B .①②③C .①③D .②③AB C DE12【答案】B【解析】试题分析:因为OA=OC,OB=OD,OA⊥OB,OC⊥OD,可得△COD≌△AOB, ∠CDO=∠ABO;∠DOC+∠AOC=∠AOB+∠AOC, OA=OC,OB=OD,所以△AOD≌△COB,所以CD=AB,∠ADO=∠CBO;所以∠CDA=∠ABC.故①②③都正确.故选B考点:三角形全等的判定和性质6.如图,△ABC中,∠B=∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是()A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°【答案】A【解析】试题分析:根据已知条件可证明△BDE≌△CFD,则∠BED=∠CDF,由∠A+∠B+∠C=180°,得∠B=,因为∠BDE+∠EDF+∠CDF=180°,所以得出a与∠A的关系2a+∠A=180°.考点:全等三角形的判定和性质,三角形的内角和定理7.如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则()A.BE+CF>EFB.BE+CF=EFC.BE+CF<EFD.BE+CF与EF的大小关系不能确定.【答案】A.8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是()A.10cm B.12cm C.15cm D.17cm【答案】C.【解析】试题分析:∵AB的垂直平分AB,∴AE=BE,BD=AD,∵AE=3cm,△ADC的周长为9cm,∴△ABC的周长是9cm+2×3cm=15cm,故选C.考点:线段垂直平分线的性质.9.如图所示,∠A+∠B+∠C+∠D+∠E的结果为()A.90° B.1 80° C.360° D.无法确定【答案】【解析】试题分析:延长BE交AC于F,∵∠A+∠B=∠2,∠D+∠E=∠1,∠1+∠2+∠C=180°,∴∠A+∠B+∠C+∠D+∠E=180°,考点:1.三角形内角和定理;2.三角形的外角性质.10.若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()A、36B、72C、108D、144【答案】C【解析】∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°,∵2(∠A+∠C)=3∠B,∴∠B=72°,11.如图,AB∥CD,∠D =∠E =35°,则∠B的度数为().A.60° B.65° C.70° D.75°【答案】C.12.如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是()A.∠1+∠0=∠A+∠2 B.∠1+∠2+∠A+∠O=180°C.∠1+∠2+∠A+∠O=360° D.∠1+∠2+∠A=∠O【答案】D.【解析】试题分析:连接AO 并延长,交BC 于点D ,∵∠BOD 是△AOB 的外角,∠COD 是△AOC 的外角,∴∠BOD=∠BAD+∠1①,∠COD=∠CAD+∠2②,①+②得,∠BOC=(∠BAD+∠CAD )+∠1+∠2,即∠BOC=∠BAC+∠1+∠2.故选D .考点:1.三角形的外角性质;2.三角形内角和定理.13.如图,BD 是∠ABC 的角平分线,DE ⊥AB 于E ,DF ⊥BC 于F ,,,,△cm 12BC cm 18AB cm 362ABC ===S 则DE 的长是( )A.2cmB.cm 512C.3cmD.cm 514 【答案】B【解析】试题分析:∵BD 是∠ABC 的角平分线,DE ⊥AB ,DF ⊥BC,由角平分线的性质可得DE=DF ∴DCB S S ∆∆+=ADB ABC S △=DF DE ⋅⨯+⋅⨯12211821=9DE+6DF=15DE=36∴DE=cm 512 所以选B.考点:角平分线的性质第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人 得分 二、填空题(题型注释)14.如图,△ABC 中,∠A =90°,DE 是BC 的垂直平分线,AD=DE ,则∠C 的度数是 °.【答案】30°.【解析】试题分析:∵DE 是BC 的垂直平分线,∴DE ⊥BC ,∵∠A =90°,AD=DE ,∴BD 平分∠AABC ,∴∠ABD=∠DBC ,∵DE 是BC 的垂直平分线,∴DC=BD ,∴∠C=∠DBC ,∴3∠C=90°,∴∠C=30°.故答案为:30°.考点:1.线段垂直平分线的性质;2.角平分线的性质.15.如图,在△ABC 中,∠ACB =90°,AB 的垂直平分线DE 交AB 于E ,交AC 于D ,∠DBC =30°,BD =4.6,则D 到AB 的距离为 。
第十三章 全等三角形 5.专项二 全等三角形的常见模型强化练

专项二 全等三角形的常见模型强化练
4. 新定义型阅读理解题 阅读材料,回答下列问题.筝形的定义:两组邻边 分别相等的四边形叫做筝形,几何图形的定义通常可作为图形的性质也可以作 为图形的判定方法.也就是说,如图,若四边形 ABCD 是一个筝形,则 DA=DC ,BA=BC;若 DA=DC,BA=BC,则四边形 ABCD 是筝形.如图,四边形 ABCD 是 一个筝形,其中 DA=DC,BA=BC.对角线 AC,BD 相交于点 O,过点 O 作 OE⊥AB,OF⊥BC,垂足分别为 E,F,求证:四边形 BEOF 是筝形.
专项二 全等三角形的常见模型强化练
解:(1)证明:∵AB⊥DC,∴∠ABC=∠DBE=90°,在△ABC 和△DBE 中, AB=DB,∠ABC=∠DBE,BC=BE,∴△ABC≌△DBE(SAS),∴DE=AC;
(2)题图 2:由平移变换知 EF⊥BC,EF=BC,DF=AB. ∴∠ABC=∠DFE=90°.在△DFE 和△ABC 中,EF=CB,∠DFE=∠ABC,DF=AB, ∴△DFE≌△ABC(SAS),∴DE=AC.故在题图 2 中的结论仍然成立.题图3,4 中 可类似地推证出(1)的结论也成立.
专项二 全等三角形的常见模型强化练
解决图形变换问题需要抓住的三个特点:(1)变化前后的结论及说理过程对 变化前后的结论起到重要的作用;(2)在图形变化前后,明确哪些关系发生变化 ,哪些关系没有发生变化,变化前的等角、等线段在变化后是否还存在;(3)几 种变化图形之间,说理思路存在内在联系,变化后的说理思路可模仿与借鉴变化 前的结论与过程.变化后的结论有时发生变化,有时不发生变化.
ቤተ መጻሕፍቲ ባይዱ 专项二 全等三角形的常见模型强化练
解:(2)AF∥CD,理由如下:如图,作 AG⊥BF 于点 G,AH⊥CE 于点 H,由(1)知△ABD≌△ACE,∴ 易知 AG=AH.∵∠AGF=∠AHF=90°,AF=AF, 又易知∠HAF=∠AFD,∴△AGF≌△FHA;∴AG=HF,∴AH=HF,∴ 易知 ∠HFA=45°,∴∠AFD=45°,∵∠BDC=135°,∴∠FDC=45°,∴∠AFD=∠FDC, ∴AF∥CD.
全等三角形专项练习及答案
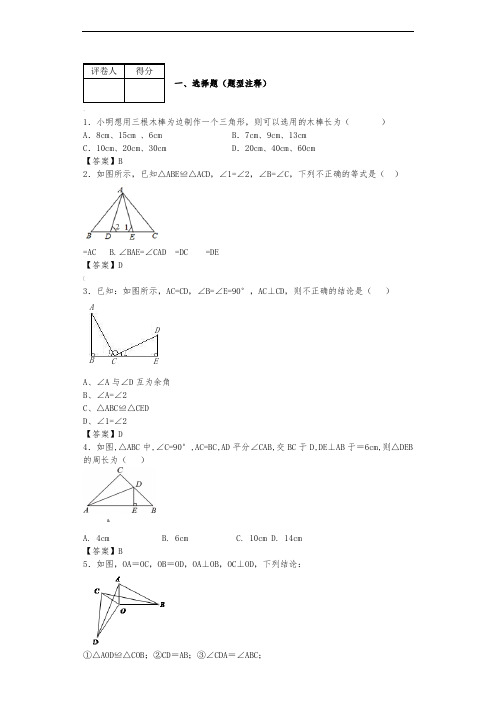
评卷人得分一、选择题(题型注释)、1.小明想用三根木棒为边制作一个三角形,则可以选用的木棒长为()A.8cm、15cm 、6cm B.7cm、9cm、13cmC.10cm、20cm、30cm D.20cm、40cm、60cm【答案】B2.如图所示,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是()=AC B.∠BAE=∠CAD =DC =DE【答案】D[3.已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A、∠A与∠D互为余角B、∠A=∠2C、△ABC≌△CEDD、∠1=∠2【答案】D4.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于=6cm,则△DEB 的周长为()A. 4cmB. 6cmC. 10cmD. 14cm【答案】B5.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC;&AB CDE1]其中正确的结论是( )A.①② B.①②③ C.①③ D.②③》【答案】B【解析】试题分析:因为OA=OC,OB=OD,OA⊥OB,OC⊥OD,可得△COD≌△AOB, ∠CDO=∠ABO;∠DOC+∠AOC=∠AOB+∠AOC, OA=OC,OB=OD,所以△AOD≌△COB,所以CD=AB,∠ADO=∠CBO;所以∠CDA=∠ABC.故①②③都正确.故选B考点:三角形全等的判定和性质6.如图,△ABC中,∠B=∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是()…A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°【答案】A【解析】试题分析:根据已知条件可证明△BDE≌△CFD,则∠BED=∠CDF,由∠A+∠B+∠C=180°,得∠B=,因为∠BDE+∠EDF+∠CDF=180°,所以得出a与∠A的关系2a+∠A=180°.考点:全等三角形的判定和性质,三角形的内角和定理7.如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则()~A.BE+CF>EFB.BE+CF=EFC.BE+CF<EFD.BE+CF与EF的大小关系不能确定.【答案】A.8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是()A.10cm B.12cm C.15cm D.17cm}【答案】C.【解析】试题分析:∵AB的垂直平分AB,∴AE=BE,BD=AD,∵AE=3cm,△ADC的周长为9cm,∴△ABC的周长是9cm+2×3cm=15cm,故选C.考点:线段垂直平分线的性质.9.如图所示,∠A+∠B+∠C+∠D+∠E的结果为()A.90° B.1 80° C.360° D.无法确定【答案】?【解析】试题分析:延长BE交AC于F,∵∠A+∠B=∠2,∠D+∠E=∠1,∠1+∠2+∠C=180°,∴∠A+∠B+∠C+∠D+∠E=180°,考点:1.三角形内角和定理;2.三角形的外角性质.10.若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()>A、36B、72C、108D、144【答案】C【解析】∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°,∵2(∠A+∠C)=3∠B,∴∠B=72°,11.如图,AB∥CD,∠D =∠E =35°,则∠B的度数为().A.60° B.65° C.70° D.75°【答案】C.~12.如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是()A .∠1+∠0=∠A+∠2B .∠1+∠2+∠A+∠O=180°C .∠1+∠2+∠A+∠O=360°D .∠1+∠2+∠A=∠O【答案】D .【解析】 试题分析:连接AO 并延长,交BC 于点D ,》∵∠BOD 是△AOB 的外角,∠COD 是△AOC 的外角,∴∠BOD=∠BAD+∠1①,∠COD=∠CAD+∠2②,①+②得,∠BOC=(∠BAD+∠CAD )+∠1+∠2,即∠BOC=∠BAC+∠1+∠2.故选D .考点:1.三角形的外角性质;2.三角形内角和定理.13.如图,BD 是∠ABC 的角平分线,DE ⊥AB 于E ,DF ⊥BC 于F ,,,,△cm 12BC cm 18AB cm 362ABC ===S 则DE 的长是( )B.cm 512 D.cm 514 ¥【答案】B【解析】试题分析:∵BD 是∠ABC 的角平分线,DE ⊥AB ,DF ⊥BC,由角平分线的性质可得DE=DF ∴DCB S S ∆∆+=ADB ABC S △=DF DE ⋅⨯+⋅⨯12211821=9DE+6DF=15DE=36∴DE=cm 512 所以选B.考点:角平分线的性质?第II卷(非选择题)请点击修改第II卷的文字说明评卷人得分~二、填空题(题型注释)14.如图,△ABC中,∠A=90°,DE是BC的垂直平分线,AD=DE,则∠C的度数是°.【答案】30°.【解析】试题分析:∵DE是BC的垂直平分线,∴DE⊥BC,∵∠A=90°,AD=DE,∴BD平分∠AABC,∴∠ABD=∠DBC,∵DE是BC的垂直平分线,∴DC=BD,∴∠C=∠DBC,∴3∠C=90°,∴∠C=30°.故答案为:30°.考点:1.线段垂直平分线的性质;2.角平分线的性质.!15.如图,在△ABC中,∠ACB=90°,AB的垂直平分线DE交AB于E,交AC于D,∠DBC=30°,BD=,则D到AB的距离为。
全等三角形专项训练及答案.解析

初中数学专项训练:全等三角形题一、选择1.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是A.AB=ADB.AC平分∠BCDC.AB=BDD.△BEC≌△DEC2.如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC ≌△DEC,不能添加的一组条件是A.BC=EC,∠B=∠EB.BC=EC,AC=DCC.BC=D,C∠A=∠DD.∠B=∠E,∠A=∠D3.如图,已知OP平分∠AOB,∠AOB=60,CP2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是A.2B.2C.3D.234.如图,在四边形ABCD中,对角线A B=AD,CB=CD,若连接A C、BD相交于【】点O,则图中全等三角形共有A.1 对B.2对C.3对D.4对5.如图,在△ABC中,AB=AC,点D、E在BC上,连接A D、AE,如果只添加()一个条件使∠DAB=∠EAC,则添加的条件不能为A.BD=CEB.AD=AEC.DA=DED.BE=CD6.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠CB.AD=CBC.BE=DFD.AD∥BC7.如图,已知△ABC中,∠ABC=9°0,AB=BC,三角形的顶点在相互平行的三l1,l2,l3上,且l1,l2之间的距离为1 , l2,l3之间的距离为2 ,条直线则AC的长是()A.26B.25C.42D.7二、填空题8.如图,已知∠C=∠D,∠ABC=∠BAD,AC与BD相交于点O,请写出图中一组相等的线段.9.如图,在Rt△ABC中,∠A=Rt∠,∠ABC的平分线B D交AC于点D,AD=3,BC=10,则△BDC的面积是。
10.如图,已知B C=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个.(答案不唯一,只需填一个)条件为11.如图,在Rt△ABC中,∠ACB=9°0,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是.12.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,.则DF的长为13.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF = CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是.(只需写一个,不添加辅助线)14.如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是。
全等三角形的证明及计算大题专项训练(30道)(含答案)

全等三角形的证明及计算大题专项训练(30道)考卷信息:本套训练卷共30题,培优篇15题,拔尖篇15题,题型针对性较高,覆盖面广,选题有深度,可深化学生对全等三角形工具的应用及构造全等三角形!1.(2021春•道里区期末)如图,点A ,C 在EF 上,AD ∥BC ,DE ∥BF ,AE =CF .(1)求证:△ADE ≌△CBF ;(2)直接写出图中所有相等的线段(AE =CF 除外).【解题思路】(1)利用ASA 证明△ADE ≌△CBF 即可;(2)根据△ADE ≌△CBF 即可得图中所有相等的线段.【解答过程】(1)证明:∵AD ∥BC∴∠DAC =∠BCA ,又∵∠DAC +∠EAD =180°,∠BCA +∠FCB =180°,∴∠EAD =∠FCB ,∵DE ∥BF ,∴∠E =∠F ,在△ADE 和△CBF 中,{∠EAD =∠FCB AE =CF ∠E =∠F,∴△ADE ≌△CBF (ASA ),(2)∵△ADE ≌△CBF ,∴ED =FB ,DA =BC ,EC =F A .∵AD ∥BC ,∴∠DAC =∠BCA ,在△ADC 和△CBA 中,{AD =CB ∠DAC =∠CBA AC =CA,∴△ADC ≌△CBA (SAS ),∴AB =CD ;∴图中所有相等的线段有:ED =FB ,DA =BC ,AB =CD ,EC =F A .2.(2021春•宁德期末)如图,AB ,CD 交于点O ,AC =DB ,∠ACD =∠DBA .(1)说明△AOC ≌△DOB 的理由;(2)若∠ACD =94°,∠CAO =28°,求∠OCB 的度数.【解题思路】(1)直接利用AAS 即可证明△AOC ≌△DOB ;(2)利用三角形外角的性质得到∠COB ,再根据△AOC ≌△DOB 得到OC =OB ,即可求得∠OCB .【解答过程】解:(1)在△AOC 和△DOB 中,{∠AOC =∠DOB ∠ACO =∠DBO AC =DB,∴△AOC ≌△DOB (AAS );(2)∵∠ACD =94°,∠CAO =28°,∴∠COB =∠ACD +∠CAO =122°,∵△AOC ≌△DOB ,∴OC =OB ,∴∠OCB =(180°﹣122°)÷2=29°.3.(2021春•沙坪坝区校级期末)如图,在△ABC 中,AC =BC ,点D 在AB 边上,点E 在BC 边上,连接CD ,DE .已知∠ACD =∠BDE ,CD =DE .(1)猜想AC 与BD 的数量关系,并证明你的猜想;(2)若AD =3,BD =5,求CE 的长.【解题思路】(1)利用AAS 证明△ADC ≌△BED ,即可得结论;(2)结合△ADC ≌△BED ,可得AC =BD =5,BE =AD =3,进而可得CE 的长.【解答过程】解:(1)AC =BD ,理由如下:∵AC =BC ,∴∠A =∠B ,在△ADC 和△BED 中,{∠A =∠B ∠ACD =∠BED CD =DE,∴△ADC ≌△BED (AAS ),∴AC =BD ;(2)由(1)知:△ADC ≌△BED ,∴AC =BD =5,BE =AD =3,∴BC =AC =5,∴CE =BC ﹣BE =2.4.(2021春•渝中区校级期末)如图,点E 在△ABC 的边AC 上,且∠ABE =∠C ,AF 平分∠BAE 交BE 于F ,FD ∥BC 交AC 于点D .(1)求证:△ABF ≌△ADF ;(2)若BE =7,AB =8,AE =5,求△EFD 的周长.【解题思路】(1)根据平行线的性质得到∠ADF =∠C ,等量代换得到∠ABF =∠ADF ,由角平分线的定义得到∠BAF =∠CAF ,根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到AD =AB =8,BF =DF ,由线段的和差得到DE =AD =AE =8﹣5=3,根据三角形的周长公式即可得到结论.【解答过程】解:(1)∵FD ∥BC ,∴∠ADF =∠C ,∵∠ABF =∠C ,∴∠ABF =∠ADF ,∵AF 平分∠BAE ,∴∠BAF =∠CAF ,在△ABF 和△ADF 中,{∠BAF =∠DAF ∠ABF =∠ADF AF =AF,∴△ABF ≌△ADF (AAS );(2)∵△ABF ≌△ADF ,∴AD =AB =8,BF =DF ,∵AE =5,∴DE =AD ﹣AE =8﹣5=3,∴△EFD 的周长=EF +DF +DE =EF +BF +DE =BE +DE =7+3=10.5.(2021春•北碚区校级期末)如图,已知D 是AC 上一点,AB =DA ,AB +DC =ED ,AE =BC .(1)求证:△ABC ≌△DAE ,(2)若∠BAE =125°,求∠DCB 的度数.【解题思路】(1)根据SSS 证明三角形全等即可.(2)利用全等三角形的性质以及三角形内角和定理求解即可.【解答过程】(1)证明:∵DE =AB +DC ,AB =AD ,∴DE =AD +DC =AC ,在△ABC 和△DAE 中,{AB =AD AC =DE BA =AE,∴△ABC ≌△DAE (SSS ).(2)解:∵△ABC ≌△DAE ,∴∠EAD =∠B ,∴∠B +∠BAC =∠EAD +∠BAC =∠EAB =125°,∴∠DCB =180°﹣(∠B +∠BAC )=180°﹣125°=55°.6.(2021春•莱芜区期末)如图,已知AD 、BC 相交于点O ,AB =CD ,AM ⊥BC 于点M ,DN ⊥BC 于点N ,BN =CM .(1)求证:△ABM ≌△DCN ;(2)试猜想OA 与OD 的大小关系,并说明理由.【解题思路】(1)根据HL 可证明:△ABM ≌△DCN ;(2)根据AAS 证明△AMO ≌△DNO 可得结论.【解答过程】(1)证明:∵BN =CM ,∴BN +MN =MN +CM ,即CN =BM ,∵AM ⊥BC 于点M ,DN ⊥BC 于点N ,∴∠AMB =∠DNC =90°,在Rt △ABM 和Rt △DCN 中,{AB =CD BM =CN, ∴Rt △ABM ≌Rt △DCN (HL );(2)解:OA =OD ,理由如下:∵Rt △ABM ≌Rt △DCN ,∴AM =DN ,在△AMO 和△DNO 中,{∠AOM =∠DNO ∠AMO =∠DNO AM =DN,∴△AMO ≌△DNO (AAS ),∴OA =OD .7.(2021春•静安区期末)如图,已知四边形ABCD 中,AB ∥CD ,AD ∥BC .E 为BD 上一点,且BE =AD ,∠DEF =∠ADC ,EF 交BC 的延长线于点F .(1)AD 和BC 相等吗?为什么?(2)BF 和BD 相等吗?为什么?【解题思路】(1)根据平行线的性质和全等三角形的判定和性质得出△ABD 与△CDB 全等,进而利用全等三角形的性质解答即可;(2)根据平行线的性质和全等三角形的判定和性质得出△EFB 与△CDB 全等,进而解答即可.【解答过程】解:(1)AD =CB ,理由如下:∵AD ∥BC ,∴∠ABD =∠CDB ,同理可得,∠ADB =∠CBD ,在△ABD 与△CDB 中,{∠ABD =∠CDB BD =DB ∠ADB =∠CBD,∴△ABD ≌△CDB (ASA ),∴AD =CB ;(2)BF =BD ,理由如下:∵AD =CB ,BE =AD ,∴BC =BE ,∵∠DEF =∠ADC ,∴∠DEF ﹣∠DBF =∠ADC ﹣∠ADB ,即∠EFB =∠CDB ,在△EFB 与△CDB 中,{∠EFB =∠CDB BC =BE ∠FBE =∠DBC,∴△EFB ≌△CDB (ASA ),∴FB =DB .8.(2021春•沙坪坝区校级月考)如图,△ABC 中,CD ⊥AB ,垂足为D .BE ⊥AC ,垂足为G ,AB =CF ,BE =AC .(1)求证:AE =AF ;(2)求∠EAF 的度数.【解题思路】(1)利用SAS 证明△AEB ≌△F AC 可证明结论;(2)由全等三角形的性质可得∠E =∠CAF ,由余角的定义可求得∠EAF 的度数.【解答过程】(1)证明:∵CD ⊥AB ,BE ⊥AC ,∴∠CAD +∠ACD =∠CAD +∠EBA =90°,∴∠ACD =∠EBA ,在△AEB 和△F AC 中,{AB =FC ∠EBA =∠ACF BE =CA,∴△AEB ≌△F AC (SAS ),∴AE =F A ;(2)解:∵△AEB ≌△F AC ,∴∠E =∠CAF ,∵∠E +∠EAG =90°,∴∠CAF +∠EAG =90°,即∠EAF =90°.9.(2021春•铁岭月考)已知:如图,AB =AC ,∠1=∠2.(1)找出图中的所有全等三角形(直接写出);(2)求证:AD =AE .【解题思路】(1)直接根据全等三角形的判定可得答案;(2)先根据SAS 证得△ABF ≌△ACF ,再根据ASA 证得△BDF ≌△CEF ,然后根据全等三角形的性质可得结论.【解答过程】解:(1)△ABF ≌△ACF ,△BDF ≌△CEF ,△ADF ≌△AEF ,△ADC ≌△AEB ;(2)证明:在△ABF 和△ACF 中,{AB =AC ∠1=∠2AF =AF,∴△ABF ≌△ACF (SAS ),∴∠B =∠C ,BF =CF .在△BDF 和△CEF 中,{∠B =∠C BF =CF ∠BFD =∠CFE,∴△BDF ≌△CEF (ASA ),∴BD =CE ,∴AB ﹣BD =AC ﹣CE ,∴AD =AE .10.(2021•南岗区模拟)已知:在△ABC 和△DBE 中,AB =DB ,BC =BE ,其中∠ABD =∠CBE .(1)如图1,求证:AC =DE ;(2)如图2,AB =BC ,AC 分别交DE ,BD 于点F ,G ,BC 交DE 于点H ,在不添加任何辅助线的情况下,请直接写出图2中的四对全等三角形.【解题思路】(1)根据SAS 证明△ABC 与△DBE 全等,利用全等三角形的性质解答即可.(2)根据全等三角形的判定解答即可.【解答过程】证明:(1)∵∠ABD =∠CBE ,∴∠ABD +∠DBC =∠CBE +∠DBC ,即∠ABC =∠DBE ,在△ABC 与△DBE 中,{AB =DB ∠ABC =∠DBE BC =BE,∴△ABC ≌△DBE (SAS ),∴AC =DE ;(2)由(1)得△ABC ≌△DBE ,∴∠A =∠D ,∠C =∠E ,AB =DB ,BC =BE ,∴AB =BE ,∵AB =BC ,∴∠A =∠C ,∴∠A =∠E ,在△ABG 与△EBH 中,{∠A =∠E AB =BE ∠ABD =∠EBC,∴△ABG ≌△EBH (ASA ),∴BG =BH ,在△DBH 与△CBG 中,{BG =BH ∠DBH =∠CBG DB =CB,∴△DBH ≌△CBG (SAS ),∴∠D =∠C ,∵DB =CB ,BG =BH ,∴DG =CH ,在△DFG 与△CFH 中,{∠DFG =∠CFH ∠D =∠C DG =CH,∴△DFG ≌△CFH (AAS ).11.(2021•三水区一模)如图,AB =AC ,直线l 过点A ,BM ⊥直线l ,CN ⊥直线l ,垂足分别为M 、N ,且BM =AN .(1)求证△AMB ≌△CNA ;(2)求证∠BAC =90°.【解题思路】(1)由HL证明△AMB≌△CNA即可;(2)先由全等三角形的性质得∠BAM=∠ACN,再由∠CAN+∠ACN=90°,得∠CAN+∠BAM=90°,即可得出结论.【解答过程】证明:(1)∵BM⊥直线l,CN⊥直线l,∴∠AMB=∠CNA=90°,在Rt△AMB和Rt△CNA中,{AB=CABM=AN,∴Rt△AMB≌Rt△CNA(HL);(2)由(1)得:Rt△AMB≌Rt△CNA,∴∠BAM=∠ACN,∵∠CAN+∠ACN=90°,∴∠CAN+∠BAM=90°,∴∠BAC=180°﹣90°=90°.12.(2021•广州模拟)如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.(1)求证:△BCE≌△CAD;(2)若BE=5,DE=7,则△ACD的周长是30.【解题思路】(1)根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC;(2)利用(1)中结论,根据全等三角形的性质即可解决问题;【解答过程】(1)证明:∵BE ⊥CE ,AD ⊥CE ,∴∠E =∠ADC =90°,∴∠EBC +∠BCE =90°.∵∠BCE +∠ACD =90°,∴∠EBC =∠DCA .在△BCE 和△CAD 中,{∠E =∠ADC ∠EBC =∠DCA BC =AC,∴△BCE ≌△CAD (AAS );(2)解:∵:△BCE ≌△CAD ,BE =5,DE =7,∴BE =DC =5,CE =AD =CD +DE =5+7=12.∴由勾股定理得:AC =13,∴△ACD 的周长为:5+12+13=30,故答案为:30.13.(2020春•越秀区校级期中)已知:△ABN 和△ACM 的位置如图所示,∠1=∠2,AB =AC ,AM =AN . 求证:(1)∠BAN =∠CAM ;(2)∠ODA =∠OEA .【解题思路】(1)由∠1=∠2,则∠1+∠MAN =∠2+∠MAN ,即∠BAN =∠CAM ;(2)先证△ACM ≌△ABN (SAS ),得∠M =∠N ,再证△ADN ≌△AEM (ASA ),即可得出结论.【解答过程】证明:(1)∵∠1=∠2,∴∠1+∠MAN =∠2+∠MAN ,即∠BAN =∠CAM ;(2)在△ACM 和△ABN 中,{AM =AN ∠CAM =∠BAN AC =AB,∴△ACM ≌△ABN (SAS ),∴∠M =∠N ,在△ADN 和△AEM 中,{∠DAN =∠EAM AN =AM ∠N =∠M,∴△ADN ≌△AEM (ASA ),∴∠NDA =∠MEA ,即∠ODA =∠OEA .14.(2020•江北区模拟)如图,在△ABC 中,AD 是BC 边上的中线,E 是AB 边上一点,过点C 作CF ∥AB ,交ED 的延长线于点F .(1)求证:△BDE ≌△CDF ;(2)当AD ⊥BC ,AE =2,CF =1时,求AC 的长.【解题思路】(1)根据平行线的性质得到∠B =∠FCD ,∠BED =∠F ,由AD 是BC 边上的中线,得到BD =CD ,于是得到结论;(2)根据全等三角形的性质得到BE =CF =1,求得AB =AE +BE =3,于是得到结论.【解答过程】证明:∵CF ∥AB ,∴∠B =∠FCD ,∠BED =∠F ,∵AD 是BC 边上的中线,∴BD =CD ,在△BDE 和△CDF 中,{∠B =∠FCD ∠BED =∠F BD =CD,∴△BDE ≌△CDF (AAS );(2)∵△BDE ≌△CDF ,∴BE =CF =1,∴AB =AE +BE =2+1=3,∵AD ⊥BC ,BD =CD ,∴AC =AB =3.15.(2020秋•萧山区月考)如图,已知在△ABC 中,BD ⊥AC 于D ,CE ⊥AB 于E ,F 是BD 上一点,BF =AC ,G 是CE 延长线上一点,CG =AB ,连接AG ,AF .(1)试说明∠ABD =∠ACE ;(2)探求线段AF ,AG 有什么关系?并请说明理由.【解题思路】(1)根据的等角的余角相等,即可证明∠ACG =∠ABF ;(2)根据SAS 推出△ABF ≌△GCA 即可解决问题;【解答过程】(1)证明:∵BD 、CE 是△ABC 的高,∴∠ADB =∠AEC =90°,∴∠ABF +∠BAD =90°,∠GCA +∠BAD =90°,∴∠ABF =∠GCA ,(2)结论:AF =AG ,AF ⊥AG .理由如下:在△ABF 和△GCA 中,{AB =CG ∠ABF =∠GCA BF =AC,∴△ABF ≌△GCA (SAS ),∴AF =AG ,∠GAC =∠AFB ,∵∠AFB=∠ADB+∠F AD,∠GAC=∠GAF+∠F AD,∴∠GAF=∠ADF,∵∠ADF=90°,∴∠GAF=90°,∴AG⊥AF,AG=AF.16.(2021•张家界模拟)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE(1)求证:△ABE≌△BCD;(2)判断线段AE与BD的数量关系及位置关系,并说明理由;(3)若CD=1,试求△AED的面积.【解题思路】(1)由平行线的性质得出∠ABE+∠C=180°,得出∠ABE=90°=∠C,再证出BE=CD,由SAS证明△ABE≌△BCD即可;(2)由全等三角形的性质得出AE=BD,证出∠ABF+∠BAE=90°,得出∠AFB=90°,即可得出结论;(3)由全等三角形的性质得出BE=CD=1,求出CE=BC﹣BE=1,得出CE=CD,△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积,即可得出答案.【解答过程】(1)证明:∵AB∥CD,∴∠ABE+∠C=180°,∵∠C=90°,∴∠ABE=90°=∠C,∵E是BC的中点,∴BC=2BE,∵BC=2CD,∴BE=CD,在△ABE和△BCD中,{AB=BC∠ABE=∠CBE=CD,∴△ABE≌△BCD(SAS);(2)解:AE=BD,AE⊥BD,理由如下:由(1)得:△ABE≌△BCD,∴AE=BD,∵∠BAE=∠CBD,∠ABF+∠CBD=90°,∴∠ABF+∠BAE=90°,∴∠AFB=90°,∴AE⊥BD;(3)解:∵△ABE≌△BCD,∴BE=CD=1,∵AB=BC=2CD=2,∴CE=BC﹣BE=1,∴CE=CD,∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=12(1+2)×2−12×2×1−12×1×1=3 2.17.(2020秋•台江区校级期中)如图,A,B,C三点共线,D,C,E三点共线,∠A=∠DBC,EF⊥AC 于点F,AE=BD.(1)求证:C是DE的中点;(2)求证:AB=2CF.【解题思路】(1)过D 作DH ⊥AC 的延长线与H ,根据全等三角形的判定证得△AEF ≌△BDH ,得到EF =DH ,再证得△EFC ≌△DHC 得到CE =CD ,即可证得即可证得结论;(2)由(1)得,△AEF ≌△BDH ,△EFC ≌△DHC ,根据全等三角形的性质得到AF =BH ,CF =CH ,再根据线段的和差即可证得结论.【解答过程】证明:(1)过D 作DH ⊥AC 的延长线与H ,∴∠EFC =∠DHC =90°,在△AEF 和△BDH 中,{∠A =∠DBC ∠AFE =∠BHD =90°AE =BD,∴△AEF ≌△BDH (AAS ),∴EF =DH ,在△EFC 和△DHC 中,{∠FCE =∠HCD ∠EFC =∠DHC =90°EF =DH,∴△EFC ≌△DHC (AAS ),∴CE =CD ,∴C 是DE 的中点;(2)由(1)得,△AEF ≌△BDH ,△EFC ≌△DHC ,∴AF =BH ,CF =CH ,∴AB +BF =BF +FH ,FH =2FC ,∴AB =FH ,∴AB =2CF .18.(2021春•铁岭月考)如图,△AOC 和△BOD 中,OA =OC ,OB =OD ,∠AOC =∠BOD =α(0<α<90°),AD 与BC 交于点P .(1)求证:△AOD ≌△COB ;(2)求∠APC (用含α的式子表示);(3)过点O 分别作OM ⊥AD ,ON ⊥BC ,垂足分别为点M 、N ,请直接写出OM 和ON 的数量关系.【解题思路】(1)由∠AOC =∠BOD ,可得∠AOD =∠COB ,然后根据SAS 可得结论;(2)根据全等三角形的性质得∠OAD =∠OCB ,再根据三角形外角性质可得答案;(3)根据全等三角形的性质得∠MAO =∠NCO ,由垂直定义得∠AMO =∠CNO ,再根据全等三角形的判定与性质可得结论.【解答过程】解:(1)∵∠AOC =∠BOD ,∴∠AOC +∠COD =∠BOD +∠COD ,∴∠AOD =∠COB ,在△AOD 和△COB 中,{OA =OC ∠AOD =∠COB OD =OB,∴△AOD ≌△COB (SAS );(2)由(1)可知△AOD ≌△COB ,∴∠OAD =∠OCB ,令AD 与OC 交于点E ,则∠AEC =∠OAD +∠AOC =∠OCB +∠APC ,∴∠AOC =∠APC ,∵∠AOC =α,∴∠APC =α;(3)∵△AOD ≌△COB ,∴∠P AP =∠BCO ,即∠MAO =∠NCO ,∵OM ⊥AD ,ON ⊥BC ,∴∠AMO =∠CNO =90°,在△AOM 和△CON 中,{∠MAO =∠NCO ∠AMO =∠CNO OA =OC,∴△AOM ≌△CON (AAS ),∴OM =ON .19.(2020秋•花都区月考)如图所示,BD 、CE 是△ABC 的高,点P 在BD 的延长线上,CA =BP ,点Q 在CE 上,QC =AB .(1)探究P A 与AQ 之间的关系;(2)若把(1)中的△ABC 改为钝角三角形,AC >AB ,∠A 是钝角,其他条件不变,上述结论是否成立?画出图形并证明你的结论.【解题思路】(1)由条件可得出∠1=∠2,可证得△APB ≌△QAC ,可得结论;(2)根据题意画出图形,结合(1)可证得△APB ≌△QAC ,可得结论.【解答过程】(1)结论:AP =AQ ,AP ⊥AQ 证明:∵BD 、CE 是△ABC 的高, ∴BD ⊥AC ,CE ⊥AB ,∴∠1+∠CAB =90°,∠2+∠CAB =90°, ∴∠1=∠2,在△QAC 和△APB 中,{QC =AB ∠1=∠2CA =BP,∴△QAC ≌△APB (SAS ),∴AQ =AP ,∠QAC =∠P ,而∠DAP +∠P =90°,∴∠DAP +∠QAC =90°,即∠QAP =90°,∴AQ ⊥AP ;即AP =AQ ,AP ⊥AQ ;(2)上述结论成立,理由如下:如图所示:∵BD 、CE 是△ABC 的高,∴BD ⊥AC ,CE ⊥AB ,∴∠1+∠CAE =90°,∠2+∠DAB =90°, ∵∠CAE =∠DAB ,∴∠1=∠2,在△QAC 和△APB 中,{QC =AB ∠1=∠2CA =BP,∴△QAC ≌△APB (SAS ),∴AQ =AP ,∠QAC =∠P ,∵∠PDA =90°,∴∠P +∠P AD =90°,∴∠QAC +∠P AD =90°,∴∠QAP =90°,∴AQ ⊥AP ,即AP =AQ ,AP ⊥AQ .20.(2020春•萍乡期末)在△ABC 中,AB =AC ,D 是直线BC 上一点,以AD 为一边在AD 的右侧作△ADE ,使AE =AD ,∠DAE =∠BAC ,连接CE ,设∠BAC =∠1,∠DCE =∠2.(1)如图①,当点D 在线段BC 上移动时,试说明:∠1+∠2=180°;(2)如图②,当点D 在线段BC 的延长线上移动时,请猜测∠1与∠2有怎样的数量关系?并说明理由.【解题思路】(1)由“SAS ”可证△BAD ≌△CAE ,可得∠ACE =∠ABD ,由三角形的内角和定理可得结论;(2)由“SAS ”可证△BAD ≌△CAE ,可得∠ACE =∠ABD ,由三角形的内角和定理和平角的定义可得结论.【解答过程】证明:(1)∵∠DAE =∠BAC ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,{AB =AC ∠BAD =∠CAE AD =AE,∴△BAD ≌△CAE (SAS ),∴∠ACE =∠ABD ,∵∠BAC +∠ABD +∠ACB =180°,∴∠BAC +∠ACB +∠ACE =∠BAC +∠BCE =180°,∴∠1+∠2=180°;(2)∠1=∠2,理由如下:∵∠DAE =∠BAC ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,{AB =AC ∠BAD =∠CAE AD =AE,∴△BAD ≌△CAE (SAS ),∴∠ACE =∠ABD ,∵∠BAC +∠ABD +∠ACB =180°,∠ACE +∠ACB +∠DCE =180°,∴∠1=∠2.21.(2020春•揭阳期末)已知△ABC ,点D 、F 分别为线段AC 、AB 上两点,连接BD 、CF 交于点E .(1)若BD ⊥AC ,CF ⊥AB ,如图1所示,试说明∠BAC +∠BEC =180°;(2)若BD 平分∠ABC ,CF 平分∠ACB ,如图2所示,试说明此时∠BAC 与∠BEC 的数量关系;(3)在(2)的条件下,若∠BAC =60°,试说明:EF =ED .【解题思路】(1)根据余角的性质得到∠DEC =∠BAC ,由于∠DEC +∠BEC =180°,即可得到结论;(2)根据角平分线的性质得到∠EBC =12∠ABC ,∠ECB =12∠ACB ,于是得到结论;(3)作∠BEC 的平分线EM 交BC 于M ,由∠BAC =60°,得到∠BEC =90°+12∠BAC =120°,求得∠FEB =∠DEC =60°,根据角平分线的性质得到∠BEM =60°,推出△FBE ≌△EBM ,根据全等三角形的性质得到EF =EM ,同理DE =EM ,即可得到结论.【解答过程】解:(1)∵BD ⊥AC ,CF ⊥AB ,∴∠DCE +∠DEC =∠DCE +∠F AC =90°,∴∠DEC =∠BAC ,∠DEC +∠BEC =180°,∴∠BAC +∠BEC =180°;(2)∵BD 平分∠ABC ,CF 平分∠ACB ,∴∠EBC =12∠ABC ,∠ECB =12∠ACB ,∠BEC =180°﹣(∠EBC +∠ECB )=180°−12(∠ABC +∠ACB )=180°−12(180°﹣∠BAC )=90°+12∠BAC ;(3)作∠BEC 的平分线EM 交BC 于M ,∵∠BAC =60°,∴∠BEC =90°+12∠BAC =120°,∴∠FEB =∠DEC =60°,∵EM 平分∠BEC ,∴∠BEM =60°,在△FBE 与△EBM 中,{∠FBE =∠EBM BE =BE ∠FEB =∠MEB,∴△FBE ≌△EBM (ASA ),∴EF =EM ,同理DE =EM ,∴EF =DE .22.(2020秋•淇滨区校级期中)(1)如图1所示,△ACB 和△ECD 都是等腰三角形,A 、C 、D 三点在同一直线上,连接BD 、AE ,并延长AE 交BD 于点F ,试判断AE 与BD 的数量关系及位置关系,并证明你的结论.(2)若△ECD 绕顶点C 顺时针转任意角度后得到图2,图1中的结论是否仍然成立?请说明理由.【解题思路】(1)根据SAS 推出△ACE ≌△BCD ,根据全等三角形的性质得出∠CAE =∠DBC ,根据∠ACB =90°求出∠CAE +∠AEC =90°,求出∠DBC +∠BEF =90°,根据三角形内角和定理求出∠BFE =90°即可;(2)根据SAS 推出△ACE ≌△BCD ,根据全等三角形的性质得出∠CAE =∠DBC ,根据∠ACB =90°求出∠CAE +∠AOC =90°,求出∠DBC +∠BOE =90°,根据三角形内角和定理求出∠BFO =90°即可.【解答过程】(1)AE ⊥BD .证明:在△ACE 和△BCD 中{AC =BC ∠ACE =∠BCD CE =CD∴△ACE ≌△BCD (SAS ),∴∠CAE =∠DBC ,∵∠ACB =90°,∴∠CAE +∠AEC =90°,∵∠CAE =∠DBC ,∠AEC =∠BEF ,∴∠DBC +∠BEF =90°,∴∠BFE =180°﹣90°=90°,∴AE ⊥BD ;(2)解:结论还成立,理由是:∵∠ACB =∠ECD ,∴∠ACB +∠BCE =∠ECD +∠BCE ,即∠ACE =∠BCD ,在△ACE 和△BCD 中{AC =BC ∠ACE =∠BCD CE =CD∴△ACE≌△BCD(SAS),∴∠CAE=∠DBC,∵∠ACB=90°,∴∠CAE+∠AOC=90°,∵∠CAE=∠DBC,∠AOC=∠BOE,∴∠DBC+∠BOE=90°,∴∠BFO=180°﹣90°=90°,∴AE⊥BD.23.(2020秋•蒙阴县期中)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕着点C旋转到如图1所示的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕着点C旋转到如图2所示的位置时,①找出图中一对全等三角形;②DE、AD、BE之间有怎样的数量关系,并加以证明.【解题思路】(1)根据余角和补角的性质易证得∠DAC=∠ECB,已知∠ADC=∠CEB=90°,AC=CB,根据全等三角形的判定AAS即可证明△ADC≌△CEB,根据各边的相等关系即可得DE=AD+BE.(2)同理可证得△ADC≌△CEB,再根据各边的相等关系可得DE=AD﹣BE.【解答过程】(1)证明:∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠ACD+∠BCE=180°﹣90°=90°,∴∠DAC=∠ECB;在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB,∴△ADC≌△CEB(AAS)①,(7分)∴DC=EB,AD=CE,∴DE=AD+BE.(9分)(2)解:同理可得△ADC≌△CEB①;(11分)∴AD=CE,CD=BE,∴DE=AD﹣BE②.(14分)24.(2018秋•环翠区期末)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF=12∠BAD,可求得EF、BE、FD之间的数量关系为BE+DF=EF.(只思考解题思路,完成填空即可,不必书写证明过程)(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF=12∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【可借鉴第(1)问的解题经验】【解题思路】(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图1中,延长CB至M,使BM =DF,连接AM,利用全等三角形的性质解决问题即可.(2)结论:EF+DF=BE.如图2中,在BE上截取BM=DF,连接AM,证明△ABM≌△ADF(SAS),推出AM=AF,∠BAM=∠DAF,再证明△AEM≌△AEF(SAS),可得结论.【解答过程】解:(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图1,延长CB至M,使BM=DF,连接AM,∵∠ABC +∠D =180°,∠ABC +∠1=180°,∴∠1=∠D ,在△ABM 和△ADF 中,{AB =AD ∠1=∠D BM =DF,∴△ABM ≌△ADF (SAS ),∴AM =AF ,∠3=∠2,∵∠EAF =12∠BAD ,∴∠4+∠4=∠EAF ,∴∠GAM =∠3+∠4=∠2+∠4=∠EAF ,在△MAE 和△F AE 中,{AM =AF ∠MAE =∠FAE AE =AE,∴△MAE ≌△F AE (SAS ),∴EF =EM ,∵EM =BM +BE =BE +DF ,∴EF =BE +FD ;故答案为:BE +DF =EF .(2)结论:EF +DF =BE .理由:在BE 上截取BM =DF ,连接AM ,∵∠B +∠ADC =180°,∠ADC +∠ADE =180°,∴∠B =∠ADF ,在△ABM 与△ADF 中,{BM =DF ∠ABM =∠ADF AB =AD,∴△ABM ≌△ADF (SAS ),∴AM =AF ,∠BAM =∠DAF ,∵∠EAF =12∠BAD ,∴∠EAF =∠EAM ,在△AEM 与△AEF 中,{AM =AF ∠EAF =∠EAM AE =AE,∴△AEM ≌△AEF (SAS ),∴EM =EF ,即BE ﹣BM =EF ,即BE ﹣DF =EF ,∴EF +DF =BE .25.(2021春•和平区期末)如图,在△ABC 中,AC =BC ,点D 在边AB 上,AB =4BD ,连接CD ,点E ,F 在线段CD 上,连接BF ,AE ,∠BFC =∠AEC =180°﹣∠ACB .(1)①∠FBC 与∠ECA 相等吗?说明你的理由;②△FBC 与△ECA 全等吗?说明你的理由;(2)若AE =11,EF =8,则请直接写出BF 的长为 3 ;(3)若△ACE 与△BDF 的面积之和为12,则△ABC 的面积为 48 .【解题思路】(1)①连接BC ,由已知及∠AEC =180°﹣∠AED ,可得到∠ACB =∠AED .再证明∠CAE =∠BCF ,由三角形内角和定理可得∠FBC =∠ECA ;②利用“ASA ”证明△FBC ≌△ECA ;(2)由(1)中全等三角形的结论及已知可得到BF 的长;(3)由(1)中结论可得S △FBC =S △ECA ,所以S △ECA +S △BDF =12=S △FBC +S △BDF =S △DBC ,根据AB =4BD ,可得到S △DBC =14S △ABC =12,从而可得△ABC 的面积.【解答过程】解:(1)①∠FBC =∠ECA ,理由如下:连接BC ,如右图.∵∠BFC =∠AEC =180°﹣∠ACB ,且∠AEC =180°﹣∠AED ,∴∠ACB =∠AED .由外角定理可得∠AED =∠ACD +∠CAE ,又∠ACB =∠ACD +∠BCF ,∴∠CAE =∠BCF ,由三角形内角和定理可得∠FBC =∠ECA .②△FBC 与△ECA 全等,理由如下:在△FBC 和△ECA 中,{∠FBC =∠ECA BC =CA ∠BCF =∠CAE,∴△FBC ≌△ECA (ASA ).(2)由(1)中②可知,FC =AE =11,BF =CE ,又EF =8,∴CE =FC ﹣EF =11﹣8=3,∴BF =3,故答案为:3.(3)由(1)中结论可知S△FBC=S△ECA,∴S△ECA+S△BDF=12=S△FBC+S△BDF=S△DBC,又AB=4BD,∴S△DBC=14S△ABC=12,∴S△ABC=48.故答案为:48.26.(2020•岱岳区一模)已知∠ABC=90°,点D是直线AB边上的点,AD=BC.(1)如图1,点D在线段AB上,过点A作AF⊥AB,且AF=BD,连接DC、DF、CF,试判断△CDF 的形状并说明理由;(2)如图2,点D在线段AB的延长线上,点F在点A的左侧,其他条件不变,以上结论是否仍然成立?请说明理由.【解题思路】(1)利用SAS证明△F AD≌△DBC,再利用全等三角形的性质得出FD=DC,即可判断三角形的形状;(2)利用SAS证明△F AD和△DBC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出结论.【解答过程】(1)△CDF是等腰直角三角形,理由如下:∵AF⊥AB,∴∠A=90°,在△F AD和△DBC中,∵{AF=BD∠A=∠B=90°AD=BC,∴△F AD≌△DBC(SAS),∴∠ADF=∠BCD,DF=DC,∵∠BDC+∠BCD=90°,∴∠ADF+∠CDB=90°,∴∠FDC=180°﹣90°=90°,又∵DF=DC,∴△CDF是等腰直角三角形;(2)仍然成立,理由如下:∵AF⊥AB,∴∠A=90°,在△F AD和△DBC中,∵{AF=BD∠A=∠DBC=90°AD=BC,∴△F AD≌△DBC(SAS),∴∠ADF=∠BCD,DF=DC,∵∠BDC+∠BCD=90°,∴∠ADF+∠BDC=90°,即∠FDC=90°,又∵DF=DC,∴△CDF是等腰直角三角形.27.如图(1),线段AD∥BC,连接AB、CD,取CD中点E,连接AE,AE平分∠BAD.(1)线段AB与AD、BC之间存在怎样的等量关系?请说明理由.(2)如果点C在AB的左侧,其他条件不变,如图(2)所示,那么(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出新的结论,并说明理由.【解题思路】(1)延长AE ,BF 交于点F ,即可求证△ADE ≌△FCE ,即可求得CF =AD ,AB =BF ,即可求得AB =AD +BC ;(2)不成立,新的结论为:AB +BC =AD .延长AE ,BF 交于点F ,可证△ADE ≌△FCE 和AB =BF ,即可解题.【解答过程】解:(1)延长AE ,BF 交于点F ,∵AE 平分∠BAD ,∴∠BAF =∠DAF ,∵AD ∥BC ,∴∠AFB =∠DAF ,∴AB =BF ,在△ADE 和△FCE 中,{∠DAE =∠EFC ∠AED =∠FEC DE =CE,∴△ADE ≌△FCE (AAS ),∴CF =AD ,∵BF =BC +CF ,∴AB =BC +AD ;(2)不成立,新结论为:AB =AD ﹣BC .延长AE ,BF 交于点F ,证明:∵AE 平分∠BAD ,∴∠BAF =∠DAF ,∵AD ∥BC ,∴∠AFB =∠DAF ,∴AB =BF ,在△ADE 和△FCE 中,{∠DAE =∠EFC ∠AED =∠FEC DE =CE,∴△ADE ≌△FCE (AAS ),∴CF =AD ,∵BF +BC =CF ,∴AB +BC =AD .28.(2021春•章丘区期末)如图,CD 是经过∠BCA 顶点C 的一条直线,CA =CB ,E 、F 分别是直线CD 上两点,且∠BEC =∠CF A =α.(1)若直线CD 经过∠BCA 的内部,且E 、F 在射线CD 上.①如图1,若∠BCA =90°,α=90°,则BE = CF ;②如图2,若0°<∠BCA <180°,请添加一个关于α与∠BCA 关系的条件 α+∠BCA =180° ,使①中的结论们然成立,并说明明理由;(2)如图3,若线CD 经过∠BCA 的外部,a =∠BCA ,请提出关于EF ,BE ,AF 三条线段数量关系的合理猜想,并简述理由.【解题思路】(1)由∠BCA =90°,∠BEC =∠CF A =α=90°,可得∠CBE =∠ACF ,从而可证△BCE ≌△CAF ,故BE =CF .(2)若BE =CF ,则可使得△BCE ≌△CAF .根据题目已知条件添加条件,再使得一对角相等,△BCE ≌△CAF 便可得证.(3)题干已知条件可证△BCE ≌△CAF ,故BE =CF ,EC =F A ,从而可证明EF =BE +AF .【解答过程】解:(1)∵∠BEC =∠CF A =α=90°,∴∠BCE +∠CBE =180°﹣∠BEC =90°.又∵∠BCA =∠BCE +∠ACF =90°,∴∠CBE =∠ACF .在△BCE 和△CAF 中,{∠BEC =∠CFA ,∠CBE =∠ACF ,BC =AC .∴△BCE ≌△CAF (AAS ).∴BE =CF .(2)α+∠BCA =180°,理由如下:∵∠BEC =∠CF A =α,∴∠BEF =180°﹣∠BEC =180°﹣α.又∵∠BEF =∠EBC +∠BCE ,∴∠EBC +∠BCE =180°﹣α.又∵α+∠BCA =180°,∴∠BCA =180°﹣α.∴∠BCA =∠BCE +∠ACF =180°﹣α.∴∠EBC =∠FCA .在△BCE 和△CAF 中,{∠CBE =∠ACF ,∠BEC =∠CFA ,BC =CA .∴△BCE ≌△CAF (AAS ).∴BE =CF .(3)EF =BE +AF ,理由如下:∵∠BCA =α,∴∠BCE +∠ACF =180°﹣∠BCA =180°﹣α.又∵∠BEC =α,∴∠EBC +∠BCE =180°﹣∠BEC =180°﹣α.∴∠EBC =∠FCA .在△BEC 和△CF A 中,{∠EBC =∠FCA ,∠BEC =∠FCA ,BC =CA .∴△BEC ≌△CF A (AAS ).∴BE =CF ,EC =F A .∴EF =EC +CF =F A +BE ,即EF =BE +AF .29.(2020春•南岸区期末)在∠MAN 内有一点D ,过点D 分别作DB ⊥AM ,DC ⊥AN ,垂足分别为B ,C .且BD =CD ,点E ,F 分别在边AM 和AN 上.(1)如图1,若∠BED =∠CFD ,请说明DE =DF ;(2)如图2,若∠BDC =120°,∠EDF =60°,猜想EF ,BE ,CF 具有的数量关系,并说明你的结论成立的理由.【解题思路】(1)根据题目中的条件和∠BED =∠CFD ,可以证明△BDE ≌△CDF ,从而可以得到DE =DF ;(2)作辅助线,过点D 作∠CDG =∠BDE ,交AN 于点G ,从而可以得到△BDE ≌△CDG ,然后即可得到DE =DG ,BE =CG ,再根据题目中的条件可以得到△EDF ≌△GDF ,即可得到EF =GF ,然后即可得到EF ,BE ,CF 具有的数量关系.【解答过程】解:(1)∵DB ⊥AM ,DC ⊥AN ,∴∠DBE =∠DCF =90°,在△BDE 和△CDF 中,∵{∠BED =∠CFD ,∠DBE =∠DCF ,BD =CD ,∴△BDE ≌△CDF (AAS ).∴DE =DF ;(2)EF =FC +BE ,理由:过点D 作∠CDG =∠BDE ,交AN 于点G ,在△BDE 和△CDG 中,{∠EBD =∠GCD BD =CD ∠BDE =∠CDG,∴△BDE ≌△CDG (ASA ),∴DE =DG ,BE =CG .∵∠BDC =120°,∠EDF =60°,∴∠BDE +∠CDF =60°.∴∠FDG =∠CDG +∠CDF =60°,∴∠EDF =∠GDF .在△EDF 和△GDF 中,{DE =DG ∠EDF =∠GDF DF =DF,∴△EDF ≌△GDF (SAS ).∴EF =GF ,∴EF=FC+CG=FC+BE.30.(2021春•揭东区期末)已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.(1)如图1,求证:△ACE≌△DCB.(2)如图1,若∠ACD=60°,则∠AFB=120°;如图2,若∠ACD=90°,则∠AFB=90°;(3)如图3,若∠ACD=β,则∠AFB=180°﹣β(用含β的式子表示)并说明理由.【解题思路】(1)求出∠ACE=∠DCB,根据SAS证出两三角形全等即可;(2)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB =180°﹣(∠EAB+∠DBC),代入求出即可;(3)根据全等三角形性质得出∠AEC=∠DBC,∠CDB=∠CAE,求出∠EAB+∠DBA=∠ACD,∠AFB =180°﹣(∠EAB+∠DBC),代入求出即可.【解答过程】(1)证明:∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE,∴∠ACE=∠DCB,在△ACE和△DCB中∵{AC=CD∠ACE=∠DCB CE=CB,∴△ACE≌△DCB;(2)解:∵∠ACD=60°,∴∠CDB+∠DBC=∠ACD=60°,∵△ACE≌△DCB,∴∠AEC=∠DBC,∠CDB=∠CAE,∴∠CAE+∠DBC=60°,∴∠AFB=180°﹣60°=120°;当∠ACD=90°时,∵∠ACD=90°,∴∠CDB+∠DBC=∠ACD=90°,∵△ACE≌△DCB,∴∠AEC=∠DBC,∠CDB=∠CAE,∴∠CAE+∠DBC=90°,∴∠AFB=180°﹣90°=90°;故答案为:120°,90°;(3)解:当∠ACD=β时,∠AFB=180°﹣β,理由是:∵∠ACD=β,∴∠CDB+∠DBC=∠ACD=β,∵△ACE≌△DCB,∴∠AEC=∠DBC,∠CDB=∠CAE,∴∠CAE+∠DBC=β,∴∠AFB=180°﹣(∠CAE+∠DBC)=180°﹣β;故答案为:180°﹣β.。
三角形全等的判定专项练习题

BcDE1234图2A图1DcBA43FBcDE图3AODcAE FDB CA第8题三角形全等的判定专项练习题一、填空题:1、如图,已知∠3=∠4,要说明△ABC≌△DCB,(1)若以“SAS”为依据,则需添加一个条件是;(2)若以“AAS”为依据,则需添加一个条件是;(3)若以“ASA”为依据,则需添加一个条件是。
2、如图,若∠1=∠2,,3=∠4,则图中共有全等三角形对,它们分别是3F在一条直线上,AB∥DE,AC DF,AC=DE,若BE=3cm,则CF=4、若DEFABC∆≅∆,△DEF周长为28 cm,DE=9 cm,EF=12 cm,则AB= ,BC=5、已知DEFABC∆≅∆,∠A=52°,∠B=31°,ED=10,那么∠F= ,AB=6、如图,在△ABC和△DEF中,AB∥DE,可以推出= ,然后加上条件AB=DE和可得到DEFABC∆≅∆,根据是7、如图,△ABD≌△ACD,AD、BC交于点D,则∠ABD= .84,则△≌△,根据是9、如图,∠xoy,分别在ox,oy上截取OA=OB,OC=OD。
连AD、BC相交于E点。
则射线OE与∠xoy的关系为。
10、如图,AB=CD,AD=CB,O为AC上一点,过O任作直线EF分别交AD、BC于E、F,要使BE=FD,则应满足的条件是。
11、等边△ABC中,D、E为BC、AC上两点,且BD=CE,连AD、BE交于O,则∠DOE= .二、选择题:12、已知△ABC≌△DEF,若∠A=500,∠C=300,则∠E的度数为()A、300B、500C、600D、100013、如图,若AC=BD,AB=DC,则图中全等三角形的对数是()A、1对B、2对C、3对D、4对14、如图,在△ABC中,AD是△BAC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,下面给出四个结论:①DA平分∠EDF;②AE=AF;③AD⊥BC;④BD=CD,其中正确的结论有()A、1个B、2个C、3个D、4个第6题CDE第7题AB CD第11题第10题第9题第1题第2题第3题15、下列说法正确的是()⑴形状相同的两个图形是全等形⑵对应角相等的两个三角形是全等形⑶全等三角形的面积相等⑷若DEFABC∆≅∆,MNPDEF∆≅∆,则MNPABC∆≅∆A、0个B、1个C、2个D、3个16、若BCDABC∆≅∆,AB=6cm,BD=7cm,AD=4cm,那么BC的长为()A、6 cmB、5 cmC、4cmD、不能确定17、若AD=BC,∠A=∠B,直接能利用“SAS”证得△ADF ≌△BCE的条件是()A、AE=BFB、DF=CEC、AF=BED、∠CEB=∠DFA18、下列能够确定△ABC的形状和大小的是()A、AB=4,BC=5,∠C=60°B、AB=6,∠C=60°,∠B=70°C、∠C=60°,∠B=70°,∠A=50°D、AB=4,BC=5,CA=1019、如图所示,已知OA=OB,则再加上下列哪个条件后,不能..判断△AOC≌△BOD的是()A、∠A=∠B B、∠C=∠DC、AC=BDD、OC=OD20、如图所示,已知AB=AC,BD=CE,则图中共有()组全等三角形A、4B、5C、6D、721、以下能够判定两个直角三角形全等的情况有()⑴两个锐角和一个锐角的对边对应相等⑵⑶一个锐角和它的对边对应相等⑷两条直角边对应相等⑸两边对应相等⑹斜边和一条直角边相等A、3B、4C、5D、622、如图,A在DE上,F在DC上,且∠1=∠2=∠3,AC=CE,则DE的等于()A.DCB.BCC.ABD.123、下列几个命题中正确的个数有()①全等三角形对应边高线相等②两边和其中一边上的高线对应的两个三角形全等③两边和第三边上的高对应相等的两个三角形全等④两边上的高对应相等的两个三角形全等A.1个B.2个C.3个D.4个24、△ABC中,AB=AC,E在BC上,D在AE上。
人教新版 八年级(上)数学 第12章 全等三角形 专项训练(含解析)

八年级(上)数学第12章全等三角形专项训练一.选择题(共10小题)1.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=()A.150°B.120°C.90°D.60°2.如图,AC与DB交于点O,下列条件不能证明△ABC≌△DCB的是()A.AB=DC,AC=DB B.∠A=∠D,∠ABC=∠DCBC.BO=CO,∠A=∠D D.AB=DC,∠ACB=∠DBC3.如图,△ABC≌△CDE,则线段AC和线段CE的关系是()A.既不相等也不互相垂直B.相等但不互相垂直C.互相垂直但不相等D.相等且互相垂直4.小明同学有一块玻璃的三角板,不小心掉到地上碎成了三块,现要去文具店买一块同样的三角板,最省事的是()A.带②去B.带①去C.带③去D.三块都带去5.在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是()A.3个B.4个C.6个D.7个6.如图,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是()A.∠B=∠D B.BC=DE C.∠1=∠2D.AB=AD7.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是()A.AD平分BC B.AD平分∠CAB C.AD平分∠CDB D.AD⊥BC8.如图,已知在△ABC中,AB=AC,∠A=50°,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于()A.55°B.60°C.65°D.70°9.如图,在△ABC中,AB=AC,BD=CD,点E,F是AD上的任意两点.若BC=8,AD=6,则图中阴影部分的面积为()A.12B.20C.24D.4810.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是()A.下滑过程中,始终有CC'=DD'B.下滑过程中,始终有CC'≠DD'C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'二.填空题(共8小题)11.已知:如图,△ABC和△BAD中,∠C=∠D=90°,再添加一个条件就可以判断△ABC≌△BAD.12.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是.13.如图,已知△ABC≌△ADE,若∠A=60°,∠B=40°,则∠BED的大小为.14.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=12cm,则D到AB的距离为cm.15.如图,在Rt△ABC中,∠C=90°,AB=16,AD平分∠BAC交BC于点D,若CD=4,则△ABD的面积为.16.如图,在△ABC中,AD⊥DE,BE⊥DE,AC、BC分别平分∠BAD和∠ABE.点C在线段DE上.若AD=5,BE=2,则AB的长是.17.如图,已知,在△ABC中,AB=AC,点D是BC中点,DE⊥AB于点E,DF⊥AC于点F,DE=3,则DF的长是.18.有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为m.三.解答题(共7小题)19.如图,已知点B,E在线段CF上,CE=BF,∠C=∠F,∠ABC=∠DEF.试说明:△ABC≌△DEF.解:因为CE=BF(已知)所以CE﹣=BF﹣BE()即=在△ABC和△DEF中,所以△ABC≌△DEF().20.已知:如图,E、F是AB上两点,AC∥BD,AC=BD,AE=BF,问:CF=DE吗?说明理由.21.如图,已知线段AC、BD相交于点E,连接AB、DC、BC,AE=DE,∠A=∠D.求证:△ABE≌△DCE.22.如图,已知在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF.BE交FC于O 点,(1)求证:BE=CF;(2)当∠BAC=70°时,求∠BOC的度数.23.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;(2)AM=AN.24.如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.(1)试判断AD与BE有怎样的位置关系,并说明理由;(2)试说明△AOD≌△EOC.25.已知OM是∠AOB的平分线,点P是射线OM上一点,点C、D分别在射线OA、OB 上,连接PC、PD.(1)如图①,当PC⊥OA,PD⊥OB时,则PC与PD的数量关系是.(2)如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当PC⊥PD时,PC与PD在(1)中的数量关系还成立吗?说明理由.参考答案一.选择题(共10小题)1.如图,△ABC≌△A'B'C',其中∠A=36°,∠C'=24°,则∠B=()A.150°B.120°C.90°D.60°解:∵△ABC≌△A'B'C',∴∠C=∠C′=24°,∵∠A=36°,∴∠B=180°﹣24°﹣36°=120°,故选:B.2.如图,AC与DB交于点O,下列条件不能证明△ABC≌△DCB的是()A.AB=DC,AC=DB B.∠A=∠D,∠ABC=∠DCB C.BO=CO,∠A=∠D D.AB=DC,∠ACB=∠DBC 解:A.在△ABC和△DCB中,∵,∴△ABC≌△DCB(SSS),故A选项不合题意;B.在△ABC和△DCB中,∵,∴△ABC≌△DCB(AAS),故B选项不合题意;C.∵BO=CO,∴∠ACB=∠DBC,在△ABC和△DCB中,∵,∴△ABC≌△DCB(AAS),故C选项不合题意;D.∵AB=DC,∠ACB=∠DBC,不能证明△ABC≌△DCB,故D选项符合题意;故选:D.3.如图,△ABC≌△CDE,则线段AC和线段CE的关系是()A.既不相等也不互相垂直B.相等但不互相垂直C.互相垂直但不相等D.相等且互相垂直解:∵△ABC≌△CDE,∴AC=CE,∠A=∠BCD,∠B=∠D,∠ACB=∠E,∴∠ACB+∠BCD=∠ACB+∠A,当∠B=∠D≠90°时,∠ACB+∠BCD=∠ACB+∠A≠90°,则∠ACE≠90°,即AC和CE不互相垂直,故选:B.4.小明同学有一块玻璃的三角板,不小心掉到地上碎成了三块,现要去文具店买一块同样的三角板,最省事的是()A.带②去B.带①去C.带③去D.三块都带去解:带③去符合“角边角”可以配一块同样大小的三角板.故选:C.5.在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是()A.3个B.4个C.6个D.7个解:如图所示:一共有6个符合题意的点.故选:C.6.如图,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌△ADE的是()A.∠B=∠D B.BC=DE C.∠1=∠2D.AB=AD解:A、添加∠B=∠D,由“AAS”可证△ABC≌△ADE,故选项A不合题意;B、添加BC=DE,由“SAS”可证△ABC≌△ADE,故选项B不合题意;C、添加∠1=∠2,由“ASA”可证△ABC≌△ADE,故选项C不合题意;D、添加AB=AD,不能证明△ABC≌△ADE,故选项D符合题意;故选:D.7.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是()A.AD平分BC B.AD平分∠CAB C.AD平分∠CDB D.AD⊥BC解:过D点分别作AB、BC、AC的垂线,垂足分别为E、G、F,∵∠ABC、∠ACB外角的平分线相交于点D,∴ED=GD,GD=DF,∴ED=DF,∴AP平分∠CAB.故选:B.8.如图,已知在△ABC中,AB=AC,∠A=50°,D为BC上一点,BF=CD,CE=BD,那么∠EDF等于()A.55°B.60°C.65°D.70°解:∵AB=AC,∠A=50°,∴∠B=∠C=65°,在△BDF和△CED中,,∴△BDF≌△CED(SAS),∴∠CDE=∠BFD,∵∠CDF=∠B+∠BFD=∠CDE+∠EDF,∴∠EDF=∠B=65°,故选:C.9.如图,在△ABC中,AB=AC,BD=CD,点E,F是AD上的任意两点.若BC=8,AD =6,则图中阴影部分的面积为()A.12B.20C.24D.48解:∵AB=AC,BD=CD,AD=AD,∴△ADC≌△ADB(SSS),∴S△ADC=S△ADB,BD=BC,∵BC=8,∴BD=4,∵S△BEF=S△CEF,AD=6,∴S阴影=S△ADB=.故选:A.10.如图,将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',则下列说法正确的是()A.下滑过程中,始终有CC'=DD'B.下滑过程中,始终有CC'≠DD'C.若OC<OD,则下滑过程中,一定存在某个位置使得CC'=DD'D.若OC>OD,则下滑过程中,一定存在某个位置使得CC'=DD'解:将一根笔直的竹竿斜放在竖直墙角AOB中,初始位置为CD,当一端C下滑至C'时,另一端D向右滑到D',可得:CD=C'D',A、下滑过程中,CC'与DD'不一定相等,说法错误;B、下滑过程中,当△OCD与△OD'C'全等时,CC'=DD',说法错误;C、若OC<OD,则下滑过程中,不存在某个位置使得CC'=DD',说法错误;D、若OC>OD,则下滑过程中,当△OCD与△OD'C'全等时,一定存在某个位置使得CC'=DD',说法正确;故选:D.二.填空题(共8小题)11.已知:如图,△ABC和△BAD中,∠C=∠D=90°,再添加一个条件AC=BD就可以判断△ABC≌△BAD.解:添加AC=BD,理由:∵∠C=∠D=90°,∴△ACB和△BDA都是直角三角形,在Rt△ABC和Rt△BAD中,∴Rt△ABC≌Rt△BAD(HL),故答案为:AC=BD.12.如图,△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是7cm.解:∵△ABC≌△ADE,BC=7,∴DE=BC=7(cm),故答案为:7cm.13.如图,已知△ABC≌△ADE,若∠A=60°,∠B=40°,则∠BED的大小为100°.解:∵△ABC≌△ADE,∴∠D=∠B=40°,∴∠BED=∠A+∠D=60°+40°=100°,故答案为:100°.14.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=12cm,则D到AB的距离为4cm.解:过点D作DE⊥AB于E,∵BD:DC=2:1,BC=12,∴DC=4,∵AD平分∠BAC,DC⊥AC,DE⊥AB,∴DE=DC=4,即D到AB的距离为4cm,故答案为:4.15.如图,在Rt△ABC中,∠C=90°,AB=16,AD平分∠BAC交BC于点D,若CD=4,则△ABD的面积为32.解:作DE⊥AB于E,∵AD平分∠BAC,∠C=90°,DE⊥AB,∴DE=DC=4,∴△ABD的面积=×AB×DE=32,故答案为:32.16.如图,在△ABC中,AD⊥DE,BE⊥DE,AC、BC分别平分∠BAD和∠ABE.点C在线段DE上.若AD=5,BE=2,则AB的长是7.解:如图,过点C作CF⊥AB于F,∵AC,BC分别平分∠BAD,∠ABE,∴∠DAC=∠F AC,∠FBC=∠EBC,在△ADC和△AFC中,∵,∴△ADC≌△AFC(AAS),∴AD=AF,在△CBE≌△CBF中,∵,∴△CBE≌△CBF(AAS),∴BE=BF,∴AB=AF+BF=AD+BE=5+2=7,故答案为:7.17.如图,已知,在△ABC中,AB=AC,点D是BC中点,DE⊥AB于点E,DF⊥AC于点F,DE=3,则DF的长是3.解:∵AB=AC,∴∠B=∠C,∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=90°,∵点D是BC中点,∴BD=CD,在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴DE=DF=3,故答案为:3.18.有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为800m.解:在△ABC和△EDC中,∴△ABC≌△EDC(SAS),∴AB=DE=800.答:A,B之间的距离为800m.故答案是:800.三.解答题(共7小题)19.如图,已知点B,E在线段CF上,CE=BF,∠C=∠F,∠ABC=∠DEF.试说明:△ABC≌△DEF.解:因为CE=BF(已知)所以CE﹣BE=BF﹣BE(等式的性质)即BC=EF在△ABC和△DEF中,所以△ABC≌△DEF(ASA).解:因为CE=BF(已知),所以CE﹣BE=BF﹣BE(等式的性质),即BC=EF,在△ABC和△DEF中,所以△ABC≌△DEF(ASA).故答案为:BE;等式的性质;BC=EF;ASA.20.已知:如图,E、F是AB上两点,AC∥BD,AC=BD,AE=BF,问:CF=DE吗?说明理由.解:CF=DE,理由:∵AE=BF,∴AF=BE.∵AC∥BD,∴∠A=∠B.在△ACF和△BDE中,,∴△ACF≌△BDE(SAS).∴CF=DE.21.如图,已知线段AC、BD相交于点E,连接AB、DC、BC,AE=DE,∠A=∠D.求证:△ABE≌△DCE.【解答】证明:在△ABE和△DCE中,∵,∴△ABE≌△DCE(ASA).22.如图,已知在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF.BE交FC于O 点,(1)求证:BE=CF;(2)当∠BAC=70°时,求∠BOC的度数.【解答】(1)证明:∵∠CAB=∠EAF,∴∠CAB+∠CAE=∠EAF+∠CAE,∴∠BAE=∠CAF,在△BAE和△CAF中∴△BAE≌△CAF(SAS),∴BE=CF;(2)∵△BAE≌△CAF,∴∠EBA=∠FCA,即∠DBA=∠OCD,∵∠BDA=∠ODC,∴∠BAD=∠COD,∵∠BAC=70°,∴∠BAD=70°,∴∠COD=70°,即∠BOC=70°.23.如图AB=AD,AC=AE,∠BAE=∠DAC.求证:(1)∠C=∠E;(2)AM=AN.【解答】证明:(1)∵∠BAE=∠DAC,∴∠BAC=∠DAE,在△ABC和△ADE中,,∴△ABC≌△ADE(SAS),∴∠C=∠E;(2)∵△ABC≌△ADE,∴∠B=∠D,在△ABM和△ADN中,,∴△ABM≌△ADN(ASA),∴AM=AN.24.如图,AB∥CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.(1)试判断AD与BE有怎样的位置关系,并说明理由;(2)试说明△AOD≌△EOC.解:(1)AD∥BE,理由:∵AB∥CD,∴∠B=∠DCE,∵∠B=∠D,∴∠DCE=∠D,∴AD∥BE;(2)∵O是CD的中点,∴DO=CO,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠OCE,在△ADO和△ECO中,∴△AOD≌△EOC(ASA).25.已知OM是∠AOB的平分线,点P是射线OM上一点,点C、D分别在射线OA、OB 上,连接PC、PD.(1)如图①,当PC⊥OA,PD⊥OB时,则PC与PD的数量关系是PC=PD.(2)如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当PC⊥PD时,PC与PD在(1)中的数量关系还成立吗?说明理由.解:(1)PC=PD,理由:∵OM是∠AOB的平分线,∴PC=PD(角平分线上点到角两边的距离相等),故答案为:PC=PD;(2)证明:过点P点作PE⊥OA于E,PF⊥OB于F,如图,∴∠PEC=∠PFD=90°,∵OM是∠AOB的平分线,∴PE=PF,∵∠AOB=90°,∠CPD=90°,∴∠PCE+∠PDO=360°﹣90°﹣90°=180°,而∠PDO+∠PDF=180°,∴∠PCE=∠PDF,在△PCE和△PDF中,∴△PCE≌△PDF(AAS),∴PC=PD.。
12.2三角形全等的判定(二)(“SAS”)练习题人教版八年级数学上册
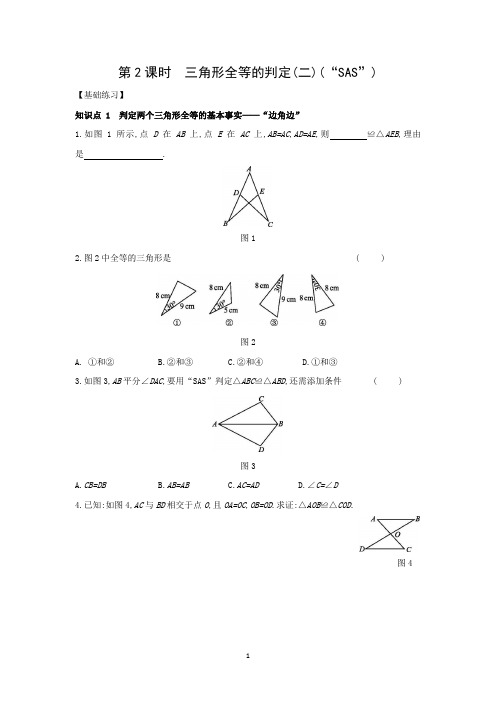
第2课时三角形全等的判定(二)(“SAS”)【基础练习】知识点 1 判定两个三角形全等的基本事实——“边角边”1.如图1所示,点D在AB上,点E在AC上,AB=AC,AD=AE,则≌△AEB,理由是.图12.图2中全等的三角形是 ()图2A.①和②B.②和③C.②和④D.①和③3.如图3,AB平分∠DAC,要用“SAS”判定△ABC≌△ABD,还需添加条件 ( )图3A.CB=DBB.AB=ABC.AC=ADD.∠C=∠D4.已知:如图4,AC与BD相交于点O,且OA=OC,OB=OD.求证:△AOB≌△COD.图45.如图5所示,CD=CA,∠1=∠2,EC=BC.求证:△ABC≌△DEC.图56.如图6所示,AD=BE,AC=DF,AC∥DF.求证:△ABC≌△DEF.图6知识点 2 全等三角形的判定(SAS)的简单应用7.如图7所示,AA',BB'表示两根长度相同的木条.若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为 ( )图7A.8 cmB.9 cmC.10 cmD.11 cm8.[2020·镇江]如图8,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC 上,BE=CD,BF=CA,连接EF.(1)求证:∠D=∠2;(2)若EF∥AC,∠D=78°,求∠BAC的度数.图8【能力提升】9.如图9所示,在△ABC和△ADC中,有下列三个论断:①AB=AD;②∠BAC=∠DAC;③BC=DC.将其中的两个论断作为条件,另一个论断作为结论写出一个真命题为.(写成“如果 ,那么 ”的形式,写一个即可)图910.[2020·江西]如图10,CA平分∠DCB,CB=CD,DA的延长线交BC于点E.若∠EAC=49°,则∠BAE的度数为.图1011.如图11,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.有下列说法:①CE=BF;②△ABD≌△ACD;③BF∥CE;④△BDF和△CDE的面积相等.其中正确的是.(填序号)图1112.:[2020·宜宾]如图12,在△ABC中,D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.(1)求证:△ABD≌△ECD;(2)若△ABD的面积为5,求△ACE的面积.图12 变式:在△ABC中,AB=7,AC=3,AD是中线,求AD的取值范围.第2课时 三角形全等的判定(二)(“SAS ”)1.△ADC SAS2.D [解析] 从图中可以看到①和③符合“SAS ”.3.C [解析] 由题意可得,在△ABC 和△ABD 中,{AC =AD,∠CAB =∠DAB,AB =AB,∴△ABC ≌△ABD (SAS).选项C 正确,其余选项都不正确. 4.证明:在△AOB 和△COD 中,{OA =OC,∠AOB =∠COD,OB =OD,∴△AOB ≌△COD (SAS).5.证明:∵∠1=∠2,∴∠1+∠ECA=∠2+∠ECA ,即∠ACB=∠DCE.在△ABC 和△DEC 中,{CA =CD,∠ACB =∠DCE,BC =EC,∴△ABC ≌△DEC (SAS).6.证明:∵AD=BE ,∴AB+BD=DE+BD ,即AB=DE.∵AC ∥DF ,∴∠A=∠FDE.在△ABC 和△DEF 中,{AB =DE,∠A =∠FDE,AC =DF,∴△ABC ≌△DEF (SAS).7.B8.解:(1)证明:在△BEF 和△CDA 中,{BE =CD,∠B =∠1,BF =CA,∴△BEF ≌△CDA (SAS).∴∠D=∠2.(2)∵∠D=∠2,∴∠2=78°.∵EF∥AC,∴∠BAC=∠2=78°.9.答案不唯一,如:如果①②,那么③(或如果①③,那么②)[解析] (1)已知AB=AD,∠BAC=∠DAC,AC=AC,可得△ABC≌△ADC(SAS),所以BC=DC;(2)已知AB=AD,BC=DC,AC=AC,可得△ABC≌△ADC(SSS),所以∠BAC=∠DAC.10.82°[解析] ∵CA平分∠DCB,∴∠BCA=∠DCA.又∵CB=CD,AC=AC,∴△ABC≌△ADC(SAS).∴∠B=∠D.∴∠B+∠ACB=∠D+∠ACD.∵∠CAE=∠D+∠ACD=49°,∴∠B+∠ACB=49°.∴∠BAE=180°-∠B-∠ACB-∠CAE=82°.故答案为82°.11.①③④[解析] ∵AD是△ABC的中线,∴BD=CD.又∠CDE=∠BDF,DE=DF,∴△BDF≌△CDE,故④正确;由△BDF≌△CDE,可知CE=BF,故①正确;∵AD是△ABC的中线,∴△ABD和△ACD等底同高,∴△ABD和△ACD的面积相等,但不一定全等,故②错误;由△BDF≌△CDE,可知∠FBD=∠ECD,∴BF∥CE,故③正确.故答案为①③④.12.解:(1)证明:∵D是边BC的中点,∴BD=CD.在△ABD 和△ECD 中,{BD =CD,∠ADB =∠EDC,AD =ED,∴△ABD ≌△ECD (SAS).(2)∵在△ABC 中,D 是边BC 的中点,∴S △ABD =S △ACD .∵△ABD ≌△ECD ,∴S △ABD =S △ECD . ∵S △ABD =5,∴S △ACE =S △ACD +S △ECD =5+5=10,即△ACE 的面积为10.变式:解:如图,延长AD 到点E ,使ED=AD ,连接BE.∵AD 是△ABC 的中线,∴BD=CD.又ED=AD ,∠ADC=∠EDB ,∴△BED ≌△CAD (SAS). ∴BE=AC=3. ∵DE=AD ,∴AE=2AD.在△ABE 中,AB-BE<AE<AB+BE , 即AB-BE<2AD<AB+BE ,∴7-3<2AD<7+3. ∴2<AD<5.。
人教版八年级上册数学《全等三角形》证明题专项训练-最新

BA DC 人教版八年级上册数学《全等三角形》证明题专项训练·最新全等三角形证明习题(1)1.在△ABC 中,AB=AC ,AD 是三角形的中线.求证:△ABD ≌△ACD2. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .3.已知,如图BD 平分∠ABC ,AB = BC 。
求证:AD = CD4.如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:AB=AC 。
CBABDC E A5. 如图,点E, F 在BC 上,BE=CF, AB=DC, ∠B=∠C. 求证: ∠A=∠D6. 如图,AB=AD, BC=DE, ∠B=∠D . 问∠BAE 与∠DAC 相等吗?为什么?7. 已知:如图,∠1=∠2,BD=CD,求证:AD 是∠BAC 的平分线.8.如图所示在△ABC 中,AB=AC , D 是BD 的中点,求证:△9.如图(2):AC ∥EF ,AC=EF ,AE=BD 。
求证:△ABC ≌△EDF 。
CO ED BA FC10.已知:如图 , AB=AE , AC=AD , BC=DE , C , D 在BE 边上. 求证:∠CAE=∠DAB .11.已知:点D 在AB 上,点E 在AC 上,BE 和CD 相交于点O ,AB=AC , ∠B=∠C 。
求证: △ABE ≌△ACD12.如图:AC=DF ,AD=BE ,BC=EF 。
求证:∠C=∠F 。
13.如图:AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF 。
DBEA OC FEB DADA14.如图,CE ⊥AB 于E , DF ⊥AB 于F , AF=BE , 且AC=BD , 求证:AC ∥BD15.如图,已知AB=DE ,BC=EF ,AF=DC ,则∠EFD=∠BCA ,请说明理由。
16.如图(6):CG=CF ,BC=DC ,AB=ED ,点A 、B 、C 、D 、E 在同一直线上。
全等三角形的性质专项练习30题

(936)全等三角形的性质专项练习30题(有答案)o k(总11页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--全等三角形的性质专项练习30题(有答案)1.如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论(请写出三个以上的结论)2.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.3.如图,AB=DC,AC=DB,你能说明图中∠1=∠2的理由吗4.已知:AB=DE,AF=CD,∠A=∠D,EF=BC,试说明:BF∥CE.5.已知△ABC≌△DEF,其中AB=2cm,BC=3cm,AC=4cm,则△DEF的三边长DE= _________ cm,EF= _________ cm,DF= _________ cm.6.如图,△ABC≌△ADE,∠B=40°,∠E=30°,∠BAE=80°,求∠BAC、∠DAC的度数.7.如图,△AOC≌△BOD,试证明AC∥BD.8.如图,△ABC≌△DEF,∠A=25°,∠B=65°,BF=3cm,求∠DFE的度数和EC的长.9.如图,△ABD≌△EBD,△DBE≌△DCE,B,E,C在一条直线上.(1)BD是∠ABE的平分线吗为什么(2)DE⊥BC,BE=EC吗为什么10.附加题:如图△ABC≌△DBC,∠A=110°,则∠D=_________ .11.如图,已知△AEC≌△BFD,则AD _________ BC.(填“>”、“=”或“<”).12.如图,△ABC≌△DEC,∠A:∠ABC:∠BCA=3:5:10,(1)求∠D的度数;(2)求∠EBC的度数.13.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.14.如图,已知△ABD≌△ACE.求证:BE=CD.15.如图,△ABC≌△DEF,BF=3,EF=2.求FC的长.16.如图,△ABC≌△BDE,M、M′分别为AB、DB中点,直线MM′交CE于K.试探索CK与EK的数量关系.17.如图,在△ABC中,BE,CF分别是AC,AB边上的高线,BE,CF相交于O,连接AO交BC于D,且△BCF≌△CBE,∠ABC=70°,求∠1和∠2的度数.18.如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.19.如图,△ABC≌△DEC,∠1与∠2相等吗请说明理由.20.如图,△ABC≌△EBD.求证:∠1=∠2.21.如图,△ABC≌△ADE,∠CAD=10度,∠B=∠D=25度,∠EAB=120度,试求∠ACB的度数.22.如图,△ABC≌△DEF,△ABC的周长是40cm,AB=10cm,BC=16cm,求△DEF中,边DF的长度.23.如图:△ABF≌△DCE,写出相等的线段.24.如图,△ABC≌△ADE中,BA⊥AE,∠BAC=30°,AD=5,求BD的长.25.如右图所示,已知△ABD≌△ACE,试说明BE=CD.26.如图,△ABC≌△EFD,你能从图中找到几组平行线请写出,并选择一组说明理由.27.如图,点B、E、C、F在一条直线上,BC=EF AB∥DE,请你添加一个条件_________ ,使△ABC≌△DE F.并写出证明过程.28.如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7,求线段AB的长.29.如图,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC的长.30.如图,△ABC≌△ADE,B点的对应顶点是D点,若∠BAD=100°,∠CAE=40°,求∠BAC的度数.参考答案1.∵△ABF≌△DCE∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;∴AF∥ED,AC=BD,BF∥CE.2.∵△ABC≌△ADE,∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°∠DGB=∠DFB﹣∠D=90°﹣25°=65°3.证明:在△ABC和△DCB中,AB=DC,AC=DB,BC=BC,∴△ABC≌△DCB(SSS),∴∠1=∠2.4.∵AB=DE,AF=CD,∠A=∠D,则可得△ABF≌△DEC,∴BF=EC,又EF=BC,∴可得四边形BCEF是平行四边形,∴BF∥EC5.∵△ABC≌△DEF∴AB=DE,BC=EF,AC=DF∴DE=2cm,EF=3cm,DF=4cm.6.①∵△ABC≌△ADE,∴∠B=∠D=40°,∠E=∠C=30°,∴∠BAC=180°﹣∠B﹣∠C=110°;②∵∠BAE=80°,∠BAC=∠DAE=110°∴∠BAD=∠DAE﹣∠BAE=30°,∴∠DAC=∠BAC+∠BAD=110°+30°=140°7. ∵△AOC≌△BOD,∴∠A=∠B(全等三角形对应角相等).∴AC∥BD(内错角相等,两直线平行)8.△ABC中∠A=25°,∠B=65°,∴∠BCA=180°﹣∠A﹣∠B=180°﹣25°﹣65°=90°,∵△ABC≌△DEF,∴∠BCA=∠DFE,BC=EF,∴EC=BF=3cm.∴∠DFE=90°,EC=3cm.9.(1)∵△ABD≌△EBD,∴∠ABD=∠EBD,∴BD是∠ABE的平分线;(2)∵△DBE≌△DCE,∴∠DEB=∠DEC,∵∠DEB+∠DEC=180°,∴∠DEB=∠DEC=90°,∴DE⊥BC,∵△DBE≌△DCE,∴BE=E C.10.解:∵△ABC≌△DBC,∠A=110°∴∠D=∠A=110°.11.∵△AEC≌△BFD∴AC=BD(全等三角形对应边相等)∴AC+CD=BD+CD,即AD=BC.12.(1)∵∠A+∠ABC+∠BCA=180°,∠A:∠ABC:∠BCA=3:5:10,∴∠A=180°×=30°,∠ABC=180°×=50°,∠BCA=180°×=100°,又∵△ABC≌△DEC,∴∠D=∠A=30°;(2)∵△ABC≌△DEC,∴∠E=∠ABC=50°,∵∠BCA=100°,∴∠EBC=∠BCA﹣∠E,=100°﹣50°=50°13.∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,∴对应边:AN与AM,BN与CM;对应角:∠BAN=∠CAM,∠ANB=∠AMC14.∵△ABD≌△ACE,∴AB=AC,AD=AE,∴AC﹣AD=AB﹣AE,即CD=BE15.∵△ABC≌△DEF∴BC=EF=2又∵FC=BF﹣BC∴FC=3﹣2=116.CK与EK的数量关系为相等,理由如下:延长MK到N,使得NK=MM',连接EM′、CM、EN,如图,可得NK+KM'=MM'+M'K,即NM'=MK,∵△ABC≌△BDE,M、M′分别为AB、DB中点,∴EM'=CM,BM'=BM,∠EM'D=∠CMB,由BM'=BM得:∠BM'M=∠BMM'=∠KM'D,∴∠NM'E=∠CMK,在△EM'N和△CMK中,NM'=MK,∠NM'E=∠CMK,EM'=CM,∴△EM'N≌△CMK,(SAS)∴CK=EN,∠N=∠CKM=∠NKE,∴EK=EN,∴CK=EK.17.∵△BCF≌△C BE,∴∠FBC=∠ECB=70°,∴∠BAC=180°﹣∠FBC﹣∠ECB=40°,AB=AC,∵BE,CF分别是AC,AB边上的高线,BE,CF相交于O,∵AD⊥BC,∴∠1=∠2=∠BAC=20°18.∵△ABC≌△ADE,∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.∵∠ADE=25°,∴∠ABC=∠ADE=25°.∵∠ACB=105°,∴∠CAB=180°﹣105°﹣25°=50°.∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°.∠AGB=∠ACB﹣∠GAC=105°﹣50°﹣10°=45°19.由题意:∵△ABC≌△DEC,∴BC=EC.∴∠1=∠220.∵△ABC≌△EBD.∴∠A=∠E.又∵∠AOD=∠BOE,∴∠A+∠AOD+∠1=∠E+∠BOE+∠2=180°,∴∠1=∠221.∵△ABC≌△ADE,∴∠CAB=∠EAD.∵∠EAB=120°,∠CAD=10°,∴∠EAB=∠EAD+∠CAD+∠CAB=2∠CAB+10°=120°,∴∠CAB=55°.∵∠B=∠D=25°,∴∠ACB=180°﹣∠CAB﹣∠B=180°﹣55°﹣25°=100°,即∠ACB的度数是100°22.已知,△ABC的周长是40cm,AB=10cm,BC=16cm,∴AC=△ABC的周长﹣AB﹣BC=40﹣10﹣16=14(cm),∵△ABC≌△DEF,∴DF=AC=14cm,所以边DF的长度为14cm23.∵△ABF≌△DCE,∴AB=DC,BF=CE,AF=DE,∠DEC=∠AFE,∴OE=OF,∴AF﹣FO=DE﹣OE,∴AO=DO,∵BF=CE,∴BF﹣FE=CE﹣EF,∴EB=FC.24.由题意得:∠BAC=∠DAE=30°,AB=AD,∠BAE=90°,∴∠CAD=30°,∴∠ABD=60°,∴△ABD是等边三角形.故可得:BD=AD=525.∵△ABD≌△ACE,∴AD=AE,AC=AB,∴AE﹣AB=AD﹣AC,即BE=CD26.AB∥EF,AC∥ED.∵△ABC≌△EFD,∴∠B=∠F,∠ACB=∠EDF,∴AB∥EF,AC∥ED27.∠ACB=∠F或AB=DE或∠A=∠D.以下证明添加条件为AB=DE时,△ABC≌△DEF.∵AB∥DE,∴∠B=∠DEF.在△ABC和△DEF中,∴△ABC≌△DEF28.∵△ACF≌△DBE,∴AC=DB,∴AC﹣BC=DB﹣BC,即AB=CD,∵AD=11,BC=7,∴AB=(AD﹣BC)=(11﹣7)=2即AB=229.∵∠A=30°,∠B=50°,∴∠ACB=180°﹣∠A﹣∠B=180°﹣30°﹣50°=100°,∵△ABC≌△DEF,∴∠DFE=∠ACB=100°,EF=BC,∴EF﹣CF=BC﹣CF,即EC=BF,∵BF=2,∴EC=230.∵△ABC≌△ADE,∴∠BAC=∠DAE,∴∠BAC﹣∠CAE=∠DAE﹣∠CAE,即∠BAE=∠DAC,∵∠BAD=100°,∠CAE=40°,∴∠BAE=(∠BAD﹣∠CAE)=(100°﹣40°)=30°,∴∠BAC=∠BAE+∠CAE=30°+40°=70。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形练习题专项训练(2)
一、填空题:
1、在△ABC 中,若AC >BC >AB ,且△DEF ≌△ABC ,则△DEF 三边的关系为___<___<___。
2、如图1,AD ⊥BC ,D 为BC 的中点,则△ABD ≌___,△ABC 是___三角形。
3、如图2,若AB =DE ,BE =CF ,要证△ABF ≌△DEC ,需补充条件____或____。
4、如图3,已知AB ∥CD ,AD ∥BC ,E 、F 是BD 上两点,且BF =DE ,则图中共有___对全等三角形,它们分别是_____。
5、如图4,四边形ABCD 的对角线相交于O 点,且有AB ∥DC ,AD ∥BC ,则图中有___对全等三角形。
6、如图5,已知AB =DC ,AD =BC ,E 、F 在DB 上两点且BF =DE ,若∠AEB =120°,∠ADB =30°,则∠BCF =____。
7、如图6,AE =AF ,AB =AC ,∠A =60°,∠B =24°,则∠BOC =____。
8、在等腰△ABC 中,AB =AC =14cm ,E 为AB 中点,DE ⊥AB 于E ,交AC 于D ,若△BDC 的周长为24cm ,则底边BC =____。
9、若△ABC ≌△A ′B ′C ′,AD 和A ′D ′分别是对应边BC 和B ′C ′的高,则△ABD ≌△A ′B ′D ′,理由是______,从而AD =A ′D ′,这说明全等三角形____相等。
10、在Rt △ABC 中,∠C =90°,∠A 、∠B 的平分线相交于O ,则∠AOB =____。
二、选择题:
11、如图7,△ABC ≌△BAD ,A 和B 、C 和D 分别是对应顶点,若AB =6cm ,AC =4cm ,BC =5cm ,则AD 的长为( )
A 、4cm
B 、5cm
C 、6cm
D 、以上都不对
1
2 图
3 图
4 图
5 A E B O F C 图
6 A C D
图7
12、下列说法正确的是( )
A 、周长相等的两个三角形全等
B 、有两边和其中一边的对角对应相等的两个三角形全等
C 、面积相等的两个三角形全等
D 、有两角和其中一角的对边对应相等的两个三角形全等
13、在△ABC 中,∠B =∠C ,与△ABC 全等的三角形有一个角是100°,那么在△ABC 中与这100°角对应相等的角是( )
A 、∠A
B 、∠B
C 、∠C
D 、∠B 或∠C
14、下列条件中,能判定△ABC ≌△DEF 的是( )
A 、A
B =DE ,B
C =E
D ,∠A =∠D
B 、∠A =∠D ,∠
C =∠F ,AC =EF
C 、∠B =∠E ,∠A =∠
D ,AC =EF
D 、∠B =∠
E ,∠A =∠D ,AB =DE
15、AD 是△ABC 中BC 边上的中线,若AB =4,AC =6,则AD 的取值范围是( )
A 、AD >1
B 、AD <5
C 、1<A
D <5 D 、2<AD <10
16、下列命题错误的是( )
A 、两条直角边对应相等的两个直角三角形全等;
B 、一条边和一个锐角对应相等的两个直角三角形全等
C 、有两边和其中一边的对角(此角为钝角)对应相等的两个三角形全等
D 、有两条边对应相等的两个直角三角形全等
17、如图8、△ABC 中,AB =AC ,BD ⊥AC 于D ,CD ⊥AB 于E ,BD 和CE 交于点O ,AO 的延长线交BC 于F ,则图中全等直角三角形的对数为( )
A 、3对
B 、4对
C 、5对
D 、6对
三、解答题与证明题:
18、如图,已知AB ∥DC ,且AB =CD ,BF =DE ,
求证:AE ∥CF ,AF ∥CE
图
8
19、如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论。
20、如图,已知AB=DC,AC=DB,BE=CE 求证:AE=DE A
C
D
B
A
B E C
D
21、已知如图,E 、F 在BD 上,且AB =CD ,BF =DE ,AE =CF
求证:AC 与BD 互相平分
22、如图,∠ABC =90°,AB =BC ,D 为AC 上一点,分别过A 、C 作BD 的垂线,垂足分别为E 、F
求证:EF =CF -AE
A
B E O F D
C
参考答案:
1、DF,EF,DE;
2、△ACD,等腰;
3、∠B=∠DEC,AB∥DE;
4、三,△ABE≌△CDF,△ADE≌△CBF,△ABD≌△CDB;
5、4;
6、90°;
7、108°;
8、10cm;
9、AAS,对应边上的高;10、135°。
11、B;12、D;13、A;14、D;15、C;16、D;17、D;
18、∵AB∥DC∴∠ABE=∠CDF,又DE=BF,∴DE+EF=BF+EF,即BE=DF;
又AB=CD,∴△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,
∴AE∥CF,再通过证△AEF≌△CFE
得∠AFE=∠CEF,∴AF∥CE
19、猜想:CE=ED,CE⊥ED,先证△ACE≌△BED
得CE=ED,∠C=∠DEB,而∠C+∠AEC=90°
∴∠AEC+∠DEB=90°
即CE⊥ED
20、先证△ABC≌△DCB
得∠ABC=∠DCB
再证△ABE≌△DCE,得AE=DE
21、由BF=DF,得BE=DF
∴△ABE≌△CDF,∴∠B=∠D
再证△AOB≌△COD,得OA=OC,OB=OD
即AC、BD互相平分
22、证△ABE≌△BCF,得BE=CF,AE=BF,
∴EF=BE-BF=CF-AE。
