全等三角形专题练习(解析版)
八年级全等三角形专题练习(解析版)

一、八年级数学全等三角形解做题压轴题〔难〕1. 〔1〕如图〔1〕,:在△ ABC中,N BAC=90.,AB二AC,直线m经过点A, 8口,直线m, CE J_直线m,垂足分别为点D、E.证实:DE=BD+CE.〔2〕如图〔2〕,将〔1〕中的条件改为:在△ ABC中,AB=AC, D、A、E三点都在直线m 上,并且有N BDA=Z AEC=Z BAC=.,其中.为任意锐角或钝角.请问结论DE=BD+CE是否成立? 如成立,请你给出证实;假设不成立,请说明理由.〔3〕拓展与应用:如图〔3〕 , D、E是D、A、E三点所在直线m上的两动点〔D、A、E 三点互不重合〕,点F为N BAC平分线上的一点,且△ ABF和^ ACF均为等边三角形,连接BD、CE,假设N BDA=Z AEC=Z BAC,试判断△ DEF 的形状.【答案】(1)见解析(2)成立(3) 4DEF为等边三角形【解析】解:(1)证实:BDL直线m, CEJ_直线m,,N BDA=N CEA=900.: Z BAC=90°, /. Z BAD+Z CAE=90°.•/ Z BAD+Z ABD=90°, /. Z CAE=Z ABD.又AB二“AC〞,「・△ ADB合△ CEA (AAS) . /. AE=BD, AD=CE./. DE=,,AE+AD=H BD+CE.(2)成立.证实如下:: Z BDA =Z BAC=a , /. Z DBA+Z BAD=Z BAD+Z CAE=180°-O r . /. Z DBA=Z CAE.Z BDA=Z AEC=., AB=AC,「・△ AD於△ CEA (AAS). /. AE=BD, AD=CE.DE二AE+AD=BD+CE.(3)△ DEF为等边三角形.理由如下:由(2)知,△ ADB合△ CEA, BD=AE, Z DBA =Z CAE,: △ ABF 和^ ACF 均为等边三角形,J Z ABF=Z CAF=60°.・•, Z DBA+Z ABF=Z CAE+Z CAF. /. Z DBF=Z FAE.; BF=AF,,•・丛DBF合△ EAF (AAS) . /. DF=EF, Z BFD=Z AFE.・•, Z DFE=Z DFA+z AFE=Z DFA+Z BFD=60°.・•.A DEF为等边三角形.(1)由于DE=DA+AE,故由AAS证△ ADB合4 CEA,得出DA=EC, AE=BD,从而证得DE=BD+CE.(2)成立,仍然通过证实△ ADB2 J CEA,得出BD=AE, AD=CE,所以DE=DA+AE=EC+BD.(3)由△ ADB2△ CEA得BD=AE, NDBA=N CAE,由△ ABF和△ ACF均等边三角形,得Z ABF=Z CAF=60°, FB=FA,所以N DBA+N ABF=N CAE+N CAF,即N DBF二N FAE,所以△ DBF^ △ EAF,所以FD=FE, Z BFD=Z AFE,再根据N DFE=Z DFA+Z AFE=Z DFA+Z BFD=60°得到△ DEF是等边三角形.2.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE, PE 交CD 于 F〔1〕证实:PC=PE;〔2〕求N CPE的度数:〔3〕如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当N ABC=12〔T时,连接【答案】(1)证实见解析(2) 90° (3) AP=CE【解析】【分析】(1)、根据正方形得出AB=BC, ZABP=ZCBP=45%结合PB=PB得出aABP g^CBP,从而得出结论:⑵、根据全等得出NBAP=NBCP, ZDAP=ZDCP,根据PA=PE得出NDAP=NE,即ZDCP=ZE,易得答案;(3)、首先证实4ABP和^CBP全等,然后得出PA=PC, NBAP=NBCP,然后得出NDCP二NE,从而得出NCPF=NEDF=60°,然后得出AEPC是等边三角形,从而得出AP=CE.【详解】⑴、在正方形ABCD 中,AB=BC, ZABP=ZCBP=45%在ZkABP 和4CBP 中,XV PB=PB AAABP^ACBP (SAS) , ,PA=PC, VPA=PE>:.PC=PE;⑵、由(1)知,A ABP^ACBP,.\ZBAP=ZBCP, JNDAP=NDCP,VPA=PE, .\ZDAP=ZE> /. ZDCP=ZE. VZCFP=ZEFD (对顶角相等), A180° - ZPFC - ZPCF=1800 - ZDFE - NE, BPZCPF=ZEDF=90<>:⑶、AP = CE理由是:在菱形ABCD 中,AB=BC, NABP二NCBP,在2\ABP ^lACBP 中,XV PB=PB /.△ABP^ACBP (SAS),,PA二PC, NBAP=NDCP,VPA=PE,,PC=PE,,NDAP=NDCP, V PA=PC,/DAP=NE, A ZDCP=ZE V ZCFP=ZEFD (对顶角相等),A180°- ZPFC - ZPCF=180° - ZDFE - NE, RPZCPF=ZEDF=180° - ZADC=180° - 120°=60°, AAEPC 是等边三角形,,PC=CE, AAP=CE考点:三角形全等的证实3.如图,在AA8C中,NAC8为锐角,点£>为射线8C上一动点,连接AO.以AO为直角边且在AD的上方作等腰直角三角形ADF.图①图②图③〔1〕假设A3 = AC, ABAC = 90°①当点.在线段BC上时〔与点3不重合〕,试探讨CF与8.的数量关系和位置关系:②当点O在线段C的延长线上时,①中的结论是否仍然成立,请在图2中而出相应的图形并说明理由;〔2〕如图3,假设ABwAC, ABAC90° , ZBC4 = 45°,点.在线段8C上运动,试探究CF与8.的位置关系.【答案】〔1〕①CF_LBD,证实见解析:②成立,理由见解析:〔2〕 CF1BD,证实见解析.【解析】【分析】〔1〕①根据同角的余角相等求出NCAF=NBAD,然后利用"边角边"证实4ACF和4ABD全等,②先求出NCAF=NBAD,然后与①的思路相同求解即可:〔2〕过点A作AE_LAC交BC于E,可得4ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE, NAED=45.,再根据同角的余角相等求出NCAF=NEAD,然后利用“边角边〞证实4ACF 和4AED全等,根据全等三角形对应角相等可得NACF=NAED,然后求出ZBCF=90°,从而得到CFJ_BD.【详解】解:〔1〕①•••NBAC=90°, 4ADF是等腰直角三角形,.\ZCAF+ZCAD=90% ZBAD+ZACD=90°,.\ZCAF=ZBAD,在4ACF和4ABD中,VAB=AC, ZCAF=ZBAD, AD=AF,.,.△ACF^AABD〔SAS〕,.・.CF=BD, ZACF=ZABD=45",ZACB=45",AZFCB=90°,.-.CF±BD:②成立,理由如下:如图2:VZCAB=ZDAF=90%,ZCAB+ ZCAD= ZDAF+ ZCAD, 即NCAF=NBAD,在aACF和AABD中,VAB=AC, ZCAF=ZBAD, AD=AF, AAACF^AABD(SAS), ACF=BD, NACF=NB,VAB=AC, ZBAC=90%AZB=ZACB=45%/. Z BCF= ZACF+ ZACB=45o+45o=90°,ACF1BD:(2)如图3,过点A作AE_LAC交BC于E,•/ ZBCA=45",••.△ACE是等腰直角三角形,,AC=AE, NAED=45°, VZCAF+ZCAD=90°, ZEAD+ZCAD=90%,NCAF=NEAD,在4ACF和4AED中,VAC=AE, NCAF=NEAD, AD=AF,.•.△ACF^AAED(SAS), /. ZACF=ZAED=45\,ZBCF= ZACF+ ZBCA=45o+45°=90°, ACF1BD.【点睛】此题考查全等三角形的动点问题,综合性较强,有一定难度,需要熟练掌握全等三角形的判定和性质进行综合运用.4.如图〔1〕,在△A3C中,ZA = 90°, A3 = AC,点.是斜边8C的中点,点E, 产分别在线段A3, 4c上,且NEDF = 90..〔1〕求证:△.所为等腰直角三角形:〔2〕假设△ABC的面积为7,求四边形AEDF•的面积:〔3〕如图〔2〕,如果点E运动到A8的延长线上时,点尸在射线C4上且保持ZEDF = 90°,△.石尸还是等腰直角三角形吗.请说明理由.【答案】〔1〕证实见解析;〔2〕 3.5:〔3〕是,理由见解析.【解析】【分析】〔1〕由题意连接AD,并利用全等三角形的判定判定△ BD年△ ADF〔ASA〕,进而分析证得△.瓦'为等腰直角三角形;〔2〕由题意分析可得S网边形AEDF=S MDF+S AADE=S ABDE+S ACDF,以此进行分析计算求出四边形AEDF的面积即可;〔3〕根据题意连接AD,运用全等三角形的判定判定△ BDE^ △ ADF〔ASA〕,进而分析证得△.所为等腰直角三角形.【详解】解:〔1〕证实:如图①,连接AD.「N BAC=90°,AB=AC,点D是斜边BC的中点,/. AD±BC , AD=BD,・•, Z 1=Z B=45°,Z EDF=90% Z 2+Z 3=90%又,Z 3+Z 4=90°,/. Z 2=Z 4,在^ BDE 和^ ADF 中,Z 1=Z B, AD=BD,Z 2=Z 4,/. △ BDE合 , ADF(ASA),・•, DE二DF,又;Z EDF=90\・•・ ADEF为等腰直角三角形.(2)由(1)可知DE=DF, NON 6=45., 又「N 2+N 3=90°, Z 2+Z 5=90%J Z 3=Z 5,A ADE级△ CDF,・' S N边H,AEDF=S AADF+S CADE二S ABDE+S^CDF,S MBC=2 S 网边毛AEDF,S wijn;AEDF=3.5.(3)是,如图②,连接AD.•/ Z BAC=90\ AB=AC, D 是斜边BC 的中点,/. AD±BC Z AD=BD ,「・Z 1=45°,Z DAF=180°-Z l=180°-45°=135% Z DBE=180°-Z ABC=180°-45°=135%/. Z DAF=Z DBE,「Z EDF=90\/. Z 3+Z 4=90%又;Z 2+Z 3=90°,「・Z 2=Z 4,在仆BDE 和a ADF 中,Z DAF=Z DBE, AD=BD,N 2=Z 4,△ BDE合△ ADF(ASA),・•.DE=DB又:Z EDF=90\.•.A DEF为等腰直角三角形.【点睛】此题考查等腰直角三角形的性质以及全等三角形的判定与性质,根据题意作辅助线构造出全等三角形是解题的关键.5.如图,在MBC中,ZC = 90°, AC = 3, BC = 7,点.是8c边上的动点,连接AD,以AO为斜边在A.的下方作等腰直角三角形AO石.(1)填空:AABC的面积等于—;(2)连接CE,求证:CE是NAC3的平分线;(3)点.在6C边上,且CO = 1,当.从点.出发运动至点3停止时,求点E相应的运动路程.王O 1 _【答案】〔I〕—:〔2〕证实见解析:〔3〕 3点【解析】【分析】〔1〕根据直角三角形的面积计算公式直接计算可得:〔2〕如下图作出辅助线,证实△AEM名ADEN 〔AAS〕,得至I] ME=NE,即可利用角平分线的判定证实:〔3〕由〔2〕可知点E在NACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=!〔AC + C.〕,根据CD的长度计算出CE的长度即可.【详解】解:〔1〕 ZC = 90°, AC = \ BC = 7= -ACxBC = -x3x7 = — ,故答案为:—2〔2〕连接CE,过点E作EMLAC于点M,作EN_LBC于点N,AZEMA=Z END=90°,XVZACB=90SAZMEN=90%AZMED+Z DEN=90°,•••△ADE是等腰直角三角形AZAED=90\ AE=DEA ZAEM+Z MED=90%, ZAEM=Z DEN,在△AEM 与ZkDEN 中,ZEMA=Z END=90% ZAEM=Z DEN, AE=DEAAAEM^ADEN 〔AAS〕/. ME=NE,点E 在NACB 的平分线上, 即CE 是NAC3的平分线工(3)由(2)可知,点E 在NACB 的平分线上,・•・当点D 向点B 运动时,点E 的路径为一条直线,VAAEM^ADEN,AM=DN,即 AC-CM=CN-CD在 RtZiCME 与 RtZkCNE 中,CE=CE, ME=NE,ARtACME^RtACNE (HL)ACM=CN.,.CN=;(AC + CO),又YNMCE 二NNCE=45°, ZCME=90\・,. CE= y/2CN = —(AC + CD).2当 AC=3, CD=CO=1 时,CE=](3 + 1) = 2&当 AC=3, CD=CB=7 时,5CE=r (3 + 7) = 5 虚,点E 的运动路程为:50-20 = 30,£【点睛】此题考查了全等三角形的综合证实题,涉及角平分线的判定,几何中动点问题,全等三角 形的性质与判定,解题的关键是综合运用上述知识点.6.如图1,在长方形ABCD 中,AB=CD=5 cm, BC=12 cm,点P 从点B 出发,以2cm/s 的 速度沿BC 向点C 运动,设点P 的运动时间为ts.(1) PC=—cm :(用含t 的式子表示)■I) I)(2)当t 为何值时,△ABPg^DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻4ABP与以P, Q, C为顶点的直角三角形全等?假设存在,请求出v的值:假设不存在,请说明理由.【答案】(1) (12-2/); (2)1 = 3;(3)存在,P = 2或忏1【解析】【分析】(1)根据P点的运动速度可得BP的长,再利用BC的长减去BP的长即可得到PC的长:(2)先根据三角形全等的条件得出当BP=CP,列方程求解即得;(3)先分两种情况:当BP=CQ, AB=PC 时,△ABPgZ\PCQ:或当BA=CQ, PB=PC 时,△ABPgaQCP,然后分别列方程计算出t的值,进而计算出v的值.【详解】解:(1)当点P以2cm/s的速度沿BC向点C运动时间为ts时3P = 2/57•・• BC = \2cin:.PC = BC-BP = (n-2i)cm故答案为:(12—27)(2) MBP = ^DCP・•. BP = CP・•・ 2/= 12-2/解得1 = 3.(3)存在,理由如下:①当BP=CQ, AB=PC 时,ZiABP名△PCQ,1. PC=AB=5.•.BP=BC-PC=12-5=7•・• BP = Item:.2t=7解得t=3.5.\CQ=BP=7,那么 3.5v=7解得y = 2.②当B4 = C.,PB = PC 时,MBP = \QCP,: BC = ncm,BP = CP = -BC = 6c7〃 2V BP = Item:.2t = 6解得/ = 3CQ = 3vcm,: AB = CQ = 5cm, 3v = 5解得U3综上所述,当u = 2或i,=,时,A48尸与以P, Q,C为顶点的直角三角形全等.【点睛】此题考查全等三角形的判定及性质和矩形的性质,解题关键是将动态情况化为某一状态情况,并以这一状态为等量关系建立方程求解.7.:在MBC中,AB = AC,ZBAC = 90° ,尸Q为过点4的一条直线,分别过B、C两点作8M_LP0,CN_L尸.,垂足分别为M、N.(1)如图①所示,当P.与BC边有交点时,求证:MN = CN — BM ;(2)如图②所示,当与6C边不相交时,请写出线段8M、CN和MN之间的数量关系,并说明理由. 【答案】(1)见解析:(2) MN = BM + CN (或BM = MN — CN或CN = MN-BM ),理由见解析【解析】【分析】(1)根据条件先证AAA/i运ACN4,得到AM = CN,BM = AN,即可证得MN = CN — BM: (2)由(1)知AAMBYACNA,得到4M =CN,8M = AN,即可确定MN = BM + CN.【详解】证实:・・・BM_LPQ,CN_LP0,・•. ZAMB=ZCAN=90°,V ZBAC=90 ° ,AZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NMM)・•. ZBAM = ZACN,在AAMB和ACN4中,'ZAMB = 4CNA・.• ZBAM = AACN , AB = CA:.AAM“ACN4(A4S),.・.AM =CN,BM =AN,,: MN = AM-AN,:.MN = CN — BM.(2) MN = BM + CN (或BM=MN-CN或CN = MN-BM) .理由:•.・BM_LPQ,CN_LP.,・•・ ZAMB=ZCAN=90°,V ZBAC=90 ° ,.\ZCAN+ZACN=90°,ZCAN+ZBAM=90°(或NCW + NAC/V = NC4N+NBAM ),:.ZBAM = ZACN,在AAMB和ACNA中,'AAMB = ZCNAZ.B\M = ZACN , AB = CA:.AAM*ACNA( AAS),.・.AM =CN,BM =AN,:.MN = AN + AM = BM+CN.【点睛】此题考察三角形全等的应用,正确确定全等三角形是解题关键,由此得到对应相等的线段,确定它们之间的和差关系得到80、CN和MN之间的关系式.8.操作发现:如图,己知"配和"DE均为等腰三角形,AB=AC, AD=AE,将这两个三角形放置在一起,使点8, D, E在同一直线上,连接CE.(1)如图1, ZABC= ZACB= ZADE= ZAED=55Q,求证:△BADgZkCAE;(2)在(1)的条件下,求N8EC的度数:拓广探索:(3)如图2,假设NC48=NEAD=120.,8D=4, CF为aBCE中8E边上的高,请直接写出讦的长度.【答案】(1)见解析:(2) 70°; (3) 2【解析】【分析】(1)根据SAS证实△BADg/kCAE即可.(2)利用全等三角形的性质解决问题即可.(3)同法可证4BAD丝ZkCAE,推出EC=BD=4,由NBEC=NBAC=12O0,推出NFCE=30°即可解决问题.(1)证实:如图1中,图1Z ABC=^ ACB = Z ADE=N AED, /. Z EAD=Z CAB,:.Z EAC=A DAB,AE=AD. AC=AB9:.△ BAD^ & CAE (SAS).(2)解:如图1中,设AC交8E于O. •「N A8C=N4C8 = 55°,/. Z 84c=180° - 110° = 70°,BAD^△ CAE,Z ABO=Z ECO,Z EOC=ZAOB,・•, Z CEO = Z 840=70°,即 N BEC= 70°.(3)解:如图2中,A图2Z C48 = N EAD=120\•. Z BAD=A CAE,:AB=AC, AD=AE.△ BAD^ 4 CAE 〔SAS〕,•. Z BAD=A ACE. 8D=EC=4,同理可证N BEC- 8AC=120°,Z F£C=60%CFLEF,Z F=90",•. Z FCE=30\1•. EF=-EC=2. 2此题属于三角形综合题,考查了全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.9.在等边aABC中,点.是边8C上一点.作射线AO,点3关于射线AO的对称点为点E.连接CE并延长,交射线AO于点〔1〕如图,连接AE,①AE与AC的数量关系是;②设NBA尸=a,用.表示NBCF的大小;〔2〕如图,用等式表示线段A尸,CF.所之间的数量关系,并证实.【答案】⑴①AB二AE;②NBCF=.:(2)AF-EF=CF,理由见详解.【解析】【分析】(1)①根据轴对称性,即可得到答案;②由釉对称性,得:AE二AB, NBAF=NEAF=.,由△A3C是等边三角形,得AB=AC, ZBAC=ZACB=60° ,再根据等腰三角形的性质和三角形内角和等于180°,即可求解:(2)作NFCG=60°交AD于点G,连接BF,易证AFCG是等边三角形,得GF=FC,再证△ACG会ABCF(SAS),从而得AG=BF,进而可得至lj结论.【详解】(1)①•・•点4关于射线的对称点为点E , AAB和AE关于射线AD的对称,AAB=AE.故答案是:AB=AE;②•.•点3关于射线的对称点为点E , ,AE二AB, NBAF=NEAF=.,•二△A3c是等边三角形,AAB=AC, ZBAC=ZACB=60" ,:.ZEAC=60° -2a, AE=AC,ZACE=1[180 - (60 - 2a)] = 60 +6?,A ZBCF=ZACE-ZACB=60 +a-60°=a .(2) AF-EF=CF,理由如下:作NFCG=60.交AD于点G,连接BF,•••NBAF=NBCF=a , NADB=NCDF,A ZABC=ZAFC=60c ,••.△FCG是等边三角形,AGF=FC,•二△A3c是等边三角形,ABC=AC, ZACB=60° , AZACG=ZBCF=« .在AACG和ABCF中,CA = CBZACG = ABCF , CG = CF,AACG 仝ABCF(SAS),.,.AG=BF,•・•点4关于射线AO的对称点为点E , .\AG=BF=EF,VAF-AG=GF,.\AF-EF=CE【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.10.如图,AA8C是等边三角形,点.在边4c上〔“点D不与A,C重合〕,点石是射线5c上的一个动点〔点E不与点8,C重合〕,连接OE,以OE为边作作等边三角形hDEF,连接CF.〔1〕如图1,当.石的延长线与A3的延长线相交,且CF在直线OE的同侧时,过点D 作DG//AB, DG 交BC 于点、G ,求证:CF = EG ;〔2〕如图2,当.石反向延长线与A8的反向延长线相交,且.,尸在直线OE的同侧时,求证:CD = CE+CF;〔3〕如图3,当OE反向延长线与线段A8相交,且.,厂在直线O石的异侧时,猜测CD、CE、CP之间的等量关系,并说明理由.【答案】〔1〕证实见详解;〔2〕证实见详解:〔3〕 CF = CO-CE,理由见详解.【解析】【分析】(1)由AABC 是等边三角形,DG//AB,得NCDG=NA=60° , NACB=60.,ACDG 是等边三角形,易证AGDE仝ACDF(SAS),即可得到结论:(2)过点D作DG〃AB交BC于点G,易证A GDE仝△ CDF(SAS),即可得到结论;(3)过点D作DG〃AB交BC于点G,易证A GDE仝A CDF(SAS),即可得到结论.【详解】(1)•・• AA3C是等边三角形,DG//AB, :.ZCDG=ZA=60° , ZACB=60° , ・•. ACQG是等边三角形,.\DG=DC.是等边三角形, .,.DE=DF, ZEDF=60° , A ZCDG-ZGDF=ZEDF-ZGDF,即:ZGDE=ZCDF, 在4 GDE和八CDF中,DE = DFNGDE = NCDF ,DG = DC.,.△GDE^A CDF(SAS),:.CF = EG ;(2)过点D作DG〃AB交BC于点G,如图2,•・• AABC是等边三角形,DG//AB、:.ZCDG=ZA=60° , ZACB=60" ,••・ACDG是等边三角形,:.DG=DC.•••ADE/是等边三角形,,DE=DF, ZEDF=60c ,A ZCDG-ZCDE=ZEDF-ZCDE> 即:ZGDE=ZCDF, 在4 GDE和^ CDF中,DE = DFNGDE = ZCDF ,DG = DC.,.△GDE^ACDF(SAS),:・CF = GE,••. CD = CG = CE+GE = CE+CF(3)CF = CD + CE,理由如下:过点D作DG〃AB交BC于点G,如图3,•・・AA8C是等边三角形,DGUAB, .,.ZCDG=ZA=60° , ZACB=60" ,,ACDG是等边三角形, ADG=DC=GC.•・• ADEF是等边三角形, ,DE=DF, ZEDF=60° ,A ZCDG+ZCDE=ZEDF+ZCDE,即:NGDE=NCDF, 在A GDE和4 CDF中,DE = DFNGDE = ZCDF , DG = DCAAGDE^ACDF(SAS),,CF = G£=GC+CE=CD+CE.【点睛】此题主要考查等边三角形的性质和三角形全等的判定和性质定理,添加辅助线,构造全等三角形,是解题的关键.。
专题01 全等三角形(解析版)

2021-2022学年人教版数学八年级上册压轴题专题精选汇编专题01 全等三角形一.选择题1.(2020秋•东城区期末)如图所示,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA,若OD=5,AB=20,则△AOB的面积是( )A.20B.30C.50D.100【思路引导】根据角平分线的性质求出OE,最后用三角形的面积公式即可解答.【完整解答】解:过O作OE⊥AB于点E,∵BO平分∠ABC,OD⊥BC于点D,∴OE=OD=5,∴△AOB的面积=,故选:C.2.(2020秋•定西期末)如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为( )A.4B.3C.2D.1【思路引导】根据垂线段最短得出当DP⊥BC时,DP的长最小,求出∠ABD=∠CBD,根据角平分线的性质得出此时DP=AD,再得出选项即可.【完整解答】解:当DP⊥BC时,DP的长最小,∵BD⊥CD,∴∠BDC=90°,∵∠A=90°,∠ADB=∠C,∠A+∠ADB+∠ABD=180°,∠BDC+∠C+∠CBD=180°,∴∠ABD=∠CBD,∵∠A=90°,∴当DP⊥BC时,DP=AD,∵AD=4,∴DP的最小值是4,故选:A.3.(2020秋•莫旗期末)如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,则PE的最小值为( )A.8B.5C.4D.2【思路引导】过E作EP⊥BC于P,此时PE的值最小,求出AD⊥CD,根据角平分线的性质求出AE=DE=PE,求出AE的长即可.【完整解答】解:过E作EP⊥BC于P,此时PE的值最小,∵AB∥CD,AD⊥AB,∴AD⊥CD,∵BE和CE分别平分∠ABC和∠BCD,∴AE=PE,ED=PE,∴AE=ED=PE,∵AD=8,∴PE=4,即PE的最小值是4,故选:C.4.(2020秋•鞍山期末)如图,Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点D作DF⊥AB,垂足为点F,点E在边AC上,若DE=DB,则下列结论不正确的是( )A.DC=DF B.DE=BF C.AC=AF D.AB=AC+CE【思路引导】根据全等三角形的判定和性质解答即可.【完整解答】解:∵Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点D作DF⊥AB,垂足为点F,∴DC=DF,故A正确,在Rt△DCE与Rt△DFB中,,∴Rt△DCE≌Rt△DFB(HL),∴CE=BF,故B错误,在Rt△ADC与Rt△ADF中,,∴Rt△ADC≌Rt△ADF(HL),∴AC=AF,故C正确,∴AB=AF+BF=AC+CE,故D正确,故选:B.5.(2020秋•新宾县期末)如图,AB=AD,AC=AE,∠DAB=∠CAE=50°,以下四个结论:①△ADC≌△ABE;②CD=BE;③∠DOB=50°;④点A在∠DOE的平分线上,其中结论正确的个数是( )A.1B.2C.3D.4【思路引导】证明△ADC≌△ABE(SAS),可得出CD=BE,∠ADC=∠ABE,则得出∠DOB=50°,连接OA,过点A作AM⊥CD于点M,AN⊥BE于点N,证明△ABN≌△ADM(AAS),则可得出点A在∠DOE的平分线上.【完整解答】解:∵∠DAB=∠CAE=50°,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE,在△ADC与△ABE中,,∴△ADC≌△ABE(SAS),∴CD=BE;故①,②正确;如图1,若AB与CD相交于点F,∵△ABE≌△ADC,∴∠ADC=∠ABE,∵∠AFD=∠CFB,∴∠DOB=∠DAB=50°.故③正确.如图2,连接OA,过点A作AM⊥CD于点M,AN⊥BE于点N,∴∠AMD=∠ANB=90°,∵△ABE≌△ADC,∴∠ABN=∠ADM,在△ABN和△ADM中,,∴△ABN≌△ADM(AAS),∴AN=AM,∴点A在∠DOE的平分线上.故④正确.故选:D.6.(2020秋•金昌期末)如图,AD是△ABC的角平分线,CE⊥AD,垂足为F.若∠CAB=30°,∠B=55°,则∠BDE的度数为( )A.35°B.40°C.45°D.50°【思路引导】根据三角形的内角和求出∠ACB=95°,利用三角形全等,求出DC=DE,再利用外角求出答案.【完整解答】解:∵∠CAB=30°,∠B=55°,∴∠ACB=180°﹣30°﹣55°=95°,∵CE⊥AD,∴∠AFC=∠AFE=90°,∵AD是△ABC的角平分线,∴∠CAD=∠EAD=×30°=15°,又∵AF=AF,∴△ACF≌△AEF(ASA)∴AC=AE,∵AD=AD,∠CAD=∠EAD,∴△ACD≌△AED(SAS),∴DC=DE,∴∠DCE=∠DEC,∵∠ACE=90°﹣15°=75°,∴∠DCE=∠DEC=∠ACB﹣∠ACE=95°﹣75°=20°,∴∠BDE=∠DCE+∠DEC=20°+20°=40°,故选:B.7.(2020秋•宜兴市期中)如图,在△ABC中,AB=4,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )A.B.C.D.【思路引导】把要求的最大值的两条线段经过平移后形成一条线段,然后再根据垂线段最短来进行计算即可.【完整解答】解:如图,过点C作CK⊥l于点K,过点A作AH⊥BC于点H,在Rt△AHB中,∵∠ABC=60°,AB=4,∴BH=2,AH=2,在Rt△AHC中,∠ACB=45°,∴AH=CH=2,∴AC===2,∵点D为BC中点,∴BD=CD,在△BFD与△CKD中,,∴△BFD≌△CKD(AAS),∴BF=CK,延长AE,过点C作CN⊥AE于点N,得矩形ENCK,∴CK=EN,∴AE+BF=AE+CK=AE+EN=AN,在Rt△ACN中,AN<AC,当直线l⊥AC时,最大值为2,综上所述,AE+BF的最大值为2.故选:B.8.(2020秋•江岸区校级月考)如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)A.28B.29C.30D.31【思路引导】当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,由此即可判断.【完整解答】解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,∴一共有:8+24﹣1=31(个)三角形与△ABC全等,故选:D.二.填空题9.(2020秋•南岗区校级月考)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=5,则CH的长为 2 .【思路引导】先由AD⊥BC,CE⊥AB,判断出∠ADB=∠AEH=90°,再判断出∠BAD=∠BCE,进而判断出△HEA≌△BEC,得出AE=EC=5,即可得出结论.【完整解答】解:∵AD⊥BC,CE⊥AB,∴∠ADB=∠AEH=90°,∵∠AHE=∠CHD,∴∠BAD=∠BCE,在△HEA和△BEC中,,∴△HEA≌△BEC(AAS),∴AE=EC=5,则CH=EC﹣EH=AE﹣EH=5﹣3=2.故答案为:2.10.(2020•松北区一模)在△ABC中,点D在AC上,AD=5,AB+AC=16,E是BD中点,∠ACB=∠ABC+2∠BCE,则CD= 2 .【思路引导】延长CE于F,使CE=EF,交AB于点G,根据SAS证明△BEF与△DEC全等,进而利用全等三角形的性质解答即可.【完整解答】解:延长CE于F,使CE=EF,交AB于点G,∵E是BD的中点,∴BE=DE,在△BEF与△DEC中,,∴△BEF≌△DEC(SAS),∴∠F=∠DCE,BF=DC,∵∠ACB=∠ABC+2∠BCE,∴∠DCE=∠ACB﹣∠BCE=∠ABC+∠BCE,∵∠AGC=∠ABC+∠BCE,∴∠AGC=∠DCE,∴∠F=∠DCE=∠AGC=∠BGF,AG=AC,∴BF=BG=CD,设BF=BG=CD=x,∵AD=5,AB+AC=16,∴,解得:x=2,∴CD=2,故答案为:2.11.(2020•荷塘区模拟)在△ABC中,若其内部的点P满足∠APB=∠BPC=∠CPA=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,PA=4,则△PAC的面积为 4 .【思路引导】如图,延长BP交AC于D,先说明△ABD是等腰直角三角形,△ADP是30°的直角三角形,可得PD和AD的长,根据费马点的定义可得∠APC=120°,从而可知△PDC也是30°的直角三角形,可得CD的长,根据三角形的面积公式可得结论.【完整解答】解:如图,延长BP交AC于D,∵∠BAC=∠PBA=45°,∴∠ADB=90°,AD=BD,∵P为△ABC的费马点,∴∠APB=∠CPA=120°,∴∠BAP=180°﹣120°﹣45°=15°,∴∠PAC=45°﹣15°=30°,∴∠APD=60°,Rt△PAD中,∵PA=4,∴PD=2,AD=2,∵∠APC=120°,∴∠CPD=120°﹣60°=60°,Rt△PDC中,∠PCD=30°,∴CD=2,∴AC=AD+CD=2+2=4,∴△PAC的面积为==4.故答案为:4.12.(2020秋•海珠区校级期中)如图,AD是△ABC的角平分线,DF⊥AB,垂足为点F,DE=DG,△ADG 和△ADE的面积分别为50和39,则△EDF的面积为 5.5 .【思路引导】在线段AC上取一点M,使DM=DE,过点D作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.【完整解答】解:如图,在线段AC上取一点M,使DM=DE,过点D作DN⊥AC于点N,∵DE=DG,∴DM=DG,∵AD是△ABC的角平分线,DF⊥AB,∴DF=DN,在Rt△DEF和Rt△DMN中,,∴Rt△DEF≌Rt△DMN(HL),∵△ADG和△AED的面积分别为50和39,∴S△MDG =S△ADG﹣S△ADM=50﹣39=11,∴S△DNM =S△EDF=S△MDG=×11=5.5.故答案是:5.5.13.(2020秋•青羊区校级月考)如图,在△ABC中,∠C=90°,D是AB中点,FD⊥ED于D,BE=,AF=,则EF= 3 .【思路引导】延长DE到H,使DH=DE,连接FH,先证△BED≌△AHD(SAS),得AH=BE,∠B=∠DAH,再求出∠FAH=90°,然后由勾股定理求出FH=3,最后由线段垂直平分线上的性质即可得出答案.【完整解答】解:如图,延长DE到H,使DH=DE,连接FH,∵D是AB中点,∴AD=BD,在△BED和△AHD中,,∴△BED≌△AHD(SAS),∴AH=BE=,∠B=∠DAH,∵∠C=90°,∴∠FAH=∠BAC+∠DAH=∠BAC+∠B=180°﹣90°=90°,由勾股定理得,FH===3,∵FD⊥ED,DE=DH,∴EF=FH=3,故答案为:3.14.(2020秋•温岭市期中)如图,AD是△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,给出下列结论:①DE=DF;②△ADF≌△ADE;③△ABD和△ACD的面积相等.其中正确结论的序号是 ①② .【思路引导】根据角平分线的性质和全等三角形的判定和性质解答即可.【完整解答】解:∵AD是△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,∴DE=DF,故①正确;在Rt△ADF与Rt△ADE中,,∴Rt△ADF≌Rt△ADE(HL),故②正确;∵得不出AB=AC,∴△ABD和△ACD的面积无法判断相等,故③错误;故答案为:①②.15.(2019秋•南岗区校级月考)如图,在△ABC中,∠ACB=90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为 4 .【思路引导】设∠BCD=α,延长AC到点G,使AG=AB,连接BG,延长EF和CA交于点H,根据已知条件证明△CEH≌△CGB,即可解决问题.【完整解答】解:设∠BCD=α,∵∠ACB=90°,∴∠ACD=90°﹣α,∵AD=AC,∴∠ADC=∠ACD=90°﹣α,∴∠CAB=180°﹣2∠ACD=2α,∴∠ABC=90°﹣2α,∵EF⊥CD,∴∠CKF=90°,∴∠DFK=90°﹣(90°﹣α)=α,∴∠CEF=90°﹣α,如图,延长AC到点G,使AG=AB,连接BG,∵AD=AC,∴CD∥GB,BD=CG=CE,∴∠GBC=∠BCD=α,∴∠G=90°﹣α,∴∠G=∠CEF,延长EF和CA交于点H,∴∠H=α=∠GBC,∵∠CAB=2α,∴∠AFH=α,∴∠H=∠AFH,∴AH=AF=2,在△CEH和△CGB中,,∴△CEH≌△CGB(ASA),∴CH=CB=8,∴DF=AD﹣AF=AC﹣AH=CH﹣2AH=8﹣4=4.故答案为:4.16.(2019秋•江汉区期中)如图,AB⊥CD于点E,且AB=CD=AC,若点I是△ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=135°;②BD=BI;③S△AIC =S△BID;④IF⊥AC.其中正确的是 ①③④ (填序号).【思路引导】如图,延长IF到G,使得FG=FI,连接DG,BG,延长FI交AC于K.利用全等三角形的判定和性质,平行四边形的判定和性质一一判断即可.【完整解答】解:如图,延长IF到G,使得FG=FI,连接DG,BG,延长FI交AC于K.∵AB ⊥CD ,∴∠AEC =90°,∴∠EAC +∠ECA =90°,∴∠IAC +∠ICA =∠EAC +∠ECA =45°,∴∠AIC =180°﹣45°=135°,故①正确,∵AB =AC ,∠IAB =∠IAC ,AI =AI ,∴△AIB ≌△AIC (SAS ),∴∠AIB =∠AIC =135°,IA =ID ,∴∠BIC =360°﹣135°﹣135°=90°,同法可证:△ICA ≌△ICD (SAS ),∴∠AIC =∠CID =135°,IA =ID ,∴∠AID =360°﹣135°﹣135°=90°,∴∠DIB +∠AIC =180°,∵DF =FB ,IF =FG ,∴四边形IBGD 是平行四边形,∴ID =BG =AI ,ID ∥BG ,∴∠DIB +∠IBG =180°,∴∠AIC =∠IBG ,∵IA =ID ,IC =IB ,∴△AIC ≌△GBI (SAS ),∴∠GIB =∠ACI ,S △AIC =S △BGI =S 平行四边形DGBI =S △BDI ,故③正确,∵∠GIB +∠CIK =90°,∴∠CIK +∠ICK =90°,∴∠IKC =90°,即IF ⊥AC ,故④正确,不妨设BI =BD ,则△BDI 是等腰直角三角形,显然ID =IB ,即AI =IC ,显然题目不满足这个条件,故②错误.故答案为①③④.17.(2018秋•襄城县期末)如图,△ABC 的内角∠ABC 和外角∠ACD 的平分线相交于点E ,BE 交AC 于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:①∠BEC=∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有 ①③④ (将所有正确答案的序号填写在横线上).【思路引导】①根据角平分线的定义得到∠EBC=∠ABC,∠DCE=ACD,根据外角的性质即可得到结论;②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;③由BG=GE,CH=EH,于是得到BG﹣CH=GE﹣EH=GH.即可得到结论;④由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.【完整解答】解:①BE平分∠ABC,∴∠EBC=∠ABC,∵CE平分∠ACD,∴∠DCE=ACD,∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,∴∠EBC+∠BEC=(∠BAC+∠ABC)=∠EBC+BAC,∴∠BEC=∠BAC,故①正确;∵②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.③BE平分∠ABC,∴∠ABE=∠CBE,∵GE∥BC,∴∠CBE=∠GEB,∴∠ABE=∠GEB,∴BG=GE,同理CH=HE,∴BG﹣CH=GE﹣EH=GH,故③正确.④过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,∵BE平分∠ABC,∴EM=ED,∵CE平分∠ACD,∴EN=ED,∴EN=EM,∴AE平分∠CAM,设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,则∠BAC=180°﹣2z,∠ACB=180﹣2x,∵∠ABC+∠ACB+∠BAC=180°,∴2y+180°﹣2z+180°﹣2x=180°,∴x+z=y+90°,∵z=y+∠AEB,∴x+y+∠AEB=y+90°,∴x+∠AEB=90°,即∠ACE+∠AEB=90°,故④正确;故答案为:①③④.18.(2019秋•潍坊月考)如图,△ABC中,AB=4,AC=7,M是BC的中点,AD平分∠BAC,过M作MF∥AD,交AC于F,则FC的长等于 5.5 .【思路引导】可通过作辅助线,即延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,从而利用角之间的关系转化为线段之间的关系,进而最终可得出结论.【完整解答】解:如图,延长FM到N,使MN=MF,连接BN,延长MF交BA延长线于E,∵M是BC中点,∴BM=CM,∠BMN=∠CMF,∴△BMN≌△CMF,∴BN=CF,∠N=∠MFC,又∵∠BAD=∠CAD,MF∥AD,∴∠E=∠BAD=∠CAD=∠CFM=∠AFE=∠N,∴AE=AF,BN=BE,∴AB+AC=AB+AF+FC=AB+AE+FC=BE+FC=BN+FC=2FC,∴FC=(AB+AC)=5.5.故答案为5.5.三.解答题19.(2021春•铁岭月考)如图,在四边形ABCD中,∠B+∠ADC=180°,CE平分∠BCD交AB于点E,连接DE.(1)若∠A=50°,∠B=70°,求∠BEC的度数;(2)若∠A=∠1,试说明∠CDE=∠DCE.【思路引导】(1)求出∠A+∠BCD=180°,求出∠BCD,求出∠BCE,根据三角形内角和定理求出即可;(2)根据三角形内角和定理和∠A+∠BCD=180°求出∠CDE=∠BCE,即可得出答案.【完整解答】解:(1)∵∠A+∠B+∠BCD+∠ADC=360°,∠B+∠ADC=180°,∴∠A+∠BCD=180°,∵∠A=50°,∴∠BCD=130°,∵CE平分∠BCD∴∠BCE=∠BCD=×130°=65°,∵∠B=70°,∴∠BEC=180°﹣65°﹣70°=45°,(2)证明:由(1)知∠A+∠BCD=180°,∴∠A+∠BCE+∠DCE=180°,∵∠CDE+∠DCE+∠1=180°,∠1=∠A,∴∠BCE=∠CDE,∵CE平分∠BCD,∴∠DCE=∠BCE,∴∠CDE=∠DCE.20.(2021•南岗区模拟)已知:点E,F在BC上,AF=DE,BE=CF,∠AFE=∠DEF.(1)如图1,求证:AB=CD;(2)如图2,连接AC,BD,AE,DF,在不添加任何辅助线的情况下,请直接写出图2中的四组平行线.【思路引导】(1)证△ABF≌△DCE(SAS),即可得出结论;(2)由全等三角形的性质得∠B=∠C,得AB∥CD,再证四边形ABDC是平行四边形,得AC∥BD,同理证出AF∥DE,AE∥DF.【完整解答】(1)证明:∵BE=CF,∴BE﹣EF=CF﹣EF,即BF=CE,∵∠AFE=∠DEF,∴∠AFB=∠DEC,在△ABF和△DCE中,,∴△ABF≌△DCE(SAS),∴AB=CD;(2)解:图2中的四组平行线为:AB∥CD,AC∥BD,AF∥DE,AE∥DF,理由如下:由(1)得:△ABF≌△DCE,∴AB=DC,∠B=∠C,∴AB∥CD,∴四边形ABDC是平行四边形,∴AC∥BD,∵∠AFE=∠DEF,∴AF∥DE,∵AF=DE,∴四边形AEDF是平行四边形,∴AE∥DF.21.(2020秋•来宾期末)如图,在五边形ABCDE中,AB=DE,AC=AD.(1)请你添加一个与角有关的条件,使得△ABC≌△DEA,并说明理由;(2)在(1)的条件下,若∠CAD =65°,∠B =110°,求∠BAE 的度数.【思路引导】(1)添加∠BAC =∠EDA ,根据SAS 即可判定两个三角形全等;(2)根据全等三角形对应角相等,运用三角形内角和定理,即可得到∠BAE 的度数.【完整解答】解:(1)添加一个角方面的条件为:∠BAC =∠EDA ,使得△ABC ≌△DEA ,理由如下:在△ABC 和△DEA 中,,∴△ABC ≌△DEA (SAS ),(2)在(1)的条件下,∵△ABC ≌△DEA ,∴∠ACB =∠DAE ,∵∠CAD =65°,∠B =110°,∴∠ACB +∠BAC =180°﹣∠B =70°,∴∠DAE +∠BAC =∠ACB +∠BAC =70°,∴∠BAE =∠DAE +∠BAC +∠CAD =70°+65°=135°.22.(2020秋•云南期末)如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是152cm 2,AB =20cm ,AC =18cm ,求DE 的长.【思路引导】根据S △ABC =S △ABD +S △ACD ,再利用角平分线的性质即可解决问题.【完整解答】解:∵AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,∴DE =DF ,∵S △ABC =S △ABD +S △ACD ,∴S △ABC =,∵△ABC 面积是152cm 2,AB =20cm ,AC =18cm ,∴152=,∴10DE +9DF =152,∵DE =DF ,∴19DE =152,∴DE =8.23.(2021春•萧山区月考)如图,在△ABC 中,OE ⊥AB 与点E ,OF ⊥AC 与点F ,且OE =OF .(1)如图①,当O 为BC 中点时,试说明AB =AC ;(2)如图②,当点O 在△ABC 内部,且OB =OC ,试判断AB 与AC 的关系.【思路引导】(1)证Rt △OBE ≌Rt △OCF (HL ),得∠B =∠C ,即可得出AB =AC ;(2)由等腰三角形的性质得∠OBC =∠OCB ,再证Rt △OBE ≌Rt △OCF (HL ),得∠ABO =∠ACO ,则∠ABC =∠ACB ,即可得出结论.【完整解答】(1)说明如下:∵O 为BC 中点,∴BO =CO ,∵OE ⊥AB ,OF ⊥AC ,∴∠OEB =∠OFC =90°,在Rt △OBE 和Rt △OCF 中,,∴Rt △OBE ≌Rt △OCF (HL ),∴∠B =∠C ,∴AB =AC ;(2)解:AB=AC,理由如下:∵OB=OC,∴∠OBC=∠OCB,∵OE⊥AB,OF⊥AC,∴∠OEB=∠OFC=90°,在Rt△OBE和Rt△OCF中,,∴Rt△OBE≌Rt△OCF(HL),∴∠ABO=∠ACO,∴∠ABC=∠ACB,∴AB=AC.24.(2021春•南山区校级期中)如图,在△ABC中,AB=AC=3,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=110°时,∠EDC= 30° ,∠AED= 70° .(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.【思路引导】(1)由平角的定义和三角形外角的性质可求∠EDC,∠DEC的度数;(2)当DC=3时,由“AAS”可证△ABD≌△DCE;(3)分AD=DE,DE=AE,AE=AD三种情况讨论,由三角形内角和和三角形外角的性质可求∠BDA 的度数.【完整解答】解:(1)∵∠ADB+∠ADE+∠EDC=180°,且∠ADE=40°,∠BDA=110°,∴∠EDC=180°﹣110°﹣40°=30°,∵AB=AC,∴∠B=∠C=40°,∴∠AED=∠EDC+∠C=30°+40°=70°,故答案为:30°,70°;(2)当DC=3时,△ABD≌△DCE,理由如下:∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠CDE,∠B=∠ADE=40°,∴∠BAD=∠CDE,且AB=CD=3,∠B=∠C=40°,∴△ABD≌△DCE(ASA);(3)若AD=DE时,∵AD=DE,∠ADE=40°,∴∠DEA=∠DAE=70°,∵∠DEA=∠C+∠EDC,∴∠EDC=30°,∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣30°=110°,若AE=DE时,∵AE=DE,∠ADE=40°,∴∠ADE=∠DAE=40°,∴∠AED=100°,∵∠DEA=∠C+∠EDC,∴∠EDC=60°,∴∠BDA=180°﹣∠ADE﹣∠EDC=180°﹣40°﹣60°=80°,若AE=AD时,∠AED=∠ADE=40°,∠DAE=180°﹣40°﹣40°=100°,此时D与B重合,不合题意,舍去.综上所述:当∠BDA=80°或110°时,△ADE的形状可以是等腰三角形.25.(2021春•沂源县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC 上,且BD=DF.(1)求证:CF=EB;(2)请你判断AE、AF与BE之间的数量关系,并说明理由.【思路引导】(1)根据角平分线的性质得到DC=DE,根据直角三角形全等的判定定理得到Rt△DCF≌Rt△DEB,根据全等三角形的性质定理得到答案;(2)根据全等三角形的性质定理得到AC=AE,根据(1)的结论得到答案.【完整解答】证明:(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,∴DC=DE,在Rt△DCF和Rt△DEB中,,∴Rt△DCF≌Rt△DEB,∴CF=EB;(2)AF+BE=AE.∵Rt△DCF≌Rt△DEB,∴AC=AE,∴AF+FC=AE,即AF+BE=AE.26.(2020秋•腾冲市期末)(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.【思路引导】(1)由条件可证明△ABD≌△CAE,可得DA=CE,AE=BD,可得DE=BD+CE;(2)由条件可知∠BAD+∠CAE=180°﹣α,且∠DBA+∠BAD=180°﹣α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论;(3)由条件可知EM=AH=GN,可得EM=GN,结合条件可证明△EMI≌△GNI,可得出结论I是EG 的中点.【完整解答】解:(1)如图1,∵BD⊥直线l,CE⊥直线l,∴∠BDA=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE;(2)DE=BD+CE.如图2,证明如下:∵∠BDA=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠DBA=∠CAE,在△ADB和△CEA中..∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE(3)如图3,过E作EM⊥HI于M,GN⊥HI的延长线于N.∴∠EMI=GNI=90°由(1)和(2)的结论可知EM=AH=GN∴EM=GN在△EMI和△GNI中,,∴△EMI≌△GNI(AAS),∴EI=GI,∴I是EG的中点.27.(2020秋•大武口区期末)如图所示,已知△ABC中,点D为BC边上一点,∠1=∠2=∠3,AC=AE,(1)求证:△ABC≌△ADE;(2)若AE∥BC,且∠E=∠CAD,求∠C的度数.【思路引导】(1)由∠1=∠2=∠3,可得∠1+∠DAC=∠DAC+∠2,即∠BAC=∠DAE,又∠1+∠B=∠ADE+∠3,则可得∠B=∠ADE,已知AC=AE,即可证得:△ABC≌△ADE;(2)由题意可得,∠ADB=∠ABD=4x,在△ABD中,可得x+4x+4x=180°,解答处即可;【完整解答】解:(1)∵∠1=∠2=∠3,∴∠1+∠DAC=∠DAC+∠2,即∠BAC=∠DAE,又∵∠1+∠B=∠ADE+∠3,则可得∠B=∠ADE,在△ABC和△ADE中,∴△ABC≌△ADE(AAS);(2)∵AE∥BC,∴∠E=∠3,∠DAE=∠ADB,∠2=∠C,又∵∠3=∠2=∠1,令∠E=x,则有:∠DAE=3x+x=4x=∠ADB,又∵由(1)得AD=AB,∠E=∠C,∴∠ABD=4x,∴在△ABD中有:x+4x+4x=180°,∴x=20°,∴∠E=∠C=20°.28.(2020秋•船营区期末)如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.【思路引导】已知等边及垂直,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.【完整解答】解:影子一样长.证明:∵AB⊥BC,A′B′⊥B′C′∴∠ABC=∠A′B′C′=90°∵AC∥A′C′∴∠ACB=∠A′C′B′在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(AAS)∴BC=B′C′即影子一样长.。
全等三角形专项练习与答案解析

一、选择题(题型注释)1.小明想用三根木棒为边制作一个三角形,则可以选用的木棒长为()A .8cm 、15cm 、6cmB .7cm 、9cm、13cmC .10cm 、20cm 、30cmD .20cm 、40cm 、60cm【答案】B2.如图所示,已知△ABE ≌△ACD ,∠1=∠2,∠B=∠C ,下列不正确的等式是()A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE【答案】D3.已知:如图所示,AC=CD ,∠B=∠E=90°,AC ⊥CD ,则不正确的结论是()A 、∠A 与∠D 互为余角B 、∠A=∠2C 、△ABC≌△CEDD 、∠1=∠2【答案】D4.如图,△ABC 中,∠C=90°,AC=BC,AD 平分∠CAB,交BC 于D,DE ⊥AB 于E.AB =6cm,则△DEB 的周长为()A. 4cmB. 6cmC. 10cmD. 14cm【答案】B5.如图,OA =OC ,OB =OD ,OA ⊥OB ,OC ⊥OD ,下列结论:①△AOD ≌△COB ;②CD =AB ;③∠CDA =∠ABC ; 其中正确的结论是()A .①②B .①②③C .①③D .②③AB C DE12【答案】B【解析】试题分析:因为OA=OC,OB=OD,OA⊥OB,OC⊥OD,可得△COD≌△AOB,∠CDO=∠ABO;∠DOC+∠AOC=∠AOB+∠AOC,OA=OC,OB=OD,所以△AOD≌△COB,所以CD=AB,∠ADO=∠CBO;所以∠CDA=∠ABC.故①②③都正确.故选B考点:三角形全等的判定和性质6.如图,△ABC中,∠B=∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是()A.2α+∠A=180°B.α+∠A=90°C.2α+∠A=90°D.α+∠A=180°【答案】A【解析】试题分析:根据已知条件可证明△BDE≌△CFD,则∠BED=∠CDF,由∠A+∠B+∠C=180°,得∠B=,因为∠BDE+∠EDF+∠CDF=180°,所以得出a与∠A的关系2a+∠A=180°.考点:全等三角形的判定和性质,三角形的内角和定理7.如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则()A.BE+CF>EFB.BE+CF=EFC.BE+CF<EFD.BE+CF与EF的大小关系不能确定.【答案】A.8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是()A.10cmB.12cmC.15cmD.17cm【答案】C.【解析】试题分析:∵AB的垂直平分AB,∴AE=BE,BD=AD,∵AE=3cm,△ADC的周长为9cm,∴△ABC的周长是9cm+2×3cm=15cm,故选C.考点:线段垂直平分线的性质.9.如图所示,∠A+∠B+∠C+∠D+∠E的结果为()A.90°B.180°C.360°D.无法确定【答案】【解析】试题分析:延长BE交AC于F,∵∠A+∠B=∠2,∠D+∠E=∠1,∠1+∠2+∠C=180°,∴∠A+∠B+∠C+∠D+∠E=180°,考点:1.三角形内角和定理;2.三角形的外角性质.10.若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()A、36B、72C、108D、144【答案】C【解析】∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°,∵2(∠A+∠C)=3∠B,∴∠B=72°,11.如图,AB∥CD,∠D=∠E=35°,则∠B的度数为().A.60°B.65°C.70°D.75°【答案】C.12.如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是()A.∠1+∠0=∠A+∠2B.∠1+∠2+∠A+∠O=180°C.∠1+∠2+∠A+∠O=360°D.∠1+∠2+∠A=∠O【答案】D.【解析】试题分析:连接AO 并延长,交BC 于点D ,∵∠BOD 是△AOB 的外角,∠COD 是△AOC 的外角,∴∠BOD=∠BAD+∠1①,∠COD=∠CAD+∠2②,①+②得,∠BOC=(∠BAD+∠CAD )+∠1+∠2,即∠BOC=∠BAC+∠1+∠2.故选D .考点:1.三角形的外角性质;2.三角形内角和定理.13.如图,BD 是∠ABC 的角平分线,DE ⊥AB 于E ,DF ⊥BC 于F ,,,,△cm 12BC cm 18AB cm 362ABC ===S 则DE 的长是()【答案】B【解析】试题分析:∵BD 是∠ABC 的角平分线,DE ⊥AB ,DF ⊥BC,由角平分线的性质可得DE=DF∴DCB S S ∆∆+=ADB ABC S △=∴所以选B.考点:角平分线的性质第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释)14.如图,△ABC 中,∠A =90°,DE 是BC 的垂直平分线,AD=DE ,则∠C 的度数是°.【答案】30°.【解析】试题分析:∵DE 是BC 的垂直平分线,∴DE ⊥BC ,∵∠A =90°,AD=DE ,∴BD 平分∠AABC ,∴∠ABD=∠DBC ,∵DE 是BC 的垂直平分线,∴DC=BD ,∴∠C=∠DBC ,∴3∠C=90°,∴∠C=30°.故答案为:30°.考点:1.线段垂直平分线的性质;2.角平分线的性质.15.如图,在△ABC 中,∠ACB =90°,AB 的垂直平分线DE 交AB 于E ,交AC 于D ,∠DBC =30°,BD =4.6,则D 到AB 的距离为。
全等三角形判定-专题复习50题(含答案解析)

全等三⾓形判定-专题复习50题(含答案解析)全等三⾓形判定⼀、选择题:1.如图所⽰,亮亮书上的三⾓形被墨迹污染了⼀部分,很快他就根据所学知识画出⼀个与书上完全⼀样的三⾓形,那么这两个三⾓形完全⼀样的依据是()A.SSS B.SAS C.AAS D.ASA2.⽅格纸中,每个⼩格顶点叫做⼀个格点,以格点连线为边的三⾓形叫做格点三⾓形.如图,在4×4的⽅格纸中,有两个格点三⾓形△ABC、△DEF,下列说法中成⽴的是()A.∠BCA=∠EDF B.∠BCA=∠EFDC.∠BAC=∠EFD D.这两个三⾓形中,没有相等的⾓3.如图所⽰,△ABD≌△CDB,下⾯四个结论中,不正确的是()A.△ABD和△C DB的⾯积相等B.△ABD和△CDB的周长相等C.∠A+∠ABD=∠C+∠CBD D.AD∥BC,且AD=BC4.下列判断中错误..的是()A.有两⾓和⼀边对应相等的两个三⾓形全等B.有两边和⼀⾓对应相等的两个三⾓形全等C.有两边和其中⼀边上的中线对应相等的两个三⾓形全等D.有⼀边对应相等的两个等边三⾓形全等5.使两个直⾓三⾓形全等的条件是()A.⼀个锐⾓对应相等B.两个锐⾓对应相等C.⼀条边对应相等D.两条边对应相等6.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于()A.∠EDB B.∠BED C.∠AFB D.2∠ABF7.在△ABC和△A/B/C/中,已知∠A=∠A/,AB=A/B/,在下⾯判断中错误的是( )A.若添加条件AC=A/C/,则△ABC≌△△A/B/C/B.若添加条件BC=B/C/,则△ABC≌△△A/B/C/C.若添加条件∠B=∠B/,则△ABC≌△△A/B/C/D.若添加条件∠C=∠C/,则△ABC≌△△A/B/C/8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪⼀个条件⽆法证明△ABC≌△DEF()A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F9.如图,在△ABC中,∠ABC=45°,AC=8cm,F是⾼AD和BE的交点,则BF的长是()A.4cm B.6cm C.8cm D.9cm10.在如图所⽰的5×5⽅格中,每个⼩⽅格都是边长为1的正⽅形,△ABC是格点三⾓形(即顶点恰好是正⽅形的顶点),则与△ABC有⼀条公共边且全等的所有格点三⾓形个数是()A.1 B.2 C.3 D.411.如图,点E在正⽅形ABCD的对⾓线AC上,且EC=2AE,直⾓三⾓形FEG的两直⾓边EF、EG分别交BC、DC于点M、N.若正⽅形ABCD的边长为a,则重叠部分四边形EMCN的⾯积为()A.a2B.a2C.a2D.a212.在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表⽰某⼈从A地到B地的不同⾏进路线(箭头表⽰⾏进的⽅向),则路程最长的⾏进路线图是()A.B.C.D.⼆、填空题:13.如图所⽰,有⼀块三⾓形的镜⼦,⼩明不⼩⼼弄破裂成1、2两块,现需配成同样⼤⼩的⼀块.为了⽅便起见,需带上块,其理由是.14.如图⽰,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加⼀个条件是__________.(填上你认为适当的⼀个条件即可)15.如图,已知∠1=∠2,AC=AD,请增加⼀个条件,使△ABC≌△AED,你添加的条件是.16.如图,∠1=∠2,要使△ABD≌△ACD,需添加的⼀个条件是(只添⼀个条件即可).17.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三⾓形对.18.如图,△ABD≌△BAC,若AD=BC,则∠BAD的对应⾓是.19.如图,已知AB⊥BD,垂⾜为B,ED⊥BD,垂⾜为D,AB=CD,BC=DE,则∠ACE= 度.20.如图,如果两个三⾓形的两条边和其中⼀条边上的⾼对应相等,那么这两个三⾓形的第三边所对的⾓的关系是.三、解答题:21.如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂⾜分别为A.B.试说明AD+AB=BE.22.如图,E、A.C三点共线,AB∥CD,∠B=∠E,,AC=CD。
中考数学复习考点题型专练19--全等三角形(解析版)

中考数学复习考点题型专练专题19全等三角形(满分:100分时间:90分钟)班级_________ 姓名_________学号_________ 分数_________ 一、单选题(共10小题,每小题3分,共计30分)1.(2022·浙江湖州市·中考真题)在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积. 如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是()A.D【答案】D【分析】根据中心对称的性质即可作出剪痕,根据三角形全等的性质即可证得EM=DN,利用勾股定理即可求得.【详解】于G.如图,EF为剪痕,过点F作FG EM∵EF 将该图形分成了面积相等的两部分,∴EF 经过正方形ABCD 对角线的交点,∴,AF CN BF DN ==.易证PME PDN ∆∆≌,∴EM DN =,而AF MG =,∴1EG EM MG DN AF DN CN DC =+=+=+==.在Rt FGE ∆中,EF ==故选:D.2.(2022·黑龙江中考真题)如图,四边形ABCD 中,AB=AD ,AC=5,∠DAB=∠DCB=90°,则四边形ABCD 的面积为( )A .15B .12.5C .14.5D .17【答案】B【分析】过A 作AE ⊥AC ,交CB 的延长线于E ,判定△ACD ≌△AEB ,即可得到△ACE 是等腰直角三角形,四边形ABCD 的面积与△ACE 的面积相等,根据S △ACE =12×5×5=12.5,即可得出结论. 【详解】如图,过A 作AE ⊥AC ,交CB 的延长线于E ,∵∠DAB=∠DCB=90°,∴∠D+∠ABC=180°=∠ABE+∠ABC,∴∠D=∠ABE,又∵∠DAB=∠CAE=90°,∴∠CAD=∠EAB,又∵AD=AB,∴△ACD≌△AEB,∴AC=AE,即△ACE是等腰直角三角形,∴四边形ABCD的面积与△ACE的面积相等,∵S△ACE=12×5×5=12.5,∴四边形ABCD的面积为12.5,故选B.3.(2022·青海中考真题)如图,把直角三角形ABO放置在平面直角坐标系中,已知30OAB∠=,B 点的坐标为()0,2,将ABO沿着斜边AB翻折后得到ABC,则点C的坐标是()A.()4B.(2,C.)D.【答案】C【分析】过点C 作CD ⊥y 轴,垂直为D ,首先证明△BOA ≌△BCA ,从而可求得BC 的长,然后再求得∠DCB=30°,接下来,依据在Rt △BCD 中,求得BD 、DC 的长,从而可得到点C 的坐标.【详解】OAB BAC 30∠∠==,BOA BCA 90∠∠==,AB AB =,BOA ∴≌BCA ,OB BC 2∴==,CBA OBA 60∠∠==,过点C 作CD y ⊥轴,垂直为D ,则DCB 30∠=,1DB BC 12∴==,DC BC 2== )C ∴, 故选C .4.(2022·新疆中考真题)如图,在△ABC 中,∠C=90°,∠A=30°,以点B 为圆心,适当长为半径的画弧,分别交BA ,BC 于点M 、N ;再分别以点M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线BP 交AC 于点D ,则下列说法中不正确的是()A .BP 是∠ABC 的平分线B .AD=BDC .:1:3CBD ABD S S D .CD=12BD 【答案】C【分析】A 、由作法得BD 是∠ABC 的平分线,即可判定;B 、先根据三角形内角和定理求出∠ABC 的度数,再由BP 是∠ABC 的平分线得出∠ABD =30°=∠A,即可判定;C ,D 、根据含30°的直角三角形,30°所对直角边等于斜边的一半,即可判定.【详解】解:由作法得BD 平分∠ABC ,所以A 选项的结论正确;∵∠C =90°,∠A =30°,∴∠ABC =60°,∴∠ABD =30°=∠A ,∴AD =BD ,所以B 选项的结论正确;∵∠CBD =12∠ABC =30°, ∴BD =2CD ,所以D 选项的结论正确;∴AD =2CD ,∴S △ABD =2S △CBD ,所以C 选项的结论错误.故选C .5.(2022·湖南张家界市·中考真题)如图,在ABC ∆中,90︒∠=C ,8AC =,13DC AD =,BD 平分ABC ∠,则点D 到AB 的距离等于( )A .4B .3C .2D .1【答案】C【分析】如图,过点D 作DE AB ⊥于E ,根据已知求出CD 的长,再根据角平分线的性质进行求解即可.【详解】如图,过点D 作DE AB ⊥于E ,AC 8=,1DC AD 3=,1CD 8213∴=⨯=+, C 90∠︒=,BD 平分ABC ∠,DE CD 2∴==,即点D 到AB 的距离为2,故选C .6.(2022·山东潍坊市·中考真题)如图,已知AOB ∠.按照以下步骤作图:①以点O 为圆心,以适当的长为半径作弧,分别交AOB ∠的两边于C ,D 两点,连接CD .②分别以点C ,D 为圆心,以大于线段OC 的长为半径作弧,两弧在AOB ∠内交于点E ,连接CE ,DE .③连接OE 交CD 于点M .下列结论中错误的是( )A .CEO DEO ∠=∠B .CM MD =C .OCD ECD ∠=∠D .12OCED S CD OE =⋅四边形 【答案】C【分析】利用基本作图得出是角平分线的作图,进而解答即可.【详解】由作图步骤可得:OE 是AOB ∠的角平分线,∴∠COE=∠DOE ,∵OC=OD ,OE=OE ,OM=OM ,∴△COE ≌△DOE ,∴∠CEO=∠DEO ,∵∠COE=∠DOE ,OC=OD ,∴CM=DM ,OM ⊥CD ,∴S 四边形OCED =S △COE +S △DOE =111222OE CM OE DM CD OE +=, 但不能得出OCD ECD ∠=∠,∴A 、B 、D 选项正确,不符合题意,C 选项错误,符合题意,故选C .7.(2022·山东临沂市·中考真题)如图,D 是AB 上一点,DF 交AC 于点E ,DE FE =,//FC AB ,若4AB =,3CF =,则BD 的长是( )A .0.5B .1C .1.5D .2【答案】B【分析】根据平行线的性质,得出A FCE ∠=∠,ADE F ∠=∠,根据全等三角形的判定,得出ADE CFE ∆≅∆,根据全等三角形的性质,得出AD CF =,根据4AB =,3CF =,即可求线段DB 的长.【详解】∵//CF AB ,∴A FCE ∠=∠,ADE F ∠=∠,在ADE ∆和FCE ∆中A FCE ADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()ADE CFE AAS ∆≅∆,∴3AD CF ==,∵4AB =,∴431DB AB AD =-=-=.故选B .8.(2022·广西河池市·中考真题)如图,在正方形ABCD 中,点E 、F 分别在BC 、CD 上,BE CF =,则图中与AEB ∠相等的角的个数是()A .1B .2C .3D .4【答案】C【分析】根据正方形的性质,利用SAS 即可证明△ABE ≌△BCF ,再根据全等三角形的性质可得∠BFC=∠AEB ,进一步得到∠DAE=∠AEB ,∠BFC=∠ABF ,从而求解.【详解】证明:∵四边形ABCD 是正方形,∴,,90AB BC AB BC ABE BCF =∠=∠=︒∕∕,在ABE ∆和BCF ∆中,AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩,∴()ABE BCF SAS ∆∆≌,∴BFC AEB ∠=∠,∴BFC ABF ∠=∠,又有EAD AEB ∠=∠故图中与AEB ∠相等的角的个数是3.故选C .9.(2022·四川宜宾市·中考真题)如图,,ABC ECD ∆∆都是等边三角形,且B ,C ,D 在一条直线上,连结,BE AD ,点M ,N 分别是线段BE ,AD 上的两点,且11,33BM BE AN AD ==,则CMN ∆的形状是()A .等腰三角形B .直角三角形C .等边三角形D .不等边三角形【答案】C【分析】先证明BCE ACD ≅,得到BE AD =,根据已知条件可得AN BM =,证明△△BCM ACN ≅,得到=60MCN ∠︒,即可得到结果;【详解】∵,ABC ECD ∆∆都是等边三角形,∴BC AC =,CE CD =,60BCA DCE ∠=∠=︒,∴+BCA ACE DCE ACE ∠∠=∠+∠,∴BCE ACD ∠=∠,在BCE 和ACD △中,BC AC BCE ACD CE CD ⎧=⎪∠=∠⎨⎪=⎩,∴()△△BCE ACD SAS ≅,∴BE AD =,CBMACN ∠=∠, 又∵11,33BM BE AN AD ==, ∴BM AN =,在BCM 和ACN △中,BM AN CBM ACN BC AC ⎧=⎪∠=∠⎨⎪=⎩,∴()△△BCM ACNSAS ≅, ∴BCM ACN ∠=∠,MC NC =,∴+60BCM ACMACN ACM ∠∠=∠+∠=︒, ∴CMN ∆是等边三角形.故答案选C .10.(2022·广西中考真题)如图,在ABC ∆中,,40AC BC A =∠=︒,观察图中尺规作图的痕迹,可知BCG ∠的度数为( )A .40︒B .45︒C .50︒D .60︒【答案】C【分析】利用等腰三角形的性质和基本作图得到CG AB ⊥,则CG 平分ACB ∠,利用A B ∠=∠和三角形内角和计算出ACB ∠,从而得到BCG ∠的度数.【详解】由作法得CG AB ⊥,∵AB AC =,∴CG 平分ACB ∠,A B ∠=∠,∵1804040100ACB ∠=︒-︒-︒=︒, ∴1502BCG ACB ∠=∠=︒. 故选:C . 二、填空题(共5小题,每小题4分,共计20分)11.(2022·广西玉林市·中考真题)如图,将两张对边平行且相等的纸条交叉叠放在一起,则重合部分构成的四边形ABCD_________菱形(是,或不是).【答案】是【分析】 如图(见解析),先根据“两张对边平行且相等的纸条”得出//,//,AB CD AD BC BE DF =,再根据平行四边形的判定可得四边形ABCD 是平行四边形,然后根据三角形全等的判定定理与性质可得AB AD =,最后根据菱形的判定即可得.【详解】如图,过点B 作BE AD ⊥,交DA 延长线于点E ,过点D 作DF AB ⊥,交BA 延长线于点F 由题意得://,//,AB CD AD BC BE DF =∴四边形ABCD 是平行四边形在ABE △和ADF 中,90BAE DAF AEB AFD BE DF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩(AAS)ABE ADF ∴≅AB AD ∴=∴平行四边形ABCD 是菱形故答案为:是.12.(2022·黑龙江鹤岗市·中考真题)如图,Rt ABC ∆和Rt EDF ∆中,//BC DF ,在不添加任何辅助线的情况下,请你添加一个条件______,使Rt ABC ∆和Rt EDF ∆全等.【答案】AB ED =,答案不唯一【分析】本题是一道开放型的题目,答案不唯一,可以是AB =ED 或BC =DF 或AC =EF 或AE =CF 等,只要符合全等三角形的判定定理即可.【详解】∵Rt ABC ∆和Rt EDF ∆中,∴90BAC DEF ∠=∠=︒,∵//BC DF ,∴DFE BCA ∠=∠,∴添加AB ED =,在Rt ABC ∆和Rt EDF ∆中DFE BCA DEF BAC AB ED ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()Rt Rt AAS ABC EDF ∆∆≌,故答案为:AB ED =答案不唯一.13.(2022·辽宁本溪市·中考真题)如图,在ABC ∆中,M ,N 分别是AB 和AC 的中点,连接MN ,点E 是CN 的中点,连接ME 并延长,交BC 的延长线于点D ,若4BC =,则CD 的长为_________.【答案】2【分析】依据三角形中位线定理,即可得到MN=12BC=2,MN //BC ,依据△MNE ≌△DCE (AAS ),即可得到CD=MN=2.【详解】解:∵M ,N 分别是AB 和AC 的中点,∴MN 是△ABC 的中位线,∴MN=12BC=2,MN ∥BC , ∴∠NME=∠D ,∠MNE=∠DCE ,∵点E 是CN 的中点,∴NE=CE ,∴△MNE ≌△DCE (AAS ),故答案为:2.14.(2022·甘肃天水市·中考真题)如图,在边长为6的正方形ABCD 内作45EAF ∠=︒,AE 交BC 于点E ,AF 交CD 于点F ,连接EF ,将ADF ∆绕点A 顺时针旋转90︒得到ABG ,若3DF =,则BE 的长为__________.【答案】2【分析】根据旋转的性质可得AG=AF ,GB=DF ,∠BAG =∠DAF ,然后根据正方形的性质和等量代换可得∠GAE =∠F AE ,进而可根据SAS 证明△GAE ≌△F AE ,可得GE=EF ,设BE=x ,则CE 与EF 可用含x 的代数式表示,然后在Rt △CEF 中,由勾股定理可得关于x 的方程,解方程即得答案.【详解】解:∵将△ADF 绕点A 顺时针旋转90︒得到△ABG ,∴AG=AF ,GB=DF ,∠BAG =∠DAF ,∵45EAF ∠=︒,∠BAD =90°,∴∠BAE +∠DAF =45°,∴∠BAE +∠BAG =45°,即∠GAE =45°,∴∠GAE =∠F AE ,又AE=AE ,∴△GAE ≌△F AE (SAS ),设BE=x ,则CE =6-x ,EF=GE=DF+BE =3+x ,∵DF =3,∴CF =3,在Rt △CEF 中,由勾股定理,得:()()222633x x -+=+,解得:x =2,即BE =2.故答案为:2.15.(2022·黑龙江齐齐哈尔市·中考真题)如图,已知在△ABD 和△ABC 中,∠DAB =∠CAB ,点A 、B 、E 在同一条直线上,若使△ABD ≌△ABC ,则还需添加的一个条件是______.(只填一个即可)【答案】AD =AC (∠D =∠C 或∠ABD =∠ABC 等)【分析】利用全等三角形的判定方法添加条件即可求解.【详解】解:∵∠DAB =∠CAB ,AB =AB ,∴当添加AD =AC 时,可根据“SAS ”判断△ABD ≌△ABC ;当添加∠D =∠C 时,可根据“AAS ”判断△ABD ≌△ABC ;当添加∠ABD =∠ABC 时,可根据“ASA ”判断△ABD ≌△ABC .故答案为AD =AC (∠D =∠C 或∠ABD =∠ABC 等).三、解答题(共5小题,每小题10分,共计50分)16.(2022·柳州市柳林中学中考真题)如图,已知OC 平分∠MON ,点A 、B 分别在射线OM ,ON 上,且OA =OB .求证:△AOC ≌△BOC .【答案】见解析【分析】根据角平分线的性质和全等三角形的判定方法可以证明结论成立.【详解】证明:∵OC 平分∠MON ,∴∠AOC =∠BOC ,在△AOC 和△BOC 中,OA OB AOC BOC OC OC =⎧⎪∠=∠⎨⎪=⎩,∴△AOC ≌△BOC (SAS ).17.(2022·江苏连云港市·中考真题)如图,在四边形ABCD 中,//AD BC ,对角线BD 的垂直平分线与边AD 、BC 分别相交于M 、N .(1)求证:四边形BNDM 是菱形;(2)若24BD =,10MN =,求菱形BNDM 的周长.【答案】(1)见解析;(2)52【分析】(1)先证明BON DOM ≌△△,得到四边形BNDM 为平行四边形,再根据菱形定义证明即可; (2)先根据菱形性质求出OB 、OM 、再根据勾股定理求出BM ,问题的得解.【详解】(1)∵//AD BC ,∴CBD ADB ∠=∠.∵MN 是对角线BD 的垂直平分线,∴OB OD =,MB MD =.在BON △和DOM △中,CBD ADB OB OD BON DOM ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BON DOM ASA ≌,∴MD NB =,∴四边形BNDM 为平行四边形.又∵MB MD =,∴四边形BNDM 为菱形.(2)∵四边形BNDM 为菱形,24BD =,10MN =.∴90BOM ︒∠=,1122OB BD ==,152OM MN ==. 在Rt BOM △中,13BM ===.∴菱形BNDM 的周长441352BM ==⨯=.18.(2022·湖南湘西土家族苗族自治州·中考真题)如图,在正方形ABCD 的外侧,作等边角形ADE ,连接BE 、CE .(1)求证:BAE CDE △≌△;(2)求AEB ∠的度数.【答案】(1)见解析;(2)15°.【分析】(1)利用正方形的性质得到AB=CD ,∠BAD=∠CDA ,利用等边三角形的性质得到AE=DE ,∠EAD=∠EDA=60°即可证明;(2)由AB=AD=AE ,得到△ABE 为等腰三角形,进而得到∠ABE=∠AEB ,且∠BAE=90°+60°=150°,再利用三角形内角和定理即可求解.【详解】解:(1)证明:∵四边形ABCD 是正方形,∴AB=CD ,且∠BAD=∠CDA=90°,∵△ADE 是等边三角形,∴AE=DE ,且∠EAD=∠EDA=60°,∴∠BAE=∠BAD+∠EAD=150°,∠CDE=∠CDA+∠EDA=150°,∴∠BAE=∠CDE ,在△BAE 和△CDE 中:=⎧⎪∠=∠⎨⎪=⎩AB CD BAE CDE AE DE ,∴()△≌△BAE CDE SAS .(2)∵AB=AD ,且AD=AE ,∴△ABE 为等腰三角形,∴∠ABE=∠AEB ,又∠BAE=150°,∴由三角形内角和定理可知:∠AEB=(180°-150°)÷2=15°.故答案为:15°.19.(2022·江苏宿迁市·中考真题)如图,在正方形ABCD 中,点E ,F 在AC 上,且AF=CE .求证:四边形BEDF 是菱形.【答案】见解析【分析】由正方形的性质可得AB=AD=CD=BC ,∠DAE=∠BAE=∠BCF=∠DCF=45°,由“SAS”可证△ABE ≌△ADE ,△BFC ≌△DFC ,△ABE ≌△CBF ,可得BE=BF=DE=DF ,可得结论.【详解】∵四边形ABCD 是正方形,∴AB=AD=CD=BC ,∠DAE=∠BAE=∠BCF=∠DCF=45°,在△ABE 和△ADE 中,AB AD BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ADE (SAS ),∴BE=DE ,同理可得△BFC ≌△DFC ,可得BF=DF ,∵AF=CE ,∴AF-EF=CE-EF ,即AE=CF ,在△ABE 和△CBF 中,AB BC BAE BCF AE CF =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△CBF (SAS ),∴BE=BF ,∴BE=BF=DE=DF ,∴四边形BEDF 是菱形.20.(2022·江苏南通市·中考真题)(1)如图①,点D 在AB 上,点E 在AC 上,AD =AE ,∠B =∠C .求证:AB =AC .(2)如图②,A 为⊙O 上一点,按以下步骤作图:①连接OA ;②以点A 为圆心,AO 长为半径作弧,交⊙O 于点B ;③在射线OB 上截取BC =OA ;④连接AC .若AC =3,求⊙O 的半径.【答案】(1)见解析;(2)⊙O【分析】(1)根据“AAS “证明△ABE ≌△ACD ,然后根据全等三角形的性质得到结论;(2)连接AB ,如图②,由作法得OA=OB=AB=BC ,先判断△OAB 为等边三角形得到∠OAB=∠OBA=60°,再利用等腰三角形的性质和三角形外角性质得到∠C=∠BAC=30°,然后根据含30度的直角三角形三边的关系求OA 的长.【详解】(1)证明:在△ABE 和△ACD 中B C A A AE AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ACD (AAS ),∴AB =AC ;(2)解:连接AB ,如图②,由作法得OA =OB =AB =BC ,∴△OAB 为等边三角形,∴∠OAB =∠OBA =60°,∵AB =BC ,∴∠C =∠BAC ,∵∠OBA =∠C+∠BAC ,∴∠C =∠BAC =30°∴∠OAC =90°,在Rt △OAC 中,OA =3AC =3×3即⊙O .。
专题01 全等三角形的性质与判定、应用(解析版)

专题01 全等三角形的性质与判定、应用全等三角形的性质1.(2022秋•鄞州区校级期末)如图,△AOB≌△ADC,∠O=∠D=90°,记∠OAD=α,∠ABO =β,当BC∥OA时,α与β之间的数量关系为( )A.α=βB.α=2βC.α+β=90°D.α+2β=180°【分析】根据全等三角形对应边相等可得AB=AC,全等三角形对应角相等可得∠BAO=∠CAD,然后求出∠BAC=α,再根据等腰三角形两底角相等求出∠ABC,然后根据两直线平行,同旁内角互补表示出∠OBC,整理即可.【解答】解:∵△AOB≌△ADC,∴AB=AC,∠BAO=∠CAD,∴∠BAC=∠OAD=α,在△ABC中,,∵BC∥OA,∴∠OBC=180°﹣∠O=180°﹣90°=90°,∴,整理得,α=2β.故选:B.2.(2022秋•嘉兴期末)如图,△ABC≌△DEF,若∠A=100°,∠F=47°,则∠E的度数为( )A.100°B.53°C.47°D.33°【分析】根据全等三角形的性质得出∠D=∠A=100°,再根据三角形内角和定理即可得出∠E 的度数【解答】解:∵△ABC≅△DEF,∠A=100°,∴∠D=∠A=100°,在△DEF中,∠F=47°,∴∠E=180°﹣∠D﹣∠E=33°,故选:D.3.(2022秋•拱墅区期末)如图,△ABC≌△EFD,则下列说法错误的是( )A.FC=BD B.EF平行且等于ABC.∠B=∠ACB D.AC平行且等于DE【分析】根据全等三角形的性质可得FD=BC,∠F=∠B,∠EDF=∠ACB,EF=AB,AC=DE,再依次判断即可.【解答】解:∵△ABC≌△EFD,∴FD=BC,∠F=∠B,∠EDF=∠ACB,EF=AB,AC=DE,∴FD﹣CD=BC﹣CD,即FC=BD,故A选项不符合题意;∵∠F=∠B,∴EF∥AB,∴EF平行且等于AB,故B选项不符合题意;没有足够的条件证明∠B=∠ACB,故C选项符合题意;∵∠EDF=∠ACB,∴AC∥DE,∴AC平行且等于DE,故D选项不符合题意,故选:C.4.(2021秋•青田县期末)如图,已知△ABC≌△DEF,B,E,C,F在同一条直线上.若BF=8cm,BE=2cm,则CE的长度( )cm.A.5B.4C.3D.2【分析】根据全等三角形的性质得出BC=EF,求出BE=CF=2cm,再求出答案即可.【解答】解:∵△ABC≌△DEF,∴BC=EF,∴BC﹣CE=EF﹣CE,∴BE=CF,∵BE=2cm,∴CF=BE=2cm,∵BF=8cm,∴CE=BF﹣BE﹣CF=8﹣2﹣2=4(cm),故选:B.5.(2022秋•仙居县期末)如图,△ABC≌△DEF,且∠A=55°,∠B=75°,则∠F= 50 °.【分析】根据全等三角形的性质求解即可.【解答】解:∵∠A=55°,∠B=75°,∠A+∠B+∠C=180°,∴∠C=50°,∵△ABC≌△DEF,∴∠C=∠F=50°,故答案为:50.6.(2022秋•宁波期末)如图,若△ABD≌△ACE,且∠1=45°,∠ADB=95°,则∠B= 50 °.【分析】根据全等三角形的性质及三角形外角性质求解即可.【解答】解:∵△ABD≌△ACE,∠ADB=95°,∴∠AEC=∠ADB=95°,∵∠AEC=∠1+∠B,∠1=45°,∴∠B=50°,故答案为:50.7.(2022秋•鄞州区校级期末)如图所示,已知△ABD≌△CFD,AD⊥BC于D.(1)求证:CE⊥AB;(2)已知BC=7,AD=5,求AF的长.【分析】(1)由△ABD≌△CFD,得出∠BAD=∠DCF,再利用三角形内角和即可得出答案;(2)根据全等三角形的性质得出AD=DC,即可得出BD=DF,进而解决问题.【解答】(1)证明:∵△ABD≌△CFD,∴∠BAD=∠DCF,又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB;(2)解:∵△ABD≌△CFD,∴BD=DF,∵BC=7,AD=DC=5,∴BD=BC﹣CD=2,∴AF=AD﹣DF=5﹣2=3.全等三角形的判定8.(2022秋•丽水期末)如图,已知AB=DC,下列条件中,不能使△ABC≌△DCB的是( )A.AC=DB B.∠A=∠D=90°C.∠ABC=∠DCB D.∠ACB=∠DBC【分析】根据全等三角形的判定定理逐个判断即可.【解答】解:A.AB=DC,BC=CB,AC=DB,符合全等三角形的判定定理SSS,能推出△ABC ≌△DCB,故本选项不符合题意;B.∠A=∠D=90°,AB=DC,BC=CB,符合两直角三角形全等的判定定理HL,能推出△ABC ≌△DCB,故本选项不符合题意;DCB,故本选不项符合题意;D.AB=DC,BC=CB,∠ACB=∠DBC,不符合全等三角形的判定定理,不能推出△ABC≌△DCB,故本选项符合题意;故选:D.9.(2021秋•湖州期末)我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图,AE=AF,GE=GF,则△AEG≌△AFG的依据是( )A.SAS B.ASA C.AAS D.SSS【分析】根据全等三角形的判定定理推出即可.【解答】解:在△AEG和△AFG中,,∴△AEG≌△AFG(SSS),故选:D.10.(2022秋•鄞州区校级期末)如图,AC和BD相交于O点,若OA=OD,不能证明△AOB≌△DOC的是( )A.AB=DC B.OB=OC C.∠A=∠D D.∠B=∠C【分析】根据全等三角形的判定定理逐个判断即可.【解答】解:A.AB=DC,OA=OD,∠AOB=∠DOC,不符合全等三角形的判定定理,不能推出△AOB≌△DOC,故本选项符合题意;B.OA=OD,∠AOB=∠DOC,OB=OC,符合全等三角形的判定定理SAS,能推出△AOB≌△DOC,故本选项不符合题意;DOC,故本选项不符合题意;D.∠B=∠C,∠AOB=∠DOC,OA=OD,符合全等三角形的判定定理AAS,能推出△AOB≌△DOC,故本选项不符合题意;故选:A.11.(2022秋•鄞州区校级期末)下列所给条件中,能画出唯一的△ABC的是( )A.AC=3,AB=4,BC=8B.∠A=50°,∠B=30°,AB=10C.∠C=90°,AB=90D.AC=4,AB=5,∠B=60°【分析】利用全等三角形的判定方法以及三角形三边关系分别判断得出即可.【解答】解:A、3+4=7<8,不符合三角形三边关系定理,即不能画出三角形,故本选项错误;B、根据∠A=50°,∠B=30°,AB=2根据ASA能画出唯一△ABC,故此选项正确;C、根据∠C=90°,AB=90,AS不能画出唯一三角形,故本选项错误;D、根据AC=4,AB=5,∠B=60°,ASS不能画出唯一三角形,故本选项错误;故选:B.12.(2022秋•新昌县期末)已知:如图,AC与DB相交于点O,∠1=∠2,∠A=∠D.求证:△AOB≌△DOC.【分析】根据∠1=∠2可得BO=CO,然后利用“角角边”证明即可.【解答】证明:∵∠1=∠2,∴BO=CO,在△AOB和△DOC中,,∴△AOB≌△DOC(AAS).13.(2022秋•镇海区校级期末)如图,在△ABC中,AC=AB,AD⊥BC,过点C作CE∥AB,∠BCE=70°,连接ED并延长ED交AB于点F.(1)求∠CAD的度数;(2)证明:△CDE≌△BDF;【分析】(1)根据平行线的性质得到∠B=∠BCE=70°,根据等腰三角形的性质得到∠ACD=∠B=70°,根据直角三角形两锐角互余,即可求得∠CAD的度数;(2)根据等腰三角形的性质得到CD=BD,根据平行线的性质得到∠E=∠DFB,∠ECD=∠B,根据全等三角形的判定定理即可得到结论;【解答】(1)解:∵CE∥AB,∠BCE=70°,∴∠B=∠BCE=70°,∵AC=AB,∴∠ACD=∠B=70°,∵AD⊥BC,∴∠ADC=90°,∴∠CAD=90°﹣70°=20°;(2)证明:∵AB=AC,AD⊥BC,∴CD=BD,∵CE∥AB,∴∠E=∠DFB,∠ECD=∠B,在△CDE与△BDF中,,∴△CDE≌△BDF(AAS).全等三角形的性质与判定14.(2022秋•江北区期末)如图,已知∠ABC,以点B为圆心,适当长为半径作弧,分别交AB,BC于P,D;作一条射线FE,以点F圆心,BD长为半径作弧l,交EF于点H;以H为圆心,PD长为半径作弧,交弧l于点Q;作射线FQ.这样可得∠QFE=∠ABC,其依据是( )A.SSS B.SAS C.ASA D.AAS【分析】根据题意得出BP=BD=FQ=FH,DP=QH,利用SSS证明△PBD≌△QFH,根据全等三角形的性质即可得出∠QFE=∠ABC.【解答】解:如图,连接DP,QH,根据题意得,BP=BD=FQ=FH,DP=QH,在△PBD和△QFH中,,∴△PBD≌△QFH(SSS),∴∠ABC=∠QFE,故选:A.15.(2023春•宁波期末)如图,△ABC的两条高AD和BF相交于点E,AD=BD=8,AC=10,AE=2,则BF的长为( )A.11.2B.11.5C.12.5D.13【分析】由高可得∠ADB=∠AFB=ADC=90°,从而可求得∠DBE=∠DAC,利用ASA可得△BDE≌△ADC,则有DE=DC,再利用等积即可求BF.【解答】解:∵△ABC的两条高AD和BF相交于点E,∴∠ADB=∠AFB=ADC=90°,∴∠DBE+∠BED=90°,∠AEF+∠EAF=90°,∵∠BED=∠AEF,∴∠DBE=∠EAF,在△BDE与△ADC中,,∴△BDE≌△ADC(ASA),∴DE=DC=AD﹣AE=6,∵,∴×14×8=×10BF,解得:BF=11.2.故选:A.16.(2021秋•海曙区校级期末)如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE 交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论有( )个.A.2B.3C.4D.5【分析】连接EG,根据等角的余角相等可判断①选项;根据BE、AG分别是∠ABC、∠DAC的平分线,∠BAD=∠C,可得到∠AFE=∠AEF,进一步即可判断②选项;假设∠EBC=∠C,根据三角形内角和定理可得∠C=30°,但∠C≠30°,可判断③选项;④证明△ABN≌△GBN (ASA),可得AN=GN,从而证出四边形AFGE是平行四边形,可判断④选项;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,可判断⑤选项.【解答】解:连接EG,如图所示:∵∠BAC=90°,AD⊥BC,∴∠C+∠ABC=90°,∠ABC+∠BAD=90°.∴∠BAD=∠C,故①选项符合题意;∵BE、AG分别是∠ABC、∠DAC的平分线,∴∠ABF=∠EBD.∵∠AFE=∠BAD+∠ABF,∠AEB=∠C+∠EBD,∴∠AFE=∠AEF,∴AF=AE,故②选项符合题意;③假设∠EBC=∠C,则有∠C=∠ABC,∵∠BAC=90°∴∠C=30°,但∠C≠30°,故③选项不符合题意;④∵AG是∠DAC的平分线,AE=AF,∴AN⊥BE,FN=EN,∴∠ANB=∠BNG=90°,在△ABN与△GBN中,,∴△ABN≌△GBN(ASA),∴AN=GN,∵FN=EN,∴四边形AFGE是平行四边形,∴GF∥AE,即GF∥AC,故④选项符合题意;⑤∵AE=AF,AE=FG,而△AEF不是等边三角形,∴EF≠AE,∴EF≠FG,故⑤选项不符合题意,故正确的选项有:①②④,故选:B.17.(2022秋•杭州期末)如图,在△ABC中,AB=AC,AD平分∠BAC,DF⊥AB于F点,DE⊥AC于点E,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等;②AD⊥BC且BD=CD;③∠BDF=∠CDE;④AE=AF.其中正确的有( )A.②③B.①③C.①②④D.①②③④【分析】由题意知,△ABC是等腰三角形,由三线合一的性质知,点D是BC的中点,AD⊥BC,故AD中BC的中垂线,也是∠BAC的平分线,进而证得△AED≌△AFD,△BFD≌△CED,故可得到5个说法均正确.【解答】解:∵AB=AC,∴△ABC是等腰三角形,∠B=∠C,∵AD平分∠BAC,DF⊥AB于F点,DE⊥AC于点E,∴AD⊥BC,BD=CD,DE=DF,故①②正确;∵DF⊥AB于F点,DE⊥AC于点E,∴∠DFB=∠DEC=90°,在△BFD和△CED中,,∴△BFD≌△CED(AAS),∴∠BDF=∠CDE,即③正确;在△AED和△AFD中,,∴△AED≌△AFD(AAS),∴AE=AF,故④正确.故选:D.18.(2022秋•鄞州区校级期末)如图,已知△ABC和△CDE都是等腰直角三角形,∠EBD=50°,则∠AEB的度数为( )A.130°B.135°C.140°D.145°【分析】由“SAS”可证△ACE≌△BCD,可得∠CBD=∠CAE,由三角形内角和定理可求解.【解答】解:∵△ABC和△CDE都是等腰直角三角形,∴AC=BC,EC=CD,∠ACB=∠ECD=90°,∴∠ACE=∠BCD,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴∠CBD=∠CAE,∵∠EBD=50°,∴∠CBE+∠CBD=50°=∠CBE+∠CAE,∵∠CAE+∠CBE+∠EAB+∠EBA=90°,∴∠EAB+∠EBA=40°,∴∠AEB=140°,故选:C.19.(2022秋•温州期末)如图,在等腰三角形ABC中,AD是底边BC上的高线,CE⊥AB于点E,交AD于点F,若∠BAC=45°,AF=6,则BD的长为 3 .【分析】证明△AEF≌△CEB(ASA),根据全等三角形的性质得出AE=BC,即可求出答案.【解答】解:∵等腰三角形ABC中,AD是底边BC上的高线,∴AB=AC,AD⊥BC,BD=CD,∴∠ADC=90°,∠B=∠BCA,∴∠CFD+∠ECB=90°,∵CE⊥AB,∠BAC=45°,∴∠BAD+∠AFE=90°,AE=CE,∵∠B=∠BCA,∴∠BAD=∠BCE,在△AEF和△CEB中,,∴△AEF≌△CEB(ASA),∴AF=BC,∵BD=CD,AF=6,∴BD=3.故答案为:3.20.(2022秋•拱墅区期末)已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A =∠E,(1)求证:△ABC≌△EDF;(2)当∠C=90°,∠CBA=60°时,求∠E的度数.【分析】(1)根据SAS即可证明:△ABC≌△EDF;(2)由全等三角形的性质及直角三角形的性质可得出答案.【解答】(1)证明:∵AD=BE,∴AB=ED,在△ABC和△EDF中,,∴△ABC≌△EDF(SAS);(2)解:∵∠C=90°,∠CBA=60°,∴∠A=90°﹣∠CBA=90°﹣60°=30°,∵△ABC≌△EDF,∴∠E=∠A=30°.21.(2022秋•鄞州区期末)如图,已知△ABC和△ADE,AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.(1)求证:BC=DE;(2)若∠B=30°,∠APC=70°.①求∠E的度数;②求证:CP=CE.【分析】(1)证明△BAC≌△DAE(ASA),由全等三角形的性质得出结论;(2)①由三角形外角的性质求出∠CAE=40°,由全等三角形的性质得出AC=AE,由等腰三角形的性质可求出答案;②证明△ACP≌△ACE(AAS),由全等三角形的性质得出结论.【解答】(1)证明:∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(ASA),∴BC=DE;(2)①解:∵∠B=30°,∠APC=70°,∴∠BAP=∠APC﹣∠B=70°﹣30°=40°,∴∠CAE=40°,∵△BAC≌△DAE,∴AC=AE,∴∠ACE=∠E===70°;②证明:∵△BAC≌△DAE,∴∠ACB=∠E=70°,∴∠ACB=∠ACE,∠APC=∠E,在△ACP和△ACE中,,∴△ACP≌△ACE(AAS),∴CP=CE.22.(2021秋•鄞州区期末)如图,△ABC中,D是BC延长线上一点,满足CD=AB,过点C作CE∥AB且CE=BC,连接DE并延长,分别交AC、AB于点F、G.(1)求证:△ABC≌△DCE;(2)若∠B=50°,∠D=22°,求∠AFG的度数.【分析】(1)根据CE∥AB可得∠B=∠DCE,由SAS定理可得结论;(2)利用全等三角形的性质定理可得∠ECD=∠B=50°,∠A=∠D=22°,由平行线的性质定理易得∠ACE=∠A=22°,由三角形的内角和定理和外角的性质可得结果.【解答】(1)证明:∵CE∥AB,∴∠B=∠DCE,在△ABC与△DCE中,,∴△ABC≌△DCE(SAS);(2)解:∵△ABC≌△DCE,∠B=50°,∠D=22°,∴∠ECD=∠B=50°,∠A=∠D=22°,∵CE∥AB,∴∠ACE=∠A=22°,∵∠CED=180°﹣∠D﹣∠ECD=180°﹣22°﹣50°=108°,∴∠AFG=∠DFC=∠CED﹣∠ACE=108°﹣22°=86°.全等三角形的应用23.(2021秋•临海市期末)如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC 与右边滑梯的水平长度DF相等,那么判定△ABC与△DEF全等的依据是( )A.HL B.ASA C.AAS D.SSS【分析】先根据BC=EF,AC=DF判断出Rt△ABC≌Rt△DEF.【解答】解:∵滑梯、墙、地面正好构成直角三角形,在Rt△ABC和Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL),故选:A.24.(2022秋•温州期末)如图是某纸伞截面示意图,伞柄AP平分两条伞骨所成的角∠BAC,AE=AF.若支杆DF需要更换,则所换长度应与哪一段长度相等( )A.BE B.AE C.DE D.DP【分析】根据平分线的定义和全等三角形的判定和性质定理即可得到结论.【解答】解:∵AP平分∠BAC.∴∠EAD=∠FAD,在△ADE与△ADF中,,∴△ADE≌△ADF(SAS),∴DF=DE,即所换长度应与DF的长度相等,故选:C.25.(2022秋•金东区期末)如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带到玻璃店( )A.①B.②C.③D.①、②、③其中任一块【分析】由图可知,第③块中,有两角及其夹边可得出这块三角形与购买的三角形全等.【解答】解:根据全等三角形的判定:两角及其夹边的两个三角形全等,即可确定这块三角形与购买的三角形全等,故选:C.26.(2022秋•武义县期末)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.(1)求证:△ADC≌△CEB;(2)求两堵木墙之间的距离.【分析】(1)根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可;(2)利用全等三角形的性质进行解答.【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC在△ADC和△CEB中,∴△ADC≌△CEB(AAS);(2)解:由题意得:AD=2×3=6(cm),BE=7×2=14(cm),∵△ADC≌△CEB,∴EC=AD=6cm,DC=BE=14cm,∴DE=DC+CE=20(cm),答:两堵木墙之间的距离为20cm.27.(2021秋•金华期末)如图,A,B两点分别位于一个池塘的两端,小明通过构造△ABC与△BCD 来测量A,B间的距离,其中AC=CD,∠ACB=∠BCD.那么量出的BD的长度就是AB的距离.请你判断小明这个方法正确与否,并给出相应理由.【分析】正确;利用全等三角形的判定定理SAS证得△ABC≌△DBC,由该全等三角形的对应边相等得到AB=DB.【解答】解:正确;理由如下:在△ABC与△DBC中,.∴△ABC≌△DBC(SAS).∴AB=DB.1.(2022秋•临海市期末)下列说法正确的是( )A.面积相等的两个三角形全等B.形状相同的两个三角形全等C.三个角分别相等的两个三角形全等D.斜边和一条直角边对应相等的两个直角三角形全等【分析】根据全等三角形的判定,逐项判断即可求解.【解答】解:A、面积相等的两个三角形不一定全等,如同底等高的2个三角形,不一定相似,不符合题意;B、形状相同的两个三角形不一定全等,相似三角形的形状相同,不符合题意;C、三个角分别相等的两个三角形不一定全等,三个角相等的三角形可能是相似三角形,不符合题意;D、斜边和一条直角边对应相等的两个直角三角形全等,符合题意.故选:D.2.(2021秋•诸暨市期末)如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB =25°,则∠ADC的度数是( )A.45°B.60°C.75°D.70°【分析】根据全等三角形的性质和三角形内角和解答即可.【解答】解:∵△ABC≌△EDC,BC⊥CD,∴∠DCE=∠ACB=25°,∠BCD=∠ACE=90°,AC=CE,∴∠ACD=90°﹣25°=65°,∵点A,D,E在同一条直线上,∴∠ADC+∠EDC=180°,∵∠EDC+∠E+∠DCE=180°,∴∠ADC=∠E+25°,∵∠ACE=90°,AC=CE,∴∠DAC+∠E=90°,∠E=∠DAC=45°,在△ADC中,∠ADC+∠DAC+∠DCA=180°,即45°+65°+∠ADC=180°,解得:∠ADC=70°,故选:D.3.(2023春•镇海区校级期末)如图,已知△OAB≌△OA1B1,AB与A1O交于点C,AB与A1B1交于点D,则下列说法中错误的是( )A.∠A=∠A1B.AC=COC.OB=OB1D.∠A1DC=∠AOC【分析】由△OAB≌△OA1B1可得选项A、C是正确的,再利用外角的性质可得D是正确的,选项B是错误的.【解答】解:∵△OAB≌△OA1B1,∴∠A=∠A1,OB=OB1,故A、C正确;∵∠A1+∠A1DC=∠A+∠AOC.∴∠A1DC=∠AOC,故D正确;∵A1B1与AO不平行,∴∠A1≠∠AOC,∴AC≠CO,故B错误.故选:B.4.(2022秋•江北区校级期末)如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )A.SSS B.SAS C.ASA D.HL【分析】根据全等三角形的判定进行判断,注意看题目中提供了哪些证明全等的要素,要根据已知选择判断方法.【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,所以用到的是两角及这两角的夹边对应相等即ASA这一方法.故选:C.5.(2022秋•义乌市校级期末)如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是 ASA .【分析】根据全等三角形的判定方法解决此题.【解答】解:由图得:遮挡住的三角形中露出两个角及其夹边.∴根据三角形的判定方法ASA可解决此题.故答案为:ASA.6.(2021秋•西湖区期末)若△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=50°,∠B =60°,则∠F= 70 °.【分析】根据三角形内角和定理可得∠ACB=180°﹣50°﹣60°=70°,再根据全等三角形的性质可得∠F=∠ACB=70°.【解答】解:∵∠A=50°,∠B=60°,∴∠ACB=180°﹣50°﹣60°=70°,∵△ABC≌△DEF,∴∠F=∠ACB=70°,故答案为:70.7.(2021秋•海曙区期末)如图,AB=DB,∠1=∠2,要使△ABC≌△DBE还需添加一个条件是 ∠A=∠D(答案不唯一) .(只需写出一种情况)【分析】此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.【解答】解:添加的条件是∠A=∠D,理由如下:∵∠1=∠2,∴∠1+∠ABE=∠2+∠ABE,即∠DBE=∠ABC,在△ABC和△DBE中,,∴△ABC≌△DBE(ASA),故答案为:∠A=∠D(答案不唯一).8.(2022秋•平湖市期末)如图,在等边三角形ABC的AC、BC边上各取一点P、Q,使AP=CQ,AQ、BP相交于点O,则∠POQ的度数为 120° .【分析】根据全等三角形的判定定理SAS证得△ABP≌△CAQ,则对应角∠ABP=∠CAQ,所以由三角形外角的性质求得∠BOQ=∠BAO+∠OAP=∠BAP=60°.【解答】解:如图,在等边△ABC中,AB=AC,∠BAP=∠C=60°.在△ABP与△CAQ中,,∴△ABP≌△CAQ(SAS),∴∠ABP=∠CAQ.∵∠BOQ=∠BAO+∠ABP,∴∠BOQ=∠BAO+∠CAQ=∠BAC=60°,∴∠POQ=180°﹣∠BOQ=120°.故答案为:120°.9.(2021秋•莲都区期末)如图,∠D=∠ACB=∠E=90°,AC=BC.求证:△ADC≌△CEB.【分析】已知∠ACB=90°,然后根据同角的余角相等求出∠B=∠ACD,再利用“角角边”证明△ADC和△CEB全等即可.【解答】证明:∵∠ACB=90°,∴∠BCE+∠ACD=90°,∵∠CBE+∠BCE=90°,∴∠CBE=∠ACD,在△ADC和△CEB中,,∴△ADC≌△CEB(AAS).10.(2021秋•临海市期末)如图,点B,E,C,F在同一条直线上,AB=DE,BE=CF,∠B=∠DEF.求证:△ABC≌△DEF.【分析】由BE=CF可得BC=EF,再有已知条件进而可得出△ABC≌△DEF.【解答】证明:∵BE=CF,∴BE+CE=CF+EC.∴BC=EF.在△ABC和△DEF中,,∴△ABC≌△DEF(SAS).11.(2022秋•余姚市校级期末)在△ABC和△ADE中,AB=AD,∠1=∠2,∠E=∠C,求证:BC=DE.【分析】根据AAS证明三角形全等即可.【解答】证明:∵∠1=∠2,∵∠DAC+∠1=∠2+∠DAC∴∠BAC=∠DAE,在△ABC和△ADE中,,∴△ADE≌△ABC(AAS)∴BC=DE.12.(2020•婺城区校级期末)如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.(2)若固定二根木条AB、BC不动,AB=2cm,BC=5cm,量得木条CD=5cm,∠B=90°,写出木条AD的长度可能取得的一个值(直接写出一个即可)(3)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.【分析】(1)相等.连接AC,根据SSS证明两个三角形全等即可.(2)由勾股定理求出AC,再根据三角形三边的关系求出AD的取值范围.(3)分两种情形①当点C在点D右侧时,②当点C在点D左侧时,分别列出方程组即可解决问题,注意最后理由三角形三边关系定理,检验是否符合题意.【解答】解:(1)相等.理由:连接AC,在△ACD和△ACB中,,∴△ACD≌△ACB,∴∠B=∠D.(2)∵AB=2cm,BC=5cm,且∠B=90°,∴AC===根据三角形三边关系可知﹣5≤AD≤+5所以AD可以为5cm.(3)设AD=x,BC=y,当点C在点D右侧时,,解得,当点C在点D左侧时,点C在D左侧时,三边之和等于第四边是构不成四边形的,不合题意,综上所述,AD=13cm,BC=10cm.。
八年级数学上册 全等三角形专题练习(解析版)

八年级数学上册全等三角形专题练习(解析版)一、八年级数学轴对称三角形填空题(难)1.在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=12BC,则△ABC的顶角的度数为_____.【答案】30°或150°或90°【解析】试题分析:分两种情况;①BC为腰,②BC为底,根据直角三角形30°角所对的直角边等于斜边的一半判断出∠ACD=30°,然后分AD在△ABC内部和外部两种情况求解即可.解:①BC为腰,∵AD⊥BC于点D,AD=12 BC,∴∠ACD=30°,如图1,AD在△ABC内部时,顶角∠C=30°,如图2,AD在△ABC外部时,顶角∠ACB=180°﹣30°=150°,②BC为底,如图3,∵AD⊥BC于点D,AD=12 BC,∴AD=BD=CD,∴∠B=∠BAD,∠C=∠CAD,∴∠BAD+∠CAD=12×180°=90°,∴顶角∠BAC=90°,综上所述,等腰三角形ABC的顶角度数为30°或150°或90°.故答案为30°或150°或90°.点睛:本题考查了含30°交点直角三角形的性质,等腰三角形的性质,分类讨论是解题的关键.2.如图,P为∠AOB内一定点,M,N分别是射线OA,OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=___________.【答案】40°【解析】【分析】作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA,OB的交点时,△PMN的周长最短,根据对称的性质可以证得:∠OP1M=∠OPM=50°,OP1=OP2=OP,根据等腰三角形的性质即可求解.【详解】如图:作P关于OA,OB的对称点P1,P2.连接OP1,OP2.则当M,N是P1P2与OA、OB 的交点时,△PMN的周长最短,连接P1O、P2O,∵PP1关于OA对称,∴∠P1OP=2∠MOP,OP1=OP,P1M=PM,∠OP1M=∠OPM=50°同理,∠P2OP=2∠NOP,OP=OP2,∴∠P1OP2=∠P1OP+∠P2OP=2(∠MOP+∠NOP)=2∠AOB,OP1=OP2=OP,∴△P1OP2是等腰三角形.∴∠OP2N=∠OP1M=50°,∴∠P1OP2=180°-2×50°=80°,∴∠AOB=40°,故答案为:40°【点睛】本题考查了对称的性质,正确作出图形,证得△P 1OP 2是等腰三角形是解题的关键.3.如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点O ,过点O 作//EF BC 交AB 于E ,交AC 于F ,过点O 作OD AC ⊥于D 下列结论:①EF BE CF =+;②点O 到ABC ∆各边的距离相等;③1902BOC A ∠=+∠;④设OD m =,AE AF n +=,则AEF S mn ∆=;⑤1()2AD AB AC BC =+-.其中正确的结论是.__________.【答案】①②③⑤【解析】【分析】由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC =90°+12∠A 正确;由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF =BE +CF 故①正确;由角平分线的性质得出点O 到△ABC 各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD =m ,AE +AF =n ,则S △AEF =12mn ,故④错误,根据HL 证明△AMO ≌△ADO 得到AM =AD ,同理可证BM =BN ,CD =CN ,变形即可得到⑤正确.【详解】∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣12∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+12∠A;故③正确;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF.∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;过点O作OM⊥AB于M,作ON⊥BC于N,连接OA.∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=12AE•OM+12AF•OD=12OD•(AE+AF)=12mn;故④错误;∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故②正确;∵AO=AO,MO=DO,∴△AMO≌△ADO(HL),∴AM=AD;同理可证:BM=BN,CD=CN.∵AM+BM=AB,AD+CD=AC,BN+CN=BC,∴AD=12(AB+AC﹣BC)故⑤正确.故答案为:①②③⑤.【点睛】本题考查了角平分线的定义与性质,等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.4.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)【答案】4【解析】【分析】①连接NP,MP,根据SSS定理可得△ANP≌△AMP,故可得出结论;②先根据三角形内角和定理求出∠CAB的度数,再由AD是∠BAC的平分线得出∠1=∠2=30°,根据直角三角形的性质可知∠ADC=60°;③根据∠1=∠B可知AD=BD,故可得出结论;④先根据直角三角形的性质得出∠2=30°,CD=12AD,再由三角形的面积公式即可得出结论.【详解】①连接NP,MP.在△ANP与△AMP中,∵AN AMNP MPAP AP=⎧⎪=⎨⎪=⎩,∴△ANP≌△AMP,则∠CAD=∠BAD,故AD是∠BAC的平分线,故此选项正确;②∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.∵AD是∠BAC的平分线,∴∠1=∠2=12∠CAB=30°,∴∠3=90°﹣∠2=60°,∴∠ADC=60°,故此选项正确;③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,故此选项正确;④∵在Rt△ACD中,∠2=30°,∴CD=12AD,∴BC=BD+CD=AD+12AD=32AD,S△DAC=12AC•CD=14AC•AD,∴S △ABC=12AC•BC=12AC•32AD=34AC•AD,∴S△DAC:S△ABC=1:3,故此选项正确.故答案为①②③④.【点睛】本题考查的是作图﹣基本作图,熟知角平分线的作法是解答此题的关键.5.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△A n B n A n+1的边长为_____.【答案】2n.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.【详解】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∵OA2=4,∴OA1=A1B1=2,∴A2B1=2,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2=32,以此类推△A n B n A n+1的边长为 2n.故答案为:2n.【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.6.如图,在平面直角坐标系中,点 A,B 的坐标分别是(1,5)、(5,1),若点 C 在 x 轴上,且 A,B,C 三点构成的三角形是等腰三角形,则这样的 C 点共有_____________个【答案】5【解析】【分析】分别以A、B为圆心,AB为半径画圆,及作AB的垂直平分线,数出在x轴上的点C的数量即可【详解】解:由图可知:点 C 在 x 轴上,且 A,B,C 三点构成的三角形是等腰三角形,则这样的 C 点共有5个故答案为:5【点睛】本题考查了等腰三角形的存在性问题,掌握“两圆一线”找等腰三角形是解题的关键7.如图,30AOB ∠=︒,P 是AOB ∠内一点,10PO =.若Q 、R 分别是边OA 、OB 上的动点,则PQR ∆周长的最小值为_______.【答案】10【解析】【分析】作点P 关于OB 的对称点P′,点P 关于OA 的对称点P″,连接P′P″交OB 于R ,交OA 于Q ,连接PR 、PQ ,如图3,利用对称的性质得到△PQR 周长=P′P″,根据两点之间线段最短可判断此时△PQR 周长最小,最小值为P′P″的长,再证明△P′OP″为等边三角形得到P′P″=OP′=OP=10,从而得到△PQR 周长的最小值【详解】解:作点P关于OB的对称点P′,点P关于OA的对称点P″,连接P′P″交OB于R,交OA于Q,连接PR、PQ,如图3,则OP=OP′,OP=OP″,RP=RP′,QP=QP″,∴△PQR周长=PR+RQ+PQ=RP′+RQ+QP″=P′P″,∴此时△PQR周长最小,最小值为P′P″的长,∵由对称性可知OP=OP′,OP=OP″,PP′⊥OB,PP″⊥OA,∴∠1=∠2,∠3=∠4,∴∠P′OP″=∠1+∠2+∠3+∠4=2∠2+2∠3=2∠BOA=60°,∴△P′OP″为等边三角形,∴P′P″=OP′=OP=10,故答案是:10.【点睛】本题考查了几何变换综合题:熟练掌握轴对称的性质和等边三角形的性质;会利用两点之间线段最短解决最短路径问题.8.如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当AP=CQ时,PQ交AC于D,则DE的长为______.【答案】1 2【解析】过点Q作AD的延长线的垂线于点F.因为△ABC是等边三角形,所以∠A=∠ACB=60°.因为∠ACB=∠QCF,所以∠QCF=60°.因为PE⊥AC,QF⊥AC,所以∠AEP=∠CFQ=90°,又因为AP=CQ,所以△AEP≌△CFQ,所以AE=CF,PE=QC.同理可证,△DEP≌△DFQ,所以DE=DF.所以AC=AE+DE+CD=DE+CD+CF=DE+DF=2DE,所以DE=12AC=12.故答案为1 2 .9.如图,在四边形ABCD中,∠A=60°,∠ADC=∠ABC=90°,在AB、AD上分别找一点F、E,连接CE、EF、CF,当△CEF的周长最小时,则∠ECF的度数为______.【答案】60°【解析】【分析】此题需分三步:第一步是作出△CEF的周长最小时E、F的位置(用对称即可);第二步是证明此时的△CEF的周长最小(利用两点之间线段最短);第三步是利用对称性求此时∠ECF的值.【详解】分别作出C关于AD、AB的对称点分别为C1、C2,连接C1C2,分别交AD,AB于点E、F再连接CE、CF此时△CEF的周长最小,理由如下:在AD、AB上任意取E1、F1两点根据对称性:∴CE=C1E,CE1=C1E1,CF=C2F,CF1=C2F1∴△CEF的周长= CE+EF+CF= C1E+EF+C2F= C1C2而△CE1F1的周长= CE1+E1F1+CF1= C1E1+E1F1+C2F1根据两点之间线段最短,故C1E1+E1F1+C2F1>C1C2∴△CEF的周长的最小为:C1C2.∵∠A=60°,∠ADC=∠ABC=90°∴∠DCB=360°-∠A-∠ADC-∠ABC=120°∴∠C C1C2+∠C C2C1=180°-∠DCB=60°根据对称性:∠C C1C2=∠E CD,∠C C2C1=∠F CB∴∠E CD+∠F CB=∠C C1C2+∠C C2C1=60°∴∠ECF=∠DCB-(∠E CD+∠F CB)=60°故答案为:60°【点睛】此题考查的是周长最小值的作图方法(对称点),及周长最小值的证法:两点之间线段最短,掌握周长最小值的作图方法是解决此题的关键.10.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为_________【答案】8 5【解析】【分析】首先根据折叠可得CD=AC=6,B′C=BC=8,∠ACE=∠DCE ,∠BCF=∠B′CF ,CE ⊥AB ,然后求得△ECF 是等腰直角三角形,进而求得∠B′FD=90°,CE=EF=4.8,由勾股定理求出AE ,得出BF 的长,即 B′F 的长.【详解】解:根据折叠的性质可知:DE=AE ,∠ACE=∠DCE ,∠BCF=∠B′CF ,CE ⊥AB ,B′F=BF ,∴B′D=8-6=2,∠DCE+∠B′CF=∠ACE+∠BCF ,∵∠ACB=90°,∴∠ECF=45°,∴△ECF 是等腰直角三角形,∴EF=CE ,∠EFC=45°,∴∠BFC=∠B′FC=135°,∴∠B′FE=90°,∵S △ABC =12AC•BC=12AB•CE , ∴AC•BC=AB•CE , ∵根据勾股定理得:22226810ABAC BC ∴ 4.8AC BC CE AB⋅== ∴EF=4.8,22 3.6AE AC EC -=∴B′F=BF=AB -AE-EF=10-3.6-4.8=1.6=85, 故答案是:85.【点睛】此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理等知识;熟练掌握翻折变换的性质,由直角三角形的性质和勾股定理求出CE 、AE 是解决问题的关键.二、八年级数学轴对称三角形选择题(难)11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )A .32B .332C .32D .不能确定【答案】B 【解析】 已知,如图,P 为等边三角形内任意一点,PD 、PE 、PF 分别是点P 到边AB 、BC 、AC 的距离,连接AP 、BP 、CP ,过点A 作AH ⊥BC 于点H ,已知等边三角形的边长为3,可求得高线AH =332,因S △ABC =12BC •AH =12AB •PD+12BC•PE +12AC •PF ,所以12×3×AH =12×3×PD +12×3×PE +12×3×PF ,即可得PD +PE +PF =AH =332,即点P 到三角形三边距离之和为332.故选B.点睛:本题考查了等边三角形的性质,根据三角形的面积求点P 到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.12.已知:如图,点D ,E 分别在△ABC 的边AC 和BC 上,AE 与BD 相交于点F ,给出下面四个条件:①∠1=∠2;②AD=BE ;③AF=BF ;④DF=EF ,从这四个条件中选取两个,不能判定△ABC 是等腰三角形的是( )A .①②B .①④C .②③D .③④【答案】C【解析】【分析】 根据全等三角形的判定和性质以及等腰三角形的判定进行判断即可.【详解】选取①②:在ADF ∆ 和BEF ∆ 中1=2{12AFD BFEAD BEADF BEFAF BFFAB FBACAB CBAAC BC∠∠∠=∠=∴∆≅∆∴=∴∠=∠∠=∠∴∠=∠∴=选取①④:在ADF ∆ 和BEF ∆ 中 1=2{12AFD BFEFD FEADF BEFAF BFFAB FBACAB CBAAC BC∠∠∠=∠=∴∆≅∆∴=∴∠=∠∠=∠∴∠=∠∴=选取③④:在ADF ∆ 和BEF ∆ 中 ={12AF BFAFD BFEFD FEADF BEFAF BFFAB FBACAB CBAAC BC∠=∠=∴∆≅∆∴=∴∠=∠∠=∠∴∠=∠∴=故选C.【点睛】本题考查了等腰三角形的性质和判定,全等三角形的性质和判定的应用,关键是熟练地运用定理进行推理,是一道开放性的题目,能培养学生分析问题的能力.13.如图所示,在ABC 中,AC BC =,90ACB ︒∠=,AD 平分BAC ∠,BE AD ⊥交AC 的延长线F ,E 为垂足.则有:①AD BF =;②CF CD =;③AC CD AB +=;④BE CF =;⑤2BF BE =,其中正确结论的个数是( )A .1B .2C .3D .4【答案】D【解析】【分析】 利用全等三角形的判定定理及其性质以及等腰三角形的三线合一的性质逐项分析即可得出答案.【详解】解:∵AC BC =,90ACB ︒∠=∴45CAB ABC ︒∠=∠=∵AD 平分BAC ∠∴22.5BAE EAF ︒∠=∠=∵90EAF F FBC F ︒∠+∠=∠+∠=∴EAF FBC ∠=∠∴ADC BFC ≅∴AD=BF ,CF=CD ,故①②正确;∵CD=CF,∴AC+CD=AC+CF=AF∵67.5F ︒∠=∵18018067.54567.5ABF F CAB ︒︒︒︒︒∠=-∠-∠=--=∴AF=AB ,即AC+CD=AB ,故③正确;由③可知,三角形ABF 是等腰三角形,∵BE AD ⊥∴12BE BF = 若BE CF =,则30CBF ∠=︒与②中结论相矛盾,故④错误;∵三角形ABF 是等腰三角形,∵BE AD ⊥∴12BE BF = ∴BF=2BE ,故⑤正确;综上所述,正确的选项有4个.故选:D .【点睛】本题考查的知识点是全等三角形的判定定理及其性质,等腰三角形的判定与性质,等腰直角三角形的性质,掌握以上知识点是解此题的关键.14.等边△ABC ,在平面内找一点P ,使△PBC 、△PAB 、△PAC 均为等腰三角形,具备这样条件的P 点有多少个?( )A .1个B .4个C .7个D .10个【答案】D【解析】试题分析:根据点P 在等边△ABC 内,而且△PBC 、△PAB 、△PAC 均为等腰三角形,可知P 点为等边△ABC 的垂心;由此可得分别以三角形各顶点为圆心,边长为半径,交垂直平分线的交点就是满足要求的.解:由点P 在等边△ABC 内,而且△PBC 、△PAB 、△PAC 均为等腰三角形,可知P 点为等边△ABC 的垂心;因为△ABC 是等边三角形,所以分别以三角形各顶点为圆心,边长为半径画弧,交垂直平分线的交点就是满足要求的,每条垂直平分线上得3个交点,再加三角形的垂心,一共10个.故选D .点评:此题主要考查等腰三角形的性质和等边三角形的性质,有一定的拔高难度,属于中档题.15.如图,AOB α∠=,点P 是AOB ∠内的一定点,点,M N 分别在OA OB 、上移动,当PMN ∆的周长最小时,MPN ∠的值为( )A .90α+B .1902α+C .180α-D .1802α-【答案】D【解析】【分析】 过P 点作角的两边的对称点,在连接两个对称点,此时线段与角两边的交点,构成的三角形周长最小.再根据角的关系求解.【详解】解:过P 点作OB 的对称点1P ,过P 作OA 的对称点2P ,连接12PP ,交点为M,N ,则此时PMN 的周长最小,且△1P NP 和△2PMP 为等腰三角形.此时∠12P PP =180°-α;设∠NPM=x°,则180°-x°=2(∠12P PP -x°) 所以 x°=180°-2α 【点睛】求出M,N 在什么位子△PMN 周长最小是解此题的关键.16.如图,ABC ∆中,60BAC ∠=︒,BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ,DE AB ⊥交AB 的延长线于点E ,DF AC ⊥于点F ,现有下列结论:①DE DF =;②DE DF AD +=;③DM 平分EDF ∠;④2AB AC AE +=,其中正确的是( )A .①②B .①②③C .①②④D .①②③④【答案】C【解析】【分析】 ①由角平分线的性质可知①正确;②由题意可知∠EAD=∠FAD=30°,故此可知ED=12AD ,DF=12AD ,从而可证明②正确;③若DM 平分∠EDF ,则∠EDM=90°,从而得到∠ABC 为直角三角形,条件不足,不能确定,故③错误;④连接BD、DC,然后证明△EBD≌△DFC,从而得到BE=FC,从而可证明④.【详解】解:如图所示:连接BD、DC.①∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴ED=DF.∴①正确.②∵∠EAC=60°,AD平分∠BAC,∴∠EAD=∠FAD=30°.∵DE⊥AB,∴∠AED=90°.∵∠AED=90°,∠EAD=30°,∴ED=12AD.同理:DF=12AD.∴DE+DF=AD.∴②正确.③由题意可知:∠EDA=∠ADF=60°.假设MD平分∠EDF,则∠ADM=30°.则∠EDM=90°,又∵∠E=∠BMD=90°,∴∠EBM=90°.∴∠ABC=90°.∵∠ABC是否等于90°不知道,∴不能判定MD平分∠EDF,故③错误.④∵DM是BC的垂直平分线,∴DB=DC.在Rt△BED和Rt△CFD中DE DFBD DC⎧⎨⎩==,∴Rt△BED≌Rt△CFD.∴BE=FC.∴AB+AC=AE-BE+AF+FC又∵AE=AF,BE=FC,∴AB+AC=2AE.故④正确.综上所述,①②④正确,故选:C.【点睛】本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质,掌握本题的辅助线的作法是解题的关键.17.如图,C 是线段 AB 上一点,且△ACD 和△BCE 都是等边三角形,连接 AE、BD 相交于点O,AE、BD 分别交 CD、CE 于 M、N,连接 MN、OC,则下列所给的结论中:①AE=BD;②CM=CN;③MN∥AB;④∠AOB=120º;⑤OC 平分∠AOB.其中结论正确的个数是()A.2 B.3 C.4 D.5【答案】D【解析】【分析】由题意易证:△ACE≅△DCB,进而可得AE=BD;由△ACE≅△DCB,可得∠CAE=∠CDB,从而△ACM ≅△DCN,可得:CM=CN;易证△MCN是等边三角形,可得∠MNC=∠BCE,即MN∥AB;由∠CAE=∠CDB,∠AMC=∠DMO,得∠ACM=∠DOM=60°,即∠AOB=120º;作CG⊥AE,CH⊥BD,易证CG=CH,即:OC 平分∠AOB.【详解】∵△ACD 和△BCE 都是等边三角形,∴AC=DC,CE=CB,∠ACE=∠DCB=120°,∴△ACE≅△DCB(SAS)∴AE=BD,∴①正确;∵△ACE≅△DCB,∴∠CAE=∠CDB,∵△ACD 和△BCE 都是等边三角形,∴∠ACD=∠BCE=∠DCE=60°,AC=DC,在△ACM 和△DCN中,∵60CAE CDB AC DCACD DCE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴△ACM ≅△DCN (ASA ),∴CM =CN ,∴②正确;∵CM =CN ,∠DCE=60°,∴△MCN 是等边三角形,∴∠MNC=60°,∴∠MNC=∠BCE ,∴MN ∥AB ,∴③正确;∵△ACE ≅△DCB ,∴∠CAE=∠CDB ,∵∠AMC=∠DMO ,∴180°-∠CAE-∠AMC=180°-∠CDB-∠DMO ,即:∠ACM=∠DOM=60°,∴∠AOB =120º,∴④正确;作CG ⊥AE ,CH ⊥BD ,垂足分别为点G ,点H ,如图,在△ACG 和△DCH 中,∵90?AMC DHC CAE CDB AC DC ∠=∠=⎧⎪∠=∠⎨⎪=⎩∴△ACG ≅△DCH (AAS ),∴CG =CH ,∴OC 平分∠AOB ,∴⑤正确.故选D.【点睛】本题主要考查全等三角形的判定定理和性质定理,等边三角形的性质定理以及角平分线性质定理的逆定理,添加合适的辅助线,是解题的关键.18.如图,等腰三角形ABC的底边BC长为4,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,若△CDM周长的最小值为8,则△ABC的面积为()A.12 B.16 C.24 D.32【答案】A【解析】【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,再根据三角形的周长求出AD的长,由此即可得出结论.【详解】连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∵△CDM周长的最小值为8,∴AD=8-12BC=8-2=6∴S△ABC=12BC•AD=12×4×6=12,故选A.【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.19.如图,已知,点A(0,0)、B(43,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于()A .201532B .201632C .3D .201932【答案】A【解析】【分析】【详解】根据锐角三函数的性质,由OB=43,OC=1,可得∠OCB=90°,然后根据等边三角形的性质,可知∠A 1AB=60°,进而可得∠CAA 1=30°,∠CA 1O=90°,因此可推导出∠A 2A 1B=30°,同理得到∠CA 2B 1=∠CA 3B 2=∠CA 4B 3=90°,∠A 2A 1B=∠A 3A 2B 2=∠A 4A 3B 3=30°,故可得后一个等边三角形的边长等于前一个等边三角形的边长的一半,即OA 1=OCcos ∠CAA 1=23,B 1A 2=1232⨯,以此类推,可知第2017个等边三角形的边长为:201713()432⨯=. 故选A.【点睛】此题主要考查了等边三角形的性质,属于规律型题目,解题关键是仔细审图,得出:后一个等边三角形的边长等于前一个等边三角形的边长的一半.20.如图,在△ABC 中,AB=AC=8,BC=5,AB 的垂直平分线交AC 于D ,则△BCD 的周长为( )A .13B .15C .18D .21【答案】A【解析】 根据线段垂直平分线的性质,可由AB=AC=8,BC=5,AB 的垂直平分线交AC 于D ,得到AD=BD ,进而得出△BCD 的周长为:CD+BD+BC=AC+BC=8+5=13.故选A .点睛:此题主要考查了线段垂直平分线的性质,关键是掌握垂直平分线上任意一点,到线段两端点的距离相等.。
专题01 全等三角形(解析版)

专题01 全等三角形【考点1全等图形的相关概念】【考点2全等三角形的性质】【考点3全等三角形的判定】【考点4直角三角形全等的判定】【考点5全等三角形的判定与性质】【考点6全等三角形的实际应用】知识点1:全等图形全等形:能够完全重合的两个图形叫做全等形。
(一)全等形的形状相同,大小相等,与图形所在的位置无关。
(二)两个全等形的面积一定相等,但面积相等的两个图形不一定是全等形。
(三)一个图形经过平移、翻折、旋转后,形状、大小都没有改变,只是位置发生了变化,即平移、翻折、旋转前后的图形全等。
知识点2:全等多边形(1)定义:能够完全重合的两个多边形叫做全等多边形.相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角.(2)性质:全等多边形的对应边相等,对应角相等.(3)判定:边、角分别对应相等的两个多边形全等.知识点3:全等三角形的性质对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.(3)有公共边的,公共边常是对应边.(4)有公共角的,公共角常是对应角.(5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键.知识点4:全等三角形的判定方法(1) 边角边定理(SAS):两边和它们的夹角对应相等的两个三角形全等.(2) 角边角定理(ASA):两角和它们的夹边对应相等的两个三角形全等.(3) 边边边定理(SSS):三边对应相等的两个三角形全等.(4) 角角边定理(AAS):两个角和其中一个角的对边对应相等的两个三角形全等.(5) 斜边、直角边定理(HL):斜边和一条直角边对应相等的两个直角三角形全等.知识点5:全等三角形的应用运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.考点剖析【考点1全等图形的相关概念】1.(2023秋•太和县期中)下列各组图形,是全等图形的是( )A.B.C.D.【答案】D【解答】解:A、不是全等图形,不符合题意;B、不是全等图形,不符合题意;C、不是全等图形,不符合题意;D、是全等图形,符合题意;故选:D.2.(2023秋•平原县期中)下列说法错误的是( )A.全等三角形的三条边相等,三个角也相等B.判定两个三角形全等的条件中至少有一个是边C.面积相等的两个图形是全等形D.全等三角形的面积和周长都相等【答案】C【解答】解:全等三角形的三条边相等,三个角也相等,A正确;判定两个三角形全等的条件中至少有一个是边,B正确;面积相等的两个图形不一定是全等形,C错误;全等三角形的面积和周长都相等,D正确,故选:C.3.(2023•东丽区一模)两个全等图形中可以不同的是( )A.位置B.长度C.角度D.面积【答案】A【解答】解:两个全等图形中对应边的长度,对应角的角度,图形的面积相等,可以不同的是位置.故选:A.4.(2022秋•东莞市期末)下列各组图形中,是全等形的是( )A.两个含60°角的直角三角形B.腰对应相等的两个等腰直角三角形C.边长为3和4的两个等腰三角形D.一个钝角相等的两个等腰三角形【答案】B【解答】解:A、两个含60°角的直角三角形,缺少对应边相等,所以不是全等形;B、腰对应相等的两个等腰直角三角形,符合AAS或ASA,或SAS,是全等形;C、边长为3和4的两个等腰三角形有可能是3,3,4或4,4,3不一定全等对应关系不明确不一定全等;D、一个钝角相等的两个等腰三角形.缺少对应边相等,不是全等形.故选:B.5.(2023秋•淮阳区期中)如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )A.135°B.125°C.120°D.90°【答案】A【解答】解:如图,在△ABC和△DEA中,,∴△ABC≌△DEA(SAS),∴∠1=∠4,∵∠3+∠4=90°,∴∠1+∠3=90°,又∵∠2=45°,∴∠1+∠2+∠3=90°+45°=135°.故选:A.6.(2022秋•西乡塘区校级期末)下列四个图形中,属于全等图形的是( )A.①和②B.②和③C.①和③D.全部【答案】D【解答】解:根据全等形的定义可知,①,②,③,④都全等.故选:D.7.(2023秋•永泰县期中)如图,四边形ABCD与四边形A'B'C'D'是全等四边形,若∠A'=95°,∠B=75°,∠D'=130°,则∠C= 60° .【答案】60°.【解答】解:∵四边形ABCD与四边形A'B'C'D'是全等四边形,∴∠A=∠A′,∠D=∠D′,∵∠A'=95°,∠D'=130°,∴∠A=95°,∠D=130°,∵∠B=75°,∴∠C=360°﹣(95°+130°+75°)=60°.故答案为:60°.【考点2全等三角形的性质】8.(2023秋•虞城县期中)如图,△ABC≌△CDA,AB=5,BC=8,AC=7,则AD的长是( )A.5B.6C.7D.8【答案】D【解答】解:∵△ABC≌△CDA,BC=8,∴AD=BC=8.故选:D.9.(2023秋•阜平县期中)如图,△ABC≌△ADE,点D在边BC上,下列结论不正确的是( )A.AD=AB B.DE=BD+DC C.∠B=∠E D.∠BAD=∠CAE【答案】C【解答】解:∵△ABC≌△ADE,∴BC=DE,AB=AD,∠BAC=∠DAE,∠C=∠E,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,DE=BD+DC,即∠BAD=∠CAE,∴选项A、选项B、选项D正确,选项C不一定正确,故选:C.10.(2023秋•丹江口市期中)如图,△ABC≌△AED,点D在BC边上.若∠EAD=85°,∠B=30°,则∠ADC的度数是( )A.50°B.55°C.65°D.30°【答案】C【解答】解:∵△ABC≌△AED,∠EAD=85°,∴∠BAC=∠EAD=85°,AC=AD,∵∠B=30°,∴∠ADC=∠C=180°﹣85°﹣30°=65°,故选:C.11.(2023秋•鹤庆县期中)如图,△ABC≌△DEF(点A,B,C的对应点分别为D,E,F),若∠B=25°,∠C=45°,则∠D的度数为( )A.110°B.105°C.100°D.90°【答案】A【解答】解:∵∠B=25°,∠C=45°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣25°﹣45°=110°,∵△ABC≌△DEF(点A,B,C的对应点分别为D,E,F),∴∠D=∠BAC=110°,故选:A.12.(2022秋•长春期末)若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )A.30B.27C.35D.40【答案】A【解答】解:∵△ABC≌△DEF,∴BC=EF=30,故选:A.12.(2023秋•文成县期中)如图,△ABC≌△DEF,BC=12,EC=7,则CF的长为( )A.5B.6C.7D.8【答案】A【解答】解:∵△ABC≌△DEF,∴BC=EF,又BC=12,∴EF=12,∴EC=7,∴CF=EF﹣EC=12﹣7=5,故选:A.13.(2023秋•天长市期中)如图,△ABD≌△ACE,BE=16,DE=10,则BC的长是( )A.24B.20C.21D.22【答案】D【解答】解:∵△ABD≌△ACE,∴BD=EC=BE﹣DE=6,∴BC=BE+EC=16+6=22,故选:D.14.(2022秋•市中区期末)如图,已知△CAD≌△CBE,若∠A=30°,∠C=80°,则∠CEB =( )A.50°B.60°C.70°D.80°【答案】C【解答】解:∵∠A=30°,∠C=80°,∴∠ADC=180°﹣80°﹣30°=70°,∵△CAD≌△CBE,∴∠CEB=∠CDA=70°;故选:C.15.(2022秋•汶上县校级期末)如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为( )A.2B.3C.4D.5【答案】A【解答】解:∵△ABC≌△DCB,∴BD=AC=7,∵BE=5,∴DE=BD﹣BE=2,故选:A.16.(2023秋•琼中县期中)如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE 交于点F,△ADC≌△BDF,若BD=4,CD=2,则△ABC的面积为( )A.24B.18C.12D.8【答案】C【解答】解:∵△ADC≌△BDF,∴AD=BD,∵BD=4,∴AD=4,∵DC=2,∴BC=BD+DC=4+2=6,∴S===12,△ABC故选:C.【考点3全等三角形的判定】17.(2023秋•社旗县期中)如图所示的四个三角形中,全等的三角形是( )A.①③B.①②C.②④D.①③④【答案】B【解答】解:根据SAS可知①和②中的两个三角形全等.故选:B.18.(2023秋•太和县期中)如图,AB∥DE,BC=EF.补充下列一个条件,不能使△ABC≌△DEF的是( )A.AC=DF B.∠A=∠D C.AB=DE D.AC∥DF【答案】A【解答】解:∵AB∥DE,∴∠B=∠DEF,且BC=EF,A、若AC=DF,不能判定△ABC≌△DEF,符合题意;B、若∠A=∠D,可根据“角角边”判定△ABC≌△DEF,不符合题意;C、若AB=DE,可根据“边角边”判定△ABC≌△DEF,不符合题意;D、若AC∥DF,则∠ACB=∠F,可根据“角边角”判定△ABC≌△DEF,不符合题意;故选:A.19.(2023秋•新和县期中)已知:如图,AB=DC,AE=BF,∠A=∠FBD,求证:△AEC ≌△BFD.【答案】见解析.【解答】证明:∵AB=DC,∴AB+BC=DC+BC,∴AC=BD,在△AEC和△BFD中,,∴△AEC≌△BFD(SAS).20.(2023•咸阳一模)已知,如图,AB=AE,AB∥DE,∠ACB=∠D,求证:△ABC≌△EAD.【答案】证明过程见解答.【解答】证明:∵AB∥DE,∴∠E=∠BAC,在△ABC和△EAD中,,∴△ABC≌△EAD(AAS).21.(2023秋•曹县期中)如图,点F,C在BE上,BF=CE,AB=DE,∠B=∠E.求证:△ABC≌△DEF.【答案】见试题解答内容【解答】证明:∵BF=CE,∴BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS).22.(2022秋•祁阳县期末)已知,如图,∠1=∠2,∠C=∠D,BC=BD,求证:△ABD≌△EBC.【答案】见试题解答内容【解答】证明:∵∠1=∠2,∴∠1+∠EBD=∠2+∠EBD,∴∠ABD=∠EBC,在△ABD和△EBC中,,∴△ABD≌△EBC(ASA).23.(2023秋•建湖县期中)已知,如图,点D、E分别在AB、AC上,AD=AE,BE、CD相交于点O,∠B=∠C,求证:(1)△ABE≌△ACD;(2)△BOD≌△COE.【答案】见试题解答内容【解答】证明:(1)在△ABE和△ACD中,,∴△ABE≌△ACD(AAS);(2)∵△ABE≌△ACD,∴AB=AC,∵AD=AE,∴BD=CE,在△BOD和△COE中,,∴△BOD≌△COE(AAS).24.(2022秋•汉阳区校级期末)如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.【答案】见试题解答内容【解答】证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,∴∠BAC=∠DAE,在△ABC和△ADE中∴△ABC≌△ADE(ASA).【考点4直角三角形全等的判定】25.(2023春•渭滨区期中)如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是( )A.AC=A′C′,BC=B′C′B.∠A=∠A′,AB=A′B′C.AC=A′C′,AB=A′B′D.∠B=∠B′,BC=B′C′【答案】C【解答】解:∵在Rt△ABC和Rt△A′B′C′中,如果AC=A′C′,AB=A′B′,那么Rt△ABC和Rt△A′B′C′一定全等,故选:C.26.(2023秋•疏勒县期中)已知:如图AD为△ABC的高,E为AC上一点BE交AD于F且有BF=AC,FD=CD.求证:Rt△BFD≌Rt△ACD.【答案】见解析.【解答】证明:∵AD是△ABC的高,∴∠ADB=∠ADC=90°.在Rt△BFD和Rt△ACD中,∴Rt△BFD≌Rt△ACD(HL).27.(2023春•怀化期末)如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.【答案】见试题解答内容【解答】证明:如图,在Rt△ACE和Rt△CBF中,,∴Rt△ACE≌Rt△CBF(HL),∴∠EAC=∠BCF,∵∠EAC+∠ACE=90°,∴∠ACE+∠BCF=90°,∴∠ACB=180°﹣90°=90°.28.(2023春•垦利区期末)如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.【答案】见试题解答内容【解答】证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE,∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,在Rt△ABF和Rt△DCE中,,∴Rt△ABF≌Rt△DCE(HL).29.(2022春•泾阳县期中)已知:如图,点E、F在线段BD上,AF⊥BD,CE⊥BD,AD=CB,DE=BF,求证:AF=CE.【答案】见试题解答内容【解答】证明:∵DE=BF,∴DE+EF=BF+EF;∴DF=BE;在Rt△ADF和Rt△CBE中,∴Rt△ADF≌Rt△CBE(HL),∴AF=CE.【考点5全等三角形的判定与性质】30.(2023秋•礼县期中)如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=∠B=40°,DE交线段AC于点E.下列结论:①∠DEC=∠BDA;②若AD=DE,则BD=CE;③当DE⊥AC时,则D为BC中点;④当△ADE为等腰三角形时,∠BAD=30°.其中正确的有( )A.1个B.2个C.3个D.4个【答案】C【解答】解:①∵∠ADC=∠B+∠BAD,∠B=∠ADE=40°,∴∠BAD=∠ADC﹣∠ADE,即∠BAD=∠CDE,∵AB=AC,∴∠B=∠C,∵∠DEC=180°﹣∠CDE﹣∠C,∠BDA=180°﹣∠BAD﹣∠B,∴∠DEC=∠BDA,故①正确;②∵AB=AC,∴∠B=∠C=40°,由①可知∠DEC=∠BDA,∵AD=DE,∴△ABD≌△DCE(ASA),∴BD=CE,故②正确;③∵D为BC中点,AB=AC,∴AD⊥BC,∴∠ADC=90°,∴∠CDE=90°﹣40°=50°,∵∠C=∠B=40°,∴∠DEC=90°,∴DE⊥AC,故③正确;④∵∠C=40°,∴∠AED>40°,∴∠ADE≠∠AED,∵△ADE为等腰三角形,∴AE=DE或AD=DE,当AE=DE时,∠DAE=∠ADE=40°,∵∠BAC=180°﹣40°﹣40°=100°,∴∠BAD=100°﹣40°=60°,故④不正确,综上所述正确的有①②③,故选:C.31.(2023秋•临颍县期中)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,B,D,E三点在一条直线上,若∠1=26°,∠3=56°,则∠2的度数为( )A.30°B.56°C.26°D.82°【答案】A【解答】解:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠1=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠2,∵∠3=∠1+∠ABD,∴∠3=∠1+∠2,∵∠1=26°,∠3=56°,∴∠2=56°﹣26°=30°,故选:A.32.(2023秋•太和县期中)如图,在△ABC中,AB=AC,∠B=∠EDF,若BE=CD=1,BC=3,则CF的长为( )A.1B.2C.3D.4【答案】B【解答】解:∵AB=AC,∴∠B=∠C,∵∠BED=180°﹣∠B﹣∠BDE,∠CDF=180°﹣∠EDF﹣∠BDE,∠B=∠EDF,∴∠BED=∠CDF,∵BE=CD,∴△BED≌△CDF(ASA),∴CF=BD,∵BC=3,CD=1,∴BD=2,∴CF=2,故选:B.33.(2023秋•鹤庆县期中)已知△ABC中AD为中线,且AB=5、AC=7,则AD的取值范围为( )A.2<AD<12B.5<AD<7C.1<AD<6D.2<AD<10【答案】C【解答】解:延长AD至点E,使DE=AD,连接EC,在△ADB和△EDC中∴△ADB≌△EDC(SAS),∴CE=AB,∵AB=5,AC=7,∴CE=5,设AD=x,则AE=2x,∴7﹣5<2x<7+5,∴1<x<6,故选:C.34.(2023秋•辉县市期中)如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,BD=6,CD=4,则线段AF的长度为( )A.1B.2C.4D.6【答案】B【解答】解:∵AD⊥BC,∴∠ADB=90°,∵∠ABC=45°,∴∠ABD=∠DAB,∴BD=AD=6,∵∠CAD+∠AFE=90°,∠CAD+∠C=90°,∠AFE=∠BFD,∴∠AFE=∠C,∵∠AFE=∠BFD∴∠C=∠BFD在△ADC和△BDF中,,∴△ADC≌△BDF(AAS),∴CD=DF=4,∴AF=AD﹣DF=6﹣4=2.故选:B.35.(2023秋•应城市期中)如图,在△ABC和△CDE中,点B,C,E在同一条直线上,∠B =∠E=∠ACD,AC=CD,若AB=1,BE=4,则DE的长为( )A.1B.2C.3D.4【答案】C【解答】解:∵∠B+∠ACB+∠BAC=180°,∠B=∠E=∠ACD,∴∠ACD+∠ACB+∠BAC=180°,∵∠ACD+∠ACB+∠DCE=180°,∴∠BAC=∠DCE,在△ABC和△CED中,,∴△ABC≌△CED(AAS),∴BC=DE,AB=CE,∵AB=1,BE=4,∴DE=BC=BE﹣CE=BE﹣AB=4﹣1=3,故选:C.36.(2022秋•阿荣旗期末)如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于点E,AE=AC,连接AD,若BC=8,则BD+DE等于( )A.6B.7C.8D.9【答案】C【解答】解:∵DE⊥AB,∴∠DEB=90°,在Rt△ACD和Rt△AED中,,∴Rt△ACD≌Rt△AED(HL),∴CD=DE,∴BD+DE=BD+CD=BC,∵BC=8,∴BD+DE=BC=8.故选:C.37.(2022秋•和平区校级期末)如图所示,BC、AE是锐角△ABF的高,相交于点D,若AD =BF,AF=7,CF=2,则BD的长为( )A.2B.3C.4D.5【答案】B【解答】解:∵BC、AE是锐角△ABF的高,∴∠BCF=∠ACD=∠AEF=90°,∴∠F+∠CAD=∠F+∠CBF=90°,∴∠CBF=∠CAD,在△BCF和△ACD中,,∴△BCF≌△ACD(AAS),∴CD=CF=2,BC=AC=AF﹣CF=5,∴BD=BC﹣CD=5﹣2=3.故选:B38.(2023秋•京口区期中)如图,点B,F,C,E在直线l上(点F,C之间不能直接测量),点A,D在l的异侧,AB∥DE,∠A=∠D,测得AB=DE.(1)求证:△ABC≌△DEF;(2)若BE=10m,BF=3m,求FC的长.【答案】(1)见解析;(2)FC=4cm.【解答】(1)证明:∵AB∥DE,∴∠ABC=∠DEF,在△ABC与△DEF中,∴△ABC≌△DEF(ASA).(2)解:∵△ABC≌△DEF,∴BC=EF,∴BF+FC=EC+FC,∴BF=EC,∵BE=10cm,BF=3cm,∴FC=10﹣3﹣3=4cm.39.(2023秋•连山区期中)如图,点D在AC边上,∠A=∠B,AE=BE,∠1=∠2.(1)求证:△AEC≌△BED;(2)若∠1=45°,求∠BDE的度数.【答案】(1)见解析;(2)67.5°.【解答】(1)证明:∵∠2+∠BDE=∠ADE=∠1+∠C,∠1=∠2∴∠C=∠BDE,在△AEC和△BED中,,∴△AEC≌△BED(AAS),(2)解:∵△AEC≌△BED,∴EC=ED,∴∠EDC=∠C,∵∠1=45°∴∴∠BDE=67.5°40.(2023秋•科尔沁区期中)如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.(2)连接AM,求证:MA平分∠EMF.【答案】见试题解答内容【解答】(1)解:结论:EC=BF,EC⊥BF.理由:∵AE⊥AB,AF⊥AC,∴∠EAB=∠CAF=90°,∴∠EAB+∠BAC=∠CAF+∠BAC,∴∠EAC=∠BAF.在△EAC和△BAF中,,∴△EAC≌△BAF(SAS),∴EC=BF.∠AEC=∠ABF∵∠AEG+∠AGE=90°,∠AGE=∠BGM,∴∠ABF+∠BGM=90°,∴∠EMB=90°,∴EC⊥BF.∴EC=BF,EC⊥BF.(2)证明:作AP⊥CE于P,AQ⊥BF于Q.∵△EAC≌△BAF,∴AP=AQ(全等三角形对应边上的高相等).∵AP⊥CE于P,AQ⊥BF于Q,∴AM平分∠EMF.41.(2023秋•合江县期中)如图,已知:∠B=∠C=90°,M是BC的中点,DM平分∠ADC.求证:(1)AM平分∠DAB;(2)AD=AB+CD.【答案】见试题解答内容【解答】(1)证明:过点M作ME⊥AD于E,∵∠B=∠C=90°,∴MB⊥AB,MC⊥CD,∵DM平分∠ADC,ME⊥AD,MC⊥CD,∴ME=MC,∵M是BC的中点,∴MC=MB,∴MB=ME,又∴MB⊥AB,ME⊥AD,∴AM平分∠DAB.(2)∵ME⊥AD,MC⊥CD,∴∠C=∠DEM=90°,在Rt△DCM和Rt△DEM中,,∴Rt△DCM≌Rt△DEM(HL),∴CD=DE,同理AE=AB,∵AE+DE=AD,∴CD+AB=AD.【考点6全等三角形的实际应用】42.(2023秋•镇平县期中)一名工作人员不慎将一块三角形模具打碎成了如图所示的四块,他需要去商店再配一块与原来大小和形状完全相同的模具.现只能拿能两块去配,其中可以配出符合要求的模具的是( )A.①③B.②④C.①④D.②③【答案】B【解答】解:根据题意得:拿①②或②④可以根据“角边角”得到原三角形全等的三角形.故选:B.43.(2023秋•昭阳区期中)如图,为了测量B点到河对面的目标A之间的距离,在B点同侧选择了一点C,测得∠ABC=60°,∠ACB=40°,然后在BC的同侧找到点M使∠MBC=60°,∠MCB=40°,得到△MBC≌△ABC,所以测得MB的长就是A,B两点间的距离,这里判定△MBC≌△ABC的理由是( )A.SAS B.AAA C.SSS D.ASA【答案】D【解答】解:在△MBC,△ABC中,,∴△MBC≌△ABC(ASA).故选:D.44.(2023春•龙岗区校级期末)如图是雨伞在开合过程中某时刻的截面图,伞骨AB=AC,点D,E分别是AB,AC的中点,DM,EM是连接弹簧和伞骨的支架,且DM=EM,已知弹簧M在向上滑动的过程中,总有△ADM≌△AEM,其判定依据是( )A.ASA B.AAS C.SSS D.HL【答案】C【解答】解:∵AB=AC,点D,E分别是AB,AC的中点,∴AD=AE,在△ADM和△AEM中,.∴△ADM≌△AEM(SSS),故选:C.45.(2023•怀化三模)如图所示,工人赵师傅用10块高度都是1.5m的相同长方体新型建筑材料,垒了两堵与地面垂直的墙ABCD和EFGH,点P在BE上,已知AP=PF,∠APF=90°.(1)求证:△ABP≌△PEF;(2)求BE的长.【答案】(1)证明见解答;(2)15m.【解答】(1)证明:∵∠ABP=∠FEP=90°,∠APF=90°,∴∠APB=∠PFE(同角的余角相等).在△ABP与△PEF中,,∴△ABP≌△PEF(AAS);(2)由题意知,AB=1.5×3=4.5(m),EF=7×1.5=10.5(m).由(1)知,△ABP≌△PEF,∴BP=EF=10.5m,AB=PE=4.5m,∴BE=BP+PE=15m.46.(2023秋•云梦县期中)在测量一个小口圆形容器的壁厚时(容器壁厚度均匀),小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,只需测得AB=a,EF=b,就可以知道圆形容器的壁厚了.(1)请你利用所学习的数学知识说明AB=CD;(2)若a=58.6mm,b=61.2mm,求出圆形容器的壁厚.【答案】(1)见解析;(2)圆形容器的壁厚为1.3mm.【解答】解:(1)在△AOB和△DOC中,,∴△AOB≌△DOC(SAS),∴AB=CD;(2)∵EF=b=61.2mm,AB=CD=a=58.6mm,∴圆形容器的壁厚为.47.(2023春•渠县校级期末)生活中的数学:(1)启迪中学计划为现初一学生暑期军训配备如图1所示的折叠凳,这样设计的折叠凳坐着舒适、稳定,这种设计所运用的数学原理是 三角形具有稳定性 .(2)图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD 的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30cm,则由以上信息可推得CB的长度也为30cm,请说明AD=CB的理由.【答案】(1)三角形具有稳定性;(2)见解答.【解答】(1)解:这种设计所运用的数学原理是三角形具有稳定性,故答案为:三角形具有稳定性;(2)证明:∵O是AB和CD的中点,∴AO=BO,CO=DO,在△AOD和△BOC中,,∴△AOD≌△BOC(SAS),∴AD=BC.过关检测一.选择题(共10小题)1.(2023秋•巴东县期中)下列汽车标志中,是由多个全等图形组成的有( )个.A.1B.2C.3D.4【答案】C【解答】解:组成第1个图形的各部分不全等,不符合题意;组成第2个图形的两个图形全等,符合题意;组成第3个图形的三个图形全等,符合题意;组成第4个图形是四个圆形全等,符合题意.故选:C.2.(2023秋•沂南县期中)如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数为( )A.30°B.31°C.32°D.33°【答案】D【解答】解:由三角形内角和定理得,∠2=180°﹣117°﹣30°=33°,∵两个三角形全等,∴∠1=∠2=33°,3.(2022秋•海淀区校级期末)如图,△ABC≌△AED,点E在线段BC上,∠1=56°,则∠AED的大小为( )A.34°B.56°C.62°D.68°【答案】C【解答】解:∵△ABC≌△AED,∴∠BAC=∠EAD,AB=AE,∴∠BAE=∠1=56°,∴∠B=∠AEB=(180°﹣56°)=62°,∴∠AED=∠B=62°,故选:C.4.(2023秋•广陵区校级月考)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90°D.∠BCA=∠DCA【答案】D【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;C、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故C选项不符合题意;D、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故D选项符合题意;5.(2023秋•张北县期中)如图,要测量池塘A,B两端的距离,作线段AC与BD相交于点O.若AC=BD=8m,AO=DO,△COD的周长为14m,则A,B两点间的距离为( )A.6m B.8m C.10m D.12m【答案】A【解答】解:∵AC=BD,AO=DO,∴AC﹣AO=BD﹣DO,即OC=OB,∵OC=OB,∠COD=∠BOA,OD=OA,∴△COD≌△BOA(SAS),∴AB=CD,∵△COD的周长为14m,∴OC+OD+CD=14m,即AC+CD=14m,∴CD=6m,∴AB=6m,故选:A.6.(2023秋•崆峒区校级期中)装修工人在搬运中发现有一块三角形的陶瓷片不慎摔成了四块(如图),他要拿哪一块回公司才能更换到相匹配的陶瓷片( )A.①B.②C.③D.④【答案】A【解答】解:②、③、④块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,只有第①块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.故选:A.7.(2023秋•青秀区校级期中)如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA′、BB'的中点.只要量出A′B′的长度.就可以知道该零件内径AB的长度.依据的数学基本事实是( )A.两角和它们的夹边分别相等的两个三角形全等B.两边和它们的夹角分别相等的两个三角形全等C.三边分别相等的两个三角形全等D.两点之间线段最短【答案】B【解答】解:∵点O为AA'、BB'的中点,∴OA=OA',OB=OB',由对顶角相等得∠AOB=∠A'OB',在△AOB和△A'OB'中,,∴△AOB≌△A'OB'(SAS),∴AB=A'B',即只要量出A'B'的长度,就可以知道该零件内径AB的长度,故选:B.8.(2022秋•正定县期末)如图,在△ABC和△AED中,已知∠1=∠2,AC=AD,添加一个条件后,仍然不能证明△ABC≌△AED,这个条件是( )A.AB=AE B.BC=ED C.∠C=∠D D.∠B=∠E【答案】B【解答】解:∵∠1=∠2,∴∠1+∠EAB=∠2+∠EAB,即∠CAB=∠DAE,A、加上条件AB=AE可利用SAS定理证明△ABC≌△AED;B、加上BC=ED不能证明△ABC≌△AED;C、加上∠C=∠D可利用ASA证明△ABC≌△AED;D、加上∠B=∠E可利用AAS证明△ABC≌△AED;故选:B.9.(2023秋•丹阳市期中)在如图所示的3×3网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )A.3个B.4个C.5个D.6个【答案】B【解答】解:如图,观察图象可知满足条件的三角形有4个.故选:B.10.(2022秋•灵宝市校级期末)现有一块如图所示的四边形草地ABCD,经测量,∠B=∠C,AB=10m,BC=8m,CD=12m,点E是AB边的中点.小狗汪汪从点B出发以2m/s的速度沿BC向点C跑,同时小狗妞妞从点C出发沿CD向点D跑,若能够在某一时刻使△BEP与△CPQ全等,则妞妞的运动速度为( )A.B.C.2m/s或D.2m/s或【答案】D【解答】解:∵AB=10m,E是AB边的中点,∴BE=5m,∵∠B=∠C,且△BEP与△CPQ全等,∴BP=CQ,BE=CP或CP=BP,BE=CQ,当BP=CQ,BE=CP时,∵BE=5m,BC=8m,设运动时间为t,8﹣2t=5,解得,∴,此时妞妞的运动速度为:m/s,当CP=BP,BE=CQ时,,t=2,此时CQ=5,妞妞的运动速度为:,故选:D.二.填空题(共5小题)11.(2023秋•武都区期中)如图,点A,D,C,E在一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为 4 .【答案】4.【解答】解:∵AB∥EF,∴∠A=∠E,在△ABC和△EFD中,,∴△ABC≌△EFD(ASA),∴AC=ED=7,又∵AE=10,∴AC+DE﹣CD=10,∴CD=14﹣10=4;故答案为:4.12.(2023秋•招远市期中)如图,已知BD=CE,∠ADB=∠AEC,若AC=9,AE=2,则线段DC的长为 7 .【答案】7.【解答】解:在△ABD和△ACE中,,∴△ABD≌△ACE(AAS),∴AD=AE=2,∵AC=9,∴DC=AC﹣AD=7,故答案为:7.13.(2023秋•湖北期中)工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别截取OM,ON,使OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C连OC.可知△OMC≌△ONC,OC便是∠AOB 的平分线.则△OMC≌△ONC的理由是 SSS .【答案】SSS.【解答】证明:由题意知;CM=CN,在△OMC和ONC中,,∴△OMC≌ONC(SSS),∴△OMC≌△ONC的理由是SSS.故答案为:SSS.14.(2023秋•宁江区期中)如图,在△ABC中,CD平分∠ACB,过点B作BE⊥CD于点D,交AC于点E.已知∠ABE=∠A,AC=10,BC=6.则BD的长为 2 .【答案】2.【解答】解:∵CD平分∠ACB,∴∠BCD=∠DCE,∵BE⊥CD,∴∠BDC=∠EDC=90°,在△CDB≌△CDE中,,∴△CDB≌△CDE(ASA),∴BD=DE,CE=BC=6,即△BCE为等腰三角形,∴AE=AC﹣CE=4,又∵∠A=∠ABE,∴BE=AE,∴BD=DE=BE=2,故答案为:2.15.(2023春•文登区期中)如图,△ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,点P、Q分别在AC和与AC垂直的射线AM上移动,当AP= 5cm或10cm 时,△ABC和△QPA全等.【答案】5cm或10cm.【解答】解:∵PQ=AB,∴根据三角形全等的判定方法HL可知,①当P运动到AP=BC时,△ABC≌△QPA,即AP=BC=5cm;②当P运动到与C点重合时,△QAP≌△BCA,即AP=AC=10cm.故答案为:5cm或10cm.三.解答题(共3小题)16.(2023•工业园区校级模拟)如图,点C、D在线段AB上,且AC=BD,AE=BF,AE∥BF,连接CE、DE、CF、DF,求证CF=DE.【答案】证明见解答过程.【解答】证明:∵AC=BD,∴AC+CD=BD+CD,即AD=BC,∵AE∥BF,∴∠A=∠B,在△ADE和△BCF中,,∴△ADE≌△BCF(SAS),∴DE=CF,即CF=DE.17.(2023秋•南川区期中)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.(1)求证:AE=AD;(2)若BD=8,DC=5,求ED的长.【答案】(1)证明见解析;(2)3.【解答】(1)证明:∵∠BAC=∠EAD,∴∠BAC﹣∠EAC=∠EAD﹣∠EAC,即:∠BAE=∠CAD,在△ABE和△ACD中,,∴△ABE≌△ACD(ASA),∴AE=AD;(2)解:∵△ABE≌△ACD,∴BE=CD,∵BD=8,DC=5,∴ED=BD﹣BE=BD﹣CD=8﹣5=3.18.(2023春•周村区期末)如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)求证:△ABC≌△ADE;(2)求∠FAE的度数;(3)求证:CD=2BF+DE.【答案】见试题解答内容【解答】证明:(1)∵∠BAD=∠CAE=90°,∴∠BAC+∠CAD=90°,∠CAD+∠DAE=90°,∴∠BAC=∠DAE,在△BAC和△DAE中,,∴△BAC≌△DAE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠E=45°,由(1)知△BAC≌△DAE,∴∠BCA=∠E=45°,∵AF⊥BC,∴∠CFA=90°,∴∠CAF=45°,∴∠FAE=∠FAC+∠CAE=45°+90°=135°;(3)延长BF到G,使得FG=FB,∵AF⊥BG,∴∠AFG=∠AFB=90°,在△AFB和△AFG中,,∴△AFB≌△AFG(SAS),∴AB=AG,∠ABF=∠G,∵△BAC≌△DAE,∴AB=AD,∠CBA=∠EDA,CB=ED,∴AG=AD,∠ABF=∠CDA,∴∠G=∠CDA,∵∠GCA=∠DCA=45°,在△CGA和△CDA中,,∴△CGA≌△CDA(AAS),∴CG=CD,∵CG=CB+BF+FG=CB+2BF=DE+2BF,∴CD=2BF+DE.。
人教八上:专题二--全等三角形的性质与判定(含解析)

专题二全等三角形的性质与判定一、单选题1.下面四个三角形中,与图中的△ABC全等的是()..23A.50°B.59°C.69°D.71°4.如图,点E、F在BC上,AB=CD,AF=DE,AF、DE相交于点G,添加下列哪一个条件,可使得△ABF≌△DCE()A.∠B=∠C B.AG=DG C.∠AFE=∠DEF D.BE=CF5.尺规作图中蕴含着丰富的数学知识和思想方法.如图,为了得到∠MBN=∠PAQ,在用直尺和圆规作图的过程中,得到△ACD≌△BEF的依据是().A.SAS B.SSS C.ASA D.AAS6.已知,如图所示的两个三角形全等,则∠1=()A.72°B.60°C.48°D.50°7.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是()A.SAS B.SSS C.ASA D.HL8.如图,点E、F在BC上,AB=DC,∠B=∠C.添加一个条件后,不能证明△ABF≌△DCE,这个条件可能是()A.∠A=∠D B.BE=CF C.BF=CE D.AF=ED9.已知图中的两个三角形全等,则∠1等于( )A.72°B.60°C.58°D.50°10.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是()A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD11.如图,已知∠CAB=∠DBA,老师要求同学们补充一个条件使△ABC≌△BAD,以下是四个同学补充的条件,其中错误的是()A.AC=BD B.CB=DA C.∠C=∠D D.∠ABC=∠BAD12.用直尺和圆规作一个角等于已知角,如图,能得出∠AOB=∠A′O′B′的依据是()A.SSS B.SAS C.ASA D.AAS13.如图,AB=4厘米,BC=6厘米,∠B=∠C,如果点P在线段BC上以2厘米/秒的速度由B点向C 点运动,同时,点Q从C点出发沿射线CD运动.若经过t秒后,△ABP与△CQP全等,则t的值是()A.1B.1.5C.1或1.5D.1或214.已知图中的两个三角形全等,则∠1的度数是()A.50°B.54°C.60°D.76°15.如图,点E、F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是( )A.∠A=∠D B.∠AFB=∠DEC C.AB=DC D.AF=DE16.如图,点B、E、C、F在一条直线上,AB=DE,∠B=∠DEF,要使得△ABC≌△DEF,不能添加的条件是()A.∠A=∠D B.AC=DF C.BE=CF D.AC∥DF17.已知图中的两个三角形全等,图中的字母表示三角形的边长,则∠1的大小是()A.64°B.65°C.51°D.55°18.如图,工人师傅设计了一种测量零件内径AB的卡钳,卡钳交叉点O为AA′、BB′的中点,只要量出A′B′的长度,就可以知道该零件内径AB的长度.其依据的数学基本据实是()A.两边及其夹角分别相等的两个三角形全等B.两角及其夹边分别相等的两个三角形全等C.等角对等边D.两点之间线段最短19.如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点A(0,a),B(b,0),C(−4,4),其中b<a<0,则a,b之间的数量关系是()A.a+b=−4B.a−b=4C.a+b=−8D.a−b=820.用尺规作图作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是()A.SAS B.ASA C.HL D.SSS21.如图,点E、F在BC上,AB=DC,AF=DE,AF、DE相交于点G,要使得△ABF≌△DCE,添加下列哪一个条件()A.∠B=∠C B.GE=GF C.∠AFE=∠DEF D.BF=CE 22.阅读以下作图步骤:①在OA和OB上分别截取OC,OD,使OC=OD;②③23A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC 24.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°25.如图,已知∠CAB=∠DAB,则添加下列一个条件不一定能使△ABC≌△ABD的是( )A.BC=BD B.∠C=∠D C.AC=AD D.∠ABC=∠ABD26.已知:如图,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A.∠A+∠D=90°B.∠A=∠2C.△ABC≌△CED D.∠1=∠227.如图,已知ΔABC,下面甲、乙、丙、丁四个三角形中,与ΔABC全等的是()A.甲B.乙C.丙D.丁二、填空题28.如图,点B、C、E三点在同一直线上,且AB=AD,AC=AE,BC=DE,若∠1+∠2+∠3=96°,则∠3的度数为.29.如图,三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,△ADE的周长为cm.30313233.已知:如图,∠B=∠C=90°,AF=DE,BE=CF.求证:AB=DC.34.如图,OA=OC,OB=OD,∠AOD=∠COB.求证:AB=CD.35.如图,四边形ABCD中,∠B=90°,AB∥CD,M是BC边上的一点,且AM平分∠BAD,DM平分∠ADC,求证:(1)BM=MC;(2)AM⊥MD.36.如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过点P作PF⊥AD 交BC的延长线于点F,PF交AC于点H,求证:(1)△ABP≌△FBP;(2)AH=AB−BD.37.如图,B、E、C、F在同一直线上,AB=DE,BE=CF,∠B=∠DEF,求证:AC=DF.38.如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD交于点O,OB=OC.求证:∠1=∠2.39.如图,在△ABC中,AB=AC,D、E是BC边上的点,且BD=CE,求证:AD=AE.40.如图,在四边形ABCD中,AB∥CD,E为AD的中点,连接CE并延长交BA的延长线于点F.(1)求证:△CDE≌△FAE.(2)连接BE,当BE⊥CF时,CD=3,AB=2,求BC的长.41.如图,点D、E在△ABC的BC边上,AB=AC,AD=AE,求证:BD=CE.42.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,AD=CD,AB=CB,对角线AC交BD与点O.(1)请根据你学过的知识直接写出一组全等的三角形______;(2)求证:AC⊥BD.43.如图,AB=CD,AE⊥BC于E,DF⊥BC于F,若CE=BF.(1)求证:AE=DF;(2)求证:AB∥CD.44.如图,BE⊥AD,CF⊥AD,垂足分别为点E,F,AF=DE,∠B=∠C,求证:AB=CD.45.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E.(1)求证:△ADC≌△CEB;(2)延长EB至点F,使得BF=DE,连接AF交CE于点G,若AD=5,BE=3,求DG的长.46.如图,AB=AE,∠B=∠AED,∠1=∠2,求证:AC=AD.47.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE.求证:∠AFB=2∠ACB.48.(变图形—平移型)如图,点C是AB的中点,AD=CE,CD=BE.求证:△ACD≌△CBE.49.如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.50.在Rt△ABC中,∠BAC=90°,AB=AC,过直角顶点A作直线MN,BD⊥MN于点D,CE⊥MN于点E.(1)如图1,当MN与BC边不相交时,判断BD,CE,DE之间的数量关系,并说明理由;(2)当MN与边BC相交时,请在图2中画出图形,并直接写出BD,CE,DE之间的数量关系.51.如图,CA=CD,∠1=∠2,BC=EC.求证:AB=DE.52.如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.53.如图,点B,E,C,F在同一直线上,相交于点E,AB=DE,AC=DF,∠A=∠D.求证:BE=CF.54.如图,点A、B、C、D在同一直线上,AE=DF,AB=CD,CE=FB.求证:AE∥DF.55.如图,已知AB=AC,BD=CD,DM⊥AB于M,DN⊥AC于N,求证:DM=DN56.如图,△ABC中,∠ACB=90°,AC=BC,将△ABC绕点C逆时针旋转角α.(0°<α<90°)得到△A1B1C1,连接BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以说明(△ABC与△A1 B1C全等除外);(2)当△BB1D是等腰三角形且BB1=BD时,求α的值.参考答案题号12345678910答案C C B D B C D D C A题号11121314151617181920答案B A C A D B A A D D题号21222324252627答案D A B B A D B1.C【分析】根据全等三角形的判定方法即可判断.【详解】解:由题可得∠A=180°−60°−54°=66°,∵A选项属于已知两边和其中一边的对角对应相等的情况,不能判定两个三角形全等,故不符合题意;∵B选项中66°角的对边不相同,不能判定两个三角形全等,故不符合题意;∵C选项中已知两边与其中一边的夹角对应相等,所以能判定全等,故C选项符合题意;∵D选项中两对应角的夹边不相等,不能判定两个三角形全等,故不符合题意;故选:C.【点睛】本题考查了全等三角形的判定,牢记判定方法以及正确找出对应边或对应角是解决本题的关键.2.C【分析】由作图可知直线MN为边AC的垂直平分线,再由BD=DC得到AD=DC=BD,利用等边对等角以及三角形内角和定理,进而得到∠B+∠C=90°.【详解】解:由作图可知,直线MN为边AC的垂直平分线,∴DC=AD,∴∠C=∠CAD,∵BD=DC,∴AD=BD,∴∠B=∠BAD,∵∠C+∠B+∠CAD+∠BAD=180°,∴∠B+∠C=90°.故选:C.3.B【分析】由全等三角形的对应角相等,结合三角形内角和定理即可得到答案.【详解】∵两个三角形全等,由全等三角形的性质可知,两幅图中边长为a、b的夹角对应相等,∴∠α=180°−50°−71°=59°,故选:B4.D【分析】根据全等三角形的判定条件逐一判断即可.【详解】解:A、由∠B=∠C,AB=CD,AF=DE,不能证明△ABF≌△DCE,不符合题意;B、由AG=DG,AB=CD,AF=DE,不能证明△ABF≌△DCE,不符合题意;C、由∠AFE=∠DEF,AB=CD,AF=DE,不能证明△ABF≌△DCE,不符合题意;D、由BE=CF即可证明BF=CE,AB=CD,AF=DE,可以由SSS证明△ABF≌△DCE,符合题意;故选D.【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定定理是解题的关键,全等三角形的判定定理有SSS,SAS,AAS,ASA,HL.5.B【分析】此题考查了全等三角形的判定定理,三边对应相等的两个三角形全等,以及作一个角等于已知角,根据用尺规画一个角等于已知角的步骤,据此即可求解,正确理解题中的作图是解题的关键.【详解】解:根据做法可知:AC=BE,AD=BF,CD=EF,∴△ACD≌△BEF(SSS),∴∠MBN=∠PAQ,故选:B.6.C【分析】本题考查了全等三角形的性质,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应边相等,对应角相等.【详解】解:∵DE=AB=a,DF=AC=c,又∵图中两个三角形全等,∴△ABC≌△DEF,∴∠D=∠A=180°−60°−72°=48°,∴∠1=48°,故选:C.7.D【分析】根据直角三角形全等的判定HL定理,可证△OPM≌△OPN.【详解】解:∵OM=ON,OP=OP,∠OMP=∠ONP=90°,∴△OPM≌△OPN所用的判定定理是HL.故选D.【点睛】本题考查学生的观察能力和判定直角三角形全等的HL定理,本题是一操作题,要会转化为数学问题来解决.8.D【分析】本题主要考查三角形全等的判定,根据SSS,ASA,SAS,AAS逐个判断即可得到答案;【详解】解:∵AB=DC,∠B=∠C,当∠A=∠D构成ASA,能得到△ABF≌△DCE,不符合题意,当BE=CF得到BF=CE构成SAS,能得到△ABF≌△DCE,不符合题意,当BF=CE构成SAS,能得到△ABF≌△DCE,不符合题意,当AF=ED不能得到三角形全等的判定,符合题意,故选:D.9.C【分析】本题主要考查了三角形内角和定理,全等三角形的性质,先根据三角形内角和为180度求出∠2的度数,再根据全等三角形对应角相等即可求出∠1的度数.【详解】解:如图所示,由三角形内角和定理得∠2=180°−50°−72°=58°,由全等三角形的性质可得∠1=∠2=58°,故选:C.10.A【分析】根据全等三角形的判定方法逐项判断即得答案.【详解】解:∵∠ABC=∠BAD,AB=BA,AC=BD,条件为边边角,∴不能证明△ABC≌△BAD,故A符合题意;∵∠ABC=∠BAD,AB=BA,∠CAB=∠DBA,条件为边角边,∴能证明△ABC≌△BAD,故B不符合题意;∵∠ABC=∠BAD,AB=BA,∠C=∠D,条件为角角边,能证明△ABC≌△BAD,故C不符合题意;∵∠ABC=∠BAD,AB=BA,BC=AD,条件为边角边,能证明△ABC≌△BAD,故D不符合题意,故选:A.【点睛】本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.11.B【分析】本题考查全等三角形的判定,根据全等三角形的判定定理,逐项分析判断,即可求解.【详解】解:∵∠CAB=∠DBA,AB=BA,∴添加的条件是:AC=BD,根据SAS可证明△ABC≌△BAD,故选项A不符合题意;添加的条件是:CB=DA,无法判断△ABC≌△BAD,故选项B符合题意;添加的条件是:∠C=∠D,根据AAS可证明△ABC≌△BAD,故选项C不符合题意;添加的条件是:∠ABC=∠BAD,根据ASA可证明△ABC≌△BAD,故选项D不符合题意;故选:B12.A【分析】本题主要考查了基本作图、全等三角形的判定与性质等知识点,明确作图过程成为解答本题的关键.通过分析作图的步骤,发现△OCD与△O′C′D′的三条边分别对应相等,于是利用边边边判定△OCD≌△O′C′D′,根据全等三角形对应角相等得∠AOB=∠A′O′B′.【详解】解:作图的步骤:①以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;②作射线O′B′,以O′为圆心,OC长为半径画弧,交O′B′于点D′;③以D′为圆心,CD长为半径画弧,交前弧于点C′;④过点C′作射线O′A′.所以∠A′O′B′就是与∠AOB相等的角.在△O′C′D′与△OCD中,O′C′=OCO′D′=OD,C′D′=CD∴△OCD≌△O′C′D′(SSS),∴∠AOB=∠A′O′B′,即运用的判定方法是SSS.故选:A.13.C【分析】本题考查了全等的性质,解一元一次方程的应用.运用分类讨论的思想是解题的关键.由题意知,BP=2t,CP=6−2t,由△ABP与△CQP全等,分△ABP≌△PCQ,△ABP≌△QCP两种情况,列方程求解即可.【详解】解:由题意知,BP=2t,CP=6−2t,∵△ABP与△CQP全等,∴分△ABP≌△PCQ,△ABP≌△QCP两种情况求解;当△ABP≌△PCQ时,PC=AB,即6−2t=4,解得t=1;当△ABP≌△QCP时,BP=CP,即2t=6−2t,解得t=1.5;综上所述,t的值是1或1.5,故选:C.14.A【分析】本题考查了全等三角形的性质,根据全等三角形的对应边相等,对应角相等去判定对应关系后计算.熟练掌握对应角的判定方法是解题的关键.【详解】解:∵两个三角形全等,∠1是边a的对角,即边b、c夹角,∴∠1的度数是180°−54°−76°=50°.故选:A.15.D【分析】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL等.根据BE=CF求出BF=CE,再根据全等三角形的判定定理进行分析即可.【详解】解:∵BE=CF,∴BE+EF=CF+EF,即BF=CE,∵∠B=∠C,∴当∠A=∠D时,利用AAS可得△ABF≌△DCE;当∠AFB=∠DEC时,利用ASA可得△ABF≌△DCE;当AB=DC时,利用SAS可得△ABF≌△DCE;当AF=DE时,无法证明△ABF≌△DCE;故选:D.16.B【分析】本题考查的是添加条件证明三角形全等,熟记全等三角形的判定方法是解本题的关键;本题根据已有的条件AB=DE,∠B=∠DEF,再逐一分析添加的条件结合ASA,SAS,AAS可得答案.【详解】解:∵AB=DE,∠B=∠DEF,∴补充∠A=∠D,可利用ASA证明△ABC≌△DEF,故A不符合题意;补充AC=DF,不能证明△ABC≌△DEF,故B符合题意;补充BE=CF,∴BC=EF,可利用SAS证明△ABC≌△DEF,故C不符合题意;补充AC∥DF,∴∠ACB=∠F,可利用AAS证明△ABC≌△DEF,故D不符合题意;故选B17.A【分析】本题考查的是全等三角形的性质,掌握全等三角形的对应角相等是解题的关键.【详解】解:∵两个三角形全等,∴∠1=64°,故选:A.18.A【分析】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握两边及其夹角分别相等的两个三角形全等.【详解】解:O为AA′、BB′的中点,∴OA=OA′,OB=OB′,∵∠AOB=∠A′OB′(对顶角相等),∴在△AOB与△A′OB′中,OA=OA′,∠AOB=∠A′OB′OB=OB∴△AOB≌△A′OB′(SAS),∴AB=A′B′,故选:A.19.D【分析】本题考查坐标与图形性质,过点C作坐标轴的垂线,利用AAS证明△BCM≌△ACN,即可求解,解题的关键是构造全等三角形.【详解】解:过点C作x轴和y轴的垂线,垂足分别M和N,∵∠CMO=∠CNO=∠MON=90°,∴四边形CMON是矩形,∴∠MCN=90°,∴∠ACN+∠ACM=90°,∵∠ACB=90°,∠BCM+∠ACM=90°,∴∠BCM=∠ACN,在△BCM和△ACN中,∠BCM=∠ACN∠BMC=∠ANC,BC=AC∴△BCM≌△ACN(AAS),∴BM=AN,又∵点C坐标为(−4,4),∴点M坐标为(−4,0),点N坐标为(0,4).∴BM=−4−b,AN=4−a∴−4−b=4−a即a−b=8.故选:D.20.D【分析】此题主要考查对尺规作图作一个角等于已知角的理解,利用全等三角形的判定方法判断即【详解】解:由作法得OD=O′D′,OC=O′C′,CD=C′D′,在△COD和△C′O′D′中,OD=O′D′OC=O′C′,CD=C′D′∴△COD≌△C′O′D′(SSS),∴∠A′O′B′=∠AOB(全等三角形的对应角相等).故选:D.21.D【分析】本题考查了全等三角形的判定.根据全等三角形的判定方法依次进行判断即可.【详解】解:A、添加∠B=∠C,不能使得△ABF≌△DCE,不符合题意;B、添加GE=GF,不能使得△ABF≌△DCE,不符合题意;C、添加∠AFE=∠DEF,不能使得△ABF≌△DCE,不符合题意;D、添加BF=CE,利用SSS,可以使得△ABF≌△DCE,符合题意;故选:D.22.A【分析】由作图过程可得:OD=OC,CM=DM,再结合DM=DM可得△COM≌△DOM(SSS),由全等三角形的性质可得∠1=∠2即可解答.【详解】解:由作图过程可得:OD=OC,CM=DM,∵DM=DM,∴△COM≌△DOM(SSS).∴∠1=∠2.∴A选项符合题意;不能确定OC=CM,则∠1=∠3不一定成立,故B选项不符合题意;不能确定OD=DM,故C选项不符合题意,OD∥CM不一定成立,则∠2=∠3不一定成立,故D选项不符合题意.故选A.【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点,理解尺规作图过程是解答本题的关键.【分析】利用全等三角形的判定依次证明即可.【详解】解:∵AE=CF,∴AE+EF=CF+EF.∴AF=CE.A.在△ADF和△CBE中,{∠A=∠CAF=CE∠AFD=∠CEB,∴△ADF≌△CBE(ASA),正确,故本选项不符合题意.B.根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项符合题意.C.在△ADF和△CBE中,{AF=CE∠AFD=∠CEBDF=BE,∴△ADF≌△CBE(SAS),正确,故本选项不符合题意.D.∵AD∥BC,∴∠A=∠C.由A选项可知,△ADF≌△CBE(ASA),正确,故本选项不符合题意.故选B.【点睛】本题考查了添加条件证明三角形全等,解题的关键是熟练运用判定三角形全等的方法.24.B【分析】本题考查了全等三角形的性质:全等三角形的对应边相等、对应角相等,找准对应角是解题的关键.根据全等三角形的对应角相等可知∠ACB=∠A′CB′,给等式的两边同时减去∠BCA′,可得到∠ACA′=∠BCB′=30°.【详解】解:∵△ACB≌△A′CB′,∴∠A′CB′=∠ACB,∵∠BCA′+∠BCB′=∠BCA′+∠A′CA,∴∠ACA′=∠BCB′,∵∠BCB′=30°,∴∠ACA′=30°.故选:B.25.A【分析】根据题目中的已知条件AB=AB,∠CAB=∠DAB,再结合题目中所给选项中的条件,利用全等三角形的判定定理进行分析即可.【详解】解;由图形可知:AB=AB,∠CAB=∠DAB,A.再加上条件BC=BD,不能证明△ABC≌△ABD,故此选项合题意;B. 再加上条件∠C=∠D,可利用AAS可证明△ABC≌△ABD,故此选项不合题意;C. 再加上条件AC=AD,可利用SAS可证明△ABC≌△ABD,故此选项不符合题意;D. 再加上条件∠ABC=∠ABD,可利用ASA可证明△ABC≌△ABD,故此选项不合题意.故选:A【点睛】本题考查全等三角形的判定定理,解题的关键是掌握全等三角形的判定定理.26.D【分析】本题主要考查全等三角形的性质.先根据角角边证明△ABC≌△CED,再根据全等三角形对应边相等,全等三角形的对应角相等的性质对各选项判断后,利用排除法求解.【详解】解:∵AC⊥CD,∴∠1+∠2=90°,∵∠B=90°,∴∠1+∠A=90°,∴∠A=∠2,在△ABC和△CED中,∠B=∠E=90°∠A=∠2,AC=CD∴△ABC≌△CED(AAS),故B、C选项正确,不符合题意;∵∠2+∠D=90°,∴∠A+∠D=90°,故A选项正确,不符合题意;∵AC⊥CD,∴∠ACD=90°,∠1+∠2=90°,但∠1不一定等于∠2,故D选项错误,符合题意.故选:D.27.B【分析】根据三角形全等的判定逐个判定即可得到答案.【详解】解:由题意可得,B选项符合边角边判定,故选B.【点睛】本题考查三角形全等的判定,解题的关键是熟练掌握三角形全等的几个判定.28.48°/48度,∴在∵∴29先长=∴∴【点睛】本题考查了翻折变换的性质,翻折变换保留原有图形的性质,而且可以使得原有的分散条件相对集中,从而有利于问题的解决.30.AB/BA【分析】本题主要考查全等三角形的判定与性质,证明△ABC≌△ADC是解题的关键.由AAS判断出△ABC≌△ADC即可得到答案.【详解】解:∵AB⊥BC,AD⊥DC,∴∠B=∠D=90°,在△ABC,△ADC中,∠1=∠2∠B=∠D,AC=AC∴△ABC≌△ADC(AAS),∴AD=AB.故答案为:AB.31.证明见解析【分析】根据平行得出∠B=∠DEF,然后用“边角边”证明△ABC≌△DEF即可.【详解】证明:∵AB//DE,∴∠B=∠DEF.∵BE=CF,∴BE+EC=CF+EC.∴BC=EF.在△ABC和△DEF中,AB=DE,∠B=∠DEF,BC=EF,∴△ABC≌△DEF.∴∠A=∠D.【点睛】本题考查了全等三角形的判定与性质,解题关键是熟练运用已知条件,推导证明出全等三角形判定所需条件,运用全等三角形判定定理证明.32.见解析【分析】利用AAS证明△ACO≌△DBO,即可得到结论.【详解】解:证明:在△ACO和△DBO中∠AOC=∠DOB∠A=∠DAC=DB∴△ACO≌△DBO(AAS).∴AO=DO,CO=BO.∴AO+BO=DO+CO∴AB=CD.【点睛】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法是解题的关键.33.详见解析【分析】运用HL定理证明直角三角形全等即可.【详解】∵BE=CF,∴BF=CE在Rt△ABF与Rt△DCE中:{AF=DE BF=CE∴Rt△ABF≌Rt△DCE(HL)∴AB =DC【点睛】本题考查了直角三角形全等的判定与性质,熟练掌握HL定理是解题关键.34.见解析【分析】根据已知条件得出∠AOB=∠COD,进而证明△AOB≌△COD,根据全等三角形的性质即可得证.【详解】证明:∵∠AOD=∠COB,∴∠AOD−∠BOD=∠COB−∠BOD,即∠AOB=∠COD.在△AOB和△COD中,OA=OC,∠AOB=∠COD,OB=OD,∴△AOB≌△COD∴AB=CD.【点睛】本小题考查等式的基本性质、全等三角形的判定与性质等基础知识,考查几何直观、推理能力等,掌握全等三角形的性质与判定是解题的关键.35.(1)见详解(2)见详解【分析】(1)作NM⊥AD,根据角平分线的性质得到BM=MN,MN=CM,等量代换得到答案.(2)根据平行线的性质得到∠BAD+∠ADC=180°,根据角平分线的定义得到∠MAD+∠ADM=90°,根据垂直的定义得到答案;【详解】(1)作NM⊥AD交AD于N,∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD,∵AM平分∠BAD,DM平分∠ADC,∴BM=MN,MN=CM,∴BM=CM;(2)证明:∵AB∥CD,∴∠BAD+∠ADC=180°,∵AM平分∠BAD,DM平分∠ADC,∴2∠MAD+2∠ADM=180°,∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM⊥DM;【点睛】本题考查的是角平分线的性质,掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键.36.(1)见详解(2)见详解【分析】(1)根据三角形内角和以及角平分线定义得出∠APB=135°,易得∠DPB=45°,可得∠BPF=135°,即可证明△ABP≌△FBP;(2)由(1)结论可得∠F=∠BAD,AP=PF,AB=BF,即可求得∠F=∠CAD,即可证明△APH≌△FPD,可得AH=DF,即可解题.【详解】(1)∵AD、BE分别平分∠BAC、∠ABC,∠ACB=90°,∴∠PAB+∠PBA=12(∠ABC+∠BAC)=45°,∴∠APB=135°,∴∠DPB=45°,∵PF⊥AD,∴∠BPF=135°,在△ABP和△FBP中,∠BPF=∠APB=135°BP=BP∠ABP=∠FBP∴△ABP≌△FBP(ASA);(2)∵△ABP≌△FBP,∴∠F=∠BAD,AP=PF,AB=BF,∵∠BAD=∠CAD,∴∠F=∠CAD,在△APH和△FPD中,∠F=∠CADAP=PF∠APH=∠FPD=90°∴△APH≌△FPD(ASA),∴AH=DF,∵BF=DF+BD,∴AB=AH+BD.∴AH=AB−BD.【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABP≌△FBP和△APH≌△FPD是解题的关键.37.见解析【分析】由BE=CF可得BC=EF,即可判定ΔABC≌ΔDEF(SAS),再利用全等三角形的性质证明即可.【详解】∵BE=CF,∴BE+EC=EC+CF,即BC=EF,又∵AB=DE,∠B=∠DEF,∴在ΔABC与ΔDEF中,AB=DE∠B=∠DEF,BC=EF∴ΔABC≌ΔDEF(SAS),∴AC=DF.【点睛】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定定理是解决本题的关键. 38.见解析【分析】先证明ΔBDO≌ΔCEO(AAS),得到OD=OE,再根据角的平行线性质判定即可.【详解】证明:∵CD⊥AB于D点,BE⊥AC于点E,∴∠BDO =∠CEO =90∘,在ΔBDO 和ΔCEO 中,∠BDO =∠CEO ∠BOD =∠COE OB =OC,ΔBDO≌ΔCEO (AAS),∴OD =OE ,∵OD ⊥AB ,OE ⊥AC ,∴OA 平分∠BAC ,∴∠1=∠2.【点睛】本题考查了三角形全等的判定和性质,角的平分线的判定定理,熟练掌握三角形全等的判定和角的平分线的判定是解题的关键.39.见解析【分析】利用等腰三角形的性质可得∠B =∠C ,再由SAS 证明△ABD≌△ACE ,从而得AD =AE .【详解】证明:∵AB =AC ,∴∠B =∠C ,在△ABD 和△ACE 中,AB =AC ∠B =∠C BD =CE,∴△ABD≌△ACE (SAS ),∴AD =AE .【点睛】本题考查等腰三角形的性质,全等三角形的性质与判定,熟练掌握相关性质定理是解题的关键.40.(1)证明见解析(2)5【分析】此题主要考查全等三角形的判定和性质,解题关键是根据AAS 证明△CDE 和△FAE 全等.(1)根据 AAS 证明△CDE 和△FAE全等即可;(2)根据全等三角形的性质结合线段垂直平分线性质解答即可.【详解】(1)证明:∵AB ∥CD ,∴∠DCE =∠F ,∵点E 是AD 中点,∴DE =AE ,在△CDE 和△FAE 中,∠DCE =∠F ∠CED =∠FEA DE =AE,∴△CDE≌△FAE (AAS);(2)由(1)知△CDE≌△FAE ,∴CE =FE ,CD =AF∵BE ⊥GF ,∴BE 垂直平分CF ,∴BC =BF ,∵CD =3,AB =2,∴AF =CD =3,∴BC =BF =AF +AB =3+2=5.41.证明见解析【分析】本题主要考查了三线合一定理,过点A 作AP ⊥B C 于P ,利用三线合一得到P 为DE 及BC 的中点,再根据线段之间的关系即可得证.【详解】证明:如图,过点A 作AP ⊥B C 于P .∵AB =AC ,∴BP =PC ;∵AD =AE ,∴DP =PE ,∴BP−DP =PC−PE ,∴BD =CE .42.(1)△ABD≌△CBD(2)证明见解析【分析】本题考查的是全等三角形的判定与性质,等腰三角形的性质;熟记等腰三角形的三线合一是解本题的关键.(1)直接利用SSS证明△ABD≌△CBD即可;(2)由△ABD≌△CBD可得∠ADB=∠CDB,再结合等腰三角形的性质可得结论.【详解】(1)解:△ABD≌△CBD,理由如下:在△ABD和△CBD中,AD=CDAB=CB,BD=BD∴△ABD≌△CBD(SSS);(2)∵△ABD≌△CBD,∴∠ADB=∠CDB,∵DA=DC,∴AD⊥AC.43.(1)证明见解析(2)证明见解析【分析】本题主要考查直角三角形的全等判定和性质,(1)根据题意得∠AEB=∠DFC=90°,由CE=BF得BE=CF,则有Rt△CDF≌Rt△BAE,结合全等的性质即可证明;(2)利用Rt△CDF≌Rt△BAE得到对应的角度相等,结合内错角相等两直线平行的判定即可证明;【详解】(1)证明:∵AE⊥BC于E,DF⊥BC于F,∴∠AEB=∠DFC=90°,∵CE=BF,∴CE−EF=BF−EF,∴BE=CF,在Rt△CDF与Rt△BAE中,CD=ABCF=BE,∴Rt△CDF≌Rt△BAE(HL)∴AE=DF,(2)由(1)可知Rt△CDF≌Rt△BAE(HL),∴∠C=∠B,∴AB∥CD.44.证明见解析【分析】本题考查了全等三角形的判定与性质等知识,证△AEB≌△DFC(AAS),即可得出结论.∴∵∴∴在∴∴45(2)((∴∴∠ACD+∠DAC=90°,∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠DAC=∠ECB.在△ADC和△CEB中,∠ADC=∠CEB,∠DAC=∠ECB, AC=CB,∴△ADC≌△CEB (AAS)(2)由(1)得△ADC≌△CEB∴CE =AD =5,CD =BE =3,∴BF =DE =CE−CD =5−3=2,∴EF =BF +BE =2+3=5,∴EF =AD .∵AD ⊥CE ,BE ⊥CE ,∴∠FEG =∠ADG =90°在△FEG 和△ADG 中,∠FEG =∠ADG,∠FGE =∠AGD,FE =AD,∴△FEG≌△ADG (AAS),∴DG =EG =12DE =1.46.证明见解析【分析】本题考查三角形全等的判定,先证明∠BAC =∠EAD ,在用ASA 证明△ABC≌△AED 即可,掌握判定三角形全等是解题的关键.【详解】证明∵∠1=∠2,∴∠1+∠EAC =∠2+∠EAC∴∠BAC =∠EAD ,在△ABC 和△AED 中,∠B =∠AED AB =AE ∠BAC =∠EAD,∴△ABC≌△AED .∴AC =AD 47.见解析【分析】先根据SSS 定理得出△ABC≌△DEB (SSS ),故∠ACB =∠EBD ,再根据∠AFB 是△BFC 的外角,可知∠AFB =∠ACB +∠EBD ,可得出∠AFB =2∠ACB,故可得出答案.【详解】解:在△ABC和△BDE中,AC=BDAB=EDBC=BE∴△ABC≌△DEB(SSS)∴∠ACB=∠EBD;∵∠AFB=∠ACB+∠EBD,∴∠AFB=2∠ACB【点睛】此题考查全等三角形的判定和性质,同时涉及三角形外角和定理,掌握相关定理知识是解题的关键.48.见解析【分析】根据中点的定义得出AC=CB,即可根据SSS证明△ACD≌△CBE.【详解】证明:∵点C是AB的中点,∴AC=CB.在△ACD和△CBE中,AD=CECD=BE,AC=CB∴△ACD≌△CBE(SSS).【点睛】本题主要考查了的三角形全等的判定,解题的关键是掌握三边都相等的两个三角形全等.49.见解析【分析】由BE=CF可得BF=CE,再结合AB=DC,∠B=∠C可证得△ABF≌△DCE,问题得证.【详解】解∵BE=CF,∴BE+EF=CF+EF,即BF=CE.在△ABF和△DCE中,AB=DC∠B=∠CBF=CE∴△ABF≌△DCE,∴∠A=∠D.【点睛】本题考查了全等三角形的判定和性质,是中考中比较常见的知识点,一般难度不大,需熟练掌握全等三角形的判定和性质.50.(1)DE=BD+CE,见解析(2)见解析,CE−BD=DE或BD−CE=DE【分析】(1)由BD⊥MN于点D,CE⊥MN于点E,得∠BDA=∠AEC=∠BAC=90°,则∠DAB=∠ECA=90°−∠EAC,而AB=CA,即可证明△DAB≌△ECA,得BD=AE,AD=CE,则BD+CE=AE+AD=DE;(2)分两种情况讨论,一是MN与边BC相交且∠BAD<45°,同理可证△DAB≌△ECA,得BD=AE,AD=CE,则CE−BD=AD−AE=DE;二是MN与边BC相交且∠BAD>45°,同理可证△DAB≌△ECA,得BD=AE,AD=CE,则BD−CE=AE−AD=DE.【详解】(1)证明:∵BD⊥MN,CE⊥MN,∴∠ADB=∠CEA=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵∠CAE+∠ACE=90°,∴∠BAD=∠ACE,在△ABD和△CAE中,∠ADB=∠CEA∠BAD=∠ACEAB=CA,∴△ABD≅△CAE(AAS);∴AD=CE,BD=AE,∵DE=AD+AE,∴DE=BD+CE;(2)解:CE−BD=DE或BD−CE=DE,理由:如图2,MN与边BC相交且∠BAD<45°,∵BD⊥MN于点D,CE⊥MN于点E,∴∠BDA=∠AEC=90°,∵∠BAC=90°,∴∠DAB=∠ECA=90°−∠EAC,在△DAB和△ECA中,∠DAB=∠ECA∠BDA=∠AEC,AB=CA∴△DAB≌△ECA(AAS),∴BD=AE,AD=CE,∴CE−BD=AD−AE=DE.如图3,MN与边BC相交且∠BAD>45°,∵BD⊥MN于点D,CE⊥MN于点E,∴∠BDA=∠AEC=90°,∵∠BAC=90°,∴∠DAB=∠ECA=90°−∠EAC,在△DAB和△ECA中,∠DAB=∠ECA∠BDA=∠AEC,AB=CA∴△DAB≌△ECA(AAS),∴BD=AE,AD=CE,∴BD−CE=AE−AD=DE.【点睛】此题重点考查直角三角形的两个锐角互余、同角的余角相等、全等三角形的判定与性质等知识,证明△DAB≌△ECA是解题的关键.51.见解析【分析】根据∠1=∠2,可得出∠ACB=∠DCE,然后利用SAS证明△ABC≌△DEC,继而可得出AB=DE.本题考查了全等三角形的判定与性质,熟练掌握SAS证三角形全等是解题的关键.【详解】证明:∵∠1=∠2,∴∠1+∠ECA=∠2+∠ECA,即∠ACB=∠DCE,在△ABC和△DEC中,CA=CD∠ACB=∠DCE,BC=EC∴△ABC≌△DEC(SAS),∴AB=DE.52.证明见解析【分析】先利用A S A证明△AOB≌△COD,得出OB=OD,根据线段垂直平分线的判定可知点O在线段BD的垂直平分线上,再由BE=DE,得出点E在线段BD的垂直平分线上,即O,E两点都在线段BD的垂直平分线上,从而可证明OE垂直平分BD.【详解】在△AOB与△COD中,∠A=∠C,OA=OC,∠AOB=∠COD,∴△AOB≌△COD(ASA),∴OB=OD,∴点O在线段BD的垂直平分线上,∵BE=DE,∴点E在线段BD的垂直平分线上,∴OE垂直平分BD.【点睛】本题考查了线段垂直平分线的判定:到一条线段两端距离相等的点在这条线段的垂直平分线上,同时考查了全等三角形的判定与性质.53.见解析【分析】根据题意可以证得△ABC≅△DEF,所以BC=EF,即可得到结论.【详解】根据题意,在△ABC和△DEF中,AB=DE∠A=∠D,AC=DF∴△ABC≅△DEF,∴BC=EF,∴BC−CE=EF−CE,∴BE=CF.【点睛】本题考查了全等三角形的判定及性质,熟练掌握全等三角形的判定及性质是解题的关键.54.见解析【分析】本题考查了全等三角形的判定和性质,平行线的判定,熟练掌握全等三角形的判定和性质定理是解题的关键.根据全等三角形的判定和性质定理和平行线的判定定理即可得到结论.【详解】证明:∵AB=CD,∴AB+BC=CD+BC,即:AC=BD,。
人教版八年级数学上册《全等三角形(SSS)》专题测试【附解析】

人教版八年级数学上册《全等三角形(SSS )》专题过关练习题(解析版)一.选择题.1. 如图,AB=DE,AC=DF,BC=EF,则∠D 等于 ( )A.30°B.50°C.60°D.100°2. 如图,在△ABC 中,AB =AC ,点D 为BC 的中点,那么以下结论不正确的是( )A .△ABD ≌△ACDB .∠B =∠CC .AD 是△ABC 的角平分线 D .AD 不是△ABC 的高3. 如图所示,在△ABC 中,AB=AC ,BE=CE ,则由“SSS ”可以直接判定( )A.△ABD ≌△ACDB. △BDE ≌△CDEC. △ABE ≌△ACED.以上都不对4. 如图,在△ABC 和△FED 中,AC=FD,BC=ED,要利用“SSS ”来判定△ABC 和△FED 全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是()A.①或②B.②或③C.①或③D.①或④5. 如图是人字型金属屋架的示意图,该屋架由BC,AC,BA,AD四段金属材料焊接而成,其中A,B,C,D四点均为焊接点,且AB=AC,点D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是 ( )A.AD和BC,点DB.AB和AC,点AC.AC和BC,点CD.AB和AD,点A二.填空题.1. 在△ABC中,AB=AC,点D在BC上(不与点B,C重合).只需添加一个条件即可证明△ABD≌△ACD,这个条件可以是(写出一个即可).2. 如图,已知AB=AD,那么添加一个条件后,能利用“SSS”判定△ABC≌△ADC的是__ __.3. 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=°.4. 工人师傅常用角尺平分一个任意角.作法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C作射线OC.由作法得△MOC≌△NOC的依据是__ __.5. 如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB 长为半径作弧,两弧交于点D;连接AD,CD.若∠B=65°,则∠ADC的大小为_ __度.6. 如图,在△ABC中,AD=DE,AB=BE,∠A=83°,则∠CED=__ __.三.解答题.1. 如图,已知AD=BC,BD=AC.求证:∠ADB=∠BCA.2. 已知AB=AC,BD=CD,试判断∠B与∠C的关系,并说明理由.3. 如图,AB=AC,DB=DC,EB=EC.(1)图中有几对全等三角形?请一一写出来.(2)选择(1)中的一对全等三角形加以证明.4. 如图,已知AD=CB,AE=CF,DE=BF.试说明:DE∥BF.5.根据图中尺规作图的痕迹,先判断得出结论,然后说明你的结论.6.如图,已知AB=AC,AD=AE,BD=CE,求证∠3=∠1+∠2.解析一.选择题.1. 如图,AB=DE,AC=DF,BC=EF,则∠D等于( D )A.30°B.50°C.60°D.100°解析:因为AB=DE,AC=DF,BC=EF,所以△ABC与△DEF全等,所以∠A=∠D,因为。
人教版八年级上册第12章12.2 全等三角形(SAS) 专题过关练习题(解析版)

《全等三角形(SAS )》专题过关练习题一.选择题.1. 如图,在△ABC 和△DEF 中,AB=DE,∠B=∠E,补充下列哪一个条件后,能直接应用“SAS ”判定△ABC ≌△DEF ( )A.∠ACB=∠DFEB.BF=ECC.AC=DFD.∠A=∠D2. 如图,等腰△ABC 中,点D ,E 分别在腰AB ,AC 上,添加下列条件,不能判定△ABE ≌△ACD 的是( )A .AD =AEB .BE =CDC .∠ADC =∠AEBD .∠DCB =∠EBC3.如图,已知,AB DC ABC DCB =∠=∠.能直接判断ABC DCB △≌△的方法是( )A. SASB. AASC. SSSD. ASA4. 如图,在△ABC 和△DEC 中,已知AB=DE,还需添加两个条件才能使△ABC ≌△DEC,不能添加的一组条件是 ( )A.BC=EC,∠B=∠EB.BC=EC,AC=DCC.BC=DC,∠A=∠DD.AC=DC,∠A=∠D5. 如图,已知点B,E,C,F 在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC ≌△DEF 的是 ( )A.AC=DFB.AB=DEC.AC ∥DFD.∠A=∠D6. 如图,在△AOB 和△COD 中,OA =OB ,OC =OD ,OA <OC ,36AOB COD ︒∠=∠=.连接AC 、BD 交于点M ,连接OM .下列结论:①36AMB ︒∠=;②AC BD =;③OM 平分AOD ∠;④MO 平分AMD ∠其中正确的结论个数有( )个.A .4B .3C .2D .1二.填空题.1. 如图,AD 和CB 相交于点E,BE=DE,请添加一个条件,能利用“SAS ”判定 △ABE ≌△CDE(只添加一个条件即可),你所添加的条件是__ _.2. 如图,点B,A,D,E 在同一直线上,BD=AE,BC ∥EF,要使△ABC ≌△DEF,则只需添加一个适当的条件是_ __.(只填一个即可)3. 如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC,BD相交于点O,则图中全等三角形共有对.4. 在△ABC中,AB=5,AC=3,AD是BC边上的中线,则AD的取值范围是 . 三.解答题.1. 如图,点E,F在BC上,BE=FC,AB=DC,∠B=∠C.试说明:∠A=∠D.2. 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)试说明:BD=CE.(2)试说明:∠M=∠N.3. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.(1)求证:△ABD≌△ACE;(2)判断△BOC的形状,并说明理由.4. 在有公共顶点的△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.(1)试说明:CE=BD.(2)若将△ADE绕A点沿逆时针方向旋转,当旋转到点C,E,D在同一条直线上时,如图所示,(1)问中的结论是否成立?如果结论成立,请说明;如果不成立,请说理由.5. 如图,△ABC和△DCE都是等边三角形.△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.《全等三角形(SAS)》专题过关练习题(解析版)一.选择题.1. 如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充下列哪一个条件后,能直接应用“SAS”判定△ABC≌△DEF ( B )A.∠ACB=∠DFEB.BF=ECC.AC=DFD.∠A=∠D解析:若用“SAS”,必须再证∠B和∠E的另一边相等,由BF=CE可得BC=EF,故选B.2. 如图,等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是( B )A.AD=AE B.BE=CD C.∠ADC=∠AEB D.∠DCB=∠EBC解析:本题考查了全等三角形的判定.由全等三角形的判定“SAS ”、“AAS ”、“ASA ”可得,添加选项A 、C 、D 都能判定两三角形全等;而添加选项B 则不能判定两三角形全等,故选B .3.如图,已知,AB DC ABC DCB =∠=∠.能直接判断ABC DCB △≌△的方法是( A )A. SASB. AASC. SSSD. ASA 解析:在△ABC 和△DCB 中,AB DC ABC DCB BC CB =⎧⎪∠=∠⎨⎪=⎩,∴ABC DCB △≌△(SAS),故选:A.4. 如图,在△ABC 和△DEC 中,已知AB=DE,还需添加两个条件才能使△ABC ≌△DEC,不能添加的一组条件是 ( C )A.BC=EC,∠B=∠EB.BC=EC,AC=DCC.BC=DC,∠A=∠DD.AC=DC,∠A=∠D解析:因为AB=DE,所以当BC=EC,∠B=∠E 时,满足SAS,可说明△ABC ≌△DEC;当BC=EC,AC=DC 时,满足SSS,可说明△ABC ≌△DEC;当BC=DC,∠A=∠D 时,在△ABC中是ASS,在△DEC 中是SAS,故不能说明△ABC ≌△DEC,故C 符合题意;当AC=DC,∠A=∠D 时,满足SAS,可说明△ABC ≌△DEC.5. 如图,已知点B,E,C,F 在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC ≌△DEF 的是 ( A )A.AC=DFB.AB=DEC.AC ∥DFD.∠A=∠D解析:因为BE=CF,所以BE+EC=EC+CF,即BC=EF,且∠ABC=∠DEF,所以当AC=DF 时,满足SSA,无法判定△ABC ≌△DEF,故A 符合题意;当AB=DE 时,满足SAS,可以判定△ABC ≌△DEF,故B 不符合题意;当AC ∥DF 时,可得∠ACB=∠F,满足ASA,可以判定△ABC ≌△DEF,故C 不符合题意;当∠A=∠D 时,满足AAS,可以判定△ABC ≌△DEF,故D 不符合题意.6. 如图,在△AOB 和△COD 中,OA =OB ,OC =OD ,OA <OC ,36AOB COD ︒∠=∠=.连接AC 、BD 交于点M ,连接OM .下列结论:①36AMB ︒∠=;②AC BD =;③OM 平分AOD ∠;④MO 平分AMD ∠ 其中正确的结论个数有( )个.A .4B .3C .2D .1 解析:本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识;证明三角形全等是解题的关键.由SAS 证明△AOC ≌△BOD ,得到∠OAC =∠OBD ,由三角形的外角性质得:∠AMB +∠OBD =∠AOB +∠OAC ,得出∠AMB =∠AOB =36°,①正确;根据全等三角形的性质得出∠OCA =∠ODB ,AC =BD ,②正确;作OG ⊥AC 于G ,OH ⊥BD 于H ,如图所示:则∠OGC =∠OHD =90°,由AAS 证明△OCG≌△ODH(AAS),得出OG=OH,由角平分线的判定方法得出MO平分AMD∠,④正确;由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA OC,故③错误;即可得出结论.正确的有①②④;故选B.二.填空题.1. 如图,AD和CB相交于点E,BE=DE,请添加一个条件,能利用“SAS”判定△ABE≌△CDE(只添加一个条件即可),你所添加的条件是__AE=CE__.解析:添加AE=CE,在△ABE和△CDE中,{BE=DE,∠AEB=∠CED, AE=CE,所以△ABE≌△CDE(SAS).2. 如图,点B,A,D,E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是__BC=EF(或∠BAC=∠EDF,答案不唯一)__.(只填一个即可)3. 如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC,BD相交于点O,则图中全等三角形共有 3 对.解析:全等的三角形有△ABC≌△ADC(SSS),△ABO≌△ADO(SAS),△BOC≌△DOC(SAS).4. 在△ABC中,AB=5,AC=3,AD是BC边上的中线,则AD的取值范围是__1<AD<4__.解析:如图,延长AD至点E使DE=AD,连接CE,因为AD是BC边上的中线,所以BD=CD,在△ABD和△ECD中,因为{BD=CD,∠ADB=∠EDC, AD=ED,所以△ABD≌△ECD(SAS),所以EC=AB=5.在△ACE中,EC-AC<AE<AC+EC. 即5-3<2AD<3+5.所以1<AD<4.三.解答题.1. 如图,点E,F 在BC 上,BE=FC,AB=DC,∠B=∠C.试说明:∠A=∠D.解析:因为BE=FC,所以BE+EF=CF+EF,即BF=CE;又因为AB=DC,∠B=∠C,所以△ABF ≌△DCE(SAS),所以∠A=∠D.2. 已知△ABN 和△ACM 位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)试说明:BD=CE.(2)试说明:∠M=∠N.解析:(1)在△ABD 和△ACE 中,{AB =AC ,∠1=∠2,AD =AE ,所以△ABD ≌△ACE(SAS),所以BD=CE.(2)因为∠1=∠2,所以∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM,由(1)得△ABD ≌△ACE,所以∠B=∠C,在△ACM 和△ABN 中,{∠C =∠B ,AC =AB ,∠CAM =∠BAN ,所以△ACM ≌△ABN(ASA),所以∠M=∠N.3. 如图,已知AB =AC ,AD =AE ,BD 和CE 相交于点O .(1)求证:△ABD≌△ACE;(2)判断△BOC的形状,并说明理由.解析:证明:(1)∵AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE (SAS);(2)△BOC是等腰三角形,理由如下:∵△ABD≌△ACE,∴∠ABD=∠ACE,∵AB=AC,∴∠ABC=∠ACB,∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,∴∠OBC=∠OCB,∴BO=CO,∴△BOC是等腰三角形.4. 在有公共顶点的△ABC和△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.(1)试说明:CE=BD.(2)若将△ADE绕A点沿逆时针方向旋转,当旋转到点C,E,D在同一条直线上时,如图所示,(1)问中的结论是否成立?如果结论成立,请说明;如果不成立,请说理由.解析:(1)因为∠CAB=∠EAD,所以∠CAB-∠EAB=∠EAD-∠EAB,即∠CAE=∠BAD.在△CAE和△BAD中,因为{AC=AB,∠CAE=∠BAD, AE=AD,所以△CAE≌△BAD(SAS),所以CE=BD.(2)当旋转到点C,E,D在一条直线上时,(1)中的结论CE=BD仍然成立.说明同(1).5. 如图,△ABC和△DCE都是等边三角形.△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.解析:(1)全等.理由是:∵△ABC和△DCE都是等边三角形,∴AC=BC,DC=EC,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△BCD和△ACE中,{CD=CE∠BCD=∠ACEBC=AC,∴△ACE≌△BCD( SAS);。
专题12.1 全等三角形(解析版)

专题12.1 全等三角形1.基本概念(1)全等形:能够完全重合的两个图形叫做全等形.(2)全等三角形:能够完全重合的两个三角形叫做全等三角形. (注意对应的顶点写在对应的位置上)(3)对应顶点:全等三角形中互相重合的顶点叫做对应顶点.(4)对应边:全等三角形中互相重合的边叫做对应边.(5)对应角:全等三角形中互相重合的角叫做对应角.2.基本性质全等三角形的性质:全等三角形的对应边相等,对应角相等.【例题1】如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:BD=CE.【答案】见解析。
【解析】证明:∵AB⊥AC,AD⊥AE,∴∠BAE+∠CAE=90°,∠BAE+∠BAD=90°,∴∠CAE=∠BAD.又AB=AC,∠ABD=∠ACE,∴△ABD≌△ACE(ASA).∴BD=CE.【点拨】在利用角边角判定该定理证明全等后,全等三角形对应边相等。
【例题2】已知,如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是()A.AC=DF B.AD=BE C.DF=EF D.BC=EF【答案】C.【解析】A.∵△ABC≌△DEF,∴AC=DF,故此结论正确;B.∵△ABC≌△DEF,∴AB=DE;∵DB是公共边,∴AB﹣BD=DE﹣BD,即AD=BE;故此结论正确;C.∵△ABC≌△DEF,∴AC=DF,故此结论DF=EF错误;D.∵△ABC≌△DEF,∴BC=EF,故此结论正确。
【点拨】考查平行线性质,全等三角形对应边相等。
【例题3】如图,若△ABC≌△DEF,∠A=45°,∠F=35°,则∠E等于()A.35°B.45°C.60°D.100°【答案】D.【解析】∵△ABC≌△DEF,∠A=45°,∠F=35°∴∠D=∠A=45°∴∠E=180°﹣∠D﹣∠F=100°.【点拨】全等三角形对应角相等。
全等三角形压轴训练(多解、动点、新定义型压轴)(解析版)—24-25学年八年级数学上册单元(人教版)

全等三角形压轴训练(多解、动点、新定义型压轴)目录题型一 利用三角形全等求时间或线段长的多解问题...........................................................................................1题型二 与全等三角形有关的多结论问题 (7)题型三 全等三角形中的动点综合问题 (13)题型四 全等三角形中的新定义型综合问题 (27)题型一 利用三角形全等求时间或线段长的多解问题【答案】4【分析】本题主要考查了全等三角形的性质和判定,解一元一次方程,先设运动全等;分两种情况:12x x -=,得出x =01 压轴总结02 压轴题型∴CAP V ≌PBQ V ;②若BP AP =,则12x x -=,解得:6x =,可知12(cm)BQ AC =¹,此时CAP V 与PQB △不全等.综上所述:运动4s 后CAP V 与PQB △全等.故答案为:4.巩固训练1.(23-24七年级下·陕西西安·期末)如图,ABC V 中,90ACB Ð=°,6cm AC =,8cm BC =,直线l 经过点C 且与边AB 相交.动点P 从点A 出发沿A C B ®®路径向终点B 运动;动点Q 从点B 出发沿B C A ®®路径向终点A 运动.点P 和点Q 的速度分别为1cm /s 和2cm /s ,两点同时出发并开始计时,当点P 到达终点B 时计时结束.在某时刻分别过点P 和点Q 作PE l ^于点E ,QF l ^于点F ,设运动时间为t 秒,则当t 为( )秒时,PEC V 与QFC V 全等.A .12或43B .2或45或10C .1或43D .2或143或12由题意得,,AP t BQ ==∵6cm,8cm AC BC ==,由题意得,,2AP t BQ ==∵6cm,8cm AC BC ==,∴6,28CP t CQ t =-=-,当PEC QFC △≌△,则PC CQ =,由题意得,AP t =,∵6cm AC =,∴6,6CP t CQ =-=,2.(23-24八年级上·重庆·阶段练习)如图,在长方形ABCD 中,4,6AB AD ==,延长BC 到点E ,使2CE =,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC CD DA →→向终点A 运动,设点P 的运动时间为t 秒,当t 的值为 秒时,ABP V 与DCE △全等.3.(23-24八年级上·山东日照·阶段练习)如图,CA AB ^,垂足为点A ,12AB =米,6AC =米,射线BM AB ^,垂足为点B ,动点E 从A 点出发以2米/秒沿射线AN 运动,点D 为射线BM 上一动点,随着E 点运动而运动,且始终保持ED CB =,当点E 经过 秒时(不包括0秒),由点D E B 、、组成的三角形与BCA V 全等.【答案】3秒或9秒或12【分析】本题考查了三角形全等的判定与性质,分四种情况:当点E 在线段AB 上,AC BE =时,ACB BED V V ≌;当E 在BN 上,AC BE =时,ACB BED V V ≌;当E 在线段AB 上,AB EB =时;当E 在BN 上,AB EB =时,ACB BDE V V ≌;分别利用三角形全等的性质进行求解即可,熟练掌握三角形全等的判定与性质是解此题的关键.【详解】解:当点E 在线段AB 上,AC BE =时,ACB BED V V ≌,6AC =Q ,6BE \=,1266AE AB BE \=-=-=,\点E 的运动时间为623¸=(秒);当E 在BN 上,AC BE =时,ACB BED V V ≌,6AC =Q ,6BE \=,12618AE AB BE \=+=+=,\点E 的运动时间为1829¸=(秒);当E 在线段AB 上,AB EB =时,此时E 在A 点未动,时间为0秒,不符合题意;当E 在BN 上,AB EB =时,ACB BDE V V ≌,12AB =Q ,12BE \=,121224AE AB BE \=+=+=,\点E 的运动时间为24212¸=(秒);综上所述,当点E 经过3秒或9秒或12秒时(不包括0秒),由点D E B 、、组成的三角形与BCA V 全等,故答案为:3秒或9秒或12.4.如图,ABC V 中,90ACB Ð=°,12AC =,16BC =,点P 从A 点出发沿A C B ®®路径向终点运动,终点为B 点;点Q 从B 点出发沿B C A ®®路径向终点运动,终点为A 点.点P 和Q 分别以2和6的运动速【答案】1或72或12【分析】根据题意分为五种情况,根据全等三角形的性质得出可.【详解】解:设点运动t秒时,以Q PE l^,QF l^,\90PEC QFCÐ=Ð=°,Q90ACBÐ=°,\90EPC PCEÐ+Ð=°,Q 由①知:PC CQ =,\212616t t -=-,=1t \;因为此时60t -<,所以此种情况不符合题意;122616PC t t =-=-,7=2t ;④当Q 到A 点停止,P 在BC ⑤因为P 的速度是每秒2,Q 题型二 与全等三角形有关的多结论问题例题:(23-24七年级下·江西吉安·期末)如图,在Rt AEB V 和Rt AFC △中,BE 与AC 相交于点M ,与CF 相交于点D ,AB 与CF 相交于点N ,90E F ÐÐ==°,EAC FAB ÐÐ=,AE AF =.给出下列结论:①B C Ð=Ð;②CD DN =;③BE CF =;④ACN ABM @V V .其中正确的结论是( )A .①③④B .①②③④C .①②③D .①②④【答案】A 【分析】本题考查了两个全等三角形的判定及性质,根据已知条件判定两个三角形全等,可得到对应边及对应角相等,据此可判断①③,再结合条件证明两个三角形全等,可得到④,即可求得结果,灵活运用两个全等三角形的条件及性质是解题的关键.【详解】解:∵EAC FAB Ð=Ð,∴EAB FAC Ð=Ð,在EAB V 和FAC V 中,90E F AE AFEAB FAC Ð=Ð=°ìï=íïÐ=Ðî,∴()ASA EAB FAC V V ≌,∴,,B C BE CF AB AC Ð=Ð==,∴①③都正确,在ACN ABM △和△中,B C AB AC CAN BAM Ð=Ðìï=íïÐ=Ðî,∴()ASA ACN ABM V V ≌,故④正确,根据已知条件无法证明②是否正确,故①③④正确,故选:A .巩固训练1.(23-24七年级下·四川巴中·期末)如图,在Rt ABC △中,点M ,N 分别是边AB BC ,上的点,且M ,N 两点满足AM CN =,BP AN ^交AC 于点P ,过点P 作PQ MC ^交AN 延长线于点Q ,交BC 于点F ,AN 与CM 交于点E ,若AB BC =,则下列结论:①连接BE ,则BE 平分ABC Ð;②AME CNE △≌△;③CFQ AME Ð=Ð;④AQ CE PQ =+.成立的是( ).A .①②③B .①②④C .②③④D .①②③④【答案】D 【分析】本题主要考查了等腰直角三角形的性质、全等三角形的判定等知识点,灵活运用全等三角形的判定与性质成为解题的关键.先证明()SAS AMC CNA V V ≌可得MCA NAC Ð=Ð,再证明()AAS AME CNE V V ≌可得ME NE =,进而证明()SSS BME BNE V V ≌得到MBE NBE Ð=Ð即可判定①;由()SAS AMC CNA V V ≌可得MCA NAC Ð=Ð,然后证明()AAS AEM CEN V V ≌即可判定②;由全等三角形的性质可得AME ENC Ð=Ð,再结合三角形外角的性质即可判定③;先证明()ASA BHE CHP ÐÐV V ≌可得EH HP =,再证明()AAS EGH PDH V V ≌可得HG HD =,然后证明()HL QGH QHD V V ≌可得QE QP =,再说明AE CE =,最后根据线段的和差及等量代换即可证明结论.【详解】解:∵AB BC =,∴BAC BCA Ð=Ð,∵AM CN =,∴()SAS AMC CNA V V ≌,∴MCA NAC Ð=Ð.∵AM CN =,AEM NEC Ð=Ð,∴()AAS AME CNE V V ≌,即②正确;∴ME NE =,∵AB BC =,AM CN =,∴MB BN =,∵BE BE =,∴()SSS BME BNE V V ≌,∴MBE NBE Ð=Ð,即BE 平分ABC Ð,故①正确;∵()AAS AEM CEN V V ≌,∴AME ENC Ð=Ð,BCM BAE Ð=Ð,∵90ENC BAE ABC BAN Ð=Ð+Ð=Ð+°,90CFQ BCM CDF BCM Ð=Ð+Ð=Ð+°,∴ENC CFQ Ð=Ð,即③正确;∴BNQ CFQ Ð=Ð∴90,90BNQ CBP BGN CBP QFC BCH QDC BCH Ð=Ð+Ð=Ð+°Ð=Ð+Ð=Ð+°,∴CBP BCM Ð=Ð,∴BH CH =,∵45MBE NBE Ð=Ð=°,45BCA Ð=°,∴EBN CBP BCA BCM Ð-Ð=Ð-Ð,即EBP ECP Ð=Ð,∵BHE CHP Ð=Ð,∴()ASA BHE CHP V V ≌,∴EH HP =,∵90EGH HDP Ð=Ð=°,EHG PHD Ð=Ð,∴()AAS EGH PDH V V ≌,∴HG HD =,如图:连接HQ ∵90QGH QDH Ð=Ð=°,HQ HQ =,∴()HL QGH QHD V V ≌,∴QE QP =,∵AEM CEN V V ≌,∴AE CE =,∴AQ AE EQ CE PQ =+=+,即④正确.故选D .2.(23-24八年级下·黑龙江哈尔滨·开学考试)如图所示,在ABC V 中,90BAC Ð=°,AD BC ^于D ,BE 平分ABC Ð交AD 于E ,F 在BC 上,并且BF AB =,则下列四个结论:①EF AC ∥,②EFB BAD Ð=Ð,③AE EF =,④ABE FBE △≌△,其中正确的结论有( )A .①③B .②④C .②③④D .①②③④【答案】D【分析】本题主要考查了全等三角形的判定与性质、角平分线的定义;根据SAS 证明ABE FBE △≌△,再利用三角形全等的性质证明EFB BAD Ð=Ð,AE EF =,进而得出EF AC ∥,熟练掌握全等三角形的判定和性质是解此题的关键.【详解】解:Q BE 平分ABC Ð交AD 于E ,ABE FBE \Ð=Ð,在ABE V 和FBE V 中,AB BF ABE FBE BE BE =ìïÐ=Ðíï=î,()SAS ABE FBE \V V ≌,故④正确;EFB BAD AE EF \Ð=Ð=,,故②③正确;90BAC Ð=°Q ,AD BC ^于D ,90BAE ABD \Ð+Ð=°,90C ABD Ð+Ð=°,C BAE EFB \Ð=Ð=Ð,EF AC ∥∴,故①正确;综上所述,正确的有①②③④,故选:D .3.(22-23七年级下·江苏南通·期末)如图,在ABC V 中,90BAC Ð=°,高AD 与角平分线BE 相交于点F ,DAC Ð的平分线AG 分别交BC ,BE 于点G ,O ,连接FG ,下列结论:①C EBG Ð=Ð;②AEF AFE Ð=Ð;③AG EF ^;④ACD ABG S S =△△,其中所有正确结论的序号是( )A .①②④B .②③C .③④D .②③④题型三 全等三角形中的动点综合问题例题:(23-24七年级下·上海闵行·期末)如图,已知在 ABC V 中, (060)AB BC ABC a a =Ð=<<°,,,射线AM AB ^,点P 为射线AM 上的动点(点P 不与点A 重合),连接BP ,将线段BP 绕点B 顺时针旋转角度α后, 得到线段BQ , 连接PQ 、QC .(1)试说明 PAB QCB V V ≌的理由;(2)延长QC 交射线AM 于点D ,在点P 的移动过程中, QDM Ð的大小是否发生变化?若改变请说明理由,若不改变,请求出 QDM Ð的大小(用含α的代数式表示);(3)当BQ AC ∥时, AB m AP n ==,, 过点Q 作QE 垂直射线AB , 垂足为E ,那么 AEQ S =V (用m 、 n 的代数式表示) .【答案】(1)理由见解析(2)不改变,QDM aÐ=(3)mn【分析】(1)先证明PBA QBC Ð=Ð,再根据两条边相等,即可证得两个三角形全等;(2)先证明()SAS DAB DCB V V ≌,得到DA DC =,DBA DBC Ð=Ð,再计算出DBA Ð的值,再证明DAC DBA Ð=Ð,最后根据三角形外角定理即可求得QDM Ð的大小;(3)证明QB 是ABE Ð的角平分线,根据角平分线定理得到BC BE =,QE QC =,再根据BC AB m ==,QC PA n ==,即可得到BE 和QE ,根据三角形面积公式进行计算即可.【详解】(1)证明:根据旋转的性质得到PN QB =,PBQ a Ð=,∴PBQ ABC Ð=Ð,∴PBA QBC Ð=Ð,∵PB QB PBA QBC AB BC =ìïÐ=Ðíï=î,∴()SAS PAB QCB V V ≌;(2)解:如下图所示,连接BD ,∵()SAS PAB QCB V V ≌,∴90QCB PAB Ð=Ð=°,∵BQ AC ∥,∴ACB CBQ CAB Ð=ÐÐ,∵ACB CAB Ð=Ð,∴QBE CBQ Ð=Ð,∴QB 是ABE Ð的角平分线,1.(23-24八年级上·湖南株洲·期末)如图,等腰Rt ACB △中,90ACB Ð=°,AC BC =,E 点为射线CB 上一动点,连接AE ,作AF AE ^且AF AE =.(1)如图1,过F 点作FG AC ^交AC 于G 点,求证:V V ≌AGF ECA ;(2)如图2,连接BF 交AC 于D 点,若3AD CD =,求证:E 点为BC 中点;(3)如图3,当E 点在CB 的延长线上时,连接BF 与AC 的延长线交于D 点,若43BC BE =,则AD CD = .AGF ECA QV V ≌,FG AC BC \==,在FGD V 和BCD △中,由(1)(2)知:V AGF CD DG \=,AG CE =\47AC AG =,\4AC =,2.(23-24八年级上·江西赣州·阶段练习)如图(1),在Rt ABC △中,90C Ð=°,8cm AC =,6cm BC =,10cm AB =,现有一动点P ,从点A 出发,沿着三角形的边AC CB BA ®®运动,回到点A 停止,速度为2cm /s ,设运动时间为s t .(1)如图(1),当t =________时,APC △的面积等于ABC V 面积的一半:(2)如图(2),在DEF V 中,90E Ð=°,4cmDE =,5cm DF =,D A Ð=Ð.在ABC V 的边上,若另外有一个动点Q ,与点P 同时从点A 出发,沿着边AB BC CA ®®运动,回到点A 停止.在两点运动过程中的某一时刻,恰好APQ △全等于DEF V ,求点Q 的运动速度.∴13cm 2CP BC ==∴()8311s 22t +==当P 在AB 上时,如图,∴12AP BP AB ===∴(6851922t ++==综上所述,当t 为(2)解:设点Q∴425x ¸=¸,解得52x =;②当点P 在AC 上,点Q 在∴5cm AP DF AQ DE ====,∴524x ¸=¸,解得85x =;③当点P 在AB 上,点Q 在∴5cm AP DF AQ DE ====,∴点P 的路程为68105++-∴19220x ¸=¸,解得4019x =;④当点P 在AB 上,点Q 在∴4cm AP DE AQ DF ===,∴点P 的路程为68104++-∴20219x ¸=¸,解得1910x =;∴Q 运动的速度为5cm/s 2或853.如图,在等腰ABC V 中,BA BC =,100ABC Ð=°,AB 平分WAC Ð.在线段AC 上有一动点D ,连接BD ,E 为直线AW 上异于A 的一点,连接BE 、DE .(1)如图1,当点E 在射线AW 上时,若DE AE DC +=,直接写出:EBD Ð=______;(2)如图2,当点E 在射线AW 的反向延长线上时,①若(1)中的结论仍成立,则DE 、AE 、DC 应满足怎样的数量关系,请证明;②若6BCD ABDE S S -=V 四边形,且25DE AE =,94AD AE =,求ABC S V 的值.4.(23-24八年级上·浙江嘉兴·期末)如图,在直角坐标系xOy 中,点()0,4A ,点B 为x 轴正半轴上一个动点,以AB 为边作ABC V ,使BC AB =,90ABC Ð=°,且点C 在第一象限内.(1)如图1,若()2,0B ,求点C 的坐标.(2)如图2,过点B 向x 轴上方作BD OB ^,且BD BO =,在点B 的运动过程中,探究点C ,D 之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)如图3,过点B 向x 轴下方作BD OB ^,且BD BO =,连结CD 交x 轴于点E ,当ABD △的面积是BEC V 的面积的2倍时,求OE 的长.【答案】(1)点C 的坐标为(6,2)(2)点C ,D 之间的距离是为定值,定值为4,理由见解析(3)6OE =【分析】本题考查坐标与图形,全等三角形的判定及性质,添加辅助线,构造全等三角形是解决问题的关键.90Q,Ð=°ABC\Ð+Ð=°,90ABO CBDÐ+Ð=°Q,OAB ABO90\Ð=Ð,OAB CBDAOBÐìï90OBA ABD Ð+Ð=°Q ,DBC ÐOBA DBC \Ð=Ð,在OAB V 和DCB △中,OB OBA AB =ìïÐíï=î()SAS OAB DCB \V V ≌.CF BO \=,BD BO =Q ,CF BD \=,4BF OA ==.CEF DEB Ð=ÐQ ,CFE Ð=()AAS CFE DBE \V V ≌,题型四 全等三角形中的新定义型综合问题例题:(23-24七年级下·辽宁本溪·期末)新定义:如果两个三角形不全等但面积相等,那么这两个三角形叫做积等三角形.【初步尝试】(1)如图1,在ABC V 中,4AB AC BC >=,,P 为边BC 上一点,若ABP V 与ACP V 是积等三角形,求BP 的长;【理解运用】(2)如图2,ABD V 与ACD V 为积等三角形,若24AB AC ==,,且线段AD 的长度为正整数,求AD 的长.【综合应用】(3)如图3,在Rt ABC △中90,BAC AB AC Ð=°=,过点C 作MN AC ^,点D 是射线CM 上一点,以AD 为边作Rt ,90,ADE DAE AD AE Ð=°=V ,连接BE .请判断BAE V 与ACD V 是否为积等三角形,并说明理由.【答案】(1)2;(2)2;(3)是积等三角形,证明见解析【分析】本题考查了等腰直角三角形的性质,三角形的中线的性质,三角形的三边关系等知识,解题的关键是正确寻找全等三角形解决问题.(1)利用三角形的中线的性质即可解决问题;(2)证明ADB NDC V V ≌,推出2AB NC ==,利用三角形的三边关系即可解决问题;(3)过过点E 作EH AB ^于点H ,先证明HAE CAD V V ≌, 则,AC AH EH CD ==,然后再依据积等三角形(2)解:如图2,延长V为积等三角形,QV与ACDABD\=BD CD(3)是积等三角形证明:如图3,过点E作^QMN AC\Ð=Ð=°ACD AHE90巩固训练1.(2024八年级下·全国·专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,ABC V 和CDE V 为“同源三角形”,AC BC =,CD CE =,ACB Ð与DCE Ð为“同源角”.(1)如图1,ABC V 和CDE V 为“同源三角形”,试判断AD 与BE 的数量关系,并说明理由.(2)如图2,若“同源三角形”ABC V 和CDE V 上的点B ,C ,D 在同一条直线上,且90ACE Ð=°,则Ð=EMD ______°.(3)如图3,ABC V 和CDE V 为“同源三角形”,且“同源角”的度数为90°时,分别取AD ,BE 的中点Q ,P ,连接CP ,CQ ,PQ ,试说明PCQ △是等腰直角三角形.【答案】(1)AD BE =,详见解析(2)45(3)见解析【分析】本题考查了新定义,全等三角形的判定与性质,等腰直角三角形的判定,三角形内角和定理等知识,(1)由“同源三角形”的定义可证ACD BCE Ð=Ð,然后根据SAS 证明≌ACD BCE V V 即可;(2)由“同源三角形”的定义和90ACE Ð=°可求出45DCE ACB Ð==°,由(1)可知≌ACD BCE V V ,得ADC BEC ÐÐ=,然后根据“8”字形图形即可求出EMD Ð的度数;(3)由(1)可知≌ACD BCE V V ,可得CAQ CBP BE AD ÐÐ=,=,根据SAS 证明ACQ BCP △≌△,可得CQ CP ACQ BCP =Ð=Ð,,进而可证结论成立;熟练掌握全等三角形的判定与性质是解答本题的关键.【详解】(1)AD BE =.理由:∵ABC V 和CDE V 是“同源三角形”,∴ACB DCE Ð=Ð,∴ACD BCE Ð=Ð.在ACD V 和BCE V 中,ACBC ACD BCE CD CE =ìïÐ=Ðíï=î,∴()SAS ACD BCE V V ≌,∴AD BE =.(2)∵ABC V 和CDE V 是“同源三角形”,∴ACB DCE Ð=Ð.∵90ACE Ð=°,∴45DCE ACB Ð=Ð=°.由(1)可知≌ACD BCE V V ,∴ADC BEC ÐÐ=.∵MOE COD Ð=Ð,∴45EMD DCE Ð=Ð=°.故答案为:45;(3)由(1)可知≌ACD BCE V V ,∴CAQ CBP Ð=Ð,BE AD =.AD ,BE 的中点分别为,Q P ,∴AQ BP =.在ACQ V 和BCP V 中,CA CB CAQ CBP AQ BP =ìïÐ=íï=î,∴()SAS ACQ BCP V V ≌,∴CQ CP =,ACQ BCP Ð=Ð.∵90BCP PCA °Ð+Ð=,∴90ACQ PCA °Ð+Ð=,∴90PCQ Ð=°,∴PCQ △是等腰直角三角形.2.(23-24七年级下·陕西宝鸡·期末)【阅读理解】定义:在同一平面内,点A ,B 分别在射线PM ,PN 上,过点A 垂直PM 的直线与过点B 垂直PN 的直线交于点Q ,则我们把AQB Ð称为APB Ð的“边垂角”.【迁移运用】(1)如图1,CD ,BE 分别是ABC V 的两条高,两条高交于点F ,根据定义,我们知道DBE Ð是DCE Ð的“边垂角”或DCE Ð是DBE Ð的“边垂角”,DAE Ð的“边垂角”是______;(2)若AQB Ð是APB Ð的“边垂角”,则AQB Ð与APB Ð的数量关系是______;(3)若ACD Ð是ABD Ð的“边垂角”,且AB AC =.如图2,BD 交AC 于点E ,点C 关于直线BD 对称点为点F ,连接AF ,EF ,且45CAF Ð=°,求证:BE CF CE =+.【答案】(1)DFEÐ(2)AQB APB Ð=Ð或180AQB APB Ð+Ð=°(3)见解析【分析】本题主要考查了全等三角形的性质与判定,四边形内角和定理:(1)根据“边垂角”的定义即可得到答案;(2)分两种情况画出图形,根据四边形的内角和定理以及等角的余角相等即可得出结论;(3)延长,BA CD 交于点G ,先证明(ASA)ABE ACG V V ≌,再证明(SAS)AGF AEF V V ≌,依据题意得出GF EC =,即可得到结论.【详解】(1)解:根据“边垂角”的定义,DAE Ð的“边垂角”是DFE Ð;(2)解:若AQB Ð是APB Ð的“边垂角”,分两种情况①如图,Q AQB Ð是APB Ð的“边垂角”,,AQ PA BQ PB \^^,190,290AQB APB \Ð+Ð=°Ð+Ð=°,12Ð=ÐQ ,AQB APB \Ð=Ð,②如图,Q AQB Ð是APB Ð的“边垂角”,,AQ PA BQ PB \^^,90,90PAQ PBQ \Ð=°Ð=°,360PAQ AQB APB PBQ Ð+Ð+Ð+Ð=°Q ,\180AQB APB Ð+Ð=°,综上所述,AQB Ð与APB Ð的数量关系是AQB APB Ð=Ð或180AQB APB Ð+Ð=°;(3)解:延长,BA CD 交于点G ,Q ACD Ð是ABD Ð的“边垂角”,∴CG BD BG AC ⊥,⊥,90,90ABE AEB ACD DEC \Ð+Ð=°Ð+Ð=°,AEB DEC Ð=ÐQ ,ABE ACF \Ð=Ð,90BAE CAG \Ð=Ð=°,AB AC =Q ,\(ASA)ABE ACG V V ≌,,AG AE BE CG \==,45FAC Ð=°Q ,9045GAF FAC \Ð=°-Ð=°,AF AF =Q ,\(SAS)AGF AEF V V ≌,GF EF \=,Q 点C 关于直线BE 对称点为点F ,EF EC \=,BE CG CF FG CF EF CF CE \==+=+=+,BE CF CE \=+;3.(23-24七年级下·辽宁沈阳·阶段练习)【阅读理解】定义:在同一平面内,点A ,B 分别在射线PM ,PN 上,过点A 垂直PM 的直线与过点B 垂直PN 的直线交于点Q ,则我们把AQB Ð称为APB Ð的“边垂角”.【迁移运用】(1)如图1,CD ,BE 分别是ABC V 的两条高,两条高交于点 F ,根据定义,我们知道DBE Ð是DCE Ð的“边垂角”或DCE Ð是DBE Ð的“边垂角”,DAE Ð的“边垂角”是 ;(2)若AQB Ð是APB Ð的“边垂角”,则AQB Ð与APB Ð的数量关系是 ;(3)若ACD Ð是ABD Ð的“边垂角”,且AB AC =.①如图2,已知B C Ð=Ð,BD 交AC 于点E ,点C 关于直线BD 对称点为点F ,连接AF ,EF ,且 45CAF Ð=°,90BAC Ð=°,求证:BE CF CE =+;对于上述问题,小明有这样的想法:在BD 上截取BH CF =,连接AH ,如图3.你明白小明的做法吗?接下来请你求证BE CF CE =+.②如图4,若92CD BD +=,直接写出四边形ABDC 的面积.【答案】(1)DFE Ð②如图,Q AQB Ð是APB Ð的“边垂角”,,AQ PA BQ PB \^^,90,90PAQ PBQ \Ð=°Ð=°,综上所述,AQB Ð与APB Ð的数量关系是AQB APB Ð=Ð或180AQB APB Ð+Ð=°;(3)解:①延长,BA CD 交于点G ,Q ACD Ð是ABD Ð的“边垂角”,90,90ABE AEB ACD DEC \Ð+Ð=°Ð+Ð=°,AEB DEC Ð=ÐQ ,ABE ACF \Ð=Ð,90BAE CAG \Ð=Ð=°,AB AC =Q ,\(ASA)ABE ACG V V ≌,,AG AE BE CG \==,45FAC Ð=°Q ,9045GAF FAC \Ð=°-Ð=°,AF AF =Q ,\(SAS)AGF AEF V V ≌,GF EF \=,Q 点C 关于直线BE 对称点为点F ,EF EC \=,BE CG CF FG CF EF CF CE \==+=+=+,BE CF CE \=+;②连接AD ,过点A 作AE AD ^与DB 延长交于点E ,Q ACD Ð是ABD Ð的“边垂角”,180ACD ABD \Ð+Ð=°,180ABE ABD Ð+Ð=°Q ,ABE ACD \Ð=Ð,90DAC BAD BAD EAB Ð+Ð=Ð+Ð=°Q ,【点睛】本题主要考查新定义,四边形的内角和定理,直角三角形的性质,全等三角形的判定与性质,熟练理解“边垂角”的定义是解题的关键.4.(22-23七年级下·江苏淮安α(0180a °<<°)得到AB ¢,把AC 绕点A 逆时针旋转β得到AC ¢,连接B C ¢¢.当180a b +=°时,我们称AB C ¢¢△是ABC V 的“旋补三角形”,AB C ¢¢△边B C ¢¢上的中线AD 叫做ABC V 的“旋补中线”,点A 叫做“旋补中心”.(1)【探索一】如图1,AB C ¢¢△是ABC V 的“旋补三角形”,AD 是ABC V 的“旋补中线”,探索AD 与BC 的数量关系.在探索这个问题之前,请先阅读材料:【材料】如图2在ABC V 中,若10AB =,8BC =.求AC 边上的中线BD 的取值范围.是这样思考的:延长BD 至E ,使DE BD =,连结CE .利用全等将边AB 转化到CE ,在BCE V 中利用三角形三边关系即可求出中线BD 的取值范围.中线BD 的取值范围是 .请仿照上面材料中的方法,猜想图1中AD 与BC 的数量关系,并给予证明.(2)【探索二】如图3,当90a b ==°时,AB C ¢¢△是ABC V 的“旋补三角形”,AE BC ^,垂足为点E ,AE 的反向延长线交B C ¢¢于点D ,探索AD 是否是ABC V 的“旋补中线”,如果是,请给出证明,如果不是,请说明理由.【答案】(1)19BD <<;2BC AD =,证明见解析;(2)AD 是ABC V 的“旋补中线”, 证明见解析【分析】(1)材料:三角形三边关系可得CE BC BE CE BC -<<+,进而可得中线BD 的取值范围;探索一:延长AD 至点E 使AD DE =,连接C E ¢,证明()SAS B DA CDE ¢≌V V ,可得AB CE ¢=,B AD E ¢Ð=Ð,求出BAC AC E ¢Ð=Ð,再证()SAS ABC C EA ¢≌V V ,根据全等三角形的性质可得结论;(2)作C H AD ¢^于H ,作B F AD ¢^交AD 延长线于F ,求出B B AF ¢Ð=Ð,证明()AAS ABE B AF ¢≌V V ,可得=B F AE ¢,同理证明()AAS ACE C AH ¢≌V V ,可得=AE C H ¢,求出=B F C H ¢¢,可证()AAS B DF C DH ¢¢≌V V ,根据全等三角形的性质可得B D C D ¢=¢,然后可得AD 是ABC V 的“旋补中线”.【详解】(1)解:材料:由题意得:10AB CE ==,8BC =,2BE BD =,由三角形三边关系可得:CE BC BE CE BC -<<+,即218BD <2<,∴19BD <<,故答案为:19BD <<;探索一:2BC AD =;证明:如图1,延长AD 至点E 使AD DE =,连接C E ¢,∵AD 是ABC V 的“旋补中线”,∴AD 是AB C ¢¢△的中线,即B D CD ¢=,又∵B DA C DE ¢¢Ð=Ð,∴()SAS B DA C DE ¢¢V V ≌,∴AB C E ¢¢=,B AD E ¢Ð=Ð,∵AB AB ¢=,∴AB C E ¢=,∵AD 是ABC V 的“旋补中线”,∴180BAC B AC BAC B AD EAC ¢¢¢Ð+Ð=Ð+Ð+Ð=°,∵180AC E E EAC ¢Ð+Ð+Ð=°,B AD E ¢Ð=Ð,∴BAC AC E ¢Ð=Ð,∵AC AC ¢=,BAC AC E ¢Ð=Ð,AB C E¢=∴()SAS ABC C EA ¢≌V V ,∴2BC AE AD ==.(2)AD 是ABC V 的“旋补中线”;证明:如图,作C H AD ¢^于H ,作B F AD ¢^交AD 延长线于F ,∵AE BC ^,∴90F BEA Ð=Ð=°,∴90BAE B Ð+Ð=°,∵90a b ==°,即90BAB CAC ¢¢Ð=Ð=°,∴90BAE B AF ¢Ð+Ð=°,∴B B AF ¢Ð=Ð,又∵¢=BA AB ,∴()AAS ABE B AF ¢≌V V ,∴=B F AE ¢,又∵90AEC C HA ¢Ð=Ð=°,90CAC ¢Ð=°,∴90CAE C Ð+Ð=°,90CAE C AH ¢Ð+Ð=°,∴C C AH ¢Ð=Ð,∵CA AC ¢=,∴()AAS ACE C AH ¢≌V V ,∴=AE C H ¢,∴=B F C H ¢¢,∵90F C HD ¢Ð=Ð=°,B DF C DH ¢¢Ð=Ð,∴()AAS B DF C DH ¢¢≌V V ,∴B D C D ¢=¢,∴AD 是AB C ¢¢△的中线,∴AD 是ABC V 的“旋补中线”.【点睛】本题主要考查了全等三角形的判定和性质、同角的余角相等,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题.。
全等三角形专项练习及答案
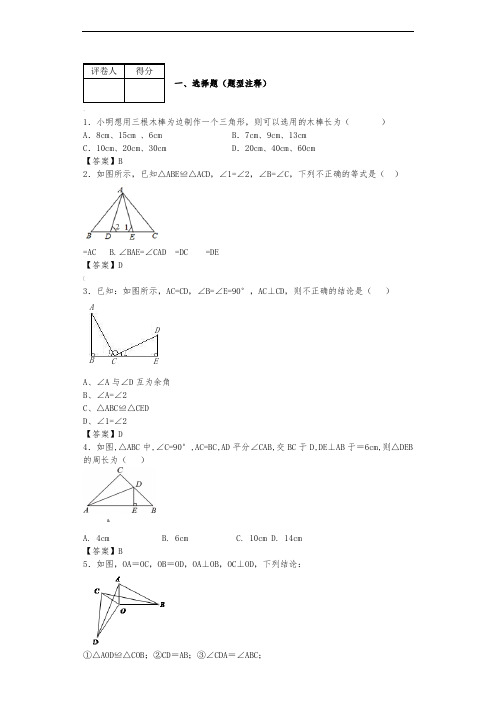
评卷人得分一、选择题(题型注释)、1.小明想用三根木棒为边制作一个三角形,则可以选用的木棒长为()A.8cm、15cm 、6cm B.7cm、9cm、13cmC.10cm、20cm、30cm D.20cm、40cm、60cm【答案】B2.如图所示,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,下列不正确的等式是()=AC B.∠BAE=∠CAD =DC =DE【答案】D[3.已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A、∠A与∠D互为余角B、∠A=∠2C、△ABC≌△CEDD、∠1=∠2【答案】D4.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于=6cm,则△DEB 的周长为()A. 4cmB. 6cmC. 10cmD. 14cm【答案】B5.如图,OA=OC,OB=OD,OA⊥OB,OC⊥OD,下列结论:①△AOD≌△COB;②CD=AB;③∠CDA=∠ABC;&AB CDE1]其中正确的结论是( )A.①② B.①②③ C.①③ D.②③》【答案】B【解析】试题分析:因为OA=OC,OB=OD,OA⊥OB,OC⊥OD,可得△COD≌△AOB, ∠CDO=∠ABO;∠DOC+∠AOC=∠AOB+∠AOC, OA=OC,OB=OD,所以△AOD≌△COB,所以CD=AB,∠ADO=∠CBO;所以∠CDA=∠ABC.故①②③都正确.故选B考点:三角形全等的判定和性质6.如图,△ABC中,∠B=∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是()…A.2α+∠A=180° B.α+∠A=90° C.2α+∠A=90° D.α+∠A=180°【答案】A【解析】试题分析:根据已知条件可证明△BDE≌△CFD,则∠BED=∠CDF,由∠A+∠B+∠C=180°,得∠B=,因为∠BDE+∠EDF+∠CDF=180°,所以得出a与∠A的关系2a+∠A=180°.考点:全等三角形的判定和性质,三角形的内角和定理7.如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF,则()~A.BE+CF>EFB.BE+CF=EFC.BE+CF<EFD.BE+CF与EF的大小关系不能确定.【答案】A.8.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是()A.10cm B.12cm C.15cm D.17cm}【答案】C.【解析】试题分析:∵AB的垂直平分AB,∴AE=BE,BD=AD,∵AE=3cm,△ADC的周长为9cm,∴△ABC的周长是9cm+2×3cm=15cm,故选C.考点:线段垂直平分线的性质.9.如图所示,∠A+∠B+∠C+∠D+∠E的结果为()A.90° B.1 80° C.360° D.无法确定【答案】?【解析】试题分析:延长BE交AC于F,∵∠A+∠B=∠2,∠D+∠E=∠1,∠1+∠2+∠C=180°,∴∠A+∠B+∠C+∠D+∠E=180°,考点:1.三角形内角和定理;2.三角形的外角性质.10.若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为何()>A、36B、72C、108D、144【答案】C【解析】∵∠A+∠B+∠C=180°,∴2(∠A+∠B+∠C)=360°,∵2(∠A+∠C)=3∠B,∴∠B=72°,11.如图,AB∥CD,∠D =∠E =35°,则∠B的度数为().A.60° B.65° C.70° D.75°【答案】C.~12.如图,已知△ABC,O是△ABC内的一点,连接OB、OC,将∠ABO、∠ACO分别记为∠1、∠2,则∠1、∠2、∠A、∠O四个角之间的数量关系是()A .∠1+∠0=∠A+∠2B .∠1+∠2+∠A+∠O=180°C .∠1+∠2+∠A+∠O=360°D .∠1+∠2+∠A=∠O【答案】D .【解析】 试题分析:连接AO 并延长,交BC 于点D ,》∵∠BOD 是△AOB 的外角,∠COD 是△AOC 的外角,∴∠BOD=∠BAD+∠1①,∠COD=∠CAD+∠2②,①+②得,∠BOC=(∠BAD+∠CAD )+∠1+∠2,即∠BOC=∠BAC+∠1+∠2.故选D .考点:1.三角形的外角性质;2.三角形内角和定理.13.如图,BD 是∠ABC 的角平分线,DE ⊥AB 于E ,DF ⊥BC 于F ,,,,△cm 12BC cm 18AB cm 362ABC ===S 则DE 的长是( )B.cm 512 D.cm 514 ¥【答案】B【解析】试题分析:∵BD 是∠ABC 的角平分线,DE ⊥AB ,DF ⊥BC,由角平分线的性质可得DE=DF ∴DCB S S ∆∆+=ADB ABC S △=DF DE ⋅⨯+⋅⨯12211821=9DE+6DF=15DE=36∴DE=cm 512 所以选B.考点:角平分线的性质?第II卷(非选择题)请点击修改第II卷的文字说明评卷人得分~二、填空题(题型注释)14.如图,△ABC中,∠A=90°,DE是BC的垂直平分线,AD=DE,则∠C的度数是°.【答案】30°.【解析】试题分析:∵DE是BC的垂直平分线,∴DE⊥BC,∵∠A=90°,AD=DE,∴BD平分∠AABC,∴∠ABD=∠DBC,∵DE是BC的垂直平分线,∴DC=BD,∴∠C=∠DBC,∴3∠C=90°,∴∠C=30°.故答案为:30°.考点:1.线段垂直平分线的性质;2.角平分线的性质.!15.如图,在△ABC中,∠ACB=90°,AB的垂直平分线DE交AB于E,交AC于D,∠DBC=30°,BD=,则D到AB的距离为。
八年级上册数学 全等三角形专题练习(解析版)

八年级上册数学全等三角形专题练习(解析版)一、八年级数学轴对称三角形填空题(难)1.如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为___________.【答案】4【解析】【分析】延长AC至E,使CE=BM,连接DE.证明△BDM≌△CDE(SAS),得出MD=ED,∠MDB=∠EDC,证明△MDN≌△EDN(SAS),得出MN=EN=CN+CE,进而得出答案.【详解】延长AC至E,使CE=BM,连接DE.∵BD=CD,且∠BDC=140°,∴∠DBC=∠DCB=20°,∵∠A=40°,AB=AC=2,∴∠ABC=∠ACB=70°,∴∠MBD=∠ABC+∠DBC=90°,同理可得∠NCD=90°,∴∠ECD=∠NCD=∠MBD=90°,在△BDM和△CDE中,BM CE MBD ECD BD CD ⎧⎪∠∠⎨⎪⎩==,=∴△BDM ≌△CDE (SAS ),∴MD=ED ,∠MDB=∠EDC ,∴∠MDE=∠BDC=140°,∵∠MDN=70°,∴∠EDN=70°=∠MDN ,在△MDN 和△EDN 中,MD ED MDN EDN DN DN ⎧⎪∠∠⎨⎪⎩==,=∴△MDN ≌△EDN (SAS ),∴MN=EN=CN+CE ,∴△AMN 的周长=AM+MN+AN=AM+CN+CE+AN=AM+AN+CN+BM=AB+AC=4;故答案为:4.【点睛】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识;证明三角形全等是解题的关键.2.在平面直角坐标系xOy 中,已知点A (2,3),在x 轴上找一点P ,使得△AOP 是等腰三角形,则这样的点P 共有_____个.【答案】4【解析】【分析】以O 为圆心,OA 为半径画弧交x 轴于点P 1、P 3,以A 为圆心,AO 为半径画弧交x 轴于点P 4,作OA 的垂直平分线交x 轴于P 2.【详解】解:如图,使△AOP 是等腰三角形的点P 有4个.故答案为4.【点睛】本题考查了在平面直角坐标系中寻找等腰三角形,掌握两圆一线找等腰三角形是解题的关键.3.等腰三角形顶角为30°,腰长是4cm ,则三角形的面积为__________【答案】4【解析】如图,根据30°角所对直角边等于斜边的一半的性质,可由等腰三角形的顶角为30°,腰长是4cm ,可求得BD=12AB =4×12=2,因此此三角形的面积为:S=12AC•BD=12×4×2=8×12=4(cm 2).故答案是:4.4.如图,在Rt ABC △中,AC BC ,D 是线段AB 上一个动点,把ACD 沿直线CD 折叠,点A 落在同一平面内的A '处,当A D '平行于Rt ABC △的直角边时,ADC ∠的大小为________.【答案】112.5︒或67.5︒ 【解析】【分析】当A D '平行于Rt ABC △的直角边时,有两种情况,一是当A D BC '时,二是当A D AC '时,两种情况根据折叠的性质及等腰三角形的性质进行角度的计算即可.【详解】如图1,当点D 在线段AB 上,且A D BC '时,45A DB B '∠=∠=︒,45180ADC A DC '∴∠+∠-=︒︒,解得112.5A DC ADC '∠=∠=︒.图1如图2,当A D AC '时,45A DB A '∠=∠=︒,45180ADC A DC '∴∠+∠+=︒︒,解得67.5A DC ADC '∠=∠=︒.图2【点睛】本题考查了翻折变换的性质,等腰直角三角形的性质,掌握折叠的性质是解题关键.5.等腰三角形一边长等于4,一边长等于9,它的周长是__.【答案】22【解析】【分析】等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形;【详解】解:因为4+4=8<9,0<4<9+9=18,∴腰的不应为4,而应为9,∴等腰三角形的周长=4+9+9=22.故答案为22.【点睛】本题主要考查了等腰三角形的性质和三角形的三边关系;求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.6.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△A n B n A n+1的边长为_____.【答案】2n.【解析】【分析】根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.【详解】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∵∠MON=30°,∵OA2=4,∴OA1=A1B1=2,∴A2B1=2,∵△A2B2A3、△A3B3A4是等边三角形,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2=32,以此类推△A n B n A n+1的边长为 2n.故答案为:2n.【点睛】本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.7.如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC=_____cm.【答案】8cm.【解析】【详解】解:如图,延长ED交BC于M,延长AD交BC于N,作DF∥BC,∵AB=AC,AD平分∠BAC,∴AN⊥BC,BN=CN,∵∠EBC=∠E=60°,∴△BEM为等边三角形,∴△EFD为等边三角形,∵BE=6cm,DE=2cm,∴DM=4,∵△BEM为等边三角形,∴∠EMB=60°,∵AN⊥BC,∴∠DNM=90°,∴∠NDM=36°,∴NM=2,∴BN=4,∴BC=8.8.如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是______________.【答案】2018180 2⎛⎫⨯ ⎪⎝⎭【解析】【分析】根据等腰三角形的性质求出∠BA1C的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律即可得出第2019个三角形中以A2019为顶点的内角度数.【详解】解:∵在△CBA1中,∠B=20°,A1B=CB,∴∠BA1C=°180-2B∠=80°,∵A1A2=A1D,∠BA1C是△A1A2D的外角,∴∠DA2A1=12∠BA1C=12×80°;同理可得∠EA3A2=(12)2×80°,∠FA4A3=(12)3×80°,∴第n个三角形中以A n为顶点的底角度数是(12)n-1×80°.∴第2017个三角形中以A2019为顶点的底角度数是(12)2018×80°,故答案为:(12) 2018×80°. 【点睛】 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠DA 2A 1,∠EA 3A 2及∠FA 4A 3的度数,找出规律是解答此题的关键.9.如图:在ABC ∆中,D ,E 为边AB 上的两个点,且BD BC =,AE AC =,若108ACB ∠=︒,则DCE ∠的大小为______.【答案】036【解析】【分析】 根据三角形内角和求出∠A+∠B,再根据AC=AE,BC=BD ,用∠A 表示∠AEC,用∠B 表示∠BDC,然后根据内角和求出∠DCE 的度数.【详解】∵∠ACB=1080,∴∠A+∠B=1800-1080=720,∵AC=AE,BC=BD,∴∠ACE=∠AEC,∠BCD=∠BDC, ∴01(180)2AEC A ∠=-∠01902A =-∠ 01(180)2BDCB ∠=-∠ =01902B -∠ ∵∠DCE+∠CDE+∠DEC=1800,∴0180DCE CDE CED ∠=-∠-∠= 00011180(90)(90)22A B --∠--∠ =1122A B ∠+∠ =1()2A B ∠+∠ =360【点睛】此题考察等腰三角形的性质,注意两条等边所在三角形,依此判断对应的两个底角相等.10.如图,在边长为6的菱形ABCD 中,∠DAB=60°,E 是AB 的中点,F 是AC 上一个动点,则EF+BF 的最小值是________ .【答案】33【解析】试题解析:∵在菱形ABCD 中,AC 与BD 互相垂直平分,∴点B 、D 关于AC 对称, 连接ED ,则ED 就是所求的EF+BF 的最小值的线段,∵E 为AB 的中点,∠DAB=60°,∴DE ⊥AB ,∴22AD AE -2263-3∴EF+BF 的最小值为3.二、八年级数学轴对称三角形选择题(难)11.已知点M(2,2),且2,在坐标轴上求作一点P ,使△OMP 为等腰三角形,则点P 的坐标不可能是( )A .2B .(0,4)C .(4,0)D .2) 【答案】D【解析】【分析】分类讨论:OM=OP ;MO=MP ;PM=PO ,分别计算出相应的P 点,从而得出答案.【详解】∵M(2,2),且2,且点P 在坐标轴上当22OM OP ==时P 点坐标为:()(22,0,0,22±± ,A 满足;当22MO MP ==P 点坐标为:()()4,0,0,4,B 满足;当PM PO =时:P 点坐标为:()()2,0,0,2,C 满足故答案选:D【点睛】本题考查动点问题构成等腰三角形,利用等腰三角形的性质分类讨论是解题关键.12.已知∠AOB =30°,点P 在∠AOB 内部,P 1与P 关于OB 对称,P 2与P 关于OA 对称,则P 1,O ,P 2三点构成的三角形是 ( )A .直角三角形B .钝角三角形C .等边三角形D .等腰三角形 【答案】C【解析】【分析】根据题意,作出相应的图形,然后对相应的角进行标记;本题先证明P 1,O ,P 2三点构成的三角形中1260POP ∠=︒,然后证边12OP OP OP ==,得到P 1,O ,P 2三点构成的三角形为等腰三角形,又因为该等腰三角形有一个角为60︒,故得证P 1,O ,P 2三点构成的三角形是等边三角形。
八年级数学上册全等三角形专题练习(解析版)

八年级数学上册全等三角形专题练习(解析版)一、八年级数学轴对称三角形填空题(难)1.如图,在锐角△ABC中,AB=5,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.【答案】5【解析】【分析】作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN为所求的最小值,再根据AD是∠BAC的平分线可知MH=MN,再由等腰直角三角形的性质即可得出结论.【详解】如图,作BH⊥AC,垂足为H,交AD于M点,过M点作MN⊥AB,垂足为N,则BM+MN 为所求的最小值.∵AD是∠BAC的平分线,∴MH=MN,∴BH是点B到直线AC的最短距离(垂线段最短).∵AB=5,∠BAC=45°,∴BH==5.∵BM+MN的最小值是BM+MN=BM+MH=BH=5.故答案为5.【点睛】本题考查了轴对称﹣最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.中取点P使得PA,PB,PC的长分别为3, 4, 5,则2.如图,在等边ABCAPC APB S S ∆∆+=_________.【答案】936 【解析】【分析】把线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ,由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS 证得△ADB ≌△APC ,连接PD ,根据旋转的性质知△APD 是等边三角形,利用勾股定理的逆定理可得△PBD 为直角三角形,∠BPD =90︒,由△ADB ≌△APC 得S △ADB =S △APC ,则有S △APC +S △APB =S △ADB +S △APB =S △ADP +S △BPD ,根据等边3S △ADP +S △BPD =332+12×3×4=936+. 【详解】将线段AP 以点A 为旋转中心顺时针旋转60︒得到线段AD ,连接PD∴AD =AP ,∠DAP =60︒,又∵△ABC 为等边三角形,∴∠BAC =60︒,AB =AC ,∴∠DAB +∠BAP =∠PAC +∠BAP ,∴∠DAB =∠PAC ,又AB=AC,AD=AP∴△ADB ≌△APC∵DA =PA ,∠DAP =60︒,∴△ADP 为等边三角形,在△PBD 中,PB =4,PD =3,BD =PC =5,∵32+42=52,即PD 2+PB 2=BD 2,∴△PBD 为直角三角形,∠BPD =90︒,∵△ADB ≌△APC ,∴S △ADB =S △APC ,∴S △APC +S △APB =S △ADB +S △APB =S △ADP +S △BPD =34×32+12×3×4=9364+.故答案为:9364 .【点睛】本题考查了等边三角形的性质与判定,解题的关键是熟知旋转的性质作出辅助线进行求解.3.如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为______.【答案】2.【解析】【分析】【详解】过点D作DF⊥B′E于点F,过点B′作B′G⊥AD于点G,∵∠B=60°,BE=BD=4,∴△BDE是等边三角形,∵△B′DE≌△BDE,∴B′F=12B′E=BE=2,3,∴GD=B′F=2,∴3∵AB=10,∴AG=10﹣6=4,∴7考点:1轴对称;2等边三角形.4.如图,在ABC ∆中,点D 是BC 的中点,点E 是AD 上一点,BE AC =.若70C ∠=︒,50DAC ∠=︒ 则EBD ∠的度数为______.【答案】10︒【解析】【分析】延长AD 到F 使DF AD =,连接BF ,通过ACD FDB ≅,根据全等三角形的性质得到CAD BFD ∠=∠,AC BF =, 等量代换得BF BE =,由等腰三角形的性质得到F BEF ∠=∠,即可得到BEF CAD ∠=∠,进而利用三角形的内角和解答即可得.【详解】如图,延长AD 到F ,使DF AD =,连接BF :∵D 是BC 的中点∴BD CD =又∵ADC FDB ∠=∠,AD DF =∴ACD FDB ≅∴AC BF =, CAD F ∠=∠,C DBF ∠=∠∵AC BE =, 70C ︒∠=, 50CAD ︒∠=∴BE BF =, 70DBF ︒∠=∴50BEF F ︒∠=∠=∴180180505080EBF F BEF ︒︒︒︒︒∠=-∠-∠=--=∴807010EBD EBF DBF ︒︒︒∠=∠-∠=-=故答案为:10︒【点睛】本题主要考查的知识点有全等三角形的判定及性质、等腰三角形的性质及三角形的内角和定理,解题的关键在于通过倍长中线法构造全等三角形.5.如图,△ABC中,AB=8,AC=6,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别交AB、AC于点D、E,则△ADE的周长为_____.【答案】14.【解析】【分析】先根据角平分线的定义及平行线的性质得BD=DF,CE=EF,则△ADE的周长=AB+AC=14.【详解】∵BF平分∠ABC,∴∠DBF=∠CBF,∵DE∥BC,∴∠CBF=∠DFB,∴∠DBF=∠DFB,∴BD=DF,同理FE=EC,∴△AED的周长=AD+AE+ED=AB+AC=8+6=14.故答案为:14.【点睛】此题考查角平分线的性质,平行线的性质,等腰三角形的等角对等边的性质.6.如图,已知每个小方格的边长为1,A 、B 两点都在小方格的格点(顶点)上,请在图中找一个格点C ,使△ABC 是等腰三角形,这样的格点C 有________个。
专题15 三角形及全等三角形(共30题)(解析版)-2023年中考数学真题分项汇编(全国通用)

专题15三角形及全等三角形(30题)一、单选题1.(2023·吉林长春·统考中考真题)如图,工人师傅设计了一种测零件内径AB 的卡钳,卡钳交叉点O 为AA '、BB '的中点,只要量出A B ''的长度,就可以道该零件内径AB 的长度.依据的数学基本事实是()A .两边及其夹角分别相等的两个三角形全等B .两角及其夹边分别相等的两个三角形全等C .两余直线被一组平行线所截,所的对应线段成比例D .两点之间线段最短【答案】A【分析】根据题意易证()SAS AOB A OB '' ≌,根据证明方法即可求解.【详解】解:O 为AA '、BB '的中点,OA OA ∴'=,OB OB '=,AOB A OB ''∠=∠ (对顶角相等),∴在AOB 与A OB ''△中,OA OA AOB A OB OB OB =⎧⎪∠=∠⎨⎪=''⎩',()SAS AOB A OB ''∴△≌△,AB A B ''∴=,故选:A .【点睛】本题考查了全等三角形的证明,正确使用全等三角形的证明方法是解题的关键.2.(2023·四川宜宾·统考中考真题)如图,AB CD ∥,且40A ∠=︒,24D ∠=︒,则E ∠等于()【答案】D 【分析】可求40ACD ∠=︒,再由ACD D E ∠=∠+∠,即可求解.【详解】解:AB CD ∥ ,40ACD A ∴∠=∠=︒,ACD D E ∠=∠+∠ ,2440E ∴︒+∠=︒,16E ∴∠=︒.故选:D .【点睛】本题考查了平行线的性质,三角形外角性质,掌握三角形外角的性质是解题的关键.3.(2023·云南·统考中考真题)如图,A B 、两点被池塘隔开,、、A B C 三点不共线.设AC BC 、的中点分别为M N 、.若3MN =米,则AB =()A .4米B .6米C .8米D .10米【答案】B 【分析】根据三角形中位线定理计算即可.【详解】解∶∵AC BC 、的中点分别为M N 、,∴MN 是ABC 的中位线,∴26(AB MN ==米),故选:B .【点睛】本题考查的是三角形中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.4.(2023·四川眉山·统考中考真题)如图,ABC 中,,40=∠=︒AB AC A ,则ACD ∠的度数为()【答案】C 【分析】根据等腰三角形的等边对等角和三角形的内角和定理,即可解答.【详解】解:,40AB AC A =∠=︒ ,180702A B ACD ︒-∠∴∠=∠==︒,110ACD A B ∴∠=∠+∠=︒,故选:C .【点睛】本题考查了等腰三角形的等边对等角性质,三角形内角和定理,熟知上述概念是解题的关键.5.(2023·湖南·统考中考真题)下列长度的各组线段能组成一个三角形的是()A .1cm,2cm,3cmB .3cm,8cm,5cmC .4cm,5cm,10cmD .4cm,5cm,6cm 【答案】D【分析】根据两边之和大于第三边,两边之差小于第三边判断即可.【详解】A.1cm+2cm=3cm ,不符合题意;B.3cm+5cm=8cm ,不符合题意;C.4cm+5cm=9cm 10cm <,不符合题意;D.4cm+5cm=9cm 6cm >,符合题意,故选:D .【点睛】本题考查了是否构成三角形,熟练掌握三角形两边之和大于第三边是解题的关键.6.(2023·山西·统考中考真题)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O 的光线相交于点P ,点F 为焦点.若1155,230∠=︒∠=︒,则3∠的度数为()A .45︒B .50︒C .55︒D .60︒【答案】C故选:C .【点睛】本题考查了平行线的性质,三角形外角的性质等知识,掌握这两个知识点是关键.7.(2023·福建·统考中考真题)阅读以下作图步骤:①在OA 和OB 上分别截取,OC OD ,使,C D 1CD 的长为半径作弧,两弧在A .12∠=∠且CM DM=C .12∠=∠且OD DM=【答案】A 【分析】由作图过程可得:OD 角形的性质可得12∠=∠即可解答.【详解】解:由作图过程可得:,OD OC CM DM ==,∵DM DM =,∴()SSS COM DOM ≌.∴12∠=∠.∴A 选项符合题意;不能确定OC CM =,则13∠=∠不一定成立,故B 选项不符合题意;不能确定OD DM =,故C 选项不符合题意,OD CM ∥不一定成立,则23∠∠=不一定成立,故D 选项不符合题意.故选A .【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点,理解尺规作图过程是解答本题的关键.8.(2023·浙江台州·统考中考真题)如图,锐角三角形ABC 中,AB AC =,点D ,E 分别在边AB ,AC 上,连接BE ,CD .下列命题中,假命题...是().A .若CD BE =,则DCB EBC∠=∠B .若DCB EBC ∠=∠,则CD BE =C .若BD CE =,则DCB EBC∠=∠D .若DCB EBC ∠=∠,则BD CE=【答案】A 【分析】由AB AC =,可得A ABC CB =∠∠,再由CD BE BC CB ==,,由SSA 无法证明BCD 与CBE 全等,从而无法得到DCB EBC ∠=∠;证明ABE ACD @V V 可得CD BE =;证明ABE ACD @V V ,可得ACD ABE ∠=∠,即可证明;证明()DBC ECB ASA ≅ ,即可得出结论.【详解】解:∵AB AC =,∴A ABC CB =∠∠,∵若CD BE =,又BC CB =,∴BCD 与CBE 满足“SSA ”的关系,无法证明全等,因此无法得出DCB EBC ∠=∠,故A 是假命题,∵若DCB EBC ∠=∠,∴ACD ABE ∠=∠,在ABE 和ACD 中,ACD ABE AB AC A A ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ABE ACD ASA ≅ ,∴CD BE =,故B 是真命题;若BD CE =,则AD AE =,在ABE 和ACD 中,AB AC A A AE AD =⎧⎪∠=∠⎨⎪=⎩,∴()ABE ACD SAS ≅ ,∴ACD ABE ∠=∠,∵A ABC CB =∠∠,∴DCB EBC ∠=∠,故C 是真命题;若DCB EBC ∠=∠,则在DBC △和ECB 中,ABC ACB BC BC DCB EBC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()DBC ECB ASA ≅ ,∴BD CE =,故D 是真命题;故选:A .【点睛】本题考查等腰三角形的判定和性质,全等三角形的判定和性质,命题的真假判断,正确的命题叫真命题,错误的命题叫假命题,判断命题的真假关键是掌握相关性质定理.9.(2023·河北·统考中考真题)在ABC 和A B C ''' 中,3064B B AB A B AC A C '''''∠=∠=︒====,,.已知C n ∠=︒,则C '∠=()A .30︒B .n ︒C .n ︒或180n ︒-︒D .30︒或150︒【答案】C 【分析】过A 作AD BC ⊥于点D ,过A '作A D B C ''''⊥于点D ¢,求得3AD A D ''==,分两种情况讨论,利用全等三角形的判定和性质即可求解.【详解】解:过A 作AD BC ⊥于点D ,过A '作A D B C ''''⊥于点D ¢,∵306B B AB A B '''∠=∠=︒==,,∴3AD A D ''==,当B C 、在点D 的两侧,B C ''、在点D ¢的两侧时,如图,∵3AD A D ''==,4AC A C ''==,∴()Rt Rt HL ACD A C D '''≌△△,∴C C n '∠=∠=︒;当B C 、在点D 的两侧,B C ''、在点D ¢的同侧时,如图,∵3AD A D ''==,4AC A C ''==,∴()Rt Rt HL ACD A C D '''≌△△,∴'''A C D C n ∠=∠=︒,即'''180'''180A C B A C D n ∠=︒-∠=︒-︒;综上,C '∠的值为n ︒或180n ︒-︒.故选:C .【点睛】本题考查了含30度角的直角三角形的性质,全等三角形的判定和性质,分类讨论是解题的关键.二、填空题10.(2023·江苏连云港·统考中考真题)一个三角形的两边长分别是3和5,则第三边长可以是__________.(只填一个即可)【答案】8【分析】利用三角形中位线定理即可求解.【详解】解:∵点C D ,分别是OA ∴12CD AB =,∴()28cm AB CD ==,故答案为:8.【点睛】本题考查了三角形中位线定理的应用,掌握12.(2023·新疆·统考中考真题)如图,【答案】52【分析】根据等边对等角得出,B C B BAD ∠∠∠∠==,再有三角形内角和定理及等量代换求解即可.【详解】解:∵AB AC =,AD BD =,∴,B C B BAD ∠∠∠∠==,∴B C BAD ∠∠∠==,∵180B C BAC ∠∠∠++=︒,∴180B C BAD CAD ∠∠∠∠+++=︒,即324180C ∠+︒=︒,解得:52C ∠=︒,故答案为:52.【点睛】题目主要考查等边对等角及三角形内角和定理,结合图形,找出各角之间的关系是解题关键.13.(2023·安徽·统考中考真题)清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论:如图,AD 是锐角ABC 的高,则2212AB AC BD BC BC ⎛⎫-=+ ⎪⎝⎭.当7,6AB BC ==,5AC =时,CD =____.【答案】1【分析】根据公式求得BD ,根据CD BC BD =-,即可求解.【详解】解:∵7,6AB BC ==,5AC =,∴2212AB AC BD BC BC ⎛⎫-=+ ⎪⎝⎭149256526-⎛⎫=+= ⎪⎝⎭∴651CD BC BD =-=-=,故答案为:1.【点睛】本题考查了三角形的高的定义,正确的使用公式是解题的关键.14.(2023·浙江·统考中考真题)如图,在ABC 中,AC 的垂直平分线交BC 于点D ,交AC 于点E ,B ADB ∠=∠.若4AB =,则DC 的长是__________.【答案】4【分析】由B ADB ∠=∠可得4AD AB ==,由DE 是AC 的垂直平分线可得AD DC =,从而可得4DC AB ==.【详解】解:∵B ADB ∠=∠,∴4AD AB ==,∵DE 是AC 的垂直平分线,∴AD DC =,∴4DC AB ==.故答案为:4.【点睛】本题主要考查了线段垂直平分线的性质以及等角对等边等知识,熟练掌握相关知识是解答本题的关键.15.(2023·湖北随州·统考中考真题)如图,在Rt ABC △中,9086C AC BC ∠=︒==,,,D 为AC 上一点,若BD 是ABC ∠的角平分线,则AD =___________.【答案】3【分析】首先证明CD DP =,6BC BP ==,设CD PD x ==,在Rt ADP 中,利用勾股定理构建方程即可解决问题.【详解】解:如图,过点D 作AB 的垂线,垂足为P ,在Rt ABC △中,∵86AC BC ==,,∴22228610AB AC BC =+=+=,∵BD 是ABC ∠的角平分线,∴CBD PBD ∠=∠,∵90C BPD BD BD ∠=∠=︒=,,∴()AAS BDC BDP ≌,∴6BC BP ==,CD PD =,设CD PD x ==,在Rt ADP 中,∵4PA AB BP =-=,8AD x =-,∴2224(8)x x +=-,∴3x =,∴3AD =.故答案为:3.【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.(2023·湖北十堰·统考中考真题)一副三角板按如图所示放置,点A 在DE 上,点F 在BC 上,若35EAB ∠=︒,则DFC ∠=___________________︒.【答案】100︒【分析】根据直角三角板的性质,得到45DFE ∠=︒,90E B ∠=∠=︒,结合12∠=∠得到35EAB BFE ∠=∠=︒,利用平角的定义计算即可.【详解】解:如图,根据直角三角板的性质,得到45DFE ∠=︒,90E B ∠=∠=︒,∵12∠=∠,∴35EAB BFE ∠=∠=︒,1803545100DFC ∠=︒-︒-︒=︒.故答案为:100︒.【点睛】本题考查了三角板的性质,直角三角形的性质,平角的定义,熟练掌握三角板的性质,直角三角形的性质是解题的关键.17.(2023·浙江杭州·统考中考真题)如图,点,D E 分别在ABC 的边,AB AC 上,且DE BC ∥,点F 在线段BC 的延长线上.若28ADE ∠=︒,118ACF ︒∠=,则A ∠=_________.【答案】90︒【分析】首先根据平行线的性质得到28B ADE ∠=∠=︒,然后根据三角形外角的性质求解即可.【详解】∵DE BC ∥,28ADE ∠=︒,∴28B ADE ∠=∠=︒,∵118ACF ︒∠=,∴1182890A ACF B ∠=∠-∠=︒-︒=︒.故答案为:90︒.【点睛】此题考查了平行线的性质和三角形外角的性质,解题的关键是熟练掌握以上知识点.18.(2023·湖北荆州·统考中考真题)如图,CD 为Rt ABC △斜边AB 上的中线,E 为AC 的中点.若8AC =,5CD =,则DE =___________.【答案】3【分析】首先根据直角三角形斜边中线的性质得出AB ,然后利用勾股定理即可得出BC ,最后利用三角形中位线定理即可求解.【详解】解:∵在Rt ABC △中,CD 为Rt ABC △斜边AB 上的中线,5CD =,∴210AB CD ==,∴22221086BC AB AC =-=-=,∵E 为AC 的中点,∴132DE BC ==故答案为:3.【点睛】本题主要考查直角三角形的性质,三角形中位线定理,掌握直角三角形中斜边上的中线等于斜边的一半是解题的关键.19.(2023·湖南·统考中考真题)如图,在Rt ABC △中,90C ∠=︒,按以下步骤作图:①以点A 为圆心,以小于AC 长为半径作弧,分别交,AC AB 于点M ,N ;②分别以M ,N 为圆心,以大于12MN 的长为半径作弧,在BAC ∠内两弧交于点O ;③作射线AO ,交BC 于点D .若点D 到AB 的距离为1,则CD 的长为__________.【答案】1【分析】根据作图可得AD 为CAB ∠的角平分线,根据角平分线的性质即可求解.【详解】解:如图所示,过点D 作DE AB ⊥于点E ,依题意1DE =,根据作图可知AD 为CAB ∠的角平分线,∵,DC AC DE AB⊥⊥∴1CD DE ==,故答案为:1.【答案】4975【分析】AM BD ⊥于点M ,AN DE ⊥根据3tan 4AM B BM ==得出16BM a =,继而求得3tan tan 4GP C B CP ===,求得3GP a =2216EN AE AN a =-=,故EG EN =【详解】由折叠的性质可知,DA 是到DM DN =,设DM DN x ==,则DG ()()()2221239a x a x a -+=+,化简得17217527AGEADG EG AN EG a DG DG AN S a S ⋅====⋅三角形三角形作AM BD ⊥于点M ,AN DE ⊥于点N ,则AM AN =,过点G 作GP BC ⊥于点P ,∵AM BD ⊥于点M ,∴3tan 4AM B BM ==,设12AM a =,则16BM a =,2220AB AM BM a =+=,又∵AB AC =,AM BD ⊥,∴12CM AM a ==,20AB AC a ==,B C ∠=∠,∵:3:1AG CG =,即14CG AC =,∴5CG a =,15AG a =,在Rt PCG △中,5CG a =,3tan tan 4GP C B CP ===,设3GP m =,则224,5CP m CG GP CP m==+=∴m a=∴3,4GP a CP a ==,∵15AG a =,12AM AN a ==,AN DE ⊥,∴229GN AG AN a =-=,∵20AB AE a ==,12AN a =,AN DE⊥∴2216EN AE AN a =-=,∴7EG EN GN a =-=,∵AD AD =,AM AN =,AM BD ⊥,AN DE ⊥,∴()HL ADM ADN △≌△,∴DM DN =,设DM DN x ==,则9DG DN GN x a =+=+,16412DP CM CP DM a a x a x =--=--=-,在Rt PDG △中,222DP GP DG +=,即()()()2221239a x a x a -+=+,三、解答题21.(2023·江苏苏州·统考中考真题)如图,在ABC 中,,AB AC AD =为ABC 的角平分线.以点A 圆心,AD 长为半径画弧,与,AB AC 分别交于点,E F ,连接,DE DF .(1)求证:ADE ADF V V ≌;(2)若80BAC ∠=︒,求BDE ∠的度数.【答案】(1)见解析(2)20BDE ∠=︒【分析】(1)根据角平分线的定义得出BAD CAD ∠=∠,由作图可得AE AF =,即可证明ADE ADF V V ≌;(2)根据角平分线的定义得出40EAD ∠=︒,由作图得出AE AD =,则根据三角形内角和定理以及等腰三角形的性质得出70ADE ∠=︒,AD BC ⊥,进而即可求解.【详解】(1)证明:∵AD 为ABC 的角平分线,∴BAD CAD ∠=∠,由作图可得AE AF =,在ADE V 和ADF △中,BAD CAD AD AD ⎪∠=∠⎨⎪=⎩,∴ADE ADF V V ≌()SAS ;(2)∵80BAC ∠=︒,AD 为ABC 的角平分线,∴40EAD ∠=︒由作图可得AE AD =,∴70ADE ∠=︒,∵AB AC =,AD 为ABC 的角平分线,∴AD BC ⊥,∴20BDE ∠=︒【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,角平分线的定义,熟练掌握等腰三角形的性质与判定是解题的关键.22.(2023·江西·统考中考真题)(1)计算:038tan 453+︒-(2)如图,AB AD =,AC 平分BAD ∠.求证:ABC ADC △△≌.【答案】(1)2(2)见解析【分析】(1)先计算立方根,特殊角三角函数值和零指数幂,再计算加减法即可;(2)先由角平分线的定义得到BAC DAC ∠=∠,再利用SAS 证明ABC ADC △△≌即可.【详解】解:(1)原式211=+-2=;(2)∵AC 平分BAD ∠,∴BAC DAC ∠=∠,在ABC 和ADC △中,BAC DAC AC AC ⎪∠=∠⎨⎪=⎩,∴()SAS ABC ADC △△≌.【点睛】本题主要考查了实数的运算,零指数幂,特殊角三角函数值,全等三角形的判定,角平分线的定义等等,灵活运用所学知识是解题的关键.23.(2023·云南·统考中考真题)如图,C 是BD 的中点,,AB ED AC EC ==.求证:ABC EDC △≌△.【答案】见解析【分析】根据C 是BD 的中点,得到BC CD =,再利用SSS 证明两个三角形全等.【详解】证明: C 是BD 的中点,BC CD ∴=,在ABC 和EDC △中,BC CD AB ED AC EC =⎧⎪=⎨⎪=⎩,()ABC EDC SSS ∴ ≌【点睛】本题考查了线段中点,三角形全等的判定,其中对三角形判定条件的确定是解决本题的关键.24.(2023·四川宜宾·统考中考真题)已知:如图,AB DE ∥,AB DE =,AF DC =.求证:B E ∠=∠.【答案】见解析【分析】根据平行线的性质得出A D ∠=∠,然后证明AC DF =,证明()SAS ABC DEF ≌△△,根据全等三角形的性质即可得证.【详解】证明:∵AB DE ∥,∴A D ∠=∠,∵AF DC =,∴AF CF DC CF+=+即AC DF=在ABC 与DEF 中AC DF A D AB DE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABC DEF ≌△△,∴B E ∠=∠.【点睛】本题考查了全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.25.(2023·福建·统考中考真题)如图,,,OA OC OB OD AOD COB ==∠=∠.求证:AB CD =.【答案】见解析【分析】根据已知条件得出AOB COD ∠=∠,进而证明△≌△AOB COD ,根据全等三角形的性质即可得证.【详解】证明:AOD COB ∠=∠ ,,AOD BOD COB BOD ∴∠-∠=∠-∠即AOB COD ∠=∠.在AOB 和COD △中,,,,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩AOB COD∴ ≌AB CD ∴=.【点睛】本小题考查等式的基本性质、全等三角形的判定与性质等基础知识,考查几何直观、推理能力等,掌握全等三角形的性质与判定是解题的关键.26.(2023·全国·统考中考真题)如图,点C 在线段BD 上,在ABC 和DEC 中,A D AB DE B E ∠=∠=∠=∠,,.求证:AC DC =.【答案】证明见解析【分析】直接利用ASA 证明ABC DEC ≌△△,再根据全等三角形的性质即可证明.【详解】解:在ABC 和DEC 中,A D AB DE B E ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASA ABC DEC ≌ ∴AC DC =.【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.27.(2023·四川乐山·统考中考真题)如图,AB 、CD 相交于点O ,AO=BO ,AC ∥DB .求证:AC=BD .【答案】见解析【分析】要证明AC=BD ,只要证明△AOC ≌△BOD ,根据AC//DB 可得∠A=∠B ,∠C=∠D ,又知AO=BO ,则可得到△AOC ≌△BOD ,从而求得结论.【详解】(方法一)∵AC//DB ,∴∠A=∠B ,∠C=∠D .在△AOC 与△BOD 中∵∠A=∠B ,∠C=∠D ,AO=BO ,∴△AOC ≌△BOD .∴AC=BD .(方法二)∵AC//DB ,∴∠A=∠B .在△AOC 与△BOD 中,∵A B AO BO AOC BOD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOC ≌△BOD .∴AC=BD .28.(2023·山东临沂·统考中考真题)如图,90,,,A AB AC BD AB BC AB BD ∠=︒=⊥=+.(1)写出AB 与BD 的数量关系(2)延长BC 到E ,使CE BC =,延长DC 到F ,使CF DC =,连接EF .求证:EF AB ⊥.(3)在(2)的条件下,作ACE ∠的平分线,交AF 于点H ,求证:AH FH =.【答案】(1)()21AB BD -=(2)见解析(3)见解析【分析】(1)勾股定理求得2BC AB =,结合已知条件即可求解;(2)根据题意画出图形,证明CBD CEF ≌,得出=45E DBC ∠=∠︒,则EF BD ∥,即可得证;(3)延长,BA EF 交于点M ,延长CH 交ME 于点G ,根据角平分线以及平行线的性质证明EG EC =,进而证明()AAS AHC FHG ≌,即可得证.【详解】(1)解:∵90,A AB AC∠=︒=∴2BC AB =,∵BC AB BD=+∴2AB AB BD =+∴90,A AB AC∠=︒=∴=45ABC ∠︒,∵BD AB ⊥,∴45DBC ∠=︒∵CE BC =,12∠=∠,CF DC=∴CBD CEF≌∴=45E DBC ∠=∠︒∴EF BD∥∴AB EF⊥(3)证明:如图所示,延长,BA EF 交于点∵EF AB ⊥,AC AB ⊥,∴ME AC ∥,∴CGE ACG∠=∠∵CH 是ACE ∠的角平分线,∴ACG ECG ∠=∠,∴CGE ECG∠=∠∴EG EC=∵CBD CEF ≌,∴EF BD =,CE CB =,∴EG CB =,又∵BC AB BD =+,∴EG AB BD AC EF =+=+,即FG EF AC EF +=+,∴AC EG =,又AC FG ∥,则HAG HFG ∠=∠,在,AHC FHG 中,HAG HFG AHG FHG AC FG ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS AHC FHG ≌,∴AH HF=【点睛】本题考查了全等三角形的与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.29.(2023·山东聊城·统考中考真题)如图,在四边形ABCD 中,点E 是边BC 上一点,且BE CD =,B AED C ∠=∠=∠.【点睛】本题考查了三角形内角和定理,全等三角形的判定和性质,等腰三角形的性质,含30︒直角三角形的性质以及勾股定理等知识,正确寻找证明三角形全等的条件是解题的关键.30.(2023·甘肃兰州·统考中考真题)综合与实践问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在OA 和OB 上分别取点C 和D ,使得OC OD =,连接CD ,以CD 为边作等边三角形CDE ,则OE 就是AOB ∠的平分线.请写出OE 平分AOB ∠的依据:____________;类比迁移:(2)小明根据以上信息研究发现:CDE 不一定必须是等边三角形,只需CE DE =即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在AOB ∠的边OA ,OB 上分别取OM ON =,移动角尺,使角尺两边相同刻度分别与点M ,N 重合,则过角尺顶点C 的射线OC 是AOB ∠的平分线,请说明此做法的理由;拓展实践:(3)小明将研究应用于实践.如图4,校园的两条小路AB 和AC ,汇聚形成了一个岔路口A ,现在学校要在两条小路之间安装一盏路灯E ,使得路灯照亮两条小路(两条小路一样亮),并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规..........在对应的示意图5中作出路灯E 的位置.(保留作图痕迹,不写作法)【答案】(1)SSS ;(2)证明见解析;(3)作图见解析;【分析】(1)先证明()SSS OCE ODE ≌,可得AOE BOE ∠=∠,从而可得答案;(2)先证明()SSS OCM OCN ≌,可得AOC BOC ∠=∠,可得OC 是AOB ∠的角平分线;(3)先作BAC ∠的角平分线,再在角平分线上截取AE AD =即可.【详解】解:(1)∵OC OD =,CE DE =,DE DE =,∴()SSS OCE ODE ≌,∴AOE BOE ∠=∠,∴OE 是AOB ∠的角平分线;故答案为:SSS(2)∵OM ON =,CM CN =,OC OC =,∴()SSS OCM OCN ≌,∴AOC BOC ∠=∠,∴OC 是AOB ∠的角平分线;(3)如图,点E 即为所求作的点;.【点睛】本题考查的是全等三角形的判定与性质,角平分线的定义与角平分线的性质,作已知角的角平分线,理解题意,熟练的作角的平分线是解本题的关键.。
全等三角形专题复习(含练习讲评)

一、全等三角形注: ① 判定两个三角形全等必须有一组边对应相等;② 全等三角形面积相等. 2. 证题的思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS例1: 如图, 在△ABE 中, AB =AE,AD =AC,∠BAD =∠EAC, BC.DE 交于点O.求证: (1) △ABC ≌△AED ; (2) OB =OE .例2: 如图所示, 已知正方形ABCD 的边BC.CD 上分别有点E 、点F, 且BE +DF =EF, 试求∠EAF 的度数.AD F例3.在△ABC中, ∠ACB=90°,AC=BC, AE是BC的中线, 过点C作CF⊥AE于F,过B作BD⊥CB 交CF的延长线于点D。
(1)求证:AE=CD, (2)若BD=5㎝,求AC的长。
例4:如图, △ABE和△ADC是△ABC分别沿着AB.AC边翻折180°形成的, 若∠1: ∠2: ∠3=28: 5: 3, 则∠a的度数为例5: 如图: 在△ABC中, ∠ACB=90°, AC=BC, D是AB上一点, AE⊥CD于E, BF⊥CD交CD的延长线于F.求证: AE=EF+BF。
练习:1.已知: 如图5—129, △ABC 的∠B.∠C 的平分线相交于点D, 过D 作MN ∥BC 交AB.AC 分别于点M 、N, 求证:BM +CN =MN2.如图(13):已知AB ⊥BD, ED ⊥BD, AB=CD , BC=DE ,请你判断AC 垂直于CE 吗? 并说明理由。
3.如图(14),已知AB=DC , DE=BF, ∠B=∠D , 试说明(1)DE ∥BF (2)AE=CFFDCABE(14)4.如图: 在△ABC中, ∠BAC=90°,∠ABD= ∠ABC, DF⊥BC, 垂足为F, AF交BD于E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在△PBD中,PB=4,PD=3,BD=PC=5,
∵32+42=52,即PD2+PB2=BD2,
∴△PBD为直角三角形,∠BPD=90 ,
∵△ADB≌△APC,
∴S△ADB=S△APC,
∴S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD= ×32+ ×3×4= .
【答案】
【解析】
过点Q作AD的延长线的垂线于点F.
因为△ABC是等边三角形,所以∠A=∠ACB=60°.
故答案为: .
【点睛】
本题考查了等边三角形的性质与判定,解题的关键是熟知旋转的性质作出辅助线进行求解.
2.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD,当△AOD是等腰三角形时,求α的角度为______
【答案】110°、125°、140°
∴α=140°;
所以当α为110°、125°、140°时,三角形AOD是等腰三角形,
故答案为:110°、125°、140°.
【点睛】
本题是对等边三角形的考查,熟练掌握等边三角形的性质定理及分类讨论是解决本题的关键.
3.如图,点 是 内任意一点, =5 cm,点 和点 分别是射线 和射线 上的动点, 的最小值是5 cm,则 的度数是__________.
【详解】
将线段AP以点A为旋转中心顺时针旋转60 得到线段AD,连接PD
∴AD=AP,∠DAP=60 ,
又∵△ABC为等边三角形,
∴∠BAC=60 ,AB=AC,
∴∠DAB+∠BAP=∠PAC+∠BAP,
∴∠DAB=∠PAC,
又AB=AC,AD=AP
∴△ADB≌△APC
∵DA=PA,∠DAP=60 ,
∴b﹣d=10°,
∴(60°﹣a)﹣d=10°,
∴a+d=50°,
即∠DAO=50°,
分三种情况讨论:
①AO=AD,则∠AOD=∠ADO,
∴190°﹣α=α﹣60°,
∴α=125°;
②OA=OD,则∠OAD=∠ADO,
∴α﹣60°=50°,
∴α=110°;
③OD=AD,则∠OAD=∠AOD,
∴190°﹣α=50°,
【答案】30°
【解析】
试题解析:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
【答案】32
【解析】
【分析】
根据底边三角形的性质求出 以及平行线的性质得出 ,以及 ,得出 , , 进而得出答案.
【详解】
解: △ 是等边三角形,
, ,
,
,
,
又 ,
,
,
,
,
△ 、△ 是等边三角形,
, ,
,
, ,
, ,
, ,
,
同理可得: ,
△ 的边长为 ,
△ 的边长为 .
故答案为: .
【点睛】
本题考查了等边三角形的性质以及30°直角三角形的性质,根据已知得出 , , 进而发现规律是解题关键.
【解析】
【分析】
先求出∠DAO=50°,分三种情况讨论:①AO=AD,则∠AOD=∠ADO,②OA=OD,则∠OAD=∠ADO,③OD=AD,则∠OAD=∠AOD,分别求出α的角度即可.
【详解】
解:∵设∠CBO=∠CAD=a,∠ABO=b,∠BAO=c,∠CAO=d,
则a+b=60°,b+c=180°﹣110°=70°,c+d=60°,
5.如图,∠AOB=45°,点M、点C在射线OA上,点P、点D在射线OB上,且OD=3 ,则CP+PM+DM的最小值是_____.
【答案】 .
【解析】
【分析】
如图,作点C关于OB的对称点C′,作点D关于OA的对称点D′,连接OC′,PC′,D′M,OD′,C′D′,根据轴对称的性质得到OC′=OC=2,OD′=OD=3 ,CP=C′P,DM=D′M,∠C′OD=′COD=∠COD′=45°,于是得到CP+PM+MD=C′+PM+D′M≥C′D′,当仅当C′,P,M,D′三点共线时,CP+PM+MD最小为C′D′,作C′T⊥D′O于点T,于是得到结论.
【详解】
解:如图,作点C关于OB的对称点C′,作点D关于OA的对称点D′,连接OC′,PC′,D′M,OD′,C′D′,
则OC′=OC=2,OD′=OD=3 ,CP=C′P,DM=D′M,∠C′OD=′COD=∠COD′=45°,
∴CP+PM+MD=C′+PM+D′M≥C′D′,
当仅当C′,P,M,D′三点共线时,CP+PM+MD最小为C′D′,
作C′T⊥D′O于点T,
则C′T=OT= ,
∴D′T=4 ,
∴C′D′= ,
∴CP+PM+DM的最小值是 .
故答案为: .
【点睛】
本题考查了最短路径问题,掌握作轴对称点是解题的关键.
6.如图,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当AP=CQ时,PQ交AC于D,则DE的长为______.
全等三角形专题练习(解析版)
一、八年级数学轴对称三角形填空题(难)
1.如图,在等边 中取点 使得 , , 的长分别为3,4,5,则 _________.
【答案】
【解析】
【Hale Waihona Puke 析】把线段AP以点A为旋转中心顺时针旋转60 得到线段AD,由旋转的性质、等边三角形的性质以及全等三角形的判定定理SAS证得△ADB≌△APC,连接PD,根据旋转的性质知△APD是等边三角形,利用勾股定理的逆定理可得△PBD为直角三角形,∠BPD=90 ,由△ADB≌△APC得S△ADB=S△APC,则有S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD,根据等边三角形的面积为边长平方的 倍和直角三角形的面积公式即可得到S△ADP+S△BPD= ×32+ ×3×4= .
∴OC=OP=OD,∠AOB= ∠COD,
∵PN+PM+MN的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
4.如图,己知 ,点 , , ,…在射线ON上,点 , , ,…在射线OM上, , , ,…均为等边三角形,若 ,则 的边长为________.
