统计学作业
统计学练习题(含作业及非官方答案)

统计学练习题(含作业及⾮官⽅答案)⼀、单项选择题1.根据样本计算的⽤于推断总体特征的概括性度量值称作(参数)A.参数B.总体C.样本D.统计量2.只能归于某⼀类别的⾮数字型数据称为(分类数据)A.分类数据B.顺序数据C.数值型数据D.数值型变量3.只能归于某⼀有序类别的⾮数字型数据称为(顺序数据)A.分类数据B.顺序数据C.数值型数据D.数值型变量4.⽤来描述样本特征的概括性数字度量称为(统计量)A.参数B.统计量C.变量D.变量值5.为了调查某校学⽣的购书费⽤⽀出,从全校抽取4个班级的学⽣进⾏调查,这种调查⽅法是(整群抽样)A.简单随机抽样B.系统抽样C.分层抽样D.整群抽样6.为了调查某校学⽣的购书费⽤⽀出,从男⽣中抽取60名学⽣调查,从⼥⽣中抽取40名学⽣进⾏调查,这种调查⽅法是(分层抽样)A.简单随机抽样B.整群抽样C.系统抽样D.分层抽样7.经验法则表明,当⼀组数据对称分布时,在平均数加减1个标准差的范围之内⼤约有(68%)A.68%B.95%C.99%D.100%8.经验法则表明,当⼀组数据对称分布时,在平均数加减2个标准差的范围内⼤约有(95%)A.68%B.95%C.99%D.100%9.离散系数的主要⽤途是(⽐较多组数据的离散程度)A.反映⼀组数据的离散程度B.反映⼀组数据的平均⽔平C.⽐较多组数据的离散程度D.⽐较多组数据的平均⽔平10.⽐较两组数据的离散程度最适合的统计量是(离散系数)A.极差B.平均差C.标准差D.离散系数11.峰态通常是与标准正态分布相⽐较⽽⾔的,如果⼀组数据服从标准正态分布,则峰态系数的值(等于0)A.等于0B.⼤于0C.⼩于0D.等于112.如果峰态系数k>0,表明该组数据是(尖峰分布)A.尖峰分布B.扁平分布C.左偏分布D.右偏分布13.某居民⼩区准备采取⼀项新的物业管理措施,为此,随机抽取了100户居民进⾏调查,其中表⽰赞成的有69户,表⽰中⽴的有22户,表⽰反对的有9户,则该组数据的中位数是(赞成)A.赞成B.69C.中⽴D.2214.某班共有25名学⽣,期未统计学课程的考试分数分别为68、73、66、76、86、74、61、89、65、90、69、67、76、62、81、63、68、81、70、73、60、87、75、64、56,那么该班考试分数的下四分位数和上四分位数分别是(64.5和78.5)A.64.5和78.5B.67.5和71.5C.64.5和71.5D.64.5和67.515.某⾏业中随机抽取10家企业,第⼀季度的利润额(单位:万元)分别是:72、63.1、54.7、54.3、29、26.9、25、23.9、23、20,该组数据的中位数为(27.95)A.28.46B.30.20C.27.95D.28.1216.⼀组数据的离散系数为0.4,平均数为20,则标准差为(8)A.80B.0.02C.4D.8 ⽅差:1)(122--=∑=nxxsnii;离散系数:xsvs=17.根据中⼼极限定理可知,当样本容量充分⼤时,样本均值的抽样分布服从正态分布,其分布的均值为(µ)A.µB.XC.2σ D.n2σ18. 根据中⼼极限定理可知,当样本容量充分⼤时,样本均值的抽样分布服从正态分布,其分布的⽅差为(n2σ)A.µB.XC.2σ D.n2σ19.假设总体服从均匀分布,从此总体中抽取容量为36的样本,则样本均值的抽样分布(近似正态分布)A.服从⾮正态分布B.近似正态分布C.服从均匀分布D.服从2χ分布20.总体均值为50,标准差为8,从此总体中随机抽取容量为64的样本,则样本均值的抽样分布的均值和标准误差分别为(50,1)A.50,8B.50,1C.50,4D.8,821.当正态总体的⽅差未知时,在⼤样本条件下,估计总体均值使⽤的分布是(正态分布)A.正态分布B.t分布C.2χ分布 D.F分布22.当正态总体的⽅差未知时,在⼩样本条件下,估计总体均值使⽤的分布是(t分布)A.正态分布B.t分布C.2χ分布 D.F分布23.根据两个匹配的⼩样本估计两个总体均值之差时,使⽤的分布是(t分布)A.正态分布B.t分布C.2χ分布 D.F分布24.估计两个总体⽅差⽐的置信区间时,使⽤的分布是(F分布)A.正态分布B.t分布C.2χ分布 D.F分布25.⼀种零件的标准长度5cm,要检验某天⽣产的零件是否符合标准要求,建⽴的原假设和备择假设应为(H0:µ=5,H1: µ≠5)A.H0:µ=5,H1: µ≠5B.H0:µ≠5,H1: µ=5C.H0:µ≤5,H1: µ≥5D.H0:µ≥5,H1: µ≤526.⼀项研究表明,中学⽣中吸烟的⽐例⾼达30%,为检验这⼀说法是否属实,建⽴的原假设和备择假设应为(H0:π=30%,H1:π≠30%)A.H0:µ=30%,H1: µ≠30%B.H0:π=30%,H1:π≠30%C.H0:π≥30%,H1:π≤30%D. H0:π≤30%,H1:π≥30%27.列联分析是利⽤列联表来研究(两个分类变量的关系)A.两个分类变量的关系B.两个数值型变量的关系C.⼀个分类变量和⼀个数值型变量的关系D.两个数值型变量的分布28.设R 为列联表的⾏数,C 为列联表的列数,则2χ分布的⾃由度为((R-1)×(C-1))A.RB.CC.R×CD.(R-1)×(C-1) 29.⽅差分析的主要⽬的是判断(分类型⾃变量对数值型因变量的影响是否显著) A.各总体是否存在⽅差B.各样本数据之间是否有显著差异C.分类型⾃变量对数值型因变量的影响是否显著D.分类型因变量对数值型⾃变量的影响是否显著30.组间误差是衡量不同⽔平下各样本数据之间的误差,它(既包括随机误差,⼜包括系统误差)A.只包括随机误差B.只包括系统误差C.既包括随机误差,⼜包括系统误差D.有时包括随机误差,有时包括系统误差 31.组内误差是衡量某⼀⽔平下样本数据之间的误差,它(只包括随机误差)A.只包括随机误差B.只包括系统误差C.既包括随机误差,⼜包括系统误差D.有时包括随机误差,有时包括系统误差 32.单因素⽅差分析是指只涉及(⼀个分类型⾃变量)A.⼀个分类型⾃变量B.⼀个数值型⾃变量C.两个分类型⾃变量D.两个数值型因变量33.双因素⽅差分析涉及(两个分类型⾃变量)A.两个分类型⾃变量B.两个数值型⾃变量C.两个分类型因变量D.两个数值型因变量34.在⽅差分析中,数据的误差⽤平⽅和来表⽰的,其中反映⼀个样本中各观测值误差⼤⼩的平⽅和称为(组内平⽅和) A.组间平⽅和 B.组内平⽅和 C.总平⽅和 D.⽔平项平⽅和 35.在⽅差分析中,数据的误差⽤平⽅和来表⽰的,其中反映各个样本均值之间误差⼤⼩的平⽅和称为(组间平⽅和) A.误差项平⽅和 B.组内平⽅和 C.组间平⽅和 D.总平⽅和 36.如果⼀个变量的取值完全依赖于另⼀个变量,各观测点落在⼀条直线上,称为两个变量之间为(完全相关关系)A.完全相关关系B.正线性相关关系C.⾮线性相关关系D.负线性相关关系37.如果相关系数r =0,则表明两个变量之间(不存在线性相关关系)A.相关程度很低B.不存在任何关系C.不存在线性相关关系D.存在⾮线性相关关系 38.在⼀元线性回归⽅程中,回归系数i β的实际意义是(当x变量1个单位时,y 增加的总数量)A.当x=0时,y 的平均变动数量B.当x 变动1个单位时,y 的平均变动数量C.当x 变动1个单位时,y 增加的总数量D.当y 变动1个单位时,x 的平均变动数量39.对不同年份的产品成本拟合的直线⽅程为x y 75.1280-=,回归系数75.11-=β表⽰(时间每增加1个单位,产品成本平均下降1.75个单位)A.时间每增加1个单位,产品成本平均增加1.75个单位B.时间每增加1个单位,产品成本平均下降1.75个单位C.产品成本每变动1个单位,平均需要1.75年时间D.时间每减少1个单位,产品成本平均增加1.75个单位 40.说明回归⽅程拟合优度的统计量是(判定系数)A.相关系数B.回归系数C.判定系数D.估计标准误差 41.各实际观测值(yi )与回归值(i y ?)的离差平⽅和称为(残差平⽅和)A.总变差平⽅和B.残差平⽅和C.回归平⽅和D.判定系数 42.回归平⽅和占总平⽅和的⽐例称为(判定系数)A.相关系数B.回归系数C.判定系数D.估计标准误差 43.若两个变量存在负线性相关关系,则建⽴的⼀元线性回归⽅程的判定系数R2的取值范围是([0,1])A.[0,1]B.[-1,0]C.[-1,1]D.⼩于0的任意数 44.若变量x 与y 之间的相关系数r =0,则下列结论中正确的是(判定系数R2=0)A.判定系数R2=1B.判定系数R2=0C.回归系数1?1=βD.估计标准误差se =045.在多元线性回归⽅程k k i x x y βββ110+++= 中,回归系数i β?表⽰(其他变量不变的条件下,⾃变量xi 变动1个单位时,因变量y 的平均变动额为i β?)A.⾃变量xi 变动1个单位时,因变量y 的平均变动额为i β?B.其他变量不变的条件下,⾃变量xi 变动1个单位时,因变量y 的平均变动额为i β?C.其他变量不变的条件下,⾃变量xi 变动1个单位时,因变量y 的变动总额为i β?D.因变量y 变动1个单位时,因变量xi 的变动总额为i β?46.设在多元线性回归⽅程k k i x x y βββ110+++= 中,若⾃变量xi 的回归系数i β?的取值接近0,这表明(⾃变量xi 对因变量y 的影响不显著)A.因变量y 对⾃变量xi 的影响不显著B.因变量y 对⾃变量xi 的影响显著C.⾃变量xi 对因变量y 的影响不显著D.⾃变量xi 对因变量y 的影响显著47.指数平滑法适合于预测(平稳序列)A.平稳序列B.⾮平稳序列C.有趋势成分的序列D.有季节成分的序列48.移动平均法适合于预测(平稳序列)A.平稳序列B.⾮平稳序列C.有趋势成分的序列D.有季节成分的序列49.⽤最⼩⼆乘法拟合直线趋势⽅程为t b b Y 10?+=,若1b 为负数,表明该现象随着时间的推移呈现(下降趋势)A.上升趋势B.下降趋势C.⽔平趋势D.随机波动 50.对某⼀时间序列拟合的直线趋势⽅程为x b b Y t 10?+=,如果b1的值等于0,则表明该序列(没有趋势)A.没有趋势B.有上升趋势C.有下降趋势 D ,有⾮线性趋势⼆、简答题1.简要区别描述统计与推断统计?答:描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等⽅法。
统计作业指导书

统计作业指导书引言概述:统计学是一门研究数据采集、分析和解释的学科,它在各个领域都有广泛的应用。
在学习统计学的过程中,作业是不可或者缺的一部份。
本文将为您提供一份统计作业指导书,匡助您更好地完成统计学作业。
一、数据采集1.1 选择适当的数据源:在开始采集数据之前,确定数据的来源是非常重要的。
可以选择公开数据集、实地调查或者自己设计实验等方式来获取数据。
1.2 数据采集方法:根据研究目的和数据类型,选择合适的数据采集方法。
例如,可以使用问卷调查、观察、实验等方法来采集数据。
1.3 数据质量控制:在数据采集过程中,要注意数据的准确性和完整性。
可以通过重复测量、数据清洗和筛选等方法来保证数据的质量。
二、数据分析2.1 数据整理和描述统计:在进行数据分析之前,首先要对数据进行整理和描述统计。
包括计算数据的均值、中位数、标准差等统计指标,绘制直方图、散点图等图表来展示数据的分布情况。
2.2 探索性数据分析:通过图表和统计分析方法,对数据进行进一步的探索。
可以使用相关分析、回归分析、方差分析等方法来探索变量之间的关系。
2.3 假设检验和判断统计:根据研究目的,进行假设检验和判断统计。
可以使用t检验、方差分析、卡方检验等方法来验证研究假设,并对总体参数进行判断。
三、数据解释和报告3.1 结果解释:在数据分析完成后,要对结果进行解释。
解释应该清晰、准确地表达出数据的含义和结果的统计学意义。
3.2 结果展示:将数据分析的结果以图表、表格等形式进行展示,使读者能够更直观地理解数据和结果。
3.3 结果报告:根据具体要求,撰写数据分析的报告。
报告应包括研究目的、数据采集和分析方法、结果和结论等内容。
四、常见问题和解决方法4.1 数据异常值处理:在数据分析过程中,可能会遇到异常值的问题。
可以通过删除异常值、替换异常值或者使用鲁棒统计方法来处理异常值。
4.2 样本量不足问题:当样本量较小时,可能会影响结果的可靠性。
可以通过增加样本量、使用非参数统计方法或者进行摹拟分析来解决样本量不足的问题。
统计学作业

统计学作业
将抗生素注入人体会产生抗生素与血浆蛋白质结合现象,以致减少了药性,下表列出5种常用的抗生素注入牛的体内时,抗生素与血浆蛋白质结合的百分比
抗生素青霉素四环素链霉素红霉素氯霉素
1 29.6 27.3 5.8 21.6 29.2
2 24.
3 32.6 6.2 17.
4 32.8
3 28.5 30.8 11.0 18.3 25.0
4 32.0 34.8 8.3 19.0 24.2
试在显著性水平a=0.05下检验这些百分比的均值有无显著性差异。
解:以u1,u2,u3,u4,u5依次表示青霉素,四环素,链霉素,红霉素,氯霉素与血浆蛋白质结合的百分比均值,本题需假设检验
Ho:u1=u2=u3=u4=u5,
H1:u1,u2,u3,u4,u5不全相等。
折线散点图:
SUMMARY
组观测数求和平均方差
青霉素 4 114.4 28.6 10.35333
四环素 4 125.5 31.375 10.05583
链霉素 4 31.3 7.825 5.6825
红霉素 4 76.3 19.075 3.2625
氯霉素 4 111.2 27.8 15.92
方差分析
差异源SS df MS F P-value F crit 组间1480.823 4 370.2058 40.88488 6.73978E-08 3.055568 组内135.8225 15 9.054833
总计1616.646 19
Fa(4,15)=3.06 <F=40.88488 所以接受H0,认为这些均值无显著性差异。
统计学作业整理

C. 某工业企业的一台设备确答案:[D ] 4. 要了解某市工业企业生产设备情况,此场合的总体单位是()A. 该市全部工业企业 B. 该市的所有企业 D. 工业企业的工人你的答案:[]正确答案:[C ] 5. A. 社会科学B. 自然科学实质性科学正确答案:[C ]多选题 1.职工人数 C. 劳动生产率正确答案:[A,D,]2.案:[A,B,C,] 5. 统计学发展历史上产生过较大影响的学派有:()A. 政治算术学派B. 社会统计学派C. 重商学派D. 数理统计学派你的答案:[] 正确答案:[A,B,D,] 判断题 1. 统计学是一门独立的社会科学。
你的答案:[] 正确答案:[F ] 2. 统计学是一门实质性科学。
你的答案:[] 正确答案:[F ] 3. 统计学是一门方法论科学。
你的答案:[] 正确答案:[T ] 4. 描述统计是用文字和图表对客观世界进行描述。
你的答案:[] 正确答案:[F ] 5. 对于有限总体不必应用推断统计方法。
你的答案:[] 正确答案:[F ] 统计资料的收集和整理单选题 1. 经国务院批准的周期性普查项目,其中每隔5年进行一次的是()A. 人口普查B. 经济普查C. 农业普查D. 人口普查和农业普查你的答案:[]正确答案:[B ] 2. 某家电生产企业为测试X型号产品的抗震力,采用()搜集相关数据资料A. 报告法B. 采访法C. 实验设计法D. 直接观察法你的答案:[]正确答案:[C ] 3. 划分全面调查与非全面调查的标志是()A. 资料是否齐全B. 调查单位是否全部C. 调查时间是否连续D. 调查项目是否齐全你的答案:[] 正确答案:[B ] 4. 在非全面调查中,最完善、最有科学根据的调查方法是()A. 重点调查B. 典型调查C. 抽样调查D. 周期性调查你的答案:[]正确答案:[C ] 5. 对家用电器的平均寿命进行调查,应该采用()A. 普查B. 重点调查C. 典型调查D. 抽样调查你的答案:[] 正确答案:[D ] 多选题 1. 在第五次全国人中普查中()A. 国籍是变异B. 全国人口数是统计指标C. 每个中国公民是调查单位D. 人的年龄是变量E. 全国男性人数是品质标志你的答案:[] 正确答案:[B,C,D,]2. 普查是()A. 专门组织的调查B. 经常调查C. 一次性调查D. 全面调查E. 可广泛采用的调查方法你的答案:[] 正确答案:[A,C,D,] 3. 对某城市居民家计调查,适宜采用()A. 全面调查B. 经常性调查C. 抽样调查D. 采访法E. 统计报表制度你的答案:[] 正确答案:[B,C,D,] 4. 我国统计调查方法改革的目标模式的内容包括()A. 以经常性的抽样调查为主体B. 以经常性的统计报表为主体C. 周期性重点调查为基础D. 周期性普查为基础E. 统计报表、重点调查为补充你的答案:[] 正确答案:[A,D,E,] 5. 频率是() A. 概率 B. 各组的次数 C. 非负数 D. 自然数E. 各组的次数占总体单位数的比重你的答案:[] 正确答案:[C,E,] 判断题 1. 组距扩大,频数就会增加。
统计学原理作业题二

又∵ F(t)=0.9545 ∴ t= 2
合格品量为:20000× (91.92%---98.08%)
即以0.9545的概率估计该批产品合格品量的在18384---19616件之间。
即91.92%--98.08%
第19页/共30页
4、一个电视节目主持人想了解观众对某个电视专题节目的喜欢情况,他选取了500个观众作样本,结果发现喜欢该节目的有175人。试以95%的概率估计观众喜欢这一专题节目的区间范围。若该节目主持人希望估计的极限误差不超过5%,问有多大把握程度?解得(1)
第2页/共30页
1、抽样调查的主要目的是( ) A)对调查单位作深入研究 B)用样本指标来推算总体指标 C)计算和控制抽样误差 D)广泛运用数学方法2、抽样调查所必须遵循的基本原则是( ) A)准确性原则 B)随机性原则 C)可靠性原则 D)灵活性原则
第6页/共30页
9、在价格不变的条件下,商品销售额与销售量之间存在( )。A)不完全的依存关系 B)不完全的随机关系 C)完全的随机关系 D)完全的依存关系 10、相关系数的取值范围是( )。 A) 0≤r≤1 B) –1<r<1 C) -1≤r≤1 D) –1≤r≤0
第11页/共30页
6、直线回归方程yc=a+bx中的b称为回归系数,回归系数的作用是( )。 A) 可确定两变量之间因果的数量关系 B) 可确定两变量的相关方向 C) 可确定两变量的实际值与估计值的变异程度 D) 可确定两变量相关的密切程度 E)可确定当自变量的增加一个单位时,因变量的平子管厂,产品质量检验是这样安排的,在一天中,每隔一小时抽取5分钟的产品进行检验,这是( )。 A) 简单随机抽样 B) 整群抽样 C) 等距抽样 D) 类型抽样8、现象之间的相关密切程度愈高,则相关系数愈接近于( )。 A) 0 B) 0.3 ~ 0.5 C) 0.8 ~ 0.9 D) ±1
统计学作业——精选推荐

作业一一、简述中心极限定理和大数定理。
答:中心极限定理:中心极限定理的具体内容是:如果从任何一个具有均值μ和方差σ2的总体(可以具有任何分布形式)中重复抽取容量为n 的随机样本,那么当n 变得很大时,样本均值X 的抽样分布接近正态,并具有均值μ和方差n2 。
大数定理:我们知道,概率论中用来阐明大量随机现象平均结果的稳定性的定理,是著名的大数定理。
其具体内容是:频率稳定于概率,平均值稳定于期望值。
二、试述正态分布的性质与特点。
——P109答:(1)正态曲线以x=μ呈钟型对称,均值=中位数=众数(2)在x=μ处,概率密度最大;当区间离μ越远,x 落在这个区间的概率越小。
(3)正态曲线的外形由σ值确定。
对于固定的σ值,不同均值μ的正态曲线的外形完全相同,差别只在于曲线在横轴方向上整体平移了一个位置 。
(4)对于固定的μ值,改变σ值,σ值越小,正态曲线越陡峭;σ值越大,正态曲线越低平。
(总之,正态分布曲线的位置是由μ决定的,而正态分布曲线的“高、矮、胖、瘦” 由σ决定的。
)(5)E(X)= μ D(X)= σ2三、简述统计量成为总体参数的合理估计的三个标准——P143答:估计量如果具有无偏性、一致性和有效性这三个要求或标准,就可以认为这种统计量是总体参数的合理估计或最佳估计。
如下:1、无偏性。
如果统计量的抽样分布的均值恰好等于被估计的参数之值,那么这一估计便可以认为是无偏估计。
换句话说,从最终的结果来看,估计量的期望值就是参数本身。
2、一致性。
虽然随机样本和总体之间存在一定的误差,但当样本容量逐渐增加时,统计量起来越接近总体参数,满足这种情况,我们就说该统计量对总体参数是一个一致的估计量。
3、有效性。
估计量的有效性指统计量的抽样分布集中在真实参数周围的程度。
如果估计是无偏的,就可以用估计量的标准差来量度这种集中程度。
标准差越小,估计量的有效性越高。
然而效率总是相对的,没有一种估计量完全有效,完全有效意味没有丝毫抽样误差。
统计学作业
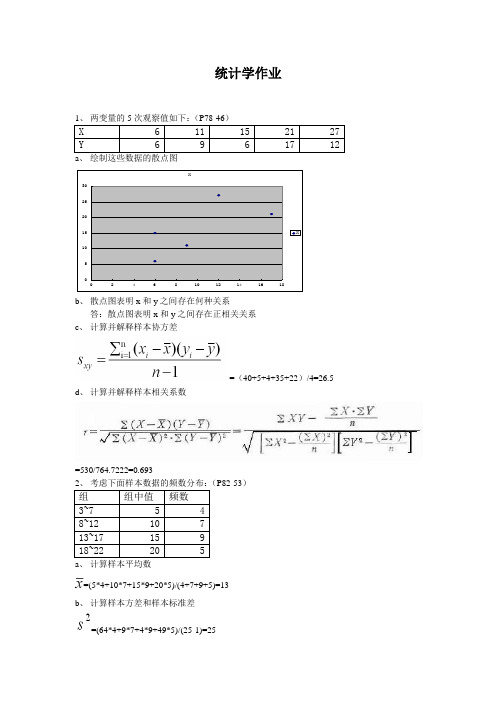
统计学作业1、 两变量的5次观察值如下:(P78-46) X6 11 15 21 27 Y 69 6 17 12 a 、 绘制这些数据的散点图X 051015202530024681012141618Xb 、 散点图表明x 和y 之间存在何种关系答:散点图表明x 和y 之间存在正相关关系c 、 计算并解释样本协方差=(40+5+4+35+22)/4=26.5d 、 计算并解释样本相关系数=530/764.7222=0.6932、 考虑下面样本数据的频数分布:(P82-53)组组中值 频数 3~75 4 8~1210 7 13~1715 9 18~22 20 5a 、 计算样本平均数=(5*4+10*7+15*9+20*5)/(4+7+9+5)=13b 、 计算样本方差和样本标准差=(64*4+9*7+4*9+49*5)/(25-1)=25=53、美国教育部报告大约有50%的在校学生利用学生贷款来帮助支付大学费用。
下面是一个利用学生贷款毕业的学生样本,数据显示的是即将毕业时的典型负债总数,以千美元计。
(P87-61)10.114.8 5.0 10.2 12.4 12.2 2.0 11.5 17.8 4.0a、对于利用学生贷款的学生来说,即将毕业时的平均贷款负债额是多少?=(10.1+14.8+5+10.2+12.4+12.2+2+11.5+17.8+4)/10=10b、方差和标准差各为多少?=(0.01+23.04+25+0.04+5.76+4.84+2.25+60.84+36)/(10-1)=24.6422=4.96414、从均值为200、标准差为50的总体,抽取n=100的简单随机样本,并利用样本均值估计总体均值(P181-18)a、的数学期望是什么?答:的数学期望为总体总体的总体均值200b、的标准差是多少?答:的标准差计算公式为50/10=5C、的抽样分布是什么?根据中心极限定理,从总体中抽取样本容量为n的简单随机样本,当样本容量很大时,样本均值的抽样分布可用正态概率分布近似。
统计学A主观题作业

《统计学A》第一次作业二、主观题(共4道小题)6. 指出下面的数据类型:(1)年龄(2)性别(3)汽车产量(4)员工对企业某项改革措施的态度(赞成、中立、反对)(5)购买商品时的支付方式(现金、信用卡、支票)参考答案:(1)年龄: 离散数值数据(2)性别: 分类数据(3)汽车产量: 离散数值数据(4)员工对企业某项改革措施的态度(赞成、中立、反对): 顺序数据(5)购买商品时的支付方式(现金、信用卡、支票): 分类数据(5)购买商品时的支付方式(现金、信用卡、支票):分类数据7. 某研究部门准备抽取2000个职工家庭推断该城市所有职工家庭的年人均收入。
要求:(1)描述总体和样本。
(2)指出参数和统计量。
参考答案:(1)总体: 全市所有职工家庭;样本: 2000个职工家庭(2)参数: 全市所有职工家庭的人均收入;统计量: 2000个职工家庭的人均收入。
统计量:2000个职工家庭的人均收入。
8. 一家研究机构从IT从业者中随机抽取1 000人作为样本进行调查, 其中60%回答他们的月收入在5 000元以上, 50%的人回答他们的消费支付方式是用信用卡。
要求:(1)这一研究的总体是什么?(2)月收入是分类变量、顺序变量还是数值型变量?(3)消费支付方式是分类变量、顺序变量还是数值型变量?(4)这一研究涉与截面数据还是时间序列数据?参考答案:(1) 所有IT从业者。
(2) 月收入十数值型变量(3)消费支付方式是分类变量(4) 涉与截面数据9. 一项调查表明, 消费者每月在网上购物的平均花费是200元, 他们选择在网上购物的主要原因是“价格便宜”。
要求:(1)这一研究的总体是什么?(2)“消费者在网上购物的原因”是分类变量、顺序变量还是数值型变量?(3)研究者所关心的参数是什么?(4)“消费者每月在网上购物的平均花费是200元”是参数还是统计量?(5)研究者所使用的主要是描述统计方法还是推断统计方法?参考答案:(1)网上购物的所有消费者(2) 分类变量(3) 所有消费者网上购物的平均花费、所有消费者选择网上购物的主要原因(4) 统计量(5) 描述统计《统计学A》第二次作业二、主观题(共1道小题)31.自填式、面访式、电话式各有什么长处和弱点?参考答案:自填式优点: 调查成本最低;适合于大范围的调查;适合于敏感性问题的调查。
统计学原理作业及答案

《统计学原理》第一次作业一、单项选择题1,统计研究在( B )阶段的方法属于大量观察法。
A,统计设计 B,统计调查 C,统计整理 D,统计分析2,把一个工厂的工人组成总体,那么每一个工人就是( A )。
A,总体单位 B,数量标志 C,指标 D,报告单位3,几位工人的工资分别为1500元、1800元和2500元,这几个数字是( C )。
A,指标 B,变量 C,变量值 D,标志4,变异的涵义是( A )。
A,统计中标志的不同表现。
B,总体单位有许多不同的标志。
C,现象总体可能存在各种各样的指标。
D,品质标志的具体表现。
5,下列各项中,属于统计指标的是( D )。
A,老王今年55岁。
B,钢材 C,宁波至北京机票1480元。
D,公司今年利润50万。
6,某市进行一次零售业质量与价格抽查,其调查单位是( C )。
A,该市所有食品商店 B,每一个食品商店 C,每一种零售食品 D,全部零售食品7,某市组织一次物价大检查,要求12月1日至12月15日全部调查完毕,这一时间规定则是( B )。
A,调查时间 B,调查期限 C,标准时间 D,登记时间8,规定普查标准时点旨在保证调查的( A )。
A,准确性 B,时效性 C,周期性 D,可比性9,对于生产过程中产品质量的检查和控制应采用( D )的方法。
A,重点调查 B,典型调查 C,普查 D,抽样检验10,对现象总体最有代表性的调查单位要推( D )单位。
A,典型调查 B,重点调查 C,抽样调查 D,普查11,某市工业企业2004年生产经营成果年报时间规定在2005年1月31日,则调查期限为( B )。
A,一日 B,一个月 C,一年 D,一年零一个月12,在全国人口普查中,( B )。
A,男性是品质标志 B,人的年龄是变量 C,人口的平均寿命是数量标志 D,全国人口是统计指标二、填空题1.社会经济统计学所研究的数量问题有自己的特点,即(数量性)、总体性和(变异性)三个。
《统计学》作业(60题)

《统计学》课程习题(修订)1.举例说明统计分组可以完成的任务。
2.举一个单向复合分组表的例子,再举一个双向复合分组表的例子。
3.某市拟对该市专业技术人员进行调查,想要通过调查来研究下列问题:(1)通过描述专业技术人员队伍的学历结构来反映队伍的整体质量;(2)研究专业技术人员总体的职称结构比例是否合理;(3)描述专业技术人员总体的年龄分布状况;(4)研究专业技术人员完成的科研成果数是否与其最后学历有关。
请回答:(1)该项调查研究的调查对象是;(2)该项调查研究的调查单位是;(3)该项调查研究的报告单位是;(4)为完成该项调查研究任务,对每一个调查单位应询问下列调查项目。
4根据上表指出:(1)变量、变量值、上限、下限、次数(频数);(2)各组组距、组中值、频率。
5注:年龄以岁为单位,小数部分按舍尾法处理。
6.对下列指标进行分类。
(只写出字母标号即可)A手机拥有量B商品库存额C市场占有率D人口数E 出生人口数F 单位产品成本G人口出生率H利税额(1)时期性总量指标有:;(2)时点性总量指标有:;(3)质量指标有:;(4)数量指标有:;(5)离散型变量有:;(6)连续型变量有:。
7.现有某地区50户居民的月人均可支配收入数据资料如下(单位:元):886 928 999 946 950 864 1050 927 949 8521027 928 978 816 1000 918 1040 854 1100 900866 905 954 890 1006 926 900 999 886 1120893 900 800 938 864 919 863 981 916 818946 926 895 967 921 978 821 924 651 850 要求:(1)试根据上述资料作等距式分组,编制次(频)数分布和频率分布数列;(2)编制向上和向下累计频数、频率数列;(3)用频率分布列绘制直方图、折线图和向上、向下累计图;(4)根据图形说明居民月人均可支配收入分布的特征。
统计学作业
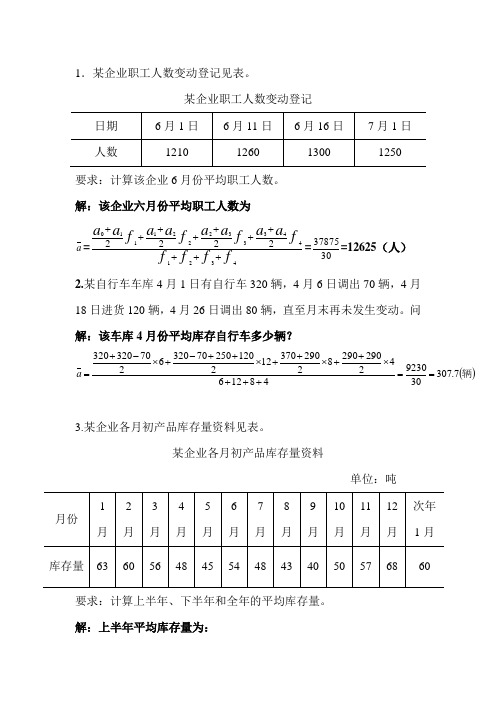
1.某企业职工人数变动登记见表。
某企业职工人数变动登记日期 6月1日 6月11日 6月16日 7月1日 人数1210126013001250要求:计算该企业6月份平均职工人数。
解:该企业六月份平均职工人数为a =ff ff f a a f a a f a a f a a 4321443332221112222++++++++++=3037875=12625(人) 2.某自行车车库4月1日有自行车320辆,4月6日调出70辆,4月18日进货120辆,4月26日调出80辆,直至月末再未发生变动。
问解:该车库4月份平均库存自行车多少辆?()辆7.307309230481264229029082290370122120250703206270320320==+++⨯++⨯++⨯++-+⨯-+=a3.某企业各月初产品库存量资料见表。
某企业各月初产品库存量资料单位:吨 月份1月 2月3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 次年1月 库存量 63 6056 48 4554 48 43 40 5057 6860要求:计算上半年、下半年和全年的平均库存量。
解:上半年平均库存量为:()吨58.48624854454856602632 (2)11=++++++=++++=-na a a a a n n下半年平均库存量为:()吨5262606857504043248=++++++=a 全年的平均库存量为:()吨54.52122606857504043485445485660263++++++++++++=a4.某企业各月份应收账款占用的资金见表。
某企业各月份账面存款余额占用的资金单位:万元时间 1月1日 4月1日 10月1日 12月31日账面存款余额326330408360要求:试计算该企业全年平均账面存款余额。
解:该企业全年平均账面存款余额为:()万元5.362124350363323604086240833032330326 (2) (22)211221110==++⨯++⨯++⨯+==+++⨯+++⨯++⨯+-f f f fa a fa a f a a a nnn n5.某企业历年的固定资产总额和折旧情况见表,求平均折旧率。
统计学练习题(含作业及非官方答案)

一、单项选择题1.根据样本计算的用于推断总体特征的概括性度量值称作(参数)A.参数B.总体C.样本D.统计量2.只能归于某一类别的非数字型数据称为(分类数据)A.分类数据B.顺序数据C.数值型数据D.数值型变量3.只能归于某一有序类别的非数字型数据称为(顺序数据)A.分类数据B.顺序数据C.数值型数据D.数值型变量4.用来描述样本特征的概括性数字度量称为(统计量)A.参数B.统计量C.变量D.变量值5.为了调查某校学生的购书费用支出,从全校抽取4个班级的学生进行调查,这种调查方法是(整群抽样)A.简单随机抽样B.系统抽样C.分层抽样D.整群抽样6.为了调查某校学生的购书费用支出,从男生中抽取60名学生调查,从女生中抽取40名学生进行调查,这种调查方法是(分层抽样)A.简单随机抽样B.整群抽样C.系统抽样D.分层抽样7.经验法则表明,当一组数据对称分布时,在平均数加减1个标准差的范围之内大约有(68%)A.68%B.95%C.99%D.100%8.经验法则表明,当一组数据对称分布时,在平均数加减2个标准差的范围内大约有(95%)A.68%B.95%C.99%D.100%9.离散系数的主要用途是(比较多组数据的离散程度)A.反映一组数据的离散程度B.反映一组数据的平均水平C.比较多组数据的离散程度D.比较多组数据的平均水平10.比较两组数据的离散程度最适合的统计量是(离散系数)A.极差B.平均差C.标准差D.离散系数11.峰态通常是与标准正态分布相比较而言的,如果一组数据服从标准正态分布,则峰态系数的值(等于0)A.等于0B.大于0C.小于0D.等于112.如果峰态系数k>0,表明该组数据是(尖峰分布)A.尖峰分布B.扁平分布C.左偏分布D.右偏分布13.某居民小区准备采取一项新的物业管理措施,为此,随机抽取了100户居民进行调查,其中表示赞成的有69户,表示中立的有22户,表示反对的有9户,则该组数据的中位数是(赞成)A.赞成B.69C.中立D.2214.某班共有25名学生,期未统计学课程的考试分数分别为68、73、66、76、86、74、61、89、65、90、69、67、76、62、81、63、68、81、70、73、60、87、75、64、56,那么该班考试分数的下四分位数和上四分位数分别是(64.5和78.5)A.64.5和78.5B.67.5和71.5C.64.5和71.5D.64.5和67.515.某行业中随机抽取10家企业,第一季度的利润额(单位:万元)分别是:72、63.1、54.7、54.3、29、26.9、25、23.9、23、20,该组数据的中位数为(27.95)A.28.46B.30.20C.27.95D.28.1216.一组数据的离散系数为0.4,平均数为20,则标准差为(8)A.80B.0.02C.4D.8 方差:1)(122--=∑=nxxsnii;离散系数:xsvs=17.根据中心极限定理可知,当样本容量充分大时,样本均值的抽样分布服从正态分布,其分布的均值为(µ)A.µB.XC.2σ D.n2σ18. 根据中心极限定理可知,当样本容量充分大时,样本均值的抽样分布服从正态分布,其分布的方差为(n2σ)A.µB.XC.2σ D.n2σ19.假设总体服从均匀分布,从此总体中抽取容量为36的样本,则样本均值的抽样分布(近似正态分布)A.服从非正态分布B.近似正态分布C.服从均匀分布D.服从2χ分布20.总体均值为50,标准差为8,从此总体中随机抽取容量为64的样本,则样本均值的抽样分布的均值和标准误差分别为(50,1)A.50,8B.50,1C.50,4D.8,821.当正态总体的方差未知时,在大样本条件下,估计总体均值使用的分布是(正态分布)A.正态分布B.t分布C.2χ分布 D.F分布22.当正态总体的方差未知时,在小样本条件下,估计总体均值使用的分布是(t分布)A.正态分布B.t分布C.2χ分布 D.F分布23.根据两个匹配的小样本估计两个总体均值之差时,使用的分布是(t分布)A.正态分布B.t分布C.2χ分布 D.F分布24.估计两个总体方差比的置信区间时,使用的分布是(F分布)A.正态分布B.t分布C.2χ分布 D.F分布25.一种零件的标准长度5cm,要检验某天生产的零件是否符合标准要求,建立的原假设和备择假设应为(H0:µ=5,H1: µ≠5)A.H0:µ=5,H1: µ≠5B.H0:µ≠5,H1: µ=5C.H0:µ≤5,H1: µ≥5D.H0:µ≥5,H1: µ≤526.一项研究表明,中学生中吸烟的比例高达30%,为检验这一说法是否属实,建立的原假设和备择假设应为(H0:π=30%,H1:π≠30%)A.H0:µ=30%,H1: µ≠30%B.H0:π=30%,H1:π≠30%C.H0:π≥30%,H1:π≤30%D. H0:π≤30%,H1:π≥30%27.列联分析是利用列联表来研究(两个分类变量的关系)A.两个分类变量的关系B.两个数值型变量的关系C.一个分类变量和一个数值型变量的关系D.两个数值型变量的分布28.设R 为列联表的行数,C 为列联表的列数,则2χ分布的自由度为((R-1)×(C-1))A.RB.CC.R×CD.(R-1)×(C-1) 29.方差分析的主要目的是判断(分类型自变量对数值型因变量的影响是否显著) A.各总体是否存在方差B.各样本数据之间是否有显著差异C.分类型自变量对数值型因变量的影响是否显著D.分类型因变量对数值型自变量的影响是否显著30.组间误差是衡量不同水平下各样本数据之间的误差,它(既包括随机误差,又包括系统误差)A.只包括随机误差B.只包括系统误差C.既包括随机误差,又包括系统误差D.有时包括随机误差,有时包括系统误差 31.组内误差是衡量某一水平下样本数据之间的误差,它(只包括随机误差)A.只包括随机误差B.只包括系统误差C.既包括随机误差,又包括系统误差D.有时包括随机误差,有时包括系统误差 32.单因素方差分析是指只涉及(一个分类型自变量)A.一个分类型自变量B.一个数值型自变量C.两个分类型自变量D.两个数值型因变量33.双因素方差分析涉及(两个分类型自变量)A.两个分类型自变量B.两个数值型自变量C.两个分类型因变量D.两个数值型因变量34.在方差分析中,数据的误差用平方和来表示的,其中反映一个样本中各观测值误差大小的平方和称为(组内平方和) A.组间平方和 B.组内平方和 C.总平方和 D.水平项平方和 35.在方差分析中,数据的误差用平方和来表示的,其中反映各个样本均值之间误差大小的平方和称为(组间平方和) A.误差项平方和 B.组内平方和 C.组间平方和 D.总平方和 36.如果一个变量的取值完全依赖于另一个变量,各观测点落在一条直线上,称为两个变量之间为(完全相关关系)A.完全相关关系B.正线性相关关系C.非线性相关关系D.负线性相关关系37.如果相关系数r =0,则表明两个变量之间(不存在线性相关关系)A.相关程度很低B.不存在任何关系C.不存在线性相关关系D.存在非线性相关关系 38.在一元线性回归方程中,回归系数iβ的实际意义是(当x变量1个单位时,y 增加的总数量)A.当x=0时,y 的平均变动数量B.当x 变动1个单位时,y 的平均变动数量C.当x 变动1个单位时,y 增加的总数量D.当y 变动1个单位时,x 的平均变动数量39.对不同年份的产品成本拟合的直线方程为x y 75.1280-=,回归系数75.11-=β表示(时间每增加1个单位,产品成本平均下降1.75个单位)A.时间每增加1个单位,产品成本平均增加1.75个单位B.时间每增加1个单位,产品成本平均下降1.75个单位C.产品成本每变动1个单位,平均需要1.75年时间D.时间每减少1个单位,产品成本平均增加1.75个单位 40.说明回归方程拟合优度的统计量是(判定系数)A.相关系数B.回归系数C.判定系数D.估计标准误差 41.各实际观测值(yi )与回归值(i yˆ)的离差平方和称为(残差平方和)A.总变差平方和B.残差平方和C.回归平方和D.判定系数 42.回归平方和占总平方和的比例称为(判定系数)A.相关系数B.回归系数C.判定系数D.估计标准误差 43.若两个变量存在负线性相关关系,则建立的一元线性回归方程的判定系数R2的取值范围是([0,1])A.[0,1]B.[-1,0]C.[-1,1]D.小于0的任意数 44.若变量x 与y 之间的相关系数r =0,则下列结论中正确的是(判定系数R2=0)A.判定系数R2=1B.判定系数R2=0C.回归系数1ˆ1=βD.估计标准误差se =045.在多元线性回归方程k k i x x y βββˆˆˆˆ110+++= 中,回归系数i βˆ表示(其他变量不变的条件下,自变量xi 变动1个单位时,因变量y 的平均变动额为i βˆ)A.自变量xi 变动1个单位时,因变量y 的平均变动额为i βˆB.其他变量不变的条件下,自变量xi 变动1个单位时,因变量y 的平均变动额为i βˆC.其他变量不变的条件下,自变量xi 变动1个单位时,因变量y 的变动总额为i βˆD.因变量y 变动1个单位时,因变量xi 的变动总额为i βˆ46.设在多元线性回归方程k k i x x y βββˆˆˆˆ110+++= 中,若自变量xi 的回归系数i βˆ的取值接近0,这表明(自变量xi 对因变量y 的影响不显著)A.因变量y 对自变量xi 的影响不显著B.因变量y 对自变量xi 的影响显著C.自变量xi 对因变量y 的影响不显著D.自变量xi 对因变量y 的影响显著47.指数平滑法适合于预测(平稳序列)A.平稳序列B.非平稳序列C.有趋势成分的序列D.有季节成分的序列48.移动平均法适合于预测(平稳序列)A.平稳序列B.非平稳序列C.有趋势成分的序列D.有季节成分的序列49.用最小二乘法拟合直线趋势方程为t b b Y 10ˆ+=,若1b 为负数,表明该现象随着时间的推移呈现(下降趋势)A.上升趋势B.下降趋势C.水平趋势D.随机波动 50.对某一时间序列拟合的直线趋势方程为x b b Y t 10ˆ+=,如果b1的值等于0,则表明该序列(没有趋势)A.没有趋势B.有上升趋势C.有下降趋势 D ,有非线性趋势二、简答题1.简要区别描述统计与推断统计?答:描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等方法。
202071 统计学 作业(专升本、高起本)

《统计学》作业一、单项选择题1.对于占全国彩电总产量绝大比重的彩电企业进行生产基本情况全面调查这是()A、典型调查B、普查C、重点调查D、抽样调查2.某地进行国有商业企业经营情况调查,则调查对象是()A 该地所有商业企业B 该地所有国有商业企业C 该地每一国有商业企业D 该地每一商业企业3.某连续变量数列,其末组为开口组,下限为100,又知其邻组的组中值为60,则末组组中值为()A 160B 140C 80D 1204.用组中值代表各组内的一般水平的假定条件是()A 各组的次数均相等B 各组的组距均相等C 各组的变量值均相等D 各组次数在本组内呈均匀分布5.根据变量数列计算平均数时,在下列哪种情况下,加权算术平均数等于简单算术平均数()A.各组次数递增B.各组次数大致相等C.各组次数相等D.各组次数不相等6.当一组数据属于左偏分布时,则()A 平均数、中位数与众数是合而为一的B 众数在左边、平均数在右边C 众数的数值较小,平均数的数值较大D 众数在右边、平均数在左边7.统计学自身的发展,沿着两个不同的方向,形成()A 描述统计学与理论统计学B 理论统计学与推断统计学C 理论统计学与应用统计学D 描述统计学与推断统计学8.某灯泡厂为了掌握该厂的产品质量,拟进行一次全厂的质量大检查,这种检查应选择()A 统计报表B 重点调查C 全面调查D 抽样调查9.下列分组中按品质标志分组的是()A 人口按年龄分组B 产品按质量优劣分组C 企业按固定资产原值分组D 乡镇按工业产值分组10.在分组时,若有某单位的变量值正好等于相邻组的下限时,一般应将其归在()A 上限所在组B 下限所在组C 任意一组均可D 另设新组11.方差是数据中各变量值与其算术平均的()A 离差绝对值的平均数B 离差平方的平均数C 离差平均数的平方D 离差平均数的绝对值12.一组数据的偏态系数为1.3,表明该组数据的分布是()A 正态分布B 平顶分布C 左偏分布D 右偏分布13.四分差排除了数列两端各()单位标志值的影响A 10%B 15%C 25%D 35%14.抽样指标与总体指标之间抽样误差的可能范围是()A 抽样平均误差B 抽样极限误差C 区间估计范围D 置信区间15.已知随机变量X服从二项分布,且E(X)=2.4,D(Y)=1.44,则二项分布的参数n,p的值为()A n=4,p=0.6B n=6,p=0.4C n=8,p=0.3D n=24,p=0.116.假设检验是检验()的假设是否成立。
统计学作业及答案

4.总体的变异性越大,抽样误差越大。对
简答题
1.请简单比较一下概率抽样和非概率抽样。
概率抽样:依据随机原则抽选样本,样本统计量的理论分布存在,可根据调查的结果推断总体
非概率抽样:不是依据随机原则抽选样本,样本统计量的分布是不确定的,无法使用样本的结果推断总体
2.举例说明统计分组应该遵循的原则。
(4)各单位的共同倾向(表现为主要的、基本的因素)决定着平均数的水平,而各单位对平均数的离差(由次要的、偶然的因素所产生的影响),则由于足够多数单位的汇总综合结果,而相互抵消,趋于消失。通过平均化的结果以抵消偶然因素的个别影响,描述现象的典型水平,并进一步推断总体的数量特征,这些都是在大数定律的作用下进行的。应该指出,大数定律的作用是帮助我们通过偶然性达到发现的必然性,认识现象规律的表现形式的目的,但它并不能说明现象的本质,这又须借助相关实质性学科的知识来解释现象的本质及其内在联系。
(4)“消费者每月在网上购物的平均花费是200元”是参数还是统计量?参数
(5)研究者所使用的主要是描述统计方法还是推断统计方法?推断统计方法
选择题
1.抽样调查应遵循的原则是()
A.准确性原则B.可靠性原则C.随机性原则D.灵活性原则
2.统计分组时,在全距一定的情况下()
A.组距越大,组数越多B.组距越大,组数越少C.组距大小与组数多少无关D.组距大小与组数多少成正比
85
85
81
75
85
97
96
60
69
64
54
85
65
60
96
82
98
60
77
46
60
86
71
《统计学》作业(60题)

《统计学》课程习题(修订)1.举例说明统计分组可以完成的任务。
2.举一个单向复合分组表的例子,再举一个双向复合分组表的例子。
3.某市拟对该市专业技术人员进行调查,想要通过调查来研究下列问题:(1)通过描述专业技术人员队伍的学历结构来反映队伍的整体质量;(2)研究专业技术人员总体的职称结构比例是否合理;(3)描述专业技术人员总体的年龄分布状况;(4)研究专业技术人员完成的科研成果数是否与其最后学历有关。
请回答:(1)该项调查研究的调查对象是;(2)该项调查研究的调查单位是;(3)该项调查研究的报告单位是;(4)为完成该项调查研究任务,对每一个调查单位应询问下列调查项目。
4根据上表指出:(1)变量、变量值、上限、下限、次数(频数);(2)各组组距、组中值、频率。
5注:年龄以岁为单位,小数部分按舍尾法处理。
6.对下列指标进行分类。
(只写出字母标号即可)A手机拥有量B商品库存额C市场占有率D人口数E 出生人口数F 单位产品成本G人口出生率H利税额(1)时期性总量指标有:;(2)时点性总量指标有:;(3)质量指标有:;(4)数量指标有:;(5)离散型变量有:;(6)连续型变量有:。
7.现有某地区50户居民的月人均可支配收入数据资料如下(单位:元):886 928 999 946 950 864 1050 927 949 8521027 928 978 816 1000 918 1040 854 1100 900866 905 954 890 1006 926 900 999 886 1120893 900 800 938 864 919 863 981 916 818946 926 895 967 921 978 821 924 651 850 要求:(1)试根据上述资料作等距式分组,编制次(频)数分布和频率分布数列;(2)编制向上和向下累计频数、频率数列;(3)用频率分布列绘制直方图、折线图和向上、向下累计图;(4)根据图形说明居民月人均可支配收入分布的特征。
统计学作业

统计学作业 Prepared on 22 November 2020第二章习题(离散程度指标)1.[习题集P23第9题]某车间有两个小组,每组都是7人,每人日产量数如下:第一组:20、40、60、70、80、100、120;第二组:67、68、69、70、71、72、73。
已知两组工人每人平均日产量件数为70件,试计算:(1)R;(2);(3),并比较哪个组的平均数代表性大要求:如计算过程有小数,请保留至小数点后两位,余均同。
试据此分别计算其平均日产量,并说明哪个班的平均日产量代表性大假定生产条件相同,试计算这两个品种的收获率(产量/播种面积),确定哪一品种具有较大的稳定性和推广价值。
注意:播种面积是“f”,而产量等于收获率乘以播种面积,因而是“xf”。
4.[习题集P25第15题]各标志值对任意数的方差为500,而这个任意数与标志值平均数之差为12,试确定标志值的方差(提示:方差是离差平方的平均数。
本题中的500是标志值与任意数的方差,即所测度的离差发生在标志值与某一任意数之间,而所求的方差是标志值与均值之间的方差)。
第二章习题(平均指标)试计算该局企业平均职工人数以及第20百分位数。
2.[习题集P21第3题]某乡播种2800亩早稻,其中35%的稻田使用良种,平均亩产750斤,其余的稻田平均亩产仅480斤。
试问:(1)全部耕地早稻平均亩产是多少(2)早稻的全部产量是多少试计算产品计划与实际的平均等级和平均出厂价格,指出两者间的经济联系(提示:可对产品等级进行赋值,尔后计算)。
根据该资料计算亩产的中位数和众数,并判断其分布态势。
第三章《时间序列分析》作业又知该厂7月初的工人数为1270人,前年12月份工业总产值为235万元。
要求计算该厂去年上半年的:(1)月平均工业总产值;(2)工业总产值的月平均增长量(以前年12月份为基期); (3)平均工人人数;(4)月平均工人劳动生产率。
要求:计算该产品的平均单位成本。
统计学作业

第一章1.简述统计的含义及其相互间的关系统计一词的三种含义:统计工作、统计资料和统计学。
(1)统计工作。
指搜集、整理和分析客观事物总体数量方面资料的工作过程,是统计的基础。
(2)统计资料。
统计工作所取得的各项数字资料及有关文字资料,一般反映在统计表、统计图、统计手册、统计年鉴、统计资料汇编和统计分析报告中。
(3)统计科学。
研究如何搜集、整理和分析统计资料的理论与方法。
(4)统计工作、统计资料、统计科学三者之间的关系是:统计工作的成果是统计资料,统计资料和统计科学的基础是统计工作,统计科学既是统计工作经验的理论概括,又是指导统计工作的原理、原则和方法。
统计工作和统计资料是过程与结果的关系,统计资料是统计工作达到成果或结晶,它来源于统计工作又服务于统计工作,统计工作和统计学是理论与实践的关系,统计学是统计活动发展到一定阶段的产物,是统计实践经验的理论概括,并用于指导统计实践,为统计工作提供理论依据。
统计工作的发展会不断完善和丰富统计理论,而统计理论的丰富又促进了统计工作的发展,使之更有效,更为科学。
2.一个完整的统计工作过程包括统计设计、统计调查、统计整理和统计分析。
3.简述统计指标和标志的关系统计指标和标志既有区别又有联系。
其区别:第一,标志说明总体单位属性或特征的名称;厄尔指标是说明总体数量特征的名称。
第二,标志有智能用文字表达的品质标志和用数量表达的数量标志两种;儿指标都只能用数值表示。
其联系:有许多指标的数值是由总体单位的数量标志值汇总而来。
第二,由于总体和总体单位是可变的,则总体的指标和反映总体单位的标志之间存在变化关系。
4.如何理解统计指标体系比同级指标的应用更为广泛和重要?第二章1.统计调查是根据调查的目的与要求,运用科学的调查方法,有计划、有组织地搜集数据信息资料的统计工作过程。
统计调查方案一般包括几项基本内容:确定调查目的;确定调查对象和调查单位;确定调查项目;设计调查问卷;选择调查方法;确定调查时间和调查期限;制定调查的组织和实施计划。
统计学作业

作业一一、单选题1、对某市分行所辖支行职工工资水平进行调查研究,则统计总体是()。
A、市分行B、全部支行C、全体职工 D、全体职工的全部工资2、进行金融系统职工普查,则总体单位是()。
A、全部金融机构 B、金融系统的全部职工 C、每个金融机构 D、金融系统的每个职工3、银行的储蓄存款余额()。
A、一定是统计指标B、一定是数量标志C、可能是统计指标,也可能是数量标志D、既不是统计指标,也不是数量标志4、下列标志中,属于品质标志的是()。
A、职称B、工资C、年龄D、体重5、下列标志中,属于数量标志的是()。
A、性别B、职称C、文化程度D、体重6、某记账员的记账差错率是()。
A、数量指标B、质量指标C、数量标志D、品质标志7、统计学中的变量是指()。
A、数量标志B、统计指标C、可变的数量标志和统计指标的统称D、品质标质、数量标志和指标的统称8、一个统计总体()。
A、只能有一个标志B、只能有一个指标C、可以有多个标志D、可以有多个指标9、某班60名学生统计课考试成绩依次是:81分、92分、65分、75分……,这些分数值是()。
A、指标B、标志C、变量D、变量值10、在全国人口普查中()。
A、“男性”是品质标志B、“文化程度”是品质标志C、“平均年龄”是数量标志D、“性别比”是品质标志二、判断题(正确的记T,错误的记F)1、“女性”是品质标志。
()2、变量值是由标志值汇总得来的。
()3、以相对数或平均数表示的指标都是质量指标。
()4、标志的承担者是总体,指标的承担者是单位。
()5、变异是指各种标志(或各种指标)之间名称的差异。
()6、任何一个统计指标值,都是总体在一定时间、地点、条件下的数量表现。
()7、统计是在质与量的辩证统一中,研究社会经济现象质的方面。
()8、构成统计总体的前提条件,是各单位的差异性。
()9、一个统计总体只有一个总体单位总量指标。
()10、变量是指可变的数量标志和统计指标。
()客观题答案分数:1:C(5分)2:D(5分)3:C(5分)4:A(5分)5:D(5分)6:C(5分)7:C(5分)8:D(5分)9:D(5分)10:B(5分)11:F(5分)12:F(5分)13:T(5分)14:F(5分)15:F(5分)16:T(5分)17:F(5分)18:F(5分)19:T(5分)20:T(5分)作业二题目内容:一、单选题(每小题4分)1、重点调查中重点单位指的是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学作业文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-第二章习题(离散程度指标)1.[习题集P23第9题]某车间有两个小组,每组都是7人,每人日产量数如下:第一组:20、40、60、70、80、100、120;第二组:67、68、69、70、71、72、73。
已知两组工人每人平均日产量件数为70件,试计算:(1)R;(2)A.D;(3)S.D,并比较哪个组的平均数代表性大?要求:如计算过程有小数,请保留至小数点后两位,余均同。
试据此分别计算其平均日产量,并说明哪个班的平均日产量代表性大?假定生产条件相同,试计算这两个品种的收获率(产量/播种面积),确定哪一品种具有较大的稳定性和推广价值。
注意:播种面积是“f”,而产量等于收获率乘以播种面积,因而是“xf”。
4.[习题集P25第15题]各标志值对任意数的方差为500,而这个任意数与标志值平均数之差为12,试确定标志值的方差(提示:方差是离差平方的平均数。
本题中的500是标志值与任意数的方差,即所测度的离差发生在标志值与某一任意数之间,而所求的方差是标志值与均值之间的方差)。
第二章习题(平均指标)试计算该局企业平均职工人数以及第20百分位数。
2.[习题集P21第3题]某乡播种2800亩早稻,其中35%的稻田使用良种,平均亩产50斤,其余的稻田平均亩产仅480斤。
试问:(1)全部耕地早稻平均亩产是多少?(2)早稻的全部产量是多少?试计算产品计划与实际的平均等级和平均出厂价格,指出两者间的经济联系(提示:可对产品等级进行赋值,尔后计算)。
根据该资料计算亩产的中位数和众数,并判断其分布态势。
第三章《时间序列分析》作业又知该厂7月初的工人数为1270人,前年12月份工业总产值为235万元。
要求计算该厂去年上半年的:(1)月平均工业总产值;(2)工业总产值的月平均增长量(以前年12月份为基期);(3)平均工人人数;(4)月平均工人劳动生产率。
要求:计算该产品的平均单位成本。
3.[P52第3题]某企业1996~2000年总增加值实际完成及计划完成程度的有关资料如试计算该企业这一时期总增加值平均计划完成程度。
试计算2001年该乡平均拥有的彩电台数。
5.[习题集P52第5题]某种产品的单位成本水平在“八五”计划期内,计划规定每年比上年的降低率分别为:5.2%、4.8%、3.8%、3.5%和2.4%。
试计算其平均每年的降低率。
6.[习题集P53第6题]某地区1985年粮食产量为25万吨。
(1)假定“七五”期间(1986~1990)每年平均增长4%,以后每年平均增长4.5%,问2000年将达到什么水平?第四章《统计指数分析》作业要求:计算三种产品的总成本指数和产量总指数。
试计算三种商品价格总指数和销售量总指数。
试分析该工厂三种产品产值的变动情况,并揭示其变动原因。
要求:(1)计算产品产量总指数及由于产量增长而增加的生产费用。
(2)单位成本总指数及由于单位成本下降而节约的生产费用。
试分别分析价格和销售量对销售额的影响。
要求:(1)分析该企业工人总平均工资的变动及其原因。
(2)分析该企业工人工资总额的变动及其原因。
提示:该题中,尽管两个小题反映的都是变动,但前者针对的是总体的平均工资;后者针对的工人的工资总额,因此,应该选用不同的指数,并涉及到不同的原因。
第六章《抽样推断》作业1.[习题集P113第1题]在稳定生产的情况下,某工厂生产的电灯泡使用时数可认为是服从正态分布,观察20个灯泡的使用时数,测得其平均寿命为1832小时,标准差为497小时。
试构造灯泡使用寿命的总体平均值95%的置信区间。
2.[习题集P113第2题]对某商场营业员的劳动效率进行纯随机不重复抽样,共抽查60人,查得每人每日平均销售额为300元,其标准差为24.50元。
该商场共有营业员600人,在概率保证程度为95%时,要求:(1)计算抽样平均误差;(2)推断该商场营业员每天平均销售额的置信区间。
3.[习题集P113第3题]某灯泡厂对生产的10000只日光灯进行质量检验,随机抽取100只,测得灯管的平均发光时间为2000小时,发光时间的标准差为50小时。
在95.45%的概率保证下,试估计这批灯管平均发光时间的范围。
如果要求最大允许误差不超过15小时,试问这批灯管的平均发光时间范围又是多少?其估计的概率保证程度是多大?4.[习题集P114第6题]某无线电厂想测定某型号收录机的功率,随机抽取121台该型号的收录机进行测试,获得其平均功率为1.98瓦,由以往的经验得知总体标准差为0.3瓦。
试以95%的置信度确定该型号收录机功率的置信区间。
5.[习题集P115第10题]某高校在一项关于旷课原因的研究中,从总体中随机抽取了200人组成样本,在对其进行问卷调查时,有60人说他们旷课是由于任课教师讲课枯燥的原因所导致。
试对由于这种原因而旷课的学生的真正比例构造95%的置信区间。
6.[习题集P118第28题]成数为30%,成数抽样误差不超过5%,在99.73%的概率保证下,试问重复抽样确定的样本容量为多少?如果成数允许误差减少40%,样本容量又为多少?7.[习题集P118第29题]某公司对发往外地的商品包装数量进行开包检查,随机检查了100包,平均每包装有99件商品,测得标准差为5件。
试用95.45%的概率保证程度估计这批货物平均每包装有商品件数的范围。
如果其他条件不变,极限误差缩小为原来的1/2,试问此时需抽查多少包?若全及总体由600群构成,试以95%的概率保证来推断该场兔子平均每只重量的范围(非统计专业不做)。
9.某厂有新、老两个车间都生产保温瓶胆。
新车间设备新颖,技术先进,产量比老车间高出一倍。
现要了解该厂产品的保温时间,按照产量比例分别在新、老两个车间进行试按95%的概率保证程度推断该厂产品的平均保温时间(非统计专业不做)。
第八章《假设检验》作业1.[习题集P132第8题]某食品厂生产果酱,标准规格是每罐净重250克,根据以往经验,标准差是3克。
现在该厂生产一批这样的罐头,从中抽取100罐进行检验,其平均净重为251克,问这批罐头是否合乎标准(显着性水平为0.05)?2.[习题集P132第9题]某公司生产电池,其寿命近似服从正态分布,该公司声称:其特定型号电池的平均寿命为21.5小时。
在实验室里测验了该公司生产的电池6只,其寿命分别为19、18、22、20、16、25小时。
问这些结果是否表明这种型号的电池寿命比该公司宣布的更短(显着性水平为0.05)?3.一种以休闲和娱乐为主题的杂志,声称其读者群中有80%为女性。
为验证这一说法是否属实,某研究部门抽取了由200人组成的一个随机样本,发现有146个女性经常阅读该杂志。
分别取显着性水平为0.05和0.01,检验该杂志读者群中女性的比率是否为80%。
4.[习题集P134第23题]某制造厂生产某装置的平均工作温度是190度。
今从一个由16台装置构成的随机样本求得的工作温度的平均数和标准差分别是194度和8度,能否说明平均工作温度比制造厂规定的要高呢?给定显着性水平为0.05,并假定工作温度服从正态分布。
5.[习题集P134第24题]某停车场管理人员估计周末汽车平均停靠时间不超过90分钟。
现抽查100辆汽车,平均停车时间为96分钟,标准差为30分钟。
试问这些数据能否说明管理人员估计的正确性?给定显着性水平0.05。
《相关与回归分析》习题答案1.已知X 、Y 两变量,6.1=xxxy L L ,y s 是x s 的两倍,求相关系数r=?解:8.0216.16.1=⨯=⨯==∴==y x yx xy xxxy s s b s s s r L L b 2.某家具厂生产家具的总成本与木材耗用量有关,根据记录资料如下表:(1)建立以总成本为因变量的回归直线方程。
(2)计算回归方程的估计标准误。
(3)计算相关系数,判断其相关程度。
解:(1)令总成本为y ,木材耗电量为x ,则计算得:b=0.7577,a=1.2655,即回归方程为:x y7577.02655.1ˆ+= (2)估计标准误:1559.022=-∑-∑-∑=n xyb y a y S yx(3)相关系数为:r=0.75393.某种机械设备已使用年限与其每年维修费用资料如下:问题:(1)试分析这种设备已使用年数长短与维修费用多少之间的相互关系方向和类型。
(2)用恰当的回归方程加以表述。
(3)当使用年数在11年时,这种机械设备的年维修费用估计是多少? (4)分析两个变量之间的密切程度。
解:(1)是正相关的直线相关类型。
(2)回归方程:x y15.7625.329ˆ+=。
(3)年维修费的点估计为:1166.9(元)。
(4)相关系数=0.89。
江西财经大学08-09第二学期期末考试试卷试卷代码:06003A 授课课时:48课程名称:统计学 适用对象:挂牌试卷命题人 试卷审核人 一、单项选择题(从下列各题四个备选答案中选出一个正确答案,并将其代号写在答题纸相应位置处。
答案错选或未选者,该题不得分。
每小题1分,共10分)1.要了解某市国有工业企业生产设备情况,则统计总体是( ) A 、该市国有的全部工业企业 B 、该市国有的每一个工业企业 C 、该市国有的某一台设备D 、该市国有工业企业的全部生产设备2.抽样调查和重点调查的主要区别是( ) A 、获取调查单位的方式不同 B 、调查的目的不同C 、调查的单位不同D 、两种调查没有本质区别3.三个班上学期统计学考试平均成绩分别是83、87和90分,且一、二班人数分别占总人数的25%和37%,则三个班统计学的总平均成绩是( )A 、数据不全,无法计算B 、87.14分C 、86.67分D 、90.21分4.下列等式中,不正确的是( ) A 、发展速度=增长速度+1B 、定基发展速度=相应各环比发展速度的连乘积C 、定基增长速度=相应各环比增长速度的连乘积D 、平均增长速度=平均发展速度-15.某种产品报告期与基期比较产量增长26%,单位成本下降32%,则生产费用支出总额为基期的( )A 、166.32%B 、85.68%C 、185%D 、54%6.在简单随机重复抽样条件下,如果允许误差缩小为原来的一半,则样本容量就要增加到原来的( )A 、5倍B 、4倍C 、3倍D 、4.5倍7.2ˆ)(y y -∑是指( )A 、残差平方和B 、回归平方和C 、总离差平方和D 、解释变差8.标准差系数抽象了( ) A 、总体指标数值大小的影响 B 、总体单位数多少的影响 C 、标志变异的影响D 、平均水平高低对离散分析的影响9.综合指数变形为加权算术平均数指数,其权数为( ) A 、该综合指数的分子 B 、该综合指数的分母 C 、固定权数D 、视具体情况而定10.简单算术平均数和加权算术平均数的计算结果相同是因为( ) A 、权数不等 B 、权数相等 C 、不存在权数作用 D 、变量值的作用 二、判断题(请在答题纸上写明题号后,在正确的命题后打√,在错误的命题后打×。
