初四数学科月考试题 Microsoft Word 文档 (2)

合集下载

初四数学测试题及答案

初四数学测试题及答案测试题：1. 某商店以原价售卖商品，现在打8.5折出售。

如果一件商品原价100元，打折后的价格是多少？2. 小明用一根长度为12厘米的铁丝做了一个正方形，求这个正方形的面积。

3. 某班级共有30名同学，其中男生占总人数的40%。

女生人数是男生人数的3倍。

那么女生人数是多少？4. 一辆汽车以每小时80公里的速度行驶，如果行驶5小时，总共行驶了多少公里？5. 某书店共有480本书，其中2/5是故事书。

那么故事书的数量是多少？答案：1. 打折后价格 = 原价 ×折扣打折后价格 = 100元 × 0.85 = 85元所以，打折后的价格是85元。

2. 正方形的边长 = 铁丝总长度 ÷ 4正方形的边长 = 12厘米 ÷ 4 = 3厘米正方形的面积 = 边长 ×边长正方形的面积 = 3厘米 × 3厘米 = 9平方厘米所以，这个正方形的面积是9平方厘米。

3. 男生人数 = 总人数 ×男生比例男生人数 = 30人 × 0.4 = 12人女生人数 = 男生人数 × 3女生人数 = 12人 × 3 = 36人所以，女生人数是36人。

4. 总行驶公里数 = 速度 ×时间总行驶公里数 = 80公里/小时 × 5小时 = 400公里所以，总共行驶了400公里。

5. 故事书的数量 = 全部书的数量 ×故事书比例故事书的数量 = 480本 × 2/5 = 192本所以，故事书的数量是192本。

以上是初四数学测试题及答案，希望对你的学习有所帮助。

初四数学试题

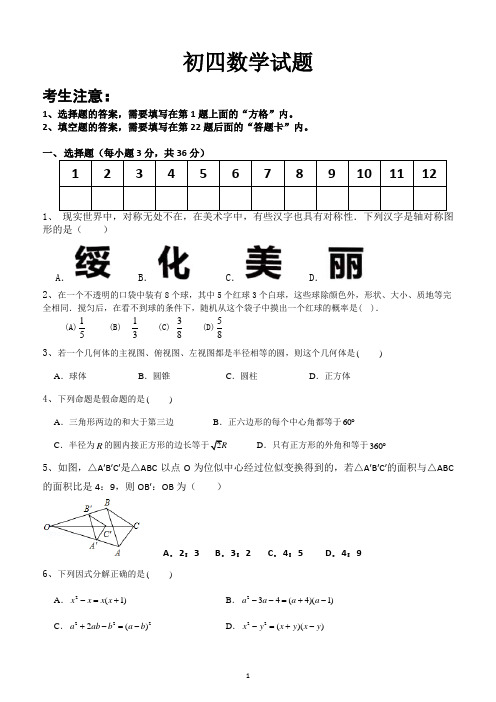
初四数学试题考生注意：1、选择题的答案，需要填写在第1题上面的“方格”内。

2、填空题的答案，需要填写在第22题后面的“答题卡”内。

1形的是（）A ．B ．C ．D ．2、在一个不透明的口袋中装有8个球，其中5个红球3个白球，这些球除颜色外，形状、大小、质地等完全相同．搅匀后，在看不到球的条件下，随机从这个袋子中摸出一个红球的概率是( )．(A)15 (B) 13 (C) 38 (D)583、若一个几何体的主视图、俯视图、左视图都是半径相等的圆，则这个几何体是( )A ．球体B ．圆锥C ．圆柱D ．正方体4、下列命题是假命题的是( )A ．三角形两边的和大于第三边B ．正六边形的每个中心角都等于60︒C ．半径为RD ．只有正方形的外角和等于360︒5、如图，△A′B′C′是△ABC 以点O 为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC 的面积比是4：9，则OB′：OB 为（）A ．2：3B ．3：2C ．4：5D ．4：96、下列因式分解正确的是( )A ．2(1)x x x x -=+B ．234(4)(1)a a a a --=+-C ．2222()a ab b a b +-=-D ．22()()x y x y x y -=+-7、小明去商店购买A 、B 两种玩具，共用了10元钱，A 种玩具每件1元，B 种玩具每件2元．若每种玩具至少买一件，且A 种玩具的数量多于B 种玩具的数量．则小明的购买方案有( )A ．5种B ．4种C ．3种D ．2种8、根据市场需求，某药厂要加速生产一批药品，现在平均每天生产药品比原计划平均每天多生产500箱，现在生产6000箱药品所需时间与原计划生产4500箱药品所需时间相同，那么原计划平均每天生产多少箱药品？设原计划平均每天可生产x 箱药品，则下面所列方程正确的是（） A ． B ． C ．D ．9、将抛物线2y x =经过下面的平移可得到抛物线2(3)4y x =++的是( )(A)向左平移3个单位，向上平移4个单位 (B)向左平移3个单位，向下平移4个单位 (C)向右平移3个单位，向上平移4个单位 (D)向右平移3个单位，向下平移4个单位10、关于x 的不等式组⎩⎨⎧1ax ＞＞x 的解集为x ＞1 ，则a 的取值范围是（）A. a ＞1B. a ＜1C. a ≥1D. a ≤111、已知在Rt △ACB 中，∠C ＝90°，∠ABC ＝75°，AB ＝5，点E 为边AC 上的动点，点F 为边AB 上的动点，则线段FE +EB 的最小值是（）A ．B.C ．D ．（第12题图）12、如图，在Rt ABC ∆中，CD 为斜边AB 的中线，过点D 作DE AC ⊥于点E ，延长DE 至点F ，使EF DE =，连接AF ，CF ，点G 在线段CF 上，连接EG ，且180CDE EGC ∠+∠=︒，2FG =，3GC =．下列结论：①12DE BC =；②四边形DBCF 是平行四边形；③EF EG =；④BC = 其中正确结论的个数是( ) A ．4个 B ．3个C ．2个D ．1个二、选择题（每小题3分，共30分）13、地球与太阳之间的距离约为149 600 000千米，用科学记数法表示约为千米．14、在函数y =x 的取值范围是．15、化简：16＝． 16、已知反比例函数y=1k x+的图象位于第一、第三象限，则k 的取值范围是． 17、方程x3x x 5-+＝0的解是． 18、某种衬衫每件的标价为150元，如果每件以8折（即按标价的80％）出售，那么这种衬衫每件的实际售价应为元．19、将一个底面半径为5cm ，母线长为12cm 的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是度． 20、观察下列图形：（第22题图）它们是按一定规律排列的，依照此规律，第19个图形中共有个★． 21、已知m ，n 是一元二次方程x 2﹣3x ﹣2＝0的两个根，则＝．22、如图，在平面直角坐标系中，O 为坐标原点，MN 垂直于x 轴，以MN 为对称轴作△ODE 的轴对称图形，对称轴MN 与线段DE 相交于点F ，点D 的对应点B 恰好落在y ＝（k ≠0，x ＜0）的双曲线上，点O 、E 的对应点分别是点C 、A ．若点A 为OE 的中点，且S △AEF ＝1，则k 的值为．填空题答题卡：三、解答题（共7道题，54分） 23、 (本题6分)（1）如图，已知线段AB 和点O ，利用直尺和圆规作ABC ∆，使点O 是ABC ∆的内心（不写作法，保留作图痕迹）；（2）在所画的ABC ∆中，若90C ∠=︒，6AC =，8BC =，则ABC ∆的内切圆半径是．（第23题图）（第24题图）24、（6分）如图，已知ABC ∆三个顶点的坐标分别为(2,4)A --，(0,4)B -，(1,1)C - （1）请在网格中，画出线段BC 关于原点对称的线段11B C ；（2）请在网格中，过点C 画一条直线CD ，将ABC ∆分成面积相等的两部分，与线段AB 相交于点D ，写出点D 的坐标；（3）若另有一点(3,3)P --，连接PC ，则tan BCP ∠= ． 25、（7分）为了解本校九年级学生体育测试项目“400米跑”的训练情况，体育教师在2019年15-月份期间，每月随机抽取部分学生进行测试，将测试成绩分为：A ，B ，C ，D 四个等级，并绘制如图两幅统计图，根据统计图提供的信息解答下列问题：（1）月份测试的学生人数最少，月份测试的学生中男生、女生人数相等；（2）求扇形统计图中D等级人数占5月份测试人数的百分比；（3）若该校2022年4月份九年级在校学生有600名，请你估计出测试成绩是A等级的学生人数．26、（8分）端午节期间，甲、乙两人沿同一路线行驶，各自开车同时去离家560千米的景区游玩，甲先以每小时60千米的速度匀速行驶1小时，再以每小时m千米的速度匀速行驶，途中休息了一段时间后，仍按照每小时m千米的速度匀速行驶，两人同时到达目的地，图中折线、线段分别表示甲、乙两人所走的路程()y km甲，()y km乙与时间()x h之间的函数关系的图象．请根据图象提供的信息，解决下列问题：（1）图中E点的坐标是，题中m=/km h，甲在途中休息h；（2）求线段CD的解析式，并写出自变量x的取值范围；（3）两人第二次相遇后，又经过多长时间两人相距20km？27、（8分）如图，AB是⊙O的直径，AC为弦，BAC∠的平分线交⊙O于点D，过点D的切线交AC的延长线于点E．求证：（1）DE AE⊥；（2）AE CE AB+=．28、（9分）如图，在正方形ABCD 中，4AB =，点G 在边BC 上，连接AG ，作DE AG ⊥于点E ，BF AG ⊥于点F ，连接BE 、DF ，设EDF α∠=，EBF β∠=，BGk BC=．（1）求证：AE BF =；（2）求证：tan α=k ×tan β（3）若点G 从点B 沿BC 边运动至点C 停止，求点E ，F 所经过的路径与边AB 围成的图形的面积．29、（10分）已知抛物线23=++的对称轴为直线1y ax bxx=，交x轴于点A、B，交y轴于点C，2且点A坐标为(2,0)=-->与抛物线交于点P、Q（点P在点Q的右边），交y A-．直线(0)y mx n m轴于点H．（1）求该抛物线的解析式；（2）若5∆的面积为3，求m的值；n=-，且CPQ（3）当1∆的面积为S，求S与m之间的函数=-，直线AQ交y轴于点K．设PQKm≠时，若3n m解析式．。

初四期末考试数学试卷

一、选择题（每题5分，共25分）1. 下列各数中，绝对值最小的是（）A. -3B. 2C. -1.5D. 0.52. 已知a > b，下列不等式中正确的是（）A. a - b > 0B. a + b > 0C. a - b < 0D. a + b < 03. 在△ABC中，若∠A = 60°，∠B = 45°，则∠C的度数是（）A. 75°B. 105°C. 120°D. 135°4. 下列函数中，是反比例函数的是（）A. y = 2x + 3B. y = 3/xC. y = x^2D. y = √x5. 下列图形中，是轴对称图形的是（）A. 等腰三角形B. 平行四边形C. 梯形D. 长方形二、填空题（每题5分，共25分）6. 已知a = -3，b = 2，则a + b = ________。

7. 下列方程中，x = 2是它的解的是（）A. 2x - 1 = 3B. 2x + 1 = 3C. 2x - 1 = 1D. 2x + 1 = 18. 若sinθ = 1/2，则cosθ的值是 ________。

9. 下列数中，有理数是 ________。

10. 若x^2 - 5x + 6 = 0，则x的值为 ________。

三、解答题（共50分）11. （15分）解下列方程组：\[\begin{cases}2x + 3y = 8 \\x - y = 1\end{cases}\]12. （15分）已知函数y = -2x + 5，求以下问题：（1）当x = 3时，y的值为多少？（2）当y = -1时，x的值为多少？13. （20分）已知直角三角形ABC中，∠A = 90°，∠B = 30°，∠C= 60°，AB = 6cm，求：（1）BC的长度；（2）AC的长度；（3）三角形ABC的面积。

初四数学答案 Microsoft Office Word 文档

2018—2019学年度第一学期期末质量检测初四数学试题答案（仅供参考）一、选择题（各小题的四个选项中，只有一项符合题意，每小题3分，共30分，请把答案写在答题框内）1.A2.B3.D4.B5.B6.C7.B8.A9.D 10.B二、填空题（每小题3分，共15分）2 15.②③④11.2000米 12.2.4 13.24 14.216.（本题满分6分）解：（1）如图所示：（2）根据题意得出：0.8×0.8×5+0.8π×0.8=（0.64π+3.2）（m2），40×（0.64π+3.2）≈208.4（元），答：一共需要花费207.4元．17. （本题满分6分）解：画树状图如下：由树状图可知，共有6种等可能结果，其中选修地理和生物的只有1种结果，所以选修地理和生物的概率为，故答案为：．18. （本题满分6分）解：（1）依题可得：∠A=45°，∠PBC=60°，∠QBC=30°，AB=10m，在Rt△PBC中，∵∠PBC=60°，∠PCB=90°，∴∠BPQ=30°；（2）设CQ=x，在Rt△QBC中，∵∠QBC=30°，∠QCB=90°，∴BQ=2x，BC=x，又∵∠PBC=60°，∠QBC=30°，∴∠PBQ=30°，由（1）知∠BPQ=30°，∴PQ=BQ=2x，∴PC=PQ+QC=3x，AC=AB+BC=10+x，又∵∠A=45°，∴AC=PC，即3x=10+x，解得：x=，∴PQ=2x=≈15.8（m），答：树PQ的高度约为15.8m.19.（本题满分6分）解：（1）∵∠EDC+∠EDA=180°、∠B+∠EDA=180°，∴∠B=∠EDC，又∵AB=AC，∴∠B=∠C，∴∠EDC=∠C，∴ED=EC；（2）连接AE，∵AB是直径，∴AE⊥BC，又∵AB=AC，∴BC=2EC=43，∵∠B=∠EDC、∠C=∠C，∴△ABC∽△EDC，∴AB：EC=BC：CD，又∵EC=23、BC=43、CD=3，∴AB=8．20. （本题满分7分）解：过点D做DF⊥BC于F由已知，BC=5∵四边形ABCD是菱形∴DC=5∵BE=3DE∴设DE=x，则BE=3x∴DF=3x，BF=x，FC=5﹣x在Rt△DFC中，DF2+FC2=DC2∴（3x）2+（5﹣x）2=52∴解得x=1∴DE=3，FD=3设OB=a则点D坐标为（1，a+3），点C坐标为（5，a）∵点D.C在双曲线上∴1×（a+3）=5a∴a=∴点C坐标为（5，）∴k=21. （本题满分8分）解：（1）根据题意，得S=x（24﹣3x），即所求的函数解析式为：S=﹣3x2+24x，又∵0＜24﹣3x≤10，∴，（2）根据题意，设AB长为x，则BC长为24﹣3x∴﹣3x2+24x=45．整理，得x2﹣8x+15=0，解得x=3或5，当x=3时，BC=24﹣9=15＞10不成立，当x=5时，BC=24﹣15=9＜10成立，∴AB长为5m；（3）S=24x﹣3x2=﹣3（x﹣4）2+48∵墙的最大可用长度为10m，0≤BC=24﹣3x≤10，∴，∵对称轴x=4，开口向下，∴当x=m，有最大面积的花圃．即：x=m，最大面积为：=24×﹣3×（）2=46.67m222. （本题满分8分）解：（1）如图作PF⊥x轴于F，QE⊥x轴于E．则OF=OP•cosα，PF=OP•sinα，∴x1=cosα，y1=sinα，故答案为cosα，sinα；（2）①结论：y1=﹣x2．理由：过点P作PF⊥x轴于点F，过点Q作QE⊥x轴于点E．∴∠PFO=∠QEO=∠POQ=90°，∴∠POF+∠OPF=90°，∠POF+∠QOE=90°，∴∠QOE=∠OPF，∵OQ=OP，∴△QOE≌△OPF，∴PF=OE，∵P（x1，y1），Q（x2，y2），∴PF=y1，OE=﹣x2，∴y1=﹣x2②当P在x轴上时，得到y1+y2的最小值为1，∵y1+y2=PF+QE=OE+OF=EF，∵四边形QEFP是直角梯形，PQ=，EF≤PQ，∴当EF=PQ=时，得到y1+y2的最大值为，∴1＜y1+y2≤．故答案为1＜y1+y2≤．23. （本题满分8分）．（2）PB=PE，理由是：如图2，连接OB，∵PB为⊙O的切线，∴OB⊥PB，∴∠OBP=90°，∴∠PBN+∠OBN=90°，∵∠OBN+∠COB=90°，∴∠PBN=∠COB，∵∠PEB=∠A+∠ACE=2∠A，∠COB=2∠A，∴∠PEB=∠COB，∴∠PEB=∠PBN，∴PB=PE；。

初四数学试题及答案

初四数学试题及答案一、选择题（每题2分，共20分）1. 下列哪个选项不是有理数？A. πB. -3C. 0.5D. √42. 如果一个数的平方等于它本身，那么这个数可能是：A. 1B. -1C. 0D. 以上都是3. 一个圆的直径是10厘米，那么它的半径是：A. 5厘米B. 10厘米C. 20厘米D. 15厘米4. 以下哪个表达式是正确的？A. (-2)^2 = -4B. √16 = 4C. (-3)^3 = -27D. √9 = -35. 如果a > b，且b > 0，那么下列哪个不等式是正确的？A. a + b < bB. a - b > 0C. a * b < 0D. a / b < 16. 下列哪个是二次根式？A. √2xB. 3x + 2C. 4x^2D. 5x^37. 一个三角形的三边长分别为3, 4, 5，这个三角形是：A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形8. 一个数的绝对值是其本身，这个数可能是：A. 正数B. 负数C. 零D. 以上都是9. 以下哪个表达式是正确的？A. 2x + 3y = 5xB. 3x - 2y = 5x + 2yC. 4x^2 - 9y^2 = (2x + 3y)(2x - 3y)D. x^2 - y^2 = (x + y)(x - y)10. 一个数的倒数是1/4，这个数是：A. 4B. 1/4C. 1/2D. 4/1二、填空题（每题2分，共20分）11. 如果一个数的相反数是-5，那么这个数是________。

12. 一个数的立方等于它本身，这个数可能是________、________、________。

13. 一个数的平方根是4，那么这个数是________。

14. 如果a + b = 10，且a - b = 2，那么2a的值是________。

15. 一个圆的周长是2πr，其中r是圆的半径，如果周长是12.56厘米，那么半径是________。

初四数学试题

参照秘密级管理☆启用前试卷类型：A初四数学试题2023.04本试题共8页，满分150分，考试时间120分钟。

考试结束后，将本试卷和答题卡一并交回。

注意事项：1．答题前，考生务必用0.5毫米黑色签字笔将学校、姓名、考试号、座号填写在答题卡和试卷规定位置，并核对条形码。

2．选择题每小题选出答案后，用2B 铅笔涂黑答题卡对应题目的答案标号；如需改动，用橡皮擦干净后，再选涂其他答案标号。

3．解答题必须用0.5毫米黑色签字笔作答，字体工整、笔迹清晰，写在答题卡各题目指定区域内；如需改动，先划掉原来答案，然后再写上新答案。

严禁使用涂改液、胶带纸修正带修改。

不允许使用计算器。

4．保证答题卡清洁、完整，严禁折叠，严禁在答题卡上做任何标记。

5．评分以答题卡上的答案为依据。

不按以上要求作答的答案无效。

一、选择题：本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

1.太阳是太阳系的中心天体，离地球最近的恒星。

太阳从中心向外可分为核反应区、辐射区、对流层和大气层，太阳的年龄约50亿年现正处于“中年阶段”。

半径为696000千米，是地球半径的109倍，696000千米用科学记数法表示为(A)56.9610⨯米(B)86.9610⨯米(C)57.010⨯米(D)87.010⨯米2.下列图形中，既是轴对称图形，又是中心对称图形的是3.在013.5-，，这四个数中，最大的数是(A)0(B)1-(C)3.5(D)(A) (B) (C) (D)4.如图，56AB BC CD DE AC CD BC =====，，⊥，点A C ，，E 在同一条直线上，则CE 的长为(A)5(B)6(C)7(D)85.不等式组2311x x ⎧+⎨⎩＞，≤的解集在数轴上表示正确的是6.不透明口袋中装有1个红球和2个白球，这些球除颜色外其余都相同，从口袋中随机摸出一个球，放回搅匀，再从口袋中随机摸出一个球，则两次摸到的球都是白球的概率是(A)23(B)19(C)29(D)497.已知函数y kx b =+的图象如图所示，则关于x 的不等式(3)0k x b ++＜的解集是(A)1x -＞(B)1x -＜(C)2x ＜(D)2x ＞8.一个圆锥的底面半径是4cm ，其侧面展开图的圆心角为120︒，则该圆锥的母线长为(A)8cm (B)12cm (C)16cm (D)24cm9.如图，在ABCD □中，3064DAB AB BC =︒==∠，，，点P 点D 出发，沿DC CB ，向终点B 匀速运动。

初中初四数学试卷

1. 下列各数中，正数是（）A. -3B. 0C. 3D. -2.52. 下列各数中，无理数是（）A. √9B. √16C. √25D. √-43. 下列各式中，正确的是（）A. a^2 = b^2 => a = bB. a^2 = b^2 => a = -bC. a^2 = b^2 => a = ±bD. a^2 = b^2 => a = 04. 若a、b是方程2x^2 - 5x + 2 = 0的两根，则a + b的值为（）A. 2B. 5C. 10D. -25. 在直角坐标系中，点A（2，3）关于x轴的对称点为（）A.（2，-3）B.（-2，3）C.（-2，-3）D.（2，-3）6. 若a、b、c是等差数列，且a + b + c = 9，则a^2 + b^2 + c^2的值为（）A. 27B. 45C. 36D. 547. 下列各函数中，是奇函数的是（）A. y = x^2B. y = x^3C. y = x^4D. y = x^58. 若sinα = 1/2，则cosα的值为（）A. √3/2B. -√3/2C. 1/2D. -1/29. 下列各三角形中，是直角三角形的是（）A. 三边长分别为3、4、5B. 三边长分别为5、12、13C. 三边长分别为6、8、10D. 三边长分别为7、24、2510. 下列各数中，是二次根式的是（）A. √4B. √-4C. √-1D. √011. 若x^2 - 4x + 3 = 0，则x的值为______。

12. 若sinα = 3/5，且α为锐角，则cosα的值为______。

13. 在等差数列{an}中，若a1 = 3，公差d = 2，则第10项an =______。

14. 若a、b、c是等比数列，且a + b + c = 24，ab = 48，则c的值为______。

15. 在直角坐标系中，点P（-3，2）到直线x + 2y - 1 = 0的距离为______。

初四数学试题

班级_____________________ 姓名____________________ 考场号____________ 考号___________----------------------------------------------------密--------------------------------封--------------------------------线------------------------------------------------ 初四数学试题班级姓名一、选择题（每小题2分）1. 在△ABC 中，90C ∠=，下列式子中必成立的是（）．Ａ．sin a c B = Ｂ．cos a c B =Ｃ．tan a c B =Ｄ．tan c a B =2. 下列函数中，二次函数是（） A ． 281y x =+ B ．81y x =+ C ．1y x=D ．211y x=+ 3. 在一坐标系内，2(0)y ax a =≠与y ax =的大致图象是（）x O yA O xyBOxyC xDO y4. 如图所示，水库大坝的横断面为梯形，坝顶宽为6米，坝高为24米，斜坡AB 的坡角为45°，斜坡CD 的坡度为i =1∶2，则坝底AD 的长为（） A ．42米B ．(30+米C ．78米D ．(30+米5. 若1)10tan(30=+α，则锐角α的度数是（）A 、200B 、300C 、400D 、5006. 某市在“旧城改造”中计划在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a 元，则购买这种草皮至少要（）A ．450a 元B ．225a 元C ．150a 元D ．300a 元7. 如图，两条宽度都是1的纸条交叉叠在一起，且它们的夹角为α，则它们重叠部分（图中阴影部分）的面积是（）A 、αsin 1B 、αcos 1C 、αsinD 、18. 如图，已知矩形ABCD 的两边AB 与BC 的比为4:5，E 是AB 上的一点，沿CE 将ΔEBC 向上翻折，若B点恰好落在边AD 上的F 点，则tan ∠DCF 等于（）．A ．43B ．34 C ．53 D ．359. 在平面直角坐标系内P 点的坐标（︒30cos ，︒45tan ），则P 点关于x 轴对称点P ／的坐标为（）A.)1,23(B.)23,1(-C.)1,23(- D.)1,23(--10. 若∠α为锐角，且αtan 是方程0322=--x x 的一个根，则αsin 等于（）A.1B.22 C.1010 D.10103 11. 如果∠A 为锐角，且cos A =41，那么∠A 的范围是（） A.0°<∠A ≤30° B .30°<∠A <45° C.45°<∠A <60° D .60°<∠A <90°班级_____________________ 姓名____________________ 考场号____________ 考号___________----------------------------------------------------密--------------------------------封--------------------------------线------------------------------------------------12. 某人沿倾斜角为β的斜坡前进100米，则他上升的最大高度是（） A ．100sin β米 B ．100sin β米 C ．100cos β米 D ．100cos β米13. 如图4，∠AOB 的顶点在坐标原点，边OB 与x 轴正半轴重合，边OA 落在第一象限，P 为OA 上一点，OP =m ，∠AOB =β，点P 的坐标为（）A ．tan tan m m ββ⎛⎫+ ⎪⎝⎭，B ．(sin cos )m m ββ，C ．tan tan m m ββ⎛⎫ ⎪⎝⎭，D ．(cos sin )m m ββ，14. 在△ABC 中，1sin cos(90)2B C =-=∠，那么△ABC 是（） A ．等腰三角形 B ．等边三角形 C ．直角三角形D ．等腰直角三角形15. 在△ABC 中，若|sin A －23|+(1－tan B )2=0，则∠C 的度数是 A.45° B.60° C.75° D.105°16. 已知△ABC 中，∠C =90°，∠A =60°，BC +AC =3+3，则BC 等于A. 3B.3C.23D.3+117. 若等腰三角形腰长为4，面积是4，则这个等腰三角形顶角的度数为 A.30°B.30°或150°C.60°D.60°或120°二、填空题（每小题3分）1. 关于x 的二次函数2(1)(1)y m xm x m =++-+，当0m =时，它是函数；当1m =-时，它是函数．2. 若二次函数2232y mx x m m =-+-的图象经过原点，则m =_________．3. 已知sin(20)cos60α+=，则α=（α为锐角）．4. 飞机在高1000m 的高空，在前进方向上同时测得桥头的俯角为30，桥尾的俯角为60，由此计算出桥长是m ．5. 已知∠B 是锐角,若1sin 22B =,则tanB 的值为_______. 6. 若α为锐角，化简αα2sin sin 21+-＝7. 函数y =622--a a ax 是二次函数，当a =_____时，其图象开口向上；当a =__ _ 时，其图象开口向下.8. 如图所示四个二次函数的图象中，分别对应的是①y ＝ax 2；②y ＝bx 2；③y ＝cx 2；④y ＝dx 2。

初四数学测试题及答案范本

初四数学测试题及答案范本题目一：简单加减法计算1. 45 + 23 = ?2. 87 - 32 = ?3. 56 + 78 = ?4. 99 - 64 = ?5. 36 + 19 = ?答案一：1. 45 + 23 = 682. 87 - 32 = 553. 56 + 78 = 1344. 99 - 64 = 355. 36 + 19 = 55题目二：乘法口诀表填空填空题：请根据乘法口诀表的规律填写下面的空格。

1 2 3 4 5 ?6 8 10 ? 15 187 ? 14 21 28 3532 ? ? ? 40 4845 54 ? ? ? ?答案二：1 2 3 4 5 66 8 10 12 15 187 9 14 21 28 3532 36 42 48 40 4845 54 63 72 81 90题目三：简单代数方程解方程：请计算下列方程中的未知数 x 的值。

1. 2x + 5 = 172. 4x - 8 = 123. 3x + 7 = 254. 5x - 10 = 205. 6x + 3 = 39答案三：1. 2x + 5 = 172x = 17 - 52x = 12x = 62. 4x - 8 = 124x = 12 + 84x = 20x = 53. 3x + 7 = 253x = 25 - 73x = 18x = 64. 5x - 10 = 205x = 20 + 105x = 30x = 65. 6x + 3 = 396x = 39 - 36x = 36x = 6题目四：几何图形计算计算下列几何图形的面积和周长。

1. 正方形：边长为8 cm2. 矩形：长为12 cm，宽为6 cm3. 圆形：半径为5 cm4. 三角形：底边长为10 cm，高为8 cm答案四：1. 正方形：边长为8 cm面积 = 边长 ×边长 = 8 cm × 8 cm = 64 cm²周长 = 4 ×边长 = 4 × 8 cm = 32 cm2. 矩形：长为12 cm，宽为6 cm面积 = 长 ×宽 = 12 cm × 6 cm = 72 cm²周长 = 2 × (长 + 宽) = 2 × (12 cm + 6 cm) = 2 × 18 cm = 36 cm 3. 圆形：半径为5 cm面积= π × 半径² = 3.14 × 5 cm × 5 cm ≈ 78.5 cm²周长= 2 × π × 半径= 2 × 3.14 × 5 cm ≈ 31.4 cm4. 三角形：底边长为10 cm，高为8 cm面积 = 1/2 ×底边长 ×高 = 1/2 × 10 cm × 8 cm = 40 cm²周长未提供足够信息，无法计算。

初四数学试题参考答案

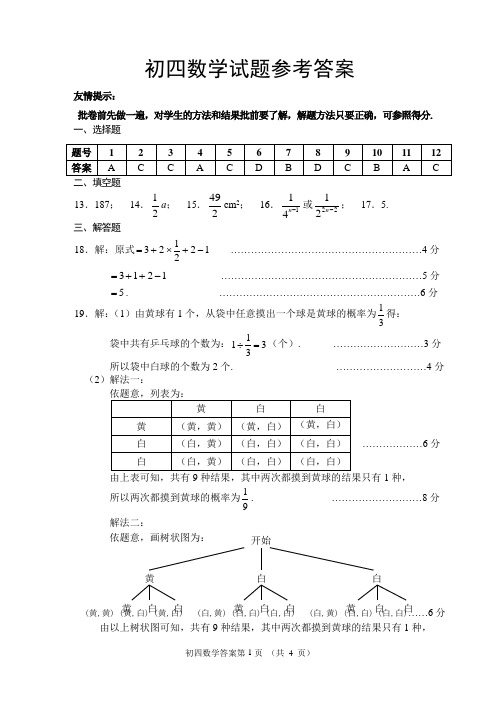
初四数学试题参考答案友情提示：批卷前先做一遍，对学生的方法和结果批前要了解，解题方法只要正确，可参照得分. 一、选择题13．187； 14．21a ； 15．492cm 2； 16．114n -或2221-n ； 17．5. 三、解答题18．解：原式122123-+⨯+= …………………………………………………4分 1213-++= ……………………………………………………5分 5=. ……………………………………………………6分19．解：（1）由黄球有1个，从袋中任意摸出一个球是黄球的概率为31得：袋中共有乒乓球的个数为：3311=÷（个）. ………………………3分所以袋中白球的个数为2个. ………………………4分（2）解法一：1种，所以两次都摸到黄球的概率为91. ………………………8分解法二：依题意，画树状图为：(黄,黄) (黄,白) (黄,白) (白,黄) (白,白) (白,白) (白,黄) (白,白) (白,白)……6分由以上树状图可知，共有9种结果，其中两次都摸到黄球的结果只有1种，………………6分开始黄白白黄白白黄白白黄白白所以两次都摸到黄球的概率为91. ………………………8分 20．（1）解：∵二次函数12)31(2-+--=a x a ax y 的对称轴是x =－2∴22)31(-=---aa ………………………2分解得a =－1 ………………………3分经检验a =－1是原分式方程的解. ………………………4分所以a =－1时，二次函数12)31(2-+--=a x a ax y 的对称轴是x =－2；…5分（2）1）当a =0时，原方程变为－x －1=0，方程的解为x = －1； ……………7分 2）当a ≠0时，原方程为一元二次方程，012)31(2=-+--a x a ax ，当△≥0时，方程总有实数根， ∵△=)12(4)31(2---a a a=122+-a a ………………………8分 =2)1(-a ≥0 ………………………9分所以a 取任何实数时，方程012)31(2=-+--a x a ax 总有实数根……10分21.（1）证明：在矩形ABCD 中，BC AD =，AD ∥BC ，︒=∠90B .∵AD ∥BC ，∴FAD BEA ∠=∠. ………………………1分 ∵DF ⊥AE ，∴︒=∠90DFA .∴DFA B ∠=∠. ………………………2分 ∵BC AE =，BC AD =，∴AD AE = ………………………3分 ∴△AEB ≌△DAF ………………………4分 ∴DF AB =. ………………………5分（2）解：由（1）可知：6==AB DF ，10==AD AE . …………………6分在Rt △AFD 中，︒=∠90DFA ，∴86102222=-=-=DF AD AF . ………………………7分 ∴2810=-=-=AF AE EF ， ………………………8分在Rt △DFE 中，︒=∠90DFE ，∴3162tan ===∠DF EF EDF . ………………………10分22.（1）证明：连接FO 并延长交⊙O 于Q ，连接DQ . ………1分∵FQ 是⊙O 直径，∴∠FDQ ＝90°.∴∠QFD ＋∠Q ＝90°.∵CD ⊥AB ，∴∠P ＋∠C ＝90°.∵∠Q ＝∠C ，∴∠QFD ＝∠P .……………3分 ∵∠FOE ＝∠POF ，∴△FOE ∽△POF .…4分 ∴OE OFOF OP=.∴OE ·OP ＝OF 2＝r 2. ………5分（2）解：（1）中的结论成立. ……………6分理由：如图2，依题意画出图形，连接FO 并延长交⊙O 于M ，连接CM . ……………7分∵FM 是⊙O 直径，∴∠FCM ＝90°，∴∠M ＋∠CFM ＝90°. ∵CD ⊥AB ，∴∠E ＋∠D ＝90°.∵∠M ＝∠D ，∴∠CFM ＝∠E. ………8分 ∵∠POF ＝∠FOE ，∴△POF ∽△FOE .…9分∴OP OFOF OE=，∴OE ·OP ＝OF 2＝r 2. ……10分 23．解：（1）设去年四月份每台A 型号彩电售价x 元，根据题意得：20004000050000=x . ………………2分解得：2500=x .经检验，2500=x 是原方程的解. ∴2500=x .答：去年四月份每台A 型号彩电售价是2500元. ………………3分（2）设电器城在此次进货中，购进A 型号彩电a 台，则B 型号彩电)20(a -台，依题意：⎩⎨⎧≤-+≥-+.33000)20(15001800,32000)20(15001800a a a a ………………5分解得：10320≤≤a . 由于a 只取非负整数，所以7=a ，8，9，10. ………………6分所以电器城在此次进货中，共有4种进货方案，分别是：方案一：购进A 型号彩电7台、B 型号彩电13台；方案二：购进A 型号彩电8台、B 型号彩电12台；方案三：购进A 型号彩电9台、B 型号彩电11台；方案四：购进A 型号彩电10台、B 型号彩电10台. ………………7分（3）设电器城获得的利润为y 元，则y 与a 的函数关系式为：6000100)20)(15001800()18002000(+-=--+-=a a a y . ……………9分 ∵6000100+-=a y ，y 随a 的增大而减小，且7=a ，8，9，10. ∴当7=a 时，y 可取得最大值，530060007100=+⨯-=最大y .第22题（图2）因此，当购进A 型号彩电7台、B 型号彩电13台时，电器城获得的利润最大，最大利润为5300元. ………………10分(注:其它解法可参照本解法给分)24. 解：（1）因为M (1,－4) 是二次函数k m x y ++=2)(的顶点坐标，所以324)1(22--=--=x x x y …………………………2分令,0322=--x x 解之得3,121=-=x x .∴A ，B 两点的坐标分别为A （－1，0），B （3,0） …………………4分（2）在二次函数的图象上存在点P ，使MAB PAB S S ∆∆=45设),,(y x p 则y y AB S PAB 221=⨯=∆，又8421=-⨯=∆AB S MAB , ∴.5,8452±=⨯=y y 即 ……5分 ∵二次函数的最小值为－4，∴5=y ……6分当5=y 时，4,2=-=x x 或.故P 点坐标为（－2，5）或（4，5）……7分（3）如图1，当直线)1(<+=b b x y 经过A 点时，可得.1=b …8分当直线)1(<+=b b x y 经过B 点时，可得.3-=b …9分由图可知符合题意的b 的取值范围为13<<-b …10分第24题。

初四数学试题

第 1 页共 3 页初四数学试题考生注意： 1、考试时间120分钟2、全卷共28题，总分120分一、选择题（本题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡相应选项上）1、若∠A 是锐角，cosA=23,则∠A 度数为（）A ．300 B. 450 C.600 D.9002、如图，在⊙O 中，直径CD 垂直于弦AB ，若∠C ＝25°，则∠BOD 的度数是（）A.25° B.30° C.40° D.50°第2题图第4题图 3、在Rt △ABC 中，∠C=90°，下列结论：①sin 2A+sin 2B=1；②cos 2A+cos 2B=1； ③tanA ﹒tanB=1；④sinA=tanA ·cosA ．正确．．的有（） A ．1个 B ．2个 C ．3个 D ．4个4、如图所示，已知⊙O 的半径为5 cm ，弦AB 的长为8 cm ，P 是AB 延长线上一点，BP ＝2 cm ，则tan ∠OPA 等于 ( ) A ．32B ．23C ．2D ．125、对于抛物线c bx ax y ++=2(a ≠0)，下面描述中错误．．的是（） A ．当a<0时，抛物线开口向下； B ．当b<0时，抛物线的对称轴在y 轴右侧； C ．当c=0时，抛物线过原点 D ．当b 2-4ac=0时，抛物线顶点在x 轴上。

6、用描点法画二次函数y ＝ax 2＋bx ＋c 图象时，某同学列出了下面的表格：x … －2 －1 0 1 2 … y … －9 －2 1 －2 －11 …由于粗心，他算错了其中一个y 的数值，则这个错误．．的数值是 ( ) A ．－9 B ．－2 C ．1 D ．－117、如图，已知河堤横断面应水坡AB 的坡比是1：3，堤高BC=5m,则坡面AB 的长度是（）A ． 15mB ．103mC ．10mD ．53m第8题图8、如图，在对角线长为2m 的正方形桌面上，用一块直径为2m 的圆桌布平铺，若四周下垂的最大长度相等，则桌布下垂的最大长度x 为（）A ．m ）1-2（2B.m ）1-2（C.m 22-2 D.m ）2-2（29、如图，图中有几对相似三角形（）A.1对B.2对C.3对D.4对10、如图，菱形ABCD 的边长是4厘米，∠B ＝60°，动点P 以1厘米秒的速度自A 点出发沿AB 方向运动至B 点停止，动点Q 以2厘米/秒的速度自B 点出发沿折线BCD 运动至D 点停止．若点P 、Q 同时出发运动了t 秒，记△BPQ 的面积为S 厘米2，下面图象中能表示S 与t 之间的函数关系的是（）A ．B ．C ．D ．二、填空题（本题共8个小题，每小题3分，共24分，答案写在答题卡上） 11、Rt △ABC 中，∠C=90°，sinA=135，则tanB= 。

初四数学试题及答案

初四数学试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是无理数？A. 3.14B. √2C. 0.33333...D. 2/3答案：B2. 一个数的平方等于它本身，这个数可能是：A. 0B. 1C. -1D. 以上都是答案：D3. 一个等腰三角形的两边长分别为3和4，那么它的周长可能是：A. 7B. 10C. 14D. 无法确定答案：B4. 如果一个二次方程的两个根的和为-5，那么这个二次方程可能是：A. x^2 - 5x + 6 = 0B. x^2 + 5x + 6 = 0C. x^2 - 5x - 6 = 0D. x^2 + 5x - 6 = 0答案：A5. 函数y = 2x + 3的图象经过的象限是：A. 第一、二、三象限B. 第一、二、四象限C. 第一、三、四象限D. 第二、三、四象限答案：C6. 一个圆的半径为5，那么它的面积是：A. 25πB. 50πC. 75πD. 100π答案：B7. 一个长方体的长、宽、高分别为2、3、4，那么它的体积是：A. 24B. 26C. 28D. 32答案：A8. 一个等差数列的前三项分别为2、5、8，那么它的第五项是：A. 11B. 14C. 17D. 20答案：B9. 函数y = x^2 - 6x + 8的最小值是：A. -1B. 0C. 1D. 8答案：A10. 一个三角形的三个内角的度数之和为：A. 90°B. 180°C. 360°D. 540°答案：B二、填空题（每题3分，共30分）11. 一个数的相反数是-5，那么这个数是_________。

答案：512. 一个数的绝对值是3，那么这个数可能是_________或_________。

答案：3或-313. 一个二次函数的顶点坐标为(2, -1)，那么它的对称轴是_________。

答案：x=214. 一个直角三角形的两直角边长分别为3和4，那么它的斜边长是_________。

初四数学联考试卷

POA· B DCEAO十二、圆一、学习目标：1、准确理解圆的有关概念及性质，会确定点与圆、直线和圆、圆和圆的位置关系；2、探索垂径定理，圆心角、弧、弦、弦心距的关系定理，圆周角与圆心角的关系定理及其推论的应用；3、探索圆的切线的性质与判定的应用；4、了解三角形的内心、外心及内切圆、外接圆的区别及联系；5、会计算弧长及扇形的面积，阴影图形的面积，圆锥的侧面积和全面积；二、知识要点：垂径定理，圆心角、弧、弦、弦心距关系定理，圆周角与圆心角关系定理；圆的切线的性质与判定的应用；圆和圆的位置关系；三角形的内切圆、外接圆的区别及联系；弧长及扇形的面积，阴影图形的面积，圆锥的侧面积和全面积；三、考点再现：1、一个点到圆的最小距离为4cm ，最大距离为9cm ，则该圆的半径是（）A 、2.5 cm 或6.5 cmB 、2.5 cmC 、6.5 cmD 、5 cm 或13cm 2、三角形的外心恰在它的一条边上，那么这个三角形是（）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、不能确定 3、如图，AB 为⊙O 的一固定直径，它把⊙O 分成上、下两个半圆，自上半圆上一点C 作弦CD ⊥AB ，∠OCD 的平分线交⊙O 于点P ，当点C 在上半圆（不包括A 、B 两点）上移动时，点P （） A 、到CD 的距离保持不变 B 、位置不变C 、等分⋂DB D 、随C 点移动而移动 4、（08长沙）如图，P 为⊙O 外一点，PA 切⊙O 于点A ，且OP=5，PA=4，则sin ∠APO 等于（A ） 54（B ） 53 （C ） 34 （D ） 435、如图，圆锥的底面半径为3cm ，高为4cm ，那么这个圆锥的侧面积是（A ）（B ）（C ）（D ）6．（08贵阳）如图，已知AB 是⊙O 的直径，点C 在O 上，且13AB =，5BC =．（1）求sin BAC ∠的值．（2）如果ODAC ⊥，垂足为D ，求AD 的长．四、典例剖析：1、（泰安）如图，AB 为⊙O 的直径，BC 与⊙O 相切与B ， AC 交⊙O 于E ，点D 是BC 边的中点，连结DE ．（1）求证：DE 与⊙O 相切；4题图PODCBA （第16题图）l43ABCD OO.A BC D E （2）若⊙O 的半径为3，3DE =，求AE ．【解析】连结BE 、OE ，利用直径、直角三角形及等腰三角形可证。