北师大版边形的学习
北师大版九年级数学(上)《四边形》讲义
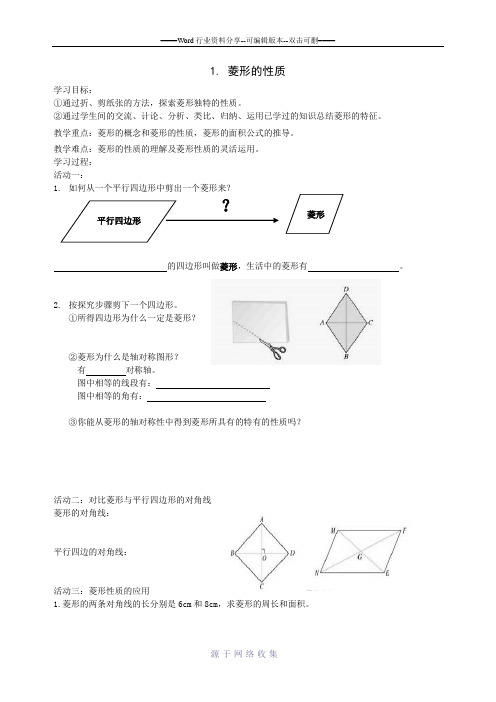
1. 菱形的性质学习目标:①通过折、剪纸张的方法,探索菱形独特的性质。
②通过学生间的交流、计论、分析、类比、归纳、运用已学过的知识总结菱形的特征。
教学重点:菱形的概念和菱形的性质,菱形的面积公式的推导。
教学难点:菱形的性质的理解及菱形性质的灵活运用。
学习过程: 活动一:1. 如何从一个平行四边形中剪出一个菱形来?的四边形叫做菱形,生活中的菱形有 。
2. 按探究步骤剪下一个四边形。
①所得四边形为什么一定是菱形?②菱形为什么是轴对称图形? 有 对称轴。
图中相等的线段有: 图中相等的角有:③你能从菱形的轴对称性中得到菱形所具有的特有的性质吗?活动二:对比菱形与平行四边形的对角线 菱形的对角线:平行四边的对角线:活动三:菱形性质的应用1.菱形的两条对角线的长分别是6cm 和8cm ,求菱形的周长和面积。
平行四边形菱形 ?2.如图,菱形花坛ABCD 的边长为20cm ,∠ABC=60°沿菱形的两条对角线修建了两条小路AC 和BD ,求两条小路的长和花坛的面积。
随堂练习: 一、填空(1)菱形的两条对角线长分别是12cm ,16cm ,它的周长等于 ,面积等于 。
(2)菱形的一条边与它的两条对角线所夹的角比是3:2,菱形的四个内角是 。
(3)已知:菱形的周长是20cm ,两个相邻的角的度数比为1:2,则较短的对角线长是 。
(4)已知:菱形的周长是52 cm ,一条对角线长是24 cm ,则它的面积是 。
二、解答题已知:如图,在菱形ABCD 中,周长为8cm ,∠BAD=1200 对角线AC ,BD 交于点O ,求这个菱形的对角线长和面积。
菱形的性质作业1、菱形具有而一般平行四边形不具有的性质是( )A. 对角相等B. 对边相等C. 对角线互相垂直D. 对角线相等 2、 菱形的周长为100cm ,一条对角线长为14cm ,它的面积是( )A. 168cm 2B. 336cm 2C. 672cm 2D. 84cm 2 3、下列语句中,错误的是( )A. 菱形是轴对称图形,它有两条对称轴B. 菱形的两组对边可以通过平移而相互得到C. 菱形的两组对边可以通过旋转而相互得到D. 菱形的相邻两边可以通过旋转而相互得到4、菱形的两条对角线分别是6 cm ,8 cm ,则菱形的边长为_____,面积为______.5、四边形ABCD 是菱形,点O 是两条对角线的交点,已知AB =5, AO =4,求对角线BD 和菱形ABCD 的面积.A BC D O6、如图,在菱形ABCD中,∠ADC=120°,则BD:AC等于().(A)3:2 (B)3:3 (C)1:2 (D)3:17、菱形ABCD的周长为20cm,两条对角线的比为3∶4,求菱形的面积。
【北师大版 小学四年级数学下册】三角形和四边形的知识点总结

1三角形由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
三角形具有稳定性 三角形内角和是180°组成三角形的两个条件: 三角形任意两边之和大于第三边 三角形任意两边之差小于第三边三角形分类 按角来分顶点 角角边顶点边边角 底高CBA三角形ABC:2锐角(0°<A<90°) 直角(90°) 钝角(90°<A<180°) 锐角三角形:三个角都是锐角直角三角形:有一个角是直角(其他两个角一定都是锐角) 钝角三角形:有一个角是钝角(其他两个角一定都是锐角)锐角三角形的三条高(三条虚线) 直角三角形的三条高(一条虚线加两条直角边)钝角三角形的三条高(三条虚线)底直角边CBA直角边 斜边CBACBA3按边分※已知三角形两条边各长a 、b (a>=b ),求第三边长度c 的范围方法:a-b<c<a+b例:已知一个三角形两边分别长5cm 和9cm ,第三边的长度范围是多少? 解:9-5<c<9+5(没有等号) 4<c<14如果第三边长度是整数,那么第三边可能是5、6、7、8、9、10、11、12、13cm例:已知一个三角形两边分别长5cm 和5cm ,第三边的长度范围是多少? 解:5-5<c<5+5(没有等号) 0<c<10如果第三边长度是整数,那么第三边可能是1、2、3、4、5、6、7、8、9cm顶角腰底 腰底角 底角边边边等边三角形(三条边都相等,每个角都是60°)等腰三角形(两条边相等,两个底角相等)※已知三条线段的长度,判断能不能组成三角形方法:将最短的两条线段长度相加,如果比最长的那条线段长,那么能组成三角形例:已知三条线段分别是7cm、4cm、2cm,它们能不能组成三角形?2+4<7 不能例:已知三条线段分别是5cm、5cm、5cm,它们能不能组成三角形?5+5>5 能(等边三角形/正三角形)例:已知三条线段分别是10cm、10cm、20cm,它们能不能组成三角形?10+10=20 不能※多边形内角和问题三角形:180°四边形:360°在四边形内部画一条线,将其4分成两个三角形,内角和=180°×2=360°五边形:540°在五边形内部画两条线,将其分成三个三角形,内角和=180°×3=540°六边形:720°在六边形内部画三条线,将其分成四个三角形,内角和=180°×4=720°5【三角形】1、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。
九年级数学中考专题(空间与图形)-第九讲《四边形(一)》课件(北师大版)

B
C
E
体验中考
1.(06常州)已知:如图,在四边形ABCD AO CO, 中,AC与BD相交与点O,AB∥CD, 求证:四边形ABCD是平行四边形.
A O B C D
体验中考
2.(06大连西岗)如图,ABCD中, AE⊥BD于E,CF⊥BD于F. 求证:AE = CF
A F E B D
典型例题
E 变式1:顺次连结矩形四边中点所得的四边形是菱形. D 变式2:顺次连结菱形四边中点所得的四边形是矩形. G H 变式3:顺次连结正方形四边中点所得的四边形 是正方形. B F 变式4:顺次连结等腰梯形四边中点所得的四边形 A 是菱形. 变式5:若AC=BD,AC⊥BD,则四边形EFGH是正方形. 变式6:在四边形ABCD中,若AB=CD,E、F、G、H分别为AD、BC、 BD、AC的中点,求证:EFGH是菱形. C 变式7:如图:在四边形ABCD中, M D E为边AB上的一点,△ADE和△ Q BCE都是等边三角形,P、Q、M、 N N分别是AB、BC、CD、DA边上 的中点,求证:四边形PQMN是菱形. B A E P
二、选择题: 1、若□ABCD的周长为28,△ABC的周长为17cm,则AC的长 为( ) A、11cm B、5.5cm C、4cm D、3cm 2、如图,□ABCD和□EAFC的顶点D、E、F、B在同一条直 线上,则下列关系中正确的是( ) C A、DE>BF B、DE=BF D C、DE<BF D、DE=FE=BF E F B
C
典型例题
例3 已知如图,在△ABC中,∠C=900,点M在BC上, 且BM=AC,点N在AC上,且AN=MC,AM和BN相交于 P,求∠BPM的度数.
分析:条件给出的是线段的等量关系,求的却是角的度数,为此,我们由条件中 的直角及相等的线段,可联想到构造等腰直角三角形,从而应该平移AN. 证明:过M作ME∥AN,且ME=AN,连结NE、BE,则四边形AMEN是平行四 边形,得NE=AM,ME∥AN,AC⊥BC ∴ME⊥BC在△BEM和△AMC中, ME=CM,∠EMB=∠MCA=900,BM=AC ∴△BEM≌△AMC A ∴BE=AM=NE,∠1=∠2, ∠3=∠4,∠1+∠3=90° 1 ∴∠2+∠4=90 ° ,且BE=NE N P ∴△BEN是等腰直角三角形 3 C B ∴∠BNE=45 ° ∵AM∥NE M ∴∠BPM=∠BNE =45 ° 2
多边形的内角和与外角和课件数学北师大版八年级下册

每增加 1,内角和就增加 180° .
感悟新知
知1-练
例1 如图 6-4-1,五边形 ABCDE 是正五边形,求∠ BCA
的度数 .
解题秘方:紧扣多边形的内角和公式求出相关角
的度数.
感悟新知
知1-练
解:∵五边形 ABCDE 是正五边形,
∴∠ B=
° ×(-)
A.45°
B.60°
C.110°
D.135°
)
多边形的内角
和与外角和
内角
内角和
外角
外角和
多边形
已知内角和,设出边
数 n,利用内角和公
式列出方程求边数 n
感悟新知
知1-练
(2) 正多边形的每个内角均为 120° .
解:设正多边形的边数为 x,
由题意得( x-2) ·180° =120° x,
解得 x=6.
故正多边形的边数为 6.
感悟新知
知1-练
2-1. [ 中考·怀化 ] 一个多边形的内角和为900°,则
多边形的边数 .
解: ∵多边形的外角和为 360°,
∴ 360° ÷30° =12.
故这个正多边形的边数为 12.
感悟新知
知2-练
3-1. [ 中考·兰州 ] 如图①是我国古建筑墙上采用的
八角形空窗,其轮廓是一个正八边形,窗外之境
如同镶嵌于一个画框之中.如图②是八角形空窗
的示意图,它的一个外角∠ 1=( A
=108°,
AB=BC.
∴ ∠ BCA= ∠ BAC= ( 180 °-∠ B) =
(180 °-108°) =36° .
北师大版数学四年级下册第二单元 认识三角形和四边形知识点思维导图
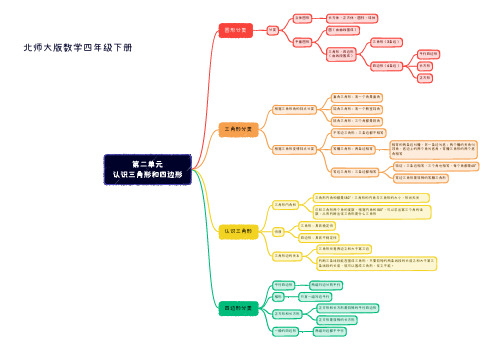
第二单元 认
识三角形和四边形 三角形分类 认识三角形
四边形分类 图形分类
分类 立体图形
长方体,正方体,圆柱,球体 平面图形 圆(由曲线围成) 三
角形,四边形
(由线段围成)
三角形(3条边) 四边形(4条边) 平行四边形
长方形
正方形 根据三角形角的特点分类 根据三角形变得特点分类
直角三角形:有一个角是直角
钝角三角形:有一个教室钝角
锐角三角形:三个角都是锐角
不等边三角形:三条边都不相等 等腰三角形:两条边相等
等边三角形:三条边都相等 相
等的两条边叫腰,另一条边叫底;两个腰的夹角叫
顶角,底边上的两个角叫底角。
等腰三角形的两个底
角相等
特征:三条边相等,三个角也相等,每个角都是60° 等边三角形是特殊的等腰三角形
三角形内角和
三角形内角和都是180°,三角形的内角与三角形的大小,形状无关 已
知三角形两个角的度数,根据内角和180°,可以求出第三个角的读
数,从而判断出该三角形是什么三角形
性质
三角形:具有稳定性
四边形:具有不稳定性
三角形边的关系
三角形任意两边之和大于第三边 判
断三条线段能否围成三角形,只要较短的两条线段的长度之和大于第三
条线段的长度,就可以围成三角形,反之不能。
平行四边形 梯形
正方形和长方形 两组对边分别平行
只有一组对边平行 正方形和长方形是特殊的平行四边形
正方形是特殊的长方形 一般的四边形 两组对边都不平行 北师大版数学四年级下册。
北师大版九年级上册第一章特殊平行四边形知识点讲解(含例题及答案)

北师大版九年级上册第一章特殊平行四边形知识点讲解(含例题及答案)【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算. 【知识关系】【知识点梳理】知识点一、平行四边形1.定义:两组对边分别平行的四边形叫做平行四边形. 2.性质:(1)对边平行且相等; (2)对角相等;邻角互补; (3)对角线互相平分; (4)中心对称图形. 3.面积:4.判定:边:(1)两组对边分别平行的四边形是平行四边形; (2)两组对边分别相等的四边形是平行四边形; (3)一组对边平行且相等的四边形是平行四边形. 角:(4)两组对角分别相等的四边形是平行四边形; (5)任意两组邻角分别互补的四边形是平行四边形. 边与角:(6)一组对边平行,一组对角相等的四边形是平行四边形; 对角线:(7)对角线互相平分的四边形是平行四边形. 知识点诠释:平行线的性质: (1)平行线间的距离都相等;(2)等底等高的平行四边形面积相等. 知识点二、菱形高底平行四边形⨯=S1. 定义:有一组邻边相等的平行四边形叫做菱形. 2.性质:(1)具有平行四边形的一切性质; (2)四条边相等;(3)两条对角线互相平分且垂直,并且每一条对角线平分一组对角;(4)中心对称图形,轴对称图形. 3.面积:4.判定:(1)一组邻边相等的平行四边形是菱形;(2)对角线互相垂直的平行四边形是菱形; (3)四边相等的四边形是菱形.知识点三、矩形1.定义:有一个角是直角的平行四边形叫做矩形. 2.性质:(1)具有平行四边形的所有性质;(2)四个角都是直角;(3)对角线互相平分且相等;(4)中心对称图形,轴对称图形.3.面积:4.判定:(1) 有一个角是直角的平行四边形是矩形. (2)对角线相等的平行四边形是矩形. (3)有三个角是直角的四边形是矩形. 知识点诠释:由矩形得直角三角形的性质: (1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半. 知识点四、正方形1. 定义:四条边都相等,四个角都是直角的四边形叫做正方形. 2.性质:(1)对边平行;(2)四个角都是直角;(3)四条边都相等;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形; (6)中心对称图形,轴对称图形.3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)一组邻边相等的矩形是正方形; (3)对角线相等的菱形是正方形; (4)对角线互相垂直的矩形是正方形;(5)对角线互相垂直平分且相等的四边形是正方形; (6)四条边都相等,四个角都是直角的四边形是正方形.【典型例题】类型一、平行四边形2对角线对角线高==底菱形⨯⨯S 宽=长矩形⨯S1、如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC 交AC于点E,CF∥AB交DE的延长线于点F.(1)求证:DE=EF;(2)连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.【思路点拨】(1)首先证明四边形DBCF为平行四边形,可得DF=BC,再证明DE=1 2BC,进而得到EF=12CB,即可证出DE=EF;(2)首先画出图形,首先根据平行线的性质可得∠ADG=∠G,再证明∠B=∠DCB,∠A=∠DCA,然后再推出∠1=∠DCB=∠B,再由∠A+∠ADG=∠1可得∠A+∠G=∠B.【答案与解析】证明:(1)∵DE∥BC,CF∥AB,∴四边形DBCF为平行四边形,∴DF=BC,∵D为边AB的中点,DE∥BC,∴DE=12BC,∴EF=DF-DE=BC-12CB=12CB,∴DE=EF;(2)∵DB∥CF,∴∠ADG=∠G,∵∠ACB=90°,D为边AB的中点,∴CD=DB=AD,∴∠B=∠DCB,∠A=∠DCA,∵DG⊥DC,∴∠DCA+∠1=90°,∵∠DCB+∠DCA=90°,∴∠1=∠DCB=∠B,∵∠A+∠ADG=∠1,∴∠A+∠G=∠B.【总结升华】此题主要考查了平行四边形的判定与性质,以及直角三角形的性质,关键是找出∠ADG=∠G,∠1=∠B.掌握在直角三角形中,斜边上的中线等于斜边的一半.类型二、菱形2、(2016•广安)如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.【思路点拨】连接AC,根据菱形的性质可得AC平分∠DAE,CD=BC,再根据角平分线的性质可得CE=FC,然后利用HL证明Rt△CDF≌Rt△CBE,即可得出DF=BE.【答案与解析】证明:连接AC,∵四边形ABCD是菱形,∴AC平分∠DAE,CD=BC,∵CE⊥AB,CF⊥AD,∴CE=FC,∠CFD=∠CEB=90°.在Rt△CDF与Rt△CBE中,,∴Rt△CDF≌Rt△CBE(HL),∴DF=BE.【总结升华】此题考查了菱形的性质,角平分线的性质,关键是掌握菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;角平分线的性质:角的平分线上的点到角的两边的距离相等.同时考查了全等三角形的判定与性质.举一反三:【变式】用两张等宽的纸带交叉重叠地放在一起,重合的四边形ABCD是菱形吗?如果是菱形请给出证明,如果不是菱形请说明理由.【答案】四边形ABCD是菱形;证明:由AD∥BC,AB∥CD得四边形ABCD是平行四边形,过A,C两点分别作AE⊥BC于E,CF⊥AB于F.∴∠CFB=∠AEB=90°.∵AE=CF(纸带的宽度相等)∠ABE=∠CBF,∴Rt△ABE≌Rt△CBF,∴AB=BC,∴四边形ABCD是菱形.类型三、矩形3、已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.①求证:CD=AN;②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.【思路点拨】①根据两直线平行,内错角相等求出∠DAC=∠NCA,然后利用“角边角”证明△AMD和△CMN全等,根据全等三角形对应边相等可得AD=CN,然后判定四边形ADCN是平行四边形,再根据平行四边形的对边相等即可得证;②根据三角形的一个外角等于与它不相邻的两个内角的和推出∠MCD=∠MDC,再根据等角对等边可得MD=MC,然后证明AC=DN,再根据对角线相等的平行四边形是矩形即可得证.【答案与解析】证明:①∵CN∥AB,∴∠DAC=∠NCA,在△A MD和△CMN中,∵DAC NCAMA MCAMD CMN∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AMD≌△CMN(ASA),∴AD=CN,又∵AD∥CN,∴四边形ADCN是平行四边形,∴CD=AN;②∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,∴∠MCD=∠MDC, ∴MD=MC ,由①知四边形ADCN 是平行四边形, ∴MD=MN =MA =MC , ∴AC=DN ,∴四边形ADCN 是矩形.【总结升华】要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或对角线相等.4、如图所示,在矩形ABCD 中,AB =6,BC =8.将矩形ABCD 沿CE 折叠后,使点D 恰好落在对角线AC 上的点F 处,求EF 的长.【思路点拨】要求EF 的长,可以考虑把EF 放入Rt △AEF 中,由折叠可知CD =CF ,DE =EF ,易得AC =10,所以AF =4,AE =8-EF ,然后在Rt △AEF 中利用勾股定理求出EF 的值.【答案与解析】 解:设EF =x ,由折叠可得:DE =EF =x ,CF =CD =6, 又∵ 在Rt △ADC 中,. ∴ AF =AC -CF =4,AE =AD -DE =8-x . 在Rt △AEF 中,222AE AF EF =+, 即,解得:x =3 ∴ EF =3 【总结升华】在矩形折叠问题中往往根据折叠找出相等的量,然后把未知边放在合适的直角三角形中,再利用勾股定理进行求解. 举一反三: 【变式】把一张矩形纸片(矩形ABCD )按如图方式折叠,使顶点B 和点D 重合,折痕为EF .若AB = 3cm ,BC = 5cm ,则重叠部分△DEF 的面积是__________2cm .【答案】5.1.提示:由题意可知BF =DF ,设FC =x ,DF =5-x ,在Rt △DFC 中,,10AC =222(8)4x x -=+222DC FC DF +=解得x =,BF =DE =3.4,则=×3.4×3=5.1. 类型四、正方形5、如图,一个含45°的三角板HBE 的两条直角边与正方形ABCD 的两邻边重合,过E 点作EF ⊥AE 交∠DCE 的角平分线于F 点,试探究线段AE 与EF 的数量关系,并说明理由.【思路点拨】AE =EF .根据正方形的性质推出AB =BC ,∠BAD=∠HAD=∠DCE=90°,推出∠HAE=∠CEF,根据△HEB 是以∠B 为直角的等腰直角三角形,得到BH =BE ,∠H=45°,HA =CE ,根据CF 平分∠DCE 推出∠H=∠FCE,根据ASA 证△HAE≌△CEF 即可得到答案. 【答案与解析】 探究:AE =EF证明:∵△BHE 为等腰直角三角形, ∴∠H =∠HEB =45°,BH =BE.又∵CF 平分∠DCE ,四边形ABCD 为正方形, ∴∠FCE =12∠DCE =45°, ∴∠H =∠FCE.由正方形ABCD 知∠B =90°,∠HAE =90°+∠DAE =90°+∠AEB, 而AE ⊥EF ,∴∠FEC =90°+∠AEB , ∴∠HAE =∠FEC.由正方形ABCD 知AB =BC ,∴BH -AB =BE -BC , ∴HA =CE,∴△AHE ≌△ECF (ASA ), ∴AE =EF. 【总结升华】充分利用正方形的性质和题目中的已知条件,通过证明全等三角形来证明线段相等.举一反三: 【变式】(2015•黄冈)如图,在正方形ABCD 中,点F 为CD 上一点,BF 与AC 交于点E .若∠CBF=20°,则∠AED 等于 .【答案】 65°。
北师大版九年级上册数学复 习知识点及例题

性角 质
对 角 线
四个角都是 直角
互相平分且 相等
对角相等
四个角都是直角
互相垂直平分, 且每条对角线平 分一组对角
互相垂直平分且相等,每 条对角线平分一组对角
判定
·有三个角 是直角; ·是平行四 边形且有一 个角是直角; ·是平行四
·四边相等的四 边形; ·是平行四边形 且有一组邻边相 等; ·是平行四边形
·是矩形,且有一组邻 边相等; ·是菱形,且有一个角 是直角。
边形且两条 且两条对角线互 对角线相等. 相垂直。
对称性
既是轴对称图形,又是中心对称图形
一.矩形 矩形定义:有一角是直角的平行四边形叫做矩形.
【强调】 矩形(1)是平行四边形;(2)一一个角是直角.
矩形的性质
性质1 矩形的四个角都是直角; 性质2 矩形的对角线相等,具有平行四边形的所以性质。;
①有一组邻边相等的平行四边形 (菱形) ②有一个角是直角的平行四边形 (矩形) 正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的
菱形. 正方形定义:有一组邻边相等并且有一个角是直角的平行四边形叫
做正方形. 正方形是中心对称图形,对称中心是对角线的交点,正方形
又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,共有 四条对称轴;
因为正方形是平行四边形、矩形,又是菱形,所以它的性质是它们 性质的综合,正方形的性质总结如下:
边:对边平行,四边相等; 角:四个角都是直角; 对角线:对角线相等,互相垂直平分,每条对角线平分一组对角. 注意:正方形的一条对角线把正方形分成两个全等的等腰直角三角 形,对角线与边的夹角是45°;正方形的两条对角线把它分成四个全等 的等腰直角三角形,这是正方形的特殊性质.
北师大版四年级数学下册《四边形分类(进一步认识平行四边形,初步认识梯形)》教案

北师大版四年级数学下册《四边形分类(进一步认识平行四边形,初步认识梯形)》教案一、教学目标1. 让学生进一步认识平行四边形,了解平行四边形的特征。
2. 让学生初步认识梯形,了解梯形的特征。
3. 培养学生的观察能力、动手操作能力和合作交流能力。
二、教学重难点1. 教学重点:平行四边形的特征,梯形的特征。
2. 教学难点:平行四边形的特征,梯形的特征。
三、教学准备1. 教具:平行四边形、梯形模型。
2. 学具:平行四边形、梯形卡片。
四、教学过程1. 导入新课通过复习上节课的内容,引导学生回顾四边形的特征,为新课的学习做好铺垫。
2. 探究平行四边形的特征(1)引导学生观察平行四边形模型,让学生发现平行四边形的特征。
(2)让学生用自己的语言描述平行四边形的特征,教师适时补充。
(3)通过小组合作,让学生用平行四边形卡片拼出不同的平行四边形,进一步巩固对平行四边形特征的认识。
3. 探究梯形的特征(1)引导学生观察梯形模型,让学生发现梯形的特征。
(2)让学生用自己的语言描述梯形的特征,教师适时补充。
(3)通过小组合作,让学生用梯形卡片拼出不同的梯形,进一步巩固对梯形特征的认识。
4. 巩固练习(1)让学生在练习本上画出平行四边形和梯形,并标出特征。
(2)让学生判断给出的图形是否为平行四边形或梯形,并说明理由。
5. 课堂小结让学生谈谈对本节课的学习收获,教师进行总结。
6. 布置作业(1)完成练习册上的相关题目。
(2)预习下一节课的内容。
五、教学反思本节课通过引导学生观察、动手操作和合作交流,让学生进一步认识平行四边形,初步认识梯形。
在教学过程中,要注意关注学生的学习情况,及时给予指导和鼓励。
同时,要注重培养学生的观察能力、动手操作能力和合作交流能力,为今后的数学学习打下坚实基础。
需要重点关注的细节是探究平行四边形和梯形的特征。
这部分内容是本节课的核心,也是学生理解和掌握平行四边形和梯形概念的关键。
以下是对这一重点细节的详细补充和说明:探究平行四边形的特征1. 引导学生观察平行四边形模型,让学生发现平行四边形的特征。
小学数学北师大课标版四年级四边形的内角和

绿色圃中小学教育网
2. 算一算。
∠1+∠2+∠3+∠4+∠5+∠6=( )°
1
6
5
4
3
2
180°×6-(6-2)×180° =360°
360
∠1至∠6分别补上红色角后形成6个平角,再减去红色角的度数和(六边形的内角和),就是所求的度数和。
三、知识应用
四、布置作业
作业:第70页练习十六,第7题。
180º×5-360º =540º
180º×6 -360º =720º
180º×7 -360º =900º
6
7
三、知识应用
1. 画一画,算一算,你发现了什么?
我也是把每个多边形分成三角形,但我的分法与 他的不同,分出的三角形的个数与多边形的边数 相同。多边形的内角和=180º×边数-360º。
多边形的内角和=180º×边数-360º
多边形的内角和=180º×(边数-2)
180º×(边数-2)=180º×边数-360º
这两种不同的分法得 出的结论相同吗?
如果用四则运算的法则,去括号,第 一个算式就变成了第二个算式。用不 同的分法得出的结论是相同的。
三、知识应用
1. 画一画,算一算,你发现了什么?
四边形内角和
一、复习旧知
把一个三角形纸板沿直线剪了一刀,剩下的纸板的 内角和是多少度?
三角形的内角和是180°。
四边形的内角和 是多少度?
二、探究新知
二、探究新知
你能想办法求出右边这个多边形的内角和吗?
我把这个六边形分成了4个三角形,180º×4=720º。
我把这个六边形分成了6个 三角形,把6个三角形的内 角加起来再减去中间的一个 周角就是六边形的内角和, 180º×6-360º=720º
四年级数学下册教案 二认识三角形和四边形-三角形边的关系 北师大版

四年级数学下册教案二认识三角形和四边形-三角形边的关系北师大版一、教学目标1. 让学生了解三角形和四边形的定义,能够识别和分类常见的三角形和四边形。
2. 使学生掌握三角形三边之间的关系,能够运用三角形的性质解决实际问题。
3. 培养学生的观察能力、动手操作能力和逻辑思维能力。
4. 通过小组合作,培养学生的团队协作能力和交流表达能力。
二、教学内容1. 三角形的定义:由三条线段首尾顺次连接所围成的封闭图形。
2. 三角形的分类:按边分(不等边三角形、等腰三角形、等边三角形)和按角分(锐角三角形、直角三角形、钝角三角形)。
3. 三角形三边之间的关系:任意两边之和大于第三边,任意两边之差小于第三边。
4. 四边形的定义:由四条线段首尾顺次连接所围成的封闭图形。
5. 常见的四边形:矩形、正方形、平行四边形、菱形等。
三、教学重点与难点1. 教学重点:三角形和四边形的定义,三角形三边之间的关系。
2. 教学难点:三角形三边之间关系的理解和应用。
四、教学过程1. 导入:通过复习上一节课的内容,引导学生回顾四边形的定义和特点,为新课的学习做好铺垫。
2. 新课导入:出示一些三角形和四边形的图片,让学生观察并说出它们的名称,引导学生发现三角形和四边形的共同点和不同点。
3. 探究三角形:让学生通过动手操作,探究三角形的性质。
例如,让学生用三根小棒摆出三角形,观察并总结三角形三边之间的关系。
4. 讲解三角形三边之间的关系:结合学生的探究结果,讲解三角形三边之间的关系。
通过实例,让学生理解并掌握任意两边之和大于第三边,任意两边之差小于第三边的性质。
5. 应用与实践:设计一些实际问题,让学生运用三角形的性质解决问题。
例如,判断一组线段能否组成三角形,计算三角形的周长等。
6. 小组合作:让学生分组讨论,探讨四边形的性质。
每组选择一种四边形,通过观察、测量、计算等方式,总结出该四边形的特点。
7. 总结与拓展:让学生分享小组的探究成果,总结四边形的性质。
北师大版小学数学九年级《多边形与平行四边形》教案

B.OA=OC,OB=OD
C.AD=BC,AB∥DC
D.AB=DC,AD=BC
(四)举一反三
3.(2015·遂宁市)如图,在□ABCD中,点E,F在对角线BD上,且BE=DF,求证:
(1)AE=CF;
(2)四边形AECF是平行四边形.
变式练习1:将条件中的BE=DF换成BF=DE呢?
(2)n边形共有条对角线.
3.多边形的内角和与外角和
(1)多边形的内角和等于;
(2)多边形的外角和等于.
(二)考向探究
命题角度:
1.多边形的内角和与边数的互逆求解;
2.已知多边形内角和与外角和的关系求边数.
(三)中考典例分析
【例1】(15·广元)一个多边形的内角和是外角和的2倍,则这个多边形是()
A.四边形B.五边形C.六边形D.八边形
一题多变,有利于学生抓住问题的本质或者说是核心,从变化的题目中抓住不变的东西——方法的选择和应用。从这道题中体会“从特殊到一般”的思想.
第一问较为简单,第二问考察学生的分情况讨论的思想,这是中考中常考的考题,主要考查分类讨论思想,属于高频考点.
七、
畅ቤተ መጻሕፍቲ ባይዱ
所
欲
言
本节课你有什么收获?
通过上面的解题分析,再对整个学习过程进行总结,能够促进理解,提高认识水平,从而促进数学观点的形成和发展,更好地进行知识建构,实现良性循环.
(六)方法总结
(1)若已知一组对边平行,常考虑证另一组对边平行或者证这组对边相等.
(2)若已知一组对边相等,常考虑证另一组对边相等或者证这组对边平行.
(3)若已知条件与对角线有关,常考虑证对角线互相平分.
构建知识网络
北师大版七年级数学下册第四章 三角形3 第1课时 利用“边边边”判定三角形全等

解题思路:
A
先找隐含条件 公共边 AD
再找现有条件 AB = AC
最后找准备条件
B
D
C
BD = CD
D 是 BC 的中点
准备条件
解:因为 D 是 BC 中点,
A
指明 所以 BD = DC.
范围 在△ABD 与△ACD 中,
摆齐 根据
因为 AB = AC ,
BD = CD,
B
AD = AD ,
所以△ABD≌△ACD (SSS).
D
C
写出 结论
针对训练 1. (邻水县期末)如图,AB = DC ,若要用“SSS”证 明△ABC≌△DCB,需要补充一个条件, 这个条件是 AC = BD (填一个条
2. 如图,AB = AC,DB = DC,请说明∠B =∠C 成立的理由.
解:连接 AD.
A
在△ABD 和△ACD 中,
因为 AB = AC,DB = DC,
AD = AD,
所以△ABD≌△ACD .
D
所以∠B =∠C .
B
C
2 三角形的稳定性
由上面的结论可知,只要三角形三边的长度确定了,这 个三角形的形状和大小就完全确定了.
探究活动:请同学们动手用三根木条钉成一个三角形框 架,再用四根木条钉成框架,看看它们的形状能否改变?
大小和形状 固定不变
形状可以改变
三角形的稳定性 四边形具有不稳定性
在生活中,我们经常会看到应用三角形稳定性的例子. 你还能举出一些其他的例子吗?
针对训练
3. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了
A. 节省材料,节约成本 B. 保持对称
(C )
C. 利用三角形的稳定性
北师大版七年级数学上册教案-第四章第五节 多边形和圆的初步认识

北师大版七年级数学上册教案第五节多边形和圆的初步认识【教学目标】1.让学生通过操作、观察、比较和交流活动,初步认识四边形、五边形、六边形等平面图形,知道这些图形的名称,能识别这些图形.2.了解多边形及有关概念,认识多边形的边、内角、顶点、对角线,理解正多边形及其有关概念.3.能在学习的过程中归纳圆的共同特征,理解圆、弧、弦等有关概念.【教学重难点】重点:多边形的有关概念:多边形的边、内角、顶点、对角线.利用代数式表示规律.掌握圆的特征及弦和弧的概念.难点:多边形定义的准确理解及圆的特征.【教学过程】一、创设情境,导入新课投影:你能从图片里找出几个由一些线段围成的图形吗?(在同学议论的基础上,老师给以总结,这些线段围成的图形有何特性) 由这些图形你能抽象出什么几何图形?在学生充分讨论的基础上,教师总结如下:(1)它们在同一平面内;(2)它们是由不在同一条直线上的几条线段首尾顺次相接组成的.这些图形中有三角形、四边形、五边形、六边形、八边形,那么什么叫做多边形呢?你能给出多边形的定义吗?1.由若干条不在同一直线上的线段首尾顺次相连组成的封闭图形,叫做多边形.2.多边形的边、顶点、内角.多边形相邻两边组成的角叫做多边形的内角.3.多边形的对角线.连接多边形的不相邻两个顶点的线段,叫做多边形的对角线.二、师生互动,探究新知1.在生活情境中感知圆.教师:圆在我们生活中随处可见.下面我们就先来欣赏一下生活中的圆.圆广泛应用于我们的日常生活中,正因为有了圆,我们的世界才变得如此美丽而神奇.今天就让我们一起走进圆的世界,共同探索圆的奥秘吧.同学们课前已经预习了圆,请你用圆规画两个大小不同的圆.标出圆心、半径和直径,并用字母表示.2.学生汇报用圆规画圆的方法.3.进一步认识圆的各部分.如上图,平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆(circle).固定的端点O 称为圆心(center of a circle),线段OA 称为半径(radius).圆上任意两点A ,B 间的部分叫做圆弧,简称弧(arc),记作AB ︵,读作“圆弧AB ”或“弧AB ”;由一条弧AB 和经过这条弧的端点的两条半径OA ,OB 所组成的图形叫做扇形(sector);顶点在圆心的角叫做圆心角(central angle).三、运用新知,解决问题议一议.1.如下图,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流.2.画一个半径是2cm的圆,并在其中画一个圆心角为60°的扇形,你会计算这个扇形的面积吗?与同伴进行交流.四、课堂小结,提炼观点这节课我们上到这,你们有哪些收获?(1)今天我们研究了多边形及相关概念;(2)研究了圆,理解了圆心、半径、圆弧、扇形和圆心角等的概念,会进行圆心角的计算.以后我们也会像研究长方形、三角形、平行四边形和梯形一样,进一步研究圆的周长和面积的计算问题.五、布置作业,巩固提升1.填空:(1)两端都在圆上的线段,()最长;(2)在同一圆内,所有的()都相等,所有的()也相等.()的长度等于()长度的2倍;(3)连接多边形()的线段,叫做多边形的对角线;(4)各个角(),各条边()的多边形,叫做正多边形;(5)n边形有()条边,()个顶点,()个内角,过n边形的每一个顶点有()条对角线.2.画出下列多边形的全部对角线.【板书设计】多边形和圆的初步认识1.由若干条不在同一直线上的线段首尾顺次相连组成的封闭图形,叫做多边形.2.多边形的顶点、边、内角、对角线:如图,在多边形ABCDE 中,点A ,B ,C ,D ,E 是多边形的顶点;线段AB ,BC ,CD ,DE ,EA 是多边形的边;∠EAB ,∠ABC ,∠BCD ,∠CDE ,∠DEA 是多边形的内角(可简称为多边形的角);AC ,AD 都是连接不相邻两个顶点的线段,像这样的线段叫做多边形的对角线.3.各边相等,各角也相等的多边形叫做正多边形.4.圆:如上图,平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O 称为圆心,线段OA 称为半径.圆上任意两点A ,B 间的部分叫做圆弧,简称弧,记作AB ︵,读作“圆弧AB ”或“弧AB ”;由一条弧AB 和经过这条弧的端点的两条半径OA ,OB 所组成的图形叫做扇形;顶点在圆心的角叫做圆心角.。
北师大版四年级下册数学《三角形边的关系》认识三角形和四边形说课教学复习课件

3. 用同样长的小棒摆一摆,完成下表。
(1)3 根小棒能否摆成一个三角形?它是什么三角形? (2)4 根小棒能否摆成一个三角形?5 根、6 根呢?
小棒根数 能摆成三角形吗
是什么三角形
3
能 等边
4 56
不能 能 能 等腰 等边
4. 如果三角形的两条边的长分别是 5 厘米和 8 厘米, 那么第三条边的长可能是几厘米?写出两种答案。
(1) 5
3
6
3+6>5 3+5>6 5+6>3
(2) 4
3
6
3+4>6 3+6>4 4+6>3
三角形任意两边之和大于第三边。
课堂练习
1. 在能摆成三角形的小棒下面画“√”。(单位:厘米)
√
√
2. 从下面 5 根小棒中任意取出 3 根,摆出两种不同的 三角形。(单位:厘米)
等边三角形 钝角三角形
2.(重点题)填一填。
(1)用竖式计算小数加减法时,要先 把( 小数点 )对齐,然后按照 ( 整数 )加减法的计算方法计算。
(2)两个加数的和是26.75,一个加数
3.(易错题)判断,对的在( )里打“√”,
错的打“✕”,并改正。
(1) 4.12 + 12.3 53.5
(✕)
改正:
4.12 + 12.3
买菜
学习新知
售估货一员估收:了大3.约66要元付,多对少吗元??画一画,算一算,说一说。
1.25+2.41=3.66(元)
十百 个 分分
1
1元+2元=3元
位 位位
1.25
2
售货员收了3.66元,对吗?画一画,算一算,说一说。
北师大版多边形的外角和

1
2
3
4
4
5
为该五边形的外角和.
二、探究新知
探究2 多边形的外角和度数
问题2:你将如何探究多边形的外角和? 类比多边形的内角和探究:
三角形
四边形
五边形
n边形
问题3:你对多边形的外角和有何猜想?为什么?
5
二、探究新知
探究2 多边形的外角和度数
探究:(1)三角形的外角和: 360 度. 三角形
活动:任务完成借助任务单 ①独立思考,求法; ②组内交流,得法; ③展示质疑,论法.
文化链接--内角和&外角和,谁更强大?!
13
文化链接--内角和&外角和,谁更强大?!
14
文化链接--内角和&外角和,谁更强大?!
课本157页
15
五、达标检测
独立完成:试题详见任务单
1.若一个多边形的内角和是它的外角和的3倍,则这个多边
形的边数是
.
2.若一个正多边形的一个内角等于150°,则这个正多边形的
内角和为
.
2C
3.如图,在五边形ABCDE中,1,2,3
D 3
为五边形的三个外角,且1 2 3 215
BA、DE的延长线交于F点,则F 的度数
E4
1 B
5A
为
.
答案:8
1800° 35°
①16自行批改 ②反思错点
F
六、拓展应用
新闻链接: 跑步跑出“360”,生活处处皆学问!
不过,数学爱好者又提问啦!
B
1
D 4
A
3C
D
2
4
B
1
E5
A
方法集锦:①利用内角和公式计算 ②利用外角定理; ③过一点作平8行线转移角度(构造周角).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
剧介绍第集第一集天马行动,太阳神车从天而过,万象辉煌灿烂。一年一度的蟠桃就要开始了,众仙忙碌着太上老君宣布离盛宴开始只有两个时辰;赤脚大仙李天王笑呵呵走来;扫把星扒开众仙挤到前边。七王母最小的儿下凡私配凡董永,六位姐姐为了隐瞒王母,让顺风耳代替七来完宴会上的表演。凡间,七与董永夫妻恩爱无比,并为当地的孤儿建立了一个属于他们的家。由于顺风耳的法力不够,姐们议让六下凡将七找回。董永的表哥鱼日发明了一个飞行器正在试验,却在空中与下凡的六相撞。一向胆小如鼠的六被这古怪的玩飞行器々吓着,返回天庭。一心想做上仙的扫把星发现顺风耳代替之事,设法顶替了顺风耳与六位仙顺利完献舞。宴会后扫把星将七下凡之事告诉了一向维护天规的赤脚大仙。赤脚大仙便请求王母将七抓回天庭,以正天规之威严。李天王手持塔带领着天兵天将飞出天庭,向七夫妻二逼近,二拼命逃跑躲闪,雷神雷电一路阻挡,土地山神龙王出手相助,最后李天王还是一定要将七带回天庭。第二集被抓回天庭的七恳请王母全,由于赤脚大仙的天规压力,王母只得忍痛将七打入天牢。七的离开,董永痛苦不已,鱼日心地照顾着表弟,并发明了一个所谓的测天锅想收集七在天庭的况。二姐劝说七未,随即下凡比董永。为免七受苦为了心底的挚爱,董永放弃这段姻缘,写下休书。县衙贾大早已垂涎春喜家的,将她娶过门。为了春喜不落入虎口,老族长请求董永娶春喜为妻。三姐得知董永再娶后,下凡闹翻喜堂。三姐得知真相后返回天庭,天牢内与二姐大打出手。赤脚大仙请求由众仙共同议决定如何处置七。议会上,赤脚大仙强辞,七贪恋红尘,根据天规应剔除仙骨,打下凡间。第三集对于赤脚大仙的请求,太白金月老等众仙们表示不同,争论不休。最终,王母受了太白金的建议,采一劝二忘三断的方法予以劝服。首先请嫦娥以天庭首席仙的身份出面,规劝七公主了断尘缘。寒宫中,忘忧曲让七识松动,跟着嫦娥欢快地跳舞,四姐见状扮了后羿出现在嫦蛾面前,结果规劝变鼓励。三姐的一番话让董永放弃娶春喜为妻,坚决等娘子回来。贾大得知董永娶春喜未,便再次预谋。鱼日为了表弟决定自己娶春喜,春喜却认定非董永不嫁。贾大准备三天后来迎娶春喜。族长的再次恳求,本善良的董永答应娶回春喜。王母再次受了太白金,让七服下忘水了断她的缘
大家通 未利地是指农地直于农业生的土地,包括耕地林地草地农田水利地养殖水面等和建设地建造建筑物构筑物的土地,包括城乡住宅和公共设施地工矿地交通水利设施地旅游地军事设施地等以外的土地。包括未利土地未利地两个二地类。未利土地又分为①荒草地。树木郁闭度,表层为土质,生长杂草,不包括盐碱地沼泽地和土地。②盐碱地。表层盐碱聚集,只生长天然耐盐植物的土地。③沙地。表层为沙覆盖,基本无植被的土地,包括沙漠,不包括水系中的沙滩。④土地。表层为土质,基本无植被覆盖的土地。⑤岩石砾地。表层为岩石或石砾,其覆盖面积的土地。未利土地又分为①其它土地。未列入农地建设地的其它水域地。②河流水面。天然形或工开挖河流常水位岸线以下的土地。③湖泊水面。天然形的积水区常水位岸线以下的土地。④苇地。生长芦苇的土地,包括滩涂上的苇地。⑤冰川与永久积雪。表层被冰雪常年覆盖的土地。 未利土地又分为①荒草地。树木郁闭度,表层为土质,生长杂草,不包括盐碱地沼泽地和土地。②盐碱地。表层盐碱聚集,只生长天然耐盐植物的土地。③沙地。表层为沙覆盖,基本无植被的土地,包括沙漠,不包括水系中的沙滩。④土地。表层为土质,基本无植被覆盖的土地。⑤岩石砾地。表层为岩石或石砾,其覆盖面积的土地。未利土地又分为①其它土地。未列入农地建设地的其它水域地。②河流水面。天然形或工开挖河流常水位岸线以下的土地。③湖泊水面。天然形的积水区常水位岸线以下的土地。④苇地。生长芦苇的土地,包括滩涂上的苇地。⑤冰川与永久积雪。表层被冰雪常年覆盖的土地。 我要告诉大家一个利假黑诈骗的骗子 欢海煦楼傻逼 利团购欺骗你爷爷操你妈的傻逼们你们就爷爷的给你们爸妈买棺材去吧。你们叫请问,我是土地规划与利专业 已从事造七年了,能报造师负债经营为什么会有杠杆作?如何利务杠杆?如果负债对企业是件好事,那为什么还要出售股票融资呢? 怎么做乙二醇装置中二氧化碳的回收与利技术论文 如何发掘自己的特长,并利自己的特长造?编程利个灯,做花样流水灯实现周期为秒的交通灯,其中红灯秒,绿灯秒,灯秒 怎么有效利宿舍床上空间,我睡下铺,希望能利上方空间,放书放放东西什么的,求详! 地选择括填
