漆安慎第二版力学基础知识总结
漆安慎《普通物理学教程:力学》第二版各单元课后习题思维方法分析

1
[3.5.3]
6
非惯性系(转动参考系)中牛顿运动定律的运用:已知受力情况(包括离心惯性力或科里奥利力)及初始条件,求运动情况
建模法、隔离法、演绎法、等效法、叠加法、图示法
3
[3.5.4][3.5.5] [3.5.6]
7
已知受力情况(包括变力 )及时间,求冲量
[4.3.7]
5
已知保守力做功,求对应势能的变化
微元法、极限法、建模法、演绎法
1
[4.4.1]
6
质点系机械能守恒定律的应用:由质点系机械能守恒,已知势能变化,求动能变化(或动能)
建模法、隔离法、演绎法
3
[4.5.1][4.5.2] [4.5.3]
7
动量守恒定律、机械能守恒定律(或动能定理)与恢复系数在对心碰撞问题中的应用
建模法、隔离法、分析法、演绎法、综合法
9
[4.6.2][4.6.3][4.6.4]
[4.6.5] [4.6.6][4.6.7] [4.6.8][4.6.9]
分析法、叠加法、演绎法
2
[2.5.4][2.5.5]
12
相遇问题:已知两质点的加速度、初速度及开始时刻的位置关系,求何时或何地相遇
叠加法、比较法
3
[2.4.5][2.4.7] [2.5.2]
13
已知自然坐标系下的运动学方程(或切向速度),求切向速度(或切向加速度或合加速度)
类比法、微元法、极限法、叠加法
漆安慎《普通物理学教程:力学》第二版
各单元课后习题思维方法分析
《质点运动学》单元中的习题分析
序号
题型
思维方法
题目数
对应习题题号
最新《力学》漆安慎(第二版)答案11章

力学(第二版)漆安慎习题解答第十一章流体力学第十一章 流体力学基本知识小结⒈理想流体就是不可压缩、无粘性的流体;稳定流动(或称定常流动)就是空间各点流速不变的流动。
⒉静止流体内的压强分布相对地球静止:gh p p gdy dp ρρ=--=21,(h 两点间高度)相对非惯性系静止:先找出等压面,再采用与惯性系相同的方法分析。
⒊连续性方程:当不可压缩流体做稳定流动时,沿一流管,流量守恒,即=∆=∆=2211s v s v Q 恒量⒋伯努力方程:当理想流体稳定流动时,沿一流线,=++221v gh p ρρ恒量⒌粘性定律:流体内面元两侧相互作用的粘性力与面元的面积、速度梯度成正比,即ηη.s f dydv ∆=为粘性系数,与物质、温度、压强有关。
⒍雷诺数及其应用 l vlR e ,ηρ=为物体某一特征长度 ⑴层流、湍流的判据:,湍流,层流;临临e e e e R R R R ><⑵流体相似律:若两种流体边界条件相似,雷诺数相同,则两种流体具有相同的动力学特征。
⒎泊肃叶公式:粘性流体在水平圆管中分层流动时,距管轴r 处的流速)(4)(2221r R lp p r v --=η11.2.1 若被测容器A 内水的压强比大气压大很多时,可用图中的水银压强计。
⑴此压强计的优点是什么?⑵如何读出压强?设 h 1=50cm,h 2=45cm,h 3=60cm,h 4=30cm ,求容器内的压强是多少大气压?解:⑴优点:可以测很高的压强,而压强计的高度不用很大 ⑵设界面处压强由右向左分别为p 0, p 1,p 2,p 3,水和水银的密度分别用ρ,ρ'表示,据压强公式,有:43323221101,',,'gh p p gh p p gh p p gh p p A ρρρρ=-=-=-=-0312*******23423434)(')(''''p h h g h h g p gh gh gh gh p gh gh gh p gh gh p gh p A +++-=++-+=+-+=++=+=∴ρρρρρρρρρρρρ用大气压表示:atm h h h h p A 43.2766050766.134530176766.1313124≈++⨯-+=++⨯-+=11.2.2 A,B 两容器内的压强都很大,现欲测它们之间的压强差,可用图中装置,Δh=50cm ,求A,B 内的压强差是多少厘米水银柱高?这个压强计的优点是什么? 解:由压强公式:11gh p p A ρ=-)(,'2221h h g p p h g p p B +∆=-∆=-ρρ h g h g h h h g p p h g gh p gh p p p B A ∆-∆=∆--+-∆++-+=-ρρρρρρ')()()()(21212211用厘米水银柱高表示:cmHg h h p p B A 3.466.13/50506.13/=-=∆-∆=-也可以忽略管中水的重量,近似认为压强差为50cmHg优点:车高雅差方便,压强计的高度不需太大。
最新力学漆安慎(第二版)答案08节

力学(第二版)漆安慎习题解答第八章弹性体的应力和应变第八章一、基本知识小结1•弹性体力学研究力与形变的规律;弹性体的基本形变有拉伸压缩形变和剪切形变,弯曲形变是由程度不同的拉伸压缩形变组成,扭转形变是由程度不同的剪切形变组成。
2•应力就是单位面积上作用的内力;如果内力与面元垂直就叫正应力,用c表示; 如果内力方向在面元内,就叫切应力,用T表示。
3•应变就是相对形变;在拉压形变中的应变就是线应变,如果10表示原长,A l表示绝对伸长或绝对压缩,则线应变c =A l/l o;在剪切形变中的应变就是切应变,用切变角书表示。
4.力与形变的基本规律是胡克定律,即应力与应变成正比。
在拉压形变中表示为c = Y c Y是由材料性质决定的杨氏模量,在剪切形变中表示为T = N书,N 是由材料性质决定的切变模量。
5.发生形变的弹性体具有形变势能:拉压形变的形变势能密度E p0弓Y 2,剪切形变的形变势能密度E p01N 26•梁弯曲的曲率与力偶矩的关系12Ybh37•杆的扭转角与力偶矩的关系NR421、思考题解答8.1作用于物体内某无穷小面元上的应力是面元两侧的相互作用力,其单位为N.这句话对不对?答:不对,应力为作用于该无穷小面元两侧单位面积上的相互作用内力,其单位为或。
其面元法向分量称正应力,切向分量称切应力。
8.2(8.1.1)式关于应力的定义当弹性体作加速运动时是否仍然适用?答:适用,(8.1.1)式中的是面元两侧的相互作用内力,它与作用于物体上的外力和物体的运动状态有关。
8.3牛顿第二定律指出:物体所受合力不为零,则必有加速度。
是否合力不为零,必产生变形,你能否举出一个合力不为零但无形变的例子?答:不一定,物体是否发生形变应看物体内应力是否为零,应力为零,则不形变。
自由落体运动,物体受重力作用,但物体内部应力为零,则不发生形变。
8. 4胡克定律是否可叙述为:当物体受到外力而发生拉伸(压缩)形变时,外力与物体的伸长(压缩)成正比,对于一定的材料,比例系数是常数,称作该材料的杨氏模量?答:不对。
最新《力学》漆安慎(第二版)答案07章

力学(第二版)漆安慎习题解答第七章刚体力学第七章 刚体力学 一、基本知识小结⒈刚体的质心定义:∑⎰⎰==dm dm r r mr m r c i i c //求质心方法:对称分析法,分割法,积分法。
⒉刚体对轴的转动惯量定义:∑⎰==dm r I r m I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量:(略) ⒊刚体的动量和质心运动定理∑==c c a m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程:∑∑==c c c c I a m F βτ(不必考虑惯性力矩)动能:221221cc c k I mv E ω+= ⒎刚体的平衡方程∑=0F, 对任意轴∑=0τ二、思考题解答7.1 火车在拐弯时所作的运动是不是平动?答:刚体作平动时固联其上的任一一条直线,在各时刻的位置(方位)始终彼此平行。
若将火车的车厢看作一个刚体,当火车作直线运行时,车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度,选取车厢上的任一点都可代替车厢整体的运动,这就是火车的平动。
但当火车拐弯时,车厢上各部分的速度和加速度都不相同,即固联在刚体上任一条直线,在各时刻的位置不能保持彼此平行,所以火车拐弯时的运动不是平动。
7.2 对静止的刚体施以外力作用,如果合外力为零,刚体会不会运动?答:对静止的刚体施以外力作用,当合外力为了零,即0i c F ma ==∑时,刚体的质心将保持静止,但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以,对某一确定点刚体所受合外力的力矩i i iM M r F ==⨯∑∑不一定为零。
由刚体的转动定律M J α=可知,刚体将发生转动。
比如,置于光滑水平面上的匀质杆,对其两端施以大小相同、方向相反,沿水平面且垂直于杆的两个作用力时,杆所受的外力的合力为零,其质心虽然保持静止,但由于所受合外力矩不为零,将作绕质心轴的转动。
漆安慎第二版力学基础知识总结

力学基础知识总结(漆安慎力学第二版)第二章⒈基本概念 22)(dt r d dt v d a dtrd v t r r====)()()(t a t v t r ⇔⇔(向右箭头表示求导运算,向左箭头表示积分运算,积分运算需初始条件:000,,v v r r t t ===)⒉直角坐标系 ,,ˆˆˆ222z y x r k z j y ix r ++=++= r与x,y,z 轴夹角的余弦分别为r z r y r x /,/,/.v v v v v k v j v i v v zy x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 v v v v v v z y x /,/,/.a a a a a k a j a i a a zy x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 ./,/,/a a a a a a z y x222222,,,,dtzd dt dv a dt y d dt dv a dt x d dt dv a dtdzv dt dy v dt dx v z z y y x x z y x =========),,(),,(),,(z y x z y x a a a v v v z y x ⇔⇔⒊自然坐标系 ||,,ˆ);(ττττv v dtds v v v s r r ====ρτττττ22222,,,ˆˆv a dts d dt dv a a a a n a a a n n n ===+=+=)()()(t a t v t s ττ⇔⇔⒋极坐标系 22,ˆˆ,ˆθθθv v v v r v v r r r r r +=+==dtd r v dt dr v r θθ==, ⒌相对运动 对于两个相对平动的参考系',0't t r r r =+=(时空变换) 0'v v v+= (速度变换) 0'a a a+= (加速度变换)若两个参考系相对做匀速直线运动,则为伽利略变换,在图示情况下,则有:zz y y x x z z y y x x a a a a a a v v v v V v v tt z z y y Vt x x =====-====-=',','',','',',',' 第三章⒈牛顿运动定律适用于惯性系、质点,牛顿第二定律是核心。
最新力学漆安慎后小结习题答案02章

力学(第二版)漆安慎习题解答第二章质点运动学第二章 质点运动学一、基本知识小结1、基本概念 22)(dtr d dt v d a dtrd v t r r====)()()(t a t v t r ⇔⇔(向右箭头表示求导运算,向左箭头表示积分运算,积分运算需初始条件:000,,v v r r t t ===)2、直角坐标系 ,,ˆˆˆ222z y x r k z j y i x r ++=++= r 与x,y,z 轴夹角的余弦分别为 r z r y r x /,/,/.v v v v v k v j v i v v z y x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 v v v v v v z y x /,/,/. a a a a a k a j a i a a z y x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 ./,/,/a a a a a a z y x222222,,,,dt zd dt dv a dt y d dt dv a dt x d dt dv a dtdzv dt dy v dt dx v z z y y x x z y x =========),,(),,(),,(z y x z y x a a a v v v z y x ⇔⇔3、自然坐标系 ||,,ˆ);(ττττv v dtds v v v s r r ====ρτττττ22222,,,ˆˆv a dts d dt dv a a a a n a a a n n n ===+=+= )()()(t a t v t s ττ⇔⇔4、极坐标系 22,ˆˆ,ˆθθθv v v v r v v r r r r r +=+== dtd rv dt dr v r θθ==,5、相对运动 对于两个相对平动的参考系 ',0't t r r r =+=(时空变换) 0'v v v+= (速度变换) 0'a a a+= (加速度变换)若两个参考系相对做匀速直线运动,则为伽利略变换,在图示情况下,则有: zz y y x x z z y y x x a a a a a a v v v v V v v t t z z y y Vt x x =====-====-=',','',','',',','y y' Vo x o' x' z z'二、思考题解答2.1质点位置矢量方向不变,质点是否作直线运动?质点沿直线运动,其位置矢量是否一定方向不变?解答:质点位置矢量方向不变,质点沿直线运动。
最新《力学》漆安慎(第二版)答案04章

力学(第二版)漆安慎习题解答第四章动能和势能第四章 动能和势能 一、基本知识小结1、功的定义式:⎰⋅=2112r r rd F A直角坐标系中:⎰⎰+==221121,,1212y x y x yxx x x dy F dx F A dx F A ,自然坐标系中:⎰=2112s s ds F A τ极坐标系中: ⎰+=2211,,12θθθθr r rrd F dr F A2、⎰⋅-=-=b ap p k r d F a E b E mv E 保势能动能)()(,212重力势能m g y y E p =)(弹簧弹性势能 2)(21)(l r k r E p -=静电势能 rQqr E p πε4)(=3、动能定理适用于惯性系、质点、质点系 ∑∑∆=+k E A A 内外4、机械能定理适用于惯性系 ∑∑+∆=+)p k E E A A (非保内外5、机械能守恒定律适用于惯性系若只有保守内力做功,则系统的机械能保持不变,C E E p k =+6、碰撞的基本公式接近速度)(分离速度(牛顿碰撞公式)动量守恒方程)e v v e v v v m v m v m v m =-=-+=+)((2010122211202101对于完全弹性碰撞 e = 1 对于完全非弹性碰撞 e = 0对于斜碰,可在球心连线方向上应用牛顿碰撞公式。
7、克尼希定理 ∑+=22'2121i i c k v m mv E绝对动能=质心动能+相对动能应用于二体问题 222121u mv E c k μ+=212121m m m m m m m +=+=μ u 为二质点相对速率二、思考题解答4.1 起重机起重重物。
问在加速上升、匀速上升、减速上升以及加速下降、匀速下降、减速下降六种情况下合力之功的正负。
又:在加速上升和匀速上升了距离h 这两种情况中,起重机吊钩对重物的拉力所做的功是否一样多?答:在加速上升、匀速上升、减速上升以及加速下降、匀速下降、减速下降六种况下合力之功的正负分别为:正、0、负、正、0、负。
最新《力学》漆安慎(第二版)课后小结习题答案02章

力学(第二版)漆安慎习题解答第二章质点运动学第二章 质点运动学一、基本知识小结1、基本概念 22)(dtr d dt v d a dtrd v t r r====)()()(t a t v t r ⇔⇔(向右箭头表示求导运算,向左箭头表示积分运算,积分运算需初始条件:000,,v v r r t t ===)2、直角坐标系 ,,ˆˆˆ222z y x r k z j y i x r ++=++= r 与x,y,z 轴夹角的余弦分别为 r z r y r x /,/,/.v v v v v k v j v i v v zy x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 v v v v v v z y x /,/,/. a a a a a k a j a i a a z y x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 ./,/,/a a a a a a z y x222222,,,,dt zd dt dv a dt y d dt dv a dt x d dt dv a dtdzv dt dy v dt dx v z z y y x x z y x =========),,(),,(),,(z y x z y x a a a v v v z y x ⇔⇔3、自然坐标系 ||,,ˆ);(ττττv v dtds v v v s r r ====ρτττττ22222,,,ˆˆv a dts d dt dv a a a a n a a a n n n ===+=+= )()()(t a t v t s ττ⇔⇔ 4、极坐标系 22,ˆˆ,ˆθθθv v v v r v v r r r r r +=+== dtd r v dt dr v r θθ==,5、相对运动 对于两个相对平动的参考系 ',0't t r r r =+=(时空变换) 0'v v v+= (速度变换) 0'a a a+= (加速度变换)若两个参考系相对做匀速直线运动,则为伽利略变换,在图示情况下,则有: zz y y x x z z y y x x a a a a a a v v v v V v v t t z z y y Vt x x =====-====-=',','',','',',','y y' Vo x o' x' z z'第2章 质点运动学 力学(第二版)漆安慎课后答案 二、思考题解答2.1质点位置矢量方向不变,质点是否作直线运动?质点沿直线运动,其位置矢量是否一定方向不变?解答:质点位置矢量方向不变,质点沿直线运动。
最新《力学》漆安慎(第二版)答案06章

力学(第二版)漆安慎习题解答第六章万有引力定律第六章万有引力定律一、基本知识小结⒈ 开普勒定律⑴ 行星沿椭圆轨道绕太阳运行,太阳位于一个焦点上⑵ 行星位矢在相等时间内扫过相等面积⑶ 行星周期平方及半长轴立方成正比 T 2/a 3=C⒉ 万有引力定律 2r mM G f =⒊ 引力势能 r mM p G r E -=)(⒋ 三个宇宙速度环绕速度 s km Rg V /9.71==脱离速度 122V V == 11.2 km/s逃逸速度 V 3 = 16.7 km/s.二、思考题解答6.1卡文迪什在1798年17卷《哲学学报》发表他关于引力常测量时,提到他实验是为测定出地球的密度。
试为什么测出G,就能测出地球的密度?答:设地面物体质量为m,地球质量为M,地球半径为R则二者之间的万有引力约为:由上式可以看出R,g都是可测量量,只要测出G,就能通过上间接测出地球密度。
6.2你有什么办法用至少那些可测量量求出地球质量、太阳质量、及地球太阳之间的距离?答:1)地球质量:设地面物体质量为m,地球质量为M,地球半径为R则二者之间的万有引力约为:因此,只要测出了地球半径R,就能求出地球质量M。
2)地球太阳之间的距离:设地球绕太阳运动的周期为,轨道半径为,太阳系的另一行星(离地球越近越好的周期为,轨道半径为,根据开普勒第三定律有:,即,由于人类早就对行星进行长期观测了, ,为已知,只需测出另一行星的轨道半径(这一距离需用视差法测量,需两个以上的天文台同时测量),便可知地球太阳之间的距离r。
3)太阳的质量:设太阳质量为M,地球质量为m,地球太阳之间的距离r,则二者之间的万有引力约为:,因此只需测得地球太阳之间的距离r,就可求出太阳质量为M。
三、习题解答6.1.1设某行星绕中心天体以公转周期T 沿圆轨道运行,试用开普勒第三定律证明:一个物体由此轨道自静止而自由下落至中心天体所需的时间为π2Tt =.证明:物体自由下落的加速度就是在行星上绕中心天体公转的向心加速度: 2222/41)2(T R RT R R v a ππ=⋅== 由自由落体公式:π2221/2,T a R t at R === (此题原来答案是:24Tt =,这里的更正及解答仅供参考)6.2.1 土星质量为5.7×1026kg ,太阳质量为2.0×1030kg ,两者的平均距离是1.4×1012m.⑴太阳对土星的引力有多大?⑵设土星沿圆轨道运行,求它的轨道速度。
力学答案(漆安慎,杜婵英)详解第一章物理学和力学

第一章 物理学和力学1.1国际单位制中的基本单位是那些?解答,基本量:长度、质量、时间、电流、温度、物质的量、光强度。
基本单位:米(m)、千克(kg)、时间(s)、安培(A)、温度(k)、摩尔(mol)、坎德拉(cd)。
力学中的基本量:长度、质量、时间。
力学中的基本单位:米(m)、千克(kg)、时间(s)。
1.2中学所学习的匀变速直线运动公式为201,2s v t at =+ 各量单位为时间:s(秒),长度:m(米),若改为以h(小时)和km(公里)作为时间和长度的单位,上述公式如何?若仅时间单位改为h,如何?若仅单位改为km/h,又如何?0v 解答,(1)由量纲,1dim v LT −=2dim a LT −=,331/10/103600/ 3.6/3600m s km h km h km h −−==×=2323221/10/()103600/ 3.623600/3600m s km h km h km h −−==×=× 改为以h(小时)和km(公里)作为时间和长度的单位时,2013.6 3.63600,2s v t at =+××(速度、加速度仍为SI 单位下的量值)验证一下: 20 2.0/, a 4.0m/s , t 3600s 1.0h v m s ==== 利用201,2s v t at =+计算得: 21236004360072002592000025927200()2s m =×+××=+= 利用2013.6 3.63600,2s v t at =+××计算得 213.621 3.63600417.22592025927.2()2s k =××+××××=+=m (2). 仅时间单位改为h由量纲,得1dim v LT −=2dim a LT −=1//3600/3600/3600m s m h m h m h === 222221//()3600/3600/3600m s m h m h m h ===2 若仅时间单位改为h,得:220136003600,2s v t a =+×t 验证一下:20 2.0/, a 4.0m/s , t 3600s 1.0h v m s ====利用201,2s v t at =+计算得: 21236004360072002592000025927200()2s m =×+××=+= 利用220136003600,2s v t a =+×t 计算得: 22136002136004172002592000025927200()2s m =××+×××=+= (3). 若仅单位改为km/h 0v 由量纲,得1dim v LT −=31/10/() 3.6/36001//3.6m s km h km h km h m s −===,仅单位改为km/h,因长度和时间的单位不变,将km/h 换成m/s 得0v 2011,3.62s v t at =+ 验证一下: 20 2.0/, a 4.0m/s , t 3600s 1.0h v m s ====利用201,2s v t at =+计算得:21236004360072002592000025927200()2s m =×+××=+= 利用2011,3.62s v t at =+计算得: 321210136004360072002592000025927200()3.61/36002s m −×=××+××=+= 1.3设汽车行驶时所受阻力f 与汽车的横截面积S 成正比,且与速率v 之平方成正比。
最新《力学》漆安慎(第二版)答案03章

力学(第二版)漆安慎习题解答第三章动量定理及其守恒定律第三章 动量定理及其守恒定律一、基本知识小结1、牛顿运动定律适用于惯性系、质点,牛顿第二定律是核心。
矢量式:22dtr d m dt v d m a m F === 分量式:(弧坐标)(直角坐标)ρτττ2,,,v m ma F dt dv m ma F ma F ma F ma F n n z z y y x x =======2、动量定理适用于惯性系、质点、质点系。
导数形式:dtp d F =;微分形式:p d dt F=;积分形式:p dt F I∆==⎰)((注意分量式的运用)3、动量守恒定律适用于惯性系、质点、质点系。
若作用于质点或质点系的外力的矢量和始终为零,则质点或质点系的动量保持不变。
即∑==恒矢量。
则,若外p F0(注意分量式的运用)4、在非惯性系中,考虑相应的惯性力,也可应用以上规律解题。
在直线加速参考系中:0*a m f-=在转动参考系中:ωω⨯=='2,*2*mv f r m f k c5、质心和质心运动定理⑴∑∑∑===i i c i i c i i c a m a m v m v m r m r m⑵∑=c a m F(注意分量式的运用)二、思考题解答3.1试表述质量的操作型定义。
解答,kgv v m m 00 ∆∆= 式中kg 1m 0=(标准物体质量);0v∆:为m 与m 0碰撞m 0的速度改变;v∆:为m 与m 0碰撞m 的速度改变,这样定义的质量,其大小反映了质点在相互作用的过程中速度改变的难易程度,或者说,其量值反映了质量惯性的大小。
这样定义的质量为操作型定义。
3.2如何从动量守恒得出牛顿第二、第三定律,何种情况下牛顿第三定律不成立? 解答,由动量守恒 )p p (p p ,p p p p 22112121-'-=-'+='+' ,p p 21∆-=∆t p t p 21∆∆-=∆∆,取极限dt p d dt p d 21 -=动量瞬时变化率是两质点间的相互作用力。
漆安慎《普通物理学教程:力学》第二版《刚体力学》单元思维方法分析一览表

匀速转动的角速度公式
演绎法、类比法
线量与角量的关系
图示法、微元法、比较法、极限法、分析法
(三)角速度矢量
角速度矢量
图示法
角加速度也是矢量
微元法、比较法、极限法
角速度和角加速度在直角坐标系中表示
分析法、等效法
(四)刚体的平面运动
刚体作平面运动的概念
抽象概括
描述刚体的平面运动方法
分析法、叠加法、等效法
等效法
滚动摩擦和滑动摩擦的比较
等效法
*(五)汽车轮的受力 汽车的极限速度
利用力偶矩和力矩平衡知识讨论汽车轮的受力和极限速度
演绎法
7.6刚体的平衡
(一)刚体的平衡方程
在平面力系作用下刚体的平衡方程
√
演绎法、综合法
刚体平衡方程的其他形式
等效法
(二)杆的受力特点
杆在三个理想条件下的受力特点
建模法
7.7自转与旋进
角坐标概念
类比法、图示法
刚位移的概念
√
比较法、类比法
瞬时角速度的概念
√
比较法、微元法、极限法
瞬时角加速度的概念
√
比较法、微元法、极限法
求角坐标随时间的变化规律
√
微元法、极限法、叠加法、类比法
求角速度随时间的变化规律
√
微元法、极限法、叠加法、类比法
匀速转动的运动学方程
(一)常平架回转仪
常平架回转仪
演绎法
(二)回转仪的旋进
用角动量定理研究旋进
演绎法
(三)地球的旋进与章动
旋进与章动的概念
等效法、图示法
漆安慎《普通物理学教程:力学》第二版
《刚体力学》单元思维方法分析一览表
最新力学漆安慎第二版答案06章

力学(第二版)漆安慎习题解答第六章万有引力定律第六章万有引力定律一、基本知识小结⒈ 开普勒定律⑴ 行星沿椭圆轨道绕太阳运行,太阳位于一个焦点上⑵ 行星位矢在相等时间内扫过相等面积⑶ 行星周期平方与半长轴立方成正比 T 2/a 3=C⒉ 万有引力定律 2rm M G f = ⒊ 引力势能 r m Mp G r E -=)(⒋ 三个宇宙速度环绕速度 s km Rg V /9.71==脱离速度 122V V == 11.2 km/s逃逸速度 V 3 = 16.7 km/s.二、思考题解答6.1卡文迪什在1798年17卷《哲学学报》发表他关于引力常测量时,提到他实验是为测定出地球的密度。
试为什么测出G,就能测出地球的密度?答:设地面物体质量为m,地球质量为M,地球半径为R则二者之间的万有引力约为:由上式可以看出R,g都是可测量量,只要测出G,就能通过上间接测出地球密度。
6.2你有什么办法用至少那些可测量量求出地球质量、太阳质量、及地球太阳之间的距离?答:1)地球质量:设地面物体质量为m,地球质量为M,地球半径为R则二者之间的万有引力约为:因此,只要测出了地球半径R,就能求出地球质量M。
2)地球太阳之间的距离:设地球绕太阳运动的周期为,轨道半径为,太阳系的另一行星(离地球越近越好的周期为,轨道半径为,根据开普勒第三定律有:,即,由于人类早就对行星进行长期观测了, ,为已知,只需测出另一行星的轨道半径(这一距离需用视差法测量,需两个以上的天文台同时测量),便可知地球太阳之间的距离r。
3)太阳的质量:设太阳质量为M,地球质量为m,地球太阳之间的距离r,则二者之间的万有引力约为:,因此只需测得地球太阳之间的距离r,就可求出太阳质量为M。
三、习题解答6.1.1设某行星绕中心天体以公转周期T 沿圆轨道运行,试用开普勒第三定律证明:一个物体由此轨道自静止而自由下落至中心天体所需的时间为π2Tt =.证明:物体自由下落的加速度就是在行星上绕中心天体公转的向心加速度:2222/41)2(T R RT R R v a ππ=⋅== 由自由落体公式:π2221/2,T a R t at R === (此题原来答案是:24Tt =,这里的更正与解答仅供参考)6.2.1 土星质量为5.7×1026kg ,太阳质量为2.0×1030kg ,两者的平均距离是1.4×1012m.⑴太阳对土星的引力有多大?⑵设土星沿圆轨道运行,求它的轨道速度。
漆安慎《普通物理学教程:力学》第二版《相对论简介》单元思维方法分析一览表
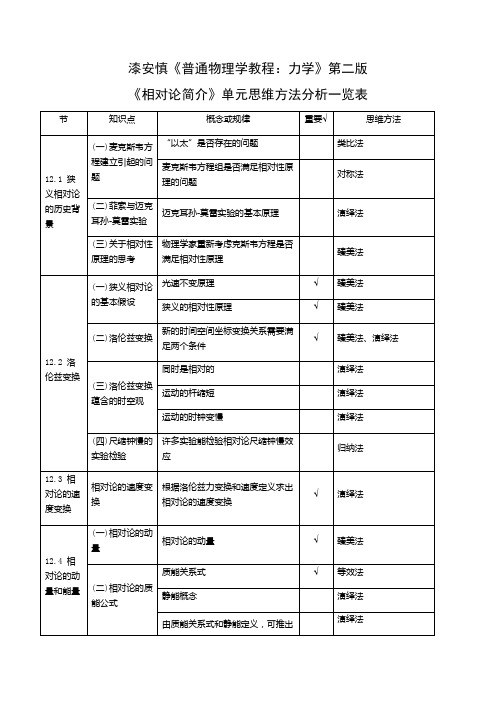
物理学家重新考虑克斯韦方程是否满足相对性原理
臻美法
12.2洛伦兹变换
(一)狭义相对论的基本假设
光速不变原理
√
臻美法
狭义的相对性原理
√
臻美法
(二)洛伦兹变换
新的时间空间坐标变换关系需要满足两个条件
√
臻美法、演绎法
(三)洛伦兹变换蕴含的时空观
同时是相对的
演绎法
运动的杆缩短
演绎法
漆安慎《普通物理学教程:力学》第二版
《相对论简介》单元思维方法分析一览表
节思维方法
12.1狭义相对论的历史背景
(一)麦克斯韦方程建立引起的问题
“以太”是否存在的问题
类比法
麦克斯韦方程组是否满足相对性原理的问题
对称法
(二)菲索与迈克耳孙-莫雷实验
迈克耳孙-莫雷实验的基本原理
演绎法
运动的时钟变慢
演绎法
(四)尺缩钟慢的实验检验
许多实验能检验相对论尺缩钟慢效应
归纳法
12.3相对论的速度变换
相对论的速度变换
根据洛伦兹力变换和速度定义求出相对论的速度变换
√
演绎法
12.4相对论的动量和能量
(一)相对论的动量
相对论的动量
√
臻美法
(二)相对论的质能公式
质能关系式
√
等效法
静能概念
演绎法
由质能关系式和静能定义,可推出总能等于动能加静能
归纳法
臻美法
(二)等效原理和广义相对性原理
弱等效原理
等效法
强等效原理
等效法
广义相对性原理
等效法
局域惯性系
微元法、建模法
*12.6引力场与弯曲时空
《力学》漆安慎答案07章

力学(第二版)漆安慎习题解答第七章刚体力学第七章刚体力学一、基本知识小结1.刚体的质心定义:r c m i r i/ m r c rdm/ dm求质心方法:对称分析法,分割法,积分法。
2.刚体对轴的转动惯量定义:I m i r i2I r2dm平行轴定理I o = l c+md2正交轴定理I z = X+I y.常见刚体的转动惯量:(略)3.刚体的动量和质心运动定理p mv c F ma c4.刚体对轴的角动量和转动定理L I I5.刚体的转动动能和重力势能E k ?I 2E p mgy c6•刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程: F ma c c I c c(不必考虑惯性力矩)动能:E k 2mv;今I c c27.刚体的平衡方程、思考题解答火车在拐弯时所作的运动是不是平动答:刚体作平动时固联其上的任一一条直线,在各时刻的位置(方位)始终彼此平行。
若将火车的车厢看作一个刚体,当火车作直线运行时,车厢上各部分具有平行运动的轨迹、相同的运动速度和加速度,选取车厢上的任一点都可代替车厢整体的运动,这就是火车的平动。
但当火车拐弯时,车厢上各部分的速度和加速度都不相同,即固联在刚体上任一条直线,在各时刻的位置不能保持彼此平行,所以火车拐弯时的运动不是平动。
对静止的刚体施以外力作用,如果合外力为零,刚体会不会运动r r答:对静止的刚体施以外力作用,当合外力为了零,即Fi ma c 0时,刚体的质心将保持静止,但合外力为零并不表明所有的外力都作用于刚体的同一点。
所以,对某一确定点刚体所受合外力的力矩M Mi r i Fi不一定为零。
由刚体的转动定律M J可知,刚体将发生转动。
比如,置于光滑水平面上的匀质杆,对其两端施以大小相同、方向相反,沿水平面且垂直于杆的两个作用力时,杆所受的外力的合力为零,其质心虽然保持静止,但由于所受合外力矩不为零,将作绕质心轴的转动。
如果刚体转动的角速度很大,那么(1)作用在它上面的力是否一定很大(2)作用在它上面的力矩是否一定很大M r i F sin j J J「答:由刚体的定轴转动定律dt可知,刚体受对轴的合外力矩正比于绕定轴转动角速度的时间变化率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力学基础知识总结(漆安慎力学第二版)第二章⒈基本概念 22)(dt r d dt v d a dtrd v t r r====)()()(t a t v t r ⇔⇔(向右箭头表示求导运算,向左箭头表示积分运算,积分运算需初始条件:000,,v v r r t t ===)⒉直角坐标系 ,,ˆˆˆ222z y x r kz j y i x r ++=++= r与x,y,z 轴夹角的余弦分别为r z r y r x /,/,/.v v v v v k v j v i v v zy x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 v v v v v v z y x /,/,/.a a a a a k a j a i a a zy x z y x ,,ˆˆˆ222++=++=与x,y,z 轴夹角的余弦分别为 ./,/,/a a a a a a z y x222222,,,,dtz d dt dv a dt y d dt dv a dt x d dt dv a dtdzv dt dy v dt dx v z z yy x x z y x =========),,(),,(),,(z y x z y x a a a v v v z y x ⇔⇔⒊自然坐标系 ||,,ˆ);(ττττv v dtdsv v v s r r ====ρτττττ22222,,,ˆˆv a dt s d dt dv a a a a n a a a n n n ===+=+=)()()(t a t v t s ττ⇔⇔⒋极坐标系 22,ˆˆ,ˆθθθv v v v r v v rr r r r +=+==dtd rv dt dr v r θθ==, ⒌相对运动 对于两个相对平动的参考系',0't t r r r =+=(时空变换)0'v v v+= (速度变换) 0'a a a+= (加速度变换)若两个参考系相对做匀速直线运动,则为伽利略变换,在图示情况下,则有:zz y y x x z z y y x x a a a a a a v v v v V v v tt z z y y Vt x x =====-====-=',','',','',',',' 第三章⒈牛顿运动定律适用于惯性系、质点,牛顿第二定律是核心。
矢量式:22dtr d m dt v d m a m F=== 分量式:(弧坐标)(直角坐标)ρτττ2,,,v m ma F dt dv m ma F ma F ma F ma F n n z z y y x x =======⒉动量定理适用于惯性系、质点、质点系。
导数形式:dt pd F =微分形式:p d dt F=积分形式:p dt F I∆==⎰)((注意分量式的运用)⒊动量守恒定律适用于惯性系、质点、质点系。
若作用于质点或质点系的外力的矢量和始终为零,则质点或质点系的动量保持不变。
即∑==恒矢量。
则,若外p F0 (注意分量式的运用)⒋在非惯性系中,考虑相应的惯性力,也可应用以上规律解题。
在直线加速参考系中:0*a m f-= 在转动参考系中:ωω⨯=='2,*2*mv f r m f k c ⒌质心和质心运动定理 ⑴∑∑∑===i i c ii c i i c a m a m v m v m r m r m⑵∑=c a m F(注意分量式的运用)第四章⒈功的定义式:⎰⋅=2112r r r d F A直角坐标系中:⎰⎰+==221121,,1212y x y x yxx x xdy F dx F A dxF A ,自然坐标系中:⎰=2112s s ds F A τ极坐标系中: ⎰+=2211,,12θθθθr r rrd F dr F A⒉⎰⋅-=-=b ap p k r d F a E b E mv E 保势能动能)()(,212重力势能 mgy y E p =)( 弹簧弹性势能 2)(21)(l r k r E p -= 静电势能 rQqr E p πε4)(=⒊动能定理适用于惯性系、质点、质点系∑∑∆=+k E A A内外⒋机械能定理适用于惯性系∑∑+∆=+)p k E E A A(非保内外⒌机械能守恒定律适用于惯性系若只有保守内力做功,则系统的机械能保持不变,C E E p k =+⒍碰撞的基本公式接近速度)(分离速度(牛顿碰撞公式)动量守恒方程)e v v e v v v m v m v m v m =-=-+=+)((2010122211202101 对于完全弹性碰撞 e = 1对于完全非弹性碰撞 e = 0对于斜碰,可在球心连线方向上应用牛顿碰撞公式。
⒎克尼希定理∑+=22'2121i i c k v m mv E 绝对动能=质心动能+相对动能 应用于二体问题 222121u mv E c k μ+=212121m m m m m m m +=+=μu 为二质点相对速率第五章⒈力矩力对点的力矩 F r o⨯=τ力对轴的力矩 ⊥⊥⨯=F r k zˆτ⒉角动量质点对点的角动量 p r L o⨯=质点对轴的角动量 ⊥⊥⨯=p r k L zˆ⒊角动量定理适用于惯性系、质点、质点系⑴质点或质点系对某点的角动量对时间的变化率等于作用于质点或质点系的外力对该点的力矩之和∑=dt L d 0 外τ⑵质点或质点系对某轴的角动量对时间的变化率等于作用于质点或质点系的外力对该轴的力矩之和∑=dtdL zz τ⒋角动量守恒定律适用于惯性系、质点、质点系⑴若作用于质点或质点系的外力对某点的力矩之和始终为零,则质点或质点系对该点的角动量保持不变⑵若作用于质点或质点系的外力对某轴的力矩之和始终为零,则质点或质点系对该轴的角动量保持不变⒌对质心参考系可直接应用角动量定理及其守恒定律,而不必考虑惯性力矩。
第六章⒈ 开普勒定律⑴ 行星沿椭圆轨道绕太阳运行,太阳位于一个焦点上 ⑵ 行星位矢在相等时间内扫过相等面积⑶ 行星周期平方与半长轴立方成正比 T 2/a 3=C ⒉ 万有引力定律 2r m M Gf = ⒊ 引力势能 rm M p G r E -=)(⒋ 三个宇宙速度 环绕速度 s km Rg V /9.71==脱离速度 122V V == 11.2 km/s逃逸速度 V 3 = 16.7 km/s.第七章⒈刚体的质心定义:∑⎰⎰==dm dm r r mr m r c i i c //求质心方法:对称分析法,分割法,积分法。
⒉刚体对轴的转动惯量定义:∑⎰==dm r I rm I ii 22平行轴定理 I o = I c +md 2 正交轴定理 I z = I x +I y.常见刚体的转动惯量:(略) ⒊刚体的动量和质心运动定理∑==c ca m F v m p⒋刚体对轴的角动量和转动定理∑==βτωI I L⒌刚体的转动动能和重力势能c p k mgy E I E ==221ω⒍刚体的平面运动=随质心坐标系的平动+绕质心坐标系的转动动力学方程:∑∑==c c ccI a m F βτ(不必考虑惯性力矩)动能:221221cc c k I mv E ω+= ⒎刚体的平衡方程∑=0F, 对任意轴∑=0τ第八章⒈弹性体力学研究力与形变的规律;弹性体的基本形变有拉伸压缩形变和剪切形变,弯曲形变是由程度不同的拉伸压缩形变组成,扭转形变是由程度不同的剪切形变组成。
⒉应力就是单位面积上作用的内力;如果内力与面元垂直就叫正应力,用σ表示;如果内力方向在面元内,就叫切应力,用τ表示。
⒊应变就是相对形变;在拉压形变中的应变就是线应变,如果l 0表示原长,Δl 表示绝对伸长或绝对压缩,则线应变ε= Δl /l 0;在剪切形变中的应变就是切应变,用切变角ψ表示。
⒋力与形变的基本规律是胡克定律,即应力与应变成正比。
在拉压形变中表示为 σ= Y ε,Y 是由材料性质决定的杨氏模量,在剪切形变中表示为 τ= N ψ,N 是由材料性质决定的切变模量。
⒌发生形变的弹性体具有形变势能: 拉压形变的形变势能密度 2210εY E p =, 剪切形变的形变势能密度 2210ψN E p =。
⒍梁弯曲的曲率与力偶矩的关系 312Ybh k τ= ⒎杆的扭转角与力偶矩的关系 lNR C C 2,4πϕτ==第九章⒈物体在线性回复力F = - kx ,或线性回复力矩τ= - c φ作用下的运动就是简谐振动,其动力学方程为 ,02022=+x dtx d ω(x 表示线位移或角位移);弹簧振子:ω02=k/m ,单摆:ω02=g/l ,扭摆:ω02=C/I.⒉简谐振动的运动学方程为 x = Acos(ω0t+α);圆频率、频率、周期是由振动系统本身决定的,ω0=2π/T=2πv ;振幅A 和初相α由初始条件决定。
⒊在简谐振动中,动能和势能互相转换,总机械能保持不变;对于弹簧振子,22021221Am kA E E p k ω==+。
⒋两个简谐振动的合成分振动特点合振动特点方向相同,频率相同与分振动频率相同的简谐振动 Δα=±2n π 合振幅最大 Δα=±(2n+1)π 合振幅最小 方向相同,频率不同,频率成整数比不是简谐振动,振动周期等于分振动周期的最小公倍数方向相同,频率不同,频率较高,又非常接近 出现拍现象,拍频等于分振动频率之差方向垂直,频率相同运动轨迹一般为椭圆Δα=±2n π 简谐振动(ⅠⅢ象限) Δα=±(2n+1)π简谐振动(ⅡⅣ象限) 方向垂直,频率不同,频率成整数比利萨如图形,花样与振幅、频率、初相有关⒌阻尼振动的动力学方程为 022022=++x dt dx dt x d ωβ。
其运动学方程分三种情况:⑴在弱阻尼状态(β<ω0),振动的方向变化有周期性,220'),'cos(βωωαωβ-=+=-t Ae x t ,对数减缩 = βT ’.⑵在过阻尼状态(β>ω0),无周期性,振子单调、缓慢地回到平衡位置。
⑶临界阻尼状态(β=ω0),无周期性,振子单调、迅速地回到平衡位置⒍受迫振动动力学方程 t f x dt dx dtx d ωωβcos 202022=++;其稳定解为 )cos(0ϕω+=t A x ,ω是驱动力的频率,A 0和φ也不是由初始条件决定,222220004)(/ωβωω+-=f A 2202ωωβωϕ--=tg 当2202βωω-=时,发生位移共振。
第十章⒈平面简谐波方程 )c o s ()(c o s kx t A t A y V xωω==; v V T v k T λπλπω====,/1,2,2。
