银行排队系统建模与仿真(1)
MATLAB模拟银行单服务台排队模型

MATLAB模拟银行单服务台排队模型银行单服务台排队模型是一种常见的排队模型,主要用于描述在银行等排队服务场所中,只有一个服务员的情况下,客户如何排队等待服务的情况。
1.模型假设在进行银行单服务台排队模型的建模过程中,我们需要进行一些假设,以简化问题的复杂性。
这些假设包括:-客户到达时间服从泊松分布:客户到达时间间隔服从泊松分布,即客户到达服从一个固定的时间间隔。
-服务时间服从指数分布:每个客户的服务时间是独立同分布的,服从指数分布。
-服务台只有一个:我们假设只有一个服务台,客户按照到达的顺序排队等待服务。
-客户不能提前离开:我们不考虑客户在等待期间可能会放弃等待而提前离开的情况。
2.模型参数在建立银行单服务台排队模型时,我们需要定义一些模型参数。
这些参数包括:-平均到达率λ:客户的平均到达率,表示单位时间内到达的客户数量的期望值。
-平均服务率μ:服务员的平均服务率,表示单位时间内服务的客户数量的期望值。
-服务台利用率ρ:服务台的利用率,表示服务台的平均使用率。
-平均等待时间W:客户平均等待服务的时间。
-平均队列长度L:客户平均排队等待的队列长度。
3.模拟过程为了模拟银行单服务台排队模型,我们使用MATLAB编程进行模拟。
以下是一个简单的模拟过程:-生成客户到达时间间隔:使用泊松分布生成客户到达时间间隔。
-生成客户服务时间:使用指数分布生成客户的服务时间。
-计算客户到达时间和服务完成时间:根据客户的到达时间间隔和服务时间,计算客户的到达时间和服务完成时间。
-计算客户的等待时间:根据客户的到达时间和服务完成时间,计算客户的等待时间。
-统计模拟结果:统计客户的等待时间、队列长度等模拟结果。
4.结果分析通过对模拟结果的分析,我们可以得到一些关键的结果,包括:-平均等待时间:通过计算客户的平均等待时间,可以评估服务台的效率和客户的等待体验。
-平均队列长度:通过计算客户的平均排队等待的队列长度,可以评估服务台的负载情况。
银行排队叫号系统设计实验报告(范本模板)

2011年至2012年第一学期《银行排队叫号系统设计》课程设计班级1006402指导教师涂立、李旎学生人数 3设计份数 12011年12月23日银行排队叫号系统设计报告一.设计时间2011年12月 19日——---12月23日二.设计地点湖南城市学院实验楼计算机机房三.设计目的1.进一步熟悉和掌握单片机的结构及工作原理。
2.掌握单片机的接口技术及相关外围芯片的外特性,控制方法。
3.通过课程设计,掌握以单片机核心的电路设计的基本方法和技术,详细使用Protel软件绘制原理图的过程.4.通过实际程序设计和调试,逐步掌握模块化程序设计方法和调试技术。
四.实验成员及分工五。
指导老师涂立副教授、李旎讲师.六.设计课题设计一个银行排队叫号系统。
理由: 1、系统原理容易理解,更贴近我们的生活。
2、怎个系统简洁明了,适于初学者。
3、能提高我们的综合应用能力。
七.基本思路及关键问题的解决方法用八个二极管表示客户取号的号码和营业员准备给那位客户办理业务的号码,用二进制表示,亮的二极管表示0,灭的二极管表示为1 。
开关KEY为客户取号码是所用,KEY闭合时八个二极管的亮灭顺序就是客户的号码。
开关KEY1,KEY2,KEY3,KEY4是分别在四个营业窗口,其中任意一个按下,八个二极管的亮灭会显示一个号码,此号码对应要办理业务客户的号码,与此同时蜂鸣器也会提醒客户。
八.算法及流程图算法:程序利用循环结构检测整个系统中的客户端和叫号端是否有按键被按下,如果检测到有按下的信号,首先判断按下按键的端口的类型,然后相应的计数变量加一,并把计数变量的信息以二进制的形式传送到相应的端口;如果没检测到按下信号,程序则跳入下一个循环继续检测按键信息。
表1 元件清单芯片晶振发光二级管电容电源按键蜂鸣器导线P87C52X2BN11.0592MHZLED10uf、30pf5V非自锁式1183181若干图1。
银行排队叫号系统原理图图2. 银行排队叫号系统流程图九、调试过程中出现的问题及相应解决办法1.开打keil软件,建立一个新工程单击【Project】在下拉菜单中找到【New project。
基于Arena的银行排队系统仿真建模与分析

III
基于 Arena 的银行排队系统仿真建模与分析
一、引言
近几年商业银行的零售业务快速发展,银行大堂是重要的零售阵地。当前,网 点转型和服务创新成为两大关注热点。很长时间以来,银行柜台零售业务一直承受 着超负荷工作压力,排队现象屡见不鲜,柜台服务质量下降,严重影响顾客满意度。 服务水平可通过内部管理进行改善。顾客增多,要减少排队等候时间就要增 加服务窗口,就要增加营业成本;而增加窗口有可能出现空闲,又浪费资源。因 此,如何找到一个平衡点,使三者达到最佳的平衡状态,是解决银行排队问题的 关键。银行的排队问题由客户人数,服务水平和服务窗口数量等因素综合决定。 其本质是柜台生产与客户需求的矛盾,是柜台生产能力与客户需求不匹配的表现。 本文尝试使用Arena仿真软件对银行排队问题进行系统仿真,根据仿真统计结 果探索银行排队问题的优化方案。
二、原理简述
排队系统基本结构由输入过程、服务机构和排队规则三个部分构成。 根据排队理论, 大部分的顾客到达间隔和服务时间的规律基本符合指数型的 概率密度函数。顾客到达银行的间隔时间的经验分布是指数分布(相继到达的间 隔时间是独立且为同负指数分布,与输入过程为泊松分布是等价的) 。到达银行的 输入过程服从泊松分布要求满足4个条件:平稳性、无后效性、普通性、有限性。 即:①平稳性:在某一时间间隔内到达的顾客数概率只与这段时间的长度和顾客 数有关;②无后效性:不相交的时间区间内到达的顾客数是相互独立的;③普通 性:在同时间点上最多到达 1个顾客,不存在同时到达2个以上顾客的情况;④有 限性:在有限的时间区间内只能到达有限位顾客,不可能有无限个顾客到达[1]。 在本仿真实验中,我们假定顾客到达间隔时间满足泊松分布条件。在高精度 的系统模型中,顾客到达间隔时间是否服从泊松分布,一般都需要进行检验。通 过检验,不仅能确定真实分布类型,还能对统计的数据进行验证。
排队系统仿真(1)

4.3 排队模型的分类
单队多服务台按FIFO规则服务的情形表示为 X/Y/Z 式中,X——相继到达时间间隔的分布; Y——服务时间的分布; Z——服务台数目。 Ek 表示相继到达间隔时间和服务时间的各种分布的符号: M——指数分布 Ek ——k阶爱尔朗分布 D——确定性时间间隔 GI——一般相互独立的随机分布 G——一般随机分布 例,M/M/1
Pk (t ) = e
− λt
(λ t ) k!
k
k = 0,1,2,L
泊松到达模式——满足 个条件 满足4个条件 泊松到达模式 满足
1.
2.
3.
4.
平稳性: 时间内有k个顾客到来的概 平稳性:在[a, a+t]时间内有 个顾客到来的概 时间内有 率与a无关,只与t, k有关。记此概率为: 率与 无关,只与 有关。记此概率为: 无关 有关 Vk(t)——在t时间间隔内到达 个顾客的概率。 时间间隔内到达k个顾客的概率 在 时间间隔内到达 个顾客的概率。 (P(k,λt)) 无后效性: 无后效性:不相交区间内到达的顾客数是相互 独立的。 到达数与[t 的到达数无关。 独立的。[t1,t2]到达数与 0,t1]的到达数无关。 到达数与 的到达数无关 普通性: 表示在长度为t的区间内至少到 普通性:令ψ(t)表示在长度为 的区间内至少到 表示在长度为 达两个顾客的概率, 达两个顾客的概率,则ψ(t)=0 当t->0; ; 有限性: 有限性:在任意有限时间区间内到达有限个顾 ∞ 客的概率之和为1。 客的概率之和为 。 ∑ Pk (t ) = 1
到达模式
到达
排队
服务机构
离去
几种常见的排队系统的结构:
动态实体到达 动态实体 服务设备 离去
(强烈推荐)单服务台排队系统建模与仿真研究报告

(强烈推荐)单服务台排队系统建模与仿真研究报告(此⽂档为word格式,下载后您可任意编辑修改!)物流系统建模与仿真单服务台排队系统仿真研究报告——选重庆⼤学A区门⼝中国银⾏分⾏某⼀服务窗⼝为单服务台排队系统研究对象⼀、系统基本背景社会的进步越来越快,⼈们的⽣活节奏也随之越来越快。
在科技的发展,新技术的普及下, 我国的银⾏业以计算机和信息技术、互联⽹技术为前提, 通过⼤量资⾦和科技的投⼊, 不断地开发出新产品和新业务。
另外有⽹上银⾏、⽀付宝等新业务的出现, ⼤⼤提⾼了⼯作效率。
然⽽现代的⾦融服务并不是都可以靠刷卡来解决, 许多技术还不完善, 这些新技术也并不适合所有顾客群,去银⾏办理业务的顾客仍然经常性地出现排队现象。
顾客等待时间过长, 造成顾客满意度下降, ⽭盾较为突出, 因此本报告试利⽤单服务台排队论的⽅法, 定性定量地对具有排队等候现象的银⾏服务系统进⾏统计调查与分析研究,希望能帮助改进银⾏⼯作效率, 优化系统的运营。
本报告研究对象为中国银⾏重庆⼤学处分⾏某⼀服务窗⼝,数据取⾃银⾏内唯⼀⾮现⾦业务柜台。
研究对象的选取虽然不是最典型的,但是综合考虑了研究地域范围和⼩组成员作业时间有限,另有其他⽅案由于各种原因⽆法进⾏,故选择离学校较近的有代表性的中国银⾏中的服务窗⼝作为最终⽅案。
中国银⾏简介:中国银⾏是中国历史最为悠久的银⾏之⼀,在⼤家对银⾏的概念中有着⼀定地位。
中国银⾏主营传统商业银⾏业务,包括公司⾦融业务、个⼈⾦融业务和⾦融市场业务。
公司业务以信贷产品为基础,致⼒于为客户提供个性化、创新的⾦融服务和融资、财务解决⽅案。
个⼈⾦融业务主要针对个⼈客户的⾦融需求,提供包括储蓄存款、消费信贷和银⾏卡在内的服务。
作为中国⾦融⾏业的百年品牌,中国银⾏在稳健经营的同时,积极进取,不断创新,创造了国内银⾏业的许多第⼀,在国际结算、外汇资⾦和贸易融资等领域得到业界和客户的⼴泛认可和赞誉。
⼆、系统描述该银⾏⼯作时间为上午8:30⾄下午16:30(周⼀⾄周⽇),另周末不办理对公业务,属于每天8⼩时⼯作制。
银行排队叫号系统需求分析设计文档(含5篇)

银行排队叫号系统需求分析设计文档(含5篇)第一篇:银行排队叫号系统需求分析设计文档银行排队叫号系统的分析与UML建模一、需求分析近年来,由于各行各业的信息化、智能化建设越来越普及,整个社会对各个行业的办事效率的要求也越来越高。
例如像银行办业务,在顾客办业务过程中排队现象在所难免,为了在排队时减少顾客的等待时间,为顾客办业务创造一个良好的环境,银行排队叫号系统应运而生。
银行排队系统的功能性需求包括以下内容:1、排队系统可以分为票务打印系统和窗口操作系统。
2、票务打印系统(1)显示发号机上的显示屏使用液晶显示,显示对待办业务的选择;(2)输入输入过程即通过触摸屏对业务进行选择的过程;(3)输出打印号票打印内容应该包括业务名称、排队号码、时间等;3、窗口操作系统基本包括显示屏、语言提示,叫号按钮(1)显示屏使用点阵式LED显示,显示内容应该是下一个号码以及办理业务窗口;(2)语音提示语音播报时用语音的形式通过广播或者音箱给人一提示信息。
语音提示不需要用户一直盯着提示屏或者排队情况。
选择使用语音芯片,实现的功能应该是当操作员按下按钮后,语音播放下一个办理者的票号。
(3)叫号按钮设置叫号按钮,以便于操作员控制窗口模块的显示屏及语音提示。
满足上述需求的系统主要包括以下几个小的系统模块:(1)派号功能模块。
派号功能模块主要是用于在用户进入服务大厅后,根据自己的业务需要,通过自助式触摸屏号票机领取票号;或者用户在服务大厅业务咨询台进行业务咨询后,咨询员可以为用户打印排队号票。
号票是由排队服务器根据当前情况自动生成。
(2)叫号功能模块。
工作人员可以通过座席软件键盘上的设置键对客户进行叫号;也可通过按键控制器对客户进行叫号;系统可以设置单语或双语进行语音播放;以及通过LED显示屏和其它视频显示设备显示票号。
(3)预约功能模块。
用户可以通过电话预约领取排队号;预约成功后取得预约号;系统将此预约号按预约时间插入当前的排队队列,在系统处理后进行优先呼叫;在同时间下办理业务时,可以进行预约服务,优先办理。
建模与仿真(petri网部分)案例分析

建模与仿真(petri网部分)案例分析建模与仿真是一种将现实世界的系统抽象成数学模型,并通过计算机模拟来分析系统行为和性能的方法。
Petri网是一种常用的建模工具,它能够描述并发系统的行为和状态变化。
以下是一个关于银行取款系统的Petri网建模与仿真案例分析: 1. 系统描述:假设有一个银行取款系统,包括一个ATM机和多个用户。
ATM机有两个状态:空闲和忙碌。
用户可以进行取款操作,当ATM机空闲时可以直接进行取款,当ATM机忙碌时需要等待。
2. 建模:首先,我们需要定义Petri网的元素。
在这个案例中,我们有以下元素:- 位置(Place):ATM空闲、ATM忙碌、用户等待队列- 变迁(Transition):用户取款、ATM机空闲、ATM机忙碌、用户离开然后,我们需要定义这些元素之间的关系。
在这个案例中,我们有以下关系:- 用户取款前需要ATM机空闲- 用户取款后ATM机变为忙碌状态- 用户等待队列中有用户时,ATM机空闲时用户可以取款- 用户取款后可以选择离开或继续等待3. 仿真:通过定义好Petri网的元素和关系,我们可以使用仿真工具来模拟系统的行为和性能。
在仿真过程中,我们可以调整系统参数(如用户到达速率、ATM机服务时间等)来观察系统的响应和效果。
例如,我们可以通过仿真来回答以下问题:- 用户平均等待时间是多少?- ATM机的利用率是多少?- 用户离开的平均时间是多少?通过不断调整参数和观察仿真结果,我们可以优化系统设计,提高系统的性能和效率。
总结:建模与仿真是一种重要的系统分析方法,可以帮助我们理解系统的行为和性能。
Petri网是一种常用的建模工具,可以描述并发系统的行为和状态变化。
通过定义Petri网的元素和关系,并使用仿真工具进行模拟,我们可以分析系统的行为和性能,并优化系统设计。
银行排队模型[1]
![银行排队模型[1]](https://img.taocdn.com/s3/m/f211b04de45c3b3567ec8b80.png)
发型师的值班问题的优化模型摘要本文主要研究的是发型师的值班系统的优化问题,针对该问题,我们组首先建立层析分析模型,目标函数为性能指标值Z.问题一:根据问访银行员工和顾客,并征求专家意见对银行排队服务过程中不同影响因子的重要程度两两比较得到比值,以此构造成对比较矩阵,通过MATLAB 6.5处理矩阵得到最大特征根对应的特征向量,归一化处理得到各因子的权重.用excel对不同时间段的数据分别进行统计,用MATLAB 6.5拟合并通过平移----标准差变换和平移----极差变换统计的各项因子标准化处理,与权重结合即得性能指标值Z.问题二:对银行排队窗口的优化,通过数学推导构建出排队论模型,由一周不同天数同一时间段的周期性特点,对数据按时间段用MATLAB 6.5进行拟合,求解过程采用时间步长法,步长取h1,给定不同的窗口数求得各个参数进而得到性能指标值Z,便可解出给定条件下的最优窗口数,从而得到一周七天内各个时间段的最优窗口数.问题三:考虑对附近系统内银行网点的工作人员进行工作统筹安排,建立排队服务系统的优化模型.在满足一定性能指标值Z的前提下,以单位时间费用的期望值最小为约束条件,而银行窗口数为整数可知费用离散函数,利用边际分析方法求出最优的窗口数,进而建立窗口业务组合模型,通过对窗口所设业务组合是优化来分配银行员工数,得到人员安排的最优化结果.所用求权向量的矩阵通过了一致性检验,故可认为合理.综上所述,我们建立的银行排队机服务系统的评价模型可较好地估计出某个银行的服务情况,而服务情况的比较标准需要对多家银行进行估计,并按比例划分来评级;对银行窗口的优化考虑了各个时间段的最优窗口数,据了解符合现实情况;而对银行系统人员的安排,我们提出了优化业务组合来优化员工数,并给出了相应的改进.关键词:层次分析排队论窗口业务组合模型边际分析一、问题重述随着人们的生活水平的提高,理发不仅仅是一种生理上的需求,而且还是心里上的需求。
第六章-排队系统建模与仿真(New)
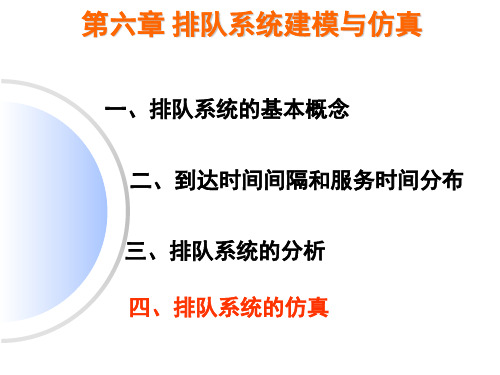
出现的次数ft 38 25 17 9 6 5 0 100
三、排队系统的分析
解:(1)计算 平均到达速度:
nfn 2.1人 / 小时
100
平均手术时间: 平均服务速度:
Ts
tft 100
0.37小时 / 人
1 1 2.5人 / 小时
Ts 0.4
(2)取λ=2.1,μ=2.5,通过统计检验方法的检验,可以认 为病人到达数服从参数为2.1的泊松分布,手术时间服从参数 为2.5的负指数分布。
服务员空闲否?
Y
开始服务
经过Si
服务完毕
N
排队等待
顾客离去
四、排队系统的仿真
仿真方法:手工仿真 仿真初始条件:系统中没有顾客,即:排队的队列中没有顾客等待,服务台 无服务对象。 仿真开始:以第一个顾客到达时刻为仿真的起始点。
四、排队系统的仿真
? 事件何时出现?
在仿真中,通过随机数来产生!
四、排队系统的仿真
• M——负指数分布 • M/M/1表示相继到达时间为负指数分布,服务时 间为负指数分布,单服务设备的模型。
三、排队系统的分析
1 单服务台M/M/1模型(M/M/1/∞/ ∞/FCFS)
(1)到达模式。动态实体源是无限的,动态实体单个 到达,相互独立,一定时间的到达数服从泊松分布。
(2)排队规则。单对,且队列长度没有限制,先到先 服务。
混合制
队列的度量
队列的度量
(1)服务强度
1
T0
n
1 Ts
ns
(2)实际业务强度u‘
u' ' 1
(3)服务设备利用率
n
三、排队系统的分析
随机排队系统的运行指标: 在系统中动态实体数量的期望值Ls, 在系统队列中等待的动态实体数量(队列长度)的 期望值Lq。 在系统中动态实体逗留时间的期望值Ws, 在队列中动态实体等待时间(排队时间)的 期望值Wq。
计算机仿真大赛作品—银行排队系统

建立模型
算法设计
编程
输出界面
顾客进来
分配顾客办理业务随机 时间t 分配下一顾客达到间隔 随机时间t0
•随机时间t1[0] •随机时间t1[1] •随机时间t1[2] 。 。 。 。
•随机时间t2[0] •随机时间t2[1] 。 。
•随机时间t3[0] 。 。
•随机时间t4[0] •随机时间t4[1] 。 。 。
(一)选择主题 假设某银行有4个对外业务办理窗口,从早 晨银行开门起不断有客户进入银行,由于每 个窗口某个时刻只能接待一个客户,因此在 客户人数众多时需要在每个窗口进行排队, 对于刚进入银行的客户,如果某个窗口空闲 ,则可立即上前办理业务;否则,就排在人 数最少的队伍后面。请模拟银行一天的业务 情况并统计客户在银行的平均停留时间。
部分 代码
document.getElementById("td00").innerHTML="";
document.getElementById("td01").innerHTML=""; if(currenttime==(t0-t)*3600) end();
}
建立模型
算法设计
编程
输出界面
部分 代码
输出界面
部分 代码
body{ padding-left:0; padding-top:0; padding-bottom:0; paddingright:0; background-image:url(bj.gif); background-repeat:repeat; } #table{ padding-top:0px; padding-left:0; padding-right:0; padding-bottom:0; } #table1{ width:810px;height:800px; border:#FFF solid 4px; }
服务台单队列排队系统仿真

服务台单队列排队系统仿真1. 引言排队是我们日常生活中常见的现象之一。
每当我们去银行、超市、餐厅等地方,总会看到人们在服务台前排长队等待接受服务。
而排队系统的效率直接影响到我们的等待时间和满意度。
为了改善排队系统的效率,许多地方引入了服务台单队列排队系统。
这种系统中,所有顾客都将排在同一个队伍中,然后按照先后顺序依次接受服务。
这种系统相比于多个队列排队系统,能够有效减少空闲时间和服务延迟。
为了对服务台单队列排队系统进行评估和优化,我们可以使用仿真技术来模拟系统的运行情况,并对其进行分析。
2. 仿真模型设计在服务台单队列排队系统的仿真模型中,我们需要考虑到以下几个方面的因素:2.1 顾客到达规律在实际排队系统中,顾客的到达时间往往是随机的,我们可以使用随机数生成器来模拟此过程。
通过设定到达时间的概率分布函数,我们可以生成一系列随机数来模拟顾客的到达间隔。
2.2 服务时间每个顾客在服务台的服务时间也是随机的。
同样地,我们可以使用随机数生成器来模拟服务时间。
通过设定服务时间的概率分布函数,我们可以生成一系列随机数来模拟顾客在服务台的停留时间。
2.3 服务台数量为了简化仿真模型,我们假设只有一个服务台。
在实际情况中,可以根据实际需求增加服务台数量,以提高系统的整体效率。
2.4 排队规则在服务台单队列排队系统中,顾客按照先后顺序依次接受服务。
当一个顾客结束服务后,下一个顾客将开始接受服务。
为了模拟这个过程,我们可以使用队列数据结构来管理顾客的排队顺序。
3. 仿真过程在进行仿真过程时,我们可以按照以下步骤进行操作:3.1 初始化仿真参数根据实际情况,我们可以设定好仿真的时间段、顾客到达规律和服务时间的概率分布函数等参数。
3.2 创建顾客队列根据顾客到达规律,我们可以按照一定的间隔时间将顾客加入到队列中。
3.3 顾客进入服务台当顾客队列不为空时,服务台将接受当前队列中的第一个顾客,并开始对其进行服务。
3.4 更新服务时间和队列在服务过程中,服务单位时间递减,直到达到零时,服务结束,当前顾客离开服务台,下一个顾客开始接受服务。
排队系统的建模仿真研究

( ) 件 表 : 件 表 列 举 了 系 统 运 行 过 程 所 发 生 的各 种 7事 事
1 排 队 系 统
1 1 基 本 概 念 . .
也就 是仿真要 解决 的问题 , 是系统调 研和建模 的依据 。 这
2 2 系统 调 研 . ’
排 队 是 生 活 中 经 常 出 现 的 现 象 。如 到 银 行 办 理 业 务 ,
系 统 结 构 调 研 的 目 的 是 为 了 深 入 了 解 系 统 的 总 体 流
13 排 队 系统 常 用 的 输 出 参 数 .
n
① 平 均 等 待 时 间 d i ∑ L —l m J i
n —一
() 1
() 2
() 3
真 的 专 业 性 特 点 , 真 模 型 和 运 行 模 型 的 工 作 一 般 由 专 业 仿 的 仿 真 人 员 来 做 。 但 是 对 系 统 的 分 析 常 常 需 要 仿 真 需 求 方 的 密 切 配 合 。为 了 使 仿 真 需 求 方 了 解 仿 真 的 一 般 过 程 , 以 配 合 仿 真 前 期 的 调 研 工 作 , 以 将 上 述 调 研 所 需 获 取 的 数 可 据 和参数 整理并列 表 , 仿真需 求 方进 行针 对性 的 填写 , 由 以 保 证资料 的完整性 和准确性 。 系 统 模 型 的形 式 可 以是 多 样 的 , 文 字 叙 述 型 、 程 图 有 流 建 立 系 统 的 流 程 图 模 型 。 流 程 图 模 型 中 应 包 含 有 : 时 实 临
银行ATM服务系统建模与仿真设计说明书

中北大学课程设计说明书学生姓名:学号:学院:机械与动力工程学院专业:工业工程题目:系统建模与仿真指导教师:职称: 副教授职称:2014年 6月 9日银行ATM服务系统建模与仿真设计说明书1 系统描述中北大学工商银行ATM自助存款机为全校师生提供自助取款服务,此服务系统由ATM机,存款人等构成。
目前工商银行只有一台自助存款机,在日常的服务过程中经常出现排队等待的现象。
在高峰期,存款人到达率服从一定的概率分布,服务速率依赖于存款人的操作时间。
建模的目的是在假定存款人到达时间间隔和存款服务花费的时间服从一定的概率分布时,考察ATM机的忙闲情况以及服务质量,并提出改进意见2 系统分析2.1 系统的实体分析在工商银行ATM是一个单台单队的服务系统,由三类实体组成:ATM机、存款人及排队队列。
ATM机是永久实体,存款人是临时实体,排队队列是一类特殊实体2.2 分析队列实体的操作由于存款服务中只有一个队列,而且存款人不会因为排队人数太多而离去,因此队列规则很简单,没有换队等特殊的队列操作。
2.3 系统的流程图描述2.4 模型参变量读者到达时间、服务时间等,这些变量由输入数据分析得出。
2.5 排队规则队列的排队规则是先到先服务,即每名读者到达时排在队尾,工作人员先为排在队首的读者服务。
3 系统仿真输入数据分析3.1 数据的收集分布的假设根据存款人到达时间分布直方图以及ATM机服务时间与已知的统计分布的比较可以假设存款人到达时间服从泊松分布和ATM机服务时间符合负指数分布。
3.3 参数估计3.3.1 样本均值和样本方差到达时间间隔样本均值:到达时间间隔样本方差:1116niiX xn===∑222111() 34.981niiS x nXn==-=-∑服务时间样本均值:服务时间样本方差:3.3.2 估计量的选取顾客到达时间服从泊松分布,其估计量选取为: 6 对于ATM 机服务时间服从负指数分布,所以,起估计量选取为:0.1673.4 拟合度检验(1)到达时间间隔拟合度检验1 0.0625 0.0588 计算得:查表得:由于故可认为顾客到达时间间隔服从泊松分布。
银行排队叫号模拟系统_实验报告及模版

综合性设计性实验报告专业:软件工程班级:*** 组别: ***——***学年第 2 学期课程名称Unix高级编程指导教师***Weibo昵称:年年有余事事顺利本组成员学号姓名实验地点逸夫楼A实验时间***-06-08实验类型实践课实验名称银行排队叫号模拟系统实验环境: VMware虚拟机实验内容:编程实现一个“银行排队模拟系统”1)该程序模拟客户到银行取号-排队-被叫号-被服务的过程;2)程序执行流程如下:Step1: 客户到达银行,并从取号机取号;Step2: 如果大厅中有空闲座位,则座下等待,否则,在大厅外等待;Step3: 银行职员如果发现有客户等待,则依次叫号服务,否则休息;Step4: step1-step4重复执行3)大厅中座椅数量为20个;4)服务窗口为2个;5)“客户到来”通过命令行输入客户名字模拟;6)为了模拟实际情况,每个客户服务时间不小于20秒,可随机确定;7)程序顺序列出不同窗口服务客户的:名称,窗口号,服务时间2、提示1)需一个主控进程,随时监控客户到来,并为之创建进程;2)取号机应视为互斥型临界资源3)座椅应视为临界资源4)客户等待及被叫号应视为进程间同步过程实验目的与要求:掌握常用IPC方法能够应用IPC方法解决实际编程问题设计思路:(设计原理、设计方案及流程等)设计原理:“银行排队模拟系统”由于进程之间通信需要进行相应进程通信机制实现,进程通信机制很多,比如信号量、管道、消息队列、套接字等通过我们组的讨论决定用信号量机制的函数来实现,因此通过我们组的讨论决定以这样的方式来进行设计:通过信号量机制<signal.h>创建子进程fork()的过程来实现设计方案:主控进程即服务进程需完成以下任务:1.创建信号量集,并为之初始化2.监督客户的到来(实时循环)3.客户输入名字后,为客户创建子进程。
4.子进程进行相关操作。
实现与主进程的同步。
5.服务进程等待有人(p操作)(P(S3))p成功,显示窗口信息6.服务进程叫号(v操作)(V(S4))7.v成功,则进行服务子进程完成的操作:1.取号(因互斥有对取号的互斥信号量S1初值1)2.申请椅子(有资源信号量S2 初值20)(P(S2))3.唤醒柜员(告知柜员有人故有同步信号量S3,初值为0) (V(S3))4.等待叫号(故有同步信号量S4,初值为0,S3,S4实现父子进程的同步) (P(S4))5.4通过,输出客户名字5.4通过,则释放椅子(V(S2))8.显示服务时间(不少于20s)程序流程:Step1: 客户到达银行,并从取号机取号;Step2: 如果大厅中有空闲座位,则座下等待,否则,在大厅外等待;Step3: 银行职员如果发现有客户等待,则依次叫号服务,否则休息;Step4: step1-step4重复执行大厅中座椅数量为20个;服务窗口为2个;“客户到来”通过命令行输入客户名字模拟;为了模拟实际情况,每个客户服务时间不小于20秒,可随机确定;程序顺序列出不同窗口服务客户的:名称,窗口号,服务时间提示:需一个主控进程,随时监控客户到来,并为之创建进程;取号机应视为互斥型临界资源座椅应视为临界资源客户等待及被叫号应视为进程间同步过程关键技术分析:1)使用信号量机制-int crt_sig(key_t key,int nsems)2)创建一个子进程 pid_t crt_child()3)使用消息队列-int msg_stat(int msqid,structmsqid_ds msg_info)4)使用sem-op函数来设置程序的申请与释放,sem_op>0对应相应进程要释放sem_op数目的共享资源;sem_op=0可以用于对共享资源是否已用完的测试; sem_op<0相当于进程要申请-sem_op个共享资源5)利用函数void srand()和rand()来获取系统的服务时间等实验步骤:编写程序:源代码为:#include<stdio.h>#include<stdlib.h>#include<unistd.h>#include<string.h>#include<sys/types.h>#include<sys/ipc.h>#include<sys/wait.h>#include<time.h>#include<sys/sem.h>#include<signal.h>#include<errno.h>#define N_SEC 20static union semun{int val;struct semid_ds *buf;unsigned short * array;struct seminfo *__buf;}arg;int BeginWaiter(int sems,int num) {int id=-1;if(!(id=fork()))//child{while(1){struct sembuf op={2,-1,0};if(-1==semop(sems,&op,1))exit(0);op.sem_num=3;op.sem_op=1;if(-1==semop(sems,&op,1))exit(0);///serviceint random=1+(int)(20.0*rand()/(RAND_MAX*1.0));printf("\n********\n%d is on duty,serve time=%d\n***********\n",num,20+random);sleep(10+random);}}elsereturn id;}int main(int argc, char *argv[]){printf("parent id=%d\n",getpid());int sems=semget(IPC_PRIVATE,5,0666);union semun arg;unsigned short init_v[5]={1,20,0,0,0};arg.array=init_v;semctl(sems,0,SETALL,arg);char custom[100]="";////////////////////////srand(0);int s1=BeginWaiter(sems,0);int s2=BeginWaiter(sems,1);printf("Waiters are:%d,%d",s1,s2);//////////////while(1){printf("Welcome!please input you name:");scanf("%s",custom);if(!strcmp(custom,"exit")){semctl(sems,0,IPC_RMID,arg);kill(SIGKILL,s1);kill(SIGKILL,s2);exit(0);}if(!fork())//child{struct sembuf ops={0,-1,0};semop(sems,&ops,1);//p mutex,alternativeops.sem_num=4,ops.sem_op=1;semop(sems,&ops/*(struct sembuf*)&{4,1,0}*/,1);//get ticketops.sem_num=0;ops.sem_op=1;semop(sems,&ops/*(struct sembuf*)&{0,1,0}*/,1);//V mutex.alternative/////////////////////ops.sem_num=1;ops.sem_op=-1;semop(sems,&ops/*(struct sembuf*)&{1,-1,0}*/,1);//compete for seatint seats=semctl(sems,1,GETVAL,arg);printf("\nThere are %d seates remained\n",seats);////////////////ops.sem_num=2;ops.sem_op=1;semop(sems,&ops/*(struct sembuf*)&{2,1,0}*/,1);//wake waiter upops.sem_num=3;ops.sem_op=-1;semop(sems,&ops/*(struct sembuf*)&{3,-1,0}*/,1);//wait for called forops.sem_num=1;ops.sem_op=1;semop(sems,&ops/*(struct sembuf*)&{1,1,0}*/,1);//release seat;//get serviceprintf("\n**********\ncustom:%s\n**************\n",custom);exit(0);}}}运行结果如下:实验分析:明确题意 ----要求的是编写小程序,非传统意义上的系统。
银行排队模型期末总结

银行排队模型期末总结1.引言银行是我们日常生活中经常接触到的金融机构之一,而排队是我们进入银行时经常遇到的问题。
银行排队模型是数学中一个重要的应用领域,对于银行的管理和服务质量有着重要的影响。
本期末总结将围绕银行排队模型展开,从排队理论的基本原理、模型假设、模型构建方法、模型的应用等方面进行详细阐述,并结合实际案例进行分析和讨论。
2.排队理论的基本原理排队理论是研究排队系统的数学理论,起源于20世纪初的概率论和统计学。
排队系统的基本组成包括顾客、服务器和队列等。
排队理论的基本原理包括到达过程、服务过程、排队规则和性能度量等。
到达过程描述顾客到达银行的时间间隔模型,服从不同的概率分布。
服务过程则描述了服务员为顾客提供服务的时间间隔模型,也服从不同的概率分布。
排队规则决定了顾客的排队顺序和服务的顺序,如先来先服务、先来后服务等。
性能度量是评价排队系统绩效的指标,包括顾客等待的平均时间、服务器的利用率等等。
3.模型的假设银行排队模型通常基于一些假设条件,这些假设条件用于简化模型,使其易于分析和计算。
常见的假设条件包括:顾客到达服从泊松分布、服务时间服从指数分布、排队规则为先来先服务、顾客在排队和服务过程中是独立的等。
这些假设条件在一定程度上接近于实际情况,并为模型的分析提供了便利。
4.模型的构建方法构建银行排队模型需要考虑到排队规则、到达过程和服务过程等因素,并利用排队理论和概率统计方法进行建模和求解。
常用的模型构建方法包括马尔可夫模型、离散事件模型和连续时间模型等。
马尔可夫模型是一种基于概率过程的模型,常用于描述排队系统的状态转移和稳定分析。
离散事件模型则将顾客到达和服务过程建模为离散事件的发生和处理过程。
连续时间模型则将时间视为连续的变量,适用于模拟和分析排队系统的动态变化过程。
5.模型的应用银行排队模型在实际中有着广泛的应用。
通过对排队模型的分析和优化,可以帮助银行管理者合理安排窗口开放数量和服务员数量,提高服务效率和客户满意度。
MMN排队系统建模与仿真

《系统仿真与matlab》综合试题....................... 错误!未定义书签。
M/M/N 排队系统的模拟仿真 (1)摘要 (1)1. 问题分析 (2)2. 模型假设 (2)3. 符号说明 (3)4. 模型准备 (3)4.1 排队系统的组成和特征 (3)4.1.1输入过程 (4)4.1.2排队规则 (4)4.1.3服务过程 (4)4.1.4排队系统的主要指标 (5)4.2输入过程与服务时间的分布 (5)4.2.1负指数分布 (5)4.2.2泊松分布 (5)4.3生灭过程 (6)5. 标准M/M/N模型 (8)5.1多服务台模型准备 (8)5.2多服务台模型建立 (9)5.2.1服务利用率 (9)5.2.2平均排队长 (9)5.2.3平均队长 (10)5.2.4平均等待时间 (10)6. 程序设计 (11)6.1动画流程图 (11)6.2 M/M/N流程图 (12)7. 程序运行实例介绍 (13)7.1动画实例讲解 (13)7.2M/M/N排队系统实例讲解 (14)8. 程序实现难点和模型评价 (17)8.1程序实现难点 (17)8.2模型评价 (17)9. 参考文献 (17)10. 附录 (17)10.1动画实现的核心程序 (17)10.2 M/M/N模型计算主要程序 (22)M/M/N 排队系统的模拟仿真摘要排队是在日常生活中经常遇到的事,由于顾客到达和服务时间的随机性,使得排队不可避免。
因此,本文建立标准的M/M/N模型,并运用Matlab软件,对M/M/N排队系统就行了仿真,从而更好地深入研究排队问题。
问题一,基于顾客到达时间服从泊松分布和服务时间服从负指数分布,建立了标准的M/M/N模型。
运用Matlab软件编程,通过输入服务台数量、泊松分布参数以及负指数分布参数,求解出平均队长、服务利用率、平均等待时间以及平均排队长等重要指标。
然后,分析了输入参数与输出结果之间的关系。
实验2单服务台单队列排队系统仿真

实验2排队系统仿真一、学习目的1.了解仿真的特点2.学习如何建构模型3.熟悉eM-Plant根本的对象和操作4.掌握排队系统的特点与仿真的实现方法二、问题描述表2.4 每个顾客效劳时间的概率分布效劳时间〔min〕概率密度累计概率123456对于上述这样一个单效劳待排队系统,仿真分析30天,分析该系统中顾客的到达、等待和被效劳情况,以及银行工作人员的效劳和空闲情况。
三、系统建模3.1 仿真目标通过对银行排队系统的仿真,研究银行系统的效劳水平和改善银行效劳水平的方法,为银行提高顾客满意度,优化顾客效劳流程效劳。
3.2.系统建模3 系统调研1. 系统结构: 银行效劳大厅的布局, 涉及的效劳设备2. 系统的工艺参数: 到达-取号-等待-效劳-离开3. 系统的动态参数: 顾客的到达时间间隔, 工作人员的效劳时间4. 逻辑参数: 排队规那么, 先到先效劳5. 系统的状态参数: 排队队列是否为空, 如果不为空队长是多少, 效劳台是否为空6. 系统的输入输出变量:输入变量确定其分布和特征值,顾客的到达时间间隔的概率分布表和每个顾客被效劳时间的概率分布. 输出变量根据仿真目标设定. 包括队列的平均队长、最大队长、仿真结束时队长、总效劳人员、每个顾客的平均效劳时间、顾客平均排队等待效劳时间、业务员利用率等。
3.系统假设1.取号机前无排队,取号时间为02.顾客排队符合先进先出的排队规那么3.一个效劳台一次只能对一个顾客效劳4.所有顾客只有一种单一效劳5.仿真时间为1个工作日〔8小时〕6.等候区的长度为无限长3系统建模系统模型:3.2.4 仿真模型1.实体:银行系统中的实体是人〔主动体〕2.属性:到达时间间隔、接受效劳的时间、接受效劳类型3.事件:顾客到达、开始取号、取号结束、进入队列、出队列、接受效劳、效劳完成、离开银行。
4.活动:到达、取号、排队、效劳、离开5.资源:取号机、排队的座椅、效劳柜台 到达离开取号机排队座椅 服务柜台到达取号排队服务离开顾客到达顾客接收服务时间顾客到达时间间隔顾客离开结束服务开始服务结束排队开始排队结束取号开始取号实体活动事件资源4 系统仿真4.1 eM-plant 界面与主要控件介绍1. 实体:eM-Plant 中包括3类实体:entity ,container ,transporter 。
银行排队信息预测系统数学建模

银行排队信息预测系统数学建模参加软件学院的一个项目,大概内容是银行的排队信息查询,预测,通过这个给客户一个有用的建议:选择附近的哪个银行更为合理。
带队老师把数学建模的任务丢给了我。
接下来我的几天时间就这么被吞噬了。
排队论,概率论,计算方法。
更要命的是写文档,几乎是痛不欲生的过程。
或许这个就是所谓的“有挑战”的事情了……的确以前文档写得太少,就当是锻炼了。
看了<排队论>和<计算方法>以后,大概有了些想法.<!--[if !supportLists]-->1.<!--[endif]-->通常顾客到达后,会排在最短的队伍后面,所以可以认为每个服务台的队伍是趋于一样长的。
<!--[if !supportLists]-->2.<!--[endif]-->银行顾客流满足平稳性,无后效性及普通性,符合Poisson流的定义。
在银行的营业时间段里可以认为来源无限。
<!--[if !supportLists]-->3.<!--[endif]-->通常不会发生顾客到达限额的情况,所以可以假设容量无限。
<!--[if !supportLists]-->4.<!--[endif]-->客户单个接受服务,服务台的服务时间具有无记忆性。
符号定义:n ––系统中的顾客数λ––平均到达率,即单位时间内平均到达的顾客数μ––平均服务率,即单位时间内服务完毕的顾客数Sn(t) ––时刻t系统中有n个顾客Pn(t) ––时刻t系统状态Sn(t) 的概率C ––服务台的个数M ––顾客相继到达的时间间隔服从负指数分布D ––顾客相继到达的时间间隔服从定长分布附:公式对于Poisson流,在[0,t]内到达K个顾客的概率分析:1.排队系统的模拟:由于已认定银行客户流为泊松流,我们在模拟的时候有了很多便利.给出曲线的定义,我们可以方便地通过随机函数来产生客流.首先,银行的客流不一定是简单的泊松流,比如在一个上午可能会有两个峰值出现,这个时候我们可以看作是两个泊松分布的叠加,依此类推。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LOGO
Add your company slogan
WITNESS环境下的仿真模型的建立 环境下的仿真模型的建立
运行结果
运行15000分钟 分钟 运行
结果分析
Байду номын сангаас
可以办理差别化服务,比如开设 窗口 可以办理差别化服务,比如开设vip窗口
可以安排劳务分工, 可以安排劳务分工,可开设不同窗口专 门办理不同业务。 门办理不同业务
多队列优点
顾客可以根据自身的喜好来选 择特定的某一服务台
改进方案
经典的排队理论已经证明, 经典的排队理论已经证明,单队列排队模式系 统和多队列排队模式系统相比, 统和多队列排队模式系统相比,在服务台个数和 服务都不变的条件下,在平均顾客数Ls、 服务都不变的条件下,在平均顾客数 、平均 排队顾客数Lq、顾客在服务系统逗留的平均时 排队顾客数 、 等各项指标上, 间Ws、顾客的平均等待时间 、顾客的平均等待时间Wq等各项指标上, 等各项指标上 均有着显著的优越性。所以我们决定将该银行的 均有着显著的优越性。 排队模式改为单队列排队模式。 排队模式改为单队列排队模式。
[Image information in product] - Title Image – www.multibits.co.kr - CD: Global Digital Design (imageState) - Note to customers: This image has been licensed to be used within this PowerPoint template only. You may not extract the image for any other use.
改进方案分析
让所有顾客都能遵循先到先服务 的规则,保证公平性。 的规则,保证公平性。
只有一条队列,所以,顾客等待的焦 只有一条队列,所以, 虑减少, 虑减少,不会因看到别人加入的队列 移动得更快而着急 。 .提高了排队系统的效率,因为缩短 了顾客排队等待的平均时间
单队列优点
改进后的模型
改进后的运行结果
LOGO
银行排队系统建模与仿真
组长: 组长:崔海龙 小组成员: 小组成员:王琮 姚进 陈旺 丁金明
任务
以东北农业大学校园内的邮政银行为研 究对象,根据其布局及排队、等待情况, 针对其面办理业务的时间,类型,实际 调查银行排队系统的各项数据。并利用 witness进行建模与仿真,对银行排队系 统进行分析及优化。
运行15000分钟 分钟 运行
前后运行结果比较
单队列模式
多队列模式
14人
3人 5.15分 2.69分
平均排队人数
18分
平均逗留时间
15分
平均等待时间
总结
古语有云, 一寸光阴一寸金, 古语有云,“一寸光阴一寸金,寸金难买寸光 阴。”良好的排队系统既是对银行营业效益的提 升也是对客户时间的节省。通过几天的调查, 升也是对客户时间的节省。通过几天的调查,我 们对邮政银行的实际问题做了初步了解, 们对邮政银行的实际问题做了初步了解,对其存 在的问题进行了讨论, 在的问题进行了讨论,我们应用课堂学习的知识 进行建模,借助Witness软件这一平台,仿真 软件这一平台, 进行建模,借助 软件这一平台 出邮政银行的业务处理模式, 出邮政银行的业务处理模式,根据其存在的问题 进行改善,科学的制定了运行模式, 进行改善,科学的制定了运行模式,减少了客户 的平均等待时间,提高的业务服务率。 的平均等待时间,提高的业务服务率。
步骤
3 1 2 3 4
对银行排队系统各项数据进行统计
针对数据利用witness进行建模 进行建模 针对数据利用
针对出现的问题进行分析
解决问题并制定改进模型
小组成员任务分工
姚进,王琮:数据调查,统计。 姚进,王琮:数据调查,统计。 崔海龙: 建模制作。 崔海龙:witness建模制作。 建模制作 陈旺: 陈旺:ppt制作 制作 丁金明:课程设计报告书编写 丁金明: 全体:小组讨论,共同讨论改进计划。 全体:小组讨论,共同讨论改进计划。
出现的问题
该银行3个窗口都办理相同的业务, 该银行 个窗口都办理相同的业务,而且学校周 个窗口都办理相同的业务 围大都是简单业务,也没必要开设vip窗口和专 围大都是简单业务,也没必要开设 窗口和专 门业务窗口,多队列的优势在此并不适合。 门业务窗口,多队列的优势在此并不适合。 根据运行结果显示,三组等候队列有一定的数据 根据运行结果显示, 波动, 号服务台的顾客平均逗留时间不到 号服务台的顾客平均逗留时间不到10 波动,2号服务台的顾客平均逗留时间不到 分钟, 分钟,而3号服务台的顾客平均逗留时间接近 号服务台的顾客平均逗留时间接近 20分钟。2号服务台的繁忙率只有 分钟。 号服务台的繁忙率只有 号服务台的繁忙率只有77%,而3 分钟 , 号服务台的防盲率接近90%。显然,该排队系 号服务台的防盲率接近 。显然, 统并没有达到理想效果,还有需要改进的地方。 统并没有达到理想效果,还有需要改进的地方。
数据统计
该银行在学校内,大多数顾客为学生,办理业务 该银行在学校内,大多数顾客为学生, 多为存取款类简单业务,时间较短。 多为存取款类简单业务,时间较短。因工作人员 工作效率不同, 个窗口的服务时间有一定的差 工作效率不同,3个窗口的服务时间有一定的差 别。1号窗口的平均服务时间为 号窗口的平均服务时间为2.5分钟,2号 分钟, 号 号窗口的平均服务时间为 分钟 窗口的平均服务时间为2.4分钟,3号窗口的平 分钟, 号窗口的平 窗口的平均服务时间为 分钟 均服务时间为2.7分钟! 分钟! 均服务时间为 分钟 银行的平均顾客到达率为60人 小时 小时, 银行的平均顾客到达率为 人/小时,平均每 队为20人 小时 小时。 队为 人/小时。
