中南大学线性代数课件-PPT精品课程
合集下载
线性代数课件PPT

线性代数课件
目录 CONTENT
• 线性代数简介 • 线性方程组 • 向量与矩阵 • 特征值与特征向量 • 行列式与矩阵的逆 • 线性变换与空间几何
01
线性代数简介
线性代数的定义和重要性
1
线性代数是数学的一个重要分支,主要研究线性 方程组、向量空间、矩阵等对象和性质。
2
线性代数在科学、工程、技术等领域有着广泛的 应用,如物理、计算机科学、经济学等。
逆矩阵来求解特征多项式和特征向量等。
06
线性变换与空间几何
线性变换的定义和性质
线性变换的定义
线性变换是向量空间中的一种变换, 它将向量空间中的每一个向量映射到 另一个向量空间中,保持向量的加法 和标量乘法的性质。
线性变换的性质
线性变换具有一些重要的性质,如线 性变换是连续的、可逆的、有逆变换 等。这些性质在解决实际问题中具有 广泛的应用。
特征值与特征向量的应用
总结词
特征值和特征向量的应用非常广泛,包括物理、工程、经济等领域。
详细描述
在物理领域,特征值和特征向量可以描述振动、波动等现象,如振动模态分析、波动分析等。在工程 领域,特征值和特征向量可以用于结构分析、控制系统设计等。在经济领域,特征值和特征向量可以 用于主成分分析、风险评估等。此外,在机器学习、图像处理等领域也有广泛的应用。
经济应用
线性方程组可用于解决经济问题,如投入产出分析、 经济预测等。
03
向量与矩阵
向量的基本概念
向量的模
表示向量的长度或大小,记作|向量|。
ቤተ መጻሕፍቲ ባይዱ
向量的方向
由起点指向终点的方向,可以通过箭头表示。
向量的分量
表示向量在各个坐标轴上的投影,记作x、y、 z等。
目录 CONTENT
• 线性代数简介 • 线性方程组 • 向量与矩阵 • 特征值与特征向量 • 行列式与矩阵的逆 • 线性变换与空间几何
01
线性代数简介
线性代数的定义和重要性
1
线性代数是数学的一个重要分支,主要研究线性 方程组、向量空间、矩阵等对象和性质。
2
线性代数在科学、工程、技术等领域有着广泛的 应用,如物理、计算机科学、经济学等。
逆矩阵来求解特征多项式和特征向量等。
06
线性变换与空间几何
线性变换的定义和性质
线性变换的定义
线性变换是向量空间中的一种变换, 它将向量空间中的每一个向量映射到 另一个向量空间中,保持向量的加法 和标量乘法的性质。
线性变换的性质
线性变换具有一些重要的性质,如线 性变换是连续的、可逆的、有逆变换 等。这些性质在解决实际问题中具有 广泛的应用。
特征值与特征向量的应用
总结词
特征值和特征向量的应用非常广泛,包括物理、工程、经济等领域。
详细描述
在物理领域,特征值和特征向量可以描述振动、波动等现象,如振动模态分析、波动分析等。在工程 领域,特征值和特征向量可以用于结构分析、控制系统设计等。在经济领域,特征值和特征向量可以 用于主成分分析、风险评估等。此外,在机器学习、图像处理等领域也有广泛的应用。
经济应用
线性方程组可用于解决经济问题,如投入产出分析、 经济预测等。
03
向量与矩阵
向量的基本概念
向量的模
表示向量的长度或大小,记作|向量|。
ቤተ መጻሕፍቲ ባይዱ
向量的方向
由起点指向终点的方向,可以通过箭头表示。
向量的分量
表示向量在各个坐标轴上的投影,记作x、y、 z等。
线性代数第一章ppt
线性代数第一章
目录
CONTENTS
• 绪论 • 线性方程组 • 向量与向量空间 • 矩阵 • 特征值与特征向量
01
绪论
线性代数的定义与重要性
线性代数是数学的一个重要分支,主要研究线性方程组、向量空间、矩阵 等线性结构。它在科学、工程、技术等领域有着广泛的应用。
线性代数的重要性在于其提供了一种有效的数学工具,用于解决各种实际 问题中的线性关系问题,如物理、化学、生物、经济等。
向量空间中的零向量是唯一确定的,且对于任意 向量a,存在唯一的负向量-a。
向量空间的运算与性质
向量空间中的加法满足交换律和结合 律,即对于任意向量a和b,存在唯一 的和向量a+b;且对于任意三个向量a、 b和c,(a+b)+c=a+(b+c)。
向量空间中的数乘满足结合律和分配 律,即对于任意标量k和l,任意向量a 和b,存在唯一的结果k*(l*a)=(kl)*a 和(k+l)*a=k*a+l*a。
圆等。
经济学问题
线性方程组可以用来描述经济现象和 规律,例如供需关系、生产成本、利
润最大化等。
物理问题
线性方程组可以用来描述物理现象和 规律,例如力学、电磁学、热力学等。
计算机科学
线性方程组在计算机科学中有广泛的 应用,例如机器学习、图像处理、数 据挖掘等。
03
向量与向量空间
向量的定义与性质
01 向量是具有大小和方向的量,通常用有向线 段表示。 02 向量具有模长,即从起点到终点的距离。
特征值与特征向量的计算方法
定义法
幂法
谱分解法
根据特征值和特征向量的定义, 通过解方程组Ax=λx来计算特征 值和特征向量。这种方法适用于 较小的矩阵,但对于大规模矩阵 来说效率较低。
目录
CONTENTS
• 绪论 • 线性方程组 • 向量与向量空间 • 矩阵 • 特征值与特征向量
01
绪论
线性代数的定义与重要性
线性代数是数学的一个重要分支,主要研究线性方程组、向量空间、矩阵 等线性结构。它在科学、工程、技术等领域有着广泛的应用。
线性代数的重要性在于其提供了一种有效的数学工具,用于解决各种实际 问题中的线性关系问题,如物理、化学、生物、经济等。
向量空间中的零向量是唯一确定的,且对于任意 向量a,存在唯一的负向量-a。
向量空间的运算与性质
向量空间中的加法满足交换律和结合 律,即对于任意向量a和b,存在唯一 的和向量a+b;且对于任意三个向量a、 b和c,(a+b)+c=a+(b+c)。
向量空间中的数乘满足结合律和分配 律,即对于任意标量k和l,任意向量a 和b,存在唯一的结果k*(l*a)=(kl)*a 和(k+l)*a=k*a+l*a。
圆等。
经济学问题
线性方程组可以用来描述经济现象和 规律,例如供需关系、生产成本、利
润最大化等。
物理问题
线性方程组可以用来描述物理现象和 规律,例如力学、电磁学、热力学等。
计算机科学
线性方程组在计算机科学中有广泛的 应用,例如机器学习、图像处理、数 据挖掘等。
03
向量与向量空间
向量的定义与性质
01 向量是具有大小和方向的量,通常用有向线 段表示。 02 向量具有模长,即从起点到终点的距离。
特征值与特征向量的计算方法
定义法
幂法
谱分解法
根据特征值和特征向量的定义, 通过解方程组Ax=λx来计算特征 值和特征向量。这种方法适用于 较小的矩阵,但对于大规模矩阵 来说效率较低。
线性代数完整版ppt课件

a11x1 a12x2 b1 a21x1 a22x2 b2
求解公式为
x1
x
2
b1a 22 a11a 22 a11b2 a11a 22
a12b2 a12a 21 b1a 21 a12a 21
请观察,此公式有何特点? Ø分母相同,由方程组的四个系数确定. Ø分子、分母都是四个数分成两对相乘再
主对角线 a 1 1 a 1 2 a 1 3
a 2 1 a 2 2 a 2 3
a11a22a33a12a23a31a13a21a32
副对角线 a 3 1 a 3 2 a 3 3
a13a22a31a12a21a33a11a23a32
称为三阶行列式.
二阶行列式的对角线法则
并不适用!
.
12
三阶行列式的计算 ——对角线法则
( a a a a ) x a b b a 12 12 12 21 2 12 11 21
当 a 1a 1 2 2a 1a 时2 2,1 该0 方程组有唯一解
x b1a22a12b2
1 a a a a
11 22
12 21
x2
a11b2 b1a21 a11a22a12a21
.
6
二元线性方程组
为列标,表明元素位于第j
列. 8
二阶行列式的计算 ——对角线法则
主对角线 a 1 1 副对角线 a 2 1
a 12 a 22
a11a22a12a21
即:主对角线上两元素之积-副对角线上两元素之积
.
9
二元线性方程组
a11x1 a12x2 a21x1 a22x2
b1 b2
若令
D a11 a12 a21 a22
显然 P n n ( n 1 ) ( n 2 )3 2 1 n !
求解公式为
x1
x
2
b1a 22 a11a 22 a11b2 a11a 22
a12b2 a12a 21 b1a 21 a12a 21
请观察,此公式有何特点? Ø分母相同,由方程组的四个系数确定. Ø分子、分母都是四个数分成两对相乘再
主对角线 a 1 1 a 1 2 a 1 3
a 2 1 a 2 2 a 2 3
a11a22a33a12a23a31a13a21a32
副对角线 a 3 1 a 3 2 a 3 3
a13a22a31a12a21a33a11a23a32
称为三阶行列式.
二阶行列式的对角线法则
并不适用!
.
12
三阶行列式的计算 ——对角线法则
( a a a a ) x a b b a 12 12 12 21 2 12 11 21
当 a 1a 1 2 2a 1a 时2 2,1 该0 方程组有唯一解
x b1a22a12b2
1 a a a a
11 22
12 21
x2
a11b2 b1a21 a11a22a12a21
.
6
二元线性方程组
为列标,表明元素位于第j
列. 8
二阶行列式的计算 ——对角线法则
主对角线 a 1 1 副对角线 a 2 1
a 12 a 22
a11a22a12a21
即:主对角线上两元素之积-副对角线上两元素之积
.
9
二元线性方程组
a11x1 a12x2 a21x1 a22x2
b1 b2
若令
D a11 a12 a21 a22
显然 P n n ( n 1 ) ( n 2 )3 2 1 n !
中南大学线性代数课件64页PPT

给出一组规则,从A中(已获得的)元素出发,依照这些 规则所获得的元素,仍然是A中的元素。这是构造A的 关键部分。
⑶ 极小化
谁 如果集合S A也满足⑴和⑵,则S = A 。这说明, A中 不 的每个元素都可以通过有限次使用⑴和⑵来获得(或称A 是 是满足条款(1)和(2)的最小集合),它保证所构造出的集
7/63
集合的比较运算
定理4.1.1设A和B是集合, A=B当且仅当A B和 BA( 的反对称性)
证明: ABBA
x(x∈Ax∈B)x(x∈Bx∈A) x((x∈Ax∈B)(x∈Bx∈A)) x(x∈Ax∈B) A=B
8/63
集合的比较运算
定义4.1.5 设A和B是集合,
如果AB且A≠B, 那么称A是B的真子集,记作
A={a|a∈I∧0<a∧a<5}, {a|a∈I∧1≤a≤50}
A={x|P(x)}, B={x|Q(x)}
若P(x)Q(x),则A = B
若P(x)Q(x),则A B
递归定义法
10/63
递归定义法(归纳定义)
用这种方法定义一个非空集合A时,一般应包括以 下三个部分:
⑴ 基本项
谁 属已于知A某,些即元S素0 (常A 。用这S0表是示构由造这A的些基元础素,组并成保的证非非空空集。合) 是 ⑵ 递归项
3/63
元素与集合的关系
a是集合A的一个元素, 则记为a∈A,读做“a属 于A”, 或说“a在A中”
a不是集合A的一个元素, 则记为aA,读做“a
不属于A”, 或说“a不在A中” 集合的元素可以是一个集合
例:A={a,b,c,{a,b}} 则{a,b}∈A且{a,b} A
4/63
有限集与无限集
长度为0的串叫做空串,记为Λ(或ε)
⑶ 极小化
谁 如果集合S A也满足⑴和⑵,则S = A 。这说明, A中 不 的每个元素都可以通过有限次使用⑴和⑵来获得(或称A 是 是满足条款(1)和(2)的最小集合),它保证所构造出的集
7/63
集合的比较运算
定理4.1.1设A和B是集合, A=B当且仅当A B和 BA( 的反对称性)
证明: ABBA
x(x∈Ax∈B)x(x∈Bx∈A) x((x∈Ax∈B)(x∈Bx∈A)) x(x∈Ax∈B) A=B
8/63
集合的比较运算
定义4.1.5 设A和B是集合,
如果AB且A≠B, 那么称A是B的真子集,记作
A={a|a∈I∧0<a∧a<5}, {a|a∈I∧1≤a≤50}
A={x|P(x)}, B={x|Q(x)}
若P(x)Q(x),则A = B
若P(x)Q(x),则A B
递归定义法
10/63
递归定义法(归纳定义)
用这种方法定义一个非空集合A时,一般应包括以 下三个部分:
⑴ 基本项
谁 属已于知A某,些即元S素0 (常A 。用这S0表是示构由造这A的些基元础素,组并成保的证非非空空集。合) 是 ⑵ 递归项
3/63
元素与集合的关系
a是集合A的一个元素, 则记为a∈A,读做“a属 于A”, 或说“a在A中”
a不是集合A的一个元素, 则记为aA,读做“a
不属于A”, 或说“a不在A中” 集合的元素可以是一个集合
例:A={a,b,c,{a,b}} 则{a,b}∈A且{a,b} A
4/63
有限集与无限集
长度为0的串叫做空串,记为Λ(或ε)
线性代数第-章1.4PPT课件

向量空间的性质
总结词
向量空间具有一些重要的性质,如加法的结合律、交换律和分配律,数乘的结合律和分配律等。
详细描述
向量空间的加法满足结合律和交换律,即对任意向量u、v、w∈V,有u+(v+w)=(u+v)+w和u+v=v+u;数乘也 满足结合律和分配律,即对任意标量k、l∈F和任意向量u∈V,有k(l(u))=(kl)(u)和k(u+v)=ku+kv。
线性组合的应用
向量表示
线性组合可以用来表示向量,使得向量的运算更加简洁明了。
线性方程组
线性组合可以用来求解线性方程组,通过将方程组中的未知数表示 为已知向量的线性组合,简化方程组的求解过程。
向量空间
线性组合是向量空间中向量运算的基本形式之一,可以用来研究向 量空间的性质和结构。
04
向量的线性相关性
中任意向量可以由这组基线性表示。
基的个数
02 一个向量空间的一组基的个数是有限的,且等于该向
量空间的维数。
基的特性
03
基中的向量是线性无关的,且可以作为该向量空间的
坐标系。
基的性质
唯一性
一个向量空间的一组基是唯一的,即如果存在另一组基也可 以表示向量空间中的任意向量,则这两组基之间存在一一对 应的关系。
05
向量组的秩
秩的定义
01
秩的定义
向量组的秩是指该向量组构成的 矩阵的秩,即该矩阵的最高阶非 零子式的阶数。
02
03
秩的符号表示
秩的性质
用符号“秩”表示,常用大写英 文字母表示,如A的秩记作r(A) 。
向量组的秩是该向量组线性无关 的向量的个数,与向量组的维数 有关。
线性代数第一章第7节PPT教学课件

解
11 1 1
12 3 4 D
1 4 9 16
1 8 27 64
(41)(42)(43)(31)(32)(21)12
1 11 1
11 11
5 23 4
D1 25
4
9
12 16
125 8 27 64
,
11 1 1
15 34
D2 1 25
48 9 16
1 125 27 64
11 1 1
12 5 4
, D3 1 4
25
72 16
1 8 125 64
12 3 5
D4 1 4 9
48 25
1 8 27 125
,
x 1 D D 1 1 , x 2 D D 2 4 , x 3 D D 3 6 , x 4 D D 4 4
三、重要定理
定理1 如果线性方程组1的系数行列式 D0, 则 1一定有解,且解是唯一的 .
“没有非零解”即“只有零解”
定理3 如果齐次线性方程组2 有非零解,则它
的系数行列式必为零.
系数行列式 D0 a11x1a12x2a1nxn0 a 2 1x1 a2 2x2 a2 nx n 0 an1x1an2x2annxn0
有非零解.
例2 问 取何值时,齐次方程组
3x1x2x3 2x2x3
思考题
当线性方程组的系数行列式为零时,能否用克拉默 法则解方程组?为什么?此时方程组的解为何?
PPT教学课件
谢谢观看
Thank You For Watching
的系数行列式不等于零,即D
a21 a22 a2n
0
an1 an2 ann
那么线性方程组1 有解,并且解是唯一的,解
中南大学线性代数课件 2-3矩阵的秩

0.
R A 2.
1 3 2 2 另解 对矩阵 A 0 2 1 3 做初等变换, 2 0 1 5 1 3 2 2 1 3 2 2 0 2 1 3 ~ 0 2 1 3 , 2 0 1 5 0 0 0 0
r3 3r2
r4 4r2
1 6 4 1 4 1 1 0 4 3 0 0 0 4 8 0 0 0 4 8 1 6 4 1 4 1 1 0 4 3 0 0 0 4 8 0 0 0 0 0
证毕
初等变换求矩阵秩的方法: 把矩阵用初等行变换变成为行阶梯形矩阵, 行阶梯形矩阵中非零行的行数就是矩阵的秩.
0 5 0 3 2 6 1 3 2 3 例4 设 A , 求矩阵 A 的 2 0 1 5 3 1 6 4 1 4 秩,并求 A 的一个最高阶非零子式 .
当A B时,分三种情况讨论:
(1)Dr中不含第i行; (2)Dr中同时含第i行和第j行; (3)Dr中含第i行但不含第j行;
ri krj
对 (1), ( 2) 两种情形,显然B 中与 Dr 对应的 子式 D r Dr 0, 故 R( B ) r .
对情形 ( 3),
则这个子式便是A 的一个最高阶非零子式.
设 n 阶可逆矩阵 A,
A 0, A的最高阶非零子式为 A ,
R( A) n, 故 A的标准形为单位阵 , A ~ E . E
可逆矩阵的秩等于阶数 ,故称可逆矩阵 为满秩矩阵. 奇异矩阵为降秩矩阵 .
1 2 2 1 1 0 2 4 8 2 例5 设A 2 4 2 3 , b 3 3 6 0 6 4
R A 2.
1 3 2 2 另解 对矩阵 A 0 2 1 3 做初等变换, 2 0 1 5 1 3 2 2 1 3 2 2 0 2 1 3 ~ 0 2 1 3 , 2 0 1 5 0 0 0 0
r3 3r2
r4 4r2
1 6 4 1 4 1 1 0 4 3 0 0 0 4 8 0 0 0 4 8 1 6 4 1 4 1 1 0 4 3 0 0 0 4 8 0 0 0 0 0
证毕
初等变换求矩阵秩的方法: 把矩阵用初等行变换变成为行阶梯形矩阵, 行阶梯形矩阵中非零行的行数就是矩阵的秩.
0 5 0 3 2 6 1 3 2 3 例4 设 A , 求矩阵 A 的 2 0 1 5 3 1 6 4 1 4 秩,并求 A 的一个最高阶非零子式 .
当A B时,分三种情况讨论:
(1)Dr中不含第i行; (2)Dr中同时含第i行和第j行; (3)Dr中含第i行但不含第j行;
ri krj
对 (1), ( 2) 两种情形,显然B 中与 Dr 对应的 子式 D r Dr 0, 故 R( B ) r .
对情形 ( 3),
则这个子式便是A 的一个最高阶非零子式.
设 n 阶可逆矩阵 A,
A 0, A的最高阶非零子式为 A ,
R( A) n, 故 A的标准形为单位阵 , A ~ E . E
可逆矩阵的秩等于阶数 ,故称可逆矩阵 为满秩矩阵. 奇异矩阵为降秩矩阵 .
1 2 2 1 1 0 2 4 8 2 例5 设A 2 4 2 3 , b 3 3 6 0 6 4
线性代数 课件-PPT精品文档

16
线性代数
出版社 科技分社
• 1.4
• 从行列式的定义看,一般低阶行列式的计 算比高阶行列式的计算简便.
• 定义2 在n阶行列式D=Δ(aij)中,把元素aij 所在的第i行和第j列划去,剩下元素按原来 的相对位置不变形成的一个n-1阶行列式, 17
线性代数
出版社 科技分社
• 称之为D中元素aij的余子式,记为Mij;称 Aij=(-1)i+jMij为aij的代数余子式.
28
线性代数
出版社 科技分社
• 2.2.3 矩阵的乘法 • 定义4 设A=(ai k)m×s,B=(bk j)s×n,则称C=(cij)m×n
为矩阵A与B的乘积,记为C=AB,
29
线性代数
出版社 科技分社
• 2.2.4
• 定义5 把矩阵A的行列依次互换得到的新 矩阵称为A的转置矩阵,记为AT.
30
• 性质1 向量组线性无关的充分必要条件是 向量组所含向量的个数等于其秩.
• 性质2 设向量组A的秩为r1,向量组B的秩 为r2,如果A组能由B组线性表示,则r1≤r2.
• 性质3 等价的向量组有相同的秩.
57
线性代数
• 证 设矩阵
• 3.4
出版社 科技分社
58
线性代数
• 定理8 正交向量组一定线性无关.
36
线性代数
出版社 科技分社
• 这里k≤min(m,n),共有CkmCkn个k阶子式. • 定义9 如果矩阵A有一个不等于零的r阶子
式D,并且所有r+1阶子式(如果有)全等于零, 则称D为矩阵A的最高阶非零子式,称r为矩 阵A的秩,记为R(A)=r,并规定零矩阵的秩 等于零.
线性代数总复习讲义PPT课件

在金融学中,线性代数用于描述资产价格和风险等经济量,以及计算收益 率和波动率等金融指标。
在计算机科学中的应用
01
Байду номын сангаас
02
03
04
线性代数在计算机科学中也有 着广泛的应用,如图像处理、 机器学习和数据挖掘等领域。
线性代数在计算机科学中也有 着广泛的应用,如图像处理、 机器学习和数据挖掘等领域。
线性代数在计算机科学中也有 着广泛的应用,如图像处理、 机器学习和数据挖掘等领域。
100%
相似变换法
通过相似变换将矩阵对角化,从 而得到其特征值和特征向量。
80%
数值计算法
对于一些大型稀疏矩阵,可以使 用数值计算方法来计算其特征值 和特征向量。
特征值与特征向量的应用
01
在物理、工程等领域中,特征值和特征向量被广泛 应用于求解振动、波动等问题。
02
在图像处理中,特征值和特征向量被用于图像压缩 和图像识别。
二次型的应用与优化问题
总结词
了解二次型在解决优化问题中的应用
详细描述
二次型的一个重要应用是在解决优化问题中, 特别是在求解二次规划问题时。通过将问题 转化为二次型的形式,可以方便地应用各种 优化算法进行求解,如梯度下降法、牛顿法 等。此外,二次型在统计分析、机器学习等 领域也有着广泛的应用。
06
矩阵的逆与行列式的值
要点一
总结词
矩阵的逆和行列式的值是线性代数中的重要概念,它们在 解决线性方程组、向量空间和特征值等问题中有着广泛的 应用。
要点二
详细描述
矩阵的逆是矩阵运算的一个重要概念,它表示一个矩阵的 逆矩阵与其原矩阵相乘为单位矩阵。逆矩阵的存在条件是 矩阵的行列式值不为零。行列式的值是一个由n阶方阵构 成的代数式,表示n个未知数的n阶线性方程组的解的系数 。行列式的值可以用来判断线性方程组是否有解以及解的 个数。同时,行列式的值也与特征值和特征向量等问题密 切相关。
在计算机科学中的应用
01
Байду номын сангаас
02
03
04
线性代数在计算机科学中也有 着广泛的应用,如图像处理、 机器学习和数据挖掘等领域。
线性代数在计算机科学中也有 着广泛的应用,如图像处理、 机器学习和数据挖掘等领域。
线性代数在计算机科学中也有 着广泛的应用,如图像处理、 机器学习和数据挖掘等领域。
100%
相似变换法
通过相似变换将矩阵对角化,从 而得到其特征值和特征向量。
80%
数值计算法
对于一些大型稀疏矩阵,可以使 用数值计算方法来计算其特征值 和特征向量。
特征值与特征向量的应用
01
在物理、工程等领域中,特征值和特征向量被广泛 应用于求解振动、波动等问题。
02
在图像处理中,特征值和特征向量被用于图像压缩 和图像识别。
二次型的应用与优化问题
总结词
了解二次型在解决优化问题中的应用
详细描述
二次型的一个重要应用是在解决优化问题中, 特别是在求解二次规划问题时。通过将问题 转化为二次型的形式,可以方便地应用各种 优化算法进行求解,如梯度下降法、牛顿法 等。此外,二次型在统计分析、机器学习等 领域也有着广泛的应用。
06
矩阵的逆与行列式的值
要点一
总结词
矩阵的逆和行列式的值是线性代数中的重要概念,它们在 解决线性方程组、向量空间和特征值等问题中有着广泛的 应用。
要点二
详细描述
矩阵的逆是矩阵运算的一个重要概念,它表示一个矩阵的 逆矩阵与其原矩阵相乘为单位矩阵。逆矩阵的存在条件是 矩阵的行列式值不为零。行列式的值是一个由n阶方阵构 成的代数式,表示n个未知数的n阶线性方程组的解的系数 。行列式的值可以用来判断线性方程组是否有解以及解的 个数。同时,行列式的值也与特征值和特征向量等问题密 切相关。
线性代数第四讲PPT课件
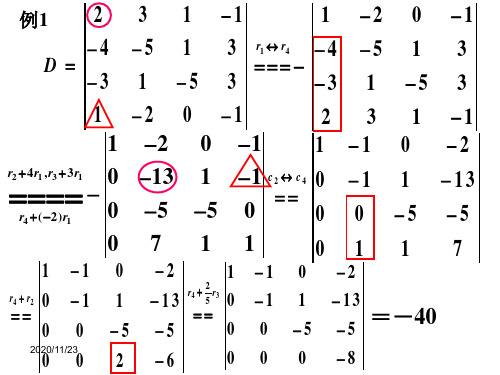
1 1 0 -5 D
记 Aij =(-1)i+j Mij , Aij 称为元素 aij 的代数余子式。
2020/11/23
2
a11 a12 a13 a14 例如四阶行列式 D a21 a22 a23 a24
a31 a32 a33 a34 a41 a42 a43 a44
元素 a32 的余子式是:
a11 a13 a14 M32 a21 a23 a24 ,
3A11 5A12 3A13 27.
2020/11/23
6
3 5 3 例2 计算行列式 D 0 1 0
7 72
解 按第二行展开,得
D1(1)223 3 72
27.
2020/11/23
7
例3 计算行列式
3 1 1 2 5 1 3 4 D 2 0 1 1 1 5 3 3
保留 a33 ,把第 3 行其余元素变为 0 ,然后按 3 行展开:
40.
2020/11/23
10
例4 证明范德蒙德(Vandermonde)行列式
1 1 1
x1 Dn x12
x2 xn
x22 xn2 (xi xj ). (1 )
nij1
比如
x1n1 x2n1 xnn1
1 1 11
4 - 1 3 2 120 16 1 9 4
64 - 1 27 8
2020/11/23
11
例4 证明范德蒙德(Vandermonde)行列式
1
x1 Dn x12
1 1
x2 xn
x22 xn2 (xi xj ). (1 )
nij1
x1n1 x2n1 xnn1
证 用数学归纳法
1 D2 x1
线性代数ppt课件

VS
线性代数的特点
线性代数具有抽象性、实用性、广泛性等 特点,是数学中重要的分支之一。
线性代数的历史背景
线性代数的起源
线性代数起源于17世纪,主要目的 是为了解决线性方程组的问题。
线性代数的发展
随着数学的发展,线性代数逐渐成为 一门独立的数学分支,并在20世纪得 到了广泛的应用和发展。
线性代数的应用领域
转置矩阵
一个矩阵A的转置矩阵是满足$A^T_{ij}=A_{ ji}$的矩阵
行列式与高斯消元
03
法
行列式的定义及性质
总结词
行列式是线性代数中重要的工具之一,它具有特殊的性质和计算规则。
详细描述
行列式是由一组方阵中的元素按照一定规则组成的,它是一个方阵是否可逆的判断标准,同时也有一 些重要的性质和计算规则,如交换两行或两列、对角线上的元素相乘等。了解行列式的定义和性质是 学习线性代数的基础。
矩阵的运算规则
加法
两个相同大小的矩阵,对应位置的元素相加
数乘
用一个数乘以矩阵的每一个元素
减法
两个相同大小的矩阵,对应位置的元素相减
乘法
要求两个矩阵满足乘法运算的规则,即第一 个矩阵的列数等于第二个矩阵的行数
矩阵的逆与转置
逆矩阵
一个矩阵A的逆矩阵是满足$AA^{-1}=I$的矩阵,其中$I$是单位矩阵
高斯消元法的原理
总结词
高斯消元法是一种解线性方程组的直接方法 ,其原理是将方程组转化为阶梯形矩阵。
详细描述
高斯消元法的基本思想是通过一系列的行变 换将线性方程组转化为阶梯形矩阵,这样就 可以直接求解方程组。高斯消元法包括三种 基本的行变换:将两行互换、将一行乘以非 零常数、将一行加上另一行的若干倍。通过 这些行变换,我们可以将矩阵转化为阶梯形 矩阵,从而求解方程组。
线性代数第一章第一节PPT课件

01递Biblioteka 公式法02递推公式法是根据行列式的性质和结构特点,利用递推公式来
计算行列式的方法。
递推公式法可以大大简化高阶行列式的计算过程,提高计算效
03
率。
行列式的计算方法
分块法
1
2
分块法是将高阶行列式分成若干个小块,然后利 用小块来计算整个行列式的方法。
3
分块法可以简化高阶行列式的计算过程,特别是 当行列式具有特定的结构特点时,分块法可以大 大提高计算效率。
01
向量空间
02
向量空间是线性代数中的一个重要概念,而行列式在向量 空间的定义和性质中也有着重要的应用。例如,通过行列 式可以判断一个向量集合是否构成向量空间,以及向量空 间的一些基本性质。
03
行列式在向量空间中的应用可以帮助我们更好地理解线性 代数的本质和结构特点。
05
特征值与特征向量
特征值与特征向量的定义
转置等特殊运算。
向量与矩阵的关系
关联性
04
向量可以用矩阵来表示,矩 阵中的每一行可以看作是一 个向量。
01 03
•·
02
向量和矩阵在数学中是密切 相关的概念,矩阵可以看作 是向量的扩展。
04
行列式
行列式的定义与性质
基本概念
行列式是由数字组成的方阵,按照一定的规则计 算出的一个数。
行列式具有一些基本的性质,如交换律、结合律、 分配律等。
向量可以用有向线段、坐 标系中的点或有序数对来 表示。
向量有大小和方向两个基 本属性,大小表示向量的 长度,方向表示向量的指 向。
矩阵的定义与运算
•·
02
基础运算
01
03
矩阵是一个由数字组成的矩 形阵列,表示二维数组。
线性代数相关知识培训教程PPT课件( 93页)

那末 A称为对称阵.
例如A162
6 8
1 0
为对称. 阵
1 0 6
说明 对称阵的元素以主对角线为对称轴对应相
等.
同型矩阵与矩阵相等
1)两个矩阵的行数相等,列数相等时,称为同型矩阵.
例如
1 5
2 6
与
14 8
3 4
为同型矩阵.
3 7 3 9
Aij (1)i j Mij, Aij叫做元素 aij的代数余子.式
A a i1 A i1 a i2 A i2 a iA n in ( i 1 ,2 , ,n ) A a i1 A j1 a i2 A j2 a iA n jn ( i j)
例1 3 1 1 2 5 1 3 4
p1p2pn
列取 . 和
N阶行列式是一个数,该数是n!项的代数和, 每项为取自表中不同行不同列n个元素的乘 积,符号由这n个元素列标排列的逆序数决定 (行标按自然顺序排列),奇排列带负号,偶排 列带正号.
2. 行列式的性质
1)行列式与它的转置行式列相等,即D DT. 2)互换行列式的两行 (列),行列式变号. 3)如果行列式有两行 (列)完全相同,则此行列式 等于零. 4)行列式的某一行(列)中所有的元素都乘以同 一数k,等于用数k 乘此行列式.
6)逆矩阵
伴随矩阵定义
行列式 A 的各个元素的代数余子式A ij 所
构成的如下矩阵
A11
A
A12
A1n
A21 An1 A22 An2 A2n Ann
称为矩阵 A 的伴随矩阵.
伴随矩阵性质
AA A AA E .
逆矩阵定义
例如A162
6 8
1 0
为对称. 阵
1 0 6
说明 对称阵的元素以主对角线为对称轴对应相
等.
同型矩阵与矩阵相等
1)两个矩阵的行数相等,列数相等时,称为同型矩阵.
例如
1 5
2 6
与
14 8
3 4
为同型矩阵.
3 7 3 9
Aij (1)i j Mij, Aij叫做元素 aij的代数余子.式
A a i1 A i1 a i2 A i2 a iA n in ( i 1 ,2 , ,n ) A a i1 A j1 a i2 A j2 a iA n jn ( i j)
例1 3 1 1 2 5 1 3 4
p1p2pn
列取 . 和
N阶行列式是一个数,该数是n!项的代数和, 每项为取自表中不同行不同列n个元素的乘 积,符号由这n个元素列标排列的逆序数决定 (行标按自然顺序排列),奇排列带负号,偶排 列带正号.
2. 行列式的性质
1)行列式与它的转置行式列相等,即D DT. 2)互换行列式的两行 (列),行列式变号. 3)如果行列式有两行 (列)完全相同,则此行列式 等于零. 4)行列式的某一行(列)中所有的元素都乘以同 一数k,等于用数k 乘此行列式.
6)逆矩阵
伴随矩阵定义
行列式 A 的各个元素的代数余子式A ij 所
构成的如下矩阵
A11
A
A12
A1n
A21 An1 A22 An2 A2n Ann
称为矩阵 A 的伴随矩阵.
伴随矩阵性质
AA A AA E .
逆矩阵定义
中南大学线性代数ppt课件

2 5 1 9
0 2 6 2 12 0 0 1 1 3
1 2 0 2
0 0
1 4
4 6
1
0
0 2
0 0
3 4
2
6
0 0 1 1 3 0 0 1 1 3
1 0 0 3 2
0
1
0
2
3
0 0 1 1 3
3 2 X 2 3.
1 3
若要求YA
C
,则可对矩阵
A
C
1
E(i(k))
k
第
i
行
1
1
以 Em (i(k)) 左乘矩阵 A,
a11
a12
Em
(
i(
k
))
A
kai1
kai 2
am1 am2
a1n
kain
第
i
行
amn
相当于以数k 乘 A的第 i 行 (ri k);
类似地,以 En(i(k)) 右乘 矩阵 A,其结果 相当于以数 k 乘 A 的第 i 列 (ci k).
例3 已知 n 阶方阵 A 0 0 1
1,
0 0 0
1
n
求 A 中所有元素的代数余子式之和 Aij . i, j1
解: A 2 0,
A 可逆. 且 A* A A1.
2 0
2 1
2 1
2 1
1 0
0 1
0 0
0 0
A E 0 0 1 1 0 0 1 0
0 0 0 1 0 0 0 1
aj2
a jn
第
i
行
ai1
ai 2
ain
中南大学线性代数PPT1-1-精选文档

(6)式称为数表(5)所确定的三阶行列式.
a11
a12
a13
D a21 a22 a23 .列标 a31 a32 a33 行标 三阶行列式的计算 a11 a12 a13 a 11 a 12
(1)沙路法 D a21 a22 a23 a31 a32 a33
a 21 a 31
a 22 a 32
a a a a a a a a D a 11 22 33 12 23 31 13 21 32 a a a a a a a a a . 11 23 32 12 21 33 13 22 31
称列)的数表
表达式 a a a a 称为数表( 4 )所确定的 11 22 12 21 a 11 a 12 行列式,并记作 ( 5 ) a 21 a 22
即
a 11 a 12 D a a a a . 11 22 12 21 a 21 a 22
二阶行列式的计算
主对角线 副对角线
对角线法则
两式相减消去 x ,得 2
( a a a a ) x b a a b ; 11 22 12 21 1 1 22 12 2
类似地,消去 x ,得 1 ( a a a a ) x a b b a , 11 22 12 21 2 11 2 1 21
方程组的解为 当 a a a a 0 时, 11 22 12 21
解
3 2 3 ( 4 ) 7 0 , D 2 1
D 1
12 2 1
3 12 21 , 14 , D2 2 1 1
D 2 21 14 D 1 3. 2, x 2 x1 7 D D 7
二、三阶行列式
定义
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A={a|a∈I∧0<a∧a<5}, {a|a∈I∧1≤a≤50}
A={x|P(x)}, B={x|Q(x)}
若P(x)Q(x),则A = B
若P(x)Q(x),则A B
递归定义法
11/63
递归定义法(归纳定义)
用这种方法定义一个非空集合A时,一般应包括以 下三个部分:
⑴ 基本项
谁 属已于知A某,些即元S素0 (常A 。用这S0表是示构由造这A的些基元础素,组并成保的证非非空空集。合) 是 ⑵ 递归项
4/63
元素与集合的关系
a是集合A的一个元素, 则记为a∈A,读做“a属 于A”, 或说“a在A中”
a不是集合A的一个元素, 则记为aA,读做“a
不属于A”, 或说“a不在A中” 集合的元素可以是一个集合
例:A={a,b,c,{a,b}} 则{a,b}∈A且{a,b} A
5/63
有限集与无限集
A = B x(xAxB) x(xA→xB)∧x(xB→xA)
否则,用A≠B表示集合A和B不相等,即
A ≠ B x(xAxB) 定义4.1.4 设A和B是集合,
如果A的每一元素是B的一个元素, 那么A是B的子集,也称B
是A的母集(或称扩集),记为AB, 读做“B包含A”或“A包含 于B”,即
ABx(xA→xB)
长度为0的串叫做空串,记为Λ(或ε)
x和y都是在Σ上的符号串,x连结(或叫并置, 毗连)y, 记为xy
x=a1a2…an,y=b1b2…bm 则 xy=a1a2…anb1b2…bm x=Λ则 xy=y
z=xy
x是z的词头, y是z的词尾 如果x≠z, 称x为真词头 如果y≠z,称y为真词尾 如果w=xyz, 则y是w的子串, 如果y≠w,称y为真子串
合A是唯一的。
12/63
例
如果全集是整数集合I, 那么能为3 整除的正 整数集合S的谓词定义如下:
S { x|x 0 y (x 3 y )}
同样集合S能归纳地定义如下: (1) (基础)3∈S; (2) (归纳)如果x∈S和y∈S, 那么x+y∈S; (3) (极小性)S的元素都是由有限次应用条款(1)和(2)得出的。
13/63
字母表与串
设Σ表示一个有限的非空的符号(字符)集合、我们 称Σ为字母表。由字母表Σ中有限个字符拼接起来 的符号串叫做字母表Σ上的一个字(或叫串) 例
(a) 如果Σ={a,b, …, z}, 那么is, then都是Σ上的字 (b) 如果Σ={你, 我, 人, 工, …, 是}, 那么“你是工人”
6/63
空集与全集
显然,空集是不含有任何元素的有限集, 常用符号Φ 表示
定义4.1.2 全集
恒用E表示,是指包含了讨论中涉及的全体元 素的特殊集合
全集也是有相对性的,不同的问题有不同的全集, 即使是同一个问题也可以有不同的全集
7/63
集合的比较运算
定义4.1.3 集合相等(外延公理)
两个集合A和B相等, 即A=B, 当且仅当它们有相同的成员
集合的表示 集合应该是充分定义(良定)的
列举法
完全列举
部分列举
将集合中的元素一一列出,写在大括号内
A={1, 2, 3, 4}, B={a,b,c,d},C={…,-4,-2,0,2,4,…}
谓词描述法(指定原理)
用谓词公式描述元素的共同属性
一般形式:
S被称为谓词P的广延
S={a|P(a)}表示a∈S当且仅当P(a)是真
给出一组规则,从A中(已获得的)元素出发,依照这些 规则所获得的元素,仍然是A中的元素。这是构造A的 关键部分。
⑶ 极小化
谁 如果集合S A也满足⑴和⑵,则S = A 。这说明, A中 不 的每个元素都可以通过有限次使用⑴和⑵来获得(或称A 是 是满足条款(1)和(2)的最小集合),它保证所构造出的集
8/63
集合的比较运算
定理4.1.1设A和B是集合, A=B当且仅当A B和 BA( 的反对称性)
证明: ABBA
x(x∈Ax∈B)x(x∈Bx∈A) x((x∈Ax∈B)(x∈Bx∈A)) x(x∈Ax∈B) A=B
9/63
集合的比较运算
定义4.1.5 设A和B是集合,
如果AB且A≠B, 那么称A是B的真子集,记作
AB , 读作“B真包Байду номын сангаасA”或“A真包含于B”,即
ABA BA≠B x(x∈Ax∈B)x(x∈Ax∈B) x(x∈Ax∈B)(x(x∈Ax∈B)x(x∈B x∈A)) (x(x∈Ax∈B)x(x∈Ax∈B))(x(x∈A x∈B) x(x∈Bx∈A))
x(x∈Ax∈B) x(x∈BxA)
10/63
是Σ上的串 (c) 如果Σ={a, b, …, z,_} , 这里“_”是代表空白。那
么that_was_long_ago是Σ上的串, 习惯上印成that was long ago (d) 如果Σ={0,1}, 那么000,010,011010等都是Σ上的串
14/63
x是Σ上的一个字, 如果x=a1a2…an, (n∈N, 1≤i≤n, ai∈Σ), 那么x中的符号个数n称为x的长度, 记为‖x‖
中南大学线性代数课件
主要内容
第4章 集合
4.1 集合的概念与表示 4.2 集合的运算 4.3 Venn氏图及容斥原理 4.4 集合的划分 4.5 自然数集与数学归纳法
第5章 二元关系
第6章 函数
2/63
第4章 集合(Set)
4.1 集合的概念与表示
集合的概念
又称为类、族或搜集 是数学中最基本的概念之一 不可精确定义(原始概念) 集合的描述
笼统地说,一些可以互相区分的任意对象(统称为元素)聚集在一 起形成的整体就叫做集合,用大写的英文字母表示,如A,B…
这些对象就是这个集合的元素(或称成员) ,一般用小写字母表示, 如a,b…
集合中的元素不计次序
{a,b,c,a}={c,b,a,d}
集合中的元素不计重度
{x,y,x} ={x,y} ={x,x,x,y}
定义4.1.1 设A是一个集合。
1. 用A或#A表示A含有的元素的个数,称做A 的基数,或阶。
2. 若#A =0,则称为空集;否则称为非空集。 3. 若#A为一非负整数,则称A为有限集;否则
称为无限集。 例:
A={a,b,{a, b}} |A|=3;|{A}|=1
基数为n的非空有限集称为n元(或n阶)集合
