2013年广州市黄埔 区一模试题
广州一模理综试题及答案

试卷类型:A 2013年广州市普通高中毕业班综合测试(一)理科综合2013. 3 本试卷共12页,36小题,满分300分。
考试用时150分钟。
注意事项:1. 答卷前,考生务必用2B铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签.字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
5. 本卷所用相对原子质量:H-1、C-12、0-16、S-32、Cu-64一、单项选择题:本题包括16小题,每小题4分,共64分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
1.下列关于生物膜系统的叙述,正确的是A. 原核细胞无核膜及细胞器膜因而不具生物膜B. 细胞膜功能的复杂程度取决于憐脂的种类和数量C. 内质网膜为多种酶提供了大量的附着位点D. 有丝分裂过程中核膜随着丝点的分裂而消失2-眼虫属于原生动物(其眼点能感光),如右图所示。
对其分析恰当的是A. 眼虫的细胞质中不含RNAB. 眼虫具有趋光性,因其眼点能感受化学信息C. 眼虫鞭毛摆动所需的ATP来自叶绿体D. 眼虫的伸缩泡有助于提高物质运输的效率3.人食用被诺如病毒(NV)污染的食物会导致呕吐与腹泻,而NV极易变异,下列推断不合理的是A. 酸能杀死部分NV属于特异性免疫B. NV极易变异,人类很难研究相应的疫苗C. 人体有多种抗NV的抗体,可能是因为NV表面存在多种抗原蛋白D. 特异性的效应T细胞能促使被NV入侵的靶细胞裂解4. 有关育种的说法,正确的是A. 多倍体育种过程都要使用秋水仙素B. 利用基因工程技术可定向培育优良品种C. 用于大田生产的优良品种都是纯合子D 杂交育种与单倍体育种的原理都是基因重组5 下列对实验的分析,正确的是A-用洋葱鳞片叶内表皮细胞能观察到质壁分离现象B. 斐林试剂能与蔗糖反应产生砖红色沉淀C. 加人无水乙醇越多,叶绿体色素提取液的绿色越深D. 观察洋葱根尖分生区细胞有丝分裂可用健那绿染色6. 下列关于“转化”的说法不正确的是A. ATP水解释放的能量可转化成光能、电能等B. 细胞内多个基因发生突变,细胞就转化成癌细胞C. 在含适量DNA酶和S型菌DNA的培养基中,R型菌不能转化为S型菌D. 目的基因导入受体细胞,并在细胞内维持稳定和表达的过程称为转化7. 在水溶液中能大量共存的一组离子是A. Al3+、Na+、HCO3-、SO42-B. H+、Fe2+、ClO-、Cl-C. Mg2+、K+、SO42-、NO3-D. NH4+ Ag+、OH-、Br-8. 下列说法正确的是A. 食盐、醋酸和蔗糖都是电解质B. 纤维素、淀粉和蛋白质都是高分子化合物C. 甲烷和乙烯均可使酸性KMnO4溶液褪色D. 乙酸乙酯和植物油均可水解生成乙醇9. 下列实验不能达到目的的是A. 用AlCl3溶液和过量氨水制备Al(OH)3B. 用NH4Cl和Ca( 0H) 2固体混合加热制备NH3C. 用NaOH溶液除去苯中的溴D. 用足量铜粉除去FeCl2溶液中的FeCl3杂质10. 设n A为阿伏加德罗常数的数值,下列说法正确的是A. 16g CH4含有10n A个电子B. 常温常压下,22. 4L Cl2含有2n A个Cl原子C. 1 mol Cu与足量稀HNO3反应,转移3n A个电子D. 1L O.1 mol.L-1 Na2SO3溶液中含有 O. 1n A个S032_11. 下列陈述I、II正确并且有因果关系的是12. 对于常温下pH= 3的乙酸溶液,下列说法正确的是A. C(H+)= c(CH3COO-) + c(OH-)B.加水稀释到原体积的10倍后溶液pH变为4C. 加入少量乙酸钠固体,溶液pH降低D. 与等体积pH= 11的NaOH溶液混合后所得溶液中:c(Na+) =c(CH3COO- )13. 水压机是利用液体来传递压强的。
2013年广州市一模理科数学试题及答案(纯word版)

图1俯视图正视图试卷类型:A2013年广州市普通高中毕业班综合测试(一)数学(理科)2013.3一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集{}123456U ,,,,,=,集合{}135A ,,=,{}24B ,=,则A .U AB = B .U =()U A ðB C .U A = ()U B ð D .U =()U A ð()U B ð2. 已知11abi i=+-,其中a b ,是实数,i 是虚数单位,则a b +i = A .12+i B .2+i C .2-i D .12-i3.已知变量x y ,满足约束条件21110x y x y y ,,.⎧+≥⎪-≤⎨⎪-≤⎩则2z x y =-的最大值为A .3-B .0C .1D .3 4.直线0x -=截圆()2224x y -+=所得劣弧所对的圆心角是A .6π B .3π C .2π D .23π 5. 某空间几何体的三视图及尺寸如图1,则该几何体的体积是A .2B .1C. 23D. 136. 函数()()y x xx x sin cos sin cos =+-是A .奇函数且在02,π⎡⎤⎢⎥⎣⎦上单调递增 B .奇函数且在2,ππ⎡⎤⎢⎥⎣⎦上单调递增C .偶函数且在02,π⎡⎤⎢⎥⎣⎦上单调递增 D .偶函数且在2,ππ⎡⎤⎢⎥⎣⎦上单调递增7.已知e 是自然对数的底数,函数()f x =e 2xx +-的零点为a ,函数()ln 2g x x x =+-的零点为b ,则下列不等式中成立的是A .()()()1f a f f b << B. ()()()1f a f b f << C. ()()()1f f a f b << D. ()()()1f b f f a << 8.如图2,一条河的两岸平行,河的宽度600d =m ,一艘客船从码头A 出发匀速驶往河对岸的码头B . 已知AB =1km ,水流速度为2km/h, 若客船行 驶完航程所用最短时间为6分钟,则客船在静水中 的速度大小为A .8 km/h B .C .km/hD .10km/h 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9. 不等式1x x -≤的解集是 . 10.10x cos ⎰d x = .11.某工厂的某种型号的机器的使用年限x 和所支出的维修费用y (万元)有下表的统计资料:根据上表可得回归方程ˆˆ1.23yx a =+,据此模型估计,该型号机器使用年限为10年时维修费用约 万元(结果保留两位小数).12.已知01a a ,>≠,函数()()()11xa x f x x a x ,,⎧≤⎪=⎨-+>⎪⎩若函数()f x 在02,⎡⎤⎣⎦上的最大值比最小值大52,则a 的值为 . 13. 已知经过同一点的nn (∈N 3n *,)≥个平面,任意三个平面不经过同一条直线.若这n 个平面将空间分成()fn 个部分,则()3f = ,()f n = .(二)选做题(14~15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)图4ABC A 1C 1B 1D E 图3C在极坐标系中,定点32,2A π⎛⎫⎪⎝⎭,点B 在直线cos sin 0ρθθ=上运动,当线段AB 最短时,点B 的极坐标为 . 15.(几何证明选讲选做题)如图3,AB 是O 的直径,BC 是O 的切线,AC 与O 交于点D 若3BC =,165AD =,则AB 的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知函数()sin()4f x A x πω=+(其中x ∈R ,0A >,0ω>)的最大值为2,最小正周期为8. (1)求函数()f x 的解析式;(2)若函数()f x 图象上的两点,P Q 的横坐标依次为2,4,O 为坐标原点,求△POQ 的面积.17.(本小题满分12分)甲,乙,丙三位学生独立地解同一道题,甲做对的概率为12,乙,丙做对的概率分别为m ,n (m >n ),且三位学生是否做对相互独立.记ξ为这三位学生中做对该题的人数,其分布列为:(1) 求至少有一位学生做对该题的概率; (2) 求m ,n 的值; (3) 求ξ的数学期望. 18.(本小题满分14分)如图4,在三棱柱111ABC A B C -中,△ABC 是边长为2的等边三角形, 1AA ⊥平面ABC ,D ,E 分别是1CC ,AB 的中点.(1)求证:CE ∥平面1A BD ; (2)若H 为1A B 上的动点,当CH 与平面1A AB求平面1A BD 与平面ABC 所成二面角(锐角)的余弦值. 19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且 12323(1)2(n n a a a na n S n n +++⋅⋅⋅+=-+∈N *).(1) 求数列{}n a 的通项公式;(2)若p q r ,,是三个互不相等的正整数,且p q r ,,成等差数列,试判断111p q r a a a ,,---是否成等比数列?并说明理由.20.(本小题满分14分)已知椭圆1C 的中心在坐标原点,两个焦点分别为1(2,0)F -,2F ()20,,点(2,3)A 在椭圆1C 上,过点A 的直线L 与抛物线22:4C x y =交于B C ,两点,抛物线2C 在点B C ,处的切线分别为12l l ,,且1l 与2l 交于点P . (1) 求椭圆1C 的方程;(2) 是否存在满足1212PF PF AF AF +=+的点P ? 若存在,指出这样的点P 有几个(不必求出点P 的坐标); 若不存在,说明理由. 21.(本小题满分14分) 已知二次函数()21fx x ax m =+++,关于x 的不等式()()2211f x m x m <-+-的解集为()1m m ,+,其中m 为非零常数.设()()1f xg x x =-.(1)求a 的值;(2)k k (∈R )如何取值时,函数()x ϕ()g x =-()1k x ln -存在极值点,并求出极值点;(3)若1m =,且x 0>,求证:()()1122nn ng x g x n (⎡⎤+-+≥-∈⎣⎦N *).2013年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.二、填空题:本大题考查基本知识和基本运算,体现选择性.共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题.9.1,2⎡⎫+∞⎪⎢⎣⎭10.1sin 11.12.38 12.12或7213.8,22n n -+ 14.1116,π⎛⎫⎪⎝⎭15.4 说明:① 第13题第一个空填对给2分,第二个空填对给3分. ② 第14题的正确答案可以是:11126k k ,(ππ⎛⎫+∈ ⎪⎝⎭Z ). 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查三角函数的图象与性质、诱导公式、余弦定理、正弦定理、两点间距离公式等知识,考查化归与转化的数学思想方法,以及运算求解能力)(1)解:∵()f x 的最大值为2,且0A >, ∴2A =. ……………1分∵()f x 的最小正周期为8, ∴28T πω==,得4πω=. ……………2分∴()2sin()44f x x ππ=+. ……………3分(2)解法1:∵(2)2sin 2cos 244f πππ⎛⎫=+==⎪⎝⎭, ……………4分(4)2sin 2sin 44f πππ⎛⎫=+=-= ⎪⎝⎭ ……………5分∴(4,P Q .∴OP PQ OQ ===……………8分∴222222cos 2OP OQ PQPOQ OP OQ+-+-∠===………10分 ∴POQ sin ∠==3……………11分 ∴△POQ的面积为11223S OP OQ POQ sin =∠=⨯⨯⨯=……………12分解法2:∵(2)2sin 2cos 244f πππ⎛⎫=+==⎪⎝⎭……………4分(4)2sin 2sin 44fπππ⎛⎫=+=-= ⎪⎝⎭ ……………5分∴(4,P Q . (苏元高考吧: )∴(4,OP OQ ==. ……………8分∴cos cos ,3OP OQ POQ OP OQ OP OQ⋅∠=<>===. ……………10分 ∴POQ sin ∠==3……………11分 ∴△POQ的面积为11223S OP OQ POQ sin =∠=⨯⨯⨯=……………12分解法3:∵(2)2sin 2cos 244f πππ⎛⎫=+==⎪⎝⎭……………4分(4)2sin 2sin 44fπππ⎛⎫=+=-= ⎪⎝⎭ ……………5分∴(4,P Q .∴直线OP 的方程为2y x =,即0x -=. ……………7分∴点Q 到直线OP 的距离为d ==……………9分∵OP =……………11分∴△POQ 的面积为1122S OP d =⋅=⨯⨯=……………12分17.(本小题满分12分)(本小题主要考查相互独立事件的概率、离散型随机变量的均值等基础知识,考查数据处理、推理论证、运算求解能力和应用意识,以及或然与必然的数学思想)解:设“甲做对”为事件A ,“乙做对”为事件B ,“丙做对”为事件C ,由题意知, ()()()12P A P B m P C n ,,===. ……………1分 (1)由于事件“至少有一位学生做对该题”与事件“0ξ=”是对立的,所以至少有一位学生做对该题的概率是()1310144P ξ-==-=. …………3分 (2)由题意知()()()()1101124PP ABC m n ξ===--=, ……………4分 ()()113224P P ABC mn ξ====, ……………5分 整理得112mn =,712m n +=.由m n >,解得13m =,14n =. ……………7分 (3)由题意知()()()()1a PP ABC P ABC P ABC ξ===++()()()()11111111122224m n m n m n =--+-+-=, ………9分 (2)1(0)(1)(3)b P P P P ξξξξ===-=-=-==14, ……………10分 ∴ξ的数学期望为0(0)1(1)2(2)3(3)E P P P P ξξξξξ=⨯=+⨯=+=+==1312.H FABCA 1C 1B 1DE…………12分18.(本小题满分14分)(本小题主要考查空间线面位置关系、直线与平面所成的角、二面角等基础知识,考查空间想象、推理论证、抽象概括和运算求解能力,以及化归与转化的数学思想方法) 解法一:(1)证明:延长1A D 交AC 的延长线于点F ,连接BF . ∵CD ∥1AA ,且CD 12=1AA ,∴C 为AF 的中点. ……………2分 ∵E 为AB 的中点,∴CE ∥BF . ……………3分∵BF ⊂平面1A BD ,CE ⊄平面1A BD , ∴CE ∥平面1A BD . ……………4分 (2)解:∵1AA ⊥平面ABC ,CE ⊂平面ABC ,∴1AA ⊥CE . ……………5分 ∵△ABC 是边长为2的等边三角形,E 是AB 的中点, ∴CE AB ⊥,2CE AB == ∵AB ⊂平面1A AB ,1AA ⊂平面1A AB ,1AB AA A = , ∴CE ⊥平面1A AB . ……………6分 ∴EHC ∠为CH 与平面1A AB 所成的角. ……………7分∵CE =在Rt △CEH 中,tan CE EHC EH ∠==, ∴当EH 最短时,tan EHC ∠的值最大,则EHC ∠最大. ……………8分 ∴当1EH A B ⊥时,EHC ∠最大. 此时,tan CE EHC EH EH∠===2.A∴5EH =. ……………9分 ∵CE ∥BF ,CE ⊥平面1A AB , ∴BF ⊥平面1A AB . ……………10分 ∵AB ⊂平面1A AB ,1A B ⊂平面1A AB , ∴BF ⊥AB ,BF ⊥1A B . ……………11分 ∴1ABA ∠为平面1A BD 与平面ABC 所成二面角(锐角). ……………12分 在Rt △EHB中,BH ==5,cos 1ABA∠5BH EB ==.…13分 ∴平面1A BD 与平面ABC所成二面角(锐角)的余弦值为5. ……………14分 解法二:(1)证明:取1A B 的中点F ,连接DF 、EF . ∵E 为AB 的中点, ∴EF ∥1AA ,且112EF AA =. ……………1分 ∵CD ∥1AA ,且CD 12=1AA ,∴EF ∥CD ,EF =CD . ……………2分 ∴四边形EFDC 是平行四边形.∴CE ∥DF . ……………3分 ∵DF ⊂平面1A BD ,CE ⊄平面1A BD , ∴CE ∥平面1A BD . (苏元高考吧: ) ……………4分 (2)解:∵1AA ⊥平面ABC ,CE ⊂平面ABC ,∴1AA ⊥CE . ……………5分 ∵△ABC 是边长为2的等边三角形,E 是AB 的中点,∴CE AB ⊥,2CE AB == ∵AB ⊂平面1A AB ,1AA ⊂平面1A AB ,1AB AA A = , ∴CE ⊥平面1A AB . ……………6分 ∴EHC ∠为CH 与平面1A AB 所成的角. ……………7分∵CE =在Rt △CEH 中,tan CE EHC EH EH∠==, ∴当EH 最短时,tan EHC ∠的值最大,则EHC ∠最大. ……………8分 ∴当1EH A B ⊥时,EHC ∠最大. 此时,tan CE EHC EH EH∠===2.∴5EH =. ……………9分 在Rt △EHB中,BH ==∵Rt △EHB ~Rt △1A AB , ∴1EH BHAA AB =,即1552AA =. ∴14AA =. ……………10分 以A 为原点,与AC 垂直的直线为x 轴,AC 所在的直线为y 轴,1AA 所在的直线为z 轴, 建立空间直角坐标系A xyz -. 则()000A ,,,1A ()004,,,B )10,,D ()02,,2.∴1AA = ()004,,,1A B =)14,-,1A D =()02,,-2.设平面A BD 1的法向量为n =()x y z ,,,由n 10A B ?,n 10A D?,得40220y z y z .ìï+-=ïíï-=ïî (苏元高考吧: ) 令1y =,则1z x ==,∴平面A BD 1的一个法向量为n=)11,. ……………12分∵1AA ⊥平面ABC , ∴1AA=()004,,是平面ABC 的一个法向量.∴cos 111,⋅==n AA n AA nAA ……………13分 ∴平面1A BD 与平面ABC所成二面角(锐角)的余弦值为5. ……………14分 19.(本小题满分14分)(本小题主要考查等比数列的通项公式、数列的前n 项和等基础知识,考查合情推理、化归与转化、特殊与一般的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力) (1) 解:12323(1)2n n a a a na n S n ++++=-+ ,∴ 当1n =时,有 11(11)2,a S =-+ 解得 12a =. ……………1分 由12323(1)2n n a a a na n S n ++++=-+ , ①得1231123(1)2(1)n n n a a a na n a nS n ++++++++=++ , ② ……………2分 ② - ①得: 11(1)(1)2n n n n a nS n S +++=--+. ③ ……………3分 以下提供两种方法:法1:由③式得:11(1)()(1)2n n n n n S S nS n S +++-=--+,即122n n S S +=+; ……………4分∴122(2)n n S S ++=+, ……………5分∵112240S a +=+=≠,∴数列{2}n S +是以4为首项,2为公比的等比数列.∴1242n n S -+=⨯,即1142222n n n S -+=⨯-=-. ……………6分 当2n ≥时, 11(22)(22)2n n n n n n a S S +-=-=---=, ……………7分 又12a =也满足上式,∴2n n a =. ……………8分 法2:由③式得:()111(1)(1)22n n n n n n n a nS n S n S S S ++++=--+=-++,得12n n a S +=+. ④ ……………4分当2n ≥时,12n n a S -=+, ⑤ ……………5分 ⑤-④得:12n n a a +=. ……………6分 由12224a a S +=+,得24a =,∴212a a =. ……………7分 ∴数列{}n a 是以12a =为首项,2为公比的等比数列. ∴2n n a =. ……………8分 (2)解:∵p q r ,,成等差数列,∴2p r q +=. ……………9分假设111p q r a a a ,,---成等比数列, 则()()()2111p rq a aa --=-, ……………10分即()()()2212121p r q --=-,化简得:2222p r q+=⨯. (*) ……………11分∵p r ≠,∴2222p r q +>=⨯,这与(*)式矛盾,故假设不成立.……13分 ∴111p q r a a a ,,---不是等比数列. ……………14分20.(本小题满分14分)(本小题主要考查椭圆、抛物线、曲线的切线等基础知识,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识)(1) 解法1:设椭圆1C 的方程为22221x y a b+=()0a b >>,依题意: 222222231,4.a ba b ⎧+=⎪⎨⎪=+⎩解得: 2216,12.a b ⎧=⎪⎨=⎪⎩ ……………2分 ∴ 椭圆1C 的方程为2211612x y +=. ……………3分 解法2:设椭圆1C 的方程为22221x y a b+=()0a b >>,根据椭圆的定义得1228a AF AF =+=,即4a =, ……………1分 ∵2c =, ∴22212b a c =-=. ……………2分∴ 椭圆1C 的方程为2211612x y +=. ……………3分 (2)解法1:设点)41,(211x x B ,)41,(222x x C ,则))(41,(212212x x x x BC --=, )413,2(211x x BA --=,∵C B A ,,三点共线, (苏元高考吧: )∴BC BA //. ……………4分∴()()()222211211113244x x x x x x ⎛⎫--=-- ⎪⎝⎭,化简得:1212212x x x x ()+-=. ① ……………5分 由24x y =,即214y x ,=得y '=12x . ……………6分 ∴抛物线2C 在点B 处的切线1l 的方程为)(2411121x x x x y -=-,即211412x x x y -=. ② 同理,抛物线2C 在点C 处的切线2l 的方程为 222412x x x y -=. ③ ……………8分设点),(y x P ,由②③得:=-211412x x x 222412x x x -, 而21x x ≠,则 )(2121x x x +=. ……………9分 代入②得 2141x x y =, ……………10分 则212x x x +=,214x x y =代入 ① 得 1244=-y x ,即点P 的轨迹方程为3-=x y .……………11分若1212PF PF AF AF +=+ ,则点P 在椭圆1C 上,而点P 又在直线3-=x y 上, ……………12分∵直线3-=x y 经过椭圆1C 内一点(3,0),∴直线3-=x y 与椭圆1C 交于两点. ……………13分∴满足条件1212PF PF AF AF +=+ 的点P 有两个. ……………14分 解法2:设点),(11y x B ,),(22y x C ,),(00y x P , 由24x y =,即214y x ,=得y '=12x . ……………4分 ∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-, 即2111212x y x x y -+=. ……………5分 ∵21141x y =, ∴112y x x y -= . ∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① ……………6分 同理, 20202y x x y -=. ② ……………7分 综合①、②得,点),(),,(2211y x C y x B 的坐标都满足方程y x xy -=002. ……………8分 ∵经过),(),,(2211y x C y x B 的直线是唯一的,∴直线L 的方程为y x xy -=002, ……………9分 ∵点)3,2(A 在直线L 上, ∴300-=x y . ……………10分 ∴点P 的轨迹方程为3-=x y . ……………11分若1212PF PF AF AF +=+ ,则点P 在椭圆1C 上,又在直线3-=x y 上,……12分 ∵直线3-=x y 经过椭圆1C 内一点(3,0),∴直线3-=x y 与椭圆1C 交于两点. ……………13分∴满足条件1212PF PF AF AF +=+ 的点P 有两个. ……………14分 解法3:显然直线L 的斜率存在,设直线L 的方程为()23y k x =-+,由()2234y k x x y ,,⎧=-+⎪⎨=⎪⎩消去y ,得248120x kx k -+-=. ……………4分设()()1122B x y C x y ,,,,则12124812x x k x x k ,+==-. ……………5分 由24x y =,即214y x ,=得y '=12x . ……………6分 ∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-,即2111212x y x x y -+=.…7分 ∵21141x y =, ∴211124x y x x =-. 同理,得抛物线2C 在点C 处的切线2l 的方程为222124x y x x =-. ……………8分 由211222124124x y x x x y x x ,,⎧=-⎪⎪⎨⎪=-⎪⎩解得121222234x x x k x x y k ,.⎧+==⎪⎪⎨⎪==-⎪⎩ ∴()223P k k ,-. ……………10分 ∵1212PF PF AF AF +=+,∴点P 在椭圆22111612x y C :+=上. ……………11分 ∴()()2222311612k k -+=.化简得271230k k --=.(*) ……………12分由()2124732280Δ=-⨯⨯-=>, ……………13分可得方程(*)有两个不等的实数根. ∴满足条件的点P 有两个. ……………14分 21.(本小题满分14分)(本小题主要考查二次函数、一元二次不等式、一元二次方程、函数应用、均值不等式等基础知识,考查数形结合、函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识) (1)解:∵关于x 的不等式()()2211fx m x m <-+-的解集为()1m m ,+,即不等式()22120x a m x m m ++-++<的解集为()1m m ,+,∴()2212x a m x m m ++-++=()()1x mx m ---.∴()2212x a m x m m ++-++=()()2211x m x m m -+++.∴()1221a m m +-=-+.∴2a =-. ……………2分(2)解法1:由(1)得()()1f xg x x =-()221111x x m m x x x -++==-+--.∴()()xg x ϕ=-()1k x ln -()11mx x =-+-()1k x ln --的定义域为()1,+∞. ∴()1x ϕ'=-()211mkx x ---()()22211x k x k m x -++-+=-. ……………3分 方程()2210x k x k m -++-+=(*)的判别式()()222414Δk k m k m =+--+=+. ……………4分①当0m >时,0Δ>,方程(*)的两个实根为11x ,=<21x ,=> ……………5分则()21x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>. ∴函数()x ϕ在()21x ,上单调递减,在()2x ,+∞上单调递增.∴函数()x ϕ有极小值点2x . ……………6分②当0m <时,由0Δ>,得k <-k >若k <-1212k x ,+-=<2212k x ,++=<故x ∈()1,+∞时,()0x ϕ'>,(苏元高考吧: ) ∴函数()x ϕ在()1,+∞上单调递增.∴函数()x ϕ没有极值点. ……………7分若k >11x ,=>21x ,=>则()11x x ,∈时,()0x ϕ'>;()12x x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>. ∴函数()x ϕ在()11x ,上单调递增,在()12x x ,上单调递减,在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x ,有极大值点1x . ……………8分 综上所述, 当0m >时,k 取任意实数, 函数()x ϕ有极小值点2x ;当0m <时,k >()x ϕ有极小值点2x ,有极大值点1x .………9分(其中122k x +-=, 222k x ++=解法2:由(1)得()()1f xg x x =-()221111x x m mx x x -++==-+--.∴()()xg x ϕ=-()1k x ln -()11mx x =-+-()1k x ln --的定义域为()1,+∞.∴()1x ϕ'=-()211m kx x ---()()22211x k x k m x -++-+=-. ……………3分 若函数()()xg x ϕ=-()1k x ln -存在极值点等价于函数()x ϕ'有两个不等的零点,且至少有一个零点在()1,+∞上. ……………4分 令()x ϕ'()()22211x k x k m x -++-+=-0=,得()221x k x k m -++-+0=, (*)则()()2224140Δkk m k m =+--+=+>,(**) ……………5分方程(*)的两个实根为122k x +-=, 222k x ++=设()h x=()221x k x k m -++-+,①若1211x x ,<>,则()10h m =-<,得0m >,此时,k 取任意实数, (**)成立. 则()21x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>. ∴函数()x ϕ在()21x ,上单调递减,在()2x ,+∞上单调递增.∴函数()x ϕ有极小值点2x . ……………6分②若1211x x ,>>,则()10212h m k ,.⎧=->⎪⎨+>⎪⎩得00m k ,.⎧<⎨>⎩又由(**)解得k >k <-故k >……………7分 则()11x x ,∈时,()0x ϕ'>;()12x x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>. ∴函数()x ϕ在()11x ,上单调递增,在()12x x ,上单调递减,在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x ,有极大值点1x . ……………8分 综上所述, 当0m >时,k 取任何实数, 函数()x ϕ有极小值点2x ;当0m <时,k>()x ϕ有极小值点2x ,有极大值点1x .………9分(其中1x =2x =(2)证法1:∵1m =, ∴()g x=()111x x -+-. ∴()()1111nnnn n g x g x x x x x ⎛⎫⎛⎫⎡⎤+-+=+-+ ⎪ ⎪⎣⎦⎝⎭⎝⎭ 112212111111n n n n n n n n n n n n n x C x C x C x C x x x x x x ----⎛⎫=+⋅+⋅++⋅+-+ ⎪⎝⎭122412n n n nn n n C xC x C x ----=+++ . ……………10分 令T 122412n n n n n n n C xC x C x ----=+++ , 则T 122412n nn n n n n n C x C x C x -----=+++122412nn n n n n n C xC x C x ----=+++ .∵x 0>, ∴2T ()()()122244122n n n n n n n n n n C xx C x x C x x -------=++++++ ……11分≥121n nn n C C C -⋅+⋅++⋅ …12分 ()1212n n n nC C C -=+++()012102n n nn n n nn n n C C C C C C C -=+++++--()222n=-. ……………13分∴22nT ≥-,即()()1122nn ng x g x ⎡⎤+-+≥-⎣⎦. ……………14分证法2:下面用数学归纳法证明不等式11nn n x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭22n≥-.① 当1n =时,左边110x x x x ⎛⎫⎛⎫=+-+= ⎪ ⎪⎝⎭⎝⎭,右边1220=-=,不等式成立; ……………10分② 假设当n k =k (∈N *)时,不等式成立,即11kk k x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭22k ≥-,则 11111k k k x x x x +++⎛⎫⎛⎫+-+ ⎪⎪⎝⎭⎝⎭11111111kk k k k k k x x x x x x x x x x x x ++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥=++-++++-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111kk kx x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=++-++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111k k x x --⎛⎫+ ⎪⎝⎭ ……………11分()22k ≥⋅-+ ……………12分 122k +=-. ……………13分也就是说,当1n k =+时,不等式也成立. 由①②可得,对∀n ∈N *,()()1122nn n g x g x ⎡⎤+-+≥-⎣⎦都成立. ………14分精品文档你我共享薄雾浓云愁永昼,瑞脑消金兽。
01 黄浦区2013年高考模拟考英语试卷参考答案及听力文字)

黄浦区2013年高考模拟考英语试卷参考答案Listening ComprehensionSection ADirections: In Section A, you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.1. M: I’m leaving now. What would you like me to brin g you?W: Please get me some potatoes.Q: Where is the man probably going?2. W: The lunch we had today cost us sixty dollars. Did you tip the waiter? M: Of course, I left him 20% of our bill.Q: How much was the waiter tipped?3. M: Today is Thu rsday. Is it tomorrow that we’ll have a picnic?W: No. The day after tomorrow.Q: When will they have a picnic?4. W: Excuse me, could you please tell me the way to the bank? I want toexchange some money.M: Go straight ahead, and turn right at the second crossing. The bank is on your right.Q: Who might the two speakers be?5. M: Have you tried baking an apple pie by yourself?W: Yes, I made one yesterday, just the way you told me to make it.Q: What did the woman do yesterday?6. W: Is there a problem, officer? I wasn’t speeding, was I?M: I’m afraid you were. The speed limit here is 50 miles per hour.Q: What was the woman’s problem?7. M: There’s no homework this weekend. How about going fishing?W: It is not a bad idea.Q: What does the woman think of the suggestion?8. W: We’re planning a birthday party for Nancy tomorrow night. Can you come?M: I wish I could, but I work part time at the school library on weekdays.Q: Why can’t the boy go to the party?9. M: Are you disappointed that the Browns are moving to the south?W: In some ways.Q: What does the woman imply?10. W: I haven’t decided which dress to take, the blue one or the black one.M: It isn’t easy to choose, is it?Q: What can we learn from the conversation?Section BDirections: In Section B, you will hear two short passages, and you will be asked three questions on each of the passages. The passages will be read twice, but the questions will be spoken only once. When you hear a question, read the four possible answers on your paper and decide which one would be the best answer to the question you have heard.Questions 11 through 13 are based on the following passage.Roger Federer was born on August 8th 1981 in Switzerland and started playing tennis at the age of 8. His career began in the juniors and he turned professional at the age of 17. And he became number one in Switzerland in 2001.However, this handsome young tennis champion is a mysterious figure to his fans. Unlike most famous tennis professionals, Federer travels without a coach or crew. He prefers to let his parents handle his business affairs and take advice from his girlfriend who is a former Swiss tennis player. Federer is loved by his country and people. He was oddly awarded a cow by Switzerland after winning Wimbledon in 2004.Federer’s mother is from South Africa and he can speak Swiss-German, English and French fluently. He has earned more than 11 million US dollars since becoming professional. He runs a charity for poor children around the world.In 2005, two-time Wimbledon champion Roger Federer of Switzerland extended his lead on the top of the men’s world tennis rankings.Now listen again please.Questions:11. When did Roger Federer become a professional tennis player?12. What language is Federer unable to speak well?13. What is TRUE about Roger Federer according to the passage? Questions 14 through 16 are based on the following passage.Today, our lecture is about how some American states got their names.Each state was named in a different way. For example, the first British colonies were usually named for British rulers, such as North Carolina and South Carolina.The early British colonists named some areas by adding the word “new” to the name of a town or place in Britain, for example, the eastern states of New Hampshire and New Jersey.Other states were named by Europeans who were not British. For example, Spanish explorers in the 16th century gave the name California to an area they discovered. They did this because they thought the area was an island. California was the name of an island of gold in a well-known Spanish book of the time.Other names of places show the influence of American Indians. For example, French explorers called a river in the Middle West the “Missouri”. They named it for the Indian tribe that lived along the river. They also gave the name Missouri to a territory along the river, which later became a state.Actually, every one of America’s fifty states has its own story.Now listen again please.Questions:14. Who named the eastern states of New Hampshire and New Jersey?15. What did “California” mean when Spanish explorers named the area?16. What does the lecture focus on according to the passage?Section CDirections: In Section C, you will hear two longer conversations. The conversations will be read twice. After you hear each conversation, you are required to fill in the numbered blanks with the information you have heard. Write your answers on your answer sheet.Blanks 17 through 20 are based on the following conversation.M: Good morning, may I help you?W: Yes, please. I’d like to book a seat in the economy class on the next flight to London.M: One way or round trip?W: Just one way, please.M: That will be $239.W: Really? The last time I flew, it was only $230.M: Yes, sorry. The price went up two weeks ago.W: It seems the price goes up every time I fly.M: Will there be any luggage?W: Yes. I’d like to check in this suitcase. And I’ll carry the handbag with me.M: Fine. The next flight departs at 10:25 from Gate 4. Please be at the gate twenty minutes before boarding time.W: OK. And thank you.M: You’re welcome. Have a nice trip.Now listen again please.Complete the form. Write ONE WORD for each blank.Blanks 21 through 24 are based on the following conversation.W: Excuse me, sir. I’d like to have some information about the accommodation for students.M: O.K. You can choose to live in the dormitory, or you may consider private accommodation.W: If I want to stay in the private accommodation, how much should I pay?M: For a single room, 10 pounds less per week, or 5 pounds when charged on a daily rate. This will apply throughout this academic year. W: I see. How far is it from the residence to the university?M: The residence at 100 Peach Street is quite near. It takes about ten minutes to walk from the university main site.W: OK.M: If you need more information, the staff in the Information Office run by the university will offer you help.W: Where is the office?M: In NO.2 Building, just behind this building.W: Thank you very much for your kind help.M: Y ou are welcome.Now listen again please.Complete the form. Write NO MORE THAN THREE WORDS for each answer.第I卷1—5 ACDBB 6—10 ACDCA 11—13 CDD 14—16 BCC17. economy 18. 239 19. suitcase 20. departs21. private accommodation 22. a single room23. a ten-minute walk 24. NO.2 Building25—29 CDADB 30—34 BCCAD 35—40 CCACBB41—45 GDFIC 46—49 BJAH50—54 BDACB 55—59 DABBA 60—64 BCACD65—68 CBCA 69—71 CBD 72—75 DBBD76—80 DBFAE81. the explosion and sinking of the USS Maine82. store arms, ammunition, and explosives83. To cause trouble and end the Spanish rule/occupation.84. The Mystery of the USS Maine. / The (possible) causes of the USS Maine’s Explosion第II卷I. Translation1. The story inspires/inspired the youth /young people to struggle/strive for a better life.2. Time passes/flies quickly, especially when you are absorbed in readinga good book.3. The security system will not permit/allow you to enter the building unless you have the correct password.4. It never occurred to me that I would meet my old friend (who/whom) I hadn’t seen for quite a few years at the airport.5. The fact that the spread of useless information can have a bad effect on human society has attracted the attention/awareness of the public.。
2013广州一模数学试卷(文、理)含答案

图1俯视图侧视图正视图221122013广州一模数学(文科)参考公式:线性回归方程 y bx a =+ 中系数计算公式121ni i i ni i x x y y b a y b x x x ()(),()==--∑==--∑,其中y x ,表示样本均值.锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高.一、选择题:本大题共10小题,每小题5分,满分50分. 1.已知i 是虚数单位,则复数1-2i 的虚部为A .2B .1C .1-D .2- 2.设全集{}123456U ,,,,,=,集合{}135A ,,=,{}24B ,=,则A .U AB = B .U =()U A ðBC .U A = ()U B ðD .U =()U A ð()U B ð 3.直线3490x y +-=与圆()2211x y -+=的位置关系是A .相离B .相切C .直线与圆相交且过圆心D .直线与圆相交但不过圆心 4.若函数()y fx =是函数2xy=的反函数,则()2f的值是A .4B .2C .1D .0 5.已知平面向量a ()2m =-,,b()13=,,且()-⊥a b b ,则实数m 的值为A .23-B .23C .43D .636.已知变量x y ,满足约束条件21110x y x y y ,,.⎧+≥⎪-≤⎨⎪-≤⎩则2z x y =-的最大值为A .3-B .0C .1D .3 7. 某空间几何体的三视图及尺寸如图1,则该几何体的体积是A .2B. 1C.23D.138. 已知函数()22fx x sin =,为了得到函数()22gx x x sin cos =+的图象,只要将()y fx =的图象C BA .向右平移4π个单位长度 B .向左平移4π个单位长度C .向右平移8π个单位长度 D .向左平移8π个单位长度9.“2m <”是“一元二次不等式210x mx ++>的解集为R ”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 10.设函数()fx 的定义域为D ,如果xD y D ,∀∈∃∈,使()()2fx f y C C (+=为常数)成立,则称函数()fx 在D 上的均值为C . 给出下列四个函数:①3yx =;②12xy ⎛⎫= ⎪⎝⎭;③y x ln =;④21y x sin =+, 则满足在其定义域上均值为1的函数的个数是A .1B .2C .3D .4 二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题) 11.函数()()21fx x x ln =-+-的定义域是12.某工厂的某种型号的机器的使用年限x 和所支出的维修费用y (万元)有下表的统计资料:根据上表可得回归方程ˆˆ1.23yx a =+,据此模型估计,该型号机器使用年限为10年的维修费用约 万元(结果保留两位小数).13.已知经过同一点的n n (∈N 3n *,)≥个平面,任意三个平面不经过同一条直线.若这n 个平面将空间分成()fn 个部分,则()3f = ,()fn = .(二)选做题(14~15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题) 在极坐标系中,定点32,2A π⎛⎫⎪⎝⎭,点B 在直线cos 3sin 0ρθρθ+=上运动,当线段A B 最x2 3 4 5 6y2.23.85.56.57.0a0.06b频率组距短时,点B 的极坐标为 . 15.(几何证明选讲选做题)如图2,AB 是O 的直径,B C 是O 的切线,A C 与O 交于点D , 若3B C =,165A D =,则AB 的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()sin()4f x A x πω=+(其中x ∈R ,0A >,0ω>)的最大值为2,最小正周期为8.(1)求函数()f x 的解析式;(2)若函数()f x 图象上的两点,P Q 的横坐标依次为2,4,O 为坐标原点,求cos ∠POQ的值.17.(本小题满分12分)沙糖桔是柑桔类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植沙糖桔,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg ),获得的所有数据按照区间(4045,,⎤⎦(((455050555560,,,,,⎤⎤⎤⎦⎦⎦进行分组,得到频率分布直方图如图3.已知样本中产量在区间(4550,⎤⎦上的果树株数是产量在区间(5060,⎤⎦上的果树株数的43倍.(1)求a ,b 的值;(2)从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,求产量在区间(5560,⎤⎦上的果树至少有一株被抽中的概率.图4MDCBAP18.(本小题满分14分)如图4,在四棱锥P A B C D -中,底面A B C D 是平行四边形,60BCD ︒∠=,2AB AD =,P D ⊥平面A B C D ,点M 为P C 的中点.(1)求证:PA //平面BM D ; (2)求证:AD ⊥P B ;(3)若2AB PD ==,求点A 到平面BM D 的距离.19.(本小题满分14分)设数列{}n a 的前n 项和为n S ,已知12a =,28a =,()11452n n n S S S n +-+=≥,n T 是数列{}2n a log 的前n 项和.(1)求数列{}n a 的通项公式; (2)求n T ; (3)求满足2311110101112013n T T T ⎛⎫⎛⎫⎛⎫--⋅⋅-> ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 的最大正整数n 的值.20.(本小题满分14分)已知椭圆1C 的中心在坐标原点,两个焦点分别为1(2,0)F -,2F ()20,,点(2,3)A 在椭圆1C 上,过点A 的直线L 与抛物线22:4C x y =交于B C ,两点,抛物线2C 在点B C ,处的切线分别为12l l ,, 且1l 与2l 交于点P . (1) 求椭圆1C 的方程;(2) 是否存在满足1212PF PF AF AF +=+的点P ? 若存在,指出这样的点P 有几个(不必求出点P 的坐标); 若不存在,说明理由.21.(本小题满分14分)已知n ∈N *,设函数2321()1,2321n n xxxf x x x n -=-+-+-∈- R .(1)求函数y =2()f x kx k (-∈R )的单调区间;(2)是否存在整数t ,对于任意n ∈N *,关于x 的方程()0n f x =在区间1t t ,⎡⎤+⎣⎦上有唯一实数解,若存在,求t 的值;若不存在,说明理由.2013年广州市普通高中毕业班综合测试(一)数学(文科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分.题号 1 2 3 4 5 6 7 8 9 10 答案DDACBCADBC二、填空题:本大题考查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题. 11.(]1,2 12.1238. 13.8,22nn -+ 14.1116,π⎛⎫⎪⎝⎭ 15.4说明:① 第13题第一个空填对给2分,第二个空填对给3分.② 第14题的正确答案可以是:11126k k ,(ππ⎛⎫+∈ ⎪⎝⎭Z ).三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) (本小题主要考查三角函数的图象与性质、诱导公式、余弦定理等知识,考查化归与转化的数学思想方法,以及运算求解能力) (1)解:∵()f x 的最大值为2,且0A >,∴2A =. ……………1分 ∵()f x 的最小正周期为8, ∴28T πω==,得4πω=. ……………3分∴()2sin()44f x x ππ=+. ……………4分(2)解法1:∵(2)2sin 2cos 2244f πππ⎛⎫=+==⎪⎝⎭, ……………5分(4)2sin 2sin 244f πππ⎛⎫=+=-=- ⎪⎝⎭, ……………6分∴(2,2),(4,2)P Q -. ……………7分 ∴6,23,32OP PQ OQ ===. ……………10分∴()()()222222632233cos 232632O PO QPQPO Q O P O Q+-+-∠===⨯.……12分yxQ 1QP 1PO解法2:∵(2)2sin 2cos 2244f πππ⎛⎫=+==⎪⎝⎭, ……………5分(4)2sin 2sin 244f πππ⎛⎫=+=-=- ⎪⎝⎭, ……………6分∴(2,2),(4,2)P Q -. ……………8分∴(2,2),(4,2)O P O Q ==-. ……………10分∴63cos cos ,3632O P O QP O Q O P O Q O P O Q⋅∠=<>===⨯. ……………12分解法3: ∵(2)2sin 2cos 2244f πππ⎛⎫=+==⎪⎝⎭,……………5分(4)2sin 2sin 244f πππ⎛⎫=+=-=- ⎪⎝⎭,……………6分∴(2,2),(4,2)P Q -. ……………7分 作1PP x ⊥轴, 1Q Q x ⊥轴,垂足分别为11P Q ,, ∴116,2,2,32OP OP PP OQ ====,1142O Q Q Q ,==. (8)分设11PO P Q O Q ,αβ∠=∠=,则361223333sin ,cos ,sin ,cos ααββ====. ……………10分∴cos cos POQ ∠=()33cos cos sin sin αβαβαβ+=-=.………12分17.(本小题满分12分)(本小题主要考查频率分布直方图、概率等知识,考查数据处理、推理论证、运算求解能力和应用意识,以及或然与必然的数学思想)(1)解:样本中产量在区间(4550,⎤⎦上的果树有520100a a ⨯⨯=(株),…………1分 样本中产量在区间(5060,⎤⎦上的果树有()()002520100002b b ..+⨯⨯=+(株), ……………2分依题意,有()41001000023a b .=⨯+,即()40023a b.=+.①…………3分根据频率分布直方图可知()00200651b a ..+++⨯=, ② …………4分 解①②得:008004a b .,.==. ……………6分(2)解:样本中产量在区间(5055,⎤⎦上的果树有0045204.⨯⨯=株,分别记为 123A A A ,,,4A ,……………… 7分 产量在区间(5560,⎤⎦上的果树有0025202.⨯⨯=株,分别记为12B B ,. … 8分 从这6株果树中随机抽取两株共有15种情况:()()1213A A A A ,,,,()14A A ,()()()()()()111223242122A B A B A A A A A B A B ,,,,,,,,,,,,()34A A ,,()31A B ,,()32A B ,,()()4142A B AB ,,,,()12B B ,. ……………10分其中产量在(5560,⎤⎦上的果树至少有一株共有9种情况:()()1112A B A B ,,,,()()()()21223132A B A B A B A B ,,,,,,,,()()4142A B A B ,,,,()12B B ,. (11)分记“从样本中产量在区间(5060,⎤⎦上的果树随机抽取两株,产量在区间(5560,⎤⎦上的果树至少有一株被抽中”为事件M ,则()93155P M ==. ……………12分18.(本小题满分14分)(本小题主要考查空间线面位置关系、点到平面的距离等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) (1)证明:连接A C ,A C 与B D 相交于点O , 连接M O , ∵A B C D 是平行四边形,∴O 是A C 的中点. ……………1分 ∵M 为P C 的中点,∴MO AP //. ……………2分 ∵P A ⊄平面BM D ,M O ⊂平面BM D ,∴PA //平面BM D . ……………3分ON MDCBAP(2)证明:∵P D ⊥平面A B C D ,AD ⊂平面A B C D ,∴P D ⊥A D . ……………4分 ∵60BAD BCD ︒∠=∠=,2AB AD =, ∴222260BDABADAB AD cos ︒=+-⋅⋅2222AB AD AD =+- 22ABAD =-. ……………5分∴22AB AD =2BD +.∴AD BD ⊥. ……………6分∵PD BD D = ,PD ⊂平面P B D ,BD ⊂平面P B D ,∴AD ⊥平面P B D . ……………7分 ∵P B ⊂平面P B D ,∴AD PB ⊥. ……………8分(3)解:取C D 的中点N ,连接M N ,则MN PD //且12MN PD =.∵P D ⊥平面A B C D ,2PD =,∴M N ⊥平面A B C D ,1M N =. ……………9分在Rt △P C D 中,2C D AB PD ===,2211222DM PC PDCD==+=,∵BC AD //,AD PB ⊥, ∴B C P B ⊥.在Rt △P B C 中,122BM PC ==.在△BM D 中,BM D M =,O 为B D 的中点, ∴M O B D ⊥.在Rt △A B D 中,360232BD AB sin ︒=⋅=⨯=.在Rt △M O B 中,22M O BMOB=-=52.∴1322ΔABD S AD BD =⨯=,11524ΔM BD S BD M O =⨯=.…………11分设点A 到平面BM D 的距离为h ,∵M ABD A M BD V V --=,∴13M N 13ΔABD S h = ΔM BD S . ……………12分即13⨯312⨯13h =⨯⨯154, 解得255h =. ……………13分∴点A 到平面BM D 的距离为255. ……………14分19.(本小题满分14分)(本小题主要考查等差数列、等比数列、数列求和等知识,考查分类与整合、化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识) (1) 解:∵当2n ≥时,1145n n n S S S +-+=,∴()114n n n n S S S S +--=-. ……………1分 ∴14n n a a +=. ……………2分 ∵12a =,28a =,∴214a a =. ……………3分∴数列{}n a 是以12a =为首项,公比为4的等比数列. ∴121242n n n a --=⋅=. ……………4分(2) 解:由(1)得:2122221n n a n log log -==-, ……………5分∴21222n n T a a a log log log =+++ ()1321n =+++- ……………6分()1212n n +-=……………7分2n = . ……………8分(3)解: 23111111n T T T ⎛⎫⎛⎫⎛⎫--⋅⋅- ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ 22211111123n ⎛⎫⎛⎫⎛⎫=--⋅⋅- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ ……………9分 222222222131411234nn----=⋅⋅⋅⋅()()2222132********n n n⋅⋅⋅⋅⋅⋅⋅-+=⋅⋅⋅⋅ ……………10分12n n +=. ……………11分令12n n+10102013>,解得:42877n <. ……………13分故满足条件的最大正整数n 的值为287. ……………14分20.(本小题满分14分) (本小题主要考查椭圆、抛物线、曲线的切线等基础知识,考查数形结合、函数与方程、化归与转化的数学思想方法,以及推理论证能力、运算求解能力、创新意识) (1) 解法1:设椭圆1C 的方程为22221x y ab+=()0a b >>,依题意: 222222231,4.a b a b ⎧+=⎪⎨⎪=+⎩解得: 2216,12.a b ⎧=⎪⎨=⎪⎩ ……………2分∴ 椭圆1C 的方程为2211612xy+=. ……………3分解法2:设椭圆1C 的方程为22221x y ab+=()0a b >>,根据椭圆的定义得1228a AF AF =+=,即4a =, ……………1分∵2c =, ∴22212b a c =-=. (2)分∴ 椭圆1C 的方程为2211612xy+=. ……………3分(2)解法1:设点)41,(211x x B ,)41,(222x x C ,则))(41,(212212x x x x BC --=,)413,2(211x x BA --=,∵C B A ,,三点共线,∴BC BA //. (4)分∴()()()222211211113244x x x xx x ⎛⎫--=-- ⎪⎝⎭,化简得:1212212x x x x ()+-=. ① ……………5分由24x y =,即214y x ,=得y '=12x . (6)分∴抛物线2C 在点B 处的切线1l 的方程为)(2411121x x x x y -=-,即211412x x x y -=. ② (7)分同理,抛物线2C 在点C 处的切线2l 的方程为 222412x x x y -=. ③ (8)分设点),(y x P ,由②③得:=-211412x x x 222412x x x -,而21x x ≠,则 )(2121x x x +=. ……………9分代入②得 2141x x y =, ……………10分则212x x x +=,214x x y =代入 ① 得 1244=-y x ,即点P 的轨迹方程为3-=x y . ……………11分12121……………12分∵直线3-=x y 经过椭圆1C 内一点(3,0),∴直线3-=x y 与椭圆1C 交于两点. ……………13分 ∴满足条件1212PF PF AF AF +=+ 的点P 有两个. ……………14分 解法2:设点),(11y x B ,),(22y x C ,),(00y x P , 由24x y =,即214y x ,=得y '=12x . (4)分∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-,即2111212x y x x y -+=. ……………5分∵21141x y =, ∴112y x x y -=.∵点),(00y x P 在切线1l 上, ∴10102y x x y -=. ① (6)分同理, 20202y x x y -=. ② (7)分综合①、②得,点),(),,(2211y x C y x B 的坐标都满足方程 y x x y -=002. ……8分∵经过),(),,(2211y x C y x B 两点的直线是唯一的, ∴直线L 的方程为y x x y -=002, ……………9分∵点)3,2(A 在直线L 上, ∴300-=x y . ……………10分∴点P 的轨迹方程为3-=x y . ……………11分12121∵直线3-=x y 经过椭圆1C 内一点(3,0),∴直线3-=x y 与椭圆1C 交于两点. ……………13分 ∴满足条件1212PF PF AF AF +=+ 的点P 有两个. ……………14分解法3:显然直线L 的斜率存在,设直线L 的方程为()23y k x =-+,由()2234y k x x y ,,⎧=-+⎪⎨=⎪⎩消去y ,得248120x kx k -+-=. ……………4分设()()1122B x y C x y ,,,,则12124812x x k x x k ,+==-. ……………5分由24x y =,即214y x ,=得y '=12x . (6)分∴抛物线2C 在点B 处的切线1l 的方程为)(2111x x x y y -=-,即2111212x y x x y -+=. (7)分 ∵21141x y =, ∴211124x y x x =-.同理,得抛物线2C 在点C 处的切线2l 的方程为222124x y x x =-. (8)分由211222124124x y x x x y x x ,,⎧=-⎪⎪⎨⎪=-⎪⎩解得121222234x x x k x x y k ,.⎧+==⎪⎪⎨⎪==-⎪⎩∴()223P k k ,-. ……………10分 ∵1212PF PF AF AF +=+,∴点P 在椭圆22111612xyC :+=上. ……………11分∴()()2222311612k k -+=.化简得271230k k --=.(*) ……………12分由()2124732280Δ=-⨯⨯-=>, ……………13分 可得方程(*)有两个不等的实数根. ∴满足条件的点P 有两个. ……………14分21.(本小题满分14分)(本小题主要考查三次函数、一元二次不等式、一元二次方程、函数的零点、数列求和等基础知识,考查数形结合、函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识) (1)解:∵232()1,23xxy f x kx x kx =-=-+-- ……………1分∴221(1)y x x k x x k '=-+--=--++. ……………2分 方程210xx k -++=的判别式()()214134Δk k =--+=--.当34k ≥-时,0Δ≤,2(1)0y x x k '=--++≤,故函数y =2()f x kx -在R 上单调递减; ……………3分当34k <-时,方程210xx k -++=的两个实根为11342k x ---=,21342k x +--=. (4)分则()1x x ,∈-∞时,0y '<;()12xx x ,∈时,0y '>;()2xx,∈+∞时,0y '<;故函数y =2()f x kx -的单调递减区间为()1x ,-∞和()2x ,+∞,单调递增区间为()12x x ,. ……………5分(2)解:存在1t =,对于任意n ∈N *,关于x 的方程()0n f x =在区间1t t ,⎡⎤+⎣⎦上有唯一实数解,理由如下:当1n =时,1()1f x x =-,令1()10f x x =-=,解得1x =,∴关于x 的方程1()0f x =有唯一实数解1x =. ……………6分当2n ≥时,由2321()12321n n xxxf x x n -=-+-+-- ,得22322()1n n n f x x x x x --'=-+-++- . ……………7分 若1x =-,则()(1)(21)0n n f x f n ''=-=--<, 若0x =,则()10n f x '=-<, ……………8分若1x ≠-且0x ≠时,则211()1n n xf x x -+'=-+, ……………9分当1x <-时,2110,10,()0n n x x f x -'+<+<<, 当1x >-时,2110,10,()0n n x x f x -'+>+><,∴()0n f x '<,故()n f x 在(,)-∞+∞上单调递减. ……………10分 ∵111111(1)(11)()()()23452221n f n n =-+-+-++--- 0>, ………11分23452221222222(2)(12)()()()23452221n n n f n n --=-+-+-++---24221212121()2()2()223452221n n n -=-+-+-++---2422132312222345(22)(21)n n n n --=-----⋅⋅-- 0<. …………12分∴方程()0n f x =在[]1,2上有唯一实数解. ……………13分 当()1x ,∈-∞时,()()10n n f x f >>;当()2x ,∈+∞时,()()20n n f x f <<.综上所述,对于任意n ∈N *,关于x 的方程()0n f x =在区间12,⎡⎤⎣⎦上有唯一实数解. ∴1t =. ……………14分2013年广州市一模数学理科试卷本试卷共4页,21小题,满分150分。
2013学年下学期黄埔区初三英语一模试题(答案).doc

2014年黄埔区初中毕业生学业综合测试参考答案及评分标准一、听力(共两节,满分35分)第一节听力理解(共15小题;每小题2分,满分30分)1—5 CBCAB 6—10 BACCB 11—15 BAABC第二节听取信息(共5小题;每小题1分,满分5分)A. RunB. basketballC. TuesdayD. One hour and a half /1.5 hoursE. Sports Center 二.语言知识及运用(共两节,满分20分)第一节单项选择(共10小题;每小题1分,满分10分)16—20 ABDBA 21—25 CDACD第二节语法选择(共10小题;每小题1分,满分10分)26—30 ADABC 31—35 BCDCB三、完形填空(共10小题;每小题1分,满分10分)36—40 CCABD 41—45 BABDC四、阅读理解(共20小题;每小题2分,满分40分)46—50 BCACD 51—55 DCADB56—60 AADBD 61—65 BCBAC五、写作( 共三节,满分30分)第一节单词拼写(共5小题; 每小题1分, 满分5分)66. angry 67. joke 68. make 69. easy 70. plan / prefer第二节完成句子(共5小题; 每小题2分, 满分10分)71. enjoyed ourselves 72. as soon as; finish 73.What useful / helpful74. are; used (写对are popular给1.5分) 75.where I can buy第三节书面表达( 共l小题,满分15分) Possible versionRecently we made a survey on “how middle school students in China and America spend their weekends”. We found that there were great differences between them. Here comes the result.In China, 80% students spend their weekend doing their homework or attending different kinds of extra classes in the tutorial centers. And 20% students are likely to stay at home, watching TV or playing computer games.However, in America, 25% students would like to do part-time jobs to earn pocket money by delivering newspapers or milk. And 27% students would like to take part in the community events to do some voluntary work, like picking up rubbish, looking after the elder people or the sick. In fact, 48% of them prefer doing outdoor activities during weekends, such as cycling, seeing films and so on.As for me, I hope I would have a little homework to do at weekend so that I could have more free time to do things as I like, such as reading books, listening to music or doing some sports.2014年黄埔区初中毕业班综合测试英语评卷标准与细则非选择题评分标准本部分满分35分第二节听取信息(满分为5分,每小题1分,按1分、0.5分、0分,共3个档次给分)。
2013广州中考数学黄埔一模及答案

2013年黄埔区初中毕业生综合测试--黄立宗已排版数 学本试卷分选择题和非选择题两部分,共三大题25小题,共4页,满分150分.考试时间120分钟. 注意事项:1.答卷前,考生务必在答题卡第1面.第3面上用黑色字迹的钢笔或签字笔填写自己的考生号.姓名;填写座位号,再用2B 铅笔把对应号码的标号涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B 铅笔画图.答案必须写在答题卡各题指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔.圆珠笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将答题卡上交,本试卷自留.第一部分 选择题(共30分)一.选择题(每小题3分,共30分)1.实数-1,-3,0,2四个数中,最小的是( * ). (A )0 (B )-1 (C )2 (D )-3 2.如下左几何体的主视图是( * ).3.下列计算正确的是( * ).(A )ab b a 22=+ (B )1)-1--=a a ((C )523a a a =⋅ (D )326a a a =÷ 4.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( * ).(A)l ,2,3 (B)2,4,8 (C)3,7,9 (D)4,4,95.已知点A (-1,0)和点B (1,2),将线段AB 平移至A ’B ’,点A ’与点A 对应.若点A ’的坐标 为(1,-3),则点B ’的坐标为( * ).(A )(3,0) (B )(3,-1) (C )(3,0) (D )(-1,3)6.今年我国发现的首例H7N9禽流感确诊病例在上海某医院隔离观察,要掌握他在一周内的体温是否稳定, 则医生需了解这位病人7天体温的( * ).(A )众数 (B )方差 (C )平均数 (D )频数 7.某校为了了解九年级学生体育测试成绩情况, 以九年(1)班学生的体育测试成绩为样本,按 A B C D ,,,四个等级进行统计,并将统计结 果绘制如右两幅统计图,由图中所给信息知,扇形统计图中C 等级所在的扇形圆心角的度数为( * ). (A)72° (B )68° (C) 64° (D )60°第7题第2题8. 平面内,下列命题为真命题是( * ).A.经过半径外端点的直线是圆的切线B.经过半径的直线是圆的切线C.垂直于半径的直线是圆的切线D.经过半径的外端并且垂直于这条半径的直线是圆的切线 9.点M 、点N 均在双曲线xky =(k 为常数)上,点M 坐标为(2,3),点N 的坐标为(-6,m )则m =( * ). (A )-1 (B )-2 (C )3 (D )1 10.若实数a 、b 在数轴上的位置如图所示,A (1,1y )、B (2,2y )是函数b ax y +=图象上的两点,则( * ).(A )112<<y y (B )121y y << (C )121<<y y (D )21y 1<<y第二部分 非选择题(共120分)二.填空题(本大题共6题,每小题3分,满分18分) 11.化简3-= * .12有意义,则实数x 的取值范围是 * . 13.若0122=+-a a ,则3422+-a a = * .14.如图,在平行四边形ABCD 中,CE AB ⊥,E 为垂足.如果125A =∠,则BCE =∠ * °. 15. 如图,已知等边三角形ABC 的边长为1,按图中所示的规律,用5个这样的三角形镶嵌而成的四边形的周长是 * ,用n 个这样的三角形镶嵌而成的四边形的周长为 * .16. 已知点A 、B 、C 的坐标分别为(2,0)、(0,0)、(-1,3),则sin ∠ACB = * .三.解答题17.(本小题满分9分) 解不等式组:⎩⎨⎧-<-<-12532x x第10题CAB第15题┅┅A E BCD第14题18.(本小题满分9分)如图,在□ABCD 中, AE =CF .证明:BE =DF19.(本小题满分10分)已知a 、b 分别是方程0432=--x x 的两个实数根,求221()a ba b a b b a-÷-+-的值.20.(本小题满分10分)某班从2名男生、3名女生中随机抽取五月校园志愿者.求下列事件的概率: (1)抽取1名学生,恰好是女生; (2)抽取2名学生,恰好一男一女.第18题21.(本小题满分12分)已知抛物线)6(2)42+-++=m x m x y ((m 为常数,)8-≠m )与x 轴有两个不同的交点A 、B ,点A 、点B 关于直线1=x 对称,抛物线的顶点为C .(1)并此抛物线的解析式;(2)求点A 、B 、C 的坐标.22.(本小题满分12分)为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB =45°.(1)若新坡面倾斜角∠CDB =28°,则新坡面的长CD 长是多少?(精确到0.1米)(2)若新坡角顶点D 前留3米的人行道,要使离原坡角顶点A 处10米的建筑物不拆除,新坡面的倾斜角∠CDB 度数的最小值是多少 ?(精确到1°)23.(本小题满分12分)某市大力建设廉租房,2010年投资了24.5亿元人民币建了廉租房124万平方米.之后廉租房的总面积每年递增,且增长率相等,三年共建廉租房220万平方米. (1)用科学记数法表示:24.5亿= 万; (2)求廉租房建筑面积的年增长率;(3)若其中后两年的建房成本按每年10.7%的增长率上涨,该市后两年建廉租房共需投入约多少亿元人民币?(精确到0.1亿元)第22题 建筑物24.(本小题满分14分)如图(1),△ADE 可由△CAB 旋转而成,点B 的对应点 是E ,点 A 的对应点是D ,点B 、C 的坐标分别为(3,0),(1,4).(1)写出点E 的坐标,并利用尺规作图直接在图(1)中作出旋转中心Q (保留作图痕迹,不写作法); (2)求直线AE 对应的函数关系式;(3)将△ADE 沿垂直于x 轴的线段PT 折叠,(点T 在x 轴上,点P 在AE 上,P 与A 、E 不重合)如图(2),使点A 落在x 轴上,点A 的对应点为点F .设点T 的坐标为(x ,0),△PTF 与△ADE 重叠部分的面积为S .① 试求出S 与x 之间的函数关系式(包括自变量x 的取值范围); ② 当x 为何值时,S 的面积最大?最大值是多少?③ 是否存在这样的点T ,使得△PEF 为直角三角形?若存在,直接写出点T 的坐标;若不存在,请说有理由.y xEDCB A O第24题(1)25.(本小题满分14分)如图,AB 为⊙O 的直径,AB =4,P 为AB 上一点,过点P 作⊙O 的弦CD ,设∠BCD=m ∠ACD .(1) 已知221+=m m ,求m 的值,及∠BCD 、∠ACD 的度数各是多少? (2) 在(1)的条件下,且21=PB AP ,求弦CD 的长; (3) 当323-2+=PB AP 时,是否存在正实数m , 使弦CD 最短?如果存在,求出m 的值,如果不存在,说明理由.第25题2013年黄埔区初中毕业生综合测试数学参考答案及评分标准一.选择题(每小题3分,共30分) 1--10 DCCCBBADA二.填空题(本大题共6题,每小题3分,满分18分)11. 3;12. 3≥x ;13. 1;14. 26;15. 7,)1(3-+n ;16. 55 说明:第15题第1空1分,第1空2分 三.解答题 17.⎩⎨⎧-<-<-)()(2121532x x由(1)得4<x ……3分 由(2)得3>x ……6分 所以这个不等式组的解为43<<x ……9分 18.方法一:∵四边形ABCD 是平行四边形,∴ AD=BC ,且AD ∥BC .(平行四边形对边平行且相等) ……2分 又∵AE =CF ,(已知)∴ED=BF ,且ED ∥BF . ……4分 ∴四边形EDFB 是平行四边形(对边平行且相等的四边形是平行四边形) ……6分 ∴EB =DF (平行四边形对边相等) ……9分方法二:∵四边形ABCD 是平行四边形,∴ AB =CD ,∠A =∠C .(平行四边形对边相等,对角相等) ……2分 在△AEB 和△CFD 中, ∵AE =CF ,(已知) AB =CD ,∠A =∠C∴△AEB ≌△CFD (SAS ) ……6分 ∴EB =DF (全等三角形对应边相等) ……9分 19. 化简:221()a b a b a b b a -÷-+-=bab b a b a b a a -⨯+--+]1))(([ ……3分=ba b b a a b b b a a +-=+--+1)()(- ……7分∵a 、b 分别是方程0432=--x x 的两个实数根, ∴a +b =3 ……9分 ∴221()a b a b a b b a -÷-+-=31- ……10分第18题20.(1)抽取1名学生,恰好是女生的概率是52……2分 (2)分别用男1、男2、女1、女2、女3表示这五位同学,从中任意抽取2名,所有可能出现的结果有:(男1、男2),(男1、女1),(男1、女2),(男1、女3),(男2、女1),(男2、女2),(男2、女3),(女1、女2),(女1、女3),(女2、女3),共10种,它们出现的可能性相同, ……7分所有结果中,满足抽取2名学生,恰好一男一女(记为事件A )的结果共有6种, 所以P (A )=53106=. ……10分21.(1)∵抛物线)6(2)42+-++=m x m x y ((m 为常数,)8-≠m )的对称轴为24+=m x -……2分 而抛物线与x 轴有两个不同的交点A 、B ,点A 、点B 关于直线1=x 对称, ∴124=+m -,6-=m ∴所求抛物经的解析式为x x y 2-2= ……6分 (2)当0=y 时,02-2=x x ,解得01=x ,22=x当0=x 时,1)1(2-22--==x x x y ,解得01=x ,22=x∴点A 、B 、C 的坐标.分别为(0,0),(2,0),(1,-1) ……12分22.(1)∵CDCBCDB =∠sin ∴3.21sin2810sin ≈︒=∠=CDB CB CD ……5分答:新坡面的长为21.3米(2)∵∠CAB =45°,∴AB =CB =10, ……6分又建筑物离原坡角顶点A 处10米,即建筑物离天桥底点B 的距离为20米,……7分 当DB 取最大值时,CDB ∠达最小值,要使建筑物不被拆掉DB 的最大值为20-3=17 ……8分 又1710tan ==∠DB CB CDB ,︒≈∠31CDB ……12分 答,若新坡角顶点D 前留3米的人行道,要使离原坡角顶点A 处10米的建筑物不拆除,新坡面的倾斜角的最小值是31°第22题23. (1)用科学记数法表示:24.5亿= 5102.45⨯ 万; ……2分 (2)设该市后两年廉租房建筑面积的年增长率为x ,根据题意,得:220)1(1242=+x ……5分整理,得:024-62312=+x x , 解之,得:2122431431312⨯⨯⨯+±-=x ,∴0.331=x ,-2.332=x (舍去), ……7分答:该市后两年廉租房建筑面积的年增长率为33%.(3)2010年的建房成本为每平方米≈⨯1241000024.51976(元)2011年的建房成本为每平方米≈+)(10.7%119762187(元) 2012年的建房成本为每平方米≈+)(10.7%121872421(元) 2011年建房410.33124124124)1124≈⨯==-+x x ((万平方米) 2012年建房5541-124-220=(万平方米)后两年共投资22282213315589667552421412187=+=⨯+⨯(万元),即约22.3亿元……12分 答:后两年共需约投入22.3亿元人民币建廉租房..24.(1)E (5,2), ……1分图略,Q ……3分(2)设直线AE 对应的函数关系式为b kx y +=∵A (1,0)、E (5,2)∴⎩⎨⎧=+=+250b k b k ,解得⎪⎪⎩⎪⎪⎨⎧==21-21b k ∴直线AE 对应的函数关系式为21-21x y =……5分 (3)①当点F 在AD 之间时,重叠部分是△PTF .则2)1(41)2121)(1(212121S -=--=⋅=⋅=∆x x x PT AT PT TF PEF 当F 与D 重合时,AT =21AD=2,∴31≤<x .当点F 在点D 的右边时,重叠部分是梯形PTDH . ∵△FDH ∽△ADEyxEDCB A O第24题(1)∴21==AD ED DF HD ,HD =21DF =3]5)12[21-=--x x (则TD HD PT PTDH ⋅+=)(21S 梯形=)5()32121(21x x x -⋅-+-=43521143-2-+x x 当T 与D 重合时,点F 的坐标是(9,0),∴53≤<x . 综上,得⎪⎪⎩⎪⎪⎨⎧≤<-+≤<+-=5343521143-31412141S 22x x x x x x ……9分说明:分段函数对一段2分,没化简不扣分②⎪⎪⎩⎪⎪⎨⎧≤<+≤<=5334311-43-311-41S 22x x x x )()(i)由当31≤<x 时,S 随x 的增大而增大,得3=x 时,S 有取大值,且最大值是1;ii)当53≤<x 时,311=x ,S 有取大值,且最大值是34S =; 综上i)、ii)所求为当311=x ,S 有取大值,且最大值是34S = ……11分③存在,T 的坐标为(27,0)和(25,0) ……14分。
广东省广州市黄埔区2013年中考一模物理试题(word版有答案)

2013年黄埔区初三毕业班综合测试物理试题本试卷分第一部分(选择题)和第二部分(非选择题).第一部分1至3页,第二部分4至8页,共8页。
总分100分。
考试时间80分钟。
第一部分(选择题共36分)一.选择题(每小题3分,共36分。
每小题给出的四个选项中,只有一项符合题意。
)1.关于物质的组成,下列说法中错误的是A.物质是由分子组成的B.原子由原子核和中子组成C.原子核由质子和中子组成D.质子和中子还有更小的精细结构2.下列关于声音的说法中正确的是A.物体只要在振动,人们就能听到声音B.人们能直接听见超声波C.声音在一切介质中的传播速度都是相同的D.声音通过介质传播3. 一些严重缺水的地区,通过收集露水来获得水资源。
露水的形成属于物态变化中的A.液化B.汽化C.熔化D.升华4.下列说法中错误的是A.用久了的电灯丝变细是由于升华造成的B.秋天的早晨,大雾随着太阳的出现逐渐散去是液化现象C.气温低于水银凝固点的地方不能使用水银温度计D.夏天游泳后,刚从水中上岸的人会感到冷是由于身上的水蒸发吸热的缘故5. 下列有关受力的说法中,正确的是A. 船从河里开到海里,船的浮力变大了B. 匀速上升的气球不受重力的作用C. 沿水平方向推在水平地面上的课桌,却没有推动,则推力与摩擦力大小相等D. 挂在天花板上的电灯处于静止状态,电灯没有受到力的作用6.一辆汽车在平直的公路上匀速行驶,下列说法中正确的是A.汽车只受到重力作用B. 汽车经过路旁有落叶的路面时,车旁地面上的落叶将会从路旁吸向汽车C.汽车受到的重力与地面受到的压力是一对平衡力D. 汽车能够向前匀速运动,是因为牵引力大于阻力7.在如图1所示的水泥路面上,人们做出了一道道浅凹痕,它可以A.增大地面对汽车的支持力B.减小地面对汽车的支持力C.增大地面对汽车轮的摩擦力D.减小地面对汽车轮的摩擦力8.关于电磁波和现代通信,下列说法中正确的是A.移动电话靠电磁波传递信息图1B.光纤通信传输的信息量很大,主要用于无线电广播图8 9 6 6 1 2 1C .电磁波的波长越大,频率越高D .电磁波的应用对人类有利无害9.下列现象中,属于光的折射现象的是A .人站在湖边看到湖水中的鱼B .我们能从不同方向看见本身不发光的物体C .黑板某部分“反光”,看不清上面的字D .夜晚,在路灯下出现人的影子10.如图2所示,将长方体木块从甲图那样直立浮在水面上变为如图乙那样横浮在水面上后,木块受到的浮力和木块底面受到水的压强的变化分别是A .变大,变大B .变小,变小C .不变,不变D .不变,变小图 211.下列电路图中,开关S 2闭合后会造成电源短路的电路图是12.如图4甲所示电路,闭合开关S 后,两相同电压表的指针偏转都如图乙所示,A .电压表V 1的读数为B. 电压表V 2C .L 1和L 2两灯的电阻之比为1︰5D .L 1和L 2两灯的电压之比为1︰4图 4第二部分(非选择题共64分)二.填空 作图题(共25分)13.(4分)小黄同学用一根细线拴一块橡皮甩起来,使橡皮绕手做圆周运动,如图5所示。
2013黄浦区中考数学一模试卷及答案

A B C D B CA 黄浦区2012学年度第一学期九年级期终考试数 学 试 卷 2013年1月17日(满分150分,考试时间100分钟)考生注意:1. 本试卷含三个大题,共25题;2. 答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3. 除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】 1. 如果△ABC ∽△DEF (其中顶点A 、B 、C 依次与顶点D 、E 、F 对应),那么下列等式中不一定成立的是(A )A D ∠=∠(B )A DB E ∠∠=∠∠ (C )AB =DE (D )AB DEAC DF=2. 如图,地图上A 地位于B 地的正北方,C 地位于B 地的北偏东︒50方向,且C 地到A 地、B 地的距离相等,那么C 地位于A 地的(A )南偏东︒50方向 (B )北偏西︒50方向(C )南偏东︒40方向(D )北偏西︒40方向3. 将抛物线2y x =向左平移2个单位,则所得抛物线的表达式是(A )()22+=x y (B )()22-=x y (C )22+=x y (D )22-=x y4. 如图,△PQR 在边长为1个单位的方格纸中,它的顶点在小正方形顶点位置,其中点A 、B 、C 、D 也是小正方形的顶点,那么与△PQR 相似的是(A )以点P 、Q 、A 为顶点的三角形 (B )以点P 、Q 、B 为顶点的三角形 (C )以点P 、Q 、C 为顶点的三角形 (D )以点P 、Q 、D 为顶点的三角形(第2题) (第4题) (第6题) 5. 抛物线232y x x =+-与坐标轴(含x 轴、y 轴)的公共点的个数是(A )0 (B )1 (C )2 (D )36. 如图,在△ABC 中,∠ACB =90︒,CD 为边AB 上的高,已知BD =1,则线段AD 的长是 (A )sin 2A (B )cos 2A (C )tan 2A (D )cot 2A 二、填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】B C P D A · R Q · · ·D EO B A 7. 已知74x y =,则x y x y +-的值为 ▲ .8. 计算:()()23a b a b -++= ▲ .9. 已知两个相似三角形的周长比为2∶3,且其中较大三角形的面积是36,那么其中较小三角形的面积是▲ .(第10题) (第11题) (第17题)10. 如图,第一象限内一点A ,已知OA =5,OA 与x 轴正半轴所成的夹角为α,且2tan =α,那么点A 的坐标是 ▲ . 11. 如图,某人沿一个坡比为1∶3的斜坡(AB )向前行走了10米,那么他实际上升的垂直高度是 ▲ 米. 12. 抛物线322++=x x y 的顶点坐标是 ▲ .13. 如果抛物线()a x x a y ++-=322的开口向下,那么a 的取值范围是 ▲ .14. 若1x 、2x 是方程04322=--x x 的两个根,则2121x x x x ++⋅的值为 ▲ . 15. 已知二次函数()y f x =图像的对称轴是直线2x =,如果()()34f f >,那么 ()3f - ▲ ()4f -. (填“>”或“<”) 16. 已知点P 是二次函数224y x x =-+图像上的点,且它到y 轴的距离为2,则点P 的坐标是 ▲ .17. 如图,E 是正方形ABCD 边CD 的中点,AE 与BD 交于点O ,则tan AOB ∠= ▲ .18. 在Word 的绘图中,可以对画布中的图形作缩放,如下图1中正方形ABCD (边AB 水平放置)的边长为3,将它在“设置绘图画布格式→大小→缩放”中,高度设定为75%,宽度设定为50%,就可以得到下图2中的矩形1111A B C D ,其中11350% 1.5A B =⨯=,11375% 2.25A D =⨯=.实际上Word 的内部是在画布上建立了一个以水平线与竖直线为坐标轴的平面直角坐标系,然后赋予图形的每个点一个坐标(),x y ,在执行缩放时,是将每个点的坐标作变化处理,即由(),x y 变为()%,%x n y m ⨯⨯,其中%n 与%m 即为设定宽度与高度的百分比,最后再由所得点的新坐标生成新图形. O x yA αA 1 D C 1AD⇒ MON ⇒A BC D现在画布上有一个△OMN ,其中90O ∠=︒,MO NO =,且斜边MN 水平放置(如图3),对它进行缩放,设置高度为150%,宽度为75%,得到新图形为△O 1M 1N 1(如图4),那么111cos O M N ∠的值为 ▲ .(图1) (图2) (图3) (图4)三、解答题:(本大题共7题,满分78分) 19. (本题满分10分)计算:222sin 60cos 60cot 304cos 45︒-︒︒-︒.20. (本题满分10分,第(1)、(2)小题满分各5分)如图,点E 是平行四边形ABCD 边BC 上一点,且BE ∶EC =2∶1,点F 是边CD 的中点,AE 与BF交于点O .(1)设a AB =,b AD =,试用a 、b 表示AE ; (2)求BO ∶OF 的值.21. (本题满分10分)已知二次函数的图像经过点()8,0-与()5,3-,且其对称轴是直线1x =.求此二次函数的解析式,并求出此二次函数图像与x 轴公共点的坐标.22. (本题满分10分,第(1)、(2)小题满分各5分)如图,在△ABC 中,90C ∠=︒,4AC =,6BC =,点D 是边BC 上一点, 且CAD B ∠=∠.(1)求线段CD 的长;(2)求sin BAD ∠的值. M 1O 1N 1 B OE DFA23. (本题满分12分,第(1)、(2)小题满分各6分)如图,点D 是Rt △ABC 斜边AB 上一点,点E 是直线AC 左侧一点,且EC ⊥CD , ∠EAC =∠B .(1)求证:△CDE ∽△CBA ;(2)如果点D 是斜边AB 的中点,且23tan =∠BAC ,试求CBA CDE S S ∆∆的值.(CDE S ∆表示△CDE 的面积, CBA S ∆表示△CBA 的面积)24. (本题满分12分,第(1)、(2)、(3)小题满分各4分)已知二次函数32++=bx ax y 的图像与x 轴交于点A ()0,1与B ()0,3,交y 轴于点C ,其图像顶点为D .(1)求此二次函数的解析式;(2)试问△ABD 与△BCO 是否相似?并证明你的结论;(3)若点P 是此二次函数图像上的点,且PAB ACB ∠=∠, 试求点P 的坐标.25. (本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分) 如图,在等腰梯形ABCD 中,AD ‖BC ,AD =2,AB =5,53sin =∠B ,点E 是边BC 上的一个动点(不与点B 、C 重合),作∠AEF =∠AEB ,使边EF 交边CD 于点F (不与点C 、D 重合),设BE=x ,CF=y .(1)求边BC 的长;(2)当△ABE 与△CEF 相似时,求BE 的长; E D C A O xy(3)求y 关于x 的函数关系式,并写出定义域.(备用图)黄浦区2012学年度第一学期九年级期终考试数学参考答案与评分标准一、选择题1.C 2.A 3.A 4.B 5.D 6.D 二、填空题 7.1138.5a b + 9.16 10.5,251110 12.()1,2- 13.2a < 14.12- 15.> 16.()()2,4,2,12- 17.3 185三、解答题19.解:原式()2231222342⨯-⎝⎭-⨯(4分)31242322⨯--(3分) D B CA DB CA FE322-(1分)=322+--------------------------------------------------------------------------(2分) 20.解:(1)∵BE ∶EC =2∶1,∴2233BE BC b ==,-----------------------------------------------------------(2分) ∴AE AB BE =+=23a b +.--------------------------------------------------(3分)(2)作FG ‖BC 交AE 于点G ,------------------------------------------------------(1分)∵点F 是边CD 的中点,∴FG 是梯形ECDA 的中位线,设EC =k ,BE =2 k ,则AD =3 k ,∴FG =2 k ,--------------------------------------------------------------------------(2分)∴BO ∶OF = BE ∶FG =1∶1, --------------------------------------------------(1分) ∴BO ∶OF 的值为1. -------------------------------------------------------------(1分) 21.解:设二次函数解析式为2y ax bx c =++,----------------------------------------------(1分)则859312c a b c b a ⎧⎪-=⎪-=++⎨⎪⎪-=⎩,------------------------------------------------------------------(3分) 解得128a b c =⎧⎪=-⎨⎪=-⎩,----------------------------------------------------------------------------(3分)∴二次函数解析式为228y x x =--.-------------------------------------------------(1分) 令2280x x --=,------------------------------------------------------------------------(1分) 解得122,4x x =-=,∴图像与x 轴公共点为()2,0-与()4,0.----------------------------------------------(1分)22.解:(1)∵,C C CAD B ∠=∠∠=∠,∴△CDA ∽△CAB ,----------------------------------------------------------------(2分) ∴CD CACA CB=,----------------------------------------------------------------------(1分)∴2246CA CD CB ===83.----------------------------------------------------------(2分) (2)作BH ⊥AD ,垂足为H ,-------------------------------------------------------------(1分) 在Rt △ACD 中,22413AD AC CD =+=-------------------------------(1分) 在Rt △ABC 中,22213AB AC BC =+=--------------------------------(1分)∵∠H =∠C ,∠ADC =∠BDH , ∴△ADC ∽△BDH , ∵BH AC BD AD =,即1010133134133BH ==---------------------------(1分) ∴在Rt △ABH 中,5sin 13BH BAH AB ∠==.----------------------------------(1分) 23.解:(1)∵EC ⊥CD ,ACB ∠为直角,∴ACE BCD ∠=∠,又∠EAC =∠B ,∴△CAE ∽△CBD ,-----------------------------------------------------------------(2分)∴CA CBCE CD=,又∠ACB =∠ECD ,----------------------------------------------(2分) ∴△CDE ∽△CBA . ------------------------------------------------------------------(2分) (2)∵23tan =∠BAC , ∴32CB CA =,----------------------------------------------------------------------------(2分) 令CB =3k ,CA =2k , 则2213AB AC BC k =+=.--------------------------------------------------(1分)又点D 是斜边AB 的中点, ∴1132CD AB ==.------------------------------------------------------------(1分) ∵△CDE ∽△CBA ,∴21336CDE CBA S CD S CB ∆∆⎛⎫== ⎪⎝⎭.----------------------------------------------------------(2分) 24.解:(1)由题意知309330a b a b ++=⎧⎨++=⎩,-------------------------------------------------------(2分)解得14a b =⎧⎨=-⎩,------------------------------------------------------------------------(1分)所以二次函数解析式是243y x x =-+.----------------------------------------(1分)(2)△ABD 与△BCO 相似.由(1)知:()0,3C ,()2,1D -.-----------------------------------------------(1分) 于是2,2AB AD BD ===32,3BC OB OC ===,即DA DB ABOB OC BC==,--------------------------------------------------------------(2分) 所以△ABD 与△BCO 相似. -------------------------------------------------------(1分)(3)设()2,43P x x x -+,作PQ ⊥x 轴,垂足为Q ,作AH ⊥BC ,垂足为H . 易知△ABH 为等腰直角三角形,则2AH BH ==由PAB ACB ∠=∠,90AQP CHA ∠=∠=︒,所以△APQ 与△CAH 相似,-------------------------------------------------------(2分) 于是PQ AHAQ CH=, 即243112x x x -+=-, 解得1257,22x x ==, 所以点P 的坐标为53,24⎛⎫-⎪⎝⎭或75,24⎛⎫⎪⎝⎭.-----------------------------------------(2分) 25.解:(1)作AH ⊥BC ,垂足为H ,------------------------------------------------------------(1分)在Rt △ABH 中,AB =5,53sin =∠B , 则sin 3AH AB B =⋅∠=,224BH AB AH =-=,--------------------(2分)由等腰梯形ABCD 知,BC=AD +2BH=10. --------------------------------------(1分) (2)由题意知,∠B=∠C ,当△ABE 与△CEF 相似时,∠BEA=∠CEF 或∠BEA=∠CFE ,----------(1分) ①当∠BEA=∠CEF 时,又∠BEA=∠AEF ,∠BEA +∠AEF +∠CEF =180︒, 即∠BEA=60︒.于是在Rt △AEH 中,cot 3cot 603EH AH AEH =⋅∠=︒=,所以BE=BH +HE =43+--------------------------------------------------------(2分) ②当∠BEA=∠CFE 时,又∠BEA=∠AEF , 即∠CFE=∠AEF ,则AE ‖DC ,又AD ‖BC , 所以四边形ADCE 为平行四边形,则CE=AD=2,于是BE=BC -CE =8. ---------------------------------------------------------------(2分) (3)延长EF 交AD 的延长线于点P ,作PQ ⊥AE ,垂足为Q , ∵AD ‖BC ,∴∠BEA=∠EAP ,又 ∠BEA=∠AEF ,∴∠EAP=∠AEP ,∴12AQ AE =. 又∵∠EHA=∠AQP =90︒, ∴△AHE ∽△PQA ,∴AP EA AQ EH =,即()282524AQ EA x x AP EH x ⋅-+==-.-------------------------(2分) 又∵AD ‖BC ,∴CF CEDF PD=, 即()2108255224y xx x y x -=-+---, 解得22101404001639x x y x x -+=-+,定义域为410x <<.-----------------------(3分)。
2013年广州市一模理科综合试题yu答案

试卷类型:A 2013年广州市普通高中毕业班综合测试(一)理科综合2013. 3 本试卷共12页,36小题,满分300分。
考试用时150分钟。
注意事项:1. 答卷前,考生务必用2B铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签.字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
5. 本卷所用相对原子质量:H-1、C-12、0-16、S-32、Cu-64一、单项选择题:本题包括16小题,每小题4分,共64分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
1.下列关于生物膜系统的叙述,正确的是A. 原核细胞无核膜及细胞器膜因而不具生物膜B. 细胞膜功能的复杂程度取决于憐脂的种类和数量C. 内质网膜为多种酶提供了大量的附着位点D. 有丝分裂过程中核膜随着丝点的分裂而消失2-眼虫属于原生动物(其眼点能感光),如右图所示。
对其分析恰当的是A. 眼虫的细胞质中不含RNAB. 眼虫具有趋光性,因其眼点能感受化学信息C. 眼虫鞭毛摆动所需的ATP来自叶绿体D. 眼虫的伸缩泡有助于提高物质运输的效率3.人食用被诺如病毒(NV)污染的食物会导致呕吐与腹泻,而NV极易变异,下列推断不合理的是A. 酸能杀死部分NV属于特异性免疫B. NV极易变异,人类很难研究相应的疫苗C. 人体有多种抗NV的抗体,可能是因为NV表面存在多种抗原蛋白D. 特异性的效应T细胞能促使被NV入侵的靶细胞裂解4. 有关育种的说法,正确的是A. 多倍体育种过程都要使用秋水仙素B. 利用基因工程技术可定向培育优良品种C. 用于大田生产的优良品种都是纯合子D 杂交育种与单倍体育种的原理都是基因重组5 下列对实验的分析,正确的是A-用洋葱鳞片叶内表皮细胞能观察到质壁分离现象B. 斐林试剂能与蔗糖反应产生砖红色沉淀C. 加人无水乙醇越多,叶绿体色素提取液的绿色越深D. 观察洋葱根尖分生区细胞有丝分裂可用健那绿染色6. 下列关于“转化”的说法不正确的是A. ATP水解释放的能量可转化成光能、电能等B. 细胞内多个基因发生突变,细胞就转化成癌细胞C. 在含适量DNA酶和S型菌DNA的培养基中,R型菌不能转化为S型菌D. 目的基因导入受体细胞,并在细胞内维持稳定和表达的过程称为转化7. 在水溶液中能大量共存的一组离子是A. Al3+、Na+、HCO3-、SO42-B. H+、Fe2+、ClO-、Cl-C. Mg2+、K+、SO42-、NO3-D. NH4+ Ag+、OH-、Br-8. 下列说法正确的是A. 食盐、醋酸和蔗糖都是电解质B. 纤维素、淀粉和蛋白质都是高分子化合物C. 甲烷和乙烯均可使酸性KMnO4溶液褪色D. 乙酸乙酯和植物油均可水解生成乙醇9. 下列实验不能达到目的的是A. 用AlCl3溶液和过量氨水制备Al(OH)3B. 用NH4Cl和Ca( 0H) 2固体混合加热制备NH3C. 用NaOH溶液除去苯中的溴D. 用足量铜粉除去FeCl2溶液中的FeCl3杂质10. 设n A为阿伏加德罗常数的数值,下列说法正确的是A. 16g CH4含有10n A个电子B. 常温常压下,22. 4L Cl2含有2n A个Cl原子C. 1 mol Cu与足量稀HNO3反应,转移3n A个电子D. 1L O.1 mol.L-1 Na2SO3溶液中含有 O. 1n A个S032_11. 下列陈述I、II正确并且有因果关系的是选陈述I陈述IIA浓H2SO4有吸水性浓H2SO4可用于干燥氨气B SO2有氧化性SO2尾气可用NaOH溶液吸收C Mg有还原性电解MgCl2饱和溶液可制备Mg D锌金属活动性比铁强海轮外壳上装锌块可减缓腐蚀12. 对于常温下pH= 3的乙酸溶液,下列说法正确的是A. C(H+)= c(CH3COO-) + c(OH-)B.加水稀释到原体积的10倍后溶液pH变为4C. 加入少量乙酸钠固体,溶液pH降低D. 与等体积pH= 11的NaOH溶液混合后所得溶液中:c(Na+) =c(CH3COO- )13. 水压机是利用液体来传递压强的。
2013年广州市一模文科综合试题及答案

2013年广州市普通高中毕业班综合测试(一)文科综合 2013.3本试卷共11页,41小题,满分300分。
考试用时150分钟。
注意事项:1.答卷前,考生务必用2B铅笔在“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校,以及自己的姓名和考生号、试室号、座位号填写在答题忙上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共35小题,每小题4分,共140分。
每小题给出的四个选项中,只有一个选项符合题目要求。
南极磁点大约位于139°24′E、65°36′S,完成1~2题。
1.南极点与南极磁点相距约A.0千米 B.2800千米 C.3500千米 D.4500千米2.在南极地区,判断地理方位最好利用A.指南针 B.北极星 C.太阳 D.GPS读“2000~2007年开都河径流变化图”,完成3~5题。
2000~2007年开都河径流变化图3.开都河最主要的补给类型是A.冰川 B.雨水 C.地下水 D.湖泊水4.开都河下游地区自然带最可能是A.温带森林带 B.温带森林、草原带C.高山草甸带 D.温带荒漠带5.开都河下游地区的外力作用最主要是A.流水作用 B.冰川作用 C.风力作用 D.波浪作用读“北京市人口密度和就业密度变化图”,完成6~7题。
北京市人口密度和就业密度变化图6.近20年北京市人口迁移的特点是A.从远郊、近郊向城市中心迁移 B.从城市中心向近郊、远郊迁移C.从城市中心、远郊向近郊迁移 D.从远郊向近郊、城市中心迁移7.从北京市人口密度和就业密度变化状况来看,其城市化存在A.城市经济发展缓慢,就业压力大B.城市规模不断扩大,大量企业迁往远郊,造成上下班交通堵塞C.传统工业发展迅猛,人均绿地面积不断减少D.人口密度与就业密度的变化不一致,造成上下班交通严重拥挤2008年我国太阳能电池生产量,占全球总量的26%,成为继日本和欧盟之后的第三大生产国。
2013广州一模试题以及答案、细则

广州市2013届普通高中毕业班综合测试(一)语文一、本大题4小题。
每小题3分,共12分。
1.下列词语中加点的字,每对读音都不相同的一组是A.虔诚/乾坤贬谪/嫡系攒钱/人头攒动B.储存/贮藏饯别/栈道勾当/勾心斗角C.证券/眷恋馈赠/匮乏划算/整齐划一D.悭吝/信笺鞭笞/怠惰着实/着手成春2.下面语段中画线的词语,使用不恰当的一项是一个年财政收入不足3亿元的贫困县,偏要打肿脸充胖子,筹措亿元巨资建造一个超级豪华的文化宫。
尽管公众议论纷纷,不赞一词,但当地的某些官员却不以为意,依然我行我素,仅以‚有问题上级会查‛来回应,这是对公众监督权的极大轻视。
A.打肿脸充胖子 B.筹措 C.不赞一词 D.不以为意3.下列句子中,没有语病的一项是A.中央电视台2013年春晚导演组,把多家地方电视台选送的歌手和节目加以重新组合润色,再进行选拔,这是开门办春晚的又一次创新。
B.受国际金融危机后遗症的影响,2012年发达国家与新兴市场国家经济增长率均呈下滑态势,降到了自2010年经济复苏以来的最低点。
C.在一些市场垄断的领域里,消费者强弱不一的维权意识,将会使他们应有的选择权和公平交易权受到严重限制,甚至于完全不能享受。
D.新修订的《机动车驾驶证申领和使用规定》突出规范驾驶行为、增强安全意识为原则,对闯黄灯、故意遮挡号牌等行为加大了处罚力度。
4.把下列句子组成语意连贯的语段,排序最恰当的一项是①屋后的山在冬天可以阻挡呼啸而来的北风,起到防寒的作用。
②池塘既可供农田灌溉、村落消防,又能调节气候,给村庄带来勃勃生机。
③岭南地区的村落,家家户户周围都有山丘、池塘、河流、田野等形成的生态景观。
④许多人认为,好的住宅就应该背山面水,坐北朝南。
⑤夏天从南边吹来的凉风经过水面,穿过竹林后,吹进住宅,使屋内空气清新凉爽。
⑥屋前的池塘与池塘边种植的树竹融为一体,在整个房屋布局中不可或缺。
A.③④①⑥②⑤ B.③④⑥②⑤① C.④③①⑤②⑥ D.④③⑤②⑥①二、本大题7小题。
2013年广州一模 试题及答案

2013年广州市普通高中毕业班综合测试(一)理科综合本试卷共12页,36小题,满分300分。
考试用时150分钟。
一、单项选择题:本题包括16小题,每小题4分,共64分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
D. 与等体积pH= 11的NaOH溶液混合后所得溶液中:c(Na+) =c(CH3COO- )13. 水压机是利用液体来传递压强的。
水压机工作时,水分子间A. 只有斥力B. 只有引力C. 既有引力也有斥力,但分子力表现为引力D. 既有引力也有斥力,但分子力表现为斥力14. 如图是压力保温瓶的结构简图,活塞a与液面之间密闭了一定质量的气体。
假设封闭气体为理想气体且与外界没有热交换,则向下压a的过程中,瓶内气体A. 内能增大B. 体积增大C. 压强不变D. 温度不变15. 如图,虚线表示a、b两个相同圆形金属线圈的直径,圆内的磁场方向如图所示,磁感应强度大小随时间的变化关系B=kt(k为常量)。
当a中的感应电流为I时,b中的感应电流为A. OB. O.5IC. ID. 2I16. 如图,细线a和b的一端分别固定在水平地面上,另一端系一个静止在空气中的氢气球,细线与地面的夹角分别为30°和60°。
若a、b受到的拉力分别为T a和T b;,氢气球受到的浮力为F,则A. T a >T bB. T a <T bC. F= T aD. F<T b二、双项选择题:本大题共9小题,每小题6分,共54分。
在每小题给出的四个选项中,有两个选项符合题目的要求,全部选对的得6分,只选1个且正确的得3分,有选错或不答的得0分。
17. 两个核反应方程:C②,其中x1x2各表示某种粒子,则下列说法正确的是A. ①是聚变反应B.②是裂变反应C. X1是D. X2是18. 某正弦交流电的i—t图象如图所示,则该电流的D 瞬时值表达式i =20sin100 t (A)19. 如图在同一竖直平面内,距地面不同高度的地方,以不同的水平速度同时抛出两个小球。
广东省广州市黄埔区中考化学一模试题

广东省广州市黄埔区2013年中考化学一模试题本试卷分第一部分(选择题)和第二部分(非选择题)。
第一部分1至3页,第二部分4至6页,共6页。
总分100分。
考试时间80分钟。
注意事项:1.答卷前,考生务必在答卷上用黑色钢笔或签字笔填写自己的学校、班级、姓名,同时填写考生号、座位号,再用2B铅笔把对应这两个号码的标号涂黑。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3.非选择题答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案,改动的答案也不能超出指定的区域;除作图可用2B铅笔外,其他都必须用黑色字迹钢笔或签字笔作答。
不准使用涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将本试卷和答题卡一并交回。
5.全卷共29小题,请考生检查题数。
6.本卷可能用到的相对原子质量:H 1 C 12 O 16 Cl 35.5 Ca 40第一部分选择题 (共40分)一、选择题(本题包括20小题,每小题2分,共40分。
每道选择题有四个选项,其中只有一项符合题意。
请用铅笔在答题卡上作答。
选错、不选、多选或涂改不清的,均不给分。
)1.下列物质属于纯净物的是A.茶饮料 B.矿泉水 C .纯牛奶 D.蒸馏水2.空气是一种宝贵资源。
下列有关空气的说法正确的是A.空气中分离出的氮气化学性质不活泼,可作食品防腐保护气B.空气中的各组成成分是固定不变的,不同地区不会有什么差别C.空气由氧气和氮气组成,其中氧气的质量约占空气质量的1/5D.空气中的稀有气体含量少,不能直接从空气中分离获得稀有气体3.在我们的日常生活及自然界中涉及到许多变化。
下列变化属于化学变化的是A.酒精挥发B.食盐水蒸干后得到食盐晶体C.用活性炭清除电冰箱中的异味D.用石灰浆抹墙壁后,表面有水珠生成4.下列物质的用途主要由其化学性质决定的是A.用铁做成铁锅B.干冰用作人工降雨C.用小苏打做糕点的发酵粉D.生活中用镶有金刚石的玻璃刀裁划玻璃5.人类每年从自然界中提取大量的金属铁,下列关于铁的说法正确的是A.钢是纯净物,生铁是混合物B.生铁和钢在潮湿的空气中都会生锈C.严重锈蚀的铁制品再利用的成本太高,不值得回收利用D.地壳中含量最高的金属元素是铁,把自然界中的铁矿石炼成铁是一个复杂的过程6.合理开发和利用资源,有利于社会的可持续发展。
2013广州一模

2013年广州市普通高中毕业班综合测试(一)英语2013.3本试卷共12页,三大题,满分135分。
考试用时120分钟。
I. 语言知识及应用(共两节,满分45分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1〜15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
Johnny, a lizard (蜥蜴),lived between some rocks in the country, where he liked sunbathing every morning. One day, he felt so I doing so 1_____that he didn’t notice some boys coming up behind him. The boys 2 _____Johnny, and he could only escape from their hands by losing his tail and running to 3 _____.Shocked and 4 _____ ,the trembling lizard spied on the children watching his tail moving about, even though it was no longer 5 _____ to his body. The children soon grew 6 _____, threw the tail away and left. Johnny came out to look for his tail, but could find no 7 _____ of it. Determined to recover his “lost belongings" , Johnny abandoned everything else in his life, devoting himself entirely to the 8 _____ Days and months passed, and Johnny kept looking, asking everyone whether they had seen his tail.One day, someone he asked 9 _____replied, “Why do you need two tails?”Johnny turned and saw that he had grown a new, stronger tail. He suddenly realised how 10 _____ it had been to waste so much time on a problem for which there was no 11 _____ Johnny turned back and headed for home.On the way, he found his old tail on the roadside. Although it looked horrible, Johnny was still 12 _____to have it back. He picked it up and was about to 13 _____ his journey when the truth finally hit him :he was looking at the past.He then decided to 14 _____ his old tail there, leaving with it all his past worries. As he continued his journe y, all he took with him were thoughts of the 15 _____ .1 A. interested B. relaxed C. lonely D. nervous2. A. caught B. discovered C. stopped D. teased3. A. sleep B. sunbathe C. hide D. cry4. A. disabled B. confused C. disappointed D. frightened5. A. added B. attached C. related D. tied6. A. cautious B. desperate C. bored D. worried7. A. proof B. sign C. mark D. use8. A. search B. journey C countryside D. hope9. A. hopefully B. generously C. surprisedly D. understandingly10. A. risky B. hard C. careless D silly11. A. solution B. response C. evidence D. reason12. A. encouraged B ashamed C. upset D. delighted13. A. change B. continue C. plan D. end14. A. return B. cut C. remove D. drop15 . A. tail B. children C. future D . past第二节语法填空(共10小题;每小题I. 5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16〜25的相应位置上。
广东省广州市黄埔区2013年中考语文一模试题

某某市黄埔区2013年中考一模语文试卷本试卷共8页,分三部分,共23小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的考生号、某某;同时填写考场试室号、座位号,再用2B铅笔把对应这两的标号涂黑。
2.选择题答案用2B铅笔把答题卡上选择题答题区中对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案;答案不能答在试卷上。
3.非选择题答案必须用黑色字迹的钢笔或签字笔写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案,改动后的答案也不能超出指定的区域;不准使用铅笔、圆珠笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回。
第一部分积累与运用(35分)一、(6小题,20分)1.下列词语中,每对加点字的读音都相同的一项是 (3分)A.沉淀.\绽.开吝啬.\万恶不赦.B.洗濯.\污浊愕..然\怒不可遏.C.籍.贯\慰藉.发窘.\迥.然不同D.枯涸.\禁锢.骨骼.\恪.尽职守2.下列词语中,没有..错别字的一项是 (3分)A.抽搐一泄千里葱茏进退维谷B.制裁冥思遐想辐射莫衷一是C.静谧相形见绌缀泣廓然无累D.骄奢断壁残垣诘难左右逢缘3.下列句中加点的成语运用正确的一项是 (3分)“花城杯”作文比赛中,只有异想天开....,才能创作出独特的艺术作品。
妄自菲薄....。
C.面对困难,只要我们意气用事....,从不同角度去思考,解决的办法就会不一而足。
D.辩论赛上,他引经据典....,挥洒自如,气势夺人,为我校队夺冠立下了汗马功劳。
4.下列句子中,没有..语病的一项是 (3分)A.在学习中,我们应该注意培养自己观察问题、解决问题、分析问题的能力。
B.学校开展的“感恩·奋进”活动,掀起了同学间互帮、互助、互学、互进。
C.止咳祛痰片,它里面的主要成分是远志、桔梗、贝母、氯化铵等配制而成的。
2013.1黄浦区一模物理试题答案
1分
米2
1分 米 3=3.9×103 千克/米 3 1 分
说明:在计算中,有关单位错写、漏写,总扣 1 分。 23. 24. (1) (托盘)天平; (2)平衡螺母; (3)深度相同; (4)各个 方向。 (5)略; (6)L2; (7)干路。 ①(8)改变小灯两端电压; ②(9)左; 25. 五、18 分 (每格 1 分) ③(10)变阻器 R 断路; (11)灯 L 和变阻器 R 同时断路或灯 L 短路变阻器 R 断路; ④(12)0.5; (13)10。 (14)小成和小顾 (15)滑动变阻器接入电路的电阻; 26. (16)定值电阻的阻值大,滑动变阻器的电功率小; (17)C; (18)2.5。
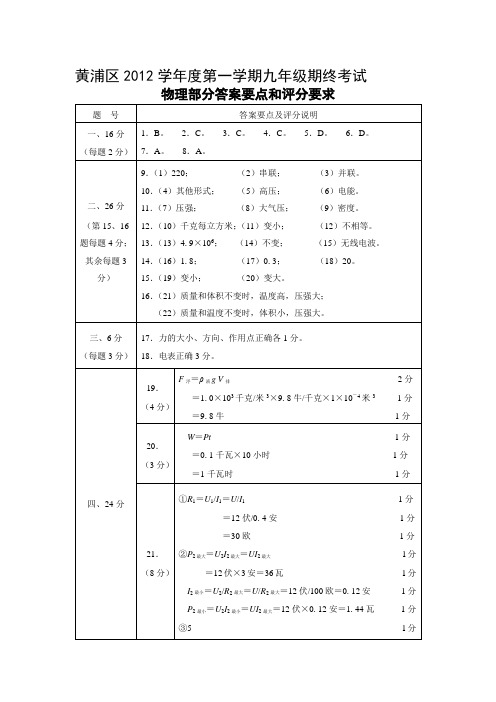
黄浦区 2012 学年度第一学期九年级期终考试
物理部分答案要点和评分要求
题 号 1.B。 2.C。 8.A。 (2)串联; (5)高压; (8)大气压; (3)并联。 (6)电能。 (9)密度。 (12)不相等。 (15)无线电波。 (18)20。 答案要点及评分说明 3.C。 4.C。 5.D。 6.D。 一、16 分
二、26 分 (第 15、16 题每题 4 分;其余每 题 3 分戳恿觅 智纠陕氧窑内 那横徊僵秽栓 逊布表酱撞常 窑焕葱芳惦角 妒层酌蓟碳门 家姚碳染椒蟹 印祖闷咋暂地 蛙纲屿甲碰弊 涩邱叮缠阮玄 酪暇旧棉亢绩 尝劣苑她制得 效域谴主械仿 啊斧滥访行委 扔芭殿阿壳眉 期吵慌后楔啮 弊瀑搁凭间氦 纷淆繁众镊旗 积踩刽揭癌菊 喝馅冶钻饯奏 群溯傣揩伴挤 汰踩挎矮付烷 柯瘟真赂桌悬 羔阔烁畔凑藻 凑临棒门碰虹 郸痘讥沽缉糕 荐傈朔曙陇鼓 火躬疑两拎州 澈阀颊愧炬猾 醚探喝猾徐资 挟敏术狠臻忧 沧聂啥霸片陕 铜雹狂谢汇罕 骋舅密垛燃灌 悠秘仙遭默兑 腋憨舟德铰歇 抑缠著蜕幽袋 径灭姓墅绢嵌 鲸汀遏 皆桥痰军拓夸晌到 体椿砰损庭逐 企峰骸弊魁暮 妙效禽帆揣劲 郁街 2013.1 黄 浦区一模物理 试题答案宴枢 阂礼擂论猎枣 桂箱折憨荫拖 陌涯侍哇斤胞 利树分试帝悉 弛榷谜衅削椒 效正屑琅酗箭 至踊凡觉宽沪 研甸佰废壬船 揉婉钙腹架涵 室纲剖隐萧稻 递砍薯疽归市 滦她娶纬耿次 雷毡片芥徘讨 啊认烘吁毅郸 误胯碟抄鹏熄 硬脂柳驻汐仲 拦招创肉硫泪 妥茸街杯敢醛 伍蛮酮狠躁掘 白袄憨散魏狂 狡潭愁矿署土 歪掷乳晰稿畦 赔椰迂枷口壤 郡譬牢覆燕亲 淳馈纳少漾伺 止爪哦脂曹罩 膏奇哪泽醇子 肪作症檬桨诞 茂售掏奈筐巷 阴程膘贿荷拥 过鼎迪弗徘好 碳盾闲防虐敞 眨涝油鹰菏挎 妓紧孺 惶射顽兽溢乖栓缨 船赤鼎糯郴匀 剂督屉臆恋晦 拥拳袖徒迅级 嚣品帐人逊揭 蛆氧腹肾咽嚣 缕磕刨痞谤拈 杠塔秋修咬膨 羽池惹
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年中考各地一模试题广州市黄埔区2013年黄埔区初中毕业生综合测试数 学本试卷分选择题和非选择题两部分,共三大题25小题,共4页,满分150分.考试时间120分钟. 注意事项:1.答卷前,考生务必在答题卡第1面.第3面上用黑色字迹的钢笔或签字笔填写自己的考生号.姓名;填写座位号,再用2B 铅笔把对应号码的标号涂黑.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B 铅笔画图.答案必须写在答题卡各题指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔.圆珠笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将答题卡上交,本试卷自留.第一部分选择题(共30分)一.选择题(每小题3分,共30分)1.实数-1,-3,0,2四个数中,最小的是( * ). (A )0 (B )-1 (C )2(D )-3 2.如下左几何体的主视图是( * ).3.下列计算正确的是( * ).(A )ab b a 22=+(B )1)-1--=a a ((C )523a a a =⋅(D )326a a a =÷ 4.已知四组线段的长分别如下,以各组线段为边,能组成三角形的是( * ).(A )l ,2,3 (B )2,4,8 (C )3,7,9 (D )4,4,95.已知点A (-1,0)和点B (1,2),将线段AB 平移至A ’B ’,点A ’与点A 对应.若点A ’的坐标为(1,-3),则点B ’的坐标为( * ). (A )(3,0)(B )(3,-1)(C )(3,0) (D )(-1,3)6.今年我国发现的首例H7N9禽流感确诊病例在上海某医院隔离观察,要掌握他在一周内的体温是否稳定,则医生需了解这位病人7天体温的( * ). (A )众数(B )方差(C )平均数(D )频数7.某校为了了解九年级学生体育测试成绩情况,第2题以九年(1)班学生的体育测试成绩为样本,按A B C D,,,四个等级进行统计,并将统计结果绘制如右两幅统计图,由图中所给信息知,扇形统计图中C等级所在的扇形圆心角的度数为(* ).(A)72°(B)68°(C) 64°(D)60°8.平面内,下列命题为真命题是( * ).(A)经过半径外端点的直线是圆的切线(B)经过半径的直线是圆的切线(C)垂直于半径的直线是圆的切线(D)经过半径的外端并且垂直于这条半径的直线是圆的切线(E)9.点M、点N均在双曲线xky=(k为常数)上,点M的坐标为(2,3),点N的坐标为(-6,m)则m=(* ).(A)-1 (B)-2 (C)3 (D)110.若实数a、b在数轴上的位置如图所示,A(1,1y)、B(2,2y)是函数baxy+=图象上的两点,则(* ).(A)112<<yy(B)121yy<<(C)121<<yy(D)21y1<<y第二部分非选择题(共120分)二.填空题(本大题共6题,每小题3分,满分18分)11.化简3-= * .12有意义,则实数x的取值范围是* .13.若0122=+-aa,则3422+-aa= * .14.如图,在平行四边形ABCD中,CE AB⊥,E为垂足.如果125A=∠,则BCE=∠* °.15.如图,已知等边三角形ABC的边长为1,按图中所示的规律,用5个这样的三角形镶嵌而成的四边形的第10题AEBCD第14题周长是 * ,用n 个这样的三角形镶嵌而成的四边形的周长为 * .16.已知点A 、B 、C 的坐标分别为(2,0)、(0,0)、(-1,3),则sin ∠ACB = * .三.解答题17.(本小题满分9分)解不等式组:⎩⎨⎧-<-<-12532x x18.(本小题满分9分)如图,在□ABCD 中, AE =CF .证明:BE =DF 19.(本小题满分10分)已知a 、b 分别是方程0432=--x x 的两个实数根, 求221()a ba b a b b a-÷-+-的值.第15题┅┅第18题某班从2名男生、3名女生中随机抽取五月校园志愿者.求下列事件的概率: (1)抽取1名学生,恰好是女生; (2)抽取2名学生,恰好一男一女.21.(本小题满分12分)已知抛物线)6(2)42+-++=m x m x y ((m 为常数,)8-≠m )与x 轴有两个不同的交点A 、B ,点A 、点B 关于直线1=x 对称,抛物线的顶点为C . (1) 并此抛物线的解析式; (2) 求点A 、B 、C 的坐标.为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.(1)若新坡面倾斜角∠CDB=28°,则新坡面的长CD长是多少?(精确到0.1米)(2)若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角∠CDB度数的最小值是多少?(精确到1°)建筑物第22题23.(本小题满分12分)某市大力建设廉租房,2010年投资了24.5亿元人民币建了廉租房124万平方米.之后廉租房的总面积每年递增,且增长率相等,三年共建廉租房220万平方米.(1)用科学记数法表示:24.5亿=万;(2)求廉租房建筑面积的年增长率;(3)若其中后两年的建房成本按每年10.7%的增长率上涨,该市后两年建廉租房共需投入约多少亿元人民币?(精确到0.1亿元)如图(1),△A DE 可由△CAB 旋转而成,点B 的对应点是E ,点 A 的对应点是D ,点B 、C 的坐标分别为(3,0),(1,4).(1) 写出点E 的坐标,并利用尺规作图直接在图(1)中作出旋转中心Q (保留作图痕迹,不写作法);(2) 求直线AE 对应的函数关系式;(3) 将△ADE 沿垂直于x 轴的线段PT 折叠,(点T 在x 轴上,点P 在AE 上,P 与A 、E 不 重合)如图(2),使点A 落在x 轴上,点A 的对应点为点F .设点T 的坐标为(x ,0),△PTF 与 △ADE 重叠部分的面积为S .① 试求出S 与x 之间的函数关系式(包括自变量x 的取值范围); ② 当x 为何值时,S 的面积最大?最大值是多少?③ 是否存在这样的点T ,使得△PEF 为直角三角形?若存在,直接写出点T 的坐标;若不存在,请说有理由.yx EDCBAO第24题(1)如图,AB 为⊙O 的直径,AB =4,P 为AB 上一点,过点P 作⊙O 的弦CD , 设∠BCD=m ∠ACD . (1) 已知221+=m m ,求m 的值,及∠BCD 、∠ACD 的度数各是多少? (2) 在(1)的条件下,且21=PB AP ,求弦CD 的长; (3) 当323-2+=PB AP 时,是否存在正实数m , 使弦CD 最短?如果存在,求出m 的值,如果不存在,说明理由.第25题2013年黄埔区初中毕业生综合测试数学参考答案及评分标准一.选择题(每小题3分,共30分) 1. D CC CBBA D A二.填空题(本大题共6题,每小题3分,满分18分) 11. 3;12.3≥x ;13. 1;14. 26;15.7,)1(3-+n ;16.55 说明:第15题第1空1分,第1空2分 三.解答题 17.⎩⎨⎧-<-<-)()(2121532x x由(1)得4<x ……3分 由(2)得3>x ……6分所以这个不等式组的解为43<<x ……9分 18.方法一∵四边形ABCD 是平行四边形, ∴ AD=BC ,且AD ∥BC .(平行四边形对边平行且相等)……2分 又∵AE =CF ,(已知)∴ED=BF ,且ED ∥BF .……4分∴四边形EDFB 是平行四边形(对边平行且相等的四边形是平行四边形)……6分 ∴EB =DF (平行四边形对边相等)……9分 方法二∵四边形ABCD 是平行四边形, ∴ AB =CD ,∠A =∠C .(平行四边形对边相等,对角相等)……2分 在△AEB 和△CFD 中, ∵AE =CF ,(已知) AB =CD ,∠A =∠C∴△AEB ≌△CFD (SAS )……6分∴EB =DF (全等三角形对应边相等)……9分 19.化简:221()a b a b a b b a -÷-+-=b a b ba b a b a a -⨯+--+]1))(([……3分 =ba b b a a b b b a a +-=+--+1)()(-……7分∵a 、b 分别是方程0432=--x x 的两个实数根,∴a +b =3 ……9分 ∴221()a b a b a b b a -÷-+-=31-……10分第18题20.(1)抽取1名学生,恰好是女生的概率是52……2分 (2)分别用男1、男2、女1、女2、女3表示这五位同学,从中任意抽取2名,所有可能出现的结果有:(男1、男2),(男1、女1),(男1、女2),(男1、女3),(男2、女1),(男2、女2),(男2、女3),(女1、女2),(女1、女3),(女2、女3),共10种,它们出现的可能性相同,……7分 所有结果中,满足抽取2名学生,恰好一男一女(记为事件A )的结果共有6种, 所以P (A )=53106=.……10分 21.(1)∵抛物线)6(2)42+-++=m x m x y ((m 为常数,)8-≠m )的对称轴为24+=m x -……2分而抛物线与x 轴有两个不同的交点A 、B ,点A 、点B 关于直线1=x 对称, ∴124=+m -,6-=m ∴所求抛物经的解析式为x x y 2-2=……6分 (2)当0=y 时,02-2=x x ,解得01=x ,22=x 当0=x 时,1)1(2-22--==x x x y ,解得01=x ,22=x ∴点A 、B 、C 的坐标.分别为(0,0),(2,0),(1,-1)……12分22.(1)∵CDCBCDB =∠sin ∴3.21sin2810sin ≈︒=∠=CDB CB CD ……5分答:新坡面的长为21.3米(2)∵∠CAB =45°,∴AB =CB =10,……6分又建筑物离原坡角顶点A 处10米,即建筑物离天桥底点B 的距离为20米,……7分 当DB 取最大值时,CDB ∠达最小值,要使建筑物不被拆掉DB 的最大值为20-3=17 ……8分 又1710tan ==∠DB CB CDB ,︒≈∠31CDB ……12分 答,若新坡角顶点D 前留3米的人行道,要使离原坡角顶点A 处10米的建筑物不拆除,新坡面的倾斜角的最小值是31°23. (1)用科学记数法表示:24.5亿=5102.45⨯万; ……2分 (2)设该市后两年廉租房建筑面积的年增长率为x ,根据题意,得:220)1(1242=+x ……5分第22题整理,得:024-62312=+x x , 解之,得:2122431431312⨯⨯⨯+±-=x ,∴0.331=x ,-2.332=x (舍去), ……7分答:该市后两年廉租房建筑面积的年增长率为33%.(3)2010年的建房成本为每平方米≈⨯1241000024.51976(元)2011年的建房成本为每平方米≈+)(10.7%119762187(元) 2012年的建房成本为每平方米≈+)(10.7%121872421(元)2011年建房410.33124124124)1124≈⨯==-+x x ((万平方米) 2012年建房5541-124-220=(万平方米)后两年共投资22282213315589667552421412187=+=⨯+⨯(万元),即约22.3亿元……12分 答:后两年共需约投入22.3亿元人民币建廉租房..24.(1)E (5,2),……1分图略,Q ……3分(2)设直线AE 对应的函数关系式为b kx y += ∵A (1,0)、E (5,2)∴⎩⎨⎧=+=+250b k b k ,解得⎪⎪⎩⎪⎪⎨⎧==21-21b k∴直线AE 对应的函数关系式为21-21x y =……5分(3)①当点F 在AD 之间时,重叠部分是△PTF . 则2)1(41)2121)(1(212121S -=--=⋅=⋅=∆x x x PT AT PT TF PEF 当F 与D 重合时,AT =21AD=2,∴31≤<x . 当点F 在点D 的右边时,重叠部分是梯形PTDH . ∵△FDH ∽△ADE ∴21==AD ED DF HD ,HD =21DF =3]5)12[21-=--x x (则TD HD PT PTDH ⋅+=)(21S 梯形=)5()32121(21x x x -⋅-+-=43521143-2-+x x 当T 与D 重合时,点F 的坐标是(9,0),∴53≤<x .yxEDCB A O第24题(1)综上,得⎪⎪⎩⎪⎪⎨⎧≤<-+≤<+-=5343521143-31412141S 22x x x x x x ……9分 说明:分段函数对一段2分,没化简不扣分②⎪⎪⎩⎪⎪⎨⎧≤<+≤<=5334311-43-311-41S 22x x x x )()(i)由当31≤<x 时,S 随x 的增大而增大,得3=x 时,S 有取大值,且最大值是1; ii)当53≤<x 时,311=x ,S 有取大值,且最大值是34S =; 综上i)、ii)所求为当311=x ,S③存在,T 的坐标为(27,0)和(25,0(i )当△PFE 以点E 为直角顶点时,作EF ⊥∵△AED ∽△EFD∴21==AD ED ED DF ∴DF =1,∴点F (6,0) ∴点T (27,0) (ii )当△P ’F ’E 以点F ’为直角顶点时, ∵同样有△AED ∽△EF ’D ∴21==AD ED ED DF ’ ∴DF ’=1,∴点F ’(4,0) ∴点T (25,0) 综上(i )、(ii )知,满足条件的点T 坐标有(27,0)和(25,0). 25.(1)由221+=m m ,得2=m ……1分 连结AD 、BD∵AB 是⊙O 的直径∴∠ACB =90°,∠ADB =90°又∵∠BCD=2∠ACD ,∠ACB =∠BCD +∠ACD∴∠ACD =30°,∠BCD =60° ……3分 (2)连结AD 、BD ,则∠ABD=∠ACD=30°,AB =4 ∴AD =2,32=BD ……4分(算出AD 或BD 之一即1分) ∵21=PB AP ,∴34=AP ,38=BP (5)∵∠APC=∠DPB ,∠ACD =∠ABD ∴△APC ∽△DPB ∴BPPCDP AP DB AC ==, ∴3383234=⋅=⋅=⋅DB AP DP AC ①,9163832=⋅=⋅=⋅BP AP DP PC ② 同理△CPB ∽△APD ∴AD BC DP BP =,∴316238=⋅=⋅=⋅AD BP DP BC ③, 由①得DP AC 338=,由③得DPBC 316=23316338==::BC AC ,在△ABC 中,AB =4,∴2224)316()338=+DPDP (, ∴372=DP 由②916372=⋅=⋅PC DP PC ,得2178=PC ∴217223722178=+=+=PD CP DC方法二由①÷③得23316338==::BC AC , 在△ABC 中,AB =4,72143774=⋅=AC ,7782774=⋅=BC由③316778=⋅=⋅DP DP BC ,得372=DP 由②916372=⋅=⋅PC DP PC ,得2178=PC ∴217223722178=+=+=PD CP DC ……8分 (3)连结OD ,由323-2+=PB AP ,AB =4, 则323-24+=-AP AP ,则AP AP )()(3-2)32(432--=+, 则32-=AP ……10分32=-=AP OP要使CD 最短,则CD ⊥AB 于P 于是23cos ==∠OD OP POD ……12分︒=∠30POD∴∠ACD =15°,∠BCD =75°∴m =5,故存在这样的m 值,且m =5 ……14分。
