2007年成都实外小升初“德瑞杯”数学知识竞赛试题
成都外国语学校小升初数学试卷必考题

成都外国语学校小升初数学试卷一.(共8题,共16分)1.一台电冰箱的原价是2100元,现在按七折出售,求现价多少元?列式是()。
A.2100÷70%B.2100×70%C.2100×(1-70%)2.某商品按20%利润定价,然后按8.8折卖出,共获利润84元,这件商品成本()元。
A.1650B.1500C.17003.已知点A和点B在同一条数轴上,点A表示数-2,点B与点A相距3.5个单位长度,那么点B表示的数是()。
A.-1.5B.5.5C.1.5或-5.5D.-1.5或3.54.一种皮衣,原价1200元,现在85折出售.现在一件这样的皮衣()。
A.1002元B.1000元C.696元D.1020元5.某地一天中午12时的气温是7℃,过5时气温下降了4℃,又过7时气温又下降了5℃,第二天零时的气温是()。
A.2°CB.-2°CC.8°CD.6°C6.用一定的钱买地砖,每块砖的价钱和买砖块数()。
A.成正比例B.成反比例C.不成比例D.不成反比例7.把38%改写成成数,正确的是()。
A.三成八B.十二成C.九成九D.二成五8.一个底面直径是8cm,高是6cm的容器,小明将这个容器装满水,再把一个底面积是3.14平方厘米、高3cm的圆锥体铁块浸入容器的水中.会溢出()立方厘米的水。
A.301.44B.9.42C.3.14D.6.28二.(共8题,共16分)1.一件工作,甲单独完成于乙单独完成所用的时间比是5:6,那么他们的工作效率比是6:5。
()2.时间一定,做每个零件的时间和零件个数成反比例。
()3.5∶8和∶可以组成比例。
()4.在比例尺的应用中,实际距离都比图上距离大。
()5.80比50多60%,50比80少37.5%。
()6.在12.2、-4、0、6、-37中,负数有3个。
()7.把一个圆形花园按1:100的比例尺画在图纸上,图纸上的花园面积与实际花园面积的比也是1:100。
成都实外小升初“德瑞杯”数学知识竞赛试题

2007年小升初“德瑞杯”数学知识竞赛试题(考试时间:60分钟 满分:100分)一、判断。
对的画√,错的画×。
(每题2分,共10分)1.所有的质数的和是一个奇数。
( )2.人的身高和体重成正比例。
( )3.两个面积相等的等腰直角三角形,能拼成一个正方形。
( )4.发芽率为90%的种子一定比发芽率为80%的种子发芽的棵数多 。
( )5.有三条对称轴的图形一定是等边三角形。
( )二、填空。
(每题3分,共30分)1.一个数精确到万位是200万,这个数最小是( )。
2.去掉一个数中所有的0,新数与原数之和是5.045,原数是( )。
3.3a 、4b 、6c 是三个最简单真分数,如果这三个分数的分子都加上c ,则这个数之和为6,这三个数是( )、( )、( )。
4.甲比乙多25%,那么乙比甲少( )。
5.甲、乙、丙三人做同样多的零件,甲每小时做20个,乙每小时做24个,丙每小时做30个,完成任务时,平均每小时做了( )多少个零件。
6.某人乘船逆流而行,在A 处不小心将一只水壶掉入水中,船又前行了15分钟后他才发现,立即返回寻找,结果在离A 处3千米的地方追到水壶。
他返回寻找水壶共用了( )分钟。
7.两个正方形的边长之和为20厘米,面积相差200平方厘米,这两个正方形的面积分别是( )平方厘米和( )平方厘米。
8.一分、二分、五分三种硬币的个数相等,共10元。
三种硬币共( )个。
9.不能写成两个不同的奇合数之和的最大偶数时( )。
10.AD 中点,线段CE 把梯形分成甲、乙两个部分,面积比是10:7。
那么梯形的上底AB 与下底CD 的长度比AB:CD =( ):( )。
三、选择。
把正确的答案的番号填在括号里。
(每题3分,共15分)(1)一个三角形三条边长比为98:99:100,这个三角形是( ) ①锐角三角形 ②直角三角形 ③钝角三角形 ④等腰三角形(2)在一个长、宽、高分别为6厘米、4厘米、3厘米的长方体上切一刀,切面最大是多少平方厘米?( )①24平方厘米 ②18平方厘米 ③12平方厘米 ④前面都不对(3)A 、B 、C 、D 、E 五人进行乒乓球比赛,每人两个人都要赛一场。
成都外国语学校2007年“德瑞杯”知识竞赛数学试卷-T版

成都外国语学校2007年“德瑞杯”知识竞赛数学试卷(90分钟完卷)一、填空。
1.今年五一黄金周,某市接待游客三十万六千八百人次,这个数写作( )人次,改写成用“万”作单位是( )人次。
实现旅游收入175030000元,这个数读作( )元,四舍五入到亿约是( )元。
解:306800;30.68万;一亿七千五百零三万;2亿。
本题的考点为数的读写。
2.有100名新生分成4个队参加军训,一队人数是二队人数的311倍,一队人 数是三队人数的411—倍,那么四队有( )人。
解:49;此题看似条件不全,只有一二三队的关系,二队是一队的43,三队是一队的54,一队的人数不可能是小数,那么一队的人数及时4的倍数又是5的倍数,即一队的人数一定是20的倍数,假如一队是20人,那么二队就是15人,三队就是16人,则四队是49人,假如一队是40人,二队就是30人,三队就是32人,则已经大于100,则不可能。
3.张村有733名村民,至少有( )位村民的生日是同一天。
解:3;典型的抽屉原理,把一年365天看作是365个抽屉,把733名抽屉看作是733个苹果,则根据抽屉原理可得答案。
4.在一个圆里画一个最大的正方形,正方形的面积与圆的面积比是( )。
解:2:π ;假设圆的半径为1,则圆的面积为π,最大正方形对角线就是圆的直径为2,那么正方形的面积=对角线的平方÷2=22÷2=2,那么正方形的面积与圆的面积比为2:π。
5.甲乙各走一段路,甲、乙所用的时间比是4:5,速度比是5:3。
则甲、乙所走路程的比是( )。
解:4:3;假设甲所用时间为4,则乙所用时间为5,设甲的速度为5,则乙的速度为3,由路程=时间×速度得到甲、乙路程比=4×5:5×3=4:3.6.一个直角三角形三边长度分别是6厘米,10厘米,8厘米,这个三角形的周长是( ),面积是( )。
解:24;24;周长=6+10+8=24(厘米),由题知这是一个直角三角形,并且直角边分别为6厘米、8厘米,则面积=6×8÷2=24(平方厘米)。
成都实验外国语学校小升初选拔考试数学试卷(1)
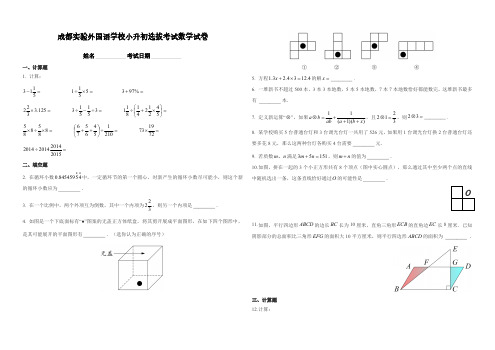
姓名 ____________ 考试日期 ____________
一、计算题 1. 计算: 311
5 2 2 3.125
3 58 58 88
1 15 5
3 97%
31 1 3 55
11 1 2 1 4 8 4 2 5
6 5 4 1 7 6 5 210
73 19 72
2014 2014 2014 2015
二、填空题
2. 在循环小数 0.845459 5 4 中,一定循环节的第一个圆心,时新产生的循环小数尽可能小,则这个新
的循环小数应为 ________ .
3. 在一个比例中,两个外项互为倒数,其中一个内项为 2 2 ,则另一个内项是 ________ . 3
17.甲容器中有纯酒精 11 升,乙容器中有水 15 升,第 1 次将甲容器中的一部分纯酒精倒入乙容器,使 酒精与水充分混合,第 2 次将乙容器中的一部分混合液倒入乙中,这样 ,甲容器中含纯酒精 55%,乙 容器中的纯酒精含量为 25%,那么,第 2 次从乙容器倒入甲容器中的混合液是多少升?
18.观察下列等式:
1 1 1 1 1 1
(6)
1
234 11
49 50 1
1 51 2 52 3 53
25 75
四、解答题
13.已知三角形
ABC
为等边三角形,其三边长如图所示,求
x2 y2 x2 2y2
1
9 25
的值.
14.艾迪、薇儿、大宽三名同学共有图书 180 本,其中艾迪的图书是薇儿的 2 倍,薇儿的图书是大宽的 3 倍,求艾迪、薇儿、大宽三名同学的图书各有多少本?
0.4
1.65 5 2 6 2.5
成都外国语学校小升初德瑞杯知识竞赛数学试题 答案2

成都外国语学校2002年“成外杯”知识竞赛数学试卷(100分钟完卷)一、直接写出结果x1.8()(1)七五折就是()%;(2)(?x))?( 30.21(34))( );(????16?256......38?1874?25判断。
正确的画√,错误的画×。
二、6个自然数,如果前三个数的和是a,那连续、1么,后三个数的和是a+3。
()的积一定能够被)整除。
(2,3,5 、2a?24?35等腰直角三角形的面积是它的斜边的平方的一、3半。
()一个数与它的倒数的和一定大于1。
()、4c?bb?c一定,那么若小于。
,、50?ba??c bac?cb)(a?()三、填空。
有一个数比一亿小,如果增加二百零三万正好、1是一亿。
用“万”作为单位,写出这个数是()。
2002年“五一”节是星期三,那么,这一年的、2国庆是星期()。
1 / 11331,把已知:ABCD四个1???D??B?CA?120%、32204数按照从大到小的顺序排列,第三个数是()。
一个半圆形铁片的周长是10.28分M,它的面积、4是()平方分M。
某个班女生人数是男生人数的一半,男生的平、5均体重是41千克,女生的平均体重是35千克,这个班的学生的平均体重是()千克。
在一块长方形的苗圃中,使用一种除草剂后,、6绝大多数杂草被杀死,但是依然很不均匀地残留着少量杂草。
如下图所示,甲棵杂30甲从左向右数,发现左右20草;乙从右往左数,发现棵杂草,但是两个人都走过了乙中线,苗圃里最多残留()棵杂草,最少有)棵杂草。
(33拿一定的钱去买一种衣服可以买件,如果用、7这些钱去买一种裤子,可以买88条,现在用这些钱买了这种衣服和裤子,可以买()套。
3,如果宽增加10厘一个长方形,宽是长的、88M,则长方形变成正方形,原来长方形的周长是2 / 11 ()厘M,面积是()平方厘M。
陈东和彰明同时各买了型号相同,车价是650、9元的自行车一辆。
他们各自都办理了自行车保险,保险费率为15%,一年过后,陈东的自行车以原价的八五折转让给了别人,而彰明的自行车因为被盗,保险公司酌情赔偿他500元。
2007年四川省成都市小升初数学试卷(解析版)

10. (3 分)把 60 分解质因数是 60=( A.1×2×2×3×5 B.2×2×3×5
11. (3 分)如果甲数和乙数都不等于 0,甲数的 等于乙数的 ,那么( A.甲数>乙数 B.乙数>甲数 C.甲数=乙数
)
12. (3 分)一钢管长 15 米,截去全长的 ,根据算式 15×(1﹣ )所求的问 题是( )
A.14 平方厘米
15. (3 分) (1)班男、女生的人数比是 8:7,女生人数占全班人数的( A. B.1 C. D.
16. (3 分)甲、乙二人合做一项工作,甲做的部分占乙的 ,乙做的占全部工作 的( A. ) B. C. D.
17. (3 分)用一张长 5 厘米,宽 4 厘米的长方形纸剪一个最大的圆,这个圆的 面积占这张纸面积的( A.20π B.4π )% C.5π D.80
四、图形题. (20 分) 18. (6 分)如图的这个图形是一个立体图形,叫四面体.它有四个面 都是三角 形,有六条棱(边) .如果把每条棱都染成白色、蓝色或红色,并且使每一个 三角形都至少有一个红色的边,那么最少有几条棱要被染成红色? 答:最少 条棱要被染成红色.
19. (7 分)一个圆管,如图,外圆半径 4 厘米,内圆半径 3 厘米,管长 20 厘米, 求这根圆管的体积?
第 4 页(共 12 页)
(2)设这个数为 x; x﹣32=8.8 x﹣32+32=8.8+32 x=40.8 x÷ =40.8÷ x=51. 答:这个数是 51. 二、判断题,对的打√,错的打×. (10 分,每题 2 分) 3. (2 分)梯形的上底与下底的和一定,它们的面积和高成正比. 【考点】6B:辨识成正比例的量与成反比例的量.
2007 年四川省成都市小升初数学试卷
成都外国语学校小升初“德瑞杯”知识竞赛数学试题答案

成都外国语学校2000年“德瑞杯”知识竞赛数学试题(100分钟完卷)一、 直接写出结果(共2分)一成七就是( )% 3:0.64的比值是( ) 31038-=( ) 40.565÷=( ) 二、 填空(共14分)1、我国的领土面积是约960万( )。
(填上适当的计量单位)4时12分=( )小时。
3.07吨=( )吨( )千克2、把一根长215米的木条,按照3:4截成两段,最短的一段长( )米。
3、如果a,b 是非零的自然数,并且a>b ,把ab ,2a ,b 2 这三个数按照从小到大排列是( )<( )< ( )。
4、甲数是a ,比乙数的23多b ,表示乙数的式子是( )。
5、一个四位小数,精确到百分位的近似数是6.70,这个四位小数最大是( )。
6、一个长方体截成两个正方体,如果这个长方体的表面积是60平方分米,那么,一个正方体的表面积是( )平方分米。
7、一个分数的分子不变,分母扩大10倍,所得到的分数与原来的分数的差是2770,那么原来的分数是( ) 8、乘数是117,积 比被乘数多14,被乘数是( )。
9、甲、乙两个商店售出的商品个数相同。
甲店的商品全部售完,乙店的商品卖掉60%,两个商店合起来算,卖掉的商品个数占商品总数的( )%。
10、 甲、乙二人从两地相向而行,相遇时乙走了全程的715。
相遇后,甲继续前行,走完全程用了45分钟。
从出发到相遇乙用的时间是( )分钟。
11、 在下图三角形ABC 中的甲、乙、丙、丁四个小三角形的面积相等。
AB 长 3.6厘米,DB 长是( )厘米。
AC D甲乙丙丁12、 一个整数乘以13后,乘积的后三位数是123,那么,这个整数最小是( )。
13、 甲、乙两个数是自然数,如果甲数的56恰好是乙数的14,那么,甲、乙两数之和的最小值是( )。
14、 将三角形ABC ,AB 四等分,BC 五等分,AC 三等分(如下图所示)那么,DEF ABC 三角形的面积三角形的面积=( )AB C F DE三、 判断(正确的打√,错误的打×。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年小升初“德瑞杯”数学知识竞赛试题
(考试时间:60分钟 满分:100分)
一、判断。
对的画√,错的画×。
(每题2分,共10分)
1.所有的质数的和是一个奇数。
( )
2.人的身高和体重成正比例。
( )
3.两个面积相等的等腰直角三角形,能拼成一个正方形。
( )
4.发芽率为90%的种子一定比发芽率为80%的种子发芽的棵数多 。
( )
5.有三条对称轴的图形一定是等边三角形。
( )
二、填空。
(每题3分,共30分)
1.一个数精确到万位是200万,这个数最小是( )。
2.去掉一个数中所有的0,新数与原数之和是5.045,原数是( )。
3.3a 、4b 、6c
是三个最简单真分数,如果这三个分数的分子都加上c ,则这
个数之和为6,这三个数是( )、( )、( )。
4.甲比乙多25%,那么乙比甲少( )。
5.甲、乙、丙三人做同样多的零件,甲每小时做20个,乙每小时做24个,
丙每小时做30个,完成任务时,平均每小时做了( )多少个零件。
6.某人乘船逆流而行,在A 处不小心将一只水壶掉入水中,船又前行了15
分钟后他才发现,立即返回寻找,结果在离A 处3千米的地方追到水壶。
他返回寻找水壶共用了( )分钟。
7.两个正方形的边长之和为20厘米,面积相差200平方厘米,这两个正方
形的面积分别是( )平方厘米和( )平方厘米。
8.一分、二分、五分三种硬币的个数相等,共10元。
三种硬币共( )
个。
9.不能写成两个不同的奇合数之和的最大偶数时( )。
10.
E 是AD 中点,线段CE 把梯形分成甲、乙
两个部分,面积比是10:7。
那么梯形的上底AB 与下底CD 的长度比AB:CD =( ):( )。
三、选择。
把正确的答案的番号填在括号里。
(每题3分,共15分)
(1)一个三角形三条边长比为98:99:100,这个三角形是( ) ①锐 ②直角三角形 ③钝角三角形 ④等腰三角形
(2)在一个长、宽、高分别为6厘米、4厘米、3厘米的长方体上切一刀,切面最大是多少平方厘米?( )
①24平方厘米 ②18平方厘米 ③12平方厘米 ④前面都不对
(3)A 、B 、C 、D 、E 五人进行乒乓球比赛,每人两个人都要赛一场。
现在A 、D 都赛了4场,B 、C 都赛了3场,E 至少赛了( )场。
①1 ②2 ③3 ④4
(4)小杨花了28元钱买了一只鸡,29元钱卖掉了。
然后他觉得不划算,花了30元钱又买回来了,31元钱卖给另外一个人。
在这个过程中小杨( )
①赚了1元钱 ②亏了1元钱 ③赚了2元钱 ④亏了2元钱
(5如图,下面圆锥形容器里有1千克水,水面在圆锥高的一半,此容器 )千克水。
①5 ②6 ③7 ④8
四、计算。
写出必要过程。
(每题3分,共9分)
(1) 95:x =54
2:1.8
(2)[(1.4+1.6×412]×(1÷198-2.375)] +2.901
(3)做一种零件,甲每小时做21个,乙每小时做13个。
要在7小时完成199个,甲乙二人至少合作多少个小时?
(4)某校四年级原有两个班,现在重新编为三个班,将原一班的31和原二班的41组成新一班,将原一班的41和原二班的31组成新二班,余下的30人组成新三班。
如果新一班的人数比新二班的人数多10%。
新一班有多少人?
(5)甲、乙二人分别从A 、B 两地同时出发,相向而行。
出发时他们的速度比是3:2,他们第一次相遇后,甲的速度提高了20%,乙的速度提高了30%,这样,当甲到达B 地时,乙离A 地还有16千米,那么A 、B 两地的距离是多少千米?
(6)一个圆柱体木桩的底面直径和高都是6厘米,把它切割成一个长方体,这个长方体的体积最大是多少立方厘米?
五、图形问题。
左图中,一只小狗被系在边长为3米的等边三角形建筑物的墙角上,绳长4米,这只小狗多能到达的总面积是多少平方米?(狗的长度不计算)
狗
六、解决问题。
1.袋鼠和兔子进行跳跃比赛,袋鼠每次跳跃214米,兔子每分钟跳跃432米,他们每秒都只跳一次。
比赛途中,从起点开始,每隔8312米设有一个气球,当他们之中的一个先踩到气球,则比赛就算结束,先踩到者为胜。
这时,另一个跳跃了多少米?
2.沿着匀速成上升的自动扶梯,甲从上朝下走到底走了150级,乙从下朝上走到顶走了75级。
如果甲每分钟走的扶梯级数是乙的3倍,那么这部自动扶梯有多少级(可见部分)?
3.如果a ▲b =b a ab +,求10▲10▲10的值。
