专题6

合集下载

人教版八年级上册数学期末复习6专题六作图专题

则H即为工厂位置．
四、网格作图
13．如图，在平面直角坐标系中，△ABC的顶点A(0，1)， B(3，2)，C(1，4)均在正方形网格的格点上．
(1)画出△ABC关于x轴的对称图形△A1B1C1； (2)将△A1B1C1沿x轴方向向左平移3个单位长度后得到
△A2B2C2，写出顶点 A2，B2，C2的坐标．
解：如图，作出AB和BC的中垂线，相交于点P，则点P是所求的到三村距离相等的点
11．如图，在△ABC中，AB＝AC，∠BAC＝120°. (1)用尺规作出AB的垂直平分线交AB于点E，交BC于点F. (2)若BF＝3，求CF的长度．
解：(1)如图所示：
(2)连接AF.
∵AB＝AC，∠BAC＝120°
∴∠B＝∠C＝
1 2
(180°－120°)＝30°
又由(1)知BF＝AF
∴∠FAB＝∠B＝30°
∴∠FAC＝120°－30°＝90°
∴CF＝2AF＝2BF＝2×3＝6
12. 如图，已知甲村和乙村靠近公路a，b，为了发展经济，甲、乙两村准备合建一个工厂，经协商，工厂必须满足以下要求：
(1)到两村的距离相等； (2)到两条公路的距离相等．你能帮忙确定工厂的位置吗？
解：如图
15.如图，在平面直角坐标系中，△ABC的三个顶点分别为 A(2，3)，B(3，1)，C(－2，－2)．
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A，B，C 的对称点分别是A′，B′，C′)，并直接写出A′，B′，C′的坐标．
(2)求△A′B′C′的面积．
解：(1)如图所示，点A′(－2，3)， B′(－3，1)，C′(2，－2)；
解：设a、b相交于点O.甲村为点E，乙村为点D.

(新课标解读)2020版语文专题 6.秋天的雨新课标改编版_6-10

字词乐园
会认字
lǎ
喇组词：喇叭
bā
叭组词：喇叭
hòu
厚组词：薄厚厚道厚此薄彼
字词乐园
会认字
qǔ
曲组词：歌曲曲子曲终人散
fēnɡ
丰组词：丰收丰富五谷丰登
他得到的天资是那样的好，没有受到正常的后天教育，尚且成为平凡的人;那么，现在那些本来就不天生聪明，本来就是平凡的人，又不接受后天的教育，难道成为普通人就为止了吗? 故事寓意：可见，一个人光有先天的智慧而不注重后天的学习是不行的，不注意接受新知识，到头来只会落在别人后面。”山羊和鸭子们围在阿索加的身边，开始唱起来：“你这只笨小马。一天，小老鼠走出茅舍，看见附近有一只大猫，吓得立即跑回去，躲在角落里瑟瑟发抖。
字词乐园Βιβλιοθήκη 易错提示颜：左部下方为三撇。
淡：右部上面的“火”的最后一笔，捺变成点。
字词乐园
会认字
yào
钥组词：钥匙一把钥匙开一把锁
shi
匙组词：钥匙
bīn
缤组词：缤纷五彩缤纷
字词乐园
会认字
méi
枚组词：一枚不胜枚举
zhēng
争组词：争先争抢争先恐后
ɡōu
勾组词：勾住勾引勾人心弦
怎么炒外汇
喇叭挖空心思唱着高调，或为自已哗众取宠，或替他人歌功颂德，整日里忙得不亦乐乎。当然，最倒霉的是主人，桌面上陈列的几件贵重古董瓷器，被它毫不客气地踢落地上摔得粉碎。，”垃圾桶忍不住发牢骚

语法专题六

语法专题探究
人教版
英语
4．For all these years I have been working for others.I’m ． hoping I’ll________my own business some day. A．turn up B．fix up ．． C．set up ．答案 C D．make up ．解析 set up one’s business“创业”。 “创业”
语法专题探究
人教版
英语
2．He will never________anything if he doesn’t work ． hard. A．hope ．解析 B．wish ． C．achieve D．succeed ．． achieve意为“完成”“做到”。其余三项均不能直意为“完成”“做到” ”“做到意为接跟名词或代词作宾语。接跟名词或代词作宾语。答案 C
语法专题探究
人教版
英语
11．The folk tales have________to us from the ancient ti ． mes. A．come back B．come out ．． C．come down D．come up ．．解析 come down“流传下来”。 “流传下来” 答案 C
语法专题探究
人教版
英语
7．With no one to ________in such a frightening ． situation，she felt very helpless. ， A．turn to B．turn on ．． C．turn off D．turn over ．．解析 turn on“打开(灯、煤气 ”；turn off“关闭”；t “打开灯煤气)” “关闭” urn over“翻转”；turn to“求助于，求救于”。 “翻转” “求助于，求救于” 答案 A

高考数学复习考点题型专题讲解6 极化恒等式、投影向量

高考数学复习考点题型专题讲解专题6 极化恒等式、投影向量极化恒等式：a ·b ＝14[(a ＋b )2－(a －b )2].(1)几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14.(2)在平行四边形PMQN 中，O 是对角线交点，则： ①PM →·PN →＝14[|PQ →|2－|NM →|2](平行四边形模式)；②PM →·PN →＝|PO →|2－14|NM →|2(三角形模式).类型一投影向量的应用由投影与投影所在的向量共线，问题转化为求向量间的投影数量与投影所在向量方向上单位向量的积.例1 已知|a |＝4，e 为单位向量，它们的夹角为2π3，则向量a 在向量e 上的投影向量是________；向量e 在向量a 上的投影向量是________. 答案－2e －18a解析由|a |＝4，e 为单位向量，它们的夹角为2π3，向量a 在向量e 上的投影数量：|a |cos 23π＝－2，向量e 在向量a 上的投影数量：|e |cos 23π＝－12，故向量a 在向量e 上的投影向量：－2e ，向量e 在向量a 上的投影向量：－12×a |a |＝－18a .训练1 (1)已知向量a 与b 的夹角为34π，且|a |＝2，|b |＝3，则a 在b 方向上的投影向量与投影向量的长度分别是( ) A.23b ，2B.23b ，－ 2 C.－23b ，2D.－23b ，－ 2 (2)已知向量a ＝(1，2)，A (6，4)，B (4，3)，b 为向量AB →在向量a 上的投影向量，则|b |＝________. 答案 (1)D (2)455解析 (1)设a 在b 方向上的投影向量为λb (λ∈R )，则a ·b ＝λb ·b ，故λ＝a ·b b 2＝|a |cos 34π|b |＝－23.故a 在b 方向上的投影向量为－23b ，a 在b 方向上的投影向量的长度为|a | cos 34π＝－ 2.(2)AB →＝(－2，－1)，由投影公式可知|b |＝|AB →·a ||a |＝|－2×1＋（－1）×2|5＝455.类型二利用极化恒等式求向量的数量积利用极化恒等式求平面向量数量积的步骤： (1)取第三边的中点，连接向量的起点与中点；(2)利用极化恒等式将数量积转化为中线长与第三边长的一半的平方差； (3)求中线及第三边的长度，从而求出数量积的值.注：对于不共起点或不共终点的向量需通过平移转化为共起点(终点)的向量，再利用极化恒等式.例2 (1)如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点.BA →·CA →＝4，BF →·CF →＝－1，则BE →·CE →的值为________.(2)如图，在平行四边形ABCD 中，AB ＝1，AD ＝2，点E ，F ，G ，H 分别是AB ，BC ，CD ，AD 边上的中点，则EF →·FG →＋GH →·HE →＝________.答案 (1)78 (2)32解析 (1)设BD ＝DC ＝m ，AE ＝EF ＝FD ＝n ，则AD ＝3n .根据向量的极化恒等式，有AB →·AC →＝AD →2－DB →2＝9n 2－m 2＝4，FB →·FC →＝FD →2－DB →2＝n 2－m 2＝－1，联立解得n 2＝58，m 2＝138.因此EB →·EC →＝ED →2－DB →2＝4n 2－m 2＝78.即BE →·CE →＝78.(2)连接EG ，FH 交于点O (图略)，则EF →·FG →＝EO →2－OH →2＝1－⎝ ⎛⎭⎪⎫122＝34，GH →·HE →＝GO →2－OH →2＝1－⎝ ⎛⎭⎪⎫122＝34，因此EF →·FG →＋GH →·HE →＝32.训练2 (1)在△ABC 中，M 是BC 的中点，AM ＝3，BC ＝10，则AB →·AC →＝________.(2)如图，在△ABC 中，已知AB ＝4，AC ＝6，∠BAC ＝60°，点D ，E 分别在边AB ，AC 上，且AB →＝2AD →，AC →＝3AE →，若F 为DE 的中点，则BF →·DE →的值为________.答案 (1)－16 (2)4解析 (1)因为M 是BC 的中点，由极化恒等式得AB →·AC →＝|AM →|2－14|BC →|2＝9－14×100＝－16.(2)取BD 的中点N ，连接NF ，EB ，因AB ＝4，AE ＝2，∠BAC ＝60°，故BE ⊥AE ，所以BE ＝2 3. 在△DEB 中，FN 綉12BE ，所以FN ＝3，故BF →·DE →＝2FB →·FD →＝2⎝ ⎛⎭⎪⎫FN →2－14DB →2＝2(3－1)＝4.类型三利用极化恒等式求数量积的最值(范围)(1)利用极化恒等式求数量积的最值(范围)时，关键在于取第三边的中点，找到三角形的中线，再写出极化恒等式.(2)难点在于求中线长的最值(范围)，可通过观察图形或用点到直线的距离等求解.例3 (1)如图，在同一平面内，点A 位于两平行直线m ，n 的同侧，且A 到m ，n 的距离分别为1，3，点B ，C 分别在m ，n 上，|AB →＋AC →|＝5，则AB →·AC →的最大值是________.(2)(2022·济南调研)在△ABC 中，点E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB →·PC →＋BC →2的最小值为________. 答案 (1)214 (2)2 3解析 (1)法一(极化恒等式法)连接BC ，取BC 的中点D ，AB →·AC →＝AD →2－BD →2，又AD ＝12|AB →＋AC →|＝52，故AB →·AC →＝254－BD →2＝254－14BC →2，又因为BC min ＝3－1＝2，所以(AB →·AC →)max ＝214.法二(坐标法)以直线n 为x 轴，过点A 且垂直于n 的直线为y 轴，建立如图所示的平面直角坐标系xOy ，如图，则A (0，3)，C (c ，0)，B (b ，2)，则AB →＝(b ，－1)，AC →＝(c ，－3) 从而(b ＋c )2＋(－4)2＝52，即(b ＋c )2＝9，又AC →·AB →＝bc ＋3≤（b ＋c ）24＋3＝214，当且仅当b ＝c 时，等号成立. (2)取BC 中点O ，PB →·PC →＝PO →2－14BC →2⇒PB →·PC →＋BC →2＝PO →2＋34BC →2≥2PO →2·34BC →2＝3|PO →||BC →|，当且仅当PO ＝32BC 时等号成立.∵PO ≥12h ，∴3|PO →||BC →|≥32h |BC →|＝3S △ABC ＝23，∴PB →·PC →＋BC →2的最小值为2 3.训练3 (1)如图所示，正方体ABCD －A 1B 1C 1D 1的棱长为2，MN 是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦)，P 为正方体表面上的动点，当弦MN 的长度最大时，PM →·PN →的取值范围是________.(2)如图所示，正方形ABCD的边长为1，A，D分别在x轴，y轴的正半轴(含原点)上滑动，则OC→·OB→的最大值是________.答案(1)[0，2] (2)2解析(1)由正方体的棱长为2，得内切球的半径为1，正方体的体对角线长为2 3.当弦MN的长度最大时，MN为球的直径.设内切球的球心为O，则PM→·PN→＝PO→2－ON→2＝|PO→2|－1.由于P为正方体表面上的动点，故|OP|∈[1，3]，所以PM→·PN→∈[0，2].(2)如图，取BC的中点M，AD的中点N，连接MN，ON，则OC →·OB →＝OM →2－14＝|OM →|2－14.因为OM ≤ON ＋NM ＝12AD ＋AB ＝32，当且仅当O ，N ，M 三点共线时取等号. 所以OC →·OB →的最大值为2.一、基本技能练1.设向量a ，b 满足|a ＋b |＝10，|a －b |＝6，则a ·b 等于( ) A.1 B.2 C.3 D.4 答案 A解析由极化恒等式得a ·b ＝14[(a ＋b )2－(a －b )2]＝14×(10－6)＝1.2.如图，在平面四边形ABCD 中，O 为BD 的中点，且OA ＝3，OC ＝5，若AB →·AD →＝－7，则BC →·DC →＝( )A.－9B.21C.－21D.9答案 D解析 AB →·AD →＝|AO →|2－14|BD →|2＝－7，∴14|BD →|2＝16，BC →·DC →＝|CO →|2－14|BD →|2＝25－16＝9.3.如图，BC ，DE 是半径为1的圆O 的两条直径，BF →＝2FO →，则FD →·FE →＝( )A.－34B.－89C.－14D.－49答案 B解析 ∵BF →＝2FO →，圆O 的半径为1，∴|FO →|＝13.法一 FD →·FE →＝(FO →＋OD →)·(FO →＋OE →)＝FO →2＋FO →·(OE →＋OD →)＋OD →·OE →＝⎝ ⎛⎭⎪⎫132＋0－1＝－89.法二由极化恒等式得FD →·FE →＝FO →2－14DE →2＝19－1＝－89.4.已知正方形ABCD 的面积为2，点P 在边AB 上，则PD →·PC →的最大值是( ) A.92B.2 C.32D.34 答案 B解析如图所示，取CD 的中点E ，连接PE ，由极化恒等式可得PD →·PC →＝PE →2－EC →2＝|PE →|2－12，所以当P 与A (B )重合时，|PE →|＝52最大，从而(PD →·PC →)max ＝2. 5.已知a ，b 是平面内两个互相垂直的单位向量，若c 满足(a －c )·(b －c )＝0，则|c |的最大值是( ) A.1 B.2 C.2D.22答案 C解析由极化恒等式(a －c )·(b －c )＝14[(a ＋b －2c )2－(a －b )2]，∵(a －c )·(b －c )＝0，所以(a ＋b －2c )2＝(a －b )2，故c 2＝(a ＋b )·c ，又因为|a |＝|b |＝1，a ⊥b ， ∴|a ＋b |＝2，于是|c |2≤|a ＋b ||c |＝2|c |， ∴|c |≤ 2.6.已知AB 为圆x 2＋y 2＝1的一条直径，点P 为直线x －y ＋2＝0上任意一点，则PA →·PB →的最小值为( )A.1B. 2C.2D.2 2答案 A解析如图所示，由极化恒等式易知，当OP与直线x－y＋2＝0垂直时，PA→·PB→有最小值，即PA→·PB→＝PO→2－OB→2＝(2)2－12＝1.故选A.7.已知AB是圆O的直径，AB长为2，C是圆O上异于A，B的一点，P是圆O所在平面上任意一点，则(PA→＋PB→)·PC→的最小值为( )A.－14B.－13C.－12D.－1答案 C解析∵PA→＋PB→＝2PO→，∴(PA→＋PB→)·PC→＝2PO→·PC→，取OC中点D(图略)，由极化恒等式得，PO→·PC→＝|PD→|2－14|OC→|2＝|PD→|2－14，又|PD →|2min ＝0，∴(PA →＋PB →)·PC →的最小值为－12.8.已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则PA →·(PB →＋PC →)的最小值为( ) A.－2 B.－32C.－43D.－1答案 B解析取BC 的中点D ，连接AD ，PD ，取AD 的中点E ，连接PE .由△ABC 是边长为2的等边三角形，E 为中线AD 的中点得AE ＝12AD ＝32，则PA →·(PB →＋PC →)＝2PA →·PD →＝2(|PE →|2－|EA →|2) ＝2⎣⎢⎡⎦⎥⎤|PE →|2－⎝ ⎛⎭⎪⎫322≥2×⎝⎛⎭⎪⎫0－34＝－32，当且仅当|PE →|＝0时，取等号， ∴PA →·(PB →＋PC →)的最小值为－32.9.已知正方形ABCD 的边长为1，点E 是AB 边上的动点，则DE →·DA →的值为________. 答案 1解析取AE 中点O ，设AE ＝x (0≤x ≤1)，则AO ＝12x ，∴DE →·DA →＝|DO →|2－14|AE |2＝12＋⎝ ⎛⎭⎪⎫12x 2－14x 2＝1. 10.在△ABC 中，AB ＝6，AC ＝5，A ＝120°，动点P 在以C 为圆心，2为半径的圆上，则PA →·PB →的最小值为________. 答案 16解析设AB 的中点为M ，则PA →·PB →＝PM →2－MA →2＝|PM →|2－9，所以要求PA →·PB →的最小值，只需求|PM →|的最小值，显然当点P 为线段MC 与圆的交点时，|PM →|取得最小值，最小值为|MC |－2. 在△AMC 中，由余弦定理得|MC |2＝32＋52－2×3×5×cos 120°＝49，所以|MC |＝7，所以|PM →|的最小值为5，则PA →·PB →的最小值为16.11.在Rt△ABC 中，CA ＝CB ＝2，M ，N 是斜边AB 上的两个动点，且MN ＝2，则CM →·CN →的取值范围是________. 答案 ⎣⎢⎡⎦⎥⎤32，2解析取MN 的中点为P ，由极化恒等式得 CM →·CN →＝|CP →|2－14|MN |2＝|CP →|2－12.当P 为AB 的中点时，|CP →|取最小值为2，则CM →·CN →的最小值为32；当M 与A (或N 与B )重合时，|CP →|取最大值为102，则CM →·CN →的最大值为2，所以CM →·CN →的取值范围是⎣⎢⎡⎦⎥⎤32，2.12.已知AB 为圆O 的直径，M 为圆O 的弦CD 上一动点，AB ＝8，CD ＝6，则MA →·MB →的取值范围是________. 答案 [－9，0]解析如图，取CD 的中点G ，连接OG ，MO ，CO ，得OG ⊥CD ，MA →·MB →＝|MO →|2－14|BA →|2＝|MO →|2－16，∵|OC →|≥|OM →|≥|OG →|， ∴7≤|OM →|≤4， ∴MA →·MB →∈[－9，0]. 二、创新拓展练13.若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为( ) A.2 B.3 C.6 D.8答案 C解析如图，由已知OF ＝1，取FO 中点E ，连接PE ，由极化恒等式得：OP →·FP →＝|PE →|2－14|OF →|2＝|PE →|2－14，∵当P 在椭圆右顶点时，|PE →|2有最大值，|PE →|2max＝254， ∴OP →·FP →的最大值为6.14.(多选)(2022·苏北四市调研)已知在△ABC 中，P 0是边AB 上一定点，满足P 0B ＝14AB ，且对于边AB 上任一点P ，恒有PB →·PC →≥P 0B →·P 0C →，则( ) A.PB →·PC →＝PD →2－DB →2B.存在点P ，使|PD →|<|P 0D →| C.P 0C →·AB →＝0 D.AC ＝BC 答案 AD解析如图所示，取BC 的中点D ，连接PD ，根据向量的极化恒等式，有PB →·PC →＝PD →2－DB →2，P 0B →·P 0C →＝P 0D →2－DB →2. 又PB →·PC →≥P 0B →·P 0C →，所以|PD →|≥|P 0D →|，A 正确；B 错误；故由点P 为边AB 上任意一点知：点D 到边AB 上点的距离的最小值为|DP 0→|，从而DP 0⊥AB ， ∴P 0C →·AB →≠0，C 错误；取AB 的中点E ，则由P 0B ＝14AB 知，CE ∥DP 0，故CE ⊥AB ，于是AC ＝BC ，D 正确.15.(2022·宁波模拟)AB 为⊙C ：(x －2)2＋(y －4)2＝25的一条弦，|AB |＝6，若点P 为⊙C 上一动点，则PA →·PB →的取值范围是( ) A.[0，100] B.[－12，48] C.[－9，64] D.[－8，72] 答案 D解析如图，取AB 中点为Q ，连接PQ .∴PA →＋PB →＝2PQ →，PA →－PB →＝BA →，∴PA →·PB →＝14[(PA →＋PB →)2－(PA →－PB →)2]＝14(4|PQ →|2－|BA →|2).又∵|BA →|＝6，|CQ |＝25－⎝ ⎛⎭⎪⎫622＝4，∴PA →·PB →＝|PQ →|2－9， ∵点P 为⊙C 上一动点， ∴|PQ |max ＝5＋|CQ |＝9， |PQ |min ＝5－|CQ |＝1，∴PA →·PB →的取值范围为[－8，72].16.在半径为1的扇形中，∠AOB ＝60°，C 为弧上的动点，AB 与OC 交于P ，则OP →·BP →的最小值为________. 答案－116解析取OB 的中点D ，作DE ⊥AB 于点E ，连接PD ，则OP →·BP →＝|PD →|2－|OD →|2＝|PD →|2－14，易知|PD →|∈[]|DE →|，|AD →|＝⎣⎢⎡⎦⎥⎤34，32，则OP →·BP →＝PD →2－14∈⎣⎢⎡⎦⎥⎤－116，12，故所求最小值为－116.17.如图，在平面四边形ABCD 中，AC ＝AD ＝2，∠DAC ＝120°，∠ABC ＝90°，则BD →·BC →的最大值为________.答案 1解析取CD 的中点E ，连接EA ，EB ，∵AC ＝AD ＝2，∠DAC ＝120°， ∴AE ⊥CD ，DE ＝AD sin 60°＝3，由∠ABC ＝∠AEC ＝90°，∴A ，B ，C ，E 四点共圆，且AC 为直径，则BD →·BC →＝|BE →|2－|ED →|2＝|BE →|2－(3)2≤|AC →|2－3＝22－3＝1，所以BD →·BC →的最大值为1.18.(2022·金丽衢12校联考)已知平面向量a ，b ，c ，d 满足|a |＝|b |＝2，a·b ＝0，|b ＋2c |＝2，若(d －a )·(d ＋2b )≤4，则|c ＋d |的取值范围为________. 答案 [0，10＋4]解析如图，因为|a |＝|b |＝2，a ·b ＝0，所以不妨设a ＝OA →＝(2，0)，b ＝OB →＝(0，2).设c ＝OC →，d ＝OD →.因为|b ＋2c |＝2，即⎪⎪⎪⎪⎪⎪c －⎝ ⎛⎭⎪⎫－12b ＝1，所以可知点C 在以(0，－1)为圆心，1为半径的圆上.设E (0，－4)，M 为AE 的中点，由(d －a )·(d ＋2b )＝AD →·ED →＝DM →2－AM →2＝DM →2－5≤4，可得点D 在以M (1，－2)为圆心，3为半径的圆内(包含边界)，所以|c ＋d |＝|d －(－c )|＝|OD →－OC ′→|＝|C ′D →|∈[0，10＋4].。

6专题六动词与动词词组

专题六动词与动词词组高考真题回顾1.Just as Professor Scotti often it, success is ninety-nine percent mentalattitude.（2009年安徽卷）A. getsB. makesC. putsD. means【考点】考查动词短语的辨析【解析】A项的get 得到，get it意为“懂得，了解,受罚”；B项的make做，制造，make it意为“成功，及时到达”；C项的put放，put it意为put it“表达”；D项的mean意味着，mean it意为“当真”。

分析语境可知这是在引用Scotti教授说的话，应该用动词puts, as sb puts it意为“正如某人所说的”，符合题意。

故答案选C。

【翻译】正如Scotti教授经常表述的一样，成功是99%的精神态度。

【扩展】连词as在这里引导的是方式状语从句，意为“依照，正如…”，又如：As I said earlier, this company has just started.正如我之前说过的，这个公司才刚刚成立。

【脱口而出】2.The Somali robbers’frequent attacks on the sea urged the United Nations to______all nations to take immediate action.（2009年福建卷）A. fight forB. apply forC. call onD. wait on【考点】考查动词短语的辨析【解析】fight for 意为“与……做斗争；为……而战”；apply for 意为“申请”；call on 意为“拜访（人）；号召”；wait for 意为“等待，伺候，服伺”。

经分析可知，只有选项C 符合句意。

【翻译】索马里海盗在海上频繁的抢劫促使联合国号召所有国家立即采取行动。

2020高考英语阅读理解解题技巧专项突破六：阅读理解专题之细节理解题(含答案)

专题 6 阅读理解专题之----细节理解题细节理解题的考查内容主要涉及时间、地点、人物、事件、原因、结果、数字、图表等例证细节和定义类细节。

这类题目的共同特点是：答案一般都能在文章中找到。

当然，答案并不一定是文章中的原句，考生需要根据文章提供的信息自己组织语句回答问题。

【设问形式】1.事实细节题：分为直接理解题和间接理解题，前者常用who, what, which, when, where, why和how提问，或判断正误，即是非判断题。

后者需与原文信息转换，表达上与原文有差异。

常见设问形式有：1) What can we learn from the passage?2) All the following are mentioned except3) Which of the following is mentioned (not mentioned)?4) Which of the following statements is true/right/false/wrong about…?2. 排列顺序题:常出现在记叙文和说明文中，一般按事件发生的顺序。

常见设问形式有：1)Wh ich of the following is the correct order of…?2）Which of the following shows the path of signals described in Paragraph…?3. 图文匹配题：设题形式：给出图表，根据图表提问问题。

4. 数字计算题：可直接找到相关细节，但需经过计算方可找到答案。

【考查方式】阅读理解细节理解题的出题形式主要有：是非判断题，同义近义（反义）转换题，例证题，定义题，年代与数字题，比较题，原因题，条件题，排序题，图表图画题等。

细节理解题需要将题目与原文进行语境上的转换，两者存在表达上的差异，需要进行加工或整理后才能得出结论，属于中档难度题。

2021年中考物理复习专题讲6-质量和密度

重难点剖析
重难点1 密度的理解及相关计算
类型一密度公式的相关计算
1.盒装牛奶，盒上“250 mL”字样。已知该牛奶的密度是1.2×103 kg/m3，
若喝掉一半后，剩余牛奶的密度是 g/cm3，剩余牛奶的质量是 kg。若宇
航员将整盒牛奶带到月球上，则1这.2盒牛奶的质量将
(选填“0.变15大”“变小”
看：使用前观察它的和。
冰的砝密度码是0，. 移动游码，使天平平衡；⑥正确读出砝码和游码的示数。正确的操作顺序是
读：读数时，视线与液体凸液面的顶部或凹液面的底部。
(
B
)
千克每立方米，符号： kg/m3
A．①②③④⑤⑥ 烧杯和烧杯中剩余液体
考点1：质量和密度的概念及应用
B．②①④③⑤⑥
考点2：质量和密度的测量
体，其密度与质量成正比
2×103 kg/m3，若喝掉一半后，剩余牛奶的密度是 g/cm3，剩余牛奶的质量是 kg。
放8×：10使3 k用g/时m3把B。量．筒放“在水铁平台杵上。磨成针”时铁的密度发生了变化
(4)性质：密度是物质的一种特性，与物质的质量和体积大小。
C．冰的密度是0.9×10 kg/m ，表明1 m 冰的质量是0.9×10 5×103 kg/m3 C．若a、b的体积相等，则a的质量小 D．a、3b的密度与它们3的质量、体积有关 3
真题精讲
考点2：质量和密度的测量
7．(2020·咸宁)用天平测小石块质量的实验中，有如下实验计划：
两个实心物体a、b的体积与质量的关系如图所示。
8下×列10说3 k法g/正m3确①。的是将( )游A．码a的密移度是至b的标密度尺的2倍左B．端a的的密度“是00.”刻度线处；②将托盘天平放置在水平工作台面上； ③

中考物理知识与专题训练6 质量与密度(含答案)

储备2020年中考物理知识库专题训练 6 质量与密度知识点1：质量1.定义：物体所含__物质的多少__叫质量，通常用字母__m __表示。

2.单位：基本单位是千克，符号是kg ，常用单位有t 、g 、mg ；换算关系： 1 t ＝__103__kg ＝__106__g ＝__109__mg 。

3.测量工具：生活常用案秤、台秤、杆秤等；实验室常用天平。

知识点2：质量的测量——天平的使用1.使用：看、放、移、调、称、读。

2.注意事项：①天平测量物体的质量时不能超出天平的称量；也不能小于天平的分度值；②砝码要用__镊子__夹取，轻拿轻放；③调节好的天平不要随意更换位置或交换托盘，否则要重新调节。

3.特殊测量：①测量轻小物体的质量时，可测出多个同样物体的质量，再求出这个物体的质量，这种方法叫“__累积法__”；②测量粉末状物体的质量时，可以在天平两盘各垫一张大小适中的相同纸片，再进行称量；③液体和潮湿的物体不能直接倒入天平盘中称量，应将它们装入容器中，再进行称量。

知识点3：密度1.定义：在物理学中，某种物质组成的物体的质量与它的体积之比叫做这种物质的密度2.单位：（1）基本单位：千克每立方米，符号是kg/m 3（2）常用单位：g/cm 3 （3）换算关系：1 g/cm 3＝__103__kg/m 33.密度与温度：温度能够改变物质的密度，常见物质受温度影响的一般规律是_热胀冷缩，一般__气体__受温度影响最大，__固体__受温度影响最小4.密度的应用：①鉴别物质；②判断实心、空心【提示】运用公式ρ＝m V及其变形式进行计算应注意：(1)公式中物理量应针对同一物体。

(2)统一公式中物理量的单位。

(3)当题中涉及几种物质时，每个物理量应采用“角标”的方式加以区分。

知识点4：体积与密度的测量1．体积的测量：2.密度的测量：（1）实验原理__ρ＝m V__（2）测量工具天平、量筒【提示】(1)测量固体的密度时，必须先测量固体的质量，然后再测量固体的体积，这样就不会因为物体表面有液体残留，造成所测质量偏大，所测密度偏大。

中考数学复习专题 6动点综合问题(含中考真题解析)学生版

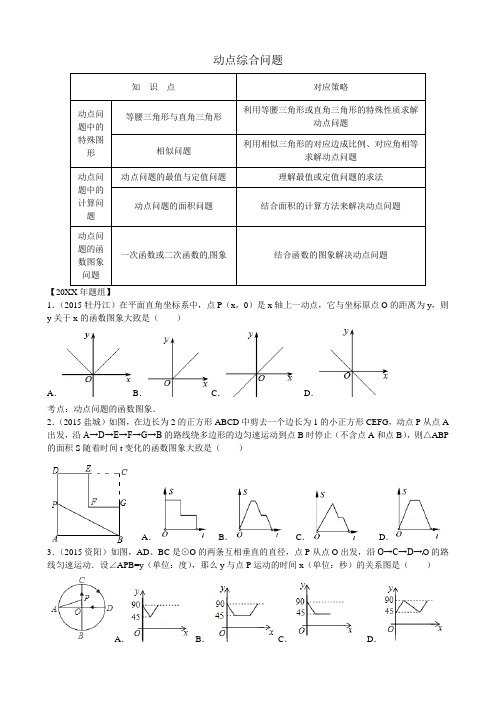
动点综合问题知识点对应策略动点问题中的特殊图形等腰三角形与直角三角形利用等腰三角形或直角三角形的特殊性质求解动点问题相似问题利用相似三角形的对应边成比例、对应角相等求解动点问题动点问题中的计算问题动点问题的最值与定值问题理解最值或定值问题的求法动点问题的面积问题结合面积的计算方法来解决动点问题动点问题的函数图象问题一次函数或二次函数的图象结合函数的图象解决动点问题【20XX年题组】1．（2015牡丹江）在平面直角坐标系中，点P（x，0）是x轴上一动点，它与坐标原点O的距离为y，则y关于x的函数图象大致是（）A．B．C．D．考点：动点问题的函数图象．2．（2015盐城）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A 出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP 的面积S随着时间t变化的函数图象大致是（）A．B．C．D．3．（2015资阳）如图，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动．设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是（）A．B．C．D．4．（2015广元）如图，矩形ABCD中，AB=3，BC=4，点P从A点出发．按A→B→C的方向在AB和BC上移动．记PA=x，点D到直线PA的距离为y，则y关于x的函数大致图象是（）A ．B ．C ．D ．5．（2015荆州）如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD ﹣DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（）A B C D6．（2015邵阳）如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t的函数关系的图象是（）A B ．C ．D ．7．（2015河池）我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：43y kx=+与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（）A．6 B．8 C．10 D．128．（2015乐山）如图，已知直线334y x=-与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB．则△PAB面积的最大值是（）A．8 B．12 C．212D．1729．（2015庆阳）如图，定点A（﹣2，0），动点B在直线y x=上运动，当线段AB最短时，点B的坐标为．10．（2015三明）如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是______ ．11．（2015凉山州）菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P 是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．12．（2015咸宁）如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂．其足为G，连结CG．下列说法：①AG＞GE；②AE=BF；③点G运动的路径长为π；④CG的最小值为51中正确的说法是．（把你认为正确的说法的序号都填上）13．（2015江西省）如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为．14．（2015鄂尔多斯）如图，甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行．若甲的速度是乙的速度的3倍，则它们第2015次相遇在边上．15．（2015柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．（1）从运动开始，当t取何值时，PQ∥CD？（2）从运动开始，当t取何值时，△PQC为直角三角形？16．（2015宿迁）已知：⊙O上两个定点A，B和两个动点C，D，AC与BD交于点E．（1）如图1，求证：EA•EC=EB•ED；（2）如图2，若»»=AB BC，AD是⊙O的直径，求证：AD•AC=2BD•BC；（3）如图3，若AC⊥BD，点O到AD的距离为2，求BC的长．17．（2015攀枝花）如图1，矩形ABCD的两条边在坐标轴上，点D与坐标原点O重合，且AD=8，AB=6．如图2，矩形ABCD沿OB方向以每秒1个单位长度的速度运动，同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动，当点P到达点C时，矩形ABCD和点P同时停止运动，设点P的运动时间为t秒．（1）当t=5时，请直接写出点D、点P的坐标；（2）当点P在线段AB或线段BC上运动时，求出△PBD的面积S关于t的函数关系式，并写出相应t的取值范围；（3）点P在线段AB或线段BC上运动时，作PE⊥x轴，垂足为点E，当△PEO与△BCD相似时，求出相应的t值．18．（2015桂林）如图，已知抛物线212y x bx c=-++与坐标轴分别交于点A（0，8）、B（8，0）和点E，动点C从原点O开始沿OA方向以每秒1个单位长度移动，动点D从点B开始沿BO方向以每秒1个单位长度移动，动点C、D同时出发，当动点D到达原点O时，点C、D停止运动．（1）直接写出抛物线的解析式：；（2）求△CED的面积S与D点运动时间t的函数解析式；当t为何值时，△CED的面积最大？最大面积是多少？（3）当△CED的面积最大时，在抛物线上是否存在点P（点E除外），使△PCD的面积等于△CED的最大面积？若存在，求出P点的坐标；若不存在，请说明理由．19．（2015淮安）如图，在Rt△ABC中，∠ACB＝900，AC=6，BC=8．动点M从点A出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动．过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒．（1）当t＝秒时，动点M、N相遇；（2）设△PMN的面积为S，求S与t之间的函数关系式；（3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由．【20XX年题组】1．（20XX年甘肃天水）如图，扇形OAB动点P从点A出发，沿»AB线段BO、OA匀速运动到点A，则OP的长度y与运动时间t之间的函数图象大致是（）A B C．D．2．（20XX年贵州安顺）如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为（）A．2B．1C．2D．223．（20XX年安徽省）如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（）A B C D4．（20XX年江苏苏州）如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A 重合），过点P作PB⊥l，垂足为B，连接PA．设PA＝x，PB＝y，则（x－y）的最大值是．5．（20XX年四川资阳）如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，则△BEQ周长的最小值为__________6．（20XX年浙江嘉兴中考）如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．下列结论：①CE=CF；②线段EF的最小值为23；③当AD=2时，EF与半圆相切；④若点F恰好落在BC上，则AD=25；⑤当点D从点A运动到点B时，线段EF扫过的面积是163．其中正确结论的序号是．7．（20XX年湖南衡阳）如图，直线AB与x轴相交于点()40A-，，与y轴相交于点()03B，，点P从点A出发，以每秒个单位长度的速度沿直线AB向点B移动．同时，将直线34y x=以每秒0.6个单位长度的速度向上平移，交OA于点C，交OB于点D，设运动时间为()05t t<<秒．⑴证明：在运动过程中，四边形ACDP总是平行四边形；⑵当t取何值时，四边形ACDP为菱形？请指出此时以点D为圆心、OD长为半径的圆与直线AB的位置关系并说明理．8．（20XX年浙江温州）如图，在平面直角坐标系中，点A，B的坐标分别是（-3，0），（0，6），动点P 从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP ，CO 为邻边构造□PCOD ，在线段OP 延长线上取点E ，使PE=AO ，设点P 运动的时间为t 秒．（1）当点C 运动到线段OB 的中点时，求t 的值及点E 的坐标；（2）当点C 在线段OB 上时，求证：四边形ADEC 为平行四边形；（3）在线段PE 上取点F ，使PF=1，过点F 作MN ⊥PE ，截取FM=2，FN=1，且点M ，N 分别在第一、四象限，在运动过程中，设□PCOD 的面积为S ．①当点M ，N 中，有一点落在四边形ADEC 的边上时，求出所有满足条件的t 的值；②若点M ，N 中恰好只有一个点落在四边形ADEC 内部（不包括边界）时，直接写出S 的取值范围．基础知识归纳：等腰三角形的两腰相等，直角三角形的两直角边的平方和等于斜边的平方，平行四边形的对边平行且相等，矩形的对角线相等，菱形的对角线互相垂直基本方法归纳：动点问题常与等腰三角形、直角三角形、平行四边形、矩形、菱形等特殊图形相结合，解决此类问题要灵活运用这些图形的特殊性质注意问题归纳：注意区分等腰三角形、直角三角形、平行四边形、矩形、菱形的性质．【例1】如图，在Rt △ABC 中，∠ACB=90º，AC=3cm ，BC=4cm ．动点P 从点B 出发，以每秒1cm 的速度沿射线BA 运动，求出点P 运动所有的时间t ，使得△PBC 为等腰三角形．归纳 2：动点问题中的计算问题基础知识归纳：动点问题的计算常常涉及到线段和的最小值、三角形周长的最小值、面积的最大值、线段或面积的定值等问题．基本方法归纳：线段和的最小值通常利用轴对称的性质来解答，面积采用割补法或面积公式，通常与二次函数、相似等内容．注意问题归纳：在计算动点问题的过程中，要注意与相似、锐角三角函数、对称、二次函数等内容的结合．【例2】如图，在Rt △ABC 中，∠ACB=90°，AC=6，BC=8，AD 是∠BAC 的平分线．若P ，Q 分别是AD 和AC 上的动点，则PC+PQ 的最小值是（）A ．125B ．4C ．245 D ．5归纳 3：动点问题的图象基础知识归纳：动点问题经常与一次函数、反比例函数和二次函数的图象相结合．BAC基本方法归纳：一次函数的图象是一条直线，反比例函数的图象是双曲线，二次函数的图象是抛物线．注意问题归纳：动点函数的图象问题可以借助于相似、特殊图形的性质求出函数的图象解析式，同时也可以观察图象的变化趋势．【例3】如图，在矩形ABCD中，AB=2，点E在边AD上，∠ABE=45°，BE=DE，连接BD，点P在线段DE上，过点P作PQ∥BD交BE于点Q，连接QD．设PD=x，△PQD的面积为y，则能表示y与x函数关系的图象大致是（）模拟1．如图1，在平行四边形ABCD中，点P从起点B出发，沿BC，CD逆时针方向向终点D匀速运动．设点P所走过的路程为x，则线段AP，AD与平行四边形的边所围成的图形面积为y，表示y与x的函数关系的图象大致如图2，则AB边上的高是（）A．3 B．4 C．5 D．62．在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M，N，直线m运动的时间为t（秒）．设△OMN的面积为S，那么能反映S与t之间函数关系的大致图象是（）A．B．C．D．3．如图，平面直角坐标系中，在边长为1的正方形ABCD的边上有一动点P沿A—B—C—D—A运动一周，则P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（）4．某景点有一座圆形的建筑，如图，小江从点A沿AO匀速直达建筑中心点O处，停留拍照后，从点O沿OB以同样的速度匀速走到点B，紧接着沿¼BCA回到点A，下面可以近似地刻画小江与中心点O的距离S随时间t变化的图象是（）．5．如图在Rt△ABC中，∠ACB=90°，∠BAC=30°，AB=2，D是AB边上的一个动点（不与点A、B重合），过点D作CD的垂线交射线CA于点E．设AD=x，CE=y，则下列图象中，能表示y与x的函数关系图象大致是（）A B C D ．【6．如图，在矩形ABCD中，AB=4cm，AD=23cm，E为CD边上的中点，点P从点A沿折线AE﹣EC运动到点C时停止，点Q从点A沿折线AB﹣BC运动到点C时停止，它们运动的速度都是1cm/s．如果点P，Q同时开始运动，设运动时间为t（s），△APQ的面积为y（cm2），则y与t的函数关系的图象可能是（）A B C D．7．已知点M，N的坐标分别为（0，1），（0，-1），点P是抛物线y=14x2上的一个动点．（1）求证：以点P为圆心，PM为半径的圆与直线y=-1的相切；（2）设直线PM与抛物线y=14x2的另一个交点为点Q，连接NP，NQ，求证：∠PNM=∠QNM．8．如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm 的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．（1）若△BPQ与△ABC相似，求t的值；（2）连接AQ、CP，若AQ⊥CP，求t的值．【答案】（1）t=1或3241时，△BPQ∽△BCA；（2）t=78．9．如图，在平面直角坐标系中，点A（5，0），B（3，2），点C在线段OA上，BC=BA，点Q是线段BC上一个动点，点P的坐标是（0，3），直线PQ的解析式为y=kx+b（k≠0），且与x轴交于点D．（1）求点C的坐标及b的值；（2）求k的取值范围；（3）当k为取值范围内的最大整数时，过点B作BE∥x轴，交PQ于点E，若抛物线y=ax2﹣5ax（a≠0）的顶点在四边形ABED的内部，求a的取值范围．10．如图，抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．（1）求A、B、C的坐标；（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若2，求点F的坐标．11．如图，在四边形ABCD中，AB⊥BC，CD⊥BC，AB=2，BC=CD=4，AC、BD交于点O，在线段BC 上，动点M以每秒1个单位长度的速度从点C出发向点B做匀速运动，同时动点N从点B出发向点C做匀速运动，当点M、N其中一点停止运动时，另一点也停止运动，分别过点M、N做BC的垂线，分别交AC、BD于点E、F，连接EF．若运动时间为x秒，在运动过程中四边形EMNF总为矩形（点M、N重合除外）．（1）求点N的运动速度；（2）当x为多少时，矩形EMNF为正方形？（3）当x为多少时，矩形EMNF的面积S最大？并求出最大值．12．如图，直线y=-12x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B，C和点A（-1，0）．（1）求B，C两点坐标；（2）求该二次函数的关系式；（3）若抛物线的对称轴与x轴的交点为点D，点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标；（4）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P 点的坐标；如果不存在，请说明问题．13．如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E．（1）求证：PA=PE；（2）若将（1）中的正方形变为矩形，其余条件不变（如图2），且AD=10，DC=8，求AP：PE；（3）在（2）的条件下，当P滑动到BD的延长线上时（如图3），请你直接写出AP：PE的比值．14．如图，抛物线y=12x2+mx+n与直线y=-12x+3交于A，B两点，交x轴与D，C两点，连接AC，BC，已知A（0，3），C（3，0）．（Ⅰ）求抛物线的解析式和tan∠BAC的值；（Ⅱ）在（Ⅰ）条件下：（1）P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ACB相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．（2）设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE以每秒一个单位速度运动到E点，再沿线段EA2A后停止，当点E的坐标是多少时，点M 在整个运动中用时最少？15．已知：如图①，在Rt△ACB中，∠C=90°，AC=4cm，BC=3cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜2），解答下列问题：（1）当t为何值时，PQ∥BC；（2）设△AQP的面积为y（cm2），求y与t之间的函数关系式；（3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；（4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．16．如图，在平面直角坐标系中，以A（3，0）为圆心，以5为半径的圆与x轴相交于B、C，与y轴的负半轴相交于D．（1）若抛物线y=ax2+bx+c经过B、C、D三点，求此抛物线的解析式，并写出抛物线与圆A的另一个交点E的坐标；（2）若动直线MN（MN∥x轴）从点D开始，以每秒1个长度单位的速度沿y轴的正方向移动，且与线段CD、y轴分别交于M、N两点，动点P同时从点C出发，在线段OC上以每秒2个长度单位的速度向原点O运动，连接PM，设运动时间为t秒，当t为何值时，MN OPMN OPg的值最大，并求出最大值；（3）在（2）的条件下，若以P、C、M为顶点的三角形与△OCD相似，求实数t的值．17．如图①，四边形ABCD中，AD∥BC，DC⊥BC，AD=6cm，DC=8cm，BC=12cm．动点M在CB上运动，从C点出发到B点，速度每秒2cm；动点N在BA上运动，从B点出发到A点，速度每秒1cm．两个动点同时出发，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t（秒）．（1）求线段AB的长．（2）当t为何值时，MN∥CD？（3）设三角形DMN的面积为S，求S与t之间的函数关系式．（4）如图②，连接BD，是否存在某一时刻t，使MN与BD互相垂直？若存在，求出这时的t值；若不存在，请说明理由．。

高一数学复习知识点讲解专题训练6---充分条件与必要条件

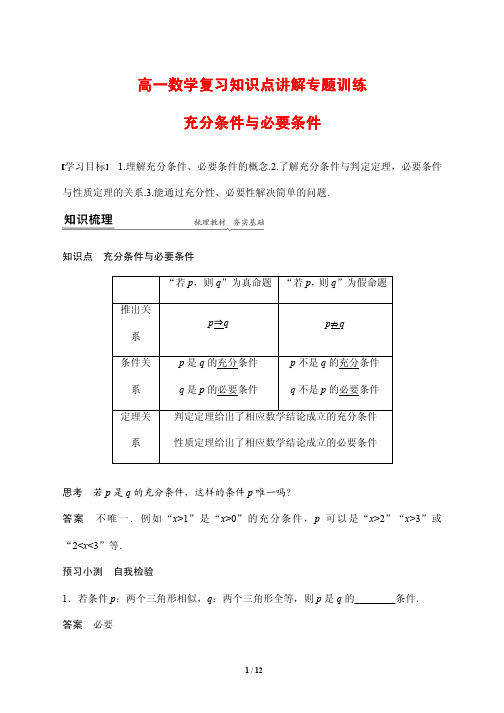
A．p：ab≠0，q：a≠0 B．p：a2＋b2≥0，q：a≥0 且 b≥0 C．p：x2>1，q：x>1 D．p：a>b，q： a> b 答案 A 解析根据充分条件的概念逐一判断． 3．“同位角相等”是“两直线平行”的( ) A．充分条件 B．必要条件 C．既是充分条件，也是必要条件 D．既不充分又不必要条件答案 C 4．若“x>1”是“x>a”的充分条件，则 a 的取值范围是________．答案 a≤1 解析因为 x>1⇒x>a，所以 a≤1. 5．“x2＝2x”是“x＝0”的________条件，“x＝0”是“x2＝2x”的________条件(用 “充分”“必要”填空)．答案必要充分解析由于 x＝0⇒x2＝2x，所以“x2＝2x”是“x＝0”的必要条件，“x＝0”是“x2＝ 2x”的充分条件．
3 / 12
(2)p：(x＋1)(x－2)＝0，q：x＋1＝0. 解 (1)由于 q⇒p，故 p 是 q 的必要条件，q 是 p 的充分条件． (2)由于 q⇒p，故 p 是 q 的必要条件，q 是 p 的充分条件．
三、充分ห้องสมุดไป่ตู้件与必要条件的应用
例 3 已知 p：实数 x 满足 3a<x<a，其中 a<0；q：实数 x 满足－2≤x≤3.若 p 是 q 的充
1．若 p 是 q 的充分条件，则 q 是 p 的( ) A．充分条件 B．必要条件 C．既不是充分条件也不是必要条件 D．既是充分条件又是必要条件答案 B 解析因为 p 是 q 的充分条件，所以 p⇒q，所以 q 是 p 的必要条件． 2．下列命题中，p 是 q 的充分条件的是( )
5 / 12
答案 A
解析 B 项中，x2＝1⇒x＝1 或 x＝－1；C 项中，当 x＝y<0 时， x， y无意义；D 项中，当 x<y<0⇒x2>y2，所以 B，C，D 中 p 不是 q 的充分条件．

高考英语复习语法知识专题讲解6---并列连词(解析版)

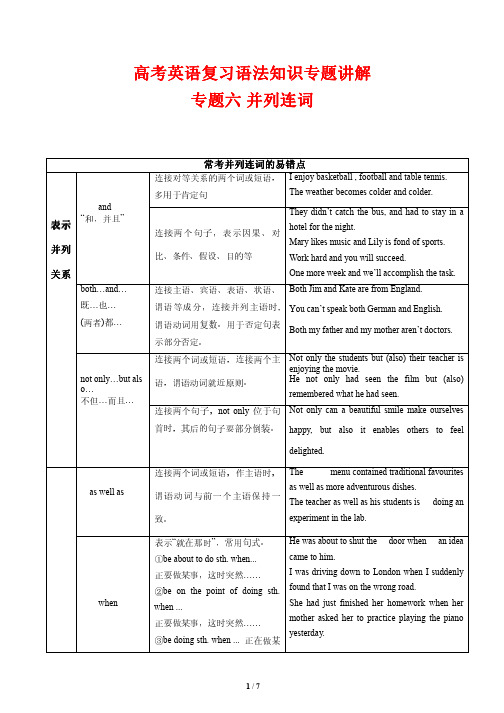
语，谓语动词就近原则。连接两个句子，not only 位于句
enjoying the movie. He not only had seen the film but (also)
remembered what he had seen.
Not only can a beautiful smile make ourselves
连接两个词或短语，连接并列主 Either you or I am right.
语时,谓语动词就近原则
Does either she or they like English?
2/7
either…or…
或者...或者...
neither...nor...
既不...也不...
由 either…or…引导的否定句是完全否定连接两个句子时，若
谓语动词用复数。用于否定句表
示部分否定。
Both my father and my mother aren’t doctors.
连接两个词或短语，连接两个主 Not only the students but (also) their teacher is
not only…but als
o不…但…而且…
traditional style.
Tom got up early, yet he failed to catch the train.
—Peter, please send us postcards so we’ll know where you have visited.
—No problem. Although history can’t be changed, yet lessons can be learned to face the future. Your composition is fairly good, however, there is still some room for improvement.

新高考数学复习考点知识与题型专题练习6---等式性质与不等式性质(解析版)

新高考数学复习考点知识与题型专题练习6 等式性质与不等式性质一、选择题：本题共8小题，在每小题给出的四个选项中，只有一项是符合题目要求的 1．在开山工程爆破时，已知导火索燃烧的速度是每秒0.5 cm ，人跑开的速度为每秒4 m ，为了使点燃导火索的人能够在爆破时跑到100 m 以外的安全区，导火索的长度x （cm ）应满足的不等式为（）A ．41000.5x ⨯≥ B ．41000.5x ⨯≤ C ．41000.5x ⨯> D ．41000.5x ⨯< 【答案】C 【解析】导火索燃烧的时间0.5x 秒，人在此时间内跑的路程为40.5x ⨯m ．由题意可得41000.5x ⨯>．故选：C.2．下列运用等式的性质，变形不正确的是（）A ．若x =y ，则x +5=y +5B ．若a =b ，则ac =bcC ．若a b c c=，则a =b D ．若x =y ，则x y a a = 【答案】D【解析】对于选项A ，由等式的性质知，若x =y ，则x +5=y +5，A 正确；对于选项B ，由等式的性质知，若a =b ，则ac =bc ，B 正确；对于选项C ，由等式的性质知，若a b c c=，则a =b ，C 正确；对于选项D ，由等式的性质知，若x =y ，则x y a a =的前提条件为a ≠0，D 错误．故选：D3．不等式a 2＋1≥2a 中等号成立的条件是（）A ．a ＝±1B ．a ＝1C ．a ＝－1D ．a ＝0【答案】B【解析】a 2＋1－2a ＝(a －1)2≥0，∴ a ＝1时，等号成立．故选：B.4．如图，在一个面积为200 m 2的矩形地基上建造一个仓库，四周是绿地，仓库的长a 大于宽b 的4倍，则表示上述的不等关系正确的是（）A ．4a b >B ．()(4200)4a b ++=C ．4(4)(4)200a b a b >⎧⎨++=⎩D ．44200a b ab >⎧⎨=⎩【答案】C 【解析】解：由题意知4a b >，根据面积公式可以得到()(4200)4a b ++=.故选:C ．5．若a ，b ，R c ∈，a b >，则下列不等式恒成立的是（）A ．11a b C ．a c b c >D ．2211a b c c >++ 【答案】D【解析】解：对于A ，若0a b >>，则11a b>，故A 错误；对于B ，取1a =，2b =-，则22a b <，故B 错误．对于C ，若0c 时，||||a c b c =，故C 错误；对于D ，因为211c +>，所以2101c >+，又a b >，所以2211a b c c >++，故D 正确；故选：D ．6．设A ＝12x x ++，B ＝34x x ++，则A 与B 的大小关系是（） A ．A <BB ．A >BC ．仅有x >0时，A <BD ．以上结论都不成立【答案】D【解析】A －B ＝12x x ++－34x x ++＝()()224x x -++，令A －B <0，得x <－4或x >－2，令A －B >0，得－4<x <－2，所以A ，B 的大小不确定．故选：D7．若0a b <<，则下列不等式错误的是（）.A ．11a b> B ．11a b a >- C ．||||a b >D ．22a b >【答案】B【解析】解：对A ，0a b <<，11a b ∴>，故A 正确；对B ，0a b <<，0b ∴->，即0a a b <-<，11a a b∴>-，故B 错误；对C ，0a b <<，0a b ∴->->，即||||a b ->-，即||||a b >，故C 正确，对D ，0a b <<，0a b ∴->->，即22()()a b ->-，即22a b >，故D 正确.故选：B.8．若a ，b ，c ∈R ，且a >b ，则下列不等式一定成立的是（）A ．a ＋c ≥b －cB ．ac >bcC ．2c a b- >0 D ．(a －b )c 2≥0 【答案】D【解析】解：由a ，b ，R c ∈，且a b >，可取2a =，1b =，3c =-，可得a b b c +<-，故A 错误；由0c ，可得22ac bc =，故B 错误；由0c ，2a =，1b =，可得20c a b=-，故C 错误；由a b >，可得0a b ->，20c ，即有2()0a b c -，故D 正确．故选：D ．二、选择题：本题共4小题，在每小题给出的选项中，有多项符合题目要求．9．设01b a <<<，则下列不等式不成立的是（）A ．ab =，所以A 错误，对于B ，取11,49a b ==1123=>=，所以B 错误，对于C ，因为01b a <<<，所以10ab>，所以11b a ab ab ⋅<⋅，即11a b <，因为01a <<，所以1101a a a <⋅<⨯，即11a <，综上111a b<<，所以C 正确，对于D ，取11,23a b ==，则21164ab a =<=，所以D 错误，故选：ABD 10．下列说法中正确的是（）A ．若a >b ，则2211a b c c >++ B ．若-2<a <3，1b >0，m >0，则m m a b< D ．若a >b ，c >d ，则ac >bd【答案】AC【解析】对于A ，因c 2+1>0，于是有211c +>0，而a >b ，由不等式性质得2211a b c c >++，A 正确；对于B ，因为1b >0，所以11a b <，又因为m >0，所以m m a b<，C 正确；对于D ，12->-且23->-，而(1)(2)(2)(3)-⋅-<--，即ac >bd 不一定成立，D 错误.故选：AC11．已知,,a b c ∈R ，若a b c >>，且230a b c ++=，则下列不等关系正确的是（）A ．ac bc C ．c c a c b c >--D ．()2a bc a b c +>+【答案】ACD【解析】230a b c ++=，a b c >>，0c ∴<，0a >，对于A ，a b >，0c <，ac bc ∴<，A 正确；对于B ，当0b =时，满足a b c >>，此时0a b c b ==，B 错误；对于C ，a b c >>，0a c b c ∴->->，11a c b c ∴<--，又0c <，c c a c b c∴>--，C 正确；对于D ，a b >，0a b ∴->，()()a a b c a b ∴->-，即2a ab ac bc ->-，整理可得：()2a bc ac ab a b c +>+=+，D 正确.故选：ACD.12．若110a b<<，则下列结论中正确的是（） A ．a 2|a ＋b | 【答案】ABC 【解析】解：因为110a b<<，所以b <a <0，所以b 2>a 2，ab 、<、=）【答案】>【解析】11221221(+)a b a b a b a b +-112221(-)+=(-)a b b a b b1212=(-)(-)b b a a ，∵1212a a b b <<，，∴1212--00b b a a <<，，即1212(-)()0-b b a a >，∴11221221++a b a b a b a b >．故答案为：>14．已知24a <<，35b <<，那么2M a b =+的取值范围是________. 【答案】{}713M M <<【解析】由已知可得428a <<，又因为35b <<，所以，7213a b <+<.因此，2M a b =+的取值范围是{}713M M <<. 故答案为：{}713M M <<.15．咖啡馆配制两种饮料，甲种饮料用奶粉、咖啡、糖分别为9g ，4g ，3g ，乙种饮料用奶粉、咖啡、糖分别为4g ，5g ，5g ．已知每天使用原料分别为奶粉3600g 、咖啡2000g 、糖3000g ，设每天配制甲种饮料x 杯，乙种饮料y 杯，则满足上述所有不等关系的不等式组为________________．【答案】943600452000353000x y x y x y x N y N +≤⎧⎪+≤⎪⎪+≤⎨⎪∈⎪∈⎪⎩，，，，【解析】设每天配制甲种饮料x 杯，乙种饮料y 杯，其中每天使用原料分别为奶粉3600g 、咖啡2000g 、糖3000g ，可得所有不等关系的不等式组为943600452000353000x y x y x y x N y N +≤⎧⎪+≤⎪⎪+≤⎨⎪∈⎪∈⎪⎩. 故答案为：943600452000353000x y x y x y x N y N +≤⎧⎪+≤⎪⎪+≤⎨⎪∈⎪∈⎪⎩. 16．给出下列命题：①a >b ⇒ac 2>bc 2；②a >|b |⇒a 2>b 2；③a >b ⇒a 3>b 3；④|a |>b ⇒a 2>b 2.其中正确命题的序号是___________.【答案】②③【解析】①当c 2=0时不成立；②因为0a b >≥，所以22a b >，即22a b >，所以②一定成立；③当a >b 时，3322()()a b a b a ab b -=-++223()24b a b a b ⎡⎤⎛⎫=-⋅++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦>0成立； ④当b <0时，不一定成立.如：|2|>-3，但22<（-3）2.故答案为：②③.四、解答题：本题共6小题．解答应写出文字说明、证明过程或演算步骤．17．比较大小.（1）比较221x y ++与()21x y +-的大小；（2）0a b >>，0m >，比较a b 与a m b m++的大小. 【答案】（1）()22121x y x y ++>+-；（2）a a m b b m+>+. 【解析】（1）因为()()()()2222211111x y x y x y ++-=-+--++，又()()2210,10x y -≥-≥，所以()()222101x y x y +--++>，所以()22121x y x y ++>+-；（2）因为()()()()ab am ab bm a b m a m b m b b m b b b m a +-+-+==+-++，又0a b >>，0m >，所以()()0a b m a m b m b b m a b --+=>++，所以a a m b b m+>+. 18．设a b c >>，求证：222222bc ca ab b c c a a b ++<++．【答案】证明见解析【解析】()()()()()()()()()()22222222220.bc ca ab b c c a a bb c a b a c ac a c b a c c a b c a ac c a c a c b b a ++---=-+-+-=+-----=---<19．已知a >b >0，c <d <0，比较b ac -与a bd -的大小．【答案】a b b d a c >--. 【解析】∵c <d <0，∴－c >－d >0．又a >b >0，∴a －c >b －d >0， ∴110b d a c>>--，又a >b >0，∴a b b d a c>--. 20．某市政府准备投资1800万元兴办一所中学．经调查，班级数量以20至30个为宜，每个初高中班硬件配置分别为28万元与58万元，该学校的规模(初高中班级数量)所满足的条件是什么？【答案】203028581800x y x y ≤+≤⎧⎨+≤⎩，．【解析】设该校有初中班x 个，高中班y 个，则有203028581800x y x y ≤+≤⎧⎨+≤⎩，． 21．（1）若bc －ad ≥0，bd >0，求证：a b b +≤c d d+；（2）已知a >b >c ，求证：a 2b ＋b 2c ＋c 2a >ab 2＋bc 2＋ca 2．【答案】（1）证明见解析；（2）证明见解析．【解析】证明（1）∵bc －ad ≥0，bd >0，∴bc ≥ad ，1bd>0， ∴c d ≥a b ，∴c d＋1≥a b ＋1，即c d d +≥a b b +，即a b b +≤c d d +．（2）a 2b ＋b 2c ＋c 2a －(ab 2＋bc 2＋ca 2)＝(a 2b －bc 2)＋(b 2c －ab 2)＋(c 2a －ca 2)＝b (a 2－c 2)＋b 2(c －a )＋ca (c －a )＝(c －a )(b 2＋ca －ba －bc )＝(c －a )(c －b )(a －b )．∵a >b >c ，∴c －a <0，c －b <0，a －b >0，∴(c －a )(c －b )(a －b )>0，即a 2b ＋b 2c ＋c 2a －(ab 2＋bc 2＋ca 2)>0， ∴a 2b ＋b 2c ＋c 2a >ab 2＋bc 2＋ca 2．22．（1）已知a ，b 均为正实数．试比较33+a b 与22a b ab +的大小；（2）已知1a ≠且a R ∈，试比较11a-与1a +的大小．【答案】（1）3322a b a b ab ++，（2）当0a =时，111a a =+-；当1a <且0a ≠时，111a a >+-；当1a >时，111a a <+-．【解析】（1）a ，b 均为正实数，332222222()()()()()()0a b a b ab a a b b a b a b a b a b a b ∴+--=---=--=-+，即3322a b a b ab ++，（2）21(1)11a a a a-+=--． ①当0a =时，201a a=-，∴111a a =+-． ②当1a <且0a ≠时，201a a>-，∴111a a >+-． ③当1a >时，201a a<-，∴111a a <+-．综上所述，当0a =时，111a a=+-；当1a <且0a ≠时，111a a>+-；当1a >时，111a a<+-．。

(新高考)高考二轮精品专题六三角函数与解三角形教师版

1．高考对三角函数的考查主要在于三角函数的定义、图象和性质、三角恒等变换，主要考查三角函数图象的变换、三角函数的性质（单调性、奇偶性、周期性、对称性及最值），三角恒等变换通常还与解三角交汇命题．2．解三角形的考查主要在具体面积、角的大小、面积与周长的最值或范围的考查，本部分要求对三角恒等变换公式熟悉．一、三角函数1．公式（1）扇形的弧长和面积公式如果半径为r 的圆的圆心角α所对的弧的长为l ，那么角α的弧度数的绝对值是l rα=．相关公式：①l =|α|r②21122S lr r α==（2）诱导公式：正弦余弦正切α+k ⋅2πsin αcos αtan αα+π―sin α―cos αtan α―α―sin αcos α―tan απ―αsin α―cos α―tan α2πα+cos α―sin α2πα-cos αsin α32πα+―cos αsin α32πα-―cos α―sin α（3）同角三角函数关系式：sin 2α+cos 2α=1，sin tan cos ααα=（4）两角和与差的三角函数：sin(α+β)=sin αcos β+cos αsin βsin(α―β)=sin αcos β―cos αsin βcos(α+β)=cos αcos β―sin αsin βcos(α―β)=cos αcos β+sin αsin βtan tan tan()1tan tan αβαβαβ++=-tan tan tan()1tan tan αβαβαβ--=+（5）二倍角公式：sin 22sin cos ααα=2222cos 2cos sin 12sin 2cos 1ααααα=-=-=-22tan tan 21tan ααα=-（6）降幂公式：21cos 2sin 2αα-=，21cos 2cos 2αα+=2．三角函数性质性质y =sin x ，x ∈Ry =cos x ，x ∈R奇偶性奇函数偶函数单调性在区间()2,222k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z 上是增函数，在区间()32,222k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z 上是减函数在区间[―π+2kπ，2kπ](k ∈Z )上是增函数，在区间[2kπ，π+2kπ](k ∈Z )上是减函数最值在()22x k k ππ=+∈Z 时，y max ；在()22x k k ππ=-∈Z 时，y min在x =2kπ(k ∈Z )时，y max ；在x =2kπ+π(k ∈Z )时，y min对称中心(kπ，0)(k ∈Z )(),02k k ππ⎛⎫+∈⎪⎝⎭Z 对称轴()2x k k ππ=+∈Z x =kπ(k ∈Z )正切函数的性质图象特点定义域为{|,}2x x k k ππ≠+∈Z 图象与直线2x k k ππ=+∈Z ，没有交点最小正周期为π在区间,22k k k ππππ⎛⎫-++∈ ⎪⎝⎭Z ，上图象完全一样在,22k k k ππππ⎛⎫-++∈ ⎪⎝⎭Z ，内是增函数图象在,22k k k ππππ⎛⎫-++∈ ⎪⎝⎭Z ，内是上升的对称中心为,02k k π⎛⎫∈⎪⎝⎭Z ，图象关于点,02k k π⎛⎫∈⎪⎝⎭Z ，成中心对称3．函数y =A sin(ωx +φ)的图象及变换（1）φ对函数y =sin(x +φ)的图象的影响（2）ω(ω>0)对y =sin(ωx +φ)的图象的影响（3）A(A >0)对y =A sin(ωx +φ)的图象的影响4．函数y =A sin(ωx +φ)的性质（1）函数y =A sin(ωx +φ)(A >0，ω>0)中参数的物理意义（2）函数y =A sin(ωx +φ)(A >0，ω>0)的有关性质二、解三角形1．正余弦定理定理正弦定理余弦定理内容(为外接圆半径)；；变形形式，，；，，；；；；2．利用正弦、余弦定理解三角形（1）已知两角一边，用正弦定理，只有一解．（2）已知两边及一边的对角，用正弦定理，有解的情况可分为几种情况．在中，已知，和角时，解得情况如下：为锐角为钝角或直角直角图形关系式解的个数一解两解一解一解上表中为锐角时，，无解．为钝角或直角时，，均无解．（3）已知三边，用余弦定理，有解时，只有一解．（4）已知两边及夹角，用余弦定理，必有一解．3．三角形中常用的面积公式（1）(表示边上的高）；（2）；（3）（为三角形的内切圆半径）．4．解三角形应用题的一般步骤一、选择题．1．在平面直角坐标系xOy 中，α为第四象限角，角α的终边与单位圆O 交于点P (x 0，y 0)，若cos 356πα⎛⎫+= ⎪⎝⎭，则x 0=（）ABCD【答案】C【解析】∵,02πα⎛⎫∈-⎪⎝⎭，∴,636πππα⎛⎫+∈- ⎪⎝⎭，又3cos 65πα⎛⎫+=< ⎪⎝⎭，所以,063ππα⎛⎫+∈- ⎪⎝⎭，所以4sin 65πα⎛⎫+=- ⎪⎝⎭，∴0cos cos cos cos sin sin 666666x ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫==+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦341552=-⨯=，故选C ．【点评】本题容易忽视6πα+的范围，而导致sin 6πα⎛⎫+⎪⎝⎭出错．2．已知 tan 2θ―4tan θ+1=0，则2cos 4πθ⎛⎫+= ⎪⎝⎭（）A ．12B ．13C ．14D ．15【答案】C（70分钟）经典训练题【解析】由 tan 2θ―4tan θ+1=0，可得1tan 4tan θθ+=，所以sin cos 4cos sin θθθθ+=，即22sin cos 4cos sin θθθθ+=⋅，即1cos sin 4θθ⋅=，211cos 2121sin 212sin cos 124cos 422224πθπθθθθ⎛⎫++-⨯⎪--⎛⎫⎝⎭+===== ⎪⎝⎭，故选C ．【点评】本题考查同角三角函数的关系、降幂公式、二倍角公式，解答本题的关键是由条件有1tan 4tan θθ+=，从而可得1cos sin 4θθ⋅=，由21cos 21sin 22cos 422πθπθθ⎛⎫++ ⎪-⎛⎫⎝⎭+== ⎪⎝⎭12sin cos 2θθ-=可解，属于中档题．3．已知函数f (x )=2sin(ωx +φ)，(0,2πωϕ><的部分图象如图所示，f (x )的图象过,14A π⎛⎫⎪⎝⎭，5,14B π⎛⎫- ⎪⎝⎭两点，将f (x )的图象向左平移712π个单位得到g (x )的图象，则函数g (x )在30,4π⎡⎤⎢⎥⎣⎦上的最小值为（）A ．―2B ．2C ．―3D ．―1【答案】A【解析】由图象知，5244T πππ=-=，∴T =2π，则1ω=，∴f (x )=2sin(x +φ)，将点,14A π⎛⎫⎪⎝⎭的坐标代入得，2sin 14πϕ⎛⎫+= ⎪⎝⎭，即1sin 42πϕ⎛⎫+= ⎪⎝⎭，又2πϕ<，∴12πϕ=-，则()2sin 12f x x π⎛⎫=-⎪⎝⎭，将f (x )的图象向左平移712π个单位得到函数()72sin 2sin 2cos 12122g x x x x πππ⎛⎫⎛⎫=+-=+= ⎪ ⎪⎝⎭⎝⎭，∴g (x )在30,4π⎡⎤⎢⎥⎣⎦上的最小值为32cos 4π=，故选A ．【点评】本题主要考了三角函数图象，以及三角函数的性质和三角函数图象的变换，属于中档题．4．已知a 、b 、c 分别是△ABC 的内角A 、B 、C 的对边，若sin cos sin CA B<，则ΔABC 的形状为（）A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等边三角形【答案】A【解析】因为在三角形中，sin cos sin CA B<变形为sin C <sin B cos A ，由内角和定理可得sin(A +B)<cos A sin B ，化简可得：sin A cos B <0，∴cos B <0，所以2B π>，所以三角形为钝角三角形，故选A ．【点评】本题考查了解三角形，主要是公式的变形是解题的关键，属于较为基础题．5．（多选）已知函数f(x)=3sin x +sin 3x ，则（）A ．f(x)是奇函数B ．f(x)是周期函数且最小正周期为2πC ．f(x)的值域是[―4，4]D ．当x ∈(0，π)时，f(x)>0【答案】ABD【解析】A ．f (―x )=3sin(―x )+sin(―3x )=―3sin x ―sin 3x =―f (x )，故f(x)是奇函数，故A 正确；B ．因为y =sin x 的最小正周期是2π，y =sin 3x 的最小正周期为23π，二者的“最小公倍数”是2π，故2π是f(x)的最小正周期，故B 正确；C ．分析f(x)的最大值，因为3sin x ≤3，sin 3x ≤1，所以f(x)≤4，等号成立的条件是sin x =1和sin 3x =1同时成立，而当sin x =1，即()22x k k ππ=+∈Z 时，()3362x k k ππ=+∈Z ，sin 3x =―1，故C 错误；D ．展开整理可得()2()3sin sin cos 2cos sin 2sin 4cos 2f x x x x x x x x =++=+，易知当x ∈(0，π)时，f(x)>0，故D 正确，故选ABD ．【点评】正确理解奇函数和偶函数的定义，必须把握好两个问题：（1）定义域关于原点对称是函数()f x 为奇函数或偶函数的必要非充分条件；（2）()()f x f x -=-或()()f x f x -=是定义域上的恒等式．奇函数的图象关于原点对称，偶函数的图象关于y 轴对称，反之也成立．利用这一性质可简化一些函数图象的画法，也可以利用它去判断函数的奇偶性．二、解答题．6．已知m =(2sin x ，sin x ―cos x )，n =(3cos x ，sin x +cos x )，函数f(x)=m ⋅n ．求函数f(x)的最大值以及取最大值时x 的取值集合．【答案】f(x)的最大值为2，,3x x k k ππ⎧⎫=+∈⎨⎬⎩⎭Z ．【解析】()()()cos sin cos sin cos f x x x x x x x =⋅=+-+m n2cos 22sin 26x x x π⎛⎫=-=- ⎪⎝⎭，所以函数f(x)的最大值为2，当2262x k πππ-=+，即,3x k k ππ=+∈Z 取得，即集合为,3x x k k ππ⎧⎫=+∈⎨⎬⎩⎭Z ．【点评】本题与向量的坐标运算结合，考查三角函数的最值，属于基础题．7．已知函数2()cos 222x x x f x =+-．（1）求函数f(x)在区间[0，π]上的值域；（2）若方程f(ωx)=3(ω>0)在区间[0，π]上至少有两个不同的解，求ω的取值范围．【答案】（1）[―2，2]；（2）5,12⎡⎫+∞⎪⎢⎣⎭．【解析】（1）()2cos 2sin(2224x x x f x x x x π=+-==+，令4U x π=+，∵x ∈[0，π]，5,44U ππ⎡⎤∴∈⎢⎥⎣⎦，由y =sin U 的图象知，sin U ⎡⎤∈⎢⎥⎣⎦，即sin 4x π⎡⎤⎛⎫+∈⎢⎥ ⎪⎝⎭⎣⎦，2sin 24x π⎛⎫⎡⎤∴+∈ ⎪⎣⎦⎝⎭，所以函数f(x)的值域为[―2，2]．（2）()2sin()(0)4f x x πωωω=+>，∵f(ωx)=3，2sin(4x πω∴+=，即sin()4x πω+=，∵x ∈[0，π]，,444x πππωωπ⎡⎤∴+∈+⎢⎥⎣⎦，且()243x k k ππωπ+=+∈Z 或()2243x k k ππωπ+=+∈Z ，由于方程f(ωx)=3(ω>0)在区间[0，π]上至少有两个不同的解，所以243ππωπ+≥，解得512ω≥，所以ω的取值范围为5,12⎡⎫+∞⎪⎢⎣⎭．【点评】考查三角函数的值域时，常用的方法：（1）将函数化简整理为f(x)=A sin(ωx +φ)，再利用三角函数性质求值域；（2）利用导数研究三角函数的单调区间，从而求出函数的最值．8．已知函数f(x)=3sin x cos x +cos 2x +1．（1）求f(x)的最小正周期和值域；（2）若对任意x ∈R ，2()()20f x k f x -⋅-≤的恒成立，求实数k 的取值范围．【答案】（1）最小正周期π，值域为15,22⎡⎤⎢⎥⎣⎦；（2）1710k ≥．【解析】（1）f(x)=3sin x cos x +cos 2x +1cos 21133212cos 2sin 222262x x x x x π+⎛⎫=++=++=++ ⎪⎝⎭，∴f(x)的为最小正周期22T ππ==，值域为()15,22f x ⎡⎤∈⎢⎥⎣⎦．（2）记f(x)=t ，则15,22t ⎡⎤∈⎢⎥⎣⎦，由f 2(x)―k ⋅f(x)―2≤0恒成立，知t 2―kt ―2≤0恒成立，即kt ≥t 2―2恒成立，∵t >0，∴222t k t t t-≥=-．∵()2g t t t =-在15,22t ⎡⎤∈⎢⎥⎣⎦时单调递增，max 5541722510g g ⎛⎫==-= ⎪⎝⎭，∴k 的取值范围是1710k ≥．【点评】本题主要考查了三角函数的恒等变换的应用，正弦函数的性质，考查了函数思想，属于中档题．9．△ABC 的内角A ，B ，C 的对边为a ，b ，c ，且3(sin B +sin C )2―3sin 2(B +C)=8sin B sin C ．（1）求cos A 的值；（2）若△ABC 的面积为，求a +b +c 的最小值．【答案】（1）13；（2）4+．【解析】（1）由3(sin B +sin C )2―3sin 2(B +C)=8sin B sin C ，∵A +B +C =π，所以228(sin sin )sin sin sin 3B C A B C +=+，由正弦定理可得228()3b c a bc +=+，则22223b c a bc +-=，由余弦定理可得2221cos 23b c a A bc +-==．（2）由1cos 3A =，得sin A =，∵1sin 2ABC S bc A ==△，∴bc =12，由22223b c a bc +-=，得222224216333a b c bc bc bc bc =+-≥-==，∴a ≥4，当且仅当b =c =23时，等号成立．又b +c ≥2bc =43，当且仅当b =c =23时，等号成立．∴a +b +c ≥4+43，当且仅当b =c =23时，等号成立．即a +b +c 的最小值为4+．【点评】求解三角形中有关边长、角、面积的最值（范围）问题时，常利用正弦定理、余弦定理与三角形面积公式，建立a +b ，ab ，a 2+b 2之间的等量关系与不等关系，然后利用函数或基本不等式求解．10．设函数f(x)=12cos 2x ―43sin x cos x ―5．（1）求f(x)的最小正周期和值域；（2）在锐角△ABC 中，角A ､B ､C 的对边长分别为a ､b ､c ．若f(A)=―5，a =3，求△ABC 周长的取值范围．【答案】（1）π，[―43+1，43+1]（2）(3+3，33]．【解析】（1）f (x )=12cos 2x ―43sin x cos x ―5=12cos 2x ―23sin 2x ―56cos 221216x x x π⎛⎫=-+=++ ⎪⎝⎭，T π∴=，值域为[―43+1，43+1]．（2）由f(A)=―5，可得212cos cos A A A =，因为三角形为锐角△ABCsin A A =，即tan A =，3A π=，由正弦定理sin sin sin a b c A B C ==，得2sin b B =，22sin 2sin()3c C B π==-，所以212sin sin()2(sin sin )32a b c B B B B B π⎡⎤++=++-=++⎢⎥⎣⎦32(sin ))26B B B π==++，因为△ABC 为锐角三角形，所以02B π<<，02C π<<，即022032B B πππ⎧<<⎪⎪⎨⎪<-<⎪⎩，解得62B ππ<<，所以2363B πππ<+<sin(16B π<+≤，即36B π+<+≤，所以周长的取值范围为区间(3+3，33]．【点评】在解三角形的周长范围时，将a +b +c 转化为含一个角的三角函数问题，利用三角函数的值域，求周长的取值范围，是常用解法．11．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且(a +b )(sin A ―sin B )=(b +c )sin C ．（1）求角A 的大小；（2）若点D 是BC 的中点，且AD =2，求△ABC 的面积的最大值．【答案】（1）23π；（2）23．【解析】（1）由题意得(a +b)(a ―b)=(b +c)c ，∴b 2+c 2―a 2=―bc ，1cos 2A ∴=-，()0,A π∈，23A π∴=．（2）1()2AD AB AC =+u u u r u u u r u u u r ，()()2222211244AD AB AC AB AC AB AC AB AC =++⋅=+-⋅u u u r u u u r u u u r u u u r u u u r ，()1224AB AC AB AC ∴≥⋅-⋅，当且仅当AB =AC 时，等号成立，∴AB ⋅AC ≤8，11sin120822S AB AC =⋅︒≤⨯=故△ABC 的面积的最大值是23．【点评】用三角形中线向量进行转化是解题关键．12．如图，在△ABC 中，AB =2AC ，∠BAC 的角平分线交BC 于点D ．（1）求ABD ADCS S △△的值；（2）若AC =1，BD =2，求AD 的长．【答案】（1）2；（2）1．【解析】（1）∵AD 为∠BAC 的角平分线，∴∠BAD =∠CAD ，即sin ∠BAD =sin ∠CAD，∴1sin 21sin 2ABDADC AB AD B AB AD S S AC AD A ACC D ⋅∠∠==⋅V V ，又∵AB =2AC ，∴2ABD ADC S S =△△．（2）由（1）知2ABD ADC S AB S AC ==△△，而1212ABDADC BC h S BC S CDCD h ⋅==⋅△△，2AB BD AC CD ∴==且AC =1，BD =2，∴2AB =，CD =∵∠BAD =∠CAD ，∴cos ∠BAD =cos ∠CAD ，在△ABD 中，22222422cos 2224AB AD BD AD AD BAD AB AD AD AD+-+-+∠===⋅⨯⨯，在△ACD 中，2222211122cos 2212AD AD AC AD CD CAD AC AD AD AD +-++-∠===⋅⨯⨯，∴2212242AD AD AD AD ++=，∴AD =1．【点评】本题考查三角形面积公式和余弦定理的应用，解题的关键在于对角平分线的性质的理解和运用，考查解题和运用能力．13．在ΔABC 中，a 、b 、c 分别是角A 、B 、C 的对边，且(a +b +c)(a +b ―c)=3ab ．（1）求角C 的值；（2）若c =2，且ΔABC 为锐角三角形，求a +b 的取值范围．【答案】（1）3C π=；（2）(23，4]．【解析】（1）由题意知(a +b +c)(a +b ―c)=3ab ，∴222a b c ab +-=，由余弦定理可知，222cos 122a b c C ab +-==，又∵C ∈(0，π)，∴3C π=．（2）由正弦定理可知，2sin sin sin 3a b A B π===a A =，b B =，∴)2sin sin sin sin 3a b A B A A π⎡⎤⎛⎫+=+=+- ⎪⎢⎥⎝⎭⎣⎦2cos 4sin 6A A A π⎛⎫=+=+ ⎪⎝⎭，又∵ΔABC 为锐角三角形，∴022032A B A πππ⎧<<⎪⎪⎨⎪<=-<⎪⎩，则2363A πππ<+<，所以4sin 46A π⎛⎫<+≤ ⎪⎝⎭，综上a +b 的取值范围为(23，4]．【点评】本题主要考查了利用正弦定理和三角函数的恒等变换求解三角形问题，对于解三角形问题，通常利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用余弦定理借助三边关系求角，利用两角和差公式及二倍角公式求三角函数值．利用正、余弦定理解三角形问题是高考高频考点，经常利用三角形内角和定理，三角形面积公式，结合正、余弦定理解题．一、选择题．1．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，则“b cos A ―c <0”，是“△ABC 为锐角三角形”的（）条件．A ．充分必要B ．充分不必要C ．必要不充分D ．既不充分也不必要【答案】C高频易错题即sin(A +B)=sin A cos B +sin B cos A >sin B cos A ，∴sin A cos B >0，因为sin A >0，∴cos B >0，所以B 为锐角．当B 为锐角时，△ABC 不一定为锐角三角形；当△ABC 为锐角三角形时，B 一定为锐角，所以“b cos A ―c <0”是“△ABC 为锐角三角形”的必要非充分条件，故选C ．【点评】判断充分必要条件，一般有三种方法：（1）定义法；（2）集合法；（3）转化法．我们要根据实际情况灵活选择方法，本题选择的是定义法判断充分必要条件．二、填空题．2．设锐角三角形ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，若a =2，B =2A ，则b 的取值范围为___________．【答案】(22，23)【解析】由sin2sin b a A A=，得4cos b A =，由0290045A A ︒<<︒⇒︒<<︒，01803903060A A ︒<︒-<︒⇒︒<<︒，故3045cos A A ︒<<︒⇒<<cos A <0，函数()2sin(2)26f x a x a b π=-+++，当0,2x π⎡⎤∈⎢⎥⎣⎦时，―5≤f (x )≤1．（1）求常数a ，b 的值；（2）设()2g x f x π⎛⎫=+ ⎪⎝⎭且lg g (x )>0，求g (x )的单调区间．【答案】（1）2a =，5b =-；（2）递增区间为,6k k k πππ⎛⎫+∈ ⎪⎝⎭Z ，；递减区间为,63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z ，．【解析】（1）由0,2x π⎡⎤∈⎢⎥⎣⎦，所以72,666x πππ⎡⎤+∈⎢⎥⎣⎦，则1sin(2),162x π⎡⎤+∈-⎢⎥⎣⎦，所以[]2sin(2)2,6a x a a π-+∈-，所以f (x )∈[b ，3a +b]，又因为―5≤f (x )≤1，可得531b a b =-⎧⎨+=⎩，解得2a =，5b =-．（2）由（1）得()4sin(2)16f x x π=-+-，则()74sin(214sin(21266g x f x x x πππ⎛⎫=+=-+-=+- ⎪⎝⎭，又由lg g (x )>0，可得g (x )>1，所以4sin(2116x π+->，即1sin(2)62x π+>，所以5222666k x k k πππππ+<+<+∈Z ，，当222662k x k k πππππ+<+≤+∈Z ，时，解得6k x k k πππ<≤+∈Z ，，此时函数g (x )单调递增，即g (x )的递增区间为,6k k k πππ⎛⎫+∈ ⎪⎝⎭Z ，；当5222266k x k k πππππ+<+<+∈Z 时，解得63k x k k ππππ+<<+∈Z ，，此时函数g (x )单调递减，即g (x )的递减区间为,63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z ，．【点评】本题主要考查了三角函数的图象与性质的综合应用，其中解答中根据三角函数的性质，求得函数的解析式，熟练应用三角函数的性质是解答的关键，着重考查推理与运算能力．一、选择题．1．如图所示，扇形OQP 的半径为2，圆心角为3π，C 是扇形弧上的动点，四边形ABCD 是扇形的内接矩形，则S ABCD 的最大值是（）AB．CD ．23【答案】A【解析】如图，记∠COP =α，在Rt △OPC 中，2cos OB α=，2sin BC α=，在Rt △OAD中，OA DA BC α===，所以2cos AB OB OA αα=-=，设矩形ABCD 的面积为S，(2cos )2sin S AB BC ααα=⋅=⋅精准预测题24sin cos 2sin 22ααααα==+-)6πα=+，由03πα<<，所以当262ππα+=，即6πα=时，S =，故选A ．【点评】本题考查在实际问题中建立三角函数模型，求解问题的关键是根据图形建立起三角模型，将三角模型用所学的恒等式变换公式进行求解．2．已知函数()2sin 26f x x π⎛⎫=+⎪⎝⎭，现将()y f x =的图象向左平移12π个单位，再将所得图象上各点的横坐标缩短为原来的12倍，纵坐标不变，得到函数y =g (x )的图象，则g (x )的解析式为（）A ．221124x y +=B ．sin 3y x π⎛⎫=+⎪⎝⎭C ．2sin 43y x π⎛⎫=+⎪⎝⎭D ．2sin 3y x π⎛⎫=+⎪⎝⎭【答案】C【解析】将()y f x =的图象向左平移12π个单位得2sin 22sin 21263y x x πππ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，再所得图象上各点的横坐标缩短为原来的12倍，纵坐标不变，得到()2sin 43y g x x π⎛⎫==+⎪⎝⎭，故选C ．【点评】在三角函数平移变换中，y =sin ωx 向左平移ϕ个单位得到的函数解析式为y =sin[ω(x +φ)]=sin(ωx +ωφ)，而不是y =sin(ωx +)，考查运算求解能力，是基础题．3．（多选）如图是函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><的部分图象，则下列说法正确的是（）A ．ω=2B ．,06π⎛⎫-⎪⎝⎭是函数，f (x )的一个对称中心C ．23πϕ=D ．函数f (x )在区间4,5ππ⎡⎤--⎢⎥⎣⎦上是减函数【答案】ACD【解析】由题知，A =2，函数f (x )的最小正周期11521212T πππ⎛⎫=⨯-=⎪⎝⎭，所以22T πω==，故A 正确；因为1111112sin 22sin 212126f πππϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以11262k ππϕπ+=+，k ∈Z ，解得423k πϕπ=-，k ∈Z ，又|φ|<π，所以23πϕ=，故C 正确；函数()22sin 23f x x π⎛⎫=+⎪⎝⎭，因为22sin 22sin 06633f ππππ⎡⎤⎛⎫⎛⎫-=⨯-+==≠ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，所以,06π⎛⎫-⎪⎝⎭不是函数f (x )的一个对称中心，故B 错误；令23222232m x m πππππ+≤+≤+，m ∈Z ，得51212m x mx πππ-≤≤+，m ∈Z ，当m =―1时，1371212x ππ-≤≤-，因为4137,,51212ππππ⎡⎤⎡⎤--⊆--⎢⎥⎢⎥⎣⎦⎣⎦，所以函数f (x )在区间4,5ππ⎡⎤--⎢⎥⎣⎦上是减函数，故D 正确，故选ACD ．【点评】已知()(sin 0,0)()f x A x A ωϕω+>>=的部分图象求其解析式时，A 比较容易看图得出，困难的是求待定系数ω和φ，常用如下两种方法：（1）由2Tπω=，即可求出ω；确定φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标0x ，则令00x ωϕ+=(或0x ωϕπ+=)，即可求出φ．（2）代入点的坐标，利用一些已知点(最高点、最低点或“零点”)坐标代入解析式，再结合图形解出ω和φ，若对A ，ω的符号或对φ的范围有要求，则可用诱导公式变换使其符合要求．二、解答题．4．已知函数f(x)=cos(ωx)(ω>0)的最小正周期为π．（1）求ω的值及函数()()0,42g x x f x x ππ⎛⎫⎡⎤=--∈ ⎪⎢⎥⎝⎭⎣⎦，的值域；（2）在△ABC 中，内角A ，B ，C 所对应的边长分别为a ，b ，c ，若0,2A π⎛⎫∈ ⎪⎝⎭，()12f A =-，△ABC 的面积为33，b ―c =2，求a 的值．【答案】（1）ω=2，值域为[―1，2]；（2）4．【解析】（1）因为函数f(x)=cos(ωx)的最小正周期为π，由2T ππω==，2ω=，又因为ω>0，所以ω=2．此时f(x)=cos 2x ，则得()2cos 24g x x x π⎛⎫=-- ⎪⎝⎭，即g(x)=3sin 2x ―cos 2x ，即()2sin 26g x x π⎛⎫=-⎪⎝⎭，当0,2x π⎡⎤∈⎢⎥⎣⎦时，52,666x πππ⎡⎤-∈-⎢⎥⎣⎦，[]2sin 21,26x π⎛⎫-∈- ⎪⎝⎭，所以所求函数的值域为[―1，2]．（2）由题意得1cos 22A =-，因为0,2A π⎛⎫∈ ⎪⎝⎭，则得2A ∈(0，π)，所以223A π=，解得3A π=，因为△ABC 的面积为33，则得1sin 2bc A =，即1sin 23bc π=，即bc =12．又因为b ―c =2，由余弦定理，得a =b 2+c 2―2bc cos A =b 2+c 2―bc =(b ―c )2+bc =22+12=4，所以a =4．【点评】本题考查求三角函数的值域，考查余弦定理解三角形，以及三角形面积公式．三角函数问题中，首先需利用诱导公式、二倍角公式、两角和与差的正弦（余弦）公式化函数为一个角的一个三角函数形式（主要是f(x)=A sin(ωx +ϕ)+k 形式），然后利用正弦函数性质确定求解．5．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a sin(A +B ―C )=c sin(B +C )．（1）求角C 的大小；（2）若2a +b =8，且△ABC 的面积为23，求△ABC 的周长．【答案】（1）3C π=；（2）6+23．【解析】（1）∵a sin(A +B ―C)=c sin(B +C)，∴sin A sin(π―2C)=sin C sin A ，∴2sin A sin C cos C =sin C sin A ，∵sin A sin C ≠0，1cos 2C ∴=，0C π<<，3C π∴=．（2）由题意可得12=∴ab =8，∵2a +b =8联立可得，a =2，b =4，由余弦定理可得，c 2=12，c =23，此时周长为6+23．【点评】本题主要考查了三角形的内角和诱导公式在三角化简中的应用，还考查了三角形的面积公式及余弦定理，属于基础题．6．如图，矩形ABCD 是某个历史文物展览厅的俯视图，点E 在AB 上，在梯形DEBC 区域内部展示文物，DE 是玻璃幕墙，游客只能在△ADE 区域内参观．在AE 上点P 处安装一可旋转的监控摄像头，∠MPN 为监控角，其中M 、N 在线段DE （含端点）上，且点M 在点N 的右下方．经测量得知：AD =6米，AE =6米，AP =2米，4MPN π∠=．记∠EPM =θ（弧度），监控摄像头的可视区域△PMN 的面积为S 平方米．（1）分别求线段PM 、PN 关于θ的函数关系式，并写出θ的取值范围；（2）求S 的最小值．【答案】（1）4sin cos PM θθ=+，PN =，30arctan 34πθ≤≤-；（2）8(2―1)平方米．【解析】（1）在△PME 中，∠EPM =θ，4PE AE AP =-=米，4PEM π∠=，34PME πθ∠=-，由正弦定理得sin sin PM PEPEM PME=∠∠，所以sin 4sin sin cos PE PEM PM PME θθ⨯∠===∠+；同理在PNE △中，由正弦定理得sin sin PN PEPEN PNE=∠∠，所以sin sin PE PEN PN PNE ⨯∠===∠当M 与E 重合时，θ=0；当N 与D 重合时，tan ∠APD =3，即∠APD =arctan 3，3πarctan 3arctan 344πθπ=--=-，所以30arctan 34πθ≤≤-．（2）△PMN 的面积214sin 2cos sin cos S PM PN MPN θθθ=⨯⨯∠=+481cos 21sin 2cos 21sin 222θθθθ===++++，因为30arctan 34πθ≤≤-，所以当242ππθ+=，即30,arctan 384ππθ⎡⎤=∈-⎢⎥⎣⎦时，S)81=-，所以可视区域△PMN 面积的最小值为8(2―1)平方米．【点评】本题考查解三角形的应用．掌握三角函数的性质是解题关键．解题方法是利用正弦定理或余弦定理求出三角形的边长，面积，利用三角函数的恒等变换化函数为基本三角函数形式，然后由正弦函数性质求最值．7．在ΔABC 中，角A ，B ，C 的对边分别为a ，b ，c ．（1）若23cos 2A +cos 2A =0，且△ABC 为锐角三角形，a =7，c =6，求b 的值；（2）若a =3，3A π=，求b +c 的取值范围．【答案】（1）5b =；（2）b +c ∈(3，23]．【解析】（1）22223cos cos 223cos 2cos 10A A A A +=+-=Q ，∴21cos 25A =，又∵A 为锐角，1cos 5A =，而a 2=b 2+c 2―2bc cos A ，即2121305b b --=，解得b =5或135b =-（舍去），∴b =5．（2）由正弦定理可得()22sin sin 2sin sin 36b c B C B B B ππ⎡⎤⎛⎫⎛⎫+=+=+-=+⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，203B π<<Q ，∴5666B πππ<+<，∴1sin 126B π⎛⎫<+≤ ⎪⎝⎭，∴b +c ∈(3，23]．【点评】本题考查三角函数的恒等变换，三角形的正弦定理和余弦定理的运用，以及运算能力，属于中档题．。

七年级数学下册专题第6讲平行线重点、考点知识总结及练习

专题第6讲平行线知识点1 平行公理及推论1. 在同一平面内，不重合的两条直线只有两种位置关系：相交和平行.直线a与直线b不相交时，直线a与b互相平行，记作a∥b.2. 平行公理：经过直线外一点，有且只有一条直线与已知直线平行.平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行. 【典例】1.如图，直线a，点B，点C.（1）过点B画直线a的平行线，能画几条？（2）过点C画直线a的平行线，它与（1）中所作的直线平行吗？【解析】解：（1）由平行公理可知，过直线a外的一点B画直线a的平行线，有且只有一条直线与直线a平行；（2）过点C画直线a的平行线，它与（1）中所作的直线平行．理由如下：如图，∵b∥a，c∥a，∴c∥b.【方法总结】本题考查了平行公理及其推论．平行公理：经过直线外一点，有且只有一条直线与这条直线平行.在公理中，要准确理解“有且只有”的含义．从作图的角度说，它是“能但只能画出一条”的意思.推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．平行公理的推论是判定两直线平行的一种常用方法，要牢固掌握.【随堂练习】1．下列说法中错误的个数是（）（1）过一点有且只有一条直线与已知直线平行；（2）过一点有且只有一条直线与已知直线垂直；（3）在同一平面内，两条直线的位置关系只有相交，平行两种；（4）不相交的两条直线叫做平行线．A．1个B．2个C．3个D．4个【解答】解：（1）在同一平面内，过直线外一点一点有且只有一条直线与已知直线平行，原来的说法错误；（2）在同一平面内，过一点有且只有一条直线与已知直线垂直，原来的说法错误；（3）在同一平面内，两条直线的位置关系只有相交，平行两种是正确的；（4）在同一平面内，不相交的两条直线叫做平行线，原来的说法错误．故说法中错误的个数是3个．故选：C．2．请你动手试试，过一条直线外的一点作这条直线的平行线，能作几条？由此能得出一个什么数学结论．____________________________．【解答】解：过一条直线外的一点作这条直线的平行线，能做1条，理由是：过直线外一点有且只有一条直线与这条直线平行．故答案为：能做一条，过直线外一点有且只有一条直线与这条直线平行．知识点2 平行线的判定1. 平行线的判定方法：判定方法1 两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：同位角相等，两直线平行.如图1，∵∠4=∠2，∴a∥b.判定方法2 两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单说成：内错角相等，两直线平行.如图2，∵∠4=∠5，∴a∥b.判定方法3 两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单说成：同旁内角互补，两直线平行.如图3，∵∠4+∠1=180°，∴a∥b.2. 重要结论：在同一平面内，垂直于同一条直线的两条直线互相平行.注意：条件“同一平面”不能缺少，否则结论不成立.【典例】1.如图，BE平分∠ABD，DE平分∠BDC，且∠E为直角，AB与CD平行吗？试说明理由.【解析】解：AB∥CD.理由：∵BE平分∠ABD（已知），∴∠ABD=2∠α（角平分线的定义）．∵DE平分∠BDC（已知），∴∠BDC=2∠β（角平分线的定义），∴∠ABD+∠BDC=2∠α+2∠β=2（∠α+∠β）（等量代换）.∵∠E为直角，即∠E=90°（已知），∴∠α+∠β=90°（直角三角形的两个锐角互余），∴∠ABD+∠BDC=180°（等量代换）．∴AB∥CD（同旁内角互补，两直线平行）．【方法总结】首先根据角平分线的定义可得∠ABD=2∠α，∠BDC=2∠β，根据等量代换可得∠ABD+∠BDC=2（∠α+∠β）.由∠E为直角可得∠α+∠β=90°，进而得到∠ABD+∠BDC=180°，然后根据“同旁内角互补，两直线平行”可得答案．此题主要考查了平行线的判定，关键是掌握角平分线的定义和平行线的判定方法．【随堂练习】1．完成下面的证明，括号内填根据．如图，直线a、b、c被直线l所截，量得∠1＝65°，∠2＝115°，∠3＝65°．求证：a∥b证明：∠1＝65°，∠3＝65°∴_______∴___________________∵∠2＝115°，∠3＝65°∴____________∴___________________∴a∥b【解答】证明：∵∠1＝65°，∠3＝65°∴∠1＝∠3，∴a∥c（同位角相等，两直线平行），∵∠2＝115°，∠3＝65°∴∠2+∠3＝180°，∴b∥c（同旁内角相等，两直线平行）∴a∥b（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）故答案为：∠1＝∠3；a∥c（同位角相等，两直线平行）；∠2+∠3＝180°；b ∥c（同旁内角相等，两直线平行）．2．如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2＝90°．求证：AB∥CD．【解答】解：∵BE平分∠ABD，DE平分∠BDC（已知），∴∠ABD＝2∠1，∠BDC＝2∠2（角平分线定义），∵∠1+∠2＝90°，∴∠ABD+∠BDC＝2（∠1+∠2）＝180°，∴AB∥CD（同旁内角互补，两直线平行）．3．如图，已知∠1＝30°，∠B＝60°，AB⊥AC，将证明AD∥BC的过程填写完整．证明：∵AB⊥AC∴∠_____＝____°（______）∵∠1＝30°∴∠BAD＝∠_____+∠___＝_____°又∵∠B＝60°∴∠BAD+∠B＝_____°∴AD∥BC（______________）【解答】证明：∵AB⊥AC∴∠BAC＝90°（垂直定义）∵∠1＝30°∴∠BAD＝∠BAC+∠1＝120°又∵∠B＝60°∴∠BAD+∠B＝180°∴AD∥BC（同旁内角互补，两直线平行）故答案为：BAC，90，垂直定义，BAC，1，120，180，同旁内角互补，两直线平行．知识点3 平行线的性质平行线的性质：性质1 两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.如图1，∵a∥b，∴∠4=∠2.性质2 两条平行线被第三条直线所截，内错角相等.简单说成：两直线平行，内错角相等.如图2，∵a∥b，∴∠4=∠5.性质3 两条平行线被第三条直线所截，同旁内角互补.简单说成：同旁内角互补，两直线平行.如图3，∵a∥b，∴∠4+∠1=180°.【典例】1.如图1，对于直线MN同侧的两个点A，B，若直线MN上的点P满足∠APM=∠BPN，则称点P为A，B在直线MN上的反射点．已知如图2，MN∥HG，AP∥BQ，点P为A，B在直线MN上的反射点，判断点B是否为P，Q在直线HG上的反射点，并说明理由．【解析】解：点B是P，Q在直线HG上的反射点，理由：∵点P为A，B在直线MN上的反射点，∴∠APM=∠BPQ，又∵HG∥MN，∴∠APM=∠BAP，∠BPQ=∠PBA，∴∠PAB=∠PBA，又∵AP∥BQ，∴∠PAB=∠QBG，∴∠PBA=∠QBG，∴点B是P，Q在直线HG上的反射点．【方法总结】依据点P为A，B在直线MN上的反射点，即可得到∠APM=∠BPQ，再根据平行线的性质，即可得到∠PAB=∠PBA，经过等量代换可得∠PBA=∠QBG，所以点B是P，Q在直线HG 上的反射点．本题是新定义题，正确理解“反射点”的概念和特征，并熟练应用平行线的性质是解题的关键.【随堂练习】1．如图，已知AB∥CD，点E在AC的右侧，∠BAE，∠DCE的平分线相交于点F．探索∠AEC与∠AFC之间的等量关系，并证明你的结论．【解答】解：∠AEC＝2∠AFC．理由：如图，分别过E，F作EG∥AB，FH∥AB，则EG∥CD，FH∥CD，∴∠AEG＝∠BAE，∠CEG＝∠DCE，∴∠AEC＝∠AEG+∠CEG＝∠BAE+∠DCE，同理可得∠AFC＝∠BAF+∠DCF，∵∠BAE，∠DCE的平分线相交于点F，∴∠BAE＝2∠BAF，∠DCE＝2∠DCF，∴∠AEC＝2（∠BAF+∠DCF）＝2∠AFC．2．课上教师呈现一个问题：已知：如图1，AB∥CD，EF⊥AB于点O，FG交CD于点P，当∠1＝30°时，求∠EFG的度数．甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如图：甲同学辅助线的做法和分析思路如下：辅助线：过点F作MN∥CD．分析思路：①欲求∠EFG的度数，由图可知只需转化为求∠2和∠3的度数之和；②由辅助线作图可知，∠2＝∠1，从而由已知∠1的度数可得∠2的度数；③由AB∥CD，MN∥CD推出AB∥MN，由此可推出∠3＝∠4；④由已知EF⊥AB，可得∠4＝90°，所以可得∠3的度数；⑤从而可求∠EFG的度数．（1）请你根据乙同学所画的图形，描述辅助线的做法，并写出相应的分析思路．辅助线：_________________分析思路：（2）请你根据丙同学所画的图形，求∠EFG的度数．【解答】解：（1）辅助线：过点P作PN∥EF交AB于点N．分析思路：①欲求∠EFG的度数，由辅助线作图可知，∠EFG＝∠NPG，因此，只需转化为求∠NPG的度数；②欲求∠NPG的度数，由图可知只需转化为求∠1和∠2的度数和；③又已知∠1的度数，所以只需求出∠2的度数；④由已知EF⊥AB，可得∠4＝90°；⑤由PN∥EF，可推出∠3＝∠4；AB∥CD可推出∠2＝∠3，由此可推∠2＝∠4，所以可得∠2的度数；⑥从而可以求出∠EFG的度数．（2）如图，过点O作ON∥FG，∵ON∥FG，∴∠EFG＝∠EON∠1＝∠ONC＝30°，∵AB∥CD，∴∠ONC＝∠BON＝30°，∵EF⊥AB，∴∠EOB＝90°，∴∠EFG＝∠EON＝∠EOB+∠BON＝90°+30°＝120°．3．问题情境：（1）如图1，AB∥CD，∠P AB＝130°，∠PCD＝120°．求∠APC度数．小颖同学的解题思路是：如图2，过点P作PE∥AB，请你接着完成解答问题迁移：（2）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β．试判断∠CPD、∠α、∠β之间有何数量关系？（提示：过点P作PE∥AD），请说明理由；（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你猜想∠CPD、∠α、∠β之间的数量关系．【解答】解：（1）过P作PE∥AB，∵AB∥CD，∴PE∥AB∥CD，∴∠APE＝180°﹣∠A＝50°，∠CPE＝180°﹣∠C＝60°，∴∠APC＝50°+60°＝110°；（2）∠CPD＝∠α+∠β，理由如下：如图3，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE+∠CPE＝∠α+∠β；（3）当P在BA延长线时，∠CPD＝∠β﹣∠α；理由：如图4，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠CPE﹣∠DPE＝∠β﹣∠α；当P在BO之间时，∠CPD＝∠α﹣∠β．理由：如图5，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE﹣∠CPE＝∠α﹣∠β．知识点4 平行线的判定与性质的综合运用两直线平行⇔同位角相等.两直线平行⇔内错角相等.同旁内角互补⇔两直线平行.“⇔”叫做“等价于”，即由左边能推出右边，由右边也能推出左边.【典例】1.如图，已知∠1=∠2，∠3=∠4，∠5=∠A，试说明：BE∥CF．【解析】解：如图，∵∠3=∠4（已知），∴AE∥BC（内错角相等，两直线平行），∴∠EDC=∠5（两直线平行，内错角相等）.∵∠5=∠A（已知），∴∠EDC=∠A（等量代换），∴DC∥AB（同位角相等，两直线平行），∴∠5+∠ABC=180°（两直线平行，同旁内角互补），即∠5+∠2+∠3=180°.∵∠1=∠2（已知），∴∠5+∠1+∠3=180°（等量代换），即∠BCF+∠3=180°，∴BE∥CF（同旁内角互补，两直线平行）.2.学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．（1）小明遇到了下面的问题：如图1，l1∥l2，点P在l1、l2内部，探究∠A，∠APB，∠B的关系．小明过点P作l1的平行线，可证∠APB，∠A，∠B之间的数量关系是：∠APB=____________________．（2）如图2，若AC∥BD，点P在AC、BD外部，∠A，∠B，∠APB的数量关系是否发生变化？（3）已知：如图3，三角形ABC，试说明：∠A+∠B+∠C=180°．【解析】解：（1）如图1，过P作PE∥l1，∵l1∥l2，∴PE∥l1∥l2，∴∠APE=∠A，∠BPE=∠B，∴∠APB=∠APE+∠BPE=∠A+∠B，故答案为：∠A+∠B.（2）如图2，过点P作PE∥AC,则∠A=∠1.∵AC∥BD，∴PE∥BD，∴∠B=∠EPB.∵∠APB=∠BPE﹣∠1，∴∠APB=∠B﹣∠A；（3）如图3，过点A作MN∥BC，则∠B=∠1，∠C=∠2.∵∠BAC+∠1+∠2=180°，∴∠BAC+∠B+∠C=180°．【方法总结】平行线的判定是由角的关系得到两直线平行，平形线的性质是由两直线平行得到角之间的关系，他们都可以作为说理的依据.其他常见的说理依据有：已知、等量代换、对顶角相等、等角的余角相等、等角的补角相等、平行于同一条直线的两条直线互相平行、三角形的内角和等于180°等.【随堂练习】1．如图，DE⊥AB，∠1＝∠A，∠2+∠3＝180°，试判断CF与AB的位置关系，并说明理由．【解答】解：CF⊥AB，理由如下：∵∠1＝∠A（已知）∴AC∥FG（同位角相等，两直线平行）∴∠2＝∠ACF（两直线平行，内错角相等）∴∠2+∠3＝180°（已知）∴∠ACF+∠3＝180°∴DE∥CF（同旁内角互补，两直线平行）∴∠DEF＝∠1+∠2∵DE⊥AB∴∠1+∠2＝90°∴CF⊥AB2．如图1，直线AG与直线BH和DI分别相交于点A和点G，点C为DI上一点，且CE⊥AG，垂足为点E，∠DCE﹣∠HAE＝90°．（1）求证：BH∥DI．（2）如图2：直线AF交DC于，AM平分∠EAF，AN平分∠BAE，证明：∠AFG ＝2∠MAN．【解答】证明：（1）因为∠DCE+∠ECG＝180°，∠CEG+∠CGA+∠ECG＝180°，所以∠DCE＝∠CEG+∠CGA因为CD⊥AG所以∠DCE﹣∠CGA＝∠CEG＝90°又因为∠DCE﹣∠HAE＝90°所以∠CGA＝∠HAE所以BH∥DI（2）因为AM平分∠EAF AN平分∠BAE所以∠EAM＝∠F AM∠EAN＝∠BAN又因为∠MAN＝∠EAN﹣∠EAM所以∠MAN＝∠BAN﹣∠F AM又因为∠BAN＝∠BAF+∠F AN∠F AM＝∠MAN+∠F AN所以∠MAN＝∠BAF﹣∠MAN所以∠BAF＝2∠MAN又所以BH∥DI所以∠AFG＝∠BAF所以∠AFG＝2∠MAN．知识点5 命题、定理、证明1. 命题：判断一件事情的语句叫做命题.数学中的命题常可以写成“如果……那么……”的形式，“如果”后接的部分是题设，“那么”后接的部分是结论.2. 真命题：如果题设成立，那么结论一定成立，这样的命题叫做真命题.假命题：题设成立时，不能保证结论一定成立，这样的命题叫做假命题.3. 定理：经过推理证实的真命题叫做定理.判断一个命题正确性的推理过程叫做证明.4. 判断一个命题是真命题，需要进行证明；判断一个命题是假命题，只要举出一个例子（反例），它符合命题的题设，但不满足结论就可以了.【典例】1.判断下列命题是真命题还是假命题．如果是真命题，请证明，如果是假命题，请举出反例．（1）两个锐角的和是钝角；（2）在同一平面内，垂直于同一条直线的两条直线互相平行．【解析】解：（1）“两个锐角的和是钝角位”是假命题，如30°和40°的和为70°；（2）“在同一平面内，垂直于同一条直线的两条直线互相平行”为真命题．已知：如图，在同一平面内，直线b⊥a，直线c⊥a.证明：如图，∵b⊥a，c⊥a，∴∠1=90°，∠2=90°，∴∠1=∠2，∴b∥c.【方法总结】要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．（1）任意找两个锐角，使它们的和为锐角或直角即可；（2）写出已知、求证，作出图形，利用平行线的判定即可证明命题为真命题.【随堂练习】1．已知：三条不同的直线a、b、c在同一平面内：①a∥b；②a⊥c；③b⊥c；④a⊥b．请你用①②③④所给出的其中两个事项作为条件，其中一个事项作为结论（用如果…那么…的形式，写出命题，例如：如果a⊥c、b⊥c、那么a∥b）．（1）写出一个真命题，并证明它的正确性；（2）写出一个假命题，并举出反例．【解答】解：（1）如果a⊥c、b⊥c、那么a∥b；理由：如图，∵a⊥c、b⊥c，∴∠1＝90°，∠2＝90°，∴∠1＝∠2，∴a∥b．（2）如果a⊥c、b⊥c、那么a⊥b；反例：见上图，如果a⊥c、b⊥c、那么a∥b．2．如图，有三个论断：①∠1＝∠2；②∠B＝∠C；③∠A＝∠D，请你从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．【解答】已知：∠1＝∠2，∠B＝∠C求证：∠A＝∠D证明：∵∠1＝∠3又∵∠1＝∠2∴∠3＝∠2∴EC∥BF∴∠AEC＝∠B又∵∠B＝∠C∴∠AEC＝∠C∴AB∥CD∴∠A＝∠D综合运用1.“垂直于同一直线的两直线平行”的题设：_______________________________________，结论:___________________________.【答案】两条直线都垂直于同一条直线这两条直线互相平行【解析】解：把命题可以写成“如果…那么…”，则如果后面为题设，那么后面为结论．“垂直于同一直线的两直线平行”改写成为“如果…那么…”的形式为：如果两条直线都垂直于同一条直线，那么这两条直线互相平行.题设：两条直线都垂直于同一条直线；结论为：这两条直线互相平行．故答案为：两条直线都垂直于同一条直线这两条直线互相平行2.如图，已知长方形ABCD，将△BCD沿对角线BD折叠，记点C的对应点为C'，若∠ADC'=24°，则∠BDC的度数为______________.【答案】57°【解析】解：如图，设AD与BC′交于点E．∵四边形ABCD是矩形，∴∠C=90°，AD∥BC，∠ADC=90°，∴∠3=∠4，∠1=∠2+∠4.∵△BDC′是由△BDC翻折得到，∴∠2=∠4，∠C=∠C′=90°，∠BDC=∠BDC′∴∠2=∠3，∵∠ADC′=24°，∴∠1=90°﹣∠EDC′=66°，∵∠1=∠2+∠4=2∠2，×66°=33°，∴∠2=∠3=12∴∠BDC=∠D-∠3=90°-33°=57°．故答案为57°.3.在同一平面内三条直线交点有多少个？甲：同一平面三直线相交交点的个数为0个，因为a∥b∥c，如图（1）所示．乙：同一平面内三条直线交点个数只有1个，因为a，b，c交于同一点O，如图（2）所示．以上说法谁对谁错？为什么？【解析】解：甲、乙说法都不对，都少了三种情况．a∥b，c与a，b相交如图（1）；a，b，c两两相交如图（2），所以三条直线互不重合，交点有0个或1个或2个或3个，共四种情况．4.如图，如果CD∥AB，CE∥AB，那么C，D，E三点是否共线？你能说明理由吗？【解析】解：C，D，E三点共线．理由：因为过直线AB外一点C有且只有一条直线与AB平行，直线CD、DE都经过点C 且与AB平行，所以直线CD、DE重合，所以点C、D、E三点共线．5.如图，已知AC⊥AE，BD⊥BF，∠1=35°，∠2=35°，AC与BD平行吗？AE与BF平行吗？【解析】解：因为∠1=35°，∠2=35°（已知），所以∠1=∠2．所以AC∥BD（同位角相等，两直线平行）．又因为AC⊥AE（已知），所以∠EAC=90°（垂直的定义）．所以∠EAB=∠EAC+∠1=125°．同理可得，∠FBG=∠FBD+∠2=125°．所以∠EAB=∠FBG（等量代换）．所以AE∥BF（同位角相等，两直线平行）．6.判断下列命题是真命题还是假命题；如果是假命题，请举一个反例.（1）两个锐角的和是锐角；（2）若a＞b，则a2＞b2；【解析】解：（1）假命题．反例为：两个锐角分别为40°，60°，它们的和为100°，为钝角；（2）假命题．反例为：a=1，b=﹣3，但是a2=1＜b2=9．7.如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE 平分∠FGD，若∠EFG=90°，∠E=35°，求∠EFB的度数．【解析】解：∵∠EFG=90°，∠E=35°，∴∠FGH=180°-∠EFG-∠E=180°-90°-35°=55°.∵GE平分∠FGD，∴∠FHG=∠HGD=55°.∵AB∥CD，∴∠FHG=∠HGD =55°.∴∠FHE=180°-∠FHG=180°-55°=125°.在△EFH中，∠EFB=180°-∠FHE-∠E=180°-125°-35°20°．8.如图，已知：AB∥CD，∠1=∠2，∠3=∠4，求证：（1）∠4=∠DAC；（2）AD∥BE．【解析】证明：（1）：∵AB∥CD，∴∠4=∠BAF（两直线平行，同位角相等）.∵∠1=∠2（已知），∴∠1+∠CAF=∠2+∠CAF（等式的性质），即∠BAF=∠DAC，∴∠4=∠DAC，（2）∵∠4=∠DAC，∠3=∠4，∴∠3=∠DAC，∴AD∥BE（内错角相等，两直线平行）．。

专题(6)三角形的“角平分线”“中线”和“高线”教师版

高三第二轮专题复习专题（6）——三角形的“角平分线”、“中线”和“高线”类型1、三角形的内角平分线问题例1、如图，在ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，ABD ∆面积是ADC ∆面积的2倍.（1）求sin sin B C；（2）若1,2AD DC ==，求BD 和AC 的长.答案：（1）12；（2）1. 变式1、已知AD 为ABC ∆内角A 的角平分线，03,5,120AB AC BAC ==∠=，求AD 的长度.答案：158.变式2、在ABC ∆中，2,1AB AC ==,角A 的平分线1AD =，求ABC ∆的面积S .类型2、三角形的中线问题例2、在ABC ∆中，2,3,AB AC BC ==边上的中线2AD =，求ABC ∆的面积S .答案：4. 变式：在ABC ∆中，内角,,A B C 的对边长分别为,,a b c ，已知函数()sin(2)6f x x π=-满足：对于任意,()()x R f x f A ∈≤恒成立．（1）求角A 的大小；（2）若a =BC 边上的中线AM 长的取值范围．解（1）由题意，∵对于任意,()()x R f x f A ∈≤恒成立， ∴()sin(2)6f x x π=-的最大值为()f A ，当()f x 取得最大值时，22,62x k k Z πππ-=+∈，即,3x k k ππ=+∈Z ， ∴,3A k k ππ=+∈Z ，又∵A 是三角形的内角，即0A π<<，∴3A π=．（2）∵AM 是BC 边上的中线，∴在ABM ∆中，2232cos 4AM AM AMB c +-∠=， ①在ACM ∆中，2232cos 4AM AM AMC b +-∠=， ② 又∵AMB AMC π∠=-∠，∴cos cos AMB AMC ∠=-∠，①＋②得 222324b c AM +=-．由余弦定理222222cos 33a b c bc b c bc π=+-=+-=， ∵2222032b c b c bc +<+-=≤，∴2236b c <+≤，∴23944AM <≤32AM <≤ 类型3、三角形的高线例3、在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且满足sin a A =. （1）求角B 的大小；（2）若点M 为BC 的中点，且AM AC =，求sin BAC ∠的值.答案：（1）3π；（2. 变式：已知ABC ∆的一个内角为0120，并且三边长构成公差为4的等差数列，求ABC ∆的面积.答案：类型4、四边形问题例4、在平面四边形ABCD 中，075,2A B C BC ====，求AB 的取值范围.答案：.变式：在平面四边形ABCD 中，内角A C 与互补，1,3,2AB BC CD DA ====.（1）求角C 和边BD ；（2）求四边形ABCD 的面积.答案：（1）,3C BD π∠==（2）。

中考总复习道德与法治6-热点专题六和平发展齐合作

①我国综合国力进一步增强 ②我国社会生产力进一步提高 ③我国
国际影响力进一步扩大
④我国人民生活水平进一步提高
A.①② B.①②④
C.②③ D.①②③④
12345678
5.2016年至2021年,中欧班列年开行数量由1702列增长到15183列,年均增长55%;运输货物品类扩大到汽车配件及整车、化工、机电、粮食等5 万余种;年运输货值由80亿美元提升至749亿美元,增长了9倍,在中欧贸易总额中的占比从1.5%提高到8%。中欧班列的开行( C ) ①促进了中欧贸易的发展 ②开启了世界经济一体化的进程 ③顺应了时代发展的潮流 ④使中国成为世界第二大经济体 A.①② B.①②④ C.①③ D.①③④
互开放的程度不断加深,在政治、经济、文化各领域的开放范围也在不断扩展;新技术、新经济、新业态不断涌现并蓬勃发展,世界正经历着新一轮大发展大变革大调整;现代交通、通信、贸易把全球各地的国家、人们联系在一起,彼此影响,休戚相关。世界的变化既给国家发展带来深远影响, 也与我们的生活息息相关。
4.经济全球化的发展趋势商品生产在全球范围内完成、商品贸易在全球范围内进行,是经济
热点专题六和平发展齐合作
热点专题六和平发展齐合作
栏目导航
1 数据链接观点归纳 2 数据共享热点聚焦
3 数据分类题组演练
1 数据链接观点归纳
1.当今时代的主题世界上维护和平的力量不断壮大,和平与发展成为时代的主题。维护
和平、促进发展,是各国人民的共同愿望,也是不可阻挡的历史潮流。 2.中国的世界角色
新征程上,中国共产党将一如既往关注人类前途命运,正确认识和处理同世界各国的关系,在习近平新时代中国特色社会主义思想指导下,领导中国始终做世界和平的建设者、全球发展的贡献者、国际秩序的维护者,不断为人类文明进步贡献智慧和力量。

高考地理专题 6土壤的有机质多少的分析思路

1．土壤的有机质多少的分析思路
(1)核心思维：土壤有机质的变化＝有机质收入量－有机质的支出量。

(2)有机质收入量：枯枝落叶多(含生物遗体多)，夏季气候温和湿润或高温多雨，雨热同期，植物生长多，冬季寒冷干燥，枯枝落叶多。

(3)有机质支出量：
①微生物消耗：气温高，微生物活跃，分解快，消耗多；气温低，微生物活动弱，分解慢，消耗少。

②植被消耗：植被生长旺盛，消耗大；某种植被生长慢或某
种植被减少，消耗少。

③土壤侵蚀或淋溶：风力、流水侵蚀会造成土壤有机质流失；降水较多，会造成有机质溶解流失。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高考总复习· 英语
3．If you miss this chance, it may be years _______ you get another one.(2015重庆) 4．I have heard a lot of good things about you ________I came back from abroad.(2013陕西) 【答案】1.before 2.before 3.before 4.since
高考总复习· 英语
4 ． Her parents passed away ________she was still at school. 5．________ she grew older she gained in confidence. 【答案】1.when 2.when 3.as/when 4.when 5.As
高考总复习· 英语
二、when，while，as引导时间状语从句的用法
用法引导时间状语从句时，既可引导“ when 时间点”，也可引导“时间段”。引导时间状语从句时，只能引导“ while 时间段”。此时可与when换用。引导时间状语从句时通常与 when通 as 用，另外它还可以表示“随着”。连词
高考总复习· 英语
选用上表中适当的连词填空 1．It was the middle of the night _______ my father woke me up and told me to watch the football game.(2014江西) 2 ． It's much easier to make friends __________you have similar interests.(2013安徽) 3 ． He smiled politely _______Mary apologized for her drunken friends.(2012山东)
连词
高考总复习· 英语
用法表示因果关系，引导并列分句，对前面分句加以解释或补充说 for 明，且只能后置，常用逗号与前面的句子隔开。 so 表示因果关系，意为“因此”。 although/though不能与but连用，特别提醒但可以和yet或still连用。
连词
高考总复习· 英语
选用上表中适当的连词填空 1. He is a shy man, _______ he is not afraid of anything or anyone.(2015北京) 2．Some animals carry seeds from one place to another, _______plants can spread to new places.(2014北京)
高考总复习· 英语
专题六
并列句和状语从句
高考总复习· 英语
一、并列连词 yet ， but ， when 折，此时注意 yet位置且前面必须加逗号。连接两个并列成分或两个并列分句，意为“但是，然而”。
高考总复习· 英语
用法作并列连词时，意义为“这时，那时”，相当于and at this/that time。常用于下列句式：①sb.was when doing sth.when…② sb.was about to/going to do sth.when„③sb.was on the point of doing sth.when„④ sb.had just done sth.when„ 作并列连词时，意为“而， while 却”，表示对比。
连词
高考总复习· 英语
用适当的连词填空 1 ． We need to get to the root of the problem______ we can solve it.(2015天津) 2 ． There is only one more day to go ______your favorite music group play live.(2015 四川)
高考总复习· 英语
3．There's no way of knowing why one man makes an important discovery________ another man, also intelligent, fails.(2013课标Ⅰ) 4．One Friday，we were packing to leave for a weekend away ________my daughter heard cries for help. 5．He found it increasingly difficult to read, _______his eyesight was beginning to fail. 【答案】1.but/yet 2.so 3.while 4.when 5.for
高考总复习· 英语
三、since，before 引导的时间状语从句的用法
用法 since从句的谓语动词一般是非延续性动词，主句谓语动词用完成时。在since从句中，如果动词是延续性的， since 则可理解为某一动作结束已经多久。用在“It is＋一段时间＋since„”中，表示“自从„„以来已经多长时间”。连词
高考总复习· 英语
用法 before表示“还未„„就„„；不到 „„就„„；„„才„„；趁„„；还没来得及„„就„„；在„„之前”。 It will be＋一段时间＋before„意为“ before 多久之后才„„”。 It won't be long before„意为“不久之后就„„”。 It was＋一段时间＋before„意为“过了多久才„„”。
高考总复习· 英语
四、表示 “ 刚 „„ 就 „„ ；一 „„ 就„„”的常用表达 1 ． as soon as, immediately, directly, instantly, the moment, the minute, the instant 2 ． no sooner„than„ ， hardly/ scarcely „when„