计算机图形学实验报告记录
计算机图形学实验一报告

计算机图形学实验一报告————————————————————————————————作者:————————————————————————————————日期:ﻩ计算机科学与通信工程学院实验报告课程计算机图形学实验题目二维图形绘制学生姓名学号专业班级指导教师日期成绩评定表评价内容具体内容权重得分论证分析方案论证与综合分析的正确、合理性20%算法设计算法描述的正确性与可读性20%编码实现源代码正确性与可读性30%程序书写规范标识符定义规范,程序书写风格规范20%报告质量报告清晰,提交准时10%总分指导教师签名二维图形的绘制1.实验内容(1)绘制金刚石图案金刚石图案的成图规则是:把一个圆周等分成n份,然后每两点之间连线。
当n取奇数时,该图案可一笔连续绘成,即用MoveTo函数确定一个当前点,然后连续用LineTo函数连点成线。
请设计连线规则并编程实现。
(2)绘制魔术三角形绘制下图所示的魔术三角形图案,采用三种可明显区分的颜色填充。
(3)绘制递归圆应用递归的方法绘制如下所示的图案。
2.实验环境软硬件运行环境:Windows XP开发工具:visual studio 20083. 问题分析根据实验需求,需要在MFC环境中建立一个由“文件”、“绘图”和“帮助”这3个菜单项目组成的菜单,其中“文件”的子菜单为“退出”,完成退出应用程序的工作,“绘图”,的子菜单为“Diamond”,用于绘制金刚石图案等,“帮助”的子菜单为“关于”,用于显示开发人员信息;定义一个输人对话框类,提供个两个参数的输入界面。
最后在客户区输出图案。
1.金刚石图案:为把一个半径为300的圆,等分绘制金刚石图案;设计该算法为避免直线段的重复连接,需设计一个二重循环,代表起点索引号的外层整型变量i从i=0循环到i=n-2,代表终点索引号的内层整型变量j从j=i+1循环到j=n-1。
以(p[i].x,p[i].y)为起点,以(p[j].x,p[j].y)为终点依次连接各线段形成金刚石图案。
计算机图形学第一次上机实验报告

计算机图形学上机实验报告实验名称:用DDA算法生成直线姓名:***班级:信息与计算科学学号:**********一:DDA 算法的思想精髓实现直线段光栅化的最简单的方法就是解直线的微分方程。
设直线的起点坐标为 (x s , y s ),终点坐标为 (x e , y e ),那么该直线的微分方程是:()m x x y y dx dy se s e =--=其离散解为:x x x y y y y y y s e s e i i i ∆--+=∆+=+1或: y y y x x x x x x s e s e i i i ∆--+=∆+=+1这里 (x i , y i ) 是直线上一点的坐标值。
式(3.2.1)和(3.2.2)表示所求直线 y 值和 x 值关于相应增量的逐次递归关系,递归初值为直线的起点。
DDA (Digital Differential Analyzer) 算法即数字微分分析算法就是基于式(3.2.1)或(3.2.2)对直线进行光栅化的算法。
在一个坐标轴上以单位间隔对直线采样,以决定另一个坐标轴上最靠近直线的对应整数值。
(1)当直线斜率 0 ≤ m ≤ 1 时,则按单位 x 间隔(D x = 1)取样并计算每个连续的 y 值:m y y i i +=+1(2)当 -1≤ m ≤ 0 时,则仍按单位 x 间隔(D x =-1)取样并计算每个连续的 y 值:m y y i i -=+1(3)当 m >1 时,则将 x 和 y 交换,这就是说,按单位 y 间隔(D y = 1) 取样并计算每个连续的 x 值:11-++=m x x i i(4)当 m <- 1 时,则同样交换 x 和 y 交换,并按 D y =- 1间隔取样计算每个连续的 x 值:11-+-=m x x i i应用上面的算式,解可以设计斜率为任意值的直线。
二:程序代码:#include<stdio.h>#include<graphics.h>#include<math.h>void lineDDA(int xs,int ys,int xe,int ye,int c){int i;float x=xs,y=ys;float xIncrement ,yIncrement,steps,dx=xe-xs,dy=ye-ys; steps=abs(dx);if(abs(dy)>abs(dx))steps=abs(dy);xIncrement=dx/steps;yIncrement=dy/steps;putpixel(x,y,c);for(i=1;i<=steps;i++){x+=xIncrement;y+=yIncrement;putpixel(x,y,c);}}main(){int gdriver=DETECT;int gmode;initgraph(&gdriver,&gmode,""); setbkcolor(MAGENTA); lineDDA(10,14,20,50,1); getch();closegraph();}三:程序截图如下:四:试验心得体会:(1)DDA算法生成直线是非常快的,但是有一点需要注意的,就是x,y的数值类型。
计算机图形学实验报告4

计算机图形学实验报告4一、实验目的本次计算机图形学实验旨在深入了解和掌握计算机图形学中的一些关键概念和技术,通过实际操作和编程实现,提高对图形生成、变换、渲染等方面的理解和应用能力。
二、实验环境本次实验使用的软件环境为_____,编程语言为_____,硬件环境为_____。
三、实验内容1、二维图形的绘制使用基本的绘图函数,如直线、矩形、圆形等,绘制简单的二维图形。
通过设置线条颜色、填充颜色等属性,增强图形的表现力。
2、图形的几何变换实现图形的平移、旋转和缩放操作。
观察不同变换参数对图形的影响。
3、三维图形的生成构建简单的三维模型,如立方体、球体等。
应用光照和材质效果,使三维图形更加逼真。
四、实验步骤1、二维图形的绘制首先,在编程环境中导入所需的图形库和相关模块。
然后,定义绘图窗口的大小和坐标范围。
接下来,使用绘图函数按照指定的坐标和参数绘制直线、矩形和圆形。
最后,设置图形的颜色和填充属性,使图形更加美观。
2、图形的几何变换对于平移操作,通过修改图形顶点的坐标值来实现水平和垂直方向的移动。
对于旋转操作,根据旋转角度计算新的顶点坐标,实现图形的绕中心点旋转。
对于缩放操作,将图形的顶点坐标乘以缩放因子,达到放大或缩小图形的效果。
3、三维图形的生成首先,定义三维模型的顶点坐标和三角形面的连接关系。
然后,设置光照的位置、颜色和强度等参数。
接着,为模型添加材质属性,如颜色、反射率等。
最后,使用渲染函数将三维模型显示在屏幕上。
五、实验结果与分析1、二维图形的绘制成功绘制出了各种简单的二维图形,并且通过颜色和填充的设置,使图形具有了更好的视觉效果。
例如,绘制的矩形和圆形边缘清晰,颜色鲜艳,填充均匀。
2、图形的几何变换平移、旋转和缩放操作都能够准确地实现,并且变换效果符合预期。
在旋转操作中,发现旋转角度的正负会影响旋转的方向,而缩放因子的大小直接决定了图形的缩放程度。
3、三维图形的生成生成的三维模型具有一定的立体感和真实感。
计算机图形学第五次实验报告

《计算机图形学》实验报告实验十一真实感图形一、实验教学目标与基本要求初步实现真实感图形, 并实践图形的造型与变换等。
二、理论基础运用几何造型, 几何、投影及透视变换、真实感图形效果(消隐、纹理、光照等)有关知识实现。
1.用给定地形高程数据绘制出地形图;2.绘制一(套)房间,参数自定。
三. 算法设计与分析真实感图形绘制过程中, 由于投影变换失去了深度信息, 往往导致图形的二义性。
要消除这类二义性, 就必须在绘制时消除被遮挡的不可见的线或面, 习惯上称之为消除隐藏线和隐藏面, 或简称为消隐, 经过消隐得到的投影图称为物体的真实图形。
消隐处理是计算机绘图中一个引人注目的问题, 目前已提出多种算法, 基本上可以分为两大类:即物体空间方法和图象空间方法。
物体空间方法是通过比较物体和物体的相对关系来决定可见与不可见的;而图象空间方法则是根据在图象象素点上各投影点之间的关系来确定可见与否的。
用这两类方法就可以消除凸型模型、凹形模型和多个模型同时存在时的隐藏面。
1).消隐算法的实现1.物体空间的消隐算法物体空间法是在三维坐标系中, 通过分析物体模型间的几何关系, 如物体的几何位置、与观察点的相对位置等, 来进行隐藏面判断的消隐算法。
世界坐标系是描述物体的原始坐标系, 物体的世界坐标描述了物体的基本形状。
为了更好地观察和描述物体, 经常需要对其世界坐标进行平移和旋转, 而得到物体的观察坐标。
物体的观察坐标能得到描述物体的更好视角, 所以物体空间法通常都是在观察坐标系中进行的。
观察坐标系的原点一般即是观察点。
物体空间法消隐包括两个基本步骤, 即三维坐标变换和选取适当的隐藏面判断算法。
选择合适的观察坐标系不但可以更好地描述物体, 而且可以大大简化和降低消隐算法的运算。
因此, 利用物体空间法进行消隐的第一步往往是将物体所处的坐标系转换为适当的观察坐标系。
这需要对物体进行三维旋转和平移变换。
常用的物体空间消隐算法包括平面公式法、径向预排序法、径向排序法、隔离平面法、深度排序法、光线投射法和区域子分法。
计算机图形学实验报告_2

计算机图形学实验报告学号:********姓名:班级:计算机 2班指导老师:***2010.6.19实验一、Windows 图形程序设计基础1、实验目的1)学习理解Win32 应用程序设计的基本知识(SDK 编程);2)掌握Win32 应用程序的基本结构(消息循环与消息处理等); 3)学习使用VC++编写Win32 Application 的方法。
4)学习MFC 类库的概念与结构;5)学习使用VC++编写Win32 应用的方法(单文档、多文档、对话框);6)学习使用MFC 的图形编程。
2、实验内容1)使用WindowsAPI 编写一个简单的Win32 程序,调用绘图API 函数绘制若干图形。
(可选任务)2 )使用MFC AppWizard 建立一个SDI 程序,窗口内显示"Hello,Thisis my first SDI Application"。
(必选任务)3)利用MFC AppWizard(exe)建立一个SDI 程序,在文档视口内绘制基本图形(直线、圆、椭圆、矩形、多边形、曲线、圆弧、椭圆弧、填充、文字等),练习图形属性的编程(修改线型、线宽、颜色、填充样式、文字样式等)。
定义图形数据结构Point\Line\Circle 等保存一些简单图形数据(在文档类中),并在视图类OnDraw 中绘制。
3、实验过程1)使用MFC AppWizard(exe)建立一个SDI 程序,选择单文档;2)在View类的OnDraw()函数中添加图形绘制代码,说出字符串“Hello,Thisis my first SDI Application”,另外实现各种颜色、各种边框的线、圆、方形、多边形以及圆弧的绘制;3)在类视图中添加图形数据point_pp,pp_circle的类,保存简单图形数据,通过在OnDraw()函数中调用,实现线、圆的绘制。
4、实验结果正确地在指定位置显示了"Hello,This is my first SDI Application"字符串,成功绘制了圆,椭圆,方形,多边形以及曲线圆弧、椭圆弧,同时按指定属性改绘了圆、方形和直线。
计算机图形学实验报告

计算机图形学实验报告
实验目的:通过本次实验,深入了解并掌握计算机图形学的基本原理和相关技术,培养对图形处理的理解和能力。
实验内容:
1. 图像的基本属性
- 图像的本质及表示方法
- 像素和分辨率的概念
- 灰度图像和彩色图像的区别
2. 图像的处理技术
- 图像的采集和处理
- 图像的变换和增强
- 图像的压缩和存储
3. 计算机图形学的应用
- 图像处理在生活中的应用
- 计算机辅助设计中的图形学应用
- 三维建模和渲染技术
实验步骤和结果:
1. 在计算机图形学实验平台上加载一张测试图像,分析其像素构成
和基本属性。
2. 运用图像处理技术,对测试图像进行模糊、锐化、色彩调整等操作,观察处理后的效果并记录。
3. 学习并掌握计算机图形学中常用的处理算法,如卷积、滤波等,
尝试应用到测试图像上并进行实验验证。
4. 探讨计算机图形学在数字媒体制作、虚拟现实、计算机辅助设计
等领域的应用案例,并总结其在实践中的重要性和价值。
结论:
通过本次实验,我对计算机图形学有了更深入的了解,掌握了图像
处理技术的基本原理和应用方法。
计算机图形学作为一门重要的学科,对多个领域有着广泛的应用前景,有助于提高数字媒体技术、虚拟现
实技术等领域的发展水平。
希望在未来的学习和工作中能进一步深化
对计算机图形学理论和实践的研究,不断提升自己在这一领域的专业
能力和创新意识。
《计算机图形学》实验4实验报告

实验4实验报告格式实验报告格式《计算机图形学》实验4实验报告实验报告实验题目:参数曲线绘制实验内容:1 圆的参数曲线绘制。
2显式数学曲线描绘程序。
显式数学曲线描绘程序。
3贝赛尔曲线绘制。
贝赛尔曲线绘制。
编写程序调用验证之。
编写程序调用验证之。
参考资料:1 circleParam.java2 explicitCurve.java3 BezierLine.java4 数学曲线绘制.ppt 和实验3的参考ppt基本概念:(详细叙述自己对实验内容的理解)(详细叙述自己对实验内容的理解)(1)圆的参数曲线绘制: 圆的参数曲线绘制就是按照圆的定义,利用步长,圆的参数曲线绘制就是按照圆的定义,利用步长,得在显示得在显示域上每一点的位置,然后绘制,圆是图形中经常使用的元素,圆是图形中经常使用的元素,圆被定义为所有离一中心位置圆被定义为所有离一中心位置),(yc xc 距离为给定值距离为给定值R 的点集,其函数方程为:222)()(R yc y xc x =-+-参数方程为:{)20(cos sin p £<+=+=t tR Xc X t R Yc Y根据已知的Xc 和Yc ,以及t 可以确定一个圆。
可以确定一个圆。
(2)显示数学曲线描绘程序:显示曲线的绘制就是在已知的坐标系上,按照方程要求在固定的点画点,然后连接成一条线,例如如果曲线的方程式:c bx ax y ++=2,利用这个公式的递推演算,我们依次从-x 到+x 来绘制。
来绘制。
(3)贝塞尔曲线的绘制:贝赛尔曲线的每一个顶点都有两个控制点,用于控制在顶点两侧的曲线的弧度。
它是应用于二维图形应用程序的数学曲线。
它是应用于二维图形应用程序的数学曲线。
曲线的定义有四个点:曲线的定义有四个点:曲线的定义有四个点:起始起始点、终止点(也称锚点)以及两个相互分离的中间点。
滑动两个中间点,贝塞尔曲线的形状会发生变化。
例如下面的公式:)10)(()(0,££=å=t t B p t p ni n i i算法设计:(详细叙述自己设计的的算法)(详细叙述自己设计的的算法)(1)圆的算法设计:本例体现的主要是圆的快速算法,这里的主要算法是:本例体现的主要是圆的快速算法,这里的主要算法是:{)20(cos sin p £<+=+=t t R Xc X t R Yc Y t 是圆的某一点与X 轴之间的夹角。
计算机图形学实验报告B样条曲线

千里之行,始于足下。
计算机图形学实验报告B样条曲线B样条曲线是计算机图形学中常用的一种曲线表示方法。
它通过插值曲线的控制点来定义曲线的形状,并且具有较好的平滑性。
本次实验中,我们使用C++语言实现了B样条曲线的生成和显示,并进行了相应的实验和分析。
实验目的:1.了解B样条曲线的原理和算法;2.掌握B样条曲线的生成和显示方法;3.通过实验观察和分析B样条曲线的性质。
一、B样条曲线的原理B样条曲线是一种基于控制点的插值曲线,它通过一系列连续的基函数(B 样条基函数)来插值控制点,从而生成曲线。
B样条曲线的基本原理如下:1.选择一组控制点P0,P1,…,PN-1;2.定义一组节点向量U={u0,u1,…,um},其中u0<=u1<=…<=um;3.通过插值曲线的标准等式,通过计算线性组合来计算曲线上每个点的坐标。
二、B样条曲线的算法1.计算节点向量U;2.定义B样条基函数;3.计算曲线上每个点的坐标。
三、实验步骤和结果1.计算节点向量U:在实验中,我们选择均匀节点向量,即ui=i,其中i=0,1,…,m。
这样的节点向量比较简单,而且能够生成比较平滑的曲线。
第1页/共3页锲而不舍,金石可镂。
2.定义B样条基函数:B样条基函数是用来插值曲线的重要部分,它可以通过递归定义来实现。
在实验中,我们使用了三次B样条基函数,其递归定义如下:N(i,1)(u)={1,u∈[ui,ui+1];0,否则}N(i,k)(u)=[(u-ui)/(ui+k-1-ui)]*N(i,k-1)(u)+(ui+1-u)/(ui+k-ui+1)*N(i+1,k-1)(u)3.计算曲线上每个点的坐标:通过计算线性组合来计算曲线上每个点的坐标。
具体计算方法如下:P(u)=sum(B(i,k)(u)*Pi,i=0 to n-1),其中B(i,k)(u)=N(i,k)(u)/sum(N(j,k)(u))四、实验结果和分析在实验中,我们通过改变控制点的位置和数量,生成了不同的B样条曲线,并进行了显示和分析。
《计算机图形学》实验报告

《计算机图形学》实验报告一、实验目的计算机图形学是一门研究如何利用计算机生成、处理和显示图形的学科。
通过本次实验,旨在深入理解计算机图形学的基本原理和算法,掌握图形的生成、变换、渲染等技术,并能够运用所学知识解决实际问题,提高对图形学的应用能力和编程实践能力。
二、实验环境本次实验使用的编程语言为 Python,使用的图形库为 Pygame。
开发环境为 PyCharm。
三、实验内容1、直线的生成算法DDA 算法(Digital Differential Analyzer)Bresenham 算法DDA 算法是通过计算直线的斜率来确定每个像素点的位置。
它的基本思想是根据直线的斜率和起始点的坐标,逐步计算出直线上的每个像素点的坐标。
Bresenham 算法则是一种基于误差的直线生成算法。
它通过比较误差值来决定下一个像素点的位置,从而减少了计算量,提高了效率。
在实验中,我们分别实现了这两种算法,并比较了它们的性能和效果。
2、圆的生成算法中点画圆算法中点画圆算法的核心思想是通过判断中点的位置来确定圆上的像素点。
通过不断迭代计算中点的位置,逐步生成整个圆。
在实现过程中,需要注意边界条件的处理和误差的计算。
3、图形的变换平移变换旋转变换缩放变换平移变换是将图形在平面上沿着指定的方向移动一定的距离。
旋转变换是围绕一个中心点将图形旋转一定的角度。
缩放变换则是改变图形的大小。
通过矩阵运算来实现这些变换,可以方便地对图形进行各种操作。
4、图形的填充种子填充算法扫描线填充算法种子填充算法是从指定的种子点开始,将相邻的具有相同颜色或属性的像素点填充为指定的颜色。
扫描线填充算法则是通过扫描图形的每一行,确定需要填充的区间,然后进行填充。
在实验中,我们对不同形状的图形进行了填充,并比较了两种算法的适用情况。
四、实验步骤1、直线生成算法的实现定义直线的起点和终点坐标。
根据所选的算法(DDA 或Bresenham)计算直线上的像素点坐标。
计算机图形学实验报告

计算机图形学实验报告引言计算机图形学是计算机科学中一个重要的研究领域,它涉及了计算机图像的生成、处理和显示等方面的技术。
本次实验旨在通过实际操作学习计算机图形学的相关知识,并利用图形学算法实现一些有趣的效果。
实验目的1. 了解计算机图形学的基本概念和发展历程;2. 掌握图形学中的基本几何变换,如平移、旋转和缩放等;3. 实现一些常见的图形学算法,如光照模型、三角形剪裁和绘制等。
实验准备在开始实验之前,我们需要准备一些实验所需的工具和环境。
首先,确保计算机上安装了图形学相关的软件,如OpenGL或DirectX等。
其次,为了编写和运行图形学程序,我们需要掌握基本的编程技巧,如C++或Python语言,并了解相关的图形库和API。
实验过程1. 实现平移、旋转和缩放首先,我们需要掌握图形学中的基本几何变换,如平移、旋转和缩放。
通过矩阵运算,我们可以很方便地实现这些变换。
例如,对于一个二维点P(x, y),我们可以通过以下公式实现平移:P' = T * P其中,P'是平移后的点,T是平移矩阵。
类似地,我们可以用旋转矩阵和缩放矩阵来实现旋转和缩放效果。
2. 实现光照模型光照模型是指在计算机图形学中模拟现实光照效果的一种方法。
它可以提供更真实的视觉效果,让计算机生成的图像更加逼真。
其中,常用的光照模型有环境光照、漫反射光照和镜面光照等。
通过计算每个像素的光照强度,我们可以实现阴影效果和光源反射等功能。
3. 实现三角形剪裁三角形剪裁是计算机图形学中一种常用的几何算法,用于确定哪些像素需要绘制,哪些像素需要剔除。
通过对三角形的边界和视口进行比较,我们可以快速计算出剪裁后的三角形顶点,以提高图形渲染的效率。
4. 实现图形绘制图形绘制是计算机图形学中的核心内容,它包括了点、线和面的绘制等。
通过设定顶点坐标和属性(如颜色、纹理等),我们可以使用算法绘制出各种形状的图像。
其中,常用的绘制算法有Bresenham算法和扫描线算法等。
计算机图形学 有效边表填充算法实验报告

实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。
7 个顶点分别为:P0(7, 8), P1(3, 12), P2(1, 7), P3(3, 1), P4(6, 5), P5(8, 1), P6(12, 9)。
在1024×768 的显示分辩率下, 将多边形顶点放大为P0(500,400), P1(350, 600), P2(250, 350), P3(350, 50), P4(500, 250), P5(600, 50), P6(800, 450)。
请使用有效边表算法填充该多边形。
图1示例多边形图2 屏幕显示多边形3.算法设计:(1)建立AET和BUCKET类;(2)初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表;(3)对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环;(4)按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间;(5)用指定颜色点亮填充区间内的所有像素, 即完成填充工作。
4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。
计算机图形学实验报告

计算机图形学实验报告计算机图形学实验报告引言计算机图形学是研究计算机生成和处理图像的学科,它在现代科技和娱乐产业中扮演着重要的角色。
本实验报告旨在总结和分享我在计算机图形学实验中的经验和收获。
一、实验背景计算机图形学实验是计算机科学与技术专业的一门重要课程,通过实践操作和编程,学生可以深入了解图形学的基本原理和算法。
本次实验主要涉及三维图形的建模、渲染和动画。
二、实验内容1. 三维图形建模在实验中,我们学习了三维图形的表示和建模方法。
通过使用OpenGL或其他图形库,我们可以创建基本的几何体,如立方体、球体和圆柱体,并进行变换操作,如平移、旋转和缩放。
这些基本操作为后续的图形处理和渲染打下了基础。
2. 光照和着色光照和着色是图形学中重要的概念。
我们学习了不同的光照模型,如环境光、漫反射和镜面反射,并了解了如何在三维场景中模拟光照效果。
通过设置材质属性和光源参数,我们可以实现逼真的光照效果,使物体看起来更加真实。
3. 纹理映射纹理映射是一种将二维图像映射到三维物体表面的技术。
通过将纹理图像与物体的顶点坐标相对应,我们可以实现更加细致的渲染效果。
在实验中,我们学习了纹理坐标的计算和纹理映射的应用,使物体表面呈现出具有纹理和细节的效果。
4. 动画和交互动画和交互是计算机图形学的重要应用领域。
在实验中,我们学习了基本的动画原理和算法,如关键帧动画和插值技术。
通过设置动画参数和交互控制,我们可以实现物体的平滑移动和变形效果,提升用户体验。
三、实验过程在实验过程中,我们首先熟悉了图形库的使用和基本的编程技巧。
然后,我们按照实验指导书的要求,逐步完成了三维图形建模、光照和着色、纹理映射以及动画和交互等任务。
在实验过程中,我们遇到了许多挑战和问题,但通过不断的尝试和调试,最终成功实现了预期的效果。
四、实验结果通过实验,我们成功实现了三维图形的建模、渲染和动画效果。
我们可以通过键盘和鼠标控制物体的移动和变形,同时观察到真实的光照效果和纹理映射效果。
计算机图形学划线实验报告

计算机图形学划线实验报告《计算机图形学》实验报告实验⼀直线、圆(弧)⽣成算法⼀、实验⽬的及要求1. 了解光栅图形显⽰器的⼯作原理和特点;2. 学习C/VC环境下的基本绘图⽅法;3. 实践与巩固直线的基本⽣成算法。
4. 掌握直线扫描转换算法的原理及实现;5. 学习圆(弧)的基本⽣成算法;6. 实践圆(弧)的基本⽣成算法;7. 掌握圆弧扫描转换算法的原理及实现;⼆、理论基础1、有关直线⽣成算法有DDA(数值微分)、中点画线线算法、Bresenham⽣成算法数值微分法先算出直线的斜率,然后从起点开始,确定最佳逼近于直线的y坐标。
假设起点的坐标为整数。
让x递增1,y相应递增k。
中点划线算法中若直线在x⽅向增加⼀个单位,y的增量只能在0、1之间。
假设当前像素点已经确定,下⼀像素点就只可能有两种情况,将这两点的中点带⼊直线⽅程中,通过中点在直线的上、下⽅来判断下⼀点的坐标。
Bresenham算法是通过各⾏、各列像素中⼼构造⼀组虚拟⽹络格线,按直线从起点到中点的顺序计算直线与各垂直⽹格线的交点,然后确定该列像素中与此交点最近的像素。
2、有关画圆的算法圆的扫描转换(中点画圆法)、Bresenham画圆算法圆的扫描转换算法同中点画线类似,将圆分为8份,先讨论圆的第⼀象限上半部分,从(0,R)点顺时针确定最佳逼近于该圆弧的像素序列。
之后通过对称画出全部圆。
Bresenham画圆算法考虑圆在第⼀象限上的点,每确定⼀像素,则下⼀像素有三种可能,通过判断右下⽅的像素与圆的位置关系再分为三种情况,之后通过这三个点与圆的距离远近确定最佳逼近像素。
三、算法设计与分析1、数值微分法int x0=0,y0=0,x1=800,y1=400; //数值微分法,|k|<=1float dx,dy,k,x,y;dx=x1-x0;dy=y1-y0;k=dy/dx;y=y0;for(x=x0;x<=x1;x++){pDC->SetPixel(x,int(y+0.5),color);y=y+k;}该程序中每⼀步的x、y值是⽤前⼀步的值加上⼀个增量来获得的。
计算机图形实验报告

计算机图形实验报告计算机图形实验报告引言:计算机图形学是一门研究如何使用计算机生成、处理和显示图像的学科。
在现代科技的发展中,计算机图形学的应用越来越广泛,涉及到许多领域,如电影制作、游戏开发、虚拟现实等。
本实验报告将介绍我在计算机图形实验中的学习和实践经验。
一、实验目的本次实验的主要目的是通过学习和实践,掌握计算机图形学的基本概念和技术。
具体来说,我们将学习如何使用计算机编程语言实现简单的图形绘制、变换和渲染等功能。
二、实验过程1. 学习基本概念在开始实验之前,我们首先学习了计算机图形学的基本概念,包括点、线、多边形等基本图元的表示方法,以及坐标系统和颜色模型等相关知识。
这些基础概念为后续的实验操作打下了坚实的基础。
2. 图形绘制在实验中,我们使用了一种编程语言来实现图形的绘制。
通过编写代码,我们可以在计算机屏幕上绘制出各种形状的图形,如直线、矩形、圆等。
这些图形的绘制是通过计算机的像素点来实现的,我们可以通过改变像素点的颜色和位置来绘制出不同的图形。
3. 图形变换除了图形的绘制,我们还学习了图形的变换技术。
通过对图形进行平移、旋转、缩放等操作,我们可以改变图形的位置、大小和形状。
这些变换操作可以通过矩阵运算来实现,通过改变矩阵的数值,我们可以对图形进行不同的变换操作。
4. 图形渲染图形渲染是计算机图形学中的一个重要环节。
通过对图形进行光照、阴影和纹理等处理,我们可以使图形看起来更加真实和逼真。
在实验中,我们学习了一些基本的渲染算法,如平均法线法、Phong光照模型等,通过应用这些算法,我们可以实现不同材质和光照条件下的图形渲染效果。
三、实验结果通过实验,我们成功地实现了一些基本的图形绘制、变换和渲染功能。
我们可以在计算机屏幕上绘制出各种形状的图形,并对其进行平移、旋转、缩放等操作。
同时,我们还实现了简单的光照和阴影效果,使图形看起来更加真实和立体。
四、实验总结通过本次实验,我对计算机图形学有了更深入的了解。
计算机图形学实验报告三

《计算机图形学》实验报告glClear(GL_COLOR_BUFFER_BIT);//glEnable(GL_SCISSOR_TEST);//glScissor(0.0f,0.0f,500,300);glutWireTeapot(0.4);glFlush();}//窗口调整子程序void myReshape(int w, int h){glViewport(500, -300, (GLsizei)w, (GLsizei)h);glMatrixMode(GL_PROJECTION);glLoadIdentity();if (w <= h)glOrtho(-1, 1, -(float)h / w, (float)h / w, -1, 1);elseglOrtho(-(float)w / h, (float)w / h, -1, 1, -1, 0.5);}2,使用opengl函数写一个图形程序,要求分别使用三个光源从一个茶壶的前右上方(偏红色),正左侧(偏绿色)和前左下方(偏蓝色)对于其进行照射,完成程序并观察效果。
}//绘图子程序void display(void){glColor3f(1.0, 1.0, 0.0);glClear(GL_COLOR_BUFFER_BIT);//glMatrixMode(GL_MODELVIEW);//glLoadIdentity();//设置光源的属性1GLfloat LightAmbient1[] = { 1.0f, 0.0f, 0.0f, 1.0f }; //环境光参数 ( 新增 )GLfloat LightDiffuse1[] = { 1.0f, 0.0f, 0.0f, 1.0f }; // 漫射光参数 ( 新增 )GLfloat Lightspecular1[] = { 1.0f, 0.0f, 0.0f, 1.0f }; // 镜面反射GLfloat LightPosition1[] = { 500.0f, 500.0f, 500.0f, 1.0f }; // 光源位置 ( 新增 ) glLightfv(GL_LIGHT0, GL_POSITION, LightPosition1);glViewport(0, 0, (GLsizei)w, (GLsizei)h);glMatrixMode(GL_PROJECTION);glLoadIdentity();3,使用opengl函数完成一个图形动画程序,显示一个球沿正弦曲线运动的过程,同时显示一个立方体沿抛物线运动过程。
《计算机图形学》实验3实验报告
实验3实验报告格式《计算机图形学》实验3实验报告实验题目:直线(光栅化)实数型Bresenham 算法在用户坐标系和Java AWT 坐标系下显示图像实验内容:1 直线(光栅化)实数型Bresenham 算法原理及程序。
2 直线(光栅化)DDA 算法原理及程序。
3 在用户坐标系和Java AWT 坐标系下显示图像的算法原理及实现。
写程序调用验证之。
参考资料:1 课件:光栅图形生成算法.PP T2 Bresenham 算法演示程序已经在MyCanvas 包里,DDA 算法applet 演示程序DDA.java3 有一个示范程序imageDrawApplet.java基本概念:(详细叙述自己对实验内容的理解) 直线(光栅化):画一条从(x1, y1)到(x2, y2)的直线,实质上是一个发现最佳逼近直线的像素序列、并填入色彩数据的过程。
这过程称为直线光栅化。
Bresenham 算法:Bresenham 直线算法是用来描绘由两点所决定的直线的算法,它会算出一条线段在 n 维光栅上最接近的点。
这个算法只会用到较为快速的整数加法、减法和位元移位,常用于绘制电脑画面中的直线。
DDA 算法:DDA 算法(Digital Differential Analyzer ),又称数值微分法,是计算机图形学中一种基于直线的微分方程来生成直线的方法。
算法设计:(详细叙述自己设计的Bresenham 算法以及程序的功能、不同坐标系下图像显示的算法)程序功能:用DDA 算法画出直线,在不同的坐标系下显示图像。
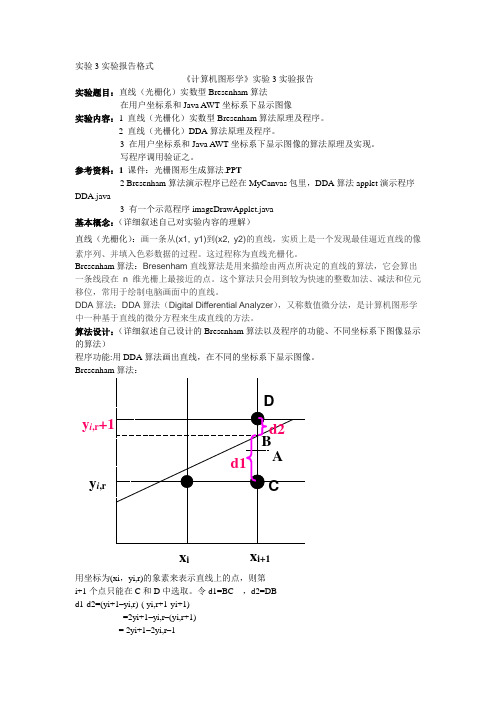
Bresenham 算法:用坐标为(xi ,yi,r)的象素来表示直线上的点,则第i+1个点只能在C 和D 中选取。
令d1=BC ,d2=DBd1-d2=(yi+1–yi,r)-( yi,r+1-yi+1)=2yi+1–yi,r –(yi,r+1)= 2yi+1–2yi,r –1x i x i+1令ε(xi+1)= yi+1–yi,r–0.5=BC-AC=BA=B-A= yi+1–(yi,r+ yi,r+1)/2当ε(xi+1)≥0时,yi+1,r= yi,r+1,即选D点,即下个点(xi+1,yi+1 )对应的象素(xi +1,yi+1,r )为(xi+1,yi,r+1 )当ε(xi+1)<0时,yi+1,r= yi,r,即选C点,即下个点(xi+1,yi+1 )对应的象素(xi +1,yi+1,r )为(xi+1,yi,r )ε(xi+1)= yi+1–yi,r–0.5ε(xi+1)≥0时,yi+1,r= yi,r+1ε(xi+1)<0时,yi+1,r= yi,r用户坐标系下图像显示算法:定义自己的坐标系,将用户坐标系转换为Java awt坐标,调用Graphics类的drawImage方法即可。
《计算机图形学》实验2实验报告

《计算机图形学》实验2实验报告《计算机图形学》实验2实验报告实验题目:多视图绘图程序实验内容:掌握多视图绘图的概念,掌握二维统计图的绘制方法。
调用实验1中自己编写的基本包,绘制自己所设计的统计图形(饼图、直方图以及折线)。
编写程序调用验证之。
基本概念:(详细叙述自己对实验内容的理解)多视图:就是将多个绘制好的图形按照一定的规则组成一个具有特定意义的图形,在同一个视图中显示出来,如下面绘制的几种统计图形(饼图、直方图以及折线)。
饼图:可以清楚的表示出各个部分所占的比例;直方图:可以清楚地的显示各部分的数量的多少;折线:可以清楚地反应各个部分的变化趋势。
算法设计:(详细叙述自己设计的多视图统计图以及程序的功能、算法及实现)public abstract void drawLine(int x1, int y1, int x2, int y2)使用当前颜色,在点(x1, y1) 和(x2, y2) 之间画线。
public abstract void drawOval(int x, int y, int width, int height) 画椭圆。
public abstract void fillOval(int x, int y, int width, int height)画实心椭圆。
public abstract void drawPolygon(int[] xPoints, int[] yPoints, int nPoints)画x和y坐标定义的多边形。
public void drawRect(int x, int y, int width, int height)画矩形。
public void drawRect(int x, int y, int width, int height)画实心矩形。
public abstract void drawRoundRect(int x, int y, int width, intheight, int arcWidth, int arcHeight) 使用当前颜色画圆角矩形。
计算机图形学实验报告

计算机图形学实验报告一、实验目的本次计算机图形学实验旨在深入了解和掌握计算机图形学的基本原理、算法和技术,通过实际操作和编程实现,提高对图形生成、处理和显示的能力,培养解决实际图形问题的思维和实践能力。
二、实验环境本次实验使用的编程语言为 Python,借助了相关的图形库如Pygame 或 matplotlib 等。
开发环境为 PyCharm 或 Jupyter Notebook。
三、实验内容(一)二维图形的绘制1、直线的绘制使用 DDA(Digital Differential Analyzer)算法或 Bresenham 算法实现直线的绘制。
通过给定直线的起点和终点坐标,在屏幕或图像上绘制出直线。
比较两种算法的效率和准确性,分析其优缺点。
2、圆的绘制采用中点画圆算法或 Bresenham 画圆算法绘制圆。
给定圆心坐标和半径,生成圆的图形。
研究不同半径大小对绘制效果和计算复杂度的影响。
(二)图形的填充1、多边形填充实现扫描线填充算法,对任意多边形进行填充。
处理多边形的顶点排序、交点计算和填充颜色的设置。
测试不同形状和复杂度的多边形填充效果。
2、图案填充设计自定义的填充图案,如纹理、条纹等,并将其应用于图形填充。
探索如何通过改变填充图案的参数来实现不同的视觉效果。
(三)图形的变换1、平移、旋转和缩放对已绘制的图形(如矩形、三角形等)进行平移、旋转和缩放操作。
通过矩阵运算实现这些变换。
观察变换前后图形的位置、形状和方向的变化。
2、组合变换将多个变换组合应用于图形,如先旋转再平移,或先缩放再旋转等。
分析组合变换的顺序对最终图形效果的影响。
(四)三维图形的表示与绘制1、三维坐标变换学习三维空间中的平移、旋转和缩放变换矩阵,并将其应用于三维点的坐标变换。
理解如何将三维坐标映射到二维屏幕上显示。
2、简单三维图形绘制尝试绘制简单的三维图形,如立方体、球体等,使用线框模型或表面模型。
探讨不同的绘制方法和视角对三维图形显示的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机图形学实验报告记录————————————————————————————————作者:————————————————————————————————日期:计算机图形学实验报告姓名:___ __________学号:_____ ________班级:______ _______时间:_____2016年12月_________实验一OpenGL编程与图形绘制1.实验目的了解OpenGL编程,并熟悉OpenGL的主要功能、绘制流程和基本语法。
学会配置OpenGL环境,并在该环境中编程绘图。
2.实验内容OpenGL的主要功能:模型绘制、模型观察、颜色模式、光照应用、图像效果增强、位图和图像处理、纹理映射、实时动画和交互技术。
OpenGL的绘制流程分为两个方面:一个完整的窗口系统的OpenGL图形处理系统的结构为:最底层为图形硬件,第二层为操作系统,第三层为窗口系统,第四层为OpenGL,最上面的层为应用软件;OpenGL命令将被放在一个命令缓冲区中,这样命令缓冲区中包含了大量的命令、顶点数据和纹理数据。
当缓冲区被清空时,缓冲区中的命令和数据都将传递给流水线的下一个阶段。
OpenGL的基本语法中相关库有:OpenGL核心库:gl、OpenGL实用程序库:glu、OpenG 编程辅助库:aux、OpenGL实用程序工具包(OpenGL utility toolkit,GLUT):glut、Windows 专用库:wgl。
OpenGL的基本语法中命名规则为:OpenGL函数都遵循一个命名约定,即采用以下格式:<库前缀><根命令><可选的参数个数><可选的参数类型>。
了解了上述基础知识后,配置好OpenGL环境,然后在该环境中编程练习图形的绘制,本次实验主要是对点的绘制、直线的绘制和多边形面的绘制。
3.实验代码及结果3.1点的绘制:#include<gl/glut.h>void Initial(void){glClearColor(1.0f,1.0f,1.0f,1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //指定设置投影参数gluOrtho2D(0.0,200.0,0.0,150.0); //设置投影参数}void Display(void){glClear(GL_COLOR_BUFFER_BIT); //用当前背景颜色填充窗口glColor3f(1.0f,0.0f,0.0f); //设置当前的绘图颜色为红// glRectf(50.0f,100.0f,150.0f,50.0f); //绘制一个矩形glPointSize(10); //三个点glBegin(GL_POINTS);glColor3f(1.0f,0.0f,0.0f);glVertex2i(2,148);glVertex2i(100,75);glVertex2i(198,2);glEnd();glFlush(); //清空OpenGL命令缓冲区,执行OpenGL程序}int main(int argc,char*argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //初始化窗口的显示模式glutInitWindowSize(400,300); //设置窗口的尺寸glutInitWindowPosition(100,120); //设置窗口位置glutCreateWindow("矩形"); //创建一个名为矩形的窗口glutDisplayFunc(Display); //设置当前窗口的显示回调函数Initial(); //完成窗口初始化glutMainLoop(); //完成窗口GLUT事件处理循环return 0;}运行结果:3.2直线的绘制:#include<gl/glut.h>void Initial(void){glClearColor(1.0f,1.0f,1.0f,1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //指定设置投影参数gluOrtho2D(0.0,200.0,0.0,150.0); //设置投影参数}void Display(void){glClear(GL_COLOR_BUFFER_BIT); //用当前背景颜色填充窗口glColor3f(1.0f,0.0f,0.0f); //设置当前的绘图颜色为红色// glRectf(50.0f,100.0f,150.0f,50.0f); //绘制一个矩形glBegin(GL_LINE_LOOP); //五角星glVertex2i(10,10);glVertex2i(30,35);glVertex2i(50,10);glVertex2i(5,25);glVertex2i(55,25);glEnd();glFlush(); //清空OpenGL命令缓冲区,执行OpenGL程序}int main(int argc,char*argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //初始化窗口的显示模式glutInitWindowSize(400,300); //设置窗口的尺寸glutInitWindowPosition(100,120); //设置窗口位置glutCreateWindow("矩形"); //创建一个名为矩形的窗口glutDisplayFunc(Display); //设置当前窗口的显示回调函数Initial(); //完成窗口初始化glutMainLoop(); //完成窗口GLUT事件处理循环return 0;}运行结果:3.3多边形面的绘制:#include<gl/glut.h>void Initial(void){glClearColor(1.0f,1.0f,1.0f,1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //指定设置投影参数gluOrtho2D(0.0,200.0,0.0,150.0); //设置投影参数}void Display(void){glClear(GL_COLOR_BUFFER_BIT); //用当前背景颜色填充窗口glColor3f(1.0f,0.0f,0.0f); //设置当前的绘图颜色为红色// glRectf(50.0f,100.0f,150.0f,50.0f); //绘制一个矩形glBegin(GL_TRIANGLES); //等边三角形glVertex2f(0.0,0.0);glVertex2f(15,25.95);glVertex2f(30,0);glEnd();glFlush(); //清空OpenGL命令缓冲区,执行OpenGL程序}int main(int argc,char*argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //初始化窗口的显示模式glutInitWindowSize(400,300); //设置窗口的尺寸glutInitWindowPosition(100,120); //设置窗口位置glutCreateWindow("矩形"); //创建一个名为矩形的窗口glutDisplayFunc(Display); //设置当前窗口的显示回调函数Initial(); //完成窗口初始化glutMainLoop(); //完成窗口GLUT事件处理循环return 0;}运行结果:实验二直线绘制实验1.实验目的为了进一步熟悉OpenGL编程,了解基本图形生成算法中的直线绘制,学会直线绘制算法中最常用的三种算法:数值微分法、中点画线算法和Bresenham算法。
2.实验内容(一)数值微分法数值微分法直接从直线的微分方程生成直线。
给定直线的两端点:P0(X0,Y0)和P1(X1,Y1),得到直线的微分方程dy/dx=△y/△x=(Y1-Y0)/(X1-X0)=k。
数值微分算法的原理是,由于直线的一阶导数是连续的,而且△x和△y是成比例的,因此通过在当前位置(Xi,Yi)分别加上两个小增量ε△x和ε△y(ε为无穷小的正数)来求下一点(X(i+1),Y(i+1))的x,y坐标。
(二)中点画线算法给定直线的两端点:P0(X0,Y0)和P1(X1,Y1),可得到直线方程F(x,y)=y-kx-b=0且k=△y/△x=(Y1-Y0)/(X1-X0)。
绘图过程如下:○1.输入直线的两端点P0(X0,Y0)和P1(X1,Y1)。
○2.计算初始值△x, △y,d=△x-2△y,x=X0,y=Y0.○3.绘制点(x,y)。
判断d的符号,若d<0,则(x,y)更新为(x+1,y+1),d更新为d+2△x-2△y;否则(x,y)更新为(x+1,y),d更新为△y。
○4.当直线没有画完时,重复步骤○3,否则结束。
(三)Bresenham算法算法步骤如下:○1.输入直线两端点P0(X0,Y0)和P1(X1,Y1)。
○2.计算初始值△x, △y,e=-△x,x=X0,y=Y0。
○3.绘制点(x,y)。
○4.e更新为e+2△y。
判断e的符号,若e>0,则(x,y)更新为(x+1,y+1),同样将e更新为e-2△x;否则(x,y)更新为(x+1,y)。
○5.当直线没有画完时,重复步骤○3和○4;否则结束。
3.实验代码及结果3.1数值微分算法编程绘制直线代码:#include<gl/glut.h>#include<windows.h>void Initial(void){glClearColor(1.0f,1.0f,1.0f,1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //指定设置投影参数gluOrtho2D(0.0,200.0,0.0,150.0); //设置投影参数}void Display(void){glClear(GL_COLOR_BUFFER_BIT); //用当前背景颜色填充窗口glColor3f(1.0f,0.0f,0.0f); //设置当前的绘图颜色为红色glBegin(GL_LINES);int x0=10;int y0=20;int x1=30;int y1=40;int color=10;int dx,dy,epsl,k;float x,y,xIncre,yIncre;dx=x1-x0;dy=y1-y0;x=x0;y=y0; //if(abs(dx)>abs(dy))epsl=abs(dx);else epsl=abs(dy);xIncre=(float)dx/(float)epsl;yIncre=(float)dy/(float)epsl;for(k=0;k<=epsl;k++){glVertex2i(int(x+0.5),(int)(y+0.5));x+=xIncre;y+=yIncre;}glEnd();glFlush(); //清空OpenGL命令缓冲区,执行OpenGL程序}int main(int argc,char*argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //初始化窗口的显示模式glutInitWindowSize(400,300); //设置窗口的尺寸glutInitWindowPosition(100,120); //设置窗口位置glutCreateWindow("矩形"); //创建一个名为矩形的窗口glutDisplayFunc(Display); //设置当前窗口的显示回调函数Initial(); //完成窗口初始化glutMainLoop(); //完成窗口GLUT事件处理循环return 0;}实验结果:2.2中点画线算法编程绘制直线代码:#include<gl/glut.h>#include<windows.h>void Initial(void){glClearColor(1.0f,1.0f,1.0f,1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //指定设置投影参数gluOrtho2D(0.0,200.0,0.0,150.0); //设置投影参数}void Display(void){glClear(GL_COLOR_BUFFER_BIT); //用当前背景颜色填充窗口glColor3f(1.0f,0.0f,0.0f); //设置当前的绘图颜色为红色glBegin(GL_POINTS);int x0=50;int y0=20;int x1=100;int y1=120;int color=10;int dx,dy,d,UpIncre,DownIncre,x,y;if(x0>x1){x=x1;x1=x0;x0=x;y=y1;y1=y0;y0=y;}x=x0;y=y0;dx=x1-x0;dy=y1-y0;d=dx-2*dy;UpIncre=2*dx-2*dy; DownIncre=2*dy;while(x<=x1){glVertex2i(x,y);x++;if(d<0){y++;d+=UpIncre;}else d+=DownIncre;}glEnd();glFlush(); //清空OpenGL命令缓冲区,执行OpenGL程序}int main(int argc,char*argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //初始化窗口的显示模式glutInitWindowSize(400,300); //设置窗口的尺寸glutInitWindowPosition(100,120); //设置窗口位置glutCreateWindow("矩形"); //创建一个名为矩形的窗口glutDisplayFunc(Display); //设置当前窗口的显示回调函数Initial(); //完成窗口初始化glutMainLoop(); //完成窗口GLUT事件处理循环return 0;}实验结果:2.3Bresenham算法编程绘制直线代码:#include <gl/glut.h>#include <windows.h>void Initial(void){glClearColor(1.0f,1.0f,1.0f,1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //指定设置投影参数gluOrtho2D(0.0,200.0,0.0,150.0); //设置投影参数}void Display(void){glClear(GL_COLOR_BUFFER_BIT); //用当前背景色填充窗口glColor3f(1.0f,0.0f,0.0f); //设置当前的绘图颜色为红色//Bresenham算法glBegin(GL_POINTS);int x0 = 10;int y0 = 20;int x1 = 90;int y1 = 90;int color=10;int x,y,dx,dy,e;dx = x1-x0;dy = y1-y0;e=-dx;x=x0;y=y0;while(x<=x1){glVertex2i(x,y);x++;e=e+2*dy;if(e>0){y++;e=e-2*dx;}}glEnd();glFlush(); //清空OpenGL命令缓冲区,执行OpenGL程序}int main(int argc,char*argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //初始化窗口的现实模式glutInitWindowSize(400,300); //设置窗口的尺寸glutInitWindowPosition(100,200); //设置窗口的位置glutCreateWindow("点"); //创建一个名为矩形的窗口glutDisplayFunc(Display); //设置当前窗口的显示函数Initial(); //完成窗口的初始化glutMainLoop(); //启动主GLUT事件处理循环return 0;}实验结果:实验三圆绘制实验1.实验目的2.实验内容(一)八分法画圆圆心位于原点的圆有4条对称轴x=0,y=0,y=x,y=-x。
