2006普通高等学校招生全国统一考试(重庆卷)
2006年普通高等学校招生全国统一考试(重庆卷)

2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(文史类)数学试题(文史类)共5页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮檫擦干净后,在选涂其他答案标号。
3.答非选择题时,必须用0.5mm 黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试卷上答题无效。
5.考试结束后,将试题卷和答题卡一并交回。
参考公式:如果事件A B 、互斥,那么()()()P A B P A P B +=+如果事件A B 、相互独立,那么()()()P A B P A P B =如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中恰好发生k 次的概率:()(1)k k n k n n P k C p p -=-一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个备选项中,只有一项是符合题目要求的。
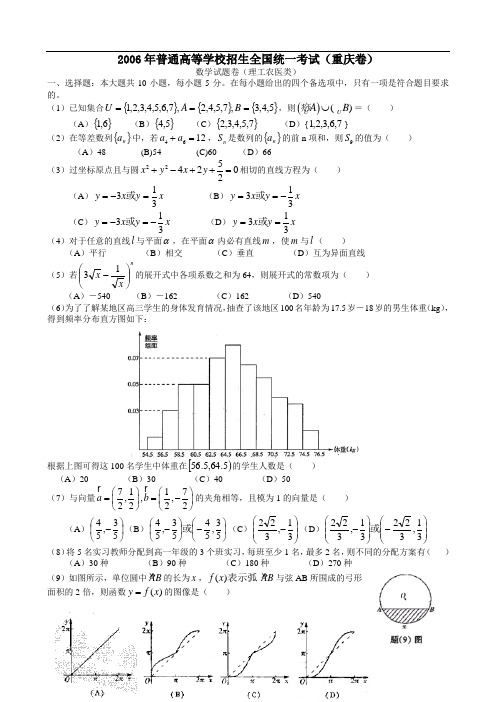
(1)已知集合{1,2,3,4,5,6,7}U =,{2,4,5,7}A =,{3,4,5}B =,则()()A B =U U 痧(A ){1,6} (B ){4,5} (C ){2,3,4,5,7} (D ){1,2,3,6,7}(2)在等差数列{}n a 中,若0n a >且3764a a =,5a 的值为(A )2 (B )4 (C )6 (D )8(3)以点(2,-1)为圆心且与直线3450x y -+=相切的圆的方程为(A )22(2)(1)3x y -++= (B )22(2)(1)3x y ++-=(C )22(2)(1)9x y -++= (D )22(2)(1)3x y ++-=(4)若P 是平面α外一点,则下列命题正确的是(A )过P 只能作一条直线与平面α相交 (B )过P 可作无数条直线与平面α垂直(C )过P 只能作一条直线与平面α平行 (D )过P 可作无数条直线与平面α平行(5)()523x -的展开式中2x 的系数为 (A )-2160 (B )-1080 (C )1080 (D )2160(6)设函数()y f x =的反函数为1()y f x -=,且(21)y f x =-的图像过点1(,1)2,则1()y f x -=的图像必过(A )1(,1)2 (B )1(1,)2(C )(1,0) (D )(0,1)(7)某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家。
高考理科综合试题及答案(重庆卷)

2006年普通高等学校招生全国统一考试(重庆)理科综合能力测试试题卷第I卷以下数据可供解题时参考:相对原子质量(原子量):H 1 O 16 S 32 Cl 35.5 Br 80 Fe 56 Pb 207选择题一(本题包括18小题。
每小题只有一个选项符合题意)1.题I图是某生态系统的食物网示意图。
甲~庚代表不同的生物,箭头表示能量流动的方向和食物联系。
下列叙述正确的是A 此食物网中有六条食物链,丁占有四个不同的营养级B 戊接受的太阳能是流经此生态系统的总能量C 丙可利用的总能量小于乙和丁可利用的总能量之和D 向此生态系统大量引入外来物种,可增强该系统的稳定性2.下列有关生物新陈代谢的叙述,正确的是A 完成有氧呼吸所需要的酶由线粒体DNA指导合成B 植物根系吸收矿质元素的速率与土壤溶液中矿质离子的浓度成正比C 用15N标记的蛋白质饲喂小白鼠,一段时间后可在其肝糖元中发现15ND 用14CO2研究玉米的光合作用过程,最早在C4化合物中检测到14C3.下列所述环境条件下的微生物,能正常生长繁殖的是A 在缺乏生长素的无氨培养基中的圆褐固氮菌B 在人体表皮擦伤部位的破伤风杆菌C 在新配制的植物矿质营养液中的酵母菌D 在灭菌后的动物细胞培养液中的禽流感病素4.下列有关生物大分子在细胞内转移的叙述,错误的是A 分泌蛋白可由核糖体进入内质网B DNA可由细胞核进入线粒体C mRNA可由细胞核进入细胞质D tRNA可由细胞质基质进入核糖体5.在用脊蛙(去除脑保留脊髓的蛙)进行反射弧分析的实验中,破坏缩腿反射弧在左上述结果表明,反射弧的被破坏部分可能是A 感受器B 感受器和传入神经C 传入神经和效应器D 效应器6.下列做法正确的是A 将浓硝酸保存在无色玻璃瓶中B 用镊子取出白磷并置于水中切割C 把氯酸钾制氧气后的残渣倒入垃圾桶D 氢气还原氧化铜实验先加热再通氢气7.设N A代表阿伏加德罗常数,下列说法正确的是A 5.6g铁与足量盐酸反应转移的电子数为0.3N AB 100mL 2.0mol/L的盐酸与醋酸溶液中氢离子数均为0.2N AC 标准状况下,22.4L氦气与22.4L氟气所含原子数均为2N AD 20g 重水(D 2O )中含有的电子数为10N A8.能正确表示下列反应的化学方程式是A 黄铁矿煅烧:2FeS 2+5O 22FeO +4SO 2B 石英与石灰石共熔:SiO 2+CaO CaSiO 3C 氨的催化氧化:4NH 3+5O 24NO +6H 2OD 氯气与石灰乳反应:2Cl 2+2Ca(OH)2=CaCl 2+CaClO 2+2H 2O9.温度相同、浓度均为0.2mol/L 的①(NH 4)2SO 4、②NaNO 3、③NH 4HSO 4、④NH 4NO 3、⑤-ONa 、⑥CH 3COONa 溶液,它们的pH 值由小到大的排列顺序是A ③①④②⑥⑤B ①③⑥④②⑤C ③②①⑥④⑤D ⑤⑥②④①③10.25℃、101kPa 下,碳、氢气、甲烷和葡萄糖的燃烧热依次是393.5kJ/mol 、285.8kJ/mol 、890.3kJ/mol 、2800kJ/mol ,则下列热化学方程式正确的是A C(s)+1/2O 2(g)=CO(g);△H =-393.5kJ/molB 2H 2(g)+O 2(g)=2H 2O(g);△H =+571.6kJ/molC CH 4(g)+2O 2(g)=CO 2(g)+2H 2O(g);△H =-890.3kJ/molD 1/2C 6H 12O 6(g)+3O 2(g)=3CO 2(g)+3H 2O(l);△H =-1400kJ/mol11.已知反应mX(g)+nY(g)qZ(g)的△H <0,m +n >q ,在恒容密闭容器中反应达到平衡时,下列说法正确的是A 通入稀有气体使压强增大,平衡将正向移动B X 的正反应速率是Y 的逆反应速率的m/n 倍C 降低温度,混合气体的平均相对分子质量变小D 增加X 的物质的量,Y 的转化率降低12.利尿酸在奥运会上被禁用,其结构简式如题12图所示。
2006年高考数学试卷(重庆卷.理)含详解
2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)一、选择题:本大题共10小题,每小题5分。
在每小题给出的四个备选项中,只有一项是符合题目要求的。
(1)已知集合{}{}{}5,4,3,7,5,4,2,7,6,5,4,3,2,1===B A U ,则()()U UA B ⋃痧=( )(A ){}6,1 (B ){}5,4 (C ){}7,5,4,3,2 (D ){7,6,3,2,1}(2)在等差数列{}n a 中,若4612a a +=,n S 是数列的{}n a 的前n 项和,则9S 的值为( ) (A )48 (B)54 (C)60 (D )66(3)过坐标原点且与圆2254202x y x y +-++=相切的直线方程为( ) (A )x y x y 313=-=或 (B )x y x y 313-==或(C )x y x y 313-=-=或 (D )x y x y 313==或(4)对于任意的直线l 与平面α,在平面α内必有直线m ,使m 与l ( )(A )平行 (B )相交 (C )垂直 (D )互为异面直线(5)若nx x ⎪⎪⎭⎫ ⎝⎛-13的展开式中各项系数之和为64,则展开式的常数项为( )(A )-540 (B )-162 (C )162 (D )540(6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg ),得到频率分布直方图如下:根据上图可得这100名学生中体重在[)5.64,5.56的学生人数是( ) (A )20 (B )30 (C )40 (D )50(7)与向量7117,,,2222a b ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭的夹角相等,且模为1的向量是( )(A )⎪⎭⎫ ⎝⎛-53,54(B )⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-53,5453,54或(C )⎪⎪⎭⎫ ⎝⎛-31,322(D )⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-31,32231,322或 (8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有( )(A )30种 (B )90种 (C )180种 (D )270种(9)如图所示,单位圆中AB 的长为x ,()f x 表示弧 AB 与弦AB 所围成的弓形面积的2倍,则函数()y f x =的图像是( )(A 1 (B 1 (C )2 (D )2 二、填空题:本大题共6小题,每小题4分,共24分。
2006年普通高等学校招生全国统一考试英语试题重庆卷

2006年普通高等学校招生全国统一考试英语试题重庆卷一、听力(共三节,满分30分)做题时,请先将答案划在试题卷上。
录音内容结束后,你将有两分钟的时间将试题卷上的答案转涂或转填到答题卡上。
第一节(共5小题;每小题1. 5分,满分7. 5分)请听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19. 15.B. £9. 15.C. £9. 18. 答案是B。
1. Where is Fred now?A. At the office.B. At home.C.In class.2. Whose dictionary is this?A. Bill’s.B. The man.C. The woman’s.3. What is the woman doing?A. Listening to the radio.B. Reading a newspaper.C. Watching television.4. What does the woman say about the question?A. She is ready to explain it.B. She doesn’t understand it.C.She has no time to answer it.5. What is the conversation mainly about?A. The car.B. The bicycle.C. The oil price.第二节(共12小题;每小题1. 5分,满分18分)请听下面4段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题卷的相应位置。
听每段对话或独白前,你将有时间阅读各小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
一般高等学校招生全国统一考试重庆卷理含详解

(A)30 种
(B)90 种
(9)如图所示,单位圆中 AAB 的长为 x , f (x)表示弧 AAB 与弦 AB 所围成的弓
形面积的 2 倍,则函数 y f (x) 的图像是( )
(C)180 种
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2006年高考重庆卷理综试卷及答案

2006年普通高等学校招生全国统一考试(重庆)理科综合能力测试试题卷第I卷以下数据可供解题时参考:相对原子质量(原子量):H 1 O 16 S 32 Cl 35.5 Br 80 Fe 56 Pb 207选择题一(本题包括18小题。
每小题只有一个选项符合题意)1.题I图是某生态系统的食物网示意图。
甲~庚代表不同的生物,箭头表示能量流动的方向和食物联系。
下列叙述正确的是A 此食物网中有六条食物链,丁占有四个不同的营养级B 戊接受的太阳能是流经此生态系统的总能量C 丙可利用的总能量小于乙和丁可利用的总能量之和D 向此生态系统大量引入外来物种,可增强该系统的稳定性2.下列有关生物新陈代谢的叙述,正确的是A 完成有氧呼吸所需要的酶由线粒体DNA指导合成B 植物根系吸收矿质元素的速率与土壤溶液中矿质离子的浓度成正比C 用15N标记的蛋白质饲喂小白鼠,一段时间后可在其肝糖元中发现15ND 用14CO2研究玉米的光合作用过程,最早在C4化合物中检测到14C3.下列所述环境条件下的微生物,能正常生长繁殖的是A 在缺乏生长素的无氨培养基中的圆褐固氮菌B 在人体表皮擦伤部位的破伤风杆菌C 在新配制的植物矿质营养液中的酵母菌D 在灭菌后的动物细胞培养液中的禽流感病素4.下列有关生物大分子在细胞内转移的叙述,错误的是A 分泌蛋白可由核糖体进入内质网B DNA可由细胞核进入线粒体C mRNA可由细胞核进入细胞质D tRNA可由细胞质基质进入核糖体5.在用脊蛙(去除脑保留脊髓的蛙)进行反射弧分析的实验中,破坏缩腿反射弧在左后肢的部分结构,观察双侧后肢对刺激的收缩反应,结果如下表:刺激部位反应破坏前破坏后左后肢左后肢收缩右后肢收缩左后肢不收缩右后肢不收缩右后肢左后肢收缩右后肢收缩左后肢不收缩右后肢收缩上述结果表明,反射弧的被破坏部分可能是A 感受器B 感受器和传入神经C 传入神经和效应器D 效应器6.下列做法正确的是A 将浓硝酸保存在无色玻璃瓶中B 用镊子取出白磷并置于水中切割C 把氯酸钾制氧气后的残渣倒入垃圾桶D 氢气还原氧化铜实验先加热再通氢气7.设N A代表阿伏加德罗常数,下列说法正确的是A 5.6g铁与足量盐酸反应转移的电子数为0.3N AB 100mL 2.0mol/L的盐酸与醋酸溶液中氢离子数均为0.2N AC 标准状况下,22.4L氦气与22.4L氟气所含原子数均为2N AD 20g 重水(D 2O )中含有的电子数为10N A8.能正确表示下列反应的化学方程式是A 黄铁矿煅烧:2FeS 2+5O 22FeO +4SO 2B 石英与石灰石共熔:SiO 2+CaO CaSiO 3C 氨的催化氧化:4NH 3+5O 24NO +6H 2OD 氯气与石灰乳反应:2Cl 2+2Ca(OH)2=CaCl 2+CaClO 2+2H 2O9.温度相同、浓度均为0.2mol/L 的①(NH 4)2SO 4、②NaNO 3、③NH 4HSO 4、④NH 4NO 3、⑤-ONa 、⑥CH 3COONa 溶液,它们的pH 值由小到大的排列顺序是A ③①④②⑥⑤B ①③⑥④②⑤C ③②①⑥④⑤D ⑤⑥②④①③10.25℃、101kPa 下,碳、氢气、甲烷和葡萄糖的燃烧热依次是393.5kJ/mol 、285.8kJ/mol 、890.3kJ/mol 、2800kJ/mol ,则下列热化学方程式正确的是A C(s)+1/2O 2(g)=CO(g);△H =-393.5kJ/molB 2H 2(g)+O 2(g)=2H 2O(g);△H =+571.6kJ/molC CH 4(g)+2O 2(g)=CO 2(g)+2H 2O(g);△H =-890.3kJ/molD 1/2C 6H 12O 6(g)+3O 2(g)=3CO 2(g)+3H 2O(l);△H =-1400kJ/mol11.已知反应mX(g)+nY(g)qZ(g)的△H <0,m +n >q ,在恒容密闭容器中反应达到平衡时,下列说法正确的是A 通入稀有气体使压强增大,平衡将正向移动B X 的正反应速率是Y 的逆反应速率的m/n 倍C 降低温度,混合气体的平均相对分子质量变小D 增加X 的物质的量,Y 的转化率降低12.利尿酸在奥运会上被禁用,其结构简式如题12图所示。
2006年普通高等学校招生全国统一考试重庆卷

2006年普通高等学校招生全国统一考试(重庆卷)语文语文试题卷共8页。
考式时间150分钟。
第1至11题为选择题,33分;第12至25题为非选择题,117分。
满分150分。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答第1至11题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答第12至25题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,将试题和答题卡一并交回。
一、(本大题共4小题,每小题3分,共12分)1.下列词语中加点的字的读音完全相同的一组是A.豁.免附和.蛊惑.人心祸.起萧墙B.遏.止扼.要鄂.伦春族厄.瓜多尔C.菁.华矜.持泾.渭分明惊.世骇俗D.撕裂.趔.趄烈.火金刚骂骂咧.咧2.下列词语中有错别的一组是A.慰藉销毁矫揉造诈瞠目结舌B.焦躁坐标变本加厉缘木求鱼C.颠簸竣工关怀备至顶礼摩拜D.盘绕静谧哄堂大笑迫不及待3.下列句子中加点的成语使用不恰当...的一项是A. 奶奶在城里呆了许多年,很少出门,从不逛街。
有一次乡下的亲戚来了,她竟然毛遂..自荐..,要带他们上街去玩。
B. 午后,我独自在花间小径上穿行,猝不及防....地被一只蝴蝶在面颊上点了一个触吻,一时,心头掠过了几许诗意般的遐想。
C. 李老汉是一知恩图报的人。
别人给他的帮助与恩惠,哪怕仅仅只是一句安慰的话,他也睚毗..。
..必报D. 植物也有“喜怒哀乐”,养植物跟养宠物一样,对它经常给予关爱,让它“心绪”良好,它就会投桃报李....,令你心旷神怡。
4.下面句子中没有..语病的一项是A. 通过仪器来观察世界开阔了人们的视野,由此也改变了我们对物质世界的认识。
B.新牌坊立交桥的建成将大大缓解交通高峰期的堵车问题。
C.由于适当的温度有助于化学反应速度,工期将选在气温较高的5、6月份。
2006年普通高等学校招生全国统一考试(重庆卷)word版

2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)一、选择题:本大题共10小题,每小题5分。
在每小题给出的四个备选项中,只有一项是符合题目要求的。
(1)已经集合{}{}{}5,4,3,7,5,4,2,7,6,5,4,3,2,1===B A U ,则())(B C A C ⋃⋃⋃=(A ){}6,1 (B ){}5,4 (C ){}7,5,4,3,2 (D )7,6,3,2,1(2)在等差数列{}n a 中,若a n s a a ,126=+是数列的{}n a 的前n 项和,则a s 的值为( ) (A )48 (B)54 (C)60 (D )66 (3)过坐标原点且与圆0252432=++-+y x y x 相切的直线方程为( )(A )x y x y 313=-=或 (B )x y x y 313-==或 (C )x y x y 313-=-=或 (D )x y x y 313==或(4)对于任意的直线l 与平面α,在平面α内必有直线m ,使m 与l ( )(A )平行 (B )相交 (C )垂直 (D )互为异面直线 (5)若nx x ⎪⎪⎭⎫⎝⎛-13的展开式中各项系数之和为64,则展开式的常数项为( )(A )-540 (B )-162 (C )162 (D )540(6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg ),得到频率分布直方图如下:根据上图可得这100名学生中体重在[)5.64,5.56的学生人数是( ) (A )20 (B )30 (C )40 (D )50 (7)与向量⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛=27,21,21,27b a 的夹角相等,且模为1的微量是( )(A )⎪⎭⎫⎝⎛-53,54 (B )⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-53,5453,54或(C)⎪⎪⎭⎫⎝⎛-31,322(D)⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛-31,32231,322或(8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有()(A)30种(B)90种(C)180种(D)270种(9)如图所示,单位圆中 AB的长为x,()f x表示弧 AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图像是()(10)若,,0a b c>且()4a abc bc+++=-则2a b c++的最小值为()(A)1(B)1(C)2(D)2二、填空题:本大题共6小题,每小题4分,共24分。
2006年普通高等学校招生全国统一考试重庆卷综
2006年普通高等学校统一招生考试文综重庆卷(新课程)第I卷国家主席胡锦涛于当地时间2006年4月18日10时50分左右(以10时50分计)到达西雅图(西八区。
当地采用夏令时,即比区时提早1小时的时间),开始了为期12天的对美国等国的国事访问。
据此回答1-3题。
1、此时北京时间为A 4月18日1时50分B、4月18日18时50分C 4月19日1时50分D 4月19日2时50分2、此时在赤道上,属于东半球并与西雅图在同一日期的白昼范围是A 20° W向东到 2 ° 30' EB 20° W向东到92° 30' EC2°30' E 向东到92° 30' ED 92° 30'E 向东到160 ° E3、访问期间A、曾母暗沙正午日影为长-短-长变化B高雄正午日影由长变短C夏威夷正午日影为长-短-长变化D西雅图正午日影由短变长图1是乌鲁木齐(43° 47' N)、拉萨(29° 40' N)、重庆(29° 31 ' N)和海口(20 ° 02' Z四城市的气温、日照年变化曲线图。
读图回答4-6题。
甲乙4、甲图中能反映气温受地势影响较大的曲线是A、①B、②C③ D、④5、乙图中代表重庆、拉萨日照年变化的曲线是A、H、IB、□、山C W、ID W、山6、四城市中气温曲线与日照曲线组合正确的是A、①—川B、②—nC③—W D④—川图2中数码①—⑦代表陆地自然带,“干”、“湿”表示水分状况。
读图回答7 —9 :题。
北 --------- 1 ----- 1——I ----------- 1------- M④③ ② ① ② ③④+ ----- 说西------- ------- 东®⑥⑦图27、甲大陆北端地处两大板块交界地带,这两大板块是A、亚欧板块、非洲板块B、亚欧板块、印度洋板块C美洲板块、非洲板块D美洲板块、印度洋板块8、两大陆陆地自然带类型相同的是A、①与⑤B、①与⑥C③与⑤ D③与⑥9、与①所处纬度相当的表层海域相对于⑦东侧表层海域A、温度高、盐度低B、温度高、盐度高图3为三个区域的人口统计图。
2006年普通高等学校招生全国统一考试(重庆卷.文)含详解-推荐下载

则“ AF , BF , CF 成等差数列”是“ x1 x2 8 ”的
(A)充要条件 (C)充分不必要条件
3
22 2
1
(C)
2
(B)必要不充分条件 (D)既非充分也非必要
(12)若 a,b, c 0 且 a2 2ab 2ac 4bc 12 ,则 a b c 的最小值是
一.选择题:本大题共 10 小题,每小题 5 分,共 50 分。在每小题给出的四个备选项中, 只有一项是符合题目要求的。
(1)已知集合U {1, 2,3, 4,5, 6, 7} , A {2, 4,5, 7} , B {3, 4,5} ,则 (ðU A) (ðU B)
(A){1, 6} (B){4,5} (C){2,3, 4,5, 7} (D){1, 2,3, 6, 7}
AB 1, BB1 3 1 , E 为 BB1 上使 B1E 1的点。
平面 AEC1 交 DD1 于 F ,交 A1D1 的延长线于 G ,
求:
(Ⅰ)异面直线 AD 与 C1G 所成角的大小;
(Ⅱ)二面角 A C1G A1 的正切值;
(21)(本小题满分 12 分)
已知定义域为
(2)在等差数列an中,若 an 0 且 a3a7 64 , a5 的值为
(A)2 (B)4 (C)6 (D)8
(3)以点(2,-1)为圆心且与直线 3x 4 y 5 0 相切的圆的方程为
(A) (x 2)2 ( y 1)2 3 (B) (x 2)2 ( y 1)2 3
设函数 f (x) 3 cos2 x sin x cosx a (其中 0, a R )。且 f (x) 的图像在
2006年高考重庆卷英语试题及参考答案

2006年普通高等学校招生全国统一考试英语试题重庆卷一、听力(共三节,满分30分)做题时,请先将答案划在试题卷上。
录音内容结束后,你将有两分钟的时间将试题卷上的答案转涂或转填到答题卡上。
第一节(共5小题;每小题1. 5分,满分7. 5分)请听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19. 15.B. £9. 15.C. £9. 18. 答案是B。
1. Where is Fred now?A. At the office.B. At home.C. In class.2. Whose dictionary is this?A. Bill’s.B. The man.C. The woman’s.3. What is the woman doing?A. Listening to the radio.B. Reading a newspaper.C. Watching television.4. What does the woman say abo ut the question?A. She is ready to explain it.B. She doesn’t understand it.C. She has no time to answer it.5. What is the conversation mainly about?A. The car.B. The bicycle.C. The o il price.第二节(共12小题;每小题1. 5分,满分18分)请听下面4段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试题卷的相应位置。
2006年普通高等学校招生全国统一考试文试题答案(重庆卷)

2006年普通高等学校招生全国统一考试(重庆卷)数学试题(文史类)答案一、选择题:每小题5分,满分60分. 1.D 2.D 3.C 4.D 5.B 6.C 7.C 8.D 9.B 10.B 11.A 12.A二、填空题:每小题4分,满分16分. 13.2-14.21-n15.(2)+,∞16.12a >三、解答题:满分74分. 17.(本小题13分) 解:(Ⅰ)由互斥事件有一个发生的概率公式和独立事件同时发生的概率公式,所求概率为33311116326p ⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(Ⅱ)这是136n p ==,的独立重复试验,故所求概率为2233155(2)C 6672P ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭. 18.(本小题13分)解:(Ⅰ)1()cos 2sin 2222f x x x a ωω=+++πsin 232x a ω⎛⎫=+++ ⎪⎝⎭. 依题意得πππ2632ω+=·. 解得12ω=.(Ⅱ)由(Ⅰ)知,π()sin 32f x x a ⎛⎫=+++ ⎪⎝⎭. 又当π5π36x ⎡⎤∈-⎢⎥⎣⎦,时,π7π036x ⎡⎤+∈⎢⎥⎣⎦,,故1πsin 123x ⎛⎫-+ ⎪⎝⎭≤≤,从而()f x 在π5π36⎡⎤-⎢⎥⎣⎦,上取得最小值12a -+.因此,由题设知122a -++= 故12a =.19.(本小题12分)解:(Ⅰ)求导得2()3f x x '=-63ax b +.由于()f x 的图象与直线1210x y +-=相切于点(111)-,,所以(1)11f =-,(1)12f '=-,即1331136312.a b a b -+=-⎧⎨-+=-⎩,解得13a b ==-,. (Ⅱ)由13a b ==-,得22()3633(23)3(1)(3)f x x ax b x x x x '=-+=--=+-. 令()0f x '>,解得1x <-或3x >;又令()0f x '<,解得13x -<<.所以当(1)x ∈--,∞时,()f x 是增函数;当(3)x ∈+,∞时,()f x 也是增函数,但(13)x ∈-,时,()f x 是减函数.20.(本小题12分)解法一:(Ⅰ)由1AD D G ∥知11C GD ∠为异面直线AD 与1C G 所成的角.连接1C F .因为AE 和1C F 分别是平行平面11ABB A 和11CC D D 与平面1AEC G 的交线,所以1AE C F ∥,由此可得1D F BE == 再由1FDG FDA △∽△得1DG = 在11Rt C DG △中,由1111C D DG =,得11π6C GD ∠=. (Ⅱ)作11D H C G ⊥于H ,连接FH .由三垂线定理知1FH C G ⊥,故1DH F ∠为二面角11F C G D --即二面角11A C G A --的平面角. 在1Rt GHD △中,由1DG =1π6D GH ∠=得1D H = EBA CDF1B1A 1D1CHG答(20)图1从而111tan 2D FD HF D H===. 解法二:(Ⅰ)由1AD D G ∥知11C GD ∠为异面直线AD 与1C G 所成的角. 因为1EC 和AF 是平行平面11BB C C 与11AA D D 与 平面1AEC C 的交线, 所以1EC AF ∥.由此可得111π4AGA EC B ∠=∠=,从而111AG AA =,于是1DG = 在11Rt C DG △中,由111C D =,1DG =11π6C GD ∠=. (Ⅱ)在11AC G △中,由11π4C A G ∠=,11π6A GC ∠=知11AC G ∠为钝角.作11A H GC ⊥交1GC 的延长线于H ,连接AH .由三垂线定理知GH AH ⊥,故1AHA ∠为二面角11A C G A --的平面角.在1Rt A HG △中,由11AG =,1π6A GH ∠=得112A H =.从而111tan 2AA AHA A H===. 解法三:(Ⅰ)以1A 为原点,11111A B A D A A ,,所在直线分别为x 轴,y 轴和z 轴建立如图所示的空间直角坐标系.于是,1(01)(110)1)A C D ,,,,,(101)(010)E AD = ,,,,,,1(011)EC =- ,,.因为1EC 和AF 分别是平行平面11BB C C 和11AA D D 与平面1AEC G 的交线,所以1EC AF ∥,答(20)图3BA CDF1B 1A1D1C GH 答(20)图2 E设(00)G y ,,,则(01)AG y =-,,.由1EC AG ∥得1y =1y =.故(010)G ,,1(C G =-. 设异面直线AD 与1C G 所成的角的大小为θ,则11cos AD C G AD C Gθ==·· 从而π6θ=. (Ⅱ)作11A H C G ⊥于H ,由三垂线定理知A H G H ⊥,故1AHA ∠为二面角11A C G A --的平面角.设(0)H a b ,,,则1(0)A H a b = ,,,1(110)C H a b =--,,. 由11A H C G ⊥得110A H C G =·,由此得0a =. ① 又由1H C G ,,共线得11C H C G ∥,从而11a -=-1)0b +-=. ②联立①和②得3144a b ==,.故H ⎝⎭.由1A H ==11A A =得111tan 2A A AHA A H=== . 21.(本小题12分)解:(Ⅰ)因为()f x 是奇函数,所以(0)0f =,即102ba-+=+,解得1b =. 从而有121()2x x f x a+-+=+.又由(1)(1)f f =--知1121241a a-+-+=-++,解得2a =.(Ⅱ)解法一:由(Ⅰ)知12111()22221x x x f x +-+==-+++.由上式易知()f x 在()-+,∞∞上为减函数,又因()f x 是奇函数,从而不等式22(2)(2)0f t t f t k -+-<等价于222(2)(2)(2)f t t f t k f t k -<--=-+.因()f x 是减函数,由上式推得2222t t t k ->-+. 即对一切t ∈R 有2320t t k -->.从而判别式4120k ∆=+<,解得13k <-. 解法二:由(Ⅰ)知121()22x x f x +-+=+.又由题设条件得2222222121212102222t tt kt t t k ---+-+-+-++<++.即2222212212(22)(21)(22)(21)0tk tttt tk-+--+-+-+++-+<,故2320t t k -->.上式对一切t ∈R 均成立,从而判别式4120k ∆=+<,解得13k <-. 22.(本小题12分)证明:(Ⅰ)对任意固定的1n ≥,因为焦点(01)F ,,所以可设直线n n A B 的方程为1n y k x -=,将它与抛物线方程24x y =联立得2440n x k x --=,由一元二次方程根与系数的关系得4n n x s =-.(Ⅱ)对任意固定的1n ≥,利用导数知识易得抛物线24x y =在n A 处的切线的斜率2n n A x =.故24x y =在n A 处的切线方程为()2n n n x y y x x -=-. ① 类似地,可求得24x y =在n B 处的切线方程为()2n n n s y t x s -=- ②由②减去①得2222n n n n n n x s x s y t x ---=-+,从而22224422n n n n n nx s x s x s x ---=-+, 2224n n n nx s x s x --=-,2n n x s x +=. ③将③代入①并注意4n n x s =-得交点n C 的坐标为12n n x s +⎛⎫- ⎪⎝⎭,.由两点间的距离公式得22222224242224442n n n n n n nn n x s x s x x FC x x ⎛⎫+⎛⎫=+=++=++=+ ⎪ ⎪⎝⎭⎝⎭. 从而22n n nx FC x =+. 现在2n n x =.利用上述已证结论并由等比数列求和公式得,12n FC FC FC +++…12121111()22n n x x x x x x ⎛⎫=+++++++ ⎪ ⎪⎝⎭ (22111)1(222)22222n n ⎛⎫=+++++++ ⎪⎝⎭…… 11(21)(22)221n n n n -+-+=-+-=-+.。
2006年普通高等学校招生全国统一考试理科综合能力测试(重庆卷)

空气水图 162006年普通高等学校招生全国统一考试理科综合能力测试(重庆卷)选择题一(每小题6分,每小题只有一个....选项符合题意) 14.如图14所示,在同一竖直平面内,小球a 、b 从高度不同的两点分别以初速度v a 和v b沿水平方向抛出,经过时间t a 和t b 后落到与两抛出点水平距离相等的P 点。
若不计空气阻力,下列说法正确的是[ A ]A .t a >t b ,v a <v bB .t a >t b ,v a >v bC .t a <t b ,v a <v bD .t a <t b ,v a >v b解析:此题平抛运动,小球在空中运动的时间由竖直方向的分运动决定,根据212h gt =,可得t a >t b ,水平方向做匀速直线运动,根据s =v 0t 可得v a <v b ,故选A 。
15.宇航员在月球上做自由落体这实验,将某物体由距月球表面高h 处释放,经时间t 后落月球表面(设月球半径为R ),据上述信息推断。
飞船在月球表面附近绕月球做匀速圆周运动所必须具有的速率为 [ B ] ABCD解析:根据自由落体知识可得:212h gt =,根据万有引力定律和圆周运动公式可得:22GMm v m R R =, 2GMmmg R=,v =v =故选B 。
16.如题16图,某同学将空的薄金属筒开口向下压入水中。
设水温均匀且恒定,筒内空气无泄漏,不计气体分子间相互作用,则被淹没的金属筒在缓慢下降过程中,筒内空气体积减小。
[ C ]A .从外界吸热B .内能增大C .向外界放热D .内能减小解析:薄金属筒可以传导热量,水温均匀且恒定,因此在缓慢下降过程中,筒内温度保持不变,由于不考虑气体分子间的相互作用,因而内能不变;体积减小,外界对空气做功,根据ΔE =Q +W 可推知,气体必须对外界放热。
故选C 。
图 1417.14C 是一种半衰期为5730年的放射性同位素。
若考古工作者探测某古木中14C 的含量为原来的14,则该古树死亡时间口中距今大约为 [ B ] A .22920年 B .11460年 C .5730年 D .2865年解析:根据半衰期公式可得:11()42t=,t=5730×2年=11460年,故应选B 。
2006年普通高等学校招生全国统一考试理试题参考答案(重庆卷)

2006年普通高等学校招生全国统一考试(重庆卷)数学试题(理工农医类)答案一、选择题:每小题5分,满分50分.(1)D (2)B (3)A (4)C (5)A (6)C (7)B (8)B (9)D (10)D 二、填空题:每小题4分,满分24分. (11)171010i + (12)12(13)5665-(14)123n +-(15)()23,(16)1a >三、解答题:满分76分.(17)(本小题13分) 解:(I )()1π2sin 2sin 223f x x x a x a ωωω⎛⎫=+=++ ⎪⎝⎭. 依题意得πππ2632ω+= ,解之得12ω=. (II )由(I )知,()πsin 3f x x a ⎛⎫=++ ⎪⎝⎭,又当π5π36x ⎡⎤∈-⎢⎥⎣⎦,时,π7π036x ⎡⎤+∈⎢⎥⎣⎦,, 故1πsin 123x ⎛⎫-+ ⎪⎝⎭≤≤,从而()f x 在π5π36⎡⎤-⎢⎥⎣⎦,上取得最小值122a -++.因此,由题设知12a -+=a = (18)(本小题13分)解法一:(I )ξ的所有可能值为0,1,2,3,4,5.由等可能性事件的概率公式得()5523203243P ξ===,()145528013243C P ξ=== ,()235528023243C P ξ=== ,()325524033243C P ξ=== ,()45521043243C P ξ=== ,()51153243P ξ===. 从而,ξ(II )由(I )得ξ的期望为32808040101012345243243243243243243E ξ=⨯+⨯+⨯+⨯+⨯+⨯40552433==. 解法二:(I )考察一位乘客是否在第20层下电梯为一次试验,这是5次独立重复试验,故153B ξ⎛⎫ ⎪⎝⎭,∼,即有()5512C 33kkk P k ξ-⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,0k =,1,2,3,4,5.由此计算ξ的分布列如解法一. (II )15533E ξ=⨯=. 解法三:(I )同解法一或解法二.(II )由对称性与等可能性,在三层的任一层下电梯的人数同分布,故期望值相等,即35E ξ=,从而53E ξ=.(19)(本小题13分) 解法一:(I )证:由已知DF AB ∥且DAB ∠为直角, 故ABFD 是矩形,从而CD BF ⊥. 又PA ⊥底面ABCD ,CD AD ⊥,故由三垂线定理知CD PD ⊥.在PDC △中,E ,F 分别为PC ,CD 的中点,故EF PD ∥,从而CD EF ⊥,由此得CD ⊥面BEF .(II )连接AC 交BF 于G ,易知G 为AC 的中点,连接EG ,则在PAC △中易知EG PA ∥.又因PA ⊥底面ABCD ,故EG ⊥底面ABCD . 在底面ABCD 中,过G 作GH BD ⊥,垂足为H ,连接EH ,由三垂线定理知EH BD ⊥,从而EHG ∠为二面角E BD C --的平面角. 设AB a =,则在PAC △中,有1122EG PA ka ==. 以下计算GH ,考虑底面的平面图(如答19图2),连接GD ,因1122BD S BD GH GB DF == △G , 故GB DFGH BD= .在ABD △中,因AB a =,2AD a =,得BD =.而1122GB FB AD a ===,DF AB =,从而得GB AB GH BD === . BA CPE FD答19图1HG答19图2A因此1tan2kaEGEHG kGH===.故0k>知EHG∠是锐角,故要使30EHG>∠,必须tan3023k>=,解之得,k的取值范围为15k>.解法二:(I)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间直角坐标系,设AB a=,则易知点A,B,C,D,F的坐标分别为()000A,,,()00B a,,,()220C a a,,,()020D a,,,()20F a a,,.从而(200)(020)DC a BF a==,,,,,,0DC BF=,故DC BF⊥.设PA b=,则(00)P b,,,而E为PC中点,故2bE a a⎛⎫⎪⎝⎭,,,从而02bBE a⎛⎫= ⎪⎝⎭,,.DC BE=,故DC BE⊥.由此得CD BEF⊥面.(II)设E在xOy平面上的投影为G,过G作GH BD⊥垂足为H,由三垂线定理知EH BD⊥.从而EHG∠为二面角E BD C--的平面角.由PA k AB= 得(00)P ka,,,2kaE a a⎛⎫⎪⎝⎭,,,(0)G a a,,.设(0)H x y,,,则(0)(20)GH x a y a BD a a=--=-,,,,,,由0GH BD=得()2()0a x a a y a--+-=,即2x y a-=-.①又因(0)BH x a y=-,,,且BH与BD的方向相同,故2x a ya a-=-,即22x y a+=.②答19图3由①②解得3455x a y a ==,,从而21055GH a a GH ⎛⎫=--= ⎪⎝⎭,,,.tan 5kaEG EHG GH=== .由0k >知EHG ∠是锐角,由30EHG ∠>︒,得tan tan30EHG >︒,即23k >. 故k的取值范围为15k >. (20)(本小题13分)解:(I )求导得2()(2)e xf x x b x b c '⎡⎤=++++⎣⎦.因24(1)b c >-,故方程()0f x '=即2(2)0x b x b c ++++=有两根:122222b b x x ++=-<=-+.令()0f x '>,解得1x x <或2x x >; 又令()0f x '<,解得12x x x <<.故当1()x x ∈-∞,时,()f x 是增函数;当2()x x ∈+,∞时,()f x 也是增函数,但当12()x x x ∈,时,()f x 是减函数.(II )易知(0)f c =,(0)f b c '=+.因此0()()(0)limlim (0)x x f x c f x f f b c x x→→--'===+. 所以,由已知条件得244(1)b c b c +=⎧⎨-⎩,≤,因此24120b b +-≤,解得62b -≤≤. (21)(本小题12分)解:(I )因为对任意x ∈R ,有22(())()f f x x x f x x x -+=-+,所以22((2)22)(2)22f f f -+=-+.又由(2)3f =,得22(322)322f -+=-+,即(1)1f =. 若(0)f a =,则22(00)00f a a -+=-+,即()f a a =. (II )因为对任意x ∈R ,有22(())()f f x x x f x x x -+=-+, 又因为有且只有一个实数0x ,使得00()f x x =, 所以对任意x ∈R ,有20()f x x x x -+=. 在上式中令0x x =,有20000()f x x x x -+=,又因为00()f x x =,所以2000x x -=,故00x =或01x =. 若00x =,则2()0f x x x -+=,即2()f x x x =-.但方程2x x x -=有两个不同实根,与题设条件矛盾,故00x ≠.若01x =,则有2()1f x x x -+=,即2()1f x x x =-+.易验证该函数满足题设条件. 综上,所求函数为2()1()f x x x x =-+∈R . (22)(本小题12分)证:(I )由题设及椭圆的几何性质有22n n n n n d P F P G =+=,故1n d =.设n c =1:n nl x c =,因此,由题意n d 应满足111n n nd c c -+1≤≤.即11101n n c c ⎧-⎪⎨⎪<<⎩≤,解之得:112n c <≤,即112<,从而对任意1n ≥,2n b ≤.(II )设点n P 的坐标为()n n x y ,,则由1n d =及椭圆方程易知11n nx c =-,()()2222211111n n n n n y b x c c ⎛⎫⎛⎫ ⎪=-=--- ⎪ ⎪⎝⎭⎝⎭()3221221nn n n c c c c =-++-. 因2n n n F G c =,故n n n P F G △的面积为n n n S c y =,答22图从而232122112n n n n n S c c c c ⎛⎫=-++-<<⎪⎝⎭. 令()32221f c c c c =-++-,由()26220f c c c '=-++=,得两根16±()f c 在12⎛ ⎝⎭,内是增函数,而在1⎫⎪⎪⎝⎭内是减函数.现在由题设取n b =,则11122n n c n n +===-++,n c 是增数列,又易知233445c c =<<=. 故由前已证,知12S S <,且()13n n S S n +> ≥.。
2006年普通高等学校招生全国统一考试(重庆卷)

绝密 * 启用前2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)数学试题(理工农医类)共5页,满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使0.5毫米黑色墨水签字笔,将答案书写在答题止规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束,监考员将试题卷和答题卡一并收回。
参考公式:如果事件A 、B 互斥,那么P (A+B )-P(A)+P(B) .如果事件A 、B 相互独立,那么P(A ·B)-P(A)·P(B) 如果事件A 在一次试验中发生的概率是P ,那么n 次独立事件重复试验中恰好发生k 次的概率P n (k)=C k n P k (1-P)n-k一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合U ={1,2,3,4,5,6,7}, A ={2,4,5,7},B ={3,4,5},则(u A )∪(u B )= (A){1,6} (B){4,5}(C){1,2,3,4,5,7} (D){1,2,3,6,7}(2)在等差数列{a n }中,若a a+a b =12,S N 是数列{a n }的前n 项和,则S N 的值为 (A )48 (B)54 (C)60 (D)66(3)过坐标原点且与x 2|y 24x |2y +25=0相切的直线的方程为 (A )y =-3x 或y =31x (B) y =-3x 或y =-31x(C )y =-3x 或y =-31x (B) y =3x 或y =31x(4)对于任意的直线l 与平同a ,在平面a 内必有直线m ,使m 与l(A)平行 (B )相交(C)垂直 (D)互为异面直线 (5)若(x 3)x1n 的展开式中各项系数之和为64,则展开式的常数项为(A)-540 (B) (c)162 (D)540(6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 (A)20 (B)30 (C)40 (D )50(7)与向量a =-⎪⎭⎫ ⎝⎛b ,21,27⎪⎭⎫ ⎝⎛27,21的夹解相等,且模为1的向量是(A) ⎪⎭⎫-⎝⎛53,54 (B) ⎪⎭⎫- ⎝⎛53,54或⎪⎭⎫ ⎝⎛-53,54 (C )⎪⎭⎫-⎝⎛31,322 (D )⎪⎭⎫- ⎝⎛31,322或⎪⎭⎫⎝⎛-31,322 (8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有(A )30种 (B )90种 (C )180种 (D )270种(9)如图所示,单位圆中弧AB 的长为x ,f (x )表示弧AB 与弦AB 所围成的弓形面积的2倍,则函数y =f (x )的图象是题 (9)图(10)若a ,b ,c >0且a (a +b +c )+bc =4-23,则2a +b +c 的最小值为 (A )3-1 (B) 3+1 (C) 23+2 (D) 23-2一、填空题:本大题共6小题,共24分,把答案填写在答题卡相应位置上 (11)复数复数2i321++i的值是_________. (12)∝-n lim=---+++12)12(312n n n _________. (13)已知βα,⎪⎭⎫⎝⎛∈ππ,43,sin(βα+)=-,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则os ⎪⎭⎫ ⎝⎛+4πα=________.(14)在数列{a n }中,若a 1=1,a n +1=2a n +3 (n ≥1),则该数列的通项a n =_________.(15)设a >0,n ≠1,函数f (x )=a lg (x 2-2n +1) 有最大值.则不等式log n (x 2-5x +7) >0的解集为_______. (16)已知变量x ,y 满足约束条件1≤x+y ≤4,-2≤x-y ≤2.若目标函数z =ax +y (其中a >0)仅在点(3,1)处取得最大值,则a 的取值范围为___________.二、解答题:本大题共6小题,共76分解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分13分) 设函数f (x )=3cos 2cos+sin ωrcos ωx+a(其中ω>0,a ∈R ),且f (x )的图象在y 轴右侧的第一个高点的横坐标为6x. (Ⅰ)求ω的值; (Ⅱ)如果f (x )在区间⎥⎦⎤⎢⎣⎡-65,3ππ上的最小值为3,求a 的值.(18)(本小题满分13分)某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有 5 位乘客,且每位乘客在这三层的每一层下电梯的概率均为31,用ξ表示这5位乘客在第20层下电梯的人数.求:(Ⅰ)随机变量ξ的分布列; (Ⅱ)随机变量ξ的期望.(19)(本小题满分13分)如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,∠DAB 为直角,AB ‖CD,AD =CD =24B,E 、F 分别为PC 、CD 的中点.(Ⅰ)试证:CD ⊥平面BEF;(Ⅱ)设P A =k ·AB ,且二面角E -BD -C 的平面角大于︒30,求k 的取值范围.(20)(本小题满分13分)已知函数f (x )=(x 2+bx +c )c x ,其中b ,c ∈R 为常数. 图(19)图 (Ⅰ)若b 2>4(a -1),讨论函数f (x )的单调性; (Ⅱ)若b 2<4(c -1),且∞→n limxcx f -)(=4,试证:-6≤b ≤2.(21)(本小题满分12分)已知定义域为R 的函数f (x )满足f (f (x )-x 2+y _=f(x )-x 2+x . (Ⅰ)若f (2)-3,求f (1);又若f (0)=a ,求f (a );(Ⅱ)设有且仅有一个实数x 0,使得f(x 0)= x 0,求函数f (x )的解析表达式.(22)(本小题满分12分)已知一列椭圆C n :x 2+22nb y =1. 0<b n <1,n=1,2. .若椭圆C 上有一点P n 使P n 到右准线l n 的距离d .是|P n F n |与|P n C n |的等差中项,其中F n 、C n 分别是C n 的左、右焦点.(Ⅰ)试证:b n ≤23(n ≥1); (Ⅱ)取b n =232++n n ,并用S A 表示∆P n F n G n 的面积,试证:S 1<S 1且S n <S n+3 (n ≥3).图(22)图(20)(本小题满分13分)已知函数f (x )=(x 2+bx +c )c x ,其中b ,c ∈R 为常数. (Ⅰ)若b 2>4(a -1),讨论函数f (x )的单调性; (Ⅱ)若b 2<4(c -1),且∞→n limxcx f -)(=4,试证:-6≤b ≤2.(21)(本小题满分12分)已知定义域为R 的函数f (x )满足f (f (x )-x 2+y _=f(x )-x 2+x . (Ⅰ)若f (2)-3,求f (1);又若f (0)=a ,求f (a );(Ⅱ)设有且仅有一个实数x 0,使得f(x 0)= x 0,求函数f (x )的解析表达式.(22)(本小题满分12分)已知一列椭圆C n :x 2+22nb y =1. 0<b n <1,n=1,2. .若椭圆C 上有一点P n 使P n 到右准线l n 的距离d .是|P n F n |与|P n C n |的等差中项,其中F n 、C n 分别是C n 的左、右焦点. (Ⅰ)试证:b n ≤23(n ≥1); (Ⅱ)取b n =232++n n ,并用S A 表示∆P n F n G n 的面积,试证:S 1<S 1且S n <S n+3 (n ≥3).图(22)图(18)(本小题13分) 解法一:(Ⅰ)ξ的所有可能值为0,1,2,3,4,5. 由等可能性事件的概率公式得P (ξ=0)=2532=24332, P (ξ=1)= =∙541532C .24380 P (ξ=2)= =∙532532C =24380, P (ξ=3)==∙542532C .24340P (ξ=4)= =∙54332C =24310, P (ξ=5)= =531.2431(Ⅱ)由(Ⅰ)得ξ的期望为 E ξ=0×24332+1×24380+2×24380+3×24340+4×24310+5×2431=243405=35. 解法二:(Ⅰ)考察一位乘客是否在第20层下电梯为一次试验,这是5次独立重复试验. 故ξ-B ⎪⎭⎫⎝⎛31,5,即有P (ξ=k )=C 25b⎪⎭⎫ ⎝⎛31k-⎪⎭⎫ ⎝⎛532,k =0,1,2,3,4,5.由此计算ξ的分布列如解法一. 解法三: (Ⅰ)同解法一或解二.(Ⅱ)由对称性与等可能性,在三层的任一层下电梯的人数同分布,故期望值相等.即3E ξ=5,从而E ξ=35. (19)(本小题13分) 解法一:(Ⅰ)证:由已知DF ∥AB 且∠DAD 为直角,故ABFD 是矩形,从而CD ⊥BF .又P A ⊥底面ABCD,CD ⊥AD ,故由三垂线定理知CD ⊥PD .在△PDC 中,E 、F 分别PC 、CD 的中点,故EF ∥PD ,从而CD ⊥EF ,由此得CD ⊥面BEF . 第(19)图1(Ⅱ)连结AC 交BF 于G .易知G 为AC 的中点.连接EG ,则在△P AC 中易知EC ∥P A .又因 P A ⊥底面ABCD ,故BC ⊥底面ABCD .在底面ABCD 中,过C 作GH ⊥BD ,垂足为H ,连接EH .由三垂线定理知EH ⊥BD .从而∠EHG 为二面角E -BD -C 的平面角.设AB=a ,则在△P AC 中,有BG =21P A =21ka . 以下计算GH ,考察底面的平面图(如答(19)图2).连结GD .因S △CBD =21BD ·GH=21GB ·OF . 故GH =BDDFGB ∙.在△ABD中,因为AB =a,AD =2A ,得BD =5a第(19)图2 而GB =21FB =21AD -a.DF-AB ,从而得GH =BD DF GB ∙= aa a 5∙=.55a因此tan EHG=GH EG =.255521k a ka=由k >0知EHG ∠是锐角,故要使EHG ∠>︒30,必须k 25>tan ︒30=,33 解之得,k 的取值范围为k >.15152解法二:(Ⅰ)如图,以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为:轴建立空间直角坐标系,设AB=a ,则易知点A,B,C,D,F 的坐标分别为 A (0,0,0),B (a ,0,0),C (2a ,2a ,0),D (0,2a ,0), F (a ,2a ,0).从而=(2a ,0,0), =(0,2a ,0),DC ·BF =0,故DC ⊥BF .设P A =b ,则P (0,0,b ),而E 为PC 中点.故 第(19)3 E ⎪⎭⎫ ⎝⎛2,,b a a .从而=⎪⎭⎫ ⎝⎛2,,0b a .·=0,故⊥.由此得CD ⊥面BEF . (Ⅱ)设E 在xOy 平面上的投影为G ,过G 作GH ⊥BD 垂足为H,由三垂线定理知EH ⊥BD. 从而∠EHG 为二面角E-BD-C 的平面角. 由PA =k ·AB 得P(0,0,ka),E ⎪⎭⎫⎝⎛2,,ka a a ,G(a,a,0). 设H(x,y,0),则=(x-a,y-a,0), =(-a,2a,0), 由·=0得=a(x-a)+2a(y-a)=0,即 x-2y=-a ①又因BH =(x,a,y,0),且BH 与BD 的方向相同,故a a x -=ay2,即2x+y=2a ② 由①②解得x =53a,y=54a,从而GH =⎪⎭⎫⎝⎛--0,51,52a a ,|GH |=55a. tan EHG=a Ka552=k 25.由k >0知,EHC 是锐角,由∠EHC >,30︒得tanEHG >tan ,30︒即k 25>.33 故k 的取值范围为k >15152. (20)(本小题13分)解:(Ⅰ)求导得f 2(x )=[x 2+(b +2)x +b+c ]e x ..因b 2>4(c-1),故方程f 2(x )=0即x 2+(b +2)x +b +c =0有两根;x 1=-2)1(422---+c b cb <x 2=-22+b .2)1(42--+c b令f ′(x )>0,解得x <x 1或x >x 1; 又令f ′(x )>0,解得x 1<x <x 2.故当x ε(-, x 1)时,f (x )是增函数,当 x ε(x 2,+)时,f(x)也是增函数,但当x ε(x 1 , x 2)时,f(x)是减函数.(Ⅱ)易知f (0)=c ,f (u )=b +c ,因此e bf xf x f x e x f +==-=-→→)0()0()(lim )(lim00. 所以,由已知条件得b +e =4 b 2≤4(e-1), 因此b 2+4b -12≤0. 解得-6≤b ≤2.(21)(本小题12分) 解:(Ⅰ)因为对任意x εR ,有f (f (x )- x 2 + x )=f (x )- x 2 +x ,所以 f (f (2)- 22+2)=f (2)- 22+2.又由f (2)=3,得f (3-22+2)-3-22+2,即f (1)=1. 若f (0)=a ,则f (a -02+0)=a -02+0,即f (a )=a .(Ⅱ)因为对任意x εR ,有f (f (x ))- x 2 +x )=f (x )- x 2 +x .又因为有且只有一个实数x 0,使得f (x 0)- x 0. 所以对任意x εR ,有f (x )- x 2 +x = x 0.在上式中令x = x 0,有f (x 0)-x 20 + x 0= x 0,又因为f (x 0)- x 0,所以x 0- x 20=0,故x 0=0或x 0=1.若x 0=0,则f (x )- x 2 +x =0,即 f (x )= x 2 –x .但方程x 2 –x =x 有两上不同实根,与题设条件矛质,故x 2≠0.若x 2=1,则有f (x )- x 2 +x =1,即f (x )= x 2 –x +1.易验证该函数满足题设条件. 综上,所求函数为 f (x )= x 2 –x +1(x ∈R ).(22)(本小题12分)证:(1)由题设及椭圆的几何性质有.1,2||||2==+=n n n n n n d G P F P d 故 设则右准线方程为,12n n b t -= .1xn e x l =因此,由题意n d 应满足.1111+≤≤-xn x e d e 即,<,解之得:<<12110111n n x e e e ≤⎪⎩⎪⎨⎧≤- 即121<n e ≤, 从而对任意.23,1≤≥n b n (Ⅱ)设点及椭圆方程易知则出)的坐标为(1,,-n n n n d f x P ,11-=nn e x ))11(1)(1()1(22222---=-=nn n n n c c x b y得两极6131±,从而易知f(c)在(21,6131±)内是增函数6131±,1)内是减函数.现在由题设取,,211211,2322c n n n b c n n b n n n +--++=-=++=则是增数列.又易知<432=c .546131n c =±< 故由前已证,知).3(121≥+n S S S S n n <,且<。
2006年高考.重庆卷.理科数学试题及详细解答

绝密 * 启用前2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)数学试题(理工农医类)共5页,满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使0.5毫米黑色墨水签字笔,将答案书写在答题止规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束,监考员将试题卷和答题卡一并收回。
参考公式:如果事件A 、B 互斥,那么P (A+B )-P(A)+P(B) .如果事件A 、B 相互独立,那么P(A ·B)-P(A)·P(B) 如果事件A 在一次试验中发生的概率是P ,那么n 次独立事件重复试验中恰好发生k 次的概率P n (k)=C k n P k (1-P)n-k一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合U ={1,2,3,4,5,6,7}, A ={2,4,5,7},B ={3,4,5},则(u A )∪(u B )= (A){1,6} (B){4,5}(C){1,2,3,4,5,7} (D){1,2,3,6,7}(2)在等差数列{a n }中,若a 4+a 6=12,S n 是数列{a n }的前n 项和,则S 9的值为 (A )48 (B)54 (C)60 (D)66(3)过坐标原点且与园x 2+y 2-4x +2y +25=0相切的直线的方程为 (A )y =-3x 或y =31x (B) y =3x 或y =-31x(C )y =-3x 或y =-31x (D) y =3x 或y =31x(4)对于任意的直线l 与平平面α,在平面a 内必有直线m ,使m 与l(A)平行 (B )相交(C)垂直 (D)互为异面直线 (5)若(x 3)x1n 的展开式中各项系数之和为64,则展开式的常数项为(A)-540 (B)-162 (c)162 (D)540(6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是(A)20 (B)30(C)40 (D)50(7)与向量a =-⎪⎭⎫⎝⎛b,21,27⎪⎭⎫⎝⎛27,21的夹解相等,且模为1的向量是(A) ⎪⎭⎫-⎝⎛53,54(B) ⎪⎭⎫-⎝⎛53,54或⎪⎭⎫⎝⎛-53,54(C)⎪⎭⎫-⎝⎛31,322(D)⎪⎭⎫-⎝⎛31,322或⎪⎭⎫⎝⎛-31,322(8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,则不同的分配方案有(A)30种(B)90种(C)180种(D)270种(9)如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是题(9)图(10)若a ,b ,c >0且a (a +b +c )+bc =4-23,则2a +b +c 的最小值为 (A )3-1 (B) 3+1 (C) 23+2 (D) 23-2一、填空题:本大题共6小题,共24分,把答案填写在答题卡相应位置上 (11)复数复数2i321++i的值是_________. (12)∝-n lim=---+++12)12(312n n n _________. (13)已知βα,⎪⎭⎫⎝⎛∈ππ,43,sin(βα+)=-,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则os ⎪⎭⎫ ⎝⎛+4πα=________.(14)在数列{a n }中,若a 1=1,a n +1=2a n +3 (n ≥1),则该数列的通项a n =_________.(15)设a >0,n ≠1,函数f (x )=a lg (x 2-2n +1) 有最大值.则不等式log n (x 2-5x +7) >0的解集为_______. (16)已知变量x ,y 满足约束条件1≤x+y ≤4,-2≤x-y ≤2.若目标函数z =ax +y (其中a >0)仅在点(3,1)处取得最大值,则a 的取值范围为___________.二、解答题:本大题共6小题,共76分解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分13分) 设函数f (x )=3cos 2cos+sin ωrcos ωx+a(其中ω>0,a ∈R ),且f (x )的图象在y 轴右侧的第一个高点的横坐标为6x. (Ⅰ)求ω的值; (Ⅱ)如果f (x )在区间⎥⎦⎤⎢⎣⎡-65,3ππ上的最小值为3,求a 的值.(18)(本小题满分13分)某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有 5 位乘客,且每位乘客在这三层的每一层下电梯的概率均为31,用ξ表示这5位乘客在第20层下电梯的人数.求:(Ⅰ)随机变量ξ的分布列; (Ⅱ)随机变量ξ的期望.(19)(本小题满分13分)如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,∠DAB 为直角,AB ‖CD,AD =CD =24B,E 、F 分别为PC 、CD 的中点.(Ⅰ)试证:CD ⊥平面BEF;(Ⅱ)设P A =k ·AB ,且二面角E -BD -C 的平面角大于︒30,求k 的取值范围.(20)(本小题满分13分)已知函数f (x )=(x 2+bx +c )c x ,其中b ,c ∈R 为常数. 图(19)图 (Ⅰ)若b 2>4(a -1),讨论函数f (x )的单调性; (Ⅱ)若b 2<4(c -1),且∞→n lim xcx f -)(=4,试证:-6≤b ≤2.(21)(本小题满分12分)已知定义域为R 的函数f (x )满足x x )x (f )x x )x (f (f 22+-=+- (Ⅰ)若f (2)=3,求f (1); 又若f (0)=a , 求f (a );(Ⅱ)设有且仅有一个实数x 0,使得f(x 0)= x 0,求函数f (x )的解析表达式.(22)(本小题满分12分) 已知一列椭圆C n :x 2+22nb y =1. 0<b n <1,n=1,2. .若椭圆C 上有一点P n 使P n 到右准线l n 的距离d .是|P n F n |与|P n C n |的等差中项,其中F n 、C n 分别是C n 的左、右焦点. (Ⅰ)试证:b n ≤23(n ≥1); (Ⅱ)取b n =232++n n ,并用S A 表示∆P n F n G n 的面积,试证:S 1<S 1且S n <S n+3 (n ≥3). 图(22)图2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)答案一、选择题:每小题5分,满分50分。
2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(理工农医类)

2006年普通高等学校招生全国统一考试(重庆卷)数学试题
卷(理工农医类)
佚名
【期刊名称】《数学教学通讯:中教版》
【年(卷),期】2006(000)007
【总页数】4页(P62-64,F0003)
【正文语种】中文
【中图分类】G4
【相关文献】
1.2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷(文科类) [J],
2.2004年普通高等学校招生全国统一考试(重庆卷)数学(理工农医类)试题 [J],
3.2004年普通高等学校招生全国统一考试(重庆卷)数学(理工农医类)试题[J],
4.2007年普通高等学校招生全国统一考试(重庆卷)——数学试题(文史类)[J], 无
5.2007年普通高等学校招生全国统一考试(重庆卷)——数学试题卷(理工农医类) [J], 无
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006普通高等学校招生全国统一考试(重庆卷)英语英语试题卷共16页。
满分150分。
考试时间120分钟。
一、听力(共三节,满分30分)做题时,请先将答案划在试题卷上。
录音内容结束后,你将有两分钟的时间将试题卷上的答案转涂或转填到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)请听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.15.C.£9.18. 答案是B。
1.Where is Fred now?A.At the office.B.At home.C.In class.2.Whose dictionary is this?A.Bill’s.B.The man.C.T he woman’s.3.What is the woman doing?A.Listening to the radio.B.Reading a newspaper.C.Watching television.4.What does the woman say about the question?A.She is ready to explain it.B.She doesn’t understand it.C.She has no time to answer it.5.What is the conversation mainly about?A.The car.B.The bicycle.C.The oil price.第二节(共12小题;每小题1.5分,满分18分)请听下面4段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试题卷的相应位置。
听每段对话或独白前,你将有时间阅读各小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
每段对话或独白读两遍。
请听第6段材料,回答第6至8题。
6.What is the man?A.A manager.B.A nurse.C.A doctor.7.Who cooks dinner on weekdays?A.Paul.B.Linda.C.Richard.8.What are the two speakers mainly talking about?A.Interesting jobs.B.Boring housework.C.Changing family roles.请听第7段材料,回答第9至11题。
9.Why is woman so happy?A.She had a pleasant walk.B.She wrote a short play.C.She met a famous poet.10.What is the man working on?A.A poem.B.An article.C.A love story.11.What is the conversation mainly about?A.How to find a way out.B.How to make friends.C.How to enjoy life.请听第8段材料,回答12至14题。
12.How did Tom spend his vacation?A.He went traveling.B.He painted pictures.C.He did some shopping.13.Why does the man come to see the woman?A.To give her a gift.B.To ask her for help.C.To tell her about his trip.14.What did the woman do for the man?A.She invited him to the cafe.B.She bought him a fridge.C.she watered his plants.请听第9段材料,回答第15至17题。
15.What is the main purpose of the talk?A.To give a prize to a musician.B.To introduce a guest speaker.C.To invite a musician to a concert.16.At what age did the pianist begin to play the own music?A.5.B.10.C.40.17.What will the pianist mainly talk about?A.His childhood.B.His music school.C.His experiences on his tours.第三节(共3小题;每小题1.5分,满分4.5分)请听下面一段独白,用所听到的独白中的词或数填空,每空限填一个词或一个数。
填入的内容要在答题卡相应的位置上。
在听本段独白前,你将有时间阅读各小题,每小题5秒钟;听完后,各小题将给出5秒钟作答时间。
本段独白读两遍。
请听第10段材料,回答题18至20题。
Courses in Harvard University二、英语知识运用(共两节,满分45分)第一节单项填空(共15小题;每小题1分,满分15分)请从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该选项的标号涂黑。
例:A computer can only do you have instructed it to do.A.howB.afterC.whatD.when答案是C。
21.I have to go to work by taxi because my car at the garage.A.will be repairedB.is repairedC.is being repairedD.has been repaired22.-Would you like some more soup?- .It is delicious,but I’ve had enough.A.Yes,pleaseB.No,thank you.C.Nothing moreD. I'd like some23.In time of serious accidents, we know some basic things about first aid,we can save lives.A.whetherB.untilC.ifD.unless24.I’ve tried very hard to improve my English. But by no means with my progress.A.the teacher is not satisfiedB.is the teacher not satisfiedC.the teacher is satisfiedD.is the teacher satisfied25.Everywhere man has cut downforests in order to grow crops,or to usewood as fuel or as building material.A.the;theB.the;/C./;theD./;/26.Isn't it time you got down to the papers?A.markB.be markedC.being markedD.marking27. and I’ll get the work finished.A.Have one more hourB.One more hourC.Given one more hourD.If I have one more hour28.——How are you managing to do your work without an assistant?——Well,I somehow.A.get alonge onC.watch outD.set off29.My grandma still treats me like a child.She can,t imagine grown up.A.myB.mineC.myselfD.me30.Customers are asked to make sure that they the right change before leaving the shop.A.will giveB.have been givenC.have givenD.will be given31.I in London for many years,but I,ve never regretted my final decision to move back to China.A.livedB.was livingC.have livedD.had lived32.-Mr.Gordon asked me to remind you of the meeting this afternoon.Don't you forgetit! -OK,I .A.won,tB.don,tC.willD.do33.Nobody believed his reason for being absent form the class he had to meet his uncle at the air port.A.whyB.thatC.whereD.because34.I saw a woman running to ward me in the dark.Before I could recognize who she was,she had run back in the direction she had come.A.of whichB.by whichC.in whichD.from which35.—How about seeing the new movie at the theatre tonight?— ,but I,ve got to go over my notes for tomorrow's exam.A.All rightB.Sounds greatC.I can,tD.No,I am terribly sorry第二节完形填空(共20小题;每小题1.5分,满分30分)请阅读下面短文,掌握其大意,然后从36-55各题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该选项的标号涂黑。
