【三维设计】高中数学教师用书第三章创新演练新人教B版必修_3
【三维设计】高中数学 教师用书 第一部分 第3章 3.4.1 第二课时 应用创新演练 苏教版必修1

一、填空题1.已知函数f (x )的图象如图,其中零点的个数与可以用二分法求解的个数分别为________.解析:图象与x 轴有4个交点,所以零点的个数为4;左、右函数值异号的有3个零点,所以可以用二分法求解的个数为3. 答案:4,32.用二分法求方程x 3-2x -5=0在区间[2,3]上的近似解,取区间中点x 0=2.5,那么下一个有解区间为__________.解析:令f (x )=x 3-2x -5,∵f (2)=-1<0,f (3)=16>0,f (2.5)=5.625,根据二分法可知,下一个有解区间为(2,2.5).答案:(2,2.5)3.若函数f (x )的零点与g (x )=4x+2x -2的零点之差的绝对值不超过0.25,则f (x )可以是下列函数中的________. ①f (x )=4x -1 ②f (x )=(x -1)2③f (x )=e x-1④f (x )=ln(x -12)解析:由g (0)=-1,g (12)=1可知g (x )的零点在(0,12)上,而f (x )=4x -1的零点为14,f (x )=(x -1)2的零点为1,f (x )=e x-1的零点为0,f (x )=ln(x -12)的零点是32,所以f (x )=4x -1满足题意.答案:①4.在用二分法求方程x 3-2x -1=0的一个近似根时,现在已经将根锁定在区间(1,2)内,则下一步可以断定根所在的区间为________. 解析:令f (x )=x 3-2x -1,则f (1.5)=(1.5)3-2×1.5-1=-0.625<0,f (1)=13-2×1-1=-2<0, f (2)=23-2×2-1=3>0,∴f (1.5)·f (2)<0,∴区间为(1.5,2). 答案:(1.5,2)5.已知图象连续不断的函数y =f (x )在区间(0,0.1)上有惟一的零点,如果用“二分法”求这个零点(精确到0.01)的近似值,则应将区间(0,0.1)等分的次数至少为________次.解析:由0.12n <0.01,得2n>10,∴n 的最小值为4.答案:46.已知函数f (x )=(13)x-log 2x ,若实数x 0是方程f (x )=0的解,且0<x 1<x 0,则f (x 1)的值与0的大小关系恒有________.解析:∵f (1)f (2)=[(13)1-0]·[(13)2-log 22]<0,∴1<x 0<2.如图所示,当0<x 1<x 0时,函数y =(13)x的图象在y =log 2x 的上方,即必有(13)x 1>log 2x 1,∴f (x 1)>0恒成立.答案:f (x 1)>0 二、解答题7.在26枚崭新的金币中,混入了一枚外表与它们完全相同的假币(重量不同,假币较轻),现在只有一台天平,请问:你最多称多少次就可以发现这枚假币?解:将26枚金币平均分成两份,放在天平上,则假币在较轻的那13枚金币里面,将这13枚金币拿出1枚,将剩下的12枚平均分成两份,若天平平衡,则假币一定是拿出的那一枚,若不平衡,则假币一定在较轻的那6枚金币里面;将这6枚平均分成两份,则假币一定在较轻的那3枚金币里面;将这3枚金币任拿出2枚放在天平上,若平衡,则剩下的那一枚即是假币,若不平衡,则较轻的的那一枚即是假币.综上可知,最多称4次就可以发现这枚假币.8.判断函数y =x 3-x -1在区间[1,1.5]内有无零点,如果有,求出一个近似零点(精确到0.1).解:因为f(1)=-1<0,f(1.5)=0.875>0,且函数y=x3-x-1的图象是连续的曲线,所以它在区间[1,1.5]内有零点,用二分法逐次计算,列表如下:因为1.312 5,1.328 125精确到0.1的近似值都为1.3,所以函数的一个近似零点为1.3.9.求函数y=ln x与函数y=3-x的图象的交点的横坐标(精确到0.1).解:求函数y=ln x与函数y=3-x的图象交点的横坐标,即求方程ln x=3-x的根.令f(x)=ln x+x-3,因为f(2)=ln 2-1<0,f(3)=ln 3>0,所以可取初始区间为(2,3),列表如下:由于2.187 5与2.218 75精确到0.1的近似值都是2.2,所以方程ln x+x-3=0在(2,3)内的一个近似根可取为2.2,即2.2可作为两函数图象交点的横坐标的近似值.。
【三维设计】高中数学 第1部分 第三章 §1-1.1 频率与概率应用创新演练 北师大版必修3

【三维设计】2013高中数学 第1部分 第三章 §1-1.1 频率与概率应用创新演练 北师大版必修31.下列事件中,属于必然事件的是( ) A .12人中至少有2人的生日在同一个月 B .13人中至少有2人的生日在同一个月 C .同一周出生的5人中至少有2人的生日相同 D .同一周出生的6人中至少有2人的生日相同解析:因为每年只有12个月,所以13人中至少有2人的生日在同一个月. 答案:B2.下列说法中不.正确的是( ) A .不可能事件的概率为0,必然事件的概率为1 B .某人射击9次,击中靶3次,则他击中靶的概率为13C .“直线y =k (x +1)过定点(-1,0)”是必然事件D .“将一个骰子抛掷两次,所得点数之和大于7”是随机事件 解析:A 显然正确;对于C ,直线y =k (x +1)是直线方程的点斜式,它表示斜率为k 且过点(-1,0)的直线,故C 正确;对于D ,“将一个骰子抛掷两次,所得点数之和大于7”可能发生,也可能不发生,所以D 也正确;B 中13只是频率,而不是概率,所以B 不正确.答案:B3.某人将一枚硬币连续抛掷了10次,正面朝上的情形出现了6次,则正面朝上的( ) A .概率为0.6 B .频率为0.6 C .频率为6D .概率接近于0.6解析:610=0.6是频率而不是概率.答案:B4.下列说法中,不.正确的是( ) A .某人射击10次,击中靶心8次,则他击中靶心的频率是0.8 B .某人射击10次,击中靶心7次,则他击中靶心的概率是0.7C .某人射击10次,击中靶心的概率为12,则他击中靶心估计有5次D .某人射击10次,击中靶心的概率为0.6,则他击不中靶心的次数估计为4 解析:概率反映了某一事件发生的可能性的大小. 答案:B5.掷一颗骰子,掷了100次,“向上的点数是2”的情况出现了19次,在这次试验中,“向上的点数是2”的频率是_______________________________________________.解析:事件发生的频率等于事件发生的次数除以试验的次数. 答案:0.196.在一次考试中,某班学生有80%及格,80%是________(填“概率”或“频率”). 解析:由概率与频率的意义可知,80%是频率. 答案:频率7.小明和小亮从同一本书中分别随机抽取了6页,在统计了各页中“的”和“了”的出现的次数后,分别求出了“的”和“了”的出现的频率,并绘制了图如下:随着统计页数的增加,试估计“的”和“了”这两个字出现的频率将如何变化?解:估计“的”字出现的频率在0.058附近摆动,“了”字出现的频率在0.01附近摆动.8.下面的表中列出10次抛掷硬币的试验结果,n 为每次试验掷硬币的次数,m 为硬币正面向上的次数.计算每次试验中“正面向上”这一事件的频率并考察它的概率.解:由P=,可分别得出这10次试验中“正面向上”这一事件出现的频率依次为n0.502,0.498,0.512,0.506,0.502,0.492,0.488,0.516,0.524,0.494.这些数字在0.5附近摆动,由概率的统计定义可得,“正面向上”的概率约为0.5.。
【三维设计】高中数学 教师用书 第1部分 第三章 3.2.2 对数函数课件 新人教版B版必修1

问题4:函数y=2x与y=log2x的图象有什么关系?定义 域、值域有什么关系?
提示:图象关于直线y=x对称,定义域和值域互换.
对数函数的图象与性质 a>1
0<a<1
图 像
定义域:(0,+∞)
性
值域:R
质
过点 (1,0) ,即当x=1时,y=0
在(0,+∞)上是 增函数 在(0,+∞)上是 减函数
0<a<1 时,若 x>1,则 y<0;若 0<x<1,则 y>0.
[例 1] 求下列函数的定义域: (1)y= lg(2-x); (2)y=log3(31x-2); (3)y=log(2x-1)(-4x+8). [思路点拨] 求与对数有关的函数的定义域,除考 虑使根式、分式有意义外,还要考虑使对数有意义,即 真数大于零,底数大于零且不等于1.
()
A.(1,2]
B.(1,2)
C.(2,+∞)
D.(-∞,2)
解析:由题意得x2--1x>>00,,解得 1<x<2.
答案:B
3.求下列函数的定义域: (1)y=loga x-1(a>0,a≠1); (2)y= -lg(1-x).
解:(1)要使函数有意义,需满足x-x-1≥1>00,,即 x>1,所 以函数 y=loga x-1的定义域是(1,+∞). (2)要使函数有意义,需满足- 1-lgx(>01,-x)≥0, 即lxg<(1,1-x)≤0,1x- <1x. ≤1,解得 0≤x<1.所以函数 y=
[精解详析] (1)由题意得l2g-(x2>-0,x)≥0,即22- -xx≥ >01. , ∴x≤1,即 y= lg(2-x)的定义域为{x|x≤1}. (2)由l3oxg-3(2>30x,-2)≠0,得33xx>-22. ≠1, 解得 x>23,且 x≠1. ∴y=log3(31x-2)的定义域为{x|x>23,且 x≠1}.
【三维设计】高中数学教师用书 课下作业 第三章 §4 对数 4.2 换底公式 应用创新演练 新人教B

1.设a =log 32,则log 38-2log 36用a 表示的形式是( ) A .a -2 B .3a -(1+a )2C .5a -2D .1+3a -a 2解析:∵a =log 32,∴log 38-2log 36=3log 32-2(log 32+1)=3a -2(a +1)=a -2.答案:A 2.1411log 9+1511log 3等于( ) A .lg3 B .-lg3C.1lg3 D .-1lg3解析:原式=log 1914+log 1315=log 94+log 35=log 32+log 35=log 310=1lg3.答案:C3.设log 34·log 48·log 8m =log 416,则m 的值为( )A.12 B .9C .18D .27解析:由题意得lg 4lg 3·lg 8lg 4·lg m lg 8=lg m lg 3=log 416=log 442=2,∴lg m lg 3=2,即lg m =2lg 3=lg 9.∴m =9.答案:B4.若lg a ,lg b 是方程2x 2-4x +1=0的两个根,则(lg a b )2的值等于( ) A .2 B.12C .4 D.14解析:由根与系数的关系,得lg a +lg b =2,lg a ·lg b =12,∴(lg a b )2=(lg a -lg b )2=(lg a +lg b )2-4lg a ·lg b=22-4×12=2.答案:A5.(lg2)3+(lg5)3+3lg2·lg5=________.解析:∵原式=(lg 2+lg 5)[(lg 2)2-lg 2·lg 5+(lg 5)2]+3lg 2·lg 5=1×[(lg 2)2-lg 2·lg 5+(lg 5)2]+3lg 2·lg 5=(lg 2)2+2lg 2·lg 5+(lg 5)2=(lg 2+lg 5)2=1.答案:16.已知f (3x )=2x ·log 23,则f (21 005)的值等于________.解析:法一:令t =3x ,∴x =log 3t ,∵f (3x )=2x ·log 23,∴f (t )=2·log 3t ·log 23=2·log 2tlog 23·log 23=2·log 2t ,∴f (x )=2·log 2x ,∴f (21 005)=2·log 221 005=2×1 005=2 010.法二:令3x =21 005,则x =log 321 005=1 005log 32∴f (22 005)=2×1 005log 32×log 23=2 010.答案:2 0107.计算下列各式的值:(1)log 2125·log 318·log 519;(2)(log 23+log 89)(log 34+log 98+log 32).解:(1)log 2125·log 318·log 519=log 25-2·log 32-3·log 53-2=-12log 25·log 32·log 53=-12·lg 5lg 2·lg 2lg 3·lg 3lg 5=-12.(2)原式=(log 23+log 3232)(log 322+log 2323+log 32)=53log 23·92log 32=152·1log 32·log 32=152.8.已知x ,y ,z 为正数,且3x =4y =6z .(1)求使2x =py 的p 的值;(2)求证:12y =1z -1x .解:(1)设3x =4y =6z =k (显然k ≠1), 则x =log 3k ,y =log 4k ,z =log 6k , 由2x =py 得2log 3k =p log 4k =p ·log 3klog 34,∵log 3k ≠0,∴p =2log 34;(2)证明:1z -1x =1log 6k -1log 3k=log k 6-log k 3=log k 2=12log k 4=12log 4k =12y .。
【三维设计】高中数学 教师用书 第1部分 第三章 3.1.1 实数指数幂及其运算课件 新人教版B版必
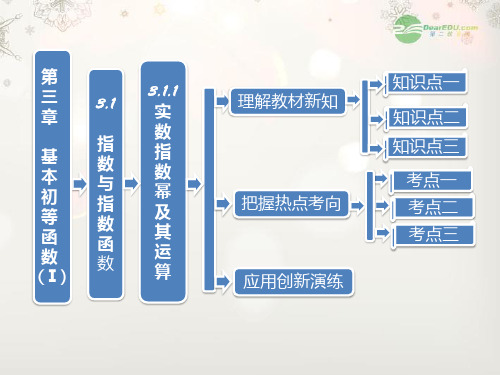
2 3
b
16 3 3 =(10a)4·(10b)-23=24·3-23= 3 .
(1)在根式的化简与运算中,一般是先将根式化成 分数指数幂,再进行运算.
(2)幂的运算中,结果不能同时含有根号和分数指 数幂,也不能同时含有分母和负分数指数幂.若无特 殊说明,结果一般用分数指数幂的形式表示.
2
5.计算(2a-3b-3)·(-3a-1b)÷(4a-4b-35)得
()
A.-32b2
B.32b2
C.-32b73
D.32b37
解析:原式=[2×(-3)÷4]a-3-1-(-4)b-32+1-(-53)
=-32a0b2=-32b2.
答案:A
6.已知a+a-1=5,则a2+a-2=________. 解析:法一:由a+a-1=5两边平方得 a2+2aa-1+a-2=25, 即a2+a-2=23. 法二:a2+a-2=a2+2aa-1+a-2-2aa-1 =(a+a-1)2-2=25-2=23. 答案:23
1.化简( a-1)2+ (1-a)2+ 3 (1 a)3 =________.
解析:由题意得a-1≥0,即a≥1. ∴原式=a-1+|1-a|+1-a
=a-1+a-1+1-a=a-1. 答案:a-1
2.计算下列各式的值: (1) 3 (4)3 ; (2) 4 (9)2 ; (3) 6 (3 )6 ; (4) 8 ( x 2)8 .
2.根式的意义和性质
n
当式子n a有意义时, a 叫做根式,n 叫做根指数. 根式的性质:
n
(1)(
a)n=
a
(n>1,且
n∈N+);
n
(2)
an=
a, |a| ,
【三维设计】高中数学 教师用书 第一部分 第3章 3.2.1 第一课时 应用创新演练 苏教版必修1

一、填空题1.把指数式(15)-2=25化成对数式________.解析:由对数的定义,得log 1525=-2.答案:log 1525=-22.方程log 5(1-2x )=1的解x =________.解析:由log 5(1-2x )=1知1-2x =5,∴x =-2.答案:-23.若log a 2=m ,log a 3=n ,则a 2m +n=________.解析:由log a 2=m 得a m =2,由log a 3=n 得a n=3.∴a 2m +n =a 2m ·a n =(a m )2·a n =22×3=12.答案:124.若f (10x )=x ,则f (1 000)的值为________.解析:令10x =t ,∴x =lg t .∴f (t )=lg t 即f (x )=lg x .∴f (1 000)=lg 1 000,∵103=1 000,∴f (1 000)=3.答案:35.若10α=2,β=lg 3,则100α-12β=________.解析:∵β=lg 3,∴10β=3.∴100α-12β=12100100a=(10α)210β=223=43.答案:436.给出以下结论:①lg(-10)=-1,②ln(lne)=0,③若lg a =10,则a =10,④若e -1=1e ,则ln 1e =-1,⑤10-log 1102=2.其中正确结论的序号是________.解析:∵零和负数没有对数,∴①不正确;∵ln(lne)=ln 1=0,∴②正确;若lg a =10,则a =1010,∴③不正确;∵e -1=1e ,∴log e 1e =ln 1e =-1,∴④正确;∵10-log 1102=(10-1)log 1102=(110)log 1102=2,∴⑤正确.答案:②④⑤二、解答题7.(1)将对数式log 139=-2,化为指数式;(2)将指数式10-3=0.001,化为对数式;(3)已知log 2(log 5x )=1,求x 的值. 解:(1)∵log 139=-2,∴(13)-2=9;(2)∵10-3=0.001,∴log 100.001=-3,即lg 0.001=-3;(3)∵log 2(log 5x )=1,∴log 5x =2,∴x =52=25.8.求下列各式中x 的值:(1)log 8x =-23;(2)log x 27=34;(3)log 2(log 5x )=0;(4)log 3(lg x )=1.解:(1)由log 8x =-23,得x =823-=(23) 23-=2-2=14.(2)由log x 27=34,得x 34=27,x =(33)43=34=81.(3)由log 2(log 5x )=0,得log 5x =1,所以x =5.(4)由log 3(lg x )=1,得lg x =3,所以x =103=1 000.9.已知log 2x =3,log 2y =5,求log 2x y 的值.解:∵log 2x =3,log 2y =5,∴x =23,y =25,x y =2325=14∴log 2x y =log 214=log 22-2=-2.。
【三维设计】高中数学教师用书第三章第一创新演练新人教B版必修

【三维设计】2013届高一数学教师用书 课下作业 第三章 3.23.2.1 第一课时 创新演练课件 必修11.使对数log a (-2a +1)有意义的a 的取值范围为( )A .a <12且a ≠1B .0<a <12C .a >0且a ≠1D .a <12解析:由对数的概念可知,使对数log a (-2a +1)有意义的a 需满足⎩⎪⎨⎪⎧a >0,a ≠1,-2a +1>0.解得0<a <12. 答案:B2.下列指数式与对数式互化不.正确的一组是( ) A .e 0=1与ln 1=0B .813-=12与log 812=-13C .log 39=2与912=3D .log 77=1与71=7解析:log 39=2应转化为32=9.答案:C3.已知log 2x =3,则x12-=( ) A.13B.12 3C.13 3D.24解析:∵log 2x =3,∴x =23=8,∴x12-=232-=24. 答案:D 4.已知2x =9,log 283=y ,则x +2y 的值为( ) A .6B .8C .4D .log 48解析:由2x=9,得log 29=x ,∴x +2y =log 29+2log 283=log 29+log 2649=log 264=6.答案:A5.已知a 23=49(a >0),则log 23a =________. 解析:法一:∵a 23=49,∴log a 49=23, ∴2log a 23=23,∴log a 23=13, ∴1log a 23=3,∴log 23a =3. 法二:∵a 23=49,∴a 2=64729, ∴a =827=(23)3, ∴log 23a =log 23(23)3=3. 答案:36.计算:823×3log 32ln e +log 4164=________. 解析:原式=(23)23×21+log 44-3 =4×21+(-3)=8-2=-4. 答案:-4 7.求下列各式的值:(1)log 535+2log 122-log 5150-log 514; (2)[(1-log 63)2+log 62·log 618]÷log 64.解:(1)原式=log 535+log 550-log 514+2log 12212=log 535×5014+log 122 =log 553-1=2.(2)原式=[(log 66-log 63)2+log 62·log 6(2×32)]÷log 64 =⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫log 6632+log 62·(log 62+log 632)÷log 622 =[(log 62)2+(log 62)2+2log 62·log 63]÷2log 62 =log 62+log 63=log 6(2×3)=1.8.已知lg x +lg y =2lg(x -2y ),求log 2x y 的值. 解:由已知得xy =(x -2y )2,即(x -y )(x -4y )=0,得x =y 或x =4y . ∵x >0,y >0,x -2y >0,∴x >2y >0. ∴x =y 应舍去,∴x =4y ,即x y =4. ∴log 2x y=log 24=4.。
【三维设计】高中数学 教师用书 第三章 3.2.2 创新演练 新人教B版必修1

1.下列各组函数中,表示同一函数的是( )A .y =x 2和y =(x )2B .|y |=|x |和y 3=x 3C .y =log a x 2和y =2log a xD .y =x 和y =log a a x 解析:对于A ,定义域不同;对于B ,对应法则不同;对于C ,定义域不同;对于D ,y =log a a x⇔y =x . 答案:D2.函数y =2+log 2x (x ≥1)的值域为( )A .(2,+∞)B .(-∞,2)C .[2,+∞)D .[3,+∞)解析:当x ≥1时,log 2x ≥0,所以y =2+log 2x ≥2.答案:C3.已知函数f (x )=log a (x -m )的图象过点(4,0)和(7,1),则f (x )在定义域上是( )A .增函数B .减函数C .奇函数D .偶函数解析:将点(4,0)和(7,1)代入函数解析式,有⎩⎪⎨⎪⎧0=log a (4-m ),1=log a (7-m ).解得a =4和m =3,则有f (x )=log 4(x -3).由于定义域是x >3,则函数不具有奇偶性.很明显函数f (x )在定义域上是增函数.答案:A4.设a =log 32,b =ln 2,c =512-,则( ) A .a <b <cB .b <c <aC .c <a <bD .c <b <a解析:a =log 32=1log 23,b =ln 2=1log 2e ,而log 23>log 2e>1,所以a <b .又c =512-=15,而5>2=log 24>log 23,所以c <a ,综上知c <a <b .答案:C5.函数y =log a (x -2)+1的图像恒过定点________.解析:令x -2=1,得x =3则,y =0+1=1.∴函数的图象恒过定点(3,1). 答案:(3,1)6.函数f (x )=2-log 2x 的定义域是________.解析:由2-log 2x ≥0 ⇒ log 2x ≤2,∴0<x ≤4.答案:(0,4]7.求下列函数的定义域:(1)y =log 2(4x -3);(2)y =log 5-x (2x -2).解:(1)要使函数有意义,必须满足:log 2(4x -3)≥0=log 21,即1≤4x -3⇒x ≥1,∴函数的定义域为[1,+∞).(2)要使函数有意义,必须满足:⎩⎪⎨⎪⎧2x -2>0,5-x >0,5-x ≠1.⇒1<x <5且x ≠4, ∴函数的定义域为(1,4)∪(4,5).8.根据函数f (x )=log 2x 的图象和性质解决以下问题:(1)若f (a )>f (2),求a 的取值范围;(2)y =log 2(2x -1)在[2,14]上的最值.解:函数y =log 2x 的图象如图.(1)因为y =log 2x 是增函数,故f (a )>f (2),即log 2a >log 22,则a >2.所以a 的取值范围为(2,+∞).(2)∵2≤x ≤14,∴3≤2x -1≤27,∴log 23≤log 2(2x -1)≤log 227.∴函数y =log 2(2x -1)在[2,14]上的最小值为log 23,最大值为log 227.。
【三维设计】高中数学 教师用书 第一部分 第3章 3.2.2 第一课时 应用创新演练 苏教版必修1

一、填空题1.函数f (x )=1-x +lg x 的定义域是________.解析:由⎩⎪⎨⎪⎧1-x ≥0,x >0,得0<x ≤1. 答案:(0,1]2.函数f (x )=log a (2x +1)+2(a >0且a ≠1)必过定点________. 解析:∵log a 1=0,∴x =0时f (x )=2.故函数f (x )过定点(0,2).答案:(0,2)3.已知a =log 23.6,b =log 43.2,c =log 43.6,则a ,b ,c 的大小关系是________. 解析:a =log 23.6=log 43.62=log 412.96,y =log 4x (x >0)是单调增函数,而3.2<3.6<12.96,∴a >c >b .答案:a >c >b4.若y =(log 12a )x 在R 上为减函数,则实数a 的取值范围是________.解析:∵函数y =(log 12a )x 在R 上为减函数,∴0<log 12a <1.∴12<a <1. 答案:(12,1) 5.函数y =log a x ,x ∈[2,4],a >0且a ≠1,若此函数的最大值比最小值大1,则a =________.解析:当a >1时,log a 4-log a 2=1,解得a =2,当0<a <1时,log a 2-log a 4=1,解得a =12. ∴a =2或12. 答案:2或126.设f (x )=⎩⎪⎨⎪⎧lg x ,x >0,10x ,x ≤0, 则f (f (-2))=________.解析:f (-2)=10-2,∴f (f (-2))=f (10-2)=lg 10-2=-2. 答案:-2二、解答题7.已知函数f (x )=log 2(x -3).(1)求f (51)-f (6)的值;(2)若f (x )≥0,求x 的取值范围.解:(1)∵f (x )=log 2(x -3),∴f (51)-f (6)=log 2(51-3)-log 2(6-3)=log 248-log 23=log 216=4.(2)f (x )≥0即log 2(x -3)≥0,∴x -3≥1解得x ≥4.所以x 的取值范围为[4,+∞).8.比较下列各组数的大小.(1)log 2π与log 20.9;(2)log 20.3与log 0.20.3;(3)log 0.76,0.76与60.7.解:(1)∵函数y =log 2x 在(0,+∞)上是增函数, π>0.9,∴log 2π>log 20.9.(2)∵log 20.3<log 21=0,log 0.20.3>log 0.21=0,∴log 20.3<log 0.20.3.(3)∵60.7>60=1,0<0.76<0.70=1,log 0.76<log 0.71=0,∴60.7>0.76>log 0.76.9.已知f (x )=log 3x .(1)作出这个函数的图象;(2)当0<a <2时,有f (a )>12,利用图象求a 的取值范围.解:(1)作出函数y =log 3x 的图象如图所示.(2)令f (x )=12,即log 3x =12,解得x = 3. 由如图所示的图象知:当0<a <2时,若f (a )>12,则3<a <2. 故当0<a <2时,满足f (a )>12的a 的取值范围为(3,2).。
【三维设计】高中数学 教师用书 第一部分 第3章 3.4.1 第一课时 应用创新演练课件 苏教版必修

一、填空题1.若函数f (x )=x 2-2x +a 有两个零点,则实数a 的取值范围是________. 解析:由条件知,Δ=(-2)2-4a >0,解得a <1.∴实数a 的取值范围是(-∞,1).答案:(-∞,1)2.若函数f (x )=mx +n 有一个零点是2,则函数g (x )=nx 2-mx 的零点是________. 解析:由条件知,f (2)=2m +n =0,∴n =-2m .∴g (x )=nx 2-mx =-2mx (x +12),由g (x )=0得 x =0或x =-12.∴g (x )的零点是0和-12. 答案:0和-123.(2012·北京高考改编)函数f (x )=x 12-⎝ ⎛⎭⎪⎫12x 的零点个数为________. 解析:因为y =x 12在x ∈[0,+∞)上单调递增,y =(12)x 在x ∈R 上单调递减,所以f (x )=x 12-(12)x 在x ∈[0,+∞)上单调递增,又f (0)=-1<0,f (1)=12>0,所以f (x )=x 12-(12)x 在定义域内有唯一零点.答案:14.已知方程a x =x +a (a >0且a ≠1)有两解,则a 的取值范围为________.解析:如图.当0<a <1时,y =a x 与y =x +a 的图象只有一个交点,当a >1时y =a x 与y =x +a 的图象必存在两个交点,故a >1.答案:(1,+∞)5.(2011·新课标高考改编)在下列区间中,函数f (x )=e x+4x -3的零点所在的区间为________.①(-14,0) ②(0,14) ③(14,12) ④(12,34) 解析:因为f (14)=e 14+4×14-3=e 14-2<0,f (12)=e 12+4×12-3=e 12-1>0, 所以f (x )=e x +4x -3的零点所在的区间为(14,12). 答案:③6.已知函数f (x )=x 2+(a -1)x +(a -2)的一个零点比1大,一个零点比1小,则实数a 的取值范围为__________.解析:∵函数f (x )的图象开口向上,又两个零点分别在1的两侧,∴f (1)=1+(a -1)+(a -2)<0,即2a -2<0.∴a <1.答案:(-∞,1)二、解答题7.求下列函数的零点:(1)f (x )=2x +7;(2)f (x )=2x 2-5x +1;(3)f (x )=(x -1)(x -2)(x +3).解:(1)令f (x )=2x +7=0,解得x =-72. ∴函数的零点为x =-72. (2)令f (x )=2x 2-5x +1=0,解得 x 1=5-174,x 2=5+174. ∴函数的零点为x 1=5-174,x 2=5+174. (3)令f (x )=(x -1)(x -2)(x +3)=0,解得x 1=-3,x 2=2,x 3=1.∴函数的零点为 x 1=-3,x 2=2,x 3=1.8.已知函数f (x )=ax 2-(a +3)x +4.若y =f (x )的两个零点为α,β,且满足0<α<2<β<4,求实数a 的取值范围.解:∵函数y =f (x )的两个零点是α,β,且α<β,则当a =0时,显然不可能有两个不同零点.则应有⎩⎪⎨⎪⎧a >0f (0)=4>0f (2)=2a -2<0f (4)=12a -8>0① 或⎩⎪⎨⎪⎧a <0f (0)<0f (2)=2a -2>0f (4)=12a -8<0②解①得23<a <1,②无解. 综上可知,a 的取值范围为{a |23<a <1}. 9.已知二次函数y =x 2-2(m -1)x +m 2-2m -3,其中m 为实数.(1)试讨论当m 取任意实数时,这个二次函数的零点个数,并证明你的结论;(2)若这个二次函数有两个零点x 1,x 2,且x 1,x 2的倒数和为23,求二次函数的解析式. 解:(1)记二次函数对应的方程为x 2-2(m -1)x +m 2-2m -3=0,则Δ=4(m -1)2-4(m 2-2m -3)=4m 2-8m +4-4m 2+8m +12=16>0,∴方程x 2-2(m -1)x +m 2-2m -3=0必有两个不相等的实数根,即不论m 取何值,这个二次函数必有两个零点.(2)依题意,x 1,x 2是方程x 2-2(m -1)x +m 2-2m -3=0的两个实数根, ∴x 1+x 2=2(m -1),x 1x 2=m 2-2m -3.又1x 1+1x 2=23,即x 1+x 2x 1x 2=23, ∴2(m -1)m 2-2m -3=23,① 解之得m =0或m =5.经检验m =0或m =5都是方程①的解.故所求二次函数的解析式为y =x 2+2x -3或y =x 2-8x +12.。
【三维设计】高中数学 第1部分 第三章 §2-2.3 互斥事件应用创新演练 北师大版必修3

【三维设计】2013高中数学 第1部分 第三章 §2-2.3 互斥事件应用创新演练 北师大版必修31.从一批产品中取出三件产品,设A =“三件产品全不是次品”,B =“三件产品全是次品”,C =“三件产品有次品,但不全是次品”,则下列结论哪个是正确的( )A .A 与C 互斥B .B 与C 互斥 C .任何两个相互斥D .任何两个都不互斥解析:由题意知事件A 、B 、C 两两不可能同时发生,因此两两互斥.答案:C2.从1,2,3,…,9中任取两数,其中:①恰有一个偶数和恰有一个奇数;②至少有一个奇数和两个都是奇数;③至少有一个奇数和两个都是偶数;④至少有一个奇数和至少有一个偶数.在上述事件中,是对立事件的是( )[A .①B .②④C .③D .①③解析:从1~9中任取两数,有以下三种情况:(1)两个均为奇数;(2)两个均为偶数;(3)一个奇数和一个偶数.答案:C3.从一批羽毛球产品中任取一个,其质量小于4.8 g 的概率为0.3,质量小于4.85 g 的概率为0.32,那么质量在[4.8,4.85)(g)范围内的概率是( )A .0.62B .0.38C .0.02D .0.68[解析:质量在 [4.8,4.85)(g )范围内的概率P =0.32-0.3=0.02.答案:C4.(2012·宁波高一检测)掷一枚硬币,若出现正面记1分,出现反面记2分,则恰好得3分的概率为( )A.58B.18C.14D.12解析:有三种可能:①连续3次都掷得正面概率为18; ②第一次掷得正面,第二次掷得反面,其概率为14;③第一次掷得反面,第二次掷得正面,其概率为14.因而恰好得3分的概率为18+14+14=58.答案:A5.某班派出甲、乙两名同学参加学校举行的数学竞赛,甲、乙两名同学夺得第一名的概率分别是316和14,则该班同学夺得第一名的概率为________. 解析:甲同学夺得第一与乙同学夺得第一是互斥事件,故该班同学夺得第一的概率P =316+14=716. 答案:7166.袋中有2个白球和3个黑球,从中任取两个球,则取得的两球中至少有1个白球的概率是________.解析:从5个球中任取两个球有10个基本事件取得的两球中没有白球有3个基本事件,∴记事件A :“取得的两球中至少有一个白球”,则P (A )=1-P (A -)=1-310=710. 答案:7107.某学校的篮球队、羽毛球队、乒乓球队各有10名队员,某些队员不止参加了一支球队,具体情况如图所示.现从中随机抽取一名队员,求:(1)该队员只属于一支球队的概率;(2)该队员最多属于两支球队的概率.解:分别令“抽取一名队员只属于篮球队、羽毛球队、乒乓球队”为事件A ,B ,C .由图知3支球队共有球员20名.则P (A )=520,P (B )=320,P (C )=420. (1)令“抽取一名队员,该队员只属于一支球队”为事件D .则D =A +B +C ,∵事件A ,B ,C 两两互斥,∴P (D )=P (A +B +C )=P (A )+P (B )+P (C )=520+320+420=35. (2)令“抽取一名队员,该队员最多属于两支球队”为事件E ,则E 为“抽取一名队员,该队员属于3支球队”,∴P (E )=1-P (E )=1-220=910.8.(2011·江西高考)某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A 饮料,另外2杯为B 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A 饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为合格.假设此人对A 和B 两种饮料没有鉴别能力.(1)求此人被评为优秀的概率;(2)求此人被评为良好及以上的概率.解:将5杯饮料编号为:1,2,3,4,5,编号1,2,3表示A 饮料,编号4,5表示B 饮料,则从5杯饮料中选出3杯的所有可能情况为:(123),(124),(125),(134),(135),(145),(234),(235),(245),(345),可见共有10种.令D 表示此人被评为优秀的事件,E 表示此人被评为良好的事件,F 表示此人被评为良好及以上的事件.则(1)P (D )=110; (2)P (E )=35,P (F )=P (D )+P (E )=710.。
【三维设计】高中数学 教师用书 第三章 章末小结 知识整合与阶段质量检测 新人教B版必修1

一、选择题(本大题共10小题,每小题5分,共50分.在每小题所给的四个选项中,只有一项是符合题目要求的)1.化简[3(-5)2]34的结果为( )A .5 B. 5 C .- 5D .-5解析:[3(-5)2]34=(352)34=522×34=512= 5. 答案:B2.函数y =log x (1+x )+(1-x )12的定义域是( ) A .(-1,0) B .(-1,1) C .(0,1)D .(0,1]解析:由题意得⎩⎪⎨⎪⎧x >0,且x ≠1,1+x >0,1-x ≥0,∴0<x <1.答案:C3.若f (x )=(2a -1)x是增函数,那么a 的取值范围为( ) A .a <12B.12<a <1 C .a >1D .a ≥1解析:由题意,即2a -1>1知a >1. 答案:C4.下列函数中,其定义域与值域相同的是( ) A .y =2xB .y =x 2C .y =log 2xD .y =2x答案:D5.已知函数f (x )=⎩⎪⎨⎪⎧3x,x ≤0,log 2x ,x >0,则f [f (12)]的值是( )A .-3B .3 C.13D .-13解析:f (12)=log 212=-1,f (f (12))=f (-1)=3-1=13.答案:C6.若a <0,则函数y =(1-a )x-1的图象必过点( ) A .(0,1)B .(0,0)C .(0,-1)D .(1,-1)解析:根据指数函数y =a x的图像恒过定点(0,1)知,函数y =(1-a )x-1恒过定点(0,0).答案:B7.某函数同时具有以下性质:①图象过点(0,1);②在区间(0,+∞)上是减函数;③是偶函数.此函数可能是( )A .f (x )=log 2|x |B .f (x )=(1π)|x |C .f (x )=2|x |D .f (x )=x 12解析:f (x )=(1π)|x |的定义域为R ,f (-x )=(1π)|-x |=(1π)|x |=f (x ),且f (0)=(1π)0=1.当x >0时,f (x )=(1π)x在(0,+∞)上为减函数.∴B 满足条件. 答案:B8.某商场宣传在节假日对顾客购物实行一定的优惠,商场规定: ①如一次购物不超过200元,不予以折扣;②如一次购物超过200元,但不超过500元,按标价予以九折优惠;③如一次购物超过500元,其中500元给予九折优惠,超过500元的给予八五折优惠. 某人两次去购物,分别付款176元和432元.如果他一次性购买同样的商品,则应付款( )A .608元B .574.1元C .582.6元D .456.8元解析:由题意得购物付款432元,实际标价为432×109=480元.如果一次购买标价176+480=656元的商品,应付款500×0.9+156×0.85=582.6元.答案:C9.三个数a =70.3,b =0.37,c =ln 0.3大小的顺序是( ) A .a >b >cB .a >c >bC .b >a >cD .c >a >b解析:a =70.3>1,0<b =0.37<1,c =ln 0.3<0, ∴a >b >c . 答案:A10.定义运算a ⊕b =⎩⎪⎨⎪⎧a , a ≤b ,b , a >b ,则函数f (x )=1⊕2x的图象是( )解析:根据题意得f (x )=1⊕2x=⎩⎪⎨⎪⎧2x, x ≤0,1, x >0.答案:A二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上) 11.函数y =log 2(2x+1)的值域为________. 解析:∵2x>0,∴2x +1>1, ∴log 2(2x +1)>0. 答案:(0,+∞)12.指数函数f (x )=a x的图象经过点(2,4),则f (-3)的值是________. 解析:由f (x )=a x的图象过点(2,4)可得a =2, 所以f (-3)=18.答案:1813.在同一平面直角坐标系中,函数y =g (x )的图象与y =e x的图象关于直线y =x 对称,而函数y =f (x )的图象与y =g (x )的图象关于y 轴对称.若f (m )=-1,则m 的值为________.解析:由题意知y =g (x )应为y =e x的反函数,即y =g (x )=ln x ,而y =f (x )与y =g (x )=ln x 图象关于y 轴对称,故可得y =f (x )=ln(-x ).又f (m )=-1,所以ln(-m )=-1,得-m =e -1,即m =-1e.答案:-1e14.下列说法中,正确的是________. ①任取x >0,均有3x>2x;②当a >0,且a ≠1时,有a 3>a 2; ③y =(3)-x是增函数;④在同一坐标系中,y =2x 的图象与y =2-x的图象关于y 轴对称.解析:②中,当a =12时,a 3=18,a 2=14,不满足a 3>a 2;③中,y =(3)-x=(33)x 是减函数.答案:①④三、解答题(本大题共4小题,共50分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分12分)计算下列各式的值: (1)( 32×3)6+(2×2)43-(-2 012)0;(2)lg 5×lg 20+(lg 2)2.解:(1)原式=(213×312)6+(2×212)12×43-1 =213×6×312×6+232×12×43-1 =22×33+21-1 =4×27+2-1 =109.(2)原式=lg 5lg (5×4)+(lg 2)2=lg 5(lg 5+lg 4)+(lg 2)2=(lg 5)2+lg 5lg 4+(lg 2)2 =(lg 5)2+2lg 5lg 2+(lg 2)2=(lg 5+lg 2)2=1.16.(本小题满分12分)20个劳动力种50亩地,这些地可种蔬菜、棉花、水稻.这些作物每亩地所需劳动力和预计产值如下表.应怎样计划才能使每亩地都能种上作物(水稻必种),所有劳动力都有工作且作物预计总产值达到最高?解:设种x 亩水稻(0<x ≤50),y 亩棉花(0≤y <50)时,总产值为h ,且每个劳动力都有工作.∴h =0.3x +0.5y +0.6[50-(x +y )],且x 、y 满足x 4+13y +12[50-(x +y )]=20,即h =-320x +27, 4≤x ≤50,x ∈N,且x =4k ,k ∈N .欲使h 为最大,则x 应为最小,故当x =4时,h max =26.4,此时y =24.故安排1个劳动力种4亩水稻,8个劳动力种24亩棉花,11个劳动力种22亩蔬菜时,作物总产值最高且每个劳动力都有工作.17.(本小题满分12分)求函数y =log a (a -a x)(a >0且a ≠1)的定义域和值域. 解:∵a -a x>0,∴a >a x. 当a >1时,x <1,则f (x )的定义域为(-∞,1); 当0<a <1时,x >1,则f (x )的定义域为(1,+∞). ∵a x>0,∴0<a -a x<a .当a >1时,log a (a -a x)<log a a =1, 函数f (x )的值域为(-∞,1); 当0<a <1时,log a (a -a x )>log a a =1, 函数f (x )的值域为(1,+∞).综上所述,当a >1时,函数f (x )的定义域与值域均为(-∞,1); 当0<a <1时,函数f (x )的定义域与值域均为(1,+∞).18.(本小题满分14分)已知函数f (x )是定义在R 上的奇函数,且当x >0时,f (x )=(12)x .(1)求函数f (x )的解析式;(2)画出函数的图象,根据图象写出f (x )的单调区间. 解:(1)因为f (x )是定义在R 上的奇函数, 所以f (0)=0. 当x <0时,-x >0,f (x )=-f (-x )=-(12)-x =-2x .所以函数的解析式为:f (x )=⎩⎪⎨⎪⎧-2x, x <0,0, x =0,(12)x, x >0.(2)函数图象如图所示.通过函数的图象可以知道,f (x )的单调递减区间是(-∞,0),(0,+∞).。
【三维设计】高中数学 教师用书 第三章 3.1.1 创新演练 新人教B版必修1

1.将 3-22化为分数指数幂,其形式是( ) A .212 B .-212C .2-12 D .-2-12 解析: 3-22=(-22)13=(-2×212)13 =(-232)13=-212.答案:B2.下列等式中,正确的个数为( )①n a n =a ;②若a ∈R,则(a 2-a +1)0=1; ③ 3x 4+y 3=x 43+y ; ④3-5=6(-5)2.A .0B .1C .2D .3 解析:①中,若n 为偶数,则不一定成立;②中,因为a 2-a +1=(a -12)2+34≠0,所以(a 2-a +1)0=1是正确的;③是错误的;④左边为负数,右边为正数,是错误的.答案:B3.(-x )2-1x 等于( ) A.xB .-x -xC .x xD .x -x 解析:由-1x 知x <0,又当x <0时,x 2=|x |=-x ,因此(-x )2 -1x =x 2·-x |x |=-x -x .答案:B4.化简(36a 9)4·(63a 9)4的结果是( ) A .a 16B .a 8C .a 4D .a 2 解析:(36a 9)4·(63a 9)4=(6a 9)43·(3a 9)46=(a 96)43·(a 93)23=a 96×43·a 93×23=a 4. 答案:C5.有下列说法: ①3-27=3;②16的4次方根是±2; ③481=±3;④ (x +y )2=|x +y |.其中,正确的有________(填上正确说法的序号).解析:负数的3次方根是一个负数,故3-27=-3,故①错误;16的4次方根有两个,为±2,故②正确;481=3,故③错误; (x +y )2是正数,故2(x +y )2=|x +y |,故④正确.答案:②④6.83-312-613+333=________. 解析:原式=83-63-23+3= 3.答案: 37.化简下列各式: (1) 3a a ; (2)(2x 14+332)(2x 14-332)-4x -12(x -x 12); (3)(m 14n -38)8.解:(1)原式=a 13·a 16=a 13+16=a 12; (2)原式=(2x 14)2-(332)2-4x -12·x +4x -12·x 12=4x 12-33-4x 12+4x 0=-23;(3)原式=(m 14)8(n -38)8=m 2n -3.8.计算:(1)(-338)-23-23+(0.002) -12-10(5-2)-1+(2-3)0; (2)(a 85·b -65)-12·5a 4÷5b 3(a >0,b >0); (3)(14) -12·(4ab -1)30.1-2(a 3b -4)12(a >0,b >0). 解:(1)原式=(-1) -23 (338)-23+(1500)-12-105-2+1=(278)-23+50012-10(5+2)+1 =49+105-105-20+1=-1679; (2)原式=a 85×(-12)·b (-65)×(-12)·a 45÷b 35=a -45·b 35·a 45÷b 35 =a -45+45b 35-35=a 0b 0=1. (3)原式=412·432100·a 32·a -32·b 12=425a 0·b 12=425b 12.。
高中数学 教师用书 第三章 3.3 创新演练 新人教B版必修1

【三维设计】2013届高一数学教师用书 课下作业 第三章 3.3创新演练课件 必修11.下列函数中,是幂函数的是( )A .y =-x 12B .y =3x 2C .y =1xD .y =2x解析:幂函数的形式为y =x α,A 是y =-1×x 12;B 是y =3×x 2;D 是指数函数,故A 、B 、D 都不是幂函数,只有y =1x=x -1符合幂函数的定义. 答案:C2.给出四个说法:①当α=0时,y =x α的图象是一个点;②幂函数的图象都经过点(0,0),(1,1);③幂函数的图象不可能出现在第四象限;④幂函数y =x α在第一象限为减函数,则α<0.其中,正确的说法个数是( )A .1B .2C .3D .4解析:显然①错误;②中y =x -1的图象不过(0,0);根据幂函数图象可知,③④正确.答案:B3.设α∈{-2,-1,-12,13,12,1,2,3},则使f (x )=x α为奇函数且在(0,+∞)上单调递减的α的值的个数是( )A .1B .2C .3D .4解析:∵f (x )=x α为奇函数,∴α=-1,13,1,3. 又∵f (x )在(0,+∞)上为减函数,∴α=-1.答案:A4.函数f (x )=(m 2-m +1)xm 2+2m -3是幂函数,且在(0,+∞)上是减函数,则实数m =( )A .0B .1C .2D .0或1 解析:由m 2-m +1=1,得m =0或m =1,再把m =0和m =1分别代入m 2+2m -3<0检验,得 m =0.答案:A5.已知幂函数y =f (x )的图象过点⎝ ⎛⎭⎪⎫2,22,则f (9)=________. 解析:设幂函数f (x )=x α.∵过点⎝ ⎛⎭⎪⎫2,22,∴2α=22, ∴α=-12,∴f (x )=x 12-, ∴f (9)=912-=13. 答案:13 6.已知幂函数f (x )=x -12,若f (a +1)<f (10-2a ),则a 的取值范围是________. 解析:∵f (x )=x -12=1x(x >0),易知f (x )在(0,+∞)上为减函数,又f (a +1)<f (10-2a ),∴⎩⎪⎨⎪⎧a +1>0,10-2a >0,a +1>10-2a 解得⎩⎪⎨⎪⎧a >-1,a <5,a >3.∴3<a <5.答案:(3,5)7.比较下列各组数中两个数的大小:(1)(25)0.5与(13)0.5; (2)(-23)-1与(-35)-1; (3)(23)34与(34)23. 解:(1)∵幂函数y =x 0.5在(0,+∞)上是单调递增的, 又25>13,∴(25)0.5>(13)0.5.(2)∵幂函数y =x -1在(-∞,0)上是单调递减的,又-23<-35, ∴(-23)-1>(-35)-1. (3)∵函数y 1=(23)x 为减函数, 又34>23,∴(23)23>(23)34. 又∵幂函数y 2=x 23在(0,+∞)上是增函数,且34>23, ∴(34)23>(23)23. ∴(34)23>(23)34. 8.已知幂函数f (x )=x a 的图像经过点A (12,2). (1)求实数a 的值;(2)判断f (x )在区间(0,+∞)内的单调性,并用定义证明.解:(1)∵f (x )=x a 的图象经过点A (12,2), ∴(12)a =2,即2-a =212,∴a =-12. (2)减函数.证明如下:任取x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 2)-f (x 1)=x 2-12-x 1-12 =1x 2-1x 1=x 1-x 2x 1x 2=x 1-x 2x 1x 2·(x 1+x 2)、 ∵x 2>x 1>0,∴x 1-x 2<0,且 x 1x 2·(x 1+x 2)>0,于是f (x 2)-f (x 1)<0,即f (x 2)<f (x 1),所以f (x )=x -12在区间(0,+∞)内是减函数.。
高中数学 教师用书 第三章 3.1.1 创新演练 新人教B版必修1

【三维设计】2013届高一数学教师用书 课下作业 第三章 3.13.1.1 创新演练课件 必修11.将 3-22化为分数指数幂,其形式是( ) A .212 B .-212C .2-12 D .-2-12 解析: 3-22=(-22)13=(-2×212)13 =(-232)13=-212.答案:B2.下列等式中,正确的个数为( )①n a n =a ;②若a ∈R,则(a 2-a +1)0=1; ③ 3x 4+y 3=x 43+y ; ④3-5=6(-5)2.A .0B .1C .2D .3 解析:①中,若n 为偶数,则不一定成立;②中,因为a 2-a +1=(a -12)2+34≠0,所以(a 2-a +1)0=1是正确的;③是错误的;④左边为负数,右边为正数,是错误的.答案:B3.(-x )2-1x 等于( ) A.xB .-x -xC .x xD .x -x 解析:由-1x 知x <0,又当x <0时,x 2=|x |=-x ,因此(-x )2 -1x =x 2·-x |x |=-x -x .答案:B4.化简(36a 9)4·(63a 9)4的结果是( ) A .a 16B .a 8C .a 4D .a 2 解析:(36a 9)4·(63a 9)4=(6a 9)43·(3a 9)46 =(a 96)43·(a 93)23=a 96×43·a 93×23=a 4. 答案:C5.有下列说法:①3-27=3;②16的4次方根是±2;③481=±3; ④ (x +y )2=|x +y |.其中,正确的有________(填上正确说法的序号).解析:负数的3次方根是一个负数,故3-27=-3,故①错误;16的4次方根有两个,为±2,故②正确;481=3,故③错误; (x +y )2是正数,故2(x +y )2=|x +y |,故④正确.答案:②④6.83-312-613+333=________. 解析:原式=83-63-23+3= 3.答案: 37.化简下列各式: (1) 3a a ; (2)(2x 14+332)(2x 14-332)-4x -12(x -x 12); (3)(m 14n -38)8.解:(1)原式=a 13·a 16=a 13+16=a 12; (2)原式=(2x 14)2-(332)2-4x -12·x +4x -12·x 12=4x 12-33-4x 12+4x 0=-23;(3)原式=(m 14)8(n -38)8=m 2n -3.8.计算:(1)(-338)-23-23+(0.002) -12-10(5-2)-1+(2-3)0; (2)(a 85·b -65)-12·5a 4÷5b 3(a >0,b >0); (3)(14) -12·(4ab -1)30.1-2(a 3b -4)12(a >0,b >0). 解:(1)原式=(-1) -23 (338)-23+(1500)-12-105-2+1=(278)-23+50012-10(5+2)+1 =49+105-105-20+1=-1679; (2)原式=a 85×(-12)·b (-65)×(-12)·a 45÷b 35=a -45·b 35·a 45÷b 35 =a -45+45b 35-35=a 0b 0=1. (3)原式=412·432100·a 32·a -32·b 12=425a 0·b 12=425b 12.。
【三维设计】高中数学 教师用书 第三章 §5 对数函数 5.1 5.2 对数函数的概念 y=log2
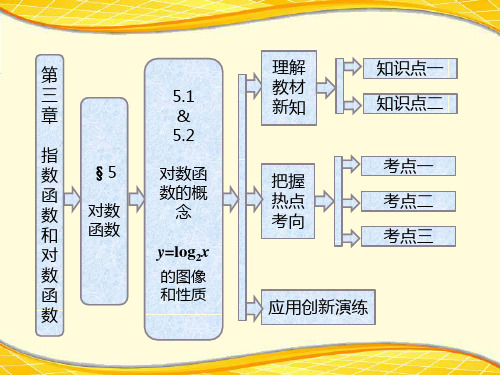
(2)由 log2x≠0,得 x>0 且 x≠1.
∴函数 y=log12x的定义域为{x|x>0,且 x≠1};
(3)由1-13x>0,得
1 x<3.
∴函数 y=log71-13x的定义域为(-∞,13).
[例 2] 求下列函数的反函数.
(1)y=10x; (2)y=(45)x; (3)y=log 1 x; (4)y=log7x.
[例3] 根据函数f(x)=log2x的图像和性质解决以下问题. (1)若f(a)>f(2),求a的取值范围; (2)求y=log2(2x-1)在x∈[2,14]上的最值. [思路点拨] 可先作出y=log2x的图像,利用图像考察单 调性解决问题.
[精解详析] 函数y=log2x 的图像如图.
(1)因为y=log2x是增函数, 若f(a)>f(2),即log2a>log22, 则a>2.所以a的取值范围为(2,+∞);
(2)∵2≤x≤14, ∴3≤2x-1≤27, ∴log23≤log2(2x-1)≤log227. ∴函数y=log2(2x-1)在x∈[2,14]上的最小值为log23,最 大值为log227.
[精解详析] (1)要使函数有意义, 需x1+ -1x>>00, , 即x>-1,
x<1. ∴-1<x<1, ∴函数的定义域为(-1,1).
(2)要使函数有意义,需
5-x>0, x-2>0, x-2≠1,
x<5, ∴x>2,
x≠3.
∴定义域为(2,3)∪(3,5).
[一点通] 求定义域有两种题型,一种是已知函数 解析式求定义域,常规为:分母不为0;0的零次幂与负 指数次幂无意义;偶次根式被开方式(数)非负;对数的 真数大于0,底数大于0且不等于1.另一种是抽象函数的 定义域问题.同时应注意求函数定义域的解题步骤.
【三维设计】高中数学 教师用书 第三章 3.2.1 第二课时 创新演练 新人教B版必修1

1.下列各式中错误的是( )A .log a b ·log b a =1B .log c d =1log d cC .log c d ·log d f =log c fD .log a b =log b clog a c答案:D2.计算log 225·log 322·log 59的结果为( )A .3B .4C .5D .6解析:原式=lg 25lg 2·lg 22lg 3·lg 9lg 5=2lg 5lg 2·32lg 2lg 3·2lg 3lg 5=6.答案:D3.1log 1419+1log 1513等于( )A .lg 3B .-lg 3C.1lg 3 D .-1lg 3解析:原式=log 1914+log 1315=log 94+log 35=log 32+log 35=log 310=1lg 3.答案:C4.若lg a ,lg b 是方程2x 2-4x +1=0的两个根,则(lg a b )2的值等于() A .2 B.12C .4 D.14解析:由根与系数的关系,得lg a +lg b =2,lg a ·lg b =12,∴(lg a b )2=(lg a -lg b )2=(lg a +lg b )2-4lg a ·lg b=22-4×12=2. 答案:A5.方程log 3(x 2-10)=1+log 3 x 的解是________.解析:原方程可化为log 3(x 2-10)=log 3(3x ),所以x 2-10=3x ,解得x =-2,或x =5.经检验知x =5.答案:x =56.已知2x =3y ,则x y =________.解析:等式2x =3y 两边取常用对数,得lg 2x =lg 3y ,即x lg 2=y lg 3,所以x y =lg 3lg 2=log 23.答案:log 237.计算下列各式的值:(1)log 2125·log 318·log 519; (2)(log 23+log 89)(log 34+log 98+log 32).解:(1)log 2125·log 318·log 519=log 25-2·log 32-3·log 53-2=-12log 25·log 32·log 53=-12·lg 5lg 2·lg 2lg 3·lg 3lg 5=-12.(2)原式=(log 23+log 3232)(log 322+log 2323+log 32)=53log 23·92log 32=152·1log 32·log 32=152. 8.测量地震级别的里氏级是地震强度(地震释放的能量)的常用对数值,显然级别越高,地震的强度也越高,如日本1923年地震是8.9级,旧金山1906年地震是8.3级,1989年地震是7.1级,试计算一下日本1923年地震强度是8.3级的几倍,是7.1级.的几倍.(lg 2≈0.3)解:由题意可设lg x =8.9,lg y =8.3,lg z =7.1,则lg x -lg y =8.9-8.3=0.6=2lg 2=lg 4,从而lg x =lg 4+lg y =lg (4y ).∴x =4y .lg x -lg z =8.9-7.1=1.8=6lg 2=lg 26=lg 64,从而lg x =lg z +lg 64=lg (64z ).∴x =64z .故8.9级地震强度是8.3级地震强度的4倍,是7.1级地震强度的64倍.。
【三维设计】高中数学 教师用书 第一部分 第3章 3

7.已知 2x=5y,则xy的值为________. 解析:令 2x=5y=k(k>0),
则 x=log2k,y=log5k, ∴xy=lloogg25kk=llooggkk52=log25. 答案:log25
8.设 A=log1519+log2319+log32 19,B=log21 π+log15 π, 试比较 A 与 B 的大小.
(4)(log66-log62)2+log62·log6(2×32) =log6622+log62·(log62+log632) =log263+log622+2log62·log63 =(log63+log62)2=1. 又 lg 10=12,ln e2=2, ∴原式=1+12-2=-12.
[一点通] 利用对数的运算性质解题时,应根据所 求式子的结构,对真数进行分解或合并,常见的方法有 两种:一种是将式中真数的积、商、幂、方根运用对数 的运算性质将它们化为对数的和、差、积、商,然后化 简求值;另一种方法是将式中的对数的和、差、积、商 运用对数的运算性质将它们化为真数的积、商、幂、方 根,然后化简求值.
第 3 章
第
3.2
二
3.2.1 课
时
把握热 点考向
应用创 新演练
考点一 考点二 考点三 考点四
3.2
对数函数
3.2.1 对数
第二课时 对数的运算性质及换底公式
[例 1] 计算下列各式的值: (1)lg25+lg 2·lg 5+lg 2; (2)2log32-log3 392+log38-5log53; (3)lg 25+23lg 8+lg 5·lg 20+lg2 2; (4)(1-log62)2+log62·log618+lg 10-ln e2.
[思路点拨] 利用对数的运算性质,将式子 转化为只含一种或几种真数的形式再进行计算.
【三维设计】高中数学 第1部分 第三章 §3 模拟方法 概率的应用应用创新演练 北师大版必修3

【三维设计】2013高中数学 第1部分 第三章 §3 模拟方法 概率的应用应用创新演练 北师大版必修31.灰太狼和红太狼计划在某日12:00~18:00这个时间段内外出捉羊,则灰太狼和红太狼在14:00~15:00之间出发的概率为( )A.12B.13C.14D.16解析:P =15-1418-12=16. 答案:D2.一个游戏转盘上有四种颜色:红、黄、蓝、黑,并且它们所占面积的比为6∶2∶1∶4,则指针停在红色或蓝色区域的概率为( )A.613 B.713 C.813 D.1013解析:P =6+16+2+1+4=713. 答案:B3.如右图所示,一半径为2的扇形(其中扇形中心角为90˚ ),在其内部随机地撒一粒黄豆,则它落在阴影部分的概率为( ) A.2πB.1πC.12 D .1-2π解析:S 扇形=14×π×22=π, S 阴影=S 扇形-S △OAB =π-12×2×2=π-2,∴P =π-2π=1-2π. 答案:D4.已知正三棱锥S -ABC 的底面边长为4,高为3,在正三棱锥内任取一点P ,使得V P -ABC <12V S -ABC 的概率是( )A.34B.78C.12D.14解析:由V P -ABC <12V S -ABC 知,P 点在三棱锥S -ABC 的中截面A 0B 0C 0的下方,P =1-VS -A 0B 0C 0V S -ABC=1-18=78. 答案:B5.如图所示,在圆心角为90°的扇形中,以圆心O 为起点作射线OC ,则∠AOC 和∠BOC 都不小于30°的概率为________.解析:设事件A 为“∠AOC 和∠BOC 都不小于30°”,则事件A 表示的区域角度为30°,所有可能结果的区域角度为90°,所以P (A )=3090=13. 答案:136.以半径为1的圆内任一点为中点作弦,则弦长超过圆内接等边三角形边长的概率为________.解析:记事件A “弦长超过圆内接等边三角形的边长”,如右图:作△BCD 的内切圆,当过小圆上任一点作弦时弦长等于等边三角形的边长,所以弦长超过内接三角形边长的条件是弦的中点在小圆内.小圆半径为12, ∴P (A )=π⎝ ⎛⎭⎪⎫122π·12=14. 答案:147.已知圆C :x 2+y 2=9.(1)若连续掷两次骰子,记向上的点数分别为m ,n ,则点(m ,n )在圆C 内的概率是多少?(2)若m ,n 是任意两个实数,且m ∈[-4,4],n ∈[-5,5],则点(m ,n )在圆C 内的概率是多少?解:(1)点在圆内需满足m 2+n 2<9,适合题意的点有(1,1),(1,2),(2,1),(2,2)共4个.而连续掷两次骰子,点数构成的基本事件共有36个,故所求概率为436=19. (2)依题意,所有可能的点(m ,n )可构成一个长、宽分别为10和8的矩形区域,如右图在此矩形内取点,则点落在圆内的概率为π×328×10=9π80. 8.如图所示,在边长为25 cm 的正方形中有两个腰长均为23 cm 的等腰直角三角形,现有粒子均匀散落在正方形中,问粒子落在中间阴影区域的概率是多少?解:因为粒子落在正方形内任何一点是等可能的,所以符合几何概型的条件.设A ={粒子落在中间阴影区域},则依题意得正方形面积为25×25=625(cm 2),两个等腰直角三角形的面积为2×12×23×23=529(cm 2),阴影区域的面积为625-529=96(cm 2),所以粒子落在中间阴影区域的概率为P (A )=96625.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【三维设计】2013届高一数学教师用书课下作业第三章 3.4
创新演练课件必修1
1.某自行车存车处在某一天总共存放车辆4 000辆次,存车费为:电动自行车0.3元/辆,普通自行车0.2元/辆.若该天普通自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4 000)
B.y=0.5x(0≤x≤4 000)
C.y=-0.1x+1 200(0≤x≤4 000)
D.y=0.1x+1 200(0≤x≤4 000)
解析:由题意得y=0.3(4 000-x)+0.2x=-0.1x+1 200.
答案:C
2.某种动物繁殖数量y(只)与时间x(年)的关系为y=a log2(x+1),设这种动物第一年有100只,到第7年它们发展到( )
A.300只B.400只
C.500只D.600只
解析:由题意得100=a log2(1+1),∴a=100,∴y=100 log2(x+1).当x=7时,y=100log2(7+1)=300.
答案:A
3.在某种金属材料的耐高温实验中,温度y(℃)随着时间t(min)变
化的情况由计算机记录后显示的图像如图所示.
现给出下列说法:
①前5 min温度增加越来越快;
②前5 min温度增加越来越慢;
③5 min后温度保持匀速增加;
④5 min后温度保持不变.
其中,说法正确的是( )
A.①④B.②④
C.②③D.①③
解析:前5 min,温度y随x增加而增加,增长速度越来越慢;5 min后,温度y随x 变化的图象是直线,即温度匀速增加.故说法②③正确.
答案:C
4.春天来了,某池塘中的荷花枝繁叶茂,已知每一天荷叶覆盖水面面积是前一天的2
倍,若荷叶20天可以完全长满池塘水面,当荷叶覆盖水面面积一半时,荷叶已生长了
( )
A .10天
B .15天
C .19天
D .2天
解析:荷叶覆盖水面面积y 与生长时间x 的函数关系式为y =2x .当x =20时,长满水面,
所以生长19天时,布满水面一半.
答案:C
5.函数y =x 2与函数y =x ln x 在区间(1,+∞)上增长较快的一个是________. 解析:当x 变大时,x 比ln x 增长要快,
∴x 2要比x ln x 增长快.
答案:y =x 2
6.某个病毒经30 分钟繁殖为原来的2倍,且知病毒的繁殖规律为y =e kt (其中k 为常数,t 表示时间,单位:小时,y 表示病毒个数),则k =________,经过5小时,1个病毒能繁殖为________个.
解析:当t =0.5时,y =2,∴2=e 12k ,
∴k =2ln 2,∴y =e
2t ln 2. 当t =5时,y =e 10ln 2=210=1 024.
答案:2ln 2 1 024
7. 在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R 与管道半径r 的四次方成正比.
(1)写出函数解析式;
(2)假设气体在半径为3 cm 的管道中,流量速率为400 cm 3/s.求该气体通过半径为r cm 的管道时,其流量速率R 的表达式;
(3)已知(2)中的气体通过的管道半径为5 cm ,计算该气体的流量速率.
解:(1)由题意,得R =kr 4(k 是大于0的常数).
(2)由r =3 cm ,R =400 cm 3/s ,得k ·34=400,∴k =
40081
, ∴速率R 的表达式为R =40081
·r 4. (3)∵R =40081
·r 4, ∴当r =5 cm 时,R =40081
×54≈3 086(cm 3/s). 8.某医药研究所开发一种新药,如果成年人按规定的剂量服用,据检测:服药后每毫升血液中的含药量y (微克)与时间t (小时)之间近似满足如图所示的曲线关系.
(1)写出y 关于t 的函数关系式y =f (t ).
(2)据进一步测定:每毫升血液中的含药量不少于0.25微克时,治疗疾病有效. ①求服药一次后治疗疾病有效的时间;
②当t =5时,第二次服药,问t ∈[5,5116
]时,药效是否连续?
解:(1)将t =1,y =4分别代入y =kt ,y =(12
)t -a ,得k =4,a =3. 从而y =f (t )=⎩⎪⎨⎪⎧4t , 0≤t ≤1,(12
)t -3,t >1. (2)①当0≤t ≤1时,由4t ≥0.25,得116
≤t ≤1; 当t >1时,由(12
)t -3≥0.25,得1<t ≤5. 因此,服药一次后治疗疾病有效的时间为5-116=41516
(小时). ②连续.因为当t =5时,第二次服药,则t ∈[5,5 116
]时,血液中的含药量增加得快,减少得慢,从而每毫升血液中的含药量还是一直不少于0.25微克的,即药效是连续的.。
