matlab初学第3章
第三章数值数组及向量化运算(matlab基础教程)

第三章数值数组及向量化运算(matlab基础教程)第3章数值数组及向量化运算数值数组(Numeric Array)和数组运算(Array Operations)始终是MATLAB的核心内容。
本书从第3章起,全部注意力将集中于数值数组及其运算。
本章系统阐述:数组浮点算法的特点;一、二维数值数组的创建和寻访;数组运算和向量化编程;实现数组运算的基本函数;常用标准数组生成函数和数组构作技法;非数NaN、“空”数组概念和应用;关系和逻辑操作。
3.1 数值计算的特点和地位【例3.1-1】已知f(t) t2cost,求s(x) (1)符号计算解法syms t x ft=t^2*cos(t) sx=int(ft,t,0,x) ft =t^2*cos(t) sx =x^2*sin(x)-2*sin(x)+2*x*cos(x)xf(t) dt。
(2)数值计算解法dt=0.05; t=0:dt:5; Ft=t.^2.*cos(t); Sx=dt*cumtrapz(Ft); t(end-4:end) Sx(end-4:end)plot(t,Sx,'.k','MarkerSize',12) xlabel('x'),ylabel('Sx'),grid onans =4.8000 4.8500 4.9000 4.95005.0000ans =-20.1144 -19.9833 -19.7907 -19.5345 -19.2131图3.1-1 在区间[0, 5]采样点上算得的定积分值【例3.1-2】已知f(t) e sin(t),求s(x) 0f(t) dt。
4(1)符号计算解法syms t xft=exp(-sin(t)) sx=int(ft,t,0,4) ft =exp(-sin(t))Warning: Explicit integral could not be found. In sym.int at 58 sx = int(exp(-sin(t)),t = 0 .. 4)(2)数值计算解法dt=0.05; t=0:dt:4; Ft=exp(-sin(t)); Sx=dt*cumtrapz(Ft); Sx(end)plot(t,Ft,'*r','MarkerSize',4) hold onplot(t,Sx,'.k','MarkerSize',15) hold off xlabel('x')legend('Ft','Sx') ans =3.0632图3.1-2 在区间[0, 4]中间的被积函数及其原函数的离散计算结果3.23.2.1 一二数值数组的创建和寻访一维数组的创建递增/减型一维数组的创建通用型一维数组的创建【例3.2-1】一维数组的常用创建方法举例。
matlab基础第3章

上一章几条重要的命令sys=tf(num,den)[num,den]=tf(sys,'v')sys=zpk([z1,z2,…,zm],[p1,p2,…,pn],k)[z p k]=zpkdata(sys,'v')sys=ss(A,B,C,D)[A,B,C,D]=ssdata(sys)sys = tf(dnum,dden,Ts)[dnum,dden,Ts]=tfdata(sys,'v')dsys=ss(Ad,Bd,Cd,Dd,T s)[Ad,Bd,Cd,Dd,T s]=ssdata(sys)要求掌握 1 系统环节的连接2 模型的转换3 系统的稳定性分析4 单输入单输出控制系统的时域分析编程5 单输入单输出控制系统的频域分析编程第3章单输入单输出控制系统的分析建立系统数学模型的主要目的是为了对系统性能进行分析与设计。
对控制系统的分析有稳态性能和动态性能分析,如系统的稳定性,稳态误差,动态响应性能参数等。
其分析方法主要有时域法和频域法两种。
时域分析法是直接在时间域内计算系统的时间响应、分析系统的稳定性、能控和能观性、动态性能等,这种分析方法的结果比较直观。
频域分析法是在系统受到频率为ω的正弦信号激励时,分析系统输出幅值和相位与输入激励之间的关系,进而得到系统的性能特性。
MATLAB 控制系统工具箱(Control System Toolbox )对控制系统,尤其是对线性时不变(Linear Time Invariant,简称LTI )系统的建模、分析和设计提供了一个完整的解决方案,也避免了繁杂的编程工作,是线性控制系统分析和设计的高效率的工具。
3.1单输入单输出(SISO )控制系统的模型及其转换在得到控制系统各个环节的MATLAB 表达之后,通常需要进行串联、并联、反馈连接等处理方式,将比较复杂的系统化成简单的系统,再进行分析和设计。
在控制系统工具箱中提供了一些函数来支持系统的连接。
第3章 MATLAB矩阵分析与处理1

(3) 希尔伯特矩阵 在MATLAB中,生成希尔伯特矩阵的函数 是hilb(n)。 使用一般方法求逆会因为原始数据的微小 扰动而产生不可靠的计算结果。MATLAB 中,有一个专门求希尔伯特矩阵的逆的函 数invhilb(n),其功能是求n阶的希尔伯特矩 阵的逆矩阵。
例3.4 求4阶希尔伯特矩阵及其逆矩阵。 命令如下: format rat %以有理形式输出 H=hilb(4) H=invhilb(4)
(5) 伴随矩阵 MATLAB生成伴随矩阵的函数是compan(p), 其中p是一个多项式的系数向量,高次幂系 数排在前,低次幂排在后。例如,为了求 多项式的x3-7x+6的伴随矩阵,可使用命令: p=[1,0,-7,6]; compan(p)
(6) 帕斯卡矩阵 我们知道,二次项(x+y)n展开后的系数随n 的增大组成一个三角形表,称为杨辉三角 形。由杨辉三角形表组成的矩阵称为帕斯 卡(Pascal)矩阵。函数pascal(n)生成一个n阶 帕斯卡矩阵。
12
(2)构造对角矩阵
如果V是一个m个元素的向量,diag(V)将产生一个m×m对角 矩阵,
其主对角线元素即为向量V的元素。
例如:
diag([1,2,-1,4])
ans =
1000
0200 0 0 -1 0 0004 例如: diag(1:3,-1)
ans = 0000 1000 0200 0030
46.7390 33.3411 25.2880 46.8095 24.1667
y = 0.6 + sqrt(0.1)*randn(5)
2024/8/10
Application of Matlab Language
2
3.1.2 用于专门学科的特殊矩阵 (1) 魔方矩阵 魔方矩阵有一个有趣的性质,其每行、每 列及两条对角线上的元素和都相等。对于n 阶魔方阵,其元素由1,2,3,…,n2共n2个整数 组成。MATLAB提供了求魔方矩阵的函数 magic(n),其功能是生成一个n阶魔方阵。
MATLAB入门教程003基础知识

MATLAB支持多种编程范式,包括命令式编程、面向对象编程以及函数式 编程。
MATLAB应用领域
A
工程与科学计算
MATLAB广泛应用于各种工程与科学计算领域 ,如信号处理、图像处理、控制系统设计等。
数据分析与可视化
数组索引
通过索引访问数组元素,多维数组使用多个索引访问,如 `A(i,j,k)`表示访问三维数组A的第i页、第j行、第k列元素 。
广播机制
MATLAB中的广播机制允许不同大小的数组进行运算,会 自动扩展较小数组的维度以匹配较大数组的维度。
04 程序设计基础
M文件编写与执行
01
M文件是MATLAB中用于存储 代作与数据导入导出
文件读写操作
读取文件
01
使用`fopen`和`fscanf`等函数读取文本或二进制文件中的数据。
写入文件
02
使用`fopen`和`fprintf`等函数将数据写入文本或二进制文件中
。
文件定位
03
使用`fseek`和`ftell`等函数在文件中进行定位,实现随机访问。
数据导入导出方法
1 2
导入数据
使用`importdata`、`xlsread`、`csvread`等函数 导入不同格式的数据文件,如Excel、CSV等。
导出数据
使用`xlswrite`、`csvwrite`等函数将数据导出为 Excel、CSV等格式的文件。
3
自定义数据格式
通过编写脚本或函数,实现特定数据格式的导入 和导出。
02
编写M文件可以使用任何文本 编辑器,将代码保存为.m文件 即可。
第3章用MATLAB进行控制系统时域分析

第3章用MATLAB进行控制系统时域分析MATLAB是一种功能强大的计算机软件,被广泛用于进行控制系统分析和设计。
在控制系统领域,时域分析是一种常用的方法,它可以用来评估和改进系统的性能及稳定性。
在MATLAB中,有几个重要的函数可以用于进行控制系统时域分析,包括step、impulse、lsim和initial等。
这些函数可以帮助我们了解系统的响应和行为。
首先,我们可以使用step函数来绘制系统的阶跃响应。
阶跃响应表示系统对输入信号的反应。
通过分析阶跃响应曲线的特性,我们可以评估系统的稳定性和性能。
例如,我们可以从阶跃响应曲线中获取系统的超调量、上升时间和峰值时间等信息。
step函数的使用方法如下:```step(sys)```其中,sys是一个控制系统的传递函数或状态空间模型。
调用step 函数后,MATLAB会自动绘制系统的阶跃响应曲线,并且返回一个包含系统响应数据的结构体。
另一个常用的时域分析函数是impulse,它可以用来绘制系统对冲击输入的响应。
冲击响应是系统对于单位冲击信号的输出。
通过分析冲击响应曲线,我们可以了解系统的固有特性,例如共振频率和阻尼比。
impulse函数的使用方法与step函数类似:```impulse(sys)```同样,调用impulse函数后,MATLAB会绘制系统的冲击响应曲线,并且返回一个包含系统响应数据的结构体。
除了阶跃响应和冲击响应外,我们还可以使用lsim函数来绘制系统对任意输入信号的响应。
lsim函数可以接受用户自定义的输入信号,并给出系统的输出响应。
通过分析系统的输出信号,我们可以更加全面地了解系统的性能和行为。
lsim函数的使用方法如下:```lsim(sys,u,t)```其中,sys是一个控制系统的传递函数或状态空间模型,u是输入信号,t是时间向量。
调用lsim函数后,MATLAB会根据输入信号和时间向量绘制系统的输出响应曲线,并返回一个包含系统响应数据的结构体。
《MATLAB程序设计教程》第3章MATLAB程序设计

《MATLAB程序设计教程》第3章MATLAB程序设计《MATLAB程序设计教程(第二版)》的第3章主要介绍了MATLAB程序设计的基本概念和基本语法。
本章内容包括MATLAB程序的基本结构、变量的定义和使用、矩阵和向量的操作、条件语句和循环语句的使用、MATLAB函数及其调用、输入和输出等。
首先,本章介绍了MATLAB程序的基本结构。
一个MATLAB程序包含多个部分,包括脚本文件、函数文件、注释等。
脚本文件是由一系列MATLAB语句组成的,按照顺序执行。
函数文件是由函数定义和函数体组成的,可以在其他脚本文件或函数文件中调用。
接着,本章介绍了MATLAB中变量的定义和使用。
MATLAB中的变量是用来存储数据的,可以是数字、字符、字符串等。
变量可以使用等号进行赋值,并且可以进行各种运算操作。
MATLAB中的变量有严格的命名规则和作用域,需要注意命名的规范。
然后,本章介绍了MATLAB中矩阵和向量的操作。
MATLAB可以通过矩阵和向量进行复杂的数值计算。
可以通过矩阵的加减乘除、转置、求逆等操作来实现各种数值运算。
MATLAB还提供了许多便捷的函数来操作矩阵和向量,例如最大最小值、平均值、排序等。
接下来,本章介绍了条件语句和循环语句的使用。
条件语句用来根据条件执行不同的操作,包括if语句和switch语句。
循环语句用来重复执行一段代码,包括for循环、while循环和do-while循环。
这些语句可以有效地控制程序的逻辑流程,并实现各种复杂的计算。
然后,本章介绍了MATLAB函数及其调用。
函数是由一系列语句组成的,可以重复使用。
可以在MATLAB程序中定义自己的函数,并在程序中调用。
函数可以接受输入参数,经过运算后返回输出结果,可以大大提高程序的重复利用性和代码的模块化程度。
最后,本章介绍了MATLAB的输入和输出。
MATLAB可以通过命令窗口进行输入输出,也可以通过文件进行输入输出。
可以使用各种函数来读取和写入数据,包括文本文件、二进制文件等。
matlab第3章

用compass和feather函数,compass函数绘制围绕原点的罗盘图,feather函数 绘制围绕x轴的羽毛图,其调用格式为
● compass(z)或compass(u,v) ● featuher(z)或faether(u,v) 其中,z为复数向量,u、v分别为复数向量的实部和虚部。
(xr,yr,zr)为半径可以画椭圆 例:[X Y Z]=ellipsoid(0,0,0,2,3,4);见例3-17
3.2.3 其他三维图形
绘制二维图形时的条形图、饼图、杆图、填充图等特殊图形可以 扩展为三维形式出现,使用的函数分别是bar3、bar3h、pie3、 stem3和fill3。
1.三维统计分析图
title(‘text’,‘property1’,propertyvalue1,‘property2’,propertyvalue2 ,...); 其中 ‘text’是要添加的文本的内容,‘property’是该文本的属性, 譬如“FontWeight”(字体粗细),“FontName”(字体名), “FontSize”(字体大小),后面的若省略就用缺省值。
元素值为纵坐标画出一条连续曲线; 若y是复数向量,则分别以向量元素实部和虚部为横、纵坐标绘 制一条曲线。见例3-1 若y是实矩阵,则按列绘制每列元素值相对其下标的曲线,曲线 条数等于输入参数矩阵的列数;若y是复数矩阵,则按列分别以 元素实部和虚部为横、纵坐标绘制多条曲线。
(3)多条曲线的绘制 见例3-2
grid on/off命令控制是画还是不画网格线,box on/off命令控制 是加还是不加边框线。 【例3.5】见P57
3.1.5 多图形显示 1.图形窗口的分割:subplot函数 见例3-5 调用格式: subplot(m,n,p) 该函数将当前图形窗口分成m × n个绘图区,即每行n个,共m行,
第三章matlab矩阵运算

3.2.3 坐标变换函数(P52)
例3-23 将迪卡尔坐标系中(1,1,1)分别转换到球坐 标系和极坐标中。 [THETA,PHI,R]=cart2sph(1,1,1) P= [THETA,PHI,R] [THETA,PHI,Z]=cart2pol(1,1,1) Q= [THETA,PHI,Z] R=[P;Q]
ankn
例3-3 求向量eye(4),magic(4)和A=[1,2,3 ;4,5,6;7,8,9]的行列式。 det(eye(4)); det(magic(4)); det(A);
4.矩阵的行列迹: 矩阵的迹定义为对角元素之和。Matlab中用函数trace( )来计算矩阵的行列式。 例3-4 求向量eye(4),magic(4)和A=[1,2,3 ;4,5,6;7,8,9]的行列式。 trace(eye(4)); trace(magic(4)); trace(A);
2.LU分解:
LU分解是将任意一个方正A分解成为一个交换下三角矩阵 L(或是排列(permuted) 的上三角形矩阵)和一个上三角矩 阵U的乘积,A=LU,在Matlab中用函数lu来计算LU分解
例3-14 求矩阵A=[1,4,2;5,6,9;4,1,8]的LU分解,
[L1,U1]=lu(A)
L1*U1
R=rref(A2)
9.矩阵空间之间的角度:
矩阵空间之间的角度代表具有相同行数的两个矩阵线性 相关程度,夹角越小代表线性相关度越高。Matlab中用函 数subspace()来计算矩阵空间之间的角度。
例3-9 求矩阵A1=[1,2,3;4,5,6;7,8,9]和A2=[1,2;3 ,4;5,6]之间的夹角Q。
MATLAB 第3章 Z变换

第三章 Z变换
例3-2 x(n)=anu(n), 求其z变换及收敛域。
解 这是一个因果序列,其z变换为
X ( z) a z
n 0
n n
1 z (az ) 1 1 az za n 0
1 n
|z|>|a|
这是一个无穷项的等比级数求和,只有在 |az-1|<1 即 |z|>|a|处收敛如图3-4所示。
1. 设zk是X(z)zn-1的单(一阶)极点,则有
Re s[ X ( z) z ]z zk [( z zk ) X ( z) z ]z zk (3-1)
2. 如果zk是X(z)zn-1的多重极点,如N阶极点,则有
n1
n1
Re s[ X ( z ) z
n 1
]z zk
1 k n 1 [( z z ) X ( z ) z ] z zk k N 1 ( N 1)! dz
1 z 由于 , 故在z=a处有一极点(用“×” 1 1 az za
表示),收敛域为极点所在圆|z|=|a|的外部。
数字信号处理
第三章 Z变换
收敛域上函数必须是解析 的,因此收敛域内不允许有极 点存在。所以,注意:右边序 列的z变换如果有N个有限极点 z1, z2 ,zN 存 在 , 那 么 收 敛 域一定在模值最大的有限极点 所在圆以外,也即
X ( z)
n
x ( n) z
n
x ( n) z
n 0
n
n
n x ( n ) z
1
|z|>Rx-
|z|<Rx+
Rx-<|z|<Rx+
matlab第3章ppt课件

fplot('[sin(x),cos(x)]',[0,2*pi,-1.5,1.5],1e-3,'r.')
观察上述语句绘制的正余弦曲线采样点的分布,可发现
曲线变化率大的区段,采样点比较密集。
16
1.图形窗口的分割 分割后的图形窗口由若干个绘图区并绘制图形。同一图形窗口中的不同图形称 为子图。 subplot(m,n,p) 该函数将当前图形窗口分成m × n个绘图区,即每行n个,共m 行,区号按行优先编号,且选定第p个区为当前活动区。在每 一个绘图区允许以不同的坐标系单独绘制图形。
18
2.图形叠加
一般情况下,绘图命令每执行一次就刷新当前图形窗口,
图形窗口原有图形将不复存在。若希望在已存在的图 形上再叠加新的图形,可使用图形保持命令hold。 hold on/off命令控制是保持原有图形还是刷新原有图 形。例如:
x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
8
表 3.1 线型选项
选项
线型
-
实线(默 认值)
:
虚线
--
双画线
-.
点画线
表 3.2 颜色选项
选项 颜色
b( blue )
蓝色
g( green )
绿色
r(red)
红色
c(cyan)
青色
选项 颜色
m(magenta) 品红色
y(yellow)
黄色
k(black)
黑色
w( whit e)
白色
表 3.3 选项 . O(字母) X(字母) + * s(square )
令来控制。grid on/off命令控制是画还是不画网格 线,box on/off命令控制是加还是不加边框线。
Matlab第三章习题答案

Matlab第三章习题答案第三章3.5计算多项式乘法()()222254x x x x ++++>> a=[1 2 2];>> b=[1 5 4];>> c=conv(a,b)c =1 7 16 18 8poly2sym(c)ans =x^4 + 7*x^3 + 16*x^2 + 18*x + 83.6计算多项式的除法()()3231368/4x x x x ++++ >> a=[3 13 6 8];>> b=[1 4];>> [q r]=deconv(a,b)q =3 1 2r =0 0 0 0>> poly2sym(q)ans =3*x^2 + x + 23.8求多项式4324121459x x x x --++的微分和积分(1)微分:>> a=[4 -12 -14 5 9];>> b=polyder(a)b =16 -36 -28 5>> poly2sym(b)ans =16*x^3 - 36*x^2 - 28*x + 5(2)积分:polyint(a)ans =0.8000 -3.0000 -4.6667 2.5000 9.00000 >> poly2sym(ans)ans =(4*x^5)/5 - 3*x^4 - (14*x^3)/3 + (5*x^2)/2 + 9*x3.9求代数⽅程32349x x x +-+=0的解。
>> [x]=solve('x^3+3*x^2-4*x+9')x =- 7/(3*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 -1/108*108^(1/2)*4703^(1/2))^(1/3) - 17/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 - (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 - 1 7/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 + (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 – 1 3.10求线性⽅程组223430x xy y x x ?++=??-+=??的解 eqn1='x^2+x*y+y=3';>> eqn2='x^2-4*x+3=0';[x,y]=solve(eqn1,eqn2)x =13y =1-3/23.11求微分⽅程64dy y x dx=+的通解。
第三章 MATLAB符号运算

第3章 MATLAB符号计算符号计算则是可以对未赋值的符号对象(可以是常数、变量、表达式)进行运算和处理。
MATLAB具有符号数学工具箱(Symbolic Math Toolbox),将符号运算结合到MATLAB的数值运算环境。
符号数学工具箱是建立在Maple软件基础上的。
3.1 符号表达式的建立3.1.1 创建符号变量和表达式Symbolic Math Toolbox规定在进行符号计算时,首先要定义基本的符号对象然后才能进行符号运算。
创建符号变量和符号表达式可以使用sym和syms命令。
1. 使用sym命令创建符号变量和表达式语法:sym(‘变量’,参数) %把变量定义为符号对象2.使用syms命令创建符号变量和符号表达式语法:syms(‘arg1’, ‘arg2’, …,参数) %把字符变量定义为符号变量syms arg1 arg2 …,参数%把字符变量定义为符号变量的简洁形式说明:syms用来创建多个符号变量,这两种方式创建的符号对象是相同的。
参数设置和前面的sym命令相同,省略时符号表达式直接由各符号变量组成。
说明:参数用来设置限定符号变量的数学特性,可以选择为’positive’、’real’和’unreal’,’positive’表示为“正、实”符号变量,’real’表示为“实”符号变量,’unreal’表示为“非实”符号变量。
如果不限定则参数可省略。
【例3.1】创建符号变量,用参数设置其特性。
>> syms x y real %创建实数符号变量>> z=x+i*y; %创建z为复数符号变量>>real(z) %复数z的实部是实数xans =x【例3.2】创建符号表达式。
>> f1=sym('a*x^2+b*x+c')f1 =a*x^2+b*x+c【例3.3】使用syms命令创建符号变量和符号表达式。
>> syms a b c x %创建多个符号变量>>f2=a*x^2+b*x+c %创建符号表达式f2 =a*x^2+b*x+c3.1.2符号表达式的代数运算符号运算与数值运算的区别主要有以下几点:▪传统的数值型运算因为要受到计算机所保留的有效位数的限制,它的内部表示法总是采用计算机硬件提供的8位浮点表示法,因此每一次运算都会有一定的截断误差,重复的多次数值运算就可能会造成很大的累积误差。
MATLAB基础与编程入门(第二版)(张威)-第3章

第三章 数 据 类 型
注意:
MATLAB和C语言在处理数据类型和变量时不同。在C语言 中,任何变量在使用之前都必须声明,然后赋值,在声明变量时 就指定了变量的数据类型。但是在MATLAB中,任何数据变量都不 需要预先的声明,MATLAB将自动地将数据类型设置为双精度类型, 若需要使用其他类型的数据,则必须通过数据类型的转换完成。 MATLAB的数据类型名称同样就是数据类型转换的函数,利用这些 函数来完成相应的数据类型转化的工作。
第三章 数 据 类 型
第三章 数 据 类 型
3.1 概述 3.2 MATLAB基本数值类型 3.3 逻辑类型和关系运算 3.4 字符串 3.5 元胞数组 3.6 结构 3.7 本章小结
第三章 数 据 类 型 3.1 概 述
MATLAB的早期版本只有非常简单的二维数组和字符类型 的数据,目前的MATLAB版本中不仅有多达十几种的基本数据类型, 在不同的专业工具箱中还有特殊的数据类型,并且MATLAB还支持 面向对象的编程技术,支持用户自定义的数据类型。
关于数据类型转换函数的使用可以参阅相应的在线帮助。
第三章 数 据 类 型
例子3-2 使用不同的数据类型。
在MATLAB命令行窗体中键入下面的指令:
>> A = [1 2 3];
>> B = [4 5 6];
>> C = A + B;
>> whos
Name
Size
Bytes Class
A
1x3
24 double
MATLAB支持的基本数据类型见图3-1。
第三章 数 据 类 型
MATLAB数据类型
基本数值类型
字符串
matlab程序设计第三章课后习题答案
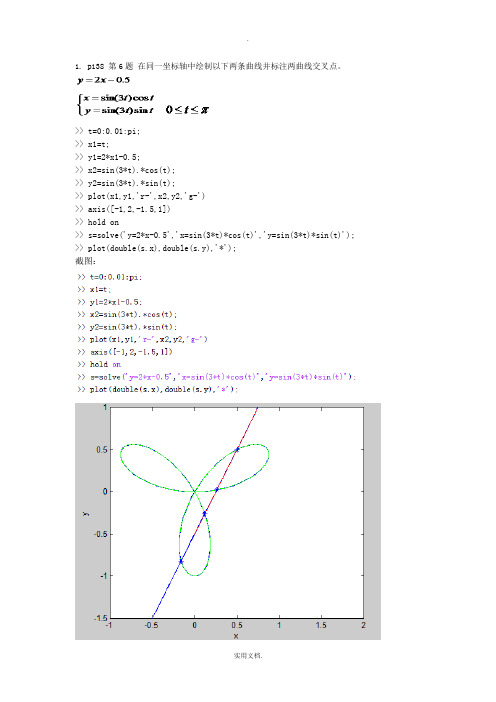
1. p138 第6题在同一坐标轴中绘制以下两条曲线并标注两曲线交叉点。
>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)'); >> plot(double(s.x),double(s.y),'*');截图:p366 第4题绘制极坐标曲线,并分析对曲线形状的影响。
function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0:0.01:2*pi;a=input('请输入a的值:');b=input('请输入b的值:');n=input('请输入n的值:');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1,b=1,n=1的极坐标图形为根底来分析a、b、n的影响。
对a的值进行改变:比照发现a只影响半径值的整倍变化对b的值进行改变:比照发现b的值使这个圆转换了一定的角度对n的值进行改变:比照发现当n>=2时有如下规律1、当n为整数时,图形变为2n个花瓣状的图形2、当n为奇数时,图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值,比照发现图形变为2n个花瓣状,并且还旋转了一定角度1 绘制sin(x)曲线,通过句柄修改曲线的颜色,要求:a)生成曲线的同时,获取句柄,再修改颜色;>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =>> set(h,'color','r');截图如下:b〕先生成曲线,然后再获取句柄,再完成颜色修改。
MATLAB实用技巧精讲之三

\sigma \delta \leq
Page 22
σ δ ≤
\Sigma \Delta \geq
Σ Δ ≥
\Phi \infty \neq
Φ ∞ ≠
数学物理建模与计算机辅助设计
MATLAB绘图和数据可视化
• 二维图形绘制
– 二维图形修饰 (3)文本标注 text(x,y,'标注文本及控制字符串')
MATLAB绘图和数据可视化
• 二维图形绘制
– 二维特殊函数图的绘制
表:Matlab中常见二维特殊图形函数
函数名
说明
函数名
说明
area bar hist
polar
填充绘图 条形图 直方图
极坐标图
feather harh pie
contour
矢量图 水平条形图 饼图
等高线图
Page 20
数学物理建模与计算机辅助设计
P数据可视化
• 【例】 clf x = 0:0.1*pi:2*pi; y=sin(x); z=cos(x); plot(x,y,x,z) xlabel('x') ylabel('y') title('y=sin(x)') legend('y=sin(x)','z=cos(x)') grid on grid off gtext('sin(1)')
Page 25
数学物理建模与计算机辅助设计
MATLAB绘图和数据可视化
• 二维图形绘制
– 复杂图形的布置和修饰:图形的保持(hold on和hold off) 例: x=0:0.1*pi:2*pi; y=sin(x); z=cos(x); plot(x,y,'-*') hold on %开启 plot(x,z,'o'); plot(x,y+z,'-h') legend('sin(x)','cos(x)','sin(x)+cos(x)',0) hold off %关闭
《Matlab入门》PPT课件

f(x) a1 b 0
bxa 其它
该分布的均值为:1/2(a+b)
方差为:1/12(a+b)2
精选PPT
8
输出噪声被均匀分布 的上限和下限
精选PPT
9
贝努利分布
泊松分布
精选PPT
10
3.1 信源、信宿和误差分析
3.1.1 信号产生设备
(4)泊松随机整数发生器
泊松分布的概率密度函数为:
(2)瑞利噪声发生器
瑞利分布等效于一个二维零均值高斯变量的均方和 (Rss—Root sum squares)。假设y1和y2是两个独立的 高斯随机变量,均值为零,方差为σ2,则服从瑞利分 布的随机变量x的表达式为:
x y12 y22
瑞利分布的概率密度函数为:
x
x2
f(x) exp( )
2
2精选P2PT
OUT = RANDINT(N) generates an N-by-N matrix of random binary numbers. The appearance of "0" and "1" have even probability.
OUT = RANDINT(N, M) generates an N-by-M matrix of random binary numbers. The appearance of "0" and "1" have even probability.
f(x)x!e
0
x0,1,2 其它
精选PPT
11
②seed 初始化“种子”值。
lambda 指定泊松参数λ。当它是标量 时,输出矢量的每一分量具 有相同的λ值。当它是矢量时, 此矢量长度须与“种子”的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)矩阵乘法 矩阵A和B进行乘法运算,要求A的列数与B的行数相等,或称A和B两矩 阵维数相容。如果两者的维数不相容,则将给出错误信息,提示用户 两个矩阵是不可乘的。例如: A=[1,2,3;4,5,6]; B=A*A ??? Error using ==> mtimes Inner matrix dimensions must agree. 在MATLAB中,还可以进行矩阵和标量相乘,标量可以是乘数也可以是 被乘数。矩阵和标量相乘是矩阵中的每个元素与此标量相乘。 (3)矩阵除法 在MATLAB中,有两种矩阵除法运算:\和/,分别表示左除和右除。如果 A矩阵是非奇异方阵,则A\B和B/A运算可以实现。A\B等效于A的逆 左乘B矩阵,也就是inv(A)*B,而B/A等效于A矩阵的逆右乘B矩阵, 也就是B*inv(A)。 (4)矩阵的乘方 一个矩阵的乘方运算可以表示成A^x,要求A为方阵,x为标量。
− 5 6 7 = 10 2 − 6 . − 2 17 10
3 4 2 1 ຫໍສະໝຸດ 1 − 1 2 1 特别: 特别: 为一阶方阵, 1 × s 与 s × 1 矩阵的乘积 为一阶方阵,即一个数
b11 b 21 = a b + a b + L a b = a b ( a11 a12 L a1 s ) M 11 11 12 21 1 s s1 ∑ 1k k 1 bs1 s × 1 与 1 × s 矩阵的乘积为 一个s阶方阵 一个s a11 a11b11 a11b12 L a11b1 s a a b a21b12 L a21b1 s 21 ( b 21 11 b12 L b1 s ) = M 11 M M M as1 a s1b11 a s1b12 L a s1b1 s
当选项省略时,MATLAB规定,线型一律用实线,颜色将根 据曲线的先后顺序依次采用表中给出的前7种颜色。
matlab7.1线形: [ + | o | * | . | x | square | diamond | v | ^ | > | < | pentagram | hexagram ] square diamond pentagram hexagram 正方形 菱形 五角星 六角星
除了设置画线的颜色,样式,符号形式。我们还可以 设置其中的4种附加的属性。
属性 说明 LineWidth MarkerEdgeColor MarkerFaceColor MarkerSize 用来指定线的宽度 用来指定标识表面的颜色 填充标识的颜色 指定标识的大小
在plot命令中,画线的属性在自变量之后被指定,形式 如下: plot(x,y,'PropertyName',value,...)
\fontsize 字体的大小
^{xxx} xxx做为某字符的上标 _{xxx} xxx做为某字符的下标
例如,下面的命令将画出一个图象,轨迹的宽度为3,颜色 为黑色,圆圈标识的宽度为6,每个标识为红色边缘和绿 色内核。 x=0:pi/15:4*pi; y=exp(2*sin(x)); plot(x,y,'-ko','LineWidth',3.0,'Markersize',6 ,... 'MarkerEdgeColor','r','MarkerFaceColor','g');
plot(x,y, ‘s’)—— 此格式用于绘制不同的线形、点 标和颜色的图形,字符串s设定曲线颜色和绘 图方式,使用颜色字符串的前1~3个字母,如 yellow—yel表示等。 或plot(x1,y1,’s1’,x2,y2,’s2’,…)
S的标准设定值如下:
字母 b g r c m y k w 颜色 蓝色 绿色 大红 亮蓝 粉红 黄色 黑色 白色 标点 · ○ × + - -· (--) ∗ : 线型 点线 圈线 ×线 +字线 实线 点划线 星形线 虚线
定义
B 若 A = (aij )m× s , = (bij ) s×n ,
s
规定 AB = C = (cij )m×n ,
= 其中 cij = ai 1b1 j + ai 2b2 j + L + ais bsj ∑ aik bkj
2Lm j 2Ln (i = 1,, , ; = 1,, , )
k=1
例1
4 − 2 4 2 C = = 1 − 2 2×2 − 3 − 6 2×2
16 − 32 − ? 16 2 × 2 8
例2
1 0 − 1 2 A = − 1 1 3 0 0 5 − 1 4
Q A = (aij )3×4 , ×
注: 1)条件 左矩阵A的列数等于右矩阵B的行数 数等于右 左行右列法——矩阵乘积 C 的元素cij 矩阵乘积 2)方法 左行右列法 等于左 等于左矩阵 A的第 i 行与右矩阵 B 的第 j 列对应元素 乘积的和. 乘积的和. 左行右列 的行数左 3)结果 左行右列——C的行数左矩阵A的行数
C的行数,C的列数为右矩阵B的列数. 的行数, 的列数为右
3.1.1 绘制二维曲线 1.plot函数 plot(x,y) 其中x和y为大小相同的向量,分别用于存储x坐标和y坐标数 据。 【例3.1】绘制曲线 3.1 t=0:0.1:8*pi; x=cos(t)+t.*sin(t); y=sin(t)-t.*cos(t);; plot(x,y);
(1)当plot函数只有一个输入参数时,即 plot(y) 若y是实型向量,则以该向量元素的下标为横坐标、元素值 为纵坐标画出一条连续曲线;若y是复数向量,则分别以 向量元素实部和虚部为横、纵坐标绘制一条曲线。若y是 实矩阵,则按列绘制每列元素值相对其下标的曲线,曲线 条数等于输入参数矩阵的列数;若y是复数矩阵,则按列 分别以元素实部和虚部为横、纵坐标绘制多条曲线。
文本字符串的高级控制
我们在画图中可能要用到文本字符串(比如标题,坐 标轴标签),这些字符串我们可以用黑体,斜体来格式化, 也包括特殊的希腊或数学符号。 文本的字体通可以通过stream modifiers修改。一 个stream modifier是一个特殊的字符序列,用来告诉编译 器改变它的行为。最普通的stream modifiers是: \bf \it \rm 黑体 斜体 正体
2.点运算 两矩阵进行点运算是指它们的对应元素进行相关运算,要求 两矩阵的维参数相同。点运算符有.*、./、.\和.^。例如: A=[1,2,3;4,5,6;7,8,9]; B=[-1,0,1;1,-1,0;0,1,1]; C=A.*B C= -1 0 3 4 -5 0 0 8 9 如果A、B两矩阵具有相同的维数,则A./B表示A矩阵除以B 矩阵的对应元素。
例:plot(x,sin(x),'-.rd')
【例3.3】在同一坐标内,分别用不同线型和颜色绘制曲线 y1 = 0.2e−0.5xcos(4πx)和y2 = 1.5e−0.5x cos(πx)。标记两曲线交叉点。 程序如下:
x=linspace(0,2*pi,1 000); y1=0.2*exp(-0.5*x).*cos(4*pi*x); y2=1.5*exp(-0.5*x).*cos(pi*x); k=find(abs(y1-y2)<1e-2); %查找y1与y2相等点(近似相等)的下标 x1=x(k);%取y1与y2相等点的x坐标 y3=0.2*exp(-0.5*x1).*cos(4*pi*x1); %求y1与y2值相等点的y坐标 plot(x,y1,x,y2,'k:',x1,y3,'bp');
y=[1,2,4,8,16,32,64,128]; plot(y)
y=[0,1,2;3,4,5;6,7,8]; plot(y)
x=[1:1:100]; y=[2:2:200]; z=x+y.*i; plot(z)
(3)当plot函数有多个输入参数,且都为向量时,即 plot(x1,y1,x2,y2,…,xn,yn) 其中,x1和y1,x2和y2,……,xn和yn分别组成一组向量对, 每一组向量对的长度可以不同。每一向量对可以绘制出一 条曲线,这样可以在同一坐标内绘制出多条曲线。例如, 在同一坐标中绘制3条幅值不同的正弦曲线,命令也可以 写成: x=0:pi/10:2*pi; y=sin(x); plot(x,y,x,y*2,x,y*3)
第3章 图形绘制
——Matlab语言丰富的图形表现方法,使得数学计算结果可 以方便地、多样性地实现了可视化,这是其它语言所不能 比拟的。 数据可视化 不管根据计算得到的数据堆还是符号堆是多么准确,人 们还是很难从这一大堆原始的数据和符号中发现它们的具体 物理含义或是内在规律,而数据图形恰能使视觉感官直接感 受到数据的许多内在本质,发现数据的内在联系。因此,数 据可视化是一项非常重要的技术。 MATLAB有两类绘图命令,一类是直接对图形句柄进行操作 的低层绘图命令,另一类是在低层命令基础上建立起来的 高层绘图命令。高层绘图命令简单明了、方便高效。利用 高层绘图函数,用户不需要过多地考虑绘图细节,只需给 出一些基本参数就能得到所需图形。
图形叠加 一般情况下,绘图命令每执行一次就刷新当前图形窗口,图 形窗口原有图形将不复存在。若希望在已存在的图形上再 叠加新的图形,可使用图形保持命令hold。hold on/off命 令控制是保持原有图形还是刷新原有图形。例如: x=0:pi/100:2*pi; y1=0.2*exp(-0.5*x).*cos(4*pi*x); plot(x,y1) hold on y2=1.5*exp(-0.5*x).*cos(pi*x); plot(x,y2); hold off
3.1.3 图形标注与坐标控制 1.图形标注 在绘制图形的同时,可以对图形加上一些说明,如图形名称、坐标轴说 明、图形某一部分的含义等,这些操作称为添加图形标注。有关图形 标注函数的调用格式如下。 ● title(图形名称) ● xlabel(x轴说明) ● ylabel(y轴说明) ● text(x,y,图形说明) ● legend(图例1,图例2,……) title和xlabel、ylabel 函数分别用于说明图形和坐标轴的名称。text函数是 在(x,y)坐标处添加图形说明。添加文本说明也可用gtext命令,执 行该命令时,十字坐标光标自动跟随鼠标移动,单击鼠标即可将文本 放置在十字光标处,如命令gtext('cos(x)'),即可放置字符串cos(x)。 legend函数用于绘制曲线所用线型、颜色或数据点标记图例,
