高中数学人教A版选修4-4创新应用教学案:第二讲第1节第1课时参数方程的概念-含答案
高中数学人教A版选修4-4第二讲 一 1. 参数方程的概念 课件

[解] 法一:设 P 点的坐标为(x,y),过
P 点作 x 轴的垂线交 x 轴于 Q.如图所示,则 Rt△OAB≌Rt△QBP.
∴xy==bascions
θ, θ.
这就是所求的轨迹方程.
9.如图所示,OA是圆C的直径,且OA=2a, 射线OB与圆交于Q点,和经过A点的切线 交于B点,作PQ⊥OA,PB∥OA,试求点P 的轨迹方程.
解:设 P(x,y)是轨迹上任意一点,取∠DOQ=θ, 由 PQ⊥OA,PB∥OA,得 x=OD=OQcosθ=OAcos2θ= 2acos2θ,y=AB=OAtan θ=2atan θ. 所以 P 点轨迹的参数方程为xy==22aatcaons2θθ,, θ∈-π2,π2.
解析:x轴上的点横坐标可取任意实数,纵坐标为0.
答案:D
2.若点P(4,a)在曲线x=2t , (t为参数)上,则a等于(
)
y=2 t
A.4
B.4 2
C.8
D.1
解析:根据题意,将点P坐标代入曲线方程中得
4=2t , a=2 t
⇒ta==84,2.
答案:B
3.在方程
参数方程是曲线方程的另一种表达形式,点与曲线 位置关系的判断,与平面直角坐标方程下的判断方法是 一致的.
1.已知点 M(2,-2)在曲线 C:x=t+1t , (t 为参数)上, y=-2
则其对应的参数 t 的值为________. 解:由 t+1t =2 知 t=1. 答案:1
2.已知某条曲线 C 的参数方程为xy==a1t+2 2t, (其中 t 为参数, a∈R).点 M(5,4)在该曲线上,求常数 a.
(人教)高中数学选修4-4课件:第2讲参数方程1第1课时

•—、曲线的参数方程•第1课时参数方程的概念、圆的参数方程卜1.理解曲线参数方程的有关概念.卜2.掌握圆的参数方程.「3一一能够根据圆的参数方程解决最值问题____ ] •1. 了解曲线的参数方程的意义.(重点)I•2.常与方程、平面几何和三角函数结合命题|I• 3.掌握圆的参数方程并用于解决最值问题. (难点)预习学案启动思维目前世界上最高的摩天轮是北京朝阳公园的朝天轮,它的轮盘直径约198米,地面高度208米,运转一周大约需要30分钟,安装在轮缘上的48个同步旋转的空调轿厢, 每个最多可截客40人・若一游客从地面搭乘摩天轮,经t秒后该游客的位置在哪里?走进教材1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标(兀,y)都是某个变数t的函数山飞⑴①,并且对于f的每一个允许值,由方程组①所确定的点M(x, y)都在这条曲线上,那么方稈①就叫做这条曲线的参数方程联系变数兀,y 的变数' 叫做参变数,简称参数.相对于参数方程而言,直接给出点的坐标间关系的方稈叫做参数普通方程 .2. 的参数方程(1)如图所示,设0的半径是r,占八、、M从初始位置A/。
出发,按逆时针方向在O上作匀速周运动,设\x=rcos 3 y=rsin 0(0为参数)y),则>4这就是心在原点0,半径为r的圆的参数方程,其中0的几何意义是0M。
绕点O逆时针旋转到I OM的位置时, OM。
转过的角度.• (2)圆心为C(o,b),半径为厂的圆的普通方程自主练习是()A.直线x+2y —2 — 0B.以(2,0)为端点的射线D.以(2Q )和(0,1)为端点的线段 C. (%—1)2+/=11・若曲线 |x =1 +cos 20, y=sin 23 (0为参数),则点(兀,y )的轨迹•解析:x = 1 + cos 20=2 - 2sin20 ,又sin?。
= %• Ax = 2 - 2y ,艮卩兀+ 2y - 2 = 0.•又y = sin20e [0,1] z•・••轨迹是以(2,0)和(0,1)为端点的线段・•答案:D•2.由方程兀2+护—4饥一2°+5Q—4=0(r为参数)所表示的一族圆的圆心轨迹是()•A. —个定点 B. —个椭圆•C・一条抛物线 D. 一条直线解析:上述方程可变形为(%—2r)2+(y—r)2:=4,・•・这组圆的圆心坐标为(2t, t).令[ =>x—2y=0.[y=t•答案:D• 3.把圆x2+y2+2x—4y+1 =0化为参数方程—4y+1 —0 的标准方程是(x+ 1)2H~ 心为(一1,2),半径为2,故参数方程为|x—— 1 +2cos 0y=2 + 2sin 3(0为参数)答案:x=— 1 +2cos 0y=2+2sin 3(0为参数)2)2=4,• 4•二个大风壬的半径为8 m,12分钟旋转一周 ,它的最低点离地面2 m(如图所示),风车翼片的一个端占为P.炎. 、•(1)点P的参数方程;•(2)点P到地面的距离加米)与时间/(分钟)之间的函数关系(用弧度制求解).解析:首先考虑建立直角坐标系,以最低点的切线作为X 轴,最低点作为坐标原点,如图建立直角坐标系.(1)设P(JG y)的初始位置在最低点,1X0ZPO l O=0,那么风车上翼片端点所在位置P可由函数兀⑴、y⑴来刻画.在RtAOrPQ中,8cos 3=~/.x(0 = 8sin 0, y(r)= — 8cos 0+8.8 ,而寻=号’所以0=自・兀x(0 = 8sin g71 ,小y(f)=_8cos g+8即点P的参数方程为7Cx=8sin ~^tTty = — 8cos g+8 ([为参数)・7Th⑴=y(D + 2, (2)Vy(O = —8cos g+8,.\/z(0=—8cos ”+10・课堂讲义典例导航2cos 0PQ (°为参数,0£0<2兀)[y=3sin 3(判断点A(2,0), B -A/3,刁是否在曲线C上?若在曲线上,\ 厶)求出点对应的参数的值.•[思路点拨](1)消参,得到普通方程•⑵将点代入普通方程判断• (3)注意变量的取值范围k==2cos 0[解题过程]将点A(2,0)的坐标代入[y=3sin0 ,得cos 3= 1Vsin 0=0,由于0解得0=0,所以点4(2,0)在曲线C上,对应0=0.将点B—A/3,\ I]的坐标代入x—• 2cos3V3 2cos 0—书cos 3=-2-• a 1sin t/=2由于0<3<2TI,解得0=5兀"6_,所以点冲一伍目在曲线C±,对应&=石・[规律方法]对于曲线C 的普通方程>,j )=0,若点M (X1, yi )在曲线上,则/Cm yJ=O,若点Ng ,丁2)不在曲线上,则Zte , 力)和.同样,对于曲线c 的参数方程¥=£;;)(》为参数),若点即参数(不存在.[变式训练]1 •已知曲线C 的参数方程为1=”_4 (/为参血,旳)在曲线上,则忙眷)对应的参数f 有解,否则无解,数)判断点4(3,0), 3(—2,2)是否在曲线C上?若在曲线上,求出点对应的参数的值.. 一\x=t+\b+l=3解析:将点4(3,0)的坐标代入(=[2_4,得(2_4=0,解得尸2,所以点A(3,0)在曲线C上,对应参数尸2.]%=/+1 ”+1 = _2将点8( — 2,2)的坐标代入[円2_4,得[—4 = 2 '即,此方程组无解,所以点3(—22)不在曲线C上.•例酬< 已知圆的普通方程界+护+2兀一6y+9 =0,将它化为参数方程.[思路点拨](1)将圆的普通方程化为参数方程,关键是引 入适合的参数.⑵将一般方程标准化I —T 引入参数I —T 化为参数方程圆的参数方程[解题过程]由x2+y2+2x-6y+9 = 0, 得(x+l)24-(j—3)2= 1. 令x+1 =cos 0, y—3 = sin 0,fx= —1+cos 0,所以参数方程为仁3 +smo(0为参数).[规律方法](1)普通方程化为参数方程关键是选参数,并且利用三角等式sin2a+cos2a = 1.(2)常见的圆的参数方程有:x=rcos q *匚、①圆x2+y2=r2的参数方程为:sin6) (0为参数);fx=x0+rcos 0,②圆(x-^o)2+(y-yo)2=r2的参数方程为[尸沟+罰0(0为参数).4/ 4r 当fHO 时,而y=tx,即2,尸l+z24? y—TT?•[变式训练]2•设丁 =饥(》为参数),求圆x2+y2 -4^=0的参数方程.解析:因为y=tx,代入x2+y2—4y=0,得x2+(/x)2—4/x—0.r r fx = 0,当f=0 时,x=0,且y=0,即< c 2=0・• 例❸《已知矩BABCD 的顶点C(4,4),点4在 圆O : x 2+y 2=%x>0, y>0)±移动,且 AD 两边始终分别平行于兀轴、评由.求矩形 4BCD 面积的;「川二斗值,以及相应的点 4的坐标.AV B参数方程的应用•[思路点拨]由题目可获取以下主要信息:①点C(4,4)是定点,点A是弧上的动点;*②*矩开如= S刊'\AD\.解答本题可以设出点A的坐标,转化为矩形白6邻边的长屢之积求最小值与最知首.[解题过程]方法一:设点A的坐标为a,y±°)' 则??+y2 = 9.S 矩形ABCD=SBI・SD=(4—兀)・(4一刃= 16—4(x+y)+xy ・_(x+y『_9 •••(x+y)2=x2+y2+2xy=9+2x”•••xy= 2 ・•••S 矩形ABCD= 16一4(x+y)+ 2Vx2+y2^(x+y)2^2(x2+y2)(x^0, y^O)・°・9W(x+y)y 18,于是3Wx+yW3边令t=x+y,贝I」S 矩形ABCD=2^t—4『+㊁.(3W T W3A J^)7 7/.当t=x+y = 4时,Smin = y 此时xy = 297所以兀、y是方程才一4z+㊁=0即2z2—8z+7=0的两根,解得z=2± 22■<x=2+ 22或V y=2+当 f=x+y=3 时,Smax=4,此时 xy =Oj 所以%、y 是方程z 2—3z=0的两根.此时点4的坐标为综上所述,S m[n =225max=4,此时点人的坐标为(3,0)或(0,3)・方法二:由于点4在圆6 x2+y2=9(x^0, y^O)上移动,7T所以设点4(3cos0, 3sin <9),且0,才S ABCD =\AB\'\AD\= (4-3cos 0)・(4一3sin 6»)=16— 12(sin 0+cos 0) + 9sin 0・cos 0.( 、令f=sin 0+cos 3=\l2sin 0+f ,#_1则sin 0・cos 3=―—,且[1, A/2].7+尹WW 边).47 当 t=sin 0 + cOS 0 = g 时,Smin = y7此时 sin 3-cos 0=込,• Q _2.2_19 I• •»矩形ABCD —2厂 2_9f_4\3丿4 7 所以sin 0、cos 0 是方程z2—^z+j^=O, 即18Z2-24Z+7= 0 的两根,解得毫盖.x=3cos 0=2+号-y=3sin <9=2-半%—3cos 0=2 —或彳J = 3sin 0=2 +当r=sin O+cos 0=1时,Smax=4, 此时sin 0・cos 0=0,所以sin 3=0, cos 3=1或sin 3=1, cos 3=0.x-— 3cos 0~— 3 丿=3sin<9=0 或| x=3cos 0=0 y = 3sin 3=3 *综上所述,5min =此时点4的坐标为2+麥,25max=4,此时点A的坐标为(3,0)或(0,3)・•[规律方法]⑴方法一:设出点4的直角坐标,将矩形的面积表示为兀+歹的二次函数,而利用基本不等式确定x + y的取值范围是难点・方法二:利用圆的参数方程,将矩形的面积表示为角0的三角函数,根据三角函数的有界性从而求出了矩形面积的最大值与最小值,这样就突破了有关不等式方面的难点・两种方法都运用了换元法,这是解决多元函数问题的常用技巧・• (2)在解答本题的过程中,易出现换元时不考虑参数的取值范围的错误,导致错误的原因•[变式训练]3.青海省玉树县2010年4月14日发生7.1级地震,灾区人民的安危牵动着全国人民的心,一批批救援物资源源不断地运往灾区•现在一架救援飞机在离灾区地面593 m 高处以150m/s的速度作水平飞行.为使投放救援物资准确落于灾区某指定的地点(不记空气阻力),飞行员应如何确定投放时机呢?解析:如图所示,物资投出机舱后,设在时刻t的水平位移为X,垂直距离为"(g = 9・8 m/s2).令J=0,得alls,代入x=150t,得x^l 650 m.所以,飞行员在离救援点的水平距离约1 650米时开始投放物资,可使其准确落在指定位置.疑难解读•1.求曲线的参数方程的方法步骤是什么?•(1)建立直角坐标系,设曲线上任一点P坐标为(x,y);•(2)选取适当的参数,与运动有关的问题选取时间"故参数,与旋转的有关问题选取角0叫做参数,或选取有向线段的数量、长度、直线的倾斜角、斜率等.•(3)根据已知条件和图形的几何性质,物理意义,建立点P坐标与参数的函数式;/八左希存旦石rh 巫施心会拓iVi丽/古姑审M的参数方程中,设点M 绕点0转动的角速度为①(① 为常数)转动的某一时刻为t,因此取时刻t 为参数可得圆的参 数方程为:若以0M 转过的角度0(ZM°OM=0)为参数,可得圆的参[FCOS 0数方程为 .a (0为参数),此时0具有明显的几何意义. y=rsin c/2・ 参数有什么实际意义?x=rcos coty = rsin cot(t 为参数),此时参数f 表示时间.。
人教版高中数学选修(4-4)-2.1《参数方程的概念》参考教案2

参数方程的概念
一、教学内容分析
本节课内容选自《普通高中课程标准实验教科书·数学选修4-4(人教A版)》第二章2.1.1参数方程的概念。
教材通过“平抛运动中运动物体的位置与时间的关系”引导学生从实际问题中体会物体的水平位移量与物体距地面的高度都与时间t有着关系,进而引出参数方程的概念。
二、学生学习情况分析
本节课是一节概念课,由于前面已经学习了曲线的普通方程,学生在学习参数方程的概念时很容易出现不重视本节课内容的情况,造成对参数方程的概念理解不透彻、不深刻的问题。
三、设计思想
鉴于学生在学习本节课可能出现的问题,在介绍参数方程概念时,应多举例子让学生体会参数方程在解决实际问题时的作用,尤其是要体会参数的设法和作用。
四、教学目标
(一)知识与技能
理解曲线参数方程的概念,能根据实际问题引进适当的参数,写出参数方程,并体会参数的意义
(二)过程与方法
在解决实际问题的过程中,体会参数的基本思想
(三)情感、态度与价值观
初步了解如何应用参数方程来解决具体问题,提高数学抽象思维能力
五、教学重点与难点
1. 重点:参数方程的概念,能根据问题列出参数方程
2. 难点:根据实际问题列出参数方程,并体会参数的意义
六、教学过程设计。
高中数学:2.1《参数方程的概念》教案(新人教A版选修4-4)

1. 参数方程的概念一)目标点击:1. 理解参数方程的概念,能识别参数方程给出的曲线或曲线上点的坐标;2. 熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3. 能掌握消去参数的一些常用技巧:代人消参法、三角消参等; 4. 能了解参数方程中参数的意义,运用参数思想解决有关问题; 二)概念理解: 1、例题回放:问题1:(请你翻开黄岗习题册P122,阅读例题)已知圆C 的方程为1)2(22=+-y x ,过点P 1(1,0) 作圆C 的任意弦,交圆C 于另一点P 2,求P 1P 2的中点M 的轨迹方程。
书中列举了六种解法,其中解法六运用了什么方法求得M 点的轨迹方程?此种方法是如何设置参数的,其几何意义是什么?设M(y x ,),由⎪⎪⎩⎪⎪⎨⎧+=++=222112k k y k k x,消去k,得41)23(22=+-y x ,因M 与P 1不重合,所以M 点的轨迹方程为41)23(22=+-y x (1≠x ) 解法六的关键是没有直接寻求中点M 的轨迹方程0),(=y x F ,而是通过引入第三个变量k(直线的斜率),间接地求出了x 与y 的关系式,从而求得M点的轨迹方程。
实际上方程⎪⎪⎩⎪⎪⎨⎧+=++=222112k k y k k x (1)和41)23(22=+-y x (1≠x )(2)都表示同一个曲线,都是M 点的轨迹方程.这两个方程是曲线方程的两种形式。
方程组(1)是曲线的参数方程,变数k 是参数,方程(2)是曲线的普通方程。
由此可以看出参数方程和普通方程是同一曲线的两种不同的表达形式.我们对参数方程并不陌生,在求轨迹方程的过程中,我们通过设参变量k ,先求得曲线的参数方程再化为普通方程,进而求得轨迹方程.参数法是求轨迹方程的一种比较简捷、有效的方法。
问题2:几何课本3.1曲线的参数方程一节中,从研究炮弹发射后的运动规律,得出弹道曲线的方程.在这个过程中,选择什么量为参数,其物理意义是什么?参数的取值范围?通过研究炮弹发射后弹道曲线的方程说明:【例1】 形如⎩⎨⎧==)()(t g y t f x 的方程组,描述了运动轨道上的每一个位置(y x ,) 和时间t 的对应关系.【例2】 我们利用“分解与合成”的方法研究和认识了形如⎩⎨⎧==)()(t g y t f x 的方程组表示质点的运动规律.3)参数t 的取值范围是由t 的物理意义限制的. 2、曲线的参数方程与曲线C 的关系在选定的直角坐标系中,曲线的参数方程⎩⎨⎧==)()(t g y t f x t D ∈(*)与曲线C 满足以下条件:(1) 对于集合D 中的每个t 0,通过方程组(*)所确定的点()(),(0t g t f )都在曲线C 上;(2) 对于曲线C 上任意点(00,y x ),都至少存在一个t 0,满足⎩⎨⎧==)()(0000t g y t f x则 曲线C ⇔ 参数方程⎩⎨⎧==)()(t g y t f x t D ∈3、曲线的普通方程与曲线的参数方程的区别与联系曲线的普通方程),(y x F =0是相对参数方程而言,它反映了坐标变量x 与y 之间的直接联系;而参数方程⎩⎨⎧==)()(t g y t f x t D ∈是通过参数t 反映坐标变量x 与y 之间的间接联系.曲线的普通方程中有两个变数,变数的个数比方程的个数多1;曲线的参数方程中,有三个变数两个方程,变数的个数比方程的个数多1个.从这个意义上讲,曲线的普通方程和参数方程是“一致”的.参数方程 普通方程 ; 普通方程 参数方程这时普通方程和参数方程是同一曲线的两种不同表达形式. 问题3:方程222a y x =+(0≠a );方程λ=-2222by a x (0≠λ)是参数方程吗?参数方程与含参数的方程一样吗?方程222a y x =+(0≠a )表示圆心在原点的圆系,方程λ=-2222by a x (0≠λ)表示共渐近线的双曲线系.曲线的参数方程⎩⎨⎧==)()(t g y t f x(t 为参数,t D ∈)是表示一条确定的曲线;含参数的方程),,(t y x F =0却表示具有某一共同属性的曲线系,两者是有原则区别的. 三)基础知识点拨:例1:已知参数方程⎩⎨⎧==θθsin 2cos 2y x ∈θ[0,2π)判断点A (1,3)和B (2,1)是否在方程的曲线上。
人教A版选修4-4参数方程的概念 教案

高中数学选修4-4全套教案第二章 参数方程【课标要求】1、了解抛物运动轨迹的参数方程及参数的意义。
2、理解直线的参数方程及其应用;理解圆和椭圆(椭圆的中心在原点)的参数方程及其简单应用。
3、会进行曲线的参数方程与普通方程的互化。
第一课时 参数方程的概念一、教学目标:1.通过分析抛物运动中时间与运动物体位置的关系,写出抛物运动轨迹的参数方程,体会参数的意义。
2.分析曲线的几何性质,选择适当的参数写出它的参数方程。
二、教学重点:根据问题的条件引进适当的参数,写出参数方程,体会参数的意义。
教学难点:根据几何性质选取恰当的参数,建立曲线的参数方程。
三、教学方法:启发诱导,探究归纳 四、教学过程(一).参数方程的概念1.问题提出:铅球运动员投掷铅球,在出手的一刹那,铅球的速度为0ν,与地面成α角,如何来刻画铅球运动的轨迹呢?2.分析探究理解: (1)、斜抛运动:为参数)t gt t v y t v x (21sin cos 200⎪⎩⎪⎨⎧-⋅=⋅=αα (2)、抽象概括:参数方程的概念。
说明:(1)一般来说,参数的变化范围是有限制的。
(2)参数是联系变量x ,y 的桥梁,可以有实际意义,也可无实际意义。
(3)平抛运动:xyOv=v 0xy 500O Av=100m/s为参数)t gt y t x (215001002⎪⎩⎪⎨⎧-== (4)思考交流:把引例中求出的铅球运动的轨迹的参数方程消去参数t 后,再将所得方程与原方程进行比较,体会参数方程的作用。
(二)、应用举例:例1、已知曲线C 的参数方程是⎩⎨⎧+==1232t y t x (t 为参数)(1)判断点1M (0,1), 2M (5,4)与曲线C 的位置关系;(2)已知点3M (6,a )在曲线C 上,求a 的值。
分析:只要把参数方程中的t 消去化成关于x,y 的方程问题易于解决。
学生练反思归纳:给定参数方程要研究问题可化为关于x,y 的方程问题求解。
人教A版高中数学选修4-4课件第二章第一节《参数方程》

,(为
参数)的右
顶点,
则常数a的值为________ .
*高考链接*
1.(2013年高考湖南卷(理))在平面直
角
坐标系xOy中,
若l
:
x y
t t
,
(t为 a
参数)
过椭圆C
:
x y
3 2
cos sin
,(为
参数)的右
顶点,
则常数a的值为____3____ .
*练习1* 曲线y x2的一种参数方程是( )
A.
x
t
2
y t 4
B.
x
sin
t
y sin2 t
C
.
x
t
y t
D.
x
t
y t 2
练习2* 参数方程
x y
|
cos
2 1 (1 2
sin
一般地,在平面直角坐标系中,如果曲线
上任意一点的坐标x,y都是某个变数t的函数
x f (t),
(2)
y g(t),
并且对于t的每一个允许值,由方程组(2)所确
定的点M(x,y)都在这条曲线上,那么方程(2)
就叫做这条曲线的参数方程,联系变数x,y
的变数t叫做参变数,简称参数。相对于参数
x
sin
t
y sin2 t
(2)
x
1 2
(et
et
)
y
高中数学 第2讲 参数方程 1.1 参数方程的概念 圆的参数方程学案 新人教A版选修4-4(202

2016-2017学年高中数学第2讲参数方程1.1 参数方程的概念圆的参数方程学案新人教A版选修4-4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2016-2017学年高中数学第2讲参数方程1.1 参数方程的概念圆的参数方程学案新人教A版选修4-4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2016-2017学年高中数学第2讲参数方程1.1 参数方程的概念圆的参数方程学案新人教A版选修4-4的全部内容。
参数方程的概念圆的参数方程1.了解曲线的参数方程的概念与特点.2.理解圆的参数方程的形式和特点.(重点)3.运用圆的参数方程解决最大值、最小值问题.(难点、易错点)[基础·初探]教材整理1 参数方程的概念阅读教材P21~P23“圆的参数方程”以上部分,完成下列问题.一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数{x=f t①,并且对于t的每一个允许值,由方程组①所确定的点M(x,y)都,y=g t在这条曲线上,那么方程组①就叫做这条曲线的参数方程,联系变数x,y的变数t叫做参变数,简称参数.相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.方程错误!(θ是参数)所表示曲线经过下列点中的( )A.(1,1) B.错误!C。
错误!D。
错误!【解析】将点的坐标代入方程:错误!,解θ的值.若有解,则该点在曲线上.【答案】C教材整理2 圆的参数方程阅读教材P23~P24“思考”及以上部分,完成下列问题.1.如图21。
1,设圆O的半径为r,点M从初始位置M0(t=0时的位置)出发,按逆时针方向在圆O上作匀速圆周运动,设M(x,y),点M转过的角度是θ,则错误!(θ为参数),这就是圆心在原点,半径为r的圆的参数方程.图2。
高中数学 2[1].1《参数方程的概念》教案 新人教选修4-4
![高中数学 2[1].1《参数方程的概念》教案 新人教选修4-4](https://img.taocdn.com/s3/m/3fa869fa16fc700aba68fc8e.png)
参数方程目标点击:1.理解参数方程的概念,了解某些参数的几何意义和物理意义; 2.熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3.会选择最常见的参数,建立最简单的参数方程,能够根据条件求出直线、圆锥曲线等常用曲线的一些参数方程并了解其参数的几何意义;4.灵活运用常见曲线的参数方程解决有关的问题. 基础知识点击: 1、曲线的参数方程在取定的坐标系中,如果曲线上任意一点的坐标x,y 都是某个变数t的函数,⎩⎨⎧==)()(t g y t f x (1) 并且对于t 的每一个允许值,由方程组(1)所确定的点M(x,y)都在这条曲线上,那么方程组(1)叫做这条曲线的参数方程.联系x 、y 之间关系的变数叫做参变数,简称参数.2、求曲线的参数方程求曲线参数方程一般程序:(1) 设点:建立适当的直角坐标系,用(x,y)表示曲线上任意一点M 的坐标;(2) 选参:选择合适的参数;(3) 表示:依据题设、参数的几何或物理意义,建立参数与x ,y 的关系式,并由此分别解出用参数表示的x 、y 的表达式. (4) 结论:用参数方程的形式表示曲线的方程 3、曲线的普通方程相对与参数方程来说,把直接确定曲线C 上任一点的坐标(x,y )的方程F (x,y )=0叫做曲线C 的普通方程. 4、参数方程的几个基本问题(1) 消去参数,把参数方程化为普通方程. (2) 由普通方程化为参数方程. (3) 利用参数求点的轨迹方程. (4) 常见曲线的参数方程. 5、几种常见曲线的参数方程 (1) 直线的参数方程(ⅰ)过点P 0(00,y x ),倾斜角为α的直线的参数方程是⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数)t 的几何意义:t 表示有向线段P P 0的数量,P(y x ,)为直线上任意一点.(ⅱ)过点P 0(00,y x ),斜率为abk =的直线的参数方程是⎩⎨⎧+=+=bt y y atx x 00 (t 为参数)(2)圆的参数方程(ⅰ)圆222r y x =+的参数方程为⎩⎨⎧==ϕϕsin cos r y r x (ϕ为参数)ϕ的几何意义为“圆心角”(ⅱ)圆22020)()(r y y x x =-+-的参数方程是⎩⎨⎧+=+=ϕϕsin cos 00r y y r x x (ϕ为参数)ϕ的几何意义为“圆心角”(3)椭圆的参数方程(ⅰ)椭圆12222=+b y a x (0>>b a ) 的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (ϕ为参数)(ⅱ)椭圆1)()(220220=-+-b y y a x x (0>>b a )的参数方程是 ⎩⎨⎧+=+=ϕϕsin cos 00b y y a x x (ϕ为参数)ϕ的几何意义为“离心角”(4)双曲线的参数方程(ⅰ)双曲线12222=-b y a x 的参数方程为⎩⎨⎧==ϕϕbtg y a x sec (ϕ为参数)(ⅱ)双曲线1)()(220220=---by y a x x 的参数方程是 ⎩⎨⎧+=+=ϕϕbtg y y a x x 00sec (ϕ为参数)ϕ的几何意义为“离心角”(5) 抛物线的参数方程px y 22= (p>0) 的参数方程为⎩⎨⎧==pty pt x 222(t 为参数) 其中t 的几何意义是抛物线上的点与原点连线的斜率的倒数(顶点除外). 考点简析:参数方程属每年高考的必考内容,主要考查基础知识、基本技能,从两个方面考查(1)参数方程与普通方程的互化与等价性判定;(2)参数方程所表示的曲线的性质. 题型一般为选择题、填空题.一、 参数方程的概念一)目标点击:1、理解参数方程的概念,能识别参数方程给出的曲线或曲线上点的坐标;2、熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3、能掌握消去参数的一些常用技巧:代人消参法、三角消参等;4、能了解参数方程中参数的意义,运用参数思想解决有关问题; 二)概念理解: 1、例题回放: 问题1:(请你翻开黄岗习题册P122,阅读例题) 已知圆C 的方程为1)2(22=+-y x ,过点P 1(1,0) 作圆C 的任意弦,交圆C 于另一点P 2,求P 1P 2的中点M 的轨迹方程.书中列举了六种解法,其中解法六运用了什么方法求得M 点的轨迹方程?此种方法是如何设置参数的,其几何意义是什么? 设M(y x ,) ,由⎪⎪⎩⎪⎪⎨⎧+=++=222112k k y k k x ,消去k,得41)23(22=+-y x ,因M 与P 1不重合,所以M 点的轨迹方程为41)23(22=+-y x (1≠x ) 解法六的关键是没有直接寻求中点M 的轨迹方程0),(=y x F ,而是通过引入第三个变量k (直线的斜率),间接地求出了x 与y 的关系式,从而求得M点的轨迹方程.实际上方程⎪⎪⎩⎪⎪⎨⎧+=++=222112k k y k k x (1)和41)23(22=+-y x (1≠x )(2)都表示同一个曲线,都是M 点的轨迹方程.这两个方程是曲线方程的两种形式.方程组(1)是曲线的参数方程,变数k 是参数,方程(2)是曲线的普通方程.由此可以看出参数方程和普通方程是同一曲线的两种不同的表达形式.我们对参数方程并不陌生,在求轨迹方程的过程中,我们通过设参变量k,先求得曲线的参数方程再化为普通方程,进而求得轨迹方程.参数法是求轨迹方程的一种比较简捷、有效的方法. 问题2:几何课本3.1曲线的参数方程一节中,从研究炮弹发射后的运动规律,得出弹道曲线的方程.在这个过程中,选择什么量为参数,其物理意义是什么?参数的取值范围?通过研究炮弹发射后弹道曲线的方程说明:1)形如⎩⎨⎧==)()(t g y t f x 的方程组,描述了运动轨道上的每一个位置(y x ,)和时间t 的对应关系.2)我们利用“分解与合成”的方法研究和认识了形如⎩⎨⎧==)()(t g y t f x 的方程组表示质点的运动规律.3)参数t 的取值范围是由t 的物理意义限制的. 2、曲线的参数方程与曲线C 的关系在选定的直角坐标系中,曲线的参数方程⎩⎨⎧==)()(t g y t f x t D ∈(*)与曲线C 满足以下条件:(1)对于集合D 中的每个t 0,通过方程组(*)所确定的点()(),(00t g t f ) 都在曲线C 上;(2)对于曲线C 上任意点(00,y x ),都至少存在一个t 0,满足⎩⎨⎧==)()(0000t g y t f x 则 曲线C ⇔ 参数方程⎩⎨⎧==)()(t g y t f x t D ∈3、曲线的普通方程与曲线的参数方程的区别与联系曲线的普通方程),(y x F =0是相对参数方程而言,它反映了坐标变量x 与y 之间的直接联系;而参数方程⎩⎨⎧==)()(t g y t f x t D ∈是通过参数t 反映坐标变量x 与y 之间的间接联系.曲线的普通方程中有两个变数,变数的个数比方程的个数多1;曲线的参数方程中,有三个变数两个方程,变数的个数比方程的个数多1个.从这个意义上讲,曲线的普通方程和参数方程是“一致”的.参数方程 普通方程 ; 普通方程 参数方程这时普通方程和参数方程是同一曲线的两种不同表达形式.问题3:方程222a y x =+(0≠a );方程λ=-2222by a x (0≠λ)是参数方程吗?参数方程与含参数的方程一样吗?方程222a y x =+(0≠a )表示圆心在原点的圆系,方程λ=-2222by a x (0≠λ)表示共渐近线的双曲线系。
数学新人教A版选修第二讲《参数方程》全部教案

数学新人教A版选修4-4 第二讲《参数方程》全部教案曲线的参数方程教学目标:1.通过分析抛物运动中时间与运动物体位置的关系,写出抛物运动轨迹的参数方程,体会参数的意义。
2.分析圆的几何性质,选择适当的参数写出它的参数方程。
3.会进行参数方程和普通方程的互化。
教学重点:根据问题的条件引进适当的参数,写出参数方程,体会参数的意义。
参数方程和普通方程的互化。
教学难点:根据几何性质选取恰当的参数,建立曲线的参数方程。
参数方程和普通方程的等价互化。
教学过程一.参数方程的概念1.探究:(1)平抛运动:练习:斜抛运动:2.参数方程的概念(见教科书第22页)说明:(1)一般来说,参数的变化范围是有限制的。
(2)参数是联系变量x,y的桥梁,可以有实际意义,也可无实际意义。
例1.(教科书第22页例1)已知曲线C的参数方程是 (t 为参数)(1)判断点M1(0,1),M2(5,4)与曲线C的位置关系;(2)已知点M3(6,a)在曲线C上,求a的值。
A、一个定点B、一个椭圆C、一条抛物线D、一条直线二.圆的参数方程说明:(1)随着选取的参数不同,参数方程形式也有不同,但表示的曲线是相同的。
(2)在建立曲线的参数方程时,要注明参数及参数的取值范围。
例2.(教科书第24页例2)思考:你能回答教科书第25页的思考吗?[来源:Z三.参数方程和普通方程的互化1.阅读教科书第25页,明确参数方程和普通方程的互化的方法。
注意,在参数方程和普通方程的互化中,必须使x,y 的取值范围保持一致。
例3.(教科书第25页例3)例4.(教科书第26页例4)2.你能回答教科书第26页的思考吗?四.课堂练习(教科书第26页习题)五.巩固与反思1.本节学习的数学知识2.本节学习的数学方法巩固与提高1.与普通方程xy=1表示相同曲线的参数方程(t为参数)是(D)A. B.C. D.2.下列哪个点在曲线上(C)[来源:]A.(2,7)B.C.D.(1,0)3.曲线的轨迹是(D)A.一条直线B.一条射线C.一个圆D.一条线段4.方程表示的曲线是(D)A.余弦曲线B.与x轴平行的线段C.直线D.与y轴平行的线段5.曲线上的点到两坐标轴的距离之和的最大值是(D)A.B.C.1D.6.方程(t为参数)所表示的一族圆的圆心轨迹是(D)A.一个定点B.一个椭圆C.一条抛物线D.一条直线7.直线与圆相切,那么直线的倾斜角为(A)A.或B.或C.或D.或8.曲线的一个参数方程为。
高二数学选修4-4:第二讲 一 曲线的参数方程 1.参数方程的概念

首页
上一页
下一页
末页
结束
求曲线参数方程的主要步骤 (1)画出轨迹草图,设 M(x,y)是轨迹上任意一点的坐标.画 图时要注意根据几何条件选择点的位置,以利于发现变量之 间的关系. (2)选择适当的参数.参数的选择要考虑以下两点:一是 曲线上每一点的坐标 x,y 与参数的关系比较明显,容易列出 方程;二是 x,y 的值可以由参数唯一确定.例如,在研究运 动问题时,通常选时间为参数;在研究旋转问题时,通常选 旋转角为参数.此外,离某一定点的“有向距离”、直线的 倾斜角、斜率、截距等也常常被选为参数. (3)根据已知条件、图形的几何性质、问题的物理意义等, 建立点的坐标与参数的函数关系式,证明可以省略.
首页
上一页
下一页
末页
结束
求曲线的参数方程
[例 2] 如图,△ABP 是等腰直角三角形, ∠B 是直角,腰长为 a,顶点 B,A 分别在 x 轴、y 轴上滑动,求点 P 在第一象限的轨迹的 参数方程.
[思路点拨] 解决此类问题关键是参数的选取.本例中由 于 A,B 的滑动而引起点 P 的运动,故可以 OB 的长为参数, 或以角为参数,此时不妨取 BP 与 x 轴正向夹角为参数来求解.
则其对应的参数 t 的值为________.
解析:由 t+1t=2,解得 t=1. 答案:1
首页
上一页
下一页
末页
结束
2.已知某条曲线 C 的参数方程为xy==a1t+2 2t, (其中 t 为参数, a∈R).点 M(5,4)在该曲线上,求常数 a. 解:∵点 M(5,4)在曲线 C 上,∴45==a1+ t2,2t, 解得ta==21,. ∴a 的值为 1.
首页Biblioteka 上一页下一页末页结束
高中数学《参数方程的概念》教案新人教A版选修4-4[1]共7页word资料
![高中数学《参数方程的概念》教案新人教A版选修4-4[1]共7页word资料](https://img.taocdn.com/s3/m/f1e2d01e3b3567ec102d8aef.png)
参数方程目标点击:1.理解参数方程的概念,了解某些参数的几何意义和物理意义;2.熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3.会选择最常见的参数,建立最简单的参数方程,能够根据条件求出直线、圆锥曲线等常用曲线的一些参数方程并了解其参数的几何意义; 4.灵活运用常见曲线的参数方程解决有关的问题.基础知识点击:1、曲线的参数方程在取定的坐标系中,如果曲线上任意一点的坐标x,y 都是某个变数t 的函数,⎩⎨⎧==)()(t g y t f x (1) 并且对于t 的每一个允许值,由方程组(1)所确定的点M(x,y)都在这条曲线上,那么方程组(1)叫做这条曲线的参数方程.联系x 、y 之间关系的变数叫做参变数,简称参数.2、求曲线的参数方程求曲线参数方程一般程序:(1) 设点:建立适当的直角坐标系,用(x,y)表示曲线上任意一点M 的坐标; (2) 选参:选择合适的参数;(3) 表示:依据题设、参数的几何或物理意义,建立参数与x ,y 的关系 式,并由此分别解出用参数表示的x 、y 的表达式. (4) 结论:用参数方程的形式表示曲线的方程 3、曲线的普通方程相对与参数方程来说,把直接确定曲线C 上任一点的坐标(x,y )的方程F (x,y )=0叫做曲线C 的普通方程. 4、参数方程的几个基本问题(1) 消去参数,把参数方程化为普通方程. (2) 由普通方程化为参数方程. (3) 利用参数求点的轨迹方程. (4) 常见曲线的参数方程. 5、几种常见曲线的参数方程 (1) 直线的参数方程(ⅰ)过点P 0(00,y x ),倾斜角为α的直线的参数方程是⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数)t 的几何意义:t 表示有向线段P P 0的数量,P(y x ,) 为直线上任意一点.(ⅱ)过点P 0(00,y x ),斜率为abk =的直线的参数方程是⎩⎨⎧+=+=bt y y atx x 00 (t 为参数)(2)圆的参数方程(ⅰ)圆222r y x =+的参数方程为⎩⎨⎧==ϕϕsin cos r y r x (ϕ为参数)ϕ的几何意义为“圆心角”(ⅱ)圆22020)()(r y y x x =-+-的参数方程是⎩⎨⎧+=+=ϕϕsin cos 00r y y r x x (ϕ为参数)ϕ的几何意义为“圆心角”(3)椭圆的参数方程(ⅰ)椭圆12222=+b y a x (0>>b a ) 的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (ϕ为参数)(ⅱ)椭圆1)()(220220=-+-by y a x x (0>>b a )的参数方程是 ⎩⎨⎧+=+=ϕϕsin cos 00b y y a x x (ϕ为参数)ϕ的几何意义为“离心角”(4)双曲线的参数方程(ⅰ)双曲线12222=-b y a x 的参数方程为⎩⎨⎧==ϕϕbtg y a x sec (ϕ为参数)(ⅱ)双曲线1)()(220220=---by y a x x 的参数方程是 ⎩⎨⎧+=+=ϕϕbtg y y a x x 00sec (ϕ为参数)ϕ的几何意义为“离心角”(5) 抛物线的参数方程px y 22= (p>0) 的参数方程为⎩⎨⎧==pty pt x 222(t 为参数) 其中t 的几何意义是抛物线上的点与原点连线的斜率的倒数(顶点除外).考点简析:参数方程属每年高考的必考内容,主要考查基础知识、基本技能,从两个方面考查(1)参数方程与普通方程的互化与等价性判定;(2)参数方程所表示的曲线的性质. 题型一般为选择题、填空题.一、 参数方程的概念一)目标点击:1、理解参数方程的概念,能识别参数方程给出的曲线或曲线上点的坐标;2、熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3、能掌握消去参数的一些常用技巧:代人消参法、三角消参等;4、能了解参数方程中参数的意义,运用参数思想解决有关问题;二)概念理解:1、例题回放: 问题1:(请你翻开黄岗习题册P122,阅读例题)已知圆C 的方程为1)2(22=+-y x ,过点P 1(1,0) 作圆C 的任意弦, 交圆C 于另一点P 2,求P 1P 2的中点M 的轨迹方程.书中列举了六种解法,其中解法六运用了什么方法求得M 点的轨迹方程?此种方法是如何设置参数的,其几何意义是什么?设M(y x ,) ,由⎪⎪⎩⎪⎪⎨⎧+=++=222112k ky k k x ,消去k,得41)23(22=+-y x ,因M 与P 1不重合,所以M 点的轨迹方程为41)23(22=+-y x (1≠x )解法六的关键是没有直接寻求中点M 的轨迹方程0),(=y x F ,而是通过引入第三个变量k (直线的斜率),间接地求出了x 与y 的关系式,从而求得M 点的轨迹方程.实际上方程⎪⎪⎩⎪⎪⎨⎧+=++=222112k k y k k x (1)和41)23(22=+-y x (1≠x )(2)都表示同一个曲线,都是M 点的轨迹方程.这两个方程是曲线方程的两种形式.方程组(1)是曲线的参数方程,变数k 是参数,方程(2)是曲线的普通方程. 由此可以看出参数方程和普通方程是同一曲线的两种不同的表达形式.我们对参数方程并不陌生,在求轨迹方程的过程中,我们通过设参变量k,先求得曲线的参数方程再化为普通方程,进而求得轨迹方程.参数法是求轨迹方程的一种比较简捷、有效的方法.问题2:几何课本3.1曲线的参数方程一节中,从研究炮弹发射后的运动规律, 得出弹道曲线的方程.在这个过程中,选择什么量为参数,其物理意 义是什么?参数的取值范围?通过研究炮弹发射后弹道曲线的方程说明:1)形如⎩⎨⎧==)()(t g y t f x 的方程组,描述了运动轨道上的每一个位置(y x ,)和时间t 的对应关系.2)我们利用“分解与合成”的方法研究和认识了形如⎩⎨⎧==)()(t g y t f x 的方程组表示质点的运动规律.3)参数t 的取值范围是由t 的物理意义限制的. 2、曲线的参数方程与曲线C 的关系在选定的直角坐标系中,曲线的参数方程⎩⎨⎧==)()(t g y t f x t D ∈ (*)与曲线C 满足以下条件:(1)对于集合D 中的每个t 0,通过方程组(*)所确定的点()(),(00t g t f ) 都在曲线C 上;(2)对于曲线C 上任意点(00,y x ),都至少存在一个t 0,满足⎩⎨⎧==)()(0000t g y t f x则 曲线C ⇔ 参数方程⎩⎨⎧==)()(t g y t f x t D ∈3、曲线的普通方程与曲线的参数方程的区别与联系曲线的普通方程),(y x F =0是相对参数方程而言,它反映了坐标变量x 与y之间的直接联系;而参数方程⎩⎨⎧==)()(t g y t f x t D ∈是通过参数t 反映坐标变量x 与y 之间的间接联系.曲线的普通方程中有两个变数,变数的个数比方程的个数多1;曲线的参数方程中,有三个变数两个方程,变数的个数比方程的个数多1个.从这个意义上讲,曲线的普通方程和参数方程是“一致”的.参数方程 普通方程 ; 普通方程 参数方程这时普通方程和参数方程是同一曲线的两种不同表达形式.问题3:方程222a y x =+(0≠a );方程λ=-2222by a x (0≠λ)是参数方程吗?参数方程与含参数的方程一样吗?方程222a y x =+(0≠a )表示圆心在原点的圆系,方程λ=-2222by a x (0≠λ)表示共渐近线的双曲线系。
高中数学 第二讲参数方程全部教案 新人教A版选修4-4

曲线的参数方程教学目标:1.通过分析抛物运动中时间与运动物体位置的关系,写出抛物运动轨迹的参数方程,体会参数的意义。
2.分析圆的几何性质,选择适当的参数写出它的参数方程。
3.会进行参数方程和普通方程的互化。
教学重点:根据问题的条件引进适当的参数,写出参数方程,体会参数的意义。
参数方程和普通方程的互化。
教学难点:根据几何性质选取恰当的参数,建立曲线的参数方程。
参数方程和普通方程的等价互化。
教学过程一.参数方程的概念1.探究:(1)平抛运动: 为参数)t gt y tx (215001002⎪⎩⎪⎨⎧-== 练习:斜抛运动:为参数)t gt t v y t v x (21sin cos 200⎪⎩⎪⎨⎧-⋅=⋅=αα2.参数方程的概念 (见教科书第22页) 说明:(1)一般来说,参数的变化范围是有限制的。
(2)参数是联系变量x ,y 的桥梁,可以有实际意义,也可无实际意义。
例1.(教科书第22页例1)已知曲线C 的参数方程是⎩⎨⎧+==1232t y tx (t 为参数) (1)判断点M 1(0,1),M 2(5,4)与曲线C 的位置关系; (2)已知点M 3(6,a )在曲线C 上,求a 的值。
)0,1(21,21()21,31()7,2()(2cos sin 2D C B A y x ,、,、,、的坐标是表示的曲线上的一个点为参数、方程θθθ⎩⎨⎧==A 、一个定点B 、一个椭圆C 、一条抛物线D 、一条直线二.圆的参数方程)(sin cos 为参数t t r y t r x ⎩⎨⎧==ωω)(sin cos 为参数θθθ⎩⎨⎧==r y r x说明:(1)随着选取的参数不同,参数方程形式也有不同,但表示的曲线是相同的。
(2)在建立曲线的参数方程时,要注明参数及参数的取值范围。
例2.(教科书第24页例2)思考:你能回答教科书第25页的思考吗?三.参数方程和普通方程的互化1.阅读教科书第25页,明确参数方程和普通方程的互化的方法。
人教版高中数学选修4-4 2.1.1参数方程的概念教案设计
3、例题讲解:
例1已知 曲线 C的参数方程是 (t为参数)
(1)判断点 ( 0,1), (5,4)与曲线C的位置关系;
(2)已知点 (6,a)在曲线C上,求a的值。
解:(1)把点 的坐标(0,1)代入方程组,解得t=0,所以 在曲线C上.
教学难点:根据几何性质选取恰当的参数,建立曲线的参数方程.
教师活动
学生活动
设计意图
第一课时
授课时间:
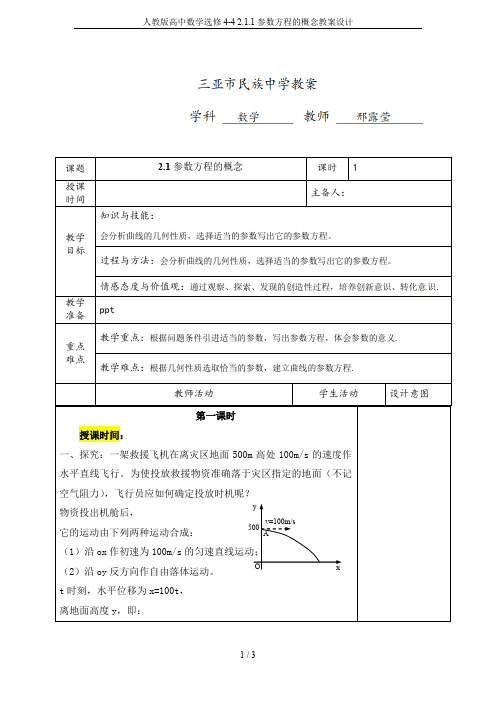
一、探究:一架救援飞机在离灾区地面500m高处100m/s的速度作水平直线飞行。为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?
物资投出机舱后,
它的运动由下列两种运动合成:
课题
2.1参数方程的概念
课时
1
授课
时间
主备人:
教学
目标
知识与技能:
会分析曲线的几何性质,选择适当的参数写出它的参数方程。
过程与方法:会分析曲线的几何性质,选择适当的参数写出它的参数方程。
情感态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识、转化意 识.
教学
准备
ppt
重点
难点
教学重点:根据问题条件引进适当的参数,写出参数方程,体会参数的意义.
六、作业:课本第26页1、2、题
板书设计
一、 参数方程的概念例1
练习
二、新课讲解
参数方程的概念:
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数 ,并且对于t的每一个允许值,由方程组所确定的点M(x, y)都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系变数x, y的变数t叫做参变数,简称参数。相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
2018-2019学年高中数学人教A版选修4-4创新应用教学案:第二讲第2节第1课时椭圆的参数方程-含答案

第1课时 椭圆的参数方程[核心必知]椭圆的参数方程中心在原点,焦点在x 轴上的椭圆x 2a 2+y 2b 2=1的参数方程是⎩⎪⎨⎪⎧x =a cos φ,y =b sin φ(φ是参数),规定参数φ的取值范围是[0,2π).[问题思考]1.中心在原点,焦点在y 轴上的椭圆y 2a 2+x 2b 2=1的参数方程是什么? 提示:由⎩⎨⎧y 2a 2=sin 2φ,x 2b 2=cos 2φ,得⎩⎪⎨⎪⎧x =b cos φ,y =a sin φ. 即参数方程为⎩⎪⎨⎪⎧x =b cos φy =a sin φ(φ为参数). 2.圆的参数方程⎩⎪⎨⎪⎧x =r cos θ,y =r sin θ中参数θ的意义与椭圆的参数方程中参数φ的意义相同吗? 提示:圆的参数方程:⎩⎪⎨⎪⎧x =r cos θ,y =r sin θ(θ为参数)中的参数θ是动点M (x ,y )的旋转角,但在椭圆的参数方程⎩⎪⎨⎪⎧x =a cos φ,y =b sin φ(φ为参数)中的参数φ不是动点M (x ,y )的旋转角,它是点M 所对应的圆的半径OA =a (或OB =b )的旋转角,称为离心角,不是OM 的旋转角.已知椭圆x 2100+y 264=1有一内接矩形ABCD ,求矩形ABCD 的最大面积. [精讲详析] 本题考查椭圆的参数方程的求法及应用.解答此题需要设出A 点的坐标,然后借助椭圆的对称性即可知B 、C 、D 的坐标,从而求出矩形的面积的表达式.∵椭圆方程为x 2100+y 264=1, ∴可设A 点的坐标为(10cos α,8sin α).则|AD |=20|cos α|,|AB |=16|sin α|,∴S 矩形=|AB |·|AD |=20×16|sin α·cos α|=160|sin 2α|.∵|sin 2α|≤1,∴矩形ABCD 的最大面积为160.利用椭圆的参数方程求函数(或代数式)最值的一般步骤为:(1)求出椭圆的参数方程;(2)利用椭圆中的参数表示已知函数(或代数式);(3)借助三角函数的知识求最值.1.已知实数x ,y 满足x 225+y 216=1,求目标函数z =x -2y 的最大值与最小值. 解:椭圆x 225+y 216=1的参数方程为⎩⎪⎨⎪⎧x =5cos φ,y =4sin φ(φ为参数). 代入目标函数得z =5cos φ-8sin φ=52+82cos (φ+φ0) =89cos (φ+φ0)(tan φ0=85). 所以目标函数z min =-89,z max =89.。
人教A版2019年高中数学选修4-4教学案: 第二讲 第1节 第1课时 参数方程的概念_含答案

第1课时 参数方程的概念[核心必知]1.参数方程在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数⎩⎪⎨⎪⎧x =f (t ),y =g (t ),①,并且对于t 的每一个允许值,由方程组①所确定的点M (x ,y )都在这条曲线上,那么方程组①叫做这条曲线的参数方程.联系变量x ,y 的变数t 叫做参变数,简称参数. 2.普通方程相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.[问题思考]1.参数方程中的参数t 是否一定有实际意义?提示:参数是联系变数x ,y 的桥梁,可以是一个有物理意义或几何意义的变数,也可以是没有明显实际意义的变数.2.曲线的参数方程一定是唯一的吗?提示:同一曲线选取参数不同,曲线参数方程形式也不一样.如⎩⎪⎨⎪⎧x =4t +1,y =2t (t ∈R )和⎩⎪⎨⎪⎧x =2m +1,y =m (m ∈R ) 都表示直线x =2y +1.已知曲线C 的参数方程是⎩⎪⎨⎪⎧x =2t ,y =3t 2-1(t 为参数). (1)判断点M 1(0,-1)和M 2(4,10)与曲线C 的位置关系; (2)已知点M (2,a )在曲线C 上,求a 的值.[精讲详析] 本题考查曲线的参数方程及点与曲线的位置关系.解答此题需要将已知点代入参数方程,判断参数是否存在.(1)把点M 1的坐标代入参数方程⎩⎪⎨⎪⎧x =2t ,y =3t 2-1, 得⎩⎪⎨⎪⎧0=2t ,-1=3t 2-1, ∴t =0.即点M 1在曲线C 上.把点M 2的坐标代入参数方程⎩⎪⎨⎪⎧x =2t ,y =3t 2-1, 得⎩⎪⎨⎪⎧4=2t ,10=3t 2-1,方程组无解.即点M 2不在曲线C 上. (2)∵点M (2,a )在曲线C 上,∴⎩⎪⎨⎪⎧2=2t ,a =3t 2-1. ∴t =1,a =3×12-1=2.即a 的值为2.已知曲线的参数方程,判断某点是否在曲线上,就是将点的坐标代入曲线的参数方程,然后建立关于参数的方程组,如果方程组有解,则点在曲线上;否则,点不在曲线上.1.已知曲线⎩⎪⎨⎪⎧x =2sin θ+1,y =sin θ+3(θ为参数,0≤θ<π),则下列各点A (1,3),B (2,2),C (-3,5)在曲线上的点是________.解析:将A (1,3)点代入方程得θ=0;将B 、C 点坐标代入方程,方程无解,故B 、C 点不在曲线上.答案:A (1,3)如图,△ABP 是等腰直角三角形,∠B 是直角,腰长为a ,顶点B 、A 分别在x 轴、y 轴上滑动,求点P 在第一象限的轨迹的参数方程.[精讲详析] 本题考查曲线参数方程的求法,解答本题需要先确定参数,然后分别用同一个参数表示x 和y .法一:设P 点的坐标为(x ,y ),过P 点作x 轴的垂线交x 轴于Q . 如图所示,则Rt △OAB ≌Rt △QBP .取OB =t ,t 为参数(0<t <a ). ∵|OA |=a 2-t 2,∴|BQ |=a 2-t 2. ∴点P 在第一象限的轨迹的参数方程为⎩⎨⎧x =t +a 2-t 2,y =t ,(0<t <a ) 法二:设点P 的坐标为(x ,y ),过点P 作x 轴的垂线交x 轴于点Q ,如图所示.取∠QBP =θ,θ为参数(0<θ<π2),则∠ABO =π2-θ.在Rt △OAB 中,|OB |=a cos (π2-θ)=a sin θ.在Rt △QBP 中,|BQ |=a cos θ,|PQ |=a sin θ. ∴点P 在第一象限的轨迹的参数方程为⎩⎪⎨⎪⎧x =a (sin θ+cos θ),y =a sin θ.(θ为参数,0<θ<π2).(1)求曲线参数方程的主要步骤:第一步,建立直角坐标系,设(x ,y )是轨迹上任意一点的坐标.画出草图(画图时要注意根据几何条件选择点的位置,以利于发现变量之间的关系).第二步,选择适当的参数.参数的选择要考虑以下两点:一是曲线上每一点的坐标x ,y 与参数的关系比较明显,容易列出方程;二是x ,y 的值可以由参数唯一确定.例如,在研究运动问题时,通常选时间为参数;在研究旋转问题时,通常选旋转角为参数.此外,离某一定点的“有向距离”、直线的倾斜角、斜率、截距等也常常被选为参数.第三步,根据已知条件、图形的几何性质、问题的物理意义等,建立点的坐标与参数的函数关系式.(2)求曲线的参数方程时,要根据题设条件或图形特性求出参数的取值范围并标注出来.2.如图所示,OA 是圆C 的直径,且OA =2a ,射线OB 与圆交于Q 点,和经过A 点的切线交于B 点,作PQ ⊥OA 交OA 于D ,PB ∥OA ,试求点P 的轨迹的参数方程.解:设P (x ,y )是轨迹上任意一点,取∠DOQ =θ,由PQ ⊥OA ,PB ∥OA ,得x =OD =OQ cos θ=OA ·cos 2θ=2a cos 2θ,y =AB =OA tan θ=2a tan θ.所以P 点轨迹的参数方程为⎩⎪⎨⎪⎧x =2a cos 2θ,y =2a tan θ,θ∈(-π2,π2).曲线参数方程的应用,是高考模拟的热点内容.本考题以实际问题为背景考查了曲线参数方程的实际应用,是高考模拟命题的一个新亮点.[考题印证]已知弹道曲线的参数方程为⎩⎨⎧x =2t cosπ6,y =2t sin π6-12gt 2.(t 为参数)(1)求炮弹从发射到落地所需时间; (2)求炮弹在运动中达到的最大高度.[命题立意] 本题主要考查曲线参数方程中参数的实际意义及其应用. [解] (1)令y =0,则2t sin π6-12gt 2=0, 解之得t =2g.∴炮弹从发射到落地所需要的时间为2g .(2)y =2t sinπ6-12gt 2=-12gt 2+t =-12g (t 2-2g t )=-12g [(t -1g )2-1g 2]=-12g (t -1g )2+12g ,∴当t =1g 时,y 取最大值12g.即炮弹在运动中达到的最大高度为12g .一、选择题1.方程⎩⎪⎨⎪⎧x =1+sin θ,y =sin 2θ(θ是参数)所表示曲线经过下列点中的( )A .(1,1) B.⎝⎛⎭⎫32,12 C.⎝⎛⎭⎫32,32 D.⎝ ⎛⎭⎪⎫2+32,-12解析:选C 将点的坐标代入方程:⎩⎪⎨⎪⎧x =1+sin θ,y =sin 2θ,解θ的值.若有解,则该点在曲线上.2.直线l 的参数方程为⎩⎪⎨⎪⎧x =a +t ,y =b +t (t 为参数),l 上的点P 1对应的参数是t 1,则点P 1与P (a ,b )之间的距离是( )A .|t 1|B .2|t 1| C.2|t 1| D.22|t 1| 解析:选C ∵P 1(a +t 1,b +t 1),P (a ,b ),∴|P 1P |=(a +t 1-a )2+(b +t 1-b )2=t 21+t 21=2|t 1|.3.已知曲线C 的参数方程为⎩⎪⎨⎪⎧x =6+4cos θ,y =5tan θ-3(θ为参数,π≤θ<2π).已知点M (14,a )在曲线C 上,则a =( )A .-3-5 3B .-3+5 3C .-3+53 3D .-3-53 3解析:选A ∵(14,a )在曲线C 上, ∴⎩⎪⎨⎪⎧14=6+4cos θ, ①a =5tan θ-3. ② 由①得:cos θ=12,又π≤θ<2π.∴sin θ=-1-(12)2=-32,∴tan θ=- 3.∴a =5·(-3)-3=-3-5 3.4.参数方程⎩⎪⎨⎪⎧x =t +1t ,y =-2(t 为参数)所表示的曲线是( )A .一条射线B .两条射线C .一条直线D .两条直线解析:选B 因为x =t +1t ∈(-∞,-2]∪[2,+∞),即x ≤-2或x ≥2,故是两条射线. 二、填空题5.由方程x 2+y 2-4tx -2ty +3t 2-4=0(t 为参数)所表示的一族圆的圆心的轨迹的参数方程为________.解析:由x 2+y 2-4tx -2ty +3t 2-4=0得: (x -2t )2+(y -t )2=4+2t 2.设圆心坐标为(x ,y ),则⎩⎪⎨⎪⎧x =2t ,y =t .答案:⎩⎪⎨⎪⎧x =2t ,y =t (t 为参数)6.已知某条曲线C 的参数方程为⎩⎪⎨⎪⎧x =1+2t ,y =at 2(其中t 为参数,a ∈R ).点M (5,4)在该曲线上,则常数a =________.解析:∵点M (5,4)在曲线C 上∴⎩⎪⎨⎪⎧5=1+2t ,4=at 2, 解得:⎩⎪⎨⎪⎧t =2,a =1.∴a 的值为1.答案:17.曲线(x -1)2+y 2=4上点的坐标可以表示为________(填序号). ①(-1+cos θ,sin θ),②(1+sin θ,cos θ), ③(-1+2cos θ,2sin θ),④(1+2cos θ,2sin θ)解析:分别将①、②、③、④代入曲线(x -1)2+y 2=4验证可知,只有④使方程成立. 答案:④8.动点M 作匀速直线运动,它在x 轴和y 轴方向的分速度分别为9和12,运动开始时,点M 位于A (1,1),则点M 的参数方程为________.解析:设M (x ,y ),则在x 轴上的位移为:x =1+9t ,在y 轴上的位移为y =1+12t . ∴参数方程为:⎩⎪⎨⎪⎧x =1+9t ,y =1+12t .答案:⎩⎪⎨⎪⎧x =1+9t ,y =1+12t (t 为参数)三、解答题9.设质点沿以原点为圆心,半径为2的圆作匀角速度运动,角速度为π60 rad/s ,运动开始时质点位于A (2,0),试以时间t 为参数,建立质点运动轨迹的参数方程.解:如图,运动开始时质点位于点A 处,此时t =0,设动点M (x ,y )对应时刻t ,由图可知:⎩⎪⎨⎪⎧x =2cos θy =2sin θ又θ=π60·t ,故参数方程为:⎩⎨⎧x =2cos π60t ,y =2sin π60t(t 为参数).10.过M (0,1)作椭圆x 2+y 24=1的弦,试求弦中点的轨迹的参数方程.解:设过M (0,1)的弦所在的直线方程为y =kx +1,其与椭圆的交点为(x 1,y 1)和(x 2,y 2),设中点P (x ,y )则有:x =x 1+x 22,y =y 1+y 22由⎩⎪⎨⎪⎧y =kx +1,x 2+y 24=1得:(k 2+4)y 2-8y +4-4k 2=0 ∴y 1+y 2=8k 2+4,x 1+x 2=-2k k 2+4. ∴⎩⎨⎧x =-kk 2+4,y =4k 2+4.(k 为参数)这就是以动弦斜率k 为参数的动弦中点的轨迹的参数方程.11.舰A 在舰B 的正东,距离6千米;舰C 在舰B 的北偏西30°,距离4千米.它们准备围捕海中某动物,某时刻A发现动物信号,4秒后B 、C 同时发现这种信号,A 于是发射麻醉炮弹,假设舰与动物都是静止的,动物信号的传播速度为1千米/秒,炮弹初速度为 203g3千米/秒,其中g 为重力加速度,空气阻力不计,求舰A 炮击的方位角与仰角.解:以BA 为x 轴,BA 中垂线为y 轴建立直角坐标系(如图),则B (-3,0),A (3,0),C (-5,23).设海中动物为P (x ,y ).因为|BP |=|CP |,所以P 在线段BC 的中垂线上,易知中垂线方程是y =33(x +7).又|PB |-|P A |=4,所以P 在以A 、B 为焦点的双曲线右支上,双曲线方程是x 24-y 25=1.从而得P (8,53).设∠xAP =α,则tan α=k AP =3,∴α=60°,这样炮弹发射的方位角为北偏东30°.再以A 为原点,AP 为x ′轴建立坐标系x ′Ay ′,(如图).|P A |=10,设弹道曲线方程是⎩⎪⎨⎪⎧x ′=v 0t cos θ,y ′=v 0t sin θ-12gt 2,(其中θ为仰角)将P (10,0)代入,消去t 便得sin 2θ=32,θ=30°或60°这样舰A 发射炮弹的仰角为30°或60°.。
高中数学 2[1].1《参数方程的概念》教案 新人教选修4-4
![高中数学 2[1].1《参数方程的概念》教案 新人教选修4-4](https://img.taocdn.com/s3/m/b79c41bbd4d8d15abe234edc.png)
参数方程目标点击:1.理解参数方程的概念,了解某些参数的几何意义和物理意义;2.熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3.会选择最常见的参数,建立最简单的参数方程,能够根据条件求出直线、圆锥曲线等常用曲线的一些参数方程并了解其参数的几何意义; 4.灵活运用常见曲线的参数方程解决有关的问题.基础知识点击:1、曲线的参数方程在取定的坐标系中,如果曲线上任意一点的坐标x,y 都是某个变数t 的函数,⎩⎨⎧==)()(t g y t f x (1) 并且对于t 的每一个允许值,由方程组(1)所确定的点M(x,y)都在这条曲线上,那么方程组(1)叫做这条曲线的参数方程.联系x 、y 之间关系的变数叫做参变数,简称参数.2、求曲线的参数方程求曲线参数方程一般程序:(1) 设点:建立适当的直角坐标系,用(x,y)表示曲线上任意一点M 的坐标; (2) 选参:选择合适的参数;(3) 表示:依据题设、参数的几何或物理意义,建立参数与x ,y 的关系 式,并由此分别解出用参数表示的x 、y 的表达式. (4) 结论:用参数方程的形式表示曲线的方程 3、曲线的普通方程相对与参数方程来说,把直接确定曲线C 上任一点的坐标(x,y )的方程F (x,y )=0叫做曲线C 的普通方程. 4、参数方程的几个基本问题(1) 消去参数,把参数方程化为普通方程. (2) 由普通方程化为参数方程. (3) 利用参数求点的轨迹方程. (4) 常见曲线的参数方程. 5、几种常见曲线的参数方程 (1) 直线的参数方程(ⅰ)过点P 0(00,y x ),倾斜角为α的直线的参数方程是⎩⎨⎧+=+=ααs i nc o s 00t y y t x x (t 为参数)t 的几何意义:t 表示有向线段P P 0的数量,P(y x ,)为直线上任意一点.(ⅱ)过点P 0(00,y x ),斜率为abk =的直线的参数方程是⎩⎨⎧+=+=bty y atx x 00 (t 为参数)(2)圆的参数方程(ⅰ)圆222r y x =+的参数方程为⎩⎨⎧==ϕϕsin cos r y r x (ϕ为参数)ϕ的几何意义为“圆心角”(ⅱ)圆22020)()(r y y x x =-+-的参数方程是⎩⎨⎧+=+=ϕϕs i n c o s 00r y y r x x (ϕ为参数)ϕ的几何意义为“圆心角”(3)椭圆的参数方程(ⅰ)椭圆12222=+b y a x (0>>b a ) 的参数方程为⎩⎨⎧==ϕϕsin cos b y a x (ϕ为参数)(ⅱ)椭圆1)()(220220=-+-by y a x x (0>>b a )的参数方程是 ⎩⎨⎧+=+=ϕϕs i nc o s 00b y y a x x (ϕ为参数)ϕ的几何意义为“离心角”(4)双曲线的参数方程(ⅰ)双曲线12222=-b y a x 的参数方程为⎩⎨⎧==ϕϕbtg y a x sec (ϕ为参数)(ⅱ)双曲线1)()(220220=---by y a x x 的参数方程是 ⎩⎨⎧+=+=ϕϕb t g y y a x x 00s ec (ϕ为参数)ϕ的几何意义为“离心角”(5) 抛物线的参数方程px y 22= (p>0) 的参数方程为⎩⎨⎧==pty pt x 222(t 为参数) 其中t 的几何意义是抛物线上的点与原点连线的斜率的倒数(顶点除外).考点简析:参数方程属每年高考的必考内容,主要考查基础知识、基本技能,从两个方面考查(1)参数方程与普通方程的互化与等价性判定;(2)参数方程所表示的曲线的性质. 题型一般为选择题、填空题.一、 参数方程的概念一)目标点击:1、理解参数方程的概念,能识别参数方程给出的曲线或曲线上点的坐标;2、熟悉参数方程与普通方程之间的联系和区别,掌握他们的互化法则;3、能掌握消去参数的一些常用技巧:代人消参法、三角消参等;4、能了解参数方程中参数的意义,运用参数思想解决有关问题;二)概念理解:1、例题回放: 问题1:(请你翻开黄岗习题册P122,阅读例题)已知圆C 的方程为1)2(22=+-y x ,过点P 1(1,0) 作圆C 的任意弦, 交圆C 于另一点P 2,求P 1P 2的中点M 的轨迹方程. 书中列举了六种解法,其中解法六运用了什么方法求得M 点的轨迹方程?此种方法是如何设置参数的,其几何意义是什么?设M(y x ,) ,由⎪⎪⎩⎪⎪⎨⎧+=++=222112k ky k k x ,消去k,得41)23(22=+-y x ,因M 与 P 1不重合,所以M 点的轨迹方程为41)23(22=+-y x (1≠x )解法六的关键是没有直接寻求中点M 的轨迹方程0),(=y x F ,而是通过引入第三个变量k (直线的斜率),间接地求出了x 与y 的关系式,从而求得M 点的轨迹方程.实际上方程⎪⎪⎩⎪⎪⎨⎧+=++=222112k k y k k x (1)和41)23(22=+-y x (1≠x )(2)都表示同一个曲线,都是M 点的轨迹方程.这两个方程是曲线方程的两种形式.方程组(1)是曲线的参数方程,变数k 是参数,方程(2)是曲线的普通方程. 由此可以看出参数方程和普通方程是同一曲线的两种不同的表达形式.我们对参数方程并不陌生,在求轨迹方程的过程中,我们通过设参变量k,先求得曲线的参数方程再化为普通方程,进而求得轨迹方程.参数法是求轨迹方程的一种比较简捷、有效的方法.问题2:几何课本3.1曲线的参数方程一节中,从研究炮弹发射后的运动规律, 得出弹道曲线的方程.在这个过程中,选择什么量为参数,其物理意 义是什么?参数的取值范围?通过研究炮弹发射后弹道曲线的方程说明:1)形如⎩⎨⎧==)()(t g y t f x 的方程组,描述了运动轨道上的每一个位置(y x ,)和时间t 的对应关系.2)我们利用“分解与合成”的方法研究和认识了形如⎩⎨⎧==)()(t g y t f x 的方程组表示质点的运动规律.3)参数t 的取值范围是由t 的物理意义限制的. 2、曲线的参数方程与曲线C 的关系在选定的直角坐标系中,曲线的参数方程⎩⎨⎧==)()(t g y t f x t D ∈ (*)与曲线C 满足以下条件:(1)对于集合D 中的每个t 0,通过方程组(*)所确定的点()(),(00t g t f ) 都在曲线C 上;(2)对于曲线C 上任意点(00,y x ),都至少存在一个t 0,满足⎩⎨⎧==)()(0000t g y t f x则 曲线C ⇔ 参数方程⎩⎨⎧==)()(t g y t f x t D ∈3、曲线的普通方程与曲线的参数方程的区别与联系 曲线的普通方程),(y x F =0是相对参数方程而言,它反映了坐标变量x 与y之间的直接联系;而参数方程⎩⎨⎧==)()(t g y t f x t D ∈是通过参数t 反映坐标变量x 与y 之间的间接联系.曲线的普通方程中有两个变数,变数的个数比方程的个数多1;曲线的参数方程中,有三个变数两个方程,变数的个数比方程的个数多1个.从这个意义上讲,曲线的普通方程和参数方程是“一致”的.参数方程 普通方程 ; 普通方程 参数方程这时普通方程和参数方程是同一曲线的两种不同表达形式.问题3:方程222a y x =+(0≠a );方程λ=-2222by a x (0≠λ)是参数方程吗?参数方程与含参数的方程一样吗?方程222a y x =+(0≠a )表示圆心在原点的圆系,方程λ=-2222by a x (0≠λ)表示共渐近线的双曲线系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1课时 参数方程的概念
[核心必知]
1.参数方程
在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数
⎩⎪⎨⎪⎧x =f (t ),y =g (t ),
①,并且对于t 的每一个允许值,由方程组①所确定的点M (x ,y )都在这条曲线上,那么方程组①叫做这条曲线的参数方程.
联系变量x ,y 的变数t 叫做参变数,简称参数. 2.普通方程
相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.
[问题思考]
1.参数方程中的参数t 是否一定有实际意义?
提示:参数是联系变数x ,y 的桥梁,可以是一个有物理意义或几何意义的变数,也可以是没有明显实际意义的变数.
2.曲线的参数方程一定是唯一的吗?
提示:同一曲线选取参数不同,曲线参数方程形式也不一样.如⎩⎪⎨⎪⎧x =4t +1,
y =2t (t ∈R )和
⎩
⎪⎨
⎪⎧x =2m +1,
y =m (m ∈R ) 都表示直线x =2y +1.
已知曲线C 的参数方程是⎩
⎪⎨⎪⎧x =2t ,
y =3t 2
-1(t 为参数). (1)判断点M 1(0,-1)和M 2(4,10)与曲线C 的位置关系; (2)已知点M (2,a )在曲线C 上,求a 的值.
[精讲详析] 本题考查曲线的参数方程及点与曲线的位置关系.解答此题需要将已知点代入参数方程,判断参数是否存在.
(1)把点M 1的坐标代入参数方程⎩⎪⎨⎪⎧x =2t ,
y =3t 2
-1, 得⎩⎪⎨⎪⎧0=2t ,
-1=3t 2
-1,
∴t =0.即点M 1在曲线C 上.
把点M 2的坐标代入参数方程⎩⎪⎨⎪⎧x =2t ,y =3t 2
-1,
得⎩
⎪⎨⎪⎧4=2t ,
10=3t 2
-1,方程组无解.即点M 2不在曲线C 上. (2)∵点M (2,a )在曲线C 上,∴⎩⎪⎨⎪⎧2=2t ,a =3t 2
-1.
∴t =1,a =3×12-1=2.即a 的值为2.
已知曲线的参数方程,判断某点是否在曲线上,就是将点的坐标代入曲线的参数方程,然后建立关于参数的方程组,如果方程组有解,则点在曲线上;否则,点不在曲线上.
1.已知曲线⎩
⎪⎨⎪⎧x =2sin θ+1,
y =sin θ+3(θ为参数,0≤θ<π),则下列各点A (1,3),B (2,2),
C (-3,5)在曲线上的点是________.
解析:将A (1,3)点代入方程得θ=0;将B 、C 点坐标代入方程,方程无解,故B 、C 点不在曲线上.
答案:A (1,3)
如图,△ABP 是等腰直角三角形,∠B 是直角,腰长为a ,顶点B 、A 分别
在x 轴、y 轴上滑动,求点P 在第一象限的轨迹的参数方程.
[精讲详析] 本题考查曲线参数方程的求法,解答本题需要先确定参数,然后分别用同一个参数表示x 和y .
法一:设P 点的坐标为(x ,y ),过P 点作x 轴的垂线交x 轴于Q . 如图所示,则Rt △OAB ≌Rt △QBP .
取OB =t ,t 为参数(0<t <a ). ∵|OA |=
a 2-t 2,∴|BQ |=
a 2-t 2.
∴点P 在第一象限的轨迹的参数方程为
⎩⎪⎨⎪⎧x =t +a 2-t 2,
y =t ,
(0<t <a ) 法二:设点P 的坐标为(x ,y ),过点P 作x 轴的垂线交x 轴于点Q ,如图所示.。
