广东省湛江二中2013届高三5月模拟测试数学(文)试题
广东省湛江市2013年高考二模数学试卷(文科)含解析

2013年广东省湛江市高考数学二模试卷(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.2解:由题意可得=1由于函数y=tanx是奇函数,故不满足条件.故选B.点评:本题主要考查函数的奇偶性和单调性,属于基础题.5.(5分)已知函数,那么=()A.2B.C.﹣2 D.﹣考点:函数的值.专题:计算题;函数的性质及应用.分析:由题意可得f()==﹣1,然后代入求解f(﹣1)即可解答:解:∵f()==﹣1<0∴f[f()]=f(﹣1)=故选B点评:本题主要考查看分段函数的函数值的求解,解题的关键是明确函数的对应关系6.(5分)若三条线段的长分别为3、5、7,则用这三条线段()A.能组成直角三角形B.能组成锐角三角形C.能组成钝角三角形D.不能组成三角形考点:三角形的形状判断.专题:计算题;解三角形.分析:根据题意,因为两条较短线段之和大于最长线段,可得三条线段能组成一个三角形.再由余弦定理算出最大角为钝角,即可得到三条线段能组成钝角三角形.解答:解:∵3+5=8且8>7,∴三条线段可以组成一个三角形,且该三角形的最大角为7所对的角设最大角为α,根据余弦定理得cosα=<0结合α∈(0,π),得α为钝角,所以此三角形为钝角三角形故选:C点评:本题给长度为3、5、7的三条线段,问它们能构成什么样的三角形,着重考查了三角形两边之和大于第三边和用余弦定理解三角形等知识,属于基础题.7.(5分)一个几何体的三视图是三个边长为1的正方形和对角线,如图所示,则此几何体的体积为()A.B.C.D.1考点:由三视图求面积、体积.专题:计算题;作图题.分析:由三视图还原原几何体,由正方体的体积减去棱角(三棱锥)的体积即可.解答:解:由三视图还原原几何体如图,所以该几何体的体积为8.(5分)运行如图的程序框图,输出的结果是()2,10.(5分)对集合A,如果存在x0使得对任意正数a,都存在x∈A,使0<|x﹣x0|<a,则称x0为集合A的“聚点”,给出下列四个集合:①;②{x∈R|x≠0};③;④Z.分析:利用“聚点”的定义可得①的聚点是1,②的聚点是0,③的聚点是0,而④无聚点.,,要使成立,只要取正整数∈③∵,由(1)可知:0为集合{},根据“聚点”的定义可知,0是其聚二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11〜13题)(二)选做题(14-15题,考生只能从中选做一题)11.(5分)(2012•房山区一模)i是虚数单位,则=1﹣i.解:∵===112.(5分)若抛物线y2=2px(p>0)的焦点与双曲线的右焦点重复,则p=8.)的焦点与双曲线的右焦点重解:双曲线中∴双曲线的右焦点为(4,0))的焦点与双曲线∴13.(5分)在圆(x﹣2)2+(y﹣2)2=4内任取一点,则该点恰好在区域内的概率为.公式,即可算出所求的概率.表示的平面区域,内任取一点,则该点恰好在区域P==故答案为:.2214.(5分)(坐标系与参数方程选做题)在直角坐标系xoy中,曲线C的参数方程是(θ∈[0,2π],θ为参数),若以O为极点,x轴正半轴为极轴,则曲线C的极坐标方程是ρ=4cosθ.分析:先求出曲线C的普通方程,再利用x=ρcosθ,y=ρsinθ代换求得极坐标方程.解:由得,两式平方后相加得(x﹣2)2+y2=4,…(4分)=.15.(2013•蓟县一模)(几何证明选讲)如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为 4.5.度.∴∴AC==4.5,三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.16.(12分)已知函数(1)求的值;(2)设,求函数f(x)的值域.2x+)从而求得)因为,再根据正弦函数的定义域和值域,求得函数=故=2=2sin=2.)因为,所以217.(12分)某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.×总计55 50 105所以18.(14分)三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=BC=AC=AA1,CD⊥AC1,E、F分别是BB1、CC1中点.(1)证明:平面DEF∥平面ABC;(2)证明:CD⊥平面AEC1.,又可得CE==由余弦定理可得:DE2=12+22=3,∴DE=,CD=CE==19.(14分)已知函数f(x)=x2﹣2x+4,数列{a n}是公差为d的等差数列,若a1=f(d﹣1),a3=f(d+1)(1)求数列{a n}的通项公式;(2)S n为{a n}的前n项和,求证:.所以,所以,≥=20.(14分)已知三角形ABC的三个顶点的坐标分别为A(3,2),B(1,3),C(2,5),l为BC边上的高所在直线.(1)求直线l的方程;(2)直线l与椭圆相交于D、E两点,△CDE是以C(2,5)为直角顶点的等腰直角三角形,求该椭圆的方程.直线l的方程为:y﹣2=(x﹣3),即:x+2y﹣7=0可得:(a2+4b2)y2﹣28b2y+49b2﹣a2b2=0,化为,,=2所以,=4,即36﹣4=4,解得:,所以,所求方程为:21.(14分)已知a<2,.(注:e是自然对数的底)(1)求f(x)的单调区间;(2)若存在x1∈[e,e2],使得对任意的x2∈[﹣2,0],f(x1)<g(x2)恒成立,求实数a的取值范围.a的取值范围.,∈[e,e]及x2∈[﹣2,0],f(x)min min1由(1),当a<2,x1∈[e,e2]时,f(x)是增函数,f(x)min=f(e)=xmin∴。
广东湛江市湛师附中2013高考复习模拟试题(2)-数学理汇总
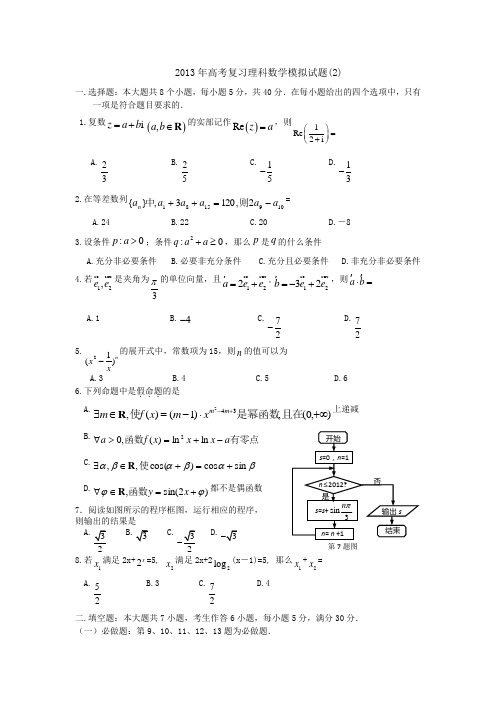
2013年高考复习理科数学模拟试题(2)一.选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数iz a b =+(),a b ∈R 的实部记作()Re z a =,则1Re 2i ⎛⎫= ⎪+⎝⎭A.23B.25C.15-D.13-2.在等差数列10915812,1203,}{a a a a a a n -=++则中=A.24B.22C.20D.-83.设条件:0p a >;条件2:0q a a +≥,那么p 是q 的什么条件A.充分非必要条件B.必要非充分条件C.充分且必要条件D.非充分非必要条件 4.若12,e e 是夹角为3π的单位向量,且122a e e =+,1232b e e =-+,则a b ⋅=A.1B.4-C.72- D.725.21()n x x-的展开式中,常数项为15,则n 的值可以为A.3B.4C.5D.66.下列命题中是假命题...的是 A.),0(,)1()(,342+∞⋅-=∈∃+-且在是幂函数使m m xm x f m R 上递减B.有零点函数a x x x f a -+=>∀ln ln )(,02C.βαβαβαsin cos )cos(,,+=+∈∃使RD.)2sin(,ϕϕ+=∈∀x y 函数R 都不是偶函数7.阅读如图所示的程序框图,运行相应的程序, 则输出的结果是8.若1x 满足2x+2x =5, 2x 满足2x+22log (x -1)=5, 那么1x +2x =A.52B.3C.72D.4二.填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题:第9、10、11、12、13题为必做题.第7题图9.设随机变量2~N 1 3X (,),且06P X P X a ≤=>-()(),则实数a 的值为______.10.函数1,(10)()cos ,(0)2x x f x x x π+-≤<⎧⎪=⎨≤≤⎪⎩的图象与x 轴所围成的封闭图形的面积为________.11.已若0x >,0y >,123x y +=,则11x y+的最小值是________. 12.一个几何体的三视图如图所示(单位:m),则该几何体的体积为_________m 3. 13.已知y x z k k y x x y x y x 3)(020,+=⎪⎩⎪⎨⎧≤++≤≥,若为常数满足条件的最大值为8,则k =______.(二)选做题:第14、15题为选做题,考生只能从中选做一题.14.(坐标系与参数方程选做题)直角坐标系xOy 中,以原点为极点,x 轴的正半轴为极轴建立极 坐标系,设点A ,B 分别在曲线C 1:=3cos =4sin x y θθ+⎧⎨+⎩ (θ为参数)和曲线C 2:ρ=1上,则|AB|的最小值为___________.15.(几何证明选讲选做题)如图,已知四边形ABCD 内接于⊙O,且AB 为⊙O 的直径,直线MN 切⊙O 于D ,∠MDA=450,则 ∠DCB=_________.三.解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(12分)已知函数()tan 34f x x π⎛⎫=+ ⎪⎝⎭. (1)求9f π⎛⎫ ⎪⎝⎭的值;(2)若234f απ⎛⎫+= ⎪⎝⎭,求cos 2α的值.PABCDE17.(12分)高考数学试题中共有8道选择题每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“每题只选1项,答对得5分,不答或答错得0分”,某考生每道题都给出了一个答案,已确定有5道题的答案是正确的,而其余题中,有一道题可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:(1)得40分的概率; (2)所得分数ξ的数学期望.18.(14分)如图,ABCD 为正方形,PD ⊥平面ABCD ,//EC PD ,且2AD PD EC ==, (1)求证:BE//平面PDA ;(2)求平面PBE 与平面ABCD 所成的二面角的余弦值;19.(14分) 在平面直角坐标系xoy 中,设点F(1,0),直线l :1x =-,点P 在直线l 上移动,R 是线段PF 与y 轴的交点, ,RQ FP PQ l ⊥⊥.(1)求动点Q 的轨迹的方程;(2)记Q 的轨迹的方程为E ,过点F 作两条互相垂直的曲线E 的弦AB 、CD ,设AB 、CD 的中点分别为M,N .求证:直线MN 必过定点R(3,0).20.(14分)数列{n a }满足112a =,112n na a +=-.(1)求数列{n a }通项公式 (2)若11n nb a =-,{b n }的前n 次和为Bn,若存在整数m ,对任意n ∈N +且n ≥2都有320n n mB B ->成立,求m 的最大值.21.(14分)(1)若任意直线l 过点)1,0(F ,且与函数241)(xx f =的图象C 交于两个不同的点A,B ,分别过点A,B 作C 的切线,两切线交于点M ,证明:点M 的纵坐标是一个定值,并求出这个定值;(2)若不等式()()f x g x ≥恒成立,)0(ln )(>=a x a x g 求实数a 的取值范围;(3)求证:44444444ln 2ln 3ln 4ln 2...234n n e++++<,(其中e 为无理数,约为2.71828).2013年高考复习理科数学模拟试题(2)答案BAAC DDBC 9.8 10.3211.269+ 12.6π+ 13.-6 14.315.135016.(1)解:9f π⎛⎫ ⎪⎝⎭tan 34ππ⎛⎫=+ ⎪⎝⎭tan tan 341tan tan34ππ+=-2==-………………4分(2)解法2:因为3tan 3444f ααπππ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭()tan α=+π tan 2α==.…7分 所以22cos 2cos sin ααα=-2222cos sin cos sin αααα-=+221tan 1tan αα-=+ 143145-==-+. 12分 17.(1)得分为40分,8道题必须全做对.在其余的三道题中,有一道题答对的概率为12,有一道题答对的概率为13,还有一道答对的概率为14,所以得分为40分的概率为:P =241413121=⋅⋅ ………(6分)(2)依题意,该考生得分的范围为{25,30,35,40}. 得分为25分表示只做对了5道题, 余各题都做错,所以概率为:414332211=⋅⋅=P :得分为30分的概率为:24114331214332214132212=⋅⋅+⋅⋅+⋅⋅=P 得分为35分的概率为:414131214132214331213=⋅⋅+⋅⋅+⋅⋅=P ; 得分为40分的概率为:⋅=2414P12365247302414041352411304125==⋅+⋅+⋅+⋅=∴ξE ………(12分)18.(1)取PD 中点Q,连结AQ ,1//,2EC PD EC PD= //,EC DQ EC DQ ∴=,∴四边形DCEQ 为平行四边形, //,EQ DC EQ DC ∴=,∵ABCD 为正方形,//,EQ AB EQ AB ∴=,∴四边形BEQA 为平行四边形,∴AQ//BE , AQ ⊆平面PAD,BE ⊄平面PAD, ∴BE//平面PAD;(2)延长PE 交DC 于点K ,连结BK ,则平面PBE 与平面ABCD 的交线为BK,PD ⊥平面ABCD,,PD BK ∴⊥ 又1//,2EC PD EC PD=易知,E 为P 、G 中点,C 为D ,K 中点,由正方形ABCD 可得BD=BK,且BD ⊥BK ,,BDPD D BK =∴⊥平面PDB,PB BK ∴⊥,PBD ∴∠为所求二面角的平面角,cos BD PBD PB ∴==所以平面PBE 与平面ABCD解法2:(1)E 201B -=(,,),设平面PDA 的法向量为n ,可取(0,1,0)n =,0,,//;n BE BE PDA BE PDA =⊄∴平面平面(2)设平面ABCD 的法向量为1n ,可取1(0,0,1)n =,设平面PBE 的法向量为2n ,2220,(2,2,2),(0,2,1),(1,1,2)0n PB PB PE n n PE ⎧=⎪=-=-∴=⎨=⎪⎩126cos ,n n ∴<>=所以平面PBE 与平面ABCD 19.解:(1)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP , ∴RQ 是线段FP 的垂直平分线.∴PQ是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF=.…4分故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x =>.…7分 (2) 设()()BB A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y (8)则⎪⎩⎪⎨⎧==)2(4)1(422BB A A x y x y (1)-(2)得k y y B A 4=+,即ky M 2=,………9分代入方程)1(-=x k y ,解得122+=kx M.所以点M的坐标为222(1,)k k +.……10分同理可得:N 的坐标为2(21,2)k k +-. 直线MN 的斜率为21k k x x y y k N M N M MN-=--=,方程为)12(1222---=+k x k k k y ,整理得)3()1(2-=-x k k y ,……12分 显然,不论k 为何值,(3,0)均满足方程,所以直线MN 恒过定点R (3,0).……14分 20.解:(1)112n na a +=-,21111111112n n n n na a a a a -===-+-----∴111111n n a a +-=--- ∴1{}1n a -为首次为-2,公差为-1的等差数列 ∴11n a -=-2+(n-1)×(-1)=-(n+1) ∴1nn a n =+(2)111n n b n n +=-= 令3111++1+23nn n n C B B n n =-=++∴111111++2+33(n+1)13n n C C n n n n+-=+---++=1111+13+23n+33n+1n n -+++ =12122-03+23n+33n+13n+33n+3n +>-= ∴C n+1-C n >0∴{C n }为单调递增数列 ∴3min62111119()345620n n B B B B -=-=+++=∴192020m <∴m<19 又m N *∈ ∴m 的最大值为1821.证明:(1)设1122(,),(,)A x y B x y ,由题意知AB 的斜率必存在 设,1:+=kx y AB 代入241xy =得 ∴4,044212-=∴=--x x kx x 2)(,41)(2x x f x x f ='=2,221x K x K BM AM==∴,)(24:1121x x x x y AM -=-∴, 化简得:42:211x x x y AM -=同理:42:222x x x y BM -=, 解得:1412-==x x y (2)令:)0,0(ln 41)()()(2>>-=-=x a x a x x g x f x F ,xa x x a x x F 222)(2-=-='∴令 0)(='x F 得:a x 2= 所以 当)2,0(a x ∈ ,时0)(<x F )(x F 在)2,0(a x ∈上单调递减;所以 当),2(+∞∈a x ,时0)(>x F )(x F 在),2(+∞∈a x 上单调递增;∴()y F x =在a x 2=时取得最小值, 要()()f x g x ≥恒成立,只要0)2≥a F (即 02ln 2≥-a a x,解得2e a ≤(3)由(2)得,取e a p =有2ln 2x ex p p≥ 化简得:22ln 1x x e ≤ 变形得:424ln 2xx e x ≤ 即442ln 2x x e x ≤ ∴44444444ln 2ln 3ln 4ln ...234n n ++++ 222221111(...)234e n<++++ 21111(...)122334(1)e n n<++++⨯⨯⨯- 21111111(1...)22334(1)e n n=-+-+-++--212(1)en e =-<。
广东省湛江二中2012-2013学年高二第一次月考数学试题

(本试卷共4页,20小题,满分150分.考试用时120分钟)注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效. 参考公式:若柱体的底面积为S ,高为h ,则柱体的体积 V Sh =.第Ⅰ卷 选择题(共50分)一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项符合题目要求.1.设集合,}2,1{=A ,}4,3,2{=B ,则)(B A U等于( )A .}2{B .}5{C .}4,3,2,1{D .}5,4,3,1{2.若222x y x y ≤⎧⎪≤⎨⎪+≥⎩,则目标函数 z = x + 2 y 的取值范围是 ( )A .[2 ,6]B . [2,5]C . [3,6]D . [3,5]3.甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若甲s ,乙s ,丙s 分别表示他们测试成绩的标准差,则( ) A .丙乙甲s s s << B .乙丙甲s s s << C .丙甲乙s s s << D .乙甲丙s s s <<4.某工厂生产A 、B 、C 三种不同型号的产品,产品数量之比依次为2:3:5.现用分层抽样的方法抽出一个容量为n 的样本,样本中A 种型号的产品共有16件,那么此n =( )A .80B .90C . 100D .120 5.以(5,6)和(3,-4)为直径端点的圆的方程是( )A .072422=+-++y x y xB .064822=-+++y x y xC .092822=---+y x y xD . 052422=-+-+y x y x6.在一次数学测验中,统计7名学生的成绩分布茎叶图如右图所示,若这7名学生的平均成绩为77分,则x 的值为( ) A.5B.6C.7D.87.已知向量(3,4),(sin ,cos ),a b αα==且a ∥b ,则αtan = ( ) A .34-B .34 C .34D .34- 8.若函数f (x )=sin ωx +cos ωx (ω>0)的最小正周期为π,则它的图象的一个对称中心为( ) A .(0,0) B.)(0,8πC .)—(0,8πD .)—(0,4π9.数列}{n a 的前n 项和为S n ,若32()n n S a n N =+∈*,则这个数列一定是( ) A .等比数列 B .等差数列 C .从第二项起是等比数列 D .从第二项起是等差数列10.方程3)2(42+-=-x k x 有两个不等实根,则k 的取值范围是( ) A .)125,0( B .]43,31[ C .),125(+∞ D .]43,125(第Ⅱ卷 非选择题(共100分)二、填空题(本大题共4小题,每小题5分,满分20分) 11.函数)5lg()(-=x x f 的定义域是______.12.一个三棱柱的底面是边长为3的正三角形,且侧棱垂直于底面, 它的三视图如下图所示.则这个三棱柱的体积是 .13.运行右图所示的程序框图,则输出的结果是_______.14.设22 (1)() (12)2 (2)x x f x x x x x +-⎧⎪=-<<⎨⎪⎩≤≥,若()3f x =,则x =_______.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分12分)如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题:(1)79.5~89.5这一组的频率、频数分别是多少?(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均分. 16.(本小题满分12分)右图是函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象.(1)求函数f (x )的解析式;(2)若f )(2α=45,0<α<π3,求cos α的值. 17.(本小题满分14分)如图,已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1)1//C O 面11AB D ; (2 )1AC ⊥面11AB D . 18.(本小题满分14分)已知圆C :226440x y x y +--+=,直线1l 被圆所截得的弦的中点为P (5,3). (1)求直线1l 的方程;(2)若直线2l :0x y b ++=与圆C 相交于两个不同的点,求b 的取值范围.19.(本小题满分14分)某漁业公司年初用98万元购买一艘捕魚船,第一年各种支出费用12万元,以后每年都增加4万元,每年捕魚收益50万元.(1)该公司第几年开始获利? (2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船; ②总纯收入获利最大时,以8万元出售渔船. 问哪种处理方案最合算?20.(本小题满分14分)设函数2()21x f x a =-+, (1) 求证:不论a 为何实数()f x 在定义域上总为增函数; (2) 确定a 的值,使()f x 为奇函数; (3) 当()f x 为奇函数时,求()f x 的值域.湛江市第二中学2014届高二级第一次月考数学试题参考答案与评分标准一、选择题:本大题共10个小题;每小题5分,共50分.二、填空题:本大题共4小题,每小题5分,满分20分.11.}{|5x x > ; 12 ; 13. 24 ; 14.3=x 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)【解】(1)由图象知A =1 .………………1分f (x )的最小正周期T =4×⎝⎛⎭⎫5π12-π6=π,故ω=2πT=2.……3分 将点⎝⎛⎭⎫π6,1代入f (x )的解析式得sin ⎝⎛⎭⎫π3+φ=1, ∴2,32k k Z ππϕπ+=+∈,即2,6k k Z πϕπ=+∈,又|φ|<π2,∴φ=π6.……………………………………………………5分故函数f (x )的解析式为f (x )=sin ⎝⎛⎭⎫2x +π6.…………………………6分 (2)由f ⎝⎛⎭⎫α2=45,得sin ⎝⎛⎭⎫α+π6=45,由0<α<π3,得 π6<α+π6<π2,∴cos ⎝⎛⎭⎫α+π6=35.………………………………9分 ∴cos α=[(α+π6)-π6]=cos ⎝⎛⎭⎫α+π6cos π6+sin ⎝⎛⎭⎫α+π6sin π6=33+410.………12分17.(本小题满分14分) 【证明】(1)连结11A C ,设11111AC B D O =,连结1AO .…1分1111ABCD A B C D -是正方体,11//AA CC ∴=,11A ACC ∴四边形是平行四边形.11//AC AC ∴且 11AC AC =,………………………………3分又1,O O 分别是11,AC AC 的中点,11//O C AO ∴且11O C AO =, 11AOC O ∴是平行四边形 ,11//,C O AO ∴…………………………5分∴1A C ⊥平面11AB D ……………………………………………………14分18.(本小题满分14分)【解】(1)由226440x y x y +--+=,得()()222323x y -+-=,∴圆心()3,2C ,半径为3.…………………2分D 1ODBAC 1B 1A 1CO 1由垂径定理知直线1l ⊥直线CP , 直线CP 的斜率321532CP k -==-,故直线的斜率112l CPk k =-=-,……………5分 ∴直线1l 的方程为()325y x -=--,即2130x y +-=.…………………………7分(2)解法1:由题意知方程组226440x y x y x y b ⎧+--+=⎨++=⎩有两组解,由方程组消去y 得()22221440x b x b b +-+++=,该方程应有两个不同的解,…………………9分∴()()22218440b b b ∆=--++>⎡⎤⎣⎦,化简得21070b b ++>,………………10分19.(本小题满分14分)【解】(1)设第n 年的纯收入为)(n f .由题设知每年的费用是以12为首项,4为公差的等差数列, 故前n 年的费用总和为()211242102n n n S n n n -=+⋅=+,………………3分 前n 年的收入总和为50n ,则)(n f =50n -(2210n n +)-98=224098n n -+-.由 )(n f >0⇒ 220490n n -+<⇒10-51<n <10+51…………………6分 又∵n ∈N , ∴n =3,4,…,17.即该公司从第三年开始获利.………………7分 (2)①年平均收入为()()49402()402127.f n n n n n =-+≤-⨯==当且仅当时等号成立 所以当n =7时,年均获利最大,此时出售所得总收益为12×7+26=110(万元).………10分②.102)10(2)(2+--=n n f ∴当n =10时,102)(max =n f .即10n =总纯收入最大,此时出售所得总收益为102+8=110万元,………………………13分∵7<10. ∴第一种方案更合算.……………………14分20.(本小题满分14分)则 22a aa a -=-⎧⎨=-⎩,解得: 1.a =2()1.21x f x ∴=-+………………………………………………………………10分 (4) 由(2)知2()121x f x =-+,211x +>,10121x ∴<<+,2220,111,1()12121x x f x ∴-<-<∴-<-<-<<++即故当()f x 为奇函数时,其值域为(1,1).-…………………………………14分另解:由(2)知2()121x f x =-+. 由2121xy =-+,得()121xy y -=--, 当1y =时,得02=-,矛盾,所以1y ≠; 故有121x y y --=-. 当x R ∈时,20x >,所以101y y -->-,解得11y -<<. 故当()f x 为奇函数时,其值域为(1,1).-…………………………………14分。
广东省六校2013届高三5月高考模拟考试数学文试题Word版含答案

2013届高三六校高考模拟考试文科数学试题命题学校:深圳实验 2013,5,17本试卷共6页,21小题,满分150分.考试用时120分钟.一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|1}A x x =≥,)}2(log |{2+==x y x B ,则=A BA .)1,2(-B .]1,2(-C .)1,2[-D .]1,2[- 2.已知i 为虚数单位,a 为实数,复数(2i)i z a =-在复平面内对应的点为M , 则“2a <-”是“点M 在第四象限”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 3.已知等比数列}{n a 中,公比0q >,若42=a , 则321a a a ++的最值情况为A .有最小值4-B .有最大值4-C .有最小值12D .有最大值12 4.由两个完全相同的正四棱锥组合而成的空间几何体的 正(主)视图、侧(左)其中四边形ABCD 是边长为1的正方形,则该几何体的表面积为A .34B .33C .32D .3 5.执行如图所示的程序框图,输出的S 是A . 0B .12C . 1D .1-6.下列四个命题中,正确的有①两个变量间的相关系数r 越小,说明两变量间的线性相关程度越低;②命题p :“R ∈∃0x ,01020>--x x ”的否定p ⌝:“R ∈∀x ,012<--x x ”; ③用相关指数2R 来刻画回归效果,若2R 越大,则说明模型的拟合效果越好;④若23.0=a ,3.02=b ,2log 3.0=c ,则b a c <<.A .①③B .①④C .②③D .③④ 7.把正奇数数列按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号一个数,第五个括号两个数,第六个括号三个数,….依次划分为)1(,)5,3(,)11,9,7(,)13(,)17,15(,)23,21,19(,)25(,….则第50个括号内各数之和为A .396B .394C .392D .390 8.已知函数)(x f y =的定义域是R ,若对于任意的正数a ,函数)()()(a x f x f x g --= 都是其定义域上的减函数,则函数)(x f y =的图象可能是A .B .C .D .9.已知定点)0,2(-A ,)0,2(B ,N 是圆O :122=+y x 上任意一点,点A 关于点N 的对称点为M ,线段AM 的中垂线与直线BM 相交于点P ,则点P 的轨迹是 A .椭圆 B .双曲线 C .抛物线 D .圆 10.设函数)(x f 在区间I 上可导,若I x x ∈∀,0,总有))(()()(000x x x f x f x f -'+≥,则称)(x f y =为区间I 上的U 函数. 在下列四个函数2x y =,xx y 1+=,xy e -=,x y 2cos =中,在区间)0,1(-上为U 函数的个数是A .1B .2C .3D .4二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题:11、12、13题为必做题. 11.如图,菱形ABCD 的边长为2,︒=∠60A ,M 为DC 的中点,则AB AM ⋅的值为 .第11题图12.设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥-≥+≤0,0121y x x y x y ,若目标函数z mx y =+(0m >)的最大值为35,则m 的值为 .13.设1>a ,则当xa y =与x y a log =两个函数图象有且只有一个公共点时,=a ln ln .(二)选做题:第14、15题为选做题,考生只能从中选做一题. 14.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=-=t y t x 23221(t 为参数),以原点O为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 2=,则l 上的动点P 与C 上的动点Q 间的最短距离为 . 15.(几何证明选讲选做题)如图,四边形ABCD 是边长为2的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的圆O 交于点F ,连接CF 并延长CF 交AB 于E .则线段BF 的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分13分)某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有630名学生,男女生人数之比为10:11,现按分层抽样方 法抽取若干名学生,每人被抽到的概率均为16. (1)求抽取的男学生人数和女学生人数;(2)通过对被抽取的学生的问卷调查,得到如下22⨯列联表:第15题图①完成列联表;②能否有97.5%的把握认为态度与性别有关?(3)若一班有5名男生被抽到,其中4人持否定态度,1人持肯定态度;二班有4名女生被抽到,其中2人持否定态度,2人持肯定态度.现从这9人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.解答时可参考下面临界值表:17.(本小题满分12分)设ABC ∆的三个内角A ,B ,C 所对的边分别为a ,b ,c .已知sin()cos 6A A π-=.(1)求角A 的大小;(2)若2a =,求b c +的最大值.18.(本小题满分14分)在四棱锥ABCD P -中,︒=∠=∠90ACD ABC ,︒=∠=∠60CAD BAC ,⊥PA 面ABCD ,E 为PD 的中点,42==AB PA .(1)求证:AE PC ⊥; (2)求证://CE 面PAB ; (3)求三棱锥ACE P -的体积V .PABCDE第18题图19.(本小题满分13分)已知数列}{n a 的前n 项和为n S ,若21=a ,()11++=⋅+n n S a n n n ,*N ∈n . (1)求数列}{n a 的通项公式: (2)令n nn S T 2=,*N ∈n . ①当n 为何正整数值时,1+>n n T T ;②若对一切正整数n ,总有m T n ≤,求m 的取值范围.20.(本小题满分14分)如图,点F 是椭圆12222=+by a x (0>>b a )的左焦点,点A ,B 分别是椭圆的左顶点和上顶点,椭圆的离心率为21,点C 在x 轴上,且BC BF ⊥,过点A 作斜率为(0)k k >的直线l 与由三点B ,F ,C 确定的圆M 相交于D ,E 两点,满足221a ME MD -=⋅.(1)若BOF ∆(2)直线l 的斜率是否为定值?证明你的结论.第20题图21.(本小题满分14分)已知函数1)1(ln )(+--=x x a x x f (R ∈a ,0≠a ),x x x g +=2)(. (1)求函数(1)()ln ()1a x h x a x g x x -=-⋅+的单调区间,并确定其零点个数;(2)若)(x f 在其定义域内单调递增,求a 的取值范围; (3)证明不等式 1ln 121715131+<+++++n n (*N ∈n ).2013年广东省六校高三年级第四次联考数学(文科)参考答案 2013.5一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.11. 4 12. 16 13.1- 14.15 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分13分)某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有630名学生,男女生人数之比为10:11,现按分层抽样方 法抽取若干名学生,每人被抽到的概率均为16. (1)求抽取的男学生人数和女学生人数;(2)通过对被抽取的学生的问卷调查,得到如下22⨯列联表:①完成列联表;②能否有97.5%的把握认为态度与性别有关?(3)若一班有5名男生被抽到,其中4人持否定态度,1人持肯定态度;二班有4名女生被抽到,其中2人持否定态度,2人持肯定态度.现从这9人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.解答时可参考下面临界值表:解:(1)共抽取6306105÷=人,…………………………………………………………1分男生 111055521⨯=人, 女生101055021⨯=人,……………………………3分 (2)①…………4分② 假设0H : 学生对体育课改上自习课的态度与性别无关220()105(45201030) 6.110()()()()75305550n ad bc k a c b d a b c d -⨯-⨯==≈++++⨯⨯⨯ 因为 6.1105.02>, 2( 5.024)0.025P K ≥= 所以 有97.5%的把握认为态度与性别有关.………………………………8分(3)记一班被抽到的男生为1234,,,,A A A A a ,1234,,,A A A A 持否定态度,a 持肯定态度;二班被抽到的女生为1212,,,B B b b ,12,B B 持否定态度,12,b b 持肯定态度. 则所有抽取可能共有20种:11(,)A B ,12(,)A B ,11(,)A b ,12(,)A b ;21(,)A B ,22(,)A B ,21(,)A b ,22(,)A b ;31(,)A B ,32(,)A B ,31(,)A b ,32(,)A b ;41(,)A B ,42(,)A B ,41(,)A b ,42(,)A b ;1(,)a B ,2(,)a B ,1(,)a b ,2(,)a b .………10分其中恰有一人持否定态度一人持肯定态度的有10种:11(,)A b ,12(,)A b ,21(,)A b ,22(,)A b ,31(,)A b ,32(,)A b ,41(,)A b ,42(,)A b ,1(,)a B ,2(,)a B .……11分记“从这9人中随机抽取一男一女,其中恰有一人持肯定态度一人持否定态度”事件为M ,则101()202P M ==. ……………………………………………………12分答:(1)抽取男生55人,女生50人;(2)有有97.5%的把握认为态度与性别有关;(3)恰有一人持肯定态度一人持否定态度的概率为12.……………………………13分17.(本小题满分12分)设ABC ∆的三个内角A ,B ,C 所对的边分别为a ,b ,c .已知sin()cos 6A A π-=.(1)求角A 的大小;(2)若2a =,求b c +的最大值. 解:(1)由已知有sin coscos sincos 66A A A ππ⋅-⋅=,………………………………1分得1cos cos 2A A A -=,则sin A A =,………………3分tan A =………………………………………………………………4分又0A π<<,故3A π=.……………………………………………………5分(2)(法一)由正弦定理得sin 2sin sin sin 3a B B b B A π⋅⋅===, sin 2sin sin sin 3a C C c C A π⋅⋅===,则sin )b c B C +=+.……………………………………………7分 而21sin sin sin sin()sin sin )32B C B B B B B π+=+-=++31sin cos ))226B B B B B π=+=+=+.…9分 则 4sin()6b c B π+=+.又 203B π<<, 所以5666B πππ<+<.……………………………10分 所以 当且仅当62B ππ+=,即3B π=时,sin()6B π+取得最大值1,11分故 max ()4b c +=. …………………………………………………………12分(法二)由余弦定理得22222cos3b c bc π=+-,即224b c bc =+-, …………7分则 24()3b c bc =+-,又 2()2b c bc +≤则 10分 22()()434b c b c ++-≤⋅…………………10分得 2()16b c +≤, 故 4b c +≤,当且仅当b c =时,max ()4b c +=.…… ………………………………………12分18.(本小题满分14分)在四棱锥ABCD P -中,︒=∠=∠90ACD ABC ,︒=∠=∠60CAD BAC ,⊥PA 面ABCD ,E 为PD 的中点,42==AB PA .(1)求证:AE PC ⊥; (2)求证://CE 面PAB ; (3)求三棱锥ACE P -的体积V .解:(1)证明 取PC 中点F ,连接,AF EF . ……1分在Rt ABC ∆中,2AB =,60BAC ∠=, 则 BC =4AC =. 而 4PA =则 在等腰三角形APC 中 PC AF ⊥. ① ………………2分又 在PCD ∆中,,PE ED PF FC ==,则 EF ∥CD ……………………………………………………………………3分因 PA ⊥面ABCD ,CD ⊂面ABCD , 则 PA ⊥CD ,又 90ACD ∠=,即CD AC ⊥, 则 CD ⊥面PAC ,……………………4分CD PC ⊥,所以 EF PC ⊥. ② ………………5分 由①②知 PC ⊥面AEF .故 PC ⊥AE .…………………………6分 (2)(法一)取AD 中点M ,连接,EM CM . 则 在PAD ∆中, EM ∥PA . 又 EM ⊄面PAB , PA ⊂面PAB则 EM ∥面PAB , …………………………………………………………………7分 在Rt ACD ∆中,60CAD ∠= 所以ACM ∆为正三角形,则 60ACM *∆= ……………………………………………………………………8分 又 60BAC ∠= 则 MC ∥AB .又 MC ⊄面PAB , AB ⊂面PABPA DBCEF MPABCDE第18题图则 MC ∥面PAB , …………………………………………………………………9分 而 EMMC M =,所以 面EMC ∥面PAB . …………………………………………………………10分 又 EC ⊂面EMC则 EC ∥面PAB . ………………………………………………………………11分 (法二)延长,DC AB 交于N ,连接PN . …………………………………………7分 在AND ∆中,60NAC DAC ∠=∠=,AC ⊥CD ,则 C 为ND 的中点…………………………………………………………………9分又 PE ED =所以 EC ∥PN ……………………………………………………………………10分 又 EC ⊄面PAB , PN ⊂面PAB则 EC ∥面PAB .…………………………………………………………………11分(3)由(1)(2)知 4AC =, CD =12EF CD ==因 CD ⊥面PAC , EF ∥CD 则 EF⊥面PAC ,……………………………………………………………12分而 1144822Rt PAC S PA AC ∆=⋅=⨯⨯=………………………………………13分故 11833P AECE PAC Rt PAC V V S EF --∆==⋅=⨯⨯=14分19.(本小题满分13分)已知数列}{n a 的前n 项和为n S ,若21=a ,()11++=⋅+n n S a n n n ,*N ∈n . (1)求数列}{n a 的通项公式:(2)令n nn S T 2=,*N ∈n .①当n 为何正整数值时,1+>n n T T ;②若对一切正整数n ,总有m T n ≤,求m 的取值范围.解:(1)在()11++=⋅+n n S a n n n 中令1n =,得2111(11)a S ⨯=+⨯+又12a =,则24a =,所以212a a -=. ………………………………………1分 当2n ≥时,()11++=⋅+n n S a n n n1(1)(1)n n n a S n n --=+-相减得 11(1)2n n n n na n a S S n +---=-+ ……………………………………3分 即 1(1)2n n n na n a a n +--=+,整理得 12(2)n n a a n +-=≥ ………4分 结合到 212a a -=,所以 数列{}n a 是以2为首项,2为公差的等差数列,………………………5分 则 2(1)2n a n =+-⨯,即2n a n =.…………………………………………6分(2)①(法一) (22)(1)2n n nS n n +==+…………………………………………7分 则 (1)22n n n nS n n T +==………………………………………………………8分 1111(1)(2)(1)1(1)(2)(22)2222n n n n n n n n n n n n n T T n n +++++++++--=-=+-=由 10n n T T +-<……………………………………………………………9分 得 2n >,即n 取不小于3的正整数. …………………………………10分 (法二) 把 12(1)n a n +=+代入()11++=⋅+n n S a n n n得 ()2(1)1n n n S n n ⨯+=++所以 (1)n S n n =+.……………………………………………7分以下同法一.② 由①知 数列{}n T 各项的大小情况为 12345T T T T T <=>>>.11分则 {}n T 的各项中数值最大的项为3222(21)322T T +===,………12分 因为对一切正整数n ,总有m T n ≤,则 32m ≥……………………13分20.(本小题满分14分)如图,点F 是椭圆12222=+by a x (0>>b a )的左焦点,点A ,B 分别是椭圆的左顶点和上顶点,椭圆的离心率为21,点C 在x 轴上,且BC BF ⊥,过点A 作斜率为(0)k k >的直线l 与由三点B ,F ,C 确定的圆M 相交于D ,E 两点,满足221a ME MD -=⋅.(1)若BOF ∆(2)直线l 的斜率是否为定值?证明你的结论.解:(1)由已知可得12c a =,12cb =2分 又222a b c =+,解得2222,6,8c b a ===. …………3分所求椭圆方程为22186x y +=.…………4分 (2)由12c a =得b =,则(,0),)F c B -……5分因BC BF ⊥ 则1-=⋅BF BC k k (斜率显然存在且不为零)……………6分 而0()FB k c -==-- 设 (,0)C t ,则BC k ==得 c t 3=,所以)0,3(c C ……………………………………………………7分则圆心M 的坐标为(,0)M c ,半径为2r c =………………………………………8分 据题意 直线l 的方程可设为 (2)y k x c =+,即20kx y ck -+=………………9分由 221a ME MD -=⋅得 2122cos 2c c DME a ⨯⨯∠=-………………………10分即 2122cos (2)2c c DME c ⨯⨯∠=-,得1cos 2DME ∠=-,而0DME π≤∠≤所以 23DME π∠=…………………………………………………………………11分在等腰三角形MED 中 由垂径定理可得点M 到直线l 的距离为c .………………12分则c =…………………………………………………………………13分解得k = 而0k > 故k =(定值)……………………………14分21.(本小题满分14分)已知函数1)1(ln )(+--=x x a x x f (R ∈a ,0≠a ),x x x g +=2)(. (1)求函数(1)()ln ()1a x h x a x g x x -=-⋅+的单调区间,并确定其零点个数;(2)若)(x f 在其定义域内单调递增,求a 的取值范围; (3)证明不等式1ln 121715131+<+++++n n (*N ∈n ). 解:(1)2()ln (0)h x a x ax ax x =-+> …………………………………………1分则 1()(21)(0)h x a x x x'=-+>2(21)a x x x --=-12(1)()2a x x x-+=-……………………………………………2分 (i )若0a >,则当(0,1)x ∈时,()0h x '>;当(1,)x ∈+∞时,()0h x '<所以 (0,1)为()h x 的增区间,(1,)+∞为()h x 的减区间. ………………3分 极大值为0111ln )1(2=⨯+⨯-=a a a h 所以)(x h 只有一个零点1=x .(ii )若0a <,则当(0,1)x ∈时,()0h x '<;当(1,)x ∈+∞时,()0h x '> 所以 (0,1)为()h x 的减区间,(1,)+∞为()h x 的增区间.极小值为0111ln )1(2=⨯+⨯-=a a a h ……………………………………4分 所以)(x h 只有一个零点1=x . 综上所述,当0a <时,(0,1)为()h x 的减区间,(1,)+∞为()h x 的增区间,)(x h 有且只有一个零点;当0a >时,(0,1)为()h x 的增区间,(1,)+∞为()h x 的减区间,)(x h 有且只有一个零点.……………………………………………………………………5分 (2) 21[1(1)]()(1)a x x f x x x +--'=-+212(1)a x x =-+ 22(22)1(0)(1)x a x x x x +-+=>+……………………………………6分 由)(x f 在其定义域内单调递增,可知(0,)x ∀∈+∞,()0f x '≥恒成立.则 2(22)10x a x +-+≥ (0,)x ∀∈+∞ 恒成立.…………………………7分(法一)由二次函数的图象(开口向上,过定点(0,1))可得10a -≤或100a ->⎧⎨∆≤⎩………………………………………………………8分则 1a ≤或210(22)40a a ->⎧⎨--≤⎩ 则 1a ≤或102a a >⎧⎨≤≤⎩得 2a ≤.可以验证 当2a =时)(x f 在其定义域(0,)+∞内单调递增故 2a ≤ (9)分(法二)分离变量 122(0)a x x x≤++>因 12224x x++≥+= (当且仅当1x x =,即1x =时取到等号)…8分所以 24a ≤, 则2a ≤.可以验证 当2a =时)(x f 在其定义域(0,)+∞内单调递增故 2a ≤……………………………………………………………………9分(3)由(2)可知 当2a =时,2(1)()ln 1x f x x x -=-+在(0,)+∞内单调递增, 而2(11)(1)ln1011f -=-=+ 所以当1x >时,()(1)0f x f >= 即 2(1)ln (1)1x x x x ->>+ (10)分令 *11()x n N n=+∈, 则 12(11)1ln(1)111n n n+-+>++ (11)分则 12ln21n n n +>+ 所以 2ln 121n n n >--,22ln 323n n n ->--,…… , 32ln 25>,22ln 13>, 以上n 个式子累加可得132222lnln ln ln 212212153n n n n n n +++++>++++-+-…………………………………12分则 131111ln(2)2()12212153n nn n n n +⋅⋅⋅>++++-+- 则 1111ln(1)2()212153n n n +>+++++-…………………………13分则 11111ln(1)2212153n n n +>+++++- 故 111135721n ++++<+(*N ∈n ).………………14分。
广东省湛江市2013届高三上学期调研测试数学(文)

广东省湛江市2013届高中毕业班调研测试数学(文)试题本试卷共4页,共21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填在答题卡上。
用2B 铅笔将答题卡试卷类型(A)填涂在答题卡上。
在答题卡右上角的"试室号"和"座位号"栏填写试室号、座位号,将相应的试室号、座位号信息点涂黑。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上求作答的答案无效。
4.考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式:V=13·S ·h ,其中S 是底面积,h 是高。
一组数据x 1,x 2,…,x n 的方差222121[()()s x x x x n=-+-+ …+2()]n x x - ,其中x 为12,,x x …nx 的平均数。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知i 是虚数单位,则复数(1)i i += ( )A .-1-iB .-1+iC .1+iD .1-i 2.函数()xxf x e e -=-是( )A .奇函数B .偶函数C .既是奇函数又是偶函数D .既不是奇函数也不是偶函数3.设集合{}{}2|2,|,U U x x A x x x A =<=<=则ð( )A .∅B .{}|12x x ≤<C .{}|012x x x ≤≤<或D .{}|102x x x ≤-≤<或4.已知函数2log ,0()1,0x x f x x x >⎧=⎨+≤⎩,若()2f a =,则a=( )A .4B .2C .1D .-15.已知等差数列{}n a 的前n 项和为S n ,若45810,8,a a S ===则 ( )A .18B .36C .54D .726.曲线()1f x nx =在x=1处的切线方程为 ( )A .y=xB .y=x -1C .y=x+1D .y =-x+17.已知m R ∈,则“m >2”是“方程2211x y m +=- 表示双椭圆”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件8.如图是一个算法的程序框图,当输入的x 等于5时,其输出的结果是( )A .12B .132C .2D .49.一个几何体的三视图及其尺寸如图所示,其中正(主)观图是直角三角形,侧(左)视图是半圆,府视图是等腰三角形,则这个几何体的体积是 ( )A .3πB .2πC .4πD .π10.函数sin ()cos 2xf x x =-的值域是( )A .[-2,2]B .[11,22-] C .[33-] D .[二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
【2013届湛江二模】广东省湛江市2013届高三普通高考模拟测试

试卷类型:A 湛江市2013年普通高考模拟测试题数学(理科)本试卷共4页,共21小题,满分150分。
考试用时120分钟。
注意事项:1. 答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上。
用2B 铅笔将答题卡试卷类型(A)填涂在答题卡上。
在答题卡右上角的“试室号”和“座位 号”栏填写试室号、座位号,将相应的试室号、座位号信息点涂黑。
2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改 动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内 相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式:13V Sh ,其中S 是底面面积,h 是高.参考数据:一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一 项是符合题目要求的.1.已知集合A= {x|x 〉1},B={X |X 2 <4},则A∩B =A. {x | x < 2}B. {x|-2<x<2}C. {x | x > 1}D. {x| 1 < x < 2}2. 复数i+12的虚部是 A. 1 B2 C.-1 D.-2 3. 如果命题“)(q p ∧⌝”是真命题,则A.命题p 、q 均为假命题B.命题p 、q 均为真命题C.命题p 、q 中至少有一个是真命题D.命题p 、q 中至多有一个是真命题4. 下列函数中既是奇函数,又在(0,+∞)上单调递增的是A. y = x 2B. y = x 3C. y = -xD. y = tanx5. 运行如图的程序框图,输出的结果是A. 510B. 1022C. 254D. 2566.函数f(x)= (x-1)cosx 2在区间[0,4]上的零点个数是A. 4B. 5C. 6D. 77. 设F 1,F 2是椭圆:)0(12222>>=+b a by a x 的左右焦点,若直线x = wa (m >1)上存在一点尸,使ΔF 2PF 1是底角为300的等腰三角形,则m 的取值范围是A. 1 < M < 2B. M > 2C. 1 < M <23D. M >238. 某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段, 在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大 值为A. 22B. 32C. 4D. 52二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9〜13题)9.曲线y= x 3-x + 3在点(1,3)处的切线方程为_______10.已知函数⎩⎨⎧>≤=)0(log )0(2)(3x x x x f x ,那么)]31([f f =_______ 11.不等式|x 2-3x+ 1|<1的解集为______.12.已知{a n }的前n 项之和为S n ,a 1 _______________________ =1, S n = 2a n+1,则S n =______13.四位学生,坐在一排有7个位置的座位上,有且只有两个空位是相邻的不同坐法有______种.(用数字作答)(二)选做题(14~15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系x 吵中,曲线C 的参数方程是⎩⎨⎧=+=θθsin 2cos 22y x (θπθ],2,0[∈为参数), 若以O 为极点,x 轴正半轴为极轴,则曲线C 的极坐标方程是________.15.(几何证明选讲选做题)如图,点A 、B 、C 都在O 上,过点C 的切线 交A B的延长线于点D,若AB = 5,BC = 3,CD = 6,则线段AC的长为_______三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.甲校:乙校:(1) 求表中x与y的值;(2) 由以上统计数据完成下面2x2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?(3) 若以样本的频率作为概率,现从乙校总体中任取3人(每次抽取看作是独立重复的),求优秀学生人数 的分布列和数学期望.(注:概率值可用分数表示)17.(本小题满分12分)。
广东省湛江市高考数学二模试卷(文科)卷

高考数学二模试卷(文科)一、选择题(本大题共12小题,共60.0分)1.若复数z满足2z=3+12i,其中i为虚数单位,是z的共轭复数,则复数|z|=()A. 3B. 2C. 4D. 52.已知集合A={1,2,3,4},B={y|y=2x-3,x∈A},则集合A∩B的子集个数为()A. 1B. 2C. 4D. 83.现有甲班A,B,C三名学生,乙班D,E两名学生,从这5名学生中选2名学生参加某项活动,则选取的2名学生来自于不同班级的概率是()A. B. C. D.4.平行四边形ABCD中,∠BAD=120°,||=2,||=3,=,则=()A. 3B. -3C. 2D. -25.有人认为在机动车驾驶技术上,男性优于女性.这是真的么?某社会调查机构与交警合作随机统计了经常开车的100名驾驶员最近三个月内是否有交通事故或交通违法事件发生,得到下面的列联表:附:K2=据此表,可得()A. 认为机动车驾驶技术与性别有关的可靠性不足50%B. 认为机动车驾驶技术与性别有关的可靠性超过50%C. 认为机动车驾驶技术与性别有关的可靠性不足60%D. 认为机动车驾驶技术与性别有关的可靠性超过60%6.在△ABC中,内角A,B,C的所对的边分别为a,b,c,且a cos B=(4c-b)cos A,则cos2A=()A. B. C. D. -7.设F1,F2分别为离心率e=的双曲线C:-=1(a>0,b>0)的左、右焦点,A为双曲线C的右顶点,以F1F2为直径的圆交双曲线的渐近线l于M,N两点,则tan∠MAN=()A. -1B. -C. -D. -28.已知实数m是给定的常数,函数f(x)=mx3-x2-2mx-1的图象不可能是()A.B.C.D.9. 在三棱锥P -ABC 中,AB =BC =2,AC =2,PB ⊥面ABC ,M ,N ,Q 分别为AC ,PB ,AB 的中点,MN =,则异面直线PQ 与MN 所成角的余弦值为( )A.B.C. D.10. 把函数y =f (x )的图象向左平移个单位长度,再把所得的图象上每个点的横、纵坐标都变为原来的2倍,得到函数g (x )的图象,并且g (x )的图象如图所示,则f (x )的表达式可以为( )A. f (x )=2sin (x +)B. f(x )=sin (4x +)C. f (x )=sin (4x -)D. f (x )=2sin (4x -)11. 设椭圆C :=1(a >b >0)的右焦点为F ,经过原点O 的直线与椭圆C 相交于点A ,B ,若|AF |=2,|BF |=4,椭圆C 的离心率为,则△AFB 的面积是( )A.B. 2C. 2D.12. 函数f (x )对于任意实数x ,都有f (-x )=f (x )与f (1+x )=f (1-x )成立,并且当0≤x ≤1时,f (x )=x 2,则方程的根的个数是A. 2020B. 2019C. 1010D. 1009二、填空题(本大题共4小题,共20.0分)13. 已知函数f (x )=e x cos x +x 5,则曲线y =f (x )在点(0,f (0))处的切线方程是______. 14. 若实数x ,y 满足不等式组,且z =x -2y 的最小为0,则实m =______.15. 一元线性同余方程组问题最早可见于中国南北朝时期(公元5世纪)的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即,一个整数除以三余二,除以五余三,求这个整数.设这个整数为a ,当a ∈[2,2019]时,符合条件的a 共有______个. 16. 圆锥Ω的底面半径为2,母线长为4.正四棱柱ABCD -A ′B ′C ′D ′的上底面的顶点A ′,B ′,C ′,D ′均在圆锥Ω的侧面上,棱柱下底面在圆锥Ω的底面上,则此正四棱柱体积的最大值为______. 三、解答题(本大题共7小题,共84.0分)17. S n 为数列{a n }的前n 项和,已知S n =.(1)求{a n }的通项公式;(2)设b n=,T n=b1+b2+…+b n,求T n.18.四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,PA=PB=PD.(1)求证:PD⊥AB;(2)若AB=6,PC=8,E是BD的中点,求点E到平面PCD的距离.19.某小区为了调查居民的生活水平,随机从小区住户中抽取6个家庭,得到数据如下:参考公式:回归直线的方程是:=x,其中,==,=.(1)据题中数据,求月支出y(千元)关于月收入x(千元)的线性回归方程(保留一位小数);(2)从这6个家庭中随机抽取2个,求月支出都少于1万元的概率.20.已知定点F(1,0),横坐标不小于0的动点在y轴上的射影为H,若|TF|=|TH|+1.(1)求动点T的轨迹C的方程;(2)若点P(4,4)不在直l:y=kx+m线上,并且直线l与曲线C相交于A,B两个不同点.问是否存在常数k使得当m的值变化时,直线PA,PB斜率之和是一个定值.若存在,求出k的值;若不存在,请说明理由.21.函数g(x)=(x-2)e x-ax+2,其中常数a∈R.(1)求f(x)=g(x)+e x+ax-2的最小值;(2)若a<0,讨论g(x)的零点的个数.22.在直角坐标系xOy中,点M(0,1),直线l:(t为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为7ρ2+ρ2cos2θ=24.(1)求曲线C的直角坐标方程;(2)设直线l与曲线C交于点A,B,求的值.23.已知函数f(x)=|x-1|,g(x)=|2x+3|.(1)解不等式f(x)-g(x)≥2;(2)若2f(x)≤g(x)+m对于任意x∈R恒成立,求实数m的最小值,并求当m 取最小值时x的范围.答案和解析1.【答案】D【解析】解:复数z=a+bi,a、b∈R,∵2z=3+12i,∴2(a+bi)-(a-bi)=3+12i,即,解得a=3,b=4,∴z=3+4i,∴|z|=.故选:D.根据复数的四则运算法则先求出复数z,再计算它的模长.本题主要考查了复数的计算问题,要求熟练掌握复数的四则运算以及复数长度的计算公式,是基础题.2.【答案】C【解析】【分析】本题主要考查列举法、描述法的定义,交集的运算,以及子集的定义及子集个数的求法,属于基础题.求出集合B,然后求出A∩B,从而可确定它的子集个数.【解答】解:B={-1,1,3,5};∴A∩B={1,3};∴A∩B的子集个数为:.故选C.3.【答案】D【解析】解:从这5名学生中选2名学生参加某项活动,基本事件总数n==10,抽到2名学生来自于同一班级包含的基本事件个数m==4,∴抽到2名学生来自于不同班级的概率是P=1-=1-.故选:D.基本事件总数n==10,抽到2名学生来自于同一班级包含的基本事件个数m==4,由此能求出抽到2名学生来自于不同班级的概率.本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,是基础题.4.【答案】B【解析】解:平行四边形ABCD中,∠BAD=120°,||=2,||=3,∴=2×=-3,∵=,∴=,,则=(•===-3.故选:B.先根据向量的数量积求出•,然后把,用,表示,代入结合已知即可求解本题考查两个向量的数量积的定义,数量积公式的应用,考查计算能力与转化能力.5.【答案】A【解析】解:由表中数据,计算K2=≈0.3367<0.455,∴认为机动车驾驶技术与性别有关的可靠性不足50%;故选:A.由表中数据计算观测值,对照临界值得出结论.本题考查独立性检验的应用,关键是理解独立性检验的思路.属中档题.6.【答案】C【解析】【分析】本题考查了正弦定理及二倍角余弦公式的灵活运用,考查计算能力,属于基础题.根据题目条件结合三角形的正弦定理以及三角形内角和定理可得cos A,进而利用二倍角余弦公式得到结果.【解答】解:在△ABC中,根据正弦定理,∵a cos B=(4c-b)cos A,∴sin A cos B=4sin C cos A-sin B cos A即4sin C cos A=sin B cos A+sin A cos B=sin(A+B)=sin C,∴sin C=4cos A sin C∵0<C<π,sin C≠0.∴1=4cos A,即cos A=,那么cos2A=2cos2A-1=-.故选:C.7.【答案】A【解析】解:离心率e===,可得b=2a,可设双曲线的渐近线l的方程为y=2x,A(a,0)为双曲线C的右顶点,以F1F2为直径的圆方程为x2+y2=c2,解得M(,)即(a,2a),N(-a,-2a),直线AN的斜率为=1,可得∠OAN=45°,且MA⊥x轴,可得tan∠MAN=tan(90°+45°)=-1.故选:A.由离心率公式和a,b,c的关系,求得直线l的方程y=2x,求得圆的方程,联立解得M,N,再由直线的斜率公式,计算可得所求值.本题考查双曲线的方程和性质,主要是离心率和渐近线方程的运用,考查方程是想和运算能力,属于基础题.8.【答案】D【解析】【分析】本题考查函数图象的识别与判断,导数的应用,考查推理能力,是基础题.令m=0,排除D,对函数求导,确定其极值点的正负即可判断.【解答】解:当m=0时,C符合题意;当m≠0时,f′(x)=3mx2-2x-2m,△=4+24m2>0,设3mx2-2x-2m=0的两根为x1,x2,则<0,则两个极值点x1,x2异号,则D不合题意.故选D.9.【答案】B【解析】【分析】本题考查异面直线所成角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.推导出AB⊥BC,PB⊥面ABC,以B为原点,BA,BC,BP所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出异面直线PQ与MN所成角的余弦值.【解答】解:∵在三棱锥P-ABC中,AB=BC=2,AC=2,∴AB2+BC2=AC2,∴AB⊥BC,又PB⊥面ABC,∴以B为原点,BA,BC,BP所在直线分别为x,y,z轴,建立空间直角坐标系,设PB=t,∵M,N,Q分别为AC,PB,AB的中点,MN=,∴P(0,0,t),N(0,0,),A(2,0,0),C(0,2,0),M(1,1,0),∴MN==,解得t=2,∴P(0,0,2),Q(1,0,0),N(0,0,1),=(1,0,-2),=(-1,-1,1),设异面直线PQ与MN所成角为θ,则cosθ===,∴异面直线PQ与MN所成角的余弦值为.故选B.10.【答案】B【解析】【分析】本题主要考查三角函数图象的应用,利用三角函数图象平移变换关系是解决本题的关键,属于中档题.根据图像可得g(x)的最大值为2,故f(x)的最大值为1,故排除AD;若f(x)=sin(4x-),则,不满足图像,进而可解.【解答】解:根据图像可得g(x)的最大值为2,故f(x)的最大值为1,故排除AD;若f(x)=sin(4x-),则,当时,g(x)=2,不满足图像,故选B.11.【答案】C【解析】解:设椭圆的左焦点为F′,由椭圆的对称性可知,|AF′|=|BF|=4,∴|AF′|+|AF|=2+4=6=2a,∴a=3,又e=,∴c=,由余弦定理可得,cos∠FAF′==-,故sin∠FAF′=.∴S△AFB=S△AFF′=|AF′||AF|sin∠FAF′==故选:C.由椭圆定义及离心率,可得a,c的值,利用余弦定理可得cos∠FAF′,进而利用面积公式得到结果.本题考查了椭圆的定义与几何性质,考查了余弦定理及面积公式,属于中档题.12.【答案】A【解析】解:由函数f(x)对于任意实数x,都有f(-x)=f(x),则函数f(x)为偶函数.又f(1+x)=f(1-x)成立,所以函数f(x)的图象关于直线x=1对称,所以f(x)=f(2+x),即函数f(x)为周期为2的周期函数.则函数y=f(x)的图象与直线y=在[0,1]有两个交点,在(1,3]有两个交点,在(3,5]有两个交点…在(2017,2019]有两个交点,在(2019,+∞)无交点,在(-∞,0)无交点,即交点个数为2020,故选:A.由函数的奇偶性及周期性,方程的解及函数图象的交点个数的转化即可得解.本题考查了函数的奇偶性及周期性,方程的解及函数图象的交点个数的转化,属中档题.13.【答案】y=x+1【解析】【分析】本题考查切线方程,求导法则及运算,考查直线方程,考查计算能力,是基础题.求导,x=0代入求k,点斜式求切线方程即可.【解答】解:函数f(x)=e x cos x+x5,f′(x)=e x(cos x-sin x)+5x4,则f′(0)=1,又f(0)=1,故切线方程为y=x+1,故答案为:y=x+1.14.【答案】【解析】解:画出可行域如图阴影部分所示:当z=x-2y过A时取得最小值,联立得A,则,解m=.故答案为:.画出可行域,由z的几何意义确定其最小值,列m的方程求解即可本题考查线性规划,z的几何意义,数形结合思想,确定取得最小值的最优解是关键,是中档题.15.【答案】135【解析】解:由题设a=3m+2=5n+3,m,n∈N*,则3m=5n+1当m=5k,n不存在;当m=5k+1,n不存在当m=5k+2,n=3k+1,满足题意当m=5k+3,n不存在;当m=5k+4,n不存在;故2≤a=15k+8≤2019,解-≤k≤,则k=0,1,2…134,共135个故答案为:135由题设a=3m+2=5n+3,m,n∈N*,得3m=5n+1,对m讨论求解即可.本题以传统文化为背景考查整数的运算性质,考查不等式性质,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.16.【答案】【解析】解:设正四棱柱的底面边长为x,设棱柱的高h,根据相似性可得:,解得:h=,(其中0<x<2).∴此正四棱柱体积为:V=x2h=x2•,V′=令V′=0,解得:x=,易得:V=x2•,在(0,)上递增,在(,2)上递减,所以此正四棱柱体积的最大值为.故答案为:.设正四棱柱的底面边长为x,设棱柱的高h,利用相似性表示h=,从而得到V的表达式,利用导数知识求最值即可.本题考查了空间几何体的结构特征及函数的最值问题,导数的应用,考查空间想象能力与计算能力,属于中档题.17.【答案】解:(1)当n≥2时,a n=S n-S n-1=+(n-1)2-(n-1)=11-n,当n=1时,满足上式,可得a n=11-n;(2)由a n=11-n,可得b n===(-),T n=(-+-+…+-)=(-)=--.【解析】(1)运用数列的递推式,当n≥2时,a n=S n-S n-1,检验n=1成立即可得到所求通项公式;(2)由b n===(-),裂项相消求和即可.本题考查数列通项公式,裂项相消求和,考查计算能力,熟记求和的基本方法,准确计算是关键,是基础题.18.【答案】(1)证明:由于四边形ABCD是菱形,∠BAD=60°,所以△ABD是正三角形.设AB的中点为K,连接PK,DK,如图所示,则AB⊥DK,又PA=PB,所以AB⊥PK,又PK,DK相交于K,面PKD,所以AB⊥平面PKD.又PD⊂平面PKD,所以AB⊥PD.(2)解:由(1)可知,AB⊥平面PKD.又AB∥CD,所以CD⊥平面PKD.又CD⊂平面PDC,所以平面PDC⊥平面PKD,设点E到平面PCD的距离为h,则由于BD=2ED,得点B到平面PCD的距离为2h.由于KB∥平面PCD,所以K,B两点到平面PCD的距离均为2h.所以点K到直线PD的距离就是2h.设△ABD的中心为H,则PH⊥平面ABD.HC=4HE=4,在Rt△PHC中,PH==4,在Rt△PHD中,PH=4,DH=2,所以PD==2.由DH=2HK,得点H到直线PD的距离为,即==,得h=.所以点E到平面PCD的距离为.【解析】本题考查线面垂直的判定,点到平面的距离,考查空间想象能力与计算能力,属于中档题.(1)设K为AB的中点,要证AB⊥PD,转证AB⊥平面PKD,即证AB⊥PK,AB⊥DK;(2)设H为△ABD的中心,点E到平面PCD的距离为h,则点K到平面PCD的距离为2h,由(1)可知,AB⊥平面PKD,得平面PDC⊥平面PKD,故H到直线PD的距离为,在Rt△AHD中计算H到PD的距离即可得出答案.19.【答案】解:(1)=38,=7;其中==≈0.2,==7-0.2×38=-0.6,故月支出y关于x月收入的线性回归方程是:=0.2x-0.6,(2)若从6个家庭中抽取2个,则基本事件为12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共15种,月支出都少于1万元的基本事件为12,13,14,15,23,24,25,34,35,45,共10种,则月支出都少于1万元的概率为P==.【解析】(1)由题意得到、,,,从而得到月支出y(千元)关于月收入x(千元)的线性回归方程;(2)从6个家庭中抽取2个,共包含15种情况,其中月支出都少于1万元的基本事件共10种,从而得到结果.本题考查线性回归方程的应用,考查最小二乘法求线性回归方程,考查古典概型概率公式,考查计算能力,是中档题.20.【答案】解:(1)设点T在直线x=-1上的射影是R,则由于T的横坐标不小于0,∴|TR|=|TH|+1,又|TF|=|TH|+1,∴|TF|=|TR|,即点T到F(1,0)的距离与T到直线x=-1的距离相等,∴T的轨迹是以F为焦点,以x=-1为准线的抛物线.即C的方程是y2=4x.(2)由于A,B在曲线C上,可设A(,a),B(,b),则PA的斜率k1==,同理PB的斜率k2=.∴k1+k2=+=.又曲线C与直线l相交于A,B两点,∴k≠0,于是联立方程,得⇒ky2-4y+4m=0,∴a+b=,ab=.∴∴k1+k2==1-,此式随着m的变化,值也在变化,所以不存在k值满足题意.【解析】(1)利用抛物线定义,即可得到动点T的轨迹C的方程;(2)设A(,a),B(,b),利用斜率计算公式可得k1+k2,利用韦达定理即可得到结果.本题考查了定义法求轨迹方程、综合考查了直线与圆锥曲线方程联立解决复杂的存在探究问题,考查了推理能力与计算能力,属于中档题.21.【答案】解:(1)f(x)=(x-1)e x在定义域R上的导数为f′(x)=xe x.∴当x<0时,f′(x)<0;当x>0时,f′(x)>0.∴f(x)的单调递减区间是(-∞,0),单调增区间是(0,+∞).∴f(x)的最小值是F(0)=-1.(2)g(x)在其定义域R上的导数是g′(x)=(x-1)e x-a.①当a≤-1时,由(1)可得g′(x)≥0,g(x)在R上是增函数,此时由g(0)=0,可得函数g(x)有唯一的零点.②当-1<a<0时,g′(0)=-1-a<0,并且对于负数2ln(-a)-5,有g′[2ln(-a)-5]=[2ln(-a)-5-1]e[2ln(-a)-5]-a=[2ln(-a)-6]e[2ln(-a)-5]-a=.又∵2a ln(-a)-6a<6<e5,∴2a ln(-a)-6a-e5<0,即g′[2ln(-a)-5]>0.∴在区间(2ln(-a)-5,0)上存在负数t,使得g′(t)=0,则在(-∞,t)上g′(x)>0,g(x)是增函数;在区间(t,0)上g′(x)<0,g(x)是减函数.则g(t)>g(0)=0,g()=()<0.∴在(-∞,0)上,g(x)有且仅有1个零点;在区间(0,+∞)上,g′(0)=-1-a<0,g′(1)=-a>0并且g′(x)是增函数.∴存在正数n,使得在(0,n)上,g′(x)<0,g(x)是减函数;在(n,+∞)上,g′(x)>0,g(x)是增函数.于是有g(n)<g(0)=0,g(2)=2-2a>0.∴在(0,+∞)上,g(x)恰有唯一的零点.∴当-1<a<0时,g(x)在R上恰有三个不同的零点.综上所述,当a≤-1时,g(x)有唯一的零点;当-1<a<0时,g(x)有三个不同的零点.【解析】(1)导数为f′(x)=xe x,研究单调性即可得到f(x)=g(x)+e x+ax-2的最小值;(2)g(x)在其定义域R上的导数是g′(x)=(x-1)e x-a,对a分类讨论,数形结合即可明确g(x)的零点的个数.本题考查了函数的最值与函数零点的个数判断,考查转化思想与函数方程思想,考查转化能力与计算能力,属于难题.22.【答案】解(1)∵7ρ2+ρ2cos2θ=24,∴7ρ2+ρ2(2cos2θ-1)=24,又∵ρ2=x2+y2,x=ρcosθ,∴曲线C的直角坐标方程为:+=1.(2)将直线l的参数方程化为标准形式为:(t为参数),代入曲线C方程,得19t2+6t-45=0>0恒成立,∴t1+t2=-,t1t2=-∴+=+===.【解析】本题考查了简单曲线的极坐标方程,考查直线参数方程t的几何意义,考查计算能力,属中档题.(1)利用极坐标与直角坐标的互化求解即可;(2)将直线l的参数方程化为标准形式为:(t为参数),与椭圆联立,利用t的几何意义求解+即可.23.【答案】解:(1)f(x)-g(x)=|x-1|-|2x+3|,当x≤-时,不等式化为x+4≥2,解得x≥-2,可得-2≤x≤;当<x<1时,不等式化为-3x-2≥2,解得x≤-,可得<x≤-;当x≥1时,不等式化为-x-4≥2,解得x≤-6,可得x∈∅.综上可得,原不等式的解集为{x|-2≤x}.(2)若2f(x)≤g(x)+m恒成立,则|2x-2|-|2x+3|≤m恒成立,∴m≥(|2x-2|-|2x+3|)max,又∵|2x-2|-|2x+3|≤|2x-2-(2x+3)|=5,∴m最小值为5.此时∴,解得x≤.【解析】(1)零点分段去绝对值化简f(x)-g(x)解不等式即可;(2)2f(x)≤g(x)+m恒成立,即|2x-2|-|2x+3|≤m恒成立,即m≥(|2x-2|-|2x+3|)max,由绝对值三角不等式求m≥(|2x-2|-|2x+3|)max,即可求解.本题考查绝对值不等式的解法,绝对值三角不等式求最值,熟记定理,准确计算是关键,绝对值三角不等式成立条件是易错点,是中档题.。
广东省六校2013届高三5月高考模拟考试数学(文)试题(无答案)

2013届高三六校高考模拟考试文科数学试题本试卷共6页,21小题,满分150分.考试用时120分钟.一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|1}A x x =≥,)}2(log |{2+==x y x B ,则=A BA .)1,2(-B .]1,2(-C .)1,2[-D .]1,2[- 2.已知i 为虚数单位,a 为实数,复数(2i)i z a =-在复平面内对应的点为M ,则“2a <-”是“点M 在第四象限”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 3.已知等比数列}{n a 中,公比0q >,若42=a , 则321a a a ++的最值情况为A .有最小值4-B .有最大值4-C .有最小值12D .有最大值12 4.由两个完全相同的正四棱锥组合而成的空间几何体的 正(主)视图、侧(左)其中四边形ABCD 是边长为1的正方形,则该几何体的表面积为A .34B .33C .32D .3 5.执行如图所示的程序框图,输出的S 是 A . 0 B .12C . 1D .1- 6.下列四个命题中,正确的有①两个变量间的相关系数r 越小,说明两变量间的线性相关程度越低;②命题p :“R ∈∃0x ,01020>--x x ”的否定p ⌝:“R ∈∀x ,012<--x x ”;③用相关指数2R 来刻画回归效果,若2R 越大,则说明模型的拟合效果越好; ④若23.0=a ,3.02=b ,2log 3.0=c ,则b a c <<.A .①③B .①④C .②③D .③④7.把正奇数数列按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号一个数,第五个括号两个数,第六个括号三个数,….依次划分为)1(,)5,3(,)11,9,7(,)13(,)17,15(,)23,21,19(,)25(,….则第50个括号内各数之和为A .396B .394C .392D .3908.已知函数)(x f y =的定义域是R ,若对于任意的正数a ,函数)()()(a x f x f x g --= 都是其定义域上的减函数,则函数)(x f y =的图象可能是A .B .C .D .9.已知定点)0,2(-A ,)0,2(B ,N 是圆O :122=+y x 上任意一点,点A 关于点N 的对称点为M ,线段AM 的中垂线与直线BM 相交于点P ,则点P 的轨迹是 A .椭圆 B .双曲线 C .抛物线 D .圆 10.设函数)(x f 在区间I 上可导,若I x x ∈∀,0,总有))(()()(000x x x f x f x f -'+≥,则称)(x f y =为区间I 上的U 函数. 在下列四个函数2x y =,xx y 1+=,xy e -=,x y 2cos =中,在区间)0,1(-上为U 函数的个数是A .1B .2C .3D .4二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题:11、12、13题为必做题. 11.如图,菱形ABCD 的边长为2,︒=∠60A ,M 为DC 的中点,则AB AM ⋅的值为 .第11题图12.设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥-≥+≤0,0121y x x y x y ,若目标函数z mx y =+(0m >)的最大值为35,则m 的值为 .13.设1>a ,则当x a y =与x y a log =两个函数图象有且只有一个公共点时,=a ln ln .(二)选做题:第14、15题为选做题,考生只能从中选做一题. 14.(坐标系与参数方程选做题)在平面直角坐标系xOy 中,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=-=t y t x 23221(t 为参数),以原点O为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为θρcos 2=,则l 上的动点P 与C 上的动点Q 间的最短距离为 . 15.(几何证明选讲选做题)如图,四边形ABCD 是边长为2的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的圆O 交于点F ,连接CF 并延长CF 交AB 于E .则线段BF 的长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分13分)某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有630名学生,男女生人数之比为10:11,现按分层抽样方 法抽取若干名学生,每人被抽到的概率均为16. (1)求抽取的男学生人数和女学生人数;(2)通过对被抽取的学生的问卷调查,得到如下22⨯列联表:BEO第15题图①完成列联表;②能否有97.5%的把握认为态度与性别有关?(3)若一班有5名男生被抽到,其中4人持否定态度,1人持肯定态度;二班有4名女生被抽到,其中2人持否定态度,2人持肯定态度.现从这9人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.解答时可参考下面临界值表:17.(本小题满分12分)设ABC ∆的三个内角A ,B ,C 所对的边分别为a ,b ,c .已知sin()cos 6A A π-=.(1)求角A 的大小;(2)若2a =,求b c +的最大值.18.(本小题满分14分)在四棱锥ABCD P -中,︒=∠=∠90ACD ABC ,︒=∠=∠60CAD BAC ,⊥PA 面ABCD ,E 为PD 的中点,42==AB PA .(1)求证:AE PC ⊥; (2)求证://CE 面PAB ; (3)求三棱锥ACE P -的体积V .PABCDE第18题图19.(本小题满分13分)已知数列}{n a 的前n 项和为n S ,若21=a ,()11++=⋅+n n S a n n n ,*N ∈n . (1)求数列}{n a 的通项公式: (2)令nnn S T 2=,*N ∈n . ①当n 为何正整数值时,1+>n n T T ;②若对一切正整数n ,总有m T n ≤,求m 的取值范围.20.(本小题满分14分)如图,点F 是椭圆12222=+by a x (0>>b a )的左焦点,点A ,B 分别是椭圆的左顶点和上顶点,椭圆的离心率为21,点C 在x 轴上,且BC BF ⊥,过点A 作斜率为(0)k k >的直线l 与由三点B ,F ,C 确定的圆M 相交于D ,E 两点,满足221a ME MD -=⋅.(1)若BOF ∆,求椭圆的方程; (2)直线l 的斜率是否为定值?证明你的结论.第20题图21.(本小题满分14分)已知函数1)1(ln )(+--=x x a x x f (R ∈a ,0≠a ),x x x g +=2)(. (1)求函数(1)()ln ()1a x h x a x g x x -=-⋅+的单调区间,并确定其零点个数;(2)若)(x f 在其定义域内单调递增,求a 的取值范围; (3)证明不等式 1ln 121715131+<+++++n n (*N ∈n ).。
广东省湛江二中2013届高三数学5月模拟测试试题 文 新人教A版

广东省湛江二中2013届高三数学5月模拟测试试题 文 新人教A 版本试卷共4页,21小题,满分150分.考试用时120分钟 2013年5月注意事项: 答卷前,考生务必用黑色字迹的钢笔或签字笔将自已的姓名和考生号、试室号、座位号填写在答题卡上,答案不能答在试卷上。
考试结束将答题卡交回。
参考公式:锥体的体积公式:13V Sh =,其中S 是锥体的底面积,h 是锥体的高; 球的体积公式:334R V ⋅=π,其中R 是球的半径. 一、选择题:(本大题共10小题,每小题5分,满分50分,每题仅有一个选项正确) 1.设全集{}1,3,5,6,8U =,{}1,6A =,{}5,6,8B =,则=B A C U )( ( )A .{}6B .{}58,C .{}68,D .{}568,,2.已知i iz+=-31,则复数z 在复平面内对应的点所在的象限是 ( ) A .第一象限B .第二象限C .第三象限D .第四象限3.已知抛物线28y x = 的准线l 与椭圆C :1222=+y ax 相切,则椭圆C 的离心率=e( ) A .23 B .21 C .33 D .55 4.已知向量)1,3(=a ,)2,1(-=b ,)2,(-=k c ,若b c a ⊥-)(,则=k ( )A .3B. 3-C.31 D .31- 5.数列}{n a 是公差为2的等差数列,且521,,a a a 成等比数列,则}{n a 的前5项和=5S( )A .20B.30C .25D .406.在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知2=b ,3=c ,C B A 2=+,则角=A( ) A .43π B .4π C .125π D .6π 7.已知变量y x ,满足约束条件2010220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩,则z x y =-的最小值是 ( )A .1B .3C .2-D .1-8.如右图是一个几何体的三视图,则该几何体的 体积为 ( ) A .321π+B .322π+C .π324+D .34212π+9.已知圆C 的圆心是直线04=+-y x 与直线022=++y x 的交点,且圆C 被直线012=+-y x 所截得的弦长为4,则圆C 的方程是 ( ) A .3)1()1(22=-++y xB .3)2()2(22=-++y xC .9)2()2(22=-++y x D .9)2()2(22=++-y x10.定义在R 上的函数()f x 满足(6)()f x f x +=.当31x -≤<-时,2()(2)f x x =-+,当13x -≤<时,()f x x=。
广东省湛江一中2013届高三5月高考模拟数学文试题 含答案

湛江一中2013届高三5月模拟考试数学(文科) 2013.5本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.参考公式:方差()()()2222121n sx x x x x x n ⎡⎤=-+-+⋅⋅⋅+-⎢⎥⎣⎦,其中12nx xx x n+++=。
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项。
1. 集合{}|(1)(2)0A x x x =-+≤,B ={}0x x <,则AB =( )A .(,0]-∞B .(,1]-∞C .[1,2]D .[1,)+∞2。
i 是虚数单位,则复数21=i z i -在复平面内对应的点在 ( )A .第一象限B 。
第二象限C 。
第三象限D .第四象限3. 已知命题:p x ∀∈R,2x ≥,那么下列结论正确的是 ( )A . 命题:2p x x ⌝∀∈R ≤,B .命题:2p x x ⌝∃∈<R ,C .命题:2p x x ⌝∀∈-R ≤, D .命题:2p x x ⌝∃∈<-R ,4。
某空间几何体的三视图如右图所示,则该几何体的表面积为 ( )A 。
180B .240C .276D .3005.()22,0,3log ,0.x f x xx x ⎧-<⎪=⎨⎪+>⎩则((1))f f -等于 ( )A 。
广东湛江二中2013高三上第一次月考--数学(文).

本试卷共4页,21小题,满分150分。
考试用时120分钟。
命题人:一、选择题:本大题共10 小题,每小题5分,满分50分.每小题给出得四个选项中,只有一项是符合题目要求得. 1.已知集合{}{}1,0,1,1,2A B =-=,则AB 等于 ( )A .{}1,0,1-B .{}0,1C .{}1D .{}1,22.已知向量(1,1),2(4,2)=+=a a b ,则向量,a b 的夹角为 ( )A .6π B .4π C .3π D .2π3.设函数22()cos ()sin (),44f x x x x Rππ=+-+∈,则函数()f x 是 ( )A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为2π的奇函数D .最小正周期为2π的偶函数4.如图,是一个几何体的正视图(主视图)、侧视图(左视图)、俯视图,正视图(主视图)、侧视图(左视图)都是矩形,则该几何体的体积是 ( ) A .24 B .12 C .8 D .4 5.已知实数x ,y 满足约束条件⎪⎩⎪⎨⎧≤-≤≥021y x y x 则z=2x-y 的取值范围( )A .[l,2]B .[1,3]C .[0,2]D .[0,1] 6. 函数21sin -2cos 21+=x x y 的值域是 ( )A 、[]1,1-B 、⎥⎦⎤⎢⎣⎡45,1C 、[]2,0D 、⎥⎦⎤⎢⎣⎡-45,17.已知i 为虚数单位,a 为实数,复数(2i)(1+i)z a =-在复平面内对应的点为M ,则“a =1”是“点M 在第四象限”的 ( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 8.函数xx y lg =的图象大致是( )9.在如下程序框图中,已知:x xe x f =)(0,则输出的是 ( )A . x x xe e +2009B .x x xe e +2008C .x x xe e +2007D .x e x +2008 10.圆心在曲线)0(2>=x xy 上,且与直线2x+y+l=O 相切的 面积最小的圆的方程为( )A .5)2()1(22=-+-y xB .5)1()2(22=-+-y xC .25)2()1(22=-+-y x D .25)1()2(22=-+-y x二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
2013年广东省高考全真模拟考试文科数学试题(五)

第8题2013年广东省高考全真模拟试卷文科数学(五)本试卷共4页,21小题, 满分150分. 考试用时120分钟.参考公式:锥体的体积公式13V Sh =,其中S 为锥体的底面积,h 为高. 一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的 1. (){},|0,,A x y x y x y R =+=∈,则集合AB =( )A .(1,1)-B .{}{}11x y ==- C .{}1,1- D .(){}1,1-2.下列函数中,在其定义域内是减函数的是( ) A .1)(2++-=x x x f B . xx f 1)(=C . 13()log f x x = D . ()ln f x x =3.已知0a >,4()4,f x x a x =-+则()f x 为( )A .奇函数B .偶函数C .非奇非偶函数D .奇偶性与a 有关4.已知向量(12)a =,,(4)b x =,,若向量a b //,则x =( ) A .2 B . 2- C . 8D .8-5.设数列{}n a 是等差数列,且5,8152=-=a a ,n S 是数列{}n a 的前n 项和,则 ( ) A.109S S <B.109S S =C.1011S S <D.1011S S =6.已知直线l 、m ,平面βα、,则下列命题中:①.若βα//,α⊂l ,则β//l ②.若βα//,α⊥l ,则l β⊥③.若α//l ,α⊂m ,则m l // ④.若βα⊥,l =⋂βα, l m ⊥,则β⊥m . 其中,真命题有( ) A .0个 B .1个 C .2个 D .3个7.已知离心率为e 的曲线22217-=x y a ,其右焦点与抛物线216=y x 的焦点重合,则e 的值为( )A .34B .42323C .43D .2348.给出计算201614121++++ 的值的一个 程序框图如右图,其中判断框内应填入的条件是( ). A .10>i B .10<i C .20>i D .20<i 9.lg ,lg ,lg x y z 成等差数列是2y xz =成立的( )ABDCOM N A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既不充分也不必要条件10.规定记号“⊗”表示一种运算,即),(2为正实数b a b a ab b a ++=⊗,若31=⊗k ,则k =( ) A .2- B .1 C .2- 或1 D .2二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
广东省湛江一中等“十校”第二学期高三联考数学(文)试题参考答案

2013届广东省湛江一中等“十校”第二学期高三联考数学(文)试题参考答案一、选择题二、填空题11.24 12.1- 13.④ 14.1个 15.4 三、解答题共6小题,共80分。
解答应写出文字说明、演算步骤或证明过程. 16.解:(1)解:由正弦定理得C cA a sin sin =,∵32sin c A a =, 32sin c C c =∴, ………2分 ∴23sin =C ……………4分 ∵ABC ∆是锐角三角形,∴3π=C . ……………6分(2)解:7=c ,3π=C ,由面积公式得2333sin 21=πab , ………………8分 ∴ 6ab =. ………………9分由余弦定理得73cos222=-+πab b a ……………11分∴ 1322=+b a ………………12分 17.解:(1)由题意可知,样本总人数为,5016.08=,04.0502==∴b 16,0.04,0.032,0.004a b x y ====.……………………4分(2)(ⅰ)由题意可知,第4组共有4人,记为,,,A B C D ,第5组共有2人,记为,X Y .从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有,,,,,,,AB AC AD BC BD CD AX AY ,,,,,,,BX BY CX CY DX DY XY共15种情况. …………………6分 设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E , …………7分 有,AX AY ,,,,,,,BX BY CX CY DX DY XY 共9种情况. ………8分 所以93()155P E ==. 答:随机抽取的2名同学中至少有1名同学来自第5组的概率35.………9分 (ⅱ)设“随机抽取的2名同学来自同一组”为事件F , ………………10分有,,,,,,AB AC AD BC BD CD XY 共7种情况. ………………11分 所以7()15P F =. 答:随机抽取的2名同学来自同一组的概率是715. …12分 18.解:(1)连接OF .由ABCD 是正方形可知,点O 为BD 中点. 又F 为BE 的中点,所以OF ∥DE ………………….2分 又,,OF ACF DE ACF ⊂⊄平面平面 所以DE ∥平面ACF ………….4分(2)证明:由EC ABCD BD ABCD ⊥⊂底面,底面, 所以,EC BD ⊥………………………………5分由ABCD 是正方形可知, ,AC BD ⊥…………………………6分又=,,AC EC C AC EC ACE ⋂⊂平面,………………………………7分 所以,BD ACE ⊥平面……………………………………8分又AE ACE ⊂平面,所以BD AE ⊥…………………………………………………9分 (3)在线段EO 上存在点G ,使CG BDE ⊥平面.理由如下:如图,取EO 中点G ,连接CG .………………………………10分在四棱锥EABCD 中,22,AB CE COAB CE ,所以CG EO ⊥ ……………11分 由(2)可知,BD ACE ⊥平面,而,BD BDE ⊂平面所以,ACE BDE ACE BDE EO ⊥⋂=平面平面且平面平面,…………12分因为,CG EO CG ACE ⊥⊂平面,所以CG BDE ⊥平面 ………………13分 故在线段EO 上存在点G ,使CG BDE ⊥平面.由G 为EO 中点,得1.2EGEO …………… 14分 19.解:(1)由已知得2b =2a =1d +, 3b =5a 14d =+, 2b =14a 113d =+, ………1分由于{}n b 为等比数列,所以2324b b b =⋅.∴2(14)d +=(1)(113)d d ++, 0,2d d >∴=. ……………2分∴21n a n =- . ………3分又2b =2a =3,3b = 5a =9 , ………………4分∴数列{n b }的公比为3, ………………5分 ∴n b =3⋅23n -=13n -. ………………6分(2)由11c b +22c b +…+n nc b =1n a + , (1) 当1n =时,11c b =2a =3, ∴1c =3. ……………8分当1n >时,11c b +22c b +…+11n n c b --= n a , (2) ………………9分 由(1)-(2)得nnc b =1n a +-n a =2 , ………………10分 ∴n c =2n b =2⋅13n -, (2)n ≥ ………………11分∴n c =13,123,2n n n -=⎧⎨⋅≥⎩ ………………12分 ∴123c c c +++…2012c =3+2⋅3+2⋅23+…+2⋅20113 ……………13分=1+2⋅03+2⋅3+2⋅23+…+2⋅20113=1+2⋅20121313--=20123 …………14分20.(1)解:设曲线C 1的方程为2221x y a+=,C 2的方程为2221x y b +=(1,01a b ><<)…2分∵C 1 ,C 2的离心率相同,∴22211a b a -=-,∴1ab =, …………………………………………3分 3,2m =∴令32y =代入曲线方程, 则22311,.42A x x a a +=∴=- 22311,42C x x b b +=∴=. ∴当m 3A 3(2a -,C 13(2a . …………………5分 又∵54AC =,115224b a ∴+=. 由521a b ab ⎧+=⎪⎨⎪=⎩,且1,01a b ><<,解得212a b =⎧⎪⎨=⎪⎩ .………………6分∴C 1 ,C 2的方程分别为2214x y +=,2241x y +=. …………………7分 (2)令m y =代入曲线方程,2221x y a+=,得,12m a x A --=2221x y b+=,得21m b x C -= ………9分由于1=ab ,所以A (-21a m -,m ),C (211m a-,m ) . ………10分 由于MN 是曲线1C 的短轴,所以)1,0(-N .∵OC ⊥AN ,∴0OC AN ⋅=(*).. .................... 11分 ∵OC =(211m a-,m ),AN =(21a m -,-1-m ), 代入(*)并整理得2m 2+m-1=0, ………………12分 ∴21=m 或1-=m (舍负) ,∴21=m . ………………14分 21.解:(1)函数的定义域为()0,+∞,222122()(1)ax x af x a x x x-+'=+-=. ………… 1分 设2()2h x ax x a =-+,①当0a =时,()20h x x =-<,2()20h x ax x a =-+<在),0(+∞上恒成立,则()0f x '<在),0(+∞上恒成立,此时()f x 在),0(+∞上单调递减. ……………2分②当0a ≠时,(I )由,0442=-=∆a 得1±=a .当1=a 时,2()2h x ax x a =-+0)1(1222≥-=+-=x x x 恒成立, )(x f ∴在),0(+∞上单调递增。
广东省湛江一中等“十校”2013届高三下学期联考数学文试题 含答案

“十校"2012——2013学年度高三联考数学(文科)试题 2013.2本试卷共4页,21小题,满分150分.考试时间120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案,不准使用铅笔和涂改液.不按以上要求作答的答案无效.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1。
已知复数1z i =+,则3z 的虚部为( )A 。
2iB 。
2i - C.2 D 。
2-2.设集合2{2}A x xx =<,集合2{log 0}B x x =>,则A B 等于( )A .{}|2x x <B .{}|x x >0C .{}|02x x <<D .{}|12x x << 3.设33tan =α,23παπ<<,则sin 2α的值为( ) A 。
32-B.12-C. 12D 。
324.已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积为( ) A. 4 B .8 C 。
12 D.245.已知cos ,0()(1)1,0xx f x f x x π≤⎧=⎨-+>⎩,则)34()34(-+f f 的值为( )A .2-B .1-C .1D .26。
下列有关命题的说法正确的是( ) A .命题“若21x=,则1=x ”的否命题为:“若21x =,则1x ≠”.B .“6x =”是“2560xx --="的必要不充分条件.C .命题“对任意,R x ∈均有210xx -+>”的否定是:“存在,R x ∈使得012<+-x x ”.D .命题“若x y =,则cos cos x y =”的逆否命题为真命题.7.已知向量(1,)x =a ,(1,)x =-b ,若2-a b 与b 垂直,则||=a ( )A .2 B .3 C .2 D .48.在等差数列{}n a 中,0>n a ,且301021=+++a a a,则65a a ⋅的最大值是( )A .3B .6C .9D .36 9.已知1F 、2F 为双曲线C :14x 22=-y 的左、右焦点,点P 在曲线C 上,∠21PF F =060,则P 到x 轴的距离为( ) A .55B .155C .2155D .152010。
广东省湛江二中2013届高三5月模拟测试化学试题Word版含答案

可能用到的相对原子质量:H-1 C-12 N-14 O-16 18O-18一、单选7.用N A表示阿伏加德罗常数,下列判断正确的是A.常温常压下,16g O2和O3的混合气体中含有N A个氧原子B.常温常压下,28 g CO与22.4 L O2的分子数都是N A个C.16 g CH4与18 g NH+4所含质子数都是10N A个D.1 mol/L Na2CO3溶液中,CO32-的离子数目小于N A个8.下列关于有机化合物的叙述正确的是A.用NaOH溶液可以除去乙酸乙酯中的乙酸B.乙烯和苯都能与溴水反应而使溴水褪色C.用新制的银氨溶液可区分甲酸甲酯和乙醛D.脂肪、糖类和蛋白质都是人体重要的营养物质9.在由水电离出的c(H+)=1×10-12 mol·L-1的溶液中,一定能大量共存的离子组是A.NH4+、Ba2+、NO3-、Cl-B.Cl-、SO42-、Na+、K+C.SO42-、NO3-、Fe2+、Mg2+D.Na+、K+、ClO-、I-10.下图是元素周期表的一部分。
A、B、C、D均为短周期元素,若C原子最外层电子数是其内层电子数的3/5,则下列说法不正确的是A.气态氢化物的稳定性:A>BB.B元素的两种同素异形体常温下都是气体C.最高价氧化物对应水化物的酸性:D>CD.原子半径从大到小的排列顺序为:C>B11.“长征三号”丙运载火箭推进器常以联氨(N2H4)为燃料、过氧化氢为助燃剂。
已知下列各物质反应的热化学方程式为:N2H4(g)+O2(g)===N2(g)+2H2O(g) ΔH1=-533.23 kJ· mol-1H2O(g)===H2O(l) ΔH2=-44 kJ· mol-12H2O2(l)===2H2O(l)+O2(g) ΔH3=-196.4 kJ· mol-1则联氨与过氧化氢反应的热化学方程式可表示为()A.N2H4(g)+2H2O2(l)===N2(g)+4H2O(g)ΔH=+817.63 kJ·mol-1B.N2H4(g)+2H2O2(l)===N2(g)+4H2O(g)ΔH=-641.63 kJ·mol-1C.N2H4(g)+2H2O2(l)===N2(g)+4H2O(g)ΔH=+641.63 kJ·mol-1D.N2H4(g)+2H2O2(l)===N2(g)+4H2O (g)ΔH=-817.63 kJ·mol-112.下列化学实验基本操作中,正确的是A.配制溶液时,将量筒中液体倒入烧杯后,应将量筒洗涤,将洗涤液也倒入烧杯B.用干燥的pH试纸分别测1 mol·L-1的NaOH溶液和1 mol·L-1的H2SO4的pHC.稀释浓硫酸时,把浓硫酸慢慢倒入盛有水的烧杯中并不断搅拌D.向酒精灯加酒精时,应将试剂瓶中的酒精直接倒入酒精灯中二、双选22.下图为氢氧燃料电池原理示意图,按照此图的提示,下列叙述不正确...的是A.a电极是负极B.电子从b电极流向a电极C.在电池工作中,a电极附近pH值降低D.b电极的电极反应为:4OH--4e-===2H2O+O2↑23.室温时,0.1 mol·L-1的HA溶液的pH=3,向该溶液中逐滴加入0.1 mol·L-1 NaOH溶液,在滴加过程中,有关叙述正确的是A.未加入NaOH溶液时,原HA溶液中c(H+)=c(OH-)+c(A-)B.向原溶液中滴入少量NaOH溶液,离子浓度可能为:c(A-)>c(Na+)>c(H+)>c(OH-) C.当滴入的NaOH与HA恰好完全中和时,溶液中c(Na+)=c(A-)D.当加入过量的NaOH溶液时,溶液可能呈中性,也可能呈碱性三、非选择题30.(16分)松油醇是一种调香精,它是α、β、γ三种同分异构体组成的混合物,可由松节油分馏产品A(下式中的18O是为区分两个羟基而人为加上去的)经下列反应制得:试回答:(1)α-松油醇的相对分子质量为_________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省湛江二中2013届高三5月模拟测试数学(文)试题本试卷共4页,21小题,满分150分.考试用时120分钟注意事项: 答卷前,考生务必用黑色字迹的钢笔或签字笔将自已的姓名和考生号、试室号、座位号填写在答题卡上,答案不能答在试卷上。
考试结束将答题卡交回。
参考公式:锥体的体积公式:13V Sh =,其中S 是锥体的底面积,h 是锥体的高; 球的体积公式:334R V ⋅=π,其中R 是球的半径. 一、选择题:(本大题共10小题,每小题5分,满分50分,每题仅有一个选项正确) 1.设全集{}1,3,5,6,8U =,{}1,6A =,{}5,6,8B =,则=B A C U )( ( )A .{}6B .{}58,C .{}68,D .{}568,, 2.已知i iz+=-31,则复数z 在复平面内对应的点所在的象限是 ( ) A .第一象限B .第二象限C .第三象限D .第四象限3.已知抛物线28y x = 的准线l 与椭圆C :1222=+y ax 相切,则椭圆C 的离心率=e( ) A .23 B .21 C .33 D .55 4.已知向量)1,3(=,)2,1(-=,)2,(-=k ,若⊥-)(,则=k ( )A .3B. 3-C.31 D .31- 5.数列}{n a 是公差为2的等差数列,且521,,a a a 成等比数列,则}{n a 的前5项和=5S( )A .20B.30C .25D .406.在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知2=b ,3=c ,C B A 2=+,则角=A( )A .43π B .4π C .125π D .6π 7.已知变量y x ,满足约束条件2010220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩,则z x y =-的最小值是 ( )A .1B .3C .2-D .1-8.如右图是一个几何体的三视图,则该几何体的 体积为 ( ) A .321π+B .322π+C .π324+D .34212π+9.已知圆C 的圆心是直线04=+-y x 与直线022=++y x 的交点,且圆C 被直线012=+-y x 所截得的弦长为4,则圆C 的方程是 ( ) A .3)1()1(22=-++y xB .3)2()2(22=-++y xC .9)2()2(22=-++y x D .9)2()2(22=++-y x10.定义在R 上的函数()f x 满足(6)()f x f x +=.当31x -≤<-时,2()(2)f x x =-+,当13x -≤<时,()f x x=。
则=++++)2013()3()2()1(f f f f ( )A .337 B.338 C.1678 D.2013 二、填空题:(本大题共5小题,每小题5分,满分20分.其中14、15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分)11.函数x x f 6log 21)(-=的定义域为 . 12.执行右边的程序框图,其输出结果是 . 13.已知方程mx x x =--112有两个不相等的实数根,则实数m 的取值范围是 .14.(坐标系与参数方程选做题)在极坐标系中,直线l 的方程为02)sin 2(cos =+-θθρ,则点π26⎛⎫ ⎪⎝⎭,到直线l 的距离为.ABCDO. 侧视图俯视图15.(几何证明选讲选做题)如图,AB 是圆O 的直径, 延长AB 至C ,使2BC OB =,CD 是圆O 的切线, 切点为D ,连接AD ,BD ,则ADBD的值为 . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数x x x f ωω2sin 3cos 2)(2+=,(0>ω,R x ∈)的最小正周期为π. (1)求ω的值; (2)若)6,0(πθ∈,且513)(=θf ,求:)6(πθ+f 的值. 17.(本小题满分12分)湛江电视台为了宣传在湛江举办的“广东省运动会”,随机对湛江市15-65岁的人群抽取了100人回答 “广东省运动会” 的有关问题,根据统计结果制作了如下的统计图表1、表2:(1)分别求出表2中的a 、x 的值;(2)若在第2、3、4组回答正确的人中用分层抽样的方法抽取6人,则各组应分别抽取多少人?(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求获奖的2人均来自第2组的概率. 18.(本小题满分14分)如图,四边形ABCD 是边长为 1 的正方形,⊥MD 平面ABCD ,⊥NB 平面ABCD , 且1==NB MD .MND0.0.0.0.0.表2(1)求证:CD AM ⊥; (2)求证:CN ∥平面AMD ; (3)求该几何体ABCDMN 的体积.19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且满足121+=n n S a (*∈N n ). (1)求数列{}n a 的通项公式; (2)若n n a b 2log =,21+⋅=n n n b b c ,数列{}n c 的前n 项和为n T ,求n T 的取值范围.20.(本小题满分14分)已知椭圆C 的两焦点为)0,1(1-F ,)0,1(2F ,并且经过点)23,1(M . (1)求椭圆C 的方程;(2)已知圆O :122=+y x ,直线l :1=+ny mx ,证明当点()n m P ,在椭圆C 上运动时,直线l 与圆O 恒相交;并求直线l 被圆O 所截得的弦长的取值范围. 21.(本题满分14分) 已知函数x k x x f ln 21)(2⋅-=(R k ∈). (1)当2=k 时,求函数在点))1(,1(f 处的切线方程; (2)求函数)(x f 的单调区间和极值; (3)设332)(x x g =,1-=k ,当),1(+∞∈x 时,比较)(x f 与)(x g 的大小.湛江二中2013届高三五月模拟考试题数学(文科)参考答案(其他答案请酌情给分!) 2013年5月一、选择题:二、填空题:11. ]6,0( 12. 127 13.)2,1()1,0( 14.51515三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数x x x f ωω2sin 3cos 2)(2+=,(0>ω,R x ∈)的最小正周期为π. (1)求ω的值; (2)若)6,0(πθ∈,且513)(=θf ,求:)6(πθ+f 的值. 解:(1) x x x f ωω2sin 3cos 2)(2+=1)62sin(22sin 32cos 1++=++=πωωωx x x (4)分∵ )(x f 的最小正周期为π, ∴ πωπ=22, ∴ 1=ω (6)分(2) 由(1),1)62s in (2)(++=πx x f∴ 5131)62sin(2)(=++=πθθf ∴ 54)62s i n (=+πθ,∵)6,0(πθ∈ ∴ )2,6(62πππθ∈+∴ 53)62c o s (=+πθ ……………………………………………… 8分 又 12c o s 21)22s i n (21]6)6(2s i n [2)6(+=++=+++⨯=+θπθππθπθf ………10分6sin )62sin(6cos )62cos(]6)62cos[(2cos ππθππθππθθ⋅++⋅+=-+=1033421542353+=⨯+⨯=∴12c o s 2)6(=+=+θπθf……… 12分17.(本小题满分12分) 的“广东省运动会”市15-65岁的人群抽取了人回答 “广东省运动会” 的有关问题,根据统计结果制作了如下的统计图表1、表2:(1)分别求出表2中的a 、x 的值;(2)若在第2、3、4组回答正确的人中用分层抽样的方法抽取6人,则各组应分别抽取多少人?0.0.0.0.0.表1表2(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求获奖的2人均来自第2组的概率.解:(1)由频率分布直方图可知,第2、3组总人数分别为:20人、30人∴ 18209.0=⨯=a (人), 9.03027==x ……………………………………………………4分 (2)在第2、3、4组回答正确的人共有54人,用分层抽样的方法抽取6人,则各组分别抽取: 第2组:265418=⨯; 第3组:365427=⨯; 第4组:16549=⨯ ∴ 应在第2、3、4组分别抽取2人、3人、1人. (8)分(3)分别记第2组的2人为1A ,2A ,第3组的3人为1B ,2B ,3B ,第4组的1人为C , 则从6人中随机抽取2人的所有可能结果为:(1A ,2A ),(1A ,1B ),(1A ,2B ),(1A ,3B ),(1A ,C ), (2A ,1B ),(2A ,2B ),(2A ,3B ),(2A ,C ),(1B ,2B ),(1B ,3B ),(1B ,C ),(2B ,3B ),(2B ,C ),(3B ,C )共15种情况,则获奖2人均来自第2组有:(1B ,2B ),(1B ,3B ),(2B ,3B )3种情况,故获奖的2人均来自第2组的概率为51153= ……………………………12分18.(本小题满分14分)如图,四边形ABCD 是边长为1的正方形,⊥MD 平面ABCD ,⊥NB 平面ABCD ,且1==NB MD .(1)求证:CD AM ⊥; (2)求证:CN ∥平面AMD ; (3)求该几何体ABCDMN 的体积.解:(1)由已知,⊥MD 平面ABCD ,⊂CD 平面ABCDMNABCD O∴ CD MD ⊥又 ∵四边形ABCD 是正方形,AD CD ⊥D AD MD =∴ ⊥CD 平面AMD ,⊂AM 平面AMD∴ CD AM ⊥ ……………………………………………… 4分 (2)由已知,⊥MD 平面ABCD ,⊥NB 平面ABCD∴ NB ∥MD , 又 ⊂MD 平面AMD ,⊄NB 平面AMD , ∴NB ∥平面AMD 同理,BC ∥平面AMD ∵ B NB BC =∴ 平面NBC ∥平面AMD ,⊂CN 平面NBC∴ CN ∥平面AMD ……………………………………………… 9分19.(本小题满分14分)已知数列{}n a 的前n 项和为n S ,且满足121+=n n S a (*∈N n ). (1)求数列{}n a 的通项公式; (2)若n n a b 2log =,21+⋅=n n n b b c ,且数列{}n c 的前n 项和为n T ,求n T 的取值范围.解:(1)由题意,121+=n n S a (*∈N n ), ∴ 12111+=--n n S a (2≥n ,*∈N n )……………………………………1分两式相减:n n n a a a 211=--, 即12-=n n a a (2≥n ,*∈N n ) (3)分又12111+=S a , ∴ 21=a ………………………………………… 4分∴ 数列{}n a 是首项为2,公比为2的等比数列,∴ nn a 2= …………………………………………………………… 6分(2)由(1)可得,n a b nn n ===2log log 22 ………………………………… 8分∴ )211(21)2(112+-=+⋅=⋅=+n n n n b b c n n n (10)分)211111151314121311(211321+-++--++-+-+-=+++++=-n n n n c c c c c T nn n )2111(2143)2111211(21+++-=+-+-+=n n n n ………………………………… 12分∴ 431<≤n T T , 即4331<≤n T所以,n T 的取值范围为:)43,31[ (14)分20.(本小题满分14分)已知椭圆C 的两焦点为)0,1(1-F ,)0,1(2F ,并且经过点)23,1(M . (1)求椭圆C 的方程;(2)已知圆O :122=+y x ,直线l :1=+ny mx ,证明当点()n m P ,在椭圆C 上运动时,直线l 与圆O 恒相交;并求直线l 被圆O 所截得的弦长的取值范围.解:(1)解法一:设椭圆C 的标准方程为)0(12222>>=+b a by a x ,由椭圆的定义知:22224,1,3a c b a c ====-= 得 3,2==b a故椭圆C 的方程为13422=+y x . (4)分解法二:设椭圆C 的标准方程为)0(12222>>=+b a by a x ,依题意,122=-b a ①, 将点⎪⎭⎫ ⎝⎛23,1M 坐标代入得12312222=⎪⎭⎫⎝⎛+b a ② 由①②解得3,422==b a ,故C 的方程为13422=+y x . …………………………………4分(2) 圆心O 到直线1:=+ny mx l 的距离221nm d +=因为点()n m P ,在椭圆C 上运动,所以22143m n +=, 则1342222=+>+n m n m ∴ r nm d =<+=1122所以直线l 与圆O 相交. (8)分直线l 被圆O 所截的弦长为22211212nm d L +-=-=341112413112222+-=⎪⎪⎭⎫ ⎝⎛-+-=m m m ………10 分,31341141,4341340222≤+≤≤+≤∴≤≤m m m ∴3362≤≤L …………………………………………14 分 21.(本题满分14分) 已知函数x k x x f ln 21)(2⋅-=(R k ∈). (1)当2=k 时,求函数在点))1(,1(f 处的切线方程; (2)求函数)(x f 的单调区间和极值;(3)设332)(x x g =,1-=k ,当),1(+∞∈x 时,比较)(x f 与)(x g 的大小. 解:(1) 当2=k 时,x x x f ln 221)(2-=又 21)1(=f 切点为)21,1(∴ x x x f 2)(-=' 切线斜率: 1)1(-='f ………………………… 2 分∴ 切线方程:)1(21--=-x y 即 022=-+y x ………………………… 3 分(2) 由已知,函数)(x f 定义域为()+∞∈,0x , xkx x k x x f -=-='2)( …………… 4 分① 0≤k 时,0)(>'x f 在()+∞∈,0x 恒时成立,故)(x f 在()+∞∈,0x 上单调递增, 函数无极值; (5)分② 0>k 时,xk x k x x k x x k x x f ))(()(2-+=-=-=', ┅┅┅┅┅┅┅6分)(x f '、)(x f 随()+∞∈,0x 的变化情况如下表:所以,函数在),0(k 上单调递减,在),(+∞k 上单调递增, …………………8分在k x =时取到极小值:)ln 1(2ln 2121)(k kk k k k f -=⋅-=…………………10分(3)设332)(x x g =,1-=k ,当),1(+∞∈x 时,比较)(x f 与)(x g 的大小. ∵ 3232ln 21)()(x x x x g x f -+=-令 3232ln 21)(x x x x F -+=,则xx x x x x x x F )12)(1(21)(22++-=-+=' ………………………………12分∵ 1x >, ∴ 0)(<x F ', 函数)(x F 在区间(1,+∞)上单调递减. 又 061)1(<-=F , ∴ )(x F 在区间(1,+∞)上,恒有)(x F <0 即 3232ln 21x x x <+,即:)(x f <)(x g (14)分。
