第五章 异方差修正
异方差的修正方法

异方差的修正方法
异方差的修正方法有以下几种:
1. 帕克-贝克修正:通过引入一个异方差函数,根据残差与预测变量之间的关系来修正异方差。
常用的帕克-贝克修正包括指数函数和对数函数。
2. 杜宾-沃森修正:基于杜宾-沃森统计量的计算,通过对残差进行变换,使其满足异方差齐次性的假设。
3. 加权最小二乘法:根据异方差函数给不同观测值赋予不同的权重,对加权后的残差进行最小二乘估计。
4. 基于泛化最小二乘估计:通过最小化泛化最小二乘估计准则,得到异方差不相关的估计。
5. Huber-White标准误差估计:利用矩阵方法计算标准误差的估计,通过估计异方差矩阵的逆矩阵来进行修正。
这些方法的选择取决于数据的特点以及研究目的。
在实际应用中,可以通过检验异方差的存在并选择适当的修正方法来解决异方差问题。
第五章_异方差性及检验

7
(四)截面数据中总体各单位的差异 例如利用截面数据研究消费与收入的关系时,不同
情况下,无法判断是哪个变量引起的异方差。
27
三、White检验
(一)基本思想: 不需要关于异方差的任何先验信息,只需要
在大样本的情况下,将OLS估计后的残差平方对 常数、解释变量、解释变量的平方及其交叉乘积 等构成一个辅助回归,利用辅助回归建立相应的 检验统计量来判断异方差性。
28
(二)检验步骤: 以一个二元线性回归模型为例,设模型为:
( xi
)2
Xi
Var(ˆ2
)
2xi2
X
2 i
(xi2 )2
于是
Var(ˆ2 ) Var(ˆ2 )
(
2xi2
xi Xi
)2
xi2
X
2 i
由于
(
xi Xi
)2
xi2
X
2 i
(
xi Xi
xi
Xi
)
(xi2 )2
所以
Var(ˆ2 Var(ˆ2
) )
1
第五章 异方差性
1
本章讨论四个问题: ●异方差的实质和产生的原因 ●异方差产生的后果 ●异方差的检测方法 ●异方差的补救
2
第一节 异方差性的概念
一、什么是异方差性
在简单线性回归模型和多元线性回归模型的基 本假定中,有同方差假定:
第五章-4异方差的解决方法

11.58966
Log likelihood
-220.1929 F-statistic
29.21043
Durbin-Watson stat 1.149682 Prob(F-statistic) 0.000008
UnWeighted Statistics
WLS处理后的残差图
2000
Hale Waihona Puke 0-2000-4000
补救异方差的基本思路:
变异方差为同方差; 尽量缓解方差变异的程度 为了补救异方差造成的(不再具有最小方差; 参数的显著性检验失效;预 测精度降低)的严重后果
方法:
一、加权最小二乘法
二、对原模型变换的方法
三、“一般解决法”(模型的对数变换)
1、加权最小二乘法的思路
根据离差平方和最小建立起来的OLS法 同方差时:认为各 ei 提供信息的重要程度是一致的,即将各样本点提供的残差一视同仁。 异方差时:离散程度大的ei 对应的回归直线的位置很不精确,拟合直线时理应不太重视 们提供的信息。即 Xi 对应的 ei 偏离大的所提供的信息贡献应打折扣,而偏离小的所提供的 信息贡献则应于重视。因此采用权数对残差提供的信息的重要程度作一番校正,以提高估计 精度。这就是 WLS(加权最小二乘法)的思路。
1
Xi
2
ui Xi
Var
ui Xi
1
X
2 i
Var
ui
2
例2 Yi 1 2 X i ui
Var(ui)
2 i
2
X
i
Yi Xi
1
Xi
2
Xi
ui Xi
Var
ui Xi
1
X
i
庞浩 计量经济学5第五章 异方差性

同方差
递增型异方差
递减型异方差
复杂型异方差
18
2.借助X-e2散点图进行判断 观察散点的纵坐标是否随解释变量Xi的变化而 变化。
~2 e2e i ei e2 ~2
X 同方差 递增异方差
X
e2
~2 e i
~2 e 2 e i
X 递减异方差 复杂型异方差
X
19
二、戈德菲尔德—夸特 (Goldfeld-Quanadt)检验
3
说明1
矩阵表示: Y X u 随机扰动项向量 其方差—协 u1 u 方差矩阵不 2 u 再是: un n1 而是:
2 2 Var Cov ( ui ) 2 nn
ei X i v i
ei
1 vi Xi
ei X i v i 1 ei vi Xi
③利用上述回归的R2、t统计量、F统计量等判断,R2 好、t统计量和F统计量显著,即可判定存在异方差。 28
说明: 1.也可以用 e i 与可能产生异方差的多个解释变 量进行回归模拟; 2.戈里瑟检验的优点在于不仅检验了异方差是否 存在,同时也给出了异方差存在时的具体表现 形式,为克服异方差提供了方便。 3.试验模型选得不好,也可能导致检验不出是否 存在异方差性。
12 2 2 Var Cov ( ui ) 2 n nn
4
说明2
随机扰动项 ui具有异方差性,可理解释为被解释变量 的条件分散程度随解释变量的变化而变化,如下图所 示:var( ui ) i2 2 f ( X i)(i 1,2,, n)
10
第二节 异方差性的后果
5 第五章异方差性(第二版)

ˆ*) Var ( 2
( x )
2 2 x i i 2 2 i
(证明见下页)
i2 未知,也不能再用 ( ei2 ) (n 2) ˆ 2 去估计, 2 ˆ * ) 无法确定。 ( i 不再是常数), Var (
2
2、如果仍然用不存在异方差性时的OLS方式估计其 方差,即用
第五章 异 方 差 性
引子:更为接近真实的结论是什么?
根据四川省2000年21个地市州医疗机构数与人口数资 料,分析医疗机构与人口数量的关系,建立卫生医疗机 构数与人口数的回归735 X Y i i
(291.5778) (0.644284) t =(-1.931062) (8.340265)
●
第五章
异方差性
本章将讨论四个问题: ●异方差的实质和产生的原因 ●异方差产生的后果 ●异方差的检测方法 ●异方差的补救
第一节 异方差性的概念
一、异方差的实质
同方差的含义 同方差性:对所有的 i (i 1,2,..., n) 有:
Var(ui ) = σ
2
因为方差是度量被解释变量
Y
的观测值围绕回归线
● 要求为大样本 ● 不仅能够检验异方差的存在性,同时在多变量 的情况下,还能判断出是哪一个变量引起的异方 差。
White 检验在EViews上的实现(用现成命令)
设 Yt 1 2 X 2t 3 X 3t t
1)Ls Y C X2 X3 2)点击 View/residual test/White/回车; 3)在出现的对话框中,选择 no cross terms(没有交叉项) /回车或 cross terms(有交叉项)/回车 4)出现输出框(比模型输出框多2行) Test直接给出了相关的统计量(F-statistic和Obs*R-squared)
计量经济学课件:第五章-异方差性汇总
第五章异方差性本章教学要求:根据类型,异方差性是违背古典假定情况下线性回归模型建立的另一问题。
通过本章的学习应达到,掌握异方差的基本概念包括经济学解释,异方差的出现对模型的不良影响,诊断异方差的方法和修正异方差的方法。
经过学习能够处理模型中出现的异方差问题。
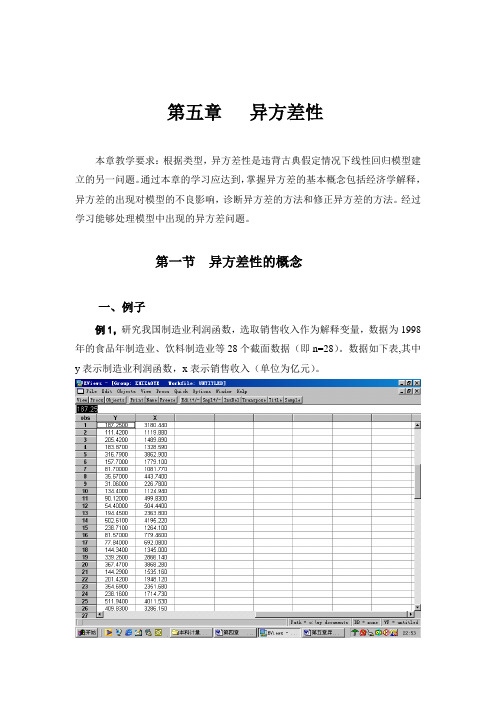
第一节异方差性的概念一、例子例1,研究我国制造业利润函数,选取销售收入作为解释变量,数据为1998年的食品年制造业、饮料制造业等28个截面数据(即n=28)。
数据如下表,其中y表示制造业利润函数,x表示销售收入(单位为亿元)。
Y对X的散点图为从散点图可以看出,在线性的基础上,有的点分散幅度较小,有的点分散幅度较大。
因此,这种分散幅度的大小不一致,可以认为是由于销售收入的影响,使得制造业利润偏离均值的程度发生了变化,而这种偏离均值的程度大小不同是一种什么现象?如何定义?如果非线性,则属于哪类非线性,从图形所反映的特征看并不明显。
下面给出制造业利润对销售收入的回归估计。
模型的书写格式为2ˆ12.03350.1044(0.6165)(12.3666)0.8547,..84191.34,152.9322213.4639,146.4905Y YX R S E FY s =+=====通过变量的散点图、参数估计、残差图,可以看到模型中(随机误差)很有可能存在一种系统性的表现。
例2,改革开放以来,各地区的医疗机构都有了较快发展,不仅政府建立了一批医疗机构,还建立了不少民营医疗机构。
各地医疗机构的发展状况,除了其他因素外主要决定于对医疗服务的需求量,而医疗服务需求与人口数量有关。
为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
根据四川省2000年21个地市州医疗机构数与人口数资料对模型估计的结果如下:i iX Y 3735.50548.563ˆ+-= (291.5778) (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表示卫生医疗机构数(个),X 表示人口数量(万人)。
第五章异方差ppt课件

f
ˆ 2
2
w i (Yˆ ( ˆ1 ˆ2 X i ))( X i ) 0
ˆ2
wi xi* yi*
w
i
x
* i
2
ˆ1 Y * ˆ 2 X *
其中, X * w i X i , Y * w iYi
wi
wi
xi*
Xi
X
* i
,
yi*
Yi
Yi*
Econometrics 2005
将是不可靠的。
Econometrics 2005
13
5.3 异方差的检验
方法有 (1)图示法( X _ e2); (2)解析法:
戈德菲尔德-匡特检验 怀特检验 ARCH检验
Econometrics 2005
14
5.3.1 图示法及其类型
1. 异方差指u的方差随着x的变化而变化。 2. 故可以根据x-e2的散点图,对异方差是否
Y的预测值的精度降低;
2
(2)由于 i 难以确定, Y的方差也就难以确定, Y
的预测区间的确定也出 现困难;
2
(3)在 = ei2 /( n k )是 2的无偏的证明中用到了
2
同方差的假定,由于异 方差性,使得 = ei2 /( n k )
是有偏的。在此区间估 计基础上区间估计和假 设检验
基本思路:
(以二元回归为例Y:t 1 2 X2t 3X3t ut)
如果有异方差,则i2与解释变量有关系。:如
i2=0
1X2i
3 X3i
2
X
2 2i
4 X32i
5 X2i
X3i+vi
但是i2一般未知,用模型回剩归余ei2作为i2的渐进
第5章 异方差性

5、计算统计量:
RSS2
F
nc ( k 1) nc nc 2 ~ F( k 1, k 1) RSS1 2 2 nc ( k 1) 2
6、在给定的显著性水平下比较判断。
注意: (1) 当模型含有多个解释变量时,应以每一个解释变 量为基准检验异方差。 (2)对于截面样本,计算F统计量之前,必须先把数据 按解释变量的值从小到大排序。 (3)G—Q检验仅适用于检验递增或递减型异方差。 (4)检验结果与数据剔除个数c的选取有关。 (5) G—Q检验无法判定异方差的具体形式。
5.2异方差性的后果
5.2.1对模型参数估计值无偏性的影响
以简单线性回归模型为例,对模型 yt = b0 + b1 xt + ut ˆ 当Var(ut) = t 2,为异方差时,以 b1 为例:
ˆ b1
k
t
yt b1 kt ut
ˆ E (b1 ) E (b1 kt ut ) b1
划分方法是: 把成对(组)的观测值按解释变量的大小顺序排列, 略去c个处于中心位置的观测值 (通常n 30时,取c n/ 4), 余下的n- c个观测值自然分成容量相等,(n- c) / 2的两 个子样本。
{x1, x2, …, xt-1, xt, xt+1, …, x n-1, xn}
n1 = (n-c) / 2
5.2.3对模型参数估计值显著性检验的影响
ee ˆ 并非随机误差项 在异方差情况下, n k 1 方差的无偏估计量。
2
ˆ 导致在此基础上估计的 s ( b j ) 也出现偏误。
ˆ bj 而变量的显著性检验中,构造了t统计量 t ˆ s(b j )
变量的显著性检验失去意义。
第五章第四节 异方差的解决方法

(5)权数的选择(**)
• 一般地,Wi=1/2i。问题在于:2i一般是未知的 • 关键:找出ui随着Xi的变化而变化的规律,对异方差
Var(ui)= 2i = 2 f( Xi )( i=1,2,…,n)的具体形式作出 合理假设。
• 怎样才能提出合理的假设呢? (1)通过对具体经济问题的经验分析,或 (2)考察OLS的ei2与Xi的关系,或 (3)通过White等检验的结果提供的信息 • 粗略做法: Wi =1/|ei|或1/ ei2 ,ei是OLS估计的残差 • 所以,利用WLS的思路是:寻找合适的“权数”,
4.WLS法在eviews中的实现
1.创建文件:File/New/Workfile/输入数据频率/Ok 2.输入数据:在主菜单,点quick / empty group/输入变量
名称和数值/ 3.产生新序列:在eviews栏,点quick/generate series/输
入w=1/sqr(x),点ok(假设w=1/sqr(x) 4.作回归:在eviews栏,点quick/ estimate equation/键入
变量和常数[如y c x],同时点右下方的option,选择 Weighted LS/TLS,键入w,点ok
同质性 权数序列名
二、对原模型变换的方法
1、模型变换法的定义
模型变换法是对存在异方差的总体回归模型作适当的代数变换,使之成为满足同方 差假定的模型 , 进而运用OLS方法估计参数。
2、模型变换法的关键是: 通过对具体经济问题的经验分析,事先对异方差
往往有较小的差异。
利用EViews对模型进行对数变换
例 ln Yi 1 2 ln Xi ui 在eviews栏,点quick/generate series/输入 LY=LOG(Y) 在eviews栏,点quick/generate series/输入 LX=LOG(X)
第五章-异方差性-答案说课讲解

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T )二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B )A. B. C. D. 7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模型时,应将模型变换为( C )。
计量经济学 第五章习题答案
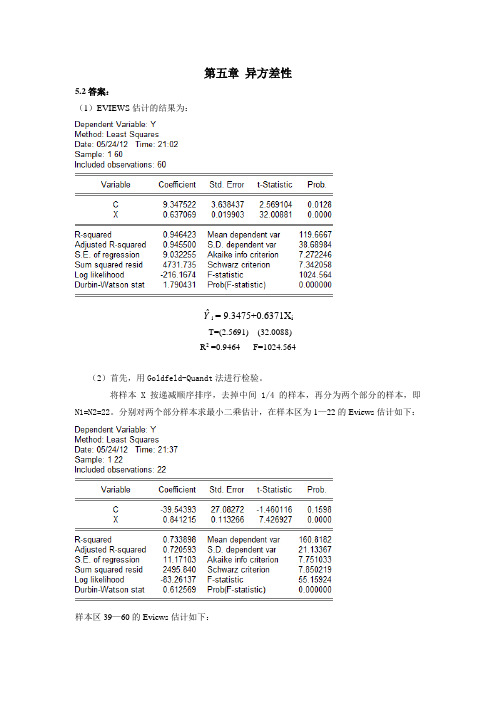
第五章异方差性5.2答案:(1)EVIEWS估计的结果为:Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564(2)首先,用Goldfeld-Quandt法进行检验。
将样本X按递减顺序排序,去掉中间1/4的样本,再分为两个部分的样本,即N1=N2=22。
分别对两个部分样本求最小二乘估计,在样本区为1—22的Eviews估计如下:样本区39—60的Eviews估计如下:得到两个部分各自的残差平方和,即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为: F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05,查F 分布表,得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值,有F =4.1390>F 0.05=(20,20)=2.12,说明该模型的随机误差项存在异方差。
其次,用White 法进行检验结果如下:给定α=0.05,在自由度为2下查卡方分布表,得χ2=5.9915。
比较临界值与卡方统计量值,即nR2=10.8640>χ2=5.9915,同样说明模型中的随机误差项存在异方差。
(2)用权数W1=1/X,作加权最小二乘估计,得如下结果用White法进行检验得如下结果:F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。
比较临界值与卡方统计量值,即nR2=5.9519<χ2=5.9915,说明加权后的模型中的随机误差项不存在异方差。
其估计的结果为:Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案:(1)EVIEWS估计结果:Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 (2)利用White方法检验异方差,则White检验结果见下表:由上述结果可知,该模型存在异方差。
计量经济学第五章 异方差

X 20000
5.3异方差的侦查
利用残差图——绘制残差平方与X散点图
(一般把异方差看成是由于解释变量的变化而引起的)
5.1异方差的概念
三、异方差产生的原因 模型设定误差:省略了重要的解释变量
例:真实模型 Yi 1 2 X 2i 3 X 3i i 采用模型 Yi 1 2 X 2i i
如果X3随着X2的不同而对Y产生不同的影响,则 该影响体现在扰动项中。
测量误差: 一方面,测量误差常常在一定时间内逐渐增加,如X 越大,测量误差就会趋于增大 另一方面,测量误差随时间变化趋于减少,如抽样技 术的改进使得测量误差减少。
)
2 i
5.1异方差的概念
6 Y
4
300 Y
200
2
100
0 0
X
0
X
10
20
30
0
5000
10000
15000
20000
250
Y
二、常见的异方差类型: 200
递增型异方差:
150
100
递减型异方差:
50
条件异方差(略):
0 0
X
10
20
30
时间序列数据和截面数据中都有可能存在异方差。
经济时间序列中的异方差常为递增型异方差。
ˆ 2 ei2 (Yi ˆX i )2 (( ˆ) X i i )2
n 1
n 1
n 1
5.2异方差的后果
E (vaˆr(ˆ ))
E(
ˆ 2
X
2 i
)
E(
(( ˆ)X
(n 1)
异方差的修正方法

异方差的修正方法在统计学和经济学中,异方差是指误差项的方差不是恒定的情况。
当误差项的方差不恒定时,会对统计分析结果产生影响,导致参数估计的不准确性。
因此,需要对异方差进行修正,以确保统计分析结果的准确性和可靠性。
异方差的修正方法主要包括加权最小二乘法(Weighted Least Squares, WLS)、异方差稳健标准误(Heteroscedasticity-Robust Standard Errors)和异方差稳健回归(Heteroscedasticity-Robust Regression)。
这些方法能够有效地处理异方差的问题,提高了统计分析结果的准确性。
加权最小二乘法是一种常用的异方差修正方法。
它通过赋予观测值不同的权重,对方差不恒定的数据进行加权处理,从而得到更为准确的参数估计值。
加权最小二乘法的核心思想是将方差不恒定的数据进行加权,使得方差较大的数据点在估计过程中起到较小的作用,从而降低了异方差对参数估计的影响。
另一种常用的异方差修正方法是异方差稳健标准误。
在普通最小二乘法中,通常假设误差项的方差是恒定的,但当误差项的方差不恒定时,普通最小二乘法的标准误就会产生偏误。
异方差稳健标准误通过对标准误进行修正,考虑了误差项方差的不恒定性,从而得到更为准确的统计推断结果。
此外,异方差稳健回归也是一种常用的异方差修正方法。
它通过对残差进行加权,从而得到更为准确的参数估计值。
异方差稳健回归在实际应用中具有较强的鲁棒性,能够有效地处理异方差的问题,提高了回归分析的准确性和可靠性。
总的来说,针对异方差的修正方法有多种选择,可以根据具体情况进行合理选择。
在进行统计分析时,需要对数据是否存在异方差进行检验,并采用适当的异方差修正方法,以确保统计分析结果的准确性和可靠性。
异方差的修正方法在实际应用中具有重要的意义,对于提高统计分析的准确性和可靠性具有重要作用。
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
第5章课程论文异方差性的检验和补救
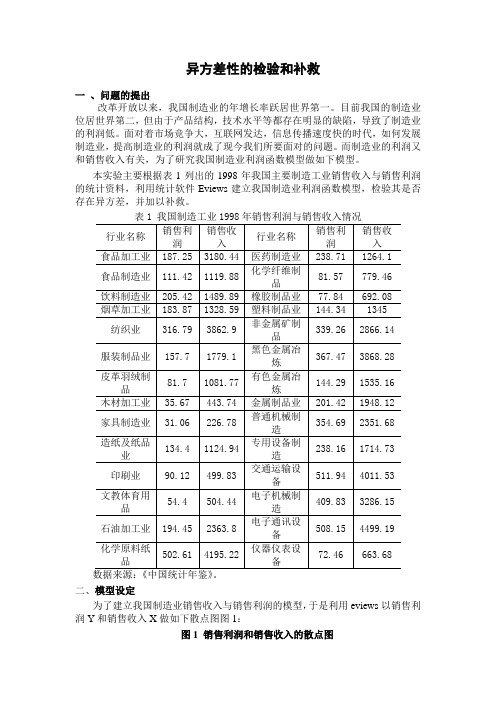
异方差性的检验和补救一、问题的提出改革开放以来,我国制造业的年增长率跃居世界第一。
目前我国的制造业位居世界第二,但由于产品结构,技术水平等都存在明显的缺陷,导致了制造业的利润低。
面对着市场竞争大,互联网发达,信息传播速度快的时代,如何发展制造业,提高制造业的利润就成了现今我们所要面对的问题。
而制造业的利润又和销售收入有关,为了研究我国制造业利润函数模型做如下模型。
本实验主要根据表1列出的1998年我国主要制造工业销售收入与销售利润的统计资料,利用统计软件Eviews建立我国制造业利润函数模型,检验其是否存在异方差,并加以补救。
表1 我国制造工业1998年销售利润与销售收入情况行业名称销售利润销售收入行业名称销售利润销售收入食品加工业187.25 3180.44 医药制造业238.71 1264.1食品制造业111.42 1119.88 化学纤维制品81.57 779.46饮料制造业205.42 1489.89 橡胶制品业77.84 692.08 烟草加工业183.87 1328.59 塑料制品业144.34 1345纺织业316.79 3862.9 非金属矿制品339.26 2866.14服装制品业157.7 1779.1 黑色金属冶炼367.47 3868.28皮革羽绒制品81.7 1081.77有色金属冶炼144.29 1535.16木材加工业35.67 443.74 金属制品业201.42 1948.12家具制造业31.06 226.78 普通机械制造354.69 2351.68造纸及纸品业134.4 1124.94专用设备制造238.16 1714.73印刷业90.12 499.83 交通运输设备511.94 4011.53文教体育用品54.4 504.44电子机械制造409.83 3286.15石油加工业194.45 2363.8 电子通讯设备508.15 4499.19化学原料纸品502.61 4195.22仪器仪表设备72.46 663.68数据来源:《中国统计年鉴》。
计量经济学 第五章 异方差 ppt课件

H0:ut不存在异方差, H1:ut存在异方差。
10
5.4 异方差检验
(2) White检验
④在同方差假设条件下,统计量
TR 2 2(5)
其中T表示样本容量,R2是辅助回归式的OLS估计的可决系数。 自由度5表示辅助回归式中解释变量项数(注意,不计算常数 项)。T R 2属于LM统计量。 ⑤判别规则是
2
1
0
-1
1
0 20 40 60 80 100 120 140 160 180 200
-2
-3 0
T
50
100
150
200
散点图
残差图
7
5.4 异方差检验
(1) Goldfeld-Quandt 检验
H0: ut 具有同方差, H1: ut 具有递增型异方差。
①把原样本分成两个子样本。具体方法是把成对(组)的观 测值按解释变量顺序排列,略去m个处于中心位置的观测值 (通常T 30时,取m T / 4,余下的T- m个观测值自然分成 容量相等,(T- m) / 2,的两个子样本。)
主对角线上的部分或全部元素都不为零,误差项就是自相关的。
异方差通常有三种表现形式,(1)递增型,(2)递减型,(3)条件自回
归型。 7
Байду номын сангаас
6
Y 6
4
DJ P Y
5
2
4
0
3
-2
2
-4
1
-6
0 20 40 60 80 100 120 140 160 180 200
-8
异方差

第一节 异方差的概念
例:以某一行业的企业为样本建立企业生产函数模 型 Yi=Ai1 Ki2 Li3ei 被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不同 ,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量观 测值的变化而呈规律性变化,呈现复杂型。
第三节 异方差性的检验
三、戈里瑟(Gleiser)检验 1969年戈里瑟提出的,它不但可以检验异方差是 否存在,而且可以近似探测随机误差项的方差是 怎样随解释变量的变化而变化的。 基本思想:由OLS法得到残差 e i ,取 e i 的绝对 值 ,然后将 对某个 X i回归,根据回归模 ei ei 型的显著性和拟合优度来判断是否存在异方差。
二、异方差性的后果
ˆ
2
e
2 i
n2
ˆ s(1 )
ˆ ki
2
2
ˆ2
(Xi X )
2
但是,在异方差的情况下
ˆ* s( i ) ˆ ki i
2 2
ˆ i ki
2 2
ˆ ki
2
2
i ki ki
2
2
=
ˆ s(i )
i Байду номын сангаасi
第三节 异方差性的检验
第五章第三节 异方差性的检验

3、 G-Q检验具体步骤
(1)将样本(观察值)按某个解释变量的大小排序;
(2)将序列中间(段)约 c = 1 / 4 个观察值除去,并使余下的头、尾两段样本容量相同,均为(n-c)/2 个;(3)提出假设:
H0 : ui为同方差; H1:ui为异方差
(4)分别对头、尾两部分样本进行回归,且计算各残差平方和分别为
对(2)式进行回归
R2
a) H0 : 1 2 P H1 : 至少一个i 0
三、Glejser (格里瑟)检验(选学)
四、Breusch—Pagan (布鲁士—佩格)检验(选学) 五、White(怀特)检验 六、ARCH检验
除了图示法以外的检验方法都是构造统计量 实施检验,称为解析法
共同思路
• 异方差性,是相对于不同的样本点,即相对于不 同的X观测值, ui具有不同的方差
ei2
图形分析法是利用残差序列绘制出各种图形,以供分析检验使用。 包括:
1、解释变量为X 轴,残差的平方ei 2 为Y轴的 散点图。
2.解释变量为X 轴,被解释变量为Y轴的X-Y散点图
异方差的类型大致可以分为递增异方差、递减异方差、 复杂异方差三种。 用Y X 作散点图的区域逐渐变宽、变窄、不规则变化, 认为存在异方差; 用ei2 X 作散点图上e2并不近似于某一常数, 则认为存在异方差。
(2)求出残差et , 进而求出et2
(3)估计et2
0
1 X 2t
2 X3t
3
X
2 2t
4
X
2 3t
5 X2t
X 3t
t
(4)针对上述模型作回归,并计算统计量nR2。其中:n为样本
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i的方差呈现单调递增型变化
以绝对收入假设为理论假设、以截面数据为样本 建立居民消费函数:
Ci=0+1Yi+i
将居民按照收入等距离分成n组,取组平均 数为样本观测值。
一般情况下,居民收入服从正态分布:中等收 入组人数多,两端收入组人数少。而人数多的 组平均数的误差小,人数少的组平均数的误差 大。
◆如果 ui 随 Xi 而变化,则表明存在异方差。
3 0
e~i 2
e~i 2
X 同方差
X 递增异方差
e~i 2
e~i 2
X 递减异方差
X 复杂型异方差
作用:检验递增性(或递减性)异方差。
2 i
2
X
2 i
,
是常数。X
i
值越大,
2 i
值也越大
基本思想:将样本分为两部分,然后分别对两个样
本进行回归,并计算两个子样的残差平方和所构成
的比,以此为统计量来判断是否存在异方差。
(一) 检验的前提条件 1、要求检验使用的为大样本容量。 2、除了同方差假定不成立外,其它假定均满足。
3 2
1.排序 将解释变量的取值按从小到大排序。
2.数据分组 将排列在中间的约1/4的观察值删除掉,记
为 c ,再将剩余的分为两个部分,每部分观察
值的个数为 (n - c) / 2 。
^
E( ) E[ ( X ' X )1 X 'u] E( )
2 2
(二)参数估计的方差不再是最小的 同方差假定是OLS估计方差最小的前提条件,所 以随机误差项是异方差时,将不能再保证最小二 乘估计的方差最小。
COV ( βˆ) E{[ βˆ E( βˆ)][ βˆ E( βˆ)]}
(三)数据的测量误差
样本数据的观测误差有可能随研究范围的扩大
而增加,或随时间的推移逐步积累,也可能随
着观测技术的提高而逐步减小。
1 8
(四)截面数据中总体各单位的差异 通常认为,截面数据较时间序列数据更容易产 生异方差。这是因为同一时点不同对象的差异, 一般说来会大于同一对象不同时间的差异。不过, 在时间序列数据发生较大变化的情况下,也可能 出现比截面数据更严重的异方差。
所以样本观测值的观测误差随着解释变量观测 值的不同而不同,往往引起异方差性。
较高收入的家庭比低收入家庭有更多的储蓄,并在储蓄过程中有更多的 变异/ 家庭的支出模式
异方差的现实情境:
(1) 边错边改学习模型。随着打字练习,出错(误差会减少) (2)随着备用收入的增加,人们支配他们的收入有着更多的选择范围 (3)异常值的出现。和其他值相比,非常大或非常小。包括或不包括 这样一个观测值,尤其是在样本很小的时候,会改变样本回归的结果。 (4) 分布偏态问题( skewness)一个或多个回归元的分布偏态,大多 数社会中收入和财富的分配都是不对称的,处在顶端少数几个人拥有大 部分的收入和财富。
2 4
尽管参数的OLS估计量仍然无偏,并且基于此的 预测也是无偏的,但是由于参数估计量不是有效 的,从而对Y的预测也将不是有效的。
所以,当模型出现异方差性时,参数OLS 估计值的变异程度增大,从而造成对Y的预测 误差变大,降低预测精度,预测功能失效。
2 5
常用检验方法:
●图示检验法 ● Goldfeld-Quanadt检验 ● White检验 ● ARCH检验
E[( βˆ β)( βˆ β)]
Hale Waihona Puke E[( X X )1 X uuX (X X )1]
( X X )1 X E(uu) X ( X X )1
( X X )1 X 2WX ( X X )1
E(uu) 2In
由于异方差的影响,使得无法正确估计参数的标 准误差,导致参数估计的 t 统计量的值不能正确 确定,所以,如果仍用 t 统计量进行参数的显著 性检验将失去意义。
3 9
(二)检验的特点 要求变量的取值为大样本 不仅能够检验异方差的存在性,同时在多变量的 情况下,还能判断出是哪一个变量引起的异方差。 怀特检验并不要求排序,也不依赖正态性假定。
4 0
(三)检验的基本步骤:
以一个二元线性回归模型为例,设模型为:
Yt = β1 + β2 X 2t + β3 X3t +ut 并且,设异方差与 X 2t , X3t 的一般关系为
3.提出假设
H0 : σi2 = σ 2,i = 1, 2,..., n;
H1
:
σ12
σ
2 2
...
σ
2 n
3 3
4.构造F统计量 分别对上述两个部分的观察值求回归模型,由此
得到的两个部分的残差平方为 和 e12i 。 e22i e12i 为前一部分样本回归产生的残差平方和, e22i 为后一部分样本回归产生的残差平方和。它 们的自由度均为 [(n - c) / 2] - k ,k 为参数的个数。
异方差:
i2 = f(Xi)
异方差一般可归结为三种类型:
(1)单调递增型: i2随X的增大而增大 (2)单调递减型: i2随X的增大而减小 (3)复 杂 型: i2与X的变化呈复杂形式
实际经济问题中的异方差性
截面资料下研究居民家庭的储蓄行为:
Yi=0+1Xi+i Yi:第i个家庭的储蓄额 Xi:第i个家庭的可支配收入。
Var(ui ) = σ 2
(5.1)
因为方差是度量被解释变量 Y的观测值围绕回归线
E(Yi ) 1 2 X 2i 3X3i ... k X ki (5.2)
的分散程度,因此同方差性指的是所有观测值的
分散程度相同。
6
设模型为
Yi 1 2 X2i 3 X3i ... k X ki ui i 1, 2,..., n
发支出等因素。
每个企业所处的外部环境对产出量的影响 程度不同,造成了随机误差项的异方差性。
这时,随机误差项的方差并不随某一个解 释变量观测值的变化而呈规律性变化,呈现 复杂型。
二、产生异方差的原因
(一)模型中省略了某些重要的解释变量 假设正确的计量模型是:
Yi 1 2 X 2i 3 X3i ui
(三)检验的特点
●要求大样本 ●异方差的表现既可为递增型,也可为递减型
●检验结果与选择数据删除的个数 c 的大小有关
●只能判断异方差是否存在,在多个解释变量的 情下,对哪一个变量引起异方差的判断存在局限。
3 8
(一)基本思想: 不需要关于异方差的任何先验信息,只需要在大 样本的情况下,将OLS估计后的残差平方对常数、 解释变量、解释变量的平方及其交叉乘积等所构 成一个辅助回归,利用辅助回归建立相应的检验 统计量来判断异方差性。
2 0
本节基本内容:
●对参数估计统计特性的影响 ●对参数显著性检验的影响 ●对预测的影响
2 1
(一)参数估计的线性性仍然满足 (二)参数估计的无偏性仍然满足
参数估计的无偏性仅依赖于基本假定中的零均值 假定(即 E(ui ) 0)。所以异方差的存在对无偏性 的成立没有影响。
ˆ ( X X )1 X Y ( X X )1 X ( Xβ + u) β ( X X )1 X u
用X-Y 的散点图进行判断看 是否存在明显的散点扩大、 缩小或复杂趋势(即不在一
个固定的带型域中)
2 9
设一元线性回归模型为: Yi β1 β2 X i ui
运用OLS法估计,得样本回归模型为: Yˆi = βˆ1 + βˆ2 Xi
由上两式得残差: ei Yi -Yˆi
绘制出 ei2 对 X i的散点图 ◆如果 ui 不随 Xi 而变化,则表明不存在异方差;
假如略去 X3i ,而采用
Yi 1 2 X 2i ui*
(5u.i*5) X3i
当被略去的
X
与
3i
X 2i 有呈同方向或反方向变
化的趋势时,随 X2i 的有规律变化会体现在(5.5)
式的
u
* i
中。
1 7
(二)模型的设定误差
模型的设定主要包括变量的选择和模型数学形式的确定。 模型中略去了重要解释变量常常导致异方差,实际就是模型 设定问题。除此而外,模型的函数形式不正确,如把变量间 本来为非线性的关系设定为线性,也可能u导i* 致异方差X3。i
式中 Y表示卫生医疗机构数(个),X 表示人口数量
(万人)
人口数量对应参数的标准误差较小;
t统计量远大于临界值,可决系数和修正的可决系 数结果较好,F检验结果明显显著; 表明该模型的估计效果不错,可以认为人口数量
每增加1万人,平均说来医疗机构将增加5.3735 人。
然而,这里得出的结论可能是不可靠的,平均说 来每增加1万人口可能并不需要增加这样多的医疗 机构,所得结论并不符合真实情况。
σt2
=
α1
+
α2
X
2t
+
α3
X
3t
+
α4
X
2 2t
+
α5
X
2 3t
+
α6
X
2t
X
3t
+
vt
其中 vt 为随机误差项。
4 1
1.求回归估计式并计算 et2
用OLS估计式(5.14),计算残差
差的平方 et2 。
et
Yt
-Yˆt
,并求残
2.求辅助函数
用残差平方
et2
作为异方差
