第五章 异 方 差
第五章 异方差性

26
异方差性的检验
问题在于用什么来表示随机误差项的方差 一般的处理方法:
Var(ui ) E(uቤተ መጻሕፍቲ ባይዱ2) ei2
图示检验法
图示检验法
(一)相关图形分析 方差描述的是随机变量取值的(与其均值的)离散程度。因为被解释
变量Y与随机误差项u有相同的方差,所以分析Y与X的相关图,可以初 略地看到Y的离散程度与X之间是否有相关关系。
ui 的某些分布特征,可通过残差 ei 的图形对异方差进行观察。
对于一元回归模型,绘制出ei2 对Xi的散点图,对于多元回归模型,绘制出ei2 对Yi的散点图或ei2 与认为和异方差有关的X的散点图。
31
图示检验法
(二)残差图形分析
e~i 2
e~i 2
X 同方差
e~i 2
X 递增异方差
e~i 2
X 递减异方差
每个企业所处的外部环境对产出量的影响被包含在随机误差项中 每个企业所处的外部环境对产出量的影响程度不同,造成了随机
误差项的异方差性
产生异方差性的原因
产生异方差性的原因
(一)模型设定误差
假设正确的模型是:
Yi 1 2 X2i 3 X3i ui
假如略去了重要的解释变量X3 ,而采用 Yi 1 2 X2i vi
排序,再按戈德菲尔德匡特检验方法回归,否则即使存在异方差,也有可能用戈德菲
尔德匡特方法检验不出来。
用 EViews 给截面数据排序的方法:在 Workfile 窗口点击 Procs 键并选 Sort current page
功能,在打开的 Sort Workfile Series 对话窗填写以哪一个序列为标准(基准序列)排
第五章异方差ppt课件

f
ˆ 2
2
w i (Yˆ ( ˆ1 ˆ2 X i ))( X i ) 0
ˆ2
wi xi* yi*
w
i
x
* i
2
ˆ1 Y * ˆ 2 X *
其中, X * w i X i , Y * w iYi
wi
wi
xi*
Xi
X
* i
,
yi*
Yi
Yi*
Econometrics 2005
将是不可靠的。
Econometrics 2005
13
5.3 异方差的检验
方法有 (1)图示法( X _ e2); (2)解析法:
戈德菲尔德-匡特检验 怀特检验 ARCH检验
Econometrics 2005
14
5.3.1 图示法及其类型
1. 异方差指u的方差随着x的变化而变化。 2. 故可以根据x-e2的散点图,对异方差是否
Y的预测值的精度降低;
2
(2)由于 i 难以确定, Y的方差也就难以确定, Y
的预测区间的确定也出 现困难;
2
(3)在 = ei2 /( n k )是 2的无偏的证明中用到了
2
同方差的假定,由于异 方差性,使得 = ei2 /( n k )
是有偏的。在此区间估 计基础上区间估计和假 设检验
基本思路:
(以二元回归为例Y:t 1 2 X2t 3X3t ut)
如果有异方差,则i2与解释变量有关系。:如
i2=0
1X2i
3 X3i
2
X
2 2i
4 X32i
5 X2i
X3i+vi
但是i2一般未知,用模型回剩归余ei2作为i2的渐进
第5章 异方差性

5、计算统计量:
RSS2
F
nc ( k 1) nc nc 2 ~ F( k 1, k 1) RSS1 2 2 nc ( k 1) 2
6、在给定的显著性水平下比较判断。
注意: (1) 当模型含有多个解释变量时,应以每一个解释变 量为基准检验异方差。 (2)对于截面样本,计算F统计量之前,必须先把数据 按解释变量的值从小到大排序。 (3)G—Q检验仅适用于检验递增或递减型异方差。 (4)检验结果与数据剔除个数c的选取有关。 (5) G—Q检验无法判定异方差的具体形式。
5.2异方差性的后果
5.2.1对模型参数估计值无偏性的影响
以简单线性回归模型为例,对模型 yt = b0 + b1 xt + ut ˆ 当Var(ut) = t 2,为异方差时,以 b1 为例:
ˆ b1
k
t
yt b1 kt ut
ˆ E (b1 ) E (b1 kt ut ) b1
划分方法是: 把成对(组)的观测值按解释变量的大小顺序排列, 略去c个处于中心位置的观测值 (通常n 30时,取c n/ 4), 余下的n- c个观测值自然分成容量相等,(n- c) / 2的两 个子样本。
{x1, x2, …, xt-1, xt, xt+1, …, x n-1, xn}
n1 = (n-c) / 2
5.2.3对模型参数估计值显著性检验的影响
ee ˆ 并非随机误差项 在异方差情况下, n k 1 方差的无偏估计量。
2
ˆ 导致在此基础上估计的 s ( b j ) 也出现偏误。
ˆ bj 而变量的显著性检验中,构造了t统计量 t ˆ s(b j )
变量的显著性检验失去意义。
计量经济学第五章异方差性
计量经济学第五章异⽅差性第五章异⽅差性本章教学要求:根据类型,异⽅差性是违背古典假定情况下线性回归模型建⽴的另⼀问题。
通过本章的学习应达到,掌握异⽅差的基本概念包括经济学解释,异⽅差的出现对模型的不良影响,诊断异⽅差的⽅法和修正异⽅差的若⼲⽅法。
经过学习能够处理模型中出现的异⽅差问题。
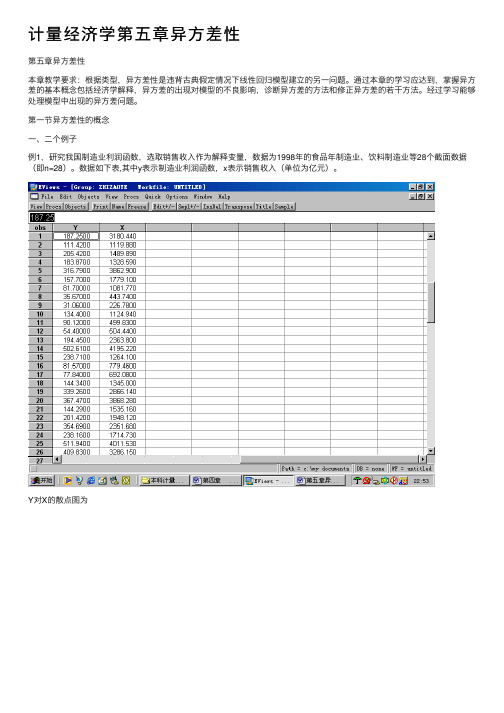
第⼀节异⽅差性的概念⼀、⼆个例⼦例1,研究我国制造业利润函数,选取销售收⼊作为解释变量,数据为1998年的⾷品年制造业、饮料制造业等28个截⾯数据(即n=28)。
数据如下表,其中y表⽰制造业利润函数,x表⽰销售收⼊(单位为亿元)。
Y对X的散点图为从散点图可以看出,在线性的基础上,有的点分散幅度较⼩,有的点分散幅度较⼤。
因此,这种分散幅度的⼤⼩不⼀致,可以认为是由于销售收⼊的影响,使得制造业利润偏离均值的程度发⽣变化,⽽偏离均值的程度⼤⼩的不同,就是所谓的随机误差的⽅差存在变异,即异⽅差。
如果⾮线性,则属于哪类⾮线性,从图形所反映的特征看,并不明显。
下⾯给出制造业利润对销售收⼊的回归估计。
模型的书写格式为212.03350.1044(0.6165)(12.3666)0.8547,..56.9046,152.9322213.4639,146.4905Y Y X R S E F Y s =+=====通过变量的散点图、参数估计、残差图,可以看到模型中(随机误差)很有可能存在异⽅差性。
例2,改⾰开放以来,各地区的医疗机构都有了较快发展,不仅政府建⽴了⼀批医疗机构,还建⽴了不少民营医疗机构。
各地医疗机构的发展状况,除了其他因素外主要决定于对医疗服务的需求量,⽽医疗服务需求与⼈⼝数量有关。
为了给制定医疗机构的规划提供依据,分析⽐较医疗机构与⼈⼝数量的关系,建⽴卫⽣医疗机构数与⼈⼝数的回归模型。
根据四川省2000年21个地市州医疗机构数与⼈⼝数资料对模型估计的结果如下:i iX Y 3735.50548.563?+-= (291.5778) (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表⽰卫⽣医疗机构数(个),X 表⽰⼈⼝数量(万⼈)。
第五章第四节 异方差的解决方法

(5)权数的选择(**)
• 一般地,Wi=1/2i。问题在于:2i一般是未知的 • 关键:找出ui随着Xi的变化而变化的规律,对异方差
Var(ui)= 2i = 2 f( Xi )( i=1,2,…,n)的具体形式作出 合理假设。
• 怎样才能提出合理的假设呢? (1)通过对具体经济问题的经验分析,或 (2)考察OLS的ei2与Xi的关系,或 (3)通过White等检验的结果提供的信息 • 粗略做法: Wi =1/|ei|或1/ ei2 ,ei是OLS估计的残差 • 所以,利用WLS的思路是:寻找合适的“权数”,
4.WLS法在eviews中的实现
1.创建文件:File/New/Workfile/输入数据频率/Ok 2.输入数据:在主菜单,点quick / empty group/输入变量
名称和数值/ 3.产生新序列:在eviews栏,点quick/generate series/输
入w=1/sqr(x),点ok(假设w=1/sqr(x) 4.作回归:在eviews栏,点quick/ estimate equation/键入
变量和常数[如y c x],同时点右下方的option,选择 Weighted LS/TLS,键入w,点ok
同质性 权数序列名
二、对原模型变换的方法
1、模型变换法的定义
模型变换法是对存在异方差的总体回归模型作适当的代数变换,使之成为满足同方 差假定的模型 , 进而运用OLS方法估计参数。
2、模型变换法的关键是: 通过对具体经济问题的经验分析,事先对异方差
往往有较小的差异。
利用EViews对模型进行对数变换
例 ln Yi 1 2 ln Xi ui 在eviews栏,点quick/generate series/输入 LY=LOG(Y) 在eviews栏,点quick/generate series/输入 LX=LOG(X)
第五章-异方差性-答案说课讲解

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T )二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B )A. B. C. D. 7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模型时,应将模型变换为( C )。
计量经济学第五章 异方差

X 20000
5.3异方差的侦查
利用残差图——绘制残差平方与X散点图
(一般把异方差看成是由于解释变量的变化而引起的)
5.1异方差的概念
三、异方差产生的原因 模型设定误差:省略了重要的解释变量
例:真实模型 Yi 1 2 X 2i 3 X 3i i 采用模型 Yi 1 2 X 2i i
如果X3随着X2的不同而对Y产生不同的影响,则 该影响体现在扰动项中。
测量误差: 一方面,测量误差常常在一定时间内逐渐增加,如X 越大,测量误差就会趋于增大 另一方面,测量误差随时间变化趋于减少,如抽样技 术的改进使得测量误差减少。
)
2 i
5.1异方差的概念
6 Y
4
300 Y
200
2
100
0 0
X
0
X
10
20
30
0
5000
10000
15000
20000
250
Y
二、常见的异方差类型: 200
递增型异方差:
150
100
递减型异方差:
50
条件异方差(略):
0 0
X
10
20
30
时间序列数据和截面数据中都有可能存在异方差。
经济时间序列中的异方差常为递增型异方差。
ˆ 2 ei2 (Yi ˆX i )2 (( ˆ) X i i )2
n 1
n 1
n 1
5.2异方差的后果
E (vaˆr(ˆ ))
E(
ˆ 2
X
2 i
)
E(
(( ˆ)X
(n 1)
计量经济学第五章 异方差性

●异方差性的概念 ●异方差产生的后果 ●异方差的检测方法 ●异方差的补救
1
第一节 异方差性的概念
一、异方差性的实质 二、异方差产生的原因
2
一、异方差性的实质
设模型为
Yi 1 2 X 2i 3 X3i ... k X ki ui
如果对于模型中随机误差项,有:
8
第二节 异方差性的后果
一、对参数估计统计特性的影响 二、对参数显著性检验的影响 三、对预测的影响
9
一、对参数估计式统计特性的影响
1、仍然具有线性性 2、仍然具有无偏性
参数估计的无偏性仅依赖于基本假定中的零 均值 假定(即 E(ui ) 0 )。所以异方差的存在对 无偏性的成立没有影响。
3、仍然具有一致性 4、不再具有最小方差性
24
4、检验的特点
(1)适用于大样本; (2)检验递增型或递减型异方差; (3)只能判断异方差是否存在,在多个解释变 量的情下,对哪一个变量引起异方差的判断存在局 限; (4)该检验的功效取决于C,C值越大,检验功 效越好; Continued
25
Continued (5)两个子样回归所用的观测值个数如果不 相等时,也可以用该检验,需要通过改变自由度 和统计量的计算公式来调整; (6)当模型中包含多个解释变量时,应对每 个可能引起异方差的解释变量都进行检验。
26
三、White检验
1、基本思想:
构造残差平方序列与解释变量之间的辅助函 数,通过判断辅助函数的显著性来判断原方程是 否存在异方差。 一般而言,辅助回归的解释变量包括常数项、 原模型中的解释变量、解释变量平方、其交叉乘 积。
27
2、检验的基本步骤:
原模型为
第五章异方差性

∑
2
ˆ σ 2 = ∑ ei2 n − k 是有偏的,在此基础上的区间估 是有偏的,
计和假设检验都将不可靠。 计和假设检验都将不可靠。
第三节 异方差性的检验
一. 图形分析法
基本思想: 基本思想: 异方差性的表现是 u i 的方差随某个解释变量的变 化而变化, 的分散程度随X的变化而变化 化而变化 , 或 Y的分散程度随 的变化而变化 。 因此可 的分散程度随 的变化而变化。 与某解释变量的散布图, 利用 u i 的代表 ei 与某解释变量的散布图,观察是否存 在异方差及其异方差的形式。 在异方差及其异方差的形式。 具体方法: 具体方法: ●假定不存在异方差,进行回归,并计算剩余平方 e 2,描绘 假定不存在异方差,进行回归, 假定不存在异方差
⋅ ⋅⋅ ⋅⋅ ⋅
Yi
⋅⋅ ⋅ ⋅ ⋅ ⋅⋅ ⋅
⋅
C个
Xi
●将前后两部分分别作回归,分别计算出各部 将前后两部分分别作回归, 分剩余 ei , 2 ● 比较前后两个回归的剩余平方和 ∑ ei : ei2 之比接近于 ,为同方差; 如果两个 ∑ 之比接近于1,为同方差; ei2 之比不同于 ,为异方差 如果两个 ∑ 之比不同于1, 前提条件: 前提条件: ●样本容量较大 服从正态分布, ● ui 服从正态分布,并除异方差外满足其他 基本假定
具体步骤: 具体步骤:
●排序 将观测值按解释变量 大小顺序排列 排序:将观测值按解释变量 排序 将观测值按解释变量X大小顺序排列 数据分组:去掉中间的 去掉中间的C个 ●数据分组 去掉中间的 个(约1/4)观测值,分别 )观测值, 进行前后两部分 (n − c) 2 个观测值的回归 ●提出假设:分别进行前后两部分回归的基础上,提出 提出假设 分别进行前后两部分回归的基础上, 分别进行前后两部分回归的基础上 检验假设: 检验假设: o : ui H 即
第五章 异方差性

• 异方差一般可归结为三种类型:
(1)单调递增型: i2随X的增大而增大; (2)单调递减型: i2随X的增大而减小; (3)复 杂 型: i2与X的变化呈复杂形式。
实际经济问题中的异方差性
(1)模型中缺失了某些解释变量 服装需求函数模型 服装需求量为被解释变量,收入、服装价 格和其他商品价格为解释变量,于是有: qi f ( I i , pi ) i i=1,2,…,n
二、 产生异方差性的原因
● 从模型中略去的变量随列入模型的解释变量 X i 的变化, 也呈现规律性的变化,导致 ●
ui
随 X i 而变化
模型设定不恰当产生的异方差。如果一些重要变量被忽
略,或把非线性差
测量误差可能随解释变量X的增大而增大
●截面数据中总体各单位的差异 一般说异方差性在截面数据中比在时间序列数据中更常出现 原因:同一时点不同对象的差异(如某年各省的GDP) 一般大于 同一对象不同时间的差异(同一个省不同年份的GDP) 注意:在经济结构发生较大变化时,时间序列也常存在异方差
因为方差是度量被解释变量
Y 的观测值围绕条件期望
E(Yi X 2 , X 3, X k ) 1 2 X 2i 3 X 3i ... k X ki
的分散程度,因此同方差性指的是所有观测值围绕回
归线的分散程度相同。
同方差性的图示
当只有一个解释变量时
概 率 分 布 密 度
2 i
(2.4.7)
一. 图形分析法
基本思想:
异方差性的表现是 u i 的方差随某个解释变量的变化 而变化,或Y的分散程度随X的变化而变化。因此可利用 u i的代表 e i 与某解释变量的散布图,观察是否存在异方差 及其异方差的形式。 具体方法: ●假定不存在异方差,进行回归,并计算剩余平方 与 ei2的散点图,作出近似判断。 X
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
计量经济学第五章-异方差

可编辑ppt
5
一、参数的OLS估计仍然是线性无偏的,但不 是最小方差的估计量
1、线性性
bˆ1
= xi yi xi 2
= b1
+ xi ui xi 2
一元线性回归模型为例
2、无偏性
E( bˆ1 )=E(
b1
+
xi ui xi 2
在同方差的假定下才被证明是服从 t 分布的。 分母变大,t 值变小,t 检验也就失去意义。
三、降低预测精度
由于存在异方差,参数的OLS估计的方差增大,参数 估计值的变异程度增大,从而造成对 Y 的预测误差变大, 降低预测的精度。
可编辑ppt
7
第二节 异方差的检验
• 1、图解法 • 2、戈德菲尔德—匡特法(双变量模型) • 3、怀特检验(White) • 4、戈里瑟(Glejser)检验 • 5、帕克(Park)检验
• 二、随着收入的增长,人们有更多的备用收入,从而如何支配 他们的收入有更大的选择范围。因此,在做储蓄对收入的回归 时,很可能发现,由于人们对其储蓄行为有更多的选择,与收 入俱增。
• 三、个体户收入随时间变化。
• 四、异方差还会因为异常值的出现而产生。一个超越正常值范 围的观测值或称异常值是指和其它观测值相比相差很多(非常 小或非常大)的观测值。
)= b1+
xi E(ui xi 2
)
=
b1
3、方差
该形式不具有最小方差
Var( bˆ1 ) =
i 2
xi 2
在同方差时,
xi2 Xi2 xi 2
该形式具有最小方差
Var(
异方差

第一节 异方差的概念
例:以某一行业的企业为样本建立企业生产函数模 型 Yi=Ai1 Ki2 Li3ei 被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不同 ,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量观 测值的变化而呈规律性变化,呈现复杂型。
第三节 异方差性的检验
三、戈里瑟(Gleiser)检验 1969年戈里瑟提出的,它不但可以检验异方差是 否存在,而且可以近似探测随机误差项的方差是 怎样随解释变量的变化而变化的。 基本思想:由OLS法得到残差 e i ,取 e i 的绝对 值 ,然后将 对某个 X i回归,根据回归模 ei ei 型的显著性和拟合优度来判断是否存在异方差。
二、异方差性的后果
ˆ
2
e
2 i
n2
ˆ s(1 )
ˆ ki
2
2
ˆ2
(Xi X )
2
但是,在异方差的情况下
ˆ* s( i ) ˆ ki i
2 2
ˆ i ki
2 2
ˆ ki
2
2
i ki ki
2
2
=
ˆ s(i )
i Байду номын сангаасi
第三节 异方差性的检验
第五章 异方差性 答案

第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T ) 二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法 3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性 4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验 5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用 6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B ) A. B.C. D.7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )A. B.C. D. ∑=ii x y n 1b ˆ8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=∑∑=2ˆxxy b 22)(ˆ∑∑∑∑∑--=x x n y x xy n b xyb=ˆ型时,应将模型变换为( C )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、异方差性的后果
计量经济学模型一旦出现异方差性,如果仍采 用OLS估计模型参数,会产生下列不良后果: 1、参数估计量非有效 OLS估计量仍然具有无偏性,但不具有有效性 因为在有效性证明中利用了 E(’)=2I 而且,在大样本情况下,尽管参数估计量具有 一致性,但仍然不具有渐近有效性。
虽然最小二乘法参数的估计量是无偏的,但 这些参数方差的估计量是有偏的。 正的偏差即OLS高估了参数估计值的真实 方差 负的偏差即OLS低估了参数估计值的真实 方差。
1 SALE
,在EVIEWS软件中,可直接给出权重
1
由软件自行进行模型转换,完成加权最小 二乘法(WLS)的线性回归方程。
SALE
procs Makபைடு நூலகம்Equation options
在Weighted LS/TSLS 上打钩 在Weight 内输入1/SQR(sale) 得到F6
E(u ) k X
2 i 2 i 2
2 i
K为常数比例因子。
Yi Xi ui 1 0 ( ) 1 ( ) ( ) Xi Xi Xi Xi
例F6 见Eviews F5 (1)平方根变换将OLS回归的残差描图, 我们可以发现误差方差正比于销售量, 因此可对模型作平方根变换后再进行回 归,即采用加权最小二乘法,权为
异方差的图示 散点图
三、实际经济问题中的异方差性
例1:截面资料下研究居民家庭的储蓄行为 Yi=0+1Xi+i Yi:第i个家庭的储蓄额 Xi:第i个家庭的可支配收入 高收入家庭:储蓄的差异较大 低收入家庭:储蓄则更有规律性,差异较小 i的方差呈现单调递增型变化
例2,以绝对收入假设为理论假设、以截面数据 为样本建立居民消费函数: Ci=0+1Yi+I 将居民按照收入等距离分成n组,取组平均数为样 本观测值。 一般情况下,居民收入服从正态分布:中等收入 组人数多,两端收入组人数少。而人数多的组平均 数的误差小,人数少的组平均数的误差大。 所以样本观测值的观测误差随着解释变量观测值 的不同而不同,往往引起异方差性。
2、变量的显著性检验失去意义
变量的显著性检验中,构造了t统计量
其他检验也是如此。
3、模型的预测失效
一方面,由于上述后果,使得模型不具有 良好的统计性质;
所以,当模型出现异方差性时,参数OLS 估计值的变异程度增大,从而造成对Y的预测 误差变大,降低预测精度,预测功能失效。
§5.3 异方差性的检验
3、怀特(White)检验
怀特检验不需要排序,且适合任何形式的异方差
怀特检验的基本思想与步骤(以二元为例): Yi 0 1 X 1i 2 X 2i i
然后做如下辅助回归
~2 X X X 2 X 2 X X e i 0 1 1i 2 2i 3 1i 4 2i 5 1i 2i i
④在同方差性假定下,构造如下满足F分布的 统计量
nc 2 ~ e2i ( 2 k 1) nc nc F ~ F( k 1, k 1) nc 2 2 2 ~ e ( k 1 ) 1i 2
⑤给定显著性水平,确定临界值F(v1,v2), 若F> F(v1,v2), 则拒绝同方差性假设,表明 存在异方差。 当然,还可根据两个残差平方和对应的子样 的顺序判断是递增型异方差还是递减异型方差。
i E(ui ) ki X i
2 k 其中, i 为常数,称为比例因子
将模型的两边同除以扰动项的标准差 k X i
Yi Xi ui 1 0 1 Xi Xi Xi Xi
情形2:假设误差的方差与X2成比例 若原回归模型的残差图类似于图5-5的 模式,则可表明误差的方差并不是与X线 性相关,而是随X的平方按比例增加
几种异方差的检验方法: 1、图示法
(1)用X-Y的散点图进行判断 看是否存在明显的散点扩大、缩小或复杂型 趋势(即不在一个固定的带型域中)
2 ~ e (2)X- i 的散点图进行判断
看是否形成一斜率为零的直线
~2 e i ~2 e i
X 同方差 递增异方差
X
~2 e i
~2 e i
X 递减异方差 复杂型异方差
异方差问题多存在于截面数据中 例如同一时间点上不同消费者或是其家 庭成员、公司、行业,或者区域上分区、 县、州或城市等等。 这些单位具有不同的规模,如小公司, 中等公司或者大公司,或是低收入、中等 收入或高收入。换言之,可能存在规模效 应(scale effect)。
二、异方差的类型
同方差性假定:i2 = 常数 f(Xi) 异方差时: i2 = f(Xi) 异方差一般可归结为三种类型: (1)单调递增型: i2随X的增大而增大 (2)单调递减型: i2随X的增大而减小 (3)复 杂 型: i2与X的变化呈复杂形式
(5-16)
变换后的扰动项是同方差的,变换 后的模型不存在异方差的问题 这种回归分析方法称为加权最小二乘 法(WLS) 这种方法估计出来的参数称为加权最 小二乘估计量 其中解释变量和被解释变量都以其标 准差的倒数为权数
二、扰动项的方差σ2i未知 情形1:扰动项的方差与X成比例:平方根 变换。 若普通OLS回归所得的残差ei对解释变 量 X ,作图得到的残差图类似于图 5-4 所 示,则表明扰动项的方差与解释变量线 性相关,或者扰动项的方差与成比例, 即有: 2 2 2
§5.1 异方差的性质
一、异方差的涵义 为了看清楚同方差性和异方差性的区别, 我们先看个实例: (5-1) Y X u
0 1
Y为储蓄,X为个人可支配收入,u为扰动项,β0, β1为参数 我们考察一下这个模型的两种情况 一种情况如图5-1(a)所示 另外一种情形如图5-1(b)所示
G-Q检验的思想:
先将样本一分为二,对子样①和子样②分别 作回归,然后利用两个子样的残差平方和之比构 造统计量进行异方差检验。
由于该统计量服从F分布,因此假如存在递增 的异方差,则F远大于1;反之就会等于1(同方 差)、或小于1(递减方差)。
G-Q检验的步骤:
①将n对样本观察值(Xi,Yi)按观察值Xi的大小 排队 ②将序列中间的c=n/4个观察值除去,并将剩 下的观察值划分为较小与较大的相同的两个 子样本,每个子样样本容量均为(n-c)/2 ③对每个子样分别进行OLS回归,并计算各自 的残差平方和
例3,以某一行业的企业为样本建立企业生产函数 模型 Yi=Ai1 Ki2 Li3ei
被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不 同,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量 观测值的变化而呈规律性变化,呈现复杂型。
E(u )
2 i
2 i
E(u )
2 i
2
异方差的概念
对于模型
Yi 0 1 X ii 2 X 2i k X ki i
如果出现
Var(i ) i2
即对于不同的样本点,随机误差项的方差不再 是常数,而互不相同,则认为出现了异方差性 (Heteroskedasticity)。
检验思路: 由于异方差性就是相对于不同的解释变量观测值, 随机误差项具有不同的方差。那么: 检验异方差性,也就是检验随机误差项的方 差与解释变量观测值之间的相关性及其相关的 “形式”。 在涉及不均匀单元的横截面数据中,异方 差性可能是一种常规而不是例外 横截面分析中,如果样本同时含有小、中 和大型厂家,则一般都预期有异方差性。
2、测量误差 一方面,测量误差常常随着时间逐渐 累积,所以扰动项的方差,趋向于随时 间增加; 另一方面,抽样技术和其他数据采集 技术的不断改进,测量误差以及扰动项 的方差也可能随时间减少 当然,这两种情况最容易出现在时 间序列数据中,故由于测量误差的影响, 时间序列数据的随机扰动项常常是不同 方差的。
问题在于用什么来表示随机误差项的方差 一般的处理方法:
首先采用 OLS 法估计模型,以求得随机误差项的 估计量 (注意, 该估计量是不严格的) , 我们称之为 “近
~ e 似估计量” ,用 i
表示。于是有
~2 Var ( i ) E ( i2 ) e i
~ y (y i ) 0ls e i i
有时经济生活中,被略去的变量又与 Xi具有某种关联,故ui就往往随着Xi的变 化而变化,从而ui的方差是Xi的函数,而 不是一个常数 方程(5-1)中,ui项就包含了除可支 配收入以外的其他因素对储蓄的影响, 但这些因素往往又与收入密切相关。因 此,在储蓄行为中,收入高的家庭其储 蓄的变动性要比收入低的家庭大得多,ui 项的方差是与Xi相关的。
Yi 0 1 X i ui
i
Yi 0 ( 1
(5-12) (5-13)
i
) 1 (
i
Xi
)
i
ui
vi2
ui2
2 i
(5-15)
i
ui2 ) 2 1
E (vi ) E (
2 i
E (ui2 )
(5-16)
E (vi )
1
i
2 i 1 2
如: 帕克检验常用的函数形式:
i f ( X ji ) 2 X e ji
或
~ 2 ) ln 2 ln X ln(e i ji i
若在统计上是显著的,表明存在异方差性。
3、戈德菲尔德-匡特(Goldfeld-Quandt)检验 G-Q检验以F检验为基础,适用于样本容量较大、 异方差递增或递减的情况。
§5.4 异方差性的补救措施 基本思想是将原模型加以“变换”, 使得“变换”后的模型具有同方差性, 但是变换的形式取决于每个扰动项方差 的真实值 σ2i 是已知还是未知,所以补救 的方法也就分为两种:当扰动项方差 σ2i 为已知和扰动项方差σ2i为未知
