机械原理(哈)课后习题

合集下载

机械原理课后习题答案

⎛ ⎜ ⎝
m / s2 mm
⎞ ⎟ ⎠
作加速度图
C
2
3
D
B
p(d) 4
(c3)
b2 (b1) (b3)
题3-8 c) 解(续2)
[解]
（3）加速度分析 aB 2 (= aB1) → aB3 → aC 3
1) 求aB2
A 1 ω1
2) 求aB3
aB3
=
an B3D
+
at B3D
=
aB
2
+
ak B3B2
得d点
p(c3)
E
vD = μv pd = 0.005 × 44.6 = 0.223 (m / s)
作 de ⊥ bc2
并使
de = DE = lDE = 40 bd BD lBD 50
得e点
vE = μv pe = 0.005 × 32.0 = 0.16 (m / s)
3) 求ω2
ω2
=
vC 2B lBC
p' = 2p'l + p'h − 3n' = 2 × 3 + 0 − 3× 2 = 0
p' = 2p'l + p'h − 3n' = 2 ×10 + 0 − 3×6 = 2
F = 3n − (2pl + ph − p') − F' = 3 × 11 − (2 × 17 + 0 − 2) − 0 =1
P24
B P23
3
2A
P12
1
4
D
P14
vE
=
vB
P13 E P13B

机械原理课后习题_答案.PPT36页

机械原理课后习题_答ห้องสมุดไป่ตู้.
31、园日涉以成趣，门虽设而常关。 32、鼓腹无所思。朝起暮归眠。 33、倾壶绝余沥，窥灶不见烟。
34、春秋满四泽，夏云多奇峰，秋月扬明辉，冬岭秀孤松。 35、丈夫志四海，我愿不知老。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非

《机械原理》课后习题附答案

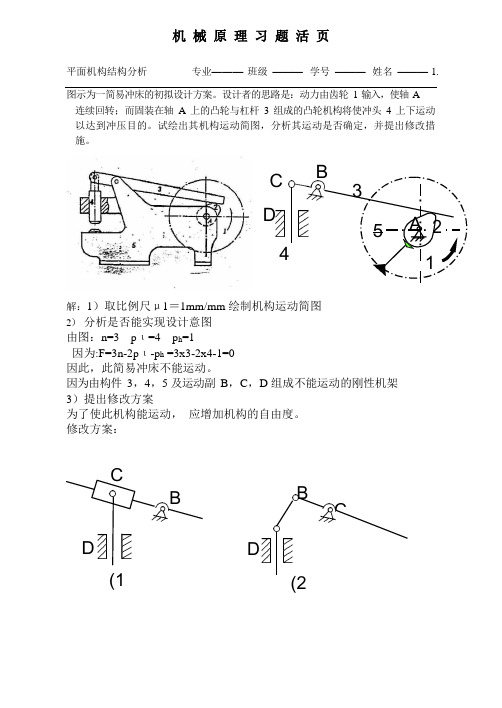
CB D BC平面机构结构分析专业———班级———学号———姓名——— 1.图示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1 输入，使轴A连续回转；而固装在轴A 上的凸轮与杠杆3 组成的凸轮机构将使冲头4 上下运动以达到冲压目的。

试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。

C B 35 A 24 1解：1）取比例尺μ1＝1mm/mm 绘制机构运动简图2）分析是否能实现设计意图由图：n=3 pι=4 p h=1因为:F=3n-2pι-p h =3x3-2x4-1=0因此，此简易冲床不能运动。

因为由构件3，4，5 及运动副B，C，D 组成不能运动的刚性机架3）提出修改方案为了使此机构能运动，应增加机构的自由度。

修改方案：D(1 (2DG7D 64C EF9 38B 2 A122如图所示为一小型压力机。

图中齿轮 1与偏心轮 1’为同一构件，绕固定轴心 o 连续转动。

在齿轮 5上开有凸轮凹槽，摆杆 4上的滚子 6嵌在凹槽中，从而使摆杆 4 绕 C 轴上下摆动。

同时，又通过偏心轮 1’、连杆 2、滑杆 3使 C 轴上下移动。

最后通过在摆杆 4的叉槽中的滑块 7和铰链 G 使冲头 8实现冲压运动。

试绘制其机构运动简图，并计算自由度。

b)解：计算该机构的自由度n=7， p ι=9， p h =2 F=3n-2p e -p h =3x7-2x8-2=13. 试计算下列二图所示齿轮连杆组合机构的自由度。

图中相切的圆周表示一对齿轮传动的节圆；凡局部自由度、复合铰链和虚约束均需明确指出。

解：a ）解n=4 P ι=5 Ph=1F=3x4-2x5-1=134 C A复合铰链1a)BD 5b）解：n＝6 Pι=7 Ph=3F＝3×6－2×7－3＝14.试计算下列二图所示压榨机的自由度。

图a 中，左右两半完全对称；图b 中，CD = FI = KL = KM = FJ = CE，LI =KF = MJ = JE = FC = ID。

机械原理课后题答案

机械原理课后题答案题目1：在机械原理中，力的合成与分解是非常重要的概念。

下面通过一个实例来解答该题。

题目：一辆汽车在直线上行驶，车上的引擎提供了一个向前的力，摩擦力与空气阻力则会对车辆施加一个向后的力。

假设引擎提供的力为50 N，摩擦力为20 N，空气阻力为30 N。

请问车辆的净力是多少？解答：根据题目要求，我们需要计算车辆的净力。

净力可以通过合成力的方式来计算。

合成力的公式为：净力 = 引擎提供的力 - 摩擦力 - 空气阻力将已知数值代入公式中，得到净力 = 50 N - 20 N - 30 N = 0 N所以，车辆的净力为0 N。

题目2：在机械原理中，杠杆原理是一种重要的基本原理。

下面我们通过一个实例来解答该题。

题目：某个平衡杠杆的左臂长为3 m，右臂长为2 m。

在左臂上施加了一个力为100 N，我们需要计算右臂上需要施加的力是多少？解答：根据杠杆原理，平衡杠杆上受力的乘积相等，即左臂上的力乘以左臂的长度等于右臂上的力乘以右臂的长度。

设左臂上的力为 F1，右臂上的力为 F2，左臂的长度为 L1，右臂的长度为 L2。

则有 F1 * L1 = F2 * L2。

已知左臂的长度 L1 = 3 m，右臂的长度 L2 = 2 m，左臂上的力 F1 = 100 N。

代入已知数值，将未知数 F2 单独列出来，得到 F2 = (F1 * L1) / L2 = (100 N * 3 m) / 2 m = 150 N。

所以，右臂上需要施加的力为 150 N。

题目3：在机械原理中，滑轮组是一种常见的简化传动装置。

下面我们来解答一个关于滑轮组的题目。

题目：一个由3个滑轮组成的滑轮组，滑轮A的直径为10 cm，滑轮B的直径为20 cm，滑轮C的直径为30 cm。

如果滑轮A的转速为300 rpm，则滑轮B和滑轮C的转速分别是多少？解答：滑轮组的转速与滑轮的直径呈反比关系，即转速和直径成反比。

设滑轮A的转速为 S1，滑轮B的转速为 S2，滑轮C的转速为 S3。

机械原理课后习题答案

机械原理课后习题答案1. 两个质量分别为m1和m2的物体，它们分别靠在光滑水平面上的两个弹簧上，两个弹簧的弹性系数分别为k1和k2。

求当两个物体分别受到的外力分别为F1和F2时，两个物体的加速度分别是多少？答，根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。

根据这个公式，可以得出两个物体的加速度分别为a1=F1/m1，a2=F2/m2。

2. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，物体的加速度是多少？答，同样根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。

根据这个公式，可以得出物体的加速度为a=F/m。

3. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，弹簧的位移是多少？答，根据胡克定律，弹簧的位移与受到的外力成正比，即F=kx，其中x为弹簧的位移。

解出x=F/k，即弹簧的位移与外力成反比。

4. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，弹簧的振动周期是多少？答，根据弹簧的振动周期公式T=2π√(m/k)，可以得出弹簧的振动周期与物体的质量和弹簧的弹性系数有关，与受到的外力无关。

5. 一个质量为m的物体，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当物体受到外力F时，弹簧的振幅是多少？答，根据弹簧振动的公式x=Acos(ωt+φ)，可以得出弹簧的振幅与受到的外力无关，只与弹簧的弹性系数和物体的质量有关。

求当物体受到外力F时，弹簧的振动频率是多少？答，根据弹簧振动的公式f=1/2π√(k/m)，可以得出弹簧的振动频率与受到的外力无关，只与弹簧的弹性系数和物体的质量有关。

7. 一个半径为r的圆盘，靠在光滑水平面上的弹簧上，弹簧的弹性系数为k。

求当圆盘受到外力F时，圆盘的加速度是多少？答，根据牛顿第二定律，物体受到的合外力等于物体的质量乘以加速度，即F=ma。

机械原理课后习题答案

第四章课后习题4—12图示为一曲柄滑块机构的三个位置，F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆，试决定在此三个位置时作用在连杆AB上的作用力的真实方向（构件重量及惯性力略去不计）。

解：上图中构件2受压力。

因在转动副A处2、1之间的夹角∠OAB在逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故FR12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA在逐渐增大，相对角速度ω23也沿顺时针方向，故FR32应切于摩擦圆的上方。

R32解：上图构件2依然受压力。

因在转动副A处2、1之间的夹角∠OAB逐渐减小，故相对角速度ω21沿顺时针方向，又因2受压力，故F R12应切于摩擦圆的下方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿逆时针方向，F R32应切于摩擦圆的下方。

解：上图构件2受拉力。

因在转动副A处2、1之间的夹角∠OAB在逐渐增大，故相对角速度ω21沿顺时针方向，又因2受拉力，故FR12应切于摩擦圆的上方；在转动副B处，2、3之间的夹角∠OBA逐渐减小，故相对角速度ω23沿顺时针方向，FR32应切于摩擦圆的下方。

4-13 图示为一摆动推杆盘形凸轮机构，凸轮1沿逆时针方向回转，F为作用在推杆2上的外载荷，试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位（不考虑构件的重量及惯性力，解：经受力分析，FR12的方向如上图所示。

在FR12的作用下，2相对于3顺时针转动，故FR32应切于摩擦圆的左侧。

补充题1 如图所示，楔块机构中，已知γ＝β＝60°，Q ＝1000N 格接触面摩擦系数f ＝0.15，如Q 为有效阻力，试求所需的驱动力F 。

解:对机构进行受力分析,并作出力三角形如图。

对楔块1，R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=））o o ① 对楔块2，同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=））o o ②sin(602sin(602F Q ϕϕ+=⋅-））o o且有2112R R F F = ，8.53arctgf ϕ＝＝o ③联立以上三式，求解得F ＝1430.65N2 如图示斜面机构，已知：f （滑块1、2与导槽3相互之间摩擦系数）、λ（滑块1的倾斜角）、Q （工作阻力，沿水平方向），设不计两滑块质量，试确定该机构等速运动时所需的铅重方向的驱动力F 。

机械原理课后习题答案部分

第二章2-1 何谓构件何谓运动副及运动副元素运动副是如何进行分类的答：参考教材5~7页;2-2 机构运动简图有何用处它能表示出原机构哪些方面的特征答：机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析;2-3 机构具有确定运动的条件是什么当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况答：参考教材12~13页;2-5 在计算平面机构的自由度时,应注意哪些事项答：参考教材15~17页;2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗为什么答：不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处;2-7 何谓机构的组成原理何谓基本杆组它具有什么特性如何确定基本杆组的级别及机构的级别答：参考教材18~19页;2-8 为何要对平面高副机构进行“高副低代"“高副低代”应满足的条件是什么答：参考教材20~21页;2-11 如图所示为一简易冲床的初拟设计方案;设计者的思路是：动力由齿轮1输入,使轴 A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的;试绘出其机构运动简图,分析其是否能实现设计意图并提出修改方案;解：1取比例尺绘制机构运动简图;2分析其是否可实现设计意图;F=3n- 2P l +P h –p’ -F’=3×3-2×4+1-0-0=0此简易冲床不能运动,无法实现设计意图;3修改方案;为了使此机构运动,应增加一个自由度;办法是：增加一个活动构件,一个低副;修改方案很多,现提供两种;※2-13图示为一新型偏心轮滑阎式真空泵;其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动;当偏心轮按图示方向连续回转时可将设备中的空气吸入,并将空气从阀5中排出,从而形成真空;1试绘制其机构运动简图；2计算其自由度;解：1取比例尺作机构运动简图如图所示;2 F=3n-2p1+p h-p’-F’=3×4-2×4+0-0-1=12-14 解：1绘制机构运动简图1）绘制机构运动简图F=3n-2P l +P h –p’-F’=3×5-2×7+0-0-0=12）弯曲90o 时的机构运动简图※2-15试绘制所示仿人手型机械手的食指机构的机构运动简图以手掌8作为相对固定的机架,井计算自由度;解：1取比倒尺肌作机构运动简图；2计算自由度1⨯=-F210⨯73=2-17 计算如图所示各机构的自由度;aF=3n- 2P l +P h–p’-F’=3×4-2×5+1 -0-0=1A处为复合铰链bF=3n-2P l +P h–p’-F’=3×7-2×8+2-0-2=12、4处存在局部自由度cp’= 2P l ’+P h ’-3n’=2×10+0-3×6=2,F=3n-2P l +P h–p’-F’=3×11-2×17+0-2-0=1C、F、K 处存在复合铰链,重复部分引入虚约束※2-21图示为一收放式折叠支架机构;该支架中的件1和5分别用木螺钉连接于固定台板1’和括动台板5’上．两者在D处铰接,使活动台板能相对于固定台极转动;又通过件1,2,3,4组成的铰链四杆机构及连杆3上E点处的销子与件5上的连杆曲线槽组成的销槽连接使活动台板实现收放动作;在图示位置时,虽在活动台板上放有较重的重物．活动台板也不会自动收起,必须沿箭头方向推动件2,使铰链B,D重合时．活动台板才可收起如图中双点划线所示;现已知机构尺寸l AB=l AD=90 mm；l BC=l CD=25 mm,其余尺寸见图;试绘制该机构的运动简图,并计算其自由度;解：F=3n-2p1+p b-p’-F’=3×5-2×6+1-0-1=12-23 图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组;有如在该机构中改选EG为原动件,试问组成此机构的基本杆组是否与前有所不同;解：1计算自由度F=3n-2P l +P h–p’-F’=3×7-2×10+0-0-0=12拆组3EG 为原动件,拆组2-24 试计算如图所示平面高副机构的自由度,并在高副低代后分析组成该机构的基本杆组;1、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×5-2×6+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图2所示 3高副低代如图3所示 4拆组如图4所示 2、解：1计算自由度F=3n-2P l +P h –p ’-F ’=3×-2×9+1-0-1=12从结构上去除局部自由度、虚约束、多余的移动副、转动副如图b 所示 3高副低代如图c 所示 4拆组如图d 所示第三章3—1 何谓速度瞬心相对瞬心与绝对瞬心有何异同点答：参考教材30~31页;3—2 何谓三心定理何种情况下的瞬心需用三心定理来确定答：参考教材31页;※3-3机构中,设已知构件的尺寸及点B 的速度v B 即速度矢量pb,试作出各机构在图示位置时的速度多边形;※3-4 试判断在图示的两机构中．B 点足否都存在哥氏加速度又在何位置哥氏加速度为零怍出相应的III 级组II 级组II 级组II 级组机构位置图;并思考下列问题;1什么条件下存在氏加速度2根椐上一条．请检查一下所有哥氏加速度为零的位置是否已全部找出;3图 a 中,a kB2B3=2ω2v B2B3对吗为什么;解：1图 a 存在哥氏加速度,图 b 不存在;2由于a kB2B3==2ω2v B2B3故ω3,v B2B3中只要有一项为零,则哥氏加速度为零;图 a 中B 点到达最高和最低点时构件1,3．4重合,此时v B2B3=0,当构件1与构件3相互垂直．即_f=；点到达最左及最右位置时ω2=ω3=0．故在此四个位置无哥氏加速度;图 b 中无论在什么位置都有ω2=ω3=0,故该机构在任何位置哥矢加速度都为零; 3对;因为ω3≡ω2;3-5 在图示的曲柄滑块机构中,已知mm l mm l mm l mm l DE BD A AB 40,50,100,30C ====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=451ϕ位置时,点D 、E 的速度和加速度以及构件2的角速度和角加速度;解：1以选定的比例尺l μ作机构运动简图（2）速度分析AB)(m/s 3.01⊥==AB B l v ωBCBCv v v v v C C C B C B C //32322⊥∨∨+=+=？方向：？0？大小：？根据速度影像原理,作BC BD bc bd //2=求得点d,连接pd;根据速度影像原理,作BDE bde ∆≈∆求得点e,连接pe,由图可知)(/r 2/m/s,175.0m/s,173.0,m/s 23.0223232顺时针s ad l bc c c v pe v pd v BC v v C C v E v D ========μωμμμ （3）加速度分析A)(B m/s 3221→==AB B l a ω根据速度影像原理作BC BD c b d b /''/''2=求得点'd ,连接''d p ;根据速度影像原理,作BDE e d b ∆≈'''∆求得点e ',连接e p '',由图可知)(/36.8//,m/s 8.2'',m/s 64.2''2'2'22222顺时针s rad l c n l a e p a d p a BC a BC B C a E a D =======μαμμτ 3-6 在图示机构中,设已知各构件的尺寸,原动件1以等角速度1ω顺时针方向转动,试用图解法求机构在图示位置时构件3上C 点速度和加速度比例尺任选;abc3-7 在图示机构中,已知mm l mm l mm l mm l mm l BC CD EF A AE 50,75,35,40,70B =====,曲柄以等角速度s rad /101=ω回转,试用图解法求机构在︒=501ϕ位置时,C 点的速度c v 和加速度c a ; 解：1以选定的比例尺l μ作机构运动简图;速度分析m/s 72.0m/s,4.01111====AF F AB B l v l v ωω AFAF EFv v v v F F F F F //15145⊥⊥∨+==方向：大小：v d 用速度影响法求2速度分析CD ED v v v CDD C ⊥⊥∨+=方向：大小： BC AB v v v CBB C ⊥⊥∨+=方向：大小：3加速度分析)(m/s 2.7A),(B m/s 42211221A F l a l a AF F AB B →==→==ωω AFA F v a a a a a F F rF F k F F F F F ///21511515145→→∨++==方向：大小：ω EFEF l a a a a a EFEF n E F E F F ⊥→++==方向：大小：2444450ωτa d 用加速度影像法求CD D C l a a a a CDCDnCD D C ⊥→∨∨++=方向：大小：23ωτ CBB C l a a a a CB CBnCB B C ⊥→∨∨++=方向：大小：22ωτ 2m/s 3''=⋅=a C c p a μ3-8 在图示凸轮机构中,已知凸轮1以等角速度s rad /101=ω转动,凸轮为一偏心圆,其半径︒====90,50,15,251B ϕmm l mm l mm R AD A ;试用图解法求构件2的角速度2ω和角加速度2α; 解：1以选定的比例尺l μ作机构运动简图;2速度分析：将机构进行高副低代,其替代机构如图b 所示;m/s 15.0141===AB B B l v v ωCDAB BD v v v B B B B //4242⊥⊥∨+=方向：大小：？？)(/3.2//222逆时针s rad l pb l v BD v BD B ===μω3加速度分析A)m/s(B 5.12141→===AB B B l a a ω其中,）（顺时针222222222242242rad/s 9.143/''/,m/s 286.0,m/s 746.02=======BD a BD D B BD n D B B B k B B l b n l a l a v a μαωωτ 3-11 试求图示机构在图示位置时的全部瞬心; 解：a 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上 d 总瞬心数：4×3/2=6对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上※3-12 标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮1与齿轮3的传动比ω1/ω3; 解：1瞬新的数目：K=NN-1/2=66-1/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置,3)ω1/ω3= P 36P 13/P 16P 13=DK/AK,由构件1、3在K 点的速度方向相同,可知ω3与ω1同向;3-13 在图示四杆机构中,s rad mm l mm l CD AB /10,90,602===ω,试用瞬心法求：1当︒=165ϕ时点C 的速度C v ；当︒=165ϕ时构件3的BC 线上或其延长线上速度最小的一点E 的位置及其速度大小；3当0=C v 时ϕ角之值有两解;解：1以选定的比例尺l μ作机构运动简图（2）因P 24为构件2、4的顺心,则m/s 4.0rad/s 5.4424242242424=⋅==⋅=⋅=CD C D P A P l v DP AP l l ωωωω，对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上（3）因构件3的BC 线上速度最小的点到绝对瞬心P 13的距离最近,故从P 13作BC 线的垂线交于E 点; 对P 13：P 12、P 23、P 13在同一直线上, P 14、P 34、P 13在同一直线上,故m/s 357.0131321313133313=⋅⋅=⋅⋅⋅=⋅⋅=⋅=E P B P l E P u B P v E P l v ABl l B l E P E ωμμωω（4）若0=C v ,则04=ω,DP AP l l DP A P 24242242424⋅=⋅=ωωω若024=A P ,则P 24与P 12重合,对P 24:P 23、P 34、P 24在同一直线上,P 12、P 14、P 24在同一直线上若024=A P ,则A 、B 、C 三点共线;︒=⋅-++︒=︒=⋅-+=6.226)2arccos(1804.26)2arccos(22222221212211ADAC D C AD AC AD AC D C AD AC ϕϕ， ※3-15 在图示的牛头刨机构中,l AB =200 mnl,l CD =960 mm,l DE =160 mm, h=800mm,h 1=360mm,h 2=120mm;设曲柄以等角速度ω1=5 rad ／s ．逆时针方向回转．试以图解法求机构在φ1=135o 位置时．刨头点的速度v C ;sm AP v v P P P l p c l /24.1,,)2(151********===μωμ出瞬心利用顺心多边形依次定所示作机构运动简图，如图（1）以:解。

机械原理课后习题答案

《机械原理》课后习题答案第2章（P27）2-2 计算下列机构的自由度，如遇有复合铰链、局部自由度、虚约束等加以说明。

（a）n=3，p l=3 F=3*3-2*3=3（b）n=3，p l=3，p h=2 F=3*3-2*3-2=1 （B处有局部自由度）（c）n=7，p l=10 F=3*7-2*10=1（d）n=4，p l=4，p h=2 F=3*4-2*4-2=2 （A处有复合铰链）（e）n=3，p l=4 F=3*3-2*4=1 （A或D处有虚约束）（f）n=3，p l=4 F=3*3-2*4=1 （构件4和转动副E、F引入虚约束）（g）n=3，p l=5 F=(3-1)*3-(2-1)*5=1 （有公共约束）（h）n=9，p l=12，p h=2 F=3*9-2*12-2=1 （M处有复合铰链，C处有局部自由度）2-3 计算下列机构的自由度，拆杆组并确定机构的级别。

（a）n=5，p l=7 F=3*5-2*7=1由于组成该机构的基本杆组的最高级别为Ⅱ级杆组，故此机构为Ⅱ级机构。

（b）n=5，p l=7 F=3*5-2*7=1此机构为Ⅱ级机构。

（c）n=5，p l=7 F=3*5-2*7=1拆分时只须将主动件拆下，其它构件组成一个Ⅲ级杆组，故此机构为Ⅲ级机构。

2-4 验算下列运动链的运动是否确定，并提出具有确定运动的修改方案。

（a）n=3，p l=4，p h=1 F=3*3-2*4-1=0 该运动链不能运动。

修改方案如下图所示：（b）n=4，p l=6 F=3*4-2*6=0 该运动链不能运动。

修改方案如下图所示：或第3章（P42）3-2 下列机构中，已知机构尺寸，求在图示位置时的所有瞬心。

（a）（b）（c）(a) v3=v P13=ω1P14P13μl3-6 在图示齿轮连杆机构中，三个圆互作纯滚，试利用相对瞬心P13来讨论轮1与轮3的传动比i13。

第5章（P80）5-2 一铰接四杆机构（2）机构的两极限位置如下图：（3）传动角最大和最小位置如下图：5-3题略解：若使其成为曲柄摇杆机构，则最短杆必为连架杆，即a 为最短杆。

机械原理课后全部习题解答

机械原理课后全部习题解答文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征机器通常由哪三部分组成各部分的功能是什么2）、机器与机构有什么异同点3）、什么叫构件什么叫零件什么叫通用零件和专用零件试各举二个实例。

4）、设计机器时应满足哪些基本要求试选取一台机器，分析设计时应满足的基本要求。

2、填空题1)、机器或机构，都是由组合而成的。

2）、机器或机构的之间，具有确定的相对运动。

3）、机器可以用来人的劳动，完成有用的。

4）、组成机构、并且相互间能作的物体，叫做构件。

5）、从运动的角度看，机构的主要功用在于运动或运动的形式。

6）、构件是机器的单元。

零件是机器的单元。

7）、机器的工作部分须完成机器的动作，且处于整个传动的。

8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。

9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。

3、判断题1)、构件都是可动的。

（）2）、机器的传动部分都是机构。

（）3）、互相之间能作相对运动的物件是构件。

（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。

（）5）、机构的作用，只是传递或转换运动的形式。

（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。

（）7）、机构中的主动件和被动件，都是构件。

（）2 填空题答案1）、构件 2）、构件 3）、代替机械功 4）、相对运动 5）、传递转换6）、运动制造 7）、预定终端 8）、中间环节 9）、确定有用构件3判断题答案1）、√ 2）、√ 3）、√ 4）、√ 5）、× 6）、√ 7）、√第二章机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。

机械原理课后答案

机械原理课后习题答案（顺序有点乱，不过不影响）第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答：参考教材5~7页。

2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，而且也可用来进行动力分析。

2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况?答：参考教材12~13页。

2-4 何谓最小阻力定律?试举出在机械工程中应用最小阻力定律的1、2个实例。

2-5 在计算平面机构的自由度时，应注意哪些事项?答：参考教材15~17页。

2-6 在图2-20所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗?为什么?答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。

2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答：参考教材18~19页。

2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答：参考教材20~21页。

2-9 任选三个你身边已有的或能观察到的下列常用装置(或其他装置)，试画出其机构运动简图，并计算其自由度。

1)折叠桌或折叠椅；2)酒瓶软木塞开盖器；3)衣柜上的弹簧合页；4)可调臂台灯机构；5)剥线钳；6)磁带式录放音机功能键操纵机构；7)洗衣机定时器机构；8)轿车挡风玻璃雨刷机构；9)公共汽车自动开闭门机构；10)挖掘机机械臂机构；…。

2-10 请说出你自己身上腿部的髋关节、膝关节和踝关节分别可视为何种运动副?试画出仿腿部机构的机构运动简图，并计算其自由度。

2-11图示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮j输入，使轴A连续回转；而固装在轴^上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。

机械原理习题及课后答案(图文并茂)

3 4
2
1 5
解答：原机构自由度 F=33- 2 4-1 = 0，不合理，改为以下几种结构均可：
2-3 图 2-39 所示为一小型压力机，其中，1 为滚子；2 为摆杆；3 为滑块；4 为滑杆；5 为齿轮及凸轮；6 为连杆；7 为齿轮及偏心轮；8 为机架；9 为压头。试绘制其机构运动简图，并计算其自由度。
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决，机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料1荷试试下卷卷高问总中题体资2配2料，置试而时卷且，调可需控保要试障在验各最；类大对管限设路度备习内进题来行到确调位保整。机使在组其管高在路中正敷资常设料工过试况程卷下中安与，全过要，度加并工强且作看尽下护可都关能可于地以管缩正路小常高故工中障作资高；料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高，核中或对资者定料对值试某，卷些审弯异核扁常与度高校固中对定资图盒料纸位试，置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置，线高尤弯中其曲资要半料避径试免标卷错高调误等试高，方中要案资求，料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高，技料课中并术3试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术，、以术来管及避架系免等统不多启必项动要方方高式案中，；资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资，中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置，作调合并试理且技利进术用行，管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵：导活在。。分对对线于于盒调差处试动，过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调，问试应题技采，术用作是金为指属调发隔试电板人机进员一行，变隔需压开要器处在组理事在；前发同掌生一握内线图部槽纸故内资障，料时强、，电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料，试试线卷卷缆试切敷验除设报从完告而毕与采，相用要关高进技中行术资检资料查料试和，卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

(完整版)机械原理课后全部习题答案

机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征？机器通常由哪三部分组成？各部分的功能是什么？2）、机器与机构有什么异同点？3）、什么叫构件？什么叫零件？什么叫通用零件和专用零件？试各举二个实例。

4）、设计机器时应满足哪些基本要求？试选取一台机器，分析设计时应满足的基本要求。

2、填空题1)、机器或机构，都是由组合而成的。

2）、机器或机构的之间，具有确定的相对运动。

3）、机器可以用来人的劳动，完成有用的。

4）、组成机构、并且相互间能作的物体，叫做构件。

5）、从运动的角度看，机构的主要功用在于运动或运动的形式。

6）、构件是机器的单元。

零件是机器的单元。

7）、机器的工作部分须完成机器的动作，且处于整个传动的。

8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。

9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。

3、判断题1)、构件都是可动的。

（）2）、机器的传动部分都是机构。

（）3）、互相之间能作相对运动的物件是构件。

（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。

（）5）、机构的作用，只是传递或转换运动的形式。

（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。

（）7）、机构中的主动件和被动件，都是构件。

（）2 填空题答案1）、构件2）、构件3）、代替机械功4）、相对运动5）、传递转换6）、运动制造7）、预定终端8）、中间环节9）、确定有用构件3判断题答案1）、√2）、√3）、√4）、√5）、×6）、√7）、√第二章机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。

机械原理课后习题答案

机械原理课后习题答案1. 机械原理是机械工程专业的重要基础课程，通过学习机械原理，可以帮助我们更好地理解和应用机械知识。

下面是一些机械原理课后习题的答案，希望对大家的学习有所帮助。

2. 习题一，已知一个力为200N的物体沿水平方向移动了5m，求所做的功。

答案，功的计算公式为W=Fs，其中W为功，F为力，s为位移。

根据题目，力F为200N，位移s为5m，代入公式计算得W=200N5m=1000J。

所做的功为1000焦耳。

习题二，一个质量为2kg的物体，受到一个力为10N的水平拉力，求物体的加速度。

答案，根据牛顿第二定律F=ma，其中F为力，m为质量，a为加速度。

代入题目数据，10N=2kga，解得a=5m/s²。

物体的加速度为5米每秒平方。

习题三，一个质量为5kg的物体，从静止开始受到一个力为20N的水平拉力，求物体移动2秒后的速度。

答案，根据牛顿第二定律F=ma和速度公式v=at，首先求加速度a=20N/5kg=4m/s²，然后代入速度公式v=4m/s²2s=8m/s。

物体移动2秒后的速度为8米每秒。

3. 通过以上习题的答案，我们可以看到机械原理课程中涉及到了力、功、加速度等重要概念的计算和应用。

这些知识对于我们理解和分析机械运动、设计机械系统等具有重要意义。

希望大家在学习机械原理课程时，能够认真对待课后习题，加强对知识点的理解和掌握，为将来的学习和工作打下坚实的基础。

4. 总之，机械原理课后习题的答案是我们学习和掌握知识的重要参考，希望大家在学习过程中能够认真对待，勤加练习，提高自己的理论水平和实际能力。

祝大家学习进步，取得优异成绩！。

机械原理课后题答案

机械原理课后题答案1. 列举并解释一下机械原理中的三大支配因素。

- 动力：指施加在机构元件上的力或力矩，用来驱动机构执行运动或产生工作效果。

- 运动：指机构元件相对运动的方式、路径和速度。

- 连结：指机构元件之间的连接方式，包括直接和间接连接两种形式。

2. 解释一下机械原理中的三大运动副类型。

- 滑动副：两个机构元件之间只能沿着一条确定的直线运动，如推拉杆、滑块等。

- 旋转副：两个机构元件之间只能绕一条确定的轴线旋转运动，如轴承、齿轮等。

- 滚动副：两个机构元件之间存在滚动运动，如滚子轴承、滚珠丝杠等。

3. 什么是机械原理中的受力分析方法？受力分析方法是指通过分析机构元件之间的力和力矩关系，找出各个元件的受力情况，以解决机构设计和运动性能分析的方法。

常用的受力分析方法包括力平衡法、力矩平衡法、虚功原理等。

4. 什么是力平衡法？力平衡法是一种受力分析方法，通过分析机构元件之间的力平衡关系，得到各个元件所受力的大小和方向。

它基于牛顿第一定律，即所有物体受力之和为零，可用来解决机构中受力平衡问题，确定力的大小和方向。

5. 解释一下力矩平衡法。

力矩平衡法是一种受力分析方法，通过分析机构元件之间的力矩平衡关系，得到各个元件所受力的大小和方向。

在机械原理中，力矩平衡法常被用于解决转动副运动问题，根据力矩平衡条件，求解未知力矩和力矩的方向。

6. 什么是虚功原理？虚功原理是一种受力分析方法，通过分析机构元件之间的虚功平衡关系，得到各个元件所受力的大小和方向。

虚功原理是基于功率平衡的原理，即虚功平衡原理，在机械原理中常用于分析运动副的受力情况和功率传递效率。

7. 介绍一下机械原理中的摩擦现象。

摩擦是指两个物体相对运动时由接触面之间的相互作用力导致的阻碍运动的力。

在机械运动中，正常情况下不可避免地存在摩擦力，摩擦力会导致机械能的损失、能量的消耗和部件的磨损。

因此在机械原理中需要对摩擦进行充分的考虑和分析。

机械原理习题及课后答案

机械原理课后习题及参考答案第二章机构的结构分析2-2 图2-38所示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1输入，使轴A连续回转；而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图，分析其运动是否确定，并提出修改措施。

4351 2解答：原机构自由度F=3⨯3- 2 ⨯4-1 = 0，不合理，改为以下几种结构均可：2-3 图2-396为连杆；7为齿轮及偏心轮；8为机架；9为压头。

试绘制其机构运动简图，并计算其自由度。

O齿轮及偏心轮ωA齿轮及凸轮BEFDC压头机架连杆滑杆滑块摆杆滚子解答：n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 = 12-6 试计算图2-42所示凸轮—连杆组合机构的自由度。

解答：a) n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 =1 L 处存在局部自由度，D 处存在虚约束b) n=5; P l =6; P h =2，F=3⨯5-2 ⨯6-2 =1 E 、B 处存在局部自由度，F 、C 处存在虚约束b)a)A EMDFELKJIFBCCDBA2-7 试计算图2-43所示齿轮—连杆组合机构的自由度。

BDCA(a)CDBA(b)解答：a) n=4; P l =5; P h =1，F=3⨯4-2 ⨯5-1=1 A 处存在复合铰链 b) n=6; P l =7; P h =3，F=3⨯6-2 ⨯7-3=1 B 、C 、D 处存在复合铰链2-8 试计算图2-44所示刹车机构的自由度。

并就刹车过程说明此机构自由度的变化情况。

解答：① 当未刹车时，F=3⨯6-2 ⨯8=2② 在刹车瞬时，F=3⨯5-2⨯7=1，此时构件EFG 和车轮接触成为一体，位置保持不变，可看作为机架。

③ 完全刹死以后，F=3⨯4-2⨯6=0，此时构件EFG 、HIJ 和车轮接触成为一体，位置保持不变，可看作为机架。

机械原理(哈)课后习题

机械原理习题第二章习题2-1 解释下列概念1. 运动副；2. 机构自由度；3. 机构运动简图；4. 机构结构分析；5.高副低代。

2-2验算下列机构能否运动，看运动是否具有确定性，并给出具有确定运动的修改方法。

a）b）题2-22-3绘出下列机构的运动简图，并计算其自由度，并说明注意事项。

a）b）题2-32-4计算下列机构自由度，并说明其自由度（其中构件1均为机架）。

a）b）c）d）e）题2-42-5计算下列机构的自由度，并确定杆组及机构的级别（如图所示机构分别以构件2、4、8为原动件）。

题2-5第三章习题3-3在图示铰链四杆机构中，已知：mm l BC 50=，mm l CD 35=，mm l AD 30=，AD 为机架，并且1）若此机构为曲柄摇杆机构，且AB 为曲柄，求AB l 的最大值；2）若此机构为双曲柄机构，求AB l 的最小值；3）若此机构为双摇杆机构，求AB l 的数值。

题 3-33-4试求图示各机构在图示位置时全部瞬心的位置。

a ）b ）c ）d ）题 3-4 3-5在图示的齿轮-连杆组合机构中，试用瞬心法求齿轮1与齿轮3的传动比31/ωω。

题 3-53-6在图示凸轮机构中，已知mm r 50=，mm l OA 22=，mm l AC 80=，οϕ901=，凸轮，凸轮1以角速度s rad /101=ω逆时针方向转动。

试用瞬心法求从动件2的角速度2ω。

题 3-63-7在的四杆机构ABCD 中，mm l AB 60=，mm l CD 90=，mm l l BC AD 120==，s rad /102=ω，试用瞬心法求：1）当οϕ165=时，点C 的速度c v ；2）当οϕ165=时，构件3的BC 线上（或其延长线上）速度最小的一点E 的位置及其速度的大小；3）当0=c v 时，ϕ角的值（有两个解）。

3-8在转动导杆机构机构中，已知mm l AC 50=，mm l BC 100=，s rad /202=ω，求在一个运动循环中，构件3的角位移、角速度和角加速度。

机械原理课后题答案

选择填空：（1）当机构的原动件数目小于或大于其自由度数时，该机构将（ B ）确定运动。

A.有；B.没有；C.不一定；（2）在机构中，某些不影响机构运动传递的重复部分所带入的约束为（ A ）。

A.虚约束；B.局部自由度；C.复合铰链；（3）机构具有确定运动的条件是（B ）。

A.机构自由度数小于原动件数；机构自由度数大于原动件数；B.机构自由度数等于原动件数；（4）用一个平面低副联二个做平面运动的构件所形成的运动链共有（ B ）个自由度。

A.3；B.4；C.5；D.6；（5）杆组是自由度等于（ A ）的运动链。

A.0；B.1；C.原动件数。

（6）平面运动副所提供的约束为（ D ）。

A.1；B.2；C.3；D.1或2；（7）某机构为Ⅲ级机构，那么该机构应满足的必要充分条件是（ D ）。

A.含有一个原动件组；B.原动件；C.至少含有一个Ⅱ级杆组；D.至少含有一个Ⅲ级杆组；（8）机构中只有一个（D ）。

A.闭式运动链；B.原动件；C.从动件；D.机架。

（9）具有确定运动的差动轮系中其原动件数目（ C ）。

A.至少应有2个；B.最多有2个；C.只有2个；D. 不受限制。

（10）在加速度多边形中，连接极点至任一点的矢量，代表构件上相应点的____B__加速度；而其它任意两点间矢量，则代表构件上相应两点间的______加速度。

A.法向; 切向B.绝对; 相对C.法向; 相对D.合成; 切向（11）在速度多边形中，极点代表该构件上_____A_为零的点。

A.绝对速度B.加速度C.相对速度D.哥氏加速度（12）机械出现自锁是由于（ A ）。

A. 机械效率小于零；B. 驱动力太小；C. 阻力太大；D. 约束反力太大；（13）当四杆机构处于死点位置时，机构的压力角＿B ＿。

A. 为00；B. 为090；C. 与构件尺寸有关；（14）四杆机构的急回特性是针对主动件＿D ＿而言的。

D. 等速运动；E. 等速移动；F. 变速转动或变速移动；（15）对于双摇杆机构，最短构件与最长构件之和＿H ＿大于其余两构件长度之和。

机械原理(哈)课后习题

机械原理 课后习题答案

机械原理课后习题_答案.PPT36页

《机械原理》课后习题附答案

机械原理课后题答案

机械原理课后习题答案

机械原理课后习题答案

机械原理课后习题答案部分

机械原理课后习题答案

机械原理课后全部习题解答

机械原理课后答案

机械原理习题及课后答案(图文并茂)

(完整版)机械原理课后全部习题答案

机械原理课后习题答案

机械原理课后题答案

机械原理习题及课后答案

机械原理(哈)课后习题

机械原理课后题答案

机械原理课后习题答案