几何光学
合集下载
几何光学

几何光学定律成立的条件
1. 光学系统的尺度远大于光波的波长。 2. 介质是均匀和各向同性的。 3. 光强不是很大。
一、基本概念
光线
波面
球面波
平面波
光线:表示光波能量传播方向的几何线。 波面:光波位相相同的同相面。
几何光学中仅讨论与光线垂直的平面或球面,分别 对应平面波或球面波。
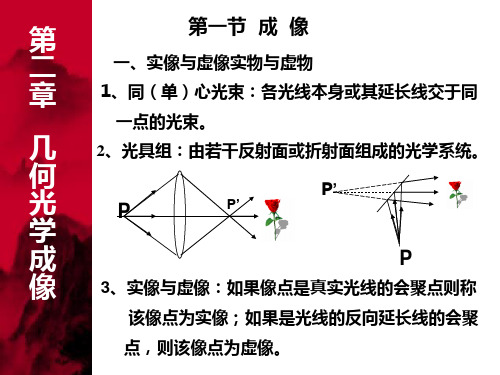
一、物和像
单心光束:相交于一点或他们的延长线交于一点的 光线称作单心光束。 非单心光束:各光线或其延长线不交于同一点的光 线称为非单心光束。 物点:入射单心光束的会聚点称为物点。 实物点:若入射光束为发散的单心光束,则物点叫 做实物点。 虚物点:若入射光束为汇聚的单心光束,则物点叫 做虚物点。 理想光学系统:不改变入射光束单心性的光学系统 称为理想光学系统。
一、物和像
像点: 出射单心光束的会聚点称为像点。 实像点:若出射光束为汇聚的单心光束,则像点为 实像点。 虚像点:若出射光束为发散的单心光束,则像点为 虚像点。 物空间:未经光学系统变换前入射的单心光束所在 的空间叫物空间。 物方折射率:物空间介质的折射率叫做物方折射率 像空间:经光学系统变换后出射的单心光束所在的 空间叫做像空间。 像方折射率:像空间介质的折射率叫做像方折射率
二、几何光学的基本实验定律
光的直线传播定律:光在同一种均匀介质中是 沿直线传播的。 光的反射和折射定律 光的独立传播定律:两列或几列光波在空间相 遇后,互不发生影响,各自保持自己的特性继 续向前传播。 光的可逆性原理:光在空间传播时,其光路是 可逆的。
三、费马原理
费马原理:光在指定的两点之间传播,其实际 光程总是一个极值。也就是说光沿光程为最大、 最小或恒定的路程传播。
1. 光学系统的尺度远大于光波的波长。 2. 介质是均匀和各向同性的。 3. 光强不是很大。
一、基本概念
光线
波面
球面波
平面波
光线:表示光波能量传播方向的几何线。 波面:光波位相相同的同相面。
几何光学中仅讨论与光线垂直的平面或球面,分别 对应平面波或球面波。
一、物和像
单心光束:相交于一点或他们的延长线交于一点的 光线称作单心光束。 非单心光束:各光线或其延长线不交于同一点的光 线称为非单心光束。 物点:入射单心光束的会聚点称为物点。 实物点:若入射光束为发散的单心光束,则物点叫 做实物点。 虚物点:若入射光束为汇聚的单心光束,则物点叫 做虚物点。 理想光学系统:不改变入射光束单心性的光学系统 称为理想光学系统。
一、物和像
像点: 出射单心光束的会聚点称为像点。 实像点:若出射光束为汇聚的单心光束,则像点为 实像点。 虚像点:若出射光束为发散的单心光束,则像点为 虚像点。 物空间:未经光学系统变换前入射的单心光束所在 的空间叫物空间。 物方折射率:物空间介质的折射率叫做物方折射率 像空间:经光学系统变换后出射的单心光束所在的 空间叫做像空间。 像方折射率:像空间介质的折射率叫做像方折射率
二、几何光学的基本实验定律
光的直线传播定律:光在同一种均匀介质中是 沿直线传播的。 光的反射和折射定律 光的独立传播定律:两列或几列光波在空间相 遇后,互不发生影响,各自保持自己的特性继 续向前传播。 光的可逆性原理:光在空间传播时,其光路是 可逆的。
三、费马原理
费马原理:光在指定的两点之间传播,其实际 光程总是一个极值。也就是说光沿光程为最大、 最小或恒定的路程传播。
大学物理--几何光学

B
B
B
ndl n dl
A
A
而由公理:两点间直线距离最短 A
B
dl 的极小值为直线AB A
所以光在均匀介质中沿直线传播
2.光的反射定律
Q点发出的光经 反射面Σ到达P点
P’是P点关于Σ 面的对称点。
P,Q,O三点 确定平面Π。
直线QP’与反射 面Σ交于O点。
nQO OP
则易知当i’=i时,QO + OP为光程最短的路径。
•直接用真空中的光速来计算光在不同介质中通过一定 几何路程所需要的时间。
t nl ct cc
•光程表示光在介质中通过真实路程所需时间内,在真空
中所能传播的路程。
分区均匀介质:
k
nili
i 1
,
t
c
1 c
k i 1
nili
连续介质:
ndl (l)
二、费马原理
1.表述:光在空间两定点间传播时,实际光程为一特 定的极值。
'
nl
nl '
n r 2 r s 2 2 r r s cos
n
r 2
s '
2
r
2
r s '
r cos
A
l
i -i` l '
P
-u
-u`
C
P` -s` O
-r
-s
对给定的物点,不同的入射点,对应着不同
的入射线和反射线,对应着不同的 。
由费马原理可知 :当 d PAP' 0 时,
2. 光的折射反射定律:
(1) 光的反射定律:反射线位于入射面内,反射线和 入射线分居法线两侧,反射角等于入射角,即
第12章 几何光学

望远镜的光路
内窥镜
水柱引导光线的行进
11
12.2 光程 费马原理
一、光程
光在均匀介质走过的几何路程 r 与
介质折射率 n 之乘积。用 L表示。
即: L= nr
光程的物理意义:光程就是光在介质中通过的 几何路程按波数相等折合到真空中的路程。
r nr
'
介质中:
折合到真
r
连续变化的介质:
空中:
nr
n
2
◆ 光的波粒二象性
• 牛顿:光的直线转播说明光是粒子流。 • 惠更斯、托马斯 · 杨、菲涅耳:光具有干涉和衍
射现象,所以光是一种波。 • 麦克斯韦:根据我的理论,光是一种电磁波,而
且是横波,转播速度为每秒30万公里。 • 迈克尔逊:我为什么测不到“以太风”。 • 爱因斯坦:用普朗克的“能量子”解释了光电效应。
y P iO
n1
γC
n2
Q
y A
p
q
m y n1q y n2 p
22
一、透镜
12.4 薄透镜成像
透镜——将玻璃、水晶等磨成两面为球面(或一面为平面) 的透明物体。
薄透镜:透镜厚度远小于两球面的曲率半径。
或 两个侧面的中心靠得很近的透镜。
凸透镜: 中间厚边缘薄 的透镜。
①
②
③
凹透镜:中间薄边缘厚
率),其定义为:
n c v
光在真空中的传播速度 光在介质中的传播速度
两种介质相比较,折射率大的介质,光在其中的
传播速度小,称为光密介质;折射率小的介质,光在
其中的传播速度大,称为光疏介质。
n21
v1 v2
n2 n1
折射定律也可表示为:
第二章几何光学
三、傍轴物点成像与横向放大率
第
二 章
PΠ
n
n’
Q
几
i
C
A
i’
Q’
-y’ P’
何
s
Σ
s’
Π’
光
学
傍轴条件:y 2 , y2 s 2 ,s2 ,r 2
成
像
对于折射球面: V y ns y ns
讨论放大率的正负 与像的虚实
对于反射球面: V y s ys
四、逐次成像
第 二
n1
n3 n2
章
二
折射面的曲 5.7mm 网膜的曲率 9.8mm
率半径R
半径R’
章
物方焦距f -17.1mm 像方焦距f ’ 22.8mm
几
何
人眼的调节功能
光
1、改变眼睛的焦距使距离不同的物体都能在视网
学
膜上形成清晰的像,这个过程称为眼睛的调节。
成
像
眼睛能看清的最远点称为远点(无穷远);
眼睛能看清的最近点称为近点(25cm)。
之,高度y(y’)<0。
(5)图示中的各个量均为正值。
第
第二节 共轴球面组傍轴成像
二
一、光在单个球面上的折射
章 几 何
nl A
P
Oφ
s
r
B
l’ C s’
P’ n’
光 学
1
l r 2 r s2 2rr scos 2
成
1
l r 2 s r 2 2rs r cos 2
像
由费马原理可得:
像
和像方主点重合的。
四、惠更斯目镜与冉斯登目镜
第 二
1、惠更斯目镜
第十四章 几何光学

n1 n2 n2 − n1 + = u1 v1 r 1
1 1.5 1.5 −1 + = 40 v1 10
解得
v1=60cm
u1
v1
第二球面成像:u2= -(v1-2r )= -40cm, n1 = 1.5, n2 = 1,r 2= -10cm
代入公式
得
n1 n2 n2 − n1 + = u2 v2 r2
第十四章 几何光学
以几何定律和某些基本实验定律为基础的光学称 为几何光学。 一、几何光学的基本定律: 几何光学的基本定律: 1、光在均匀介质中的直线传播定律。 2、光通过两种介质分界面时的反射定律和折射定律。 折射定律:n1 sin i1= n2 sin i2 3、光的独立传播定律和光路可逆原理。
第一节 球面折射
第二节 透镜 透镜(lens)
把玻璃等透明物质磨成薄片,其表面都为球面或 有一面为平面,即组成透镜,如下图所示。 中间部分比 边缘部分厚的 透镜叫凸透镜。 中间部分比 边缘部分薄的 透镜叫凹透镜。
+r −r2 r = ∞ −r2 1 1
双凸 平凸
−r −r2 1
弯凸
−r +r2 1
双凹
−r r2 = ∞ −r −r2 1 1
如果用v1表示上一个球面像距,u2表示下一个球面 的物距,d 表示上下两球面之间的距离,则 u2=d-v1 上式适用于所有的情况,其中,u2、v1都带符号。 例如,求得上一球面像距v1= -5cm(成一虚像),上下 两球面之间的距离d=10cm,则 u2=d-v1=10-(-5)=15cm (实物) --
v2=11.4cm
2.像与物的关系 用逐个球面成像法求解共轴系统成像问题时,关键 要弄清楚上一个球面的像是下一球面的实物还是虚物。 当成像是从左到右依次进行时,如果上一个球面 所成像(虚、实)的位置在下一个球面的左边,对下 一个球面来说,该像是实物,u>0;反之,如果上一 u>0 个球面所成像(实)的位置在下一个球面的右边,对 下一个球面来说,该像是虚物,u<0。 就是说,若上一球面成一虚像,则对下一球面来说, 它一定是实物。若上一球面所成的像为实像,则要根 据此像的像距与上、下两球面之间的距离进行比较, 判断是实物还是虚物。
光学第三章几何光学

2、c —— 光速
联系光与电磁波
3、λ ——光波长
是否趋近于零 区分几何光学与波动光
学 4、χ ——介质的电极化率
其对光场响应是线性与非线性区分线性 与非线性光学
费马原理
一、费马原理:光在指定的两点间传播时,
实际的光程总是一个极值。其数学表达式为:
B nds 极值(极大值、极小值或恒定值) A
射光束都是单心光束的成像。这也是我们
着重研究的情况。
3、物、像与人眼
问题:
‘
这里的像就是人眼视网膜上所成的
像吗?人眼能否区分物与像?
结论:
对人眼来所,物与像都是进入瞳孔的发
射光束的顶点。物、像、虚像人眼不能分辨。
但对于像,其光束有一定的限制,必须在特定
的范围才能观察到。
光在平面界面上的反射和折射 光学纤维 棱镜
第 三 章 几 何 光 学
三角形孔夫琅禾费衍射图像
本章内容
光线的概念 几何光学的基本定律 费马原理 光束 实象和虚像 平面反射和折射,棱镜的最小偏向角,光
学纤维 光在球面界面上的反射和折射、符号法则 近轴物点近轴光线成像的条件 薄透镜 理想光具组的基点和基面
光线的概念、几何光学的基本定律
B
或: nds 0 A
或:t 1
B
nds 0
ccA
二、几何光学的基本实验定律与费马原理
1、几何光学的基本实验定律或费马原理都可以 作为几何光学出发点,从而建立几何光学内容 体系。 2、由费马原理可以推导几何光学的基本实验 定律。 (1)、光在均匀介质中的直线传播
S
1
l = ([ - r)2 +(r - s)2 + (2 - r)( r - s)cos ] 2
联系光与电磁波
3、λ ——光波长
是否趋近于零 区分几何光学与波动光
学 4、χ ——介质的电极化率
其对光场响应是线性与非线性区分线性 与非线性光学
费马原理
一、费马原理:光在指定的两点间传播时,
实际的光程总是一个极值。其数学表达式为:
B nds 极值(极大值、极小值或恒定值) A
射光束都是单心光束的成像。这也是我们
着重研究的情况。
3、物、像与人眼
问题:
‘
这里的像就是人眼视网膜上所成的
像吗?人眼能否区分物与像?
结论:
对人眼来所,物与像都是进入瞳孔的发
射光束的顶点。物、像、虚像人眼不能分辨。
但对于像,其光束有一定的限制,必须在特定
的范围才能观察到。
光在平面界面上的反射和折射 光学纤维 棱镜
第 三 章 几 何 光 学
三角形孔夫琅禾费衍射图像
本章内容
光线的概念 几何光学的基本定律 费马原理 光束 实象和虚像 平面反射和折射,棱镜的最小偏向角,光
学纤维 光在球面界面上的反射和折射、符号法则 近轴物点近轴光线成像的条件 薄透镜 理想光具组的基点和基面
光线的概念、几何光学的基本定律
B
或: nds 0 A
或:t 1
B
nds 0
ccA
二、几何光学的基本实验定律与费马原理
1、几何光学的基本实验定律或费马原理都可以 作为几何光学出发点,从而建立几何光学内容 体系。 2、由费马原理可以推导几何光学的基本实验 定律。 (1)、光在均匀介质中的直线传播
S
1
l = ([ - r)2 +(r - s)2 + (2 - r)( r - s)cos ] 2
第一章 几何光学

第一章 几何光学
以光线概念为基础研究光的 传播和成像规律
§1.1 光线传播的基本定律
一.几何光学的实验定律
1.光的直线传播定律。(各向同性介质中)
共面
2.反射定律和折射定律:
分于法线两侧 角度关系
3.光的独立传播定律和光路可逆原理(各向同性介质中)
几何光学中常用的器件-----棱镜
作用:改变光路 色散分光
s
2 2 2
n (s r)
n
s
/2
/2
0
/ 2
(s r )
1 n (s r )
2
n
1
/2
0
(s r)
/
求出上两式联立方程的解,可得一对特殊的共轭点, 称为球面折射的齐明点或不晕点 对一对齐明点,宽光束经球面折射仍能成像。
(二)把光束限制在傍轴区,即
则有:
2
cos 1
共轴球面系统的基点基面
(1) 焦点与焦平面
焦平面的普遍意义:顶点位于焦平面上的光束,其共轭光束为平行光束; 顶点位于焦点上的光束,其共轭光束与主光轴平行。 物(像)方焦点F( F'):与无限远处像(物)点共轭的轴上物(像)点。 物(像)方焦平面:过物(像)方焦点F( F' )的垂轴平面。
2
在傍轴区d<<s,s/,|r|;略去二阶以上无穷小量得
d (r s) PM s 1 2 s
d (r s' ) M P s ' 1 2 s'
因此,光程
d (r s) d (r s' ) [ PMP ' ] ns 1 2 2 ns ' 1 s s'
以光线概念为基础研究光的 传播和成像规律
§1.1 光线传播的基本定律
一.几何光学的实验定律
1.光的直线传播定律。(各向同性介质中)
共面
2.反射定律和折射定律:
分于法线两侧 角度关系
3.光的独立传播定律和光路可逆原理(各向同性介质中)
几何光学中常用的器件-----棱镜
作用:改变光路 色散分光
s
2 2 2
n (s r)
n
s
/2
/2
0
/ 2
(s r )
1 n (s r )
2
n
1
/2
0
(s r)
/
求出上两式联立方程的解,可得一对特殊的共轭点, 称为球面折射的齐明点或不晕点 对一对齐明点,宽光束经球面折射仍能成像。
(二)把光束限制在傍轴区,即
则有:
2
cos 1
共轴球面系统的基点基面
(1) 焦点与焦平面
焦平面的普遍意义:顶点位于焦平面上的光束,其共轭光束为平行光束; 顶点位于焦点上的光束,其共轭光束与主光轴平行。 物(像)方焦点F( F'):与无限远处像(物)点共轭的轴上物(像)点。 物(像)方焦平面:过物(像)方焦点F( F' )的垂轴平面。
2
在傍轴区d<<s,s/,|r|;略去二阶以上无穷小量得
d (r s) PM s 1 2 s
d (r s' ) M P s ' 1 2 s'
因此,光程
d (r s) d (r s' ) [ PMP ' ] ns 1 2 2 ns ' 1 s s'
第十一章 几何光学181212

n1 n2 n2 n1
uv
r
f2
n2 r n2 n1
f1
n1 r n2 n1
f2
n2 r n2 n1
①f1 、f2可正可负, F1、F2可以是实焦点,也可 以是虚焦点,单球面对光线可以起到会聚作用, 也可以起到发散作用。
②当f1 、f2为正时, F1、F2是实际光线交汇点, 就是实焦点,对光线起会聚作用;
1 1 n 1( 1 1 )
uv
r1 r2
透镜有两个焦点;若薄透镜两侧介质n不同时,
两焦距不等;当薄透镜两侧介质n相同时,两焦
距也相等。
薄透镜焦距公式
f
n
n0 n0
1 ( r1
1 1
r2
)
比
薄透镜公式 1 1 n n0 ( 1 1 )
较
例11-2 从几何光学的角度来看,人眼可简化为 高尔斯特兰简化眼模型。这种模型将人眼成像归 结成一个曲率半径为5.7mm、媒质折射率为1.33 的单球面折射成像。⑴试求这种简化眼的焦点位 置和焦度;⑵若已知某物在膜后24.02mm处视网 膜上成像,求该物应放在何处。
解⑴:已知n1=1.0, n2=1.33, r=5.7mm
ur
a.从F1到折射面顶点的距离(物距)叫第一焦距,f1 u=f1,v =∞
n1 n2 n2 n1
uv
r
f1
n1 r n2 n1
n1
n2
平行主光轴光线成像 于F2处,F2称为折 射面的第二焦点。
F2
v r
b.从F2到折射面顶点的距离(像距)叫第二焦距,f2
u= ∞ ,v =f2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代入n1 sin i1 n2 sin i2得:
n1
y u
n2
y v
所以,球面折射成像的横向放大率表达式为:
M y n1v y n2u
3.焦度、焦点和焦距
• •
焦度:
(1)
n2
n1
r
• (2)意义:表示球面的折射本领
• (3)单位:屈光度,符号:D
1D 100度
焦点,焦距:
① 第一焦点: F1 第一焦距: f1
解:第一折射面,n1=1.0,n2=1.5,u1=40cm,r=10cm
代入
n1 u
n2 v
n2
r
n1
1.0
有:
40
1.5 v1
1.5 - 1.0 10
解得:v1=60cm
第二折射面,n1=1.5,n2=1.0,u2=-(60-20)=-40cm,r=-10cm
代入
n1 u
n2 v
n2
r
n1
横向放大率:M
y y
n1v n2u
4. 共轴球面系统
第二节 透 镜
一 . 薄透镜成像公式 二 . 薄透镜的组合 三.共轴球面系统的三对基点几作图成像法 四.非对称折射系统与柱面透镜 五.透镜的像差
一 . 薄透镜成像公式
透镜(lens)是由两个共轴 折射面系统组成,两个折 射面之间是均匀透明介 质.透镜两折射面与主光 轴交点的距离 d 称为透 镜的厚度. 若透镜的厚度与焦距相比可以忽略时,则称其为 薄透镜,厚度不可忽略者为厚透镜.
f1 f2
r
例10-1:如图所示,有一折射率为1.5的玻璃棒,一端为 r=30cm的光滑凸球面,另一端为磨砂平面,试问该棒多长时, 正好使无限远处物体经球面后清晰的成像在磨砂平面上?
P
F
n1
n2
• 解:
根据单球面折射公式:
n1 n2 n2 n1
uv r
代入数据: 1 1.5 1.5 1
第一节 球面折射
一 . 单球面折射 二 . 共轴球面折射
一.什么是单球面折射系统
像
点光源 球面顶点
曲率中心
球面半径
• 如图所示:两种介质的分界面是球面的一部分,这样的装置就是 一个单球面折射系统。
• 几个概念: • 主光轴——通过曲率中心C的直线OCI; • 物 距 ——物点O到球面顶点P的距离(OP),用u表示; • 像 距 ——像点I到球面顶点P的距离(PI),用v表示;
1.5
有:
- 40
1.0 v2
1.0 -
1- 01.5解得:v2=11.4cm
小结:
1.单球面折射成像公式:
n1 n2 n2 n1 uv r
符号规定:实物、实像取正;虚物、虚像取负。
入射光线
对着凸面,r取正。 对着凹面,r取负。
2. 焦度: Φ n1 n2 n2 n1
f1 f2
r
3.
(重要结论)
单球面折射成像公式:
n1 n2 n2 n1
适用条件: u v
r
1.近轴光线; 2.任何凸、凹球面
符号法则:
①如果从物点到折射面的方向与入射光的方向相同,则物距为正, 反之为负,即实物的物距为正,虚物的物距为负;
②如果从折射面到像的方向与折射光的方向相同,则像距为正, 反之为负,即实像的像距为正,虚像的像距为负。
像在无穷远处的物点
n1
n2
n1 f1
f1n2
n2
nn12 nr1
n1
rF1Leabharlann f1② 第二焦点: F2 第二焦距: f2
物在无穷远处的像点
n1
n2
n1f
2nf22n2n2nn21
r r
n1
F2
f2
f1 f2
0, F1为实焦点 0,F2为实焦点
折射面对入射光线会聚
(3)焦距和焦度的关系
Φ n1 n2 n2 n1
③若实际入射光线对着凸球面,则r取正值,反之,如实际入射光 线对着凹球面,则r取负值。
④n1,n2的顺序以实际入射光线的行进为准。
o
u>0
图①
r >0
I
v >0
oI
图② u<0 v >0
r >0
u>0 v <0
r <0
oI
图③
(3)单球面成像的放大率
y sin i1 tan i1 u
y sin i2 tan i2 v
n0
O
I
I1
u=u1
v2= v
u2=- v1
n n0 n0 n
v1 v
r2
两式相加得
1 1 n n0 ( 1 1 ) u v n0 r1 r2
若透镜处在空气中,这时n0=1,则上式可简化为
1 1 (n 1)( 1 1 )
uv
v 30
解得:
v 90cm
二、共轴球面系统
如果两个或两个以上折射球面的曲率中心和球面 顶点都在同一直线上,它们便组成共轴球面系统.
在成像过程 中,前一个折射面所成的像,即为 相邻的后一个折射面的物。
采用逐次成像法,应用单球面折射成像公式,求共 轴球面系统的像。
例10-2:一点光源放在球前40cm处,已知玻璃球的直径 为20cm,折射率n2=1.5。求近轴光线通过玻璃球后所成 像的位置。
当d0时,两球面顶点重合为一点,称为光心.
根据几何形状透镜分为二类: 一类中间厚边缘薄的叫凸透镜.
双凸 平凸 弯凸
一类中间薄边缘厚的叫凹透镜.
双凹 平凹
弯凹
根据透镜对光线的作用也分为二类:
会聚透镜
发散透镜
一.薄透镜
❖ 薄透镜公式
对第一折射面
n0 n n n0
u v1
r1
对第二折射面
n
n0
贵阳医学院
医学生物工程系 喻贡友
第十章 几 何 光 学
本章内容概述:
一、几何光学的理论基础: 1.直线传播定律;2.独立传播定律;3.反射定律;4.折射定律
二、学习内容: 1.熟练掌握单球面折射系统和共轴球面折射系统的成像规律, 薄透镜的成像规律,显微镜的放大率和分辨本领概念; 2.理解眼睛的成像特点,掌握非正常眼屈光不正的矫正理论; 3.了解厚透镜的成像特点、几种特殊显微镜原理和医用内镜的工 作原理
球 面半径
n (折射定律) 1
sin
i1
n2
sin
i2
(近轴近似) i1 sin i1
i2 sin i2
n1 n2 n2 n1
tan h / u
tan h / v
tan h / r
像
n1 i1 n2 i2
i1 i2
n1 n2 n2 n1 uv r
• 近轴光线——OA、AI(α、β很小)。
• 近轴近似关系:
sin tan sin tan
二.什么单球面折射 (1)定义:在单球面折射系统中,光从一种介质射
向另一种介质时,在球状面发生的折射称为单球面折射
思考:单球面折射的成像规律是什么?
(2)单球面成像公式
点光源 球面顶点
曲率中心
