Leslie模型(数学建模)
leslie人口增长模型

人口增长预测模型摘要本文建立了我国人口增长的预测模型,对各年份全国人口总量增长的中短期和长期趋势作出了预测,并对人口老龄化、人口抚养比等一系列评价指标进行了预测。
最后提出了有关人口控制与管理的措施。
模型Ⅰ:建立了Logistic人口阻滞增长模型,利用附件2中数据,结合网上查找补充的数据,分别根据从1963年、1980年、2005年到2012年四组总人口数据建立模型,进行预测,把预测结果与附件1《国家人口发展战略研究报告》中提供的预测值进行分析比较。
得出运用1980年到2005年的总人口数建立模型预测效果好,拟合的曲线的可决系数为0.9987。
运用1980年到2005年总人口数据预测得到2010年、2020年、2033年我国的总人口数分别为13.55357亿、14.18440亿、14.70172亿。
模型Ⅱ:考虑到人口年龄结构对人口增长的影响,建立了按年龄分布的女性模型(Leslie模型):以附件2中提供的2001年的有关数据,构造Leslie矩阵,建立相应Leslie模型;然后,根据中外专家给出的人口更替率1.8,构造Leslie矩阵,建立相应的 Leslie模型。
首先,分别预测2002年到2050年我国总人口数、劳动年龄人口数、老年人口数(见附录8),然后再用预测求得的数据分别对全国总人口数、劳动年龄人口数的发展情况进行分析,得出:我国总人口在2010年达到14.2609亿人,在2020年达到14.9513亿人,在2023年达到峰值14.985亿人;预测我国在短期内劳动力不缺,但须加强劳动力结构方面的调整。
其次,对人口老龄化问题、人口抚养比进行分析。
得到我国老龄化在加速,预计本世纪40年代中后期形成老龄人口高峰平台,60岁以上老年人口达4.45亿人,比重达33.277%;65岁以上老年人口达3.51亿人,比重达25.53%;人口抚养呈现增加的趋势。
再次,讨论我国人口的控制,预测出将来我国育龄妇女人数与生育旺盛期育龄妇女人数,得到育龄妇女人数在短期内将达到高峰,随后又下降的趋势的结论。
Leslie人口模型及例题详解

Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化。
如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型。
20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变 化。
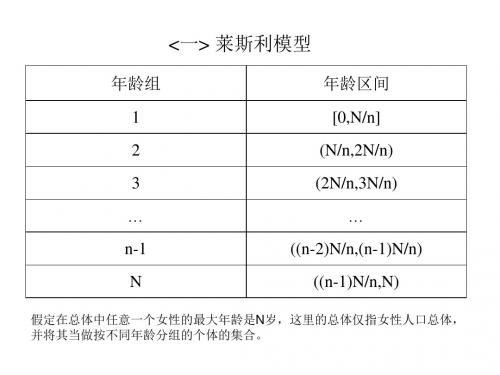
假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔人口数量的变化;(2) 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记)](,),(),([)(21t n t n t n t n m =第i 年龄组女性生育率为i b (注:所谓女性生育率指生女率),女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;(3) 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;(4) 生育率仅与年龄段有关,存活率也仅与年龄段有关。
建立模型与求解根据以上假设,可得到方程 )1(1+t n =∑=mi i i t n b 1)()()1(1t n s t n i i i =++ 1=i ,2.…,m -1 写成矩阵形式为)()1(t Ln t n =+其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000000121121m m m s s s b b b b(1) 记)]0(,),0(),0([)0(21m n n n n = (2)假设n (0)和矩阵L 已经由统计资料给出,则t1+t()(0),0,1,2,t n t L n t ==为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:(i) s i > 0,i =1,2,…,m -1;(ii) b i 0≥,i =1,2,…,m ,且b i 不全为零。
Leslie人口模型及例题详解

Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化。
如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型。
20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变 化。
假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔内人口数量的变化;(2) 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记)](,),(),([)(21t n t n t n t n m =第i 年龄组女性生育率为i b (注:所谓女性生育率指生女率),女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;(3) 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;(4) 生育率仅与年龄段有关,存活率也仅与年龄段有关。
建立模型与求解根据以上假设,可得到方程 )1(1+t n =∑=mi ii t n b 1)( )()1(1t n s t n i i i =++ 1=i ,2.…,m -1 写成矩阵形式为)()1(t Ln t n =+其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000000121121m m m s s s b b b b (1) 记)]0(,),0(),0([)0(21m n n n n = (2)假设n (0)和矩阵L 已经由统计资料给出,则t1+t()(0),0,1,2,t n t Ln t ==为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:(i) s i > 0,i =1,2,…,m -1;(ii) b i 0≥,i =1,2,…,m ,且b i 不全为零。
Leslie人口模型及例题详解

L e s l i e人口模型及例题详解The saying "the more diligent, the more luckier you are" really should be my charm in2006.Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化;如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型;20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型;模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变 化;假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔内人口数量的变化;2 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记第i 年龄组女性生育率为i b 注:所谓女性生育率指生女率,女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;3 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;4 生育率仅与年龄段有关,存活率也仅与年龄段有关;建立模型与求解根据以上假设,可得到方程 )1(1+t n =∑=mi i i t n b 1)()()1(1t n s t n i i i =++ 1=i ,2.…,m -1 写成矩阵形式为其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000000121121m m m s s s b b b b 1 记)]0(,),0(),0([)0(21m n n n n = 2假设n 0和矩阵L 已经由统计资料给出,则为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:i s i > 0,i =1,2,…,m -1;ii b i 0≥,i =1,2,…,m ,且b i 不全为零;易见,对于人口模型,这两个条件是很容易满足的;在条件i 、ii 下,下面的结果是成立的: 定理1t1+tL 矩阵有唯一的单重的正的特征根0λλ=,且对应的一个特征向量为*n =1,s 1/0λ,s 1s 2/20λ,…,s 1s 2 …s m -1/10-m λT3 定理2若1λ是矩阵L 的任意一个特征根,则必有01λλ≤;定理3若L 第一行中至少有两个顺次的0,1>+i i b b ,则i 若1λ是矩阵L 的任意一个特征根,则必有01λλ<;ii t t t n 0/)(lim λ+∞>-=*cn , 4 其中c 是与n 0有关的常数;定理1至定理3的证明这里省去;由定理3的结论知道,当t 充分大时,有*)(0n c t n t λ≈ 5 定理4记121i i i b s s s β-=,q λ=1β/λ+2β/λ2+…+m β/m λ,则λ是L 的非零特征根的充分必要条件为q λ=1 6所以当时间充分大时,女性人口的年龄结构向量趋于稳定状态,即年龄结构趋于稳定形态,而各个年龄组的人口数近似地按λ-1的比例增长;由5式可得到如下结论:i 当λ>1时,人口数最终是递增的;ii 当λ<1时,人口数最终是递减的;iii 当λ=1时,人口数是稳定的;根据6式,如果λ=1,则有b 1 + b 2s 1 + b 3s 1s 2 + … + b m s 1 s 2…s m-1=1记R = b 1 + b 2s 1 + b 3s 1s 2 + … + b m s 1 s 2…s m-1 7R 称为净增长率,它的实际含义是每个妇女一生中所生女孩的平均数;当R >1时,人口递增;当R <1时,人口递减;Leslie 模型有着广泛应用,这里我们给出一个应用的例子,供大家参考;公园大象管理南非的一家大型自然公园放养了大约11000头大象,管理部门希望为大象创造一个健康的生存环境,将大象的总数控制在11000头左右;每年,公园的管理人员都要统计当年大象的总数;过去20年里,公园每年都要处理一些大象,以便保持大象总数维持在11000头左右,通常都是采用捕杀或者迁移的方法来实现;统计表明,每年约处理600-800头大象;近年来,公众强烈反对捕杀大象行为,而且即使是迁移少量的大象也是不允许的;但是一种新的给大象打避孕针的方法也被研制成功;一只成年母象打了避孕针后,两年内不再怀孕;公园有一些关于大象的资料,供建模参考:1几乎不再迁入或迁出大象;2目前性别比接近1:1,采取控制后,也希望维持这个比例;3初生象的性别比也是大约1:1,生双胎的比例为%4母象初次怀孕大约在10-12岁,一直到60岁大约每年怀胎一次,60岁后不再受孕,怀孕期为22个月;5避孕针可能引起大象每个月都发情,但不受孕,因为大象通常每年生育1次,所以按月循坏的方案是不足取的;6避孕针对母象没有副作用,打了避孕针的母象2年内不再受孕;7初生象存活到1岁的比例为70%-80%,此后,直至60岁前,存活率都比较均匀,大约在95%以上,大象一般只活到70岁;8公园里不存在捕杀行为,偷猎可以不考虑;公园管理部门有一份过去两年移出公园大象的粗略统计,不幸的是没有捕杀或公园大象的具体数据;你的任务是,构造一个模型,利用模型研究如何采用避孕措施控制公园大象的总数.同时需要完成以下任务:1 建立并利用模型推算2-60岁大象可能的存活率,以及目前的大象年龄结构;2估计每年需要避孕多少大象,才能保证大象总数控制在11000头左右,说明数据不确定性对你的结论的影响,评价一下年龄结构的变化以及对旅游的影响,你可能被要求观察30-60年;3假设每年可以移出50-300头大象,避孕大象数可以减少多少,评价如何根据经济效益平衡两种方案;4有一些反对观点认为,假如出现疾病或者失控的偷猎,使大象总数突然大幅度下降,即使停止避孕,也会对大象群的恢复存在不良影响,研究并回答这个问题;5公园公管理部门正在构造模型,特别希望批驳那些以缺乏完整数据为由而嘲笑利用模型指导决策的观点.希望你的模型包括一份技术报告能给公园管理部门提一些建议,提高公园管理部门的信心,除此之外,你的报告,还应该包括一个详细的技术流程最多3页回答公共关心的问题;6假如非洲其它公园对你的模型感兴趣,有意利用你的模型,请为公园大象数在300-25000头规模的公园提供一份避孕计划,顺便考虑一下存活率稍有不同或者可以有迁移的情况.附过去两年的迁出数据年龄 0 1 2 3 4 5 6 7 8 9总量1 103 77 71 70 68 61 58 51 52 51母象1 50 36 41 29 31 30 28 24 22 29总量2 98 74 69 61 60 54 52 59 58 57母象2 57 34 33 29 34 28 27 31 25 25年龄 10 11 12 13 14 15 16 17 18 19总量1 51 50 51 48 47 49 48 47 43 42母象1 27 27 26 27 26 25 28 27 19 25总量2 60 63 64 60 63 59 52 55 49 50母象2 26 36 38 30 33 34 24 30 21 30年龄 20 21 22 23 24 25 26 27 28 29总量1 42 37 39 41 42 43 45 48 49 47母象1 18 16 19 24 17 25 21 26 29 27总量2 53 57 65 53 56 50 53 49 43 40母象2 29 27 40 23 29 24 21 26 24 16年龄 30 31 32 33 3 4 35 36 37 38 39总量1 46 42 44 44 46 49 47 48 46 41母象1 24 22 20 22 24 24 23 25 21 24总量2 38 35 37 33 20 33 30 29 29 26母象2 17 16 18 18 15 18 12 17 16 13年龄 40 41 42 43 4 4 45 46 47 48 49总量1 41 42 43 38 34 34 33 30 35 26母象1 24 19 26 20 20 15 16 13 20 11总量2 10 24 25 22 21 22 11 21 21 19母象2 6 11 14 10 10 12 8 11 12 9年龄 50 51 52 53 54 55 56 57 58 59总量1 21 18 14 5 9 7 6 0 4 4母象1 10 9 8 4 4 4 3 0 3 2总量2 15 5 10 9 7 6 5 4 7 0母象2 6 4 5 4 4 2 3 2 4 0年龄 60 61 62 63 64 65 66 67 68 69 70总量1 4 3 2 2 1 3 0 2 1 0 2母象1 2 1 1 1 0 3 0 0 1 0 2总量2 2 3 0 2 0 2 0 1 0 0 0母象2 2 1 0 0 0 1 0 1 0 0 0假设与分析1大象性别比接近1:1,初生象的性别比也是大约1:1,采取控制后,也希望维持这个比例;2过去两年迁出的大象是随机抽样,其结构反映了象群总体的年龄结构;3 避孕是随机的,母象是否避孕是不可识别的,假设各个年龄的母象是等比例避孕的,比例系数为k,仅通过调节k 来控制公园大象数量;4母象初次怀孕大约在10-12岁,简化假设大象初孕时间为11岁,当前状态下,成年象的成活率为s,生育母象率为r ,老年象的成活率是线性逐渐递减的,因此其成活率可表示为设初生象活到1岁的存活率为0s ;5避孕针对母象没有副作用,打了避孕针的母象2年内不再受孕;且无论打避孕针前母象是否怀孕,一旦打了避孕针,母象就被避孕或中止怀孕,平均每年有γ比例的母象处于避孕状态;每年母象的避孕率为η,每年的避孕方案时瞬时完成的;6 假设大象的年龄结构是稳定的;数据处理与分析12-60岁大象的存活率与年龄结构母象生育率为r =1/+1+/2=头/年12岁的母象生育母象的生育率为r /6;由题设知道存活率)99.0,95.0(∈s ;以下是第一年迁移出0至70岁大象数据x1=103,77,71,70,68,61,58,51,52,51,51,50,51,48,47,49,48,47,43,42,42,37,39,41,42,43,45,48,49,47,46,42,44,44,46,49,47,48,46,41,41,42,43,38,34,34,33,30,35,26,21,18,14,5,9,7,6,0,4, 4, 4 ,3,2,2,1,3,0,2,1,0,2 ;以下是第二年迁移的0-70岁大象数据x2=98,74 69 61 60 54 52 59 58 57 60 63 64 60 63 59 52 55 49 50 53 57 65 53 56 50 53 49 43 40 38 35 37 33 20 33 30 29 29 26 10 24 25 22 21 22 11 21 21 19 15 5 10 9 7 6 5 4 7 0 2 3 0 2 0 2 0 1 0 0 0;x=x1+x2;x0=x/normx,1;以下是第一年迁移的0-59岁母象数据y1=50 36 41 29 31 30 28 24 22 29 27 27 26 27 26 25 28 27 19 25 18 16 19 24 17 25 21 26 29 27 24 22 20 22 24 24 23 25 21 24 24 19 26 20 20 15 16 13 20 11 10 9 8 4 4 4 3 0 3 2;以下是第二年迁移的0-59岁母象数据y2=57 34 33 29 34 28 27 31 25 25 26 36 38 30 33 34 24 30 21 30 29 27 40 23 29 24 21 26 24 16 17 16 18 18 15 18 12 17 16 13 6 11 14 10 10 12 8 11 12 9 6 4 5 4 4 2 3 2 4 0;考虑到有些数据较小及抽样的随机性,我们取两次抽样的平均值作为分析的基本数据;t1=x12:11;t2=x22:11;tt=t1+t2;tt1=tt1:9;tt2=tt2:10;tn=tt2./tt1;meantnans =t1=x112:21;t2=x212:21; tt=t1+t2; tt1=tt1:9;tt2=tt2:10;tn=tt2./tt1; meantnans =t1=x112:31;t2=x212:31; tt=t1+t2; tt1=tt1:19;tt2=tt2:20;tn=tt2./tt1; meantnans =t1=x112:41;t2=x212:41; tt=t1+t2; tt1=tt1:29;tt2=tt2:30;tn=tt2./tt1; meantnans =t1=x112:51;t2=x212:51; tt=t1+t2; tt1=tt1:39;tt2=tt2:40;tn=tt2./tt1; meantnans =t1=x112:60;t2=x212:60; tt=t1+t2;tt1=tt1:48;tt2=tt2:49;tn=tt2./tt1; meantnans =n1=zeros1,71;n11=1;n12=;for i=3:61n1i=n1i-1;endn1;for i=62:71n1i=n1611-i-61/10;endn1;N1=n112:50;xx=x12:50;xx=100xx/normxx,1;N1=100N1/normN1,1;t=1:39;plott,N1,t,xx;axis10,40,0,5;title'图1'通过以上分析大致可以得到,1-60岁大象的存活率约为;0-70岁年龄结构向量见图2; y0=100x0/normx0,1;a=0:70;bara,y0,'stacked';title'图2'下面我们取0120.75,0.98s s s ===;m1=zeros1,71;m11=1;m12=;for i=3:61m1i=m1i-1;endm1;for i=62:71m1i=m1611-i-61/10;endm1;m1=100m1/normm1,1;bara,m1,'stacked';title'图3 稳定的年龄结构'plota,m1,'r-',a,y0,'b-.';title'图4 年龄结构当前状态与稳定状态比较'polyfity0,m1,1ans =从所给的数据来看,象群的年龄结构还没有达到相对稳定的状态;根据以上数据,大体可以得到l=zeros71,71; l1,13=6;l2,1=;for i=14:61l1,i=;endl;for j=3:61lj,j-1=;end; l;for k=62:71lk,k-1=eigl;矩阵的唯一正特征值为;对于不同的存活率,得到的唯一正特征值为:下面我们估计每年处于避孕状态母象的比率γ;此时,女性生育率为0.1448(1)γ-;记由6式得解得1-1/^111/6+ans =即每年应该有%的母象处于避孕状态;为了保证有%的母象处于避孕状态,下面分析每年应该打避孕针母象的比例η;在假设3和假设5的前提下,如果每年打避孕针母象比例为η;母象可以分成3类:即当年被打避孕针而上一年没有被打避孕针或上一年被打避孕针而本年没有被打避孕针,比例为2(1)ηη-;连续两年被打避孕针2η;连续两年没有被打避孕针;只有最后一类母象具有生育能力;因此,只需要η满足方程1-sqrtans =ans =5500ans =+003解得 0.387η=,即每年大约需要给2127头母象打避孕针;在方案实施过程中,实际上根本不需要打这么多针,因为许多小象还是可以识别的;可以采取随机抽样的打针方式,对于抽到的小象只计数不打针,直至计满2127头母象,就算完成当年任务;采取打避孕针的方案对象群的年龄结构是由一些影响的,下面给出了打与不打避孕针情况下稳定的象群年龄结构与各你阿爸年龄段象群数的比较;m1=zeros1,71;m11=1;m12=;for i=3:61m1i=m1i-1;end; m1;for i=62:71m1i=m1611-i-61/10;end; m1;n1=zeros1,71;n11=1;n12=;for i=3:61n1i=n1i-1;end; n1;for i=62:71n1i=n1611-i-61/10;end;n1;subplot1,2,1a=0:70;plota,m1,'r-',a,n1,'b--';title'图5年龄结构比较';axis0,70,0,1;M1=5500m1/normm1,1;N1=5500n1/normn1,1;a=0:70;subplot1,2,2plota,M1,'r-',a,N1,'b--'title'图5各年龄段大象数比较图'axis-0,70,0,300通过以上两个图的比较,可以发现采取避孕措施,将使幼象、小象数减少,中老年象数增加;由于采取避孕措施,使得初生小象数减少,因此会不可避免地引起象群年龄结构的改变,下面分析,15年、30年、60年后的象群年龄结构;L=zeros71,71;L1,13=6;L2,1=;for i=14:61L1,i=;end; L;for j=3:61Lj,j-1=; end; L;for k=62:71Lk,k-1= end; L;eigL;n15=L^15x0';n30=L^15n15;n60=L^30n30;n15=100n15/normn15,1;n30=100n30/normn30,1;n60=100n60/normn60,1;M15=5500n15/normn15,1;M30=5500n30/normn30,1;M60=5500n60/normn60,1;bara,55y0title'图6a 避孕前种群量分布';axis0,70,0,250bara,M15title'图6b 避孕15年后种群量分布';axis0,70,0,250bara,M30title'图6c避孕30年后种群量分布';axis0,70,0,250M60=5500n60/normn60,1;bara,M60title'图6d 避孕前种群量分布';axis0,70,0,250n70=L^70x0';n70=100n70/norm n70,1;k1=100m1/normm1,1;图7给出了避孕前后年龄结构稳定状态的比较plot a,k 1,'r-',a,n70,'b-.';title'图7 避孕前后稳定的年龄结构';axis0,70,0,5数据不确定性对结果的影响分别取0120.7,0.8,0.95,0.99s s s ===1-1/^111/6+ans =1-sqrtans =1-1/^111/6+ans =1-sqrtans =每年需避孕的母象比例为%—% ;对于每年可以迁移50-300头大象及0120.75,0.98s s s ===,下面分析避孕方案的变化及最经济的方案;设增长率为p ,对于 0120.75,0.98s s s ===令当 1.01p =,每年的避孕率为%,每年迁出110头; 当 1.02p =,每年的避孕率为%,每年迁出220头; 当 1.025p =,每年的避孕率为%,迁出275头;1-1/^111/6+ans =1-sqrtans =p=;1-p ^12./^111/6+./p-./p.^49/./pans =1-sqrtans =p=;1-p.^12./^111/6+./p-./p^49/pans =1-sqrtans =p=;1-p.^12./^111/6+./p-./p^49/pans =1-sqrtans =进一步分析可以知道,对于 0120.75,0.98s s s ===,如果增长率为(1 1.0322,11000(p-1))p p ≤≤即每年移,令每年需要避孕的母象为5500'γ,每年需要迁移的大象数为11000(1)p -;从相关的文献中我们大致可以得到,设平均每迁移一头大象的成本约避孕一头大象费用的λ倍,由此得到增长率为p 时的总费用函数为记易见,1,0.3868, 1.01,0.346, 1.02,0.396p y p y p y ======clear ;p=1::;q =1-p.^12./^111/6+./p-./p.^49././pq =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 17a =1-sqrt1-qa =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 17y=a+15p-1y =Columns 1 through 5Columns 6 through 10Columns 11 through 15Columns 16 through 17。
leslie模型

1,模型的建立
我们将人口的年龄按大小分为n 个年龄组,记为1,2,3,,i n =
同时将时间离散为时间段,长度与年龄组区间相等,记为1,2,3,
t
= 定义()i x t 为第t 年第i 年龄组的女性人口数;()i b t 为第t 年第i 年龄组女性生育率;()i d t 为第t 年第i 年龄组的女性人口的死亡率;()i s t 为第t 年第i 年龄组女性的存活率,即()1()i i s t d t =-;()w t 为第t 年出生人口中女性所占比例。
则第1t +年为第1年龄组的女性人数为:
11(1)()()()m
i i i x t b t w t x t =+=∑
第1t +年为第1i +年龄组的女性人口是从第t 年第i 年龄组存活下来的人数:
1(1)()()i i i x t s t x t ++=
构造Leslie 矩阵: []12112121 0 0 0 0 ,0 0 0 0 0 0n n i n wb wb wb wb s L s i i i b s --⎡⎤⎢⎥⎢⎥⎢⎥=∉=⎢⎥⎢⎥⎢⎥⎣
⎦
其中时, 那么我们可以得到:
(1)()x t Lx t += 进一步可以得到Leslie 矩阵模型的预测公式:
()(0)x t L x '=
所以只要已知L 矩阵及初始女性人口分布向量(0)x ,就可以求出第t 年女性人口分布的数列,再根据男女性别比例即可推算出总人口的各项指标。
Leslie种群年龄结构的差分方程模型

Leslie种群年龄结构的差分方程模型摘要本文对带年龄结构的单个生物种群的增长状况的问题建立了差分方程模型进行分析,用MATLAB做出其图像讨论这种昆虫各种周龄的昆虫数目在不同条件下的演变趋势。
针对问题一,用k时段2周后幼虫数量、2到4周虫的数量、4到6周虫数量之间的关系建立了差分方程模型一,利用MATLAB计算得出结果。
针对问题二,用MATLAB做出差分方程模型一在0-50时段的各种周龄的昆虫数目的演变趋势,分析年份足够长时的情况。
得出的结论:各周龄的昆虫比例没有一个稳定值,整个昆虫的数量在无限增长。
针对问题三,把差分方程模型一中的成活率改成原来的一半得到了差分方程模型二,用MATLAB做出图像进行分析。
得出结论:这种除虫剂的效果不明显。
关键词:Leslie矩阵,差分方程,MATLAB,除虫剂一 、问题重述已知一种昆虫每两周产卵一次,六周以后死亡(给除了变化过程的基本规律)。
孵化后的幼虫2周后成熟,平均产卵100个,四周龄的成虫平均产卵150个。
假设每个卵发育成2周龄成虫的概率为0.09,(称为成活率),2周龄成虫发育成4周龄成虫的概率为0.2。
(1) 假设开始时,0-2,2-4,4-6周龄的昆虫数目相同,计算2周、4周、6周后各种周龄的昆虫数目;(2) 讨论这种昆虫各种周龄的昆虫数目的演变趋势:各周龄的昆虫比例是否有一个稳定值?昆虫是无限地增长还是趋于灭亡?(3) 假设使用了除虫剂,已知使用了除虫剂后各周龄的成活率减半,问这种除虫剂是否有效?二、 问题分析本问题是要解决带年龄结构的单个生物种群的增长状况的问题,我们考虑用Leslie 矩阵模型进行分析。
问题一建立0-2,2-4,4-6周龄的昆虫数目之间的关系的模型,从而计算出结果;问题二用问题一的模型画出图像来分析各种周龄的昆虫数目的演变趋势;问题三只要把问题一的模型的成活率改成原来的一半建立新的模型,画出图像来分析昆虫数量的变化趋势,从而分析除虫剂的效果。
人口模型

Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化。
如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型。
20 世纪40 年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型假设模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变化。
假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔S / m 年观察一次,不考虑同一时间间隔内人口数量的变化; (2) 记ni (t ) 为第i 个年龄组t 次观察的女性总人数,记n(t ) = [n1 (t ), n 2 (t ),L , n m (t )] 第i 年龄组女性生育率为bi (注:所谓女性生育率指生女率),女性死亡率为d i ,记si = 1 di , 假设bi , di 不随时间变化; (3) 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响; (4) 生育率仅与年龄段有关,存活率也仅与年龄段有关。
建立模型与求解根据以上假设,可得到方程t n1 (t + 1) = ∑ bi ni (t ) i =1 m ni +1 (t + 1) = si ni (t ) 写成矩阵形式为i = 1 ,2.…, m -1 t +1 n(t + 1) = Ln(t ) b1 b2 L bm 1 bm 0 0 s1 0 L 0 其中,L= 0 s 2 0 L M O O O M 0 K 0 s m1 0 (1)记n(0) = [n1 (0), n2 (0),L, nm (0)] 假设n(0)和矩阵L 已经由统计资料给出,则(2)n(t ) = Lt n(0), t = 0,1, 2,L 为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:(i) si> 0,i=1,2,…,m-1; (ii) bi ≥ 0 ,i=1,2,…,m,且bi 不全为零。
基于leslie模型的中国人口预测模型

= 其中矩阵 L [
1 d (0)
]
1 d (6) 0 给出 x(k,i),A 就可求出 x(k+1,) MATLAB 程序为:
名词定义:x(k,i) :在第 k 时期内的女性人口数量;
b(i):第 i 组女性的生育率;
d(i) ; 第 i 组女性的死亡率;
根据以上假设可以得出 k + 1 时段各组人数与 k 时段各组人数之间的转换关系:
X(k+1)=L*x(k) ,(a 为女婴所占的百分比)。
a * b(0) a * b(1) ... a * b(7)
i
0
1
2
3
4
5
Hale Waihona Puke 67年龄组 0
1~15 16~30 31~45 46~60 61~75 76~90 90~
注:0 组表示婴儿。
2.考虑到我国近三十年国家整体处于稳定状态没有大的灾难,战争等突发事件,所以假设
各年龄组死亡率 d(i) ,(i=0,1,…7),不随时间变化。
3.各年龄组女性的生育率 b(i),(i=0,1,…7)在较短的时期变化不大。
基于 Leslie 矩阵的中国人口预测模型
问题提出:
中国是一个人口大国,人口问题始终是制约我国发展的关键因素之一。根 据已有数据,运用数学建模的方法,对中国人口做出分析和预测是一个重要问 题。20 世纪 40 年代提出的 Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型建立:
基本假设:1.假设各年龄段的男女比例保持不变(以 05 年男女性别比例为例: 106.30:100,)所以可以由女性人口数量来计算总人口 SP。将女性分为 8 组见下表
leslie模型的求解

9879292
9829885
72
3449237
3443988
27
9801611
9679225
73
3149307
3194562
28
11271599
11050548
74
2964127
3116046
29
9914552
9653457
75
2690547
2941930
30
9604727
9323642
76
2454168
Z=X+Y; %总人数
T=sum(Z);
g1=2011:2061;
plot(g1,T,'r')
2010年分年龄、性别人口数
年龄
男性
女性
年龄
男性
女性
0
7461199
6325235
46
11867147
11488631
1
8574973
7082982
47
13803796
13168361
2
8507697
7109678
17
10760828
10014541
63
5492805
5298828
18
10744556
10010718
64
5015412
4936055
19
11079367
10464099
65
4564266
4509145
20
14201091
13825863
66
4391409
4249556
21
13357755
Leslie模型(数学建模)

提出问题:
我们首先考虑Malthus 模型: x(t)为人口总数,r为自然增长率; 于是可以得出:
x(t)=x0er(t-t0)改进的模型设地球能容纳的总人数为k,随着人口的增 长,出生率必然会下降,于是r与x存在 着一定的关系。基于上述假设,我们选 择一种简单的函数。 r(x)=r0(1-x/k) r0为特定的常数
控制论模型常采取一些评价函数来评判控制 模型的效果,对于人口模型,可类似连续型模型, 引入以下一些人口指数: (1)人口总量 不妨以N(j)记j时段的人口总量, N(j)= N(i,j). (2)平均年龄 y(j)=(1/ N(j)) i N(i,j). (3)平均寿命 Q(j)= exp [- (1-Pi(j))],其中(1Pi(j))为j时段i组人的死亡率。 (4)p社会人口老龄化指数 w(j)=y(j)/Q(j)
目前我国人口中中年青人的比例很大,加上计 划生育降低出生率,必然造成若干年后社会人 口的严重老龄化,待这一代人越出m组后,又 会使人口迅速青年化而走向另一个极端。
为减少这种年龄结构上的振荡,人们又引入了一 个控制变量h(i,j),使bi(j)=h(i,j)
且 h(i,j)=1 h(i,j)称为女性的生育模式,用来调整育龄妇 女在不同年龄组内生育率的高低。为简便可通过 控制结婚年龄和两胎之间的年龄差来接近h(i,j)的 理想值。 于是Leslie模型可以如下形式上的改变: N j+1=[A(j)+B(j)]N j
n0 .
A属于1的特征向量N=
.
nk
解线性方程组 AN= 1N
1k/(P0P1…P k-1)
数学建模-莱斯利模型

x1
(k )
a 1 x1
( k 1)
a2 x2
( k 1)
... a n x n
( k 1)
.
(5.1) (5.2)
x i 1 bi x i
(k )
( k 1)
, i 1, 2, ..., n 1 .
将(5.1)式和(5.2)用矩阵表示即得
同样,至少有一个 a i 是正的,这样就保证有n个女儿出生了。与正的 a i 对应的年龄组称为生育年龄组。
记 x i 是在时刻个 年龄组中的女性数目,则称
(i)
X
(k )
x1 (k ) x2 k xn
(k )
为在时刻 t k 时年龄分布向量。在时刻 t k ,第一个年龄组中的女性数恰 好就是在 t k 1 和 t k 之间出生的女孩数,即
(1 ) (0)
<二> 极限状态
(5.5)式给出了总日在任意时间的年龄分布,但是它并不能直接反映增长过 程动态的情况。 为此我们需要考虑莱斯利矩阵L的特征值和特征向量,L的特征根是它的特 征多项式的根,这个特征多项式为
p ( ) | E L | a1
n
n 1
a 2 b1
a 1 a 2 b1 a 3 b1b 2 ... a n b1b 2 ...b n 1 1
时才有 1 1 。 表达式
(5.15)
R a 1 a 2 b1 a 3 b1b 2 ... a n b1b 2 ...b n 1
(5.16)
称为总体的净繁殖率。因此,总体的净繁殖率为1时,一个总体有 零总体增长。
Leslie模型

Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化。
如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型。
20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变化。
假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔内人口数量的变化;(2) 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记)](,),(),([)(21t n t n t n t n m =第i 年龄组女性生育率为i b (注:所谓女性生育率指生女率),女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;(3) 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;(4) 生育率仅与年龄段有关,存活率也仅与年龄段有关。
建立模型与求解根据以上假设,可得到方程 t)1(+t n =∑=mi i i t n b 1)()()1(1t n s t n i i i =++ 1=i ,2.…,m -1写成矩阵形式为)()1(t Ln t n =+其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--000000000121121m m m s s s b b b b(1)记)]0(,),0(),0([)0(21m n n n n =(2)假设n (0)和矩阵L 已经由统计资料给出,则()(0),0,1,2,t n t L n t ==为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件:(i) s i > 0,i =1,2,…,m -1;(ii) b i 0≥,i =1,2,…,m ,且b i 不全为零。
Leslie矩阵模型预测人口

L e s l i e矩阵模型预测人口4.1Leslie矩阵模型的基本概念4.1.1参数定义[11]我们将中国人口按年龄段分成数段,因此当段数到达一定大小的时候就能包含全部年龄层的人。
再将时间序列也分割成数段(一年为一段即可研究年度人口总数),得到:——在时间周期k第i个年龄段的人数注:这里的;一定存在整数n 使得表示的是年龄最高的人的人数,如“100岁以上的人”的数量。
其他关于人口的参数:1)——在时间周期k第i年龄组的女性的生育率,即女性生的孩子的人数与女性数的比例,我们也称其为年龄别生育率2)——在时间周期k第i年龄组的死亡率,即死亡人数除以这一年龄组总人数,我们也称其为年龄别死亡率4.1.2Leslie矩阵1.转移过程在一个时间周期内里的人数转移到里,考虑死亡的人数我们得到如下式子:11(1)()(1()),1,2,k k kx i x i d i i n--+=-=(4-1)下面来讨论的情况,即新生儿人数,在这里我们做了一个假设,女性人口大致占总人口的一半(通过以往的人口普查可以得到证实),因此在时间周期k的第个i年龄段的女性人数为1()2kx i,则可以通过女性的年龄别生育率预测第一个递推关系如下:1111()()()2nk k kix i b i x i--==∑(4-2) 2.人口发展模型111111111111(0)(1)(1)()22221(0)00001(1)0001(1)0k k k kkk kkkb b b n b ndx xdd n--------⎛⎫-⎪⎪-⎪=⨯⎪-⎪⎪⎪--⎝⎭(4-3) 其中(0)(1)()k k k k x x x x n ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭1111(0)(1)()k k k k x x x x n ----⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭(4-4)为了化简,我们记:11111111111(0)(1)(1)()22221(0)00001(1)00001(1)0k k k k k k k b b b n b n d L d d n -------⎛⎫- ⎪⎪- ⎪=⎪- ⎪ ⎪⎪--⎝⎭(4-5)则有简写:1k k x L x -=(4-6)则有递推公式:10k kk x L x L x -==(4-7)通过这种方法,我们把人口预测问题的重点落到了一个n 维矩阵运算上。
Leslie模型

Leslie 人口模型现在我们来建立一个简单的离散的人口增长模型,借用差分方程模型,仅考虑女性人口的发展变化。
如果仅把所有的女性分成为未成年的和成年的两组,则人口的年龄结构无法刻划,因此必须建立一个更精确的模型。
20世纪40年代提出的Leslie 人口模型,就是一个预测人口按年龄组变化的离散模型。
模型假设(1) 将时间离散化,假设男女人口的性别比为1:1,因此本模型仅考虑女性人口的发展变 化。
假设女性最大年龄为S 岁,将其等间隔划分成m 个年龄段,不妨假设S 为m 的整数倍,每隔m S /年观察一次,不考虑同一时间间隔内人口数量的变化;(2) 记)(t n i 为第i 个年龄组t 次观察的女性总人数,记)](,),(),([)(21t n t n t n t n m =第i 年龄组女性生育率为i b (注:所谓女性生育率指生女率),女性死亡率为i d ,记1,i i s d =-假设,i i b d 不随时间变化;(3) 不考虑生存空间等自然资源的制约,不考虑意外灾难等因素对人口变化的影响;(4) 生育率仅与年龄段有关,存活率也仅与年龄段有关。
建立模型与求解根据以上假设,可得到方程)1(+t n =∑=mi i i t n b 1)()()1(1t n s t n i i i =++ 1=i ,2.…,m -1 写成矩阵形式为)()1(t Ln t n =+其中,L =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--00000000121121m m m s s s b b b b(1) 记)]0(,),0(),0([)0(21m n n n n = (2)假设n (0)和矩阵L 已经由统计资料给出,则()(0),0,1,2,tn t L n t ==t1+t为了讨论女性人口年龄结构的长远变化趋势,我们先给出如下两个条件: (i) s i > 0,i =1,2,…,m -1;(ii) b i 0≥,i =1,2,…,m ,且b i 不全为零。
考虑年龄结构的人口模型Leslie模型

考虑年龄结构的人口模型(Leslie 模型)对Logistic 模型的批评意见除了实际统计时常采用离散变化的时间变量外,另一种看法是种群增长不应当只和种群总量有关,也应当和种群的年龄结构有关。
不同年龄的个体具有不同的生育能力和死亡率,这一重要特征没有在Logistic 模型中反映出来。
基于这一事实,Leslie 在20世纪40年代建立了一个考虑种群年龄结构的离散模型。
由于男、女性人口(或雌、雄性个体)通常有一定的比例,为了简便起见,建模时可以只考虑女性人数,人口总量可以按比例折算出来。
将女性按年龄划分成m +1个组,即0,1,…,m 组,例如,可5岁(或10岁)一组划分。
将时间也离散成间隔相同的一个个时段,即5年(或10年)为一个时段。
记j 时段年龄在i 组中的女性人数为N (i ,j ),b i 为i 组每一妇女在一个时段中生育女孩的平均数,i p 为i 组女性存活一时段到下一时段升入i +1组的人数所占的比例(即死亡率d i =1-i p )同时假设没有人能活到超过m 组的年龄。
实际上可以这样来理解这一假设,少量活到超过m 组的妇女(老寿星)人数可以忽略不计,她们早已超过了生育期,对人口总量的影响是微小的而且是暂时性的,对今后人口的增长和人口的年龄结构不产生任何影响,假设b i 、i p 不随时段的变迁而改变,这一假设在稳定状况下是合理的。
如果研究的时间跨度不过于大,人们的生活水平、整个社会的医疗条件及周围的生活环境没有过于巨大的变化,b i 、i p 事实上差不多是不变的,其值可通过统计资料估算出来。
根据以上假设可以得出以下j +1时段各组人数与j 时段各组人数之间的转换关系:⎪⎪⎩⎪⎪⎨⎧-=+=++++=+-),1()1,(),0()1,1(),(),0(),0()1,0(1010j m N p j m N j N p j N j m N b j N b j N b j N m m 显然,0,≥i j p b 。
数学建模莱斯利模型
1 X ( k 1) ,
(5.14)
这说明对于足够大的时间值,每个年龄分布向量是前一个年龄分 布向量的一个数量倍数,这个数量就是矩阵的正特征值。因此, 在每一个年龄组中的女性比例据变为常量。 由给出常时期人口的年龄分布向量(5.12)式 (k ) k 1 1
C X , 根据正特征值 1 的数值,会有三种情况: X
(0)
因此,对于任意初始年龄分布向量 X
就有
X ( k ) Lk X (0)
1k 0 P 0
0
2k
0
0 0 1 (0) P X , k 1, 2,... k n
此等式两边除以
1k ,就得出
0 P 1 X (0) . (n / 1 ) k 0
k 1, 2,...,
(5.4)
其中
a1 a2 b 0 1 L 0 b2 0 0
a3 0 0 0
an 1 an 0 0 0 0 bn 1 0
称为莱斯利矩阵。由(5.4)式可得
X (1) LX (0) , (2) (1) 2 (0) X LX L X , (3) (2) 3 (0) X LX L X , ........ (5.5) X ( k ) LX ( k 1) Lk X (0) , (0) 因此,如果已知初始年林分布 X 及莱斯利矩阵L,就能求出在以后任何时
(5.8)
由于 1 是单根,它相应的特征空间是一维的,因而任意它所对应的特 征向量 X 1 是某个倍数,则有定理
定理1 一个莱斯利矩阵L有一个唯一的正特征值 1 ,并且有一个所有元 素均为正的特征向量。 总体年龄分布的长期行为是由正的特征值 1 及它的特征向量 X 1 来决定 的。实际应用中,由数学软件很容易求出矩阵的特征值与特征向量,请 读者参阅第四章相关内容。 定理2 如果 1 为莱斯利矩阵L的唯一的正特征值,i 是L的特征值,它 可以是任意实数或复数,则 | i | 1 。 称为L的严格主特征值。并不是所有的莱斯利矩阵都满足这个条件,例如
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P(0)
P(1)
Nt(0)
Nt(1)
K=
I(t)=
… …
P(n)
… …
Nt(n)
数学表达:
第一年新生儿的总数: F(0)•P(0)+ F(1)•P(1)+ ••• +F(n)•P(n) 第一年x岁人口总数: N1(x)=S(x-1)•P(x-1) 第一年末人口总数:F(0)•P(0)+ F(1)•P(1)+ ••• +F(n)•P(n)+ S(0)•P(0)+ S(1)•P(1)+ ••• +S(n-1)•P(n-1)
解得:
x(t)=k/[1+(k/x0-1)e-r(t-t0)]
分析以上两个模型:
每个个体的出生率与死亡率是相同的。但实 际上不同年龄的年的生育率与死亡率有很大 的不同。
基于这种考虑,下面将建立一个人口按 年龄分布的模型
定义
r表示年龄,函数F(r,t)为t时刻年龄小于r的人口总数,称 其为人口分布函数 令p(r,t)= F/ r p(r,t)为年龄密度函数
建立模型:
a(0) a(1) a(2) • • • a(n) b(0)
构造n+1阶方阵 L=
b(1) b(2) •••
b(n-1)
那么I (1)=(L-H)K ; I (t)=(L-H) I (t-1) I (t)= (L-H) tK
定理:Leslie矩阵具有唯一的正特征根1,
与之对应的特征向量为 N=( 1k/(P0P1…P k-1), 1k-1(P1…P k-1),…, 1/P k-1,1)T
另外在这个模型中我们还加上了人口迁移对起其总数 的影响.
一些定义:
n为人类的年龄上限 a(x)=x岁的妇女所生的婴数/x岁的妇女总数 b(x)=x岁人的存活率 h(x)= x岁的妇女迁移数/x岁的妇女总数 Nt(x)=距离初始t年时x岁的总人口数
Nt(0) Nt(1) h(0) h(1)
控制论模型常采取一些评价函数来评判控制 模型的效果,对于人口模型,可类似连续型模型, 引入以下一些人口指数: (1)人口总量 不妨以N(j)记j时段的人口总量, N(j)= N(i,j). (2)平均年龄 y(j)=(1/ N(j)) i N(i,j). (3)平均寿命 Q(j)= exp [- (1-Pi(j))],其中(1Pi(j))为j时段i组人的死亡率。 (4)p社会人口老龄化指数 w(j)=y(j)/Q(j)
目前我国人口中中年青人的比例很大,加上计 划生育降低出生率,必然造成若干年后社会人 口的严重老龄化,待这一代人越出m组后,又 会使人口迅速青年化而走向另一个极端。
为减少这种年龄结构上的振荡,人们又引入了一 个控制变量h(i,j),使bi(j)=h(i,j)
且 h(i,j)=1 h(i,j)称为女性的生育模式,用来调整育龄妇 女在不同年龄组内生育率的高低。为简便可通过 控制结婚年龄和两胎之间的年龄差来接近h(i,j)的 理想值。 于是Leslie模型可以如下形式上的改变: N j+1=[A(j)+B(j)]N j
则t时刻年龄处在[r,r+dr)的人口总数为p(r,t)dr
设µ (r,t)为t时刻年龄为r的人的死亡率,t时刻年龄在[r,r+dr) 单位时间死亡的人数为µ (r,t)p(r,t)dr
分析:
下面考虑从t到t+dt这一过程的人口变化: 年龄处在[r,r+dr)到t+dt时刻活着的人的年龄变为 [r+dt,r+dr+dt)而这一时刻死亡的人数为µ (r,t)p(r,t)drdt 则p(r,t)dr-p(r+dt,t+dt)dr= µ (r,t)p(r,t)drdt
记R=f1(1)=b0+P0b1+…+(P0…P k-1)b k
易见R即为女性一生所生女孩的平均值。
有 定理: 1 =1的充要条件为R=1
但并非每一个均能活到足够的年龄并生下R个女孩, 每一妇女可生子女数可定为某一略大于2的数, 称为临界生育率。据统计,中国妇女的临界生育 率为2.2左右。
要实现对人口增长的控制只能采取降低人口出 生率的办法。 记j时段I年龄组中女性所占的百分比为Ki(j) 并设i1,…,i2为育龄年龄组,则j时段新生儿总数 为 N(0,j+1)=bi(j)K i(j)N(i,j) N(i,j+1)=Pi-1N(i-1,j) i=1,…,m
n0 .
A属于1的特征向量N=
.
nk
解线性方程组 AN= 1N
1k/(P0P1…P k-1)
N=
1k-1(P1…P k-1)
1/P k-1 1
当且仅当1=1时,N j N,人口总量将趋于稳定 且各年龄人数在总人口数中所占的比例也将趋于 一个定值。
在1固定的情况下,N只和Pi有关。Pi为i组人的 存活率。在一定时期内,它们基本上是一些常数, 事实上人们只能通过控制b j的值来保证1=1。
关于建立人口增长模型,我们考虑了两条 主要思路: 一.以微分方程为主要手段: 二.以高等代数为主要手段:
提出问题:
我们首先考虑Malthus 模型: x(t)为人口总数,r为自然增长率; 于是可以得出:
x(t)=x0er(t-t0)
改进的模型
设地球能容纳的总人数为k,随着人口的增 长,出生率必然会下降,于是r与x存在 着一定的关系。基于上述假设,我们选 择一种简单的函数。 r(x)=r0(1-x/k) r0为特定的常数
其中 0
P0(j) A(j)= 0
…
…
… 0
0 B(j)= 0 0 … … … …
0 P m-1(j) 0 0 … … … … … … 0 … … 0
0 … b`i1(j) … b`i2(j) 0 …
b`i(j)=(j)h(i,j)K i(j) 在一定时期内,Pi(j),(I=0,…,m-1), (j),h(i,j) 和K i(j)可视为与j无关的常数, 从而在这一时期内A(j),B(j)取常数矩阵 A,B。
p/ r + p/ t=- µ (r,t)p(r,t)
p(r,0)=p0(r) p(0,t)=f(t)
在社会比较安定的情况下,死亡 率大致与时间无关. μ (r,t)=μ (r) p(r,t)= p0(r-t)e f(t-r)e
( s)ds
r t r0≤t≤r Fra bibliotek>r (s)ds
定理:若Leslie矩阵A的第一行中至少有两个相
邻的bi>0则 |i|< |1|且N j/ 1j Pi及N0决定
CN其中C为某一常数,由值bi,
本定理的条件通常能够得到满足,故在j充分大 时有N j=C 1j N,即各年龄组的人口比例总会趋 于稳定,且N j+1= 1N j。若1 >1,种群增大, 1 <1时,种群减小。
建立模型:
F(0) F(1) F(2) • • • F(n) S(0)
构造n+1阶方阵 M=
S(1) S(2) •••
S(n-1)
那么I (1)=MK I (t)=MtK
考虑到在一段稳定的时间段内:总的女性人口数比上总 的男性人口数为一个近似为1的定值.为了更为确切地分 析女性个体数量的分布对总人口数的影响,我们单独把 女性人口数作为研究对象.
0
r
分析:
1.当t<r时,p(r,t)完全由年龄为r-t的人口的初始密度及 这些人的死亡率决定。 2.t>r 时,p(r,t)完全由未来的生育状况f(t-r)及死亡率决 定。
两个重要模型:
Keyfitz Leslie
一些定义:
n为人类的年龄上限 F(x)=x岁的妇女所生的婴儿数/x岁的总人口数 S(x)=x岁人的存活率 P(x)=初始时x岁的总人口数 Nt(x)=距离初始t年时x岁的总人口数
K= I(0)
I(t)=
H(t)=
… …
Nt(n)
…..
h(n)
数学表达:
第一年新生女婴的总数: a(0)•Nt(0)+ a(1)•Nt(1)+ ••• +a(n)• Nt(n) 第一年x岁女性人口总数: N1(x)=b(x-1)•Nt(x-1)- h(x-1)•b(x1)•Nt(x-1)=(1- h(x-1) )•b(x-1)•Nt(x-1) 第一年末女性人口总数: a(0)•Nt(0)+ a(1)•Nt(1)+ ••• +a(n)• Nt(n)+ (1- h(0) )•b(0)•Nt(0)+ ••• + (1- h(n-1) )• b(n-1)•Nt(n-1)
(5)依赖性指数 设l1,…,l2与l`1,…,l`2分别为男性 与女性中具有劳动能力的年龄组,则j时段具有劳 动能力的人口数
L(j)= [1-Pi(j)]N(i,j)+ K i(j)N(i,j)。而N(j)-L(j) 为j时段由社会抚养的失去劳动能力的老人或尚未 具有劳动能力的未成年人的数量。定义社会的依 赖性指数(j)=[N(j)-L(j)]/L(j),即平均每一劳动者抚 养的无劳动能力的人数。
