(MBA课程)管理运筹学:第二章 线性规划的图解法
管理运筹学第二章 线性规划的图解法

B、约束条件不是等式的问题:
若约束条件为 ai1 x1+ai2 x2+ … +ain xn ≤ bi 可以引进一个新的变量si ,使它等于约束右 边与左边之差 si=bi–(ai1 x1 + ai2 x2 + … + ain xn ) 显然,si 也具有非负约束,即si≥0, 这时新的约束条件成为 ai1 x1+ai2 x2+ … +ain xn+si = bi
第二章 线性规划 的图解法
一、线性规划的概念 二、线性规划问题的提出 三、线性规划的数学模型 四、线性规划的图解法 五、线性规划解的情况 六、LP图解法的灵敏度分析
一、线性规划的概念
线性规划Linear Programming 简称LP,是一 种解决在线性约束条件下追求最大或最小的 线性目标函数的方法。 线性规划的目标和约束条件都可以表示成线 性的式子。
max z 3 x1 2 x2
2 x1 x2 ≤ 10 设备B台时占用 s.t. x1 x2 ≤ 8 x , x ≥ 0 产量非负 1 2
决策变量 (decision variable) 目标函数 (objective function) 约束条件 (subject to)
-ai1
x1-ai2 x2- … -ain xn = -bi 。
例1.3:将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x 1 , x 2 , x3 ≥ 0
MBA2 管理运筹学讲义:线性规划

• 约束条件
任何管理决策问题都是限定在一定的条件下求解 把各种限制条件表示为一组等式或不等式,称之为约束条件 约束条件是决策方案可行的保障 LP的约束条件,都是决策变量的线性函数
• 目标函数
衡量决策方案优劣的准则,如时间最省、利润最大、成本最低 目标函数是决策变量的线性函数 有的目标要实现极大,有的则要求极小
24
上海财经大学国际工商管理学院 上海财经大学国际工商管理学院
4
SHUFE
第一节 线性规划的标准型
≤8 2x2 ≤12 3x1 +4 x2 ≤36 x1 ≥0, x2 ≥0 x1
x1 ≥0, x2 ≥0
• 例2. 运输问题 某名牌饮料在国内有三个生产厂,分布在城市A1、A2、 A3, 其一级承销商有 4 个,分布在城市 B1 、 B2 、 B3 、 B4,已知各厂的产量、各承销商的销售量及从Ai到Bj 的每吨饮料运费为 Cij ,为发挥集团优势,公司要统 一筹划运销问题,求运费最小的调运方案。
二、非标准型向标准型转化
• 目标函数极小化问题
minZ=CTX,只需将等式两端乘以 -1 即变为极大化问题。
• 右端常数项非正
两端同乘以 -1
• 为了求解方便,特规定一种线性规划的标准形式, 非标准型可以转化为标准型。标准形式为:
目标函数极大化 约束条件为等式 右端常数项bi≥0 决策变量非负
12
x1
17
上海财经大学国际工商管理学院 上海财经大学国际工商管理学院
18
3
SHUFE
第二节 线性规划的图解法
SHUFE
第二节 线性规划的图解法
二 、解的可能性 • 唯一最优解:只有一个最优点。 • 多重最优解:无穷多个最优解。若在两个顶点同时 得到最优解,则它们连线上的每一点都是最优解。
管理运筹学第二章线性规划的图解法

02
图解法的基本原理
图解法的概念
图解法是一种通过图形来直观展示线性规划问题解的方法。它通过在坐标系中绘 制可行域和目标函数,帮助我们理解问题的结构和最优解的位置。
图解法适用于线性规划问题中变量和约束条件较少的情况,能够直观地展示出最 优解的几何意义。
图解法的步骤
确定决策变量和目标函数
明确问题的决策变量和目标函数,以便在图 形中表示。
目标函数是要求最小化或最大化的函数,通常表示为 $f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
04
约束条件是限制决策变量取值的条件,通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
LINDO是一款开源的线性规划求解器,用 户可以免费使用。
软件工具的使用方法
Excel
用户需要先在Excel中设置好线性规划模型,然后使 用“数据”菜单中的“规划求解”功能进行求解。
Gurobi/CPLEX/LINDO
这些软件通常需要用户先在软件界面中输入线性规划 模型,然后通过点击“求解”按钮进行求解。
实例三:分配问题
总结词
分配问题是指如何根据一定的分配原则 或目标,将有限的资源分配给不同的需 求方,以最大化整体效益。
VS
详细描述
分配问题在实际生活中广泛存在,如物资 分配、任务分配等。通过图解法,可以将 分配问题转化为线性规划模型,并利用图 形直观地展示最优解的资源分配方案。在 分配问题中,通常需要考虑不同需求方的 重要性和优先级,以及资源的有限性等因 素,以实现整体效益的最大化。
韩伯棠教授《管理运筹学》第三版习题答案 高等教育出版社
6 、解: b 1 ≤ c1 ≤ 3
c 2 ≤ c2 ≤ 6
d x1 = 6 x2 = 4
e x1 ∈ [4,8] x2 = 16 − 2x1
f 变化。原斜率从 − 2 变为 −1 3
7、解: 模型:
max z = 500x1 + 400x2
2x1 ≤ 300 3x2 ≤ 540 2x1 + 2x2 ≤ 440 1.2x1 +1.5x2 ≤ 300 x1, x2 ≥ 0
h 100×50=5000 对偶价格不变 i能 j 不发生变化 允许增加的百分比与允许减少的百分比之和没有超出 100% k 发生变化 2、解:
a 4000 10000 62000 b 约束条件 1:总投资额增加 1 个单位,风险系数则降低 0.057
约束条件 2:年回报额增加 1 个单位,风险系数升高 2.167 c 约束条件 1 的松弛变量是 0,约束条件 2 的剩余变量是 0
f 600000 + 300000 = 100% 故对偶价格不变 900000 900000
4、解:
a x1 = 8.5 x2 = 1.5 x3 = 0 x4 = 1 最优目标函数 18.5
b 约束条件 2 和 3
对偶价格为 2 和 3.5
c 选择约束条件 3,最优目标函数值 22
d 在负无穷到 5.5 的范围内变化,其最优解不变,但此时最优目标函数值变化
课后吧 kehou8.com
第 2 章 线性规划的图解法
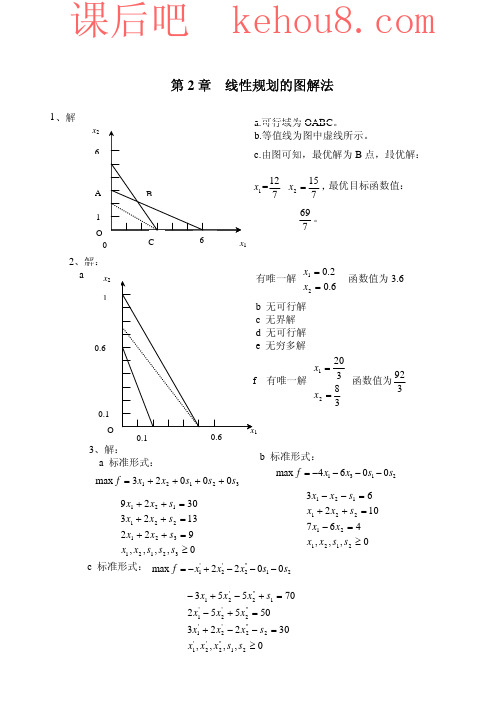
1、解:
x2
6
a.可行域为 OABC。 b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解:
A
B
12 x1 = 7
x2
【运筹学】2第二章线性规划图解法

(7, 0)
56
78
9 10
x1
Example 1: Graphical Solution
x2
• Optimal Solution
8 7 6 5 4 3 2 1
12
Objective Function 5x1 + 7x2 = 46
Optimal Solution (x1 = 5, x2 = 3)
34
56
78
9 10
x1
•画图求解 •2)Max z= 7x1 + 5x2 •3)Max z= 5x1 + 10x2 •4)Max z= 5x1 + 5x2
Example 1: Graphical Solution
x2
• Optimal Solution
8 7 6 5 4 3 2 1
12
Objective Function 5x1 + 7x2
第2章 线性规划图解法
第2章 线性规划图解法
2.1 线性规划问题 2.2 图解法 2.3 极点和最优解 2.4 计算机求解 2.5 最小化问题 2.6 特例
2.1 线性规划问题
• 在一定的约束条件(限制条件)下,使得 某一目标函数取得最大(或最小)值,当 规划问题的目标函数与约束条件都是线性 函数,便称为线性规划。 •Linear programming (LP)
2.2 图解法
•唯一解 •无穷多个最优解 •无界解 •无可行解
Example 1: A Maximization Problem
• LP Formulation • •
Max z= 5x1 + 7x2
•
s.t.
x1
管理运筹学_第二章_线性规划的图解法

线性规划中超过约束最低限的部分,称为剩余量。 记s1,s2为剩余变量,s3为松弛变量,则s1=0, s2=125,
s3=0,加入松弛变量与剩余变量后例2的数学模型变为 标准型: 目标函数: min f =2x1+3x2+0s1+0s2+0s3 约束条件: x1+x2-s1=350, x1-s2=125, 2x1+x2+s3=600, x1, x2, s1,s2,s3≥0.
阴影部分的每 一点都是这个线 性规划的可行解, 而此公共部分是 可行解的集合, 称为可行域。
B
X2=250
100
100
300
x1
B点为最优解, X1+X2=300 坐标为(50, 250), Z=0=50x1+100x2 此时Z=27500。 Z=10000=50x1+100x2 问题的解: 最优生产方案是生产I产品50单位,生产Ⅱ产品250单位,可得 最大利润27500元。
Z=10000=50x1+50x2
线段BC上的所有点都代表了最优解,对应的最优值相 同: 50x1+50x2=15000。
10
3. 无界解,即无最优解的情况。对下述线性规划问题:
目标函数:max z =x1+x2 约束条件:x1 - x2≤1 -3x1+2x2≤6 x1≥0, x2≥0.
x2 -3x1+2x2=6 3
其中ci为第i个决策变量xi在目标函数中的系数, aij为第i个约束条件中第j个决策变量xj的系数, bj(≥0)为第j个约束条件中的常数项。
16
灵敏度分析
灵敏度分析:求得最优解之后,研究线性规划的
04第二章 线性规划的图解法 管理运筹学课件

③
10
20
30
40
50
x1
一、目标函数中的系数的灵敏度分析
• -, • 0 ≤ c1≤3750,最优解不变
•当c1 =1500不变时,
• 1000 ≤ c2,最优解不变
二、约束条件中常数项的灵敏度分析
max Z=1500x1+2500x2 s.t. 3x1+2x2 65 ① 2x1+ x2 40 ② 3x2 75 ③ 30 x1,x2 0 ④ 3x1+2x2 66 20 x1=16/3 x2=25 Z=70500 可见资源A每增加一个单 位就可以多获得500元的 利润.
n
i 1,2,… , m j 1,2,… , n
2、矩阵式
…… …… ………………... ……
… … …
3、向量式
…
…
…
…
…
当z值不断增加时,该直线
§2
线性规划的图解法
②
50 40
x2 = -(3/5)x1 +Z/2500
沿着其法线方向向右上方移 动。
唯一最优解
max Z=1500x1+2500x2 ① 30 s.t. 3x1+2x2 65 ① 2x1+ x2 40 ② 3x2 75 ③ x1,x2 0 ④ 20 由图示可知最优点为B (5,25),最优值为70000 10 可行域、可行解 最优解、最优值
线性规划问题解的特点和几种 可能情况:
• 线性规划问题的可行解的集合是凸集
• 凸集的极点(顶点)的个数是有限的 • 最优解如果存在只可能在凸集的极点上取 得,而不可能发生在凸集的内部 • 线性规划问题的解可能是:唯一解、无穷 多最优解、无界解和无可行解(无解)
第二章 线性规划的图解法(简)

第二节 图解法
在线性规划中,对一个约束条件中没使用的资源或能力的大小称 之为松弛量。记为Si。
第二节 图解法
像这样把所有的约束条件都写成等式 ,称为线性规划模型的标准化,所得结果 称为线性规划的标准形式。
第二节 图解法
同样对于≥约束条件中,可以增加一些代表
最低限约束的超过量,称之为剩余变量,把≥约
第二章 线性规划的图解法
主要内容:
§1 问题的提出 (什么是线性规划) §2 图解法 §3 图解法的灵敏度分析
重点和难点
重点: (1)线性规划问题的主要概念 (2)线性规划问题的数学模型 (3)线性规划图解法的过程 (4)阴影价格的定义和灵敏度分析 难点: 灵敏度分析
第一节 问题的提出
约束条件对偶价格小于零时,约束条件
右边常数增加一个单位,就使得最优目
标函数值减少一个其对偶价格。
第三节 图解法的灵敏度分析
对目标函数值求最小值的情况下, 当对偶价格大于零时,约束条件右边常数增加 一个单位就使其最优目标函数值减少一个其对 偶价格; 当对偶价格等于零时,约束条件右边常数增加 一个单位,并不影响其最优目标函数值; 当对偶价格小于零时,约束条件右边常数增加 一个单位,就使得其最忧目标函数值增加一个 其对偶价格。
具有上述3个特征的问题为线性规划问题。
第一节 问题的提出
我们的仸务就是要选择一组或多组方案,使目
标函数值最大或最小。从选择方案的角度说,
这是规划问题。从使目标函数值最大或最小的
角度说,就是优化问题。
线性规划数学模型的一般表示方式
max(min) f ( x) c1 x1 c2 x2 cn xn a11 x1 a12 x2 a1n xn a x a x a x 21 1 22 2 2n n s.t. a x a x a x m2 2 mn n m1 1 x1 , x2 , , xn n : 变量个数 ; m : 约束行数 ; n m : 线性规划问题的规模 c j : 价值系数 ; b j : 右端项; aij : 技术系数 (, )b1 (, )b2 (, )bm 0
管理运筹学 线性规划的图解法课件

线性规划的应用领域
生产计划
线性规划可以用于制定生产计划,优 化资源配置,提高生产效率。
物流优化
线性规划可以用于优化物流配送路线 、车辆调度等问题,降低运输成本。
金融投资
线性规划可以用于金融投资组合优化 ,实现风险和收益的平衡。
资源分配
线性规划可以用于资源分配问题,如 人员、资金、设备等资源的合理分配 ,提高资源利用效率。
束条件。
线性规划的目标是在满足一系列 限制条件下,使某一目标函数达
到最优值。
线性规划问题通常表示为求解一 组变量的最优值,使得这些变量 满足一系列线性等式或不等式约
束。
线性规划的数学模型
线性规划的数学模型由决策变量、目标函数和约束条 件三部分组成。
输标02入题
决策变量是问题中需要求解的未知数,通常表示为 $x_1, x_2, ldots, x_n$。
01
03
约束条件是限制决策变量取值的条件,通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
04
目标函数是问题要优化的函数,通常表示为$f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
03
绿色发展与线性规 划的结合
将可持续发展理念融入线性规划 ,实现资源节约、环境友好的发 展目标。
THANKS
[ 感谢观看 ]
约束条件
生产计划问题通常受到资源限制、市场需求和生 产能力等约束条件的限制。
详细描述
生产计划问题通常涉及到如何分配有限的资源, 以最大化某种目标函数(如利润)。通过图解法 ,我们可以将约束条件和目标函数在二维平面上 表示出来,从而找到最优解。
[管理学]第2章 线性规划的图解法
![[管理学]第2章 线性规划的图解法](https://img.taocdn.com/s3/m/adb09ff987c24028915fc3fc.png)
x1 , x2 ≥ 0
h
管理运筹学
3
§1 问题的提出
• 建模过程
1.理解要解决的问题,了解解题的目标和条件;
2.定义决策变量( 案;
x1
,x2
,…
,xn
),每一组值表示一个方
3.用决策变量的线性函数形式写出目标函数,确定最大化或最 小化目标;
坐标系上作图表示线 性规划问题的有关概 念,并求解。
下面通过例1详细 讲解其方法:
s.t.
x1 + x2 ≤ 300 (A) 2 x1 + x2 ≤ 400 (B)
x2 ≤ 250 (C) x1 ≥ 0 (D) x2 ≥ 0 (E) 得到最优解:
x1 = 50, x2 = 250 最优目标值 z = 27500
4.用一组决策变量的等式或不等式表示解决问题过程中必须遵 循的约束条件
• 一般形式
目标函数: 约束条件:
Max (Min) z = c1 x1 + c2 x2 + … + cn xn
s.t.
a11 x1 + a12 x2 + … + a1n xn a21 x1 + a22 x2 + … + a2n xn
说明:生产50单位Ⅰ产品和250单位Ⅱ产品将消耗完所有
可能的设备台时数及原料B,但原料A则还剩余50千克。
h
管理运筹学
10
§2 图 解 法
• 重要结论:
– 如果线性规划有唯一最优解,则一定有一个可 行域的顶点对应最优解;
– 无穷多个最优解。若将例1中的目标函数变为 max z=50x1+50x2,则线段BC上的所有点都代表 了最优解;
《管理运筹学》第二版习题答案(韩伯棠教授)1

3第 2 章 线性规划的图解法1、解:x 26A B1O 01C6x 1a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O0.1 0.6x 1有唯一解x 1 = 0.2函数值为 3.6x 2 = 0.6b 无可行解c 无界解d 无可行解e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 = 3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 303x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9 x 1 , x 2 , s 1 , s 2 , s 3 ≥= −4 x 1 − 6x 3 − 0s 1 − 0s 23x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x ' − 2 x ''− 0s − 0s'''− 3x 1 + 5x 2 − 5x 2 + s 1 = 70 2 x ' − 5x ' + 5x '' = 50122' ' ''3x 1 + 2 x 2 − 2x 2 − s 2 = 30'' ''4 、解:x 1 , x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 203x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36 x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6 x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
第二章 线性规划的图解法

例2.某工厂在计划期内要安排Ⅰ、Ⅱ两种产 品的生产,已知生产单位产品所需的设备台 时及A、B两种原材料的消耗、资源的限制, 如下表:
设备 原料 A 原料 B 单位产品获利 Ⅰ 1 2 0 50 元 Ⅱ 1 1 1 100 元 资源限制 300 台时 400 千克 250 千克
问题:工厂应分别生产多少单位Ⅰ、Ⅱ 产品才能使工厂获利最多?
第二章 线性规划的图解法
问题1具体数据如表所示:
资源 单耗 资源 煤(t) 电(kw.h) 油(t) 单位产品价格 9 4 3 7 4 5 10 12 360 200 300 产品 甲 乙 资源限量
提出和形成问题
建立模型
求解
结果的分析和应用
第二章 线性规划的图解法
在本例中
决策变量: 甲、乙产品的计划产量,记为x1 ,x2; 目标函数: 总收入记为f,则 f=7x1 +12x2 ,为体现对其求极大化, 在f 的前面冠以极大号Max,
第二章 线性规划的图解法 例2:.某公司由于生产需要,共需要A,B两种原料至 少350吨(A,B两种材料有一定替代性),其中A原 料至少购进125吨。但由于A,B两种原料的规格不同, 各自所需的加工时间也是不同的,加工每吨A原料需 要2个小时,加工每吨B原料需要1小时,而公司总共 有600个加工小时。又知道每吨A原料的价格为2万元, 每吨B原料的价格为3万元,试问在满足生产需要的 前提下,在公司加工能力的范围内,如何购买A,B 两种原料,使得购进成本最低?
第二章 线性规划的图解法
★线性规划模型的三个基本要素:
(也是所有规划问题的三个基本要素):
(1)决策变量:甲、乙产品的产量x1 ,x2 决策变量:需要决策的量,即等待求解的未知数。 (2)目标函数:总收入最大,Max f = 7 x 1 +12 x 2 目标函数:想要达到的目标,用决策 变量的表达式表示。 (3)约束条件: 约束条件:由于资源有限,为了实现 目标有哪些资源限制,用决策变量的 等式或不等式表示。
管理运筹学第2章 线性规划的图解法

i
i
MinZ e1i e2i
i
i
s.t.eβ10i-,eβ21i无 符yi 号 β限0 制β1xi
e1i , e2i 0,i 1,2,, n
还可以加上一些特定的需求.例如,要求必须过某 一点.
16
线性规划问题的应用举例(回归分析)
新标准:最小化最大绝对误差.
–整数规划问题
• 考虑短期排班的问题
–对午休换班进行建模
• 考虑每个工人
–允许工人有不同的偏好
29
套裁下料问题
例某工厂要做100套钢架,每套用长为2.9 m,2.1 m,1.5 m的圆钢
各一根。已知原料每根长7.4 m,问:应如何下料,可使所
用原料最省?
方案 1 方案 2 方案 3 方案 4 方案 5 方案 6 方案 7 方案 8
产品名称
规格要求
单价(元/kg)
甲 原材料 1 不少于 50%,原材料 2 不超过 25%
50
乙 原材料 1 不少于 25%,原材料 2 不超过 50%
35
丙
不限
25
原材料名称
1 2 3
每天最多供应量
100 100 60
单价(元/kg) 65 25 35
9
线性规划应用举例
解:设 xij 表示第 i 种(甲、乙、丙)产品中原料 j 的含量。 这样我们建立数学模型时,要考虑:
x1 + x2 ≥ 70 x2 + x3 ≥ 60 x3 + x4 ≥ 50 x4 + x5 ≥ 20 x5 + x6 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0
20
关于决策变量的选择的启示
第2章 线性规划的图解法

在标准形式中,要求右端项必须每一个分量非 对各个约束引进不同的松弛变量。 负。当某一个右端项系数为负时,如 bi<0,则把该 等式约束两端同时乘以-1,得到:-ai1 x1-ai2 x2… -ain xn = -bi。
管 理 运 筹 学
7
§2 图 解 法
对于只有两个决 策变量的线性规划问 题,可以在平面直角 坐标系上作图表示线 性规划问题的有关概 念,并求解。 下面通过例1详细 讲解其方法:
例1.目标函数: Max z = 50 x1 + 100 x2 约束条件: s.t. x1 + 2 x1 + x2 ≤ x2 ≤ x2 ≤ x1 ≥ x2 ≥ 300 (A) 400 (B) 250 (C) 0 (D) 0 (E)
X2=0
x1
管 理 运 筹 学
x1
9
§2 图 解 法
(2)对每个不等式(约束条件),先取其等式在坐标系中作直 线,然后确定不等式所决定的半平面。
400 300 200 100 100 200 300 300
x1+x2=300
200 100
2x1+x2=400
2x1+x2≤400
100
200
300
x1+x2≤300
x2 B C z=27500=50x1+100x2 z=20000=50x1+100x2 D z=0=50x1+100x2 E x1
A z=10000=50x1+100x2
图2-2
管 理 运 筹 学
12
§2 图 解 法
• 线性规划的标准化内容之一:——引入松驰变量(含义是 线性规划的标准化内容之一: 资源的剩余量) 例1 中引入 s1, s2, s3 模型化为 目标函数:Max z = 50 x1 + 100 x2 + 0 s1 + 0 s2 + 0 s3 约束条件:s.t. x1 + x2 + s1 = 300 2 x1 + x2 + s2 = 400 x2 + s3 = 250 x1 , x2 , s1 , s2 , s3 ≥ 0 对于最优解 x1 =50 x2 = 250 , s1 = 0 s2 =50 s3 = 0 说明:生产50单位Ⅰ产品和250单位Ⅱ产品将消耗完所有 可能的设备台时数及原料B,但对原料A则还剩余50千克。
运筹学课件1-2-1线性规划图解法

x2
4x1 ≤ 16 C D
| 1 | 2 | 3 | 4
4 x2 ≤ 16
最优解 (4, 2)
x1 + 2x2 ≤ 8
| 6 | 7 | 8 | 9
A
0
E
| 5
x1 下页 返回
上页
图解法求解步骤
• 由全部约束条件作图求出可行域; 由全部约束条件作图求出可行域; 可行域 • 作目标函数等值线,确定使目标函数最 作目标函数等值线, 等值线
E (8,0)
| 6
| 8
| | 10 12
| | | 14 16 18
x1 下页 返回
上页
练习) 图解法 —(练习)
18 — 16 — 14 — 12 — 10 — B 8—
x2
2x1 + x2 ≤ 16 2x1 + 2x2 ≤ 18 C 4x1 + 6x2 ≤ 48 D
| 2 | 4 | 6 | 8 | | 10 12 | | | 14 16 18
上页 下页 返回
x2
6 ① ③ 4
④
2
(4,2)
Zmax ②
0
2 Z=0
4 Z=6
6
8
x1
返回
上页
下页
练习: 练习:
用图解法求解LP问题
Max Z = 34 x1 + 40 x2
4 x1 + 6 x2 ≤ 48 2 x1 + 2 x2 ≤ 18 2 x1 + x2 ≤ 16 x1、 x2 ≥ 0
A
x1 下页 返回
上页
练习) 图解法 —(练习)
18 — 16 — 14 — 12 — 10 — B 8—
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
广西大学 王中昭 制作
目标函数: max Z=50x1+100x2, 满足约束条件:x1+x2≤300, 2 x1+x2≤400, x2≤250, x1≥0, x2≥0. 由于上述数学模型的目标函数为变量的线性函数, 约束条件也为变量的线性等式或不等式,故此模型称 之为线性规划。 把满足所有约束条件的解称为该线性规划的可行 解。把使得目标函数值最大(即利润最大)的可行解称 为该线性规划的最优解,此目标函数值称为最优目标 函数值,简称最优值。
这表明了生产50单位Ⅰ产品和250单位Ⅱ产品将消 耗完所有可使用的设备台时数和原料B,但对原料A来 说只消耗了350千克,还有(400—350)=50千克没有 使用。在线性规划中,对一个≤约束条件中没使用的资 源或能力的大小称之为松弛量。 12
广西大学 王中昭 制作
松弛变量和线性规划标准化
8
广西大学 王中昭 制作
§2.2 图 解 法
对于只包含两个决策变量的线性规划问题,可 以用图解法来求解。大于两个决策变量不能用图解 法来解了。 图解法.首先把每个约束条件(代表一个平面) 画在二维坐标轴上。
300 x2
X1+X2=300
100
100
300
x1
9
广西大学 王中昭 制作
1
广西大学 王中昭 制作
3.投资问题。从许多不同的投资项目中选 出一个投资方案,使得投资的回报为最大。 4.产品生产计划。合理充分地利用厂里 现有的人力、物力、财力,作出最优的产品 生产计划,使得工厂获利最大。 5.劳动力安排。某单位由于工作需要, 在不同时间段需要不同数量的劳动力,在每 个劳动力工作日连续工作八小时的规则下, 如何安排劳动力,才能用最少的劳动力来满 足工作的需要。
Z=0=X1+X2
Z=1=X1+X2
18
广西大学 王中昭 制作
4.线性规划存在无可行解的情况。若在 例1的数学模型中再增加一个约束条件 4x1+3x2≥1200,显然可见新的线性规划的可行 域为空域,出现这种情况是由于约束条件自相 矛盾导致的建模错误。
400
x2 X2=250
100 100 300
广西大学 王中昭 制作
3
广西大学 王中昭 制作
§2.1 问题的提出
生产,已知生产单位产品所需的设备台时及A,B两 种原材料的消耗,以及资源的限制,如下表所示。 设备 原料A 原料B Ⅰ 1 2 0 Ⅱ 1 1 1 资源限制 300台时 400千克 250千克
例1.某工厂在计划期内要安排Ⅰ、Ⅱ两种产品的
20
广西大学 王中昭 制作
x2 500
用图解法来解:
2x1+ห้องสมุดไป่ตู้x2=1200
300
Q点坐标为 x1=250, x2=100
2x1+3x2=800
100
Q
100
300
500
600 X1+X2=350
x1
X1=125
2X1+X2=600
21
广西大学 王中昭 制作
目标函数在可行域内Q点处取得最小 值。Q点
x1 X1+X2=300
19
4x1+3x2=1200
广西大学 王中昭 制作
目标函数最小化的线性规划问题
例2 某公司由于生产需要,共需要A,B两种原料至 少350吨(A,B两种材料有一定替代性),其中A原料 至少购进125吨。但由于A,B两种原料的规格不同, 各自所需的加工时间也是不同的,加工每吨A原料需 要2个小时,加工每吨B原料需要1小时,而公司总共 有600个加工小时。又知道每吨A原料的价格为2万元, 每吨B原料的价格为3万元,试问在满足生产需要的 前提下,在公司加工能力的范围内,如何购买A,B 两种原料,使得购进成本最低? 解:设x1为购进原料A的吨数,x2为购进原料B的 吨数。得到了此线性规划的数学模型如下: 目标函数: min f=2x1+3x2, 约束条件: x1+x2≥350, x1≥125,2x1+x2≤600, x1,x2≥0.
400
x2
2X1+X2=400
100 100 300 x2
x1
X2=250
100
100
300
x1
10
广西大学 王中昭 制作
2x1+x2=400
400 x2 B Z=27500=50x1+100x2 X2=250
阴影部分的每 一点(包括边界 线)都是这个线 性规划的可行 解,
此公共部分也 称为可行域。
2
6.运输问题。一个公司有若干个生产单位与销售单
位,根据各生产单位的产量及销售单位的销量,如何制 定调运方案,将产品运到各销售单位而总的运费最小。 以上的这些问题都有一个共同的特点。 首先,每个例子中都要求达到某些数量上的最大化 或最小化的目标。 如问题1,是要求使用原料钢管最少;问题2是要求 利润最大;问题3是要求投资回报最大等等。在所有线 性规划的问题中某些数量上的最大化或最小化就是线性 规划问题的目标。 其次,所有线性规划问题都是在一定的约束条件下 来追求其目标的。 例如问题1,是在满足生产需要的一定数量、不同 规格的钢管的约束下来追求原材料钢管的最小使用量。 而在问题2中是在原料供应量的限制和保证产品成分的 含量约束下来追求最大利润的。
6
广西大学 王中昭 制作
对于一般线性规划问题的建模过程。应注意 如下几个问题:
1.要正确理解所要解决的问题,要搞清在什么条件
下,追求什么样的目标。 2.定义决策变量,每一个问题都用一组决策变量(X1, X2, …, Xn)表示任何一个方案;这组决策变量的值就代 表一个具体方案,一般这些变量取值是非负的。 3.用决策变量的线性函数形式写出所要追求的目标, 称之为目标函数,按问题的不同,要求目标函数实现最 大化或最小化。 4.用一组决策变量的等式或不等式来表示在解决问 题过程上所必须遵循的约束条件。 满足以上2、3、4三个条件的数学模型称之为线性规 划的数学模型,其一般形式为: 7
广西大学 王中昭 制作
第二章 线性规划的图解法
线性规划(Linear Programming,简称LP)是运筹 学的一个重要分支。它是现代科学管理的重要手段之 一,是帮助管理者作出最优决策的一个有效的方法。 下面看看一些在管理上经常应用的典型线性规划问题: 1.合理利用线材问题。现有一批长度一定的钢管, 由于生产的需要,要求截出不同规格的钢管若干。试 问应如何下料,既满足了生产的需要,又使得使用的 原材料钢管的数量最少。 2.配料问题。用若干种不同价格不同成分含量的 原料,用不同的配比混合调配出一些不同价格不同规 格的产品,在原料供应量的限制和保证产品成分的含 量的前提下,如何获取最大的利润。
广西大学 王中昭 制作
2x1+x2=400
400 x2 B Z=15000=50x1+50x2 X2=250
100 100 300
x1 X1+X2=300
Z=0=50x1+50x2
Z=10000=50x1+50x2
16
广西大学 王中昭 制作
线性规划存在无界解,即无 最优解的情况。对下述线性规划问 题: 目标函数: max z =x1+x2 约束条件: x1-x2≤1 - 3x1+2x2≤6 x1≥0,x2≥0.
广西大学 王中昭 制作
线性规划的数学模型的一般形式为:
目标函数: max (min) Z=c1x1+c2x2+…+cnxn 约束条件: a11x1+a12x2+…+a1nxn≤( =, ≥) b1, a21x1+a22x2+…+a2nxn≤( =, ≥) b2, ………………………… am1x1+am2x2+…+amnxn≤( =, ≥) bm, x1, x2, …, xn≥0.
为了把一个线性规划标准化,需要有代表没使用的
资源或能力的变量,称之为松弛变量,记为Si。显 然这些松弛变量对目标函数不会产生影响,可以在 目标函数中把这些松弛变量的系数看成零,加了松 弛变量后我们得到如下的例1的数学模型: 目标函数: max Z=50x1+100x2+0s1+0s2+0s3, 约束条件: x1+x2+s1=300, 2x1+x2+s2=400, x2+s3=250, x1,x2,s1,s2,s3≥0
广西大学 王中昭 制作
其中max为最大化的符号(最小化为min);50和100分别为单位产
品 Ⅰ、 Ⅱ的利润。同样也可以用x1和x2的线性不等式来表示问 题的约束条件。对于台时数的限制可以表示为: X1+X2≤300.
同样,两种原材料的限量可分别表示为:
2X1+X2≤400, X2≤250. 显然还应该有x1≥0,x2≥0,因为Ⅰ产品, Ⅱ产品的 产量是不 能取负值的。综上所述,就得到了例1的数学模型如下:
13
广西大学 王中昭 制作
像这样把所有的约束条件都写成等式,称为线性 规划模型的标准化,所得结果称为线性规划的标准形 式。在标准型中 bj(右边常量)都要大于等于零, 对某 个bj小于零时,只要方程两边都乘以(-1)即可。 实际上以后可看到应同时具备如下三个条件的模型 才是标准型: 一是约束条件必须化为等式;二是所有变量必须化 为大于或者等于零;三是约束条件中的右端常数项必 须是大于或者等于零。 对例1 的最优解 x1=50,x2=250来说,松弛变量的值 如下所示: 约束条件 松弛变量的值 设备台时数 s1=0 原料A s2=50 原料B s3=0 14
