5.8 二次函数的应用 第1课时
《二次函数的应用》第1课时教案

《二次函数的应用》第1课时教案教学目标:1、经历数学建模的基本过程。
2、会运用二次函数求实际问题中的最大值或最小值。
3、体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值。
教学重点和难点:重点:二次函数在最优化问题中的应用。
难点:例1是从现实问题中建立二次函数模型,学生较难理解。
教学设计:一、创设情境、提出问题出示引例 (将作业题第3题作为引例)给你长8m 的铝合金条,设问:①你能用它制成一矩形窗框吗?②怎样设计,窗框的透光面积最大?③如何验证?二、观察分析,研究问题演示动画,引导学生观察、思考、发现:当矩形的一边变化时,另一边和面积也随之改变。
深入探究如设矩形的一边长为x 米,则另一边长为(4-x)米,再设面积为ym 2,则它们的函数关系式为x x y 42+-=⎩⎨⎧-ox x 40 40 x ∴并当x =2时(属于40 x 范围)即当设计为正方形时,面积最大=4(m 2)引导学生总结,确定问题的解决方法:在一些涉及到变量的最大值或最小值的应用问题中,可以考虑利用二次函数最值方面的性质去解决。
步骤:第一步设自变量;第二步建立函数的解析式;第三步确定自变量的取值范围;第四步根据顶点坐标公式或配方法求出最大值或最小值(在自变量的取值范围内)。
三、例练应用,解决问题在上面的矩形中加上一条与宽平行的线段,出示图形设问:用长为8m的铝合金条制成如图形状的矩形窗框,问窗框的宽和高各是多少米时,窗户的透光面积最大?最大面积是多少?引导学生分析,板书解题过程。
变式(即课本例1):现在用长为8米的铝合金条制成如图所示的窗框(把矩形的窗框改为上部分是由4个全等扇形组成的半圆,下部分是矩形),那么如何设计使窗框的透光面积最大?(结果精确到0.01米)练习:课本作业题第4题四、知识整理,形成系统这节课学习了用什么知识解决哪类问题?解决问题的一般步骤是什么?应注意哪些问题?学到了哪些思考问题的方法?五、布置作业:作业本。
5.8二次函数的应用

8 3x y x 2
3 2 x 4x 2 3 4 2 8 8 (x ) (0 x ) 3 2 3 3
所以:当窗框的宽为:X=4/3m,高为:2m时,
窗框的透光面积最大。最大面积是8/3平方米.
例1、如图窗户边框的上部分是由4个全等扇形组成的半
圆,下部分是矩形。如果制作一个窗户边框的材料的总 长度为6米,那么如何设计这个窗户边框的尺寸,才能使 窗户的透光面积最大(结果精确到0.01米)?
例1、如图窗户边框的上部分是由4个全等扇形组成的半
圆,下部分是矩形。如果制作一个窗户边框的材料的总 长度为6米,那么如何设计这个窗户边框的尺寸,才能使 窗户的透光面积最大(结果精确到0.01米)?
解:设半圆的半径为x米,如图,矩形的一边长为y米,
根据题意,有5x+πx+2x+2y=6,
即:y=3-0.5(π+7)x
∴3-0.5(π +7)x>0
π 2 π 2 故透光面积:S= x +2xy= x +2x[3-0.5(π +7)x] 2 2 6 ( 7) x 2 6 x (0<x< ) 7 2
(2,-10)
解:设y=ax2 +bx+c 又过O(0,0),B(2,-10)顶 (?,2/3) 点的纵坐标为2/3,得: 4a+2b+c= -10 (0,0) c=0 4ac - b2 2 = 4a 3 25 3 a = a=或 6 2 10 或 b= b = -2 3 c =0 c = 0 (2,-10) 又∵抛物线对称轴在y轴右侧 所以a,b异号
o
x
最新北师大版九年级数学下册《二次函数的应用(第1课时)》精品教学课件

y=x
坐标系,其函数的关系式为
25 ,当水面离桥拱顶的高度DO是4 m时,这时水面宽度
AB为 ( C )
A.-20 m
B.10 m
C.20 m
D.-10 m
4.某广场有一个喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面
直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最
结合图象可知,点 C 的坐标为(6+2 15,0).
所以 OC=6+2 15≈13.75(米).
答:该男生把铅球推出去约 13.75 米.
第二章
第1课时
几何图形问题
知识要点基础练
综合能力提升练
拓展探究突破练
-6-
7.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,
不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)
(2)求△PBQ的面积的最大值.
1
解:(1)∵S△PBQ=2PB·BQ,PB=AB-AP=18-2x,BQ=x,
1
∴y=2x(18-2x),即 y=-x2+9x(0<x≤4).
(2)由(1)知 y=-x2+9x,
9 2
81
∴y=- - 2 + 4 .
9
∵当 0<x≤2时,y 随
x 的增大而增大,又∵0<x≤4,
大高度为 ( A )
A.4米 B.3米
C.2米 D.1米
第二章
第1课时
几何图形问题
知识要点基础练
综合能力提升练
拓展探究突破练
-4-
5.8二次函数的应用

合作探究 某广告公司要设计一个周长为20 米的矩形广告牌.当矩形的一边 为何值时,广告牌的面积最大.
例2.如图,ABCD是一块边长为2m的正方形铁板,在 边AB上选取一点M,分别以AM和BM为边截取两块相 邻的正方形铁板。当AM的长为何值时,截取的板料 面积最小?
D C
A
2m
M
B
新课标教学网()--海 量教学资源欢迎下载!
如图,一位篮球运动员跳起投篮,球沿抛物线 1 y=- 5 x2+3.5运行,然后准确落入篮框内.已
知篮框的中心离地面的距离为3.05米. (1) 球在空中运行的最大高度为多少米? ( 2) 如果该运动员跳投时,球出手离地面的高度 为2.25 米,请问他距离篮框中心的水平距离是多少? B A
→数学问题 ↖ ↙
实际问题 求解数学问题
拓展提升
• 某商场销售一批名牌衬衫,平均每天可 售出20件,每件盈利40元。为了扩大销 售,商场决定采取适当的降价措施。经 调查发现,如果每件衬衫每降价一元, 商场平均每天可多售出2件。问每件衬 衫降价多少元时,商场平均每天盈利最 多?最大盈利为多少?
挑战自ቤተ መጻሕፍቲ ባይዱ:
复习旧知:
1、二次函数 y=x2-8x+12图象的开口向 上 , 对称轴是 直线x=4 ,顶点坐标为 (4,-4). 。 2、二次函数y=-3(x-1)2+5的图象开口 向 下 ,对称轴是 直线x=1 ,当x= 1 时 函数有最 大 值为 5 。当x <1 时,y 随x的增大而增大。
自主学习
如图所示,修建有一条边靠墙的矩形菜园,不 靠墙的三边的长度之和为60米. (1)如图,设长方形的一条边长为x米,则另一 条边长为多少米? (2)设长方形的面积为y平方米,写出 y与x之间 的关系式。 (3)怎样设计才能使菜园的面积最大?最大面积 是多少?
九年级数学上册二次函数的应用第1课时二次函数的应用1教案新版沪科版

21.4 二次函数的应用第1课时二次函数的应用(1)【知识与技能】经历探究图形的最大面积问题的过程,进一步获得利用数学方法解决实际问题的经验.【过程与方法】经历探索问题的过程,获得利用数学方法解决实际问题的经验,感受数学模型和数学应用的价值,通过观察、比较、推理、交流等过程,发展获得一些研究问题与合作交流的方法与经验.【情感态度】通过动手实做及同学之间的合作与交流,让学生积累经验,发展学习动力.【教学重点】会根据不同的条件,利用二次函数解决生活中的实际问题.【教学难点】从几何背景及实际情景中抽象出函数模型.一、情景导入,初步认知问题:某开发商计划开发一块三角形土地,它的底边长100米,高80米.开发商要沿着底边修一座底面是矩形的大楼,这座大楼地基的最大面积是多少?要解决这些实际问题,实际上也就是求面积最大的问题,在数学中也就是求最大值的问题.这节课我们看能否用已学过的数学知识来解决以上问题.【教学说明】通过几个实际情景设置悬念,引入新课.二、思考探究,获取新知探究:在第21.1节的问题中,要使围成的水面面积最大,则它的边长应是多少米?它的最大面积是多少平方米?根据题意,可得,S=x(20-x)问题:①这是一个什么函数?②要求最大面积,就是求的最大值.③你会求S的最大值吗?将这个函数的表达式配方,得S=-(x-10)2+100(0<x<20)这个函数的图象是一条开口向下抛物线中的一段,如图,它的顶点坐标是(10,100),所以,当x=10时,函数取最大值,即S最大值=100(m2)此时,另一边长=20-10=10(m)答:当围成的矩形水面边长都为10m时,它的面积是最大为100m2.你能总结此类题目的解题步骤吗?【归纳结论】在一些涉及到变量的最大值或最小值的应用问题中,可以考虑利用二次函数最值方面的性质去解决.其步骤为:第一步设自变量;第二步建立函数的解析式;第三步确定自变量的取值范围;第四步根据顶点坐标公式或配方法求出最大值或最小值(在自变量的取值范围内).【教学说明】由于学习本节课所用的基本知识点是求二次函数的最值,因此首先和同学们一起复习二次函数最值的求法,对于一般式,要求掌握配方法的同时,也能利用基本结论,对于顶点式,要求能直接说出其最值及取得最值时自变量的值.三、运用新知,深化理解1.教材P37例2.2.求下列函数的最大值或最小值.(1)y=2x2-3x-5;(2)y=-x2-3x+4.【分析】由于函数y=2x 2-3x-5和y=-x 2-3x+4的自变量x 的取值范围是全体实数,所以只要确定它们的图象有最高点或最低点,就可以确定函数有最大值或最小值.解:(1)二次函数y=2x 2-3x-5中的二次项系数2>0,因此抛物线y=2x 2-3x-5有最低点,即函数有最小值.因为y=2x 2-3x-5=2(x-43)2-849, 所以当x=43时,函数y=2x 2-3x-5有最小值是-849. (2)二次函数y=-x 2-3x+4中的二次项系数-1<0, 因此抛物线y=-x 2-3x+4有最高点,即函数有最大值.因为y=-x 2-3x+4=-(x+23)2+425, 所以当x=-23时,函数y=-x 2-3x+4有最大值是425. 3.要用总长为20m 的铁栏杆,一面靠墙,围成一个矩形的花圃,怎样围法才能使围成的花圃的面积最大?【分析】先写出函数关系式,再求出函数的最大值.解:设矩形的宽AB 为xm,则矩形的长BC 为(20-2x)m,由于x >0,且20-2x >0,所以0<x <10.围成的花圃面积y 与x 的函数关系式是y =x(20-2x),即y =-2x 2+20x.配方得y =-2(x -5)2+50所以当x =5时,函数取得最大值,最大值y =50.因为x =5时,满足0<x <10,这时20-2x =10.所以应围成宽5m,长10m 的矩形,才能使围成的花圃的面积最大.4.在一个直角三角形的内部作一个矩形ABCD,其中AB 和AD 分别在两直角边上.如果设矩形的一边AB=xm,那么当x 为多少时,矩形面积最大?最大面积是多少?5.如图,在Rt △ABC 中,∠C=90°,BC=4,AC=8,点D 在斜边AB 上,分别作DE ⊥AC,DF ⊥BC,垂足分别为E 、F,得四边形DECF,设DE=x,DF=y.(1)用含y 的代数式表示AE ;(2)求y 与x 之间的函数关系式,并求出x 的取值范围;(3)设四边形DECF 的面积为S,求S 与x 之间的函数关系,并求出S 的最大值.解:(1)由题意可知,四边形DECF 为矩形,因此AE=AC-DF=8-y.(2)由DE ∥BC,得ACAE BC DE ,即884y x -=, 所以,y=8-2x,x 的取值范围是0<x <4.(3)S=xy=x(8-2x)=-2x 2+8x=-2(x-2)2+8所以,当x=2时,S 有最大值8.【教学说明】应用所学知识解决实际问题,使学生明白数学来源于生活,适用于生活.四、师生互动、课堂小结先小组内交流收获和感想而后以小组为单位派代表进行总结.教师作以补充.布置作业:教材“习题21.4”中第1、2题.在教学中一定要注意学生易错地方:学生往往列出表达式后不根据背景写出自变量的范围;求最值时,只知代入顶点坐标公式,不考虑自变量范围.。
《二次函数的应用》第一课时练习题
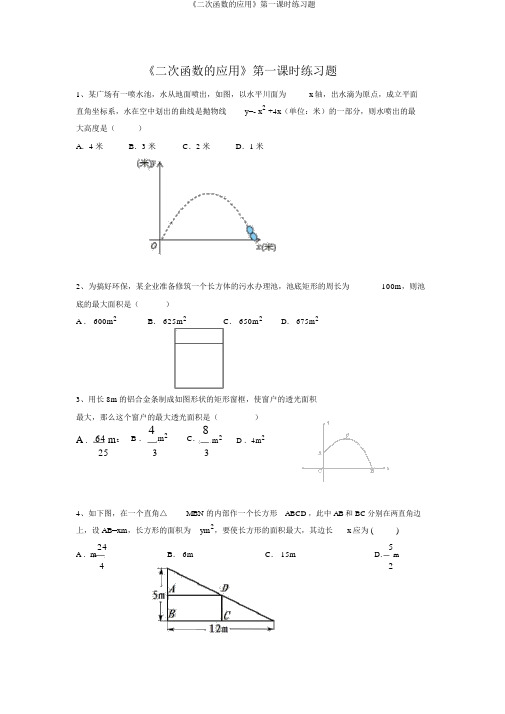
《二次函数的应用》第一课时练习题1、某广场有一喷水池,水从地面喷出,如图,以水平川面为x轴,出水滴为原点,成立平面直角坐标系,水在空中划出的曲线是抛物线y=- x2 +4x(单位:米)的一部分,则水喷出的最大高度是()A.4米B.3米C.2米D.1米2、为搞好环保,某企业准备修筑一个长方体的污水办理池,池底矩形的周长为100m,则池底的最大面积是()A . 600m2B. 625m2C. 650m2D. 675m23、用长 8m的铝合金条制成如图形状的矩形窗框,使窗户的透光面积最大,那么这个窗户的最大透光面积是()A. 64 m2 B .4m2C.8m2 D .4m225334、如下图,在一个直角△MBN 的内部作一个长方形ABCD ,此中 AB和 BC分别在两直角边上,设 AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为 ()24B. 6m C. 15m 5A .m D. m425、将一张边长为 30cm 的正方形纸片的四角分别剪去一个边长为xcm 的小正方形,而后折叠成一个无盖的长方体.当x 取下边哪个数值时,长方体的体积最大()A .7B .6C . 5D .46 、如 图,铅球运动员掷铅球的高度 y ( m ) 与水平距离x( m ) 之间的函数关系式是 :y1 x2 2 x 5 ,则该运动员此次掷铅球的成绩是 ()12 3 3A . 6mB . 12mC . 8mD .10m7、小明在某次投篮中,球的运动路线是抛物线圈中心,则他与篮底的距离L 是()y1 x2 3.5 的一部分,如图,若命中篮5A4 .6m B4 .5m C 4m D3 .5m.. ..8、某广场中心有高低不一样的各样喷泉,此中一支高度为3米的喷2水管喷水最大高度为4米,此时喷水水平距离为1米,在如下图2的坐标系中,这支喷泉的函数关系式是()A . y= 1 x 2+4B . y=- 10(x+ 1) 2+422C . y=4( x- 1 )2+ 3D . y=- 10( x-1)2+42 2 29、已知边长为 4的正方形截去一个角后成为五边形 ABCDE (如图),此中 AF=2,BF =1. 试在AB 上求一点 P ,使矩形 PNDM 有最大面积 .10、小明的家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修筑一个矩形花园,他买回了 32米长的不锈钢管准备作为花园的围栏,为了浇花和赏花的方便,准备在花园的中间再围出一条宽为一米的通道及在左右花园各放一个1米宽的门(木质).花园的长与宽怎样设计才能使花园的面积最大?11、一座拱桥的轮廓是抛物线型( 如图 a所示 ) ,拱高 6m,跨度 20m,相邻两支柱间的距离均为 5m.( 1)将抛物线放在所给的直角坐标系中( 如图 b所示 ) ,求抛物线的分析式;(2)求支柱 EF 的长度;(3)拱桥下地平面是双向行车道 ( 正中间是一条宽 2m的隔绝带 ) ,此中的一条行车道可否并排行驶宽 2m、高 3m的三辆汽车 ( 汽车间的间隔忽视不计 ) ?请说明你的原因.12、如下图,在生产中,为了节俭原资料,加工部件经常用一些边角余料,△ ABC为锐角三角形废料.此中BC =12cm,BC边上高 AD = 8cm,在△ ABC上截取矩形 PQM N,与 BC边重合,画出草图说明P, N两点落在什么地点上,才能使它的面积最大?最大面积是多少?并求出这时矩形的长和宽.答案:1、A2、 B3、 C4、D5、D6、D7、 B8、 D9、解:设矩形 PNDM 的边 DN x, NP y,则矩形 PNDM 的面积 Sxy(2 x4)易知 CN=4- x , EM=4- y.过点作BH PN 于点 H ,则有B 有△ AFB ∽△ BHPAF BH 即2 4 x BFPH1 y 3y1x 5 2Sxy1 x2 5x(2 x 4)2此二次函数的图象张口向下,对称轴 x 5当 x5时,函数值 y 随 x 的增大而增大,关于 2 x 4 来说,当 x 4 时,10、 解:设花园的宽为 x 米,面积为 S 平方米 则长为: 32 4x 2 34 4x )则: Sx(344 x)4x 2 34x 4( x17) 2 28944S 最大1 42 5 4 12344x 102617x21764S 与 x 的二次函数的极点不在自变量 x 范围内,而在x17 内, S 随 x 的增大而减小62当时,x 6答:可设计成宽176米,2长28910米的矩形花2圃,这样的花园面积最大.S 最大4(6)4 60( m )411、解:( 1)依据题目条件,A、B、C的坐标分别是(- 100, 0),( 10, 0),( 0, 6) .设抛物线的分析式为y ax2c则由题意可得:6c解得 a 3, c 6 .0100a c50( 2)可设 F( 5,y F),于是 y F3526 4.550进而支柱MN的长度是10 4.5 55米 .-= .( 3)设 DN 是隔绝带的宽, NG是三辆车的宽度和,则 G点坐标是( 7、0) .过 GH点作 GH 垂直 AB交抛物线于 H,则y H3726 3.06 350依据抛物线的特色,可知一条行车道能并排行驶这样的三辆汽车.12、解:设 ED = x cm,则 AE=( 8- x) cm,由矩形的性质可得:ED =PQ=MN ,PN // BC△APN∽△ ABCPN AEBC AD则 PN 8 x128PN 12 3 x2设矩形的面积为Scm23S x(12x)3x2 12x23( x 4) 22420 x8当 x =4cm时,矩形的最大面积为24cm2,这时,矩形的长PN为6cm,宽PQ为4cm。
《二次函数的应用》二次函数PPT教学课件(第1课时)

1.25米 O
当堂练习
y B
解:建立如图坐标系,设抛物线顶点 为B,水流落水处与x轴交于C点.
A 1.25
由题意可知A( 0,1.25)、
O
Cx
B( 1,2.25 )、C(x0,0).
设抛物线为y=a(x-1)2+2.25 (a≠0),
把点A坐标代入,得a= - 1;
∴抛物线为y=-(x-1)2+2.25.
当堂练习
(2)请你设计一个方案,使获得的设计费最多,并求 出这个费用. (2)S=-x2+6x=-(x-3)2+9; ∴当x=3时,即矩形的一边长为3m时,矩形面积 最大,为9m2.
这时设计费最多,为9×1000=9000(元)
当堂练习
5.公园要建造圆形的喷水池,在水池中央垂直于水面处安装 一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶 端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物 线路线落下.为使水流较为漂亮,要求设计成水流在离OA 距离为1米处达到距水面最大高度2.25米.如果不计其他因素, 那么水池的半径至少要多少米,才能使喷出的水流不落到 池外?
∴当x=2时,y取最小值,最小值为-9;
(2)∵a=-1<0,对称轴为x=
-
3 2
,顶点坐标为( -
3 2
,25
4
),
∴当x=
-3 2
时,y取最大值,最大值为
25 4
;
讲授新课
例2 已知二次函数y=ax2+4x+a-1的最小值为2,
则a的值为( C )
A.3
B.-1
C.4
D.4或-1
解析:∵二次函数y=ax2+4x+a-1有最小值2,
二次函数的应用第一课时教案

二次函数的应用(1)教学目标:1、经历数学建模的基本过程。
2、会运用二次函数求实际问题中的最大值或最小值。
3、体会二次函数是一类最优化问题的重要数学模型,感受数学的应用价值。
教学重点和难点:重点:二次函数在最优化问题中的应用。
难点:例1是从现实问题中建立二次函数模型,学生较难理解。
教学过程:由合作学习3引入:拟建中的一个温室的平面图如图,如果温室外围是一个矩形,周长为120m , 室内通道的尺寸如图,设一条边长为x (cm), 种植面积为y (m2)。
试建立y与x的函数关系式,并当x取何值时,种植面积最大?最大面积是多少?y=(x-2)(56-x)=-x2+58x-112=-(x-29)2+729 (自变量取值范围2<x<56)解题循环图:例1:图中窗户边框的上半部分是由四个全等扇形组成的半圆,下部分是矩形。
如果制作一个窗户边框的材料总长为6米,那么如何设计这个窗户边框的尺寸,使透光面积最大(结果精确到课内练习P45(1,2)及作业题补充练习1.如图,用长20cm的篱笆,一面靠墙围成一个长方形的园子,怎样围才能使园子的面积最大?最大面积是多少?2.如图在Rt△ABC中,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,已知AC=1,AB=2,求:(1)何时矩形PMCN的面积最大,把最大面积是多少?(2)当AM平分∠CAB时,矩形PMCN的面积.3.(06金华)23.初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:图案(1) 图案(2) 图案(3) 请根据以上图案回答下列问题:(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是▲ m2;(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为x m,长方形框架ABCD的面积为S=▲ (用含x的代数式表示);当AB=▲ m时, 长方形框架ABCD的面积S最大;在图案(3)中,如果铝合金材料总长度为l m, 设AB为x m,当AB= ▲ m时, 长方形框架ABCD的面积S最大.(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律.…探索:如图案(4),如果铝合金材料总长度为l m共有n条竖档时, 那么当竖档AB多少时,长方形框架ABCD的面积最大. 图案(4)小结:实际问题转化为数学模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,顶点坐标是_________. (h,k) ,它
b 4ac b 2 , 4a 抛物线
的对称轴是
,顶点坐标是___________.
低 点,函数
当a>0时,抛物线开口向 上 ,有最 有最 小 值,是 向 下 ,有最
4ac b 2 __________. 4a
的关系式为: y=(600-5x)(100+x)=-5x²+100x+60000
验证猜想
y=(600-5x)(100+x )=-5x²+100x+60000 解: =-5(x-10)2+60500 ∵当x=10时,y最大=60500 ∴增种10棵树时, 总产量最多,是60500个
“二次函数应用”的思路
某旅行社组团去外地旅游,30人起组团,每人单价800 元。旅行社对超过30人的团给予优惠,即旅行团每增加一 人,每人的单价就降低10元。当一个旅行团的人数是多少 时,旅行社可以获得最大营业额?
解:设一个旅行团有x人时,旅行社营业额为y元.则 y=〔 800-10(x-30) 〕·x =-10x2+1100x
25 个正方形面积之和的最小值是 2 或12.5 cm2.
3.(2010·兰州中考)如图,小明的父亲
在相距2米的两棵树间拴了一根绳子,给小
明做了一个简易的秋千.拴绳子的地方距地 面高都是2.5米,绳子自然下垂呈抛物线状, 身高1米的小明距较近的那棵树0.5米时,头部刚好接触 到绳子,则绳子的最低点距地面的距离为 0.5 米.
当销售单价为 润是
9112.5
9.25 元时,可以获得最大利润,最大利
元.
何时橙子总产量最大? 某果园有100棵橙子树,每一棵树平均结600个橙子.现准备 多种一些橙子树以提高产量,但是如果多种树,那么树之间 的距离和每一棵树所接受的阳光就会减少.根据经验估计, 每多种一棵树,平均每棵树就会少结5个橙子. 如果增种x棵树,果园橙子的总产量为y个,那么y与x之间
4ac b 2 4a
;当 a<0时,抛物线开口 大 值,是
高
点,函数有最
3.二次函数y=2(x-3)2+5的对称轴是 直线x=3
,顶点坐标 5
是
(3 ,5) 。当x= 3 时,y的最 小 值是
。
,顶点
4.二次函数y=-3(x+4)2-1的对称轴是 坐标是 是 (-4 ,-1)
直线x=-4
。当x= -4 时,函数有最 大 值,
4.(2010·昭通中考)某种火箭被竖直向上发射时,它的 高度h(m)与时间t(s)的关系可以用公式h=-5t2+150t+10表 示.经过______s 15 ,火箭达到它的最高点.
5.(2010·武汉中考)某宾馆有50个房间供游客住宿,当 每个房间的房价为每天180元时,房间会全部住满.当每个 房间每天的房价每增加10元时,就会有一个房间空闲.宾馆 需对游客居住的每个房间每天支出20元的各种费用.根据规 定,每个房间每天的房价不得高于340元.设每个房间的房 价每天增加x元(x为10的整数倍).
会导致销售量的减少,即销售单价每提高1元,销售量相应减 少20件.售价提高多少元时,才能在半个月内获得最大利润?
解:设售价提高x元时,半月内获得的利润为y元.则 y=(x+30-20)(400-20x) =-20x2+200x+4000
=-20(x-5)2+4500
∴当x=5时,y最大 =4500 答:当售价提高5元时,半月内可获最大利润4500元
-1 。
5.二次函数y=2x2-8x+9的对称轴是 直线x=2 ,顶点坐标
是 (2 ,1).当x= 2 时,函数有最 小 值,是 1
。
某商店经营T恤衫,已知成批购进时单价
是2.5元.根据市场调查,销售量与单价满足如
下关系:在一段时间内,单价是13.5元时,销售 量是500件,而单价每降低1元,就可以多售出 200件.请你帮助分析,销售单价是多少时, 可以获利最多?
5.8 二次函数的应用
第1课时
1、让学生进一步熟悉点的坐标和线段之间的转化. 2、让学生学会用二次函数的知识解决有关的实际问题. 3、掌握数学建模的思想,体会到数学来源于生活,又
服务于生活.
1. 二次函数y=a(x-h)2+k的图象是一条 抛物线 的对称轴是 直线x=h
直线x b 2a
,它
回顾本课“最大面积(利润)”解决问题的过程,你能总结 一下解决此类问题的基本思路吗? 1.理解问题; 2.分析问题中的变量和常量,以及它们之间的关系; 3.用数学的方式表示出它们之间的关系; 4.做数学求解; 5.检验结果的合理性,拓展等.
某商店购进一批单价为20元的日用品,如果以单价30元
销售,那么半个月内可以售出400件.根据销售经验,提高单价
1.(2010·甘肃中考)向空中发射一枚炮弹,经x秒后的
高度为y米,且时间与高度的关系为y=ax2bx+c
(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则 在下列时间中炮弹所在高度最高的是( B ) A.第8秒 C.第12秒 B.第10秒 D.第15秒
2.(2010·包头中考)将一条长为20cm的铁丝剪成两段, 并以每一段铁丝的长度为周长各做成一个正方形,则这两
=-10(x-55)2+30250
∴当x=55时,y最大=30250 答:一个旅行团有55人时,旅行社可获最大利润30250元
解这类题目的一般步骤 (1)列出二次函数的解析式,并根据自变量的实际意义, 确定自变量的取值范围; (2)在自变量的取值范围内,运用公式法或通过配方求
出二次函数的最大值或最小值。
若设销售价为x元(x≤13.5元),那么 销售量可表示为: 销售额可表示为:
500 20013.5 x
件;
x500 20013.5 x 元;
x 2.5500 20013.5 x 元; 所获利润可表示为:_______________________
(1)设一天订住的房间数为y,直接写出y与x的函数关系式 及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润 是多少元?
