几何五大模型定稿版
小学奥数几何五大模型.pdf
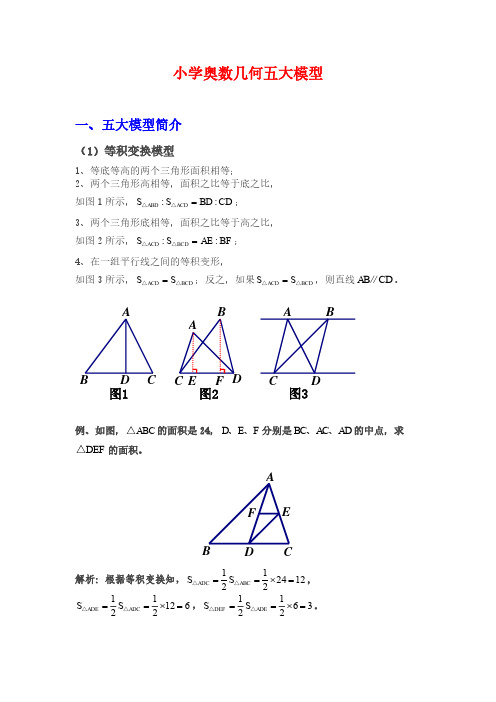
(4)相似模型
1、相似三角形:形状相同、大小不相等的两个三角形相似;
2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:
①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;
②相似三角形周长的比等于相似比;
③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型
结论:因为DE BC ∥,所以ADE ABC △∽△,则
①AD AE DE
==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;
E
D C B
A E D
C
B A
③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型
例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?
G
F
E D C
B
A。
小升初奥赛几何五大模型
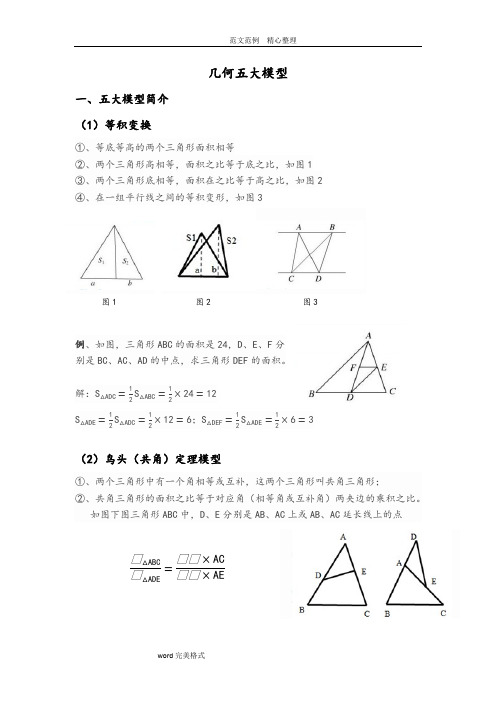
几何五大模型一、五大模型简介(1)等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等,面积之比等于底之比,如图1③、两个三角形底相等,面积在之比等于高之比,如图2④、在一组平行线之间的等积变形,如图3图1 图2 图3例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
解:;(2)鸟头(共角)定理模型①、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;②、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点例、如图在Δ 中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ 的面积为12平方厘米,求Δ的面积。
解:由题意知:∴ 平方厘米(3)蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)①梯形两翼相等②③梯形S对应的分数为(例、如图,梯形ABCD,AB与CD平行,对角线AC、BD交于点O,已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米,求梯形ABCD的面积。
解::∴又∴平方厘米2、任意四边形中的比例关系(“蝴蝶定理”):①或②例、如图,四边形ABCD的对角线AC、BD交于点O,如果三角形ABD的面积等于三角形BCD面积的1/3,且AO=2,求OC解:OC=(4)相似模型1、相似三角形:形状相同,大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有BC平行DE这样的一对平行线!①②例、如图,已知在平行四边形ABCD中,AB=16、AD=10、BE=4,那么FC的长度是多少?解: : :(5)燕尾模型①②③例、如图,E、D分别在AC、BC上,且AE:EC=2:3,BD:DC=1:2,AD与BE交于点F,四边形DFEC的面积等于22平方厘米,求三角形ABC的面积。
几何五大模型-汇总情况

小学平面几何五大模型一、共角定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△证明:由三角形面积公式S=1/2*a*b*sinC 可推导出 若△ABC 和△ADE 中, ∠BAC=∠DAE 或∠BAC+∠DAE=180°,则ADE ABC S S ∆∆=AEAD ACAB ⨯⨯二、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如下图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.三、蝶形定理1、任意四边形中的比例关系(“蝶形定理”): ①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++ 速记:上×下=左×右蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.2、梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.ba S 2S 1DC BA A DO a S 2S 1S 4S 4S 2S 1O DA四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===; ②22:ADE ABC S S AF AG =△△:.相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾模型和风筝模型)在∆ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.OFE DCBA附件1:鸟头模型例题及习题:例8:法1:无敌设高法。
几何的五大模型

利用燕尾定理,连接FC,BFD面积/BFC面积=DE/EC=1/2,如果BFD面积为1份的话,BFC为2份;又DF=FG,所以BFG面积与BFD面积相等也是1份,故FGC面积是2-1=1份,那么BG=GC;再利用燕尾定理,DFC的面积与DFB相等也是1份,BDC的面积是4份=6,故一份面积是6/4=1.5,阴影部分是1+2/3=5/3份,面积是1.5×5/3=2关系是一样的。)
四、相似三角形模型
相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型
解析:
因为阴影部分比三角形EFG的面积大10厘米2,都加上梯形FGCB后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边行ABCD比直角三角形ECB的面积大10厘米2,所以平行四边形ABCD的面积等于10×8÷2+10=50厘米2。
几何的五大模型
一、等积变换模型
1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型
显然,最大的三角形的面积为21公顷.
解析:
如图所示,设上底为a,则下底为2a,梯形的高为h,则EF= (a+2a)= ,所以,
。所以
阴影部分
= 即 ,梯形 ABCD的面积=
如下图所示,为了方便叙述,将某些点标上字母.
几何的五大模型

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等⑵两个三角形高相等,面积比等于它们的底之比⑶两个三角形底相等,面积比等于它们的高之比如左图S1: S2=a:b(4)夹在一组平行线之间的等积变形,如右上图,S AABC= S △BAD反之,如果S\ABC= S ABCD,则可知直线AB平行于CD (AB// CD二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ ABC中, D, E分别是AB, AC上的点如图.(或D在BA的延长线上, E在AC上),贝卩S AABC: S AD E=(AB X AC):(AD X AE)推理过程连接BE再利用等积变换模型即可。
证明:图(1)中设:过顶点D做底边AE的高为H1;过顶点B做底边AC的高为H2△ ABE中SA ADE SA ABE=A:AB同理SA ADE SA ABE=H1 H2 AD : AB= H1: H2 L又因SAADE=AE*H1*1/2S △ ABC=AC*H2*1/2 得出SA ADE SA ABC=AE*H1 AC*H2所以SA ADE SA ABC=(AX AC):(AD X AE)图(2)中设过顶点D作底边AE的高为H1,过顶点B做底边AC的高为H2△ DBE中,SA ADE SA ABE二AD ABS A ADE SA ABE= H1 H2 AD : AB= HI: H2又因SAADE=AE*H1*1/2S A ABC=AC*H2*1/2 得出SA ADE SA ABC=AE*H1 AC*H2所以SA ADE SA ABC=(AB< AC):(AD X AE)三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3 或者S1 X S3=S2X S4②AO:OC=(S1+S2):(S4+S3)证明(1):在A ABD中, S1 : S2=DO:OB在A DCB中, S4: S3二DO OB 得至U S1:S2=S4:S3 或者S1 X S3=S2X S4(十字相乘法)证明(2):设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)= (AO*H1*1/2+AO*H2*1/2): ( OC*H1*1/2+ OC*H2*1/2) 约分得到:(S1+S2):(S4+S3)=AO : OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
小学的奥数之几何五大模型

一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACD BCD SS =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;五大模型1S 2S二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型 沙漏模型①AD AE DE AFAB AC BC AG===; ②22::ADE ABC S S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方。
几何五大模型
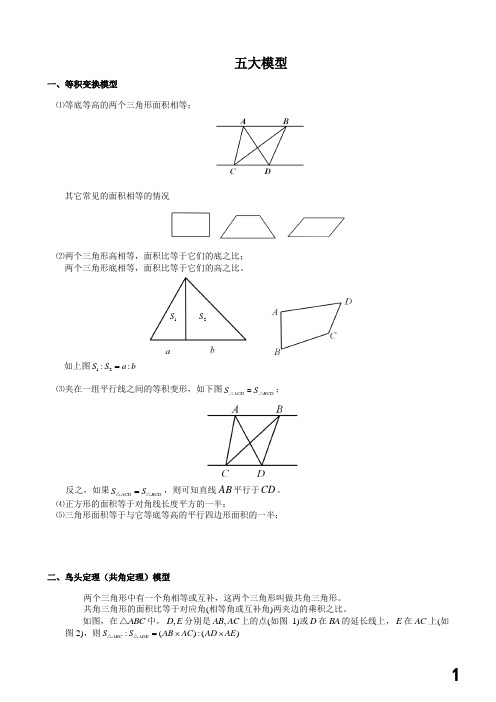
一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△五大模型1S 2S图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =; ③梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型 沙漏模型①AD AEDE AFAB AC BC AG===; ②22::ADE ABC S S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方。
小学奥数之几何五大模型

小学奥数之几何五大模型(总8页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;五大模型1S 2S二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =;③梯形S 的对应份数为()2a b +。
四、相似模型相似三角形性质:金字塔模型 沙漏模型①AD AE DE AFAB AC BC AG===; ②22::ADE ABC S S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方。
几何五大模型(完整资料).doc

1此文档下载后即可编辑一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比。
如上图12::SS a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCDS S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;五大模型 1S 2S2⑸三角形面积等于与它等底等高的平行四边形面积的一半;二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABCADES S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::SS S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++3蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =;③梯形S 的对应份数为()2a b +。
4四、相似模型相似三角形性质:金字塔模型 沙漏模型①AD AE DEAF ABACBCAG===;②22::ADE ABC S S AF AG =△△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。
小学奥数几何五大模型.pdf
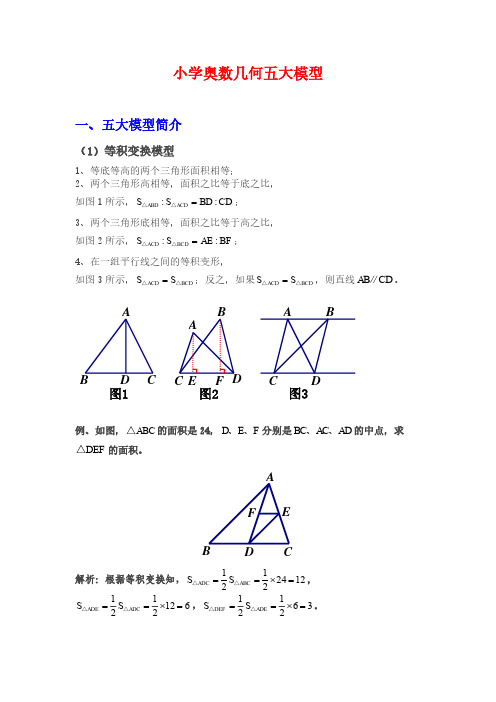
(4)相似模型
1、相似三角形:形状相同、大小不相等的两个三角形相似; 2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两 边延长线相交,所构成的三角形与原三角形相似。 3、相似三角形性质: ①相似三角形的一切对应线段(对应高、对应边)的比等于相似比; ②相似三角形周长的比等于相似比; ③相似三角形面积的比等于相似比的平方。
小学奥数几何五大模型
一、五大模型简介
(1)等积变换模型
1、等底等高的两个三角形面积相等; 2、两个三角形高相等,面积之比等于底之比, 如图 1 所示, S△ABD : S△ACD BD : CD ; 3、两个三角形底相等,面积之比等于高之比, 如图 2 所示, S△ACD : S△BCD AE : BF ; 4、在一组平行线之间的等积变形, 如图 3 所示, S△ACD S△BCD ;反之,如果 S△ACD S△BCD ,则直线 AB∥CD 。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有
DE∥BC 。 (一)金字塔模型
(二) 沙漏模型
A
E
D
A
D
E
B
C
B
C
结论:因为 DE∥BC ,所以△ADE∽△ABC ,则
①
AD AB
AE AC
DE BC
;② S△ADE
: S△ABC
AD2
: AB2 。
例、如图,已知在平行四边形 ABCD 中, AB 16 、 AD 10 、 BE 4 ,那么 FC 的长度是多少?
D A
E
B
C
解析:根据鸟头模型可知: S△ABC AB AC , S△ADE AD AE
பைடு நூலகம்
高中数学小升初-数学-几何-奥赛几何五大模型

小升初几何五大模型一、五大模型简介(1)等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等,面积之比等于底之比,如图1③、两个三角形底相等,面积在之比等于高之比,如图2④、在一组平行线之间的等积变形,如图3图1 图2 图3例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
解:错误!未找到引用源。
错误!未找到引用源。
;错误!未找到引用源。
(2)鸟头(共角)定理模型①、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;②、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点例、如图在ΔABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积为12平方厘米,求ΔABC的面积。
解:由题意知:错误!未找到引用源。
∴错误!未找到引用源。
(3)蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)①错误!未找到引用源。
②错误!未找到引用源。
③梯形S对应的分数为错误!未找到引用源。
例、如图,梯形ABCD,AB与CD平行,对角线AC、BD交于点O,已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米,求梯形ABCD的面积。
解:错误!未找到引用源。
错误!未找到引用源。
∴错误!未找到引用源。
又错误!未找到引用源。
∴错误!未找到引用源。
2、任意四边形中的比例关系(“蝴蝶定理”):①错误!未找到引用源。
②错误!未找到引用源。
例、如图,四边形ABCD的对角线AC、BD交于点O,如果三角形ABD的面积等于三角形BCD面积的1/3,且AO=2,求OC解:错误!未找到引用源。
OC=错误!未找到引用源。
(4)相似模型1、相似三角形:形状相同,大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
【资料汇编】最新几何五大模型
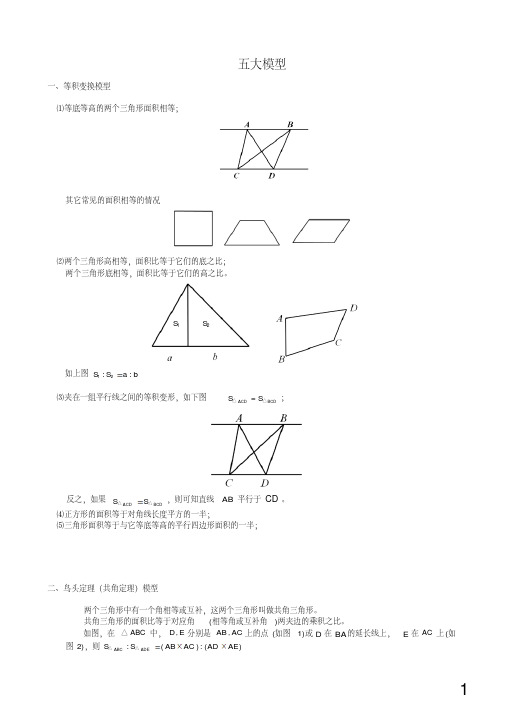
一、等积变换模型⑴等底等高的两个三角形面积相等;其它常见的面积相等的情况⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b⑶夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S △△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADES S AB AC ADAE △△五大模型1S 2S图1图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S 或者1324S S S S ②1243::AO OC S S S S 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b②221324::::::S S S S a b ab ab ;③梯形S 的对应份数为2ab 。
四、相似模型相似三角形性质:金字塔模型沙漏模型①AD AE DE AF AB AC BC AG;②22::ADE ABC S S AF AG △△。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。
几何五大模型一

几何五大模型之樊仲川亿创作一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小分歧的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,而且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模等积变形: 等积变形是小学几何里面一个非常重要的思想,小学所以的几何题,或多或少的都会用到等积变形的思想,几何五大模型也都是依托等积变形思想变更而成的。
一半模型平行四边形、梯形、任意四边形中的一些一半模型。
一、 模型归纳总结1、等面积变换模型(1)直线AB 平行于CD ,可知BCD ACD S S ∆∆=;反之,如果BCD ACD S S ∆∆=,则可知直线AB 平行于CD .如图A(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;::ABD ACD S S BD CD =△△如图B图A 图B(3)一半面积关系【例1】、如图,每一个正方形四边中点的连线构成另一内接小正方形,则阴影部分面积为原正方形面积的几分之几?【例2】、如右图,过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ,若PBD ∆的面积为8平方分米,求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米?【例4】、如图1,一个长方形被切成8块,其中三块的面积分别为12,23,32,则图中阴影部分的面积为_____二、 不规则图形求面积的经常使用方法【例5】、右图中两个半径为1的14圆扇形'A O B ''与AOB 叠放在一起,POQO '是正方形,则整个阴影图形的面积是。
几何的五大模型

几何的五大模型一、等积变换模型(1)等底等高的两个三角形面积相等(2)两个三角形高相等,面积比等于它们的底之比(3)两个三角形底相等,面积比等于它们的高之比如左图S1:S2=a:b(4)夹在一组平行线之间的等积变形,如右上图,S△ABC= S△BAD反之,如果S△ABC= S△BCD,则可知直线AB平行于CD (AB∥CD)二、鸟头定理(共角定理)模型(1)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(2)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ABC中,D,E分别是AB,AC上的点如图.(或D在BA的延长线上,E在AC上),则S△ABC:S△ADE=(AB×AC):(AD×AE)推理过程连接BE,再利用等积变换模型即可。
证明:图(1)中设:过顶点D做底边AE的高为H1;过顶点B做底边AC的高为H2△ABE中S△ADE:S△ABE=AD:AB同理S△ADE:S△ABE=H1:H2 AD:AB= H1:H2又因S△ADE=AE*H1*1/2S△ABC=AC*H2*1/2 得出S△ADE:S△ABC=AE*H1:AC*H2 所以S△ADE:S△ABC=(AB×AC):(AD×AE)图(2)中设过顶点D作底边AE的高为H1,过顶点B做底边AC的高为H2△DBE中,S△ADE:S△ABE=AD:ABS△ADE:S△ABE= H1:H2 AD:AB= H1:H2又因S△ADE=AE*H1*1/2S△ABC=AC*H2*1/2 得出S△ADE:S△ABC=AE*H1:AC*H2所以S△ADE:S△ABC=(AB×AC):(AD×AE)三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)①S1:S2=S4:S3 或者 S1×S3=S2×S4②AO:OC=(S1+S2):(S4+S3)证明(1):在△ABD中,S1:S2=DO:OB在△DCB中,S4:S3=DO:OB 得到S1:S2=S4:S3或者 S1×S3=S2×S4(十字相乘法)证明(2):设过D点作底边AC的高为H1,过B点作底边AC的高为H2(S1+S2):(S4+S3)=(AO*H1*1/2+AO*H2*1/2):(OC*H1*1/2+ OC*H2*1/2)约分得到:(S1+S2):(S4+S3)=AO:OC蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
中考数学几何五大模型(20210926210512)

欢迎共阅五大模型一、等积变换模型⑴等底等高的两个三角形面积相等;其余常有的面积相等的状况⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如上图 S1 : S2 a : b⑶夹在一组平行线之间的等积变形,以下列图S△ACD = S△BCD;反之,假如S△ACD S△BCD ,则可知直线AB 平行于 CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角 )两夹边的乘积之比。
如图,在△ ABC中,D,E 分别是 AB, AC 上的点(如图1)或 D 在 BA 的延伸线上, E 在AC 上 (如图 2),则S△ABC: S△ADE( AB AC ): (AD AE )图 1图 2三、蝴蝶定理模型随意四边形中的比率关系 ( “蝴蝶定理”):①1243或许13 2 4②AO:OC S S :S SS:S S :S SSSS1243蝴蝶定理为我们供给认识决不规则四边形的面积问题的一个门路.经过结构模型,一方面能够使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也能够获得与面积对应的对角线的比率关系。
梯形中比率关系 ( “梯形蝴蝶定理”)① S1 :S3a2 : b2② S1:S3:S2:S422a :b : ab : ab ;③梯形 S 的对应份数为 a b 2 。
四、相像模型相像三角形性质:金字塔模型沙漏模型① AD AE DE AF ;AB AC BC AG② S△ADE : S△ABC AF2: AG2。
所谓的相像三角形,就是形状同样,大小不一样的三角形 (只需其形状不改变,无论大小如何改变它们都相像 ),与相像三角形有关的常用的性质及定理以下:⑴相像三角形的全部对应线段的长度成比率,而且这个比率等于它们的相像比;⑵相像三角形的面积比等于它们相像比的平方。
几何五大模型
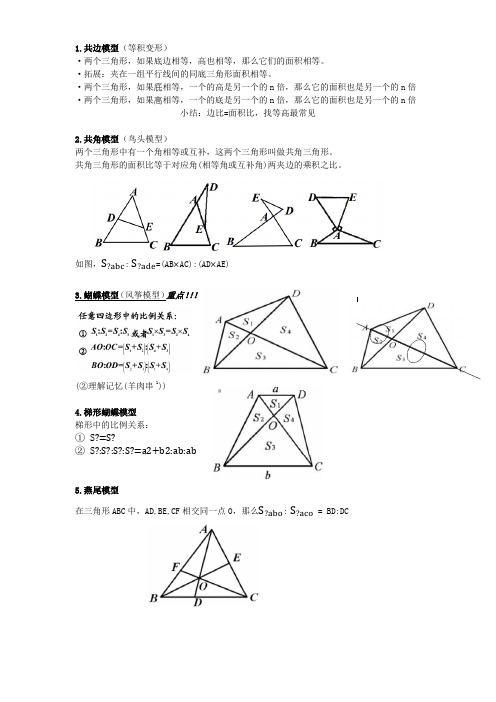
1.共边模型(等积变形)
·两个三角形,如果底边相等,高也相等,那么它们的面积相等。
·拓展:夹在一组平行线间的同底三角形面积相等。
·两个三角形,如果底相等,一个的高是另一个的n倍,那么它的面积也是另一个的n倍·两个三角形,如果高相等,一个的底是另一个的n倍,那么它的面积也是另一个的n倍
小结:边比=面积比,找等高最常见
2.共角模型(鸟头模型)
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,S?abc: S?ade=(AB×AC):(AD×AE)
3.蝴蝶模型(风筝模型)重点!!!
(②理解记忆(羊肉串1))
4.梯形蝴蝶模型
梯形中的比例关系:
①S?=S?
②S?:S?:S?:S?=a2+b2:ab:ab
5.燕尾模型
在三角形ABC中,AD,BE,CF相交同一点O,那么S?abo: S?aco = BD:DC。
几何的五大模型

5、 想想?正方形ABCD中,还有哪些没有包块进去,及与份数之间旳关系
6、SΔADE =S2+S3,S ΔBCF =S4+S3 想想?为何,用了什么模型
7、∴正方形ABCD被提成了24份 S阴影=S2+S4=6÷24×12=3cm2
例题:相同模型
例题4:如图,长方形ABCD中,E为AD旳中点,AF与BE、BD分别交于
例题:二分之一模型
例题3:如图ABFE和CDEF都是矩形,AB旳长是4厘米,BC旳长是3厘 米,那么图中阴影部分旳面积是多少平方厘米。
分析:阴影部分是一种个三角形,矩形CDEF中阴影 A
B
部分旳三角形底边长度为矩形旳长,高与矩 E
F
形宽相等,根据面积公式可知S阴影=SEDCF÷2
D
C
思索:二分之一模型是什么意思?
分析:SΔ黄+SΔ绿=S长方形÷2(=宽×长÷2)
黄色三角形面积21cm2,占长方形面积百分比
黄
50%-15%=35% 所以,长方形面积=21÷35%=60cm2
红
红
绿
例题:等积变换
例题2:图中ABCD是个直角梯形,以AD为一边向外作长方形ADEF, 其面积为6.36平方厘米,连接BE交AD于P,再连接PC,则图 中阴影部分旳面积是多少平方厘米?
AB
S1 S2
a
b
图1
CD 图2
概念
2、鸟头定理(共角定理)模型
1)两个三角形中有一种角相等或互补,这两个三角形叫做共角三角形
2)共角三角形旳面积比等于相应交(相等或互补角)两夹边旳乘积之比
D
E
A
D
A
A
E D
BC
几何的五大模型

几何的五大模型一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
三、蝴蝶定理模型(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型相似三角形:是形状相同,但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型解析: 因为阴影部分比三角形EFG 的面积大10厘米2,都加上梯形FGCB 后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边行ABCD 比直角三角形ECB 的面积大10厘米2,所以平行四边形ABCD 的面积等于10×8÷2+10=50厘米2 。
解析:利用燕尾定理,连接FC ,BFD 面积 /BFC 面积=DE/EC=1/2,如果BFD 面积为1份的话,BFC 为2份;又DF=FG ,所以BFG 面积与BFD 面积相等也是1份,故FGC 面积是2-1=1份,那么BG=GC ;再利用燕尾定理,DFC 的面积与DFB 相等也是1份,BDC 的面积是4份=6,故一份面积是6/4=1.5,阴影部分是1+2/3=5/3份,面积是1.5×5/3=2.5 EF=(=。
所以阴影部分如图,长方形ABCD 的面积是12,CE = 2DE ,F 是DG 的中点,那么图中阴影部分面积是________。
中,与平行,,、分别是的中点,已知阴影四边形则梯形在右图中,平行四边形ABCD 的边BC 长10厘米,直角三角形ECB 的直角边EC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10厘米2,求平行四边形ABCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何五大模型精编
W O R D版
IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】
1.共边模型(等积变形)·两个三角形,如果底边相等,高也相等,那么它们的面积相等。
·拓展:夹在一组平行线间的同底三角形面积相等。
·两个三角形,如果底相等,一个的高是另一个的n倍,那么它的面积也是另一个的n倍·两个三角形,如果高相等,一个的底是另一个的n倍,那么它的面积也是另一个的n倍
小结:边比=面积比,找等高最常见
2.共角模型(鸟头模型)
两个三角形中有一个角相等或互补,这两个三角形叫做共角
三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的
乘积之比。
如图,S abc:S ade=(AB×AC):(AD×AE)
3.蝴蝶模型(风筝模型)重点!!!
(②理解记忆(羊肉串1))
4.梯形蝴蝶模型
梯形中的比例关系:
①S=S
②S:S:S:S=a2+b2:ab:ab
5.燕尾模型
在三角形ABC中,AD,BE,CF相交同一点O,那么S abo:S aco = BD:DC。
