第3章用统计量描述数据22年课件
合集下载
《统计描述》课件
05
统计描述的注意事项
数据来源的可靠性
01 确保数据来源的可靠性和权威性，避免使用不可 靠的数据源。
02 在数据收集过程中，应遵循科学的方法和程序， 确保数据的准确性和客观性。
02 对于网络数据，需要注意数据的来源和可信度， 避免使用虚假或错误的数据。
数据的异常值处理
在数据分析前，需要对异常值进 行识别和处理。
《统计描述》ppt课 件 (2)
目录
• 统计描述概述 • 数据收集与整理 • 数值型数据的统计描述 • 分类数据的统计描述 • 统计描述的注意事项
01
统计描述概述
定义与目的
定义
统计描述是对数据进行整理、归纳和总结，以简明的方 式呈现数据的基本特征和规律。
目的
帮助人们更好地理解数据，为进一步的数据分析提供基 础。
03
数值型数据的统计描述
平均数
01 平均数
表示一组数据的总体“平 均水平”的统计量。
03 计算方法
将一组数据加起来，然后
除以这组数据的个数。
02 分类
算术平均数、调和平均数
、几何平均数等。
04 应用场景
分析数据集中各数值的一
般水平，如工资、成绩等。Βιβλιοθήκη 中位数和众数中位数
将一组数据从小到大排列 后，位于中间位置的数。
根据实际情况，可以采用不同的 方法处理异常值，如删除、替换 或保留异常值并对其进行合理的
解释。
处理异常值时应保持客观和科学 ，避免主观臆断或随意处理。
数据的可视化呈现
数据可视化是统计描述的重要 部分，通过图表、图像等形式 呈现数据。
选择合适的图表类型，如柱状 图、折线图、饼图等，以便更 直观地展示数据的特点和趋势 。
应用统计学(第三章 数据的描述性分析)
累积频率 Cumulative P
0.02 0.09 0.28 0.63
0.84 0.95 1.00
a.自然值进行分组，最大值17，最小值11 b.数据主要集中在14，向两侧分布逐渐减少
(3)计量数据
100例健康男子血清总胆固醇(mol/L)测定结果
4.77 3.37 6.14 3.95 3.56 4.23 4.31 4.71 5.69 4.12 4.56 4.37 5.39 6.30 5.21 7.22 5.54 3.93 5.21 6.51 5.18 5.77 4.79 5.12 5.20 5.10 4.70 4.74 3.50 4.69 4.38 4.89 6.25 5.32 4.50 4.63 3.61 4.44 4.43 4.25 4.03 5.85 4.09 3.35 4.08 4.49 5.30 4.97 3.18 3.97 5.16 5.10 5.85 4.79 5.34 4.24 4.32 4.77 6.36 6.38 4.88 5.55 3.04 4.55 3.35 4.87 4.17 5.85 5.16 5.09 4.52 4.38 4.31 4.58 5.72 6.55 4.76 4.61 4.17 4.03 4.47 3.40 3.91 2.70 4.60 4.09 5.96 5.48 4.40 4.55 5.38 3.89 4.60 4.47 3.64 4.34 5.18 6.14 3.24 4.90
15
21
0.21
0.84
16
11
0.11
0.95
17
5
0.05
1.00
表 2-2 100只梅花鸡每月产蛋数次数分布表
每月产蛋数
11 12 13 14 15 16 17
第3章 平均数、标准差与变异系数
复习题
试分别写出样本平均数、方差和标准差的统计量及参数 符号. 试写出平均数、方差、标准差、几何平均数、变异系数 的计算公式. 平方和的计算公式有-----、-------和-------。 已知∑xi2=45180，平均值=67，n=10，则其方差和标准 差分别为------和------ 。 已知样本平方和为360，样本容量为10，则其标准差等 于-------。
S
x ( x ) / n
2 2
n 1
2955000 5400 / 10
2
10 1
65.828
三、标准差的特性
1、各观测值间变异大，标准差也大，反之则小。 2、各观测值加或减一个常数，其标准差值不变。 3、每观测值乘或除一个常数a，则标准差是原来的
a倍或1/a倍。
Excel计算统计量
二、几何平均数
使用（适用）条件； 定义； 计算方法； 实例。
一、几何平均数适用条件
呈倍数关系或偏态分布的资料，描述
其集中性时可用几何平均数表示。
如畜禽 、水产养殖的增长率，抗体的滴度，药 物的效价，畜禽疾病的潜伏期等，可用几何平均 数表示其平均水平。
2、几何平均数定义
n个观测值相乘之积开n次方所得的方根， 称为几何平均数，记为G。
S
x
2
(
x)
2
n
n 1
6、
测定北京肉鸭周龄(x)与体重(g , y)如下:
周龄：0 1 2 3 4 5 体重 48.5 206 535 969 1467 1975 相对数： 4.25 2.60 1.81 1.51 1.35
试求其周平均生长速度。
第3章 用统计量描述数据(1)PPT课件
STATISTICS (第三版)
加权平均数
(例题分析)
某电脑公司销售量数据分组表
按销售量分组
140~150 150~160 160~170 170~180 180~190 190~200 200~210 210~220 220~230 230~240
合计
组中值(Mi) 145 155 165 175 185 195 205 215 225 235
➢ 由此可见，在射击比赛中，运动员能否取得好的成绩， 发挥的稳定性至关重要。那么，怎样评价一名运动员 的发挥是否稳定呢？通过本章内容的学习就能很容易 回答这样的问题
3-6
统计学
STATISTICS (第三版)
数据分布的特征
数据水平 (位置)
数据差异 (分散程度)
分布形状 (偏态和峰态)
3-7
第 3 章 用统计量描述数据
x
x
3 - 10
统计学
STATISTICS (第三版)
简单算数平均
(Simple mean)
设一组数据为：x1 ，x2 ，… ，xn (总体据xN)
样本平均数
n
xx1 x2
xn
xi i1
n
n
总体平均数
N
x1 x2
xN
xi i1
N
N
3 - 11
统计学
STATISTICS (第三版)
加权平均数
3.1 水平的度量
3.1.1 平均数 3.1.2 中位数和分位数 3.1.3 用哪个值代表一组数据？
3.1 水平的度量 3.1.1 平均数
统计学
STATISTICS (第三版)
平均数
(mean)
1. 也称为均值，常用的统计量之一
加权平均数
(例题分析)
某电脑公司销售量数据分组表
按销售量分组
140~150 150~160 160~170 170~180 180~190 190~200 200~210 210~220 220~230 230~240
合计
组中值(Mi) 145 155 165 175 185 195 205 215 225 235
➢ 由此可见，在射击比赛中，运动员能否取得好的成绩， 发挥的稳定性至关重要。那么，怎样评价一名运动员 的发挥是否稳定呢？通过本章内容的学习就能很容易 回答这样的问题
3-6
统计学
STATISTICS (第三版)
数据分布的特征
数据水平 (位置)
数据差异 (分散程度)
分布形状 (偏态和峰态)
3-7
第 3 章 用统计量描述数据
x
x
3 - 10
统计学
STATISTICS (第三版)
简单算数平均
(Simple mean)
设一组数据为：x1 ，x2 ，… ，xn (总体据xN)
样本平均数
n
xx1 x2
xn
xi i1
n
n
总体平均数
N
x1 x2
xN
xi i1
N
N
3 - 11
统计学
STATISTICS (第三版)
加权平均数
3.1 水平的度量
3.1.1 平均数 3.1.2 中位数和分位数 3.1.3 用哪个值代表一组数据？
3.1 水平的度量 3.1.1 平均数
统计学
STATISTICS (第三版)
平均数
(mean)
1. 也称为均值，常用的统计量之一
第3章 数据的分析 单元备课 2022—2023学年鲁教版(五四制)八年级数学上册
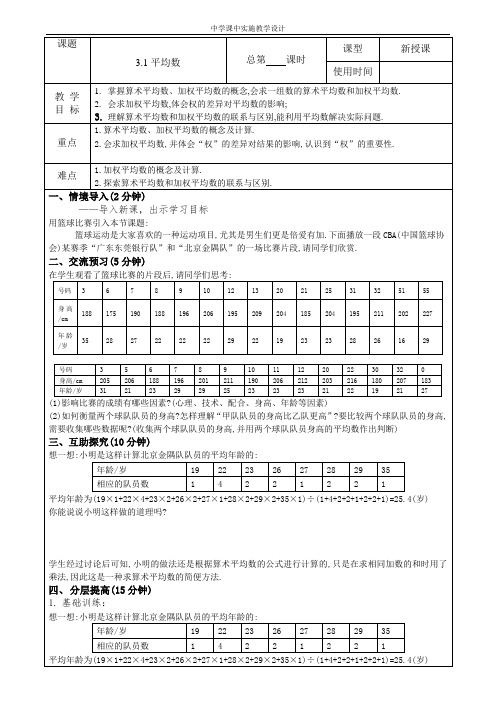
课题3.1平均数总第课时课型新授课使用时间教学目标1.掌握算术平均数、加权平均数的概念,会求一组数的算术平均数和加权平均数.2.会求加权平均数,体会权的差异对平均数的影响;3.理解算术平均数和加权平均数的联系与区别,能利用平均数解决实际问题.重点1.算术平均数、加权平均数的概念及计算.2.会求加权平均数,并体会“权”的差异对结果的影响,认识到“权”的重要性.难点1.加权平均数的概念及计算.2.探索算术平均数和加权平均数的联系与区别.一、情境导入(2分钟)——导入新课，出示学习目标用篮球比赛引入本节课题:篮球运动是大家喜欢的一种运动项目,尤其是男生们更是倍爱有加.下面播放一段CBA(中国篮球协会)某赛季“广东东莞银行队”和“北京金隅队”的一场比赛片段,请同学们欣赏.二、交流预习(5分钟)在学生观看了篮球比赛的片段后,请同学们思考:号码3678910121320212531325155身高/cm188175190188196206195209204185204195211202227年龄/岁352827222222292219232328261629号码356789101112202230320身高/cm205206188196201211190206212203216180207183年龄/岁3121232929252323232122192127(1)影响比赛的成绩有哪些因素?(心理、技术、配合、身高、年龄等因素)(2)如何衡量两个球队队员的身高?怎样理解“甲队队员的身高比乙队更高”?要比较两个球队队员的身高,需要收集哪些数据呢?(收集两个球队队员的身高,并用两个球队队员身高的平均数作出判断)三、互助探究(10分钟)想一想:小明是这样计算北京金隅队队员的平均年龄的:年龄/岁1922232627282935相应的队员数14221221平均年龄为(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁)你能说说小明这样做的道理吗?学生经过讨论后可知,小明的做法还是根据算术平均数的公式进行计算的,只是在求相同加数的和时用了乘法,因此这是一种求算术平均数的简便方法.四、分层提高(15分钟)1.基础训练：想一想:小明是这样计算北京金隅队队员的平均年龄的:年龄/岁1922232627282935相应的队员数14221221平均年龄为(19×1+22×4+23×2+26×2+27×1+28×2+29×2+35×1)÷(1+4+2+2+1+2+2+1)=25.4(岁)你能说说小明这样做的道理吗?学生经过讨论后可知,小明的做法还是根据算术平均数的公式进行计算的,只是在求相同加数的和时用了乘法,因此这是一种求算术平均数的简便方法.2.提升训练：某市是一个严重缺水的城市,为鼓励市民珍惜每一滴水,某居委会表扬了100个节约用水模范户,5月份这100户节约用水的情况如下表:每户节约用水量(单位:t)1 1.2 1.5节水户数523018那么5月份这100户平均每户节约用水的吨数为 t.教师引导师友订正答案，对师友出现的错题和重点题目进行有选择性讲解、点拨，组织师友有针对性地进行互助交流。
医学统计学PPT课件
验结果,每次都有如此好的吻合. 的概率约10万分之4。 6
绪论 Introduction
讲授内容：
一、医学统计学的意义
二、统计学中的几个基本概念
三、统计资料的类型
四、医学统计工作的基本步骤
五、学习医学统计学应注意的问题
.
7
一、医学统计学的意义
• 1.统计学（statistics）:应用数学的原理与 方法,研究数据的搜集、整理与分析的科 学，对不确定性数据作出科学的推断。
例如：某药治疗高血压患者30名
样本含量（n）为30
.
21
二、统计学中的几个基本概念
• 4、参数（parameter）和统计量（statistic）
• （1）参数（parameter）：根据总体个体 值统 计计算出来的描述总体的特征量。
• 一般用希腊字母表示
• （2）、统计量（statistic）：根据样本个体值统 计计算出来的描述样本的特征量。
（120.2cm,118.6cm,121.8cm,…)
研究某人群性别构成 变量值：男、女。
.
15
二、统计学中的几个基本概念
• 2、同质（homogeneity）和变异 （variation）
• （1）、同质（homogeneity）：根据研究 目的给研究单位确定的相同性质。
• 研究长沙市2004年7岁 男孩身高的正常值范围？
.
27
二、统计学中的几个基本概念
• （3）、抽样误差（sampling error）：由 于抽样所造成的样本统计量与总体参数 的差别。
• 例如：=120.0cm
n=100
•
N=5万 → X =118.6cm
• 特点:1)不可避免性
第3章用统计量描述数据习题答案(可编辑修改word版)
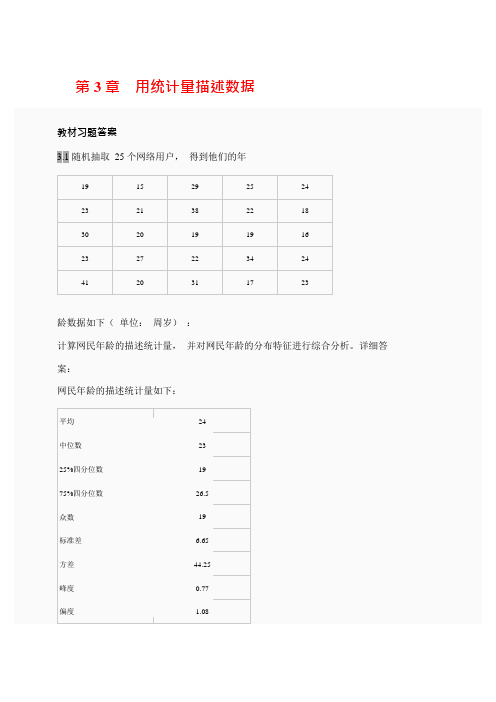
第3 章用统计量描述数据从集中度来看，网民平均年龄为24 岁，中位数为23 岁。
从离散度来看，标准差在为6.65 岁，极差达到26 岁，说明离散程度较大。
从分布的形状上看，年龄呈现右偏，而且偏斜程度较大。
3.2 某银行为缩短顾客到银行办理业务等待的时间，准备采用两种排队方式进行试验。
一种是所有顾客都进入一个等待队列；另一种是顾客在 3 个业务窗口处列队3 排等待。
为比较哪种排队方式使顾客等待的时间更短，两种排队方式各随机抽取9 名顾客，得到第一种排队方式的平均等待时间为7.2 分钟，标准差为 1.97 分钟，第二种排队方式的等待时间（单位：分钟）如下：5.56.6 6.7 6.87.1 7.3 7.4 7.8 7.8(1)计算第二种排队时间的平均数和标准差。
(2)比两种排队方式等待时间的离散程度。
(3)如果让你选择一种排队方式，你会选择哪一种？试说明理由。
详细答案：（1）（岁）；（岁）。
（2）；。
第一中排队方式的离散程度大。
（3）选方法二，因为平均等待时间短，且离散程度小。
3.3 在某地区随机抽取120 家企业，按利润额进行分组后结果如下：300～400 30400～500 42500～600 18600 以上11合计120计算120 家企业利润额的平均数和标准差（注：第一组和最后一组的组距按相邻组计算）。
详细答案：=426.67（万元）；（万元）。
3.4一家公司在招收职员时，首先要通过两项能力测试。
在 A 项测试中，其平均分数是100 分，标准差是15 分；在B 项测试中，其平均分数是400 分，标准差是50 分。
一位应试者在A 项测试中得了115 分，在B 项测试中得了425 分。
与平均分数相比，该位应试者哪一项测试更为理想？详细答案：通过计算标准化值来判断，，，说明在Ａ项测试中该应试者比平均分数高出 1 个标准差，而在 B 项测试中只高出平均分数0.5 个标准差，由于 A 项测试的标准化值高于 B 项测试，所以 A 项测试比较理想。
(03)第3章-用统计量描述数据1资料
1. 也称为内距或四分间距 2. 上四分位数与下四分位数之差：Qd = QU – QL
25% 75%
平均差
1. 各变量值与其平均数离差绝对值的平均数 2. 能全面反映一组数据的离散程度
3. 计算公式为
未分组数据
n
xi x
Md i1 n
组距分组数据
k
Mi x fi
Md i1 n
某电脑公司销售量数据分组表
k
(Mi x)3 fi
SK i1 ns 3
偏态系数
(例题分析)
某电脑公司销售量偏态及峰度计算表
按销售量份组(台) 组中值(Mi)
频数 fi
(Mi x)3 fi
140 ~ 150
145
4
-256000
150 ~ 160
155
9
-243000
160 ~ 170
165
16
-128000
170 ~ 180
Md i1
n
平均差
(例题分析)
k
Md
i 1
Mi x n
fi
2040 17(台) 120
含义：每一天的销售量平均数相比， 平均相差17台
3.2 离散程度的度量 3.2.3 方差和标准差
方差和标准差
(variance and standard deviation)
1. 数据离散程度的最常用测度值 2. 反映各变量值与均值的平均差异
（1）粗略地估计一下，男生中有百分之几的人 体重在55~65kg之间。
（2）粗略地估计一下，女生中有百分之几的人 体重在40~60kg之间。
例 ：一条生产线平均每天的产量为3700件，标准 差50件。如果某一天的产量低于或高于平均产量， 并落入正负两个标准差的范围之外，就认为该生
25% 75%
平均差
1. 各变量值与其平均数离差绝对值的平均数 2. 能全面反映一组数据的离散程度
3. 计算公式为
未分组数据
n
xi x
Md i1 n
组距分组数据
k
Mi x fi
Md i1 n
某电脑公司销售量数据分组表
k
(Mi x)3 fi
SK i1 ns 3
偏态系数
(例题分析)
某电脑公司销售量偏态及峰度计算表
按销售量份组(台) 组中值(Mi)
频数 fi
(Mi x)3 fi
140 ~ 150
145
4
-256000
150 ~ 160
155
9
-243000
160 ~ 170
165
16
-128000
170 ~ 180
Md i1
n
平均差
(例题分析)
k
Md
i 1
Mi x n
fi
2040 17(台) 120
含义：每一天的销售量平均数相比， 平均相差17台
3.2 离散程度的度量 3.2.3 方差和标准差
方差和标准差
(variance and standard deviation)
1. 数据离散程度的最常用测度值 2. 反映各变量值与均值的平均差异
（1）粗略地估计一下，男生中有百分之几的人 体重在55~65kg之间。
（2）粗略地估计一下，女生中有百分之几的人 体重在40~60kg之间。
例 ：一条生产线平均每天的产量为3700件，标准 差50件。如果某一天的产量低于或高于平均产量， 并落入正负两个标准差的范围之外，就认为该生
数理统计CH3描述统计32ppt课件
2 99 100 9801
3 104 108 10816
4 96 97 9216
5 94 93 8836
合计 489 496 47885
y2 9604 10000 11664 9409 8649 49326
x 97.8
xy 9408 9900 11232 9312 8742 48594
变异系数
cv
48594 1 489 496 85.2 5
2020/1/20
王玉顺：数理统计03_描述统计
18
3.4 基于观测的统计计算
x 489 y 496
(4)计算样本协方差 xy 48594 SPxy 85.2
序号 x y
x2
y2
xy
1 96 98 9216 9604 9408
2 99 100 9801 10000 9900
3 104 108 10816 11664 11232
4 96 97 9216 9409 9312
5 94 93 8836 8649 8742
合计 489 496 47885 49326 48594
y2 y2 n
sxx
n1
syy
n1
2020/1/20
王玉顺：数理统计03_描述统计
22
3.4 基于观测的统计计算
Pearson Correlation
Coefficient
(5)计算样本相关系数
样本相关系数
样本协方差
Correlation Coefficient
SPxy
r SPxy
n1
sxy
SSx SS y
SSx SS y
第3章用统计量描述数据22年课件
QL位置
n3 4
QU位置
3n 1 4
如果位置不是整数，则按比例分摊位置两侧数值的差值
3 - 17
2020-1-16
统计学
STATISTICS (第四版)
四分位数的计算
(数据个数为奇数)
【例3-4】 9个家庭的人均月收入数据(4种方法计算)
原始数据: 1500 750 780 1080 850 960 2000 1250 1630 排 序: 750 780 850 960 1080 1250 1500 1630 2000
合计
组中值(Mi) 145 155 165 175 185 195 205 215 225 235
—
频数(fi) 4 9
16 27 20 17 10
8 4 5
120
3-9
Mi fi 580 1395 2640 4725 3700 3315 2050 1720 900 1175
22200
k
Mi fi
位 置: 1 2 3 4 5 6 7 8 9
方法4—Excel公式
QL 位置
9
4
3
3
QU 位置
3
9 4
1
7
QL 850
QU 1500
统计函数—QUARTILE
3 - 21
2020-1-16
统计学
STATISTICS (第四版)
众数
(mode)
1. 一组数据中出现次数最多的变量值 2. 适合于数据量较多时使用 3. 不受极端值的影响 4. 一组数据可能没有众数或有几个众数
2. 如果平均收入的多少代表了该地区的生活水平，你 能否认为甲地区的平均生活水平就高于乙地区呢？
第三章_统计量描述统计
数据除了具有集 中趋势特征外， 还有分散趋势的 特征
乙商店
10 10
甲商店
0 可口 可乐 雪碧 杏 仁露 新 骑士 醒目
0 可口 可乐
雪碧
杏 仁露
新 骑士
醒目
Mo=可口可乐
Mo=可口可乐
虽然两商店软饮料购买频数的众数都是 可口可乐，但数据的离散程度不同。
23
离散趋势
二、离散趋势
乙城市 甲城市
非常不 满意
4. 均值
对组距数 据频数分 布表求均 值方法— 用组中值 代替该组 的各个值
__
x1 f1 x2 f 2 xn f n x 76 f
16
均值
4. 均值
___ xi x 0 1.所有观测值与其均值的离差之和等于0。 i 1 n
均值的性质
2.所有观测值与其均值的离差平方和最小。
2
fm
Me L x
n S 2 m1
利用两个三角形相 似原理，得到比例 关系，从中求出x
S m 1
x
i
L
11
四分位数
3. 四分位数
有50%的观测值小 于中位数
有50%的观测值 大于中位数
占25%数 据量位置 的分位数 最 小 观测值 下 四 分位数 （low quartile）
50%位置 的分位数
33 28 5 75 33 28 33 26
7
众数
由组距式频数分布表计算众数的原理
i
利用两个三角形相 似原理，得到比例 关系，从中求出x
x
f f 1
f f 1
x f f 1 i x f f 1
8
第三章 描述性统计量
▪ （三）众数（Mode)
▪ 1.概念：众数是数据集中出现次数最多或最常见的 数值。
▪ 2.众数的确定 （1）对于未列表的数据和列表（不分组）的数据， 可直接观察来确定。
2020/6/24
第一节 刻画数据集中程度的特征量
例 下表是关于交通事故的统计Fra bibliotek料，忽略交通事故的
等级，事故的频数统计如下：
事故次数 0
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 依据各种统计指标的具体代表意义和计算方 式的不同，可以将其归纳为数值平均数和位 置平均数两大类。
▪ 数值平均数就是对所有各项数据计算的平均 数。因此它能够概括反映所有各项数据的平 均水平。
▪ 常用的数值平均数有算术平均数、调和平均 数和几何平均数。
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 由未列表数据或列表（不分）组数据计算四分位数，首先要求 求出它们所在的位置点，然后根据位置点确定四分位数。
▪ 例 某单位12个部门的费用月支出如下：4138，2894，5154， 4006，3285，3985，5007，5248，4862，7500，6124，7003。 试确定四分位数。
▪ 四分位数(quartile)是能够将数据集按数据大小等分为四部分 的三个数据，分别记为Q1、Q2、Q3。
▪ Q1：从最小值开始位于第（n+1）/4数据处的那个数据称为1/4 分位数或下四分位数
▪ Q2：中位数 ▪ Q3：从最小值开始位于第3（n+1）/4数据处的那个数据称为
3/4分位数或上四分位数
2020/6/24
第二节 刻画数据离散程度的特征量
▪ 变异指标又称为变动度，是描述统计数据差 异程度或离散程度的指标。
▪ 1.概念：众数是数据集中出现次数最多或最常见的 数值。
▪ 2.众数的确定 （1）对于未列表的数据和列表（不分组）的数据， 可直接观察来确定。
2020/6/24
第一节 刻画数据集中程度的特征量
例 下表是关于交通事故的统计Fra bibliotek料，忽略交通事故的
等级，事故的频数统计如下：
事故次数 0
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 依据各种统计指标的具体代表意义和计算方 式的不同，可以将其归纳为数值平均数和位 置平均数两大类。
▪ 数值平均数就是对所有各项数据计算的平均 数。因此它能够概括反映所有各项数据的平 均水平。
▪ 常用的数值平均数有算术平均数、调和平均 数和几何平均数。
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 由未列表数据或列表（不分）组数据计算四分位数，首先要求 求出它们所在的位置点，然后根据位置点确定四分位数。
▪ 例 某单位12个部门的费用月支出如下：4138，2894，5154， 4006，3285，3985，5007，5248，4862，7500，6124，7003。 试确定四分位数。
▪ 四分位数(quartile)是能够将数据集按数据大小等分为四部分 的三个数据，分别记为Q1、Q2、Q3。
▪ Q1：从最小值开始位于第（n+1）/4数据处的那个数据称为1/4 分位数或下四分位数
▪ Q2：中位数 ▪ Q3：从最小值开始位于第3（n+1）/4数据处的那个数据称为
3/4分位数或上四分位数
2020/6/24
第二节 刻画数据离散程度的特征量
▪ 变异指标又称为变动度，是描述统计数据差 异程度或离散程度的指标。
常用统计量及其应用课件
应用
在科学、工程、医学等领 域广泛使用，例如在产品 质量检测、医学诊断等方 面。
方差分析
定义
方差分析是一种统计方法，用于 比较两个或多个样本均值是否存
在显著差异。
方法
通过计算方差，将样本均值与总体 均值的差异分解为可解释部分和不 可解释部分，从而判断不同样本之 间是否存在显著差异。
应用
在工业、农业、社会科学等领域都 有广泛的应用，例如在生产过程控 制、市场调研等方面。
极差是描述一组数据离散程度 的另一个常用统计量，是最大 值与最小值的差。
优点：计算简单，直观易懂。
缺点：不能反映数据的整体分 布情况，容易受到极端值的影响。
03
推论性统计量
假设检验
01
02
03
定义
假设检验是统计推断的重 要组成部分，通过样本数 据对总体参数进行推断。
方法
根据样本数据做出假设， 然后利用适当的统计量进 行检验，根据检验结果判 断原假设是否合理。
缺点：不适用于所有数据分布，有些 数据分布可能没有标准差。
方差
方差是描述一组数据离散程度的另一个常用统计量，是 标准差的平方。
优点：能够反映数据的波动情况，计算简单。
计算方法：先求出每个数据与平均数的差值，然后平方 这些差值，最后求平均数。
缺点：不适用于所有数据分布，有些数据分布可能没有 方差。
极差
统计量的意义
统计量的意义在于它能够帮助我们更 好地理解数据，掌握数据的分布特征 和规律，为决策提供科学依据。
通过统计量，我们可以对数据样本进 行比较和分析，从而得出有关总体分 布的结论，为进一步研究和应用提供 支持。
统计量的分类
常用统计量包括平均数、中位数、众数、方差、标准差、四 分位数等。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n
x甲i1 nxi 0121 010 100 88(2分 )
n
xi
x乙i1n
082 0110101(2 分 ) 10
3 - 10
3.1 水平的度量 3.1.2 中位数和分位数
统计学
STATISTICS (第四版)
中位数
(median)
1. 排序后处于中间位置上的值。不受极端值影响
50%
50%
合计
组中值(Mi) 145 155 165 175 185 195 205 215 225 235
—
频数(fi) 4 9
16 27 20 17 10
8 4 5
120
Mi fi 580 1395 2640 4725 3700 3315 2050 1720 900 1175
22200
k
M i fi
x i1 n
位 置: 1 2 3 4 5 6 7 8 9
位置 n1915 22
中位数 1080
3 - 13
统计学
STATISTICS (第四版)
中位数的计算
(数据个数为偶数)
【例3-3】 10个家庭的人均月收入数据
排 序: 750 780 850 960 1080 1250 1500 1630 2000 2800
统计学
STATISTICS (第四版)
3-2
统计学
STATISTICS (第四版)
3-3
统计学
STATISTICS (第四版)
3-6
统计学
STATISTICS (第四版)
简单算数平均
(Simple mean)
设一组数据为：x1 ，x2 ，… ，xn (总体数据xN)
样本平均数 总体平均数
位 置: 1 2 3 4 5 6 7 8 9 10
位 置 n110 15.5 22
中位 1数 18 102510165 2 统计函数—MEDIAN
3 - 14
统计学
STATISTICS (第四版)
四分位数—用3个点等分数据
(quartile)
1. 排序后处于25%和75%位置上的值
25% 25% 25% 25%
统计学
STATISTICS (第四版)
四分位数的计算
(数据个数为奇数)
【例3-4】 9个家庭的人均月收入数据(4种方法计算)
原始数据: 1500 750 780 1080 850 960 2000 1250 1630 排 序: 750 780 850 960 1080 1250 1500 1630 2000
Q L 位 9 4 置 1 2 .5Q U 位 3 (9 置 4 1 ) 7 .5
Q L7 2 8805 801Q U 5 15 2 1 06 0 1 35 06
3 - 19
统计学
STATISTICS (第四版)
四分位数的计算
(数据个数为奇数)
【例3-4】 9个家庭的人均月收入数据
四分位数的计算
(位置的确定)
方法3：
Q位置
n 1 2
2
1
其中[ ]表示中位数的位置取整。这样计算出的四分位数的
位置，要么是整数，要么在两个数之间0.5的位置上
方法4： Excel给出的四分位数位置的确定方法
QL位置
n3 4
QU位置
3n1 4
如果位置不是整数，则按比例分摊位置两侧数值的差值
3 - 17
22200 185 120
3-9
统计学
STATISTICS (第四版)
加权平均数
(权数对均值的影响)
【例】甲乙两组各有10名学生，他们的考试成绩及其分布数 据如下
甲组： 考试成绩（x ）: 0 20 100
人数分布（f ）：1 1 8
乙组： 考试成绩（x）: 0 20 100
人数分布（f ）：8 1 1
2. 位置确定 3. 数值确定
Me
中位数位 n置 1 2
Me
x
n1 2
12x
n 2
x
n1 2
n为奇数 nΒιβλιοθήκη 偶数3 - 12统计学
STATISTICS (第四版)
中位数的计算
(数据个数为奇数)
【例3-3】 9个家庭的人均月收入数据
原始数据: 1500 750 780 1080 850 960 2000 1250 1630 排 序: 750 780 850 960 1080 1250 1500 1630 2000
Mi fi i1
n
k
总体加权平均：
M1f1f1 Mf22f 2 fkMkfk
Mi fi i1
N
3-8
统计学
STATISTICS (第四版)
加权平均数
(例题分析)
某电脑公司销售额数据分组表
按销售额分组
140~150 150~160 160~170 170~180 180~190 190~200 200~210 210~220 220~230 230~240
QL
QM
QU
2. 不受极端值的影响
3 - 15
统计学
STATISTICS (第四版)
四分位数的计算
(位置的确定)
方法1：定义算法
Q
L
位置
n 4
Q
U
位置
3n 4
方法2：较准确算法 (SPSS的算法)
3 - 16
Q
L
位置
n 1 4
Q
U
位置
3(n 1) 4
统计学
STATISTICS (第四版)
n
xx1 x2 xn i1 xi
n
n
N
x1x2 xN i1 xi
N
N
统计函数—AVERAGE
3-7
统计学
STATISTICS (第四版)
加权平均数
(Weighted mean)
设各组的组中值为：M1 ，M2 ，… ，Mk 相应的频数为： f1 ， f2 ，… ，fk
k
样本加权平均：
xM1f1f1 Mf22f 2 fkMkfk
四分位数的计算
(数据个数为奇数)
【例3-4】 9个家庭的人均月收入数据
原始数据: 1500 750 780 1080 850 960 2000 1250 1630 排 序: 750 780 850 960 1080 1250 1500 1630 2000
位 置: 1 2 3 4 5 6 7 8 9
方法2—SPSS公式
位 置: 1 2 3 4 5 6 7 8 9
方法1—定义公式
Q L 位 9 4 置 2 .25 Q U 位 3 4 置 9 6 .75
QL78(0857 08)00.25 Q U125(1050 10 2) 50.7 05
79.57
14.537
3 - 18
统计学
STATISTICS (第四版)
原始数据: 1500 750 780 1080 850 960 2000 1250 1630 排 序: 750 780 850 960 1080 1250 1500 1630 2000
位 置: 1 2 3 4 5