三角高程测量原理(2).pptx
《三角高程测量》课件

80%
测量过程
通过在建筑物顶部和底部设置测 点,利用全站仪或经纬仪等测量 设备,对测点进行角度和距离测 量,计算出建筑物的垂直度。
大跨度桥梁的高程测量
桥梁监测
大跨度桥梁在施工和运营过程 中需要进行高程测量,以监测 桥梁的变形和沉降情况。
跨度大
大跨度桥梁的跨度较大,传统 的水准测量方法难以满足精度 要求,而三角高程测量方法则 能够提供更高的测量精度。
将处理后的结果以图表、地图 等形式进行展示,以便更好地 理解和应用。
总结与报告编写
对整个测量过程进行总结,编 写详细的测量报告和技术文档
,以便后续使用和参考。
03
三角高程测量的误差来源与控制
误差来源分析
仪器误差
由于仪器本身精度限制 ,导致测量结果存在误
差。
观测误差
观测过程中由于人为因 素或环境因素引起的误
3
自动化巡检与监测
利用无人机和传感器技术,实现测量设施的自动 化巡检和监测,提高设施运行安全性和可靠性。
在其他领域的应用拓展
城市规划与建设
利用三角高程测量技术获取城市 地形数据,为城市规划、建设和
管理工作提供基础数据支持。
农业领域应用
利用三角高程测量技术获取农田地 形数据,为农业灌溉、土地整治和 农业机械化等工作提供技术支持。
加强质量控制
建立完善的质量控制体系,对测量过 程和结果进行严格的质量控制和检查 。
04
三角高程测量的实际应用案例
高层建筑物的垂直度测量
80%
垂直度测量
三角高程测量方法常用于高层建 筑物的垂直度测量,以确保建筑 物垂直且符合设计要求。
100%
精度要求高
由于高层建筑物的垂直度对结构 安全和稳定性至关重要,因此需 要高精度的测量方法来确保垂直 度在允许的误差范围内。
三角高程测量
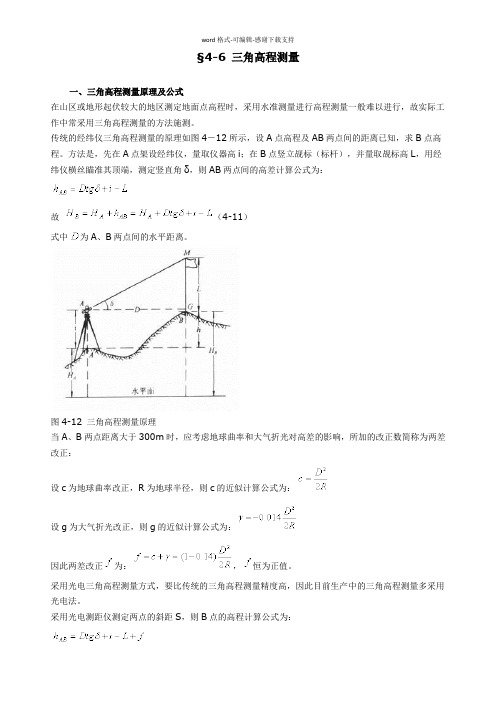
§4-6 三角高程测量一、三角高程测量原理及公式在山区或地形起伏较大的地区测定地面点高程时,采用水准测量进行高程测量一般难以进行,故实际工作中常采用三角高程测量的方法施测。
传统的经纬仪三角高程测量的原理如图4-12所示,设A点高程及AB两点间的距离已知,求B点高程。
方法是,先在A点架设经纬仪,量取仪器高i;在B点竖立觇标(标杆),并量取觇标高L,用经纬仪横丝瞄准其顶端,测定竖直角δ,则AB两点间的高差计算公式为:故(4-11)式中为A、B两点间的水平距离。
图4-12 三角高程测量原理当A、B两点距离大于300m时,应考虑地球曲率和大气折光对高差的影响,所加的改正数简称为两差改正:设c为地球曲率改正,R为地球半径,则c的近似计算公式为:设g为大气折光改正,则g的近似计算公式为:因此两差改正为:,恒为正值。
采用光电三角高程测量方式,要比传统的三角高程测量精度高,因此目前生产中的三角高程测量多采用光电法。
采用光电测距仪测定两点的斜距S,则B点的高程计算公式为:(4-12)为了消除一些外界误差对三角高程测量的影响,通常在两点间进行对向观测,即测定hAB和hBA,最后取其平均值,由于hAB和hBA反号,因此可以抵销。
实际工作中,光电三角高程测量视距长度不应超过1km,垂直角不得超过15°。
理论分析和实验结果都已证实,在地面坡度不超过8度,距离在1.5km以内,采取一定的措施,电磁波测距三角高程可以替代三、四等水准测量。
当已知地面两点间的水平距离或采用光电三角高程测量方法时,垂直角的观测精度是影响三角高程测量的精度主要因素。
二、光电三角高程测量方法光电三角高程测量需要依据规范要求进行,如《公路勘测规范》中光电三角高程测量具体要求见表4-6。
表4-6 光电三角高程测量技术要求往返各注:表4-6中为光电测距边长度。
对于单点的光电高程测量,为了提高观测精度和可靠性,一般在两个以上的已知高程点上设站对待测点进行观测,最后取高程的平均值作为所求点的高程。
全站仪三角高程测量的原理、方法、精度分析

摘要在工程建设的勘测、施工中常常涉及到高程测量,现场采用的测量方法主要是水准测量和三角高程测量。
水准测量精度高,但是速度比较慢,效率低。
此外,水准测量的转点多,而且标尺与仪器也存在下沉误差,如果在丘陵、山区等地使用水准测量进行高程传递是非常困难的,有时甚至是不可能的。
近些年来,由于全站仪的发展,使得测角、测距的精度不断提高。
三角高程测量传递高程比较灵活、方便、受地形条件限制较少等优点,因此全站仪三角高程测量补充了水准测量不能在山区等地形起伏较大的地区施测的不足,成为水准测量的重要方法。
本文对全站仪三角高程测量的原理、方法、精度等进行了分析,认为用全站仪代替水准仪进行高程测量,在一定范围内可达到三等水准测量要求。
关键词:全站仪三角高程精度分析等级水准AbstractIn the construction survey, construction often involve the height measurement, the scene is the leveling measurement method is mainly used and trigonometric leveling. Leveling precision, but at a slower speed, low efficiency. In addition, the turning point of leveling and gauge and instrument is also sinking error, if in the hills, mountains and other places using the leveling elevation transfer is very difficult, sometimes even impossible. In recent years, due to the development of the total station, the accuracy of Angle, distance to improve. Trigonometric leveling elevation is more flexible and convenient, and the advantages of less restricted by terrain conditions, so the triangle elevation surveying added leveling can't in mountainous terrain volatile regions such as measured by the insufficiency, has become an important method of leveling. In this paper, the principle and method of total station triangle elevation measurement, precision are analyzed, such as that using total station to replace the level height measurement, within a certain range can be up to three, the fourth level measurement requirements.Key Words:Total station, Triangle elevation, Accuracy analysis, Order leveling目录摘要 (I)ABSTRACT (II)第1章绪论 (1)1.1 前言 (1)1.1.1 研究目的与意义 (1)1.2 国内外研究现状 (2)1.2.1 国内研究现状 (2)1.2.2 国外研究现状 (2)1.3 本文研究内容 (3)第2章全站仪三角高程测量原理和观测方法 (4)2.1 全站仪三角高程的基本理论 (4)2.1.1 全站仪三角高程测量的原理 (4)2.1.2三角高程测量的基本公式 (5)2.2 全站仪三角高程测量的方法 (7)2.2.1对向观测法 (7)2.2.2中间测量法 (8)第3章三角高程与几何水准高程误差及精度的对比研究 (9)3.1 全站仪对向观测法的精度分析 (9)3.2 全站仪中间观测法的精度分析 (11)3.3 三角高程测量方法的比较 (13)第4章实例分析 (15)4.1 测量过程 (15)4.2 观测结果分析 (17)第5章结论与展望 (19)致谢 (20)参考文献 (21)第1章绪论1.1 前言测量地面待定点的高程,传统的方法是通过仪器测量待测点与已知点间的高差,然后计算出待测点的高程。
三角高程测量.ppt

• 计算竖直角:各按三丝所测得的L和R分别计算出相应
的竖角,最后取平均值为该竖角的角值。
22
2021年3月23日星期二
五、指标差的检验与校正
1.测定指标差 盘左、盘右瞄准同一明显目标,观测多个测回 求得指标差。 2.求出盘左或盘右的正确读数(读数减指标 差)。 3.微调竖盘指标水准管,使竖盘位于正确读数。 4.调节竖盘水准管校正螺丝,使气泡居中。
小,一般来说,瞄准目标的竖角都比较小,所
以要注意竖盘偏心的影响。
当α=0°时,Δx=0,随着α的增大,Δx将逐增
大,所以检验指标差时,以视线水平为好。
31
2021年3月23日星期二
三、如何消除竖角误差Δα对高差的影响
在A、B两点分别安置仪器进行相对观测, 且i = v,则两竖角一个为正,一个为负,当 存在竖盘偏心时,相对观测的竖角就其绝对 值而言,其中一个竖角将大一个改正数,而 另一个竖角却小一个改正数,因此,取相对 观测竖角(绝对值)的平均值将消除竖盘偏 心的影响。
25
2021年3月23日星期二
竖
盘
指
标
自
动
归
零
26
旋 2021年3月23日星期二
竖盘指标自动归零补偿器的构造形式
《城市测量规范》规定,对于DJ6级光学经纬仪,竖盘指标 自动归零补偿器的补偿范围为±2′,安平中误差为±1″。
27
2021年3月23日星期二
§10.3 单指标竖盘的偏心问题
竖直度盘偏心与水平度盘偏心的异同:
2.在靠近A点处(距离2m左右) 安置经纬仪,盘左并顾及指标差使望远 镜视线水平,在A标尺上读数设为a,转 动照准部,瞄准B标尺读数为a处,读取 竖盘读数;然后在盘右位置进行观测, 并读取竖盘读数。
三角高程测量原理

三角高程测量原理
三角高程测量原理是通过测量不同位置的角度来计算地面上的高程差。
这个原理是基于三角形的性质,根据三角形的内角和外角之间的关系,可以推导出高程差的计算公式。
测量过程中,需要选取两个测量点A和B,并在这两个点之间选择一个基准点O。
然后,用仰角仪或望远镜等测量工具,分别测量AOB、BOA和AOB三个角的大小。
测量出这三个角度后,可以根据三角形的内角和外角之间的关系来计算高程差。
根据三角形的内角和外角之间的关系,可以得到如下公式:
AOB + BOA + AOB = 180°
将测量的角度代入公式中,可以得到:
AOB + BOA + AOB = 180°
2AOB + BOA = 180°
AOB = (180° - BOA) / 2
根据这个公式,可以计算出AOB的角度,然后利用三角函数计算出高程差。
具体的计算方法可以根据具体的测量设备和测量要求进行选择和调整。
总之,三角高程测量原理是一种通过测量角度来计算地面高程
差的方法。
它利用了三角形的性质,通过测量不同位置的角度来计算地面高程差,可以广泛应用于地质勘探、土地测量和工程测量等领域。
测量学课件第四章距离测量与三角高程测量

20
二.视线倾斜时视距测量公式
n'
二.视线倾斜 时视距测量
公式
n’为水准尺与视线 垂直时的尺间隔
1.视距公式:
n'ncos
S'100ncos
则 DS'cos 100nco2s
2.高差公式:高差主值 h'Dtan
(4-2-8)
2019/11/4
AB高差
hh' 课件ilDtanil
2往
3 0.4 + 10 .4 11 9.970 + 15 .0 11 9.985 0
返
3 0.5 + 10 .5 11 9.970 + 15 .1 11 9.985 1
3 往 1 0 :40 3 0.2 + 10 .2 11 9.972 + 14 .7 11 9.986 7
返
3 1.1 + 11 .1 11 9.973 + 16 .0 11 9.989 0
k kl
检定场:在平整的条形场地两端地面埋
设两个稳定的标志,其间距比待检定钢 尺长度n倍略短一些。高精度测量两标志 的间距作为标准长度S标准。
设尺子的温度膨胀系数已知。用待检定 的尺子(先假定Δk=0),在工作时的正 常拉力下,测量检定场两标志的间距S’。 从而可得
k
S标准S' n
用途:主要用于地形图测绘 (地形点的距离与高差)。
201(一)视线水平时
十字丝板上有两根视距丝,它们在物镜光心
处的张角φ基本是不变的。两根视距丝在物方
象的间距与距离成正比
an f s
所以 S ' n f n c
三角高程测量

图根三角高程路线的布设
在地势起伏较大的测区,图根点高程除尽量在 坡缓地区,用水准测量的方法测定少量图根点 高程作为图根三角高程测量起、终点外,其余 图根点,可根据分布情况,尽量沿最短边和最 短路线组成三角高程闭合路线或附合路线,测 定图根点高程。 三角高程路线发展层次一般不多于两级,一级 起闭于水准测量的固定点,二级在一级的基础 上发展。 以交会定点的方法测定图根点高程,可由几个 已知高程的平面控制点,用三角高程测量方法 独立交会确定其高程
图根三角高程测量路线计算的目的,是求出路 线上各图根点的高程。计算前,首先要检查外 业观测手簿,确认无误后才能开始计算 高差计算 高差闭和差的计算与调整 高程计算 从路线起始点出发,根据改正后的高差,逐点 计算各点高程
学而不思则罔●▂●思而不学则殆 专业分享,敬请收藏 7
独立交会高程点的计算 Nhomakorabea角高程测量的方 法,是在相邻两 点间观测其竖直 角,再根据这两 点间的水平距离, 应用三角学的原 理计算出两点间 的高差,进而推 算出点的高程
学而不思则罔●▂●思而不学则殆 专业分享,敬请收藏 3
地球曲率和大气折光对高差的 影响
以水平面作为起算面的, 即把地球表面视为平面, 但大地水准面并不是平 面而是曲面。如图AF为 过A点的水准面,AE为 过A点的水平面,而EF 为水平面代替水准面对 高差的影响,称为球差, 若不改正,就使高差变 小了
三角高程测量
用水准测量方法测定图根点的高程,其 精度较高,但在地形起伏变化较大的山 区、丘陵地区,使用该法就十分困难。 在这种情况下,通常要采用三角高程测 量的方法
学而不思则罔●▂●思而不学则殆 专业分享,敬请收藏
三角高程测量的原理

2 即圆弧PN的弦切角∠MPN等于圆心角 ε的一半。
三角高程测量
因ε很小, PN PN D,由图可
得 MPN MN MN
2 PN D
即
MN D
2
因
PN D
R' R'
所以
MN D2
若令
k
R
2R ' ,k称为大气折光系数
R' ,则 R ' R,代入上式得
hAB =D·tanα + i - v + f1 - f2
三角高程测量
在三角高程测量中,由于球 差f1使高差减小,气差f2使高差 增大,因此,在高差中应进行“ 加入球差减去气差”的改正,即 球气差改正,亦称两差改正,通 常用 f 表示。即
f = f1 - f2 将上式代入hAB =D·tanα + i v + f1 - f2 ,并整理得:
k f2
MN
D2 2R
k
三角高程测量
D2 f1 CE 2R
f2
MN
D2 2R
k
将上式代入 f = f1 - f2 得
f D2 D2 k (1 k) D2
2R 2R
2R
三角高程测量
4. 三角高程测量的观测方法
(1)直、反觇观测 由已知高程点设站观测待定高程点的垂直角叫直
觇。 由待定高程点设站观测已知高程点的垂直角叫反
由于R>>i+HA,故可以用R代替
i+HA+R,则
R2+D2=(CE+R)2
展开得 R2+D2=CE2+2R·CE+R2
则
高程测量(2-三角高程测量)

高程控制测量
二、三角高程测量
当使用椭球面上的边长计算单向现测高差的公式为:
h12 s tan Hm 2 1 C i1 v2 s 12 R
(5-50)
当使用高斯平面上的边长计算单向观测高差的公式
h12 d tan 12
d tan 12
Hm y2m Cd i1 v2 d tan 12 ( ) 2 R 2R
高程控制测量
二、三角高程测量
Ⅰ、三角高程测量原理
一、三角高程测量原理 (一)三角高程测量的基本公式 h12=BF=MC+CE+EF-MN-NB
CE MN 1 K 2 S-48) (5-49)
MC=S0tanδ12
h12 S tan12 CS 2 0 i1 v2
高程控制测量
二、三角高程测量
大,且具有相同的符号,此时很可能是本点仪器高或觇标高量测存 在粗差。
(4)对于边长相差悬殊的平面网,可以酌情舍弃某些边的成果,否 则反而会影响最后成果的精度。
(四)三角高程起算点的密度
规定:高程起算点应尽量布设在平面网的两端或网的边缘。在平面 网进行整体平差时,其密度使平面网中任一平面点与最近高程起算 点间隔的边数(即三角高程推算边数)不超过表5—28的规定。
三角高程的精度,必须满足基本等高距为1m、2m的大比例尺测图 的需要。为此,三角高程网(或符合路线)中的最弱点相对于邻近 水准点的高程中误差,不得超过1/20基本等高距,即对于1m和2m 的等高距来说,其高程中误差分别不得大于0.05m和0.10m。
高程控制测量
二、三角高程测量
二、电磁波测距三角高程测量 h12= S斜sinδ
高程控制测量
二、三角高程测量
中间法三角高程测量基本原理

中间法三角高程测量基本原理嘿,朋友们!今天咱来聊聊中间法三角高程测量的基本原理哈。
你看哈,这中间法三角高程测量就像是我们走路找方向一样。
我们要知道从哪儿出发,到哪儿去,中间经过哪些地方。
三角高程测量呢,就是要搞清楚地面上不同点之间的高差。
想象一下,我们在两个点之间拉一条线,就像搭了一座小桥。
然后呢,我们通过测量角度和距离,来算出这座“小桥”的坡度,这就是高差啦!这是不是很神奇呢?它呀,就像是一个聪明的小侦探,能通过各种线索找出地面的高低起伏。
我们用全站仪或者经纬仪这些厉害的工具,就像小侦探的放大镜和显微镜一样,去捕捉那些关键的信息。
比如说,我们在这边的点上观测那边的点,测量出角度,再量一下距离,然后通过一些巧妙的计算,就能得出高差啦!这可不像我们平时走路那么简单哦,这里面可有大学问呢!这中间法呀,就像是走在一条中间的道路上,不偏不倚,能更准确地测量出那些高差。
为啥要这么做呢?这就好比我们要去一个地方,走直路肯定比绕弯路来得快、来得准呀!你说这中间法三角高程测量是不是很有意思呢?它能帮我们搞清楚大地的起伏,就像给大地画了一幅立体的图画。
我们工程师们就靠着它来修路、建桥、盖房子呀!没有它,那可真是不行呢!而且哦,它还很实用呢!不管是在高山上,还是在平原上,都能发挥它的作用。
就好像一把万能钥匙,能打开各种地形的秘密之门。
你想想,如果没有它,我们怎么知道这里高那里低呀?那不就像闭着眼睛走路一样,容易摔跤嘛!所以说呀,这中间法三角高程测量可真是我们工程建设的好帮手呢!总之呢,中间法三角高程测量是个非常重要的测量方法,它就像我们生活中的指南针一样,指引着我们在工程建设的道路上稳步前行。
让我们好好利用它,为我们的生活创造更多美好的建筑和设施吧!。
三角高程原理_图文

HB
A、B两点间的高差hAB为:
h AB
D AB
tan
iv
B点的高程HB为:H B
H A
h AB
H A
D AB
tan
i
v
注意:当两点距离较大(大于300m)时:
加球气差改正数:
f
0.43 D 2 R
;即有:hAB
i Dtg
l
f
解决方法:可采 用对向观测后取 平均的方法,抵 消球气差的影响
球差为正,气差为负
7
课程 设置
教学 设计
组织 实施
考核 评价
2
3
目录页
1
Contents Page
4
8
水准测量
多维评价 拓展思维
课程设计 教学设计 组织实施 考核评价
过程评价:在学生制作过程中对优秀学生进行正面
1 评价,以激励中间学生,提点相对落后点的学生。
2 结果评价:对学生的成品进行整体评价。
3
学生自评:让学生对自己的作品进行阐述, 以提高学生的表达能力与总结能力。
课程目标
理实一体,工作 学习一体化
理论结合实践, 在工作中学习,在学 习中工作
3
课程 设置
教学 设计
组织 实施
考核 评价
2
3
目录页
1
Contents Page
4
4
水准测量
课程设计 教学设计 组织实施 考核评价
教学模式
以设计项目为导向,实 行 “做学做”一体化 的教学模式。
教学方法
问题驱动 现场教学 项目演练
4 学生互评:同学间进行相互评价,看到别人
的长处也看到自己的不足,能做到取长补短。
三角高程测量的基本原理

三角高程测量的基本原理
嘿,朋友们!今天咱来聊聊三角高程测量的基本原理呀!
你看哈,这三角高程测量就像是我们在探索大地这个大宝藏时的秘密武器。
想象一下,我们站在这头,要知道远处那个点有多高,就好像我们想知道山顶上那棵树比我们高多少一样。
它的原理其实并不复杂。
我们通过测量一个角度和一段距离,就能算出那个神秘点的高度啦!就好像我们知道了从我们这儿到山顶的倾斜角度,还有我们和山顶之间的距离,那就能大概算出山顶有多高啦,是不是挺神奇的?
这其中啊,角度就像是一个关键的线索。
我们得精确地测量出这个角度,就像我们要准确抓住小偷的蛛丝马迹一样重要!而距离呢,就是另一个重要的元素啦,要是距离都没搞对,那后面的计算不就全乱套啦?
而且哦,这三角高程测量可不仅仅是在平地上有用,在那些高低起伏的地方,它更是大显身手呢!比如在山里,我们没法直接量高度,这时候它就派上大用场啦。
你说这是不是很有意思呀?就像我们解开一个又一个谜题,一步步靠近真相。
它让我们能够跨越那些难以直接到达的地方,去了解它们的高度秘密。
在实际操作中,我们可得认真对待每一个步骤哦。
测角度的时候要稳稳的,不能手抖;量距离的时候要精确,不能马虎。
这就好像做饭一样,每一种调料都要放得恰到好处,不然味道可就不对啦!
三角高程测量呀,就像是我们探索大地的神奇魔法,让我们能够知晓那些隐藏在地形中的秘密。
它让我们在面对高山、低谷的时候不再迷茫,能够准确地知道它们的高度信息。
所以呀,大家可别小瞧了它哦!这可是我们测量领域的宝贝呢!
总之呢,三角高程测量就是这么一个厉害又有趣的东西,让我们能够更好地了解我们脚下的这片大地呀!。
三角高程测量原理

§5.9 三角高程测量三角高程测量的基本思想是根据由测站向照准点所观测的垂直角或天顶距和它们之间的水平距离;计算测站点与照准点之间的高差..这种方法简便灵活;受地形条件的限制较少;故适用于测定三角点的高程..三角点的高程主要是作为各种比例尺测图的高程控制的一部分..一般都是在一定密度的水准网控制下;用三角高程测量的方法测定三角点的高程..5.9.1 三角高程测量的基本公式1.基本公式关于三角高程测量的基本原理和计算高差的基本公式;在测量学中已有过讨论;但公式的推导是以水平面作为依据的..在控制测量中;由于距离较长;所以必须以椭球面为依据来推导三角高程测量的基本公式..如图5-35所示..设0s 为B A 、两点间的实测水平距离..仪器置于A 点;仪器高度为1i ..B 为照准点;砚标高度为2v ;R 为参考椭球面上B A ''的曲率半径..AF PE 、分别为过P 点和A 点的水准面..PC 是PE 在P 点的切线;PN 为光程曲线..当位于P 点的望远镜指向与PN 相切的PM 方向时;由于大气折光的影响;由N 点出射的光线正好落在望远镜的横丝上..这就是说;仪器置于A 点测得M P 、间的垂直角为2,1a ..由图5-35可明显地看出;B A 、 两地面点间的高差为NB MN EF CE MC BF h --++==2,1 5-54式中;EF 为仪器高NB i ;1为照准点的觇标高度2v ;而CE 和MN 分别为地球曲率和折光影响..由2021s R CE =2021s R MN '=式中R '为光程曲线PN 在N 点的曲率半径..设,K R R='则 20202.21S RK S R R R MN ='=K 称为大气垂直折光系数..图5-35由于B A 、两点之间的水平距离0s 与曲率半径R 之比值很小当km s 100=时;0s 所对的圆心角仅5'多一点;故可认为PC 近似垂直于OM ;即认为 90≈PCM ;这样PCM ∆可视为直角三角形..则5-54式中的MC 为2,10tan αs MC =将各项代入5-54式;则B A 、两地面点的高差为21202,102201202,102,121tan 221tan v i s RK s v s R K i s R s h -+-+=--++=αα 令式中C C RK,21=-一般称为球气差系数;则上式可写成 21202,102.1tan v i Cs s h -++=α 5-555-55式就是单向观测计算高差的基本公式..式中垂直角a ;仪器高i 和砚标高v ;均可由外业观测得到..0s 为实测的水平距离;一般要化为高斯平面上的长度d .. 2.距离的归算在图5-36中;B A H H 、分别为B A 、两点的高程此处已忽略了参考椭球面与大地水准面之间的差距;;其平均高程为mM H H H B A m ),(21+=为平均高程水准面..由于实测距离0s -般不大工程测量中一般在l0km 以内;所以可以将0s 视为在平均高程水准面上的距离.. 由图5-36有下列关系)1(100RH s s RH R H R s s mm m +=+=+= 5-56这就是表达实测距离0s 与参考椭球面上的距离s 之间的关系式..参考椭球面上的距离s 和投影在高斯投影平面上的距离d 之间有下列关系)21(22Ry d s m-= 5-57式中m y 为B A 、两点在高斯投影平面上投影点的横坐标的平均值..关系式5-57的推导将在第八章中讨论..将5-57式代入5-56式中;并略去微小项后得)21(220R y R H d s mm -+= 5-58图5-363.用椭球面上的边长计算单向观测高差的公式 将5-56式代入5-55式;得2122,12,1)1(tan v i Cs RH s h m-+++=α 5-59 式中2Cs 项的数值很小;故未顾及0s 与s 之间的差异.. 4.用高斯平面上的边长计算单向观测高差的公式 将5-57式代入5-59式;舍去微小项后得)2(tan )2(tan tan 222122,1222,12122,12.1RyR H h v i Cd d R y R H d v i Cd d h m m mm -'+-++=-+-++=ααα 5-60 式中2,1tan αd h ='..令 h h '=∆2,1)2(22R y R H mm - 5-61则5-60式为2,12122,12,1tan h v i Cd d h ∆+-++=α 5-625-61式中的m H 与R 相比较是一个微小的数值;只有在高山地区当m H 甚大而高差也较大时;才有必要顾及R H m 这一项..例如当m h m H m 100,1000='=时;RHm 带这一项对高差的影响还不到0.02m;一般情况下;这一项可以略去..此外;当时m h km y m 100,300='=;222Ry m这-项对高差的影响约为0.llm..如果要求高差计算正确到0.lm;则只有h Ry m'222项小于0.04m 时才可略去不计;因此;5-62式中最后一项2,1h ∆只有当h H m ',或m y 较大时才有必要顾及..5.对向观测计算高差的公式一般要求三角高程测量进行对向观测;也就是在测站A 上向B 点观测垂直角2,1α;而在测站B 上也向A 点观测垂直角1,2α;按5-62式有下列两个计算高差的式子.. 由测站A 观测B 点2,122,1212,12,1tan h d C v i d h ∆++-+=α则测站B 观测A 点1,22121,21,21,2tan h d C v i d h ∆++-+=α式中;11v i 、和22v i 、分别为A 、B 点的仪器和觇标高度;2,1C 和1,2C 为由A 观测B 和B 观测A 时的球气差系数..如果观测是在同样情况下进行的;特别是在同一时间作对向观测;则可以近似地假定折光系数K 值对于对向观测是相同的;因此1,22,1C C =..在上面两个式子中; 2,1h ∆与1,2h ∆的大小相等而正负号相反.. 从以上两个式子可得对向观测计算高差的基本公式2,122111,22,1)(2,1)(21)(21)(21tan h v i v i d h ∆+--++-=αα对向 5-63式中h Ry R H h mm '⋅-=∆)2(222,1)(21tan 1,22,1αα-='d h6.电磁波测距三角高程测量的高差计算公式由于电磁波测距仪的发展异常迅速;不但其测距精度高;而且使用十分方便;可以同时测定边长和垂直角;提高了作业效率;因此;利用电磁波测距仪作三角高程测量已相当普遍..根据实测试验表明;当垂直角观测精度,0.2''±≤a m 边长在2km 范围内;电磁波测距三角高程测量完全可以替代四等水准测量;如果缩短边长或提高垂直角的测定精度;还可以进一步提高测定高差的精度..如5,1''±≤a m ; ;边长在3.5km 范围内可达到四等水准测量的精度;边长在1.2km 范围内可达到三等水准测量的精度.. 电磁波测距三角高程测量可按斜距由下列公式计算高差Z i RD K D h -+-+=αα22cos 2)1(sin 5-64式中;h 为测站与镜站之间的高差;α为垂直角;D 为经气象改正后的斜距;K 为大气折光系数;i 为经纬仪水平轴到地面点的高度;Z 为反光镜瞄准中心到地面点的高度..5.9.2 垂直角的观测方法垂直角的观测方法有中丝法和三丝法两种.. 1.中丝法中丝法也称单丝法;就是以望远镜十字丝的水平中丝照准目标;构成一个测回的观测程序为:在盘左位置;用水平中丝照准目标一次;如图5-37a 所示;使指标水准器气泡精密符合;读取垂直度读数;得盘左读数L ..在盘右位置;按盘左时的方法进行照准和读数;得盘右读数R ..照准目标如图5-37b 所示..2.三丝法三丝法就是以上、中、下3条水平横丝依次照准目标..构成一个测回的观测程序为:在盘左位置;按上、中、下3条水平横丝依次照准同一目标各一次;如图5-38a所示;使指标水准器气泡精密符合;分别进行垂直度盘读数;得盘左读数L ..图5-37 图5-38 在盘右位置;再按上、中、下3条水平横丝依次照准同一目标各一次;如图5-38b 所示;使指标水准器气泡精密符合.分别进行垂直度盘读数;得盘右读数R..在一个测站上观测时;一般将观测方向分成若干组;每组包括2~4个方向;分别进行观测;如通视条件不好;也可以分别对每个方向进行连续照准观测..根据具体情况;在实际作业时可灵活采用上述两种方法;如T3光学经纬仪仅有一条水平横丝;在观测时只能采用中丝法..按垂直度盘读数计算垂直角和指标差的公式列于表5-10..表5-10仪器类型计算公式各测回互差限值垂直角指标差垂直角指标差J1T3 J2T2;010RL-=α]180)[(21--=LRα180)(-+=RLi]360)[(21-+=RLi10″15″10″15″5.9.3 球气差系数C值和大气折光系数K值的确定大气垂直折光系数K;是随地区、气候、季节、地面覆盖物和视线超出地面高度等条件不同而变化的;要精确测定它的数值;目前尚不可能..通过实验发现;K值在一天内的变化;大致在中午前后数值最小;也较稳定;日出、日落时数值最大;变化也快..因而垂直角的观测时间最好在地方时10时至16时之间;此时K值约在0.08~0.14之间;如图5-39所示..不少单位对K值进行过大量的计算和统计工作;例如某单位根据16个测区的资料统计;得图5-39出107.0=K ..在实际作业中;往往不是直接测定K 值;而是设法确定C 值;因为RKC 21-=..而平均曲率半径R 对一个小测区来说是一个常数;所以确定了C 值; K 值也就知道了..由于K 值是 小于1的数值;故C 值永为正.. 下面介绍确定C 值的两种方法..1.根据水准测量的观测成果确定C 值在已经由水准测量测得高差的两点之间观测垂直角;设由水准测量测得的高差为h ;那么;根据垂直角的观测值按5-55式计算两点之间的高差;如果所取的C 值正确的话;也应该得到相同的高差值;也就是21202,10tan v i Cs s h -++=α在实际计算时;一般先假定一个近似值0C ;代人上式可求得高差的近似值0h ;即212002,100tan v i s C s h -++=α即2000)(s C C h h -=-或200sh h C C -=- 5-65令式中C C C ∆=-0;则按5-65式求得的C ∆值加在近似值0C 上;就可以得到正确的C 值..2.根据同时对向观测的垂直角计算C 值设两点间的正确高差为h ;由同时对向观测的成果算出的高差分别为2,1h 和1,2h 由于是同时对向观测;所以可以认为01,22,1C C C ==;则202,1Cs h h ∆+=201,2Cs h h ∆+=-由以上两式可得1,22,12s h h C +=∆ 5-66从而可以按下式求出C 值C C C ∆+=0无论用哪一种方法;都不能根据一两次测定的结果确定一个地区的平均折光系数;而必须从大量的三角高程测量数据中推算出来;然后再取平均值才较为可靠..5.9.4 三角高程测量的精度1.观测高差中误差三角高程测量的精度受垂直角观测误差、仪器高和觇标高的量测误差、大气折光误差和垂线偏差变化等诸多因素的影响;而大气折光和垂线偏差的影响可能随地区不同而有较大的变化;尤其大气折光的影响与观测条件密切相关;如视线超出地面的高度等..因此不可能从理论上推导出一个普遍适用的计算公式;而只能根据大量实测资料;进行统计分析;才有可能求出一个大体上足以代表三角高程测量平均精度的经验公式.. 根据各种不同地理条件的约20个测区的实测资料;对不同边长的三角高程测量的精度统计;得出下列经验公式s P M h ⋅= 5-67式中; h M 为对向观测高差中数的中误差;s 为边长;以km 为单位;P 为每公里的高差中误差;以m/km 为单位..根据资料的统计结果表明;P 的数值在0.013~0.022之间变化;平均值为0.018;一般取P =0.02;因此5-67式为s M h 02.0±= 5-68 5-68式可以作为三角高程测量平均精度与边长的关系式..考虑到三角高程测量的精度;在不同类型的地区和不同的观测条件下;可能有较大的差异;现在从最不利的观测条件来考虑;取P =0.025作为最不利条件下的系数;即s M h 025.0= 5-69 公式5-69说明高差中误差与边长成正比例的关系;对短边三角高程测量精度较高;边长愈长精度愈低;对于平均边长为8km 时;高差中误差为士0.20m ;平均边长为4.5km 时;高差中误差约为0.llm..可见三角高程测量用短边传递高程较为有利..为了控制地形测图;要求高程控制点高程中误差不超过测图等高的1/10;对等高距为lm 的测图;则要求m M h 1.0±≤..5-69式是作为规定限差的基本公式.. 2.对向观测高差闭合差的限差同一条观测边上对向观测高差的绝对值应相等;或者说对向观测高差之和应等于零;但实际上由于各种误差的影响不等于零;而产生所谓对向观测高差闭合差..对向观测也称往返测;所以对向观测高差闭合差也称为往返测高差闭合差;以W 表示1,22,1h h W += 5-70以W m 表示闭合差W 的中误差;以0h m 表示单向观测高差h 的中误差;则由5-70式得222h W m m = 取两倍中误差作为限差;则往返测观测高差闭合差限W 为0222h W m m W ±==限 5-71若以h W 表示对向观测高差中误差;则单向观测高差中误差可以写为h h M m 20=顾及5-69式;则上式为s m h 2025.00=再将上式代入5-71式得s s W 1.02025.022±=⨯±=限 5-725-72式就是计算对向观测高差闭合差限差的公式.. 3.环线闭合差的限差如果若干条对向观测边构成一个闭合环线;其观测高差的总和应该等于零;当这一条件不能满足时;就产生环线闭合差..最简单的闭合环是三角形;这时的环线闭合差就是三角形高差闭合差..321h h h W ++= 以W m 表示环线闭合差中误差;i h m 表示各边对向观测高差中数的中误差;则2222321h h h W m m m m ++= 对向观测高差中误差i h m 可用5-69式代入;再取两倍中误差作为限差;则环线闭合差限W 限为205.02i W s m W ∑±==限 5-73。
全站仪三角高程测量不同方法的分析与应用概要课件

精密工程测量
在精密工程中,需要高精度地测量各种物体的位置和尺寸,以确保工程的精度和质量。全站仪三角高程测量方法可以满足精 密工程测量的高精度要求。
在实际应用中,可以在工程现场设置基准点和测点,利用全站仪对测点进行高程测量,获取各个位置的高程数据。这些数据 可以用于分析工程的精度和质量,及时发现误差和异常情况,为调整和修复提供依据。同时,全站仪三角高程测量方法也可 以与其他测量方法相结合,形成更加完善的测量系统,提高工程测量的精度和效率。
THANKS
感谢观看
在实际应用中,可以在矿山的周围设置基准点和监测点,利用全站仪对监测点进 行高程测量,通过与基准点的高程比较,计算出矿山的垂直位移量。同时,可以 定期进行监测,形成位移曲线,分析位移趋势,预测未来的位移情况。
水利工程的高程测量
水利工程建设和维护过程中,需要高精度地测量水库大坝、堤防等位置的高程,以确保水利工程的安 全。全站仪三角高程测量方法可以在各种复杂环境下进行高程测量。
特点
能够克服河流的障碍,快速准确地测量两岸的高程。但需要解决对 岸点的通视问题,以及考虑地球曲率和大气折射等因素的影响。
应用场景
适用于河流两岸的高程测量和工程规划等场合。
PART 03
全站仪三角高程测量的精 度分析
测量误差来源
仪器误差
气象条件影响
观测环境
操作者技能
全站仪本身存在的误差, 如望远镜、测距仪、电
子系统等部件的精度限制。
如大气折射、温差、气 压等因素对测距和角度
距离测量与三角高程测量PPT课件

+4.07
1.42
95027 5027
150.83
+14.39
2.15
88025 1035 57.76
-2.33
注:竖盘公式 : L 90
第16页/共23页
高程 H
25.47
35.79
19.07
返回
第四节 三角高程测量
进行三角高程测量时,应测定两点间的平距或斜距以及垂直角。 一.三角高程测量的计算公式
K D往 D返 D 1 D往 D返 D M 2
M D D
两点间水平距离为:
D
1 2
D往
D返
第5页/共23页
(三). 精密量测
当量距精度要求在
1
以上时,要用精密量测法。
10000
(四). 钢尺量距成果整理
1. 尺长改正
钢尺名义长度 一般l0和实际长度不相等,每量一段都需加 入尺长改正。在标准拉力、标准温度下经过检定实际长
钢尺量距中辅助工具还有测钎、花杆、垂球、弹簧秤和温度计。 花杆用于定直线。 测钎用来标志所量尺段的起、止点 。 垂球用于不平坦地面将尺的端点垂直投影到地面 弹簧秤和温度计,用于控制拉力和测定温度。
第1页/共23页
二. 直线定线
将所量尺段标定在待测二点间一条直线上的工作称为直线定线。
第2页/共23页
第15页/共23页
测站:A
照准点号
下丝读数 上丝读数 视距间隔
1.768
1
0.934
0.834
2.182
2
0.660
1.522
2.440
3
1.862
0.578
视距测量记录
测站高程:21.40m
