自由基聚合反应动力学
自由基聚合反应简介

高分子化学
3.5 影响自由基聚合反应的因素
2、匀速聚合 当引发剂的半衰期适当时,正常聚合速率的衰减与凝胶效应的 自动加速部分可互补,从而可做到匀速反应。 3、前快后慢的聚合反应 当采用引发剂活性很高时,聚合 初期引发剂大量分解,使正常聚 合速率很大,聚合中后期,因引 发剂残留量少,正常聚合速率下 降幅度大,以致于凝胶效应的自 动加速部分还不足以弥补,故总 聚合速率降低,甚至为零。
CH2 CHR + O 苯醌
CH O CH2 CHR O CHR + HO HO CH2 CHR O O
O
CH2 CHR O
O
(17)
生成的自由基由于有苯环的强共振作用而稳定,引发活性低。
极性效应对苯醌(缺电子物质)的阻聚作用有显著影响。
18
高分子化学
3.6 阻聚和缓聚
• 芳族硝基化合物
(iii) 硝基化合物:硝基苯、多硝基苯
高分子化学
3.5 影响自由基聚合反应的因素
(3)链自由基卷曲、包埋的程度以及聚合速率的大小受聚合物在单 体或溶剂中溶解性能的好坏的影响。通常,自动加速现象在良溶剂 中较少出现,在非溶剂(沉淀剂)中出现得早、显著,在不良溶剂 中自动加速现象介于以上两种情况。
图2 溶剂对MMA聚合时自动加速效应的影响 (1~3—采用非溶剂;4~5—采用不良溶剂;8~10—采用良溶剂)
氯化铁不仅阻聚效率高,并能化学计量地消灭一个自由基,因 此,可用于测定引发速率。
22
高分子化学
第三章4:自由基聚合动力学

转化率与反应速率的关系
转化率:C=([M]0-[M])/[M]0 (单位?) dC/dt=Rp/[M]0 Rp =[M]0(dC/dt);单位:mol.L-1 .s-1 [M]0:单体的起始浓度
转化率C的测定:测定生成聚合物的质量
转化率–时间曲线
利用聚合物、单体在 某溶剂中的溶解度不同, 从反应混合物中分离出聚 合物,经多次沉淀并干燥 称重所得聚合物量。测定 不同时间形成聚合物的量, 得到转化率与时间的曲 线。
转化率,%
12
3
4
反应时间/min
反应速率–时间曲线
12
3
4
聚合反应速率
反应时间/min
MMA 50℃,BPO PMMA (s形)
讨论1
R ki[R][M] k p1[M1][M]k p2[M 2][M]......k pn[M n][M]
How and Why???
R ki[R][M]?
链增长反应(chain propagation)
M1M k p1 MM
MM M kp2MMM
郑军峰 2016-11-8
第四节:自由基聚合反应动力学
4.1聚合反应速率的表征及测定 4.2自由基聚合反应动力学和速度方程
4.1聚合反应速率的表征及测定
以单体消耗速率表征,哪几步消耗了单体?
4.1聚合反应速率的表征及测定
单体消耗速率:-d[M]/dt=Ri+Rp 聚合物生成速率: d[P]/dt
原理:聚合物的密度比单体大,聚合后发生体积收缩。测定聚 合反应中随时间发生的体积变化。体积收缩与转化率成正比。
膨胀计法测定聚合速率
第二章 自由基聚合-2.4 自由基聚合反应动力学

Rd=d[R·]/dt=2kd[I] Ri =-d[M]/dt=ki[R·][M] Rp1=-d[M]/dt =kp1[M][M1·] Rp2=-d[M]/dt =kp2[M][M2·]
••••••
Rpn=-d[M]/dt=kpn[M][Mn·]
Rtc=-d[Mx·]/dt=ktc[Mx·][My ·]
2.4.1聚合反应动力学研究方法 二、聚合速率的测定-间接法
C% V Vo K
K Vm Vp 100% Vm
其中,Vo为起始体积,△V为t时刻的
体积收缩值,由高度变化计算得到
Rp
d[M ] dt
[M ]2 t2
[M ]1 t1
C2[M ]o C1[M ]o t2 t1
••••••
Rpn=-d[M]/dt=kpn[M][Mn·]
2.4.2自由基聚合初期反应速率 一 动力学方程的推导
d[M ] R dt Ri Rp1 Rp2 ... Rpn
ki[R][M ] k p1[M1][M ] k p2[M 2][M ] ...... k pn[M n ][M ]
(7) Mx • M y • ktcMxy
(8) Mx • M y • ktd Mx M y
(9) M x • XH kts M x H X •
(无活性)
(10) M x • M ktr,M Mx M • (11) Mx • S ktr,s Mx S • (12) M x • I ktr,I M x I •
H
2.4.2自由基聚合初期聚合反应速率 一 动力学方程的推导
空间效应
空间效应对不同链长自由基的活性影响相同
第六章 自由基聚合反应

铵(NH4)2S2O8 ,是这类引发剂的代表, 能溶于水,多用于乳液聚合和水溶液聚 合的场合。
分离产物SO4-.既是离子,又是自由
基.可称做离子自由基或自由基离于。
4.氧化—还原引发体系
许多氧化“还原反应”可以产生自由基,
用来引发聚合,这类引发剂称做氧化— 还原引发体系。这一体系的优点是活化 能较低(约40~60kJ/mol),可在较低温度 (0~50 ℃)下引发聚合,而有较快的聚合 速度。体系组分可以是无机和有机化合 物,性质可以是水溶性和油溶性的,反 应机理是直接电荷转移或先形成中间络 合物。
链增长的立体结构
在链增长反应中,结构单元问的结合可能存在“头-尾”
和“头-头”或“尾-尾”两种形式
经实验证明主要以头—尾形成连接。原因有电子效应和
位阻效应。按头—尾形式连接时,取代基与独电子连在 同一碳原子上,苯基一类的取代基对自由基有共扼稳定 作用,加上相邻次甲基的超共扼效应,自由基得以稳定。 而按头-头形式连接时,无共扼效应.自由基比较不稳定。 对于共扼稳定较差的单体.如醋酸乙烯酌,会有一些 头—头形式连接出现。聚合温度升高时,头—头形式结 构将增多。另一方面,次甲基一端的空间位阻较小,有 利于头尾连接
一般在45~65 ℃下使用,其特点是分解均匀,
只形成一种自由基,无其他副反应;另一优点 是比较稳定,可以纯粹状态安全储存.但 80~90 ℃时也急剧分解。缺点是有一定毒性, 分解速率较低,属于低活性引发剂。 AIBN分解后形成的异丁腈(二甲基一氰基一 甲基)自由基是碳自由基,缺乏脱氢能力,因此 不能用作接枝聚合的引发剂。
(1)水溶性氧化-还原引发体系
这类体系的氧化剂有过氧化氢、过硫酸
第三章自由基聚合(第7周)动力学概论
直径约1mm 长500mm
4
3.7 聚合速率
膨胀计法:
测定原理:利用聚合过程的体积收缩与转化率的线性关系。
随聚合反应发生,分子间形成了键。反应时,从π键变为σ键, 键长有所增加,但低分子间力转变成链节间的共价键,比未成键 前单体分子间距离要短得多:
22
-d[M]/dt
可用C ~t 曲线表示聚合过程中速率的变化
通常呈S 型。据此,
率自
-
时 间 关 系
由 基 聚 合
曲反
线应
图转
化
转
化 率
中 期
诱
导 期
初 期
S型
后 期
t
聚合过程
诱 初中 后
导
期期 期
期 ︵
零 速
︵︵ ︵ 匀加 减 速速 速
期
期期 期
︶ ︶︶ ︶
诱导期:初级自由基为阻聚杂质所终止,无聚合物形成,聚合速率为零。 初期:单体开始正常聚合,转化率在5%~10%以下(研究聚合时)或10%~20%(工
由于副反应和诱导分解,初级自由基或分解的引
发剂并不全部参加引发反应,故须引入引发剂效 率f。
引发速率(Ri)方程为:
Ri =2fkd[ I ]
B 链增长
单体自由基连续加上大量单体分子的反应
RM M RM2 M RM3 M
kp1
kp 2
kp 3
RMx
∲ 根据等活性理论,链自由基的活性与链长基本无关, 即各步速率常数相等。这是处理自由基动力学的 第一个假定。(低转化率5%-10%)
上述公式一般只适用于聚合初期 (低转化率5%~10%), 为什么?
3.7 聚合速率
自由基聚合过程中反应速度和聚合物分子量

自由基聚合过程中反应速度和聚合物分子量自由基聚合是一种常见的加聚反应,它是指由自由基作为活性种,与烯类单体发生连锁反应,形成高分子的过程。
自由基聚合的反应速度和聚合物分子量是两个重要的参数,它们反映了聚合反应的动力学和热力学特征,也影响了聚合物的性能和应用。
本文将介绍自由基聚合过程中反应速度和聚合物分子量的影响因素和控制方法。
反应速度是指聚合反应的进行速率,它与聚合反应的转化率和反应时间有关。
反应速度受到以下因素的影响:聚合温度。
聚合温度是影响反应速度的主要因素,一般来说,升高聚合温度,可以增加分子的热运动,提高引发剂的分解速率,增加自由基的浓度,促进链增长反应,从而提高反应速度。
但是,过高的聚合温度,也会加速链终止和链转移反应,降低聚合反应的选择性,导致聚合物分子量的降低和分布的变宽,甚至引起反应失控和爆聚。
因此,聚合温度应根据不同的单体和引发剂的特性,选择适当的范围,以保证反应速度和聚合物质量的平衡。
引发剂的种类和浓度。
引发剂是自由基聚合的启动剂,它可以在一定的温度下分解生成自由基,引发单体的聚合。
引发剂的种类和浓度决定了自由基的数量和活性,从而影响反应速度。
一般来说,引发剂的分解温度越低,分解速率越快,生成的自由基越多,反应速度越高。
引发剂的浓度越高,自由基的浓度越高,反应速度越高。
但是,引发剂的种类和浓度也会影响聚合物分子量,因为引发剂的残基会存在于聚合物的链端,增加聚合物的分子量分布,降低聚合物的均一性。
因此,引发剂的种类和浓度应根据不同的单体和聚合条件,选择合适的类型和用量,以保证反应速度和聚合物质量的平衡。
单体的种类和浓度。
单体是自由基聚合的原料,它与自由基发生链增长反应,形成聚合物。
单体的种类和浓度影响反应速度,主要是通过影响链增长反应的速率常数和反应级数。
一般来说,单体的反应活性越高,链增长反应的速率常数越大,反应速度越高。
单体的浓度越高,链增长反应的反应级数越大,反应速度越高。
第二章 自由基聚合-2.4 自由基聚合反应动力学2

2. Rp∝[I]n
Rp=kp[M][M ·]
=kp[M]Ri/kt′ =kp[M]Ri1/kt =kp(2fkd/kt )[M][I]1
条件II: 低转化率 假设III:自由基稳态 Ri=Rt 条件III:单基终止 Rt=kt[M·][RH]= [M·] kt′ [M·]=Rt/ kt′= Ri/ kt′
2
ER
Ep (29)
Ed 2
(125)
Et 2
(17)
83k J
/
mol
0
2.4.2自由基聚合初期聚合反应速率 三、反应温度对聚合反应速率的影响
2. 分析
ቤተ መጻሕፍቲ ባይዱ
ER
Ep (29)
Ed 2
(125)
Et 2
(17)
83kJ
/ mol
0
• ①ER>0, T反升高, kR增大,且ER越大,升温影响越 显著
2.4.2自由基聚合初期反应速率 一 动力学方程的推导
1
R
k p
fkd kt
2
[M
][
I
1
]2
6.0 2.0
1
Rp104/(mol/L s·)
实验验证Ⅱ
0.6
2
3 0.2
0.06 10-4 10-3 10-2 10-1 [I] /(mol/L)
图3-5 [M]恒定下聚合速率与[I]的关系
Rt=2kt[M·]2
1
R
Rp
k p[M ]
Ri 2kt
2
普适方程
2.4.2自由基聚合初期反应速率 一 动力学方程的推导
自由基聚合机理

Rp kpM M *
高分子聚合度很大,用于引发的单体远少于用于增 长的单体,即:Ri<<Rp
RCH 2CH
特点:
X
X
•放热反应(exothermal reaction);
•Ei低,约20-34KJ/mol;
•反应速率快。
2. 链增长(chain propagation):迅速形成大 分子链
RCH 2CH +CH 2=CH
RCH 2CHCH 2CH ......
X
X
XX
RCH 2CH CH 2CH nCH 2CH
二、引发剂分解动力学
(kinetics of initiator decomposition) ——研究引发剂浓度与时间、温度间的定量关系
1. 分解动力学方程 一级反应
I kd 2R•
Rd
d I
dt
kd
I
积分得: [I ]
ln [I ]0
kd t
Kd——分解速率常数,时间-1
物理意义:单位引发剂浓度时的 分解速率
由基数目并无增减,但消耗了一分子引发剂,从而使引发剂 效率降低。
过氧类引发剂、引发剂浓度大时易发生诱导分解。
2 . 笼蔽效应(cage effect)
引发剂分解产生的初级自由基,处于周围分子(如溶 剂分子)的包围,像处在笼子中一样,形成稳定分子, 使引发剂效率降低。这一现象称之为笼蔽效应。 大多数引发剂均可观察到些现象,偶氮类引发剂易发生。
链终止和链增长是一对竞争反应 终止速率常数远大于增长速率常数,但由于体系中, [M](monomer concentration)(1-10mol/l)>> [M.] (radical concentration)(10-7-10-9mol/l) Rp (增长总速率) > >Rt(终止总速率)
自由基
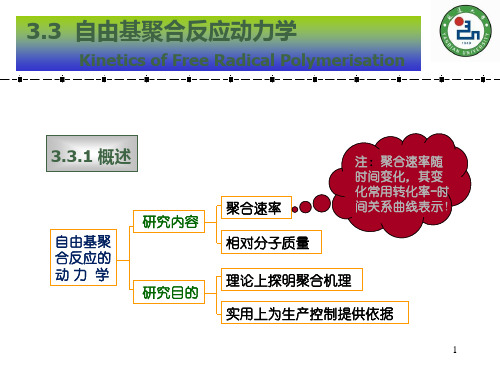
说明:组成自由基聚合的三步主要基元反应:链引发、链增长
和链终止对总聚合速率均有所贡献;链转移反应一般不 影响聚合速率。
4
3.3 自由基聚合反应动力学
聚合速率的测定方法
①直接法(常用沉淀法测定聚合物量) 加入沉淀剂使聚合物沉淀,或蒸馏出单 体,使聚合中断,然后经分离、精制、 干燥、称重等程序,求出聚合物的质量。 ②间接法(常用膨胀计法测定比体积) 测定聚合过程中比容、粘度、折光率、 吸收光谱等物理性质的变化,间接求出 聚合物量,从而可得到聚合速率。最常 用的是比容的测定——膨胀计法。
聚合物的 强度、力 学性能、 加工性能
引发剂的浓度、聚合温度等诸因素 以不同方式影响聚合速率和分子量
无 影 响 重大影响
链转移反应
23
3.4 聚合物的平均聚合度
动力学链长 表达相对分子质 量的两个物理量 平均聚合度 表示无链转移时聚 合物相对分子质量
表示有链转移时聚 合物相对分子质量
3.4.1 无链转移时的相对分子质量(动力学链长)
(10)3-33
Hale Waihona Puke 133.3 自由基聚合反应动力学
4、聚合总速率的推导
I、聚合总速率通常以单体消耗速率(-d[M]/dt)表示。
(3)推导自由基聚合动力学方程的第三个假定:聚合度大
自由基聚合三步主要基元反应中,链引发和链增长这两步都消耗 单体,高分子聚合度很大,用于引发的单体远远少于增长消耗的 单体,即 Ri<< Rp,可忽略不计,聚合总速率就等于链增长速率。 (11) 将稳定态时自由基浓度,即(10)3-33代入(6)3-31,得总聚合 速率的普适方程(适合于引发剂、光、热和辐射等不同作用引发 的聚合反应):
第三章-4:自由基聚合动力学

(2)温度对反应速率的影响
1
Rp
kp
fkd kt
2
[M
]
1
[I]2
1
kR
ER
ARe RT
kp
kd kt
1
2
EP
APe RT
Ed
Ade RT
Et
Ate RT
2
A A e P
d
( EP Ed Et ) RT 2RT 2RT
1
Rp
-
d[M dt
]
kp
fkd kt
2
[M
1
][I]2
速率微分方程
注:此时[I]和[M]为某一时刻的浓度
低转化率
1)微分方程所有条件和假设 2)[I]和f恒定
3)kp、kt 、kd 恒定
1
ln [M ]0 [M ]
kp
fkd kt
2 1 [I]02
Rp=k[M ]1~2 [I]0~1
?
聚合 反应 速率
聚合时间
自由基聚合动力学曲线
4.2.2 自由基聚合中期聚合反应速率
1、自动加速现象 2、自动加速现象的形成原因
凝胶效应 沉淀效应 3、影响因素
1、自动加速现象
1
Rp
kp
fkd kt
2
[M
]
1
[I]2
R [M] [I]
随着反应进行,聚合 反应速率不仅不随单 体和引发剂浓度的降 低而减慢,反而增大 的现象。这种聚合反 应速率自动加快的现 象称为自动加速现象。
第三章 自由基聚合-2

3.4
自由基聚合反应动力学
当体系中存在阻聚剂时,引发剂开始分解后,并不能
马上引发单体聚合,必须在体系中的阻聚剂全部消耗完后
,聚合反应才会正常进行。即从引发剂开始分解到单体开 始转化存在一个时间间隔,称诱导期 (induction period, ti).
单体在贮存、运输过程中常加入阻聚剂以防止单体聚
3.4
自由基聚合反应动力学
曲线1—纯净单体聚合,无诱导期,聚合速率正常。
曲线2—典型的阻聚作用,存在诱导期,诱导期间聚合完 全停止。但诱导期过后,聚合速率正常(Rp与1相同)。
曲线3—典型的缓聚作用,无诱导期,不会使聚合反应停 止,但聚合速率降低。
曲线4—兼有阻聚作用与缓聚作用,既产生诱导期,诱导 期过后聚合速率又降低。 3.4.4.1 阻聚剂与阻聚机理
3.4
自由基聚合反应动力学
3.4.1.1 各基元反应速率方程 ( 1)链引发 M M· 链引发速率 Ri =d[M•]/dt (2)链增长 RM· k R MM· k R MMM· k p p p M ¨¨¨ RMi · k RMi+1 · (i=1→∞)
p
M
M
M
根据等活性假设,各步增长反应的速率常数相等。 链增长速率 Rp =kp[M] ∑[RMi•] = kp[M][M•] kp—链增长速率 常数 ( [M•]= ∑[RMi•] )
3.4
自 由 基 聚 合 反 应 动 力 学
3.4.1自由基聚合动力学方程 基本假设: (1)忽略链转移反应,终止方式为双基终止; (2)等活性理论:链自由基的活性与链长无关,即各步链 增长速率常数相等,用一个速率常数kp表示。 (3)聚合产物Xn 很大,链增长所消耗的单体远远大于链引 发反应,因此认为单体主要消耗于链增长反应,聚合总速率 可以用链增长速率表示 R = -d[M]/dt= Ri +Rp≈ Rp (4)稳态假设:反应开始很短一段时间后,链自由基的生 成速率等于其消失速率(Ri =Rt),即体系中自由基的浓度恒 定,进入“稳态”;
高分子材料的自由基聚合反应动力学

高分子材料的自由基聚合反应动力学高分子材料是一类重要的工程材料,具有广泛的应用领域,如塑料、橡胶、纤维等。
高分子材料的制备主要依靠聚合反应,其中自由基聚合反应是最常用的方法之一。
了解高分子材料的自由基聚合反应动力学是实现高性能高分子材料的关键。
自由基聚合反应是通过自由基间的链式传递反应来实现高分子物质的形成。
这个过程包括引发、链增长和链传递三个阶段。
首先是引发步骤,当外部因素,如热、光、辐射等作用于起始物质时,可以产生自由基。
这些自由基具有高度反应性,会引发聚合反应。
然后是链增长步骤,起始物质中的自由基可以与单体分子发生反应,将单体分子加入到聚合链的末端,使聚合链得到延长。
最后是链传递步骤,聚合链中的自由基可以与其他自由基发生反应,导致链的断裂或交联,从而影响聚合过程。
在高分子材料的自由基聚合反应过程中,动力学参数对于控制聚合反应的速度和分子量分布至关重要。
其中,聚合反应速率常数(kp)和转移速率常数(kt)是反映反应速率的重要参数。
聚合反应速率常数是指在特定条件下,自由基与单体之间发生反应的速率常数。
转移速率常数是指自由基与其他基团之间转移反应的速率常数。
这两个参数的大小直接影响聚合物的分子量增长速率和分子量分布。
动力学模型是研究高分子材料自由基聚合反应动力学的重要工具。
根据反应过程的特点,常用的动力学模型有糖分级数动力学模型、时段动力学模型、可逆转移模型等。
这些模型可以通过数学公式来描述聚合反应过程中自由基浓度、聚合物分子量等参数的变化规律。
了解自由基聚合反应的动力学特点有助于优化聚合反应条件,提高聚合物的质量和性能。
一方面,可以通过调节引发剂的浓度或类型来改变聚合反应速率,控制聚合物的分子量分布。
另一方面,可以通过调节反应温度和环境条件来控制转移反应的发生,从而影响聚合物的结构和性能。
此外,了解自由基聚合反应的动力学特点还有助于预测聚合过程中可能产生的副反应和副产物。
例如,聚合过程中可能发生分支反应,导致聚合物结构的分岔和交联。
自由基聚合微观动力学方程

自由基聚合微观动力学方程自由基聚合是一种在化学反应中发生的重要过程。
在聚合反应中,自由基通过相互结合形成长链分子。
这种反应过程常见于合成高分子材料,例如聚乙烯和聚丙烯等。
自由基聚合的微观动力学方程可以描述为以下几个步骤:1.初始化:初始化时,反应体系中存在着自由基单体和引发剂。
引发剂在适当条件下可以产生自由基,从而引发聚合反应的开始。
2.引发剂生成自由基:引发剂在引发剂反应中产生自由基,这些自由基有机会与单体发生反应。
3.自由基引发反应:引发剂生成的自由基会与单体分子发生反应,形成新的自由基和聚合物链。
这些新生成的自由基会继续引发新的反应。
4.终止反应:在整个聚合反应中,还会发生终止反应。
终止反应是指两个自由基相互结合或与其他物质发生反应,从而停止自由基聚合反应的进行。
以上描述的微观动力学方程可以用数学公式表示如下:d[M] / dt = k*p*f[A]*[M]其中,d[M] / dt是单体浓度随时间的变化率,k是聚合速率常数,p是引发剂浓度,f[A]是引发剂的活化因子,[A]是引发剂浓度,[M]是单体浓度。
这个方程可以描述单体浓度随时间的变化。
引发剂生成自由基可以用以下公式表示:[A] = [A0]*exp(-kt)其中,[A0]是引发剂初始浓度,k是引发剂的速率常数,t是反应时间。
终止反应可以用以下公式表示:d[P] / dt = k't*[I]*[P]其中,d[P] / dt是聚合物浓度随时间的变化率,k'是终止反应速率常数,[I]是终止剂浓度,[P]是聚合物浓度。
这个方程可以描述聚合物浓度随时间的变化。
以上是自由基聚合微观动力学方程的基本描述。
在实际应用中,还可以根据反应体系的具体条件和反应特点进行相应的修正和扩展。
此外,还需要考虑一些其他因素,比如溶剂效应、温度效应等。
总结而言,自由基聚合微观动力学方程对于理解聚合反应的机理和控制聚合反应具有重要意义。
通过对微观动力学方程的建立和求解,可以更好地预测和调控聚合反应的过程和产物,为合成高分子材料提供理论基础和指导。
自由基反应动力学

自由基聚合速率方程
因此总的聚合速率的普适方程为
当用引发剂引发时,将式
代入上式
得
聚合速率
引发剂浓度的 平方根成正比
单体浓度的一次方成正比
15
16
对引发剂反应级数介于0.5~1.0之间
0.5级和1.0级是双基终止和单基终止的两 种极端情况
往往是单基终止和双基终止并存,其对 引发剂浓度的反应级数介于0.5~1.0之间
2
3.4.1 本体聚合的反应特征
聚合速率也可用 单位时间内的转化率变化表示:
或
3
C%
t
图 转化率~聚合时间关系
诱导期、聚合初期、聚合中期、聚合后期
4
转化率随聚合时间变化的测定
分为直接法和间接法两类 常用的直接法为沉淀法
一定温度下聚合,定时取样,求得不同t时的 聚合物量
也可通过分析单体的浓度而求得某时刻的转化 率
约 20 kJ/mol 温度对聚合速率的影响较小,在较低的温度
下(0℃)也能聚合
24
3.4.4 各基元反应速率常数及 聚合主要参数
自由基聚合各基元反应速率常数的测定 各基元反应速率常数及主要动力学参数
25
(1)各基元反应速率常数的测定
链引发反应 链增长反应 链终止反应
26
动力学稳态处理,消去[M·] ,得到聚 合速率方程
6
3.4.2 自由基聚合动力学方程
(1)各基元反应的速率方程 (2)自由基聚合速率方程
7
(1)各基元反应的速率方程
自由基聚合是由三个基元反应组成 链引发 链增长 链终止
各基元反应对总聚合速率都有贡献 链转移反应一般不影响速率,可略之
8
① 引发剂的链引发反应的速率方程
自由基稳态假定

自由基稳态假定(Radical Stabilization Assumption)是自由基聚合(free radical polymerization)动力学中的一个重要概念。
在自由基聚合过程中,自由基是引发聚合反应的活性种,它们会不断生成新的自由基和聚合物链。
稳态假定认为,在聚合反应达到一定阶段后,自由基的生成速率和聚合速率之间达到平衡,即自由基的浓度保持恒定。
这个假定的基础是自由基的生成速率和聚合速率都与自由基的浓度有关。
在聚合反应的初期,自由基的浓度较高,因此生成速率较快。
随着聚合物链的增长,自由基的浓度逐渐降低,生成速率也会相应减慢。
但是,由于聚合物链的增长也会产生新的自由基,这些新产生的自由基会继续引发聚合反应,使得聚合速率保持稳定。
稳态假定通常用于描述聚合反应进入稳定生长阶段后的动力学行为。
在这个阶段,聚合速率主要受到聚合反应器中自由基浓度的控制。
因此,稳态假定可以用来预测聚合物的分子量分布和分子量增长规律。
自由基聚合反应动力学

§1-4 自由基聚合反应动力学
〆引发剂引发时复杂情况的自由基聚合微观动力学方程
R P K I M
n
m
式中的n=0.5~1.0,m=1~1.5。
▲其他引发方程下的自由基聚合微观动力学方程 引发方式 引发速率方程 Ri 聚合速率方程 RP
kP fk d 2k t
fk d k t
fk i kP k t
2
2 I 0 M
直接光引发
I 0 kP k t
I 0 kP k t
1 2Fra bibliotekM 3 2
2 I 0 I
I M
§1-4 自由基聚合反应动力学
二、自由基聚合反应宏观动力学
R i k i R M
由于链引发受引发剂分解过程控制,所以 ▲链增长:
RM
1
R i R d 2 fk d I
R P 1 k P RM
1
M RM
k
kP
2
3
P RM 2 M RM ……………
R P 2 k P RM
R Pn k P RM
§1-4 自由基聚合反应动力学
一、自由基聚合反应微观动力学方程
●推导微观动力学方程的基本假设 ▲聚合度很大假设( R i R P )
R 总= d M dt
Ri R P R P
▲自由基等活性假设
k P 1 k P 2 k P 3 k Pn k P
▲“稳态”假设
根据稳态假设得:
Ri M 2k t
高化之自由基聚合的微观动力学

2.2.3 自由基聚合的微观动力学 自由基聚合的微观动力学是研究聚合反 应初期聚合速率R与引发浓度[I]、单体浓度
[M]、时间t等参数之间的定量关系。
t1/2↓(或kd↑) 活性↑
d[ I ] 1 d[ R ] - ——— = — · ——— = kd [ I ] dt 2 dt
引发剂分解:-d[ I ] / dt = kd [ I ] ( 2 )
●
●
(1)
初级自由基生成: d[ R ] / dt = 2 kd [ I ] ( 3 ) 在链引发反应的动力学研究中,要研究 的是自由基的生成。 用式(3) d[ R ] ——— = 2 kd [ I ] dt
● ●
偶合终止速率 Rtc = 2 ktc [M ]2 (9) ktd Mm + Mn Mm + Mn
● ● ●
歧化终止速率 Rtd = 2 ktd [M ]2
●
( 10 )
终止总速率 Rt = Rtc + Rtd = 2 (ktc + ktd) [M ]2 = 2 kt [M ]2
● ●
( 11 )
ln([M0]/[M]) = kP (f kd/kt )1/2 [ I ]1/2 t
式中 [M0] 起始浓度 ( t = 0 ) [M] 时间t时的浓度 适用条件同 ( 16 )
( 17 )
RM + M → …… → ~~~~~~ M R + M → RM
● ●
●
●
引发消耗的单体所占的比例很小,Ri<<RP, 可忽略不计。(假定三)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M 2
M
M
RM
n
M RM
kP
n 1
n
由于:
RP
R
Pi
R P 1 R P 2 R Pn
1
R P k P RM
RM
2
RM
n
M
所以:
R P k P M M
fk i kP k t
2
2 I 0 M
直接光引发
I 0 kP k t
I 0 kP k t
1 2
M
3 2
2 I 0 I
I M
§1-4 自由基聚合反应动力学
二、自由基聚合反应宏观动力学
聚合时间/min
第三阶段:聚合中期(或加速阶段)20%~80%
产生的原因:随着体系内大分子数量的增加,黏度不断增大,造成长链自由基活动受 阻,甚至活性自由基被包裹,双基终止困难,链终止速率常数下降;而单体分子因体积小, 活动自由,能继续与长链自由基碰撞反应,使增长速率常数下降较少或不下降;故此,产 生自动加速。这种由于体系黏度增加所引起的不正常的动力学现象称为凝胶效应。 第四阶段:聚合后期(或降速阶段)X≥80% 产生的原因:体系黏度更大,单体浓度减少。
§1-4 自由基聚合反应动力学
〆引发剂引发时复杂情况的自由基聚合微观动力学方程
R P K I M
n
m
式中的n=0.5~1.0,m=1~1.5。
▲其他引发方程下的自由基聚合微观动力学方程 引发方式 引发速率方程 Ri 聚合速率方程 RP
kP fk d 2k t
fk d k t
Ri Rt 或
d M dt
0
其中第一、二点假设在聚合转化率高时,不存在。
§1-4 自由基聚合反应动力学
●自由基聚合反应微观动力学方程
推导依据:自由基聚合机理、质量作用定律、基本假设 ▲链引发:
I 2R
i R M RM
kd
R d 2 fk d I
1
k
fk i k t
2 fk d I
引发剂引发
2 fk d I M
k i M
1 2
I M
1 2
1 2
kP
I M
1 2
3 2
1
2
2
kP
3
M 2
M
1 2
5 2
热引发
1
k i M
§1-4 自由基聚合反应动力学
〆自动加速现象的数据解释
转化率 0 10 20 30 40 50 60 70 80 聚合速率 自由基寿命 3.5 2.7 6.0 15.4 23.4 24.5 20.0 13.1 2.6 0.80 1.14 2.21 5.0 6.3 9.4 26.7 79.3 216
2
I M
1 2
引发剂引发时,聚合速率与单体浓度的一次方成正比,与引发剂浓度的平方根成正比。 〆引发剂引发的非正常自由基聚合微观动力学方程 此时的链引发形式为
其微观动力学方程为:I M R M
1 2
R i 2 fk
d
I M
3 1 fk d 2 I M 2 RP kP k 结果表明: t 聚合速率与单体浓度的3/2次方成正比,与引发剂浓度的平方根成正比。
§1-4 自由基聚合反应动力学
一、自由基聚合反应微观动力学方程
●推导微观动力学方程的基本假设 ▲聚合度很大假设( R i R P )
R 总= d M dt
Ri R P R P
▲自由基等活性假设
k P 1 k P 2 k P 3 k Pn k P
▲“稳态”假设
〆工业生产中“自动加速”现象的危害与控制办法 危害:放热集中、爆聚使生产难于控制;单体气化,产物中有气泡,影响质量。 控制办法:关键是降低体系的黏度。具体办法:溶液聚合;提高聚合温度;低温乳液 聚合;加入链转移剂。另外,还要注意单体的结构与单体对聚合物的溶解情况。 ●高转化率下的宏观动力学方程 因无固定的表述形式,暂不介绍。
§1-4 自由基聚合反应动力学
●对自由基聚合微观动力学方程的讨论
▲引发剂引发的自由基聚合微观动力学方程 〆引发剂引发的正常自由基聚合微观动力学方程 将引发速率方程 R i R d 2 fk d I 代入一般式之中,整理得:
1
RP
结果表明:
fk d kP 2k t
●自由基聚合全过程的聚合速率变化曲线(“S”型曲线) 第一阶段: 诱导期, X=0。 转 化 率 x% 产生的原因:引发剂产生的初级自由基被阻 聚杂质所消耗。诱导期的长短取决于阻 聚杂质的多少。
1
2
3
4
第二阶段:聚合初期(或等速阶段)X≤20% 产生的原因:阻聚杂质耗尽,体系的大分子 数量较少,黏度较低,大分子和单体均 能自由运动,体系处于稳态阶段。
kP
384 234 267 303 368 256 74 16 1
k t 10
5
k
P
/ k t 2 10
1
5
442 273 72.6 14.2 8.93 4.03 0.498 0.0564 0.0076
5.78 4.58 8.81 25.5 38.9 40.6 33.2 21.3 3.59
§1-4 自由基聚合反应动力学
▲链终止
M
n
M m M M M m
nm
R tc 2 k tc M
m
2
n
n
M
R td 2 k td M
2
2
R t R tc R td 2 ( k tc k td ) M 2 k P M
R i k i R M
由于链引发受引发剂分解过程控制,所以 ▲链增长:
RM
1
R i R d 2 fk d I
R P 1 k P RM
1
M RM
k
kP
2
3
P RM 2 M RM ……………
R P 2 k P RM
R Pn k P RM
根据稳态假设得:
Ri M 2k t
1 2
2
代入链增长速率方程得:自由基聚合微观动力学方程一般表达式
1
RP
该式表明:
Ri k P M 2k t
2
聚合速率正比于单体浓度的一次方,正比于引发速度的平方根,后者产生的原因是双 基终止。不同的引发方式,其引发速率方程不同,结果聚合速率方程必然不同。
