NOIP2010复习资料
复赛noip2010提高组题解[新版]
![复赛noip2010提高组题解[新版]](https://img.taocdn.com/s3/m/7b1ee1c3b8f3f90f76c66137ee06eff9aef84965.png)
1.translate(20分)简单模拟。
开一个1000的队列,时刻保持队列长度不大于M,每次接受翻译请求时,先在队列中查找,查找失败则将单词加入队列。
查找使用Hash则为O(N),直接扫描O(MN),都在可接受范围内。
考试时只打了20分,原因至今不明,告诫大家对于水题不要多想,就像这道题最好不开hash,因为一个系统的可靠度是该系统所有子系统可靠度之积,程序越复杂越可能出错。
4.tortoise(50分)基础动规。
可以从题目背景中抽象出这样的问题:有一四维立方体(这里的立方体棱长不必相等,每一维对应一种卡片,每维的棱长对应该种卡片个数),每走一格(即使用一张卡片)的收益是当前位置坐标的函数。
求从(0,0,0,0)走到(a1,a2,a3,a4)最大收益。
故有方程f[x,y,z,t]=max{f[x-1,y,z,t], f[x,y-1,z,t], f[x,y,z-1,t], f[x,y,z,t-1]} + w[1 + x + y*2 + z*3 + t*4]目标状态: f[a1,a2,a3,a4]O(b^4)的代价,数据保证b<=40,完全满足要求5.prison(70分)问题可以重新描述为:寻找最小的冲突值c,使得存在一种方案,将原图分为两部分,并去掉这两部分之间的所有边后,余下的边权都不大于c。
对于这个问题我们可以二分查找c,并判定其可行性。
判定可行性的方法至今没想好。
考试的时候我是用并查集,将所有与u相连并与u之间边权大于c的点(设为点集Zu)必然不与u在同一集合中,枚举所有的u,每次将Zu合并成为一个集合,若存在某点u和Zu某个点处于同一个集合中,则c不可行,反之则可行。
但这种方法貌似存在bug,能拿70分。
如果把并查集合并查找的时间代价看作常数,则这种做法的时间代价为O(elogK),e是边数,K为最大的冲突值。
6.flow(100分)先用floodfill预处理出上方的每个格子能覆盖到下方的格子,构造一个布尔矩阵,行下标表示最上方的某个点,列下标表示最下方的某个点,矩阵对应点的值表示相应两个点的覆盖关系。
(完整word)NOIP2010提高组初赛试题及详细解析

第十六届全国青少年信息学奥林匹克联赛初赛试题( 提高组 C++ 语言 两小时完成 )• • 全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效 ••、单项选择题 (共 10 题,每题 1.5 分,共计 15 分。
每题有且仅有一个正确选项。
)1.与十六进制数 A1.2 等值的十进制数是( )A . 101.2B . 111.4C . 161.125D . 177.25&主存储器的存取速度比中央处理器 (CPU )的工作速度慢的多,从而使得后者的效率受到影响。
而根据局部性原理,CPU 所访问的存储单元通常都趋于一个较小的连续区域中。
于是,为了提高系统 整体的执行效率,在 CPU 中引入了( )。
A .寄存器B .高速缓存C .闪存D .外存9.完全二叉树的顺序存储方案,是指将完全二叉树的结点从上到下、从左到右依次存放到一个顺序 结构的数组中。
假定根结点存放在数组的 1 号位置上,则第 k 号结点的父结点如果存在的话,应当 存放在数组中的( )号位置。
A .2kB .2k+1C .k/2 下取整D .(k+1)/22.一个字节( byte )由( )个二进制组成。
A .8B .16上都有可能3.以下逻辑表达式的值恒为真的是( )。
A . P V (n P A Q )V (n P 心 Q )BC . P V Q V ( P A n Q )V (n P A Q )D 4 . Linux 下可执行文件的默认扩展名是 ( ) 。
A.exe B. com都不是C .32 D .以Q V( n P A Q )V (P A n Q )P V n Q V( P A n Q V (n P A n Q)C. dllD.以上5 .如果在某个进制下等式 7*7=41 成立,那么在该进制下等式 12*12= ( A. 100B. 144C. 164 )也成立。
D. 1966 .提出“存储程序”的计算机工作原理的是(A. 克劳德 ?香农B. 戈登?摩尔)。
NOIP 2010

全国信息学奥林匹克联赛复赛试题提高组3小时完成题目一览题目名称统计数字字符串的展开矩阵取数游戏树网的核代号count expand game core输入文件count.in expand.in game.in core.in输出文件count.out expand.out game.out core.out时限1秒1秒1秒1秒说明:1. 文件名(程序名和输入输出文件名)必须使用小写2. C/C++中函数main()的返回值必须是int,程序正常结束时返回值必须是0。
3. 全国统一评测时采用的机器参考配置为:CPU 2.0GHz,内存256M。
1、统计数字(count.pas/c/cpp)【问题描述】某次科研调查时得到了n个自然数,每个数均不超过1500000000(1.5*109)。
已知不相同的数不超过10000个,现在需要统计这些自然数各自出现的次数,并按照自然数从小到大的顺序输出统计结果。
【输入】输入文件count.in包含n+1行;第一行是整数n,表示自然数的个数;第2~n+1每行一个自然数。
【输出】输出文件count.out包含m行(m为n个自然数中不相同数的个数),按照自然数从小到大的顺序输出。
每行输出两个整数,分别是自然数和该数出现的次数,其间用一个空格隔开。
【输入输出样例】count.in count.out8 2 4 2 4 5 100 2 100 2 34 25 1 100 2【限制】40%的数据满足:1<=n<=100080%的数据满足:1<=n<=50000100%的数据满足:1<=n<=200000,每个数均不超过1500 000 000(1.5*109)2、字符串的展开(expand.pas/c/cpp)【问题描述】在初赛普及组的“阅读程序写结果”的问题中,我们曾给出一个字符串展开的例子:如果在输入的字符串中,含有类似于“d-h”或者“4-8”的字串,我们就把它当作一种简写,输出时,用连续递增的字母获数字串替代其中的减号,即,将上面两个子串分别输出为“defgh”和“45678”。
NOIP2010题解

总分
400 380 340 330 320 310 300 300 290 280 280 270 270 260 260 260 260 250 250 250 240 240 240
姓名
徐明昭 张硕基 徐子尧 崔灏 田博 李光谱 吕诚 魏鑫鼎 马龙 李昭 吴文彬 李金培 李栋 李昂 杨帅 李怡君 杨东 王子晗 谢志聪 周梦溪 苏畅 许可 常泽昊
240 240 240 240 240 240 230 230 230 230 230 230 220 210 210 210 210 210 200 200
noip普及组赛前冲刺资料全

数组一、数字数组ex1_1_1.pas级数求和(NOIP2002)【题目描述】已知:Sn=1+1/2+1/3+…+1/n。
显然对于任意一个数K,当n.足够大的时候,Sn大于K。
现给出一个整数K(1≤K≤15),要求计算出一个最小的n,使得Sn>K【输入】一行,一个整数K【输出】一行,一个整数n【输入样例】1【输出样例】2ex1_1_2.pas陶陶摘苹果(NOIP2005)【题目描述】陶陶家的院子里有一棵苹果树,每到秋天树上就会结出10个苹果。
苹果成熟的时候,陶陶就会跑去摘苹果。
陶陶有个30厘米高的板凳,当她不能直接用手摘到苹果的时候,就会踩到板凳上再试试。
现在已知10个苹果到地面的高度,以及陶陶把手伸直的时候能够达到的最大高度,请帮陶陶算一下她能够摘到的苹果的数目。
假设她碰到苹果,苹果就会掉下来。
【输入】两行数据。
第一行包含10个100到200之间(包括100和200)的整数(以厘米为单位)分别表示10个苹果到地面的高度,两个相邻的整数之间用一个空格隔开。
第二行只包括一个100到120之间(包含100和120)的整数(以厘米为单位),表示陶陶把手伸直的时候能够达到的最大高度。
【输出】一行,这一行只包含一个整数,表示陶陶能够摘到的苹果的数目。
【输入样例】100 200 150 140 129 134 167 198 200 111110【输出样例】5ex1_1_3.pas数字统计(NOIP2010)【题目描述】请统计某个给定范围[L, R]的所有整数中,数字2 出现的次数。
比如给定范围[2, 22],数字2 在数2 中出现了1 次,在数12 中出现1 次,在数20 中出现1 次,在数21 中出现1 次,在数22 中出现2 次,所以数字2 在该范围内一共出现了6次。
【输入】共1 行,为两个正整数L 和R,之间用一个空格隔开。
【输出】共1 行,表示数字2 出现的次数。
【输入样例】2 22【输出样例】6【输入输出样例2】2 100【输出】20【数据范围】1 ≤ L ≤ R≤ 10000。
深入Noip2010初赛试题和全解

作者:钟野梓序今年Noip2010初赛刚结束,网上便铺天盖地地响起了“今年初赛好容易”“分数线一定很高,怎么办……”之类的声音。
确实,自2008年起,Noip初赛难度确有逐年下降的趋势,然而这并不是出题水平降低的缘故,相反,我认为这是中国计算机协会(下称CCF)对于N oip考核目的的审视和改变所导致的必然结果。
因此,我试图通过深入解析本届Noip初赛试囗题,来探寻这种变化下面深层的规律,从而令信息学竞赛选手能更好地备战往后数届的Noip初赛,让初赛不再成为一个问题。
由于条件所限,本文仅以Pascal语言的提高组试囗题作为对象进行分析,相对于普及组而言提高组试囗题一向具有较高的难度和较好的区分度,作为研究对象是个很好的选择;至于说语言的选择,仅是因为笔者个人选择原因。
一、概况本届题目在设置方面与往年相似,由选择题(普及组仅有单项选择题,提高组则有单项选择题与不定项选择题)、问题求解、阅读程序写结果及完善程序四大部分组成;但值得注意的是,今年提高组试囗题的分值设计与往年出现了较大的不同,除了选择题仍然是30分(15分单项+15分不定项),其余部分分值均发生了变化,其中问题求解由10分上升到15分,阅读程序由32分下降到28分,完善程序由28分下降到27分。
由于是第一年实行这种分值,目前暂时无法定言背后的含义,然而或许CCF在初赛更加重视选手的数学素质,而弱化了对于阅读程序能力的考察。
众所周知,阅读程序的能力并不能非常真实地反映选手的程序能力,并且纵观近几年的阅读程序题已没有了什么新意,这也可看做是一个“求新求变”的信号。
至于试囗题整体难度方面较上年有了明显下降,其中问题求解第一题可以看做是考察选手的语文水平,而阅读程序更是没有了以往的“死算”题(即给定若干常数,在程序中设置一系列运算过程,让选手进行阅读计算类型的题目),完善程序给定的源代码风格良好,第二题竟然还加上了注释,这不能不说就是一种降低难度的举动。
NOIP2010普及组复赛试题

NOIP2010普及组复赛试题1.数字统计(two.pas/c/cpp) 【问题描述】请统计某个给定范围[L,R]的所有整数中,数字2出现的次数。
【输入格式】共1行,为两个正整数L 和R ,之间用一个空格隔开。
(1≤L ≤R ≤10000)。
【输出格式】仅1行,表示数字2出现的次数。
2.接水问题(water.pas/c/cpp) 【问题描述】学校里有一个水房,水房里一共装有m 个龙头可供同学们打开水,每个龙头每秒钟的供水量相等,均为1。
现在有n 名同学准备接水,他们的初始接水顺序已经确定。
将这些同学按接水顺序从1到n 编号,i 号同学的接水量为w i 。
接水开始时,1到m 号同学各占一个水龙头,并同时打开水龙头接水。
当其中某名同学j 完成其接水量要求w j 后,下一名排队等候接水的同学k 马上接替j 同学的位置开始接水。
这个换人的过程是瞬间完成的,且没有任何水的浪费。
即j 同学第x 秒结束时完成接水,则k 同学第x+1秒立刻开始接水。
若当前接水人数n 不足m ,则只有n 个龙头供水,其它m?n 个龙头关闭。
现在给出n 名同学的接水量,按照上述接水规则,问所有同学都接完水需要多少秒。
【输入格式】第1行2个整数n 和m ,用一个空格隔开,分别表示接水人数和龙头个数。
第2行n 个整数w 1、w 2、……、w n ,每两个整数之间用一个空格隔开,wi 表示i 号同学的接水量。
1≤n ≤10000,1≤m ≤100且m ≤n ;1≤w i ≤100。
【输出格式】仅一行,1个整数,表示接水所需的总时间。
3.导弹拦截(missile.pas/c/cpp) 【问题描述】经过11年的韬光养晦,某国研发出了一种新的导弹拦截系统,凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。
当工作半径为0时,则能够拦截与它位置恰好相同的导弹。
但该导弹拦截系统也存在这样的缺陷:每套系统每天只能设定一次工作半径。
而当天的使用代价,就是所有系统工作半径的平方和。
备战NOIP2010提高组初赛复习——数据结构

通常高级程序设计语言都提供了各种简单类型和静态构造类型的数据结构。例如PASCAL就提供了12种类型的定义。这12种类型中除了文件和指针属于动态结构的构造类型外,其余10种均属于简单类型和静态构造类型。在上表的数据结构中,像数组、栈、串和队列等数据结构属于线性数据结构,而树和图属于非线性数据结构。线性数据结构易于表示各结点之间的联系,其存储方式相对简单;非线性数据结构往往能比较形象地反映各结点之间的层次关系。无论是线性结构或非线性结构,若采用数组方式存储,则属于静态数据类型;若采用指针类型存储,则属于动态数据类型。考虑到篇幅限制和读者大多具备pascal语言或c语言的基础,本书侧重讲解线性结构和非线性结构两种。
数据结构和算法有着密切的联系,简洁有效的算法很大程度上出自于对数据结构的正确选取。奥林匹克信息学竞赛的试题大都属于非数值计算问题,从问题中抽象出的数据多半是结构类型的,因此,对于参与这项活动的学生来说,学好、用好数据结构尤为重要。为此。我们在本书中详尽地介绍了数据结构的有关概念和基本操作,同时辅之于一些实例,围绕编程实际展开讨论,尽可能多给读者一点启示。
据,这两种数据类型足以应付当时多数的科学计渐应用于数据处理和非数值计算问题,从客观事物中抽象出的数据日益显现出多样化的特征,简单的数据类型已远远不能满足需要,各数据元素之间的复杂联系已经不是普通的数学方程式所能表达的了。在这种背景下,一种专门研究数据之间结构关系的学科—数据结构便应运而生。
数据结构专门研究各种数据的表示、数据的类型以及它们之间关系的集合,其研究范围主要包括各种数据结构的性质,即它们的逻辑结构、物理结构以及施于其上的操作。数据结构的类型种类繁多,可以从不同的角度来划分:若从数据元素的值在使用时具有不可分割的性质或者是它可以由更基本的成份组成这个角度来划分,数据结构可以分成简单类型和构造类型两大类;如果从数据所占据的内存空间在程序执行期间是否发生变化这个角度来划分,数据结构又可以分成静态结构和动态结构两大类;如果从数据结点后继关系的多少和是否具有层次性的角度划分,数据结构还可以分成线性结构和非线性结构两大类。
Noip2010提高组初赛试题及详细解析(C语言)

第十六届全国青少年信息学奥林匹克联赛初赛试题(提高组C 语言二小时完成)●● 全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一.单项选择题(共10题,每题1.5分,共计15分。
每题有且仅有一个正确选项。
)1.与16进制数A1.2等值的10进制数是(C )A.101.2B.111.4C.161.125D.177.25解析1:看进制转换的表原式等于10(A)×161+1×160+2×16-1=161.1252.一个字节(byte)由()个二进制位组成。
A.8B.16C.32D.以上都有可能解析2: 一个字节(byte)由( 8 )个二进制位组成,即一个字节等于八比特3.一下逻辑表达式的值恒为真的是()A.P∨(┐P∧Q)∨(┐P∧┐Q)B.Q∨(┐P∧Q)∨(P∨┐Q)C.P∨Q∨(P∧┐Q)∨(┐P∧Q)D.P∨┐Q∨(P∧┐Q)∨(┐P∧┐Q)解析3:各个逻辑符号的问题,可以进行一定的假设。
设P,Q都为假"∨" 表示"或" 相当于生活中的“或者”, "∧" 表示"与". 相当于生活中说的“并且” "┐"表示"非". 真或真为真:真或假为真:假或假为假:假与假为假,假与真为假,真与真为真。
真为真,非真为假,假为假,非假为真。
4.Linux下可执行文件的默认扩展名为()A.exe Baaa C.dll D.都不是解析4:Linux下常见的文件名后缀、文件类型1、系统文件*.conf配置文件*.rpm rpm包*.a 一种存档文件*.lock 一种琐文件*.~ 备份文件*. 隐藏文件2:程序或脚本*.c c语言源程序文件*.cpp c++语言源程序*.h c或c++头文件*.o 程序对象文件*.pl perl语言源程序*. php php语言源程序*.tcl tcl脚本程序*.so/.lib 库文件*.sql sql语言文件3:格式文件*.txt 无格式的ascii码文件*.html/.htm 静态web页*.ps postScipt文件*.au 一种声音文件*.wav 一种声音文件*.xpm一种图像文件*.png一种图形,图像文件4:存档与压缩文件*.tar tar归档文件*.Z/.gz/.bz2压缩文件*.tar.gz/.tgz/.tar.bz2/.tbz为压缩后的tar 包linux本身是没有扩展名这个概念的。
NOIP2010初赛普及组C++题目及参考答案

第十六届全国青少年信息学奥林匹克联赛初赛试题(普及组C++语言两小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共20题,每题1.5分,共计30分。
每题有且仅有一个正确选项。
)1.2E+03表示()。
A. 2.03B.5C.8D.200023A.PC.P4.5A.2n6A.7.设式8.A.910在CPUA.寄存器B.高速缓存C.闪存D.外存11.一个字长为8位的整数的补码是11111001,则它的原码是()。
A.00000111B.01111001C.11111001D.1000011112.基于比较的排序时间复杂度的下限是(),其中n表示待排序的元素个数。
A.Θ(n)B.Θ(nlogn)C.Θ(logn)D.Θ(n2)13.一个自然数在十进制下有n位,则它在二进制下的位数与()最接近。
A.5nB.n*log210C.10*log2nD.10n log2n14.在下列HTML语句中,可以正确产生一个指向NOI官方网站的超链接的是()。
A.<aurl="">欢迎访问NOI网站</a>B.<ahref="">欢迎访问NOI网站</a>C.<a></a>D.<aname="">欢迎访问NOI网站</a>15.元素R1、R2、R3、R4、R5入栈的顺序为R1、R2、R3、R4、R5。
如果第1个出栈的是R3,那么第5个出栈的不可能是()。
A.R1B.R2C.R4D.R516.双向链表中有两个指针域llink和rlink,分别指向该结点的前驱及后继。
设p指向链表中的一个结点,它的左右结点均非空。
现要求删除结点p,则下面语句序列中错误的是()。
A.p->rlink->llink=p->rlink;p->llink->rlink=p->llink;deletep;1718A.B.C.D.19置。
NOIP2010提高组初赛试题及详细解析

第十六届全国青少年信息学奥林匹克联赛初赛试题(提高组 C++语言两小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共10题,每题1.5分,共计15分。
每题有且仅有一个正确选项。
)1.与十六进制数 A1.2等值的十进制数是()A.101.2 B.111.4 C.161.125 D.177.252.一个字节(byte)由()个二进制组成。
A.8 B.16 C.32 D.以上都有可能3.以下逻辑表达式的值恒为真的是()。
A.P∨(┓P∧Q)∨(┓P∧┓Q) B.Q∨(┓P∧Q)∨(P∧┓Q)C.P∨Q∨(P∧┓Q)∨(┓P∧Q) D.P∨┓Q∨(P∧┓Q)∨(┓P∧┓Q)4.Linux下可执行文件的默认扩展名是( )。
A. exeB. comC. dllD. 以上都不是5.如果在某个进制下等式7*7=41成立,那么在该进制下等式12*12=()也成立。
A. 100B. 144C. 164D. 1966.提出“存储程序”的计算机工作原理的是()。
A. 克劳德•香农B. 戈登•摩尔C. 查尔斯•巴比奇D. 冯•诺依曼7.前缀表达式“+ 3 * 2 + 5 12 ”的值是()。
A. 23B. 25C. 37D. 6 58.主存储器的存取速度比中央处理器(CPU)的工作速度慢的多,从而使得后者的效率受到影响。
而根据局部性原理,CPU所访问的存储单元通常都趋于一个较小的连续区域中。
于是,为了提高系统整体的执行效率,在CPU中引入了( )。
A.寄存器 B.高速缓存 C.闪存 D.外存9.完全二叉树的顺序存储方案,是指将完全二叉树的结点从上到下、从左到右依次存放到一个顺序结构的数组中。
假定根结点存放在数组的1号位置上,则第k号结点的父结点如果存在的话,应当存放在数组中的()号位置。
A.2k B.2k+1 C.k/2下取整 D.(k+1)/210.以下竞赛活动中历史最悠久的是()。
NOIP2010终极资料(打印版)

数论算法1.求两数的最大公约数【注释①】function gcd(a,b:integer):integer;beginif b=0 then gcd:=aelse gcd:=gcd (b,a mod b);end;2.求两数的最小公倍数function lcm(a,b:integer):integer;beginif a<b then swap(a,b);【注释②】lcm:=a;while lcm mod b>0 do inc(lcm,a);end;3.素数的求法1)小范围内判断一个数是否为质数function prime(n:integer):boolean;var i:integer;beginfor i:=2 to trunc(sqrt(n)) doif n mod i=0 then beginprime:=false;exit;end;prime:=true;end;2)判断longint范围内的数是否为素数(包含求50000以内的素数表)【注释①】procedure getprime; {50000以内的素数表}var i,j:longint;p:array[1..50000] of boolean;beginfillchar(p,sizeof(p),true);p[1]:=false;i:=2;while i<50000 do beginif p then beginj:=i*2;while j<50000 do beginp[j]:=false;inc(j,i);end;end;inc(i);end; l:=0;for i:=1 to 50000 doif p then begininc(l);pr[l]:=i;end;end;{getprime}function prime(x:longint):integer; {判断}var i:integer;beginprime:=false;for i:=1 to l doif pr[i]>=x then breakelse if x mod pr[i]=0 then exit; prime:=true;end;4.进制转换1)任意正整数进制间的互化除n(倒)取余2)实数任意正整数进制间的互化乘n(正)取整3)负数进制:(noip2001进制转换)设计一个程序,读入一个十进制数的基数和一个负进制数的基数,并将此十进制数转换为此负进制下的数:-R∈{-2,-3,-4,....,-20}const d='123456789ABCDEFGHiJK';var n,m,i:longint;procedure work(n,m:longint);var a,b,i:longint;str:ansistring;begini:=1; a:=n;repeatb:=a mod m;a:=a div m;if b<0 then begin b:=b-m; inc(a); end;str:=d[b]+str;until a=0;writeln(n,'=',str,'(','base',m,')');end;{end work}beginwhile not(eof) dobeginreadln(n,m);work(n,m);注:①最大公约数,最小公倍数关系:gcd(a,b)*lcm(a,b)=a*b其中a,b为正整数满足:gcd(a,b)<=a,b<=lcm(a,b) ②swap(a,b)不能直接用在程序中procedure swap(a:b:integer); var t:integer;begint:=a;a:=b;b:=t;end; 注:①var n,i,x:longint;f:boolean;a:array[1..100000] of boolean;beginreadln(n);for i:=2 to n doif a[i]=false then begin{a[i]在之前没有被筛掉为质数} writeln(i);x:=i*2; {进行筛选,x初始化}while x<=n do begin{x≤n,进入循环,进行筛选}a[x]:=true;x:=x+i;end;end;{end if}end.注:hp[0]用来存储数字的位数end; end.5.全排列与组合的生成【注释①】1)排列的生成:(1..n )procedure solve(dep:integer); var i:integer; beginif dep=n+1 then begin writeln(s);exit; end; for i:=1 to n doif not used then begins:=s+chr(i+ord('0'));used:=true; solve(dep+1);s:=copy(s,1,length(s)-1); used:=false; end; end;2)组合的生成(1..n 中选取k 个数的所有方案) procedure solve(dep,pre:integer); vari:integer; beginif dep=k+1 then begin writeln(s);exit;end; for i:=1 to n doif (not used) and (i>pre) then begin s:=s+chr(i+ord('0'));used:=true; solve(dep+1,i);s:=copy(s,1,length(s)-1); used:=false; end; end;高精度计算高精度数的定义: typehp=array[0..maxlen] of integer;1.高精度加法procedure plus ( a,b:hp; var c:hp); var i,len:integer; beginfillchar(c,sizeof(c),0);if a[0]>b[0] then len:=a[0] else len:=b[0]; for i:=1 to len do begin inc(c[i],a[i]+b[i]);if c[i]>10 then begin dec(c[i],10); inc(c[i+1]); end; {进位} end;if c[len+1]>0 then inc(len); c[0]:=len;end;{plus} 2.高精度减法procedure substract(a,b:hp;var c:hp); var i,len:integer; beginfillchar(c,sizeof(c),0);if a[0]>b[0] then len:=a[0] else len:=b[0]; for i:=1 to len do begin inc(c[i],a[i]-b[i]); if c<0 then begin inc(c[i],10);dec(c[i+1]); end; while (len>1) and (c[len]=0) do dec(len); c[0]:=len; end;3.高精度乘以低精度procedure multiply(a:hp;b:longint;var c:hp); var i,len:integer; beginfillchar(c,sizeof(c),0); len:=a[0];for i:=1 to len do begin inc(c[i],a[i]*b);inc(c[i+1],(a[i]*b) div 10); c[i]:=c[i] mod 10; end;inc(len);while (c[len]>=10) do begin {处理最高位的进位} c[len+1]:=c[len] div 10; c[len]:=c[len] mod 10; inc(len); end;while (len>1) and (c[len]=0) do dec(len); {若不需进位则调整len} c[0]:=len; end;{multiply}4.高精度乘以高精度procedure high_multiply(a,b:hp; var c:hp} var i,j,len:integer; beginfillchar(c,sizeof(c),0); for i:=1 to a[0] dofor j:=1 to b[0] do begin inc(c[i+j-1],a[i]*b[j]);inc(c[i+j],c[i+j-1] div 10); c[i+j-1]:=c[i+j-1] mod 10; end;len:=a[0]+b[0]+1;while (len>1) and (c[len]=0) do dec(len); c[0]:=len; end;5.高精度除以低精度procedure devide(a:hp;b:longint; var c:hp;var d:longint);{c:=a div b; d:= a mod b} var i,len:integer; beginfillchar(c,sizeof(c),0); len:=a[0]; d:=0;for i:=len downto 1 do begin d:=d*10+a[i]; c[i]:=d div b;注:①注:①相当于d[i]:=d[i]*10+a[i],移一位接着除②function compare(d,b:hp):boolean;var i:integer;beginif d[0]>b[0] then exit(true);if d[0]<b[0] then exit(false);for i:=d[0] downto 1 dobeginif b[i]>d[i] then exit(true);if b[i]<d[i] then exit(false); end;if d[1]=b[1] then exit(true);end; 注:①此处为二分快排。
全国信息学奥林匹克联赛(NOIP2010)复赛模拟赛六重点
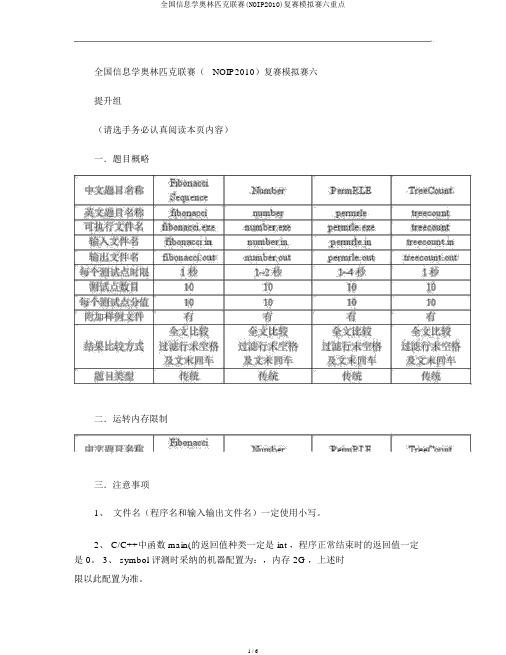
全国信息学奥林匹克联赛(NOIP2010)复赛模拟赛六提升组(请选手务必认真阅读本页内容)一.题目概略二.运转内存限制三.注意事项1、文件名(程序名和输入输出文件名)一定使用小写。
2、 C/C++中函数 main(的返回值种类一定是 int ,程序正常结束时的返回值一定是 0。
3、 symbol 评测时采纳的机器配置为:,内存 2G ,上述时限以此配置为准。
【问题描绘】f(n =f(n-1 +f(n-2 *n≥ 3, f(1 =1, f(2,=1+这就是有名的Fibonacci sequence。
现在给你两个数 x, y, 此中 x ≤y, y≤231。
-1( 你的任务就是求出∑y即Fibonacci数列第x~y项的和除以10000i=xfi mod 10000。
的余数。
【输入】第一行是一个整数T(T≤1000 ,表示有多少组数据。
接下来T行,每行两个整数 x ,y ,意义如上述。
【输出】( 输出 T 行,关于每组数据,输出∑ yi=xfi mod 10000。
【输入输出样例】【数据商定】关于 80%的数据, T=1,且 y ≤106关于 100%的数据, T≤1000,且 y ≤231-12. N umber【问题描绘】有 N(2≤N ≤15个数 a1,a2,, an-1, an,假如在这 N 个数中,有且仅有一个数能整除 m ,那么整数 m 就是一个好运数,你的任务就是在给定 a1,a2, , an-1, an 的状况下,求出第 K 小的好运数。
【输入】第一行为一整数数N ,K(2≤N ≤15, 1≤K ≤231- ,意义如上述。
接下来一行有 N 个整数, a1,a2,, an-1, an,这 N 个整数均不超出231-1 。
【输出】输出一行,仅包括一个整数ans ,表示第 K 小的好运数。
答案保证不超出1015。
【输出输出样例】【数据商定】关于 50%的数据, N ≤5,ans ≤100000关于 80%的数据, N ≤10, ans≤1015关于 100%的数据, N ≤15,ans ≤10153. P ermRLE【问题描绘】文本压缩的算法有好多种,这里给出一种叫做PermRLE 的压缩算法。
noip2010

《NOIP竞赛完善程序测试》试题班级____________ 姓名____________ 得分____________第1题(14分)以下程序是将一组整数按从小到大的顺序排列。
排序的方法是将长度为n的数a分为两个长度分别为(n div 2)与(n-n div 2)的子数组a1,a2。
然后递归调用排序过程,将a1,a2分别排序,最后将a1,a2归并成数组a。
例如a=(3,1,2,4),那么a1=(3,1),a2=(2,4)。
调用排序过程将a1,a2排序,得到a1=(1,3),a2=(2,4),然后进行合并排序。
从键盘输入数的长度n以及n个整数,存在数组a中,调用子过程sort进行排序,最后输出排序结果。
program wsh;const maxn=100;type arr:array[1..maxn] of integer;vara:array[1..maxn] of integer;n,i:integer;procedure sort(n:integer; var a:arr);vari, p1, p2, n1, n2: integer;a1,a2 :arr;beginif n = 1 then exit;fillchar(a1,sizeof(a1) ,0); fillchar(a2,sizeof(a2) ,0); n1:=0; n2:=0;n1:=n div 2; n2:=(____(1)____);for i:= 1 to n1 do a1[i]:=a[i];for i:= 1 to n2 do a2[i]:=____(2)____;____(3)____;sort(n2, a2);p1:=1; p2:=1;n:=0;while (p1 <= n1) and (____(4)____) dobeginn:=n+1;if ____(5)____then begin a[n]:=a1[p1] ;inc (p1); endelse begin ____(6)____; inc (p2) ;end;end;if p1 <= n1then for i:= ____(7)____ to n1 do begin n:=n+1;a[n]:=a1[i] endelse for i:=p2 to n2 do begin n:=n+1; a[n]:=a2[i]; end;end;beginwrite('n = '); readln (n);for i:= 1 to n do read(a[i]);readln; sort(n,a);for i:=1 to n do write(a[i],'');writeln;end.第2题(8分)有n(1≤n≤100)个同学种m(1≤n≤m≤100)种小树苗,例如:4个同学(1、2、3、4)每小时种4种树苗(A、B、C、D)的数量估算如下表所示,编程输出每人种1种苗所用的总时间最少的安排方案和所花费的时间。
NOIP初赛知识点2010(提高组)

◆ 计算机结构与组成原理 ◆ 基本的数学知识 (集合的运算、排列与组合)
◆ 计算机结构与组成原理
一、计算机发展及应用
1、第一台电子计算机的诞生: ENIAC
1946年,世界上第一台数字式电于计算机是由美固宾夕法尼亚大学的物理 学家约翰·莫克利(John Mauchly)和工程师普雷斯伯·埃克特 (J.hesper.Eckert)领导研制的取名为ENIAC(Elecotmnic Nurnerical Integrator And Calculator)的计算杌。
)存储器 (NOIP7) D)高速缓冲
C)可擦除可编程只读
4、下面哪个部件对于个人桌面电脑的正常运行不是必需的( )。NOIP10 A.CPU B. 图形卡(显卡) C. 光驱 D. 主板 E. 内存 5、用静电吸附墨粉后转移到纸张上,是哪种输出设备的工作方式( )。NOIP10 A.针式打印机 B. 喷墨打印机 C. 激光打印机 D. 笔式绘图仪 E. 喷墨绘 图仪 6、下列哪个(些)不是计算机的存储设备( )。NOIP10 A.文件管理器 B. 内存 C. 显卡 D. 硬盘 E. U盘 7 、下列说法中正确的有( )。NOIP10 A.CPU的基本功能就是执行指令。 B.CPU的主频是指CPU在1秒内完成的指令周期数,主频越快的CPU速度一定越快。 C.内部构造不同的CPU运行相同的机器语言程序,一定会产生不同的结果。 D.在一台计算机内部,一个内存地址编码对应唯一的一个内存单元。 E.数据总线的宽度决定了一次传递数据量的大小,是影响计算机性能的因素之 一。 8、彩色显示器所显示的五彩斑斓的色彩,是由哪三色混合而成的( )。NOIP10 A.红 B. 白 C. 蓝 D. 绿 E. 橙 9、下列哪个(些)是64位处理器( )。NOIP10 A. Intel Itanium B. Intel Pentium III C. AMD Athlon64 D. AMD Opteron E. IBM Power 5 C,C,C,ADE,ACD,ACDE
(2021年整理)NOIP2010集训小资料

NOIP2010集训小资料编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(NOIP2010集训小资料)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为NOIP2010集训小资料的全部内容。
NOIP2010集训小资料目录1.最短路floyed2.矩阵乘法3.并查集4。
空间的计算5.快速幂6.位运算7。
卡特兰数8.各类背包问题分析9.循环小数转分数10.Fibonacci数列11.反约瑟夫问题12.拓扑排序13.最短路SPFA14。
字典序法生成排列15最小生成树Kruskal16.过程fillchar的使用技巧17。
move函数的用法18。
中缀转后缀19.后缀转中缀20。
关键路径21。
求最大公约数(欧几里德算法)做题心得算法精华1。
最短路floyedFor k:=1 to n doFor i:=1 to n doIf i<〉j thenFor j:=1 to n doIf (j〈>i) and (j〈>k) thenIf map[i,j]>map[I,k]+map[j,k] thenMap[I ,j ]:=map[I,k]+map[k,j];注意:中间值k 必须放在最外层循环。
2.矩阵乘法.),(),(..),1()1,(......)1,(),(....)1,1()1,(A :......::......:),(),1(..),1()1,1(......)1,b (),1(....)1,1()1,1(A ),(B ..........)1,(:..........::..........:),1(..........)1,1()b ,a (..........)1,a (:..........::...........:)b ,1(..........)1,1(c b B b a A c B a A b B b a A B a c b B b A c B A B b A B c b b B c B B A A A A ⨯+⨯⨯++⨯⨯+⨯⨯++⨯=⨯∑=⨯=b 1],[],[],[k j k B k i A j i C矩阵乘法主要应用于求n 值较大的递推关系,难点在于构造矩阵。
NOIP10(pty)
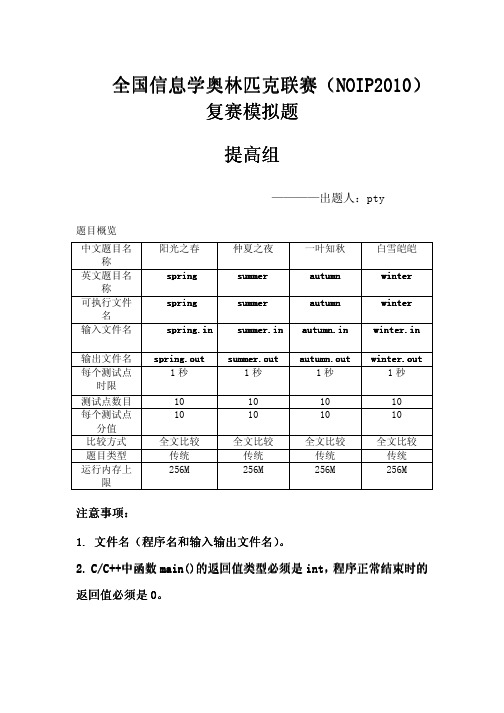
全国信息学奥林匹克联赛全国信息学奥林匹克联赛((NOIP2010NOIP2010))复赛模拟题复赛模拟题提高组提高组————出题人:pty题目概览 中文题目名称 阳光之春 仲夏之夜 一叶知秋 白雪皑皑 英文题目名称 spring spring summer summer autumn autumn winter winter 可执行文件名 spring spring summer summer autumn autumn winter winter 输入文件名 spring spring..in in s ummer ummer.in .in .in autumn autumn.in .in .in w inter inter.in .in .in 输出文件名 spring spring.out .out .out s ummer ummer.out .out .outa utumn utumn.out .out .out winter winter.out .out .out 每个测试点时限 1秒1秒1秒1秒测试点数目 10 10 10 10 每个测试点分值 10 10 10 10 比较方式 全文比较 全文比较 全文比较 全文比较 题目类型 传统 传统 传统 传统 运行内存上限256M256M256M256M注意事项注意事项::1. 1. 文件名文件名文件名((程序名和输入输出文件名程序名和输入输出文件名)。
)。
C/C++2. C/C++中函数中函数main()main()的返回值类型必须是的返回值类型必须是int int,,程序正常结束时的返回值必须是0。
1、阳光之春阳光之春spring.pas/c/cpp).pas/c/cpp)(spring.pas/c/cpp)【问题描述】春天静悄悄地来了。
HJ站在窗前,欣赏着这和谐的万物。
他背着手,慢步踱行,吟诵道:“春色满园关不住,一枝红杏出墙来”,好诗啊!(HJ不愧是有知识的人)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP图论相关内容1.图的存储相邻矩阵a[I,j]表示结点I到结点j的距离边集数组I,j,k 表示结点I与结点j相连接,权值为k邻接表方法一浪费空间tot[I]表示第I个结点连接边的数量a[I,j]表示第I个结点第j个连接的结点的结点序号方法二模拟链表节省空间last[点]=边记录和这个点相连的最后一条边pre[边]=边记录和同一点相连的上一条边other[边]=点记录的这条边的另一个点建图readln(x,y);inc(e);pre[e]:=last[x];last[x]:=e;other[e]:=y;2.图的遍历DFSProcedure dfs(x:longint);BeginBool[x]:=true;For I:=1 to n doIf I未被访问 and 与I连接 then dfs(i); End;BeginFor I:=1 to n doIf bool[I]=false then dfs(i);End;BFSProcedure (x:longint);Var I,l,r,j:longint;BeginL:=0;r:=1;Bool[x]:=true;Q[r]:=x;While l>r doBeginInc(l);I:=q[l];For j:=1 to n doIf (a[I,j]=1) and (bool[j]=false) then Begin inc(r);q[r]:=j;bool[j]:=true; end; End;End;3.传递闭包for k:=1 to n dofor I:=1 to n dofor j:=1 to n dof[I,j]=f[I,j] or (f[I,k] and f[k,j]);4.最短路径floyed O(N^3)多源最短路径(多源最长路径)当计算最短路径时,要求图中不能有负权回路当计算最长路径时,要求图中不能有正权回路f[I,j]表示i到j的最短路径for k:=1 to n dofor I:=1 to n dofor j:=1 to n do最短路径 f[I,j]=min(f[I,j],f[I,k]+f[k,j]); 最长路径 f[I,j]=max(f[I,j],f[I,k]+f [k,j]);Dijkstra O(N^2)单源最短路径运用松弛技术,逐步更新两结点的距离,图中不能有负权fillchar(bool,sizeof(bool),false);f[1]=0 f[I]=+oo (1<I<=n)for I:=1 to n domin:=+oo;for j:=1 to n doif (not(bool[j])) and (f[j]<min) thenbegin min:=f[j];q:=j; end;bool[q]:=true;for j:=1 to n doif (not(bool[j])) and (f[j]<f[q]+dis[q,j]) then f[j]:=f[q]+dis[q,j] end;writeln(f[x]);end.Bellman-ford O(NM)单源最最路径运用松弛计数,可以计算负权,逐步更新两点的距离For i:=1 to m doReadln(e[i].a,e[i].r,e[i].w); //边集数组输入F[1]:=0; f[i]:=+oo; (1<I<=n)For i:=1 to n-1 dochange:=false;for j:=1 to m dobeginif f[e[j].a]+e[j].w<f[e[j].b] thenf[e[j].b]:=f[e[j].a]+e[j].w;change:=true;end;if not(change) then break;end;writeln(f[k]);end.SPFA单源最短路Bellman-ford 的队列实现方式,SPFA采用邻接表的数据结构Tot[i]表示第i个结点相邻的结点数F[i]表示结点1到i的最短距离map[I,j]表示i结点第j个结点的序号Que[i]当前队列F[0]:=0;F[i]:=+oo;L:=0;r:=1;Que[r]:=1;while l<r dobegininc(l);q:=que[l];for i:=1 to tot[q] doif a[q,map[q,i]]+f[q]<f[map[q,i]] then begininc(r);f[map[q,i]]:=a[q,map[q,i]]+f[q];que[r]:=map[q,i];end;end;writeln(f[x]);end;5.最小生成树(MST)Kruskal o(eloge) 适合于边稀疏贪心+快速排序+并查集Kuai(1,tot) 升序排列For i:=1 to tot doBeginX:=find(e[i].l); y:=find(e[i].r); If x<>y thenBeginSum:=sum+e[i].w;S[x]:=y;Inc(t);If t=n-1 then break;End;End;Prim o(n^2) 适合于点密集Cost[i]表示结点i到集合的距离Index[i]表示第i个点连接的点每次扩展距离集合最短的结点For i:=1 to n doBeginCost[i]:=a[1,i];Index[i]:=1;End;For i:=1 to n-1 doBeginMin:=+oo;For j:=1 to n doIf (cost[j]<min) and (cost[j]<>0) then BeginMin:=cost[j];K:=j;End;Cost[k]:=0;For j:=1 to n doIf a[k,j]<cost[j] thenBeginCost[j]:=a[k,j];Index[j]:=k;End;End;For i:=2 to n doMax:=max+a[I,index[i]];Writeln(max);End.6.并查集①返回集合跟结点function find(x:longint):longint; beginif x=s[x] then exit(s[x]) else begins[x]:=fins(s[x]);exit(s[x]);end;end;②合并procedure bing(a,b:longint);var v1,v2:longint;beginv1:=find(a); v2:=find(b);if v1<>v2 then s[v1]:=v2;end;③查询集合个数(hash)for i:=1 to n doif bool[find(i)]=false then begin bool[find(i)]:=true;inc(tot); end;7.二分图匹配function dfs(a:longint):longint;var i:longint;beginfor i:=1 to n doif bool[i]=false thenbeginbool[i]:=true;if (seat[i]=0) and (dfs(seat[i])=1) then beginseat[i]=a;exit(1);end;end;exit(0);end.For i:=1 to n doBeginFillchar(bool,sizeof(bool),false);Dfs(i);End;NOIP树相关内容1.树的遍历procedure bian(x:longint);var i:longint;beginfor I:=1 to n doif 未被访问 and i是x的儿子 then bian(i); 访问处理(i);end;2. 二叉树树的存储一般存储方法Const m=树的结点数TypeNode=recordData:datatypeL,r,f:0..m; 左儿子,右儿子,父亲结点End;Treetype=array[1..m] of node;var tree:treetype特殊存储完全二叉树父节点I 左儿子2*I 右儿子 2*I+1 由于以上二叉树性质,完全二叉树可以由线性数组存储(堆)3.二叉树的遍历前序遍历Procedure preorder(i:longint);BeginIf bool[i]=true thenBegin访问处理 a[i].dataPreorder(a[i].l);Preorder(a[i].r);End;End;中序遍历Procedure inorder(i:longint);BeginIf bool[i]=true thenBeginInorder(a[i].l);访问处理 a[i].dataInorder(a[i].r);End;End;后序遍历Procedure postorder(i:longint); BeginIf bool[i]=true thenBeginPostorder(a[i].l);Postorder(a[i].r);访问处理a[i].dataEnd;End;中序遍历+后序遍历求前序遍历vars1,s2:string;procedure try(s3,s4:string);var p,i:longint;beginif length(s3)=0 then exit;if length(s3)=1 then begin write(s3);exit; end; p:=length(s4);write(s4[p]);i:=pos(s4[p],s3);try(copy(s3,1,i-1),copy(s4,1,i-1));try(copy(s3,i+1,p-i),copy(s4,i,p-i));end;beginreadln(s1);readln(s2);try(s1,s2);end.4. 森林与多叉树转2叉树处理 O(n)左儿子,右兄弟原则Ft[i]表示i是否有孩子A[i].right\a[i].left 表示i结点的左儿子、右儿子Num[i]表示i结点的最后一个儿子的结点号readln(n,m);for i:=1 to n dobeginreadln(x,y); //x表示x是i的父亲,y为数据 if ft[x]=false thenbegina[x].left:=i;num[x]:=i;ft[x]:=true;endelsebegina[num[x]].right:=i;num[x]:=i;end;a[i].data:=y;end;5.堆堆排序O(nlogn)procedure down(i:longint);var j:longint;beginj:=i*2;while j<=ed dobeginif (j<ed) and (a[j+1]>a[j]) then inc(j); if a[j]>a[i] thenbeginswap(i,j);i:=j;j:=i*2;endelse j:=maxlongint;end;end;建堆for i:=ed div 2 downto 1 do堆排序建堆后,最上面即为最值(max或min),和堆中最和一个元素交换,down(1)维护堆性质6.求树的直径 O(n)从任意一点出发,搜索到的最远点,则这个最远点必定在数的直径上,再从最远点搜索一次它的最远点既为树的直径typetxt=recorddata:char;f,l,r:longint;end;var a:array[0..1000] of txt;t:array[-1..1000] of boolean;i,j,n,max,node,m:longint;procedure dfs(x,l:longint);beginif l>max then begin max:=l;node:=x; end; t[x]:=false;if t[a[x].f] then dfs(a[x].f,l+1);if t[a[x].l] then dfs(a[x].l,l+1);if t[a[x].r] then dfs(a[x].r,l+1);end;beginreadln(m);read(a[1].data);a[1].f:=-1;a[1].r:=3;a[1].l:=2;for i:=2 to m dobeginread(a[i].data);a[i].f:=i div 2;if i*2<=m then a[i].l:=i*2;if i*2+1<=m then a[i].r:=i*2+1; end;max:=0;fillchar(t,sizeof(t),false);for i:=1 to m dot[i]:=true;dfs(1,0);max:=0;fillchar(t,sizeof(t),false);for i:=1 to m dot[i]:=true;dfs(node,0);writeln(max);end.7. 线段树typenode=recordp,r,m:longint; //[p,r) m = (p+r) div 2 k:longint;left,right:longint;end;vara:array[0..1000000] of node;data:array[0..1000000] of longint;i,j,n,m,tot,x,y,p,c:longint;function min(a,b:longint):longint;beginif a>b then exit(b) else exit(a);end;procedure buildtree(t:longint); beginif a[t].p+1=a[t].r thenbegina[t].k:=data[a[t].p];exit;end;a[t].m:=(a[t].p+a[t].r) div 2; //leftinc(tot);a[t].left:=tot;a[tot].p:=a[t].p;a[tot].r:=a[t].m;buildtree(tot);//rightinc(tot);a[t].right:=tot;a[tot].p:=a[t].m;a[tot].r:=a[t].r;buildtree(tot);a[t].k:=min(a[a[t].left].k,a[a[t].right].k);end;procedure change(t,i,v:longint);beginif a[t].p+1=a[t].r thenbegina[t].k:=v;data[i]:=v;exit;end;if i<a[t].m then change(a[t].left,i,v) else change(a[t].right,i,v); a[t].k:=min(a[a[t].left].k,a[a[t].right].k);end;function answer(t,x,y:longint):longint;beginif (a[t].p=x) and (a[t].r=y) then exit(a[t].k);if (y<=a[t].m) then exit(answer(a[t].left,x,y)) elseif (x>=a[t].m) then exit(answer(a[t].right,x,y)) elseexit(min(answer(a[t].left,x,a[t].m),answer(a[t].right,a[t].m,y))); end;beginreadln(n,m);for i:=1 to n doread(data[i]);tot:=1;a[tot].p:=1;a[tot].r:=n+1;buildtree(1);for i:=1 to m dobeginreadln(c,x,y);if c=1 thenwrite(answer(1,x,y+1),' ')else change(1,x,y);end;writeln;end.NOIP排序相关内容1.选择排序 o(n^2)for i:=1 to n-1 dofor j:=i+1 to n doif a[i]>a[j] then swap(i,j);2.快速排序procedure quick-sort(l,r:longint);var i,j,k,t:longint;begini:=l;j:=r;k:=a[(i+j) div 2];repeatwhile a[i]<k do inc(i);while a[j]>k do dec(j);if i<j thenbeginswap(i,j);inc(i);dec(j);end;until i>j;if i<r then quick-sort(i,r); if l<j then quick-sort(l,j); end.3.记数排序readln(n);for i:=1 to n dobeginread(a);inc(c[a]);if a>max then max:=a;end;for i:=1 to max doif c[i]<>0 thenfor j:=1 to c[i] dowrite(i,' ');4.堆排序procedure down(i:longint);var j:longint;beginj:=i*2;while j<=ed dobeginif (j<ed) and (a[j+1]>a[j]) then inc(j); if a[j]>a[i] thenbeginswap(i,j);i:=j;j:=i*2;endelse j:=maxlongint;end;end;建堆for i:=ed div 2 downto 1 doNOIP基本数论相关内容1.求最大公约数、最小公倍数function gcd(a,b:longint):longint;beginif b=0 then gcd:=a else gcd:=gcd(b,a mod b);end;function lcm(g:longint):longint;beginlcm:=a*b div g;end;2.2分法求解方程的近似解2分法确定方程近似解①确定区间[a,b],验证f(a)*f(b)<0,给定精度ε② c=(a+b)/2③ if f(c)=0 then writeln(c);if f(c)*f(a)<0 then b=c;if f(c)*f(b)<0 then a=c;④if abs(a-b)<ε then writeln((a+b) div 2);牛顿迭代法求平方根f(x)=x^2-a x^2的导数是2x,根据斜率,求得表达式 (x+a/x)/2=x0 重复迭代即可( 4 + 2/ 4 ) / 2 = 2.25 4为x的初值( 2.25 + 2/ 2.25) / 2 = 1.56944..( 1.56944..+ 2/1.56944..) / 2 = 1.42189..( 1.42189..+ 2/1.42189..) / 2 = 1.41423..3.求素数①判断某一数字是否为素数function sushu(x:longint):boolean; var i:longint;beginif (x=1) or (x=0) then exit(false); for i:=2 to trunc(sqrt(x)) doif x mod i=0 then exit(false);exit(true);end;②筛法求1-n的素数readln(n);fillchar(a,sizeof(a),true);for i:=2 to n-1 doif a[i] thenfor j:=i+1 to n doif j mod i=0 then a[j]:=false;write(1,' ');for i:=2 to n doif a[i] then write(i,' ');4.闰年判定if (year能被4整除 and 不能被100整除) or year能被400整除then 该年为闰年else 该年为平年5.构造排列①递归构造排列procedure try(k:longint);var i:longint;beginfor i:=1 to n dobeginx[k]:=i;if c[i]=false thenif k=n then begin for j:=1 to n do write(x[j]);writeln; end elsec[i]:=true;try(k+1);c[i]:=false;end;end;end;②模拟根据当前排列求下一组排列readln(n);readln(m);for i:=1 to n doread(a[i]);repeatdec(m);p:=n-1;while a[p]>a[p+1] do dec(p); if p>0 thenbeginwhile a[q]<a[p] do dec(q); swap(q,p);x:=p+1; y:=n;while x<y dobeginswap(x,y);inc(x);dec(y);end;end;until (m=0) or (p=0);6.构造组合①递归构造procedure try(k:longint);var i:longint;beginfor i:=1 to m dobeginx[k]:=i;if place(k) thenif k=n then begin for j:=1 to n do write(x[j]);writeln; end else try(k+1);end;end;②模拟根据当前组合构造下一组合readln(n);readln(m);for i:=1 to n doread(a[i]);repeatprint;i:=n;while (i>0) and (a[i]=m-n+i) do dec(i);if i>0 thenbegininc(a[i]);for j:=i+1 to n doa[j]:=a[j-1]+1;end;until i=0;7.进制转换①10进制转n进制(整数部分)采用“除以n倒取余法”,将十进制数除以n,记下余数……,直到商为0,最后将余数倒的输出即为所求。
