Wild ramification and a vanishing cycles formula
2020年在nature catalysis上发表重要成果

2020年在nature catalysis上发表重要成果
2020年,在《Nature Catalysis》杂志上发表了一项重要成果,该成果由某科研团队经过多年努力终于成功研发出一种新型的催化剂,能够有效地将废弃塑料转化为高附加值的产品。
这项成果的研发背景是,随着人类对塑料的依赖程度不断加深,废弃塑料的污染问题日益严重,给生态环境带来了巨大的压力。
因此,科研团队一直在寻找一种能够有效处理废弃塑料的方法。
该科研团队通过多年的研究,成功研发出这种新型催化剂。
该催化剂能够在常温常压下将废弃塑料中的聚乙烯和聚丙烯等塑料成分转化为燃料和化学品等高附加值的产品。
这种转化过程不仅能够有效处理废弃塑料,而且能够产生经济效益,具有很高的应用价值。
该成果的发表引起了广泛关注。
在《Nature Catalysis》杂志上,该论文被选为封面文章,并得到了编辑部的特别推荐。
该论文的发表不仅证明了该科研团队在催化剂研究方面的实力,也标志着人类在解决废弃塑料污染问题方面取得了重要进展。
未来,该科研团队将继续优化这种新型催化剂的制备工艺和应用范围,希望能够为解决全球废弃塑料污染问题做出更大的贡献。
同时,他们也希望通过与产业界的合作,将这种技术应用于实际生产中,为人类创造更加美好的生态环境和可持续发展未来。
贺兰山东坡直翅目昆虫群落的边缘效应英文

S tud y o n th e Ed g e Effe c t of O rth op te ra n C om m u n ity i n N i n g x ia H e la n M o u n ta i nHE H a i 2m i n g 1,Y AN G G u i 2ju n 2,HE L i 2ro n g 2,WAN G Xi n 2p u3,431.Sci e nce and Tech no l o gy Dep a rt m e nt,N i ng xi a U nivers i ty,Yi nchua n 750021;2.Schoo l o f L i fe Sc i en ce ,Yi nchua n 750021;3.Schoo l o fAg ri cu lt u re,N i n gxi a U n i ve rs it y,Yi nchua n 750021; 4.Ke y Labo ra t o ry f o r R es t o rat i o n a nd R econ s tru cti o n o f D eg raded Eco sy s t em i n No rth 2we s tern C h i na of M i n is try o f Edu ca ti o n,Yinchuan 750021Ab s t ra ct [O bject i ve]The s tudy a i m ed t o d iscus s the i nfl uen ce s o f ed ge effect on o rtho p t e ran comm un it y i n ea st s l o p e o f Helan Mo un t a i n.[M eth od ]Sam p l e s a re co l l e cted by u s i ng samp l e zo ne m e t ho d.The d i ffe ren t sp ecies o f o rt hop terans i n d i ffe ren t hab i ta ts are reco rded.[Resul t]Th e p ercen tage of O ed i po di d ae,C atan t op i dae and Pamp hg i dae i n t o t a l are 42.65%,29.15%a nd 12.76%re sp ecti ve l y .From scat t e red g ras s 2l a nd i n teri o r t o e dge and then t o des ert g ras s l an d,abun dance i n crea se i n t u rn,bu t d i ve rs it y i n the edge is the h i ghe s t .The d i vers i ty i nde x o f o r 2thop t e ran comm un i ty decrea se w i th the dis t a nce aw ay fr om edge i nc rea s i ng.The ri chne ss chang es w it h the dis t a nce aw ay fr om the edge.The re are 4t ype s o f edg e effect s i n cl ud i ng ha bitat gene ralis t,hab it a t gene ra l is t edge e xp l o it e r,hab i ta t spec i a l is t e dge exp l o i te r and h abitat s p ec i alist edge a vo i de r i n the sca ttered g ras s l an d 2d es ert gra s s l and eco t on e acco rd i ng t o Sisk a nd M arg ul e s πs crit e ri o n.[C on clus i on ]The re se arch p rov i de s da t a an d theo retical ba s i s fo r t he b i od i ve rs it y p ro tect i o n,devel opm en t a nd ut i li zati o n o f o rtho p t e ran ,and t he d evel opm en t o f co n se rva ti o n bi o l o 2gy .Key w o rds O rt hop tera;Edg e effec t ;D i vers i ty;Sca ttered gra s sland 2de se rt gra s s l and Eco sys tem ;He l an M oun ta i nR D , M ,S y M y f ,N y x T S (N T 22)32x @y The re se a rch o n the beha vi o ra l re spo nse s or se l e ct trends o f spe c i e s to ha bita t edge is ve ry i m po rta nt t o unde r 2stand the edge e ffec t [1].The re ac ti o ns t o the e dge a re va ri e d a cco rdi ng to t he bi o l o g i ca l a nd e xte rna l co nditi o ns,a nd m any othe r fa cto rs.B ec ause i n se c ts a re hi ghl y sen siti ve t o habita t cha nge s,som e i n sec ts a re use d a s environ m enta l i ndi ca 2t o rs [2,3].O rthop t e ra n i n e a st sl ope of He lan M ounta i n a re m a inl y distribu t e d in sc a tte red gra ssland and de se rt g ra ss 2l and .Through the s t udy o f e dge e ffec t fo r o rthop te ra i nse ct comm unitie s i n e a st sl ope of He l a n Mo un t a in,we discus s the diffe re nc e s am ong di ffe ren t o rthop te ran sp ec i e s t o the sam e ty p e of edge re a cti on so tha t we could ca rry ou t p reve nti o n a nd con tro l li ng wo rk rea sonab l y a nd app rop ri a te ly on the l o 2cu st,p re se rve a nd m a inta i n the e xisti ng ba l a nce of the e co 2system sta te ,a nd give ce rta in da ta a nd theo re ti c a l ba sis t o bi odive rsity con se rva ti on .E xp e ri m e n ta l S ite sR e se a rch a rea is l o ca te d in Ningxi a He l a n M ounta i n Na 2ti ona l Na ture R e se rve ,no rthwe st of N i ngxi a ,whi ch borde rs Inne r M ongoli a Autonom ous Re gi on i n we st a nd no rth,a nd sp i ns t he tem pe ra te steppe and de se rt i n the t wo vege ta ti o n re gi ons .Annua l a ve ra ge t em pe ra ture is -0.8℃,a nnua l a v 2e rage sunsh i ne i s ove r 3000h,fro st 2free pe ri od a re 128-175days,a ve rage ra i nfa l l is be t w e e n 200-400mm ,and a nnua l e vapo ra ti o n i s ove r 2000mm.S ca tt e re d gra ssl a nd a nd de se rt gra ss l and a re the i m po rtan t ve ge ta ti on i n ea s t sl ope of He l a n M oun ta i n .Sc a tte red gra ss l and is m a i nl y distri buted i n a lt .1500-2100m i n a ri d l ow 2mo un t a i n .Xe ri c shrub such a s U l 2m us g l a uce sc en s,P runu s m ongolica a nd A j a ni a fruti cul o sa a re spa rse l y dis tri buted,wh il e S ti pa ,Se t a ri a viri dis a nd A rt e 2m isi a su t d i gita ta e t a l .a re grow i ng th i ckl y .Ave rage ra infa ll is 250-300mm.De se rt gra ssland is i n a lt .1200-1500m ,a ve rage tem pe ra ture is 8℃,a ve rage ra infa ll is 200-250mm.M a ny pa rts of the bed r o ck e xpo se s,soil is infe rtil e si 2e ro zem.M a i n ve ge t a ti on type s a re S ti pa gra sse s,xe ri c a nd de se rt xe ri c sem i 2sh rubs a j a ni a.In a dditi on,fo re land p l uvi a l fan gra ss l and is i nc lude d .Re sea rch p l ots a re l o c a ted i n the geographica l coordi na te s of 105°56′-106°03′E,38°27′-39°50′N,e l e va ti o n ra nge i s 1400-1600m.It is the tran si 2ti ona l re gi on o f sc a tte red gra ssland a nd de se rt gra s sl a nd.M e th o d sE xp e ri m en ta l de s ignF i ve sam p l e zo ne s w it h t he width of 5m we re se l e c ted i n the ve rtica l dire c ti on of the edge.The inte rva l be t we e n eve ry zone w a s 10-20m ,9p l o ts we re cho sen i n e a ch zone.The a re a of the pl o t se l e c ted i n sca tt e re d g ra ss l a nd,de se rt g ra s s 2l a nd a nd edge l a nd wa s 5m ×5m.The inte rva l be t w ee n e a ch p l o t wa s 20m.S pec ifi c samp li ng prog ram is shown i n F i g.1(show i ng t w o zone s )[4-7].Samp li ng wo rks we re conduc te d be t we en June and August in 2008.Ac co rd i ng to the di ffe ren t spe c i e s a nd habita ts i n cap turing p roce ss,we u se d ne tm e th 2od,fre e 2ha nd c ap t u re and trapp i ng m e thod e tc .I nse ct spe c i 2m e ns we re b r o ught bac k to the l a b afte r the po isoning,i den ti 2fied a nd reco rde d t he spe c i e s a nd qua ntiti e s of orthop te ra n a cco rding t o the l ite ra ture m onograph [8].F x (I ;II )D y R f M f f 2Agri cu l tu ral Sc i ence &Techno l o gy,2010,11(2):113-116,145C op yright κ2010,I nf o r m at i o n I n s ti tu t e of HAAS.All ri gh ts res erved.Ani m a l S ciencee ce i ve d:ecem be r 242009Accep t e d:a rch 192010uppo rted b i n i s tr o Educa ti o n ew C en tur E ce ll en t al e n ts chem e C E 070470.C o rre spo n di n g au tho r .E m ail :w ang i npu i g.1E pe ri m en t p l o ts de s i gn :scatte red g ras s l an d :d es ert g ras s l an d a ta an a l s i sich ne ss o sp ec ies ea su rem ent o the nu m be r o sp ec i e s i n comm uniti e s,ofte n c ha ra cte rized w ith"S".S ha nno n2W ie ne r d ive rs ity inde x(H′) H′=-∑P i l nP iH′is the Sha nno n2W i e ne r di ve rsity inde x;P i is the p ro2 po rti on o f i th ta xa i ndividua l num be rs i n the t o ta l i ndi vidua l nu m be rs.S is the nu m be r o f spe c i e s i n comm un i ty.E ve nn es s ind ex(E) E=H′/l o g2(S)o r E=H′/ln(S)E is t he e venne ss i nde x i n t he form ul a.D om ina nc e Ind ex(D) B e rge r2P a rke r i nde x is adop ted.D=Nm a x/NTD is the dom i na nce i ndex i n the fo r m u l a;Nm ax i s the popula ti on of dom i na nt spe c i e s;NT is the popul a ti on of a ll ty p e spe c i e s i n comm un i ty.Com m u nity s i m ila rity ind ex S i m il a ri ty coe ffi c i e nt fo r m ula ra ised by Ja c ca rd(1901)is a dop ted:q=c/(a+b-c)I n the fo r m ula,q is t he comm unity inde x;c is the com2 mo n spec ie s i n sam p l e A and B;a is the tota l spe c i e s in sam2 pl e A;b is the t o ta l spe c i e s i n sam p l e B.Sp e c ie s ab unda nc e va lue The t o ta l num be r o f i ndi vidua l spe c i e s pe r25m2i n eve ry sam p l e i s counte d a s the abun2 dance of e ac h i nse c t.I ndi vi dua l a ve rage of fi ve p l o ts w ith a ce rta i n distance away from the edge is shown a s the sp ec i e s a bunda nce va lue[5].R e s u lts a n d A n a lys isCom p os ition o f O rthop te ran C omm un itySpe c i m e ns o f4874orthop te ra n w e re collec te d a nd i den2 ti fied a s28spe c i e s,be l o ng i ng to9fam ili e rge st num be r of i ndi vi dua ls a re O ed i p odida e,C a tan t opida e a nd P am pha gi2 dae,a ccoun ti ng fo r42.65%,29.15%a nd12.76%in to t a lo r2 t hop te ra n re spe c ti ve l y,they a re the dom i na nt sp ec i e s i n the su rve y a re a(F i g.1);Foll owe d by A rcyp te ri da e,a c counti ng fo r7.29%i n t o ta l o rthop te ran.B radyporida e,Te tri go i dae, Conocep ha l ida e,P yrgom o r p hi da e a nd Ac ri di da e a re the com2 mo n spe c i e s i n t he surve y a rea,a cco unti ng fo r1%-5%.In a ll co ll e c ted spe cie s,C a lli ptam us ba rba rus ba rba rus, C.ba r2 ba ru s,O eda leu s i nfe rna lis and O.deco rus a sia ti c us a re the dom i na nt spe cie s in the surve y a re a,a cco un ti ng fo r53.48% i n tota l.D ive rs ity of O rthop te ra n Com m u n ityThe edge of sca tte red g ra s sl a nd a nd de se rt gra ssland is the comm on e dge ha bit a t type s e xi s t e d in e a st sl op e of He l a n M oun ta i n.Acco rdi ng t o the distance awa y from edge,45re2 se a rc h p l o ts(5samp l e zo ne s,ea ch zone conta i n s9p l o ts) a re ga the re d t o three gr o up s:sca tte re d gra ssl a nd habita t (p l o ts s1t o s15)conta ins three dista nce group s(40m,60m a nd80m)de ep i n t o the sc a tte red gra s sl a nd inte ri or.D e se rt g ra ss l a nd ha bita t(p l o ts s31t o s45)co nta i n s three dista nce g r o up s(40m,60m a nd80m)de ep int o the de se rt gra ssl a nd i nte ri o r;Edge l a nd habita t(p l o ts s16t o s30)co nta i ns t he o th2 e r th re e d i s tance group s(e dge l a nd,deep i nto the sca tte re d g ra ss l a nd i nte ri o r fo r25m,de ep i nto the de se rt gra ssland in2 te ri o r fo r25m)(Ta bl e2).O rthopte ra n di ve rsity inde x i n edge l a nd is sli ghtl y h i ghe r tha n t he t w o adjac en t e co system s,a nd de se rt gra ss l and inte ri or is hi ghe r tha n sca tte re d gra ss l a nd in2 te ri o r.The re i s s i gni fi c an t diffe re nc e in H′i ndex be t we en edge l a nd a nd sca tte re d gra ssl a nd(P<0.05),but no si gni fi c an td i ffe re nce be t w ee n e dge l a nd a nd de se rt gra s sl a nd(P>0.05).B e ca use the re a re so m a ny suitab l e ha bita t fra g m e nts fo r o rt hop te ra n i n sca tte re d g ra ss l a nd,no t on l y the surviva l of l ocus ts a re re stricte d,but a lso t he sp re a d a nd distr i bu ti on of them a re li m ited,so the di ve rsity is l ow.Tre nd s of e ve nne s s E is a s foll ow s:sca tte re d gra ssl a nd>e dge l a nd>de se rt g ra ss l a nd.Tab le1 Sp eci e s com po s i t i o n in su rvey area sFam i l y S p ec i e sA mo2untP e rce n2tage∥% B radypori da e Zi chya p i ec hockii Ce j cha n250.51Zi chya a l a san i ca B2B i e nk1142.34 Conocepha li da e Conoc epha l us c hi nens i s Re dtenbac he r781.60 Te tri goi dae Fo r mosa te tti x he l a nshane nsis Zhe ng410.84P a ra t e tt ix uva r ovi S eme nov701.44 Pampha gi da e Hap l otr op i s ne i m ongol e nsis Yi n1232.52F i lchne re ll a be i cki Ramme1362.79F i lchne re ll a he l a nsha nens i s Zhe ng1022.09P se udo t m e t his bra chypte rus Li480.98P se udo t m e t his a l a sha ni cus B.2B i enko1493.06Eo t me thi s ho l ane nsis Zheng e t G ow641.31 Pyrgomo r p hi da e Atra c t omorpha s i ne nsis Bo li v a r641.31 C a t a nt opida e O xya a de nt a ta W i ll e m se721.48Ca ll i p t amus ba r ba rus ba rba rus Go sta76215.63Ca ll i p t amus ba r ba rus(Co sta)52310.73 A rcypte ri da e Cho rthi p pu s a l bonemus Che ng e t Tu2074.25Cho rthi p pu s hsi a i Cheng e t Tu1483.04 O e di p odi da e O eda l e us de corus a si a ti cu s B.B i e nk o63813.09O eda l e us i nf e r na li s Sa ussure68414.03Anga ra c ri s rhodop a(Fisc he rW a l he i m)891.83Bryodema koz l oviB.B i e nk o1643.36Bryodeme l l a ho l de re ri ho l de re ri(Kr a uss)1553.18Bryodema n i g r opte ra Zheng e t G ow1072.20Ce l e s ska l o z uboviA de l.581.19Comp so r h i p i s da vi di ana(S aus sure)1072.20Sp hi ngono t us ni ngsi a nu s Zhe ng e t G ow360.74Lep t opte rni s grac il is(Eve rsma nn)410.84 Ac ri d i da e Ac ri da c i ne re a(Thunbe rg)691.42 T o ta l4874100 Ta b l e2 D i ve rs it y index o f o rthop t e ran comm unity i n s urvey a reaR i chn es s of spec i es(S)D i ve rsity i nde x(H′)E ven nes s i ndex(E)Dom i nance i nde x(D) Scatte red g ras s l and SG16 2.16050.78320.2924 Edge l and SG2DG25 2.84350.87670.1633De se rt gras s l and D G28 2.79760.84040.2183 S i m il a rity of o rt hop te ra n i n sca tte re d gra ssl a nd,edge l a nd and de se rt g ra ss l a nd a re shown i n Table3.De se rt gra ss l and ind i ca te s a hi gh si m il a rity with edge l a nd and m iddle y Sy B f y(f f2ond com po ne nts is92.32%)(F i g.2),we fi nd t ha t the re a re g re a t di ffe rence am ong sca tte red g ra ss l a nd i n te ri o r,e dge l a nd a nd de se rt gra ssland i nte ri o r,no ove rl ap i n the so rti ng m ap,y T22 y411Ag ri cu l tu ral Sc i ence&Tech no l o gy Vo l.11,No.2,2010dis si m i la rit w ith sca tt e re d g ra ss l a nd.ca tte re d gra ssl a nd show s l o w s i m ila rit with e dge l a nd.a se d on the PCA o o rthop te ra n comm unit com po siti o n a ccum ula ted va riance contri bu ti on ra te o the irst a nd se c but de se rt gra s sl a nd is re l a tive l c l o se t o e dge l a nd.he re sult show s tha t orthop t e ra n i n de se rt gra ss l a nd ha s the t e nd e nc t o sp re a d t o sca tte re d gra s sl a nd.Ta b l e 3 The s i m il a rit y co effi cient o f o rtho p t e ran i n d i ffe ren t hab it a tsScatte red gras s l andEdge g ra s sl a nd De se rt gra s sland Scatte red g ras s l and 10.52000.4643Edge g ra ss l and 0.520010.8929De se rt gras s l and0.46430.89291F ig.2 The PCA o rd i na ti on o f O rt hop tera n comm un i t i esO rthop te ra n d ive rs ity w ith d iffe re n t d is ta nc e aw a y f rom e dgeW e compa re the d i ve rsit y o f o rthop te ran a nd the com po 2siti on o f spe c i e s with di ffe ren t dista nce awa y from edge ,the re sults a re shown i n Fig .3.The re is a te nde nc y tha t the di ve r 2sity o f o rthop te ra n comm unity de c re a se s w ith t he d i s tance a 2wa y from e dge i nc rea si ng both i n sca tte re d gra s sl a nd o r de s 2e rt gra ss l and .The d i ve rs it y of sca tte re d g ra ss l a nd 80m awa y from e dge dec rea se 0.9542com pa red w ith e dge l a nd,but the re is no s i gni fican t di ffe re nce of di ve rsity i n de se rt g ra ss 2l and w ith t he dista nce aw ay from edge inc rea si ng .Sp ec i e s com po siti o n of o rthop te ran comm un i ti e s in sc a tte red gra ssl a nd dec rea se with the dista nce awa y fr om e dge inc re a s i ng .16spe c i e s a re co ll ec te d i n sc a tte red gra s sl a nd 40m aw ay from e dge ,a ccounting fo r 57.14%i n t o ta l am oun t in survey a rea ;13sp ec i e s a re co ll e c ted i n sca tte re d gra ssland 80m awa y from e dge ,a cco un ti ng fo r 46.42%i n t o t a l am ount;Sp ec i e s com po siti o n of o rthop t e ra n comm uniti e s i n de se rt gra ssl a nd i nc rea se w ith the dista nce awa y from e dge i nc rea si ng .All spe c i e s c an be fo und i n de se rt g ra ss l a nd 40m aw ay from edge.F ig.3 Comm unity d i vers i ty and n um be r o f spec i e s o f O rthop 2teran i n d i ffe ren t edg e di a tanceE dg e e ffe c t of C om m un ityEdge effe ct of comm unity is ge ne ra l ity in eco t one e co sys 2t em.Thr o ugh the s t udy of edge e ffec t,we coul d unde rstand t he e dge i m pa c t on t he spe ci e s distri buti on pa tte rn and fo r m a ti on,f y,y,y S M [],y f ff 2de se rt g ra ss l a nd e cotone (F ig .4).Eo t m e this ho l a ne ns i s,Zi c hya p i ec hockii ,P se udot m e t his bra chy p te rus a nd Sphin 2gonotu s n i ngsi a nus be l o ng t o hab it a t spe cia list e dge avo i de r .The se ki nds of i n se c ts adap t t o d i s tri bute i n de se rt xe ri c ve ge 2ta ti on w it h e xpo sed be drock i n m a ny pa rts a nd i nfe rtil e de se rt g ra ss l a nd,no distribu ti on i n the edge of sca tt e re d gra ssland 2de se rt gra ss l and .P seudo t m e this a l a sha nicus be l ongs to ha bi 2ta t sp ec i a l ist edge e x p l o i te r,distri buti ng in de se rt gra ssl a nd a nd e dge l a nd .Zi chya a l a sa ni ca ,Co nocepha lus ch i ne ns i s,F il chne re l la be i c ki ,B ryodem a koz l ovi and B ryodem e ll a ho l 2de re ri ho l de re ri be l o ng t o hab i ta t gene ra list edge e xpl o ite r,the y a dap t t o distribu t e i n the edge shrub zone of sca tte re d g ra ss l a nd 2de se rt g ra ss l a nd .It is m o re suitable fo r the ir su rvi v 2a l beca use of the abunda nt food a nd cha nge d m ic r o 2envir o n 2m e nt i n e dge land a nd becom e the i de a l e co l o g i ca l p l a ce com 2pa red with the ha bita t i nte ri o r .For m o sa te tti x he l a nsha ne ns i s,P a ra te tti x uva rovi ,Atra ctomo rpha s i nen sis,O xya a den t a ta,Ca l li p tam u s ba rba rus ba rba ru s,C a ll i p tam u s ba rba rus,C ho r 2thi pp us a l bonem us,C ho rt h i p pu s hs i a i,O e da l e us de co rus a si 2a ti cu s,Oe da l e us infe rna lis,C e le s ska l oz ubo vi,Com p so rhi p is da vi di a na,Lep top te rnis g ra c i lis,Ac ri da cine re a ,Hap l o tr op is ne i m ongo l e nsis,Anga ra cris rhodopa and B ryodem a ni g r op 2te ra be l ong t o ha bita t gene ra list,the y d i s tri bute i n sca tte re d g ra ss l a nd 2de se rt g ra ss l a nd a nd edge land w it h e xten si ve a 2dap tab i lity .The i ndi vi dua l c an succ e ssfu ll y c ro ss the bo unda 2ri e s be t we e n fragm e nts a nd a dap t the cha nge d e nviron m en t d i ffe re nt fr om the inte rna l hab i ta t .The y rega rd t his type of ha bita t a s a ne a r 2homo ge neous w it h s m a ll envir onm e nta l c ha nge ,ha ving no si gni fica nt e ffe ct o n t he ir survi va l .B ut they do n πt show a ve ry uniform distribu ti on of adap tab i lity i n sca t 2te re d g ra s sl a nd 2de se rt g ra ss l a nd a nd e dge l a nd.W hen the d i s t a nce awa y from e dge i nc rea se s,the amo unt of Ca l li p ta 2m u s ba rba rus ba rba rus a nd C a lli p tam us ba rba rus i nc re a se i n de se rt g ra s sl a nd i ncre a se ,but de c re a se i n sca tt e re d g ra s s 2l a nd.The dis tri buti o n of O eda leu s de co ru s a si a ti c us a nd O e da leu s i nfe rna lis show oppo site trend w ith t hem.The d i s tri 2buti o n of Hap l o trop is ne i m ongo l e nsis,F il chne re lla he lan s 2hane nsis,Anga ra c ris rho dop a and B ry odem a ni grop t e ra i n sca tt e re d g ra ss l a nd is few.D is c u s s io nThe s tudy shows tha t o rt hop te ra n comm unity ha s s i gn i fi 2c ant di ffe rence s be t w e e n sca tte red g ra ss l a nd a nd de se rt g ra ss l a nd.The re a re appa re nt di ffe re nti a ti o n i n e dge land a nd sca tt e re d gra ss l a nd comm unit y com pos iti on,be i ng a m ixtu re of f o re st spe cie s and de se rt gra ss l a nd spe c i e s .Edge a nd de se rt gra s sl a nd comm unity com pos iti on a re si m il a r .B a sed on the compo siti on a ttri bute so rt of orthop te ra n comm uniti e s,orthop t e ra n i n de se rt gra ssland have the t e nd 2e nc y t o sp re a d t o the sca tte re d g ra s sl a nd .Edge e ffe ct of o rthop te ra n dec re a se s w ith the dista nce awa y from edge i ncre a si ng .Spe c i e s com po siti on of o rt hop te r 2a n comm un i ti e s in sca tte re d gra ssland de cre a se s w it h the d is 2tance aw ay fr om e dge inc re a s i ng,w hi le show i ng the oppo site trend i n de se rt gra ss l and .The re is no endem i c spe c i e s i n sca tt e re d g ra ss l a nd .The re a re 4ty p e s of e dge e ffe c ts for o rthopte ran i n sca t 2te re d gra s s 2de se rt gra ssl a nd e co t o ne.The a na l ysis of d i ffe r 2x f ff f ff x ff [35]N ff f y ,x yz ff f y T 511HE Ha i 2m i ng e t a l .Study o n the Ed ge Effect o f O rt hop t e ran Comm un it y in Ningx i a He l a n M ou nta i n t h i s w i ll provi de a theo re ti ca l ba sis o r conse rva ti on bi o l og bi odi ve rsit bi ol ogi ca l contr o l a nd i nse ct p e stm a na gem ent .Acco rdi ng t o the c rite ri on ra ised b isk a nd a rgu l e s 9the re a re 4t p e s o e dge e ec ts i n the sc a tte red gra ssl a nd e nt t a a o o rt hop te ra n to e dge e e c t shows tha t re sults romd ie re nt ta a a re di e re nt -.e vill e e t a l .po i n ted tha t ba se d on the di e rence o t h is ana l s is we m u st e nsure the ta a wh il e a na l i ng the edge e ec t o bi o l o g .he conc ep tF i g.4 4t ype s of respo n se of O rtho p t e ran t o e dge"Anca nc e li ng 2out e ffe ct"we re propose d when the y ana l yze dorde rs taxa of inse c ts [10].The study fi nds tha t suc h p he nom e 2non e xists i n P am phagida e a nd O ed i p odida e ,it i ndica te s tha t dom i na nt popul a ti on m a y de te r m i ne the em e rge nce of t h is phe nom e non.The re fore ,the study of b i o l ogy rea c ti on t ype s t o e dge e ffec t ha s g rea t sign i fi ca nce on eco sys tem re s t o ra ti o n a fte r la rge 2sca le disturba nce a nd the e col ogica l re se a rc h inc l u 2di ng t he ana lys is of bi o 2a rea trend .A t the sam e ti m e w e ca n se e tha t diffe re nt spe c i e s of gra sshoope r ha ve d i ffe re nt re a c 2ti on t o the sam e edge type ,re fl e c ti ng ha bi ta t se lec ti ve diffe r 2e nc e of gra s shoope r .R e fe re n c e s[1]HA I L A Y,H ANSKI I K,N I E M ELA J ,e t a l .Fo res try and bo real fau 2na:m atchi ng m ana gem ent w it h na t u ral f o re s t dynam i cs [J ].Ann Zoo l Fenn i ci ,1994,30:17-30.[2]EY R E MD,LO TT DA,GAR S I D E A.As se ss i ng the po t en ti a l fo r en 2v i ronm en t a l mo n i t o ri ng us i ng ground beetl e s (Co l eop t e ra:C arab i 2dae )wit h ri ve rs i de and Sco tti sh da ta[J ].Ann Zoo l Fenn i ci ,1996,33:157-163.[3]L I A N Z M (廉振民),Y U GZ (于广志).Edge effect and b i od i ve rs it y(边缘效应与生物多样性)[J ].C h i nese B i od i vers it y (生物多样性),2000,8(1):120-125.[4]L I U C M (刘缠民),L I A N Z M (廉振民).The s tudy o n d i versity o fg ra sshopp ers com m unit y i n No rth Shaanxi(陕西北部蝗虫群落多样性研究)[J ].J ou rnal of Xuzho u No r m a lU ni vers i ty (徐州师范大学学报),2001,19(2):63-65.[5]L I U C M (刘缠民),L I A N Z M (廉振民).Gras shoppe r comm unit ys truct u re o n the no rt he rn s l ope of Tai ba iM oun t a i n of Q inli ng (秦岭太白山北坡蝗虫的群落结构)[J ].Zoo l og i cal R es earch (动物学研究),2002,23(4):301-305.[6]L I A N Z M (廉振民),Y U GZ (于广志).Ana l ys i s o n t he edge re s po n 2se s of g ras shoppe rs t o the edge zone bet ween fi e l dl an d andwas tel and (农田-荒地边缘地带中蝗虫边缘反应分析)[J ].Acta Eco l o gi ca Si n i ca (生态学报),2001,21(8):1270-1277.[7]Y U X D (于晓东),LUO TH(罗天宏),ZHOU HZ (周红章),et a l .I n 2fl uence o f edge effect o n d i versity o f g r o und 2dwe l li ng be etl e s a cr o s s a fo res t 2g ras s l and eco t o ne i n Wo l o ng Na t u ral Re se rve ,S (边缘效应对卧龙自然保护区森林草地群落交错 带地表甲虫多样性的影响)[J ].Ac t a En t om o l og i ca Si n i ca (昆虫学报),2006,49(2):277-286.[8]ZHENG Z M (郑哲民),WAN LS (万力生).Gras shopp er i n N i ngxi a(宁夏蝗虫)[M ].Xi ’an:Shaanxi Norma l Unive rs i ty Pre s s (西安:陕西师范大学出版社),1993:1-147.[9]S I SK TD,MAR GULES CR.Hab i tat edge s an d re sto rati on:m e t h 2o ds fo r quantifyi ng edge effects an d p red i c ti ng the re sults of r e s t o 2ra ti o n eff o rts [M ]//SA UNDERS DA,HOBB S RJ ,EHRL I CH PR .Na t u re con serva ti o n 3-t he recon s tructi on o f fragm en t e d eco sys 2tem s .Pert h:Su rrey B eatty a nd Son s,1993:57-68.[10]NEV I L LE PJD,B LAC KDG.An i m a l s on t he edge:the can ce l i n g 2o ut effect[J ].Mem o irs o f t he M us eum of Vi ct o ri a,1997,56(2):623-630.[11]L I S M (李淑梅),MA KS (马克世),L I J P (李季平).Study o n the bi od i versit y o f so il fauna i n d i ffe rent l and use type (土地不同利用类型下土壤动物群落多样性研究)[J ].J o urna l o f Anhui Ag ri cu l tur 2al Sci ences (安徽农业科学),2008,36(2):309-310,358.[12]WA N G Y H (王玉红).S t ud i e s on p es tspec i es of Hem i p tera a nd O r 2thop teran on fruit trees i n Q i nhuangd ao area (秦皇岛地区半翅目、直翅目果树害虫种类研究)[J ].Heb ei Fruits (河北果树),2009(6):6.[13]TENG Z Q (滕兆乾),L I N YZ (林育真),WANG Y W (王裕文).Studi e s o n comm un i ty d i ve rs it y of O rt hop teran s i n J i nan (济南市郊直翅目(O rt hop tera )昆虫群落多样性研究)[J ].Ludo ng Un i versit y J ou rna l (鲁东大学学报):Na t u ral Sci ence Ed i ti on (自然科学版),2003,19(1):35-40.[14]XI E GL (谢广林),WAN G W K (王文凯).A p reli m inary study onO rthop t e ra i n Houhe N ati ona l Na t u re R es erve (后河国家自然保护区直翅目昆虫初步研究)[J ].J ou rnal o f Yangtze Un i ve rs it y (长江大学学报):Na t u ral Sci ence Ed i ti o n (自科版),2006,3(1):110-112.[15]ZHEN G Z M (郑哲民),ZHONG Y L (钟玉林).Three new s p eci e so f O rthop t e ra fr om Hube i P r o vi nce (湖北省直翅目三新种(直翅目))[J ].En t om o t a xonom i a (昆虫分类学报),2005,27(4):249-256.[16]ZHENG Z M (郑哲民),L IM (李敏),W EIXJ (魏秀娟).A new spe 2ci es of the genu s cho rthi ppu s fi ebe r fr om Q i nli ng Mou ntai n Area (O rt hop t e ra:A rcyp te ri dae)(秦岭地区雏蝗属1新种记述(直翅目:网翅蝗科))[J ].J o urna l o f Huazhong Ag ri cult u ral Un i versit y (华中农业大学学报),,(3)66R Z NG 2 R YI N 2 R f WU X 2y (下转第5页)611Ag ri cu l tu ral Sc i ence &Tech no l o gy Vo l .11,No.2,2010ou thwes t C hi na -200928:28-29.es p o n s i b le e d it o r:HA C a i l i e s p o n s ib le t ra n s la to r:J i a n l i e s p o n s ib l e p ro o rea d e r:iao an14Ne t B e an s I D E5.0wa s deve l opm en t langua ge.The co rre 2spo nd i ng re tri e va l sys tem a i m i ng a t c rop p e sts w a s c re a te d a nd com pa re d w it h tra diti ona l se a rch e ngine (Ta bl e 1).The first 20e ffec ti ve info r m a ti on we re a dopte d .Ta b l e 1 Com pa rison o f re trieval sys tem p e rf o rm ance %D i s eas es and i n se ct p es ts Goo g l e B a i du Yahoo C I S B acte ri a l s talk r o t30352560Dac t y l ispa se ti fe ra (chap uis )30453570R ou nd spo t35352565He l o tr o pha l euco s ti gm a l aw is40553060 AC I S ga ve the fu l l con si de ra ti ons t o u se r re quirem e nt a ndit wa s cons truc te d on the ba s is of g ramm a r,sem a ntic a ndpragm a ti c.The re tri e va l e nvi ronm e nt and ta rge t w e re unde r 2st ood t o som e e xt e nt,the refo re ,the required i nfo r m a ti o n could be found mo re a cc ura te.C o n c lu s io n sThe com p re he ns i ve i nfo r m a ti on t heo ry is sta rti ng sta ge inCh i na a nd fo re i gn co un tri e s,whil e di ffi cu l ty is the comp lex conve rs i o n p roce ss fr om i nf o r m a ti on t o know l e dge a nd from know l edge t o i n te lli ge nce ,be side s;the re i s no unive rsa l prin 2c i p l e a l go rith m w ith str o ng m a ne uve rability t o suppo rt .S tud 2yi ng conve rsi o n a l go ri thm o f i nf o r m a ti on,know l e dge a nd inte l 2li gence by re fe rri ng da ta m i ni ng a nd re la ted tec hno l ogy of know l edge d iscove ry w ill becom e a re sea rch focu s .R e fe re n c e s[1]WANG SQ (王世耆).R evi ew o f i nforma ti on t echno l o gy app li ca ti oni n agri cult u re (信息技术农业应用述评)[J ].C om pu t e r and Agri cul 2t u re (计算机与农业),1996(3):1-5.[2]ZH ONG YX(钟义信).Pri nci p l es o f i nf o r m ati on sc i ence (信息科学原理)[M ].3r ded (第3版).B eij i n g:B e i ji ng Un i versit y of Po s ts and Tel e comm un i cati on s Pre ss (北京:北京邮电大学出版社),2002:45-48.[3]H AN J W ,K A MBER M.Da t a m ini ng co ncep ts and t echn i que s[M ].San Ma t eo ,CA:Mo rgan Kauf mm an Publi s hers,2000.[4]DUB O I S D,PRADE H .Fuzzy se ts and s ystem s (t h eo ry an d app l i 2ca ti o n)[M ].O xf o rd,U K :Academ i c Pre ss ,1980.R es p o n s i b le e d it o r:C HEN Xiu 2ch e n R es p o n s ib le t ran s la to r:L I Zh u 2le R e s p o n s ib l e p ro o fread er:WU Xiao 2y an基于全信息理论的农业信息检索系统吴启明3 (河池学院,广西宜州546300)摘要 通过分析语法、语义、语用信息,建立了基于全信息的农业信息检索系统AC IS 。
英文文献翻译

铅污染土壤的生物修复实验室进行了利用培养好的白腐菌和秸秆对被铅污染的土壤进行生物修复模拟。
监测了土壤的pH值,铅浓度,土壤微生物,微生物代谢商,微生物商和微生物生物量C和N的比值。
以上指标用来学习土壤中铅的强度和微生物在生物修复过程中的影响。
研究表明被施以白腐菌和秸秆的土壤含有更低的可溶性交换铅,更低的生物商和生物量C和N的比值(0 mg /kg 干土,1.9 mg CH2-C,生物量C 和4.9 在60天时),和更高的微生物生物量和微生物代谢商(2258 mg /kg 干土和7.86% 在第60天)。
另外,在logistic 等式中的动力参数是用BIOLOG数据进行计算。
对动力参数进行分析后,就能得到一些微生物群的微生物量的信息。
所有数据显示含铅土壤的生物利用度被减少,这样潜在铅的强度被缓解,并且土壤微生物影响和微生物群的微生物量有所提高。
1.简介土壤中的重金属是最常见的环境污染。
铅被认定是所有重金属中危害最为严重的。
铅污染的主要来源是采矿、冶炼、含铅汽油、污水污泥、废弃电池以及其他含铅产品。
这些种类繁多的铅来源导致土壤中含铅量偏高。
Linet al的报道指出在瑞典Falun西南部大量工厂废物聚集地,土壤含铅量超1000 mg /kg。
Buatier et al.指出在法国一个污染地,地表铅浓度达到460–2670 mg/kg。
铅的毒性和生物利用度受土壤pH、氧化还原和铅种类的影响。
土壤中的含铅化合物主要通过可交换物、碳酸盐类、Fe/Mn 氧化物有机物和残留态流失。
可溶性可交换状态铅的最大危害是铅非常容易浸入地下水,地表以及农作物。
然而铅在有机物和残留状态却无害,这是由于有机健的强度和硫化物,特别是在重污染土壤中。
因此,相对其他状态下的铅,铅在可溶状态时对环境,生态和人类更加有害。
这样怎样减小土壤中铅变为可溶状态是值得关注的。
相比传统的物理化学方法,生物修复是一种既不会加剧其他污染又能有效修复污染甚至还原土壤原先状态的技术。
英文文献翻译

十溴联苯醚与四溴双酚A的复合物对土壤微生物和酶活性的毒性效应研究张卫,陈磊,安帅, 刘怐,林匡飞,赵丽摘要: 十溴联苯醚和四溴双酚A是生态垃圾回收站点中主要的污染物,并且他们潜在的毒性效应已经引起广泛的关注。
然而,这两种物质的复合物对土壤可培养微生物种群以及酶活性的影响仍然是未知的。
因此,本文首次通过实验室孵化试验,将未污染的土壤样本与受土壤污染的样本在十溴联苯醚和四溴双酚A的复合作用下产生的毒理学效应进行对照。
结果证明,毒理学效应的产生是由于土壤长期暴露在一种或两种污染物中。
微生物种群的抑制率随着培养时间延长和污染物浓度增大而逐渐增大,并且表现出明显的剂量和时间效应关系。
反应灵敏度排序依次为:真菌 >细菌>放线菌。
这两种化学物质对土壤酶的影响达到峰值7天,这与对照组的观察有着显著的差异(P < 0.01)。
对于这两种化学物质,脲酶比过氧化氢酶和蔗糖酶更敏感。
一般来说,这两种污染物的复合作用对土壤微生物、过氧化氢酶或蔗糖酶的活性产生相反的效果。
然而,对于脲酶的活性, 四溴双酚A的影响占主导地位。
这样的观察结果为解决溴化火焰阻燃剂对生态环境的潜在污染提供了有用的信息。
关键词:十溴联苯醚;四溴双酚A;土壤微生物;土壤酶;复合效应1.引言随着各种电器、电子设备的不断更新换代,电子垃圾的产生速度也越来越快,或者由于科学技术的快速和持续的改善,他们都将被更好的电子设备替代,更多的电子垃圾将被处理。
据估计,全球50%-80%的电子垃圾通过合法或非法的途径被输送到亚洲,其中90%的被运往中国。
然而,由于缺乏有效的回收技术和足够的设备处理大量的电子垃圾,在中国,许多的电子垃圾回收站点的土壤受到严重的污染。
大约75%的商用溴化火焰阻燃剂目前正用于全球范围生产耐火电子设备。
十溴联苯醚和四溴双酚A是溴化阻燃剂的主要成分,他们主要存在于预警雷达附近的土壤和沉积物中。
此外,从中国南部的东江河核心处收集的浓度分别从3.8到230ng/g蒸馏水的第15层表面沉积物及浓度从30到5700ng/g蒸馏水的第二层表面沉积物样品中都发现了四溴双酚A和十溴联苯醚。
法国Carbios公司生物回收技术取得进展

43T echnological Innovation了一种以海藻为原材料的吸管制作技术,它看上去和塑料很像,但却是可食用的。
同时,制造商很容易在这种材料中添加香料和营养物质,使得这种吸管的口感更好,对健康也更有益。
来自纽约帕森设计学院的切尔西-布里甘地是一名环保爱好者,她早在大学时期就发明了一种可以食用的杯子,这些利用生物可降解材料制作的杯子可以大大缓解一次性塑料制品带来的污染问题。
陶氏在印推完全可回收聚乙烯包装解决方案陶氏化学公司旗下陶氏包装与特种塑料事业部开发出创新的聚乙烯(PE)树脂配方,为印度带来一种新型、可持续、全PE 复合软包装的解决方案。
目前的软包装解决方案是不同的聚合物和添加剂的多层结构,它们在回收过程中不相容,需要复杂的过程分解。
陶氏的革命性全PE 复合软包装解决方案,在不影响美感、品牌认知和性能的同时,能够让包装在用完之后实现100%可回收。
陶氏包装与特种塑料业务部亚太区商务副总裁李明壮(Bambang Candra)表示:“陶氏鼓励负责任地生产、处理和回收塑料,我们新推出的全PE 复合软包装解决方案支持完全回收,旨在解决印度的软塑料垃圾管理问题。
我们对这款新产品感到非常兴奋,而且将与当地品牌商紧密合作,利用我们的新解决方案帮助他们通过减少使用多聚合物塑料,从而满足法规要求,和保护环境。
”神奇水解酶专“吃”塑料从中科院天津工业生物技术研究所传来最新信息,一种专门用于分解PET 塑料的水解酶研究取得重要突破,未来将据此培育出专“吃”PET 塑料的新酶种,通过生物降解方法帮助解决日益严重的塑料垃圾污染问题。
该研究成果已发表在最新一期《自然·通讯》杂志。
PET 全称“聚对苯二甲酸乙二酯”,是以石油为原料的常见化工材料,广泛用于生产食品容器和电子产品,PET 塑料已占全球聚合物总量18%,废弃后在自然界中极难降解,是白色污染的重要来源。
长久以来科学界一直在寻找有效的PET 生物降解方法。
采用锰矿从水溶液中吸附铅和镉离子(英文)

采用锰矿从水溶液中吸附铅和镉离子(英文)
Aylin S NMEZAY;M.SALIM NCEL;Nihal BEKTAS
【期刊名称】《中国有色金属学报:英文版》
【年(卷),期】2012(022)012
【摘要】采用低成本的本地可得的天然锰矿作为吸附剂,研究吸附工艺从水溶液中脱除铅离子和镉离子。
利用伪一级、伪二级动力学和颗粒内扩散模型检验动力学吸附数据,计算和比较这些动力学模型的吸附速率常数,发现用伪二级动力学模型能最佳地描述吸附动力学。
将 Langmuir 和 Freundlich 等温吸附模型用来拟合不同温度下的平衡数据,发现实验数据与 Langmuir 模型拟合得更好。
采用 Langmuir 等温吸附模型计算出锰矿吸附铅离子和镉离子的最大容量分别为 98 和 6.8 mg/g。
计算了热力学参数,如吸附吉布斯自由能的变化、焓变与熵变。
结果表明,锰矿作为吸附剂对铅和镉的吸附反应是自发的吸热反应。
因此,锰矿作为一种天然的矿物吸附剂,可以替代现有的吸附剂来脱除水溶液中的铅离子和镉离子。
【总页数】9页(P3131-3139)
【作者】Aylin S NMEZAY;M.SALIM NCEL;Nihal BEKTAS
【作者单位】
Gebze;Institute;of;Technology,;Department;of;Environmental;Engineering,;4 1400;Gebze,;Turkey
【正文语种】中文
【中图分类】TG146
因版权原因,仅展示原文概要,查看原文内容请购买。
环境工程专业英语文献中英双语版

Treatment of geothermal waters for production ofindustrial, agricultural or drinking waterDarrell L. Gallup ∗Chevron Corporation, Energy Technology Company, 3901 Briarpark Dr., Houston, Texas 77042, USAReceived 14 March 2007; accepted 16 July 2007Available online 12 September 2007AbstractA conceptual study has been carried out to convert geothermal water and condensate into a valuable industrial, agricultural or drinking water resource. Laboratory and field pilot test studies were used for the conceptual designs and preliminary cost estimates, referred to treatment facilities handling 750 kg/s of geothermal water and 350 kg/s of steam condensate. The experiments demonstrated that industrial, agricultural and drinking water standards could probably be met by adopting certain operating conditions. Six different treatments were examined. Unit processes for geothermal water/condensate treatment include desilication of the waters to produce marketable minerals, removal of dissolved solids by reverse osmosis or evaporation, removal of arsenic by oxidation/precipitation, and removal of boron by various methods including ion exchange. The total project cost estimates, with an accuracy of approximately ±25%, ranged from US$ 10 to 78 million in capital cost, with an operation and maintenance (or product) cost ranging from US$ 0.15 to 2.73m−3 of treated water.© 2007 CNR. Published by Elsevier Ltd. All rights reserved. Keywords:Geothermal water treatment; Water resources; Desilication; Arsenic; Boron1. IntroductionWith the world entering an age of water shortages and arid farming land, it is increasingly important that we find ways of recycling wastewater. The oil, gas and geothermal industries, for example, extract massive amounts of brine and water from the subsurface, most of which are injected back into underground formations. Holistic approaches to water management are being adopted ever more frequently, and produced water is now being considered as a potential resource. In the oil and gas arena, attempts have been made to convert produced water for drinking supply or other reuses (Doran et al., 1998). Turning oilfield-produced water into a valuable resource entails an understanding of the environmental and economic implications, and of the techniques required to remove dissolved organic and inorganic components from the waters. Treatments of geothermal water and condensate for beneficial use, on the other hand, involve the removal of inorganic components only.We have explored the technical and economic feasibility of reusingwaters and steam condensates from existing and future geothermal power plants. Produced geothermal fluids, especially in arid climates, should be viewed as valuable resources for industry and agriculture, as well as for drinking water supplies. This paper presents the results of laboratory and field pilot studies designed to convert geothermal-produced fluids into beneficially usable water. The preliminary economics of several water treatment strategies are also provided.2. Design layoutThe layout for the treatment strategies (units of operation) have been designed specifically for a nominal 50Mwe geothermal power plant located in an arid climate of the western hemisphere, hereafter referred to as the test plant. The average concentration of constituents in the produced water is shown in Table 1. The amount of spent water from the test flashplant is ∼750 kg/s. The potential amount of steam condensate that could be produced at the plant is ∼350 kg/s. Table 1includes the compositionof the steam condensate derived from well tests. The six treatment cases considered in the study are given in Table 2, together with product flows and unit operations of treatment. Fig. 1 provides simplified schematic layouts of the unit operations for each case.3. Evaluation of treatment optionsIn this section the various operations considered for each case are described.3.1. Arsenic removalT he techniques considered viable for removing traces of arsenic (As) from condensate or from water are ozone oxidation followed by iron co-precipitation or catalyzed photo-oxidation processes (Khoe et al., 1997). Other processes for extracting As from geothermal waters (e.g. Rothbaum and Anderton, 1975; Umeno and Iwanaga, 1998; Pascua et al., 2007) have not been considered in the present study. In the case of the test plant, ozone (O3) would be generated on-site using parasitic power, air and corona-discharge ultra-violet (UV) lamps, and iron in the form of ferric sulfate [Fe2(SO4)3] or ferric chloride (FeCl3) that would be delivered to the geothermal plant. The photo-oxidation processes consist of treating the condensate or water with Fe2+ in the form of ferrous sulfate (FeSO4) or ferrous chloride (FeCl2), or with SO2 photo absorbers. The latter is generated from the oxidation of H2S in turbine vent gas (Kitz and Gallup,1997).The photo-oxidation process consists of sparging air through the photo- adsorber-treated fluid, and then irradiating it with UV lamps or exposing it to sunlight to oxidize As3+ to As5+. In the Fe photo-oxidation mode, the Fe2+ is oxidized to Fe3+, which not only catalyzes the oxidation reaction, but also co-precipitates the As. In the SO2 photo-oxidation mode,after oxidizing the As, FeCl3 or Fe2(SO4)3 is added to the water to precipitate the As5+ as a scorodite-like mineralTable 1Approximate geothermal water and steam condensate compositions assumed in the studya Total dissolved solids.Table 2Summary of the six cases of geothermal fluid treatment to produce marketable watera On treatment of water, clays are produced at a rate of 7.4 ton/h.(FeAsO4·2H2O). In the laboratory and field pilot tests, the photo-absorber and UV dosages were varied to decrease the As concentration in geothermal fluids to below the detection limit of 2 ppb (Simmons et al., 2002). Residual As in the precipitate may be slurry-injected into a water disposal well or fixed/stabilized for land disposal to meet United States Environmental Protection Agency (USEPA) Toxicity Characterization Leach Procedure (TCLP) limits using special cement formulations (Allen, 1996).3.2. Ion exchangeStrong-base anion exchange resins have been shown to remove traces of As in geothermal fluids provided that the amorphous silica is decreased below its saturation point or the water stabilized against silica scaling by acidification. The ion exchange alternative to As removal by oxidation/precipitation has proven successful in reducing the concentrations of this element to below the limits set for drinking water standards. As part of the present study, laboratory and field columnar tests were successfully conducted with geothermal hot spring water containing 30 ppm As. Pre-oxidation of As3+ is required to achieveacceptable As removal by ion exchange. In these columnar tests, NaOCl and H2O2 were used to pre-treat the hot spring water to oxidize As3+ to As5+. Chloride-rich water, which had been treated with lime (CaOH2) and filtered to reduce amorphous silica to well below its saturation point, successfully regenerated the resin. In the field, and for simplicity of operation, we concluded that ozone/Fe co-precipitation or catalyzed photo-oxidation would be preferred for water treatment over ion exchange as this would eliminate the need to purchase and transport additional chemicals. On the other hand, ion exchange is an attractive option for extracting As from condensate.Special ion-exchange resins have proven successful in removing boron (B) from geothermal fluids (Recepoglu and Beker, 1991; Gallup, 1995). Hot spring water from the geothermal field, containing 25 ppm B, had its B content decreased to <1 ppm in a laboratory columnar test. The resin was regenerated with sulfuric acid (H2SO4). No deterioration in resin performance was observed up to 10 loading and regenerationcycles.Fig. 1. Flow chart of the basic unit operations involved in treatment cases 1–6.3.3. pH adjustmentThe majority of the cases considered in this study require adjustment to pH. Adding soda ash (Na2CO3) can increase the buffering capacity of the water and condensate. Soda ash or lime treatment can also be used to enhance precipitation of certain species. Purchased H2SO4, on-site generated sulfurous acid (H2SO3) or on-site generated hydrochloric acid (HCl) can be used to acidify waters to meet reuse requirements or to inhibit silica scaling (Hirowatari, 1996; Kitz and Gallup, 1997; Gallup, 2002). A number of geothermal power plants around the world utilize water acidification to inhibit silica scaling. Unocal Corporation commenced this practice of pH adjustment of hot and cold geothermal fluids in commercial operations in the early 1980s (Jost and Gallup, 1985; Gallup et al., 1993; Gallup, 1996). In water acidification the pH is reduced slightly so as to slow down the silica polymerization reaction kinetics without significantly increasing corrosion rates.3.4. Cooling pondsIn this water processing option, the water is cooled in open, lined ponds prior to injection or treatment for beneficial use. The flashed water is allowed to flow into the pond where it “ages” for up to 3 days; this is a sufficient length of time to achieve amorphous silica saturation at ambient temperature, which is assumed to be below 20 ◦C most of the year. Adjustment of the water pH to 8.0±0.5 with soda ash or lime enhances water desilication, resulting in undersaturation with respect to amorphous silica (Gallup et al., 2003). At 15 ◦C, the solubility of amorphous silica in the water in our test field is predicted to be about 90 ppm (Fournier and Marshall, 1983). In a large bottle, field water wasadjusted from pH 7.2 to 8.1 with soda ash and allowed to cool to 15 ◦C over a period of 90 min. The resultant dissolved silica [Si(OH)4] concentration in the supernatant fluid was 54 ppm (undersaturated by about 40%).3.5. FiltrationSand and plate/frame filters were adopted in this study to polish water and dewater sludges, respectively. This does not mean that other filters could not be used in the water treatment project. At the Salton Sea (California, USA) geothermal field, for example, flocculated secondary clarifiers and pressure or vacuum filters have been adopted with success for many years as alternatives to media and plate/frame filters, respectively (Featherstone et al., 1989).3.6. Multi-stage vacuum-assisted evaporatorIn this unit of operation, cool, ponded water is combined with cooled and re-circulated water (from the evaporator heat rejection stages), and pumped to the heat recovery portion of the evaporator system. The cool water provides the thermal sink for the vapors from the final stages of the evaporator concentrate. The inlet water and concentrate flow countercurrent in the evaporator. After flowing through the heat recovery stages, the water temperature has increased somewhat. Most of this heated water is sent to a separate cooling pond before returning to the heat recovery stages. A portion of the heated water continues on through the heat recovery stages; the water also functions as the heat sink for this portion of the process.After the heat recovery stages, the water is heated with steam and returned to the heat recovery stages for flashing. The water proceeds through the heat recovery and rejection stages until it is fully concentrated. The concentrate is sent to an injection well, while the distillate is collected and re-routed for pH adjustment, as required, before passing to other treatments discussed here. The evaporator has not yet been tested at the field; the present discussion is provided for conceptualization only.3.7. Reverse osmosisThe reverse osmosis (RO) process removes dissolved salts through fine filtration at the molecular level of water. The RO membrane allows water to pass through but blocks 98% of the salts. The typical RO operating pressure is 2760–3100 kPa, which is achieved by gravity flow from the power plant to the RO unit located 300m downhill. The RO feed is pre-treated with a 2 _m cartridge filter. The rejected fluid is injected into a disposal well, while the permeate can be sent to other treatment units for polishing.The RO unit has not yet been tested at the field; the present discussion is again provided for conceptualization only. However, RO has been successfully tested at the Mammoth Lakes, California, USA, field to recover useable silica (Bourcier et al., 2006).3.8. Desilication and production of claysSilica can be eliminated from the water by holding the latter in cooling ponds for up to 3 days. Soda ash or lime can be added to the water to enhance silica precipitation. Laboratory and field jar test experiments showed that desilication of the water can also be achieved by treating with various metal cations at elevated pH to precipitate metal silicates. Below ∼90 ◦Cand at elevated pH (typically 9–10) treatments with caustic soda (NaOH), magnesium hydroxide [Mg(OH)2], lime, strontium hydroxide [Sr(OH)2], barium hydroxide [Ba(OH)2], ferric hydroxide [Fe(OH)3], birnessite [(Na,Ca)0.5(Mn4+,Mn3+)2O4· 1.5H2O], copper hydroxide, [Cu(OH)2] and zinc hydroxide [Zn(OH)2] precipitated only amorphous or poorly crystalline metal-rich silicates of little commercial value. Treatment of water with alkaline-earth metals below ∼90 ◦C, except magnesium, tended to co-precipitate metal carbonates. Laboratory reactions conducted at ∼130 ◦C demonstrated that certain metal ions may react with the silica in the water to precipitate crystalline compounds of commercial value. For example, kerolite1 clay was precipitated upon treating synthetic and field waters with magnesium at 130 ◦C, whereas, under similar conditions, sodalite (Na4Al3 Si3O12Cl) and Zeolite P2 were precipitated upon treatment with aluminum hydroxide or sodium aluminate (Gallup et al., 2003; Gallup and Glanzman, 2004). Treatment of waters with a combination of magnesium and iron precipitated hectorite (i.e. a lithium-rich clay mineral of the montmorillonite group).The desilication process designed for the field consists of a crystallizer-clarifier similar to those used at the Salton Sea field (Newell et al., 1989). For kerolite production, magnesium chloride (MgCl2) is added at slightly above stoichiometric proportions (3Mg:4Si) and the pH is increased to ∼10.0 with caustic soda or lime. The crystallizer and clarifier include sludge recirculation to maximize the “seed crystal” effect, thus providing a high surface area for precipitation. After precipitation, the water is clarified, possibly treated further to meet industrial water specifications, cooled to pipeline specifications, and finally sent to a pipeline for transport to the industrial site. The kerolite sludge is dewatered using a filter, as discussed earlier. The dewatered sludge can be dried in a steam-heated kiln or in an arid, but cool environment at the power plant. Dried kerolite is transported off-site for commercial refining and use. In zeolite manufacture, sodium aluminate (NaAlO2) is used both as the Al and base source. Hectorite or saponite (i.e. a magnesium-rich clay mineral of the montmorillonite group) are made1 Kerolite is a disordered form of talc.2 Zeolite P refers to various forms of gismodine.Table 3Quality of the water end-product estimated from actual testing and from vendor treatment specifications for the six treatment cases described in Table 2a TDS: total dissolved solids.in a similar fashion by treating water with Mg2+ and Fe2+ salts and a base (Gallup et al., 2003). Adding a little brucite [Mg(OH)2] or MgCl2 will also produce a nearly pure silica by-product for industrial uses (Lin et al., 2001). Desilication of water with precipitation of valuable minerals is a preferred option as opposed to simply allowing the silica to deposit in cooling ponds as it adds value to the geothermal power project by simultaneously controlling scale deposition and producing marketable products. Once the water is treated for desilication, any metals of commercial value can be extracted by means of well-documented processes (Maimoni, 1982; Featherstone, 1988; Duyvesteyn, 1992; Featherstone and Furmanski, 2004). This approach is particularly important if ion exchange or solvent extraction techniques have been used to concentrate and recover lithium, base and precious metals.4. Quality of the water end-productTable 3 gives details on the estimated quality of the water produced after each of the six treatment cases (see Table 2 for initial concentrations). The water qualities meet or exceed perceived drinking, agriculture and industrial standards at the location of the test plant.5. Preliminary cost estimatesTable 4 is a summary of the estimated capital and operating (product water) costs, based on construction of the geothermal power plant for the six treatment processes. Local market prices for chemicals such as H2SO4, CaO, flocculents, NaCl, Na2CO3, FeSO4, MgCl2, NaAlO2, etc., were used in the calculations. The product cost does not include a productstorage reservoir at the end of the pipeline where the treated water can be made available for industrial, agricultural or drinking uses. The anticipated selling price for finished minerals, such as kerolite, saponite, sepiolite (a magnesium-rich clay mineral), etc. was set at US$ 0.45 kg −1. For comparison, the cost of injecting all of the waste geothermal fluids back into the field (using wells with gravity feed) is ∼US$ 10,000,000. The latter is the estimated capital cost of drilling sufficient injection wells for water disposal, but does not include poten- Table 4Preliminary cost estimates (US$) for the six treatment cases described in Table 2a Water treatment cost offset by 7.5 ton/h of clay sales.tially high maintenance costs for acidification treatment and/or for re-drilling these injection wells.6. ConclusionsA preliminary study has been made of combining water treatment/reuse and electricity generation in a geothermal power plant located in an arid region of the western hemisphere. It has been assumed that good-quality water is scarce in the area and that there is a local demand for potable, agricultural and industrial water resources. Geothermal water and steam condensate require treatment prior to reuse. A variety of treatment scenarios have been considered to achieve water quality ranging from potable to industrial standards. Some proof-of-concept testing in the laboratory and the field has been conducted to ensure that certain qualities can be attained. Preliminary cost estimates have been made for the treatment schemes considered in the study. Promising processes have been developed to produce marketable water and silicate minerals. Desilication and removal of arsenic and boron from the water have also proved useful with a view to subsequent extraction of lithium, base and precious metals.AcknowledgmentsThe authorwould like to thank Chevron Corporation management for permission to publish this paper. CH2MHILL, Irvine, CA, provided many of the process ideas and cost estimates included here. The author appreciates the many useful comments and suggestions provided by the editors and by Mr. Paul Hirtz in his review of the manuscript.ReferencesAllen, W.C., 1996. Superplasticizer-cement composition for waste disposal. US Patent 5,551,976.Bourcier, W., Ralph, W., Johnson, M., Bruton, C., Gutierrez, P., 2006. Silica extraction at Mammoth Lakes, California.Lawrence Berkeley National Laboratory Report UCRL-PROC-224426. Livermore,CA, USA, 6 pp.Doran, G.F.,Williams, K.L., Drago, J.A., Huang, S.S., Leong, L.Y.C., 1998. Pilot study results to convert oil field producedwater to drinking water or reuse. Paper presented at 1998 SPE Annual Technical Conference and Exhibition, 27–30September. New Orleans, LA, USA, SPE Paper 49124, 15 pp.Duyvesteyn, W.P.C., 1992. Recovery of base metals from geothermal waters. Geothermics 21, 773–799.Featherstone, J.L., 1988. Process for removing silica from silica-rich geothermal water. US Patent 4,765,913.Featherstone, J.L., Furmanski, G., 2004. Process for producing electrolytic manganese dioxide from geothermal brine.US Patent 6,682,644.Featherstone, J.L., Spang, T., Newell, D.G., Gallup, D.L., 1989. Process and apparatus for reducing the concentration ofsuspended solids in clarified geothermal water. US Patent 4,874,529. Fournier, R.O., Marshall, W.L., 1983. Calculation of amorphous silica solubilities at 25◦ to 300 ◦C and apparent cationhydration numbers in aqueous salt solutions using the concept of effective density of water. Geochim. Cosmochim.Acta 47, 587–596.Gallup, D.L., 1995. Agricultural uses of excess steam condensate—Salton Sea geothermal field. Geotherm. Sci. Technol.4, 175–187.Gallup, D.L., 1996. Water pH modification scale control technology. Geotherm. Resour. Counc. Trans. 20, 749–755.Gallup, D.L., 2002. Method for simultaneously abating H2S and producing acid for water treatment. US Patent 6,375,907.Gallup, D.L., Barnes, M.L., Cope, D., Kolimlim, Q.S., Leong, J.K., 1993. Water heat exchanger treatment method. USPatent 5,190,664.Gallup, D., Sugiaman, F., Capuno, V., Manceau, A., 2003. Laboratory investigation of silica removal from geothermalwaters to control silica scaling and produce usable silicates. Appl. Geochem. 18, 1597–1612.Gallup, D.L., Glanzman, R.K., 2004. Method for synthesizing crystalline magnesium silicates from geothermal water.US Patent 6,761,865.Hirowatari, K., 1996. Scale prevention method bywater acidification with biochemical reactors. Geothermics 25, 259–270.Jost, J.W., Gallup, D.L. 1985. Inhibiting scale precipitation from high temperature water. US Patent 4,500,434.Khoe, G.H., Emett, M.T., Robins, R.G., 1997. Photoassisted oxidation of species in solution. US Patent No. 5,688,378.Kitz, K.R., Gallup, D.L., 1997. pH modification of geothermal water with sulfur-containing acid. US Patent 5,656,172.Lin, M.S., Premuzic, E.T., Zhou,W.M., Johnson, S.D., 2001. Mineral recovery: a promising geothermal power productionco-product. Geotherm. Resour. Counc. Trans. 25, 497–500.Maimoni, A., 1982. Mineral recovery from Salton Sea geothermal waters: a literature review and proposed cementationprocess. Geothermics 11, 239–258.Newell, D.G., Whitescarver, O.D., Messer, P.H., 1989. Salton Sea Unit 3;47.5MWe geothermal power plant. Geotherm.Resour. Counc. Bull. 18 (5), 3–5.Pascua, C.S., Minato, M., Yokoyama, S., Sato, T., 2007. Uptake of dissolved arsenic during the retrieval of silica fromspent geothermal brine. Geothermics 36, 230–242.Recepoglu, O., Beker, U., 1991. A preliminary study of boron removal from Kizildere/Turkey geothermal waste water.Geothermics 20, 83–89.Rothbaum, H.P., Anderton, B.H., 1975. Removal of silica and arsenic from geothermal discharge waters by precipitationof useful calcium silicates. Geothermics 2, 1417–1425.Simmons, M., Gallup, D., Harden, D., 2002. Photo-oxidation, removal and stabilization of arsenic residuals in drinkingwater, wastewater and process water systems. Trends Geochem. 2, 73–84. Umeno, J., Iwanaga, T., 1998. A study on the abatement technology of the harmful chemical components in geothermalhot water. In: Proceedings of the 20th New Zealand Geothermal Workshop, pp. 209–213.处理地热废水来生产工业用水、农业用水或生活饮用水达雷尔L.盖洛普能源技术公司,雪佛龙公司Briarpark博士,美国德克萨斯州休斯顿摘要:一个概念的研究已经进行了转换成有价值的工业、农业和饮用水资源地热水和凝析油。
国外放牧方法研究概述

国外放牧方法研究概述赵瑞雪,程钰宏,董宽虎山西农业大学动物科技学院,山西太谷(030801)mail zhaoruixue1234@E-:摘要:放牧方法是在长期的放牧实践和研究中得出的,其能够平衡饲草供给、满足家畜需要、增加畜产品以满足人们需求。
本文对国外放牧方法:连续放牧、季节适宜性放牧、延迟放牧/休牧、高密度放牧方法进行详细的介绍。
关键词:连续放牧,季节适宜性放牧,延迟放牧/休牧,高密度放牧人们在长期的放牧实践和研究中,为了平衡饲草供给,满足人们需求,得出了许多优良的、适应时代发展要求的放牧方法。
放牧是草地利用的基本方式,它既关系到草地放牧业的稳定和发展,也关系到草地保护和生产效率的提高。
目前世界各国草地畜牧业中,放牧仍然是主要的饲养方式。
当今社会,在同一放牧地上用运两种或两种以上的放牧方法已成为一种趋势,不同放牧方法有机结合更有利于提高家畜产量,为长久利用草地提供了合理的理论依据。
这些不同放牧方法的有机结合,形成了不同的放牧制度,从历史发展来看,放牧制度大体经历了原始游牧制、季节性游牧制、半定居放牧制和定居放牧制四个阶段。
各个历史阶段则是生产与生产能力的适应。
放牧制度是草地用于放牧时的基本利用体系,其规定了家畜对牧草地利用的时间和空间上的通盘安排。
为了选择合理的放牧制度,本文就以下放牧制度及其包含的放牧方法进行详细地介绍,以利于人们合理利用草地资源,为在我国草原地区的推广利用,提供基础资料。
1.放牧方法的作用优良的放牧方法或放牧制度是非常实际有效的,可以根据当地气候条件机动调节并应用于生产,实现最优饲草转化。
放牧方法和放牧管理的结合用运已成为一种趋势,根据实际情况进行科学管理是牧场获利的最佳途径。
由于饲草供给、气候变化、目标转换,经济波动等原因,复杂的放牧方法在实践中经常被相应的调整,达到最优的放牧强度以适应生产发展需要。
Heady认为实现饲草最优化转化的处理方法是不同的,但它们遵循以下法则[1]:第一、必须遵循主要饲草植物的生理生态学需要;第二、改善植物生长条件,维持较高的生长活力;第三、提供良好的牧草生长环境,防止过度放牧;第四、提高植物的适口性和饲草产量;第五、在草地上维持草畜平衡;第六、在实际操作过程中执行理论和实际相结合的原理;为了使草地生态系统有高的第二性生产,必须保证有足够的第一性生产,科学合理地选择放牧方法是关键,管理者在选择放牧方法时,必须优先考虑如下目标:表1 选择放牧方法需考虑达到的目标植物/生存条件要达到的目标动物/市场经济需要达到的目标1、改善植物生长条件,提高植物生长活力1、在市场低峰期购买家畜2、维持植物高的生长条件2、维持高的饲草营养水平3、合理分配利用牧草3、保证高的营养水平在动物生长敏感期4、减少动物对植物的选择性4、合理的放牧管理计划5、合理的载畜量6、保证饲草供应充足7、在干旱或其它紧急情况下采取延迟放牧或休牧2.放牧方法的适应性放牧方法得到人们的认可,是因为其不是单纯的实验研究,而是在实践中产生,在实践中有强的适应性和高的经济回报。
油橄榄叶提取物对铅中毒小鼠大脑海马组织抗氧化酶及NO与NOS的影响

氧化氮合酶 ( NOS 活性及丙二醛 ( A) ) MD
、
,
变化・ 结果 表 明: 与模 型对照 组相 比 , 鼠灌 胃 OI 小 E后海 马组织 S D O
、
C AT、 NO、 s水 平 均 升 高 , A 含 量 降 N0 MD
、
低 ・ 明油 橄 榄 叶 提取 物对 铅 中 毒 小 鼠有 一 定 的 疗 效 说
Efe t fo i e l a xt a to n a i x d n n y f c s o lv e f e r c i n o nto i a te z me
,
N O S a tv t nd N O o e ti i p c m p c i iy a c nt n n h p o a us
-
( DA ) i ip c m p so c t e d p io ig,h e lhm iewe ec o e n aI t M n h p o a u fmiewih la o s n n t eh at c r h s n a d d i i yn
.
r ga t i d~ a s rca
m m ̄taln wi e d a ea ea d wi ifr n o eo sr t t la c t t n t dfee td s fOLE f r3 a s Th c i iy o OD , o h h o 0 d y e a tv t f S CAT n ad NOS a l a h o tn fM DA n swel st ec n e to a d NO n hp o a u f iewe ed tr ie _ er s l i i p c mp so c r e em n Th e u t m d ss o d h we t a o p r d wi h d l r u t ec n e ta in fS h tc m a e t t emo e o p,h o c n r t so OD CAT , h g o NO nd NOS i c nty i r as d a sgni a l nc e e
WILEY期刊清单
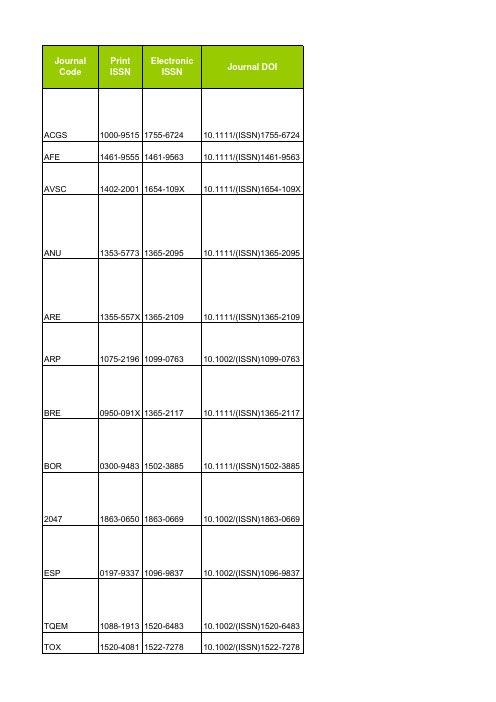
Print ISSN
1000-9515 1461-9555 1402-2001 1353-5773 1355-557X 1075-2196 0950-091X 0300-9483 1863-0650 0197-9337 1088-1913 1520-4081 0730-7268 1351-0754 1467-2960 0969-997X 1054-6006 0883-6353 1472-4677 1468-8115 0072-1050 0266-6979 0016-8025 1639-4488 0142-5242 1744-6961 1551-3777 0899-8418 1047-482X 1038-4871 0931-2250 0175-8659 0022-1112 0140-7775 1088-1980 0263-4929 0141-6421 1436-8730 0893-8849 1100-9233 1320-5331 1085-3278 0024-1164 1086-9379 1350-4827 1545-7893 0165-0203 0031-0239 1051-5658 1344-1698 1535-1459 0037-0746 0266-0032
0954-4879 0035-9009 1747-6585 0043-1656 1444-6162 0043-1737 0024-3590 0003-8504 0171-5445 0932-8351 0005-9900 1061-3773 1093-9687 0098-8847 0424-7760 1942-9533 1944-7442 0266-4720 0308-0501 1865-7362 0172-6145 0017-467X 1069-3629 1099-2871 1090-8471 0885-6087 1931-4973 0905-6947 0363-9061 2040-7939 0029-5981 0271-2091 0890-6327 0098-9886 1074-5351 0363-907X 0894-3370 1096-4290 1049-8923 1542-0973 1430-144X 1531-0353 1556-4959 1071-7641 1093-474X 0954-0075 1432-3427 0895-2477 0143-2087 0894-3214 1059-1478 1062-7995 0748-8017 0038-9145 1867-0520 0039-2103 1464-4177
锂同位素在稀有金属成矿过程的分馏机制——以川西打枪沟为例

作者简介:(1989-),,。
6Li和7Li作为锂的两种稳定同位素,易产生分馏,为利用锂同位素示踪各种地质过程提供可能条件。
锂同位素被广泛用于陨石研究、壳幔作用、岩浆演化、热液成矿过程等方面[1]。
锂元素为中等不相容元素,使其倾向于在岩浆演化的晚期富集[2]。
富锂铍的稀有金属花岗岩经历了广泛的岩浆分异和热液过程[3]。
锂在稀有金属花岗岩的岩浆分异和热液作用过程中含量和同位素组成变化较大[4]。
因此,锂同位素是岩浆演化和热液作用过程物理化学条件演化的有效示踪剂。
打枪沟锂铍矿床位于松潘-甘孜造山带主体的雅江被动陆缘中央褶皱推覆带[5],是近年来新发现的中型锂铍矿床[6]。
矿区内出露可能与伟晶岩具同源岩浆演化关系的几类岩浆岩,为锂同位素方法实验、研究提供了理想条件。
1矿区地质特征打枪沟锂铍矿矿区出露三叠系新都桥组白云母黑云千枚状片岩、含炭质黑云母石英千枚状片岩。
构———何成麟1,2,张博2,殷聃2,成欣怡2,张姚2(1.成都理工大学地球科学学院,四川成都610059;2.四川省冶金地质勘查局水文工程大队,四川成都611730)摘要:本文首次尝试将锂同位素研究应用于打枪沟锂铍矿床岩浆演化与热液作用研究中。
对打枪沟与伟晶岩有关的中-酸性岩体进行了系统的采样、测试,结果表明,岩体δ7Li 值主要分布于-1.16‰~+1.59‰,伟晶岩δ7Li 值分布于-4.55‰~+12.4‰,表明锂的两种同位素在岩浆演化阶段未发生明显的分馏,而在形成伟晶岩的熔体相-流体相之间交代作用阶段表现出在不同矿物中差异化的分配行为,热液交代作用为锂同位素分馏的主控因素。
关键词:打枪沟;伟晶岩;锂同位素;热液作用过程中图分类号:P618文献标志码:AFractionation Mechanism of Lithium Isotopes in the Ore-forming processes of Rare Metals:A CaseStudy from Daqianggou,Western Sichuan HE Chenglin 1,2,ZHANG Bo 2,YIN Dan 2(1.College of Earth Science,Chengdu University of Technology,Chengdu 610059,China ;2.Hydro-EngineeringParty of Sichuan Metallurgical Geology&Exploration Bureau,Chengdu 611730,China)Abstract:This study utilizes lithium isotopes for the first time in an attempt to trace the magmatic evolution and hydrothermal processes of Daqianggou deposit.Systematic sampling were conducted on ore-related intermediate-felsic plutons and pegmatites.Consequently,the δ7Li values range from -1.16to +1.59‰for felsic plutons,-4.55to +12.4‰for pegmatites,indicating slight lithium fractionation in the magmatic evolutionary stage and strong lithium fractionation in the hydrothermal metasomatism stage.We propose that hydrothermal metasomatism might be a main controlling factor in lithium fractionation.Key words:Daqianggou;pegmatite;lithium isotope;hydrothermal processes2造单一,主要为褶皱构造。
保护森林的有效途径

V'7傥磧養森林对地球上的生命至关重要,但世界各地的森林正在迅速消失,我们该如何应对这场全球危机?Effective ways to conserve forests保护森林的有效途径重庆谈增胜体裁文章词数建议用时信息性文本约4298分钟/难词探意1.deforestation/.dil.fDri'steiJn/n.滥伐森林2.cubic/'kjulbik/adj.立方的3.rotational/r藜尬teij藜nl/adj.交替的;轮流的4.friction/'frikjn/n.摩擦5.negligence/neglid30ns/n.疏忽Forests are critical to life on earth.1.6billion people rely on them directly for food,shelter,fuel and income.But they are rapidly disappearing all over the world,alarming many people. How can we prevent this global crisis?Here are 16Crazy English2021.2some effective ways to conserve forests.Planned and regulated tree-cuttingThe commercial felling of trees is one of the main reasons for deforestation.According to an estimate,about1,600million cubic meters of wood has been used for various purposes in the world.If trees are cut down at this level, their revival cannot be possible.Therefore,cutting should be regulated.野Sustainable yield冶methodThis technique is adopted by many coun-tries.In regulated cutting,only one-tenth of the forest area is selected for use,and the rotational system is always followed for theirprotection.The time gap between these cuttings is helpful in the regrowth of trees.ReforestationThe野sustainable yield冶method also requires that every tree that gets cut down must be re-planted.Similarly,any tree that gets burned down due to forest fires or mining activities must also get replanted.This may be done by natural or artificial methods.Control forest firesForest fires also contribute to deforestation. Forest fires occur in the following ways.Natural disasters:Some forest fires are caused by nature through lightning,or trees rubbing against each other during a strong wind and creating friction.We can do the least about it.Manmade:Most forest fires are due to human negligence.There are ways to prevent this from happening such as:•Do not make open fires•Do not throw your cigarette on the ground•Maintain electricity wires properlyReading fCheckDo you have any other ways to conserve forests apart from the ways mentioned in the text?Sentence for writingThe commercial felling of trees is one of the main reasons for deforestation.商业砍伐树木是滥伐森林的主要原因之一。
赣锋锂业铊超标小作文

赣锋锂业铊超标小作文英文回答:Recently, there has been a lot of talk about Ganfeng Lithium's excessive thallium levels. Thallium is a toxic heavy metal that can have serious health effects ifingested or inhaled. As a concerned citizen, I believe itis important to address this issue and discuss thepotential consequences.Firstly, it is crucial to understand the dangers of thallium. Exposure to high levels of thallium can lead to symptoms such as hair loss, skin rashes, and even neurological disorders. Long-term exposure can have even more severe effects, including damage to the kidneys, liver, and lungs. Therefore, it is essential for Ganfeng Lithiumto take immediate action to reduce thallium levels and ensure the safety of the surrounding communities.Furthermore, the excessive thallium levels not onlypose a threat to human health but also to the environment. Thallium can contaminate water sources, soil, and vegetation, leading to a disruption of the ecosystem. This can have a detrimental impact on wildlife and biodiversityin the area. It is crucial for Ganfeng Lithium to implement effective measures to prevent further contamination and mitigate the environmental damage caused by thallium.In addition to the health and environmental concerns, the excessive thallium levels also raise questions aboutthe company's commitment to corporate social responsibility. Companies have a responsibility to prioritize the well-being of their employees, customers, and the communities they operate in. By allowing thallium levels to exceed the acceptable limits, Ganfeng Lithium is failing to fulfillthis responsibility. It is important for the company totake accountability for their actions and work towards rectifying the situation.中文回答:最近,关于赣锋锂业铊超标的问题引起了广泛关注。
富含锂的冶金矿渣[发明专利]
![富含锂的冶金矿渣[发明专利]](https://img.taocdn.com/s3/m/ca10308958fafab069dc02f0.png)
专利名称:富含锂的冶金矿渣
专利类型:发明专利
发明人:马尔滕·奎西,大卫·范胡蕾比克,托马斯·休特恩斯申请号:CN201780005822.0
申请日:20170104
公开号:CN108474061A
公开日:
20180831
专利内容由知识产权出版社提供
摘要:本发明涉及具有高锂含量的矿渣组合物,其适合作为制造最终用户产品的添加剂或用于含锂的经济回收。
实际上锂浓度与锂辉石浓度相媲美,锂辉石是生产锂的经典矿物。
该矿渣的特征在于根据以下的组成:3%
申请人:尤米科尔公司
地址:比利时布鲁塞尔
国籍:BE
代理机构:中原信达知识产权代理有限责任公司
更多信息请下载全文后查看。
国际视角

国际视角作者:暂无来源:《科技传播》 2017年第12期加拿大变废为宝:废旧轮胎可解决混凝土开裂难题加拿大不列颠哥伦比亚大学(UBC)的研究人员正在尝试不同的研究方向,通过使用废旧轮胎获得的聚合物纤维来阻止混凝土继续开裂。
将聚合物纤维添加到现有的混凝土中,有弹性纤维使混凝土微小的裂缝不会继续变大。
研究人员在UBC的McMillan 建筑中使用了这种加入纤维的混凝土。
利用嵌入在混凝土中的传感器,他们正在监测开裂等因素。
日本研发新技术通过泉水确定野生动物种类近日,由日本千叶县立中央博物馆等研究人员组成的研究小组开发出一种新技术,通过分析森林中泉水的成分即可判断出在此栖息的野生动物的种类。
研究人员表示,该技术可用于在广袤的热带雨林中确定濒临灭绝的野生动物的位置,以便更好地保护这些动物。
日本千叶县立中央博物馆等研究小组此次开发出的新技术计划用于东南亚等地的野生动物保护活动。
澳大利亚“太阳能油漆”将空气中的水蒸汽转化为氢燃料澳大利亚的研究人员目前取得了一项重大突破,开发了一种可以将空气中的水蒸汽转化为氢燃料的“太阳能油漆”。
这种“太阳能油漆”的关键是一种新开发的类似于硅胶的化合物。
这种化合物被称为合成硫化钼,它可用作半导体,引发水原子分解成氢气和氧气。
然后,团队发现将该化合物与二氧化钛颗粒混合后可形成能吸收太阳光、产生氢能的油漆。
俄罗斯科学家研制出特殊材料永久电池将不是梦近日,俄罗斯国家研究型工艺技术大学节能中心的工作人员研制出了航天器高效热电发生器所需材料的经济快速的制作方法,这种材料直接将热能转化为电能。
研制出的热电材料含有两种原子:固定在晶格内、保障高导电性的原子和自由移动、大大降低热导率的原子。
这种组合通过创建金属互化物的方式获得,金属互化物的晶体结构含有空隙,可用原子填充。
美国研究人员尝试用光合作用治疗心脏缺氧斯坦福大学的研究人员正在尝试利用光合作用和光合细菌,帮助血管堵塞的患者运输氧气。
日前,斯坦福大学的心胸外科主任Joseph Woo 博士表示,他正在研究多种开箱即用式的心脏治疗方法。
废干电池制取锰锌铁氧体过程中锰的测定

--●Vol.31,No.112013年11月中国资源综合利用China Resources Comprehensive Utilization利用废干电池制备锰锌铁氧体,既避免了环境污染,又回收利用了资源,产品附加值高[1-2]。
在制备过程中,需要准确测定锰的含量,目前,锰的分析方法主要有:原子吸收光谱法、等离子光谱法、硝酸铵氧化法、K 2Cr 2O 7-Na 3AsO 3联合氧化法等[3-5]。
前两种方法分析速度快,但是需要昂贵的分析仪器;硝酸铵氧化法,由于磷酸冒烟时温度难以控制,因而重复性不好,并且分析的时间比较长;K 2Cr 2O 7-Na 3AsO 3联合氧化法,因三氧化二砷是一种剧毒物品,对分析人员的身体健康影响比较大。
本试验应用硫酸亚铁铵氧化还原滴定法,用硫酸亚铁铵作为标准溶液直接滴定试样中的锰的含量,而无需考虑铁、锌的影响。
此法试剂、仪器常见,操作简单,过程中颜色变化的分界点较明显。
1试验原理及方法1.1试验原理在稀硫酸溶液中,以银离子为催化剂,用过硫酸铵将锰氧化成高价锰,以二苯胺磺酸钠为指示剂,用硫酸亚铁铵标准溶液滴定。
反应原理如下:2Mn 2++5S 2O 82-+8H 2O ═2MnO 4-+10SO 42-+16H +(1)5Fe 2++MnO 4-+8H +═5Fe 3++Mn 2++4H 2O (2)1.2主要试剂硫酸,1∶1;磷酸,1∶1;过硫酸铵,固体;硝酸银溶液,1%;二苯胺磺酸钠指示剂,0.5%;Mn 2+标准溶液,1g/L;Zn 2+标准溶液,10g/L;Fe 2+标准溶液,10g/L;重铬酸钾标液,0.01mol/L;硫酸亚铁铵标准溶液,锰的滴定度为0.5504mg/mL。
硫酸亚铁铵标准溶液配制:称取10g 硫酸亚铁废干电池制取锰锌铁氧体过程中锰的测定张晓东1,2,刘晓静1,冷士良1,刘兵1,李宗磊1(1.徐州工业职业技术学院;2.江苏省化工新材料工程技术研究开发中心,江苏徐州221000)摘要:利用废干电池制取锰锌铁氧体过程中需要准确测定锰含量。
芬顿氧化处理工业废水的应用概述

芬顿氧化处理工业废水的应用概述摘要:本文提供了作为工业废水先进处理方法的芬顿氧化法在应用流程的最新的信息。
这种技术作为一个化学氧化法处理已经在最近几十年里被应用,能满足多种目标包括最终抛光,减少化学需氧量或总有机碳的有机负荷的高百分比和去除顽固和有毒污染物从而允许进一步传统生物处理。
这项技术的效率和灵活性已经被证明,它具有广泛的多样性,与废水化学和其他相关行业的或活动相关,包括制药、纸浆和造纸、纺织、食品、软木加工、填埋的垃圾等。
关键词:芬顿过程;化学氧化;工业废水处理;废物最少化;渗滤液前言工业活动产生废水与各种各样的污染物,如酚及其衍生品、碳氢化合物、卤代硫和流变的有机化合物,重金属乙腈化物和其他有机复合物的形式。
这些废水经常在大范围的浓度内含有混合池中的污染物。
这个开发低成本的技术解决方案需要成功地应对工业废水领域内引起的日益复杂的问题。
在最近几十年,化学处理方法涉及生成的羟基自由基被称为高级氧化过程(AOPs),在其强氧化性的基础上已经成功应用于去除或降解顽固污染物。
在这些高级氧化过程中,芬顿过程是一个被广泛研究的和采用催化法根据生成的羟基自由基(HO·)通过过氧化氢与铁离子作为均相催化剂在酸性pH和环境条件下的研究过程[1]。
HO·有一个高的标准氧化电位(2.80 V),与其他传统的氧化剂像Cl2、O2、O3,过氧化氢或KMnO4相比有很高的反应速度。
这个羟基自由基与大多数有机和许多无机溶质以高速率反应。
普遍接受的机理,提出了芬顿过程生产的羟基自由基依照方程(1),而催化剂再生通过方程(2),或从反应Fe3 +中间的有机自由基(方程(3)-(5)):[2-6]Fe2+ + H2O2 →Fe3+ + HO·+ HO?k = 76 Lmol-1 s-1 (1)Fe3+ + H2O2 →Fe2+ + HO2·+ H+k = 0.01 Lmol-1 s-1 (2)RH + HO·→R · +H2O (3)R· + Fe3+→R+ + Fe2+(4)R+ + HO? →R-OH (5)然而,一批有竞争力的反应也会发生(方程(6)-(9)),它影响氧化过程:Fe2+ + HO·→Fe3+ + HO?k = 3.2 × 108 Lmol-1 s-1 (6)H2O2 + HO·→HO2 · + H2Ok = 2.7 × 107Lmol-1 s-1 (7)HO2· + HO·→O2 + H2O (8)HO· + HO·→H2O2k = 5.2 × 109 Lmol-1 s-1 (9)芬顿法的速度强烈依赖于自由基清除剂如t-丁醇或氯离子,但在某些情况下,即使在高浓度的这些物种也没有发现大幅降低[7]。
雅思考试中和

雅思考试中和雅思考试中和“污染”有关的词汇来源:exam8采矿废物Mining wastes机动车辆排放物Motor vehicle emissions城市废物Municipal waste氮氧化物Nitrogen oxides噪声污染Noise pollution恶臭公害Odour nuisance有机物污染Organic pollutants难降解有机污染物Persistent organic pollutants 有机溶剂Organic solvents有机卤化物Organohalogen compounds医药废物Pharmaceutical wastes塑料废物Plastic wastes多氯联苯Polychlorinated biphenyls聚合物废物Polymer wastes放射性物质Radioactive substances氡Radon橡胶废物Rubber waste锯屑Sawdust污水Sewage屠宰场废物Slaughterhouse waste固体废物Solid wastes热污染Thermal pollution有毒物质Toxic substances采矿废物Mining wastes机动车辆排放物Motor vehicle emissions城市废物Municipal waste氮氧化物Nitrogen oxides噪声污染Noise pollution恶臭公害Odour nuisance有机物污染Organic pollutants难降解有机污染物Persistent organic pollutants 有机溶剂Organic solvents有机卤化物Organohalogen compounds医药废物Pharmaceutical wastes塑料废物Plastic wastes多氯联苯Polychlorinated biphenyls聚合物废物Polymer wastes放射性物质Radioactive substances氡Radon橡胶废物Rubber waste锯屑Sawdust污水Sewage屠宰场废物Slaughterhouse waste 固体废物Solid wastes热污染Thermal pollution有毒物质Toxic substances有毒废物Toxic waste毒素Toxins痕量元素Trace elements痕量物质Trace materials交通噪音Traffic noise废物,垃圾Trash废热Waste heat木材废料Wood waste对流层臭氧Tropospheric ozone 污染源Pollution sources生物武器Biological weapons水泥工业Cement industry化学武器Chemical weapons烟囱Chimneys冷却水Cooling waters机动车辆Motor vehicles摩托车Motorcycles核武器Nuclear weapons海洋倾倒Ocean dumping石油泄漏Oil spills废金属Scrap metals挖掘堆积Excavation heaps污染治理Pollution abatement隔音Acoustic insulation化学污染清除Chemical decontamination燃料脱硫Desulphurization of fuels过滤器Filters噪音治理Noise abatement污染治理设备Pollution abatement equipment 污染控制技术Pollution control technology辐射防护Radiation protection洗涤器Scrubbers分离器Separators防烟Smoke prevention废物最少化Waste minimization废物Wastes电池处理Battery disposal废物的化学处理Chemical treatment of waste 处置场所Disposal sites废物焚烧Incineration of waste矿山回填Mine filling残油回收Oil residue recuperation放射性废物管理Radioactive waste management回收的材料Recycled materials回收Recycling材料再利用Reuse of materials卫生填埋Sanitary landfills海洋排泄口Sea outfall化粪池Septic tanks污水处置Sewage disposal污水处理系统Sewage treatment systems固体废物处置Solid waste disposal废物同化处置Waste assimilation capacities废物转化技术Waste conversion techniques废物处置Waste disposal废物土地处置Waste disposal in the ground废物处置税Waste disposal taxes废物回收Waste recovery废物利用Waste use水的再利用Water reuse人体健康HUMAN HEALTH污染物的危害Hazards of pollutants在人体组织中的积累Accumulation in body tissues镉污染Cadmium contamination环境健康危害Environmental health hazards人体接触污染物Human exposure to pollutants 污染物的长期效应Long-term effects of pollutants核安全Nuclear safety污染物的影响Pollutant effects污染风险Pollution risk辐射效应Radiation effects药物的副作用Side effects of pharmaceutical drugs有毒物质的协同效应Synergistic effects of toxic substances。
沙丘芦苇特有内含物PAAC与蛋白质的相互作用的开题报告

沙丘芦苇特有内含物PAAC与蛋白质的相互作用的开题报告1. 研究背景沙丘芦苇是一种耐盐碱的植物,常用于沙漠植被恢复和生态环境治理。
它的种子和茎叶中含有一种独特的内含物质PAAC(Poly-Acetylenic Acid Complex),具有抗氧化、抗菌、抗肿瘤等生物活性。
近年来,研究发现PAAC还能与蛋白质发生相互作用,影响蛋白质的结构和功能。
因此,深入研究PAAC与蛋白质的相互作用机制,对于进一步发掘沙丘芦苇的生物活性成分和应用价值,以及解析PAAC作为一种天然生物活性物质的生物合成和代谢途径具有重要意义。
2. 研究目的本研究旨在探讨沙丘芦苇内含物PAAC与蛋白质的相互作用机制,包括PAAC对蛋白质的结构影响、PAAC与蛋白质的结合模式、PAAC对蛋白质的生物活性调节作用等方面,为深入认识PAAC的生物活性和生物合成机制提供理论基础和实验依据。
3. 研究内容本研究将从以下几个方面展开:(1)分离提取PAAC和蛋白质采用生物化学方法和高水平液相色谱技术,分离提取沙丘芦苇茎叶中的PAAC和蛋白质,并进行纯化和鉴定。
(2)研究PAAC对蛋白质结构的影响利用荧光光谱、CD光谱等生物物理手段,研究PAAC对蛋白质二级结构和三级结构的影响,探讨PAAC与不同类型蛋白质的结合亲和力和空间构象的关系。
(3)探究PAAC与蛋白质的结合模式采用原位荧光探针和分子对接技术等手段,研究PAAC与蛋白质结合时的区域和模式,揭示PAAC与蛋白质相互作用的分子机制。
(4)研究PAAC对蛋白质生物活性的影响通过酶活性测定、生物学活性指标检测等方法,研究PAAC对蛋白质催化活性、抗氧化活性、抗肿瘤活性等生物学功能的影响。
同时,探讨PAAC对蛋白质激活、抑制、修饰等的生物调节作用。
4. 研究意义PAAC与蛋白质的相互作用是沙丘芦苇作为一种重要生物资源的研究热点之一,但相关研究还未被深入探究。
本研究将为深入研究PAAC的生物功能和生物合成机制提供重要的实验基础和理论支持,有助于进一步解析PAAC作为一种生物活性物质的结构、性质和功能,为沙丘芦苇及其内含物的利用和植物资源开发提供科学依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a r X i v :m a t h /0106248v 1 [m a t h .A G ] 28 J u n 2001Wild ramification and a vanishing cycles formulaMohamed Sa ¨ıdiAbstract In this paper we prove an explicit formula which compares the dimensions of the spaces of vanishing cycles in a Galois cover of degree p between formal germs of curves over a complete discrete valuation ring of inequal characteristics (0,p ).This formula can be easily generalised to the case of a Galois cover with group which is nilpotent or which has a normal p -sylow subgroup.The results of this paper play a key role in [Sa-1]where is studied the semi-stable reduction of Galois covers of degree p above semi-stable curves over a complete discrete valuation ring of inequal characteristics (0,p ),as well as the Galois action on these covers.0.Introduction.Let R be a complete discrete valuation ring of inequal characteristics,with uniformiser π,fraction field K ,and algebraically closed residue field k of characteristic p .In this paper we investigate Galois covers of degree p between formal germs of R -curves at closed points.Our main result is the following formula which compares the dimensions of the spaces of vanishing cycles at the corresponding closed points.More precisely we have the following:Theorem (2.4).Let X :=Spf ˆO x be the formal germ of an R -curve at a closed point x ,with X k reduced.Let f :Y →X be a Galois cover of group Z /p Z with Y normal and local.Assume that the special fibre Y k :=Y ×R k of Y is reduced.Let {℘i }i ∈I be the minimalprime ideals of ˆOx which contain πand which correspond to the branches (ηi )i ∈I of the special fibre X k :=X ×R k of X at x ,and let X i :=Spf ˆO ℘ibe the formal completion of the localisation of X at ℘i .For each i ∈I ,the above cover f induces a torsor f i :Y i →X i under a finite and flat R -group scheme G i of rank p ,above the boundary X i .For each i ∈I ,let (G k,i ,m i ,h i )be the reduction type of f i as defined in [Sa]3.2.Let y be the closed point of Y .Then one has the following “local Riemman-Hurwitz formula”:2g y −2=p (2g x −2)+d η−d sWhere g y (resp.g x )denotes the genus of the singularity at y (resp.x ),d ηis the degreeof the divisor of ramification in the morphism f η:Y η→X ηinduced by f on the generic fibre,and d s := i ∈I rad (m i −1)(p −1)+ i ∈I et (m i −1)(p −1),where I rad is the subset of I consisting of those i for which G k,i is radicial,and I et is the subset of I consisting of those i for which G k,i is ´e tale and m i =0.Hier G i,k denotes the special fibre of the group scheme G i .In particular the genus g y of y depends only on the genus g x of x ,the ramification datas on the generic fibre in the above morphism f :Y →X ,and its degeneration type on the boundaries of the formal fibre X .The above formula can be easily extended to the case of a Galois cover with group G which is nilpotent,or a group which has a normal p -Sylow subgroup.Our method to prove such a formula is to construct,using formal patchingtechniques `a la Harbater,a compactification ˜f:Y →X of the above cover f :Y →X (cf.2.3.2).The formula follows then by comparing the genus of the special and the generic fibres of Y in this compactification.As an application,and using the above formula one can obtain interesting results in the case where X is the formal germ of a semi-stable R -curve (cf.3.1and 3.2),in particular one can predict in this case if Y is semi-stable or not.We give several examples which illustrate this situation namely the case of Galois covers of degree p between formal germs of semi-stable R -curves (cf. 3.1.3,3.1.4and 3.2.4).In particular one can classify ´e tale Galois covers of degree p between annuli (cf.3.2.5).The above results play a key role in[Sa-1]in order to exhibit and realise the “degeneration datas”associated to Galois covers of degree p above a proper semi-stable R -curve.I.Formal and rigid patching.In what follows we explain the procedure which allows to construct (Galois)-covers of curves in the setting of formal or rigid geometry by glueing together covers of formal affine or affinoid rigid curves with covers of formal fibres at closed points of the special fibre.We refer the reader to the exposition in [Pr]for a discussion of patching results and for detailled references on the subject.Let R be a complete discrete valuation ring with fractions field K ,residue field k ,and uniformiser π.Let X be an admissible formal R -scheme which is an R -curve ,by which we mean that the special fibre X k :=X ×R k is a reduced one dimensional k -scheme of finitetype.Let Z be a finite set of closed points of X k .For a point x ∈Z ,let X x :=Spf ˆOX,x be the formal completion of X at x ,which is the formal fibre at the point x .Also let X ′be a formal open subset of X whose special fibre is X k −Z .For each point x ∈Z ,let {℘i }n i =1be the set of minimal prime ideals of ˆO X,x which contain π,they correspondto the branches (ηi )n i =1of the completion of X k at x ,and let X x,i :=Spf ˆO x,℘i be the formal completion of the localisation of X x at ℘i .The ring ˆO x,℘iis a complete discretevaluation ring.The set{X x,i}n i=1is the set of boundaries of the formalfibre X x.For each i∈{1,n}we have a canonical morphism X x,i→X x.1.1.Definition.With the same notations as above a(G)-cover patching data for the pair(X,Z)consists of the following:a)Afinite(Galois)cover Y′→X′(with group G).b)For each point x∈Z,afinite(Galois)cover Y x→X x(with group G).The above datas a)and b)must satisfy to the following condition:c)If{X x,i}n i=1are the boundaries of the formalfibre at the point x,then for each i∈{1,n} is given a(G-equivariant)isomorphismσi:Y x×XxX x,i≃Y′×X′X x,i.1.2.Proposition/Formal patching.Given a(G)-cover patching data as in1.1 there exists a unique,up to isomorphism,(Galois)cover Y→X(with group G)which induces the above(G)-covers in a)(resp.in b)when restricted to X′(resp.when pulled back to X x for each point x∈Z).The proof of1.2is an easy consequence of theorem3.4.in[Pr],and which is due to Ferrand and Raynaud.1.3.Remark.With the same notations as above let x∈Z and let˜X k be the normali-sation of X k.There is a one to one correspondance between the set of points of˜X k above x and the set of boundaries of the formalfibre at the point x.Let x i be the point of˜X k above x which corresponds to the boundary X x,i,for i∈{1,n}.Assume that the point x∈X k(k)is rational.Then the completion of˜X k at x i is isomorphic to the spectrum of a ring of formal power series k[[t i]]in one variable over k,where t i is a local parameterat x i.The complete local ringˆO x,℘iis a two dimensional discrete valuation ring whoseresiduefield is isomorphic to k((t i)).Let T i be an element ofˆO x,℘iwhich lifts t i,suchan element is called a parameter ofˆO x,℘i.Then it follows from[Bo]that there exists anisomorphismˆO x,℘i ≃R[[T i]]{T−1i},where R[[T i]]{T−1i}is the ring of formal power seriesi∈Za i T i with lim i→−∞|a i|=0,and where||is an absolute value of K associated to its valuation.1.4.Rigid patching.The analog of the above result is well known in rigid geometry, which is not surprising because of the link between rigid and formal geometry(cf.[Ra],[Bo-Lu]).We explain briefly the patching procedure in this context locally.Let X:=Spm A be an affinoid reduced curve,and let X be a formal model of X with specialfibre X k. Let x be a closed point of X k,and let X x be the formalfibre of X at x,which is a non quasi-compact rigid space and which consists of the set of points of X which reduce to the point x.The structure of the boundary of X x is well known and depends functorially onthe normalisation of the complete local ringˆO Xk ,x(cf.[Bo-Lu-1]).Namely this boundarydecomposes into a disjoint union of semi-open annuli X i:=X x,i one corresponding to eachminimal prime idealηi ofˆO Xk ,x.Let X′:=X−X x which is a quasi-compact rigid space.Let f′:Y′→X′and f x:Y x→X x be(Galois)-covers(with group G).The(G)-cover f′:Y′→X′extends to(G)-covers f i:Y i→X i of each of the components of the boundary of X x,and the germ of such an extension is unique(cf.[Ra]).A(G)-patching data in this context are(G-equivariant)isomorphisms between the germs of f i:Y i→X i and the restriction of the initial(G)-cover f x:Y x→X x to X i.The rigid patching result is that given a(G)-patching data as above then there exists a unique,up to isomorphism, (G)-cover f:Y→X which induces the above covers above X′and X x when restricted to this analytic subspaces.X1.5.Local-global principle.As a direct consequence of the above patching results one obtains a local-global principle,which is certainly well known to the experts,for lifting of covers of curves.More precisely we have the following:1.6.Proposition.let X be a proper andflat algebraic(or formal)R-curve and let Z:={x i}n i=1be afinite set of closed points of X.Let f k:Y k→X k be afinite generically separable(Galois)-cover(of group G)whose branch locus is contained in Z.Assume that for each i∈{1,n}there exists a(Galois)-cover f i:Y i→SpfˆO X,xi(of group G)whichlifts the coverˆY k,i→SpecˆO Xk ,x iinduced by f k,whereˆY k,i denotes the completion of Y kabove x i.Then there exists a unique,up to isomorphism,(Galois)-cover f:Y→X(of group G)which lifts the cover f k,and which is isomorphic to the cover f i when pulled back to SpfˆO X,xi,for each i∈{1,n}.Proof.After passing to the formal completion of X along its specialfibre we may reduced to the case where X is a formal R-curve.We treat the case where Z={x}consists of one point(the general case is similar).Let U k:=X k−{x},and let U be a formal open in X whose specialfibre equals U k.The´e tale cover f′k:V k→U k induced by f k aboveU k can be lifted,uniquely,by the theorems of lifting of´e tale covers(cf.[Gr])to an´e tale formal cover f′:V→U.Let{℘i}n i=1be the minimal prime ideals ofˆO X,x which containbe the formal completion of the localisation ofˆO X,x at π,and let X i:=X x,i:=SpfˆO x,℘i℘i.We have canonical morphisms X i→X,and X i→SpfˆO X,x.The cover f′(resp the given cover f i:Y i→SpecˆO X,x)induces(by pull back)a cover f′i:Y i→X i(resp.aicover f i:Y i→X i).For each i∈{1,n},the cover f i and f′i by construction are isomorphic when restricted to the specialfibre Spec k((t i))of X i.Since both f i and f′i are´e tale and X i is local and complete we deduce that they are isomorphic.Hence we obtain a patchingin order to data which allows us to patch the covers f′:V→U and f i:Y i→SpfˆO X,xiobtain a cover f:Y→X with the required properties.Now thanks to the formal GAGA theorem this cover is algebraic f:Y→X and has the desired properties.Moreover if the starting datas are Galois then the constructed cover is also Galois with the same Galois group.1.7.Remark.Although the formal patching result1.2and the rigid patching result1.4 are equivalent,we opted in this paper to use the formal patching result and the framework of formal geometry since this seems to be more convenient for most readers.However it should be clear that one could also use the framework of rigid geometry and adapt the content of this paper to this setting.putation of vanishing cycles.The main result of this section is2.4which gives a formula which compares the dimensions of the space of vanishing cycles in a Galois cover˜f:Y→X of group Z/p Z between formal germs of R-curves,where R is a complete discrete valuation ring of in-equal characteristic which contains a primitive p-th root of unity,where p is the residue characteristic,in terms of the degeneration type of˜f above the boundaries of X.2.1.In this section we consider a complete discrete valuation ring R of inequal character-istic,with residue characteristic p>0,and which contains a primitive p-th root of unity ζ.We denote by K the fractionfield of R,πa uniformising parameter of R,k the residue field of R,andλ:=ζ−1.We also denote by v K the valuation of K which is normalised by v K(π)=1.We assume that the residuefield k is algebraically closed.By a (formal)R-curve we mean a(formal)R-scheme offinite type which is normal,flat,and whosefibres have dimension1.For an R-scheme X,we denote by X K:=X×Spec R Spec K the genericfibre of X,and X k:=X×Spec R Spec k its specialfibre.In what follows by a (formal)germ X of an R-curve we mean that X:=Spec O X,x is the(resp.X:=SpfˆO X,x is the formal completion of the)spectrum of the local ring of an R-curve X at a closed point x.Let O x be the local ring of X k at x.Letδx:=dim k˜O x/O x where˜O x is the normalisation of O x in its total ring of fractions,and let r x be the number of maximalideals in˜O x.The contribution to the arithmetic genus of the point x is by definition g x:=δx−r x+1.We will call the integer g x the genus of the point x.The following lemma is easy to prove(cf.for example[Bo-Lu-1]).2.1.1.Lemma.Let X k be a proper reduced algebraic curve over k.Let˜X k→X k be the normalisation of X k,and let{X i}i∈I be the irreducible components of˜X k.Let {x j}j∈J be the singular point of X k,which we assume to be rational.Let g(X k)(resp. g(X i))be the arithmetic genus of X k(resp.the arithmetic genus of X i).Then g(X k)=i∈I g(X i)+j∈Jg xj.2.2.Let f:Y→X be afinite cover between R-curves.Assume that the specialfibres X k and Y k are reduced.Let y be a closed point of Y and let x be its image in X,which we assume to be a rational point.Let(x j)j∈J be the points of the normalisation˜X k of X k above x,and for afixed j let(y i,j)i∈Ijbe the points of the normalisation˜Y k of Y k which are above x j.Assume that the morphism f k:Y k→X k is generically´e tale.Under this assumption we have the following local Riemann-Hurwitz formula which is due to Kato (cf.[Ka],and[Ma-Yo]):(1)(g y+δy−1)=n(g x+δx−1)+d K−d w kWhere n is the local degree at y,which is the degree of the morphism SpecˆO Y,y→SpecˆO X,x between the completion of the local rings of Y(resp X)at the point y(resp. x),d K is the degree of the divisor of ramification in the morphism Spec(ˆO Y,y⊗R K)→Spec(ˆO X,x⊗R K).Let d w i,j:=v xj (δyi,j,x j)−e i,j+1,whereδyi,j,x jis the discriminantideal of the extensionˆO˜X k,x j →ˆO˜Y k,y i,jof complete discrete valuation ring,and e i,j itsramification index.The integer d w k is equal to the sumi,jd w i,j.In2.4we will obtain aformula similair to(1)in the case where f is Galois of group Z/p Z and which includes the case where f k is generically radicial.pactification process.Let X:=SpfˆO X,x be the formal germ of an R-curve at a closed point x.Let˜f:Y→X be a Galois cover of group Z/p Z with Y local. We assume that the specialfibre of Y k is reduced(this can alaways be achieved after a finite extension of R).We will construct a compactification of the above cover˜f which will allows us to compute the arithmetic genus of the closed point of Y.More precisely we will construct a Galois cover f:Y→X of degree p,between proper algebraic R-curves,a closed point y∈Y and its image x=f(y),such that the formal germ of X(resp.Y)at x (resp.at y)equals X(resp.Y),and such that the Galois cover f x:SpfˆO Y,y→SpfˆO X,x induced by f between the formal germs at y and x is isomorphic to the above given cover ˜f:Y→X.The construction of such a compactification is well known in the case where˜f has´e tale reduction type on the boundaries(cf[Ma-Yo]and[Ra-2]).In the case of radicialreduction type of degree p on the boundaries one is able to carry out such a construction using the formal patching result in1.2and the result3.1in[Sa].In fact it suffices to be able to treat the case of one boundary,which is easily done using the next proposition and the formal patching result.2.3.1.Proposition.Let D:=Spf R<1/T>be the formal closed disc centered at ∞.Let D:=Spf R[[T]]{T−1},and let D→D be the canonical morphism.Let˜f:Y→D be a non trivial torsor under afinite andflat R-group scheme of rank p,such that the specialfibre of Y is reduced.Then there exists a Galois cover f:Y→D with group Z/p Z whose pull back to D is isomorphic to the above given torsor˜f.More precisely,with the same notations as in[Sa]3.1we have the following depending on the several cases that occur there:case a)consider the cover f:Y→D given generically by an equation Z p=λp T m+1.This cover is an´e tale torsor above D under the group scheme H vK (λ)and induces an´e taletorsor f k:Y k→D k in reduction.Moreover the genus of the smooth compactification of Y k equals(m−1)(p−1)/2.case b-1)Consider the cover f:Y→D given generically by an equation Z p=T−r where r:=p−h.This cover is ramified at the genericfibre only above the point at infinity,thefinite morphism f k:Y k→X k is aµp-torsor outside infinity,and Y k is smooth at infinity.Moreover the genus of the smooth compactification of Y k equals0.case b-2)Consider the cover f:Y→D given generically by an equation Z p= T−α(T−m+1),whereαis an integer such that m+α≡0mod(p).This cover is ramified at the genericfibre above infinity and above the distincts m-th root of unity.Thefinite morphism f k:Y k→D k is aµp-torsor outside infinity and the distincts m-th root of unity, and Y k is smooth.Moreover the genus of the smooth compactification of Y k equals0.case c)First if m≤0consider the cover f:Y→D given generically by an equation Z p=1+πnp T m.This cover is a torsor under the group scheme H n,and its specialfibre f k:Y k→X k is a torsor underαp.The affine curve Y k has a unique singular point y which is the point above infinity and g y=(−m−1)(p−1)/2.Secondly if m≥0consider the cover f:Y→D given generically by an equation Z p=T−α(T−m+πpn)whereαis as in b-2.This cover is ramified above infinity and the m distinct roots ofπ−np.Thefinite morphism f k:Y k→X k is anαp-torsor outside infinity,and the specialfibre Y k of Y is smooth.Moreover in both cases the smooth compactification of the normalisation of Y k has genus0.Proof.Case a is straitforward.In case b-1one has only to justify that Y k is smooth at infinity.the cover f is given by the equation Z p=T−r,and after using the Bezout identity one reduces to an equation Z′p=T−1from which it follows directly that the complete local ring at the point above infinity is B=R[[Z′]]hence this point is smooth.In caseb-2one deduces in a similar way as above that Y k is smooth.Case c:if m is negatif the αp -torsor f k :Y k →X k is given locally for the ´e tale topology above the point at infinity by an equation z p =t −m where t :=T mod (π).The computation of the arithmetic genus of the singularity above infinity follows then by a direct calculation (cf.example [Ra-1],or[Sai],2.9).If m is positive and in order to see that Y k is smooth one considers the Galois cover f ′:Y ′→P above the formal R -projective line P ,obtained by gluing D with the formal unit closed disc D ′:=Spf R <T >centered at 0,and given by the (same)equation Z p =1+πnp T m .The genus of the generic fibre of Y ′is (m −1)(p −1)/2.The finitemorphism f ′k :Y ′k →P k is an αp -torsor outside infinity,and outside 0coincides with themorphism f k .Above 0this torsor is given locally for the ´e tale topology by an equation z p =t m where t :=T mod (π),hence the arithmetic genus above 0equals (m −1)(p −1)/2from which one deduces that Y k issmooth.Y D and b-2)cases a) b-1)g=(-m-1)(p-1)/2yDkcase c) m<0Yk f 2.3.2.Proposition .Let X :=Spf ˆOx be the formal germ of an R -curve at a closedpoint x ,and let {X i }n i be the boundaries of X .Let ˜f :Y →X be a Galois cover of groupZ /p Z with Y local.Assume that Y k and X k are reduced.Then there exists a Galois cover f :Y →X of degree p ,between proper algebraic R -curves,a closed point y ∈Y and its image x =f (y ),such that the formal germ of X (resp.Y)at x (resp.at y )equals X(resp.Y ),and such that the Galois cover Spf ˆOY,y →Spf ˆO X,x induced by f between the formal germs at y and x is isomorphic to the above given cover ˜f:Y →X .Moreover the formal completion of X along its special fibre has a covering which consists of n closed formal discs D i which are patched with X along the boundaries D i ,and the special fibre X k of X consists of n smooth projective lines which intersect at the point x .xX kn componentsProof.Let {℘i }n i =1be the minimal prime ideals of ˆO x which contain πand which corre-spond to the branches (ηi )n i =1of X k at x ,and let D i :=Spf ˆO ℘i be the formal completionof the localisation of X at ℘i .If T i is a lifting of a uniformising parameter of the branche(ηi )of X k at x then ˆO ℘i is isomorphic to R [[T i ]]{T −1i}.For each i ∈{1,n }consider a formal closed disc D i :=Spf R <1/T i >centered at infinity,and the canonical morphism D i :=Spf R [[T i ]]{T −1i }→D i .As a consequence of the formal patching result,which isvalid for coherent sheaves (cf.[Pr]theorem 3.4),one can patch X :=Spf ˆOx with the D i ,via the choice for each i of an automorphism of D i ,in order to construct a proper formal R -curve X ,and a closed point x ∈X ,such that the formal completion of X at x equals X .The special fibre X k of X is a union of n smooth k -projective lines which intersect atthe point x .Now the given cover ˜finduces a torsor f i :Y i →D i ,under a finite and flat R -group scheme of rank p for each i ,and by the above lemma 3.3.1one can find Galois covers Y i →D i of degree p which after pull back to D i coincide with f i ,for each i ∈{1,n }.The formal patching result again allows us then to patch these covers in order to construct a Galois cover f :Y →X of degree p with the desired properties.The formal R -curve is proper.By the formal GAGA theorems X is algebraic and the Galois cover f :Y →X is alsoalgebraic.Y kX k The next result is the main one of this paper,it gives a formula which compares the dimensions of the space of vanishing cycles in a Galois cover of degree p between formal fibres.2.4.Theorem.Let X :=Spf ˆOx be the formal germ of an R -curve at a closed point x ,with X k reduced.Let ˜f:Y →X be a Galois cover of group Z /p Z with Y local,and Y k reduced.Let {℘i }i ∈I be the minimal prime ideals of ˆOx which contain πand which correspond to the branches (ηi )i ∈I of X k at x ,and let X i :=Spf ˆO ℘i be the formal completion of the localisation of X at ℘i .For each i ∈I ,the above cover ˜finduces a torsor ˜f i :Y i →X i under a finite and flat R -group scheme of rank p ,above the boundaryX i .For each i ∈I ,let (G k,i ,m i ,h i )be the reduction type of ˜f i (cf.[Sa]3.2).Let y be theclosed point of Y .Then one has the following “local Riemman-Hurwitz formula”:(2)2g y −2=p (2g x −2)+d η−d sWhere d ηis the degree of the divisor of ramification in the morphism ˜f K :Y K →X K induced by ˜f ,where X K :=Spec(ˆO x ⊗R K )and Y K :=Spec(ˆO Y ,y ⊗R K ),and d s := i ∈I rad (m i −1)(p −1)+ i ∈I et (m i −1)(p −1),where Irad is the subset of I consisting of those i for which G k,i is radicial,and I et is the subset of I consisting of those i for which G k,i is ´e tale and m i =0.Proof.By 2.3.2one can compactify the given morphism ˜f.More precisely we constructed a Galois cover f :Y →X of degree p between proper algebraic R -curves,a closed point y ∈Y and its image x =f (y ),such that the formal germ of X (resp.Y)at x (resp.aty )equals X (resp.Y ),and such that the Galois cover Spf ˆOY,y →Spf ˆO X,x induced by f between the formal germs at y and x is isomorphic to the given cover ˜f:Y →X .The special fibre of X consists (by construction)of n -ditincts smooth projective lines which meet at the closed point x .The formal completion of X along its special fibre has a covering which consists of |I |formal closed unit discs which are patched with the formal fibre X along the boundaries X i .The above formula (2)follows then by comparing the arithmetic genus of the generic fibre Y K of Y and the one of the special fibre Y k .By the precise informations given in 3.3.1one can easily deduce that g (Y K )=pg x +(1−p )+d η/2+ i ∈I b (−m i +1)(p −1)/2+ i ∈I c,>(−m i +1)(p −1)where I b is the subset of I consisting of those i for which the degeneration data correspond to the one in case b of[Sa]3.1,and I c,>is the subset of I consisting of those i for which the degeneration data correspond to the one in case c in [Sa]3.1,and with m positif.On the other hand one has g (Y k )=g y + i ∈I a,>(−m i −1)(p −1)/2+ i ∈I c,<(−m i +1)(p −1),where I a,>is the subset of I consisting of those i for which the degeneration data correspond to the one in case a of 2.4.1with m i =0,and I c,<is the subset of I consisting of those i for which the degeneration data correspond to the one in case c in [Sa]3.1,and with m i <0.Now since Y is flat g (Y K )=g (Y k )from which directly follows the formula (2).III.Galois covers of degree p above germs of semi-stable curves.In what follows we use the same notations as in 2.1.As a consequence of the above result 2.4we will deduce some interesting results in this section in the case of a Galois cover Y →X ,where X is the formal germ of a semi-stable R -curve at a closed point.These results willplay an important role in the paper [Sa-1]in order to exhibit,and realise,the degeneration datas which describe the semi-stable reduction of Galois covres of degree p .3.1.We start with the case of a Galois cover of degree p above a germ of a smooth point.3.1.1.Proposition.Let X :=Spf R [[T ]]be the germ of a formal R -curve at a smooth point x .Let ηbe the generic point of the special fibre X k of X .The completion of the localisation of X at ηis X η:=Spf R [[T ]]{T −1},which is the boundary of X .Let f :Y →X be a Galois cover of degree p ,with Y local.Assume that the special fibre of Y is reduced.Let y be the unique closed point of Y k .Let δK :=r (p −1)be the degree of the divisor of ramification in the morphism f :Y K →X K .We distinguish two cases:case 1)Y k is unibranche at y .Let (G k ,m,h )be the degeneration type of f above the boundary X η.Then necessarily r −m −1≥0,and g y =(r −m −1)(p −1)/2.case 2)Y k has p -branches at y .Then the cover f has an ´e tale completely split reduction of type (Z /p Z ,0,0)on the boundary,i.e.the induced torsor above Spf R [[T ]]{T −1}is trivial,in which case g y =(r −2)(p −1)/2.xxcase 1)case 2)y y p branchesWith the same notations as in 3.1.1,and as an immediate consequence,one can immediately see whether the point y is smooth or not.More precisely we have the following:3.1.2.Corollary.We use the same notations as in 3.1.1Then y is a smooth point,which is equivalent to g y=0,if and only if r=m+1.This in the case of radicial reduction type on the boundary is equivalent to r=−ord(ω),whereωis the associated differential form.In particular if the reduction is of multiplicative type on the boundary,i.e.G k=µp, then g y=0only if r=1or r=0,since ord(ω)≥−1in this case.Also if r=1and g y=0 then necessarily G k=µp.Next we give some examples of Galois covers of degree p above the formal germ of a smooth point which cover all the possibilities for the genus and the degeneration type on the boundary.Both in3.1.3and3.1.4we use the same notations as in3.1.1.Wefirst begin with examples with genus0.3.1.3.Examples.The following are examples given by explicit equations of the different cases,depending on the possible degeneration type,of Galois covers f:Y→X of degree p above X=Spf R[[T]],and where g y=0.1)For m>0an integer prime to p,consider the cover given generically by the equation X p=1+λp T−m.Hier r=m+1,and this cover has a reduction of type (Z/p Z,m,0)on the boundary.2)For h∈F∗p,consider the cover given generically by the equation X p=T h.Hier r=1,and this cover has a reduction of type(µp,0,h)on the boundary.3)Consider the cover given generically by the equation X p=1+T.Hier r=0,and this cover has a reduction of type(µp,−1,0)on the boudary.4)For n<v K(λ),and m<0,consider the cover given generically by the equation X p=1+πnp T m.Hier r=−m+1,and this cover has a reduction of type(αp,−m,0)on the boudary.5)For n<v K(λ),consider the cover given generically by the equation X p=1+πnp T. Hier r=0,and this cover has a reduction of type(αp,−1,0)on the boudary.Next we give examples of Galois covers of degree p above formal germs of smooth points which lead to a singularity with positive genus.3.1.4.Examples.The following are examples given by explicit equations of the different cases,depending on the possible reduction type,of Galois covers f:Y→X of degree p above X=Spf R[[T]],and where g y>0.1)For m>0an integer prime to p,and m′>m,consider the cover given generically by the equation X p=1+λp(T−m+πT−m′).Hier r=m′+1,and this cover has a reduction of type(Z/p Z,m,0)on the boundary.Moreover the genus g y of the closed point y of Y equals(m′−m)(p−1)/2.2)For h∈F∗p,and m>0an integer prime to p,consider the cover given generically by the equation X p=T h′(T m+a),where h′is a positif integer such that m+h′≡h mod(p), and a∈πR.Hier r=m+1,and this cover has a reduction of type(µp,0,h)on the。
