大学物理基础教程答案1-6力-6

合集下载

大学基础物理学课后习题答案_含思考题(1)

大学基础物理课后答案主编：习岗高等教育出版社第一章思考题：<1-4> 解：在上液面下取A 点，设该点压强为A p ，在下液面内取B 点，设该点压强为B p 。

对上液面应用拉普拉斯公式，得 A A R p p γ20=- 对下液面使用拉普拉斯公式，得 BB 02R p p γ=- 又因为 gh p p ρ+=A B 将三式联立求解可得 ⎪⎪⎭⎫ ⎝⎛-=B A 112R R g h ργ<1-5> 答：根据对毛细现象的物理分析可知，由于水的表面张力系数与温度有关，毛细水上升的高度会随着温度的变化而变化，温度越低，毛细水上升的高度越高。

在白天，由于日照的原因，土壤表面的温度较高，土壤表面的水分一方面蒸发加快，另一方面土壤颗粒之间的毛细水会因温度升高而下降，这两方面的原因使土壤表层变得干燥。

相反，在夜间，土壤表面的温度较低，而土壤深层的温度变化不大，使得土壤颗粒间的毛细水上升；另一方面，空气中的水汽也会因为温度下降而凝结，从而使得清晨时土壤表层变得较为湿润。

<1-6> 答：连续性原理是根据质量守恒原理推出的，连续性原理要求流体的流动是定常流动，并且不可压缩。

伯努利方程是根据功能原理推出的，它的使用条件是不考虑流体的黏滞性和可压缩性，同时，还要求流动是定常流动。

如果流体具有黏滞性，伯努利方程不能使用，需要加以修正。

<1-8> 答：泊肃叶公式适用于圆形管道中的定常流动，并且流体具有黏滞性。

斯托克斯公式适用于球形物体在黏滞流体中运动速度不太大的情况。

练习题：<1-6> 解：设以水坝底部作为高度起点，水坝任一点至底部的距离为h 。

在h 基础上取微元d h ，与之对应的水坝侧面面积元d S （图中阴影面积）应为坡长d m 与坝长l 的乘积。

练习题1-6用图d h d F由图可知 osin60d sin d d hh m ==θ 水坝侧面的面积元d S 为 d d d sin 60hS l m l °== 该面积元上所受的水压力为 0d d d [(5)]sin 60hF p S p ρg h l°==+-水坝所受的总压力为 ()[]N)(103.760sin d 5d 855o0⨯=-+==⎰⎰h l h g p F F ρ（注：若以水坝的上顶点作为高度起点亦可，则新定义的高度5h h ¢=-,高度微元取法不变，即d d h h ¢=，将h ¢与d h ¢带入水坝压力积分公式，同样可解出水坝所受压力大小。

大物书后习题答案整理(杨晓峰版)-习题06

22
波向 x 轴的正方向传播，波动方程为
y
t 0.1cos[2 (
x )
] SI
22 2
y
tx Leabharlann 振动速度为v 0.1 cos[2 ( ) ]
t
22 2
弦上任一点的最大振动速度
tx 由于 cos[2 ( ) ] 1
22 2
所以v max 0.1 m s 1 0.314 m s1
习题 6-3 解答：基本思路：由旋转矢量法可知坐标原点处的初相位，然后根据题中已知的其它的物理量，写出原点处的振动方程，再写出波动方程，由波动方程可以求出在 x 150 cm 处质点的振动方程。
习题 6-1 解答：基本思路：将题中波的表达式和标准的波的表达式比较，直接得出振幅、波速、频率和波长；波函数对时间一次倒数为速度，速度对时间一次倒数为加速度，从
而可以求出最大速度和加速度；再根据波函数可以写出 x1 0.2 m 处和 x2 0.7 m 两处的相位，然后求出两点的相位差。
x 计算过程：（1）标准的波的表达式 y Acos[2 (t )]
到
2π 位移 y 0.01cos (0.25 0.1 2) 0.01cos19.75 m
0.2
速度 v
2 A
u sin
2π (ut
x)
0.025
sin 19.75
m s 1
加速度 a
2 A(
u)2
cos
2π
(ut
x)
0.0625
2
cos19.75
m s 2
习题 6-7 解答：解： (1) 通过截面的平均能流 P = 2.7 ×10−2 = 2.7 ×10−3 J⋅ s−1
22 2

大学物理1-6章课后习题答案1

二、课后习题解答1-1、一飞轮直径为0.2m ，质量为5.00kg ，t 边缘饶一轻绳，现用恒力拉绳子的一端，使其有静止均匀地加速，经0.50s 转速达10转/s 。

假定飞轮可看作实心圆柱体。

求；飞轮的角加速度及在这段时间转过的转数拉力及拉力所做的功从拉动后t=10s 时飞轮的角速度及边缘上一点的速度和切向加速度及发向速度。

解：,/1058.1,/6.12,/126,/1026.1)3(3.4921212125232202s m r a s m r a s m r v s t J J J J A t n t t z z z ⨯======⨯====-=ωβωβωωωωτ1-2、有一根长为l 、质量为m 的匀质细杆，两端各牢固的连接一个质量为m 的小球，整个系统可绕一过O 点并垂直于杆的水平轴无摩察的转动，如图。

当系统转到水平位置时，求：系统所受的和力矩系统的转动惯量系统的角加速度解：（1）设垂直纸面向里为z 轴的正方向（即力矩的正方向），合力矩为两小球及杆的重力矩之和。

mgl M M M M lmg r g dr rg rgdm M l mlmg M lmg M F r M z z zz l l l l z zzz 4341243,4190,4/34/24/34/0=+'+'=∴======'-='=⨯=--⎰⎰杆右左杆右左杆所受重力矩：其中两小球所受重力矩：ρρρθ224/34/34/34/24/34/222483748731)41(,)43()2(ml J J J J ml r dr r dm r J l m J l m J z z zz l l l l l l z z z=+'+'=∴====='='---⎰⎰杆右左杆右左杆的转动惯量：两小球的转动惯量：转动惯量之和，小球的转动惯量和杆的系统的转动惯量等于两λλ（3）由转动定理lg J M J M z z z z 3736==⇒=ββ1-3、有一质量为m 1、 m 2（m 1>m 2）两物体分别悬挂在两个半径不同的组合轮上，如图。

大学物理六习题集答案

大学物理六习题集答案大学物理六习题集答案大学物理是一门重要的基础学科，它涵盖了广泛的知识领域，包括力学、电磁学、光学等等。

在学习大学物理的过程中，做习题是非常重要的一部分，它能够帮助我们巩固知识，提高解题能力。

本文将为大家提供一些大学物理六习题集的答案，希望能够对大家的学习有所帮助。

第一题：力学题目：一个物体以速度v沿着水平方向匀速运动，突然受到一个水平方向的恒力F作用，物体在经过一段时间t后速度变为v'，求恒力F的大小。

解答：根据牛顿第二定律，力等于质量乘以加速度。

由于物体在经过一段时间t 后速度变为v'，可以得出加速度a=(v'-v)/t。

所以恒力F=m*a，其中m为物体的质量。

将a带入公式，可以得到F=m*(v'-v)/t。

第二题：电磁学题目：一根长直导线通有电流I，求导线周围的磁场强度B。

解答：根据安培定律，长直导线周围的磁场强度与电流成正比，与距离成反比。

具体公式为B=μ0*I/(2πr)，其中μ0为真空中的磁导率，约等于4π×10^-7T·m/A，r为导线到观察点的距离。

第三题：光学题目：一束光从空气射入玻璃，求光的折射角。

解答：根据斯涅尔定律，光线从一个介质射入另一个介质时，入射角和折射角满足sinθ1/sinθ2=n2/n1，其中θ1为入射角，θ2为折射角，n1为入射介质的折射率，n2为折射介质的折射率。

对于空气和玻璃的界面，空气的折射率近似为1，玻璃的折射率可以通过查表得到。

第四题：热学题目：一定质量的物体从温度T1升到温度T2，求物体所吸收的热量。

解答：物体所吸收的热量可以通过热容公式计算，即Q=m*c*(T2-T1)，其中Q为所吸收的热量，m为物体的质量，c为物体的比热容，T2-T1为温度的变化。

第五题：波动题目：一条绳子上有一定张力的波动传播，求波速。

解答：波速可以通过绳子的线密度和张力计算，即v=sqrt(T/μ)，其中v为波速，T为绳子的张力，μ为绳子的线密度。

大学物理教程第二版-第1章答案

1 -5 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s ．求：(1) 质点在运动开始后4.0 s 内的位移的大小； (2) 质点在该时间内所通过的路程；(3) t ＝4 s 时质点的速度和加速度．分析位移和路程是两个完全不同的概念．只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等．质点在t 时间内的位移Δx 的大小可直接由运动方程得到：0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了．为此,需根据0d d =tx来确定其运动方向改变的时刻t p ,求出0～t p 和t p ～t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t ＝4.0 s 时质点速度和加速度可用tx d d 和22d d t x两式计算．题 1-5 图解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x(2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t ＝0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t ＝4.0 s 时1s0.4s m 48d d -=⋅-==t t xv2s0.422m.s 36d d -=-==t t x a1 -6 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为ｓ．求： (1) 质点的运动轨迹；(2) t ＝0 及t ＝2ｓ时,质点的位矢；(3) 由t ＝0 到t ＝2ｓ内质点的位移Δr 和径向增量Δr ；分析质点的轨迹方程为y ＝f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到．对于r 、Δr 、Δr 、Δs 来说,物理含义不同,(详见题1-1分析).解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -= 这是一个抛物线方程,轨迹如图(a)所示．(2) 将t ＝0ｓ和t ＝2ｓ分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t ＝0ｓ和t ＝2ｓ时质点所在位置． (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r题 1-6 图1 -9 质点沿直线运动,加速度a ＝4 -t2 ,式中a 的单位为m·ｓ-2 ,t 的单位为ｓ．如果当t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1 ,求质点的运动方程．分析本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决．由t a d d v =和txd d =v 可得t a d d =v 和t x d d v =．如a ＝a (t )或v ＝v (t ),则可两边直接积分．如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分．解由分析知,应有⎰⎰=tt a 0d d 0vv v得 03314v v +-=t t (1)由⎰⎰=txx t x 0d d 0v得 00421212x t t t x ++-=v (2) 将t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1代入(1)、(2)得v 0＝-1 m·ｓ-1, x 0＝0.75 m于是可得质点运动方程为75.0121242+-=t t x 1 -10 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a ＝A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程．分析本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v ＝a (v )d t 分离变量为t a d )(d =v v后再两边积分．解选取石子下落方向为y 轴正向,下落起点为坐标原点．(1) 由题意知 v vB A ta -==d d (1) 用分离变量法把式(1)改写为t B A d d =-vv(2)将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v vvvv得石子速度 )e 1(Bt BA--=v 由此可知当,t →∞时,BA→v 为一常量,通常称为极限速度或收尾速度． (2) 再由)e 1(d d Bt BAt y --==v 并考虑初始条件有 t BA y t Bt y d )e 1(d 00⎰⎰--= 得石子运动方程)1(e 2-+=-Bt BAt B A y 1 -12 质点在Oxy 平面内运动,其运动方程为r ＝2.0t i ＋(19.0 -2.0t 2 )j ,式中r 的单位为m,t 的单位为s ．求：(1)质点的轨迹方程；(2) 在t 1＝1.0s 到t 2 ＝2.0s 时间内的平均速度；(3) t 1 ＝1.0ｓ时的速度及切向和法向加速度；(4) t ＝1.0s 时质点所在处轨道的曲率半径ρ．分析根据运动方程可直接写出其分量式x ＝x (t )和y ＝y (t ),从中消去参数t ,即得质点的轨迹方程．平均速度是反映质点在一段时间内位置的变化率,即tΔΔr=v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v ．切向和法向加速度是指在自然坐标下的分矢量a ｔ和a n ,前者只反映质点在切线方向速度大小的变化率,即tt te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a ｔ得到．在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ．解 (1) 由参数方程x ＝2.0t , y ＝19.0-2.0t 2消去t 得质点的轨迹方程：y ＝19.0 -0.50x 2(2) 在t 1 ＝1.00ｓ到t 2 ＝2.0ｓ时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 22222s m 0.4d d d d )(-⋅-=+=tyt x t则t 1 ＝1.00ｓ时的速度v (t )｜t ＝1ｓ＝2.0i -4.0j切向和法向加速度分别为t t y x t t ttt e e e a 222s1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t ＝1.0ｓ质点的速度大小为122s m 47.4-⋅=+=y x v v v则m 17.112==na ρv1 -18 一质点在半径为0.10 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为ｓ．(1) 求在t ＝2.0ｓ时质点的法向加速度和切向加速度．(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少？(3) t 为多少时,法向加速度和切向加速度的值相等？分析掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到．解 (1) 由于342t θ+=,则角速度212d d t tθω==．在t ＝2 ｓ时,法向加速度和切向加速度的数值分别为22s2s m 30.2-=⋅==ωr a t n2s2s m 80.4d d -=⋅==tωra t t(2) 当22212/t n t a a a a +==时,有223nt a a =,即 ()()422212243t r rt =得 3213=t此时刻的角位置为rad 15.3423=+=t θ(3) 要使t n a a =,则有()()422212243t r rt =t ＝0.55ｓ。

大学物理基础教程答案ppt课件

F
相同
在质心参照系中： aF dLC dt
LC IC
15
IC为通过质心垂直于棒轴的转动惯量，已知： IC mk 2
(0) 0
mk2 (t) (0) aF t
(t )
aF mk 2
t
在L系中若要
vQ 0
vQ vC b
F aF m t mk2 t b 0
b k2 a
2
22
R
M 2m
4-8 有一线绕圆盘半径为R、质量为m在其重量作用下滚落,显
得上端固定在天花板上。求圆盘中心从静止下落h高度时的转动
动能和质心速度?
解: 质心运动定理
mg T ma C
质心系中的角动量定理
TR 1 mR 2 d
2
dt
6
角量、线量的关系张力的作用点是瞬时不动点
aC R
i
i 末
初 Fi外
drCO
末 T
初
drCO
(1 2
i
mv
2 C末
1 2
mv
2 C初
)
(ECp末
ECp初 )
（2）
两式相加
0
1 2
mv
2 C末
mgh C
1 2
IC2 末
7
在惯性系中绳张力不作功。
v
2 C末
R 2C2 末
v
2 C
R 2C2
4
vC
gh 3
E kC
1 2
I(
vC R
)2
1 3
mgh
解：以知 1=2n接合过程中,摩擦属内力,又
无其他外力矩，角动量守恒I1 = (I1+I2)

大学物理基础教程答案

第一章质点运动学习题解答1-1质点作曲线运动,在时刻质点的位矢为,速度为,速率为,在至时间内的位移为, 路程为, 位矢大小的变化量为( 或称),平均速度为,平均速率为．(1) 根据上述情况,则必有( B )(A)(B) ，当时有(C) ，当时有(D) ，当时有(2) 根据上述情况,则必有( C )(A) ，(B) ，(C) ，(D) ，1-2一运动质点在某瞬时位于位矢的端点处,对其速度的大小有四种意见,即(1)；(2)；(3)；(4)．下述判断正确的是( D )(A) 只有(1)(2)正确(B) 只有(2)正确(C) 只有(2)(3)正确(D) 只有(3)(4)正确1-3质点作曲线运动,表示位置矢量,表示速度,表示加速度,表示路程,表示切向加速度．对下列表达式,即(1)；(2) ；(3) ；(4) 。

下述判断正确的是( D )(A) 只有(1)、(2)是对的(B) 只有(3)、(4)是对的(C) 只有(2)是对的(D) 只有(3)是对的1-4一个质点在做圆周运动时,则有( B )习题1-1图(A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变 1-5 一质点沿轴运动，其坐标与时间的关系为，则该质点速度方向沿轴正向的时间区间为( A )。

(A)(B)(C) (D)1-6 质点的运动方程为，则质点在秒时到原点的距离为m ，速度矢量为m/s 。

1-7 一质点做半径为、周期为的匀速率圆周运动，试问经过四分之一周期的时间间隔内，质点所发生的位移的大小是（），走过的路程是（）。

1-8 已知质点以初速度、加速度作直线运动（），则速度与时间的关系式为（）。

1-9 一质点沿半径米的圆周运动，其所走路程与时间的关系为，则在秒时速率为（），切向加速度的值为（）。

1-10飞机驾驶员想往正北方向航行，而风以的速度由东向西刮来，如果飞机的航速(在静止空气中的速率)，试问驾驶员应取什么航向？飞机相对于地面的速率为多少？试用矢量图说明。

大学物理基础教程答案1-6力ppt课件

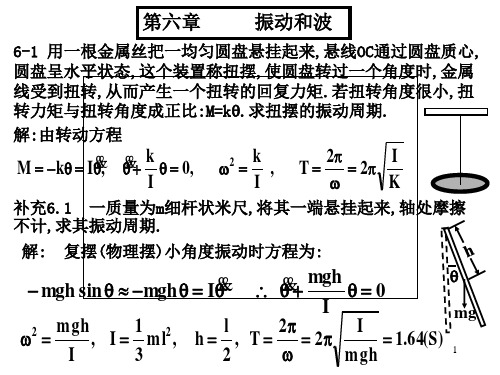
解:(1)振动频率 1 g 1.6(Hz) 2 2 l
k
(2)振幅
A
x
2 0
( v0 )2
0.02(m)
m
(3)初相位
cos1 x0 cos1 0.9 0.46(rad)
A
(v0>0取正号, v0 <0取负号)
(4)振动表达式. X=0.02cos(10t-0.46) (m)
4
最大响度的音（即拍声),问拍频是多少？音叉的频率可能是多
少？为了进一步唯一确定其值，可以在待测测音叉上滴上一点
石蜡，重做上述实验,若此时拍频变低,则说明待测音叉的频率
是多少？
解：以知T=0.5s，得拍频
f 1 2 0.5
f2 f1 2 f2 2 f1 440(Hz)
或
f2 f1 2 438(Hz)
求(1)振动的圆频率、周期、振幅和初始相位；(2)振动的速度
和加速度(函数式)；(3)振动的总能量E(4)振动的平均动能和平
均势能；(5) t =1.0秒、10秒等时刻的相位。
11
解：
(1)
x
0.5cos(8t
)
与振动表达式
x Acos(t )
3
比较便直接可得:
2 1
A 0.5(cm) , 8 T (s)
t3ln2
A A0 ,A A0 ,
16
3213
6-9 火车在铁轨上行驶，每经过铁轨接轨处即受一次震动，使装在弹簧上面的车厢上下振动。设每段铁轨长12.5米，弹簧平均负重5.5吨，而弹簧每受1.0吨力将压缩16毫米。试问，火车速度多大时，振动特别强？
解: 固有振动周期等于强迫力周期时发生共振
分深度为a.若用力稍稍压下,使其浸入水中深度为b,如图所示,然后放手,任其作自由振动,求其振动的周期和振幅.

武汉理工大学大学物理练习题1-6答案

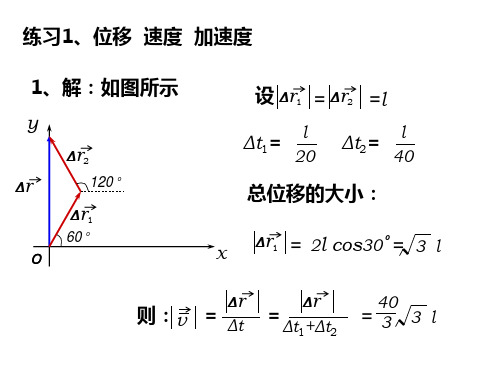
t 1s
an 3.6 1.9m/s
2
2、解：
1 2 由 θ ω 0t β t 2
代入 θ 75rad
t 5s
β 2rad/s
75 5ω0 25
求出 ω 0 10rad/s
ω0 ω β t 再由求出 t 5s 0 β
练习3、牛顿定律及其应用
②滑块相对小车的速度
v v V 0.55 m / s
∴
1.1 t 2s 0.55
练习6、角动量和角动量守恒
1、解：
r 3i 8 j L r mv 3(3i 8 j ) (5 i 6 j )
174 k (kg m / s )
2
M r F (3i 8 j ) (7 i ) 56 k (N s )
1、解：
设阻力 f = -kv
dv 由牛顿定律： f = -kv = ma = m
dt
k dv 分离变量：- dt = m v
k 0 dt m
t
dv v0 v
v
v k ln t v0 m dx v0 由 v dt m ∴ x v0 k
k t e m
∴
x
v v0
积分
v
∴
dv ktdt 2 v
t dv v0 v 2 0 ktdt
1 1 1 2 kt 得： v0 v 2
即：
1 1 2 1 kt v 2 v0
练习2、自然坐标 1、解：
圆周运动
相对运动
dx 1 ① vx dt dy 2 vy 3t dt dv x 0 ② ax dt dv y ay 6t dt

大学物理基础教程答案1-6力-6ppt课件

2 k
m1 m2
此系统作振幅为A,圆频率为.的简振动.
Al-l
5
6-4一只鸟落在树枝上每4秒摆动6次,鸟飞走后,用一千克砝码系在
鸟呆过地方树枝弯下12厘米,问这只鸟的质量是多少？解:树技与乌组成一个谐振子
kmg81.ห้องสมุดไป่ตู้6(kg/m) T2
l
3
k 2
k
9.42(ra)d mT
m2 0.92(kg)
2
2
A m v0 k(mm)
k
mm
k
2
m’ m
v0
0
x
x Acos(t ) m v0 cos( k t )
k(mm)
mm 2
补充6.4 图所示振动系统，振子是一个作纯滚动的圆柱体，以
知圆柱体的质量为m,半径为R，弹簧的倔强系数为k，并且弹簧
是系于圆柱体的中心旋转对称轴上.试求这一振动系统的频率。
解：设平衡点为弹簧原长时，又
弹簧质量不计，对圆柱体在运动
中受力有：
.
k
m
7
kxc f mxc
fR(12mR2)
1mR2 xc 2R
f 12mxc
kxc 12mxc mxc
xc (32mk)xc
22k, 3m
1(2k)1 2 23m
6-6 如图弹簧的倔强系数为k,定滑轮的质量为m’,半径为R,转动惯量为k，物体的质量为m。轴处摩擦不计，弹簧和绳的质量也不
电能q2/2c,通过电感电流为i,此时电感储有磁能Li2/2,i=dq/dt,
且 q2/2c+ Li2/2=常量,试求LC电路的固有振荡频率.
解: 1q21L2iC 2c 2

大学物理上册课后习题答案

大学物理上册课后习题答案大学物理上册课后习题答案大学物理是一门重要的基础学科，它为我们提供了理解自然界的物质和能量运动规律的工具。

然而，学习物理并不仅仅是理论知识的学习，更需要通过实践和习题的解答来巩固和应用所学的知识。

本文将为大家提供大学物理上册课后习题的答案，希望能够帮助大家更好地学习和理解物理知识。

第一章：运动的描述1. 一个物体从静止开始做匀加速直线运动，经过2秒后速度达到10m/s，求物体的加速度和位移。

答案：加速度a = (10m/s - 0m/s) / 2s = 5m/s²，位移s = (0m/s + 10m/s) / 2 ×2s = 10m。

2. 一个物体做直线运动，已知它的初速度为20m/s，加速度为4m/s²，求它在5秒内的位移。

答案：位移s = 20m/s × 5s + 1/2 × 4m/s² × (5s)² = 100m + 50m = 150m。

第二章：力学1. 一个质量为2kg的物体受到一个10N的水平力，求物体的加速度。

答案：根据牛顿第二定律F = ma，可得加速度a = F / m = 10N / 2kg = 5m/s²。

2. 一个质量为0.5kg的物体受到一个向上的力10N和一个向下的力5N，求物体的加速度。

答案：合力F = 10N - 5N = 5N，根据牛顿第二定律F = ma，可得加速度a = F / m = 5N / 0.5kg = 10m/s²。

第三章：能量守恒1. 一个质量为0.1kg的物体从地面上抛起，初速度为10m/s，求物体达到最高点时的动能、势能和总机械能。

答案：最高点时，物体的速度为0，所以动能为0；势能由重力势能计算，势能mgh = 0.1kg × 9.8m/s² × h，总机械能为动能和势能之和。

2. 一个质量为2kg的物体从高度为5m的斜面上滑下，摩擦系数为0.2，求物体滑到底部时的动能损失。

《大学物理学》第1-6章课后习题解答

大学物理学习题答案习题一答案习题一1.1 简要回答下列问题：(1) 位移和路程有何区别？在什么情况下二者的量值相等？在什么情况下二者的量值不相等？(2) 平均速度和平均速率有何区别？在什么情况下二者的量值相等？(3) 瞬时速度和平均速度的关系和区别是什么？瞬时速率和平均速率的关系和区别又是什么？(4) 质点的位矢方向不变，它是否一定做直线运动？质点做直线运动，其位矢的方向是否一定保持不变？ (5) r ∆和r ∆有区别吗？v ∆和v ∆有区别吗？0dvdt =和0d v dt=各代表什么运动？ (6) 设质点的运动方程为：()x x t =，()y y t =，在计算质点的速度和加速度时，有人先求出22r x y =+，然后根据drv dt= 及 22d r a dt =而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即22dx dy v dt dt ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭ 及 222222d x d y a dt dt ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭你认为两种方法哪一种正确？两者区别何在？(7) 如果一质点的加速度与时间的关系是线性的，那么，该质点的速度和位矢与时间的关系是否也是线性的？(8) “物体做曲线运动时，速度方向一定在运动轨道的切线方向，法向分速度恒为零，因此其法向加速度也一定为零.”这种说法正确吗？(9) 任意平面曲线运动的加速度的方向总指向曲线凹进那一侧，为什么？(10) 质点沿圆周运动，且速率随时间均匀增大，n a 、t a 、a 三者的大小是否随时间改变？ (11) 一个人在以恒定速度运动的火车上竖直向上抛出一石子，此石子能否落回他的手中？如果石子抛出后，火车以恒定加速度前进，结果又如何？1.2 一质点沿x 轴运动，坐标与时间的变化关系为224t t x -=，式中t x ,分别以m 、s 为单位，试计算：(1)在最初s 2内的位移、平均速度和s 2末的瞬时速度；(2)s 1末到s 3末的平均加速度；(3)s 3末的瞬时加速度。

大学物理基础教程答案1-6力-6

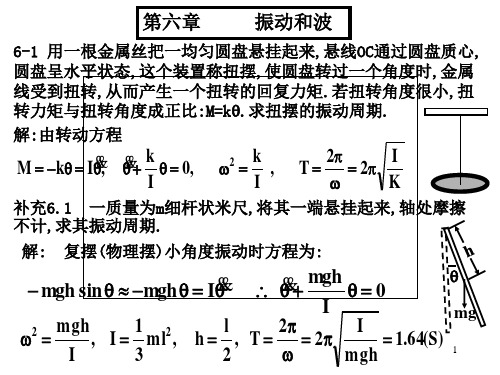
a b − 5 r r
求:(1)用a和b表示平衡位置;(2)证明其振动圆频率 = 8b ( b )3/ 4 :(1)用表示平衡位置;(2)证明其振动圆频率 ;(2) ω
m 5a
保守力平衡点f=0 解:(1)保守力平衡点保守力平衡点
5a b f =− 6 + 2 =0 r r
5a 1 / 4 r0 = ( ) b
ρgas = mg ⇒ m = ρas mg − ρg(a + x)s = m&& x ρgs g x ρgxs+ m&& = 0∴ω = = m a
2
b
a
2π a T= = 2π g ω
6-2一质量为1.0x10-3 千克的质点,作简谐振动,其振幅为2.0x10-4 一质量为1.0x10 千克的质点,作简谐振动,其振幅为2.0x10 米,质点在离平衡位置最远处的加速度为8.0 x103米/秒.(1) 试计质点在离平衡位置最远处的加速度为8.0 算质点的振动频率;(2) 质点通过平衡位置的速度;(3) 算质点的振动频率;(2) 质点通过平衡位置的速度;(3) 质点位移米时的速度;(4) ;(4)写出作用在这质点上的力作为位置为1.2 0x10-4 米时的速度;(4)写出作用在这质点上的力作为位置的函数合作为时间的函数. 的函数合作为时间的函数.
定滑轮的质量为m 半径为R, R,转动 6-6 如图弹簧的倔强系数为k,定滑轮的质量为m’,半径为R,转动物体的质量为m 轴处摩擦不计，惯量为k，物体的质量为m。轴处摩擦不计，弹簧和绳的质量也不绳与滑轮间无相对滑动,(1)试求这一振动系统的振动频率,(2) ,(1)试求这一振动系统的振动频率计,绳与滑轮间无相对滑动,(1)试求这一振动系统的振动频率,(2) 如果在弹簧处于原长时由静止释放物体m, m向下具有最大速度时如果在弹簧处于原长时由静止释放物体m, m向下具有最大速度时的正坐标, 振动表达式。开始计时, 开始计时,并令m向下运动为x的正坐标,试写出m振动表达式。解：(1)设弹簧原长l0平衡时伸长x0 (1)设弹簧原长l 平衡时伸长x 设弹簧原长为坐标原点，运动中，有: 为坐标原点，运动中， mg以伸长时m kx0= mg以x0伸长时m所在点

大学物理课后答案详解

大学物理课后答案详解第一章：力学1.1 牛顿定律的三种形式第一种形式：惯性定律牛顿的第一定律，也被称为惯性定律。

它的表述为：一个物体如果没有外力作用，将保持静止或匀速直线运动的状态。

这意味着在没有外力作用时，物体的加速度为零，速度保持不变。

这个定律的重要性在于它说明了运动的惯性特性。

举个例子，当我们在车上紧急刹车时，我们的身体会有向前的惯性，因为车突然减速，而我们的身体仍保持原来的运动状态。

第二种形式：动量定律牛顿的第二定律，也被称为动量定律。

它的表述为：一个物体的加速度正比于作用在它上面的合外力，反比于物体的质量。

通过数学表达式可以得到 F = ma，其中 F表示物体所受合外力的大小，m表示物体的质量，a表示加速度。

这个定律说明了力是一种导致物体加速度变化的物理量。

第三种形式：作用与反作用定律牛顿的第三定律，也被称为作用与反作用定律。

它的表述为：如果物体A对物体B施加了一个力，那么物体B对物体A也会施加一个大小相等、方向相反的力。

这一个定律解释了为什么当我们敲击桌子时，手感到疼痛，因为我们的手会受到桌子的反作用力。

同样地，当我们踢足球时，脚球会受到我们脚的力的影响而向前踢出。

1.2 动力学动力学是力学的一个重要分支，它研究的是物体在受力作用下的运动规律。

其中最常见的运动学参数有位移、速度和加速度。

1.2.1 位移位移是一个矢量量，它表示物体从初始位置到最终位置的改变。

位移的大小等于物体在运动过程中实际移动的距离。

位移的方向由初始位置和最终位置的连线所决定。

1.2.2 速度速度是一个矢量量，它表示物体单位时间内移动的位移。

速度的大小等于单位时间内移动的位移，而速度的方向由位移的方向和时间的方向所决定。

1.2.3 加速度加速度是一个矢量量，它表示单位时间内速度的变化量。

加速度的大小等于单位时间内速度的改变量，而加速度的方向由速度的方向和时间的方向所决定。

1.3 弹力和重力1.3.1 弹力弹力是一种垂直于两个物体接触面的力，它是由于两个物体之间的接触而产生的。

大学物理课后习题答案(全册)

《大学物理学》课后习题参考答案习题11-1. 已知质点位矢随时间变化函数形式为)ωｔsin ωｔ(cos j i R r其中为常量．求：（1）质点轨道；(2)速度和速率。

解：1）由)ωｔsin ωｔ(cos j i R r知t cos R x ωtsin R yω消去t 可得轨道方程222Ryx2）jr vt Rcos sin ωωt ωR ωdtd iRωt ωR ωt ωR ωv2122])cos ()sin [(1-2. 已知质点位矢随时间变化的函数形式为j ir )t 23(t 42，式中r 的单位为m ，t 的单位为s .求：（1）质点的轨道；（2）从0t到1t 秒的位移；（3）0t 和1t 秒两时刻的速度。

解：1）由j ir)t 23(t 42可知2t 4x t23y消去t 得轨道方程为：2)3y(x2）jir v 2t 8dtd jij i v r 24)dt2t 8(dt101Δ3）jv 2(0)jiv 28(1)1-3. 已知质点位矢随时间变化的函数形式为j ir t t 22，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。

解：1）ji r v2t 2dtd iv a2dtd 2）212212)1t(2]4)t 2[(v1tt 2dtdv a 2t22221nta aat 1-4. 一升降机以加速度a 上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。

解：以地面为参照系，坐标如图，升降机与螺丝的运动方程分别为20121att v y （1）图 1-420221gttv h y （2）21y y （3）解之2d tg a 1-5. 一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程；（3）落地前瞬时小球的td dr ，td dv ，tv d d .解：（1）t v x 0式（1）2gt21hy 式（2）jir )gt 21-h (t v (t)20（2）联立式（1）、式（2）得22v 2gx hy （3）ji r gt -v td d 0而落地所用时间gh 2t所以j i r 2gh -v t d d 0jv g td d 2202y2x)gt (vvvv 211222222[()](2)g ghg t dv dtvgt vgh 1-6. 路灯距地面的高度为1h ，一身高为2h 的人在路灯下以匀速1v 沿直线行走。

大学物理学课后习题答案-赵近芳-全

习题及解答〔全〕习题一1-1 ｜r ∆｜与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明．解：〔1〕r ∆是位移的模，∆r 是位矢的模的增量，即r ∆12r r -=，12r r r -=∆；〔2〕t d d r 是速度的模，即t d d r ==v tsd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =〔式中r ˆ叫做单位矢〕，则t ˆr ˆt r t d d d d d d r rr += 式中t rd d 就是速度径向上的分量，∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模，即t v a d d =，t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢〕，所以t v t v t v d d d d d d ττ +=式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂，超出教材规定，故不予讨论) 1-2 设质点的运动方程为x =x (t )，y =y (t )，在计算质点的速度和加速度时，有人先求出r ＝22y x +，然后根据v =t rd d ，及a ＝22d d t r 而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确？为什么？两者差异何在？解：后一种方法正确.因为速度与加速度都是矢量，在平面直角坐标系中，有j y i x r+=，jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点，其一是概念上的错误，即误把速度、加速度定义作22d d d d t r a trv ==其二，可能是将22d d d d t r tr 与误作速度与加速度的模。

大学物理1-6章课后习题答案1

⼤学物理1-6章课后习题答案1⼆、课后习题解答1-1、⼀飞轮直径为0.2m ，质量为5.00kg ，t 边缘饶⼀轻绳，现⽤恒⼒拉绳⼦的⼀端，使其有静⽌均匀地加速，经0.50s 转速达10转/s 。

假定飞轮可看作实⼼圆柱体。

求；飞轮的⾓加速度及在这段时间转过的转数拉⼒及拉⼒所做的功从拉动后t=10s 时飞轮的⾓速度及边缘上⼀点的速度和切向加速度及发向速度。

解：,/1058.1,/6.12,/126,/1026.1)3(3.4921212125232202s m r a s m r a s m r v s t J J J J A t n t t z z z ?======?====-=ωβωβωωωωτ1-2、有⼀根长为l 、质量为m 的匀质细杆，两端各牢固的连接⼀个质量为m 的⼩球，整个系统可绕⼀过O 点并垂直于杆的⽔平轴⽆摩察的转动，如图。

当系统转到⽔平位置时，求：系统所受的和⼒矩系统的转动惯量系统的⾓加速度解：（1）设垂直纸⾯向⾥为z 轴的正⽅向（即⼒矩的正⽅向），合⼒矩为两⼩球及杆的重⼒矩之和。

m gl M M M M lm g r g dr rg rgdm M l mlm g M lm g M F r M z z zz l l l l z zzz 4341243,4190,4/34/24/34/0=+'+'=∴======'-='=?=--??杆右左杆右左杆所受重⼒矩：其中两⼩球所受重⼒矩：ρρρθ224/34/34/34/24/34/222483748731(,)43()2(m l J J J J m l r dr r dm r J l m J l m J z z zz l l l l l l z z z=+'+'=∴====='='---?杆右左杆右左杆的转动惯量：两⼩球的转动惯量：转动惯量之和，⼩球的转动惯量和杆的系统的转动惯量等于两λλ（3）由转动定理lg J M J M z z z z 3736===ββ1-3、有⼀质量为m 1、 m 2（m 1>m 2）两物体分别悬挂在两个半径不同的组合轮上，如图。

大学物理课后答案第1章质点运动学习题解答

第1章质点运动学习题解答1-1如图所示,质点自A 点沿曲线运动到B 点A 点与B 点的矢径分别为°与g的头3s 内质点的位移、平均速度、平均加速度与所通过的路程解：y 5 24t 2t 3,v 24 6t 2,a 12ty y(3) y(0) 18(m ) v - 6(m/s)3v(3) v(0)2、a18(m/ s )3t 2s 时,v 0,质点作反向运动s y(2)y(0) |y(3)y(2) | 46(m)1-3 一质点沿x 轴作直线运动，图示为其v t 曲线图。

设t 0时,x 5m 。

试根据v t 图画出:(1) 质点的a t 曲线图;(2)质点的x t 曲线图。

试在图中标出位移 r 与路程s,同时对| r |与r 的意义及它们与矢径的关系进1-2 一质点沿y 轴作直线运动，其运动方程为y 5 24t 2t 3(SI)。

求在计时开始20 20t 解: 15 2.5t75 7.5t(0(2(6t 2)6)10)(1)20 20t 15 2.5t 75 7.5t(0(2(62)6)10)质点的a t曲线图如右图所示⑵v dxdt Xdxtvdt，可求得:t 2时,xdx 5 t0(20 20t)dt, 10t 2 20tt 6时,xdx 5 20(20 20t )dtt2(152.5t)dt ,5t215t 30410时,xdx20(20 20t)dt62(15 2.5t)dtt6(75 7.5t)dt , 75t 210210t 20t 5 (0 t 2)5t215t4%2 75t 4 门気105)30 (2 t 6)开口制上的覚皙變210 (6 t 10)质点的x t曲线图如右图所示。

1-4如图所示,路灯距地面的高度为H,在与路灯水平距离为s处,有一气球由离t 1 0 时,x(0) 0, y(0) 19,v x (0) 2—(0) 0地面h 处开始以匀速率v o 上升(h H )。

大学物理 - 1-6章练习附答案

第一章质点运动学1、已知一质点作直线运动，其加速度为 a ＝4+3t 2s m -⋅，开始运动时，x ＝5 m ，v =0，求该质点在t ＝10s 时的速度和位置。

解：∵ t tva 34d d +==分离变量，得 t t v d )34(d += 积分，得 12234c t t v ++= 由题知，0=t ,00=v ,∴01=c故 2234t t v += 又因为 2234d d t t t x v +==分离变量， t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x 所以s 10=t 时m70551021102s m 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v2、质点沿x 轴运动，其加速度和位置的关系为 a ＝2+62x ，a 的单位为2s m -⋅，x 的单位为 m 。

质点在x ＝0处，速度为101s m -⋅,试求质点在任何坐标处的速度值。

解： ∵ xv v t x x v t v a d d d d d d d d ===分离变量： 2d (26)d v v adx x x ==+ 两边积分得c x x v ++=322221 由题知，0=x 时，100=v ,∴50=c∴ 13s m 252-⋅++=x x v第二章质点动力学1、质量为M 的大木块具有半径为R 的四分之一弧形槽，如图所示。

质量为m 的小立方体从曲面的顶端滑下，大木块放在光滑水平面上，二者都作无摩擦的运动，而且都从静止开始，求小木块脱离大木块时的速度。

解: m 从M 上下滑的过程中，机械能守恒，以m ，M ，地球为系统，以最低点为重力势能零点，则有222121MV mv mgR +=又下滑过程，动量守恒，以m 、M 为系统，则在m 脱离M 瞬间，水平方向有0=-MV mv联立以上两式，得2MgR v m M =+2、哈雷彗星绕太阳运动的轨道是一个椭圆。