八年级数学上学期期末复习教案1(新版)苏科版
八年级数学上册《一次函数》复习学案 苏科版
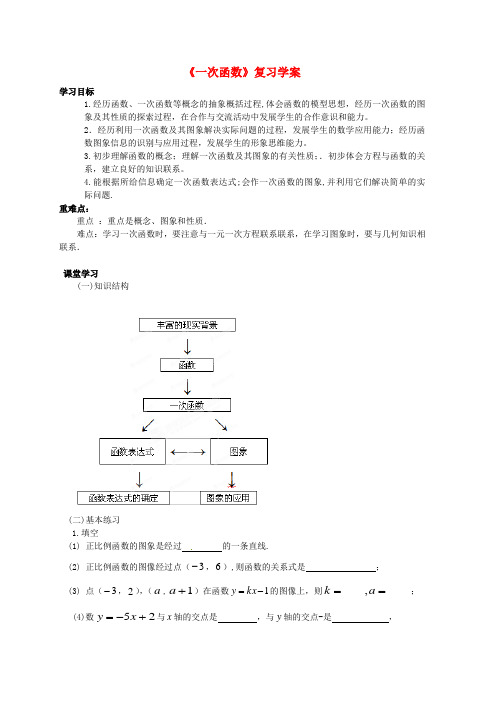
《一次函数》复习学案学习目标1.经历函数、一次函数等概念的抽象概括过程,体会函数的模型思想,经历一次函数的图象及其性质的探索过程,在合作与交流活动中发展学生的合作意识和能力。
2.经历利用一次函数及其图象解决实际问题的过程,发展学生的数学应用能力;经历函数图象信息的识别与应用过程,发展学生的形象思维能力。
3.初步理解函数的概念;理解一次函数及其图象的有关性质;.初步体会方程与函数的关系,建立良好的知识联系。
4.能根据所给信息确定一次函数表达式;会作一次函数的图象,并利用它们解决简单的实际问题.重难点:重点 :重点是概念、图象和性质.难点:学习一次函数时,要注意与一元一次方程联系联系,在学习图象时,要与几何知识相联系.课堂学习(一)知识结构(二)基本练习1.填空(1) 正比例函数的图象是经过 的一条直线.(2) 正比例函数的图像经过点(3-,6),则函数的关系式是 ;(3) 点(3-,2),(a ,1+a )在函数1-=kx y 的图像上,则______,==a k ;(4)数25+-=x y 与x 轴的交点是 ,与y 轴的交点-是 ,2.选择题(1) 下列函数中,正比例函数是 ( ) A x y 2= B xy 21= C 2x y = D 4--=x y (2)下列一次函数中,y 的值随着x 值的增大而减小的是( ) A y =10x-9 B y =-0.3x+2 C y =5x-4 D y =(3-2 )x(三)例题尝试[例题1]:已知:28(3)1m y m x m -=-++是一次函数,求m 的值.<点拨>一次函数y kx b =+中:k ≠0,自变量x 的最高次项的次数为1.解:由题意得:3m -≠0,且281m -= 29m =,3m =-或3m =(舍去)因此,3m =-.<解后反思>易错点:忽视3m -≠0这一限制条件而出错.变式:一次函数y kx b =+中,如何确定函数值的增减性?如果把本题改为28(2)1m y m x m -=-++是一次函数,且y 随着x 的增大而减小,你能求m 值吗?指明板演,统一订正..[例题2] 如图1所示,已知直线l 交x 轴于点B ,交y 轴于点A ,求:(1)y 与x 的函数关系式;(2) AOB 的周长和面积;<点拨>(1)确定一次函数的表达式,就是求待定系数k ,b .一般已知直线上两双不同对应值可以得到两个方程,求出k ,b .(2)第二小题,是涉及函数与几何的综合题,根据勾股定理、三角形有关性质等知识,运用数形结合的思想求得.解:(1)直线l 中,设:y kx b =+,点A (0,2)在直线上,20,2k b b ∴=⨯+=;又B (3,0)在直线上,2032,3k k =+=-; 因此,223y x =-+. (2)从图象观察得,OA=2,OB=3,∴由勾股定理得,AB ==∴ AOB 的周长为:; ∴ AOB 的面积为:S 1123322OA OB ==⨯⨯= (单位平方)<解后反思>易错点:用坐标表达线段长度时,要注意加绝对值符号,如P (0,-7),则OP=|-7|=7 本例题由学生回答,师板书.变式:如果本题改为直线2y kx =-+交x 轴于点A ,交y 轴于点B ,且 AOB 的面积为3,求k 的值.指名板演,统一订正.[例题3]妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系 如折线图所示:根据图象解答下列问题:1.洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?2.已知洗衣机的排水速度为每分钟19升;○1求排水时y 与x 之间的关 系式。
八年级上册数学期末复习教案

八年级上册数学期末复习教案八年级上册数学期末复习教案1一、内容和内容解析1.内容二次根式的性质。
2.内容解析本节教材是在学生学习二次根式概念的基础上,结合二次根式的概念和算术平方根的概念,通过观察、归纳和思考得到二次根式的两个基本性质.对于二次根式的性质,教材没有直接从算术平方根的意义得到,而是考虑学生的年龄特征,先通过“探究”栏目中给出四个具体问题,让学生学生根据算术平方根的意义,就具体数字进行分析得出结果,再分析这些结果的共同特征,由特殊到一般地归纳出结论.基于以上分析,确定本节课的教学重点为:理解二次根式的性质.二、目标和目标解析1.教学目标(1)经历探索二次根式的性质的过程,并理解其意义;(2)会运用二次根式的性质进行二次根式的化简;(3)了解代数式的概念.2.目标解析(1)学生能根据具体数字分析和算术平方根的意义,由特殊到一般地归纳出二次根式的性质,会用符号表述这一性质;(2)学生能灵活运用二次根式的性质进行二次根式的化简;(3)学生能从已学过的各种式子中,体会其共同特点,得出代数式的概念.三、教学问题诊断分析二次根式的性质是二次根式化简和运算的重要基础.学生根据二次根式的概念和算术平方根的意义,由特殊到一般地得出二次根式的性质后,重在能灵活运用二次根式的性质进行二次根式的化简和解决一些综合性较强的问题.由于学生初次学习二次根式的性质,对二次根式性质的灵活运用存在一定的困难,突破这一难点需要教师精心设计好每一道习题,让学生在练习中进一步掌握二次根式的性质,培养其灵活运用的能力.本节课的教学难点为:二次根式性质的灵活运用.四、教学过程设计1.探究性质1问题1 你能解释下列式子的含义吗?,,, .师生活动:教师引导学生说出每一个式子的含义.【设计意图】让学生初步感知,这些式子都表示一个非负数的算术平方根的平方.问题2 根据算术平方根的意义填空,并说出得到结论的依据.; ; ; .师生活动学生独立完成填空后,让学生展示其思维过程,说出得到结论的依据.【设计意图】学生通过计算或根据算术平方根的意义得出结论,为归纳二次根式的性质1作铺垫.问题 3 从以上的结论中你能发现什么规律?你能用一个式子表示这个规律吗?师生活动:引导学生归纳得出二次根式的性质: ( ≥0).【设计意图】让学生经历从特殊到一般的过程,概括出二次根式的性质1,培养学生抽象概括的能力.例2 计算(1) ;(2) .师生活动:学生独立完成,集体订正.【设计意图】巩固二次根式的性质1,学会灵活运用.2.探究性质2问题4 你能解释下列式子的含义吗?,,, .师生活动:教师引导学生说出每一个式子的含义.【设计意图】让学生初步感知,这些式子都表示一个数的平方的算术平方根.问题5 根据算术平方根的意义填空,并说出得到结论的依据.= , = , = , = .师生活动学生独立完成填空后,让学生展示其思维过程,说出得到结论的依据.【设计意图】学生通过计算或根据算术平方根的意义得出结论,为归纳二次根式的性质2作铺垫.问题 6 从以上的结论中你能发现什么规律?你能用一个式子表示这个规律吗?师生活动:引导学生归纳得出二次根式的性质: ( ≥0)【设计意图】让学生经历从特殊到一般的过程,概括出二次根式的性质2,培养学生抽象概括的能力.例3 计算(1) ;(2) .师生活动:学生独立完成,集体订正.【设计意图】巩固二次根式的性质2,学会灵活运用.3.归纳代数式的概念问题7 回顾我们学过的式子,如,,,,,,, ( ≥0),这些式子有哪些共同特征?师生活动:学生概括式子的共同特征,得出代数式的概念.【设计意图】学生通过观察式子的共同特征,形成代数式的概念,培养学生的概括能力.4.综合运用(1)算一算:; ; ; .【设计意图】设计有一定综合性的题目,考查学生的灵活运用的能力,第(2)、(3)、(4)小题要特别注意结果的符号.(2)想一想:中,的取值范围是什么?当≥0时,等于多少?当时,又等于多少?【设计意图】通过此问题的设计,加深学生对的理解,开阔学生的视野,训练学生的思维.(3)谈一谈你对与的认识.【设计意图】加深学生对二次根式性质的理解.5.总结反思(1)你知道了二次根式的哪些性质?(2)运用二次根式性质进行化简需要注意什么?(3)请谈谈发现二次根式性质的思考过程?(4)想一想,到现在为止,你学习了哪几类字母表示数得到的式子?说说你对代数式的认识.6.布置作业:教科书习题16.1第2,4题.五、目标检测设计1. ; ; .【设计意图】考查对二次根式性质的理解.2.下列运算正确的是( )A. B. C. D.【设计意图】考查学生运用二次根式的性质进行化简的能力.3.若,则的取值范围是 .【设计意图】考查学生对一个数非负数的算术平方根的理解.4.计算: .【设计意图】考查二次根式性质的灵活运用.八年级上册数学期末复习教案2教学目标1.等腰三角形的概念.2.等腰三角形的性质.3.等腰三角形的概念及性质的应用.教学重点: 1.等腰三角形的概念及性质. 2.等腰三角形性质的应用.教学难点:等腰三角形三线合一的性质的理解及其应用.教学过程Ⅰ.提出问题,创设情境在前面的学习中,我们认识了轴对称图形,探究了轴对称的性质,•并且能够作出一个简单平面图形关于某一直线的轴对称图形,•还能够通过轴对称变换来设计一些美丽的图案.这节课我们就是从轴对称的角度来认识一些我们熟悉的几何图形.来研究:①三角形是轴对称图形吗?②什么样的三角形是轴对称图形?有的三角形是轴对称图形,有的三角形不是.问题:那什么样的三角形是轴对称图形?满足轴对称的条件的三角形就是轴对称图形,•也就是将三角形沿某一条直线对折后两部分能够完全重合的就是轴对称图形.我们这节课就来认识一种成轴对称图形的三角形──等腰三角形.Ⅱ.导入新课:要求学生通过自己的思考来做一个等腰三角形.作一条直线L,在L上取点A,在L外取点B,作出点B关于直线L的对称点C,连结AB、BC、CA,则可得到一个等腰三角形.等腰三角形的定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.同学们在自己作出的等腰三角形中,注明它的腰、底边、顶角和底角.思考:1.等腰三角形是轴对称图形吗?请找出它的对称轴.2.等腰三角形的两底角有什么关系?3.顶角的平分线所在的直线是等腰三角形的对称轴吗?4.底边上的中线所在的直线是等腰三角形的对称轴吗?•底边上的高所在的直线呢?结论:等腰三角形是轴对称图形.它的对称轴是顶角的平分线所在的直线.因为等腰三角形的两腰相等,所以把这两条腰重合对折三角形便知:等腰三角形是轴对称图形,它的对称轴是顶角的平分线所在的直线.要求学生把自己做的等腰三角形进行折叠,找出它的对称轴,并看它的两个底角有什么关系.沿等腰三角形的顶角的平分线对折,发现它两旁的部分互相重合,由此可知这个等腰三角形的两个底角相等,•而且还可以知道顶角的平分线既是底边上的中线,也是底边上的高.由此可以得到等腰三角形的性质:1.等腰三角形的两个底角相等(简写成“等边对等角”).2.等腰三角形的顶角平分线,底边上的中线、•底边上的高互相重合(通常称作“三线合一”).由上面折叠的过程获得启发,我们可以通过作出等腰三角形的对称轴,得到两个全等的三角形,从而利用三角形的全等来证明这些性质.同学们现在就动手来写出这些证明过程).如右图,在△ABC中,AB=AC,作底边BC的中线AD,因为所以△BAD≌△CAD(SSS).所以∠B=∠C.]如右图,在△ABC中,AB=AC,作顶角∠BAC的角平分线AD,因为所以△BAD≌△CAD.所以BD=CD,∠BDA=∠CDA= ∠BDC=90°.[例1]如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求:△ABC各角的度数.分析:根据等边对等角的性质,我们可以得到∠A=∠ABD,∠ABC=∠C=∠BDC,•再由∠BDC=∠A+∠ABD,就可得到∠ABC=∠C=∠BDC=2∠A.再由三角形内角和为180°,•就可求出△ABC的三个内角.把∠A设为x的话,那么∠ABC、∠C都可以用x来表示,这样过程就更简捷.解:因为AB=AC,BD=BC=AD,所以∠ABC=∠C=∠BDC.∠A=∠ABD(等边对等角).设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x.于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,解得x=36°. 在△ABC中,∠A=35°,∠ABC=∠C=72°.[师]下面我们通过练习来巩固这节课所学的知识.Ⅲ.随堂练习:1.课本P51练习 1、2、3. 2.阅读课本P49~P51,然后小结.Ⅳ.课时小结这节课我们主要探讨了等腰三角形的性质,并对性质作了简单的应用.等腰三角形是轴对称图形,它的两个底角相等(等边对等角),等腰三角形的对称轴是它顶角的平分线,并且它的顶角平分线既是底边上的中线,又是底边上的高.我们通过这节课的学习,首先就是要理解并掌握这些性质,并且能够灵活应用它们.Ⅴ.作业:课本P56习题12.3第1、2、3、4题.板书设计12.3.1.1 等腰三角形一、设计方案作出一个等腰三角形二、等腰三角形性质: 1.等边对等角 2.三线合一八年级上册数学期末复习教案3教学目标1、理解并掌握等腰三角形的判定定理及推论2、能利用其性质与判定证明线段或角的相等关系.教学重点:等腰三角形的判定定理及推论的运用教学难点:正确区分等腰三角形的判定与性质,能够利用等腰三角形的判定定理证明线段的相等关系.教学过程:一、复习等腰三角形的性质二、新授:I提出问题,创设情境出示投影片.某地质专家为估测一条东西流向河流的宽度,选择河流北岸上一棵树(B点)为B标,然后在这棵树的正南方(南岸A点抽一小旗作标志)沿南偏东60°方向走一段距离到C处时,测得∠ACB为30°,这时,地质专家测得AC 的长度就可知河流宽度.学生们很想知道,这样估测河流宽度的根据是什么?带着这个问题,引导学生学习“等腰三角形的判定”.II引入新课1.由性质定理的题设和结论的变化,引出研究的内容——在△ABC中,苦∠B=∠C,则AB= AC吗?作一个两个角相等的三角形,然后观察两等角所对的边有什么关系?2.引导学生根据图形,写出已知、求证.2、小结,通过论证,这个命题是真命题,即“等腰三角形的判定定理”(板书定理名称).强调此定理是在一个三角形中把角的相等关系转化成边的相等关系的重要依据,类似于性质定理可简称“等角对等边”.4.引导学生说出引例中地质专家的测量方法的根据.III例题与练习1.如图2其中△ABC是等腰三角形的是 [ ]2.①如图3,已知△ABC中,AB=AC.∠A=36°,则∠C______(根据什么?).②如图4,已知△ABC中,∠A=36°,∠C=72°,△ABC是______三角形(根据什么?).③若已知∠A=36°,∠C=72°,BD平分∠ABC交AC于D,判断图5中等腰三角形有______.④若已知 AD=4cm,则BC______cm.3.以问题形式引出推论l______.4.以问题形式引出推论2______.例:如果三角形一个外角的平分线平行于三角形的一边,求证这个三角形是等腰三角形.分析:引导学生根据题意作出图形,写出已知、求证,并分析证明.练习:5.(l)如图6,在△ABC中,AB=AC,∠ABC、∠ACB的平分线相交于点F,过F作DE//BC,交AB于点D,交AC于E.问图中哪些三角形是等腰三角形?(2)上题中,若去掉条件AB=AC,其他条件不变,图6中还有等腰三角形吗?练习:P53练习1、2、3。
八年级数学上册期末复习教学案-苏科版
期末复习教学案(1)-----轴对称与轴对称图形一、知识点:1. 什么叫轴对称:如果把一个图形沿着某一条直线折叠后,能够与另一个图形重合,那么这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做对称点。
2. 什么叫轴对称图形:如果把一个图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
3.轴对称与轴对称图形的区别与联系: 区别:①轴对称是指两个图形沿某直线对折能够完全重合,而轴对称图形是指一个图形的两个部分沿某直线对折能完全重合。
②轴对称是反映两个图形的特殊位置、大小关系;轴对称图形是反映一个图形的特性。
联系:①两部分都完全重合,都有对称轴,都有对称点。
②如果把成轴对称的两个图形看成是一个整体,这个整体就是一个轴对称图形;如果把一个轴对称图形的两旁的部分看成两个图形,这两个部分图形就成轴对称。
常见的轴对称图形有:圆、正方形、长方形、菱形、等腰梯形、等腰三角形、等边三角形、角、线段、相交的两条直线等。
4.线段的垂直平分线: 垂直并且平分一条线段的直线,叫做这条线段的垂直平分线。
(也称线段的中垂线)ﻩ 5.轴对称的性质:⑴成轴对称的两个图形全等。
⑵如果两个图形成轴对称,那么对称轴是对称点连线的垂直平分线。
6.怎样画轴对称图形:画轴对称图形时,应先确定对称轴,再找出对称点。
二、举例:例1:判断题:① 角是轴对称图形,对称轴是角的平分线; ( ) ②等腰三角形至少有1条对称轴,至多有3条对称轴; ( ) ③关于某直线对称的两个三角形一定是全等三角形; ( ) ④两图形关于某直线对称,对称点一定在直线的两旁。
( )例2:下图曾被哈佛大学选为入学考试的试题.请在下列一组图形符号中找出它们所蕴含的内在规律,然后把图形空白处填上恰当的图形.例3:如图,由小正方形组成的L 形图中,请你用三种方法分别在下图中添画一个小正方形使它成为一个轴对称图形:例4:如图,已知:ΔAB C和直线l ,请作出ΔAB C关于直线l 的对称三角形。
苏科版八年级上册《 一次函数》复习(1)学案

苏科版八年级上册《 一次函数》复习(1)学案——基于江苏省“十二五”规划课题《实施促进式教学,提升学生学习力的研究》的学案设计常州市初中数学促进式教学吕水庚名教师工作室 丁峰 2013.01.11.【复习目标】1、掌握一次函数和正比例函数的概念,了解一次函数和正比例函数的关系.2、能结合图象理解一次函数(含正比例函数)的性质.3、能合理的运用关系式、表格、图像三种方式来解决一次函数的有关问题。
4、培养分析、类比和综合、归纳的能力和用“转化”、“数形结合”、“分类讨论”的思想与方法解决数学问题.【知识回顾】1、一次函数(正比例函数)的概念当m 时,函数(1)3m y m x =-+是一次函数解题感悟:理解一次函数概念应注意那些细节2、一次函数的图象(1)动手画一画,一次函数y=kx+b 的图像大致有几种形状,并判断k 、b 的符号解题感悟:k 、b 的符号与函数图象的关系(2)若直线y=mx+n 不过第三象限,则m 0 n 03、一次函数y=kx+b(k ≠ 0)的增减性:一次函数y=-x+1的图象过第 象限,y 随x 的增大而 。
【自主尝试】1、 已知一次函数的图像经过点(1,2),(3,-2),在平面直角坐标系中,作出这个一次函数的图像,并回答下列问题:(1) 求出函数解析式(2)直线与x 轴交点坐标是 ,与y 轴交点坐标是 ,直线与坐标轴围成的图形面积是变式题:直线l 过点(2,0),且与坐标轴围成的三角形面积是4,求直线l 的函数解析式(3)若你所画直线经过点A 1(,)2m -,点B (3,)n ,请判断m 、n 的大小,说明理由。
变式题:直线2(2)6y a x =+-过点A (,)x m ,点B (1,)x n -,请判断m 、 n 的大小,说明理由。
(4)结合图像回答当x 时,y=0;当x 时,y<0;当x 时,y>0(5)若将你所画的直线沿y 轴向下平移3个单位,得到直线的解析式是(6)若有一条直线和你所画直线平行,且过点(3,2),求这条直线的解析式。
八年级上学期数学期末复习教案

八年级数学·上新课标[人]1.进一步掌握三角形的有关线段(边、高、中线、角平分线)的概念,能正确应用三角形三边关系解题.2.巩固三角形内角、外角的概念,领会三角形内角和、外角和之间的内在联系.3.深刻理解多边形的内角和与外角和,建立三角形和多边形之间的联系.1.通过准确理解概念,领会相关知识的推导过程.2.通过必要的练习,达到巩固知识、整合知识、运用知识的目的.培养学生严密的思维习惯,初步领略分类讨论的数学思想.【重点】1.三角形三边关系以及三角形中的重要线段.2.三角形和多边形中的有关计算.【难点】三角形和多边形的相关知识的综合应用.专题一三角形三边的关系【专题分析】三角形的三边关系是不等式与几何知识的重要结合点,经常利用这种关系结合不等式进行考查.利用此定理可以判断三条线段能否组成三角形,确定三角形第三边的取值范围,也可以作为不等式计算的重要依据.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()A.5B.6C.11D.16〔解析〕已知三角形两边的长分别是4和10,∴第三边x的取值范围是6<x<14,在这个范围内,只有11符合.故选C.[解题策略]解此类题,设三角形第三条边的长为x,根据三角形的三边关系列出不等式,求出x的取值范围,找出符合条件的x值即可.【针对训练1】已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形的个数为()A.2B.3C.5D.13〔解析〕由三角形的三边关系可知11<x<15,∵x为正整数,∴x为12,13,14,则三角形的个数为3个.故选B.[方法归纳]解决这类问题时,要明确构成三角形的条件,即其他两边之差<第三边<其他两边之和,再根据条件确定具体的值.已知在ΔABC中,三边长a,b,c都是整数,且满足a>b>c,a=8,那么满足条件的三角形共有多少个?〔解析〕此题是典型的讨论类题目,为了不重复、不漏解,可以采用列表法.解:由三角形的三边关系知b+c>a,而由b>c,a=8可知b>4,且b<8,又b是整数,所以b=5,6,7,如此分类可得c,列表讨论如下:a8 8 8b 5 6 7c 4 5,4,3 6,5,4,3,2因此,满足条件的三角形共有1+3+5=9(个).[解题策略]此类题要防止重复或漏解,办法是列表,先把大边固定,然后根据三边关系限制较小的两边.【针对训练2】如图所示,点P是ΔABC内一点,试说明AB+AC>PB+PC.〔解析〕本题可适当添加辅助线解答.解:如图所示,延长CP交AB于点D.在ΔADC中,AD+AC>PC+PD,在ΔBPD中,BD+PD>BP,∴BD+PD+AD+AC>PC+PD+BP,即AB+AC+PD>PD+PC+PB,∴AB+AC>PB+PC.[解题策略]本题充分运用了三角形的三边关系.利用转化思想解决问题,相当于寻找另一种解决问题的办法.专题二三角形的高、角平分线和中线【专题分析】三角形的中线、角平分线和高是三角形的三条重要线段,它们具有十分重要的性质,三角形的高构造了垂直的条件,三角形的中线隐含线段相等,三角形的中线可以把三角形分成面积相等的两部分,三角形的角平分线提供了角相等的条件,掌握这些性质,对解与三角形有关的问题十分重要.如图所示,在ΔABC中,BD=DC,∠1=∠2,则ΔABC的一条中线是,一条角平分线是.〔解析〕在ΔABC中,BD=DC,∠1=∠2,则ΔABC的一条中线是线段AD,一条角平分线是线段BE.〔答案〕线段AD 线段BE【针对训练3】如图所示,在ΔABC中,D是BC边上的任意一点,AH⊥BC于H,图中以AH为高的三角形有 ()A.3个B.4个C.5个D.6个〔解析〕AH是图中所有三角形的高.故选D.[方法归纳]对于本题,以AH为高的三角形的个数实际就是图中三角形的总个数,即3+2+1=6.在ΔABC中,AB=AC,BD为ΔABC的中线,且BD将ΔABC的周长分为12 cm与15 cm两部分,求三角形各边长.〔解析〕根据中线的定义得到AD=CD,设AD=CD=x cm,则AB=2x cm,分类讨论:①x+2x=12,BC+x=15;②x+2x=15,BC+x=12.分别求出x和BC,即可得到三角形三边的长.解:如图所示,∵BD为ΔABC的中线,∴AD=CD.设AD=CD=x cm,则AB=2x cm.当x+2x=12,BC+x=15时,解得x=4,BC=11 cm,此时ΔABC的三边长为:AB=AC=8 cm,BC=11 cm;当x+2x=15,BC+x=12时,解得x=5,BC=7 cm,此时ΔABC的三边长为:AB=AC=10 cm,BC=7 cm.【针对训练4】如图所示,在ΔABC中(AB>BC),AC=2BC,BC边上的中线AD把ΔABC的周长分成60和40两部分,求AC和AB的长.〔解析〕先根据AD是BC边上的中线得出BD=CD,设BD=CD=x,AB=y,则AC=4x,再分AC+CD=60或AB+BD=60两种情况进行讨论即可.解:∵AD是BC边上的中线,∴BD=CD.设BD=CD=x,AB=y,则AC=4x.分为两种情况:①AC+CD=60,AB+BD=40,则4x+x=60,x+y=40,解得x=12,y=28,∴AC=4x=48,AB=28;②AC+CD=40,AB+BD=60,则4x+x=40,x+y=60,解得x=8,y=52,∴AC=4x=32,AB=52,BC=2x=16,此时不符合三角形三边关系定理.综合上述,AC=48,AB=28.专题三多边形内角和与外角和定理【专题分析】用三角形的内角和定理可以推出多边形的内角和定理及外角和定理,在推导的过程中体现了转化思想,在解有关多边形的问题,如求多边形的内角、外角、边数及对角线等问题时,这两个定理都很重要.如图所示,AB∥CD,∠CED=90°,∠AEC=35°,则∠D的大小为 ()A.65°B.55°C.45°D.35°〔解析〕∵AB∥CD,∴∠C=∠AEC=35°,∵∠D=180°-∠C-∠CED,∠CED=90°,∴∠D=180°-35°-90°=55°.故选B.[方法总结]求一个角的大小,可以先转化为求一个和它相等的角的大小,然后运用平行线的性质、三角形内角和定理等知识去解决.求角的度数常用的方法有两种:(1)直接根据条件去求,(2)运用转化思想把所求的角转化为另一个角去求.【针对训练5】已知ΔABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于()A.40°B.60°C.80°D.90°〔解析〕用代数方法根据几何图形间的数量关系建立方程是求解几何问题的重要方法.由题意得∠B=2∠A,∠C=∠A+20°,所以∠A+∠B+∠C=∠A+2∠A+∠A+20°=180°,解得∠A=40°.故选A.七边形的内角和的度数为()A.540°B.720°C.900°D.1080°〔解析〕根据多边形内角和定理可以直接计算出答案为(7-2)×180°=900°.故选C.[解题策略]此题主要考查了多边形内角和定理,关键是熟练掌握计算公式(n-2)×180°(n≥3,且n为整数).【针对训练6】若n边形的内角和为1440°,则从一个顶点出发引的对角线的条数最多是条.〔解析〕n边形从一个顶点出发引的对角线的条数为(n-3),由(n-2)×180°=1440°得n=10.故填7.一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的23,求这个多边形的边数及内角和.〔解析〕此题要结合多边形的内角与外角的关系来寻求等量关系,构建方程求解.解:设该多边形的一个内角为x°,则一个外角为23x°,依题意得x+23x=180,53x=180,x=108,360°÷(23×108°)=5, (5-2)×180°=540°.答:这个多边形的边数为5,内角和是540°.【针对训练7】一个多边形除一个内角∠A外,其余所有内角之和为2190°,你能求出这个多边形的边数及∠A的度数吗?〔解析〕根据多边形的内角和公式(n-2)·180°可知用2190除以180,商就是(n-2),余数就是与∠A相邻的外角的度数,进而可以算出这个多边形的边数.解:2190÷180=12……30,则边数n=15,这个内角∠A的度数是180°-30°=150°,故这个多边形的边数是15,∠A的度数是150°.[解题策略]解答多边形的有关问题,关键要掌握多边形的内角和公式、相邻内外角之间的互补关系、多边形的对角线的条数与边数的关系.专题四三角形的外角【专题分析】三角形每个顶点处有两个外角,它们是对顶角,所以一个三角形共有六个外角.通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.因为三角形的每个外角和与它相邻的内角是邻补角,所以由三角形的内角和是180°可推出三角形的三个外角和是360°.三角形内角和定理和三角形外角的性质是求角度及论证与角有关的结论时经常使用的理论依据,另外,在证角的不等关系时也常用到外角的性质.如图所示,在RtΔABC中,∠BAC=90°,∠B=30°,∠C=60°,AT平分∠BAC,AH⊥BC,垂足为H,则∠TAH=.〔解析〕根据三角形的外角等于与它不相邻的两个内角之和进行求解.因为AH⊥BC,所以∠TAH=90°-∠ATH.由三角形外角性质可知∠ATH=∠B+∠BAT.因为∠BAT=12∠BAC=12(180°-∠B-∠C)=90°-12(∠B+∠C),所以∠ATH=∠B+90°-12(∠B+∠C),所以∠TAH=90°-∠B-90°+12(∠B+∠C)=12(∠C-∠B)=15°.故填15°.[规律总结]三角形中,同一个顶点处的角平分线和高线的夹角等于其余两内角差(较大的角-较小的角)的一半,如本题中∠TAH=12(∠C-∠B).【针对训练8】如图所示,在折纸活动中,小明制作了一张ΔABC纸片,点D,E分别在边AB,AC上,将ΔABC沿着DE折叠压平,A与A'重合,若∠DAE=75°,则∠1+∠2等于()A.150°B.210°C.105°D.75°〔解析〕方法1:由折叠知∠DA'E=∠DAE=75°,∵∠DAE+∠AED +∠ADE =∠DA'E+∠A'ED+∠A'DE=180°,∴∠DAE+∠AED +∠ADE +∠DA'E+∠A'ED+∠A'DE=360°,∵∠1+∠AED +∠A'ED=∠2+∠ADE +∠A'DE=180°,∴∠1+∠AED +∠A'ED +∠2+∠ADE +∠A'DE=360°,∴∠1+∠2=∠DAE+∠DA'E=2∠DAE=150°.方法2:如图所示,连接AA',根据三角形外角的性质可知∠1=∠EA A'+∠E A'A ,∠2=∠DA A'+∠D A'A ,∴∠1+∠2=∠EA A'+∠E A'A +∠DA A'+∠D A'A =∠DAE+∠D A'E,由折叠知∠D A'E=∠DAE=75°,∴∠1+∠2=150°.故选A.[方法归纳]同一个问题在解决的过程中可以有不同的方法,在解答之前要认真分析题目中的已知条件,选择合理的方法进行解答.1.回顾全等三角形的概念,能熟练运用全等三角形的对应边相等、对应角相等.2.能熟练利用三角形全等的性质和判定进行相关的证明.3.进一步掌握角的平分线的性质和判定.1.在解决问题的过程中,培养学生解决问题的能力.2.让学生在证明过程中掌握推理的思路和方法.1.体验数学知识与其他知识的联系,培养积极的学习态度.2.在解决问题的过程中,体验几何证明的严谨性与表述的规范性.【重点】三角形全等的判定和性质.【难点】相关知识的综合应用.专题一三角形全等的判定与性质的综合应用【专题分析】三角形全等的判定要根据具体题目的具体情况确定采用SAS,ASA,AAS,SSS,HL中的哪个方法,在解题过程中往往要结合其性质综合运用.如图所示,AC,BD相交于点O,且OA=OC,OB=OD.求证AD∥BC.〔解析〕根据SAS证ΔAOD≌ΔCOB,推出∠A=∠C,根据平行线的判定定理即可得出结论.证明:在ΔAOD和ΔCOB中,∵{AO=OC,∠AOD=∠COB, OD=OB,∴ΔAOD≌ΔCOB(SAS),∴∠A=∠C,∴AD∥BC.【针对训练1】如图所示,点E,F分别是AD上的两点,AB∥CD,AB=CD,AF=DE.则线段CE,BF有什么数量关系和位置关系?并加以证明.〔解析〕CE和BF的关系是CE=BF(数量关系),CE∥BF(位置关系),理由是根据平行线性质求出∠A=∠D,根据SAS证ΔABF≌ΔDCE,推出CE=BF,∠AFB=∠DEC即可.解:CE和BF的数量关系是CE=BF,位置关系是CE∥BF.证明如下:∵AB∥CD,∴∠A=∠D.在ΔABF和ΔDCE中,∵{AB=CD,∠A=∠D, AF=DE,∴ΔABF ≌ΔDCE ,∴CE =BF ,∠AFB =∠DEC ,∴CE ∥BF ,即CE 和BF 的数量关系是CE =BF ,位置关系是CE ∥BF.[规律方法] 全等三角形的判定和性质是证明线段相等、线段的位置关系、角相等的重要手段.证明线段的位置和数量关系可通过先证三角形全等,然后利用全等三角形的性质来实现.专题二 全等三角形的性质及判定的实际应用【专题分析】全等三角形的知识在实际问题中的应用是常见的一种类型题,解题的关键是将实际问题抽象成几何问题来解决,一般难度不大.如图所示,要测量河岸相对的两点A ,B 之间的距离,先从B 处出发,沿与AB 成90°角的方向,向前走40米到C 处,在C 处立一根标杆,然后方向不变继续朝前走40米到D 处,在D 处转90°沿DE 方向再走28米,到达E 处,此时A ,C 与E 在同一直线上,求点A 、点B 之间的距离.〔解析〕 根据已知条件可证ΔABC ≌ΔEDC ,利用其对应边相等的性质即可求得AB 的长.解:∵先从B 处出发,沿与AB 成90°角的方向向前走,∴∠ABC =90°,易知BC =40米,CD =40米,∠EDC =90°,在ΔABC 和ΔEDC 中,{∠ABC =∠EDC =90°,BC =DC ,∠ACB =∠ECD ,∴ΔABC ≌ΔEDC ,∴AB =ED ,∵沿DE 方向再走28米,到达E 处,∴DE=28米,∴AB=28米.∴点A,点B之间的距离为28米.【针对训练2】如图所示,广场上有两根旗杆,都垂直于地面放置.已知太阳光线AB与DE是平行的,经过测量,这两根旗杆在太阳光下的影子一样长,那么这两根旗杆的高度相等吗?说说你的理由.〔解析〕根据太阳光线AB与DE平行,可得∠B=∠E,再根据两根旗杆都垂直于地面可得∠C=∠F=90°,然后利用“角边角”证明ΔABC和ΔDEF全等,根据全等三角形对应边相等即可得解.解:两根旗杆的高度相等.理由如下:∵太阳光线AB与DE是平行的,∴∠B=∠E.∵两根旗杆都垂直于地面放置,∴∠C=∠F=90°.∵两根旗杆在太阳光下的影子一样长,∴BC=EF.在ΔABC和ΔDEF中,{∠B=∠E, BC=EF,∠C=∠F,∴ΔABC≌ΔDEF(ASA),∴AC=DF,即两根旗杆的高度相等.[方法归纳]本类题考查了全等三角形的应用,根据题意找出三角形全等的条件,然后证明两三角形全等,最后根据全等三角形的性质得出线段相等.专题三角平分线的性质及判定的应用【专题分析】此部分内容单独考查时难度不大,但要注意角平分线的性质和判定方法的区别和联系.“角的平分线上的点到角两边的距离相等”这是角的平分线的性质,而“角的内部到角的两边的距离相等的点在角的平分线上”这是角的平分线的判定,性质和判定互为逆命题.如图所示,在ΔABC中,∠BAC=90°,BE平分∠ABC,ED⊥BC于D,DE=DC.求证BC=AB+AE.〔解析〕需先证ΔBDE≌ΔBAE,则BD=BA,AE=DE=DC,从而可得BC=BD+DC=AB+AE.证明:∵∠BAC=90°,BE平分∠ABC,ED⊥BC于D,∴AE=DE.∵BE是公共边,∴RtΔBDE≌RtΔBAE(HL),∴BD=BA,AE=DE=DC,∴BC=BD+DC=AB+AE.【针对训练3】如图所示,已知在RtΔABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.(1)求证BD平分∠ABC;(2)若∠A=36°,求∠DBC的度数.〔解析〕(1)根据已知条件结合角平分线的判定方法即可证明;(2)根据直角三角形的两个锐角互余求解.证明:(1)∵DC⊥BC,DE⊥AB,DE=DC,∴点D在∠ABC的平分线上,∴BD平分∠ABC.解:(2)∵∠C=90°,∠A=36°,∴∠ABC=54°,∵BD平分∠ABC,∴∠DBC=∠ABD=27°.[注意事项]在利用角的平分线的性质和判定方法时,要注意格式的规范,一定要体现“到角两边的距离”的书写格式,即要交待清楚哪些线段互相垂直.专题四利用尺规作图,作一个三角形与已知三角形全等或作一个角的平分线【专题分析】尺规作图是数学的重要知识之一,作一个角的平分线和作一个三角形与已知三角形全等是尺规作图中的基本作图,很多复杂的图形都是通过这些简单的基本图形得出来的.如图所示,已知直线l1,l2,l3表示三条相互交叉的公路,交点分别为A,B,C,现要建一个塔台,若要求它到三条公路的距离都相等,那么:(1)可选择的地点有几处?(2)你能画出塔台的位置吗?〔解析〕(1)根据角平分线的性质易得出符合条件的点有4处.(2)由角平分线的性质可知该点可在ΔABC的内部,也可以在ΔABC的外部,分别作出即可.解:(1)可选择的地点有4处.(2)能,如图所示,根据角平分线的性质,可知该点可以在ΔABC的内部,也可以在ΔABC的外部,若在ΔABC 的内部,则为两内角平分线的交点,若在ΔABC的外部,则为两内角的邻补角的平分线的交点,如图所示的P1,P2,P3,P4即为所求的塔台的位置.【针对训练4】如图所示,已知ΔABC.(1)请用直尺和圆规作一个三角形,使所作三角形与ΔABC全等.(2)请简要说明你所作的三角形与ΔABC全等的依据.〔解析〕(1)首先作一条射线,在射线上截取DF=BC,再以D为圆心,AB长为半径画弧,以F为圆心,AC 长为半径画弧,交点设为E点,即可得出符合题意的三角形.(2)利用三角形全等的判定方法得出即可.解:(1)如图所示.首先作一条射线,在射线上截取DF=BC,再以D为圆心,AB长为半径画弧,以F为圆心,AC长为半径画弧,交点设为E点,连接DE,EF,即可得出符合题意的三角形,ΔEDF即为所求.(2)在ΔEDF和ΔABC中,{DE=AB, DF=BC, EF=AC,∴ΔEDF≌ΔABC(SSS).[规律方法]在作图时要掌握角平分线的性质和判定方法,以及全等三角形的判定方法,作图要规范,要利用直尺和圆规正确地作图,保留作图痕迹.专题五分类讨论思想【专题分析】对于三角形全等的性质和判定的问题,由于已知条件的不确定性或开放性,常用到分类讨论思想.如图所示,点F,C在线段BE上,且∠1=∠2,AC=DF,若使ΔABC≌ΔDEF,则需补充的一个条件是或或.〔解析〕要使ΔABC≌ΔDEF,已知∠1=∠2,AC=DF,因此只需添加一组对应角相等或BC=EF即可得出两三角形全等的结论.〔答案〕BC=EF ∠A=∠D ∠B=∠E(答案不唯一)【针对训练5】如图所示,已知AB=AC,用“SAS”证明ΔABD≌ΔACE,还需添加一个条件:;若用“ASA”证明,还需添加一个条件:;若用“AAS”证明,还需添加一个条件:.图中除了ΔABD≌ΔACE之外,还有Δ≌Δ.〔解析〕本题要判定ΔABD≌ΔACE,已知AB=AC,∠A是公共角,具备了一组边、一组角相等,故添加AD=AE,∠C=∠B,∠ADB=∠AEC后可分别根据SAS,ASA,AAS判定ΔABD≌ΔACE.证明ΔABD≌ΔACE后可进一步证明ΔDFC≌ΔEFB.〔答案〕AD=AE ∠C=∠B ∠ADB=∠AEC DFC EFB[规律方法]本类题考查三角形全等的判定方法.判定两个三角形全等的一般方法:SSS,SAS,ASA,AAS,HL(只适用于直角三角形).同时注意:AAA,SSA不能判定两个三角形全等,根据已知条件,结合图形及判定方法正确添加条件是解答本类题的关键.专题六转化思想【专题分析】三角形全等是证明线段相等、角相等最常用的方法,证明线段(或角)相等,往往转化为证明线段(或角)所在的两个三角形全等.当线段(或角)所在的两个三角形明显不全等时,还要添加辅助线,构造全等三角形.如图所示,D,E分别是等边三角形ABC的边BC,CA延长线上的点,且CD=AE,连接AD,BE,求证AD=BE.〔解析〕根据ΔABC为等边三角形可以得到∠BAC=∠ACB=60°,AC=AB,则∠EAB=∠ACD,根据SAS即可证得ΔABE≌ΔCAD,然后根据全等三角形的对应边相等,即可证得AD=BE.证明:∵ΔABC是等边三角形,∴∠BAC=∠ACB=60°,AC=AB,∴∠EAB=∠ACD=120°.在ΔABE 和ΔCAD 中,∵{AE =CD ,∠EAB =∠DCA ,BA =AC ,∴ΔABE ≌ΔCAD (SAS),∴AD =BE.【针对训练6】 在ΔABC 中,∠ACB =2∠B ,如图(1)所示,当∠C =90°,AD 为∠BAC 的平分线时,在AB 上截取AE =AC ,连接DE ,易证AB =AC +CD.(1)如图(2)所示,当∠C ≠90°,AD 为∠BAC 的平分线时,线段AB ,AC ,CD 又有怎样的数量关系?请写出你的猜想并证明.(2)如图(3)所示,当AD 为ΔABC 的外角∠CAF 的平分线时,线段AB ,AC ,CD 又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.〔解析〕 (1)首先在AB 上截取AE =AC ,连接DE ,易证ΔADE ≌ΔADC (SAS),则可得∠AED =∠ACD ,ED =CD ,又由∠ACB =2∠B ,得∠AED =2∠B ,即∠B =∠BDE ,易得DE =CD =BE ,则可得AB =AC +CD.(2)首先在BA 的延长线上截取AE =AC ,连接ED ,易证ΔEAD ≌ΔCAD ,可得ED =CD ,∠AED =∠ACD ,又由∠ACB =2∠B ,易证DE =EB ,则可得AC +AB =CD.解:(1)猜想:AB =AC +CD.证明如下:如图(1)所示,在AB 上截取AE =AC ,连接DE ,∵AD 为∠BAC 的平分线,∴∠BAD=∠CAD.∵AD=AD,∴ΔADE≌ΔADC(SAS),∴∠AED=∠ACD,ED=CD.∵∠ACB=2∠B,∴∠AED=2∠B.∵∠AED=∠B+∠EDB,∴∠B=∠EDB,∴EB=ED,∴EB=CD,∴AB=AE+BE=AC+CD.(2)猜想:AB+AC=CD.证明如下:如图(2)所示,在BA的延长线上截取AE=AC,连接ED.∵AD平分∠EAC,∴∠EAD=∠CAD.在ΔEAD与ΔCAD中,AE=AC,∠EAD=∠CAD,AD=AD,∴ΔEAD≌ΔCAD(SAS).∴ED=CD,∠AED=∠ACD.∴∠FED=∠ACB,又∵∠ACB=2∠B,∴∠FED=2∠B,∵∠FED=∠B+∠EDB,∴∠EDB=∠B,∴EB=ED.∴EA+AB=EB=ED=CD.∴AC+AB=CD.[规律方法]在几何证明的过程中,当题目中的已知条件无法解决问题时,我们可以适当地添加辅助线来构造全等三角形,添加辅助线时要先分析题目中的已知条件,然后合理地作辅助线,辅助线添加得正确与否是解决问题的关键.专题七数学建模思想【专题分析】全等三角形在实际生活中有很多的应用.比如,测量零件内槽宽的工具——卡钳,它可以测量不能直接测量的两点间的距离.对于这些实际问题,往往是根据实际情况建立数学模型,利用数学原理解决问题.如图所示,有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,但A,B间的距离不能直接测得,请你用已学过的知识按以下要求设计测量方案.(1)画出测量图;(2)写出测量方案;(3)写出推理过程.〔解析〕(1)根据题意及所给图形,结合全等三角形的相关知识画出测量图;(2)根据画好的测量图,写出测量方案;(3)可通过证ΔACB≌ΔDCE来验证方案的合理性.解:(1)如图所示.(2)①找个能同时看见A点和B点的C点,然后连接AC并延长到D,使DC=AC;②连接BC并延长至E,使EC=BC;③测量DE的长度,即为A,B间的距离.(3)在ΔACB和ΔDCE中,{AC=DC,∠ACB=∠DCE, CB=CE,∴ΔACB≌ΔDCE(SAS),∴AB=DE.【针对训练7】某班同学到野外活动,为测量一池塘两端A,B间的距离,设计了几种方案,下面介绍两种:①如图(1)所示,先在平地上取一个可以直接到达A,B的点C,并分别延长AC到D,BC到E,使DC=AC,EC=BC,最后测出DE的长,即为A,B间的距离.②如图(2)所示,先过B点作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,测出DE的长,即为A,B间的距离.阅读后回答下列问题:(1)方案①是否可行?并说明理由.(2)方案②是否可行?并说明理由.〔解析〕(1)由题意可证明ΔACB≌ΔDCE,得出AB=DE,故方案①可行;(2)由题意可证明ΔABC≌ΔEDC,故AB=ED,故方案②可行.解:(1)方案①可行.理由如下:∵DC=AC,EC=BC且有对顶角∠ACB=∠DCE,∴ΔACB≌ΔDCE(SAS),∴AB=DE,∴测出DE的长,即为A,B间的距离.故方案①可行.(2)方案②可行.理由如下:∵AB⊥BC,DE⊥CD,∴∠ABC=∠EDC=90°.又∵BC=CD,∠ACB=∠ECD,∴ΔABC≌ΔEDC,∴AB=ED,∴测出DE的长,即为A,B间的距离.故方案②可行.[规律方法]本类题考查了全等三角形的应用.此类题带有一定的主观性,学生要根据已学过的知识对新问题进行探索,同时对基础知识进行巩固,这种题型较常见,要熟练掌握.专题八类比思想【专题分析】对于几何图形的运动问题(如平移、旋转等)以及一些规律探究题,常常会出现一个基本图形,无论从图形上还是从解题方法上都比较简单,而其他的较复杂的图形,都是由基本图形通过变化得到的,它与基本图形有很多类似的条件和结论,类比基本图形,可以解决复杂图形的问题,主要考查观察、推理、猜想的能力.如图所示,ΔABC中,AB=AC,∠BAC=90°,D,E是BC上的两点,且∠DAE=45°.将ΔAEC绕着点A顺时针旋转90°后,得到ΔAFB,连接DF.(1)请猜想DF与DE之间有何数量关系;(2)证明你的猜想.〔解析〕(1)猜想:DF=DE.(2)ΔAEC绕点A顺时针旋转90°后,得到ΔAFB,根据旋转的知识得AE=AF,∠FAB=∠EAC,而∠DAE=45°,易得∠DAF=45°,根据SAS证出ΔADF≌ΔADE,则DF=DE.解:(1)猜想:DF=DE.证明:(2)∵∠BAC=90°,∠DAE=45°,∴∠BAD+∠EAC=45°.∵将ΔAEC绕着点A顺时针旋转90°后,得到ΔAFB,∴AF=AE,∠FAB=∠EAC,∴∠FAD=∠FAB+∠BAD=45°=∠DAE.在ΔADF和ΔADE中,{AF=AE,∠FAD=∠EAD, AD=AD,∴ΔADF≌ΔADE(SAS),∴DF=DE.【针对训练8】直线CD经过∠BCA的顶点C,CA=CB.E,F是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图(1)所示,若∠BCA=90°,∠α=90°,判断EF与|BE-AF|的数量关系;②如图(2)所示,若0°<∠BCA<180°,若使①中的结论仍然成立,则∠α与∠BCA应满足什么数量关系?理由是什么?(2)如图(3)所示,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF,BE,AF三条线段之间的数量关系,并给予证明.〔解析〕(1)①由∠BCA=90°,∠α=90°可得∠CBE+∠BCE=90°,∠BCE+∠ACD=90°,可推得∠CBE=∠ACD,且已知CA=CB,∠BEC=∠CFA,可证ΔBEC≌ΔCFA,得BE=CF,EC=AF,又知EF=CF-CE,所以可得EF与|BE-AF|的关系.②只有满足ΔBEC≌ΔCFA,才有①中的结论,即∠BCE=∠CAF,∠CBE=∠ACF.由三角形内角和等于180°,可知∠α+∠BCE+∠CBE=180°,即∠α+∠BCE+∠FCA=180°,即可得到∠α+∠BCA=180°.(2)通过条件证明ΔBEC≌ΔCFA(可通过AAS证得),可得BE=CF,EC=AF,即可得到EF=EC+CF=BE+AF.解:(1)①∵∠BCA=90°,∠α=90°,∴∠CBE+∠BCE=90°,∠BCE+∠ACD=90°,∴∠CBE=∠ACD,在ΔBEC与ΔCFA中,∵{∠BEC=∠CFA,∠CBE=∠ACF, BC=CA,∴ΔBEC≌ΔCFA(AAS),∴BE=CF,EC=FA.∵EF=CF-CE,∴EF=|BE-AF|.②∠α与∠BCA应满足的数量关系是∠α+∠BCA=180°,理由如下:∵∠α+∠BCA=180°,∴∠α+∠BCE+∠FCA=180°,∵∠α+∠BCE+∠CBE=180°(三角形内角和等于180°),∴∠CBE=∠ACD,又∵∠BEC=∠CFA,CA=CB,∴ΔBEC≌ΔCFA(AAS),∴BE=CF,EC=FA,∵EF=CF-CE,∴EF=|BE-AF|.(2)EF=BE+AF.证明如下:如图所示,∵∠1+∠2+∠BCA=180°,∠2+∠3+∠CFA=180°,∠BCA=∠α=∠CFA,∴∠1=∠3.又∵∠BEC=∠CFA=∠α,CB=CA,∴ΔBEC≌ΔCFA(AAS),∴BE=CF,EC=FA,∴EF=EC+CF=BE+AF.[规律方法]本类题主要考查三角形全等的判定,涉及三角形内角和定理、线段比较长短等知识点.题目的阅读量大,因此在解决此类问题时一定要仔细阅读,理解题目中的已知条件,寻找解题思路,并要在不断地探索中发现规律和总结规律.1.进一步掌握轴对称的性质、会画轴对称图形.2.掌握等腰三角形和等边三角形的性质和判定方法.3.掌握含30°角的直角三角形的性质.1.通过练习巩固所学的知识,提高学生解决问题的能力.2.培养学生对知识的综合运用能力.通过对问题的解决,使学生树立认真、严谨的科学态度.【重点】轴对称的性质;等腰三角形和等边三角形的性质和判定.【难点】等腰三角形和等边三角形的性质和判定.专题一轴对称及轴对称图形【专题分析】轴对称和轴对称图形的概念是本章的重点,通过观察日常生活中的轴对称现象,理解轴对称图形和轴对称的概念的区别与联系;学习轴对称变换,不但要会画一个图形关于某直线对称的图形,还要学会通过轴对称设计确定最短路线等.【针对训练1】从对称轴角度看,和其他三个不一样的图形是()〔解析〕A,C,D都只有两条对称轴,只有B有无数条对称轴.故选B.[规律方法]判断某图形是否为轴对称图形(或两个图形是否成轴对称),关键是能否找到一条直线,将这个图形(或两个图形)沿着这条直线对折,使对折后的两部分(或两个图形)完全重合.如果能,就是轴对称图形(或成轴对称),这条直线就是它的对称轴.专题二利用轴对称作变换后的图形及设计图案【专题分析】利用轴对称变换设计精美图案,当对称轴改变方向时,原图形的对称图形也改变方向,一个图形经过若干次轴对称变换,再结合平移、旋转等,就可以得到非常美丽的图案.经过轴对称变换将甲图案变成乙图案的是()〔解析〕A,B,D中的甲图案通过旋转或平移,和乙图案中各点对应,均错误;C.经过轴对称变换将甲图案变成乙图案,故此选项正确.故选C.[解题策略]本题考查了利用轴对称设计图案,属于基础题,关键是掌握几何变换不改变图形的大小.【针对训练2】如图所示的是三个小正方形组成的图形,现再给你一个同样的小正方形“接”在原图形上,使其变成一个轴对称图形,请你分别在图a,b,c,d中画出不同的拼接方案,并画出对称轴.。
苏科版八年级数学上册第1章《全等三角形》复习教案

苏科版八年级数学上册第1章《全等三角形》复习教案知识梳理:1.全等三角形的由来:全等三角形是从__________分离出来的一个常用模型,从________到全等三角形是一种从_________到___________的关系,这是我们在数学学习当中常用的一种思维方法。
2.全等三角形的定义定义:_____________的两个三角形叫做全等三角形。
1.全等三角形中,对应边_______,对应角______;对应边上的________;3.全等三角形的性质2.全等三角形的对应线段对应边上的________;对应___的______________;3.全等三角形的周长,面积。
4.全等三角形的判定(4+1)1._________相等的两个三角形全等,简称“_______”(_S_):2._____和___________对应相等的两个三角形全等,简称“______”(_A_):斜三角形3._____和___________对应相等的两个三角形全等,简称“_______”(A__);4._____和___________对应相等的两个三角形全等,简称“_______”(__S);直角三角形:____________________的两个直角三角形全等,简称“________”(___):5.全等三角形的证明思路:(1)已知两边:①找夹角→ ②找直角→ ③找第三边→ ___(2)已知一边一角:①边角相对→找另外任一角→ ___②边角相邻→⎪⎩⎪⎨⎧→→→AAS ASASAS 找边的对角找边的另一邻角找角的另一邻边6.全等三角形的简单应用利用全等三角形可以测出不能(或不易)直接测量长度的线段长,例如,河宽,或利用全等测量小口瓶的内径等。
同步题型复习(一)全等的定义和性质例1.已知如图(1),≌,其中的对应边:____与____,____与____,____与____,ABC ∆DCB ∆对应角:______与_______,______与_______,______与_______。
【K12教育学习资料】八年级数学上学期期末复习教案1 (新版)苏科版

1.下列图形中:①平行四边形;②有一个角是30°的直角三角形;③长方形;④等腰三角形.其中是轴对称图形有()个
A.1个B.2个C.3个D.4个
2.下列几组数中不能作为直角三角形三边长度的是()
A. B.
C. D.
3.下列函数中,正比例函数是:()
A. B. -1C. D.
4.一次函数y=2x+3的图象不经过的象限是()
(三).解答题
9.点A(2,0),点B(4,0),点C在y轴上,如果△ABC的面积为5,求点C的坐标.
10.已知正比例函数 的图像与一次函数 的图像交于点P(3,-6)。
(1)求 、 的值;
(2)如果一次函数 的图像与 轴交于点A,求点ΔA0P的面积。
三.收取试卷。
板书设计
(用案人完成)
教学札记
江苏省新沂市第二中学八年级数学上学期期末复习教案1
课题
期末复习(1)
课型
新授课
教学目标
回顾和整理各章的知识点,使其成为知识框架。
通过试卷检测同学们对整册书的掌握情况,以便教师有针对性复习。
重点
各章节知识点
难点
各章节知识点
教法及教具
教
学
过
程
教学内容
个案调整
教师主导活动
学生主体活动
组织教学
教师分发试卷
初二年级数学期末试卷(1)
A.第一象限B.第二象限C.第三象限D.第四象限
教
学
过
程
Байду номын сангаас教学内容
个案调整
教师主导活动
学生主体活动
填空题
5、当x=时,点P(x-3,2)在y轴上。
6.已知一次函数 +3,则 =.
最新苏科版八年级(上)数学期末复习精品教学案

八年级(上)数学期末复习(1)矩形、菱形、正方形一、知识点:1、矩形的定义:有一个角是直角的平行四边形叫做矩形,通常也叫长方形。
2、矩形的性质:①矩形是特殊的平行四边形,它具有平行四边形的一切性质;②矩形既是轴对称图形也是中心对称图形,对称轴是对边中点连线所在直线,有两条,对称中心是对角线的交点。
③矩形的对角线相等; ④矩形的四个角都是直角。
3、矩形的判定:①有一个角是直角的平行四边形是矩形;②对角线相等的平行四边形是矩形;③有3个角是直角的四边形是矩形。
4、菱形的定义:有一组邻边相等的平行四边形叫做菱形。
5、菱形的性质:①菱形是特殊的平行四边形,它具有平行四边形的一切性质;②菱形既是轴对称图形也是中心对称图形,对称轴是两条对角线所在直线,对称中心是对角线的交点。
③菱形的四条边相等;④菱形的对角线互相垂直,并且每一条对角线平分一组对角。
6、菱形的判定:①有一组邻边相等的平行四边形是菱形;②四边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形。
7、菱形的面积:S 菱形=12AC ·BD 8、正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
9、正方形的性质:①正方形具有矩形的性质,同时又具有菱形的性质。
②正方形既是轴对称图形也是中心对称图形,对称轴有四条,对称中心是对角线的交点。
10、正方形的判定:①有一组邻边相等并且有一个角是直角的平行四边形是正方形;②有一组邻边相等矩形形是正方形;DCD③有一个角是直角的菱形是正方形。
11、平行四边形、矩形、菱形、正方形之间的关系:二、举例:例1:选择和填空:1.矩形ABCD 的长为5,宽为3,点E 、F 将AC 三等分,则⊿BEF 的面积为( ) A 、23; B 、35; C 、25; D 、5; 2.已知:矩形ABCD 的AB=2BC ,在CD 上取点E ,使AE=EB ,那么∠EBC 等于( ) A 、60°; B 、45°; C 、30°; D 、15°; 3.下列叙述错误的是( )A 、平行四边形的对角线互相平分;B 、矩形的对角线相等;C 、对角线互相平分的四边形是平行四边形;D 、对角线相等的四边形是矩形。
苏科版数学八年级上册复习课:第六章一次函数复习 教案

一次函数复习一、教材分析:本课是在学习完函数的概念及其表示法,学习了一次函数的有关知识后,进行全章内容的回顾与复习活动,整理全章的知识结构,概括函数研究的思想方法,抽象的思想、模型的思想、对应的思想、数形结合的思想。
二、学情分析:学生已经学习了一次函数的有关知识,能够对全章内容的回顾与复习,整理全章的知识结构。
三、学习目标:1、知识目标:了解一次函数的概念,掌握一次函数的图象和性质;能正确画出一次函数的图象,并能根据图象探索函数的性质;能利用待定系数法求一次函数的关系式。
2、能力目标:理解数形结合和分类讨论的数学思想,强化数学的建模意识,提高利用演绎和归纳进行复习的能力。
3、情感目标:通过对零散知识点的系统整理,让学生认识到事物是有规律可循的,同时帮助他们提高复习的效果,增进数学学习的兴趣。
四、教学重难点:正确求出一次函数及正比例函数的解析式,并能运用图象及性质解决问题。
五、教具准备:投影片六、教学过程;(一)复习(基本知识提炼整理)1、函数的概念2、一次函数和正比例函数概念3、一次函数和正比例函数的图像及性质(二) 情景导入: 如图是一个一次函数图像,你能说出哪些信息?合作探究:(1) 若将上题中的直线向下平移4个单位,则所得函数的表达式是此时,它也可以看作上题中的直线向 (左、右)平移 个单位得到。
(2) 直线AB 关于y 轴对称的直线的表达式是(3)若点P 是直线AB 上一动点,直线OP 平分△AOB 的面积,试求点P 的坐标(3) 若点P 是直线AB 上的一动点,当△AOP 与 △AOB 的面积之比为1:2,试求点P 的坐标。
若为2:3呢A BAB A BAB(5)若直线DF:y2=-x-1与x轴交于点F,与y轴交于点D,与直线AB:y1=x+2交于点E(1)试求点E的坐标(2)当x取何值时,y1<y2(3)试求两条直线与x轴围成的面积(三)课堂小结:今天你有哪些收获?(四)课堂作业:课课练同步AB。
八年级数学上期末复习教案

21DCBAD CB ADCBA八年级上期末复习第一章 三角形的初步知识1、 三角形的定义:由不在同一直线上的三条线段首尾顺次相接组成的图形叫做三角形.2、 三角形的分类:(1)按角分类: (2)按边分类:3、 三角形的主要线段的定义:(1)三角形的中线: 三角形中,连结一个顶点和它对边中点的线段. 表示法:① AD 是△ABC 的BC 上的中线.② BD=DC=12BC. ③ BC =2BD =2DC 注意:①三角形的中线是线段;②三角形三条中线全在三角形的内部; ③三角形三条中线交于三角形内部一点; ④中线把三角形分成两个面积相等的三角形.(2)三角形的角平分线: 三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段表示法:① AD 是△ABC 的∠BAC 的平分线.② ∠1=∠2=12∠BAC. ③ ∠BAC=2∠1=2∠2注意:①三角形的角平分线是线段;②三角形三条角平分线全在三角形的内部; ③三角形三条角平分线交于三角形内部一点;(3)三角形的高:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段. 表示法:① AD 是△ABC 的BC 上的高线.② AD⊥BC 于D. ③∠ADB=∠ADC=90°.注意:①三角形的高是线段;②锐角三角形三条高全在三角形的内部,直角三角形有两条高是边,钝角三角形有两条高在形外;③三角形三条高所在直线交于一点.4、三角形的三边关系: 三角形的任意两边之和大于第三边;任意两边之差小于第三边. 注意:(1)三边关系的依据是:两点之间线段是短;(2)围成三角形的条件是任意两边之和大于第三边. 5、 三角形的角与角之间的关系: (1)三角形三个内角的和等于180 ;三角形直角三象形 锐角三角形钝角三角形三角形等腰三角形不等边三角形底边和腰不相等的等腰三角形 等边三角形(2)三角形的一个外角等于和它不相邻的两个内角的和; (3)三角形的一个外角大于任何一个和它不相邻的内角. (4)直角三角形的两个锐角互余. 6、三角形的稳定性:三角形的三边长确定,则三角形的形状就唯一确定,这叫做三角形的稳定性. 注意:(1)三角形具有稳定性; (2)四边形没有稳定性. 7、全等三角形(1)全等三角形的概念: 能够完全重合的两个三角形叫做全等三角形。
八年级数学苏科版上册 第一单元《单元复习》教学设计 教案(1)

主备人用案人授课时间20 年月日总第课时课题第1章三角形全等复习1课型教学目标1、了解全等形及全等三角形的概念,理解全等三角形的性质2、掌握全等三角形的判定3、灵活运用全等三角形的判定定理和性质定理,证明简单的全等三角形问题重点运用全等三角形的判定定理和性质定理难点掌握角平分线的性质与判定以及综合运用角平分线的性质与判定教法及教具教学过程教师活动学生活动一课前导读思考一下几个问题1、全等形,全等三角形的定义2、全等三角形的性质有哪些?从哪几方面考虑?为什么?3、全等三角形有哪些判定?(1)文字语言(2)符号表示4、角的平分线性质和判定是什么?两者区别和联系5、证明两个三角形全等的基本思路:二自主先学例:已知:如图,AC=AB,AE=AD,∠1=∠2.求证:∠3=∠4小组讨论1. 两个三角形只有以下元素对应相等,不能判定两个三角形全等的是()A. 两角和其中一角的对边B. 两边及夹角C. 三个角D. 三条边2. 能使两个直角三角形全等的条件是( )C.一条边对应相等D.两直角边对应相等3. 在△ABC和△A′B′C′中,已知∠A=∠A′,AB= A′B′,在下面判定中错误的是( )A. 若添加条件AC=A′C′则△ABC ≌△A′B′C′B. 若添加条件BC=B′C′则△ABC ≌△A′B′C′C. 若添加条件∠B=∠B′则△ABC ≌△A′B′C′D. 若添加条件∠C=∠C′则△ABC ≌△A′B′C′4. 在△ABC和△A′B′C′中,①AB= A′B′,②BC= B′C′,③AC= A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥∠C=∠C′,则下列条件组不能保证△ABC≌△A′B′C′的是( )A.①②③B.①②⑤C.②④⑤D.①③⑤3四交流展示1、如图,AC=AD,BC=BD,图中有相等的角吗?请找出来,并说明你的理由.2、如图,BD=CD,BF⊥AC,CE⊥AB.求证:点D在∠BAC的平分线上.3、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,求∠EFD的度数.五检测反馈补充习题对应练习六课堂小结通过今天的活动你有何收获呢?七作业布置板书设计(用案人完成)当堂作业课外作业教学札记。
最新苏科版八年级数学上册《勾股定理复习课》教学设计

《勾股定理》期末专项复习教学目标:1、会用勾股定理解决较综合问题2、树立数形结合的思想教学重难点:勾股定理的综合应用教学过程:勾股定理:1、已知△ABC是直角三角形,两直角边长分别为5, 12,则斜边长为勾股定理的逆定理:2、已知三边长分别为5,12,13,则△ABC为三角形.常见的勾股数:3 4 5 ; 6 8 10 ;5 12 13;9 12 15;8 15 17 ; 9 40 41 ;9 12 15;12 16 20……一、勾股树1、如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为5,则正方形A,B,C,D的面积的和为。
S1S2S42、如图所示,图中所有三角形是直角三角形,所有四边形是正方形,s1=9,s3=144,s4=169 ,则s2= .二、分类讨论思想1、已知直角三角形的两直角边长分别是5和12,则第三边为。
2、已知直角三角形的两条边长分别是5和12,则第三边为。
3、已知在ΔABC中,AB=10,AC=17,BC边的高为8,则边BC的长为()A 21B 6C 21或 6D 以上都不对三、方程思想1、如左图所示,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=___________。
2、如右图所示,把长方形ABCD沿BD对折,使C点落在C’的位置时,BC’与AD交于E,若AB=6,BC=8,求重叠部分△BED的面积。
4、如图,铁路上A、B两点相距25km, C、D为两村庄若DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E 站的距离相等.(1)求E应建在距A多远处?(2)DE和EC垂直吗?试说明理由四、整体思想1、一个直角三角形的周长为2+ ,斜边长为2,则其面积为_______2、已知Rt△ABC中,∠C=90°,若a+b=14,c=10,则Rt△ABC的面积是_______63、一个直角三角形的周长为24cm,面积为24cm²,则斜边长为_____五、直角三角形斜边上的高的求法1.若直角三角形两条直角边长分别为5㎝,12㎝,则斜边上的高为 ____________.2.某校要把一块形状是直角三角形的废地开发为生物园,如图AC=80米,BC=60米,若线段CD为一条水渠,且D在边AB上,己知水渠的造价是10元/米,则点D在距A点多远,水渠的造价最低,最低价是多少?CB A六、勾股定理与等腰(边)三角形1、在ΔABC中, AB=AC=10, BC=12,则ΔABC 的面积为___________2、等边三角形的边长为2,则该三角形的面积为______七、勾股定理与平面直角坐标系1、在平面直角坐标系中,已知点P的坐标是(1,2),则OP的长为()八、勾股定理与最短距离问题如图,要在河边修建一个水泵站,分别向A村庄和B村庄送水,已知A、B两村庄到河边的距离分别为2km和7km,且二村庄相距13km.(1)水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置。
苏科版八年级上一次函数复习教学案
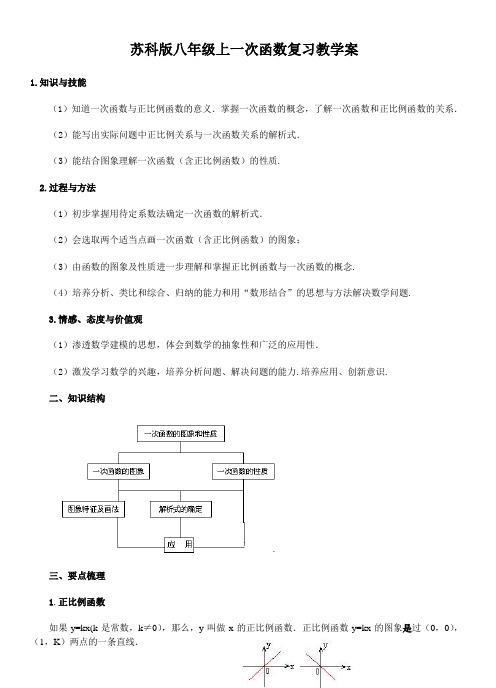
苏科版八年级上一次函数复习教学案1.知识与技能(1)知道一次函数与正比例函数的意义.掌握一次函数的概念,了解一次函数和正比例函数的关系.(2)能写出实际问题中正比例关系与一次函数关系的解析式.(3)能结合图象理解一次函数(含正比例函数)的性质.2.过程与方法(1)初步掌握用待定系数法确定一次函数的解析式.(2)会选取两个适当点画一次函数(含正比例函数)的图象;(3)由函数的图象及性质进一步理解和掌握正比例函数与一次函数的概念.(4)培养分析、类比和综合、归纳的能力和用“数形结合”的思想与方法解决数学问题.3.情感、态度与价值观(1)渗透数学建模的思想,体会到数学的抽象性和广泛的应用性.(2)激发学习数学的兴趣,培养分析问题、解决问题的能力.培养应用、创新意识.二、知识结构三、要点梳理1.正比例函数如果y=kx(k是常数,k≠0),那么,y叫做x的正比例函数.正比例函数y=kx的图象是过(0,0),(1,K)两点的一条直线.性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小2.常数函数函数y=b,(b是常数)叫做常数函数即对自变量x不管取它的允值范围内的任何一个值,函数值都取同一个常数值,这样的函数叫常函数.3.一次函数如果y=kx+b(k,b是+常数,k≠0),那么y叫做x的一次函数.直线y=kx+b,与y轴的交点是(o,b),与x轴的交点是线在x轴上的截距,叫做横截距.即直线与y轴的交点的纵坐标叫做纵截距.直线与x轴的交点的横坐标叫做横截距.4.一次函数y=kx+b的图象两个一次函数y1=k1x+b1,y2=k2x+b2的图象当一次项系数相等(k1=k2)且常数项不等(b1≠b2)时,它们平行.反之,若它们的图象平行,必有k1=k2,且b1≠b2已知:L1∥L2结论:k1=k2,b1≠b2反之,已知:k1=k2,b1≠b2L1∥L2.四.重难点重点:一次函数(含正比例函数)的图象的画法及性质.因为函数图象是研究性质的前提,而函数性质又是研究其图象的基础.一次函数的图象虽然比较简单,但同学们对函数图象不太熟悉,在画图过程中还会出现一些问题.在不断的探索实践中,促成学生对规律性的总结.难点:①选取适当两点画一次函数y=Kx+b 的图象;②结合一次函数(含正比例函数)图象说出它们的性质.五.思想方法本章主要的数学思想方法有数形结合、联系与转化、待定系数法、分类讨论、图象的平移等方法. 六、典例解析 1.有关函数的概念对有关函数概念的考查,主要是考查考生是否理解正比例函数、一次函数等有关概念.有时单独命题专门考查,有时则结合其他题目来考查.【例1】 已知正比例函数y=kx (k ≠0)的函数值y 随x 的增大而减小,则一次函数y=x +k 的图象大致是图中的 ( )1.一次函数y=2x+3的图象不经过的象限是 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限2. 已知一次函数y=kx+b 的图象如图所示,则 ( ) A.k>0,b>0 B. k<0,b<0 C. k>0,b<0 D.k<0,b>03.已知一次函数y=(m -1)x+1的图象上两点A (x 1,y 1),B (x 2,y 2),当x 1>x 2时,有y 1<y 2,那么m 的取值范围是 ( )A.m>0B. m<0C. m>1D. m<1 4.一次函数y=kx+b 与y=kbx ,它们在同一坐标系内的图象可能为 ( )xy 0xyyyy5.有下列函数:①y =6x-5, ②y =5x,③y =x +4, ④y =-4x +5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省新沂市第二中学八年级数学上学期期末复习教案1
中国书法艺术说课教案
今天我要说课的题目是中国书法艺术,下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。
一、教材分析:
本节课讲的是中国书法艺术主要是为了提高学生对书法基础知识的掌握,让学生开始对书法的入门学习有一定了解。
书法作为中国特有的一门线条艺术,在书写中与笔、墨、纸、砚相得益彰,是中国人民勤劳智慧的结晶,是举世公认的艺术奇葩。
早在5000年以前的甲骨文就初露端倪,书法从文字产生到形成文字的书写体系,几经变革创造了多种体式的书写艺术。
1、教学目标:
使学生了解书法的发展史概况和特点及书法的总体情况,通过分析代表作品,获得如何欣赏书法作品的知识,并能作简单的书法练习。
2、教学重点与难点:
(一)教学重点
了解中国书法的基础知识,掌握其基本特点,进行大量的书法练习。
(二)教学难点:
如何感受、认识书法作品中的线条美、结构美、气韵美。
3、教具准备:
粉笔,钢笔,书写纸等。
4、课时:一课时
二、教学方法:
要让学生在教学过程中有所收获,并达到一定的教学目标,在本节课的教学中,我将采用欣赏法、讲授法、练习法来设计本节课。
(1)欣赏法:通过幻灯片让学生欣赏大量优秀的书法作品,使学生对书法产生浓厚的兴趣。
(2)讲授法:讲解书法文字的发展简史,和形式特征,让学生对书法作进一步的了解和认识,通过对书法理论的了解,更深刻的认识书法,从而为以后的书法练习作重要铺垫!
(3)练习法:为了使学生充分了解、认识书法名家名作的书法功底和技巧,请学生进行局部临摹练习。
三、教学过程:
(一)组织教学
让学生准备好上课用的工具,如钢笔,书与纸等;做好上课准备,以便在以下的教学过程中有一个良好的学习气氛。
(二)引入新课,
通过对上节课所学知识的总结,让学生认识到学习书法的意义和重要性!
(三)讲授新课
1、在讲授新课之前,通过大量幻灯片让学生欣赏一些优秀的书法作品,使学生对书法产生浓厚的兴趣。
2、讲解书法文字的发展简史和形式特征,让学生对书法作品进一步的了解和认识通过对书法理论的了解,更深刻的认识书法,从而为以后的书法练习作重要铺垫!
A书法文字发展简史:
①古文字系统
甲古文——钟鼎文——篆书
早在5000年以前我们中华民族的祖先就在龟甲、兽骨上刻出了许多用于记载占卜、天文历法、医术的原始文字“甲骨文”;到了夏商周时期,由于生产力的发展,人们掌握了金属的治炼技术,便在金属器皿上铸上当时的一些天文,历法等情况,这就是“钟鼎文”(又名金文);秦统一全国以后为了方便政治、经济、文化的交流,便将各国纷杂的文字统一为“秦篆”,为了有别于以前的大篆又称小篆。
(请学生讨论这几种字体的特点?)古文字是一种以象形为主的字体。
②今文字系统
隶书——草书——行书——楷书
到了秦末、汉初这一时期,各地交流日见繁多而小篆书写较慢,不能满足需要,隶书便在这种情况下产生了,隶书另一层意思是平民使用,同时还出现了一种草写的章草(独草),这时笔墨纸都已出现,对书法的独立创作起到了积极的推动作用。
狂草在魏晋出现,唐朝的张旭、怀素将它推向顶峰;行书出
现于晋,是一种介于楷、行之间的字体;楷书也是魏晋出现,唐朝达到顶峰,著名的书法家有欧阳询、颜真卿、柳公权。
(请学生谈一下对今文字是怎样理解的?),教师进行归纳:它们的共同特点是已经摆脱了象形走向抽象化。
B主要书体的形式特征
①古文字:甲骨文,由于它处于文明的萌芽时期,故字形错落有致辞,纯古可爱,目前发现的总共有3000多字,可认识的约1800字。
金文,处在文明的发展初期,线条朴实质感饱满而丰腴,因它多附在金属器皿上,所以保存完整。
石鼓文是战国时期秦的文字,记载的是君王外出狩猎和祈祷丰年,秦篆是一种严谨刻板的纯实用性的字体,艺术价值很小。
②今文字:隶书是在秦篆严谨的压抑下出现的一种潇洒开放型的新字体,课本图例《张迁碑》结构方正,四周平稳,刚劲沉着,是汉碑方笔的典范,章草是在隶书基础上更艺术化,实用化的字体,索靖《急就章》便是这种字体的代表作,字字独立,高古凝重,楷书有两大部分构成:魏碑、唐楷魏碑是北魏时期优秀书法作品的统称。
《郑文公碑》和《始平公造像》是这一时期的代表,前者气势纵横,雄浑深厚,劲健绝逸是圆笔的典型;唐楷中的《醴泉铭》法度森严、遒劲雄强,浑穆古拙、浑厚刚健,《神策军碑》精练苍劲、风神整峻、法度谨严,以上三种书体分别代表了唐楷三个时期的不同特点。
《兰亭序》和《洛神赋》作者分别是晋代王羲之、王献之父子是中国书法史上的两座高峰,前者气骨雄骏、风神跌宕、秀逸萧散的境界,后者在技法上达到了由拙到巧、笔墨洗练、丝丝入扣的微妙的境界。
他们都是不拘泥于传统的章法和技能,对后世
学书者产生了深远的影响;明代文征明的书法文雅自如,现代书家沈尹默在继承传统书法方面起到了不可魔灭的作用。
3、欣赏要点:
先找几位同学说一下自己评价书法作品的标准或原则是什么?[或如何来欣赏一幅书法作品?]学生谈完后,对他们的观点进行归纳总结。
然后自己要谈一下自己的观点:书法艺术的欣赏活动,有着不同于其它艺术门类的特征,欣赏书法伤口不可能获得相对直接的印象、辨识与教益,也不可能单纯为了使学生辨识书写的内容,去探讨言词语汇上的优劣。
进而得出:书法主要是通过对抽象的点画线条、结构形态和章法布局等有“情趣意味“的形式,从客观物象各种美的体态,安致这些独有的特性中,使人们在欣赏时得到精神上健康闲静的愉悦和人们意念境界里的美妙享受(结合讲授出示古代书法名作的图片,并与一般的书法作品进行比较,让学生在比较中得出什么是格调节器高雅,什么是粗庸平常)。
书法可以说是无声的音乐,抽象的绘画,线条流动的诗歌。
四、课堂评价:
根据本节课所学的内容结合板书。
让学生体会到祖国书法艺术的博大精深,着重分析学生在书体形式特点和审美欣赏方面表现出的得失。
让学生懂得在欣赏书法时主要是通过对抽像的点画线条、结构形态和章法布局等有“情趣意味“的形式,从客观物象各种美的体态,安致这些独有的特性中,使人们在欣赏时得到精神上健康闲静的愉悦和人们意念境界里的美妙享受。
