中考数学二轮综合训练 圆的弧长和图形面积的计算
考点集训25 圆的弧长和图形面积的计算 浙江《中考面对面》课件PPT

解:(1)如图;
(2)过点 O 作 OC⊥AB 于 D,交弧 AB 于 C,则 CD=6cm.∵OC⊥AB, ∴BD=AD=12AB,∴BD=AD=6 3cm,设半径为 r,则 OD=(r- 6)cm,在 Rt△BOD 中,BD2+OD2=BO2,∴(6 3)2+(r-6)2=r2,解 得 r=12,∴这个圆形截面的半径为 12cm.又∵设弧长 AB 所对圆心
考点集训25 圆的弧长和图形面积的计算
一、选择题 1.扇形的半径为30cm,圆心角为120°,此扇形的弧长是( A) A.20πcm B.10πcm C.10cm D.20cm
【解析】圆心角 120°即32π.弧长=32π·30=20πcm
2.已知圆锥的底面半径为 4cm,高为 3cm,则圆锥的侧 面积是( B )
∴劣弧B︵C长为601π8×0 1=π3.
12.某公园管理人员在巡视公园时,发现有一条圆柱形的输水管 道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有
水部分的截面图(如图). (1)请你帮忙补全这个输水管道的圆形截面(不写作法,但应保留
作图痕迹); (2)维修员量得这个输水管道有水部分的水面宽 AB=12 3cm,水
4.如图,点 O 是圆形纸片的圆心,将这个圆形纸片按下列顺序
折叠,使A︵B和B︵C都经过圆心 O,则阴影部分的面积是⊙O 面积的( B )
1
1
2
3
A.2
B.3
C.3
D.5
【解析】折叠 AC,会发现A︵C也会经过圆心 O, 此时观察图像易 发现阴影部分面积占全圆的13.
5.如图,AB 为⊙O 的切线,切点为 B,连接 AO,AO 与⊙O 交
圆的弧长和扇形面积计算

圆的弧长和扇形面积计算在数学中,圆是一个非常重要的几何形状。
对于圆,我们通常需要计算它的弧长和扇形的面积。
在本文中,我将介绍如何准确计算圆的弧长和扇形的面积。
1. 圆的弧长计算圆的弧长是圆周上两点之间的曲线距离。
要计算圆的弧长,我们需要知道圆的半径和圆心角的度数。
圆的弧长公式为:弧长 = (圆心角度数/ 360) × 2πr其中,r代表圆的半径,π是一个常数,约等于3.14159。
举个例子,假设一个圆的半径为5cm,圆心角为60度。
我们可以使用上述公式计算弧长:弧长 = (60 / 360) × 2π × 5 = 5.24cm因此,这个圆的弧长为5.24cm。
2. 扇形的面积计算扇形是由圆周上两条半径之间的部分组成。
要计算扇形的面积,我们同样需要圆的半径和圆心角的度数。
扇形的面积公式为:面积 = (圆心角度数/ 360) × πr²举个例子,假设一个圆的半径为8cm,圆心角为45度。
我们可以使用上述公式计算扇形的面积:面积= (45 / 360) × π × 8² = 25.13cm²因此,这个扇形的面积为25.13cm²。
总结:在计算圆的弧长和扇形的面积时,使用公式可以帮助我们准确计算结果。
记住圆的弧长公式为(圆心角度数/ 360) × 2πr,扇形的面积公式为(圆心角度数/ 360) × πr²。
以上就是关于圆的弧长和扇形面积计算的介绍。
通过掌握这些计算方法,我们可以更好地理解和应用圆的相关知识。
希望本文对你有所帮助!。
2024中考备考数学重难点05 圆的综合压轴题(6大题型+满分技巧+限时分层检测
重难点05 圆的综合压轴题中考数学中《圆的综合压轴题》部分主要考向分为六类:一、圆中弧长和面积的综合题二、圆与全等三角形的综合题三、圆的综合证明问题四、圆与等腰三角形的综合题五、圆的阅读理解与新定义问题六、圆与特殊四边形的综合题圆的综合问题是中考数学中的压轴题中的一类,也是难度较大的一类,所以,对应的训练很有必要。
考向一:圆中弧长与面积的综合题1.(2023•河北)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.计算:在图1中,已知MN=48cm,作OC⊥MN于点C.(1)求OC的长.操作:将图1中的水槽沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动.如图2.其中,半圆的中点为Q,GH与半圆的切点为E,连接OE交MN于点D.探究:在图2中.(2)操作后水面高度下降了多少?(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.2.(2023•乐山)在学习完《图形的旋转》后,刘老师带领学生开展了一次数学探究活动.【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容:如图1,将一个三角形纸板△ABC绕点A逆时针旋转θ到达的位置△AB′C′的位置,那么可以得到:AB=AB′,AC=AC′,BC=B′C′;∠BAC=∠B′AC′,∠ABC=∠AB′C′,∠ACB=∠AC′B′.(_____)刘老师进一步谈到:图形的旋转蕴含于自然界的运动变化规律中,即“变”中蕴含着“不变”,这是我们解决图形旋转的关键.故数学就是一门哲学.【问题解决】(1)上述问题情境中“(_____)”处应填理由:;(2)如图2,小王将一个半径为4cm,圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A′B′C′的位置.①请在图中作出点O;②如果BB′=6cm,则在旋转过程中,点B经过的路径长为;【问题拓展】小李突发奇想,将与(2)中完全相同的两个扇形纸板重叠,一个固定在墙上,使得一边位于水平位置.另一个在弧的中点处固定,然后放开纸板,使其摆动到竖直位置时静止.此时,两个纸板重叠部分的面积是多少呢?如图3所示,请你帮助小李解决这个问题.考向二:圆与全等三角形综合题1.(2023•济宁)如图,已知AB是⊙O的直径,CD=CB,BE切⊙O于点B,过点C作CF⊥OE交BE于点F,EF=2BF.(1)如图1,连接BD,求证:△ADB≌△OBE;(2)如图2,N是AD上一点,在AB上取一点M,使∠MCN=60°,连接MN.请问:三条线段MN,BM,DN有怎样的数量关系?并证明你的结论.2.(2023•哈尔滨)已知△ABC内接于⊙O,AB为⊙O的直径,N为的中点,连接ON交AC于点H.(1)如图①,求证:BC=2OH;(2)如图②,点D在⊙O上,连接DB,DO,DC,DC交OH于点E,若DB=DC,求证OD∥AC;(3)如图③,在(2)的条件下,点F在BD上,过点F作FG⊥DO,交DO于点G,DG=CH,过点F 作FR⊥DE,垂足为R,连接EF,EA,EF:DF=3:2,点T在BC的延长线上,连接AT,过点T作TM ⊥DC,交DC的延长线于点M,若FR=CM,AT=4,求AB的长.3.(2023•长春)【感知】如图①,点A、B、P均在⊙O上,∠AOB=90°,则锐角∠APB的大小为45度.【探究】小明遇到这样一个问题:如图②,⊙O是等边三角形ABC的外接圆,点P在弧AC上(点P不与点A、C重合),连接PA、PB、PC.求证:PB=PA+PC.小明发现,延长PA至点E,使AE=PC,连接BE,通过证明△PBC≌△EBA.可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:证明:延长PA至点E,使AE=PC,连接BE.∵四边形ABCP是⊙O的内接四边形,∴∠BAP+∠BCP=180°,∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE,∵△ABC是等边三角形,∴BA=BC,∴△PBC≌△EBA(SAS).请你补全余下的证明过程.【应用】如图③,⊙O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在⊙O上,且点P与点B在AC的两侧,连接PA、PB、PC,若,则的值为.考向三:圆的综合证明问题1.(2023•黄石)如图,AB为⊙O的直径,DA和⊙O相交于点F,AC平分∠DAB,点C在⊙O上,且CD ⊥DA,AC交BF于点P.(1)求证:CD是⊙O的切线;(2)求证:AC•PC=BC2;(3)已知BC2=3FP•DC,求的值.2.如图,在⊙O中,直径AB垂直弦CD于点E,连接AC,AD,BC,作CF⊥AD于点F,交线段OB于点G(不与点O,B重合),连接OF.(1)若BE=1,求GE的长.(2)求证:BC2=BG•BO.(3)若FO=FG,猜想∠CAD的度数,并证明你的结论.3.(2023•永州)如图,以AB为直径的⊙O是△ABC的外接圆,延长BC到点D.使得∠BAC=∠BDA,点E在DA的延长线上,点M在线段AC上,CE交BM于N,CE交AB于G.(1)求证:ED是⊙O的切线;(2)若,BD=5,AC>CD,求BC的长;(3)若DE•AM=AC•AD,求证:BM⊥CE.4.(2023•广东)综合探究如图1,在矩形ABCD中(AB>AD),对角线AC,BD相交于点O,点A关于BD的对称点为A′.连接AA′交BD于点E,连接CA′.(1)求证:AA'⊥CA';(2)以点O为圆心,OE为半径作圆.①如图2,⊙O与CD相切,求证:;②如图3,⊙O与CA′相切,AD=1,求⊙O的面积.考向四:圆与等腰三角形的综合1.(2023•宁波)如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D,连结AD,BE=3,BD=3.P是AB边上的动点,当△ADP为等腰三角形时,AP的长为.2.(2023•上海)如图(1)所示,已知在△ABC中,AB=AC,O在边AB上,点F是边OB中点,以O 为圆心,BO为半径的圆分别交CB,AC于点D,E,连接EF交OD于点G.(1)如果OG=DG,求证:四边形CEGD为平行四边形;(2)如图(2)所示,连接OE,如果∠BAC=90°,∠OFE=∠DOE,AO=4,求边OB的长;(3)连接BG,如果△OBG是以OB为腰的等腰三角形,且AO=OF,求的值.3.(2023•泰州)已知:A、B为圆上两定点,点C在该圆上,∠C为所对的圆周角.知识回顾(1)如图①,⊙O中,B、C位于直线AO异侧,∠AOB+∠C=135°.①求∠C的度数;②若⊙O的半径为5,AC=8,求BC的长;逆向思考(2)如图②,若P为圆内一点,且∠APB<120°,PA=PB,∠APB=2∠C.求证:P为该圆的圆心;拓展应用(3)如图③,在(2)的条件下,若∠APB=90°,点C在⊙P位于直线AP上方部分的圆弧上运动.点D在⊙P上,满足CD=CB﹣CA的所有点D中,必有一个点的位置始终不变.请证明.考向五:圆的阅读理解与新定义问题1.(2023•青海)综合与实践车轮设计成圆形的数学道理小青发现路上行驶的各种车辆,车轮都是圆形的.为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如下的探究活动:将车轮设计成不同的正多边形,在水平地面上模拟行驶.(1)探究一:将车轮设计成等边三角形,转动过程如图1,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是,BA=CA=DA=2,圆心角∠BAD=120°.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是BD(水平线),请在图2中计算C 到BD的距离d1.(2)探究二:将车轮设计成正方形,转动过程如图3,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是,BA=CA=DA=2,圆心角∠BAD=90°.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是BD(水平线),请在图4中计算C到BD的距离d2(结果保留根号).(3)探究三:将车轮设计成正六边形,转动过程如图5,设其中心到顶点的距离是2,以车轮转动一次(以一个顶点为支点旋转)为例,中心的轨迹是,圆心角∠BAD=.此时中心轨迹最高点是C(即的中点),转动一次前后中心的连线是BD(水平线),在图6中计算C 到BD的距离d3=(结果保留根号).(4)归纳推理:比较d1,d2,d3大小:,按此规律推理,车轮设计成的正多边形边数越多,其中心轨迹最高点与转动一次前后中心连线(水平线)的距离(填“越大”或“越小”).(5)得出结论:将车轮设计成圆形,转动过程如图7,其中心(即圆心)的轨迹与水平地面平行,此时中心轨迹最高点与转动前后中心连线(水平线)的距离d=.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.2.(2023•陕西)(1)如图①,∠AOB=120°,点P在∠AOB的平分线上,OP=4.点E,F分别在边OA,OB上,且∠EPF=60°,连接EF.求线段EF的最小值;(2)如图②,是一个圆弧型拱桥的截面示意图.点P是拱桥的中点,桥下水面的宽度AB=24m,点P到水面AB的距离PH=8m.点P1,P2均在上,=,且P1P2=10m,在点P1,P2处各装有一个照明灯,图中△P1CD和△P2EF分别是这两个灯的光照范围.两灯可以分别绕点P1,P2左右转动,且光束始终照在水面AB上.即∠CP1D,∠EP2F可分别绕点P1,P2按顺(逆)时针方向旋转(照明灯的大小忽略不计),线段CD,EF在AB上,此时,线段ED是这两灯照在水面AB上的重叠部分的水面宽度.已知∠CP1D=∠EP2F=90°,在这两个灯的照射下,当整个水面AB都被灯光照到时,求这两个灯照在水面AB上的重叠部分的水面宽度.(可利用备用图解答)3.(2023•北京)在平面直角坐标系xOy中,⊙O的半径为1.对于⊙O的弦AB和⊙O外一点C给出如下定义:若直线CA,CB中一条经过点O,另一条是⊙O的切线,则称点C是弦AB的“关联点”.(1)如图,点A(﹣1,0),B1(,),B2(,).①在点C1(﹣1,1),C2(,0),C3(0,)中,弦AB1的“关联点”是;②若点C是弦AB2的“关联点”,直接写出OC的长;(2)已知点M(0,3),N(,0),对于线段MN上一点S,存在⊙O的弦PQ,使得点S是弦PQ的“关联点”.记PQ的长为t,当点S在线段MN上运动时,直接写出t的取值范围.4.在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面内,一组对角互补的四边形的四个顶点共圆.请应用此结论,解决以下问题:如图1,△ABC中,AB=AC,∠BAC=α(60°<α<180°).点D是BC边上的一动点(点D不与B,C重合),将线段AD绕点A顺时针旋转α到线段AE,连接BE.(1)求证:A,E,B,D四点共圆;(2)如图2,当AD=CD时,⊙O是四边形AEBD的外接圆,求证:AC是⊙O的切线;(3)已知α=120°,BC=6,点M是边BC的中点,此时⊙P是四边形AEBD的外接圆,直接写出圆心P与点M距离的最小值.考向六:圆与特殊四边形综合1.(2023•威海)已知:射线OP平分∠MON,A为OP上一点,⊙A交射线OM于点B,C,交射线ON 于点D,E,连接AB,AC,AD.(1)如图1,若AD∥OM,试判断四边形OBAD的形状,并说明理由;(2)如图2,过点C作CF⊥OM,交OP于点F;过点D作DG⊥ON,交OP于点G.求证:AG=AF.2.(2023•益阳)如图,线段AB与⊙O相切于点B,AO交⊙O于点M,其延长线交⊙O于点C,连接BC,∠ABC=120°,D为⊙O上一点且的中点为M,连接AD,CD.(1)求∠ACB的度数;(2)四边形ABCD是否是菱形?如果是,请证明;如果不是,请说明理由;(3)若AC=6,求的长.(建议用时:80分钟)1.(2023•宜昌)如图1,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于点C,AB=4,PB=3.(1)填空:∠PBA的度数是,PA的长为;(2)求△ABC的面积;(3)如图2,CD⊥AB,垂足为D.E是上一点,AE=5EC.延长AE,与DC,BP的延长线分别交于点F,G,求的值.2.(2023•台州)我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置.如图,AB是⊙O的直径,直线l是⊙O的切线,B为切点.P,Q是圆上两点(不与点A重合,且在直径AB的同侧),分别作射线AP,AQ交直线l于点C,点D.(1)如图1,当AB=6,弧BP长为π时,求BC的长;(2)如图2,当,时,求的值;(3)如图3,当,BC=CD时,连接BP,PQ,直接写出的值.3.(2023•遂宁)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,AD=CD,过点D的直线l交BA的延长线于点M.交BC的延长线于点N且∠ADM=∠DAC.(1)求证:MN是⊙O的切线;(2)求证:AD2=AB•CN;(3)当AB=6,sin∠DCA=时,求AM的长.4.(2023•丽水)如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H.(1)求证:AD∥HC;(2)若=2,求tan∠FAG的值;(3)连结BC交AD于点N,若⊙O的半径为5.下面三个问题,依次按照易、中、难排列.请根据自己的认知水平,选择其中一道问题进行解答.①若OF=,求BC的长;②若AH=,求△ANB的周长;③若HF•AB=88,求△BHC的面积.5.(2023•长沙)如图,点A,B,C在⊙O上运动,满足AB2=BC2+AC2,延长AC至点D,使得∠DBC =∠CAB,点E是弦AC上一动点(不与点A,C重合),过点E作弦AB的垂线,交AB于点F,交BC 的延长线于点N,交⊙O于点M(点M在劣弧上).(1)BD是⊙O的切线吗?请作出你的判断并给出证明;(2)记△BDC,△ABC,△ADB的面积分别为S1,S2,S,若S1•S=(S2)2,求(tan D)2的值;(3)若⊙O的半径为1,设FM=x,FE•FN•=y,试求y关于x的函数解析式,并写出自变量x的取值范围.6.(2023•宁波)如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG =∠AFC.(1)求∠BGC的度数.(2)①求证:AF=BC.②若AG=DF,求tan∠GBC的值.(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.(建议用时:80分钟)1.(2023•东营区校级一模)如图,PA、PB是⊙O的切线,切点分别为A、B,BC是⊙O的直径,PO交⊙O于E点,连接AB交PO于F,连接CE交AB于D点.下列结论:①PA=PB;②OP⊥AB;③CE 平分∠ACB;④;⑤E是△PAB的内心;⑥△CDA≌△EDF.其中一定成立的有()个.A.5B.4C.3D.22.(2023•鹿城区校级三模)如图1,在△ABC中,∠ACB=90°,BC=2AC=2,过BC上一点D作DE ⊥BC,交AB于点E,以点D为圆心,DE的长为半径作半圆,交AC,AB于点F,G,交直线BC于点H,I(点I在H左侧).当点D与点C重合时(如图2),GH=;当EF=GH时,CD=.3.(2023•湖北模拟)如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为D,直线DC与AB的延长线交于点P,弦CE平分∠ACB,交AB于点F,连接BE,BE=7,下列四个结论:①AC平分∠DAB;②PF2=PB•PA;③若BC=OP,则阴影部分的面积为;④若PC=24,则tan∠PCB=;其中,所有正确结论的序号是.4.(2024•鄞州区校级一模)如图1,AB,CD是⊙O的两条互相垂直的弦,垂足为E,连结BC,BD,OC.(1)求证:∠BCO=∠ABD.(2)如图2,过点A作AF⊥BD,交CD于G,求证:CE=EG.(3)如图3,在(2)的条件上,连结BG,若BG恰好经过圆心O,若⊙O的半径为5,,求AB的长.5.(2024•常州模拟)对于⊙C和⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q 可以与点P重合,且,则点P称为点A关于⊙C的“阳光点”.已知点O为坐标原点,⊙O 的半径为1,点A(﹣1,0).(1)若点P是点A关于⊙O的“阳光点”,且点P在x轴上,请写出一个符合条件的点P的坐标;(2)若点B是点A关于⊙O的“阳光点”,且,求点B的横坐标t的取值范围;(3)直线与x轴交于点M,且与y轴交于点N,若线段MN上存在点A关于⊙O的“阳光点”,请直接写出b的取值范围是或.6.(2024•广东一模)如图1,在⊙O中,AB为⊙O的直径,点C为⊙O上一点,点D在劣弧BC上,CE ⊥CD交AD于E,连接BD.(1)求证:△ACE~△BCD;(2)若cos∠ABC=m,求;(用含m的代数式表示)(3)如图2,DE的中点为G,连接GO,若BD=a,cos∠ABC=,求OG的长.7.(2024•镇海区校级模拟)在矩形ABCD中,M、N分别在边BC、CD上,且AM⊥MN,以MN为直径作⊙O,连结AN交⊙O于点H,连结CH交MN于点P,AB=8,AD=12.(1)求证:∠MAD=∠MHC;(2)若AM平分∠BAN,求MP的长;(3)若△CMH为等腰三角形,直接写出BM的长.8.(2024•浙江一模)如图,在⊙O中,AB是一条不过圆心O的弦,C,D是的三等分点,直径CE交AB于点F,连结BD交CF于点G,连结AC,DC,过点C的切线交AB的延长线于点H.(1)求证:FG=CG.(2)求证:四边形BDCH是平行四边形.(3)若⊙O的半径为5,OF=3,求△ACH的周长.9.(2024•五华区校级模拟)如图,AB,CD是⊙O的两条直径,且AB⊥CD,点E是上一动点(不与点B,D重合),连接DE并延长交AB的延长线于点F,点P在AF上,且∠PEF=∠DCE,连接AE,CE分别交OD,OB于点M,N,连接AC,设⊙O的半径为r.(1)求证:PE是⊙O的切线;(2)当∠DCE=15°时,求证:AM=2ME;(3)在点E的移动过程中,判断AN•CM是否为定值,若是,求出该定值;若不是,请说明理由.10.(2024•福建模拟)已知:如图,⊙O内两条弦AB、CD,且AB⊥CD于E,OA为⊙O半径,连接AC、BD.(1)求证:∠OAC=∠BCD;(2)作EN⊥BD于N,延长NE交AC于点H.求证:AH=CH;(3)在(2)的条件下,作∠EHF=60°交AB于点F,点P在FE上,连接PC交HN于点L,当EL=HF=,CL=8,BE=2PF时,求⊙O的半径.11.(2024•鹿城区校级一模)如图1,锐角△ABC内接于⊙O,点E是AB的中点,连结EO并延长交BC 于D,点F在AC上,连结AD,DF,∠BAD=∠CDF.(1)求证:DF∥AB.(2)当AB=9,AF=FD=4时,①求tan∠CDF的值;②求BC的长.(3)如图2,延长AD交⊙O于点G,若,求的值.12.(2024•正阳县一模)【材料】自从《义务教育数学课程标准(2022年版)》实施以来,九年级的晏老师通过查阅新课标获悉:切线长定理由“选学”改为“必学”,并新增“会过圆外的一个点作圆的切线”,在学习完《切线的性质与判定》后,她布置一题:“已知:如图所示,⊙O及⊙O外一点P.求作:直线PQ,使PQ与⊙O相切于点Q.李蕾同学经过探索,给出了如下的一种作图方法:(1)连接OP,分别以O、P为圆心,以大于的长为半径作弧,两弧分别交于A、B两点(A、B 分别位于直线OP的上下两侧);(2)作直线AB,AB交OP于点C;(3)以点C为圆心,CO为半径作⊙C,⊙C交⊙O于点Q(点Q位于直线OP的上侧);(4)连接PQ,PQ交AB于点D,则直线PQ即为所求.【问题】(1)请按照步骤完成作图,并准确标注字母(尺规作图,保留作图痕迹);(2)结合图形,说明PQ是⊙O切线的理由;(3)若⊙O半径为2,OP=6.依据作图痕迹求QD的长.13.(2024•泌阳县一模)小贺同学在数学探究课上,用几何画板进行了如下操作:首先画一个正方形ABCD,一条线段OP(OP<AB),再以点A为圆心,OP的长为半径,画⊙A分别交AB于点E.交AD于点G.过点E,G分别作AB,AD的垂线交于点F,易得四边形AEFG也是正方形,连接CF.(1)【探究发现】如图1,BE与DG的大小和位置关系:.(2)【尝试证明】如图2,将正方形AEFG绕圆心A转动,在旋转过程中,上述(1)的关系还存在吗?请说明理由.(3)【思维拓展】如图3,若AB=2OP=4,则:①在旋转过程中,点B,A,G三点共线时,CF的值为;②在旋转过程中,CF的最大值是.14.(2024•秦都区校级一模)问题提出:(1)如图①,⊙O的半径为4,弦AB=4,则点O到AB的距离是.问题探究:(2)如图②,⊙O的半径为5,点A、B、C都在⊙O上,AB=6,求△ABC面积的最大值.问题解决:(3)如图③,是一圆形景观区示意图,⊙O的直径为60m,等边△ABP的边AB是⊙O的弦,顶点P在⊙O内,延长AP交⊙O于点C,延长BP交⊙O于点D,连接CD.现准备在△PAB和△PCD 区域内种植花卉,圆内其余区域为草坪.按照预算,草坪的面积尽可能大,求草坪的最大面积.(提示:花卉种植面积尽可能小,即花卉种植面积S△PAB +S△PCD的最小值)15.(2024•碑林区校级一模)问题探究(1)寒假期间,乐乐同学参观爸爸的工厂,看到半径分别为2和3的两个圆形零件⊙A、⊙B按如图1所示的方式放置,点A到直线m的距离AC=4,点B到直线m的距离BD=6,CD=5,M是⊙A上一点,N是⊙B上一点,在直线m上找一点P,使得PM+PN最小.请你在直线m上画出点P的位置,并直接写出PM+PN的最小值.问题解决(2)如图2,乐乐爸爸的工厂欲规划一块花园,如图所示的矩形ABCD,其中米,BC=30米,点E、F为花园的两个入口,米,DF=10米.若在△BCD区域内设计一个亭子G(亭子大小忽略不计),满足∠BDG=∠GBC,从入口到亭子铺设两条景观路.已知铺设小路EG所用的景观石材每米的造价是400元,铺设小路FG所用的景观石材每米的造价是200元,你能否帮乐乐同学分析一下,是否存在点G,使铺设小路EG和FG的总造价最低?若存在,求出最低总造价,并求出此时亭子G到边AB的距离;若不存在,请说明理由.16.(2024•雁塔区校级一模)问题发现(1)在△ABC中,AB=2,∠C=60°,则△ABC面积的最大值为;(2)如图1,在四边形ABCD中,AB=AD=6,∠BCD=∠BAD=90°,AC=8,求BC+CD的值.问题解决(3)有一个直径为60cm的圆形配件⊙O,如图2所示.现需在该配件上切割出一个四边形孔洞OABC,要求∠O=∠B=60°,OA=OC,并使切割出的四边形孔洞OABC的面积尽可能小.试问,是否存在符合要求的面积最小的四边形OABC?若存在,请求出四边形OABC面积的最小值及此时OA的长;若不存在,请说明理由.17.(2024•东莞市校级一模)如图①,点C,D在线段AB上,点C在点D的左侧,若线段AC,CD,DB 满足AC2+BD2=CD2,称C,D是线段AB的勾股点.(1)如图②,C,D是线段AB的勾股点,分别以线段AC,CD,DB为边向AB的同侧作正△ACE,正△CDF,正△DBG,已知正△ACE、正△CDF的面积分别是3,5,则正△DBG的面积是;(2)如图①,AB=12,C,D是线段AB的勾股点,当AC=AB时,求CD的长;(3)如图③,C,D是线段AB的勾股点,以CD为直径画⊙O,P在⊙O上,AC=CP,连接PA,PB,若∠A=2∠B,求∠B的度数.18.(2023•西湖区模拟)如图,已知CE是圆O的直径,点B在圆O上,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.(1)若圆O的半径为2,且点D为弧EC的中点时,求线段CD的长度;(2)在(1)的条件下,当DF=a时,求线段BD的长度;(答案用含a的代数式表示)(3)若AB=3AE,且CD=12,求△BCD的面积.19.古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”.小明决定研究一下圆,如图,AB是⊙O的直径,点C是⊙O上的一点,延长AB至点D,连接AC、BC、CD,且∠CAB=∠BCD,过点C 作CE⊥AD于点E.(1)求证:CD是⊙O的切线;(2)若OB=BD,求证:点E是OB的中点;(3)在(2)的条件下,若点F是⊙O上一点(不与A、B、C重合),求的值.。
中考件圆的弧长和图形面积的计算PPT学习教案

第21页/共32页
【典例 2】 扇形的半径为 30cm,圆心角为 120°,用它做 成一个圆锥的侧面,求圆锥的侧面积.
【错解】 设圆锥的底面半径为 r,母线长为 l. ∵132600πr2=πrl,∴132600π×302=π×30×l,解得 l=10, ∴S 侧面积=πrl=300πcm2.
r2,
2
∵r>0,∴S 与 r 之间是二次函数关系.
【答案】 (1)3-1π (2)C 3
第15页/共32页
题型三 圆锥
就圆锥而言,“底面圆的半径”和“侧面展开图的扇 形半径”是两个完全不同的概念,要注意其区别和联系, 其中扇形的弧长为圆锥底面圆的周长,扇形的半径为圆锥 的母线长;求圆锥或圆柱中的最短距离问题,通常借助于 展开图来解决,在将立体图形转化为平面图形后,应把题 中的已知条件转化到具体的线段中,最后构造直角三角形 解题.
第22页/共32页
【析错】 上述解答错将圆锥底面半径与圆锥侧面展开图的半
径混淆.
【纠错】 设圆锥的底面半径为 r,母线长为 l,已知 l=30.
∵r×360°=120°,∴r=10,∴S l
侧面积=πrl=300π(cm2).
另解:S 侧面积=S 扇形=3n60×πr2=132600×π×302=300π(cm2).
名师指津 (1)虽然本题两种解法的答案是一样的,但这只不过
是题设中数据的一种巧合而已.
(2)圆锥底面半径≠扇形半径,圆锥的侧面 展开图是一个扇形,如果设圆锥的母线
长为 l,底面圆的半径为 r,那么这个扇 形的半径为 l,扇形的弧长为 2πr,面积
S 圆锥侧=12(2πr)·l=πrl,S 圆锥表=πr2+πrl, 扇形的圆心角θ=rl×360°,如图 28-12.
中考数学复习《圆的弧长和图形面积的计算》

3.(2018· 预测)如图,AB 为⊙O 的直径,点 C 在⊙O 上,若∠OCA=50°, ︵ AB=4,则BC的长为( B ) 10 10 A. π B. π 3 9 5 5 C. π D. π 9 18
【解析】∵∠OCA=50°,OA=OC,∴∠A=50°,∴∠BOC=100°,∵AB= 100π×2 10 ︵ 的长= 4,∴BO=2,∴BC 180 = 9 π.故选 B.
第25讲 圆的弧长和图形面积的计算
数 学
1.(2017· 重庆)如图,在矩形 ABCD 中,AB=4,AD=2,分别以 A,C 为 圆心,AD,CB 为半径画弧,交 AB 于点 E,交 CD 于点 F,则图中阴影部分的 面积是( C ) π A.4-2π B.8- 2 C.8-2π D.8-4π 1 【解析】∵AD=CB=2,∴S 阴影=S 矩形-S 半圆=2×4-2π×22=8-2π,故
6.如图,有一直径是 2米的圆形铁皮,现从中剪出一个圆周角是 90°的 最大扇形 ABC,求: (1)AB 的长; (2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
【解析】由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的
周长,从而可求半径.
2 解: (1)∵∠BAC=90°, ∴BC 为⊙O 的直径, 即 BC= 2, ∴AB= BC 2 90· π·1 =1 (2)设所得圆锥的底面圆的半径为 r,根据题意得 2πr= ,解得 180 1 r= 4
12.如图,在△ABC 中,∠C=90°,∠BAC 的平分线交 BC 于点 D,点 O 在 AB 上,以点 O 为圆心,OA 为半径的圆恰好经过点 D,分别交 AC,AB 于 点 E,F. (1)试判断直线 BC 与⊙O 的位置关系,并说明理由; (2)若 BD=2 3,BF=2,∥OC,得到∠OCF=∠AEC=90°,于是得到结
初中数学圆的弧长与扇形面积知识点总结

初中数学圆的弧长与扇形面积知识点总结圆是初中数学中的重要内容,其中涉及到的弧长与扇形面积是基础且常见的问题。
本文将对这两个知识点进行总结,并给出相关的公式和例题。
一、弧长的计算公式与例题弧长是指一段圆周上的弧所对应的长度,计算弧长需要知道圆的半径r和弧度θ的数值。
弧度是角度的一种度量方式,定义为圆心角所对应的弧长与半径之比。
1. 弧长的计算公式:弧长L = rθ其中,L表示弧长,r表示圆的半径,θ表示弧度。
2. 弧长的例题:例题1:已知一个半径为6 cm的圆的弧度为π/3 rad,求弧长。
解题过程:已知半径 r = 6 cm,弧度θ = π/3 rad。
根据弧长的计算公式L = rθ,代入已知条件计算,得到 L = 6 cm ×π/3 rad = 2π cm ≈ 6.28 cm。
例题2:已知一个扇形的半径为8 cm,弧度为4π/5 rad,求扇形的弧长。
解题过程:已知半径 r = 8 cm,弧度θ = 4π/5 rad。
扇形的弧长等于扇形的圆心角所对应的弧长,即L = rθ。
代入已知条件计算,得到L = 8 cm × (4π/5) rad = 6.4π cm ≈ 20.09 cm。
二、扇形面积的计算公式与例题扇形是指圆内的一个圆锥体,其中包含了圆心角和弧所围成的部分。
计算扇形面积需要知道圆的半径r和圆心角θ的数值。
1. 扇形面积的计算公式:扇形面积S = (1/2)r²θ其中,S表示扇形面积,r表示扇形的半径,θ表示圆心角的度数。
2. 扇形面积的例题:例题1:已知一个扇形的半径为5 cm,圆心角度数为60°,求扇形的面积。
解题过程:已知半径 r = 5 cm,圆心角度数θ = 60°。
将圆心角的度数转换为弧度,θ = 60° × π/180° = π/3 rad。
代入扇形面积的计算公式S = (1/2)r²θ,计算得到 S = (1/2) × 5 cm ×5 cm × π/3 rad = (25/6)π cm² ≈ 13.09 cm²。
中考数学复习----《弧长的计算》知识点总结与专项练习题(含答案解析)

中考数学复习----《弧长的计算》知识点总结与专项练习题(含答案解析) 知识点总结1. 圆的周长计算公式:r C π2=2. 弧长计算公式:︒=180r n l π(弧长为l ,圆心角度数为n ,圆的半径为r ) 练习题1.(2022•丹东)如图,AB 是⊙O 的直径,C 是⊙O 上一点,连接AC ,OC ,若AB =6,∠A =30°,则BC ⌒的长为( )A .6πB .2πC .πD .π【分析】先根据圆周角定理求出∠BOC =2∠A =60°,求出半径OB ,再根据弧长公式求出答案即可.【解答】解:∵直径AB =6,∴半径OB =3,∵圆周角∠A =30°,∴圆心角∠BOC =2∠A =60°,∴的长是=π,故选:D .2.(2022•广西)如图,在△ABC 中,CA =CB =4,∠BAC =α,将△ABC 绕点A 逆时针旋转2α,得到△AB ′C ′,连接B ′C 并延长交AB 于点D ,当B ′D ⊥AB 时,BB ′⌒的长是( )A .332πB .334πC .938πD .9310π 【分析】证明α=30°,根据已知可算出AD 的长度,根据弧长公式即可得出答案.【解答】解:∵CA =CB ,CD ⊥AB ,∴AD =DB =AB ′.∴∠AB ′D =30°,∴α=30°,∵AC =4,∴AD =AC •cos30°=4×=2,∴, ∴的长度l ==π. 故选:B .3.(2022•河北)某款“不倒翁”(图1)的主视图是图2,PA ,PB 分别与AMB ⌒所在圆相切于点A ,B .若该圆半径是9cm ,∠P =40°,则AMB ⌒的长是( )A .11πcmB .211π cmC .7πcmD .27π cm 【分析】根据题意,先找到圆心O ,然后根据PA ,PB 分别与所在圆相切于点A ,B .∠P =40°可以得到∠AOB 的度数,然后即可得到优弧AMB 对应的圆心角,再根据弧长公式计算即可.【解答】解:OA ⊥PA ,OB ⊥PB ,OA ,OB 交于点O ,如图,∴∠OAP =∠OBP =90°,∵∠P =40°,∴∠AOB =140°,∴优弧AMB 对应的圆心角为360°﹣140°=220°,∴优弧AMB 的长是:=11π(cm ),故选:A . 4.(2022•湖北)如图,在Rt △ABC 中,∠C =90°,∠B =30°,AB =8,以点C 为圆心,CA 的长为半径画弧,交AB 于点D ,则AD ⌒的长为( )A .πB .34πC .35πD .2π【分析】连接CD ,根据∠ACB =90°,∠B =30°可以得到∠A 的度数,再根据AC =CD 以及∠A 的度数即可得到∠ACD 的度数,最后根据弧长公式求解即可.【解答】解:连接CD ,如图所示:∵∠ACB =90°,∠B =30°,AB =8,∴∠A =90°﹣30°=60°,AC ==4,由题意得:AC =CD ,∴△ACD 为等边三角形,∴∠ACD =60°,∴的长为:, 故选:B .5.(2022•甘肃)如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧(AB ⌒),点O 是这段弧所在圆的圆心,半径OA =90m ,圆心角∠AOB =80°,则这段弯路(AB ⌒)的长度为( )A .20πmB .30πmC .40πmD .50πm【分析】根据题目中的数据和弧长公式,可以计算出这段弯路()的长度. 【解答】解:∵半径OA =90m ,圆心角∠AOB =80°,∴这段弯路()的长度为:=40π(m ),故选:C . 6.(2022•丽水)某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2m ,高为23m ,则改建后门洞的圆弧长是( )A .π35m B .π38m C .π310m D .(π35+2)m 【分析】先作出合适的辅助线,然后根据题意和图形,可以求得优弧所对的圆心角的度数和所在圆的半径,然后根据弧长公式计算即可.【解答】解:连接AC,BD,AC和BD相交于点O,则O为圆心,如图所示,由题意可得,CD=2m,AD=2m,∠ADC=90°,∴tan∠DCA===,AC==4(m),∴∠ACD=60°,OA=OC=2m,∴∠ACB=30°,∴∠AOB=60°,∴优弧ADCB所对的圆心角为300°,∴改建后门洞的圆弧长是:=(m),故选:C.7.(2022•枣庄)在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为.(结果保留π)【分析】由含30度直角三角形的性质求出AB,根据弧长公式即可求出结论.【解答】解:∵∠C=90°,∠ABC=30°,AC=2,∴AB=2AC=4,∠BAC=60°,由旋转的性质得,∠BAB′=∠BAC=60°,∴B点通过一次旋转至B′所经过的路径长为=,故答案为:.8.(2022•沈阳)如图,边长为4的正方形ABCD内接于⊙O,则AB⌒的长是(结果保留π).【分析】连接OA、OB,可证∠AOB=90°,根据勾股定理求出AO,根据弧长公式求出即可.【解答】解:连接OA、OB.∵正方形ABCD内接于⊙O,∴AB=BC=DC=AD,∴===,∴∠AOB=×360°=90°,在Rt△AOB中,由勾股定理得:2AO2=42,解得:AO=2,∴的长==π,故答案为:π.9.(2022•大连)如图,正方形ABCD的边长是2,将对角线AC绕点A顺时针旋转∠CAD 的度数,点C旋转后的对应点为E,则弧CE的长是(结果保留π).【分析】先根据正方形的性质得到∠CAD=45°,AC=AB=×=2,然后利用弧长公式计算的长度.【解答】解:∵四边形ABCD为正方形,∴∠CAD=45°,AC=AB=×=2,∵对角线AC绕点A顺时针旋转∠CAD的度数,点C旋转后的对应点为E,∴的长度为=π.故答案为:π.10.(2022•青海)如图,从一个腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,则此扇形的弧长为cm.【分析】根据等腰三角形的性质得到OE的长,再利用弧长公式计算出弧CD的长.【解答】解:过O作OE⊥AB于E,当扇形的半径为OE时扇形OCD最大,∵OA=OB=60cm,∠AOB=120°,∴∠A=∠B=30°,∴OE=OA=30cm,∴弧CD的长==20πcm,故答案为:20π.11.(2022•广州)如图,在△ABC中,AB=AC,点O在边AC上,以O为圆心,4为半径的圆恰好过点C,且与边AB相切于点D,交BC于点E,则劣弧DE⌒的长是.(结果保留π)【分析】连接OD,OE,根据等腰三角形的性质和三角形内角和定理可得∠A=∠COE,再根据切线的性质和平角的定义可得∠DOE=90°,然后利用弧长公式进行计算即可解答.【解答】解:连接OD,OE,∵OC=OE,∴∠OCE=∠OEC,∵AB=AC,∴∠ABC=∠ACB,∵∠A+∠ABC+∠ACB=∠COE+∠OCE+∠OEC,∴∠A=∠COE,∵圆O与边AB相切于点D,∴∠ADO=90°,∴∠A+∠AOD=90°,∴∠COE+∠AOD=90°,∴∠DOE=180°﹣(∠COE+∠AOD)=90°,∴劣弧的长是=2π.故答案为:2π.。
中考数学二轮复习专题 与圆有关的计算及答案详解

中考数学二轮复习专题与圆有关的计算一、单选题1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为()A.B.C.D.2.如图,的半径为1,弦在圆心O的两侧,求上有动点于点E,当点D从点C运动到点A时,则点E所经过的路径长为()A.B.C.D.3.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为()A.B.C.D.4.刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为()A.1B.3C.D.5.如图,菱形中,,.以A为圆心,长为半径画,点P为菱形内一点,连,,.若,且,则图中阴影部分的面积为()A.B.C.D.6.我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是()A.1B.C.D.7.如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则的值是()A.B.3πC.5πD.8.如图,六位朋友均匀的围坐在圆桌旁聚会.圆桌的半径为80cm,每人离桌边10cm,又后来两位客人,每人向后挪动了相同距离并左右调整位置,使8个人都坐下,每相邻两人之间的距离与原来相邻两人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为xcm.则根据题意,可列方程为()A.B.C.2π(80+10)×8=2π(80+x)×10D.2π(80﹣x)×10=2π(80+x)×89.如图,在菱形中,,.以点A为圆心,为半径作,向菱形内部作,使,则图中阴影部分的面积为()A.B.C.D.10.如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是()A.B.C.D.二、填空题11.如图,△ABC内接于半径为的半圆O中,AB为直径,点M是的中点,连结BM 交AC于点E,AD平分∠CAB交BM于点D,∠ADB=135°且D为BM的中点,则DM的长为;BC的长为.12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为.13.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是.14.如图,半圆O的直径AE=4,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为.15.如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为.16.如图,正△ABO的边长为2,O为坐标原点,A在轴上,B在第二象限。
初中数学中的弧长与扇形面积解题技巧详解

初中数学中的弧长与扇形面积解题技巧详解在初中数学中,弧长与扇形面积是一个重要的概念,在解题过程中需要掌握一些解题技巧。
本文将详细介绍解决弧长与扇形面积问题的方法和技巧。
一、弧长的计算方法弧长是指圆周上的一段弧的长度。
计算弧长时需要知道圆的半径和弧度,弧度是指弧对应的圆心角所包的角度。
1. 当已知圆的半径和圆心角的度数时,可以使用如下公式计算弧长:弧长 = (圆心角 / 360)* 2πr其中,r为圆的半径,π为圆周率。
2. 当已知圆的半径和圆心角的弧度时,可以使用如下公式计算弧长:弧长 = 弧度 * r其中,r为圆的半径。
二、扇形面积的计算方法扇形是指由圆心和圆周上的两点所围成的图形,计算扇形面积时需要知道圆的半径和圆心角的度数或弧度。
1. 当已知圆的半径和圆心角的度数时,可以使用如下公式计算扇形面积:扇形面积 = (圆心角 / 360)* πr²其中,r为圆的半径,π为圆周率。
2. 当已知圆的半径和圆心角的弧度时,可以使用如下公式计算扇形面积:扇形面积 = 0.5 * 弧度 * r²其中,r为圆的半径。
三、解题技巧在解决弧长与扇形面积问题时,可以运用以下技巧:1. 将问题转化为已知数据和未知数之间的关系,建立方程或比例,然后进行求解。
2. 注意单位换算,确保所有的数值具有相同的单位。
3. 理解并运用相似三角形的性质,可以简化计算过程。
4. 将问题转化为几何图形的面积问题,利用面积公式求解。
5. 多进行反思与总结,在解题过程中不断优化自己的思考方式和解题方法。
四、例题演练下面通过几个例题演练来更好地掌握弧长与扇形面积的解题技巧:例题1:半径为8cm的圆的弧长是12cm,求圆心角的度数。
解题步骤:设圆心角为x度,根据弧长的计算公式可得:12 = (x / 360)* 2π * 8通过移项和化简计算得:x = 540 / π ≈ 172.18所以,圆心角的度数约为172.18度。
中考数学二轮复习专题 圆的基本性质及答案详解

中考数学二轮复习专题圆的基本性质一、单选题1.如图,AB是⊙O的弦,圆心O到弦AB的距离,点C是弧AB中点,点D是优弧AB上的一点,,则弦AB的长为()A.6B.9C.10D.122.如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2 ,则的长为()A.πB.πC.2πD.π3.如图,菱形中,,.以A为圆心,长为半径画,点P为菱形内一点,连,,.若,且,则图中阴影部分的面积为()A.B.C.D.4.如图,中,,,,,为,边上的两个动点,且,为中点,则的最小值为()A.B.C.D.5.如图,上有A、B两点,点C为弧AB上一点,点P是外一点,且,,则的度数为()A.B.C.D.6.如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=2,CD=3,则AE的长为()A.2B.2.5C.3D.3.57.如图,点是以为直径的半圆上的动点,于点,连接,设,则下列函数图象能反映与之间关系的是()A.B.C.D.8.以为中心点的量角器与直角三角板按如图方式摆放,量角器的0刻度线与斜边重合.点为斜边上一点,作射线交弧于点,如果点所对应的读数为,那么的大小为()A.B.C.D.9.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是()A.∠B B.∠C C.∠DEB D.∠D10.如图,点C,D是劣弧上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则所在圆的半径长为()A.B.C.2 D.二、填空题11.如图,点A、B、C在⊙O上,∠ACB+∠AOB=90°,则∠ACB的大小为12.如图,水平放置的圆柱形油桶的截面半径是,油面高为,截面上有油的弓形(阴影部分)的面积为.13.如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为.14.如图5,AB是半圆O 的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为cm.15.如图,AB是的直径,点C,D,E都在上,∠1=55°,则∠2=°16.在中,若,,则的面积的最大值为. 17.已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由,线段CD和线段BD所围成图形的阴影部分的面积为.18.如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点,点O为坐标原点.(1)该图中弧所在圆的圆心D的坐标为;.(2)根据(1)中的条件填空:①圆D的半径=(结果保留根号);②点(7,0)在圆D(填“上”、“内”或“外”);③∠ADC的度数为.三、作图题19.如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm, CD=8cm(1)求作此残片所在的圆(不写作法,保留作图痕迹)(2)求(1)中所作圆的半径四、解答题20.如图,在⊙O中,半径OC垂直弦AB于D,点E在⊙O上,∠E=22.5°,AB=2.求半径OB 的长.21.小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD.[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M.线段D′M与DM相等吗?请说明理由.[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P,N(如图3),发现线段DN,MN,PN存在一定的数量关系,请写出这个关系式,并加以证明.五、综合题22.如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.(1)求证:四边形DCFG是平行四边形;(2)当BE=4,CD=AB时,求⊙O的直径长.23.以的一条边AC为直径的⊙O与BC相交于点D,点D是BC的中点,过点D作⊙O的切线交AB于点E.(1)求证:AB=AC;(2)若BE=1,,求⊙O的半径.24.如图,在等腰△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作DE⊥AB,垂足为E.(1)求证:DE是⊙O的切线.(2)若DE= ,∠C=30°,求的长。
初中数学 圆的弧长及扇形面积公式 (含答案)

弧长及扇形面积第一部分 知识梳理(一)、圆的弧长及扇形面积公式在半径为R 的圆中,n °的圆心角所对的弧长为C 1,以n °为圆心角的扇形面积为S 1弧长公式 : 弧长C 1=180n R π 扇形面积公式: S 1=2360n R π=12C 1R注意:计算不规则图形的面积时,要转化成规则图形的面积进行计算。
(二)、圆锥的侧面积:注意:圆锥的侧面展开图是一个扇形 其中:(1)h 是圆锥的高,r 是底面半径;(2)l 是圆锥的母线,其长为侧面展开后所得扇形的半径R ;(3)圆锥的侧面展开图是半径等于 l ,弧长等于圆锥底面 周长C 的扇形.即: ①l =R ②180n Rπ=2πr ③h 2+r 2=l 2圆锥的侧面积 S 侧面积= πrl圆锥的全面积 S 全面积= πrl +πr 2第二部分 中考链接一、有关弧长计算 (一)、选择题1、(2018•淄博)如图,⊙O 的直径AB=6,若∠BAC=50°,则劣弧AC 的长为( )A 、2π B. 83π C 34π D. 43π1题图2题图 3题图 4题图 5题图2、(2018•黄石)如图,AB 是⊙O 的直径,点D 为⊙O 上一点,且∠ABD=30°,BO=4,则的长为( )A .23πB .43πC .2πD .83π3、(2018•沈阳)如图,正方形ABCD 内接于O ,AB=2,则的长是( )A .πB .πC .2πD .π4、(2018•陵城区二模)一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B 点从开始至结束所走过的路径长度为( )A .B .C .4D .2+5、(2018•明光市二模)如图,AB 与⊙O 相切于点B ,OA=2,∠OAB=30°,弦BC ∥OA ,则劣弧的长是( )A .B .C .D .6、(2019青岛)如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为()A.π B.2π C.2π D.4π6题图 7题图 8题图7、(2019烟台)如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=,CE=3,则的长为()A.B.πC.πD.π8、(2019泰安)如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为()A.πB.πC.2πD.3π(二)、填空题1、(2018•潍坊)如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=x于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则的长是..1题图 3题图 4题图5题图8题图2、(2018•连云港)一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为cm.3、(2018•永州)如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则的长为.4、(2018•盐城)如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为cm(结果保留π).5、(2018常州)如图,△ABC是⊙O的内接三角形,∠BAC=60°,的长是,则⊙O的半径是.6、(2018•温州)已知扇形的弧长为2π,圆心角为60°,则它的半径为..7、(2018•白银)如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为.8.(2019泰州)如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为cm.(三)、解答题1.(2018•湖州)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.(1)求证:AE=ED;(2)若AB=10,∠CBD=36°,求的长.二、、有关扇形面积计算(一)、选择题1、(2018•德州)如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为()A.2B.C.πm2 D.2πm21题图2题图 3题图4题图2、(2018•广安)如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为()A.π﹣2B.π﹣C.π﹣2D.π﹣3、(2018•成都)如图,在▱ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是()A.πB.2πC.3πD.6π4、(2018•绵阳)如图,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25πm2,圆柱高为3m,圆锥高为2m的蒙古包,则需要毛毡的面积是()A.(30+5)πm2B.40πm2C.(30+5)πm2D.55πm25.(2018•十堰)如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是()A.12π+18B.12π+36C.6D.66、(2018•山西)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为()A.4π﹣4 B.4π﹣8 C.8π﹣4 D.8π﹣85题图6题图7题图8题图7、(2018•广西)如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为()A.B.C.2 D.28、(2018•威海)如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是()A.18+36πB.24+18πC.18+18πD.12+18π9题图10题图11题图12题图13题图9、(2019枣庄)如图,在边长为4的正方形ABCD中,以点B为圆心,AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)()A.8﹣πB.16﹣2πC.8﹣2πD.8﹣12π10、(2019临沂)如图,⊙O中,=,∠ACB=75°,BC=2,则阴影部分的面积是()A.2+πB.2++πC.4+πD.2+π11、(2019宿迁)如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是()A.63﹣πB.63﹣2πC.63+πD.63+2π12. (2019四川南充)如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为()A. 6π B. 33π C. 23π D. 2π13.(2019四川资阳)如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为()A. 5πB. 6πC. 20πD. 24π(二)、填空题1、(2018青岛)如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是.1题图2题图3题图4题图2、(2018•安顺)如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为cm2.3、(2018•荆门)如图,在平行四边形ABCD中,AB<AD,∠D=30°,CD=4,以AB为直径的⊙O 交BC于点E,则阴影部分的面积为.4、(2018•重庆)如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)5、(2018•重庆)如图,在矩形ABCD中,AB=3,AD=2,以点A为圆心,AD长为半径画弧,交AB于点E,图中阴影部分的面积是(结果保留π).5题图6题图8题图9题图10题图6.(2018•香坊区)如图,点A、B、C是⊙O上的点,且∠ACB=40°,阴影部分的面积为2π,则此扇形的半径为.7、(2018•哈尔滨)一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是cm2.8、(2019日照)如图,已知动点A 在函数4(0y x x=>)的图象上,AB ⊥x 轴于点B ,AC ⊥y 轴于点C ,延长CA 交以A 为圆心AB 长为半径的圆弧于点E ,延长BA 交以A 为圆心AC 长为半径的圆弧于点F ,直线EF 分别交x 轴、y 轴于点M 、N ,当NF =4EM 时,图中阴影部分的面积等于 .9、(2019泰安)如图,∠AOB =90°,∠B =30°,以点O 为圆心,OA 为半径作弧交AB 于点A 、点C ,交OB于点D ,若OA =3,则阴影都分的面积为 .10、(2019德州)如图,O 为Rt △ABC 直角边AC 上一点,以OC 为半径的⊙O 与斜边AB 相切于点D ,交OA 于点E ,已知BC =,AC =3.则图中阴影部分的面积是 .11、(2019无锡市)如图,在△ABC 中,AC :BC :AB =5:12:13,⊙O 在△ABC 内自由移动,若⊙O 的半径为1,且圆心O 在△ABC 内所能到达的区域的面积为103,则△ABC 的周长为 . A BABCOOCOOI HF GED11题图 12题图 12、(2019四川内江)如图,在平行四边形ABCD 中,AB <AD ,∠A =150°,CD =4,以CD 为直径的⊙O 交AD 于点E ,则图中阴影部分的面积为 . (三)、解答题1、(2019东营)如图,AB 是⊙O 的直径,点D 是AB 延长线上的一点,点C 在⊙O 上,且AC =CD ,∠ACD =120°.(1)求证:CD 是⊙O 的切线,(2)若⊙O 的半径为3,求图中阴影部分的面积.2、(2019无锡市)一次函数b kx y +=的图像与x 轴的负半轴相交于点A ,与y 轴的正半轴相交于点B ,且sin ∠ABO 3OAB 的外接圆的圆心M 的横坐标为﹣3. (1)求一次函数的解析式; (2)求图中阴影部分的面积.xy M BAO3.(2019·武汉)已知AB 是⊙O 的直径,AM 和BN 是⊙O 的两条切线,DC 与⊙O 相切于点E ,分别交AM 、BN于D 、C 两点(1) 如图1,求证:AB 2=4AD ·BC(2) 如图2,连接OE 并延长交AM 于点F ,连接CF .若∠ADE =2∠OFC ,AD =1,求图中阴影部分的面积ODEMF EMO图1 图2 4.(2019·衡阳)如图,点A 、B 、C 在半径为8的⊙O 上,过点B 作BD ∥AC ,交OA 延长线于点D ,连接BC ,且∠BCA =∠OAC =30°.(1)求证:BD 是⊙O 的切线;(2)求图中阴影部分的面积.DAOCB三、圆锥(一)、选择题2、(2018•自贡)已知圆锥的侧面积是8πcm 2,若圆锥底面半径为R (cm ),母线长为l (cm ),则R 关于l 的函数图象大致是( )A .B .C .D .3、(2018•遵义)若要用一个底面直径为10,高为12的实心圆柱体,制作一个底面和高分别与圆柱底面半径和高相同的圆锥,则该圆锥的侧面积为( )A.60πB.65πC.78πD.120π4、(2018•遂宁)已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是()A.4πB.8πC.12πD.16π5、(2018•东阳市模拟)已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为()A.30πcm2B.50πcm2C.60πcm2D.3πcm26、(2019东营)如图所示是一个几何体的三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为()A.3B.C.3 D.3(二)、填空题1、(2018烟台)如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON 的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=.1题图2题图3题图7题图8题图2、(2018徐州)如图,扇形的半径为6,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为.3、(2018•郴州)如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为cm.(结果用π表示)4、(2018•聊城)用一块圆心角为216°的扇形铁皮,做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是cm.5、(2018•黑龙江)用一块半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则此圆锥的高为.6、(2018•扬州)用半径为10cm ,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为cm.7、(2018•苏州)如图,8×8的正方形网格纸上有扇形OAB和扇形OCD,点O,A,B,C,D 均在格点上.若用扇形OAB围成一个圆锥的侧面,记这个圆锥的底面半径为r1;若用扇形OCD围成另个圆锥的侧面,记这个圆锥的底面半径为r2,则12rr的值为8、(2019聊城)如图是一个圆锥的主视图,根据图中标出的数据(单位:cm),计算这个圆锥侧面展开图圆心角的度数为.9.(2019无锡市)已知圆锥的母线成为5cm,侧面积为15πcm 2,则这个圆锥的底面圆半径为cm .答案与提示:一、弧长计算(一)、选择题1、D2、D3、A4、B5、B6、B7、D8、C1、解:如图,连接CO,∵∠BAC=50°,AO=CO=3,∴∠ACO=50°,∴∠AOC=80°,∴劣弧AC的长为=,故选:D.1题图2题图3题图6题图8题图2、解:连接OD,∵∠ABD=30°,∴∠AOD=2∠ABD=60°,∴∠BOD=120°,∴的长==,故选:D.3、解:连接OA、OB,∵正方形ABCD内接于O,∴AB=BC=DC=AD,∴===,∴∠AOB=×360°=90°,在Rt△AOB中,由勾股定理得:2AO2=(2)2,解得:AO=2,∴的长为=π,故选:A.4、BC=AB=AC=1,∠BCB′=120°,∴B点从开始至结束所走过的路径长度为2×弧BB′=2×12014=1803ππ⨯故选B.5、连接OB,OC,∵AB为圆O的切线,∴∠ABO=90°,在Rt△ABO中,OA=2,∠OAB=30°,∴OB=1,∠AOB=60°,∵BC∥OA,∴∠OBC=∠AOB=60°,又OB=OC,∴△BOC为等边三角形,∴∠BOC=60°,则劣弧长为6011= 1803ππ⨯.6、解:连接OC、OD,∵AC,BD分别与⊙O相切于点C,D.∴OC⊥AC,OD⊥BD,∵∠A=45°,∴∠AOC=45°,∴AC=OC=4,∵AC=BD=4,OC=OD=4,∴OD=BD,∴∠BOD=45°,∴∠COD=180°﹣45°﹣45°=90°,∴的长度为:=2π,故选:B.7、解:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACD+∠BCE=90°,∵AD⊥DE,BE⊥DE,∴∠DAC+∠ACD=90°,∴∠DAC=∠ECB,∵∠ADC=∠CEB=90°,∴△ADC∽△CEB,∴=,即=,∵tan∠ABC==,∴∠ABC=30°,∴AB=2AC,∠AOC=60°,∵直线DE与⊙O相切于点C,∴∠ACD=∠ABC=30°∴AC=2AD=2,∴AB=4,∴⊙O的半径为2,∴的长为:=π,故选:D.8、解:连接OA.OB,作OC⊥AB于C,由题意得,OC=OA,∴∠OAC=30°,∵OA=OB,∴∠OBA=∠OAC=30°,∴∠AOB=120°,∴的长==2π,故选:C.(二)、填空题1、201923π2、2π3、24π4、83π5、26、67、πa8、6π1、解:直线y=x,点A1坐标为(2,0),过点A1作x轴的垂线交直线于点B1可知B1点的坐标为(2,2),以原O为圆心,OB1长为半径画弧x轴于点A2,OA2=OB1,OA2==4,点A2的坐标为(4,0),这种方法可求得B2的坐标为(4,4),故点A3的坐标为(8,0),B3(8,8)以此类推便可求出点A2019的坐标为(22019,0),则的长是=.故答案为:.2、1203=2 180ππ⨯3、解:∵点A(1,1),∴OA==,点A在第一象限的角平分线上,∵以点O为旋转中心,将点A逆时针旋转到点B的位置,∴∠AOB=45°,∴的长为=.故答案为.4、解:由图1得:的长+的长=的长 ∵半径OA=2cm ,∠AOB=120°则图2的周长为:=故答案为:.5、连接OB.OC ,由∠BAC=60°得∠BOC=120°,1204=1803r ππ⨯ 得:r=26、解:设半径为r ,60=2180rππ⨯,解得:r=6,故答案为:6 7、解:如图.∵△ABC 是等边三角形,∴∠A=∠B=∠C=60°,AB=BC=CA=a , ∴的长=的长=的长==,∴勒洛三角形的周长为×3=πa .故答案为πa .(三)、解答题1、证明:(1)∵AB 是⊙O 的直径,∴∠ADB=90°, ∵OC ∥BD ,∴∠AEO=∠ADB=90°,即OC ⊥AD ,∴AE=ED ; (2)∵OC ⊥AD ,∴,∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°=72°,∴.二、有关扇形面积计算1、A2、C3、C4、A5、C6、A7、D8、C9、C 10、A 11、A 12、A 13、A 1、解:连接AC ,∵从一块直径为2m 的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°, ∴AC 为直径,即AC=2m ,AB=BC ,∵AB 2+BC 2=22,∴AB=BC=m ,∴阴影部分的面积是=(m 2),故选:A .2、解:连接OB 和AC 交于点D ,如图所示:∵圆的半径为2,∴OB=OA=OC=2,又四边形OABC 是菱形,∴OB ⊥AC ,OD=OB=1, 在Rt △COD 中利用勾股定理可知:CD==,AC=2CD=2,∵sin ∠COD==,∴∠COD=60°,∠AOC=2∠COD=120°,∴S 菱形ABCO =OB ×AC=×2×2=2,S 扇形AOC ==,则图中阴影部分面积为S 菱形ABCO ﹣S 扇形AOC =π﹣2,故选:C .1题图 2题图 5题图 7题图 8题图3、解:∵在□ABCD 中,∠B=60°,⊙C 的半径为3,∴∠C=120°, ∴图中阴影部分的面积是:=3π,故选:C .4、解:设底面圆的半径为R ,则πR 2=25π,解得R=5, 圆锥的母线长==,所以圆锥的侧面积=•2π•5•=5π;圆柱的侧面积=2π•5•3=30π,所以需要毛毡的面积=(30π+5π)m 2.故选:A .5、解:如图,连接OD ,AD ,∵点C 为OA 的中点,∴OC=OA=OD , ∵CD ⊥OA ,∴∠CDO=30°,∠DOC=60°,∴△ADO 为等边三角形,OD=OA=12,OC=CA=6,∴CD=,6,∴S 扇形AOD ==24π,∴S 阴影=S 扇形AOB ﹣S 扇形COE ﹣(S 扇形AOD ﹣S △COD )=﹣﹣(24π﹣×6×6)=18+6π.故选:C .6、解:利用对称性可知:阴影部分的面积=扇形AEF 的面积﹣△ABD 的面积=﹣×4×2=4π﹣4,故选:A . 7、解:过A 作AD ⊥BC 于D ,∵△ABC 是等边三角形,∴AB=AC=BC=2,∠BAC=∠ABC=∠ACB=60°, ∵AD ⊥BC ,∴BD=CD=1,AD=BD=, ∴△ABC 的面积为=,S 扇形BAC ==π,∴莱洛三角形的面积S=3×π﹣2×=2π﹣2,故选:D .8、解:作FH ⊥BC 于H ,连接FH ,如图,∵点E 为BC 的中点,点F 为半圆的中点,∴BE=CE=CH=FH=6, 226+125Rt △ABE ≌△EHF ,∴∠AEB=∠EFH , 而∠EFH+∠FEH=90°,∴∠AEB+∠FEH=90°,∴∠AEF=90°,∴图中阴影部分的面积=S正方形ABCD +S半圆﹣S△ABE﹣S△AEF=12×12+12•π•62﹣12×12×6﹣12•65×65 =18+18π.故选:C.9、解:S阴=S△ABD﹣S扇形BAE=×4×4﹣=8﹣2π,故选:C.10、解:∵=,∴AB=AC,∵∠ACB=75°,∴∠ABC=∠ACB=75°,∴∠BAC=30°,∴∠BOC=60°,∵OB=OC,∴△BOC是等边三角形,∴OA=OB=OC=BC=2,作AD⊥BC,∵AB=AC,∴BD=CD,∴AD经过圆心O,∴OD=OB=,∴AD=2+,∴S△ABC=BC•AD=2+,S△BOC=BC•OD=,∴S阴影=S△ABC+S扇形BOC﹣S△BOC=2++﹣=2+π,故选:A.12.连接OA、OB,则S阴=S扇形OAB=2606360π⨯=6π故选A13、圆所扫过的图形面积=长方形的面积+圆的面积=2π×2+π=5π二、填空题1、734-23π2、4π3、40π4、14π5、43π﹣36、8﹣2π7、6﹣π8、3 9、6π10、2.5π 11、34π 12、 13、25 14、233π+解:∵∠B=90°,∠C=30°,∴∠A=60°,∵OA=OF,∴△AOF是等边三角形,∴∠COF=120°,∵OA=2,∴扇形OGF的面积为:=∵OA为半径的圆与CB相切于点E,∴∠OEC=90°,∴OC=2OE=4,∴AC=OC+OA=6,∴AB=AC=3,∴由勾股定理可知:BC=3∴△ABC的面积为:×3×3=∵△OAF的面积为:×2×=,∴阴影部分面积为:﹣﹣π=﹣π故答案为:﹣π1题图 3题图 8题图2、解:∵∠BOC=60°,△B′OC′是△BOC 绕圆心O 逆时针旋转得到的,∴∠B′OC′=60°,△BCO=△B′C′O ,∴∠B′OC=60°,∠C′B′O=30°,∴∠B′OB=120°, ∵AB=2cm ,∴OB=1cm ,OC′=,∴B′C′=,∴S 扇形B′OB ==π,S 扇形C′OC ==,∴阴影部分面积=S 扇形B′OB +S △B′C′O ﹣S △BCO ﹣S 扇形C′OC =S 扇形B′OB ﹣S 扇形C′OC =π﹣=π;3、解:连接OE 、AE ,∵AB 是⊙O 的直径,∴∠AEB=90°,∵四边形ABCD 是平行四边形,∴AB=CD=4,∠B=∠D=30°,∴AE=AB=2,BE==2,∵OA=OB=OE ,∴∠B=∠OEB=30°,∴∠BOE=120°,∴S 阴影=S 扇形OBE ﹣S △BOE ,=﹣×,=﹣,=﹣,4、解:S 阴=S △ABD ﹣S 扇形BAE =×4×4﹣=8﹣2π,故答案为8﹣2π.5、解:∵矩形ABCD ,∴AD=2,∴S 阴影=S 矩形﹣S 四分之一圆=2×3﹣π×22=6﹣π,6、解:∵在⊙O 上,∠ACB=40°,∴∠AOB=2∠ACB=80°, ∴此扇形的半径为:=3.故答案为:3.7、解:设扇形的半径为Rcm ,∵扇形的圆心角为135°,弧长为3πcm , ∴=3π,解得:R=4,所以此扇形的面积为=6π(cm 2),故答案为:6π.8.解:作DF ⊥y 轴于点D ,EG ⊥x 轴于G ,∴△GEM ∽△DNF ,∵NF =4EM ,∴==4,设GM =t ,则DF =4t ,∴A (4t ,),由AC =AF ,AE =AB ,∴AF =4t ,AE =,EG =, ∵△AEF ∽△GME ,∴AF :EG =AE :GM ,即4t :=:t ,即4t 2=,∴t 2=,图中阴影部分的面积=+=2π+π=2.5π,11、解:连接OC ,作CH ⊥OB 于H ,∵∠AOB =90°,∠B =30°,∴∠OAB =60°,AB =2OA =6, 由勾股定理得,OB ==3,∵OA =OC ,∠OAB =60°,∴△AOC 为等边三角形,∴∠AOC =60°,∴∠COB =30°, ∴CO =CB ,CH =OC =, ∴阴影都分的面积=﹣×3×3×+×3×﹣=π,故答案为:π.11题图12题图 13题图解:在Rt △ABC 中,∵BC =,AC =3.∴AB ==2,∵BC ⊥OC ,∴BC 是圆的切线,∵⊙O 与斜边AB 相切于点D ,∴BD =BC ,∴AD =AB ﹣BD =2﹣=,在Rt △ABC 中,∵sinA ===,∴∠A =30°,∵⊙O 与斜边AB 相切于点D ,∴OD ⊥AB ,∴∠AOD =90°﹣∠A =60°, ∵=tanA =tan30°,∴=,∴OD =1,∴S 阴影==.故答案是:.13、如图,圆心O 在△ABC 内所能到达的区域是△O 1O 2O 3,∵△O 1O 2O 3三边向外扩大1得到△ACB ,∴它的三边之比也是5∶12∶13, ∵△O 1O 2O 3的面积=103,∴O 1O 2=53,O 2O 3=4,O 1O 3=133,连接AO 1 与CO 2,并延长相交于I ,过I 作ID ⊥AC 于D ,交O 1O 2于E ,过I 作IG ⊥BC 于G 交O 3O 2于F ,则I 是Rt △ABC 与Rt△O 1O 2O 3的公共内心,四边形IEO 2F 四边形IDCG 都是正方形,∴IE =IF = 1223122313O O O O O O O O O O ⨯++ =23,ED =1,∴ID =IE +ED =53,设△ACB 的三边分别为5m 、12m 、13m ,则有ID =AC BC AC BC AB ⨯++=2m =53,解得m =56,△ABC 的周长=30m =25.14、连接OE,则S 阴=S 扇形OEC +S △OED =260212123336023ππ⨯+⨯⨯=(三)、解答题 1、(1)证明:连接OC .∵AC =CD ,∠ACD =120°∴∠A =∠D =30°.∵OA =OC ,∴∠ACO =∠A =30°.∴∠OCD =∠ACD ﹣∠ACO =90°.即OC ⊥CD ,∴CD 是⊙O 的切线. (2)解:∵∠A =30°,∴∠COB =2∠A =60°.∴S 扇形BOC =,在Rt △OCD 中,CD =OC ,∴,∴,∴图中阴影部分的面积为.2、作MN ⊥OB,垂足为N,连接OM,则MN=12OA=3,OA=6 ,A(-6,0)由sin ∠ABO 3则∠A=60°tan ∠BAO=OBOA∴3 ∴B (0,3)设直线AB:y=kx+b,将A,B 点的坐标代入得:3,b=3∴3x+3 S 阴=S 扇形MAO -S △MAO 2120(23)1634332ππ⨯-⨯-3、证明:(1)如图1,连接OD ,OC ,OE .∵AD ,BC ,CD 是⊙O 的切线, ∴OA ⊥AD ,OB ⊥BC ,OE ⊥CD ,AD =ED ,BC =EC ,∠ODE =12∠ADC ,∠OCE =12∠BCD ∴AD //BC ,∴∠ODE +∠OCE =12(∠ADC +∠BCD )=90°, ∵∠ODE +∠DOE =90°,∴∠DOE =∠OCE . 又∵∠OED =∠CEO =90°,∴△ODE ∽△COE .∴OE ECED OE=,OE 2=ED ·EC ∴4OE 2=4AD ·BC ,∴AB 2=4AD ·BC (2)解:如图2,由(1)知∠ADE =∠BOE ,∵∠ADE =2∠OFC ,∠BOE =∠2COF ,∴∠COF =∠OFC ,∴△COF 等腰三角形。
2020年中考数学二轮专项特训——圆的综合应用(含详细解答)

2020年中考数学二轮专项特训——圆的综合应用专训1圆中常见的计算题型名师点金:与圆有关的计算主要涉及圆与其他几何图形结合,利用圆周角定理求角度,利用垂径定理构造直角三角形并结合勾股定理,已知弦长、弦心距、半径三个量中的任意两个量时,可求出第三个量,利用弧长、扇形面积公式计算弧长、扇形面积等.有关角度的计算1.如图,⊙I是△ABC的内切圆,D,E,F为三个切点.若∠DEF=52°,则∠A的度数为()A.76°B.68°C.52°D.38°(第1题)(第2题) 2.如图,有一圆经过△ABC 的三个顶点,且弦BC 的中垂线与AC ︵相交于D点.若∠B =74°,∠C =46°,则AD ︵所对圆心角的度数为( )A .23°B .28°C .30°D .37°3.(中考·娄底)如图,在⊙O 中,AB ,CD 是直径,BE 是切线,B 为切点,连接AD ,BC ,BD.(1)求证:△ABD ≌△CDB ;(2)若∠DBE =37°,求∠ADC 的度数.(第3题)半径、弦长的计算4.(中考·南京)如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 2 cm,∠BCD=22°30′,则⊙O的半径为________.(第4题)(第5题)5.如图,AB 为⊙O 的直径,延长AB 至点D ,使BD =OB ,DC 切⊙O 于点C ,点B 是CF ︵的中点,弦CF 交AB 于点E.若⊙O 的半径为2,则CF =________.6.如图,在⊙O 中,直径AB 与弦AC 的夹角为30°,过点C 作⊙O 的切线交AB 的延长线于点D ,OD =30 cm .求直径AB 的长.(第6题)面积的计算7.(2015·丽水)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.(第7题)专训2圆中常用的作辅助线的方法名师点金:在解决有关圆的计算或证明题时,往往需要添加辅助线,根据题目特点选择恰当的辅助线至关重要.圆中常用的辅助线作法有:作半径,巧用同圆的半径相等;连接圆上两点,巧用同弧所对的圆周角相等;作直径,巧用直径所对的圆周角是直角;证切线时“连半径,证垂直”以及“作垂直,证半径”等.作半径,巧用同圆的半径相等1.如图,两正方形彼此相邻,且大正方形ABCD的顶点A,D在半圆O上,顶点B,C在半圆O的直径上;小正方形BEFG的顶点F在半圆O上,E点在半圆O的直径上,点G在大正方形的边AB上.若小正方形的边长为4 cm,求该半圆的半径.(第1题)连接圆上两点,巧用同弧所对的圆周角相等2.如图,圆内接三角形ABC的外角∠ACM的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BM,垂足为H,求证:AP=BH.(第2题)作直径,巧用直径所对的圆周角是直角3.如图,⊙O的半径为R,弦AB,CD互相垂直,连接AD,BC.(1)求证:AD2+BC2=4R2;(2)若弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),求⊙O的半径及点O到AD的距离.(第3题)证切线时辅助线作法的应用4.如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.判断CD与⊙O的位置关系,并说明理由.(第4题)遇弦加弦心距或半径5.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为()A.3 B.4 C.3 2 D.4 2(第5题)(第6题)6.(中考·贵港)如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=23,OH=1,则∠APB=________.遇直径巧作直径所对的圆周角7.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC 于点D,E,且点D是BC的中点.(1)求证:△ABC为等边三角形.(2)求DE的长.(第7题)遇切线巧作过切点的半径8.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA 切⊙O于点A,且PA=PB.(1)求证:PB是⊙O的切线;(2)已知PA=3,∠ACB=60°,求⊙O的半径.(第8题)巧添辅助线计算阴影部分的面积9.(中考·自贡)如图,点B ,C ,D 都在⊙O 上,过点C 作AC ∥BD 交OB 的延长线于点A ,连接CD ,且∠CDB =∠OBD =30°,DB =6 3 cm .(1)求证:AC 是⊙O 的切线;(2)求由弦CD ,BD 与BC ︵所围成的阴影部分的面积(结果保留π).(第9题)专训3圆的实际应用名师点金:与圆有关的知识在实际生活中有着广泛的应用,从实际生活中抽象出数学问题,并运用圆的相关知识解决这些问题,可以达到学以致用的目的.利用垂径定理解决台风问题1.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30 km/h,受影响区域的半径为200 km,B市位于点P北偏东75°的方向上,距离P点320 km处.(1)试说明台风是否会影响B市;(2)若B市受台风的影响,求台风影响B市的时间.(第1题)利用圆周角知识解决足球射门问题(转化思想)2.如图,在“世界杯”足球比赛中,队员甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴队员乙已经助攻冲到B点,现有两种射门方式:一是由队员甲直接射门;二是队员甲将球迅速传给队员乙,由队员乙射门.从射门角度考虑,你认为选择哪种射门方式较好?为什么?(第2题)利用直线与圆的位置关系解决范围问题3.已知A,B两地相距1 km.要在A,B两地之间修建一条笔直的水渠(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一个以C为圆心,350 m为半径的圆形公园,则修建的这条水渠会不会穿过公园?为什么?(第3题)利用圆锥侧面展开图解决材料最省问题4.如图,某工厂要选一块矩形铁皮加工成一个底面半径为20 cm,高为40 2 cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?(第4题)专训4与圆有关的动态问题名师点金:对于与圆有关的运动情形下的几何问题,在探究求值问题时,通常应对运动过程中所有可能出现的不同情形进行分析,如果符合某些条件的点、线等几何图形不唯一,要注意分类讨论,在探究确定结论成立情况下的已知条件时,可以把确定结论当作已知用.利用圆探究运动中形成的特殊几何图形问题1.如图,AB是半圆O的直径,BC是弦,点P从点A开始,沿AB向点B以1 cm/s的速度移动,若AB长为10 cm,点O到BC的距离为4 cm.(1)求弦BC的长;(2)经过几秒△BPC是等腰三角形?(PB不能为底边)(第1题)2.如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P 是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.(第2题)利用圆探究运动中的特殊位置关系问题3.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=12 cm,AD =8 cm,BC=22 cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1 cm/s的速度运动,动点Q从点C开始沿CB边向点B以2 cm/s的速度运动,P,Q分别从点A,C同时出发.当其中一动点到达终点时,另一个动点也随之停止运动.设运动时间为t s.当t为何值时,PQ与⊙O相切?(第3题)利用圆探究运动中的面积问题4.如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.(1)求∠AOC的度数;(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.(第4题)专训5几种常见的热门考点名师点金:圆的知识是初中数学的重点内容,也是历年中考命题的热点.本章题型广泛,主要考查圆的概念、基本性质以及圆周角定理及其推论,直线与圆的位置关系,切线的性质和判定,正多边形与圆的计算和证明等,通常以这些知识作为载体,与函数、方程等知识综合考查.垂径定理及其推论的应用1.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为()A.95B.245C.185D.52(第1题)(第2题)2.如图是一圆柱形输水管的横截面,阴影部分为有水部分.如果水面AB 的宽为8 cm,水的最大深度为2 cm,那么该输水管的半径为() A.3 cm B.4 cm C.5 cm D.6 cm圆心角与圆周角3.如图所示,AB是⊙O的直径,AB⊥弦CD于点E,∠BOC=70°,则∠ABD =()A.20°B.46°C.55°D.70°(第3题)(第4题)4.如图,A ,B ,C ,D 四个点均在⊙O 上,∠AOD =70°,AO ∥DC ,则∠B 的度数为( )A .40°B .45°C .50°D .55°5.如图所示,C 为半圆上一点,AC ︵=CE ︵,过点C 作直径AB 的垂线CP ,P 为垂足,弦AE 交PC 于点D ,交CB 于点F.求证:AD =CD.(第5题)点、直线与圆的位置关系6.已知⊙O的半径为4 cm,A为线段OP的中点,当OP=7 cm时,点A 与⊙O的位置关系是()A.点A在⊙O内B.点A在⊙O上C.点A在⊙O外D.不能确定7.在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心,r 为半径作圆,若⊙C与直线AB相切,则r的值为()A.2 cm B.2.4 cm C.3 cm D.4 cm8.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程2x2-22x+m-1=0有实数根,则直线l与⊙O()A.相离或相切B.相切或相交C.相离或相交D.无法确定切线的判定与性质(第9题)9.(中考·哈尔滨)如图,AB是⊙O的直径,AC是⊙O的切线,连结OC交⊙O于点D,连结BD,∠C=40°,则∠ABD的度数是()A.30°B.25°C.20°D.15°10.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E.(1)若BC=3,CD=1,求⊙O的半径;(2)取BE的中点F,连结DF,求证DF是⊙O的切线.(第10题)与圆有关的计算11.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为()(第11题) A.25π-6B.252π-6C.256π-6D.258π-612.(2015·兰州)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°,①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和π)(第12题)圆与其他知识的综合类型1:圆与三角形的综合13.(2015·成都)如图,在Rt △ABC 中,∠ABC =90°,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F ,且BF =BC.⊙O 是△BEF 的外接圆,连结BD.(1)求证:△ABC ≌△EBF ;(2)试判断BD 与⊙O 的位置关系,并说明理由.(第13题)类型2:圆与四边形的综合14.(2015·天津)已知A ,B ,C 是⊙O 上的三个点,四边形OABC 是平行四边形,过点C 作⊙O 的切线,交AB 的延长线于点D.(1)如图①,求∠ADC 的大小;(2)如图②,经过点O 作CD 的平行线,与AB 交于点E ,与AB ︵交于点F ,连结AF,求∠FAB的大小.(第14题) 类型3:圆与函数的综合15.如图,直线y=-34x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.(1)如图①,当四边形OBCE是矩形时,求点C的坐标;(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径r;(3)在⊙C的移动过程中,能否使△OEF是等边三角形?(只回答“能”或“不能”)(第15题)专训6圆与二次函数的综合名师点金:圆与二次函数的综合,一般会涉及勾股定理、相似三角形的判定、求二次函数的表达式、求直线对应的函数表达式、切线的判定与性质,综合考察的知识点较多,同学们注意培养自己解答综合题的能力,关键还是基础知识的掌握,要能将所学知识融会贯通,有的问题的解法不止一种,同学们可以积极探索其他解法.二次函数中利用全等证明圆与直线的位置关系1.如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).(1)求经过B、C、D三点的抛物线对应的函数表达式;(2)设抛物线的顶点为E,证明:直线CE与⊙A相切.(第1题)利用直线与圆的位置关系求直线对应的函数表达式2.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).(1)求抛物线对应的函数表达式;(2)以AB为直径作⊙M,一直线经过点E(-1,-5),并且与⊙M相切,求该直线对应的函数表达式.(第2题)利用圆的有关性质求抛物线对应的函数表达式3.(2015·烟台节选)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧ED上的点F作FH⊥AD于点H,且FH=1.5.(1)求点D的坐标及该抛物线对应的函数表达式;(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标.(第3题)二次函数中利用勾股定理的逆定理证明直线与圆的位置关系4.如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.(1)求D点的坐标和圆D的半径;(2)求sin∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;(3)设抛物线的顶点为F,证明直线AF与圆D相切.(第4题)答案专训1 1.A2.B 点拨:∵有一圆经过△ABC 的三个顶点,且弦BC 的中垂线与AC ︵相交于D 点,∴AB ︵所对的圆心角的度数=2∠C =2×46°=92°,ADC ︵所对的圆心角的度数=2∠B =2×74°=148°=AD ︵所对的圆心角的度数+DC ︵所对的圆心角的度数=AD ︵所对的圆心角的度数+BAD ︵所对的圆心角的度数=AD ︵所对的圆心角的度数+AB ︵所对的圆心角的度数+AD ︵所对的圆心角的度数,∴AD ︵所对的圆心角的度数=12(148°-92°)=28°.故选B .3.(1)证明:∵AB ,CD 是直径,∴∠ADB =∠CBD =90°. 在Rt △ABD 和Rt △CDB 中, ⎩⎨⎧AB =CD ,BD =DB ,∴Rt △ABD ≌Rt △CDB(HL ).(2)解:∵BE 是切线,∴AB ⊥BE.∴∠ABE =90°. ∵∠DBE =37°,∴∠ABD =53°.∵OD =OA ,∴∠ODA =∠BAD =90°-53°=37°, 即∠ADC 的度数为37°.4.2 cm 点拨:连接OB ,∵∠BCD =22°30′,∴∠BOD =2∠BCD =45°.∵AB ⊥CD ,∴BE =AE =12AB =12×22=2(cm ),△BOE 为等腰直角三角形,∴OB =2BE =2 cm ,故答案为2 cm .5.2 36.解:连接OC.∵∠A =30°,∴∠COD =60°. ∵DC 切⊙O 于C ,∴∠OCD =90°.∴∠D =30°.∵OD =30 cm ,∴OC =12OD =15 cm . ∴AB =2OC =30 cm .(第7题) 7.(1)证明:如图,连接OD,∵OB=OD,∴∠ABC=∠ODB.∵AB=AC,∴∠ABC=∠ACB.∴∠ODB=∠ACB.∴OD∥AC.∵DF是⊙O的切线,∴DF⊥OD.∴DF⊥AC.(2)解:如图,连接OE,∵DF⊥AC,∠CDF=22.5°,∴∠ABC=∠ACB=67.5°,∴∠BAC=45°.∵OA=OE,∴∠AOE=90°.∵⊙O的半径为4,∴S扇形AOE =4π,S△AOE=8.∴S阴影=S扇形AOE-S△AOE=4π-8.专训2(第1题)1.解:连接OA ,OF ,如图.设OA =OF =r cm ,AB =a cm .在Rt △OAB 中,r 2=⎝ ⎛⎭⎪⎫a 22+a 2,在Rt △OEF 中,r 2=42+⎝ ⎛⎭⎪⎫4+a 22,∴a 24+a 2=16+16+4a +a24,解得a 1=8,a 2=-4(舍去).∴r 2=⎝ ⎛⎭⎪⎫822+82=80,∴r 1=45,r 2=-45(舍去),即该半圆的半径为4 5 cm .点拨:在有关圆的计算题中,求角度或边长时,常连接半径构造等腰三角形或直角三角形,利用特殊三角形的性质来解决问题.2.证明:连接AD ,BD.∵∠DAC ,∠DBC 是DC ︵所对的圆周角. ∴∠DAC =∠DBC.∵CD 平分∠ACM ,DP ⊥AC ,DH ⊥CM ,∴DP =DH. 在△ADP 和△BDH 中, ⎩⎨⎧∠DAP =∠DBH ,∠DPA =∠DHB =90°,DP =DH ,∴△ADP ≌△BDH ,∴AP =BH.点拨:本题通过作辅助线构造圆周角,然后利用“同弧所对的圆周角相等”得到∠DAC =∠DBC ,为证两三角形全等创造了条件.3.(1)证明:过点D 作⊙O 的直径DE ,连接AE ,EC ,AC. ∵DE 是⊙O 的直径,∴∠ECD =∠EAD =90°. 又∵CD ⊥AB ,∴EC ∥AB , ∴∠BAC =∠ACE. ∴BC ︵=AE ︵.∴BC =AE.在Rt △AED 中,AD 2+AE 2=DE 2, ∴AD 2+BC 2=4R 2.(2)解:过点O作OF⊥AD于点F.∵弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),∴AD=5,BC=1.由(1)知,AD2+BC2=4R2,∴52+12=4R2,∴R=26 2.∵∠EAD=90°,OF⊥AD,∴OF∥EA.又∵O为DE的中点,∴OF=12AE=12BC=12,即点O到AD的距离为12.点拨:本题作出直径DE,利用“直径所对的圆周角是直角”构造了两个直角三角形,给解题带来了方便.4.解:CD与⊙O相切,理由如下:如图,作直径CE,连接AE.∵CE是直径,∴∠EAC=90°.∴∠E+∠ACE=90°.∵CA=CB,∴∠B=∠CAB.∵AB∥CD,∴∠ACD=∠CAB.∵∠B=∠E,∴∠ACD=∠E,∴∠ACE+∠ACD=90°,即OC⊥DC.又OC为⊙O的半径,∴CD与⊙O相切.(第4题)(第7题) 5.C 6.60°7.(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°.∵点D是BC 的中点,∴AD是线段BC的垂直平分线,∴AB=AC.∵AB=BC,∴AB=BC=AC,∴△ABC为等边三角形.(2)解:连接BE.∵AB是直径,∴∠AEB=90°,∴BE⊥AC,∵△ABC是等边三角形,∴AE=EC,即E为AC的中点.∵D是BC的中点,故DE为△ABC的中位线.∴DE=12AB=12×2=1.8.(1)证明:连接OB,∵OA=OB,∴∠OAB=∠OBA.∵PA=PB,∴∠PAB=∠PBA.∴∠OAB+∠PAB=∠OBA+∠PBA,即∠PAO=∠PBO.又∵PA是⊙O的切线,∴∠PAO=90°.∴∠PBO=90°.∴OB⊥PB. 又∵OB是⊙O的半径,∴PB是⊙O的切线.(2)解:连接OP,∵PA=PB,∴点P在线段AB的垂直平分线上.∵OA=OB,∴点O在线段AB的垂直平分线上.∴OP为线段AB的垂直平分线,又∵BC⊥AB,∴PO∥BC.∴∠AOP=∠ACB=60°.∴∠OPA=30°. 在Rt△APO中,AO2+PA2=PO2,即AO2+3=(2AO)2.又∵AO>0,∴AO=1.∴⊙O的半径为1.(第8题)(第9题) 9.(1)证明:如图,连接CO,交DB于点E,∴∠O=2∠CDB=60°.又∵∠OBE=30°,∴∠BEO=180°-60°-30°=90°.∵AC∥BD,∴∠ACO=∠BEO=90°,即OC⊥AC.又∵点C在⊙O上,∴AC是⊙O的切线.(2)解:∵OE⊥DB,∴EB=12DB=3 3 cm.在Rt△EOB中,∵∠OBE=30°,∴OE=12OB.∵EB=3 3 cm,∴由勾股定理可求得OB=6 cm. 又∵∠D=∠DBO,DE=BE,∠CED=∠OEB,∴△CDE≌△OBE,∴S△CDE =S△OBE,∴S阴影=S扇形OCB=60360π·62=6π(cm2).专训31.解:(1)如图,过B作BH⊥PQ于H,在Rt△BHP中,由条件易知:BP=320 km,∠BPQ=30°.∴BH=12BP=160 km<200 km.∴台风会影响B市.(2)如图,以B为圆心,200 km为半径作圆,交PQ于P1,P2两点,连接BP1,由垂径定理知P1P2=2P1H.在Rt△BHP1中,BP1=200 km,BH=160 km,∴P1H=2002-1602=120(km).∴P1P2=2P1H=240 km.∴台风影响B市的时间为24030=8(h).点拨:本题在图形中画出圆,可以非常直观地构造数学模型,然后利用垂径定理解决生活中的实际问题.(第1题)(第2题) 2.解:选择射门方式二较好,理由如下:设AQ与圆的交点为C,连接PC,如图所示.∵∠PCQ是△PAC的外角,∴∠PCQ>∠A.又∵∠PCQ=∠B,∴∠B>∠A.∴在B点射门比在A点射门好.∴选择射门方式二较好.点拨:本题运用转化思想,将射门角度大小的问题,建模转化到圆中,根据圆周角的相关知识来解决实际问题.3.解:修建的这条水渠不会穿过公园.理由:过点C作CD⊥AB,垂足为D.∵∠CBA=45°,∴∠BCD=45°,CD=BD.设CD=x km,则BD=x km.易知∠CAB=30°,∴AC=2x km,AD=(2x)2-x2=3x km.∴3x+x=1,解得x=3-1 2,即CD=3-12km≈0.366 km=366 m>350 m,也就是说,以点C为圆心,350 m为半径的圆与AB相离.即修建的这条水渠不会穿过公园.4.解:∵圆锥形漏斗的底面半径为20 cm,高为40 2 cm,∴圆锥的母线长为202+(402)2=60(cm).设圆锥的侧面展开图的圆心角为n°,则有nπ×60180=2π×20,解得n=120.方案一:如图①,扇形的半径为60 cm,矩形的宽为60 cm,易求得矩形的长为60 3 cm.此时矩形的面积为60×603=3 6003(cm2).方案二:如图②,扇形与矩形的两边相切,有一边重合,易求得矩形的宽为60 cm,长为30+60=90(cm),此时矩形的面积为90×60=5 400(cm2).∵3 6003>5 400,∴方案二所用材料最省,即选长为90 cm,宽为60 cm的矩形铁皮,才能使所用材料最省.(第4题)专训41.解:(1)作OD⊥BC于D.由垂径定理知,点D是BC的中点,即BD=12BC,∵OB=12AB=5 cm,OD=4 cm,由勾股定理得,BD=OB2-OD2=3 cm,∴BC=2BD=6 cm.(2)设经过t s,△BPC是等腰三角形.①当PC为底边时,有BP=BC,即10-t=6,解得t=4;②当BC为底边时,有PC=PB,此时P点与O点重合,t=5.∴经过4 s或5 s△BPC是等腰三角形.2.解:(1)线段AB长度的最小值为4.理由如下:连接OP.∵AB切⊙O于P,∴OP⊥AB.取AB的中点C,则AB=2OC,当OC=OP时,OC最短,即AB最短,此时AB=4.(2)存在.假设存在符合条件的点Q.如图①,设四边形APOQ为平行四边形,∵∠APO=90°,∴四边形APOQ为矩形.又∵OP=OQ,∴四边形APOQ为正方形,∴OQ=QA.∴∠QOA=45°,在Rt△OQA中,根据OQ=2,∠AOQ=45°,得Q点的坐标为(2,-2).(第2题)如图②,设四边形APQO为平行四边形,连接OP,∵OQ∥PA,∠APO=90°,∴∠POQ=90°.又∵OP=OQ,∴∠PQO=45°,∵PQ∥OA,∴PQ⊥y轴.设PQ交y轴于点H,在Rt△OHQ中,根据OQ=2,∠HQO=45°,得Q点的坐标为(-2,2).∴符合条件的点Q的坐标为(2,-2)或(-2,2).3.解:如图,设PQ与⊙O相切于点H,过点P作PE⊥BC,垂足为E.(第3题)∵在四边形ABCD中,AD∥BC,∠ABC=90°,∴PE=AB.由题意可知:AP=BE=t cm,CQ=2t cm,∴BQ=BC-CQ=(22-2t) cm,EQ=BQ-BE=22-2t-t=(22-3t) cm.∵AB 为⊙O 的直径,∠ABC =∠DAB =90°, ∴AD ,BC 为⊙O 的切线.∴AP =PH ,HQ =BQ. ∴PQ =PH +HQ =AP +BQ =t +22-2t =(22-t) cm . 在Rt △PEQ 中,PE 2+EQ 2=PQ 2, ∴122+(22-3t)2=(22-t)2,即 t 2-11t +18=0,解得t 1=2,t 2=9.∵P 在AD 边运动的时间为AD 1=81=8(s ),而t =9>8,∴t =9(舍去). ∴当t =2 s 时,PQ 与⊙O 相切.4.解:(1)∵在△ACO 中,∠OAC =60°,OC =OA , ∴△ACO 是等边三角形. ∴∠AOC =60°. (2)如图,(第4题)①作点C 关于直径AB 的对称点M 1,连接AM 1,OM 1. 易得S △M 1AO =S △CAO ,∠AOM 1=60°,∴AM 1︵=4π180×60=43π.∴当点M 运动到M 1时,S △MAO =S △CAO ,此时动点M 经过的弧长为43π.②过点M 1作M 1M 2∥AB 交⊙O 于点M 2,连接AM 2,OM 2,易得S △M 2AO =S △CAO ,∴∠OM 1M 2=∠AOM 1=60°.又∵OM 1=OM 2,∴∠M 1OM 2=60°,∴∠AOM 2=120°.∴AM 2︵=4π180×120=83π.∴当点M 运动到M 2时,S △MAO =S △CAO ,此时动点M 经过的弧长为83π. ③过点C 作CM 3∥AB 交⊙O 于点M 3,连接AM 3,OM 3,易得S △M 3AO=S △CAO ,∠AOM 3=120°.∴AM 2M 3︵=4π180×240=163π.∴当点M 运动到M 3时,S △MAO =S △CAO ,此时动点M 经过的弧长为163π. ④当点M 运动到C 时,M 与C 重合,S △MAO =S △CAO ,此时动点M 经过的弧长为4π180×300=203π.综上所述,当S △MAO =S △CAO 时,动点M 所经过的弧长为43π或83π或163π或203π.专训51.C 2.C 3.C 4.D(第5题)5.证明:如图,连结AC. ∵AB 为⊙O 的直径, ∴∠ACB =90°,∴∠ACD +∠DCB =90°. ∵CP ⊥AB 于点P , ∴∠B +∠DCB =90°, ∴∠ACD =∠B.又∵AC ︵=CE ︵,∴∠B =∠CAD =∠ACD ,∴AD =CD. 6.A 7.B 8.B 9.B(第10题)10.(1)解:设⊙O 的半径为r ,∵AB 是⊙O 的直径,BC 是⊙O 的切线, ∴AB ⊥BC ,在Rt △OBC 中,∵OC 2=OB 2+CB 2, ∴(r +1)2=r 2+(3)2,解得r =1,∴⊙O 的半径为1. (2)证明:连结OF , ∵OA =OB ,BF =EF , ∴OF 是△BAE 的中位线, ∴OF ∥AE ,∴∠A =∠2,∠1=∠ADO , 又∵∠ADO =∠A ,∴∠1=∠2,在△OBF 和△ODF 中,⎩⎨⎧OB =OD ,∠2=∠1,OF =OF ,∴△OBF ≌△ODF , ∴∠ODF =∠OBF =90°,即OD ⊥DF ,又OD 是⊙O 的半径, ∴FD 是⊙O 的切线. 11.D(第12题)12.解:(1)相切,理由如下: 如图,连结OD , ∵AD 平分∠BAC , ∴∠1=∠2.∵OA =OD ,∴∠1=∠3, ∴∠2=∠3,∴OD ∥AC. 又∠C =90°,∴OD ⊥BC , ∴BC 与⊙O 相切. (2)①设⊙O 的半径为r. ∵AC =3,∠B =30°,∴AB =6. 又OA =OD =r ,∴OB =2r.∴2r +r =6,解得r =2,即⊙O 的半径是2.②由①得OD =2,则OB =4,BD =23,S 阴影=S △OBD -S 扇形ODE =12×23×2-60π×22360=23-2π3.13.(1)证明:在Rt △CED 中,∠C +∠CED =90°,在Rt △BFE 中,∠EFB +∠BEF =90°.∵∠CED =∠BEF ,∴∠C =∠EFB.在Rt △ABC 和Rt △EBF 中, ⎩⎨⎧∠C =∠EFB ,BC =BF ,∠ABC =∠EBF ,∴△ABC ≌△EBF.(2)解:BD 与⊙O 相切,理由如下: 连结BO ,∵OB =OF , ∴∠OBF =∠OFB.∵FD 垂直平分AC ,∴D 为AC 的中点,又∵△ABC 为直角三角形. ∴BD =CD ,∴∠DCB =∠DBC.由(1)知∠ACB =∠EFB , ∴∠DBC =∠DFB =∠OBF.∵∠CBF =∠CBO +∠OBF =90°, ∴∠DBO =∠CBO +∠DBC =90°, ∴BD 为⊙O 的切线.14.解:(1)∵CD 是⊙O 的切线,C 为切点, ∴OC ⊥CD ,即∠OCD =90°. ∵四边形OABC 是平行四边形,(第14题)∴AB ∥OC ,即AD ∥OC. ∴∠ADC +∠OCD =180°, ∴∠ADC =180°-∠OCD =90°.(2)如图,连结OB ,则OB =OA =OC. ∵四边形OABC 是平行四边形, ∴OC =AB , ∴OA =OB =AB.即△AOB 是等边三角形. 于是,∠AOB =60°.由OF ∥CD ,又∠ADC =90°,得∠AEO =∠ADC =90°.∴OF ⊥AB ,有BF ︵=AF ︵.∴∠FOB =∠FOA =12∠AOB =30°.∴∠FAB =12∠FOB =15°.15.解:(1)∵直线y =-34x +3与x 轴交于点A(4,0),与y 轴交于点B(0,3),∴OA =4,OB =3,∴AB =32+42=5.连结CF ,∵四边形OBCE 是矩形,∴CE =OB =3.设OE =x ,则由切线长定理知AF =AE =x +4,∴BF =x +4-5=x -1.在Rt △CBF 中,∵BC =OE =x ,CF =CE =3,BF =x -1,BC 2=CF 2+BF 2,∴x 2=32+(x -1)2,解得x =5,即OE =5,∴点C 的坐标为(-5,3).(2)连结CE ,CD ,易知四边形CEOD 是正方形,∴OE =OD =r.由切线长定理知BF =BD =3-r ,AE =AF ,又∵AE =AO +OE =4+r ,AF =AB +BF =5+3-r =8-r ,∴4+r =8-r ,∴r =2.(3)不能.专训61.(1)解:设过点B 、C 、D 三点的抛物线对应的函数表达式为y =ax 2+bx+c ,则⎩⎨⎧4=c ,0=4a -2b +c ,0=64a -8b +c ,解得⎩⎪⎨⎪⎧a =14,b =52,c =4.∴经过B 、C 、D 三点的抛物线对应的函数表达式为y =14x 2+52x +4. (2)证明:∵y =14x 2+52x +4=14(x +5)2-94,∴E ⎝ ⎛⎭⎪⎫-5,-94. 设直线CE 对应的函数表达式为y =mx +n ,直线CE 与y 轴交于点G ,则⎩⎪⎨⎪⎧0=-2m +n ,-94=-5m +n ,解得⎩⎪⎨⎪⎧m =34,n =32,∴直线CE 对应的函数表达式为y =34x +32. 在y =34x +32中,当x =0时,y =32,∴点G 的坐标为⎝ ⎛⎭⎪⎫0,32.如图,连结AB 、AC 、AG ,则BG =OB -OG =4-32=52,CG =OC 2+OG 2=22+⎝ ⎛⎭⎪⎫322=52,∴BG =CG.又∵AB =AC ,AG =AG , ∴△ABG ≌△ACG , ∴∠ACG =∠ABG.∵⊙A 与y 轴相切于点B(0,4), ∴∠ABG =90°,。
2010年中考数学二轮复习专题水平测试-正多边形与圆、弧长、扇形面积
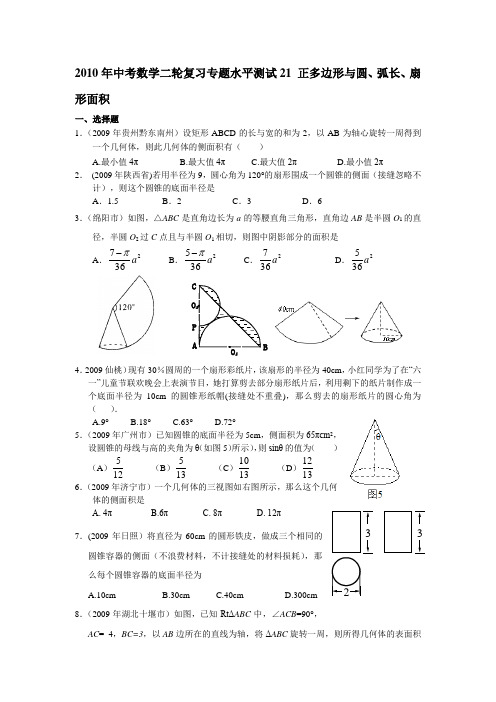
2010年中考数学二轮复习专题水平测试21 正多边形与圆、弧长、扇形面积一、选择题1.(2009年贵州黔东南州)设矩形ABCD 的长与宽的和为2,以AB 为轴心旋转一周得到一个几何体,则此几何体的侧面积有( )A.最小值4πB.最大值4πC.最大值2πD.最小值2π2. (2009年陕西省)若用半径为9,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是 A .1.5 B .2 C .3 D .6 3.(绵阳市)如图,△ABC 是直角边长为a 的等腰直角三角形,直角边AB 是半圆O 1的直径,半圆O 2过C 点且与半圆O 1相切,则图中阴影部分的面积是 A .2367a π- B .2365a π- C .2367a D .2365a4.2009仙桃)现有30%圆周的一个扇形彩纸片,该扇形的半径为40cm ,小红同学为了在“六一”儿童节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为10cm 的圆锥形纸帽(接缝处不重叠),那么剪去的扇形纸片的圆心角为( ).A.9°B.18°C.63°D.72° 5.(2009年广州市)已知圆锥的底面半径为5cm ,侧面积为65πcm 2,设圆锥的母线与高的夹角为θ(如图5)所示),则sinθ的值为( ) (A )125 (B )135 (C )1310 (D )13126.(2009年济宁市)一个几何体的三视图如右图所示,那么这个几何体的侧面积是A. 4πB.6πC. 8πD. 12π7.(2009年日照)将直径为60cm 的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为 A.10cmB.30cmC.40cmD.300cm8.(2009年湖北十堰市)如图,已知RtΔABC 中,∠ACB =90°,AC = 4,BC=3,以AB 边所在的直线为轴,将ΔABC 旋转一周,则所得几何体的表面积是( ). A .π5168 B .π24 C .π584 D .π129.(2009年台州市),⊙O 的内接多边形周长为3 ,⊙O 的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( ) A. B. C .10 D10.(2009年天津市)边长为a 的正六边形的内切圆的半径为( )A .2aB .a C.2a D .12a11.(2009年济南)在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径6cm O B =,高8cm O C =.则这个圆锥漏斗的侧面积是( )A .230cmB .230cm πC .260cm πD .2120cm 12.(2009年茂名市)如图,一把遮阳伞撑开时母线的长是2米,底面半径为1米,则做这把遮阳伞需用布料的面积是( ) A .4π平方米 B .2π平方米 C .π平方米 D .1π2平方米二、选择题13.(2009年江苏省)已知正六边形的边长为1cm ,分别以它的三个不相邻的顶点为圆心,1cm 长为半径画弧(如图),则所得到的三条弧的长度之和为 cm (结果保留π).14.(2009年黄冈市) 矩形ABCD 的边AB =8,AD =6,现将矩形ABCD 放在直线l 上且沿着l 向右作无滑动地翻滚,当它翻滚至类似开始的位置1111A B C D 时(如图所示),则顶点A 所经过的路线长是_________.15.(2009年兰州)兰州市某中学的铅球场如图10所示,已知扇形AOB的面积是36米2,弧AB 的长度为9米,那么半径OA = 米.16.(2009年凉山州)将A B C △绕点B 逆时针旋转到A BC ''△使A B C '、、在同一直线上,若90B C A ∠=°,304cm BAC AB ∠==°,,则图中阴影部分面积为cm 2.17.(2009年常德市)一个圆锥的母线长为5cm ,底面圆半径为3 cm ,则这个圆锥的侧面积是 cm 2(结果保留π).B18.(2009泰安)如图,(1)是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图(2)所示,ABCD 是正方形,⊙O 是该正方形的内切圆,E 为切点,以B 为圆心,分别以BA.BE 为半径画扇形,得到如图所示的扇环形,图(1)中的圆与扇环的面积比为 。
中考数学复习《圆的弧长和图形面积的计算》练习题含答案

中考数学复习 圆的弧长和图形面积的计算一、选择题1.扇形的半径为30 cm ,圆心角为120°,此扇形的弧长是( A ) A .20π cm B .10π c m C .10 cm D .20 cm【解析】弧长=120π×30180=20π(cm),故选A.2.如图,⊙O 是△ABC 的外接圆,BC =2,∠BAC =30°,则劣弧BC 的长等于( A ) A.2π3 B.π3 C.23π3 D.3π3【解析】如图,连结OB ,OC ,∵∠BAC =30°,∴∠BOC =2∠BAC =60°,又OB =OC ,∴△OBC 是等边三角形,∴BC =OB =OC =2,∴劣弧BC 的长为60π×2180=2π3.,第2题图) ,第3题图)3.如图,在Rt △ABC 中,AC =5 cm ,BC =12 cm ,∠ACB =90°,把Rt △ABC 所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( B )A .60π cm 2B .65π cm 2C .120π cm 2D .130π cm 2【解析】∵在Rt △ABC 中,AC =5 cm ,BC =12 cm ,∠ACB =90°,∴由勾股定理得AB=13 cm ,∴圆锥的底面周长=10π cm ,∴几何体的侧面积=12×10π ×13=65π (cm 2) .故选B.4.如图,⊙O 的半径为3,四边形ABCD 内接于⊙O ,连结OB ,OD ,若∠BOD =∠BCD ,则BD ︵的长为( C )A .π B.32π C .2π D .3π【解析】根据圆内接四边形对角互补可得∠BCD +∠A =180°,由圆周角定理可得∠BOD =2∠A ,再由∠BOD =∠BCD 可得2∠A +∠A =180°,所以∠A =60°,即可得∠BOD =120°,所以BD ︵的长=120π×3180=2π;故选C.,第4题图) ,第5题图)5.用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影部分面积为( A )A .π-332B .π-3 3 C.332 D .π-334【解析】如图,设AB 的中点P ,连结OA ,OP ,AP ,△OAP 的面积是:34×12=34,扇形OAP 的面积是:S 扇形=π6,AP 直线和AP 弧面积:S 弓形=π6-34,阴影面积:3×2S 弓形=π-332. 二、填空题6.如图,扇形纸扇完全打开后,外侧两竹条AB ,AC 的夹角为120°,AB 长为30 cm ,求则BC ︵的长为__20π_cm __.(结果保留π)【解析】根据弧长公式l =n πr 180可得:弧BC 的长=n πr 180=120×π×30180=20π (cm).7.120°的圆心角所对的弧长是6π,则此弧所在圆的半径是__9__.【解析】根据弧长的公式l =n πr 180,得到6π=120πr180,解得r =9.8.如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD 变形为以A 为圆心,AB 为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD 的面积为__25__.【解析】扇形ABD 的弧长DB ︵=BC +DC =10,扇形ABD 的半径为正方形的边长5,∴S扇形ABD =12×10×5=25.9.如图,在▱ABCD 中,AB 为⊙O 的直径,⊙O 与DC 相切于点E ,与AD 相交于点F ,已知AB =12,∠C =60°,则FE ︵的长为__π__.【解析】如图连结OE ,OF ,∵CD 是⊙O 的切线,∴OE ⊥CD ,∴∠OED =90°,∵四边形ABCD 是平行四边形,∠C =60°,∴∠A =∠C =60°,∠D =120°,∵OA =OF ,∴∠A =∠OF A =60°,∴∠DFO =120°,∴∠EOF =360°-∠D -∠DFO -∠DEO =30°,FE ︵的长=30π×6180=π.故答案为π.三、解答题10.如图,AB 切⊙O 于点B ,OA =2,∠OAB =30°,弦BC ∥OA .求劣弧BC 的长.(结果保留π)解:连结OC ,OB ,∵AB 为圆O 的切线,∴∠ABO =90°,在Rt △ABO 中,OA =2,∠OAB =30°,∴OB =1,∠AOB =60°,∵BC ∥OA ,∴∠OBC =∠AOB =60°,又OB=OC ,∴△BOC 为等边三角形,∴∠BOC =60°,∴劣弧BC 长为60π×1180=π311.如图,在平面直角坐标系中,点A ,B ,C 的坐标分别为(-1,3),(-4,1),(-2,1),先将△ABC 沿一确定方向平移得到△A 1B 1C 1,点B 的对应点B 1的坐标是(1,2),再将△A 1B 1C 1绕原点O 顺时针旋转90°得到△A 2B 2C 2,点A 1的对应点为点A 2.(1)画出△A 1B 1C 1,△A 2B 2C 2;(2)求出在这两次变换过程中,点A 经过点A 1到达A 2的路径总长.解:(1)如图,△A 1B 1C 1,△A 2B 2C 2即为所作(2)OA 1=42+42=42,点A 经过点A 1到达A 2的路径总长=52+12+90π×42180=26+22π12.如图,AB 与⊙O 相切于点C ,OA ,OB 分别交⊙O 于点D ,E ,CD ︵=CE ︵. (1)求证:OA =OB ;(2)已知AB =43,OA =4,求阴影部分的面积.解:(1)连结OC ,则OC ⊥AB.∵CD ︵=CE ︵,∴∠AOC =∠BOC.在△AOC 和△BOC 中, ⎩⎨⎧∠AOC =∠BOC ,OC =OC ,∠OCA =∠OCB =90°,∴△AOC ≌△BOC (ASA ),∴OA =OB(2)由(1)可得AC =BC =12AB =23,∴在Rt △AOC 中,OC =2,∴∠AOC =∠BOC =60°,∴S △BOC =12BC· OC =12×23×2=23,S 扇形EOC =60°×π×22360°=23π,∴S 阴影=S △BOC -S 扇形EOC =23-23π13.如图,在正方形ABCD 中,AD =2,E 是AB 的中点,将△BEC 绕点B 逆时针旋转90°后,点E 落在CB 的延长线上点F 处,点C 落在点A 处.再将线段AF 绕点F 顺时针旋转90°得线段FG ,连结EF ,CG .(1)求证:EF ∥CG ;(2)求点C ,A 在旋转过程中形成的,与线段CG 所围成的阴影部分的面积.解:(1)在正方形ABCD 中,AB =BC =AD =2,∠ABC =90°,∵△BEC 绕点B 逆时针旋转90°得到△ABF ,∴△ABF ≌△CBE ,∴∠FAB =∠ECB ,∠ABF =∠CBE =90°,AF =EC ,∴∠AFB +∠FAB =90°,∵线段AF 绕点F 顺时针旋转90°得线段FG ,∴∠AFB +∠CFG =∠AFG =90°,∴∠CFG =∠FAB =∠ECB ,∴EC ∥FG ,∵AF =EC ,AF =FG ,∴EC =FG ,∴四边形EFGC 是平行四边形,∴EF ∥CG(2)∵AD =2,E 是AB 的中点,∴FB =BE =12AB =12×2=1,∴AF =AB 2+BF 2=22+12=5,由平行四边形的性质,△FEC ≌△CGF ,∴S △FEC =S △CGF ,∴S 阴影=S 扇形BAC+S △ABF +S △FGC -S 扇形FAG =90·π·22360+12×2×1+12×(1+2)×1-90π×(5)2360=52-π4。
圆的弧长和图形面积的计算

∴点 A 所经过的路线 AA′ 的半径为 1 的小圆在半径为 9 的大圆内滚动, 且始终与大圆相切,则小圆扫过的阴影部分的面积为( ) A.17π B.32π C.49π D.80π
答案 B 解析 如图,可知外圆的半径为 9, 内圆的半径为 7,S 圆环=S 外圆-S 内圆 =π×92-π×72=81π-49π=32π.
基础知识 自主学习
要点梳理
1.弧长及扇形的面积: (1)半径为r,弧为n°的圆心角所对的弧长公式:
l=n18π0r
(2) 半径为r,孤为n°的圆心角所对的扇形面积公式:
S=n3π6r02=12lr
2.圆锥的侧面积和全面积: 圆锥的侧面展开图是一个扇形,若设圆锥的母线长为 l,底面 半径为 r,那么这个扇形的半径为 l,扇形的弧长为 2πr. (1)圆锥侧面积公式: S 圆锥侧=πrl; (2)圆锥全面积公式: S 圆锥全=πrl+πr2; (3)圆锥侧面展开图扇形圆心角公式: θ=rl·360°.
再由图②到图③,∠O=60°,OA=1.求O点所运动的路 径长.
解 点 O 运动路径第一段弧长为901π8×0 1=12π;第二段路径的弧长为601π8×0 1=13π; 第三段路径的弧长为901π8×0 1=12π. 即点 O 所运动的路径长为12π+13π+12π=43π.
探究提高 本题中所求点O经过的路线是由三条不同的弧组 合而成的,在求每段弧长时,要注意确定每段弧的半径及 所对圆心角的度数.
S 阴影=S 扇 AOB-S 扇 COD =14π(OA2-OC2) =14π×(652-152)=1000π. 答:刮雨刷 BD 扫过的面积是 1000π (cm2).
弦 BC∥OA,则劣弧 BC 的弧长为( )
3 A. 3 π
初中数学知识归纳圆的弧长面积及相关计算

初中数学知识归纳圆的弧长面积及相关计算圆的弧长与面积是初中数学中重要的内容,我们通过归纳总结可以更好地理解和应用这些知识。
在本文中,我们将重点讨论圆的弧长与面积的相关计算方法。
一、圆的弧长圆的弧长指的是圆周上的一部分弧所对应的长度。
首先,我们需要了解以下两个概念:1. 弧度制:弧度制是一种表示角度大小的单位,用弧长所对应的弧度数来度量,通常用符号"rad"表示。
一个圆的周长等于2π,也可以表示为360°。
根据这个规定,一个弧度等于圆的周长的1/2π。
2. 圆心角:圆心角是圆心所夹的两个半径所对应的角度。
一个圆的圆心角大小为360°或2π弧度。
在计算圆的弧长时,我们首先需要知道弧度制的概念。
通常情况下,我们可以利用以下公式计算弧长:s = rθ其中,s表示弧长,r表示半径,θ表示圆心角的大小(用弧度制表示)。
例如,如果半径为5cm的圆的圆心角大小为π/3弧度(即60°),那么可以通过代入公式计算出弧长:s = 5 * (π/3) ≈ 5.24cm二、圆的面积圆的面积是指圆内部所包围的平面部分的大小。
圆的面积计算公式是:A = πr²其中,A表示面积,r表示半径,π是一个数学常数,近似取3.14。
例如,如果半径为7cm的圆的面积可以通过代入公式计算出:A = 3.14 * 7² ≈ 153.86cm²三、相关计算除了圆的弧长和面积的计算外,还有一些相关的计算方法需要了解。
1. 弧长与角度之间的关系:我们已经知道,圆的周长等于2π 或360°。
因此,在计算弧长时,可以利用以下关系:弧长/周长 = 圆心角/360° = 弧度数/2π2. 弧长与半径之间的关系:如果已知圆心角度数和半径,可以利用以下关系计算弧长:弧长= (2π/360°) * 半径 * 圆心角度数3. 部分圆的弧长与面积的计算:如果我们考虑的不是完整的圆周,而是部分圆的弧长和面积,可以根据圆心角度数和半径利用上述公式进行运算。
中考数学专项训练圆的弧长和图形面积的计算含解析试题

卜人入州八九几市潮王学校圆的弧长和图形面积的计算一、选择题1.假设圆锥的轴截图为等边三角形,那么称此圆锥为正圆锥,那么正圆锥的侧面展开图的圆心角是〔〕A.90°B.120°C.150°D.180°2.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形〔阴影局部〕图案,那么树叶形图案的周长为〔〕A.πa B.2πa C.D.3a3.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是〔〕A.πB.πC.πD.π4.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,那么图中阴影局部的面积是〔〕A.﹣B.﹣ C.π﹣D.π﹣5.如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点.假设∠CDE=x°,∠ECD=y°,⊙B 的半径为R,那么的长度是〔〕A.B.C.D.二、填空题6.圆锥的侧面积为6πcm2,底面圆的半径为2cm,那么这个圆锥的母线长为cm.7.如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影局部的面积为〔结果保存π〕.8.如图,从半径为9cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥〔接缝处不重叠〕,那么这个圆锥的高为cm.9.如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠局部的量角器弧〔〕对应的圆心角〔∠AOB〕为120°,OC的长为2cm,那么三角板和量角器重叠局部的面积为.10.把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处〔即点B处〕,点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为,经过61次旋转后,顶点O经过的总路程为.三、解答题〔一共40分〕11.如图,⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.〔1〕求证:AB为⊙O的切线;〔2〕求弦AC的长;〔3〕求图中阴影局部的面积.12.如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=cm.〔1〕求证:AC是⊙O的切线;〔2〕求由弦CD、BD与弧BC所围成的阴影局部的面积.〔结果保存π〕13.如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切于点B,连接BA并延长交⊙A于点D,交ON于点E.〔1〕求证:ON是⊙A的切线;〔2〕假设∠MON=60°,求图中阴影局部的面积.〔结果保存π〕14.如图①,在矩形纸片ABCD中,AB=+1,AD=.〔1〕如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,那么折痕AE的长为;〔2〕如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,那么四边形B′FED′的面积为;〔3〕如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长.〔结果保存π〕圆的弧长和图形面积的计算参考答案与试题解析一、选择题1.假设圆锥的轴截图为等边三角形,那么称此圆锥为正圆锥,那么正圆锥的侧面展开图的圆心角是〔〕A.90°B.120°C.150°D.180°【考点】圆锥的计算.【分析】设正圆锥的底面半径是r,那么母线长是2r,底面周长是2πr,然后设正圆锥的侧面展开图的圆心角是n°,利用弧长的计算公式即可求解.【解答】解:设正圆锥的底面半径是r,那么母线长是2r,底面周长是2πr,设正圆锥的侧面展开图的圆心角是n°,那么=2πr,解得:n=180°.应选D.【点评】正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决此题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.2.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形〔阴影局部〕图案,那么树叶形图案的周长为〔〕A.πa B.2πa C.D.3a【考点】弧长的计算.【分析】由图可知,阴影局部的周长是两个圆心角为90°、半径为a的扇形的弧长,可据此求出阴影局部的周长.【解答】解:∵四边形ABCD是边长为a正方形,∴∠B=∠D=90°,AB=CB=AD=CD=a,∴树叶形图案的周长=×2=πa.应选A.【点评】此题考察了弧长的计算.解答该题时,需要牢记弧长公式l=〔R是半径〕.3.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是〔〕A.πB.πC.πD.π【考点】扇形面积的计算;钟面角.【专题】几何图形问题.【分析】从9点到9点30分分针扫过的扇形的圆心角是180°,利用扇形的面积公式即可求解.【解答】解:从9点到9点30分分针扫过的扇形的圆心角是180°,那么分针在钟面上扫过的面积是:=π.应选:A.【点评】此题考察了扇形的面积公式,正确理解公式是关键.4.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,那么图中阴影局部的面积是〔〕A.﹣B.﹣ C.π﹣D.π﹣【考点】扇形面积的计算;全等三角形的断定与性质;菱形的性质.【专题】几何图形问题;压轴题.【分析】根据菱形的性质得出△DAB是等边三角形,进而利用全等三角形的断定得出△ABG≌△DBH,得出四边形GBHD 的面积等于△ABD的面积,进而求出即可.【解答】解:连接BD,∵四边形ABCD是菱形,∠A=60°,∴∠ADC=120°,∴∠1=∠2=60°,∴△DAB是等边三角形,∵AB=2,∴△ABD的高为,∵扇形BEF的半径为2,圆心角为60°,∴∠4+∠5=60°,∠3+∠5=60°,∴∠3=∠4,设AD、BE相交于点G,设BF、DC相交于点H,在△ABG和△DBH中,,∴△ABG≌△DBH〔ASA〕,∴四边形GBHD的面积等于△ABD的面积,∴图中阴影局部的面积是:S扇形EBF﹣S△ABD=﹣×2×=﹣.应选:B.【点评】此题主要考察了扇形的面积计算以及全等三角形的断定与性质等知识,根据得出四边形EBFD的面积等于△ABD的面积是解题关键.5.如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E是切点.假设∠CDE=x°,∠ECD=y°,⊙B 的半径为R,那么的长度是〔〕A.B.C.D.【考点】弧长的计算;多边形内角与外角;圆周角定理;切线的性质;切线长定理.【专题】压轴题.【分析】点C、D、E都在⊙P上,由圆周角定理可得:∠DPE=2y°;然后在四边形BDPE中,求出∠B;最后利用弧长公式计算出结果.【解答】解:根据题意,由切线长定理可知:PC=PD=PE,即点C、D、E在以P为圆心,PC长为半径的⊙P上,由圆周角定理得:∠DPE=2∠ECD=2y°.如图,连接BD、BE,那么∠BDP=∠BEP=90°,在四边形BDPE中,∠B+∠BDP+∠DPE+∠BEP=360°,即:∠B+90°+2y°+90°=360°,解得:∠B=180°﹣2y°.∴的长度是:=.应选B.【点评】此题考察圆的相关性质.解题关键是确定点C、D、E在⊙P上,从而由圆周角定理得到∠DPE=2∠ECD=2y°.二、填空题6.圆锥的侧面积为6πcm2,底面圆的半径为2cm,那么这个圆锥的母线长为3 cm.【考点】圆锥的计算.【专题】压轴题.【分析】圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.【解答】解:设母线长为R,底面半径是2cm,那么底面周长=4π,侧面积=2πR=6π,∴R=3.故答案为:3.【点评】此题利用了圆的周长公式和扇形面积公式求解.比较根底,重点是掌握公式.7.如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影局部的面积为〔结果保存π〕π﹣2.【考点】扇形面积的计算.【分析】先根据扇形面积公式计算出扇形面积,然后计算出三角形AOB的面积,继而用扇形面积﹣三角形面积可得出阴影的面积.【解答】解:S扇形===π,S△AOB=×2×2=2,那么S阴影=S扇形﹣S△AOB=π﹣2.故答案为:π﹣2.【点评】此题考察了扇形面积的计算,难度一般,解答此题的关键是纯熟掌握扇形面积的计算公式.8.如图,从半径为9cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥〔接缝处不重叠〕,那么这个圆锥的高为3cm.【考点】圆锥的计算.【分析】首先求得扇形的弧长,即圆锥的底面周长,那么底面半径即可求得,然后利用勾股定理即可求得圆锥的高.【解答】解:圆心角是:360×〔1﹣〕=240°,那么弧长是:=12π〔cm〕,设圆锥的底面半径是r,那么2πr=12π,解得:r=6,那么圆锥的高是:=3〔cm〕.故答案是:3.【点评】正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决此题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.9.如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠局部的量角器弧〔〕对应的圆心角〔∠AOB〕为120°,OC的长为2cm,那么三角板和量角器重叠局部的面积为+2〔cm2〕.【考点】扇形面积的计算.【专题】数形结合.【分析】在Rt△OBC中求出OB、BC,然后求出扇形OAB及△OBC的面积即可得出答案.【解答】解:∵∠AOB=120°,∴∠BOC=60°,在Rt△OBC中,OC=2cm,∠BOC=60°,∴∠OBC=30°,∴OB=4cm,BC=2cm,那么S扇形OAB==〔cm2〕,S△OBC=OC×BC=2〔cm2〕,故S重叠=S扇形OAB+S△OBC=+2〔cm2〕故答案为:+2〔cm2〕.【点评】此题考察了扇形的面积计算,解答此题关键是求出扇形的半径,注意纯熟掌握扇形的面积公式,难度一般.10.把边长为1的正方形纸片OABC放在直线m上,OA边在直线m上,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时,点O运动到了点O1处〔即点B处〕,点C运动到了点C1处,点B运动到了点B1处,又将正方形纸片AO1C1B1绕B1点,按顺时针方向旋转90°…,按上述方法经过4次旋转后,顶点O经过的总路程为,经过61次旋转后,顶点O经过的总路程为.【考点】弧长的计算;正方形的性质;旋转的性质.【专题】压轴题.【分析】为了便于标注字母,且更明晰的观察,每次旋转后向右略微平移一点,作出前几次旋转后的图形,点O的第1次旋转道路是以正方形的边长为半径,以90°圆心角的扇形,第2次旋转道路是以正方形的对角线长为半径,以90°圆心角的扇形,第3次旋转道路是以正方形的边长为半径,以90°圆心角的扇形;①根据弧长公式列式进展计算即可得解;②求出61次旋转中有几个4次,然后根据以上的结论进展计算即可求解.【解答】解:如图,为了便于标注字母,且位置更明晰,每次旋转后不防向右挪动一点,第1次旋转道路是以正方形的边长为半径,以90°圆心角的扇形,道路长为=;第2次旋转道路是以正方形的对角线长为半径,以90°圆心角的扇形,道路长为=;第3次旋转道路是以正方形的边长为半径,以90°圆心角的扇形,道路长为=;第4次旋转点O没有挪动,旋转后与最初正方形的放置一样,因此4次旋转,顶点O经过的道路长为++=;∵61÷4=15…1,∴经过61次旋转,顶点O经过的路程是4次旋转路程的15倍加上第1次道路长,即×15+=.故答案为:;.【点评】此题考察了旋转变换的性质,正方形的性质以及弧长的计算,读懂题意,并根据题意作出图形更形象直观,且有利于旋转变换规律的发现.三、解答题〔一共40分〕11.如图,⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.〔1〕求证:AB为⊙O的切线;〔2〕求弦AC的长;〔3〕求图中阴影局部的面积.【考点】切线的断定;扇形面积的计算.【分析】〔1〕如图,连接OA,欲证明AAB为⊙O的切线,只需证明AB⊥OA即可;〔2〕如图,连接AD,构建直角△ADC,利用“30度角所对的直角边是斜边的一半〞求得AD=4,然后利用勾股定理来求弦AC的长度;〔3〕根据图示知,图中阴影局部的面积=扇形ADO的面积+△AOC的面积.【解答】解:〔1〕证明:如图,连接OA.∵AB=AC,∠ABC=30°,∴∠ABC=∠ACB=30°.∴∠AOB=2∠ACB=60°,∴在△ABO中,∠BAO=g地0°﹣∠ABO﹣∠AOB=90°,即AB⊥OA,又∵OA是⊙O的半径,∴AB为⊙O的切线;〔2〕解:如图,连接AD.∵CD是⊙O的直径,∴∠DAC=90°.∵由〔g〕知,∠ACB=30°,∴AD=CD=4,那么根据勾股定理知AC==4,即弦AC的长是4;〔3〕解:由〔2〕知,在△ADC中,∠DAC=90°,AD=4,AC=4,那么S△ADC=AD•AC=×4×4=8.∵点O是△ADC斜边上的中点,∴S△AOC=S△ADC=4.根据图示知,S阴影=S扇形ADO+S△AOC=+4=+4.【点评】此题考察了切线的断定,圆周角定理以及扇形面积的计算.解答〔3〕时,求△AOC的面积的面积的技巧性在于利用了“等边同高〞三角形的面积相等的性质.12.如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=cm.〔1〕求证:AC是⊙O的切线;〔2〕求由弦CD、BD与弧BC所围成的阴影局部的面积.〔结果保存π〕【考点】切线的断定;扇形面积的计算.【专题】压轴题.【分析】〔1〕求出∠COB的度数,求出∠A的度数,根据三角形的内角和定理求出∠OCA的度数,根据切线的断定推出即可;〔2〕如解答图所示,解题关键是证明△CDM≌△OBM,从而得到S阴影=S扇形BOC.【解答】如图,连接BC,OD,OC,设OC与BD交于点M.〔1〕证明:根据圆周角定理得:∠COB=2∠CDB=2×30°=60°,∵AC∥BD,∴∠A=∠OBD=30°,∴∠OCA=180°﹣30°﹣60°=90°,即OC⊥AC,∵OC为半径,∴AC是⊙O的切线;〔2〕解:由〔1〕知,AC为⊙O的切线,∴OC⊥AC.∵AC∥BD,∴OC⊥BD.由垂径定理可知,MD=MB=BD=.在Rt△OBM中,∠COB=60°,OB===6.在△CDM与△OBM中,∴△CDM≌△OBM〔ASA〕,∴S△CDM=S△OBM∴阴影局部的面积S阴影=S扇形BOC==6π〔cm2〕.【点评】此题考察了平行线性质,切线的断定,扇形的面积,三角形的面积,圆周角定理的应用,主要考察学生综合运用定理进展推理和计算的才能.13.如图,OC平分∠MON,点A在射线OC上,以点A为圆心,半径为2的⊙A与OM相切于点B,连接BA并延长交⊙A于点D,交ON于点E.〔1〕求证:ON是⊙A的切线;〔2〕假设∠MON=60°,求图中阴影局部的面积.〔结果保存π〕【考点】切线的断定;扇形面积的计算.【分析】〔1〕首先过点A作AF⊥ON于点F,易证得AF=AB,即可得ON是⊙A的切线;〔2〕由∠MON=60°,AB⊥OM,可求得AF的长,又由S阴影=S△AEF﹣S扇形ADF,即可求得答案.【解答】〔1〕证明:过点A作AF⊥ON于点F,∵⊙A与OM相切于点B,∴AB⊥OM,∵OC平分∠MON,∴AF=AB=2,∴ON是⊙A的切线;〔2〕解:∵∠MON=60°,AB⊥OM,∴∠OEB=30°,∴AF⊥ON,∴∠FAE=60°,在Rt△AEF中,tan∠FAE=,∴EF=AF•tan60°=2,∴S阴影=S△AEF﹣S扇形ADF=AF•EF﹣×π×AF2=2﹣π.【点评】此题考察了切线的断定与性质、扇形的面积以及三角函数的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.14.如图①,在矩形纸片ABCD中,AB=+1,AD=.〔1〕如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,那么折痕AE的长为;〔2〕如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,那么四边形B′FED′的面积为﹣;〔3〕如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长.〔结果保存π〕【考点】翻折变换〔折叠问题〕;矩形的性质;弧长的计算.【专题】探究型.【分析】〔1〕先根据图形反折变换的性质得出AD′,D′E的长,再根据勾股定理求出AE的长即可;〔2〕由〔1〕知,AD′=,故可得出BD′的长,根据图形反折变换的性质可得出B′D′的长,再由等腰直角三角形的性质得出B′F的长,根据梯形的面积公式即可得出结论;〔3〕先根据直角三角形的性质求出∠BEC的度数,由翻折变换的性质可得出∠DEA的度数,故可得出∠AEA′=75°=∠D′ED″,由弧长公式即可得出结论.【解答】解:〔1〕∵△ADE反折后与△AD′E重合,∴AD′=AD=D′E=DE=,∴AE===;〔2〕∵由〔1〕知AD′=,∴BD′=1,∵将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,∴B′D′=BD′=1,∵由〔1〕知AD′=AD=D′E=DE=,∴四边形ADED′是正方形,∴B′F=AB′=﹣1,∴S梯形B′FED′=〔B′F+D′E〕•B′D′=〔﹣1+〕×1=﹣;故答案为:〔1〕;〔2〕﹣;〔3〕∵∠C=90°,BC=,EC=1,∴tan∠BEC==,∴∠BEC=60°,由翻折可知:∠DEA=45°,∴∠AEA′=75°=∠D′ED″,∴==.【点评】此题考察的是图形的翻折变换,熟知图形翻折不变性的性质是解答此题的关键.。
中考数学《圆的弧长及面积计算》复习共76页

Evaluation only. Evaluation only. Created with Aspose.Slides for .NET 4.0 Client Profile reated with Aspose.Slides for .NET 4.0 Client Profile 17.
17.1. Copyright 2019-2019Aspose Pty Ltd. Copyright 2019-2019Aspose Pty Ltd.
Evaluation only. Evaluation only. Created with Aspose.Slides for .NET 4.0 Client Profile reated with Aspose.Slides for .NET 4.0 Client Profile 17.
17.1. Copyright 2019-2019Aspose Pty Ltd. Copyright 2019-2019Aspose Pty Ltd.
Evaluation only. Evaluation only. Created with Aspose.Slides for .NET 4.0 Client Profile reated with Aspose.Slides for .NET 4.0 Client Profile 17.
17.1. Copyright 2019-2019Aspose Pty Ltd. Copyright 2019-2019Aspose Pty Ltd.
Evaluation only. Evaluation only. Created with Aspose.Slides for .NET 4.0 Client Profile reated with Aspose.Slides for .NET 4.0 Client Profile 17.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学二轮综合训练28 圆的弧长和图形面积的计算一、选择题1.(2011·潜江)如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A 、B 、C 为格点,作△ABC 的外接圆⊙O ,则 AC 的长等于( )A.34π B.54π C.32π D.52π 答案 D解析 如图,易知AC =BC ,AC ⊥BC ,所以AB 是⊙O 的直径,连OC ,则∠AOC =90°,AC 的长等于90180π×5=52π . 2.(2010·丽水)小刚用一张半径为24 cm 的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10 cm ,那么这张扇形纸板的面积是( )A .120π cm 2B .240π cm 2C .260π cm 2D .480π cm 2答案 B解析 根据圆的周长公式,得圆的底面周长=2π ×10=20π ,即扇形的弧长是20π ,所以扇形的面积=12lr =12×20π ×24=240π ,故选B.3.(2011·广安)如图,圆柱的底面周长为6 cm ,AC 是底面圆的直径,高BC =6 cm ,点P 是母线BC 上一点,且PC =23BC .一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是( )A .(4+6π) cm B .5 cmC .3 5cmD .7 cm答案 B解析 如图,将圆柱的侧面展开,可求得AC =12×6=3,PC =23BC =23×6=4.在Rt △PAC 中,PA =32+42=5,所以从A 点到P 点的最短距离是5.4.(2011·常德)已知圆锥底面圆的半径为6 cm ,高为8 cm ,则圆锥的侧面积为( )cm 2. A .48 B .48π C .120π D .60π 答案 D解析 ∵r =6,h =8,又r 2+h 2=l 2,∴l =62+82=10, ∴S 圆锥侧=πrl =π×6×10=60π.5.(2011·泉州)如图,直径AB 为6的半圆,绕A 点逆时针旋转60°,此时点B 到了点B ′,则图中阴影部分的面积是( )A .3πB .6πC .5πD .4π 答案 B解析 设AB ′与半圆周交于C ,半圆圆心为O ,连接OC .∵∠B ′AB =60°,OA =OC ,∴△AOC 是等边三角形,∠AOC =60°,∠BOC =120°,S 扇形ABB ′=60360π×62=6π,∴S 阴影=S 半圆AB ′+S 扇形AB ′B -S 半圆AB =S 扇形AB ′B =6π. 二、填空题6.(2011·德州)母线长为2,底面圆的半径为1的圆锥的侧面积为___________. 答案 2π解析 S 圆锥侧=π×1×2=2π.7.(2011·绍兴)一个圆锥的侧面展开图是半径为4,圆心角为90°的扇形,则此圆锥的底面半径为______.答案 1解析 圆锥展开图扇形面积为90360π×42,圆锥的侧面积为π×r ×4,∴90360π×42=π×r ×4,r =1. 8.(2011·重庆)在半径为4π的圆中,45°的圆心角所对的弧长等于________.答案 1解析 据弧长公式,l =n πr180=45×π×4π180=1.9.(2011·台州)如图,CD 是⊙O 的直径,弦AB ⊥CD ,垂足为点M ,AB =20.分别以DM 、CM 为直径作两个大小不同的⊙O 1和⊙O 2,则图中所示的阴影部分面积为___________.(结果保留π)答案 50π解析 ∵直径DC ⊥AB ,∴AM =BM =12×20=10.由相交弦定理,得CM ·DM =AM ·BM =10×10=100,∴S 阴影=π×⎝ ⎛⎭⎪⎫12CD 2-π×⎝ ⎛⎭⎪⎫12DM 2-π×⎝ ⎛⎭⎪⎫12CM 2=14π×(CD 2-DM 2-CM 2) =14π×[(CM +DM )2-DM 2-CM 2] =14π×(2CM ×DM ) =12π×CM ×DM =12π×100=50π.10.(2011·泉州)如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形AB C.那么剪下的扇形ABC (阴影部分)的面积为______;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r =______.答案 2π;33解析 连接OA 、OB ,画OD ⊥AC 于D .∵扇形ABC 为最大圆心角为60°的扇形, ∴点B 、O 、D 在同一条直线上,BD ⊥AC .∵OA =OB ,∴∠ABD =∠BAO =30°,∠OAD =30°. 在Rt △OAD 中,OA =2,∴OD =1,AD =3,AC =2AD =2 3.∴S 阴影=60360π×(2 3)2=2π.∵弧 BC的长=60180π×2 3,∴2πr =60180π×2 3,∴r =33. 三、解答题 11.(2011·汕头)如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿着x 轴向右平移4个长度单位得⊙P 1.(1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系;(2)设⊙P 1与x 轴正半轴、y 轴正半轴的交点为A 、B ,求劣弧 AB 与弦AB 围成的图形的面积(结果保留π).解 (1)如图所示,两圆外切.(2)劣弧的长度l =90π·2180=π.劣弧和弦围成的图形的面积为S =14π·4-12×2×2=π-2.12.(2011·杭州)在△ABC 中,AB =3,AC =2,BC =1.(1)求证:∠A ≠30°;(2)将△ABC 绕BC 所在直线旋转一周,求所得几何体的表面积.解 (1)证明:在△ABC 中,∵AB 2=3,AC 2+BC 2=2+1=3,∴AC 2+BC 2=AB 2,∴∠ACB =90°,∴sin A =BC AB =3≠12,∴∠A ≠30°.(2)将△ABC 绕BC 所在直线旋转一周,所得的几何体为圆锥,由题意得r =2,l = 3.∴S 圆锥侧=π×2×3=6π,S 底=π×(2)2=2π. ∴S 表面积=6π+2π.13.(2011·湖州)如图,已知AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,∠AOC =60°,OC =2.(1)求OE 和CD 的长;(2)求图中阴影部分的面积.解 (1)在△OCE 中,∵∠CEO =90°,∠EOC =60°,OC =2,∴OE =12OC =1,∴CE =32OC = 3.∵OA ⊥CD ,∴CE =DE ,∴CD =2 3.(2) ∵S △ABC =12AB ·CE =12×4×3=2 3,∴S 阴影=12π×22-2 3=2π-2 3.14.(2011·泉州)如图,在△ABC 中,∠A =90°,O 是BC 边上一点,以O 为圆心的半圆分别与AB 、AC 边相切于D 、E 两点,连接OD .已知BD =2,AD =3.求:(1)tan C ;(2)图中两部分阴影面积的和.解 (1)如图,连接OE .∵AB 、AC 分别切⊙O 于D 、E 两点, ∴∠ADO =∠AEO =90°. 又∵∠A =90°,∴四边形ADOE 是矩形. ∵OD =OE ,∴四边形ADOE 是正方形. ∴OD ∥AC ,OD =AD =3. ∴∠BOD =∠C .在Rt △BOD 中,tan ∠BOD =BD OD =23.∴tan C =23.(2)如图,设⊙O 与BC 交于M 、N 两点. 由(1)得,四边形ADOE 是正方形, ∴∠DOE =90°.∴∠COE +∠BOD =90°.∵在Rt△EOC 中,tan C =23,OE =3,∴EC =92.∴S 扇形DOM +S 扇形EON =S 扇形DOE =14S ⊙O =14π×32=94π.∴S 阴影=S △BOD +S △COE -()S 扇形DOM +S 扇形EON =12×2×3+12×3×92-94π=394-94π.∴图中两部分阴影面积的和为394-94π.15.(2011·怀化)如图,已知AB 为⊙O 的直径,CD 是弦,AB ⊥CD 于E ,OF ⊥AC 于F ,BE =OF .(1)求证:OF ∥BC ;(2)求证:△AFO ≌△CEB ;(3)若EB =5 cm ,CD =103cm ,设OE =x ,求x 值及阴影部分的面积. 解 (1)∵AB 为⊙O 的直径, ∴∠ACB =90°.又∵OF ⊥AC 于F ,∴∠AFO =90°, ∴∠ACB =∠AFO . ∴OF ∥BC .(2)由(1)知,∠CAB +∠ABC =90°. ∵AB ⊥CD 于E ,∴∠BEC =90°,∠BCE +∠ABC =90°, ∴∠BCE =∠CAB .又∵∠AFO =∠BEC ,BE =OF , ∴△AFO ≌△CEB .(3)∵AB 为⊙O 的直径,CD 是弦,AB ⊥CD ,∴∠OEC =90°,CE =12CD =12×10 3=5 3.在Rt △OCE 中,OE =x ,则OB =5+x =OC ,由勾股定理得:OC 2=OE 2+EC 2,∴(5+x )2=()5 32+x 2,解得x =5. 在Rt △OCE 中,tan ∠COE =5 35= 3.∵∠COE 为锐角, ∴∠COE =60°.由圆的轴对称性可知阴影部分的面积为: S 阴影=2(S 扇形OBC -S ΔOEC )=2×(60π×102360-12×5 3×5)=100π3-25 3(cm 2).。
