大学物理第三篇ppt
合集下载
大学物理-第3章-静电场中的导体

R2 R1
在金属球壳与导体球之间(r0 < r < R1时):
q r0
作过 r 处的高斯面S1
q
S1 E2 dS 0
得
E2 r
q
40r 2
q
E2 40r 2 er
在金属球壳内(R1< r < R2时):电场 E3 0
在金属球壳外( r > R2时): 作过 r 处的高斯面 S 2
S2
E4
dS
在它形成的电场中平行放置一无限大金属平板。求:
金属板两个表面的电荷面密度?
解:带电平面面电荷密度0 ,导体两面感应电荷面密度分 别为1 和 2,由电荷守恒有
1 2 0 (1)
导体内场强为零(三层电荷产生)
σ0 σ1
σ2
E0 E1 E2 0
(2)
E0
0 1 2 0
(3)
20 20 20
导体表面任一点的电场强度都与导体表面垂 直。
20
2.导体在静电平衡状态下 的一些特殊性质
❖ 导体是等势体,导体表面是等势面。
在导体内部任取两点P和Q,它们之间的电势差可以表示为
VP VQ
Q
E
dl
0
P
❖ 导体表面的电场强度方向与导体的表面相垂直。
❖ 导体上感应电荷对原来的外加电场施加影响,改
Q1
Q2
0
q
q
0
得
E4r
q
4 0 r 2
E4
q
4 0 r 2
er
43
思考:(3)金属球壳和金属球的电势各 为多少?
解:设金属球壳的电势为U壳 ,则:
U壳
R2 E4 dl
大学物理第三章刚体和流体运动

2
返回
退出
对刚体内各个质点的相应式子,相加得:
F r sin f
i i i i i
i i
r sin i ( mi ri )
2 i
对于成对的内力,对同一转轴的力矩之和为零,则:
f
i
i
ri sin i 0
2 i i i
F r sin ( m r
r
问题中包括平动和转动。
T1 m1 g m1a m2 g T2 m2a T2 r T1r M r J
轮不打滑: 联立方程,可解得 T1 ,T2,a, 。
此装置称阿特伍德机——可用于测量重力加速度 g
返回
退出
例3-4 一半径为R,质量为m匀质圆盘,平放在粗糙的 水平桌面上。设盘与桌面间摩擦系数为 ,令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转,问它 经过多少时间才停止转动? 解: 把圆盘分成许多环形 质元,每个质元的质量 dm=rddre , e 是 盘 的 厚 度,质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为:
刚体定轴转动的动能定理:总外力矩对刚体所做的功 等于刚体转动动能的增量。
返回
退出
四、刚体的重力势能 以地面为势能零点,刚体和地 球系统的重力势能:
z
i
O
返回
退出
例3-5 一质量为m ,长为 l 的均质细杆,转轴在O点, 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动,求(1)水平位置的角速度和角加速度。(2)垂直位 置时的角速度和角加速度。
第三章 刚体和流体的运动
§3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系
返回
退出
对刚体内各个质点的相应式子,相加得:
F r sin f
i i i i i
i i
r sin i ( mi ri )
2 i
对于成对的内力,对同一转轴的力矩之和为零,则:
f
i
i
ri sin i 0
2 i i i
F r sin ( m r
r
问题中包括平动和转动。
T1 m1 g m1a m2 g T2 m2a T2 r T1r M r J
轮不打滑: 联立方程,可解得 T1 ,T2,a, 。
此装置称阿特伍德机——可用于测量重力加速度 g
返回
退出
例3-4 一半径为R,质量为m匀质圆盘,平放在粗糙的 水平桌面上。设盘与桌面间摩擦系数为 ,令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转,问它 经过多少时间才停止转动? 解: 把圆盘分成许多环形 质元,每个质元的质量 dm=rddre , e 是 盘 的 厚 度,质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为:
刚体定轴转动的动能定理:总外力矩对刚体所做的功 等于刚体转动动能的增量。
返回
退出
四、刚体的重力势能 以地面为势能零点,刚体和地 球系统的重力势能:
z
i
O
返回
退出
例3-5 一质量为m ,长为 l 的均质细杆,转轴在O点, 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动,求(1)水平位置的角速度和角加速度。(2)垂直位 置时的角速度和角加速度。
第三章 刚体和流体的运动
§3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系
大学物理静电场3(电势)ppt课件
最新课件
9
单个点电荷的场的电势 U q
2)电势叠加原理(标量叠加)
q
Up Edl
Eidl
1
4
0r r1 r2
p
p
P Ei dl
qi
q2
4 0ri
或对连续分布带电体
U p
dq
4 0r
q
最新课件
dq
r
p
r3
ri
q3
qi
p
Up=?
10
Ua
i
qi
40ri
一个点电荷系的电场中,任一点的电势等于每一个点电 荷单独存在时在该点所产生电势的代数和。——电势 叠加原理
电势叠加原理 习题最指新课导件 P65 16
34
形状如图所示的绝缘细线,其上均匀分布着
正电荷。已知电荷线密度为λ,两段直线长 均为a,半圆环的半径为a。求环心O点的电 势?
电势叠加原理
求电势能和电力
习题指导P65 17
最新课件
35
3.有一边长为a的正方形平面,在其中垂线上距 中心O点a/2处,有一电量为q的正点电荷,如图所 示,则通过该平面的电场强度通量为:
b
W a W bA a bq 0 aE d r
二、电势差:
移动单位正电荷从电场中a 点到b点,静电力所做 的功,为静电场中两点的电势差:
U abU aU ba bEdr最 新W 课q 件aW qb 描只述与电电场场的有性关质6
➢某点 (a点) 的电势:
首先设定电势0点(b点):
Ua
b
Edr
积分与路径无关
最新课件
4
对任何静电场,电场强度的线积分都只取决于起 点和终点的位置而与积分路径无关--静电场的
大学物理 第3章-1刚体

定轴转动:
转轴固定不动的转动。
显然,刚体是个理想化的模型,但是它有 实际的意义。 刚体是特殊的质点系, 其上各质点间的相对 位置保持不变。 质点系的规律都可用于刚体, 而且考虑到刚体的特点,规律的表示还可较一 般的质点系有所简化。
刚体的一般运动可看作: 随质心的平动
+
绕质心的转动
的合成
一般运动
2
I1
1 3
m2r
4 3
mr 2
r
摆锤转动惯量:
I 2 I C md
2
1 2
mr 2
2
I I1 I 2
4 3
mr
2
19 2
mr
2
65 6
mr
3-1-4
刚体对定轴的角动量定理 和转动定律
由质点系对轴的角动量定理,可得
dm 2π rdr
2
I r dm 2π r 3dr
o R
r
dr
I 2π r dr
3 0
R
π R 2
4
1 2
mR
2
转动惯量的大小取决于刚体的质量、形 状及转轴的位置 . a) 平行轴定理 质量为 m 的刚体,如果对 其质心轴的转动惯量为 I C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量
d
d
3g 2l
π 2 0
cos d
3g 2l cos d
A
π 2 0
0
d
C O
B
1 2
2
3g 2l
l
sin
3g 2l
大学物理学3ppt课件

0 . 15 10 sin( 30 60 ) F 0 . 15 9 . 8 175 N 0 . 01 sin 60
小球对地面的平均冲力是的反作用力,其大小为175N, 方向与相反,沿法线方向竖直向下。
3.1.2 质点系的动量定理
在研究多个有相互作用的物体的运动情况时,可以把这些 物体作为整体系统来研究,称为物体系。若其中的每一个物体 都能抽象为质点,则该物体系就可以抽象为质点系。在一个由 质点系构成的力学系统中,我们把系统外的物体对系统内各质 点的作用力称为外力;把系统内各质点间的相互作用力称为内 力。 如右图所示,两质点的质量分别为m1和 m2,在t1到t2时间内,除有相互作用的内力 为f12和f21外,它们还分别受到外力F1和F2的 作用,其速度分别从v10和v20变为v1和v2。分 别对两质点应用动量定理,有:
上式为矢量式,它在直角坐标系中的分量式为:
I x Fx dt mv 2 x mv1x
t1 t2
I y Fy dt mv 2 y mv1 y
t1
t2
I z Fz dt mv 2 z mv1z
t1
t2
【例3-1】如下图所示,质量m=0.15kg的小球以v0= 10m/s的速度射向光滑地面,入射角θ1=30°,然后沿θ2= 60°的反射角方向弹出。设碰撞时间Δt=0.01s,计算小球对 地面的平均冲力。 【解】选小球为研究对象。因地面光 滑,碰撞时小球在水平方向上不受作用力 ,地面对小球的作用力沿法线方向竖直向 上。设地面对小球的平均冲力为 F ,碰后 小球速度为v。建立坐标系如右图所示, 根据质点的动量定理有:
I 0 mv sin mv sin x 2 0 1
I ( F mg ) Δ t mv cos ( mv cos ) y 2 0 1
小球对地面的平均冲力是的反作用力,其大小为175N, 方向与相反,沿法线方向竖直向下。
3.1.2 质点系的动量定理
在研究多个有相互作用的物体的运动情况时,可以把这些 物体作为整体系统来研究,称为物体系。若其中的每一个物体 都能抽象为质点,则该物体系就可以抽象为质点系。在一个由 质点系构成的力学系统中,我们把系统外的物体对系统内各质 点的作用力称为外力;把系统内各质点间的相互作用力称为内 力。 如右图所示,两质点的质量分别为m1和 m2,在t1到t2时间内,除有相互作用的内力 为f12和f21外,它们还分别受到外力F1和F2的 作用,其速度分别从v10和v20变为v1和v2。分 别对两质点应用动量定理,有:
上式为矢量式,它在直角坐标系中的分量式为:
I x Fx dt mv 2 x mv1x
t1 t2
I y Fy dt mv 2 y mv1 y
t1
t2
I z Fz dt mv 2 z mv1z
t1
t2
【例3-1】如下图所示,质量m=0.15kg的小球以v0= 10m/s的速度射向光滑地面,入射角θ1=30°,然后沿θ2= 60°的反射角方向弹出。设碰撞时间Δt=0.01s,计算小球对 地面的平均冲力。 【解】选小球为研究对象。因地面光 滑,碰撞时小球在水平方向上不受作用力 ,地面对小球的作用力沿法线方向竖直向 上。设地面对小球的平均冲力为 F ,碰后 小球速度为v。建立坐标系如右图所示, 根据质点的动量定理有:
I 0 mv sin mv sin x 2 0 1
I ( F mg ) Δ t mv cos ( mv cos ) y 2 0 1
大学物理 第三篇 电磁感应(法拉第电磁感应定律 )

da
ox
普遍
.
把感应电动势分为两种基本形式 动生电动势 motional emf 感生电动势 induced emf
下面 从场的角度研究电磁感应 电磁感应对应的场是电场
它可使静止电荷运动 研究的问题是:
动生电动势的非静电场? 感生电动势的非静电场?性质?
.
§2 动生电动势
一. 典型装置
l
导线 ab在磁场中运动
非静电力--洛仑兹力
Ef Km qvqqBv vB B
a B
vB dl e v
fm
i
a
v
B
dl
b
a
b
i vBdl vBl>0
i
ba
b
.
讨论
d i dt 适用于一切产生电动势的回路
i vBdl 适用于切割磁力线的导体
di bav B dl i d i
z
B
例 在空间均匀的磁场中 BBz
若绕行方向取如图所示的回路.方.向.L. .L. .
按约定 磁通量为正 即 BS
由
i
d
dt
dB S < 0 dt
负号 电动势的方向
S i
说明 与所设的绕行方向相反 .
若绕行方向取如图所示的方向L
..
均.匀.磁场. B.
.
按约定 磁通量取负
. . S. . . . .
BS
. . .L. . . .
NN BdS N
Bds
d a
N
I
ldx
S
S
d 2 x
NIl da
2 ln d
L
2N I0lsintlndda
I ds l
ox
普遍
.
把感应电动势分为两种基本形式 动生电动势 motional emf 感生电动势 induced emf
下面 从场的角度研究电磁感应 电磁感应对应的场是电场
它可使静止电荷运动 研究的问题是:
动生电动势的非静电场? 感生电动势的非静电场?性质?
.
§2 动生电动势
一. 典型装置
l
导线 ab在磁场中运动
非静电力--洛仑兹力
Ef Km qvqqBv vB B
a B
vB dl e v
fm
i
a
v
B
dl
b
a
b
i vBdl vBl>0
i
ba
b
.
讨论
d i dt 适用于一切产生电动势的回路
i vBdl 适用于切割磁力线的导体
di bav B dl i d i
z
B
例 在空间均匀的磁场中 BBz
若绕行方向取如图所示的回路.方.向.L. .L. .
按约定 磁通量为正 即 BS
由
i
d
dt
dB S < 0 dt
负号 电动势的方向
S i
说明 与所设的绕行方向相反 .
若绕行方向取如图所示的方向L
..
均.匀.磁场. B.
.
按约定 磁通量取负
. . S. . . . .
BS
. . .L. . . .
NN BdS N
Bds
d a
N
I
ldx
S
S
d 2 x
NIl da
2 ln d
L
2N I0lsintlndda
I ds l
大学物理第三章动量守恒定律和能量守恒定律

动量守恒定律的表述
总结词
动量守恒定律表述为系统不受外力或所 受外力之和为零时,系统总动量保持不 变。
VS
详细描述
动量守恒定律是自然界中最基本的定律之 一,它表述为在一个封闭系统中,如果没 有外力作用或者外力之和为零,则系统总 动量保持不变。也就是说,系统的初始动 量和最终动量是相等的。
动量守恒定律的适用条件
能量守恒定律可以通过电磁学 的基本公式推导出来。
能量守恒定律可以通过相对论 的质能方程推导出来。
能量守恒定律的应用实例
01
02
03
04
机械能守恒
在无外力作用的系统中,动能 和势能可以相互转化,但总和
保持不变。
热能守恒
在一个孤立系统中,热量只能 从高温物体传递到低温物体,
最终达到热平衡状态。
电磁能守恒
详细描述
根据牛顿第三定律,作用力和反作用力大小相等、方向相反。如果将一个物体施加一个力F,则该力会产生一个 加速度a,进而改变物体的速度v。由于力的作用是相互的,反作用力也会对另一个物体产生相同大小、相反方向 的加速度和速度变化。因此,在系统内力的相互作用下,系统总动量保持不变。
02
能量守恒定律
能量守恒定律的表述
感谢观看
01
能量守恒定律表述为:在一个封闭系统中,能量不能被创造或消灭, 只能从一种形式转化为另一种形式。
02
能量守恒定律是自然界的基本定律之一,适用于宇宙中的一切物理过 程。
03
能量守恒定律是定量的,可以用数学公式表示。
04
能量守恒定律是绝对的,不受任何物理定律的限制。
能量守恒定律的适用条件
能量守恒定律适用于孤立系统,即系统与外界没有能量 交换。
大学物理课件第3章-刚体

大学物理课件第3章-刚体
刚体力学是大学物理课程的重要组成部分。它涵盖了刚体的定义、运动学、 动力学、静力学、力学、弹性和应用等多个方面内容,为学习者提供了全面 的知识体系。
刚体的定义
刚体的概念
刚体是指具有固定形状和 大小,并且内部各点相对 位置保持不变的物体。
理想刚体的定义
理想刚体是指无限刚度、 无限强度、不变形且能够 保持自身形状和大小的物 体。
刚体的动力学
刚体的动量
刚体的动量是其质 量乘以速度,刚体 受到外力时动量会 发生变化。
刚体的角动量
刚体的角动量是其 惯性矩乘以角速度, 刚体绕固定轴旋转 时角动量会发生变 化。
刚体的动能
刚体的动能是其质 量乘以速度的平方, 与速度和质量有关。
刚体的动力学定 理
动力学定理描述了 刚体受力和加速度 之间的关系,F = ma。
实际刚体的特点
实际刚体在外力作用下会 发生微小的形变,但变形 较小,可以近似看作刚体。
刚体的运动学
1
刚体的运动状态
刚体可以既进行平动运动,也可以进行转动运动。
2
刚体的平动运动
刚体的平动运动包括直线运动和曲线运动,由质心位置和速度决定。
3
刚体的转动运动
刚体的转动运动包括绕固定轴的转动,由角位移和角速度决定。
刚体的静力学
1 刚体的平衡条件
刚体在平衡状态下,力 矩和力的合力为零。
2 刚体的平衡性质
刚体在平衡状态下,质 心位置不变,不会发生 任何运动。
3 刚体的平衡实例
如天平平衡ቤተ መጻሕፍቲ ባይዱ桥梁平衡 等实际应用中,刚体的 平衡性质起到重要作用。
刚体的力学
刚体的受力分析
通过力的分析,可以确定刚体 受力的大小、方向和作用点。
刚体力学是大学物理课程的重要组成部分。它涵盖了刚体的定义、运动学、 动力学、静力学、力学、弹性和应用等多个方面内容,为学习者提供了全面 的知识体系。
刚体的定义
刚体的概念
刚体是指具有固定形状和 大小,并且内部各点相对 位置保持不变的物体。
理想刚体的定义
理想刚体是指无限刚度、 无限强度、不变形且能够 保持自身形状和大小的物 体。
刚体的动力学
刚体的动量
刚体的动量是其质 量乘以速度,刚体 受到外力时动量会 发生变化。
刚体的角动量
刚体的角动量是其 惯性矩乘以角速度, 刚体绕固定轴旋转 时角动量会发生变 化。
刚体的动能
刚体的动能是其质 量乘以速度的平方, 与速度和质量有关。
刚体的动力学定 理
动力学定理描述了 刚体受力和加速度 之间的关系,F = ma。
实际刚体的特点
实际刚体在外力作用下会 发生微小的形变,但变形 较小,可以近似看作刚体。
刚体的运动学
1
刚体的运动状态
刚体可以既进行平动运动,也可以进行转动运动。
2
刚体的平动运动
刚体的平动运动包括直线运动和曲线运动,由质心位置和速度决定。
3
刚体的转动运动
刚体的转动运动包括绕固定轴的转动,由角位移和角速度决定。
刚体的静力学
1 刚体的平衡条件
刚体在平衡状态下,力 矩和力的合力为零。
2 刚体的平衡性质
刚体在平衡状态下,质 心位置不变,不会发生 任何运动。
3 刚体的平衡实例
如天平平衡ቤተ መጻሕፍቲ ባይዱ桥梁平衡 等实际应用中,刚体的 平衡性质起到重要作用。
刚体的力学
刚体的受力分析
通过力的分析,可以确定刚体 受力的大小、方向和作用点。
大学物理课课件第3章_刚体的定轴转动

G2 G1
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
(支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统,忽略轴摩擦,脱离驱动力矩后,系 统受合外力矩为零,角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间,系统在
铅直位置,受合外力矩为零,角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体(上某点)的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
(支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统,忽略轴摩擦,脱离驱动力矩后,系 统受合外力矩为零,角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间,系统在
铅直位置,受合外力矩为零,角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体(上某点)的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
大学物理课件:第三篇 热物理学与非线性现象

热学参量(如:温度)
化学参量 (如:混合气体各化学组分的质量和摩尔数等)
电磁参量 (如:电场和磁场强度,电极化和磁化强度等)
如果在所研究的问题中既不涉及电磁性质又无须考虑与化学成
分有关的性质,系统中又不发生化学反应,则不必引入电磁参
量和化学参量。
此时只需体积和压强就可确定系统的平衡态,我们称这种系统
B
(a)
A
通过导热板进行热接触的两个系统 导热板 组成一复合系统,当复合系统达到 平衡态时,我们就说两个系统处于热平衡。
7
B
(b)
10:08:35
热力学第0定律 如果两个系统分别与处于确定状态的第三个系统 达到热平衡,则这两个系统彼此也将处于热平衡。
温度 互为热平衡的几个热力学系统,必然具有某 种共同的宏观性质,我们将这种决定系统热平衡的宏 观性质定义为温度。
• 统计物理学是研究物质热运动的微观理论。从物质由
大量微观粒子组成这一基本事实出发,运用统计方法,把物 质的宏观性质作为大量微观粒子热运动的统计平均结果,找 出宏观量与微观量的关系,进而解释物质的宏观性质。 在对物质微观模型进行简化假设后,应用统计物理可求出具体 物质的特性;还可应用到比热力学更为广阔的领域,如解释 涨落现象。
为简单系统(或 p—V 系统)。
6
10:08:35
热平衡
将两个分别处于平衡态的系统A和B用一刚性隔板分隔
开。若隔板为“绝热板”(如图(a)),
则A,B两系统的状态可独立地
变化而互不影响。
绝热板
A
若隔板为“导热板”(如图(b)),则A,B两 系统状态不能独立地改变, 一个系统状态的 变化会引起另一系统状态的变化. 通过导热板两个系统的相互作用叫热接触。
大学物理课件第三章 刚体和流体

2 绳子,绳子下端挂一质量 m1=1.0 kg 的物体,如图 所示。起初在圆盘上加一恒力矩使物体以速率 v0=0.6 m/s 匀速上升,若撤去所加力矩,问经历多 少时间圆盘开始做反向转动?
r O
m1
弹穿出后棒的角速度。已知棒长为l,质量为M。
解:子弹和木棒组成的系统对轴O的 角动量守恒
1
mv0l 4 mv0l Jω
M
其 中J 1 Ml 2
3
3mv0l 9mv0
4J 4Ml
v0
mv
3-5 力矩的功
➢力矩的功
设刚体上P点受到外力
F的作用,位移为
d
r,
功为dW
dW
3. 两种运动的结合 一般运动可分解为以下两种刚体的基本运动:
随基点O(可任选)的平动 绕通过基点O的瞬时轴的定点转动 常选质心为基点。
定轴转动:各质元均作圆周运动,其圆心都在一条固 定不动的直线(转轴)上。
各质元的线量一般不同(因为半径不同),但角量(角 位移、角速度、角加速度)都相同。
设刚体绕固定轴 z 转动,转动
3
2
3-3 刚体对定轴的角动量定理和转动定律
由质点系对轴的角动量定理,可得
d L d( J)
Mz dt dt
两边乘以dt,并积分
M t2
t1
z
d
t
L2
L1
刚体对定轴的角动量定理:在某一时间段内,作用
在刚体上的外力之冲量矩等于刚体的角动量增量。
Mz
dL dt
d( J)
dt
当 J 转动惯量是一个恒量时,有
此时滑轮的角速度。 解:据机械能守恒定律:
r O
m1
弹穿出后棒的角速度。已知棒长为l,质量为M。
解:子弹和木棒组成的系统对轴O的 角动量守恒
1
mv0l 4 mv0l Jω
M
其 中J 1 Ml 2
3
3mv0l 9mv0
4J 4Ml
v0
mv
3-5 力矩的功
➢力矩的功
设刚体上P点受到外力
F的作用,位移为
d
r,
功为dW
dW
3. 两种运动的结合 一般运动可分解为以下两种刚体的基本运动:
随基点O(可任选)的平动 绕通过基点O的瞬时轴的定点转动 常选质心为基点。
定轴转动:各质元均作圆周运动,其圆心都在一条固 定不动的直线(转轴)上。
各质元的线量一般不同(因为半径不同),但角量(角 位移、角速度、角加速度)都相同。
设刚体绕固定轴 z 转动,转动
3
2
3-3 刚体对定轴的角动量定理和转动定律
由质点系对轴的角动量定理,可得
d L d( J)
Mz dt dt
两边乘以dt,并积分
M t2
t1
z
d
t
L2
L1
刚体对定轴的角动量定理:在某一时间段内,作用
在刚体上的外力之冲量矩等于刚体的角动量增量。
Mz
dL dt
d( J)
dt
当 J 转动惯量是一个恒量时,有
此时滑轮的角速度。 解:据机械能守恒定律:
大学物理:第三章 理想光学系统

2. 像的大小;
3. 物右移200mm,像移动多大距离?
例:有一光组将物放大3倍,成像在影屏上,当透镜向物 体方向移动18mm时,物象放大率为4倍。求光组焦距。
三、由多个光组组成的理想光学系统
相应于高斯公式:
l2 l1 d1
………
d1 H1H 2
lk …lk1 d k1 (主面间隔)
相应于牛顿公式:
l HA,l H A
由图,有: x l f , x l f
代入牛顿公式,得: lf lf ll
f f 1 l l
n n n n l l f f
放大率公式为:
f f f f l nl
x f x f l n l
x f f f f f x f
x2 x1 1
………
1 F1F2
xk … xk 1 k1 (光学间隔)
光学间隔Δ和主面间隔d 的关系为:
1 d1 f1 f 2
………
k 1 …d k 1 f k1 f k 1
垂轴放大率为: yk y1 y2 yk
y1 y1 y2
yk
1 2 k
四、光学系统的光焦度
f h tgU
象方主点H′到象方焦点F′的距离称为象方 焦距(后焦距或第二焦距)
f h tgU
说明:
1)对于理想光学系统,不管其结构(r,d,n)如何,只 要知道其焦距值和焦点或主点的位置,其光学性质就确 定了。
2) f n n =n′ f f
fn
h ltgU ltgU
x f tgU x f tgU
§ 3-2 理想光学系统的基点、基面
1. 焦点、焦平面 物方焦点:对应像点在像方光轴上无限远处
焦点 像方焦点:对应物点在物方光轴上无限远处
3. 物右移200mm,像移动多大距离?
例:有一光组将物放大3倍,成像在影屏上,当透镜向物 体方向移动18mm时,物象放大率为4倍。求光组焦距。
三、由多个光组组成的理想光学系统
相应于高斯公式:
l2 l1 d1
………
d1 H1H 2
lk …lk1 d k1 (主面间隔)
相应于牛顿公式:
l HA,l H A
由图,有: x l f , x l f
代入牛顿公式,得: lf lf ll
f f 1 l l
n n n n l l f f
放大率公式为:
f f f f l nl
x f x f l n l
x f f f f f x f
x2 x1 1
………
1 F1F2
xk … xk 1 k1 (光学间隔)
光学间隔Δ和主面间隔d 的关系为:
1 d1 f1 f 2
………
k 1 …d k 1 f k1 f k 1
垂轴放大率为: yk y1 y2 yk
y1 y1 y2
yk
1 2 k
四、光学系统的光焦度
f h tgU
象方主点H′到象方焦点F′的距离称为象方 焦距(后焦距或第二焦距)
f h tgU
说明:
1)对于理想光学系统,不管其结构(r,d,n)如何,只 要知道其焦距值和焦点或主点的位置,其光学性质就确 定了。
2) f n n =n′ f f
fn
h ltgU ltgU
x f tgU x f tgU
§ 3-2 理想光学系统的基点、基面
1. 焦点、焦平面 物方焦点:对应像点在像方光轴上无限远处
焦点 像方焦点:对应物点在物方光轴上无限远处
大学物理第三篇导体壳与静电屏蔽 ppt课件
结论
在腔内 E壳外表 E壳 面外 0
电量 带电体
二.腔内有带电体
电量分布
Q腔内 q
表面
用高斯定理可证
q
腔内的电场 1)与电量 q有关;
2)与腔内带电体、几何
因素、介质有关。
未提及 的问题
1)壳是否带电?2)腔外是否有带电体?
结论
腔内的场只与腔内带电体及腔内的几
何因素、介质有关
或说 在腔内 E壳外表 E壳 面外 0
具体作法: 用与原电荷相似的若干点电荷或线电荷 代替实际导体上的感应电荷, 来计算原电荷与感应电荷合成的场。 这些相似的电荷称为镜象电荷。
例 无限大接地导体平板附近有一点电荷 q
求:1)点电荷一侧的场的分布
aq
2)导体表面的感应电荷面密度
解: 域内解唯一 镜象电荷与原电荷产生的 合场满足同样的边界条件
电量 带电体
三.静电屏蔽的装置---接地导体壳 静电屏蔽: 腔内、腔外的场互不影响
腔内场 只与内部带电量及内部几何条件 及介质有关
腔外场 只由外部带电量和外部几何条件 及介质决定
例 导体 A和B 同心放置 如图
欲求壳B的电 只 势需知壳外表面的带电量 和球壳B的外半径
A
R qB
则
UBREdl
q
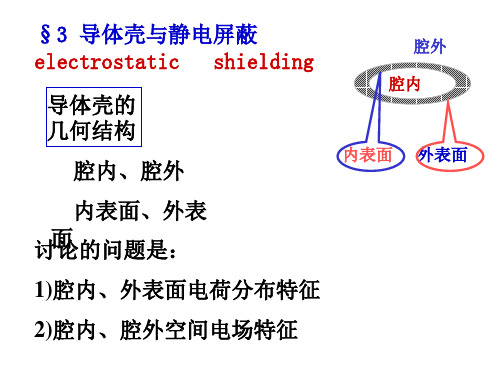
§3 导体壳与静电屏蔽 electrostatic shielding
导体壳的 几何结构
腔内、腔外
腔外 腔内
内表面 外表面
内表面、外表 讨面论的问题是:
1)腔内、外表面电荷分布特征
2)腔内、腔外空间电场特征
一.腔内无带电体
内表面处处没有电
荷
即 E腔内0
或腔说内,无腔电内场电势处处相等。
大学物理 第三篇 电磁场的物质性 统一性 相对性

大量实验证明场有
质量和动量
如 引力红移 引力偏折
场与实物相互转化
光压
等
如同步辐射光源
正负电子对湮没
e e
二.电磁场的统一性相对性
电场、磁场均由带电体产生,统一是必然的。
1. 洛仑兹不变量与洛仑兹不变式
基础是洛仑兹力公式 洛仑兹不变式
f qE qv B f qE qv B
磁场分量 相等
讨论
在运动方向上
在垂直运动方向上 电场
磁场之间有关系
如果产生场的电荷在某个惯性系中静止,则在
这个系中只有静电场,没有磁场。
正变换 Ex Ex
Ey E y vBz
z z y
E E
vB
Bx Bx v By By 2 Ez c v Bz Bz 2 E y c
1 B 2 vE c 很容易得到
在S系内
求:平板以速度 v 高速运动时的电磁场 解: 设平板静止的参考系为 S y y
相对实验室参考系(S系)
例1 均匀带电的无限大平面 电荷面密度
运动速度为
v vx
v
S 系中
只有静电场
z z
^ E E y y 2 0
0
v B 2 2c 0
与
B
0j
2
1 j v 只需注意到 0 0 2 c 在S系中用E 的高斯定理和 B 的环路定理计算
电量不变 带电板在运动方向的长度缩短
电荷面密度变为 s s 0 js v 0 s E B 2 0 2 0 2 2
大学物理第三章刚体力学 ppt课件

M F2d F2r sin
ppt课件
5
若F位于转动平面内,则上式简化为
M Fd Frsin
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
或 L 常矢量
dt
如果对于某一固定点,质点所受的合外力矩为零, 则质点对该固定点的角动量矢量保持不变—角动量守 恒定律 。
角动量守恒定律是自然界普遍适用的一条基本规律。
力矩M = 0的条件:(1)力臂 r = 0 (有心力作用),
(2)力F = 0,(3) r 与F 相互平行。
ppt课件
29
例9 行星运动的开普勒第二运动定律:行星对太阳 的位矢在相等的时间内扫过相等的面积。
d
C
JC 、 JD 分别是刚体对过质心轴, 和与之相平行的另一转轴的转动 惯量。两转轴间距为d
z ▪薄板的正交轴定理:
Jz Jx Jy
o
y
x
X,Y 轴在薄板面上,Z轴与薄板垂直。
ppt课件
14
例3、质量m,长为l 的四根均匀细棒, O
组成一正方形框架,绕过其一顶点O
并与框架垂直的轴转动,求转动惯量。
解:行星在太阳引力(有心力) 作用下沿椭圆轨道运动,因而 行星在运行过程中,它对太阳 的角动量守恒不变。
L rmv sin 常量
因而掠面速度:
dS r dr sin 1 rv sin 常 量 dt 2dt 2
ppt课件
30
例10 发射一宇宙飞船去考察一质量为m1,半径为R 的行星。当飞船静止于空间中距行星中心r=4R时,以
ppt课件
5
若F位于转动平面内,则上式简化为
M Fd Frsin
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
或 L 常矢量
dt
如果对于某一固定点,质点所受的合外力矩为零, 则质点对该固定点的角动量矢量保持不变—角动量守 恒定律 。
角动量守恒定律是自然界普遍适用的一条基本规律。
力矩M = 0的条件:(1)力臂 r = 0 (有心力作用),
(2)力F = 0,(3) r 与F 相互平行。
ppt课件
29
例9 行星运动的开普勒第二运动定律:行星对太阳 的位矢在相等的时间内扫过相等的面积。
d
C
JC 、 JD 分别是刚体对过质心轴, 和与之相平行的另一转轴的转动 惯量。两转轴间距为d
z ▪薄板的正交轴定理:
Jz Jx Jy
o
y
x
X,Y 轴在薄板面上,Z轴与薄板垂直。
ppt课件
14
例3、质量m,长为l 的四根均匀细棒, O
组成一正方形框架,绕过其一顶点O
并与框架垂直的轴转动,求转动惯量。
解:行星在太阳引力(有心力) 作用下沿椭圆轨道运动,因而 行星在运行过程中,它对太阳 的角动量守恒不变。
L rmv sin 常量
因而掠面速度:
dS r dr sin 1 rv sin 常 量 dt 2dt 2
ppt课件
30
例10 发射一宇宙飞船去考察一质量为m1,半径为R 的行星。当飞船静止于空间中距行星中心r=4R时,以
《大学物理》第三章 刚体的定轴转动

P
t
=
1 2
ω J 2 自
t
=
ω J 2 自 2P
=
2×105× (30π)
2×736×103
2
=
1.21×103s
(2) ω进 = 1度 秒 = 0.0175rad/s
ω进 =
M
Jω自
M = Jω进ω自
M = 2×105×0.0175×30π= 3.3×105 N返回.m退出
3-14 在如图所示的回转仪中,转盘的 质量为 0.15kg , 绕其轴线的转动惯量为: 1.50×10-4 kg.m2 ,架子的质量为 0.03kg, 由转盘与架子组成的系统被支持在一个支柱 的尖端O,尖端O到转盘中心的距离为0.04 m , 当转盘以一定角速度ω 绕其轴旋转时, 它便在水平面内以1/6 rev/s的转速进动。
为25cm,轴的一端 A用一根链条挂起,如
果原来轴在水平位置,并使轮子以ω自=12 rad/s的角速度旋转,方向如图所示,求:
(1)该轮自转的角动量;
(2)作用于轴上的外力矩;
(3)系统的进动角速度, ω
并判断进动方向。
AO
B
R
l 返回 退出
解:
(1)
J
=
m
R
2
回
=
5×(0.25 )2
ω
= 0.313 kg.m2
a
=
m
1+
m m
1g 2+
J
r2
T1 =
m 1g (m 2+ J m 1+m 2 + J
r 2) r2
T2 =
m 1m 2g m 1+m 2 + J
大学物理课件第3章 动量与角动量

§3.3 动量守恒定律 质点系所受合外力为零, Σ 时间改变,即
Fi = 0 总动量不随
N P pi 常矢量
i 1
1. 合外力为零,或外力与内力相比小很多;
2. 合外力沿某一方向为零;
p i
i
const .
3. 只适用于惯性系; 4. 比牛顿定律更普遍的最基本的定律。
M r F
力
M F d F r sin
提问:力矩为0的情况?
力矩
Lrp
动量
N m 矢量性: r F
单位:
三、角动量定理
pr p v pr F Lr 角动量定理: r F M (力矩)
q
v
V
v sinq
v cosq V
解:设车相对地面的反冲速度为V,方向水平向左 炮弹相对地面的速度水平分量为 v cosq V mv cosq 水平方向动量守恒 m(v cosq V ) MV 0 解得V
炮弹相对地面的速度竖直分量为 v sinq
m M
v sinq tg v cosq V
t2
mg
3秒时物是否被拉起?
F cos f 0 N F sin mg 0 f N t1 1.9 s
I x 0.62 Kgm / s
t1
F
x
dt 1.12t (cos sin ) mg dt
3
I x mvx 0 0.62Kgm / s
6
h
v
0
N =
m 2gh
τ
m 工件
mg
《大学物理》第三篇电磁学

找比较对象 类象
重要作用: (1) 是提出科学假说的重要途径; (2) 是科学阐述或理论证明的辅助手段; (3) 在解决问题的过程中起启发思路、触类旁通的作用。
注意:类比推理所得结论是或然的,需证实或证伪。
3-15-2
磁场
静电场 电
感生 场 电场
一般 电场
高斯定理
SB dS 0
S D0 dS
物质存在的两种基本形式:实物和场
共性:能量、动量、质量
•场能对其中的物体做功 ——表明场有能量
•引力红移与偏折、光压等实验 ——表明场有质量和动量
可相互转化(如正负电子对湮没、同步辐射)
1、电磁场的能量密度与能量
电场能量密度
1 we 2 E D
磁场能量密度
wm
1 2
BH
电磁场能量密度
w
we
S D0 dS
ρdV
V
L E0 dl 0
SB dS 0
D
LH dl S ( j t ) dS
SB dS 0
LH dl S j dS
静电场 基本方程
静电场 基本方程
麦克斯韦方程组是对电磁场宏观规律的 全面总结和概括!
是经典物理三大支柱之一。
再看积分形式的麦克斯韦方程组
jE
2 t
由矢量运算公式: a (b c ) (a b) c b (a c )
(H E) ( H ) E H ( E)
1
(D E
BH)
(H
E)
jE
2 t
(E H ) j E
dW 1
dt
2 V t (D E B H )dV
jD πr 2
2) r >R
最新大学物理第3章-刚体力学基础课件ppt

对所有质元的同样的式子求和:
∑Fi risini+ ∑ fi rsi ini = (∑ mi ri2 )
一对内力的力矩之和为零,所以有
∑ Fi ri sini = (∑mi ri2)
只与刚体的形状、质量分布和转轴位置有关
大学物理学A
第一篇 力学基础
第3章 刚体力学基础
令J= ∑mi ri2 J为刚体对于定转轴的转动惯量
对平动的刚体列出牛顿第二定律方程,对定轴转动的刚体 列出定轴转动定律方程;
注意利用角量与线量的关系。
大学物理学A
第一篇 力学基础
第3章 刚体力学基础
例5: 已知光滑桌面,滑轮半径R,质量为Mc,两物体质 量分别为m1 m2 ,求两物体的加速度和绳的张力.
m2
a
m1
g
m1 解:
m1 m 2
T m 1m 2 g
1 3
mLL2
Jo
2 5
mo
R2
mO
J L 2 J 0 m 0 d 2 J 0 m 0 ( L R ) 2
J1 3m L L 25 2m oR 2m o(L R )2
大学物理学A
第一篇 力学基础
大学物理学A
匀质矩形薄板
转轴通过中
心垂直板面
I=
m 12
(a2 + b2
)
匀质细圆环
转轴通过中 心垂直环面
FT 1mAa
m BgF T2 m Ba
RTF 2 RTF 1 J
a R
FN
PmAAO
FT1
x
第3章 刚体力学基础
FT1
FC
PC
FT 2
FT 2
O
mB
∑Fi risini+ ∑ fi rsi ini = (∑ mi ri2 )
一对内力的力矩之和为零,所以有
∑ Fi ri sini = (∑mi ri2)
只与刚体的形状、质量分布和转轴位置有关
大学物理学A
第一篇 力学基础
第3章 刚体力学基础
令J= ∑mi ri2 J为刚体对于定转轴的转动惯量
对平动的刚体列出牛顿第二定律方程,对定轴转动的刚体 列出定轴转动定律方程;
注意利用角量与线量的关系。
大学物理学A
第一篇 力学基础
第3章 刚体力学基础
例5: 已知光滑桌面,滑轮半径R,质量为Mc,两物体质 量分别为m1 m2 ,求两物体的加速度和绳的张力.
m2
a
m1
g
m1 解:
m1 m 2
T m 1m 2 g
1 3
mLL2
Jo
2 5
mo
R2
mO
J L 2 J 0 m 0 d 2 J 0 m 0 ( L R ) 2
J1 3m L L 25 2m oR 2m o(L R )2
大学物理学A
第一篇 力学基础
大学物理学A
匀质矩形薄板
转轴通过中
心垂直板面
I=
m 12
(a2 + b2
)
匀质细圆环
转轴通过中 心垂直环面
FT 1mAa
m BgF T2 m Ba
RTF 2 RTF 1 J
a R
FN
PmAAO
FT1
x
第3章 刚体力学基础
FT1
FC
PC
FT 2
FT 2
O
mB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
o
i
i
即作用在各质元的力矩的z分量之和
2、刚体定轴转动定理
由于刚体只能绕z轴转动,引起转动的
力矩只有 Mz,因此转动动力学方程
Li
Mz
dLz dt
Ri mivi
dL
M
oo
ri dtmi
vi
z o
Li
ri
vi
mi
由于
oo
vi
垂直于z轴
Ri
o
y
Liz ri mivi mi ri2 x
结论:
1.由于考虑了滑轮的质量,使得 T1 T2
2. 若m1m2则T1T2
【例 】“打击中心”问题 细杆:m, l ,轴O,在竖直位置静止.若在某 时刻有力作用在A处,求轴对杆的作用力。
解:可通过转动定理求细杆的转动,再求 质心加速度。利用质心运动定理求支反力。
.O
l0 C .
.A
如图示,除力F外,系统还受重力、 轴的支反力等。但这两个力对轴的力矩=0。 只有F对细杆的转动有影响,对转轴O的力矩为:
i
Ai
i
0
M
i
d
0
i
M i d Md
0
3、刚体定轴转动的动能定理
M J d J d d J d
dt d dt
d
Md
0
0
Jd
1 2
J2
1 2
J02
4、刚体的重力势能
刚体和地球系统的重力势能: 以地面为零势能点,质元i:
E pi mi gzi
Z
o
rc i
mi g
E p
i3
如:车轮滚动 i 11
4 刚体的一般运动可以分解为随质心的平移 和绕质心的定点转动
i 33
二、刚体的受力
力是滑移矢量,只能在力的方向上移动
力的三要素:大小、方向、作用线。
F F
§3.2 刚体的定轴转动
一、定轴转动的描述
p点:角位置 角位移
d
dt
d 2
dt 2
角速度,角加速度
转动平面
平行轴定理
刚体对任一转轴的转动惯量J等于对通过质心的平行
转轴的转动惯量Jc加上刚体质量m乘以两平行转轴间
距离d的平方
J Jc md 2
J miri2 miri ri
Jc J
criz
d
ri
o ri
mi
Ri
i
mi ri d ri d
i
miri2 md 2 2d
Lz Liz rimivi
i
i
( miri2 ) J
i
式中 J miri2
i
称为刚体对转轴 z 的转动惯量
代入
Mz
dLz dt
得到 M dJ
dt
J为常量 M = J dω J
dt
刚体定轴转动定理
z o
Li
ri
vi
mi
Ri
x o
y
F ma
M dL dt
L J
【解 】 盘由许多环组成
dJ r 2dm
z dr
r
y
J r2dm r2 2πr hdr
x
2πh R r 3dr 0
1 πhR4 1 m R2
2
2
【例 】圆盘:m,R,求以直径为轴的转动惯量
J 1 m R2 4
【例 】挂钟摆锤的转动惯量
o ml
1
J
1 3
m1l 2
1 2
m2 R2
i
mi gzi mg
i
mi zi m
mgz c
5、刚体定轴转动的功能原理
将重力矩作的功用重力势能差表示
0 M pd (mgzc mgzc0)
得
0
Md
(mgzc
1 2
J2 )
(mgzc0
1 2
J02 )
其中,M为除重力以外的其它外力矩
若M=0, 则
mgzc
1 2
J2
常量
即刚体的机械能守恒定律
A
i
【例 】摩擦离合器 飞轮1:J1 1飞轮2: J2 静止 两轮沿轴向结合,结合后两轮达到的共 同角速度。
解:两轮对共同转轴的角动量守恒 12
J11 J1 J2
J11 J1 J2
【例 】均质细棒:m1、 l ,水平轴O,小球:m2与棒
相碰,碰前 碰后 如图,设碰撞时间很短,棒保
持竖直,求碰后棒的角速度。
M0
Lhd
dt
Lh
2mb22 sin cos
d
Lh
3、 刚体的转动惯量
转动惯量的计算
J miri2
i
刚体对某一转轴的转动惯量等于每个质点 的质量与这一质点到转轴的距离平方的乘 积之和。
m1
r1
r2 m2
物理意义:转动惯量是对刚体转动惯性大小的量度,其大小 反映了改变刚体转动状态的难易程度。
mgL1
c
os
m
ax
c os m ax
3 4
max 41.1o
oo
i Ri
o
Fi
y
x
oo
Fi
ri
Fi
z轴 // z轴
M iz
ri Fi
ri Fi sin i
z
Fi 对参考点 o 的力矩在z轴上的分量
就等于力 Fi 对z 轴的垂足o(转心)
o
的力矩(简称力 Fi 对转轴的力矩)
相对于定轴的合外力矩
oo
ri mi
i Ri
Fi
y
M z M iz ri Fi sin i
5
5
【例 】圆柱体:m,r,l,求转动惯量
z z
dJ 1 r 2dm 1 r 2m dx
4
4l
r
dJ dmx2 dJ m dx x2 1 r2m dx
l
4l
ox
x
l
J
l
2 l
2
m
dx l
x2
1 4
r 2m dx l
mr 2 4
ml 2 12
三、定轴转动刚体的角动量守恒定律
p
o
qx
o
q点:角位置 角位移
d
dt
d 2
dt 2
按SI, 的单位分别是
rad, rad/s,rad/s2
对于匀角加度速转动,则有:
0 t
0
0t
1 2
t
2
2
2 0
2 (
0)
式中 0, 0
是t=0时刻的角速度和角位置
角量与线量之关系
v r
at
dv dt
d
dt
r
r
an
v2 r
2r
v
r
角速度矢量
d
大小为
方向由右螺旋法则确定
dt
规定顺着刚体转动的右螺旋前进方向为 角速度矢量的方向
在定轴转动下,转轴任取一点为坐标原点
v
r
r
r
sin
v
角加速度矢量
d
dt
角速度矢量再研究 定义角位移 是否矢量?
O P
1
2
2 1
1 2 2 1
有限大角位移相加时不满足交换律,不是矢量
Mdt dL dJ
推广到 J 可变情形(保持所有质点 相同)
t
J
Mdt
t0
d J
J 00
J J00
t
Mdt t0
称为在t0到t时间内作用在刚体上的冲量矩
【例 】定滑轮: m r J 物体: m1 m2
轻绳不能伸长,与滑轮间无相对滑动。
求滑轮转动的角加速度和绳的张力。
【解】m1 g T1 m1a T2 m2 g m2a
为其转过的角度。
【例 】 旋转哑铃。 求角动量及外力矩(o点)
(1) v r
vA vB bsin
L
r
mv
L 2L
L 2bmbsin 2mb2 sin
L 2bmbsin 2mb2 sin
L Lz Lh
Lz Lsin 2mb2 sin 2
LhMoLcods(Lzdt 2Lmh )b2dsdiLnth cos
定轴转动角动量定理:
M dJ
dt
当 M=0 有 dJ 0
dt
J J00 常量
定轴转动角动量守恒定律:刚体在定轴转动中,当对转 轴的合外力矩为零时,刚体对转轴的角动量保持不变。
• 茹可夫斯基凳
若系统由几个物体组成,当系统受到 的外力对轴的力矩的矢量和为零,则系统的
总角动量守恒: Jii 常量
2 转动:刚体上所有各点绕同一直线作圆周 运动,这一直线称为转轴。
(1)定轴转动:转轴固定于参考系
如:门 窗
i 1 ()
p
o
x
(2)定点转动:转轴上有一点静止于参考系
如:玩具陀螺
i3
(转轴方向2,绕轴转角1)
3 平面平行运动:刚体上每一质元的运动都 平行于某一固定平面
可以分解为刚体随质心的平移(2)和绕质心 垂直于运动平面的定轴转动(1)
细杆遵从如下动力学方程:
质心运动定律分量式:
.O l0 C .
.A
.O l0 C .
.A
讨论
打击中心
• 网球拍
the sweet spot
【例 】一半径为R,质量为m的均匀圆盘平放在粗糙的 水平面上。若它的初角速度为0,绕中心o旋转,问经 过多长时间圆盘才停止?(设摩擦系数为)
解:
