2012年福建省莆田市中考真题(word版含答案)

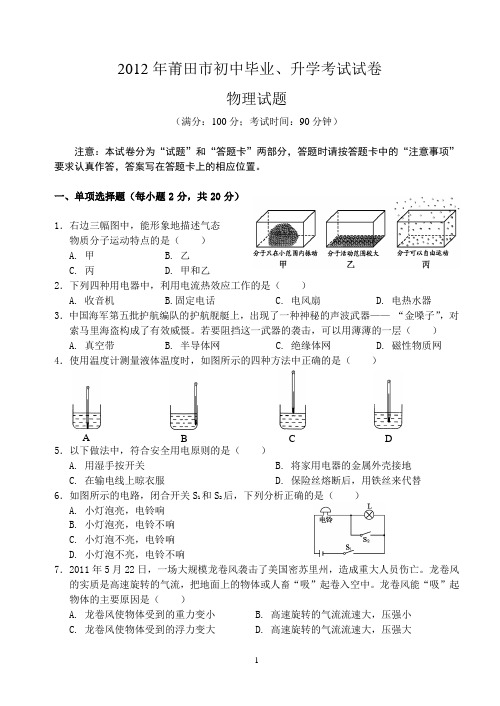
2012年莆田市初中毕业、升学考试试卷数学试题（满分：150分；考试时间：120分钟）注意：本试卷分为“试题”和“答题卡”两部分，答题时请按答题卡中的“注意事项”要求认真作答，答案写在答题卡上的相应位置．一、精心选一选：本大题共8小题，每小题4分，共32分．每小题给出的四个选项中有且只有一个选项是符合题目要求的．答对的得4分，答错、不答或答案超过一个的一律得0分． 1．下列各数中，最小的数是（ ）（A ）－l （B ）0 （C ）1 （D 2．下列图形中，是．中心对称图形，但不是．．轴对称图形的是（ ）3．下列运算正确的是（ ）（A ）33a a -= （B ）33a a a ÷=（C ）235a a a ⋅= （D ）222()a b a b +=+4．在一次芭蕾舞比赛中，甲、乙、丙、丁四队女演员的人数相同，身高的平均数均为166 cm ，且方差分别为2 1.5S =甲，2 2.5S =乙，2 2.9S =丙，23.3S =丁，则这四队女演员的身高最整齐的是（ ）（A ）甲队 （B ）乙队 （C ）丙队 （D ）丁队 5．方程()()120x x -+=的两根分别为（ ） （A ）11x =-，2x ＝2 （B ）1x ＝1，2x ＝2 （C ）11x =-，22x =- （D ）1x ＝1，22x =-6．某几何组合体的主视图和左视图为同一个视图，如图所示，则该几何组合体的俯视图不可能．．．是（ ）7．甲、乙两班学生参加植树造林．已知甲班每天比乙班少植2棵树，甲班植60棵树所用天数与乙班植70棵树所用天数相等．若设甲班每天植树x 棵，则根据题意列出方程正确的是（ ） （A ）60702x x =+ （B ）60702x x =+（C ）60702x x =- （D ）60702x x =-8．如图，在平面直角坐标系中，(11)A ，，(11)B -，，(12)C --，，(12)D -，．把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处，并按A →B →C →D →A →…的规律紧绕在四边形ABCD 的边上，则细线另一端所在位置的点的坐标是（ ） （A ）(11)-， （B ）(11)-，（C ）(12)--， （D ）(12)-，二、细心填一填：本大题共8小题，每小题4分，共32分．9．如图，A B C '''△是由ABC △沿射线AC 方向平移2cm 得到，若AC ＝3cm ，则A C '＝ cm ．10．2012年6月15日，中国“蛟龙号”载人潜水器在太平洋马里亚纳海沟区域进行下潜试验中，成功突破6500米深度，创中国载人深潜新纪录．将6500用科学记数法表示为 . 11．将一副三角尺按如图所示放置，则1∠＝ 度． 12．如果单项式13a x y +与32b x y 是同类项，那么ba = ．13．某学校为了做好道路交通安全教育工作，随机抽取本校100名学生就上学的交通方式进行调查，根据调查结果绘制扇形图如图所示．若该校共有1000名学生，请你估计全校步行上学的学生人数约有 人．14．若扇形的圆心角为60°，弧长为２π，则扇形的半径为 ．15．当12a =时，代数式22221a a ---的值为 ． 16．点A 、B 均在由面积为1的相同小矩形组成的网格的格点上，建立平面直角坐标系如图所示．若P 是x 轴上使得PA PB -的值最大的点，Q是y 轴上使得QA QB +的值最小的点，则OP OQ ＝ ．三、耐心做一做：本大题共9小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤．17．(本小题满分8分)计算：()221--18．(本小题满分8分)已知三个一元一次不等式：26x >，21x x +≥，40x -<，请从中选择你喜欢的两个不等式，组成一个不等式组，求出这个不等式组的解集，并把解集在数轴上表示出来．(1)(2分)你组成的不等式组是()()12⎧⎪⎨⎪⎩＿＿＿＿＿＿＿＿＿＿＿＿＿＿ (2)(6分)解：19．(本小题满分8分)如图，四边形ABCD 是平行四边形，连接AC ．(1)(4分)请根据以下语句画图．．，并标上相应的字母(用黑色字迹的钢笔或签字笔画)． ①过点A 画AE BC ⊥于点E ；②过点C 画CF AE ∥，交AD 于点F ；(2)(4分)在完成(1)后的图形中(不再添加其它线段和字母)， 请你找出一对全等三角形，并予以证明．20．(本小题满分8分)已知甲、乙两个班级各有50名学生．为了了解甲、乙两个班级学生解答选择题的能力状况，黄老师对某次考试中8道选择题的答题情况进行统计分析，得到统计表如下：请根据以上信息解答下列问题：(1)(2分)甲班学生答对的题数的众数是＿＿＿＿＿＿；(2)(2分)若答对的题数大于或等于7道的为优秀，则乙班该次考试中选择题答题的优秀率＝＿＿＿＿＿＿(优秀率＝班级优秀人数班级总人数×100％)；(3)(4分)从甲、乙两班答题全对的学生中，随机抽取2人作选择题解题方法交流，则抽到的2人在同一个班级的概率等于＿＿＿＿＿＿．21．(本小题满分8分)如图，某种新型导弹从地面发射点L 处发射，在初始竖直．．加速飞行阶段，导弹上升的高度(km)y 与飞行时间(s)x 之间的关系式为211186y x x =+ (010)x ≤≤．发射3s 后，导弹到达A 点，此时位于与L 同一水平面的R 处雷达站测得AR 的距离是2 km ，再过3s 后，导弹到达B 点． (1)(4分)求发射点L 与雷达站R 之间的距离；(2)(4分)当导弹到达B 点时，求雷达站测得的仰角(即BRL ∠)的正切值．22．(本小题满分10分)如图，点C 在以AB 为直径的半圆O 上，延长BC 到点D ，使得CD BC =，过点D 作DE AB ⊥于点E ，交AC 于点F ，点G 为DF 的中点，连接CG 、OF 、FB ． (1)(5分)求证：CG 是O ⊙的切线；(2)(5分)若AFB △的面积是DCG △的面积的2倍，求证：OF BC ∥．23．(本小题满分10分)如图，一次函数1y k x b =+的图象过点(03)A ，，且与反比例函数2(0)k y x x=>的图象相交于B C 、两点．(1)(5分)若(12)B ，，求12k k 的值； (2)(5分)若AB BC =，则12k k 的值是否为定值?若是，请求出该定值；若不是，请说明理由．24．(本小题满分12分)(1)(3分)如图①，在Rt ABC △中，90ABC ∠=°，BD AC ⊥于点D ． 求证：2AB AD AC =∙；(2)(4分)如图②，在Rt ABC △中，90ABC ∠=°，点D 为BC 边上的点，BE AD ⊥于点E ，延长BE 交AC 于点F ．若1AB BD BC DC ==，求AFFC的值； (3)(5分) 在Rt ABC △中，90ABC ∠=°，点D 为直线．．BC 上的动点．．(点D 不与B 、C 重合)，直线BE AD ⊥于点E ，交直线AC 于点F ．若AB BD n BC DC ==，请探究并直接写出AFFC所有可能的值(用含n 的式子表示)，不必证明．25，(本小题满分14分)如图，在平面直角坐标系中，矩形OABC 四个顶点的坐标分别为(00)O ，，(03)A ，，(63)B ，，(60)C ，，抛物线2y ax bx c =++(0)a ≠过点A ．(1)(2分)求c 的值；(2)(6分)若1a =-，且抛物线与矩形有且只有三个交点A 、D 、E ，求ADE △的面积S 的最大值；(3)(6分)若抛物线与矩形有且只有三个交点A 、M 、N ，线段MN 的垂直平分线l 过点O ，交线段BC 于点F ．当1BF =时，求抛物线的解析式．2012年莆田市初中毕业、升学考试试卷数学参考答案及评分标准说明：（一）考生的解法与“参考答案”不同时，可参照“答案的评分标准”的精神进行评分．（二）如解答的某一步计算出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得分数的二分之一；如属严重的概念性错误，就不给分． （三）以下解答各行右端所注分数表示正确做完该步骤应得的累计分数． （四）评分的最小单位1分，得分或扣分都不能出现小数点． 一、精心选一选（本大题共8小题，每小题4分，共32分）1．A 2．B 3．C 4．A 5．D 6．C 7．B 8．B 二、细心填一填（本大题共8小题，每小题4分，共32分）9．1 l0．36.510⨯ 11．105 12．8 13．400 14．6 15．1 16．5 三、耐心做一做（本大题共9小题，共86分） 17．（本小题满分8分）解：原式＝2＋2－l ＝3 ····················（8分）（注：｜－2｜＝22，（一1）2＝1各2分） 18．（本小题满分8分） （1）第一种26 21 x x x >⎧⎨≥+⎩ ① ②第二种2640 x x >⎧⎨-<⎩ ① ②第三种21 40x x x ≥+⎧⎨-<⎩ ① ②（注：每写对一个不等式得1分） （2）第一种解答：解不等式①，得3x >． ··································································································· （4分） 解不等式②，得1x ≥． ·································································································· （6分） 把不等式①和②的解集在数轴上表示 ∴ 不等式组解集为3x > ································································································· （7分）······································································· （8分）（注：第二种、第三种参照第一种解答并评分.） 19．（本小题满分8分） （1）（每画对一条线段得2分） ···························································································· （4分） （2）①ABC CDA △≌△． ································································································ （5分） 证明：∵四边形ABCD 是平行四边形， ∴AB CD BC DA ==，， ······················ （7分） ∵AC CA =， ·········································· （8分） ∴ABC CDA △≌△． ②AEC CFA △≌△． ···························· （5分） 证明：∵四边形ABCD 是平行四边形， ∴AD BC ∥，∴DAC ACE ∠=∠． ··········································································· （6分） ∵AE CF ∥，∴EAC ACF ∠=∠ ． ··········································································· （7分） ∵AC CA =， ·················································································································· （8分）∴AEC CFA △≌△． ③ABE CDF △≌△． ····································································································· （5分） 证明：∵四边形ABCD 是平行四边形， ∴ AD BC ∥，B D ∠=∠，AB CD =． ······································································ （7分） 又∵AE CF ∥，∴四边形AECF 是平行四边形． ∴AEC AFC ∠=∠，∴AEB CFD ∠=∠． ··································································· （8分） ∴ABE CDF △≌△． 20.（本小题满分8分） （1）6（或6道） ·················································································································· （2分） （2）30% ····························································································································· （4分） （3）13································································································································ （8分） 21．（本小题满分8分） 解：（1）把3x =代入211186y x x =+，得1y =，即1AL =． ········································ （2分）在Rt ARL △中，2AR =，∴LR ． ·········· （4分） （2）把336x =+=代入211186y x x =+，得3y =，即3BL =． ·· （6分）∴ tan BRL ∠＝BL LR ······················································· （8分）答：发射点L 与雷达站R 22．证明：（1）如图，连接OC ， ····················································· （1分）∵AB 为O ⊙的直径， ∴90ACB ∠=°． ································· （2分） 在Rt DCF △中，DG FG =． ∴CG DG FG ==，∴∠3＝∠4． ∵∠3＝∠5，∴∠4＝∠5． ··························································· （3分） ∵OA OC =，∴∠1＝∠2．又∵DE AB ⊥，∴ ∠1＋∠5＝90°． ∴ ∠2＋∠4＝90°．即90GCO ∠=°． ········································································································· （4分） ∴CG 为O ⊙的切线． ··································································································· （5分） （2）∵DG FG =，∴2DCF DCG S S ∆∆=． ·········································································· （6分） ∵DC CB =，∴DCF BCF S S ∆∆=，∴2BCF DCG S S ∆∆=． ················································· （7分） 又∵2ABF DCG S S ∆∆=，∴ABF BCF S S ∆∆=． ········································································ （8分） ∴AF FC =． ···················································································································· （9分） 又∵OA OB =，∴OF BC ∥． ···················································································· （10分） 23．（本小题满分10分）解：（1）把(12)B ，代入 2k y x=，得22k =． ····································································· （2分） 把(03)A ，，(12)B ，代入1y k x b =+，得132b k b =⎧⎨+=⎩，，解得131b k =⎧⎨=-⎩，··························· （4分）∴ 122k k ∙=-． ········································································································· （5分） （2） 122k k ∙=-． ············································································································· （6分） 过点B 作BG y ⊥轴于点G ，过点C 作CH y ⊥轴于点H ，∴BG CH =．∵AB BC =，∴AG GH =，∴2CH BG =． ························· （7分） 设2()kB m m ，，则2(2)2kC m m，．∴23k AG m =-，222k k GH m m =-． ∴23km -＝222k k m m -． ·········································································································· （8分）∴22k m =,B （22k，2）． ······································································································· （9分）把2(2)2k B ，代入13y k x =+，得21232kk =∙+，∴122k k ∙=-． ································ （10分） 24．（本小题满分12分）（1）证明：如图①，∵BD AC ⊥，90ABC ∠=°，∴∠ADB ＝∠ABC. 又∵ ∠A ＝∠A ，∴△ADB ∽△ABC ． ··········································································· （2分） ∴ AB AD AC AB=，∴ 2AB AD AC =∙． ······································································ （3分）（2）解：方法一：如图②，过点C 作CG AD ⊥交AD 的延长线于点G ． ···················· （4分） ∵BE AD ⊥，∴ 90CGD BED ∠=∠=°，CG BF ∥．又∵1AB BDBC DC== ∴22AB BC BD DC ===，BD DC =．又∵BDE CDG ∠=∠，∴BDE CDG △≌△．∴12ED GD EG ==． ········································································································· （5分）由（1）可得：2AB AE AD =∙，2BD DE AD =∙．∴ 2222(2)4AE AB BD DE BD BD === ，∴4AE DE =， ∴422AE DE EG DE ==． ··················· （6分）又∵CG BF ∥，2AF AEFC EG==． ····················································································· （7分） 方法二：如图③，过点D 作DG BF ∥交AC 于点G ． ···················································· （4分）∴1AB BD BC DC ==， 12BD DC BC ==，AB BC =． ∵DG BF ∥，∴2FC BCFG BD==，2FC FG =．·········· （5分） 由（1）可知： 2AB AE AD =∙，2BD DE AD =∙．∴22224AE AB BC DE BD BD ===． ····························································································· （6分） ∵DG BF ∥，∴4AF AE FG ED ==，∴22AF AFFC FG==． ·············································· （7分） （3） ①当点D 在BC 边上时，AF FC 的值为2n n +.②当点D 在BC 延长线上时，AF FC 的值为2n n -．③当点D 在BC 延长线上时，AF FC的值为2n n -．（注：写对一种得1分，写对二种得3分，写对三种得5分） 25．（本小题满分14分）解：（1）∵ 抛物线2y ax bx c =++过点(03)A ，， ∴3c =． ································································································································ （2分） （2） ∵1a =-，∴23y x bx =-++如图①，当抛物线与矩形的两个交点D 、E 分别在AB 、OC 边上时， 抛物线与直线6x =的交点应落在C 点或C 点下方．∴ 当6x =时，0y ≤， ∴ 26630b -++≤，即112b ≤又∵对称轴在y 轴右侧，∴0b >，∴1102b <≤． ·························································· （3分） 由抛物线的对称性可知：()22221b b AD b a ⎡⎤⎛⎫=⨯-=⨯-=⎢⎥ ⎪⨯-⎝⎭⎣⎦． 又∵ADE △的高＝BC ＝3，∴S ＝12×b ×3＝32b ． ·················································· （4分）。