matlab 第三章作业
数字信号处理及MATLAB实现第三章答案

3-11设是周期为N的周期序列,通过系统H(z)以后,求证序列为 证明:
在单位圆上对H(z)N等分采样,x(n)通过系统H(z)以后,输出频谱为
3-1求序列的DFS展开 解: 已知 ,则 3-2 (1) (2)
(3) (4) (5) (6) 解:(1) (2) (3) (4)
(5) 由,得 所以 (6) 因为,所以 3-3.答案略 3-4若,,,证明 证明: 3-5若,求证 证: 而
(为整数) 0 所以 于是 3-6令表示N点序列的N点DFT,试证明: (1)如果满足关系式,则。 (2)当N为偶数时,如果,则。 证: (1) N为偶数:N奇数: 而中间的一项应当满足:
因此必然有
这就是说,当N为奇数时,也有。 (b)当N为偶数:
当N为偶数时,为奇数,故;又由于故有 3-7 已知是N点有限长序列,。现将的每两点之间补进个零值点,得到 一个点的有限长序列
试求点DFT[]与的关系。 解:由 可得 而 所以是将(周期为N)延拓次形成的,即周期为。 3-8答案略 3-9设是一个2N点序列,具有如下性质
信号与系统_MATLAB_实验_课后习题答案
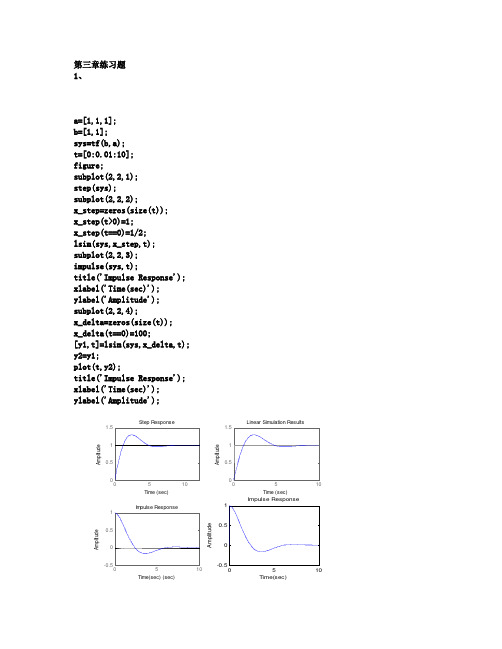
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下:t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下:function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同(b)Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数:Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统:Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统:Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。
matlab第三章答案

matlab第三章答案第1题:从键盘输入一个3位数,将它反向输出。
如输入639输出936、n1=fix(n/100);n2=rem(fix(n/10),10);n3=rem(n,10);m=n3*100+n2*10+n1;disp(m)请输入一个三位数:489984第2题:输入一个百分制成绩,要求输出成绩等级A、B、C、D、E。
其中90~100分为A,80~89分为B、70~79分为C、60~69分为D,60分以下为E。
要求:(1)分别用if语句与switch语句实现。
(2)输入百分制成绩后要判断成绩得合理性,对不合理得成绩应输出错信息。
If语句:>> s=input('请输入成绩分数:');if s>=90&s<=100disp('A');elseif s>=80&s<=89disp('B');elseif s>=70&s<=79disp('C');elseif s>=60&s<=69disp('D');elseif s>=0&s<60disp('E');elsedisp('false');end请输入成绩分数:89BSwitch语句:>> s=input('请输入成绩分数:');switch fix(s/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {5,4,3,2,1,0}disp('E');otherwisedisp('false');end请输入成绩分数:88B第3题输入20个数,求其中最大数与最小数。
数字信号处理Matlab练习第三章-080802084朱桂香

1.编写一个Matlab程序,用一个N点的复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换,并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
n=0:11; %设定n的范围x1=cos(pi/6.*n); %给定序列x1[n]x2=(4/5).^n; %给定序列x2[n]w1=x1+1i*x2; %由序列x1[n]和x2[n]组成复数序列w1[n]w2=x1-1i*x2; %序列w1[n]的共轭序列w2[n]figure,subplot(2,1,1),stem(n,x1); %指定位置1,绘制序列x1[n]xlabel('n'); %设定序列x1[n]的横轴标注和纵轴标注ylabel('x1[n]');subplot(2,1,2),stem(n,x2); %指定位置2,绘制序列x2[n]xlabel('n'); %设定序列x2[n]的横轴标注和纵轴标注ylabel('x2[n]');figure,subplot(4,1,1),stem(abs(w1)); %指定位置1,绘制序列w1[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W1的幅度谱');subplot(4,1,2),stem(angle(w1)); %指定位置2,绘制序列w1[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W1的相位谱');subplot(4,1,3),stem(abs(w2)); %指定位置3,绘制序列w2[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W2的幅度谱');subplot(4,1,4),stem(angle(w2)); %指定位置4,绘制序列w2[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W2的相位谱');X1=fft(x1); %求序列x1[n]的离散傅里叶变换X1(k)X2=fft(x2); %求序列x2[n]的离散傅里叶变换X2(k)W1=fft(w1); %求序列w1[n]的离散傅里叶变换W1(k)W2=fft(w2); %求序列w2[n]的离散傅里叶变换W2(k)Y1=(1/2)*(W1+W2); %由W1(k)和W2(k)来求X1(k)Y2=(1/(2*1i))*(W1-W2); %由W1(k)和W2(k)来求X2(k)figure,subplot(2,1,1),stem(abs(X1)); %指定位置1,绘制|X1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X1(k)|');subplot(2,1,2),stem(abs(Y1)); %指定位置2,绘制|Y1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|Y1(k)|');figure,subplot(2,1,1),stem(abs(X2)); %指定位置1,绘制|X2(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X2(k)|');subplot(2,1,2),stem(abs(Y2)); %指定位置2,绘制|Y2(k)|xlabel('k'); %设定横轴标注和纵轴标注 ylabel('|Y2(k)|');结果图:nx 1[n]024681012nx 2[n ]图1 序列x1[n]和x2[n]02468101212nm a g n i t u d eW1的幅度谱24np h a s eW1的相位谱02468101212nm a g n i t u d eW2的幅度谱024681012-4-20np h a s e图2 w1和w2的幅度谱和相位谱图246k|X 1(k )|246k|Y 1(k )|图3 两种计算X1(k)的方法比较024681012246k|X 2(k )|024681012246k|Y 2(k )|图4 两种计算X2(k)的方法比较2.编写一个Matlab 程序,用两个N 点的复数离散傅里叶变换计算一个长度为2N 的实数序列的2N 点离散傅里叶变换,并将结果同直接使用一个2N 点离散傅里叶变换得到的结果进行比较。
MATLAB语言与控制系统仿真-参考答案-第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MA TLAB 绘图的基本知识;2.掌握MA TLAB 子图绘制、图形注释、图形编辑等基本方法;3.学会通过MA TLAB 绘图解决一些实际问题;4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法;5.学会制作简单的MATLAB 动画。
图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题(1)炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。
)cos()(0αtv t x = %水平方向的行程;205.0)sin()(gt tv t y -=α %垂直方向的行程; 其中,0v 是初速度;g 是重力加速度,为9.82m/s ;t 是时间。
(2)炮弹发射程序举例:分析以下程序以及图3-47各个图形的实际意义。
a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos(a);y=t*v0*sin(a)-0.5*g*t.^2;subplot(221);plot(t,x);grid;title(‘时间-水平位移曲线'); subplot(222);plot(t,y);grid;title(‘时间-垂直位移曲线');subplot(223);plot(x,y);grid;title(‘水平位移-垂直位移曲线'); subplot(224);plot(y,x);grid;title(‘垂直位移-水平位移曲线');图3-4745角发射曲线 (3)编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程;绘图要求:◆ 标题设为“炮弹垂直发射问题”; ◆ 在图上通过添加文本的方式表明初速度; ◆ 在x 轴标注“时间”; ◆ 在y 轴上标注“垂直距离”; ◆ 添加网格线; ◆ 将310m/s 的曲线改为线粗为2的红色实线; ◆ 将290m/s 的曲线改为线粗为3的绿色点划线; ◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线;a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos(a);y1=t*v1*sin(a)-0.5*g*t.^2;plot(t,y1);grid; title('炮弹垂直发射问题'); xlabel('时间'); ylabel('垂直距离'); hold on; v2=290;x2=t*v2*cos(a);y2=t*v2*sin(a)-0.5*g*t.^2; plot(t,y2); v3=270;x3=t*v3*cos(a);y3=t*v3*sin(a)-0.5*g*t.^2; plot(t,y3);zgsc=[max(y1); max(y2); max(y3)] %三次发射的最高射程 运行结果如下:zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。
MATLAB语言与控制系统仿真_参考题答案_第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MATLAB 绘图的基本知识;2.掌握MATLAB 子图绘制、图形注释、图形编辑等基本方法;3.学会通过MATLAB 绘图解决一些实际问题;4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法;5.学会制作简单的MATLAB 动画。
图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题〔1炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。
)cos()(0αtv t x = %水平方向的行程; 205.0)sin()(gt tv t y -=α %垂直方向的行程;其中,0v 是初速度;g 是重力加速度,为9.82m/s ;t 是时间。
〔2炮弹发射程序举例:分析以下程序以及图3-47各个图形的实际意义。
a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos<a>;y=t*v0*sin<a>-0.5*g*t.^2;subplot<221>;plot<t,x>;grid;title<‘时间-水平位移曲线'>; subplot<222>;plot<t,y>;grid;title<‘时间-垂直位移曲线'>; subplot<223>;plot<x,y>;grid;title<‘水平位移-垂直位移曲线'>; subplot<224>;plot<y,x>;grid;title<‘垂直位移-水平位移曲线'>; 图3-4745角发射曲线 〔3编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程;绘图要求:◆ 标题设为"炮弹垂直发射问题";◆ 在图上通过添加文本的方式表明初速度; ◆ 在x 轴标注"时间";◆ 在y 轴上标注"垂直距离"; ◆ 添加网格线;◆ 将310m/s 的曲线改为线粗为2的红色实线; ◆ 将290m/s 的曲线改为线粗为3的绿色点划线;◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线;a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos<a>;y1=t*v1*sin<a>-0.5*g*t.^2;plot<t,y1>;grid; title<'炮弹垂直发射问题'>; xlabel<'时间'>; ylabel<'垂直距离'>; hold on; v2=290;x2=t*v2*cos<a>;y2=t*v2*sin<a>-0.5*g*t.^2; plot<t,y2>; v3=270;x3=t*v3*cos<a>;y3=t*v3*sin<a>-0.5*g*t.^2; plot<t,y3>;zgsc=[max<y1>; max<y2>; max<y3>] %三次发射的最高射程 运行结果如下: zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。
最新matlab第三章课后部分答案

习题三3-2 从键盘输入一个三位整数,将它反向输出。
如输入639,输出为936程序如下:m=input('请输入一个三位整数:');m1=fix(m/100);%求m的百位整数m2=rem(fix(m/10),10);%求m的十位数字m3=rem(m,10);%求m的个位数字m=m3*100+m2*10+m1%反向输出m3-3 输入一个百分制成绩,要求输出成绩等级A,B,C,D,E。
其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下为E。
要求:(1)分别用if语句和switch语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
程序如下:(1)if语句c=input('请输入成绩:');if c>=90&c<=100disp('A 成绩合理');elseif c>=80&c<=89disp('B 成绩合理');elseif c>=70&c<=79disp('C 成绩合理');elseif c>=60&c<=69disp('D 成绩合理');elseif c<60disp('E 成绩合理');elsedisp('成绩错误');end(2)switch语句c=input('请输入成绩:');switch fix(c)case num2cell(90:100)disp('A 成绩合理');case num2cell(80:89)disp('B 成绩合理');case num2cell(70:79)disp('C 成绩合理');case num2cell(60:69)disp('D 成绩合理');case num2cell(0:59)disp('E 成绩合理');otherwisedisp('成绩错误');end3-4 建立5*6矩阵,要求输出矩阵第N行元素。
matlab程序设计第三章课后习题答案资料

m a t l a b程序设计第三章课后习题答案1. p138 第6题在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。
>> t=0:0.01:pi;>> x1=t;>> y1=2*x1-0.5;>> x2=sin(3*t).*cos(t);>> y2=sin(3*t).*sin(t);>> plot(x1,y1,'r-',x2,y2,'g-')>> axis([-1,2,-1.5,1])>> hold on>> s=solve('y=2*x-0.5','x=sin(3*t)*cos(t)','y=sin(3*t)*sin(t)');>> plot(double(s.x),double(s.y),'*');截图:p366 第4题绘制极坐标曲线,并分析对曲线形状的影响。
function [ output_args ] = Untitled2( input_args )%UNTITLED2 Summary of this function goes here% Detailed explanation goes heretheta=0:0.01:2*pi;a=input('请输入a的值:');b=input('请输入b的值:');n=input('请输入n的值:');rho=a*sin(b+n*theta);polar(theta,rho,'k');end下面以a=1,b=1,n=1的极坐标图形为基础来分析a、b、n的影响。
对a的值进行改变:对比发现a只影响半径值的整倍变化对b的值进行改变:对比发现b的值使这个圆转换了一定的角度对n的值进行改变:对比发现当n>=2时有如下规律1、当n为整数时,图形变为2n个花瓣状的图形2、当n为奇数时,图形变为n个花瓣状的图形分别让n为2、3、4、5同时改变b和n的值,对比发现图形变为2n个花瓣状,并且还旋转了一定角度1 绘制sin(x)曲线,通过句柄修改曲线的颜色,要求:a)生成曲线的同时,获取句柄,再修改颜色;>> x=0:pi/50:2*pi;>> y=sin(x);>> h=plot(x,y)h =174.0101>> set(h,'color','r');截图如下:b)先生成曲线,然后再获取句柄,再完成颜色修改。
MATLAB程序设计与应用 刘卫国第三章作业
(6)从矩阵A提取主对角线元素,并以这些元素构成对角阵B。
MATLAB程序:
2.使用函数,实现方阵左旋90度或者右旋90度的功能。例如,原矩阵为A,A左旋后得到B,右旋后得到C。
MATLAB程序:
3.建立一个方阵A求A的逆矩阵和A的行列式的值,并验证A与B是互逆的。
MATLAB程序:
5.求下列矩阵得主对角线元素,上三角阵,下三角阵,秩,范数,条件数和迹。
(1).MATLAB程序:
(2)MATLAB程序:
6.求矩阵A的特征值和相应的的特征向量。
MATLAB程序:
第三章作业
1.写出完成下列操作的命令。
(1)建立3阶单位矩阵。
MATLAB程序:
(2)建立5 6随即矩阵A,其元素为[100,200]范围内的随机整数。MATL NhomakorabeaB程序:
(3)产生均值为1,方差为0.2的500个正态分布的随机数。
(4)产生和A同样大小的幺矩阵。
MATLAB程序:
(5)将矩阵A的对角线元素加30.
Matlab第三章习题答案

Matlab第三章习题答案第三章3.5计算多项式乘法()()222254x x x x ++++>> a=[1 2 2];>> b=[1 5 4];>> c=conv(a,b)c =1 7 16 18 8poly2sym(c)ans =x^4 + 7*x^3 + 16*x^2 + 18*x + 83.6计算多项式的除法()()3231368/4x x x x ++++ >> a=[3 13 6 8];>> b=[1 4];>> [q r]=deconv(a,b)q =3 1 2r =0 0 0 0>> poly2sym(q)ans =3*x^2 + x + 23.8求多项式4324121459x x x x --++的微分和积分(1)微分:>> a=[4 -12 -14 5 9];>> b=polyder(a)b =16 -36 -28 5>> poly2sym(b)ans =16*x^3 - 36*x^2 - 28*x + 5(2)积分:polyint(a)ans =0.8000 -3.0000 -4.6667 2.5000 9.00000 >> poly2sym(ans)ans =(4*x^5)/5 - 3*x^4 - (14*x^3)/3 + (5*x^2)/2 + 9*x3.9求代数⽅程32349x x x +-+=0的解。
>> [x]=solve('x^3+3*x^2-4*x+9')x =- 7/(3*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 -1/108*108^(1/2)*4703^(1/2))^(1/3) - 17/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 - (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 - 1 7/(6*(15/2 - (108^(1/2)*4703^(1/2))/108)^(1/3)) + (15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)/2 + (3^(1/2)*i*(7/(3*(15/2 -(108^(1/2)*4703^(1/2))/108)^(1/3)) - (15/2 - 1/108*108^(1/2)*4703^(1/2))^(1/3)))/2 – 1 3.10求线性⽅程组223430x xy y x x ?++=??-+=??的解 eqn1='x^2+x*y+y=3';>> eqn2='x^2-4*x+3=0';[x,y]=solve(eqn1,eqn2)x =13y =1-3/23.11求微分⽅程64dy y x dx=+的通解。
MATLAB第三章和第四章作业

习题三1.选择题(1)已知a=4,b='4',下面说法错误的为C 。
A. 变量a比b占用的存储空间大B. 变量a和b可以进行加、减、乘、除运算C. 变量a和b的数据类型相同D. 变量b可以用eval命令执行(2)已知s='显示"hello"',则s的元素个数是B 。
A. 12B. 9C. 7D. 18(3)运行命令>>a=sym('pi','d')则对于变量a的描述D是正确的。
A. a是符号变量B. a显示为10位的数值C. a显示为32位的数值D. a不存在(4)对于符号表达式g=sym('sin(a*z)+cos(w*v)'),如果运行命令diff(g),则求导自变量是D。
A. aB. zC. wD. v(5)运行命令>>a=double(sym('sin(pi/2)')),则变量a是 C。
A. 符号变量B. 字符串'1'C. double型的数值1D. 出错(6)运行命令>>y=dsolve('x*D2y-3*Dy=x^2','t')求解微分方程,则D。
A. Dy是指dy/dxB. 得出的y是通解有一个常数符C1C. D2y是指d2y/dxD. 得出的y是通解有两个常数符C1和C2(7)有一个2行2列的元胞数组c,则c(2)是指C 。
A. 第1行第2列的元素内容B. 第2行第1列的元素内容C. 第1行第2列的元素D. 第2行第1列的元素(8)对于一个2行2列的元胞数组c,如果要删除第二列的元素,应该使用的命令是B 。
A.c{:,2}=[]B.c(:,2)=[]C.A、B两种方式均可D.A、B两种方式均不可(9)有一个3行10列的构架数组student,每个构架有name(姓名)、scores两个字段,其中scores是以1×5数组表示的五门课的成绩,那么要查看第4个学生的第2门课成绩,采用的命令中达不到要求的是。
matlab作业第3章

3-1 编写程序,建立向量N=【1,2,3,4,5】,然后利用向量N产生下列向量:(1)2,4,6,8,10>> N=[1,2,3,4,5];>> 2*Nans =2 4 6 8 10(2)1/2,1,3/2,2,5/2>> 1/4*Nans =0.2500 0.5000 0.7500 1.0000 1.2500(3)1,1/2,1/3,1/4,1/5>> 1./Nans =1.0000 0.5000 0.3333 0.2500 0.2000(4)1,1/4,1/9,1/16,1/25>> 1./(N.*N)ans =1.0000 0.2500 0.1111 0.0625 0.04003-2 从键盘输入一个三位整数,将它反向输入。
如输入639,输出936.x=input('百位');y=input('十位');z=input('个位');a=x*100+y*10+zt=x;x=z;z=t;a=x*100+y*10+z>> f1百位3十位2个位1a =321a =1233-3输入一个百分制成绩,要求输出成绩等级A,B,C,D,E.其中90~100分为A,80~89分为B,70~79分为C,60~69分为D,60分以下的为E。
A='A';B='B';C='C';D='D';E='E';x=input('x=');if x>=90disp (A);elseif x>=80disp(B);elseif x>=70sisp(C);elseif x>=60disp(D);elseif x<60disp(E);end>> f1x=92A>> f1x=65D>> f1x=32E3-6输入20个数,求其中最大数和最小数。
matlab3作业

1.1 b=2; a=[1 0]; sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(1,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); t=0:0.1:3; y=impulse(b,a,t); subplot(1,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81零极点图tI m a g i n a r y A x i s012311.21.41.61.822.22.42.62.83t冲激响应h(t)b=2;a=conv([1 7j],[1 -7j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(1,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); t=0:0.1:3; y=impulse(b,a,t); subplot(1,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')-1-0.500.51-8-6-4-22468零极点图tI m a g i n a r y A x i s0123-0.4-0.3-0.2-0.10.10.20.3t冲激响应h(t)b=2;a=conv([1 0.5+12j],[1 0.5-12j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(2,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); [h,w]=freqs(b,a); subplot(2,2,3);plot(w,abs(h));xlabel('w ');title('幅频特性 '); subplot(2,2,4);plot(w,angle(h));xlabel('w ');title('相频特性 '); t=0:0.1:3; y=impulse(b,a,t); subplot(2,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')-0.8-0.6-0.4-0.20-20-1001020零极点图tI m a g i n a r y A x i s5010000.050.10.150.2w幅频特性50100-4-3-2-10w相频特性0123-0.2-0.100.10.2t冲激响应h(t)b=[2,-2];a=conv([1 3+9j],[1 3-9j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(2,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); [h,w]=freqs(b,a); subplot(2,2,3);plot(w,abs(h));xlabel('w ');title('幅频特性 '); subplot(2,2,4);plot(w,angle(h));xlabel('w ');title('相频特性 '); t=0:0.1:3; y=impulse(b,a,t); subplot(2,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')5010000.10.20.30.4w幅频特性50100-2024w相频特性0123-112t冲激响应h(t)零极点图tI m a g i n a r y A x i s1.5 b=[2,-12];a=conv([1 -3+20j],[1 -3-20j]); sys=tf('s'); sys=tf(b,a); z=roots(b); p=roots(a); subplot(1,2,1); pzmap(p,z); xlabel('t'); title('零极点图'); t=0:0.1:3; y=impulse(b,a,t); subplot(1,2,2);plot(t,y);xlabel('t');title('冲激响应h(t)')零极点图tI m a g i n a r y A x i s0123-1.5-1-0.50.514t冲激响应h(t)02462.1高通滤波器 b= [0 0 1];a=conv([1 85+157j],[1 85-157j]); sys=tf('s'); sys=tf(b,a) p=roots(a); z=roots(b); figure(1)subplot(1,2,1); %零极点图 pzmap(p,z); xlabel('t');title('零极点图'); subplot(1,2,2); %对应的冲激响应h(t) plot(h); xlabel('t');title('冲激响应h(t)'); [H,w]=freqs(b,a); figure(2) %频谱图plot(w,abs(H));xlabel('w');title('频谱图');零极点图tI m a g i n a r y A x i s010203040-112345t冲激响应h(t)-100-500-200-150-100-5050100150200010020030040050060070080090010000.20.40.60.811.21.4w频谱图2.2低通滤波器 b=70* [0 0 1]; a=[1 8 70]; sys=tf('s'); sys=tf(b,a) p=roots(a); z=roots(b);pzmap(p,z); xlabel('t');title('零极点图'); subplot(1,2,2); %对应的冲激响应h(t) plot(h); xlabel('t');title('冲激响应h(t)'); [H,w]=freqs(b,a); figure(2) %频谱图plot(w,abs(H));xlabel('w');title('频谱图'); grid on-4-3-2-10零极点图tI m a g i n a r y A x i s10203040-112345t冲激响应h(t)01020304050607080901000.20.40.60.811.21.4w频谱图。
Matlab 第三章作业

第三章MATLAB符号计算1.创建符号表达式
2.创建符号矩阵
3.分别对矩阵A和矩阵B进行加减乘除和点乘、点除、和点幂运算。
4.执行sym(pi/3)、sym(pi/3,’d’)和sym(‘pi/3’)语句,然后将exp(2)和sin(0.3*pi)代替pi/3分别执行前面3个语句,并观察结果。
5.确定下面个符号表达式的自由符号变量:
6.对式用simple 命令进行化简,并按排版形式显示。
7.已知表达式,,计算当x=1时f的值;计算f和g的复合函数,以及f,g的逆函数。
8.已知表达式,将其转化为多项式系数并将f中的X用5、a代替。
9.符号函数,分别对x、y、c、d进行微分,对y趋向于1求极限。
并计算对X的二次、三次微分,用findsym得出符号变量。
10.符号函数 ,分别对X 、y 进行定积分和不定积分,对y 的定积分区间为(0,1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章作业
第一题:
format long
syms x
c1=int((x^4*(1-x)^4)/(1+x^2),0,1); %符号工具箱int计算
c1=eval(c1); %指令eval一般应用于int后结果较复杂时,进一步求数值解。
f=@(x)(x.^4.*(1-x).^4)./(1+x.^2);
c2=quad(f,0,1); %数值积分指令quad要求积分限为常数
第二题:
format long
f=@(x)((2/sqrt(pi))*exp(-x.^2)); %定义误差函数
for k=0.1:0.1:1.0
c1=quad(f,0,k);
c2=erf(k);
c=abs(c1-c2);
bar(k,c)
hold on
end
第三题:
vp=1578;
f=@(v)((4/sqrt(pi))*((v.^2)/vp^3).*exp((-v.^2)/vp^2));
c1=quad(f,0,vp)
c2=quad(f,0,3.3*vp)
c3=quad(f,3e4,3e8)
结果:c1 =0.427593285448571
c2 =0.999927444001040 在0~3.3间的分子数接近为全部
c3 =3.520658577050803e-151 速度很大的分子数很少
第四题:
clear;
R=1; y=-4:0.11:4; z=-4:0.11:4 ;
the=-0.5*pi : pi/400 : 0.5*pi;
[Y, Z,T]=meshgrid(y,z,the);
r=sqrt(cos(T).^2+Z.^2+(Y-sin(T)).^2);
dv = 1./r ;
v=trapz(dv,3);
[ey,ez]=gradient(-v,0.5);
figure(1)
subplot(2,2,1)
contour(Y(:,:,1),Z(:,:,1),v,10)
subplot(2,2,2)
[SY,SZ]=meshgrid(-4:0.2:4,[0.1,-0.1]);
streamline(Y(:,:,1),Z(:,:,1),ey,ez,SY,SZ); [SY,SZ]=meshgrid([-4:0.2:4],[-0.005,0.005]); streamline(Y(:,:,1),Z(:,:,1),ey,ez,SY,SZ);
R=1; the= 0: pi/20 :2* pi;
x= -0.2:0.11:3; y= -0.2:0.11:3; z= -0.2:0.11:3 ; [X,Y, Z,T]=ndgrid(y,x,z,the);
r=sqrt((X-cos(T)).^2+(Y-sin(T)).^2+Z.^2);
dv = 1./r ;
v=trapz(dv,4);
[ex,ey,ez]=gradient(-v,0.5);
[XX,YY,ZZ]=meshgrid( -0.2:0.11:3);
[SX,SY,SZ]=meshgrid(0:0.5:3, 0:0.5:3, [0.05]); subplot(2,2,3)
Zmin=min(Z(:)); Zmax=max(Z(:));
streamslice(XX,YY,ZZ,ex,ey,ez,[],[],0.01)
subplot(2,2,4)
x=cos(the);y=sin(the);z=zeros(1,length(the)); plot3(x,y,z,'LineWidth',3,'Color','r');
hold on
h1=streamline(XX,YY,ZZ,ex,ey,ez,SX,SY,SZ) ;
h2=copyobj(h1,gca);
rotate(h2,[1,0,0],180,[0 0 0]);
h3=copyobj(allchild(gca),gca);
rotate(h3,[0,1,0],180,[0 0 0]);
view(-28,8)
第五题:
%亥姆霍兹线圈组成
clear all
M0=4*pi*1e-7; %初始化, 给定环半径、电流、图形
I0=5.0; Rh=1;
C0=M0 /(4* pi)* I0;
Nx=21; Ny=21; % 设定观测点网格数
x=linspace(-Rh,Rh,Nx); %设定观测点范围及数组
y=linspace(-Rh,Rh,Ny);
Nh=20; %电流环分段
T0= linspace( 0, 2*pi, Nh+1); % 环的圆周角分段
T1= T0( 1: Nh) ;
yb= Rh* cos( T1);
zb= Rh* sin(T1); % 设置环各段向量的起点坐标yb, zb
T2= T0( 2: Nh+ 1) ;
ye= Rh* cos( T2) ;
ze= Rh* sin( T2) ; %设置环各段向量的终点坐标ye, ze
dlx=0; dly=ye- yb; dlz=ze- zb; % 计算环各段向量dl的三个长度分量
xc=0; yc=( yb+ ye) /2; zc= ( zb+ ze) /2; %计算环各段向量中点的三个坐标分量for i=1:Ny %循环计算各网格点上的B( x, y)值
for j=1:Nx
rx=x(j) - xc; ry= y(i) - yc; rz= 0- zc; %观测点在z= 0平面上
r3= sqrt( rx.^2+ ry.^2+ rz.^2).^3;
dlXr_x=dly.*rz- dlz.*ry; %计算叉乘积dlX r的x 和y的分量
dlXr_y=dlz.*rx- dlx.*rz;
Bx(i,j)=sum(C0*dlXr_x./r3); %把环各段产生的磁场分量累加
By(i,j)=sum(C0*dlXr_y./r3);
end
end
Bax= Bx(:,11:21) + Bx(:,1:11) ;
Bay= By(:,11:21) + By(:,1:11) ;
subplot(1,2,1);
mesh(x(11:21),y,Bax); xlabel(x); ylabel(y) ; % 画出其B分布三维图
subplot(1,2,2);
plot(y,Bax), grid, xlabel(y); ylabel(Bx);。
