PPT-动力学-第12章 动能定理
合集下载
动能 动能定理(精品课件)

4.4
动能 动能定理
向睿
物体由于运 动而具有的能 量叫做动能
动能的大小 跟哪些因素有关?
物体动能的大小与物 体的质量和速度有关
寻找动能的表达式? 重力做功WG
WG EP
重力势能:EP=mgh
弹力做功WF
W弹=-E p
弹性势能:E p
1 kl 2 2
外力做功W
动能表达式?
请同学们推导出恒力F做功的表达式
③ ④
把F、x的表达式代入W =Fx,
可得F做的功: W =ma (v22 -v12 )/2a
⑤
得:
1 1 2 2 W mv m v 2 1 2 2
⑥
1 2 1 2 左边W是合外力所做的功,所以右边的 mv1 和 mv2 2 2
应当是物体在初末两个状态的某种能量,这种能量跟 物体的质量和速度直接相关,它就是物体的动能,用 EK表示,即
1 1 2 2 m v2 m v 从W 1 这个式子可以看出, 2 2
1 2 E K mv 2
物体的动能等于物体质量与 物体速度大小的二次方乘积的 一半。
对动能表达式的理解:
1 2 EK mv 2
1、国际单位:焦耳 1kg· m2/s2=1N· m=1J 2、动能是标量,且只有正值,动能只与物体的速度大小有关,
v=60m/s
s=5.3×102m
v0=0m/s
N
f mg F
v=60m/s
s=5.3×102m
解法一:飞机做匀加速直线运动,受力分析如图所示,
其合力为: F合 F kmg
根据牛顿第二定律得: 由运动学公式得: v
2
① ② ③ ④
F合 ma
v 2as
动能 动能定理
向睿
物体由于运 动而具有的能 量叫做动能
动能的大小 跟哪些因素有关?
物体动能的大小与物 体的质量和速度有关
寻找动能的表达式? 重力做功WG
WG EP
重力势能:EP=mgh
弹力做功WF
W弹=-E p
弹性势能:E p
1 kl 2 2
外力做功W
动能表达式?
请同学们推导出恒力F做功的表达式
③ ④
把F、x的表达式代入W =Fx,
可得F做的功: W =ma (v22 -v12 )/2a
⑤
得:
1 1 2 2 W mv m v 2 1 2 2
⑥
1 2 1 2 左边W是合外力所做的功,所以右边的 mv1 和 mv2 2 2
应当是物体在初末两个状态的某种能量,这种能量跟 物体的质量和速度直接相关,它就是物体的动能,用 EK表示,即
1 1 2 2 m v2 m v 从W 1 这个式子可以看出, 2 2
1 2 E K mv 2
物体的动能等于物体质量与 物体速度大小的二次方乘积的 一半。
对动能表达式的理解:
1 2 EK mv 2
1、国际单位:焦耳 1kg· m2/s2=1N· m=1J 2、动能是标量,且只有正值,动能只与物体的速度大小有关,
v=60m/s
s=5.3×102m
v0=0m/s
N
f mg F
v=60m/s
s=5.3×102m
解法一:飞机做匀加速直线运动,受力分析如图所示,
其合力为: F合 F kmg
根据牛顿第二定律得: 由运动学公式得: v
2
① ② ③ ④
F合 ma
v 2as
第十二章---动能定理

又 Mz(F) = Mz(Ft) = Ft R = Mz
∴力 F的元功为 δW = Mzd x
ω
F
o1 Fz Fr
A
Ft
or y
刚 力体F从作角的功1转为到2时,W12
2 1
M
z
(F
)d
⒋力偶的功
M
M=Fr
δW = Fds+F’ ·0 = Fr d
F ds
d r
F'
即力偶M的元功为
当刚体转过角时,
δW = FR'·drc +MC d
•平面运动刚体上力系的功
W12
M d 2
1
C
C2 C1
FR'
drC
结 平面运动刚体上力系的功等于力系向 论 质心简化所得的力和力偶作功之和。
⒍纯滚动刚体上静滑动摩擦力的功 ω
δW = F'·drD =F ·vD dt=0
• drD----接触点的位移; • D为速度瞬心, vD=0 • 静滑动摩擦力F----阻碍滑
力偶M的功为
δW = Md
W12
Md
0
⒌平面运动刚体上力系的功
• 设刚体在力系F1、F2、…Fn作
用下作平面运动,
在dt内,刚体质心位移drc,转角d ,
则Mi的位移 dri = drC +driC
Fi
dric θ
d
Mi
δWi = Fi ·dri = Fi ·drc + Fi ·driC
drc C
W12
2 1
M C d
C2 C1
FR'
drC
§12-2 质点和质点系动能 与动量比较?
∴力 F的元功为 δW = Mzd x
ω
F
o1 Fz Fr
A
Ft
or y
刚 力体F从作角的功1转为到2时,W12
2 1
M
z
(F
)d
⒋力偶的功
M
M=Fr
δW = Fds+F’ ·0 = Fr d
F ds
d r
F'
即力偶M的元功为
当刚体转过角时,
δW = FR'·drc +MC d
•平面运动刚体上力系的功
W12
M d 2
1
C
C2 C1
FR'
drC
结 平面运动刚体上力系的功等于力系向 论 质心简化所得的力和力偶作功之和。
⒍纯滚动刚体上静滑动摩擦力的功 ω
δW = F'·drD =F ·vD dt=0
• drD----接触点的位移; • D为速度瞬心, vD=0 • 静滑动摩擦力F----阻碍滑
力偶M的功为
δW = Md
W12
Md
0
⒌平面运动刚体上力系的功
• 设刚体在力系F1、F2、…Fn作
用下作平面运动,
在dt内,刚体质心位移drc,转角d ,
则Mi的位移 dri = drC +driC
Fi
dric θ
d
Mi
δWi = Fi ·dri = Fi ·drc + Fi ·driC
drc C
W12
2 1
M C d
C2 C1
FR'
drC
§12-2 质点和质点系动能 与动量比较?
第十二章 动能定理1

(2) 定轴转动刚体的动能
z
T
1 2
mivi2
1 2
miri2 2
1 2
(mi ri 2
)
2
T
1 2
J z2
ri
vi
mi
(3) 平面运动刚体的动能
T
1 2
J P 2
(P 为瞬心)
1 2
(JC
md T
2 )2
1 2
mvC2
1 2
J C 2
d
C P
平面运动刚体的动能,等于随质心平移的动能与绕质心转
动的动能的和。
23
1 (1 ml2 )2
29
1 m( 3 v)2 1 1 ml 2 ( v )2
23
2 12 l sin 60
1 ml 2 2
6
1 ml22
18
2 mv2 9
y
45º 2a
a
x
R
v R
a
T 1 J 2
2
5 ma2 2
12
T 1 J 2
2
1 ( 3 mR2 ) 2
22
3 mR22
2. 弹性力的功
F k(r l0 ) er
W12
A2
F
d
r
A1
A2 A1
k
(r
l0
)
er
d
r
erd r
r
d
r
r
1
d(r r)
2r
dr2 2r
dr
W12
r2 r1
k
(r
l0
)dr
k 2
[(r1
l0
)2
理论力学第十二章 动能定理

解:
2υC ω= = CP l cosθ
υC
T = 0, 1
成 θ 角时
1 1 1 1 2 2 2 T2 = mυC + JCω = m1+ υC 2 2 2 2 3cos θ
1 1 2 l mg (1− sin θ ) = m1+ υ 2 C 2 2 3cos θ
压力角为
20o
M − mraA 1 F 1 x = 0.364 O r M − mraA 1 F 1y = m g − O 1 r
′ = tan 20o ⋅ P′ = 0.364P′ P n t t
F 1 x + P′ = 0 O n
F 1 y + P′− m g = 0 O t 1
研究物块A 研究物块
解:
1 1 3 2 2 2 T = m C + JCω = m C υ υ 2 2 4
重力的功率
ds r r ds r r r ds r P = mg ⋅υ = mg ⋅ τ = m g ⋅τ = m ( −g sinθ ) dt dt dt ds = −mg sinθ dt
例5 已知: 为弹簧原长, 为常力偶 为常力偶. 已知:m,R, k, CA=2R为弹簧原长,M为常力偶 为弹簧原长 无初速度由最低点到达最高点时, 处约束力 处约束力. 求:圆心C无初速度由最低点到达最高点时,O处约束力 圆心 无初速度由最低点到达最高点时
A
其中
利用
1 dh = rdϕ 2 dT = ∑δW dt rα1 α1 aA = ,α2 = 2 2
M
2(2M − mAgr) a A= (2mA + 4m1 + 4m2 + m3 ) r
理论力学课件 第十二章 动能定理

FRO
r1 r2 O
mg
解:取整体为研究对象,受力分析如图所示。 v1
A
v2
B
系统对O点的动量矩为
m1 g
m2 g
LO m1v1r1 m2v2r2 J0 (m1r12 m2r22 JO )
系统所受全部外力对O点的动量矩为
MO (F e ) m1gr1 m2gr2
质点系的动量矩定理为 dLO dt
WFN 0
WF F s fmgs cos 30 8.5 J
WF
1 2
k
(12
2 2
)
100 (0 0.52) 2
12.5 J
W Wi 24.5 0 8.512.5 3.5 J
12.2 质点和质点系的动能
12.2.1 质点的动能
设质量为m的质点,某瞬时的速度为v,则质点质量与其速度平方乘积的
路径无关。若质点下降,重力的功为正;若质点上升,重力的功为负。
对于质点系,重力的功等于各质点的重力功的和,即
上式也可写为
W12 mi g(zi1 zi2) W12 mg(zC1 zC2 )
2.弹力的功
设有一根刚度系数为k,自由长为l0的弹 簧, 一端固定于点O, 另一端与物体相连接,
如图所示。求物体由M1移动到M2过程中,弹 力F所做的功。
W12
M2 M1
(Fx
d
x
Fy
d
y
Fz
d
z)
12.1.3 常见力的功
1.重力的功
z M1 M
mg
设质点M的重力为mg,沿曲线由M1运动到
M2
M2,如图所示。因为重力在三个坐标轴上的
投影分别为Fx=Fy=0,Fz=-mg,故重力的功为
第十二章动能定理

d
若 Mz(F) 是一个常量
F
W M z (F ) d
1
2
r
W M z (F )(2 1 )
假设力偶 M 作用在刚体上:
W Md
1
2
若M 是常量
W M (2 1 )
Part A 动能和功
10 平面运动刚体上力系的功
Fi
取刚体的质心C 为基点,当刚体有无穷 小位移时,任一力Fi作用点 Mi 的位移是:
vB 0.8 2.5 2.0 m/s vB 2.0 BC 2.5rad / s BI 0.8
vB
0.8m
vG G
B
vC
0.8 m
CD
C
vC BCCI 2.5 0.8 2.0m/ s vC 2.0 CD 5rad/s CD 0.4
杆BC 的质心G 的速度
Part A 动能和功
8 作用在平移刚体上的力做功
W
M2
M1
F dr
i C
M2
M1
FR drC 动能和功
9 作用在定轴转动刚体上的力做功
z
F
d 'W F ds F r d M z (F ) d
若存在
2 1
l0
Part B 动能定理
[解]
A
E k1 0
在位置 I, AB 处于水平位置,圆 柱体达到一个最右侧的极限位 置,则有 B=0 并且 vB=0 位置I 时系统的动能
Ek 2 Ek ( AB) 1 1 2 2 m AB vC J C AB 2 2
I II
30
B
l0
Part B 动能定理
理论力学12—动能定理

解:滑块在任一瞬时受力如图。由于 P与N始终垂直于滑块位移,因此,它们 所作的功为零。所以只需计算T 与F的功。 先计算T 的功:
在运动过程中,T 的大小不变,但 方向在变,因此T 的元功为
δWT T cos d x
cos (20 x) (20 x)2 152
因此T在整个过程中所作的功为
T
A
vA2
(
1 2
l)2
2vA
1 2
l
cosj
vA2
1 4
l 22
lvA
cosj
则杆的动能
A
vA
jl
B
A
j
vA vCA vC
vA
B
T
1 2
mvC2
1 2
JC2
1 2
m(vA2
1 4
l 22
lvA
cosj)
1 2
(
1 12
ml2 )2
1 2
m(vA2
1 3
l
2
2
lvA
cosj)
12.3 动能定理
上,有长为b的一段悬挂下垂,如图。初始链条静止,在自 重的作用下运动。求当末端滑离桌面时,链条的速度。
解:链条在初始及终了两状态的动能分 别为
T1 0
T2
1 2
lv22
在运动过程中所有的力所作的功为
l b b
由
W12
gb(l
b)
g(l
b)
1 2
(l
b)
1 2
g(l 2
b2 )
T2 T1 W12
质心转动的动能的和。
牢记均质圆盘在地面上作纯滚动时的动能:
C
vC
在运动过程中,T 的大小不变,但 方向在变,因此T 的元功为
δWT T cos d x
cos (20 x) (20 x)2 152
因此T在整个过程中所作的功为
T
A
vA2
(
1 2
l)2
2vA
1 2
l
cosj
vA2
1 4
l 22
lvA
cosj
则杆的动能
A
vA
jl
B
A
j
vA vCA vC
vA
B
T
1 2
mvC2
1 2
JC2
1 2
m(vA2
1 4
l 22
lvA
cosj)
1 2
(
1 12
ml2 )2
1 2
m(vA2
1 3
l
2
2
lvA
cosj)
12.3 动能定理
上,有长为b的一段悬挂下垂,如图。初始链条静止,在自 重的作用下运动。求当末端滑离桌面时,链条的速度。
解:链条在初始及终了两状态的动能分 别为
T1 0
T2
1 2
lv22
在运动过程中所有的力所作的功为
l b b
由
W12
gb(l
b)
g(l
b)
1 2
(l
b)
1 2
g(l 2
b2 )
T2 T1 W12
质心转动的动能的和。
牢记均质圆盘在地面上作纯滚动时的动能:
C
vC
理论力学第十二章 动能定理

§12-1 力的功
II. 弹性力的功
一端固定的弹簧与一质点M相连接,弹簧的原始长 度为l0,在弹性变形范围内,弹簧弹性力F的大小与其 变形量δ成正比,即
F=kδ
当质点M由M运动时,弹性力的功仍按上式计算,即弹性力的功也 只决定于弹簧初始位置与终了位置的变形量,而与质点的运动轨迹无关。
由于功只有正负值, 不具有方向意义,所 以功是代数量。
§12-1 力的功
II. 变力的功
设质点M在变力F作用下作曲线运动,当质点从M1 沿曲线运动到M2时,力F所做的功的计算可处理为: (1)整个路程细分为无数个微段dS;(2)在微小路程上, 力 F 的 大 小 和 方 向 可 视 为 不 变 ; (3)dr 表 示 相 应 于 dS 的微小位移,当dS足够小时,∣dr∣=dS。根据功的 定义,力F在微小位移dr上所做的功(即元功)为
直角坐标形式为
力F在曲线路程 上所做的功等于该力在各微段的元功之和,即
§12-1 力的功
Ⅲ. 合力的功
合力在任一路程上所做的功等于各分力在同一路程上所作功的代数和。即
常见力的功
I. 重力的功
设有一重力为G的质点,自位置M1沿某曲线运动至M2 ,
上式表明,重力的功等于质点的重量与其起始位置与终了位置 的高度差的乘积,且与质点运动的轨迹形状无关.
第十二章 动能定理
主要研究内容
力的功 功率与机械效率 动能 动能定理
§12-1 力的功
功的概念
功是度量力的作用的一个物理量。它反映的是力在一段路程上对物体作用 的累积效果,其结果是引起物体能量的改变和转化。力的功包含力和路程 两个因素。
I. 常力的功
设有大小和方向都不变的力F作用在物体上,力的 作用点向右作直线运动。则此常力F在位移方向的投 影Fcosα与位移的大小S的乘积称为力F在位移S上所 做的功,用W表示,即 W=S·Fcosa 。可知,当a<90 度时,功W为正值,即力F做正功;当a>90度时,功 W为负值,即力F做负功;当a=90度时,功为零,即 力与物体的运动方向垂直,力不做功。
理论力学-动能定理
刚体的动能
● 定轴转动刚体的动能
刚体以角速度 绕定轴 z 转动时,其上-点的速度
为:
vi ri
因此,定轴转动刚体的动能为
T 1 2
i
mi (ri )2
12(
2
i
miri2 )
1 2
J z
2
其中 J z miri2 为刚体对定轴z的转动惯量。
质点系的动能与刚体的动能
刚体的动能
● 平面运动刚体的动能
M z (F ) F R ——力 F 对轴 z 的矩
于是,力在刚体上由 1 转到 2 时所作的功为
W12
2 1
M
z
(
F
)
d
力的功
作用在刚体上力的功、力偶的功 定轴转动刚体上外力偶的功
若力偶矩矢量为 M ,则力偶所作之功为
W M zd
W12
2 1
M
zd
其中Mz 为力偶矩矢 M 在 z 轴上的投影,即力偶对转轴 z 的矩。
dT dt
P输入
P输出 P损耗
P输入
dT dt
P输出
P损耗
第12章 动能定理
功率方程 、机械效率
任何机器在工作时都需要从外界输入功率,同时也不可避免的 要消耗一些功率,消耗越少则机器性能越好。工程上,定义机械
效率为
P有效
P有用 100%=
dT dt
100% 1
P输入
P输入
其中
P有效
dT dt
止状态。现在圆盘A的质心处加一不计质量的弹簧,弹簧刚 度系数为k 求:系统的等效质量、等效刚度与系统的固有频率。
动能定理及其应用
动能定理应用举例——例 题 4
解:这是一个单自由度振动的刚体 系统,现研究怎样将其简化为弹簧 -质量模型。
● 定轴转动刚体的动能
刚体以角速度 绕定轴 z 转动时,其上-点的速度
为:
vi ri
因此,定轴转动刚体的动能为
T 1 2
i
mi (ri )2
12(
2
i
miri2 )
1 2
J z
2
其中 J z miri2 为刚体对定轴z的转动惯量。
质点系的动能与刚体的动能
刚体的动能
● 平面运动刚体的动能
M z (F ) F R ——力 F 对轴 z 的矩
于是,力在刚体上由 1 转到 2 时所作的功为
W12
2 1
M
z
(
F
)
d
力的功
作用在刚体上力的功、力偶的功 定轴转动刚体上外力偶的功
若力偶矩矢量为 M ,则力偶所作之功为
W M zd
W12
2 1
M
zd
其中Mz 为力偶矩矢 M 在 z 轴上的投影,即力偶对转轴 z 的矩。
dT dt
P输入
P输出 P损耗
P输入
dT dt
P输出
P损耗
第12章 动能定理
功率方程 、机械效率
任何机器在工作时都需要从外界输入功率,同时也不可避免的 要消耗一些功率,消耗越少则机器性能越好。工程上,定义机械
效率为
P有效
P有用 100%=
dT dt
100% 1
P输入
P输入
其中
P有效
dT dt
止状态。现在圆盘A的质心处加一不计质量的弹簧,弹簧刚 度系数为k 求:系统的等效质量、等效刚度与系统的固有频率。
动能定理及其应用
动能定理应用举例——例 题 4
解:这是一个单自由度振动的刚体 系统,现研究怎样将其简化为弹簧 -质量模型。
动能定理(共7张PPT)
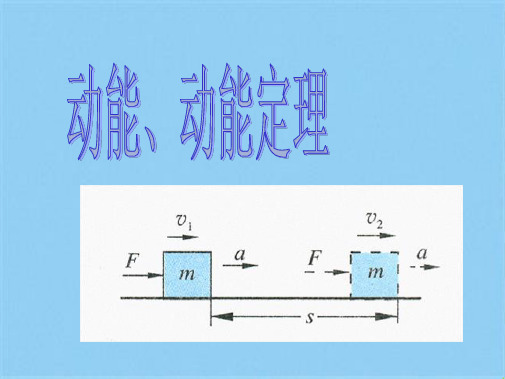
(1)7.5×104N;(2)1.5× ×106W (3)16km
出,物体落地时的速度为13m/s,求物体在运动过程中克服空气
阻力做的功。
11.2J
例2、一架小型喷气式飞机的质量为5×103kg,在跑道上从静止开始滑 行时受到的发动机牵引力为1.8×104N,设运动中的阻力是它所受重力的 0.2倍,飞机离开跑道的起飞速度是60m/s,求飞机在跑道上滑行的距离.(g 取10米/秒2.)
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度 恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才
能到达斜面顶端?
V2 0
4gh
例8、质量为3000t的列车, 在恒定的额定功率下, 由静止开始出发, 运动 过程中受到的阻力大小恒定, 经过1000s速度达到最大行驶速度72km/h. 此时司机发现前方4km处的铁轨被洪水冲毁, 便立即紧急刹车, 结果列车 正好到达铁轨冲毁处停止, 若所加的制动力为7.5×104N. 求:(1) 列车在 行驶过程中所受阻力多大? (2) 列车的额定功率多大? (3) 列车的总行程 多长?
动能定理的解题步骤:
1125m
1、确定研究对象和研究过程
2、确定始末状态的动能
3、写出过程中合力的功或各力做的总功,明确各力做功的正负
4、利用动能定理,写出等式,左边写功(合力的功或各力的总功), 右边写末动能-初动能
例4、(1999广东高考)如图,一弹簧振子,物块的质量为m,它与
水平桌面间的动摩擦因数为μ,起初用手按住物块,弹簧的伸长量为x,
N
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才能到达斜面
出,物体落地时的速度为13m/s,求物体在运动过程中克服空气
阻力做的功。
11.2J
例2、一架小型喷气式飞机的质量为5×103kg,在跑道上从静止开始滑 行时受到的发动机牵引力为1.8×104N,设运动中的阻力是它所受重力的 0.2倍,飞机离开跑道的起飞速度是60m/s,求飞机在跑道上滑行的距离.(g 取10米/秒2.)
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度 恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才
能到达斜面顶端?
V2 0
4gh
例8、质量为3000t的列车, 在恒定的额定功率下, 由静止开始出发, 运动 过程中受到的阻力大小恒定, 经过1000s速度达到最大行驶速度72km/h. 此时司机发现前方4km处的铁轨被洪水冲毁, 便立即紧急刹车, 结果列车 正好到达铁轨冲毁处停止, 若所加的制动力为7.5×104N. 求:(1) 列车在 行驶过程中所受阻力多大? (2) 列车的额定功率多大? (3) 列车的总行程 多长?
动能定理的解题步骤:
1125m
1、确定研究对象和研究过程
2、确定始末状态的动能
3、写出过程中合力的功或各力做的总功,明确各力做功的正负
4、利用动能定理,写出等式,左边写功(合力的功或各力的总功), 右边写末动能-初动能
例4、(1999广东高考)如图,一弹簧振子,物块的质量为m,它与
水平桌面间的动摩擦因数为μ,起初用手按住物块,弹簧的伸长量为x,
N
例7、一个物体从高为h的斜面顶端以初速v0下滑到斜面底端时的速度恰好为0,则使该物体由这个斜面底端至少以多大初速v上滑,才能到达斜面
第十二章 动能定理

③ 作用在纯滚轮上的摩擦力的功 接触点为瞬心,滑动摩擦力 作用点没动,此时滑动摩擦 力也不做功。
W F d rp 0
如果不是纯滚动,有相对滑 动,则摩擦力作负功。
13
§13 - 2 质点和质点系的动能 1 质点的动能
T
2 2
1 2
mv
2
动能是恒正的标量,
单位:
是瞬时量。
2
kg m / s kg m / s m N m J
( mi ri )
2
所以,刚体定轴转动的动能为:
Jz
T
1 2
J z
2
15
(3) 平面运动刚体的动能
设刚体作平面运动,如图。
C
由定轴转动刚体动能的公式
T
1 2
1
J p
2
rc p
2 C
由平行轴定理,有: 所以:
2
J p JC m r
1 2
2 C 2
T J C m r
m2g
2
d T [] 2vB d vB
Wi m3 g d s
2
vB
ds
m3g
d vB ds 两边同除d t,得: []v m3 g B dt dt m3 所以: a g B []
29
例 3
已知:两相同均质杆, m, l , 水平面光滑。初始静 止,高为h。设杆在铅垂 面内落下。 求:铰链D与地面接触时 的速度。
1
FDy
vo
F
m1g
FDx m2g m3g
2
vB
FN
受力如图。 求加速度可用动能定理的微分形式。
计算一般位置的动能
第12章 动能定理

图12-2
1.2 变力的功
这时可将路程 s 分为无限多个微段 ds,则微段路程 ds 可以近似为直线,且力 F 在位移 dr 中
可视为常力,dr 可视为沿点 M 的切线。力 F 在该微小路径上所做的功称为元功,用W 表示,且
有
W F dr
(12-3)
质点 M 沿曲线由 M1 运动到 M2 的过程中,变力 F 做的功为
迹无关。
1.4 几种常见力的功
3.摩擦力的功
如图 12-6 所示,由于质点受到的滑动摩擦力 F μFN 的方向总是与质点运动的方向相反,所 以滑动摩擦力做功恒为负,且有
W M2 Fds M1
M2 M1
μFNds
(12-10)
式(12-10)为曲线积分,因此,滑动摩擦力的功,不仅与起止位置有关,还与路径有关。
图12-6
02
质点和质点系的动能
质点的动能 质点系的动能 刚体的动能
2.1 质点的动能
动能是指物体由于本身的运动而具有的能量。实践表明,物体动能的大小与物体的质量及 运动速度有关。一切做机械运动的物体,质量越大,运动速度越快,其动能也就越大。因此, 动能是度量物体机械运动强度的物理量。
研究表明,质点的动能等于它的质量 m 与速度 v 平方的乘积的一半,即质点的动能为 mv2 /2 。 动能是一个恒为正值的标量。在国际单位制中,动能的单位与功的单位相同,都为 J。
的单位来决定。在国际单位制中,功的单位是 J。
如果路程用矢量 s 表示,则力 F 的功可以写成
W Fs
(12-2)
图12-1
1.2 变力的功
如图 12-2 所示,设质点 M 在变力 F 作用下,沿曲线从位置 M1 运动到位置 M2 ,现求力 F 在 路径 M1M 2 上做的功。由于从 M1 运动到 M2 的过程中,力 F 的大小和方向在不断变化,因此,力 F 的功不能直接用式(12-1)来计算。
1.2 变力的功
这时可将路程 s 分为无限多个微段 ds,则微段路程 ds 可以近似为直线,且力 F 在位移 dr 中
可视为常力,dr 可视为沿点 M 的切线。力 F 在该微小路径上所做的功称为元功,用W 表示,且
有
W F dr
(12-3)
质点 M 沿曲线由 M1 运动到 M2 的过程中,变力 F 做的功为
迹无关。
1.4 几种常见力的功
3.摩擦力的功
如图 12-6 所示,由于质点受到的滑动摩擦力 F μFN 的方向总是与质点运动的方向相反,所 以滑动摩擦力做功恒为负,且有
W M2 Fds M1
M2 M1
μFNds
(12-10)
式(12-10)为曲线积分,因此,滑动摩擦力的功,不仅与起止位置有关,还与路径有关。
图12-6
02
质点和质点系的动能
质点的动能 质点系的动能 刚体的动能
2.1 质点的动能
动能是指物体由于本身的运动而具有的能量。实践表明,物体动能的大小与物体的质量及 运动速度有关。一切做机械运动的物体,质量越大,运动速度越快,其动能也就越大。因此, 动能是度量物体机械运动强度的物理量。
研究表明,质点的动能等于它的质量 m 与速度 v 平方的乘积的一半,即质点的动能为 mv2 /2 。 动能是一个恒为正值的标量。在国际单位制中,动能的单位与功的单位相同,都为 J。
的单位来决定。在国际单位制中,功的单位是 J。
如果路程用矢量 s 表示,则力 F 的功可以写成
W Fs
(12-2)
图12-1
1.2 变力的功
如图 12-2 所示,设质点 M 在变力 F 作用下,沿曲线从位置 M1 运动到位置 M2 ,现求力 F 在 路径 M1M 2 上做的功。由于从 M1 运动到 M2 的过程中,力 F 的大小和方向在不断变化,因此,力 F 的功不能直接用式(12-1)来计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求:切削力F的最大值。 解: P P P 3.78kW 无用 输入 有用
60 60 3.78 F P有用 17.19kN πdn π 0.1 42 当 n 112 r / min 时
60 3.78 F 6.45kN π 0.1 112
d πn P有用 Fv F · 2 30
W12 T2 T1
T1 0
1
vC v , 2 C R1 R2
1 1 1 1 2 2 2 T2 ( m1 R1 )1 m2 v2 ( m2 R2 2 )22 2 2 2 2
vC 2 M m2 gs sin (2 m1 3m2 ) 4 s ( M m2 gR1 sin ) s
W12 mg ( zC1 zC 2 )
重力的功只与始、末位置有关,与路径无关。
2.弹性力的功 弹簧刚度系数k(N/m) 弹性力的功为
W12 F dr A k ( r l0 )er dr
A1
1
A2
A2
er dr
r 1 1 dr d( r r ) d( r 2 ) dr r 2r 2r
T2 T1 W
(a)
6M 12 M 求导得 2 2 ( 2 m 9 m ) l (2m 9m1 )l 1
注意:轮Ⅰ、Ⅱ接触点C是理想约束,其摩擦力Fs尽管在
空间是移动的,但作用于速度瞬心,故不作功.
例12-7
已知:均质杆OB=AB=l, m,在铅垂面内;M=常量,初始静止, 不计摩擦. 求:当A 运动到O点时,
F
C
P FS FN
§12-2
1.质点的动能
质点和质点系的动能
1 2 T mv 2 1 T mi vi 2 2
1 2 T mv 即 C 2
2.质点系的动能
(1)平移刚体的动能
1 1 2 2 T mi vi vC mi 2 2 (2)定轴转动刚体的动能
1 1 1 2 2 2 2 2 T mi vi mi ri mi ri 2 2 2
2 得 W12 r r1 k ( r l0 )dr
即 W k ( 2 2 ) 12 1 2
2
1 r1 l0 , 2 r2 l0
弹性力的功也与路径无关
3. 定轴转动刚物体上作用力的功
δW F dr Ft ds Ft Rd
由
M z Ft R
R1
(a)
vC 2
R1 (2m1 3m2 )
式(a)是函数关系式,两端对t 求导,得
vC 1 (2 m1 3m2 )vC aC M m2 gvC sin 2 R1 2 ( M m2 gR1 sin )
aC (2 m1 3m2 ) R1
例12-4 已知:冲击试验机m=18kg, l=840mm, 杆重不计,在 1 70 时静止释放,冲断试件后摆至 2 29 求:冲断试件需用的能量。
2
T1
(a)
2 ( F 2mgf ) 得 a0 3m
v0 a0 , , r r
例12-6 已知: r1 , m1 均质;杆m 均质, O1O2 =l , M=常量,小轮纯滚动, 大轮静止,处于水平面内,初始静止.
求: O1O2 转过φ角的 ,
O1 , O2
解:
研究整个系统
系在绝对运动中的动能等于它随质心平移的动能与相对于 质心平移坐标系运动的动能之和。
§12-3
1.质点的动能定理
动能定理
dv 将 m F 两端点乘 vdt dr , dt 1 2 mv dv d( mv ), F dr δW 得 mv dv F dr 2 1 2 因此 d( mv ) δW --质点动能定理的微分形式 2
第十二章 动 能 定 理
§12-1 力的功
一、常力在直线运动中的功
W F cos s F s
二、变力在曲线运动中的功
元功
δW F cos ds
δW F dr
F Fx i Fy j Fz k dr dxi dyj dzk
记
W Fx dx Fy dy Fz dz
解:
T1 0, T2 0
0 0 mgl (1 cos 1 )
mgl (1 cos 2 ) Wk
得冲断试件需要的能量为
Wk 78.92J
Wk k A
冲击韧度:衡量材料抵抗冲击能力的指标。
例12-5
已知:均质圆盘R ,m ,F=常量,且很大,使O 向右运动, f 为动摩擦因
vA ?
解:
l W M 2mg (1 cos ) 2 T1 0 vB vB 3 C ABC C l AB AB , OB l l 2
AB OB
v A AB · 2l
1 2 T2 TAB TOB mvC 2 4 1 1 2 2 2 ml 2 AB J C AB J 0 OB
--质点系动能定理的微分形式
dT δWi T2 T1 Wi
质点系动能的增量,等于作用于质点系全部力所作的元功的和. --质点系动能定理的积分形式
质点系在某一段运动过程中,起点和终点的动能改变量,等
于作用于质点系的全部力在这段过程中所作功的和.
3.理想约束及内力的功
光滑固定面、固定铰支座、光滑铰链、不可伸长的柔 索等约束的约束力作功等于零. 为什么? 称约束力作功等于零的约束为理想约束.
1 ml 2 2 1 1 m1r1 2 T2 ( ) m1 01 ( ) 2 2 3 2 2 2
T1 0
2
1 m 3m1 2 2 ( )l 2 3 2
01 l ( 01 l , 1 ) r1 r1
W M
1 m 3m1 2 2 M ( )l 2 3 2
数,初静止。
求:O 走过S 路程时ω, 。
解: 圆盘速度瞬心为C
W Fs 2mgfs W T
3 Fs 2mgfs mv0 2 4
s v0 2 ( F 2mgf ) 3m 将式(a)两端对t 求导,并利用
v0 R T1 0 2 1 1 mR 3 2 2 T2 mv0 ( ) mv0 2 2 2 2 4
即:功率等于切向力与力作用点速度的乘积. 作用在转动刚体上的力的功率为
δW d P Mz M z dt dt 单位W(瓦特),1W=1J/S
2.功率方程
n n δWi dT Pi dt i 1 dt i 1
功率方程:即质点系动能对时间的一阶导数,等于作用于质点 系的所有力的功率的代数和.
max
mg 1 m 2 g 2 2kmgh k k
例12-3 已知:轮O :R1 ,m1 ,质量分布在轮缘上; 均质轮C :R2 , m2 ,纯滚动, 初始静止 ;θ ,M 为常力偶。 求:轮心C 走过路程s 时的速度和加速度
解:
轮C与轮O共同作为一个质点系
W12 M m2 gs sin
对理想约束,在动能定理中只计入主动力的功即可.
内力作功之和不一定等于零.
思考:
当轮子在固定面只滚不滑时,接触处是否为理想约束?
例12-2 已知:m, h, k, 其它质量不计.
求:
max
解:
T1 0, T2 0
k 2 0 0 mg ( h max ) max 2
M2 2 W12 M δ W M1 M 1 F ·dr
三、几种常见力的功 1.重力的功 质点
Fx Fy 0 Fz mg W12 z z mgdz mg ( z1 z 2 )
2 1
质点系
W
由 得
12
mzC mi zi
m i g ( z i1 z i 2 )
质点动能的增量等于作用在质点上力的元功。
1 1 2 mv2 mv12 W12 2 2
--质点动能定理的积分形式
在质点运动的某个过程中,质点动能的改变量等于作用 于质点的力作的功.
2.质点系的动能定理
由 得
1 d( mi vi 2 ) δWi 2
1 2 d( 2mi vi ) δWi
将力系向刚体上任一点简化,一般简化为一个力和一个力
偶。由力系的等效原理,这个力和力偶所作的元功等于力 系中所有力所作元功的和,有
δW δWi FR ' drC M C d
平面运动刚体
δW FR ' drC M C d
当质心由 C1 ~ C2 ,转角由 1
C2
~ 2 时,力系的功为
W1 F R
W2 0
W1 W1 W2 F R
例12-1 已知:均质圆盘R ,m ,F =常量,且很大,使O 向右运动, f , 初静止。 求: O 走过S 路程时力的功。
F
解: 重力,摩擦力,法向约束力都不作功,只有力F作功,
将力F向质心简化,得
W F ' s M C 2 Fs
2
W12 FR drC M C d
C1
1
说明:1.对任何运动的刚体,上述结论都适用;
2.C点不是质心,而是刚体上任意一点时,上述结论也成立
3.计算力系的主矢、主矩时,可以不包含不作功的力。
思考:
W1 F s
W2 0
W1 W1 W2 F s
F 的功为
δW M z d
从角 1转动到角 2 过程中力
60 60 3.78 F P有用 17.19kN πdn π 0.1 42 当 n 112 r / min 时
60 3.78 F 6.45kN π 0.1 112
d πn P有用 Fv F · 2 30
W12 T2 T1
T1 0
1
vC v , 2 C R1 R2
1 1 1 1 2 2 2 T2 ( m1 R1 )1 m2 v2 ( m2 R2 2 )22 2 2 2 2
vC 2 M m2 gs sin (2 m1 3m2 ) 4 s ( M m2 gR1 sin ) s
W12 mg ( zC1 zC 2 )
重力的功只与始、末位置有关,与路径无关。
2.弹性力的功 弹簧刚度系数k(N/m) 弹性力的功为
W12 F dr A k ( r l0 )er dr
A1
1
A2
A2
er dr
r 1 1 dr d( r r ) d( r 2 ) dr r 2r 2r
T2 T1 W
(a)
6M 12 M 求导得 2 2 ( 2 m 9 m ) l (2m 9m1 )l 1
注意:轮Ⅰ、Ⅱ接触点C是理想约束,其摩擦力Fs尽管在
空间是移动的,但作用于速度瞬心,故不作功.
例12-7
已知:均质杆OB=AB=l, m,在铅垂面内;M=常量,初始静止, 不计摩擦. 求:当A 运动到O点时,
F
C
P FS FN
§12-2
1.质点的动能
质点和质点系的动能
1 2 T mv 2 1 T mi vi 2 2
1 2 T mv 即 C 2
2.质点系的动能
(1)平移刚体的动能
1 1 2 2 T mi vi vC mi 2 2 (2)定轴转动刚体的动能
1 1 1 2 2 2 2 2 T mi vi mi ri mi ri 2 2 2
2 得 W12 r r1 k ( r l0 )dr
即 W k ( 2 2 ) 12 1 2
2
1 r1 l0 , 2 r2 l0
弹性力的功也与路径无关
3. 定轴转动刚物体上作用力的功
δW F dr Ft ds Ft Rd
由
M z Ft R
R1
(a)
vC 2
R1 (2m1 3m2 )
式(a)是函数关系式,两端对t 求导,得
vC 1 (2 m1 3m2 )vC aC M m2 gvC sin 2 R1 2 ( M m2 gR1 sin )
aC (2 m1 3m2 ) R1
例12-4 已知:冲击试验机m=18kg, l=840mm, 杆重不计,在 1 70 时静止释放,冲断试件后摆至 2 29 求:冲断试件需用的能量。
2
T1
(a)
2 ( F 2mgf ) 得 a0 3m
v0 a0 , , r r
例12-6 已知: r1 , m1 均质;杆m 均质, O1O2 =l , M=常量,小轮纯滚动, 大轮静止,处于水平面内,初始静止.
求: O1O2 转过φ角的 ,
O1 , O2
解:
研究整个系统
系在绝对运动中的动能等于它随质心平移的动能与相对于 质心平移坐标系运动的动能之和。
§12-3
1.质点的动能定理
动能定理
dv 将 m F 两端点乘 vdt dr , dt 1 2 mv dv d( mv ), F dr δW 得 mv dv F dr 2 1 2 因此 d( mv ) δW --质点动能定理的微分形式 2
第十二章 动 能 定 理
§12-1 力的功
一、常力在直线运动中的功
W F cos s F s
二、变力在曲线运动中的功
元功
δW F cos ds
δW F dr
F Fx i Fy j Fz k dr dxi dyj dzk
记
W Fx dx Fy dy Fz dz
解:
T1 0, T2 0
0 0 mgl (1 cos 1 )
mgl (1 cos 2 ) Wk
得冲断试件需要的能量为
Wk 78.92J
Wk k A
冲击韧度:衡量材料抵抗冲击能力的指标。
例12-5
已知:均质圆盘R ,m ,F=常量,且很大,使O 向右运动, f 为动摩擦因
vA ?
解:
l W M 2mg (1 cos ) 2 T1 0 vB vB 3 C ABC C l AB AB , OB l l 2
AB OB
v A AB · 2l
1 2 T2 TAB TOB mvC 2 4 1 1 2 2 2 ml 2 AB J C AB J 0 OB
--质点系动能定理的微分形式
dT δWi T2 T1 Wi
质点系动能的增量,等于作用于质点系全部力所作的元功的和. --质点系动能定理的积分形式
质点系在某一段运动过程中,起点和终点的动能改变量,等
于作用于质点系的全部力在这段过程中所作功的和.
3.理想约束及内力的功
光滑固定面、固定铰支座、光滑铰链、不可伸长的柔 索等约束的约束力作功等于零. 为什么? 称约束力作功等于零的约束为理想约束.
1 ml 2 2 1 1 m1r1 2 T2 ( ) m1 01 ( ) 2 2 3 2 2 2
T1 0
2
1 m 3m1 2 2 ( )l 2 3 2
01 l ( 01 l , 1 ) r1 r1
W M
1 m 3m1 2 2 M ( )l 2 3 2
数,初静止。
求:O 走过S 路程时ω, 。
解: 圆盘速度瞬心为C
W Fs 2mgfs W T
3 Fs 2mgfs mv0 2 4
s v0 2 ( F 2mgf ) 3m 将式(a)两端对t 求导,并利用
v0 R T1 0 2 1 1 mR 3 2 2 T2 mv0 ( ) mv0 2 2 2 2 4
即:功率等于切向力与力作用点速度的乘积. 作用在转动刚体上的力的功率为
δW d P Mz M z dt dt 单位W(瓦特),1W=1J/S
2.功率方程
n n δWi dT Pi dt i 1 dt i 1
功率方程:即质点系动能对时间的一阶导数,等于作用于质点 系的所有力的功率的代数和.
max
mg 1 m 2 g 2 2kmgh k k
例12-3 已知:轮O :R1 ,m1 ,质量分布在轮缘上; 均质轮C :R2 , m2 ,纯滚动, 初始静止 ;θ ,M 为常力偶。 求:轮心C 走过路程s 时的速度和加速度
解:
轮C与轮O共同作为一个质点系
W12 M m2 gs sin
对理想约束,在动能定理中只计入主动力的功即可.
内力作功之和不一定等于零.
思考:
当轮子在固定面只滚不滑时,接触处是否为理想约束?
例12-2 已知:m, h, k, 其它质量不计.
求:
max
解:
T1 0, T2 0
k 2 0 0 mg ( h max ) max 2
M2 2 W12 M δ W M1 M 1 F ·dr
三、几种常见力的功 1.重力的功 质点
Fx Fy 0 Fz mg W12 z z mgdz mg ( z1 z 2 )
2 1
质点系
W
由 得
12
mzC mi zi
m i g ( z i1 z i 2 )
质点动能的增量等于作用在质点上力的元功。
1 1 2 mv2 mv12 W12 2 2
--质点动能定理的积分形式
在质点运动的某个过程中,质点动能的改变量等于作用 于质点的力作的功.
2.质点系的动能定理
由 得
1 d( mi vi 2 ) δWi 2
1 2 d( 2mi vi ) δWi
将力系向刚体上任一点简化,一般简化为一个力和一个力
偶。由力系的等效原理,这个力和力偶所作的元功等于力 系中所有力所作元功的和,有
δW δWi FR ' drC M C d
平面运动刚体
δW FR ' drC M C d
当质心由 C1 ~ C2 ,转角由 1
C2
~ 2 时,力系的功为
W1 F R
W2 0
W1 W1 W2 F R
例12-1 已知:均质圆盘R ,m ,F =常量,且很大,使O 向右运动, f , 初静止。 求: O 走过S 路程时力的功。
F
解: 重力,摩擦力,法向约束力都不作功,只有力F作功,
将力F向质心简化,得
W F ' s M C 2 Fs
2
W12 FR drC M C d
C1
1
说明:1.对任何运动的刚体,上述结论都适用;
2.C点不是质心,而是刚体上任意一点时,上述结论也成立
3.计算力系的主矢、主矩时,可以不包含不作功的力。
思考:
W1 F s
W2 0
W1 W1 W2 F s
F 的功为
δW M z d
从角 1转动到角 2 过程中力
