初中动点问题题目汇总

合集下载

初中数学动点题试卷及答案

一、选择题（每题5分，共50分）1. 下列关于动点的说法正确的是（）A. 动点在平面直角坐标系中一定沿着直线运动B. 动点的运动轨迹可以是曲线C. 动点的速度和加速度都是不变的D. 动点的位置随时间变化而变化2. 设动点P的坐标为（x，y），则下列关于P点的运动轨迹方程正确的是（）A. x+y=0B. x-y=0C. x^2+y^2=1D. x^2-y^2=13. 一个动点在平面直角坐标系中，从原点出发，先向x轴正方向运动2个单位，然后向y轴负方向运动3个单位，最后向x轴负方向运动4个单位。

则该动点的运动轨迹是（）A. 直线B. 抛物线C. 圆D. 双曲线4. 设动点P的坐标为（x，y），则下列关于P点的运动轨迹方程正确的是（）A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=4然后向y轴负方向运动3个单位，最后向x轴负方向运动4个单位。

则该动点的运动轨迹是（）A. 直线B. 抛物线C. 圆D. 双曲线6. 设动点P的坐标为（x，y），则下列关于P点的运动轨迹方程正确的是（）A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=47. 一个动点在平面直角坐标系中，从原点出发，先向x轴正方向运动2个单位，然后向y轴负方向运动3个单位，最后向x轴负方向运动4个单位。

则该动点的运动轨迹是（）A. 直线B. 抛物线C. 圆D. 双曲线8. 设动点P的坐标为（x，y），则下列关于P点的运动轨迹方程正确的是（）A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=4然后向y轴负方向运动3个单位，最后向x轴负方向运动4个单位。

则该动点的运动轨迹是（）A. 直线B. 抛物线C. 圆D. 双曲线10. 设动点P的坐标为（x，y），则下列关于P点的运动轨迹方程正确的是（）A. x^2+y^2=1B. x^2+y^2=4C. x^2-y^2=1D. x^2-y^2=4二、填空题（每题5分，共50分）1. 动点的运动轨迹可以是（）、（）、（）等。

初二数学动点练习题

初二数学动点练习题1. 直线上的动点问题- 题目：在直线AB上，点C是动点，当点C沿着直线AB移动时，求证∠ACB是一个恒定的角度。

2. 圆上的动点问题- 题目：圆O的半径为5，点P是圆上的动点。

求证：无论点P在圆上如何移动，OP的长度始终为5。

3. 动点与线段的关系- 题目：线段AB的长度为10，点C是线段AB上的动点。

当点C从A向B移动时，求线段AC的长度与线段BC的长度之和是否恒定。

4. 动点与三角形的面积- 题目：三角形ABC的面积为30平方单位，点D是边AB上的动点。

求证：无论点D在AB上如何移动，三角形ACD的面积始终是三角形ABC面积的一半。

5. 动点与平行四边形的对角线- 题目：平行四边形ABCD中，点E是边AB上的动点，点F是边CD 上的动点，且EF始终是平行四边形的对角线。

求证：无论点E和点F如何移动，EF的长度始终等于AB和CD的长度之和。

6. 动点与圆的切线- 题目：圆O的半径为6，点P是圆O外的一点，点Q是圆O上的动点。

当点Q沿着圆O移动时，求证：点P到圆O的切线长度始终等于点P到点Q的距离。

7. 动点与相似三角形- 题目：三角形ABC与三角形DEF相似，点G是三角形ABC的动点，点H是三角形DEF的动点，且GH始终是三角形ABC和三角形DEF的对应边的平行线。

求证：无论点G和点H如何移动，三角形AGH与三角形DEF始终相似。

8. 动点与坐标系- 题目：在平面直角坐标系中，点A的坐标为(2,3)，点B的坐标为(5,6)。

点C是线段AB上的动点，其坐标为(x,y)。

求证：无论点C如何移动，x和y的和始终等于点A和点B坐标的和。

练习题答案提示：- 对于直线上的动点问题，可以利用角度的恒定性，结合直线的性质来证明。

- 对于圆上的动点问题，可以利用圆的半径性质来证明。

- 对于动点与线段的关系问题，可以利用线段长度的加法性质来证明。

- 对于动点与三角形的面积问题，可以利用三角形面积的计算公式来证明。

八年级数学动点题型归纳

八年级数学动点题型归纳一、动点与三角形相关题型1. 动点在三角形边上运动求线段长度或周长题目：在等腰三角形公式中，公式，公式，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，设运动时间为公式秒。

当公式时，求公式的长度。

解析：过点公式作公式于点公式。

因为公式，等腰三角形三线合一，所以公式。

在公式中，根据勾股定理公式。

当公式时，公式，则公式。

在公式中，根据勾股定理公式。

2. 动点运动过程中三角形面积的变化题目：在公式中，公式，公式，公式，点公式从点公式出发，沿公式向点公式以每秒公式个单位长度的速度运动，同时点公式从点公式出发，沿公式向点公式以每秒公式个单位长度的速度运动，设运动时间为公式秒公式，求公式的面积公式与公式的函数关系式。

解析：已知公式，则公式，公式。

根据三角形面积公式公式，对于公式，底为公式，高为公式。

所以公式。

二、动点与四边形相关题型1. 动点在四边形边上运动判断四边形形状题目：在矩形公式中，公式，公式，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，设运动时间为公式秒。

当公式时，四边形公式是什么四边形？解析：当公式时，公式，公式。

因为四边形公式是矩形，所以公式，公式。

则公式，公式。

在四边形公式中，公式（因为公式），公式，公式（此时公式运动到公式点），公式。

因为公式且公式，所以四边形公式是梯形。

2. 动点运动过程中四边形面积的变化题目：在平行四边形公式中，公式，公式，公式，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，设运动时间为公式秒。

求四边形公式的面积公式与公式的函数关系式。

解析：四边形公式的面积公式。

过点公式作公式于点公式，在公式中，公式，公式，则公式，公式。

所以公式。

因为公式，则公式。

公式。

所以公式。

三、动点与函数图象相关题型1. 根据动点运动情况确定函数图象题目：如图，在边长为公式的正方形公式中，点公式以每秒公式个单位长度的速度从点公式出发，沿公式的路径运动，到点公式停止。

初一动点问题题目

初一动点问题题目主要涉及数轴、方程、几何等知识点。

下面是一些具体的题目例子：
1. 数轴动点问题：在数轴上，点A表示的数为3，点B表示的数为9。

点P是数轴上的一点，表示的数为x。

当点P在点A和点B之间移动时，求线段AP和线段BP的长度。

2. 方程动点问题：已知一次函数y = kx + b的图像上，点A的横坐标为2，纵坐标为6；点B 的横坐标为4，纵坐标为10。

求k和b的值。

3. 几何动点问题：在平面直角坐标系中，点A的坐标为(2, 3)，点B的坐标为(8, 7)。

点P是坐标系上的一点，坐标为(x, y)。

当点P在直线AB上移动时，求线段AP和线段PB的长度。

4. 三角形动点问题：在平面直角坐标系中，点A的坐标为(0, 0)，点B的坐标为(6, 0)，点C 的坐标为(3, 4)。

点P是坐标系上的一点，坐标为(x, y)。

当点P在三角形ABC内部移动时，求线段AP、线段BP和线段CP的长度。

5. 圆形动点问题：在平面直角坐标系中，圆心O的坐标为(0, 0)，半径为5。

点P是坐标系上的一点，坐标为(x, y)。

当点P在圆内部移动时，求线段OP的长度。

以上是一些初一动点问题的题目例子，涉及数轴、方程、几何等知识点。

在解决这些题目时，学生需要掌握数轴的概念、一次函数的性质、几何图形的特点等，并能灵活运用所学的知识。

通过不断的练习，学生能够提高解题能力，培养逻辑思维和空间想象能力。

初一年级数学动点问题例题集

初一数学动点问题集锦1、如图,已知中,厘米,厘米,点为的中点.(1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,与就是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使与全等？(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿三边运动,求经过多长时间点P 与点Q 第一次在的哪条边上相遇？解:(1)①∵秒,∴厘米, ∵厘米,点为的中点,∴厘米.又∵厘米, ∴厘米,∴. 又∵, ∴,∴. (4分)②∵, ∴,又∵,,则,∴点,点运动的时间秒,AQDB∴厘米/秒. (7分) (2)设经过秒后点与点第一次相遇,由题意,得,解得秒.∴点共运动了厘米.∵,∴点、点在边上相遇,∴经过秒点与点第一次在边上相遇. (12分)2、直线与坐标轴分别交于两点,动点同时从点出发,同时到达点,运动停止.点沿线段运动,速度为每秒1个单位长度,点沿路线→→运动. (1)直接写出两点的坐标;(2)设点的运动时间为秒,的面积为,求出与之间的函数关系式;(3)当时,求出点的坐标,并直接写出以点为顶点的平行四边形的第四个顶点的坐标.解(1)A(8,0)B(0,6)1分xAOQPBy(2)点由到的时间就是(秒)点的速度就是(单位/秒) 1分当在线段上运动(或0)时,1分当在线段上运动(或)时,, 如图,作于点,由,得, 1分1分(自变量取值范围写对给1分,否则不给分.)(3)1分3分3如图,在平面直角坐标系中,直线l:y=－2x－8分别与x轴,y轴相交于A,B 两点,点P(0,k)就是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P、(1)连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点与圆心P为顶点的三角形就是正三角形？解:(1)⊙P与x轴相切、∵直线y=－2x－8与x轴交于A(4,0),与y轴交于B(0,－8),∴OA=4,OB=8、由题意,OP=－k,∴PB=PA=8+k、在Rt△AOP中,k2+42=(8+k)2,∴k=－3,∴OP等于⊙P的半径,∴⊙P与x轴相切、(2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E、∵△PCD为正三角形,∴DE=CD=,PD=3,∴PE=、∵∠AOB=∠PEB=90°, ∠ABO=∠PBE,∴△AOB∽△PEB,∴,∴∴,∴,∴、当圆心P在线段OB延长线上时,同理可得P(0,－－8),∴k=－－8,∴当k=－8或k=－－8时,以⊙P与直线l的两个交点与圆心P为顶点的三角形就是正三角形、4 如图1,在平面直角坐标系中,点O就是坐标原点,四边形ABCO就是菱形,点A的坐标为(－3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的解析式;(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位／秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.解:BEQDA C图165在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间就是t秒(t＞0).(1)当t = 2时,AP = ,点Q 到AC 的距离就是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与 t 的函数关系式;(不必写出t 的取值范围)(3)在点E 从B 向C 运动的过程中,四边形QBED 能否成为直角梯形？若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接写出t 的值.解:(1)1,;(2)作QF ⊥AC 于点F,如图3, AQ = CP= t,∴.由△AQF ∽△ABC,,得.∴.∴,即.(3)能.①当DE ∥QB 时,如图4.∵DE ⊥PQ,∴PQ ⊥QB,四边形QBED 就是直角梯形. 此时∠AQP=90°. 由△APQ ∽△ABC,得,即. 解得.②如图5,当PQ ∥BC 时,DE ⊥BC,四边形QBED 就是直角梯形. 此时∠APQ =90°. 由△AQP ∽△ABC,得,即. 解得.(4)或.A CBPQED图4初一年级数学动点问题例题集①点P 由C 向A 运动,DE 经过点C. 连接QC,作QG ⊥BC 于点G,如图 6.,.由,得,解得.②点P 由A 向C 运动,DE 经过点C,如图7.,】6如图,在中,,.点就是的中点,过点的直线从与重合的位置开始,绕点作逆时针旋转,交边于点.过点作交直线于点,设直线的旋转角为.(1)①当度时,四边形就是等腰梯形,此时的长为 ; ②当度时,四边形就是直角梯形,此时的长为 ;(2)当时,判断四边形就是否为菱形,并说明理由.解(1)①30,1;②60,1、5; ……………………4分 (2)当∠α=900时,四边形EDBC 就是菱形、 ∵∠α=∠ACB=900,∴BC//ED 、∵CE//AB, ∴四边形EDBC 就是平行四边形、 ……………………6分在Rt △ABC 中,∠ACB=900,∠B=600,BC=2, ∴∠A=300、∴AB=4,AC=2、∴AC (E ) BPQD图6GA C (E )B PQD图7GO E CB DAlOCA(备用图)AO== 、 ……………………8分在Rt △AOD 中,∠A=300,∴AD=2、 ∴BD=2、 ∴BD=BC 、又∵四边形EDBC 就是平行四边形,∴四边形EDBC 就是菱形 ……………………10分7如图,在梯形中,动点从点出发沿线段以每秒2个单位长度的速度向终点运动;动点同时从点出发沿线段以每秒1个单位长度的速度向终点运动.设运动的时间为秒.(1)求的长.(2)当时,求的值.(3)试探究:为何值时,为等腰三角形. 解:(1)如图①,过、分别作于,于,则四边形就是矩形 ∴1分在中,2分在中,由勾股定理得,∴ 3分ADCBN(图①)ADCBK H(图②)ADCBG MN(2)如图②,过作交于点,则四边形就是平行四边形∵ ∴ ∴ ∴4分由题意知,当、运动到秒时,∵∴又∴∴ 5分即解得, 6分(3)分三种情况讨论: ①当时,如图③,即∴ 7分ADCBMN(图③)(图④)AD CBM NH E②当时,如图④,过作于解法一:由等腰三角形三线合一性质得在中,又在中,∴解得 8分解法二: ∵∴∴即∴ 8分③当时,如图⑤,过作于点、解法一:(方法同②中解法一)(图⑤)ADCBH N MF解得解法二:∵∴∴即∴综上所述,当、或时,为等腰三角形9分8如图1,在等腰梯形中,,就是的中点,过点作交于点.,、(1)求点到的距离;(2)点为线段上的一个动点,过作交于点,过作交折线于点,连结,设、①当点在线段上时(如图2),的形状就是否发生改变？若不变,求出的周长;若改变,请说明理由;②当点在线段上时(如图3),就是否存在点,使为等腰三角形？若存在,请求出所有满足要求的的值;若不存在,请说明理由、初一年级数学动点问题例题集解(1)如图1,过点作于点1分∵为的中点,∴在中,∴2分∴即点到的距离为 3分 (2)①当点在线段上运动时,的形状不发生改变. ∵∴∵∴,同理 4分如图2,过点作于,∵∴∴A D EB FC 图4(备用) ADE BF C 图5(备用) A D E BF C 图1 图2 AD E B F C P NM图3 A D E BFCP N M (第25题) 图1A D EBF CG图2A D EBFCPNMG H∴则在中,∴的周长=6分②当点在线段上运动时,的形状发生改变,但恒为等边三角形.当时,如图3,作于,则类似①, ∴ 7分∵就是等边三角形,∴此时,8分当时,如图4,这时此时,当时,如图5,则又∴图3A D E BFCPN M 图4A D EBF CP M N 图5A D EBF (P ) CMN GGRG因此点与重合,为直角三角形.∴此时,综上所述,当或4或时,为等腰三角形. 10分 9如图①,正方形 ABCD 中,点A 、B 的坐标分别为(0,10),(8,4),点C 在第一象限.动点P 在正方形 ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴正半轴上运动,当P 点到达D 点时,两点同时停止运动,设运动的时间为t 秒.(1)当P 点在边AB 上运动时,点Q 的横坐标(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q 开始运动时的坐标及点P 运动速度;(2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标; (4)如果点P 、Q 保持原速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由.解:(1)(1,0)1分点P 运动速度每秒钟1个单位长度. 2分(2) 过点作BF ⊥y 轴于点,⊥轴于点,则＝8,.∴. 在Rt △AFB 中, 3 过点作⊥轴于点,与的延长线交于点.∵ ∴△ABF ≌△BCH.∴.∴.∴所求C 点的坐标为(14,12). 4分AB CDEF G H M N PQOxy(3) 过点P作PM⊥y轴于点M,PN ⊥轴于点N,则△APM∽△ABF.∴. .∴. ∴.设△OPQ 的面积为(平方单位)∴(0≤≤10) 5分说明:未注明自变量的取值范围不扣分.∵<0 ∴当时, △OPQ的面积最大. 6分此时P的坐标为(,) . 7分(4) 当或时, OP与PQ相等. 9分10数学课上,张老师出示了问题:如图1,四边形ABCD就是正方形,点E就是边BC的中点.,且EF 交正方形外角的平行线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证,所以.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E就是边BC的中点”改为“点E就是边BC 上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,您认为小颖的观点正确不？如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E就是BC的延长线上(除C点外)的任意一点,其她条件不变,结论“AE=EF”仍然成立.您认为小华的观点正确不？如果正确,写出证明过程;如果不正确,请说明理由.A DFC GEB图1 A DFC GEB图2A DFC GEB图3解:(1)正确. (1分) 证明:在上取一点,使,连接. (2分).,.就是外角平分线,, . .,,.(ASA). (5分).(6分)(2)正确. (7分) 证明:在的延长线上取一点.使,连接. (8分)..四边形就是正方形,.. .(ASA). (10分).(11分)11已知一个直角三角形纸片,其中.如图,A DF C GEBM ADFC GE BN将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边交于点,与边交于点.(Ⅰ)若折叠后使点与点重合,求点的坐标;(Ⅱ)若折叠后点落在边上的点为,设,,试写出关于的函数解析式,并确定的取值范围;(Ⅲ)若折叠后点落在边上的点为,且使,求此时点的坐标.解(Ⅰ)如图①,折叠后点与点重合,则、设点的坐标为、则、于就是、在中,由勾股定理,得,即,解得、点的坐标为、 4分(Ⅱ)如图②,折叠后点落在边上的点为,y BO Ay BOAyBO A则、由题设,则,在中,由勾股定理,得、,即6分由点在边上,有,解析式为所求、当时,随的增大而减小,的取值范围为、7分(Ⅲ)如图③,折叠后点落在边上的点为,且、则、又,有、、有,得、 9分在中,设,则、由(Ⅱ)的结论,得,解得、点的坐标为、 10分 12问题解决如图(1),将正方形纸片折叠,使点落在边上一点(不与点,重合),压平后得到折痕.当时,求的值.类比归纳在图(1)中,若则的值等于 ;若则的值等于 ;若(为整数),则的值等于 .(用含的式子表示)联系拓广如图(2),将矩形纸片折叠,使点落在边上一点(不与点重合),压平后得到折痕设则的值等于 .(用含的式子表示)解:方法一:如图(1-1),连接.方法指导: 为了求得的值,可先求、的长,不妨设:=2图(2)N ABCD EFM图(1)A BCDEFMN N 图(1-1)A BCDEFM由题设,得四边形与四边形关于直线对称.∴垂直平分.∴1分 ∵四边形就是正方形,∴∵设则在中,.∴解得,即 3分在与在中,, , 5分设则∴解得即 6分∴ 7分方法二:同方法一, 3分如图(1－2),过点做交于点,连接N 图(1-2)A BCDEFMG∵∴四边形就是平行四边形.∴同理,四边形也就是平行四边形.∴∵与中∴５分∵6分∴7分类比归纳(或);; 10分联系拓广12分。

中考动点问题经典题型归类总结附答案

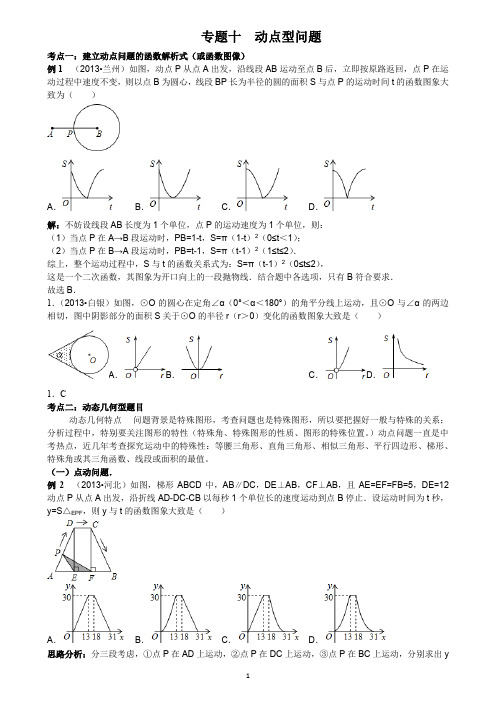
专题十动点型问题考点一：建立动点问题的函数解析式（或函数图像）例1 （2013•兰州）如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为（）A．B．C．D．解：不妨设线段AB长度为1个单位，点P的运动速度为1个单位，则：（1）当点P在A→B段运动时，PB=1-t，S=π（1-t）2（0≤t＜1）；（2）当点P在B→A段运动时，PB=t-1，S=π（t-1）2（1≤t≤2）．综上，整个运动过程中，S与t的函数关系式为：S=π（t-1）2（0≤t≤2），这是一个二次函数，其图象为开口向上的一段抛物线．结合题中各选项，只有B符合要求．故选B．1．（2013•白银）如图，⊙O的圆心在定角∠α（0°＜α＜180°）的角平分线上运动，且⊙O与∠α的两边相切，图中阴影部分的面积S关于⊙O的半径r（r＞0）变化的函数图象大致是（）A．B．C．D．1．C考点二：动态几何型题目动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

（一）点动问题．例2 （2013•河北）如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止．设运动时间为t秒，y=S△EPF，则y与t的函数图象大致是（）A．B．C．D．思路分析：分三段考虑，①点P在AD上运动，②点P在DC上运动，③点P在BC上运动，分别求出y与t 的函数表达式，继而可得出函数图象．解：在Rt △ADE 中，AD=2213AE DE +=，在Rt △CFB 中，BC=2213BF CF +=，①点P 在AD 上运动：对应训练2．（2013•北京）如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2．设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（）A ．B ．C ．D ．2．A（二）线动问题例3 （2013•荆门）如右图所示，已知等腰梯形ABCD ，AD ∥BC ，若动直线l 垂直于BC ，且向右平移，设扫过的阴影部分的面积为S ，BP 为x ，则S 关于x 的函数图象大致是（）A．B．C．D．解：①当直线l经过BA段时，阴影部分的面积越来越大，并且增大的速度越来越快；②直线l经过DC段时，阴影部分的面积越来越大，并且增大的速度保持不变；③直线l经过DC段时，阴影部分的面积越来越大，并且增大的速度越来越小；结合选项可得，A选项的图象符合．故选A．对应训练3．（2013•永州）如图所示，在矩形ABCD中，垂直于对角线BD的直线l，从点B开始沿着线段BD匀速平移到D．设直线l被矩形所截线段EF的长度为y，运动时间为t，则y关于t的函数的大致图象是（）A．B．C．D．3．A（三）面动问题例4 （2013•牡丹江）如图所示：边长分别为1和2的两个正方形，其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内去掉小正方形后的面积为s，那么s与t的大致图象应为（）A．B．C．D．解：根据题意，设小正方形运动的速度为V，分三个阶段；①小正方形向右未完全穿入大正方形，S=2×2-Vt×1=4-Vt，②小正方形穿入大正方形但未穿出大正方形，S=2×2-1×1=3，③小正方形穿出大正方形，S=Vt×1，分析选项可得，A符合；故选A．对应训练4．（2013•衡阳）如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t，正方形除去圆部分的面积为S（阴影部分），则S与t的大致图象为（）A．B．C．D．4．A究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．（4）△QMN 为等腰三角形的情形有两种，需要分类讨论，避免漏解．解：（1）∵C （7，4），AB ∥CD ，∴D （0，4）．∵sin ∠DAB=22， ∴∠DAB=45°，∴OA=OD=4，∴A （-4，0）．设直线l 的解析式为：y=kx+b ，则有4-40b k b =⎧⎨+=⎩，解得：k=1，b=4，∴y=x+4．∴点A 坐标为（-4，0），直线l 的解析式为：y=x+4．（2）在点P 、Q 运动的过程中：①当0＜t≤1时，如答图1所示：过点C 作CF ⊥x 轴于点F ，则CF=4，BF=3，由勾股定理得BC=5．过点Q 作QE ⊥x 轴于点E ，则BE=BQ•cos ∠CBF=5t•35=3t ． ∴PE=PB -BE=（14-2t ）-3t=14-5t ，S=12PM•PE=12×2t×（14-5t ）=-5t 2+14t ； ②当1＜t≤2时，如答图2所示：过点C、Q分别作x轴的垂线，垂足分别为F，E，则CQ=5t-5，PE=AF-AP-EF=11-2t-（5t-5）=16-7t，S=12PM•PE=12×2t×（16-7t）=-7t2+16t；③当点M与点Q相遇时，DM+CQ=CD=7，即（2t-4）+（5t-5）=7，解得t=167．当2＜t＜167时，如答图3所示：MQ=CD-DM-CQ=7-（2t-4）-（5t-5）=16-7t，S=12PM•MQ=12×4×（16-7t）=-14t+32．（3）①当0＜t≤1时，S=-5t2+14t=-5（t-75）2+495，∵a=-5＜0，抛物线开口向下，对称轴为直线t=75，∴当0＜t≤1时，S随t的增大而增大，∴当t=1时，S有最大值，最大值为9；②当1＜t≤2时，S=-7t2+16t=-7（t-87）2+647，∵a=-7＜0，抛物线开口向下，对称轴为直线t=87，∴当t=87时，S有最大值，最大值为647；③当2＜t＜167时，S=-14t+32∵k=-14＜0，∴S随t的增大而减小．又∵当t=2时，S=4；当t=167时，S=0，∴0＜S＜4．综上所述，当t=87时，S有最大值，最大值为647．（4）△QMN为等腰三角形，有两种情形：①如答图4所示，点M在线段CD上，MQ=CD-DM-CQ=7-（2t-4）-（5t-5）=16-7t，MN=DM=2t-4，由MN=MQ，得16-7t=2t-4，解得t=209；②如答图5所示，当点M运动到C点，同时当Q刚好运动至终点D，此时△QMN为等腰三角形，t=125．故当t=209或t=125时，△QMN为等腰三角形．对应训练5．（2013•长春）如图①，在▱ABCD中，AB=13，BC=50，BC边上的高为12．点P从点B出发，沿B-A-D-A 运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A运动时的速度为每秒8个单位长度．点Q从点B出发沿BC方向运动，速度为每秒5个单位长度．P、Q两点同时出发，当点Q到达点C时，P、Q 两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）．（2）连结AQ，在点P沿B-A-D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式．（3）过点Q作QR∥AB，交AD于点R，连结BR，如图②．在点P沿B-A-D运动过程中，当线段PQ 扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值．（4）设点C、D关于直线PQ的对称点分别为C′、D′，直接写出C′D′∥BC时t的值．5．解：（1）当点P沿A-D运动时，AP=8（t-1）=8t-8．当0＜t＜1时，如图①．作过点Q作QE⊥AB于点E．S△ABQ=12AB•QE=12BQ×12，4当0＜t≤1时，如图③．∵S △BPM =S △BQM ，∴PM=QM ．∵AB ∥QR ，∴∠PBM=∠QRM ，∠BPM=∠MQR ，在△BPM 和△RQM 中PBM QRMBPM MQR PM QM∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BPM ≌△RQM ．∴BP=RQ ，∵RQ=AB ，∴BP=AB∴13t=13，解得：t=1当1＜t≤83时，如图④．∵BR 平分阴影部分面积，∴P 与点R 重合．34∵S△ABR=S△QBR，∴S△ABR＜S四边形BQPR．∴BR不能把四边形ABQP分成面积相等的两部分．综上所述，当t=1或83时，线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分．（4）如图⑥，当P在A-D之间或D-A之间时，C′D′在BC上方且C′D′∥BC时，∴∠C′OQ=∠OQC．∵△C′OQ≌△COQ，∴∠C′OQ=∠COQ，∴∠CQO=∠COQ，∴QC=OC，∴50-5t=50-8（t-1）+13，或50-5t=8（t-1）-50+13，解得：t=7或t=95 13．当P在A-D之间或D-A之间，C′D′在BC下方且C′D′∥BC时，如图⑦．同理由菱形的性质可以得出：OD=PD，∴50-5t+13=8（t-1）-50，解得：t=121 13．∴当t=7，t=9513，t=12113时，点C、D关于直线PQ的对称点分别为C′、D′，且C′D′∥BC．中考真题演练一、选择题1．（2013•新疆）如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E 以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为（）A．2B．2.5或3.5C．3.5或4.5D．2或3.5或4.51．D2．（2013•安徽）图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是（）A．当x=3时，EC＜EMB．当y=9时，EC＞EMC．当x增大时，EC•CF的值增大D．当y增大时，BE•DF的值不变2．D3．（2013•盘锦）如图，将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合．正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动，当点A和点E重合时正方形停止运动．设正方形的运动时间为t秒，正方形ABCD与Rt△GEF重叠部分面积为s，则s关于t的函数图象为（）A．B．C．D．3．B4．（2013•龙岩）如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是（）A．2B．3C．4D．54．B5．（2013•武汉）如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是．516、如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE．连接DE，DF，EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE不可能为正方形，③DE长度的最小值为4；④四边形CDFE的面积保持不变；⑤△CDE面积的最大值为8．其中正确的结论是（）A、①②③B、①④⑤（3）若⊙P与线段QC只有一个交点，请直接写出t的取值范围．6．解：（1）∵A（8，0），B（0，6），8．（2013•宜昌）半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上．（1）过点B作的一条切线BE，E为切点．①填空：如图1，当点A在⊙O上时，∠EBA的度数是；②如图2，当E，A，D三点在同一直线上时，求线段OA的长；（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF 重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．7．解：（1）①∵半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，当点A在⊙O如图，过O 点作OK ⊥MN 于K ，∴∠MON=2∠NOK ，MN=2NK ，在Rt △ONK 中，sin ∠NOK=2NK NK ON =， ∴∠NOK 随NK 的增大而增大，∴∠MON 随MN 的增大而增大，∴当MN 最大时∠MON 最大，当MN 最小时∠MON 最小，①当N ，M ，A 分别与D ，B ，O 重合时，MN 最大，MN=BD ，∠MON=∠BOD=90°，S 扇形MON 最大=π（cm 2），②当MN=DC=2时，MN 最小，∴ON=MN=OM ，∴∠NOM=60°，S 扇形MON 最小=23π（cm 2）， ∴23π≤S 扇形MON ≤π．故答案为：30°．9．（2013•重庆）已知：如图①，在平行四边形ABCD 中，AB=12，BC=6，AD ⊥BD ．以AD 为斜边在平8．解：（1）∵四边形ABCD是平行四边形，∴AD=BC=6．在Rt△ADE中，AD=6，∠EAD=30°，∴AE=AD•cos30°=33，DE=AD•sin30°=3，∴△AED的周长为：6+33+3=9+33．（2）在△AED向右平移的过程中：（I）当0≤t≤1.5时，如答图1所示，此时重叠部分为△D0NK．∵DD0=2t，∴ND0=DD0•sin30°=t，NK=ND0•tan30°=3t，∴S=S△D0NK=12ND0•NK=12t•3t=32t2；（II）当1.5＜t≤4.5时，如答图2所示，此时重叠部分为四边形D0E0KN．∵AA0=2t，∴A0B=AB-AA0=12-2t，∴A0N=12A0B=6-t，NK=A0N•tan30°=33（6-t）．∴S=S四边形D0E0KN=S△ADE-S△A0NK=12×3×33-12×（6-t）×33（6-t）=-36t2+23t-332；（III）当4.5＜t≤6时，如答图3所示，此时重叠部分为五边形D0IJKN．∵AA 0=2t，∴A0B=AB-AA0=12-2t=D0C，∴A0N=12A0B=6-t，D0N=6-（6-t）=t，BN=A0B•cos30°=3（6-t）；易知CI=BJ=A0B=D0C=12-2t，∴BI=BC-CI=2t-6，S=S梯形BND0I-S△BKJ=12[t+（2t-6）]• 3（6-t）-12•（12-2t）•33（12-2t）=-1336t2+203t-423．综上所述，S与t之间的函数关系式为：S=2223(0 1.5)2333-23-(1.5 4.5)62133-203-423(4.56)6t tS t t tt t t⎧≤≤⎪⎪⎪⎪=+<≤⎨⎪⎪+<≤⎪⎪⎩．（3）存在α，使△BPQ为等腰三角形．理由如下：经探究，得△BPQ∽△B1QC，故当△BPQ为等腰三角形时，△B1QC也为等腰三角形．（I）当QB=QP时（如答图4），则QB1=QC，∴∠B1CQ=∠B1=30°，即∠BCB1=30°，∴α=30°；（II）当BQ=BP时，则B1Q=B1C，若点Q在线段B1E1的延长线上时（如答图5），∵∠B1=30°，∴∠B1CQ=∠B1QC=75°，即∠BCB1=75°，∴α=75°．10．（2013•吉林）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D、E、F分别是边AB、（2）在点P 从点F 运动到点D 的过程中，某一时刻，点P 落在MQ 上，求此时BQ 的长度；（3）当点P 在线段FD 上运动时，求y 与x 之间的函数关系式．11．解：（1）当点P 运动到点F 时，∵F 为AC 的中点，AC=6cm ，∴AF=FC=3cm ，∵P 和Q 的运动速度都是1cm/s ，∴BQ=AF=3cm ，∴CQ=8cm -3cm=5cm ，故答案为：5．（2）设在点P 从点F 运动到点D 的过程中，点P 落在MQ 上，如图1，则t+t -3=8，t=112， BQ 的长度为112×1=112（cm ）；（3）∵D 、E 、F 分别是AB 、BC 、AC 的中点，∴DE=12AC=12×6=3， DF=12BC=12×8=4， ∵MQ ⊥BC ，∴∠BQM=∠C=90°，∵∠QBM=∠CBA ，∴△MBQ ∽△ABC ，∴BQ MQ BC AC=， ∴86x MQ =，MQ=34x，分为三种情况：①当3≤x＜4时，重叠部分图形为平行四边形，如图2，y=PN•PD=34x（7-x）即y=-34x2+214x；②当4≤x＜112时，重叠部分为矩形，如图3，y=3[（8-X）-（X-3））]即y=-6x+33；③当112≤x≤7时，重叠部分图形为矩形，如图4，y=3[（x-3）-（8-x）]即y=6x-33．213．解：（1）如图，2如图2，由（1）知：抛物线的对称轴l为x=4，因为A、B两点关于l对称，连接CB交l于点P，则AP=BP，所以AP+CP=BC的值最小∵B（6，0），C（0，2）（3）如图3，连接ME ，∵CE 是⊙M 的切线∴ME ⊥CE ，∠CEM=90°由题意，得OC=ME=2，∠ODC=∠MDE ∵在△COD 与△MED 中COA DEMODC MD EOC ME∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△COD ≌△MED （AAS ），∴OD=DE ，DC=DM设OD=x 则CD=DM=OM -OD=4-x 则RT △COD 中，OD 2+OC 2=CD 2， ∴x 2+22=（4-x ）2∴x=32，∴D （32，0）设直线CE 的解析式为y=kx+b ∵直线CE 过C （0，2），D （32，0）两点，则3022k b b ⎧+=⎪⎨⎪=⎩，解得：432k b ⎧=-⎪⎨⎪=⎩。

九年级中考压轴——动点问题集锦

九年级中考压轴——动点问题集锦1、已知等边三角形ABC的边长为4厘米，长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动。

过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点，线段MN运动的时间为t秒。

1) 当四边形MNQP为矩形时，有MN=QP，即MN在运动t秒后，线段QP的长度为3+t。

因为三角形ABC是等边三角形，所以三角形ABC的高等于边长的一半，即2根号3.因此，四边形MNQP的面积为2根号3*t平方+2t。

2) 四边形MNQP的面积为S，运动时间为t。

因为三角形ABC是等边三角形，所以三角形ABC的高等于边长的一半，即2根号3.因此，四边形MNQP的高为2根号3.由于四边形MNQP是矩形，所以MN=QP=3+t，PQ=2根号3.因此，S=PQ*MN=2根号3*(3+t)。

函数关系式为S=2根号3*t+6根号3，t的取值范围为t≥0.2、在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=42，∠B=45度。

动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动。

设运动的时间为t 秒。

1) 因为三角形ABD和三角形CBD相似，所以BD=AB-AD=39.由于三角形BCD是直角三角形，所以BC=BD/根号2=39/根号2.2) 当MN∥AB时，由于三角形BMD和三角形BAC相似，所以BD/AB=MD/MN，即39/42=2t/(3+t)，解XXX13秒。

3) 当△MNC为等腰三角形时，由于三角形MNC和三角形ABD相似，所以CN/AD=MN/BD，即CN/3=(3+t)/39，XXX13秒。

3、在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为(6，0)，点B的坐标为(4，3)，点C在y轴的正半轴上。

动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点。

初中动点问题题目汇总定稿版

初中动点问题题目汇总精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】一.选择题1.（2015湖南邵阳第9题3分）如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t的函数关系的图象是（）2.（2015湖北荆州第9题3分）如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A 点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（）A B C．D．3．（2015?甘肃武威,第10题3分）如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P与点B、C都不重合），现将△PCD沿直线PD折叠，使点C落到点F处；过点P作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（）4．（2015?四川资阳,第8题3分）如图4，AD、BC是⊙O的两条互相垂直的直径，点P 从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是5. （2015?四川省内江市，第11题，3分）如图，正方形ABCD 的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（）A．B．2C．2D．6. （2015?山东威海，第 11题3分）如图，已知△ABC为等边三角形，AB=2，点D为边AB上一点，过点D作DE∥AC，交BC于E点；过E点作EF⊥DE，交AB的延长线于F点．设AD=x，△DEF的面积为y，则能大致反映y与x函数关系的图象是（）7. （2015山东省德州市，11，3分）如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：①OA=OD;②AD⊥EF;③当∠A=90°时，四边形AEDF是正方形；④AE2+DF2=AF2+DE2.其中正确的是（）A. ②③B. ②④C. ①③④D.②③④二.解答题1. （2015?四川甘孜、阿坝，第28题12分）如图，已知抛物线y=ax2﹣5ax+2（a≠0）与y轴交于点C，与x轴交于点A（1，0）和点B．（1）求抛物线的解析式；（2）求直线BC的解析式；（3）若点N是抛物线上的动点，过点N作NH⊥x轴，垂足为H，以B，N，H为顶点的三角形是否能够与△OBC相似？若能，请求出所有符合条件的点N的坐标；若不能，请说明理由．2. （2015?山东威海，第25题12分）已知：抛物线l1：y=﹣x2+bx+3交x轴于点A，B，（点A在点B的左侧），交y轴于点C，其对称轴为x=1，抛物线l2经过点A，与x轴的另一个交点为E（5，0），交y轴于点D（0，﹣）．（1）求抛物线l2的函数表达式；（2）P为直线x=1上一动点，连接PA，PC，当PA=PC时，求点P的坐标；（3）M为抛物线l2上一动点，过点M作直线MN∥y轴，交抛物线l1于点N，求点M自点A 运动至点E的过程中，线段MN长度的最大值．3.（2015?山东日照，第22题14分）如图，抛物线y=x2+mx+n与直线y=﹣x+3交于A，B两点，交x轴与D，C两点，连接AC，BC，已知A（0，3），C（3，0）．（Ⅰ）求抛物线的解析式和tan∠BAC的值；（Ⅱ）在（Ⅰ）条件下：（1）P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ACB相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．（2）设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE以每秒一个单位速度运动到E点，再沿线段EA以每秒个单位的速度运动到A后停止，当点E的坐标是多少时，点M在整个运动中用时最少？4.（2015?山东聊城,第25题12分）如图，在直角坐标系中，Rt△OAB的直角顶点A在x 轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N 从点O 出发，以每秒1.25个单位长度的速度，沿OB 向终点B 移动．当两个动点运动了x 秒（0＜x ＜4）时，解答下列问题：（1）求点N 的坐标（用含x 的代数式表示）；（2）设△OMN 的面积是S ，求S 与x 之间的函数表达式；当x 为何值时，S 有最大值最大值是多少（3）在两个动点运动过程中，是否存在某一时刻，使△OMN 是直角三角形？若存在，求出x 的值；若不存在，请说明理由．5．(2015·深圳，第22题分)如图1，水平放置一个三角板和一个量角器，三角板的边AB 和量角器的直径DE在一条直线上，,3,6cm OD cm BC AB ===开始的时候BD =1cm ,现在三角板以2cm /s 的速度向右移动。

初一数学动点问题20题及答案

初一数学动点问题20题及答案数轴上动点问题1．已知：如图，数轴上点A表示的数为6，点B表示的数为2，点C表示的数为﹣8，动点P从点A出发，沿数轴向左运动，速度为每秒1个单位长度．点M为线段BC中点，点N为线段BP中点．设运动时间为t秒．（1）线段AC的长为__________个单位长度；点M表示的数为；（2）当t=5时，求线段MN的长度；（3）在整个运动过程中，求线段MN的长度．（用含t的式子表示）．2．已知数轴上点A，B，C所表示的数分别是x，﹣6，4．（1）线段BC的长为_________，线段BC的中点D所表示的数是；（2）若AC=8，求x的值；（3）在数轴上有两个动点P，Q，P的速度为1个单位长度/秒，Q的速度为2个单位/秒，点P，Q分别从点B，C同时出发，在数轴上运动，则经过多少时间后P，Q两点相距4个单位？3．动点A、B同时从数轴上的原点出发向相反的方向运动，且A、B的速度之比是1：4（速度单位：长度单位/秒），3秒后，A、B两点相距15个单位长度．（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置．（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间？4．如图A、B两点在数轴上分别表示﹣10和20，动点P从点A出发以10个单位每秒的速度向右运动，动点Q从点B出发以每秒5个单位的速度出向右运动．设运动时间为t．（1）当点P运动到B点时，求出t的值；（2）当t为何值时，P、Q两点相遇，并求出此时P点对应的数？（3）在此运动过程中，若P、Q相距10个单位，直接写出运动时间t？5．已知a，b满足（a+2）2+|b﹣1|=0，请回答下列问题：（1）a=_______，b=_______；（2）a，b在数轴上对应的点分别为A，B，在所给的数轴上标出点A，点B；（3）若甲、乙两个动点分别从A，B两点同时出发沿x轴正方向运动，已知甲的速度为每秒2个单位长度，乙的速度为每秒1个单位长度，更多好题请进入：437600809，请问经过多少秒甲追上乙？6．在数轴上有A、B两动点，点A起始位置表示数为﹣3，点B起始位置表示数为12，点A的速度为1单位长度/秒，点B的运动速度是点A速度的二倍．（1）若点A、B同时沿数轴向左运动，多少秒后，点B与点A相距6单位长度？（2）若点A、点B同时沿数轴向左运动，是否有一个时刻，表示数﹣3的点是线段AB 的中点？如果有，求出运动时间；如果没有，说明理由．7．如图，已知数轴上点A表示的为8，B是数轴上一点，且AB=14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；（2）动点H从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、H 同时出发，问点P运动多少秒时追上点H？8．如图，数轴上的点A，B对应的数分别为﹣10，5．动点P，Q分别从A，B同时出发，点P以每秒3个单位长度的速度沿数轴向右匀速运动，点Q以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．（1）求线段AB的长；（2）直接用含t的式子分别表示数轴上的点P，Q对应的数；（3）当PQ=AB时，求t的值．9．如图，已知数轴上点A表示的数为6，B是你数轴上一点，且AB=10，动点P从点O 出发，以每秒6个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B所表示的数______；当t=3时，OP=_______．（2）动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R 同时出发，问点R运动多少秒时追上点P？10．如图．点A、点C是数轴上的两点，0是原点，0A=6，5AO=3CO．（1）写出数轴上点A、点C表示的数；（2）点P、Q分别从A、C同时出发，点P以每秒1个单位长度的速度沿数轴向右匀速运动，点Q以每4个单位长度的速度沿数轴向左匀速运动，问运动多少秒后，这两个动点到原点O的距离存在2倍关系？11．已知数轴上两点A，B对应的数分别为﹣1，3，P为数轴上的动点，其对应的数为x．（1）数轴上是否存在点P，使P到点A、点B的之和为5？若存在，请求出x的值；若不存在，说明理由；（2）当点P以每分钟1个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度的速度向左运动，点B以每分钟20个单位长度的速度向左运动．问，它们同时出发几分钟时点P到点A、点B的距离相等？12．A、B两个动点在数轴上做匀速运动，它们的运动时间以及位置记录如下．（1）根据题意，填写下列表格；（2）A、B两点能否相遇？如果相遇，求相遇时的时刻及在数轴上的位置；如果不能相遇，请说明理由；（3）A、B两点能否相距18个单位长度？如果能，求相距18个单位长度的时刻；如不能，请说明理由．13．如图1，点A，B是在数轴上对应的数字分别为﹣12和4，动点P和Q分别从A，B 两点同时出发向右运动，点P的速度是5个单位/秒，点Q的速度是2个单位/秒，设运动时间为t秒．（1）AB=．（2）当点P在线段BQ上时（如图2）：①BP=______________（用含t的代数式表示）；②当P点为BQ中点时，求t的值．。

七年级数学动点题50道

七年级数学动点题50道一、数轴上的动点问题（20道）1. 已知数轴上点A表示的数为 3，点B表示的数为1，点P以每秒2个单位长度的速度从点A出发向左运动，同时点Q以每秒3个单位长度的速度从点B出发向右运动，设运动时间为t秒。

（1）当t = 1时，求PQ的长度。

（2）求经过多少秒后，PQ = 5。

解析：（1）当t = 1时，点P表示的数为公式，点Q表示的数为公式。

所以公式。

（2）运动t秒后，点P表示的数为公式，点Q表示的数为公式。

则公式。

当公式时，即公式。

则公式或公式。

当公式时，公式，公式（舍去，因为时间不能为负）。

当公式时，公式，公式。

2. 数轴上点A对应的数为 2，点B对应的数为4，点C对应的数为x，若点C在点A、B之间，且公式，求x的值。

解析：因为点C在点A、B之间，公式，公式。

又因为公式，所以公式。

去括号得公式。

移项得公式。

合并同类项得公式。

解得公式。

3. 数轴上有A、B两点，A表示的数为 1，B表示的数为3，点P以每秒1个单位长度的速度从点A出发向右运动，设运动时间为t秒。

（1）当t为何值时，点P到点B的距离为2？（2）点Q以每秒2个单位长度的速度从点B出发向左运动，当公式时，求t的值。

解析：（1）点P表示的数为公式。

当点P到点B的距离为2时，公式。

则公式或公式。

解得公式或公式。

（2）点Q表示的数为公式，公式。

当公式时，公式。

即公式。

则公式或公式。

当公式时，公式，公式。

4. 数轴上点A表示的数为5，点B表示的数为 3，点M从点A出发，以每秒1个单位长度的速度向左运动，点N从点B出发，以每秒2个单位长度的速度向右运动，设运动时间为t秒。

（1）求t秒后，点M表示的数和点N表示的数。

（2）当t为何值时，点M与点N相距4个单位长度？解析：（1）t秒后，点M表示的数为公式，点N表示的数为公式。

（2）当点M与点N相距4个单位长度时，公式。

则公式或公式。

当公式时，公式，公式。

初中动点问题题目

选择题在数轴上，点A从原点出发，以每秒2个单位的速度向右移动，同时点B从数轴上的-5点出发，以每秒3个单位的速度向左移动，经过多少秒后，A、B两点相距15个单位？A. 2秒B. 3秒C. 4秒（正确答案）D. 5秒直角三角形ABC中，∠C=90°，AC=3，BC=4，点P从A出发沿AC边以每秒1个单位的速度向C移动，同时点Q从C出发沿CB边以每秒2个单位的速度向B移动，设移动时间为t秒，则当t为何值时，∠PCQ的面积等于2？A. t=1/2（正确答案）B. t=1C. t=3/2D. t=2在平行四边形ABCD中，AB=6，AD=8，∠B=60°，点E从A出发沿AB边以每秒2个单位的速度向B移动，点F从D出发沿DA边以每秒1个单位的速度向A移动，若E、F同时出发，设移动时间为x秒，则当以E、F为端点的线段与BC平行时，x的值为？A. 2秒B. 2.4秒（正确答案）C. 3秒D. 3.6秒点M、N分别在等腰三角形ABC的底边BC、顶角A的角平分线AD上，且BM=CN，若点M 从B出发沿BC以每秒3个单位的速度向C移动，同时点N从A出发沿AD以每秒2个单位的速度向D移动，当其中一个点到达终点时，另一个点也停止移动，则当MN∠AC时，移动的时间为？A. 1秒B. 1.5秒（正确答案）C. 2秒D. 2.5秒在矩形ABCD中，AB=6，BC=8，点E从A出发沿AB边以每秒1个单位的速度向B移动，同时点F从C出发沿CD边以每秒2个单位的速度向D移动，设移动时间为t秒，则当四边形AECF为菱形时，t的值为？A. 2秒（正确答案）B. 3秒C. 4秒D. 5秒在梯形ABCD中，AD∠BC，AD=3，BC=7，AB=CD=4，点P从A出发沿AD边以每秒1个单位的速度向D移动，同时点Q从C出发沿CB边以每秒2个单位的速度向B移动，设移动时间为x秒，则当PQ∠BC时，x的值为？A. 1秒B. 1.5秒C. 2秒（正确答案）D. 2.5秒在∠ABC中，AB=AC=5，BC=6，点D、E分别是AB、AC上的动点，且保持DE∠BC，若DE=x，∠ADE的面积为y，则y与x之间的函数关系式及x的取值范围是？A. y=3/5x2, 0<x<5（正确答案）B. y=4/5x2, 0<x<6C. y=3/5x, 0<x<5D. y=4/5x, 0<x<6在正方形ABCD中，边长为4，点E从A出发沿AB边以每秒1个单位的速度向B移动，同时点F从B出发沿BC边以每秒2个单位的速度向C移动，设移动时间为t秒，则当∠EBF的面积为3时，t的值为？A. 1秒B. 1.5秒（正确答案）C. 2秒D. 2.5秒。

初中数学动点题

初中数学动点题
以下是一些初中数学动点题的例子:
1. 一个人在跑步，每分钟跑 100 米。

他的速度是 6 米/秒。

如果他以这个速度向前跑，那么他能够追上自己吗？如果会，那么他需要多少时间才能追上自己？
2. 一个篮球运动员在比赛中得到了 5 个进球，共得分 10 分。

他平均每场得分是多少？如果他在比赛中平均每场得分 2 分，那么他需要多少场比赛才能得满 10 分？
3. 一列火车长 200 米，以每秒 8 米的速度通过一座长 240 米的桥，需要 4 秒。

求这座桥的长度是多少？
4. 一个长度为 20 厘米的线段，在两端点各燃烧 1 秒钟，共烧了 2 秒钟。

求这条线段的总长度是多少？
5. 一个时钟的分针长为 5 厘米，每秒钟走过一格。

如果这只时钟的分钟数是 30，那么它的一面需要多少时间才能转完一圈？
希望这些例子能够提供帮助。

如果需要更多的帮助，请随时提问。

七年级动点问题大全

七年级动点问题大全（一）例1:如图，在数轴上A点表示数a，B点表示数b，AB表示A点和B点之间的距离，且a、b满足|a+2|+（b+3a）2=0（1）求A、B两点之间的距离；（2）若在数轴上存在一点C，且AC=2BC，求C点表示的数；（3）若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以2个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为t（秒），①分别表示甲、乙两小球到原点的距离（用t表示）；①求甲、乙两小球到原点的距离相等时经历的时间．例2:如图，有一数轴原点为O，点A所对应的数是-12，点A沿数轴匀速平移经过原点到达点B．（1）如果OA=OB，那么点B所对应的数是什么？（2）从点A到达点B所用时间是3秒，求该点的运动速度．（3）在（2）的条件下，从点A沿数轴匀速平移经过点K到达点C，所用时间是9秒，且KC=KA，分别求点K和点C所对应的数。

例3动点A从原点出发向数轴负方向运动，同时，动点B也从原点出发向数轴正方向运动，3秒后，两点相距15个单位长度．已知动点A、B的速度比是1：4．（速度单位：单位长度/秒）（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置；（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间；（3）在（2）中A、B两点继续同时向数轴负方向运动时，另一动点C同时从B点位置出发向A运动，当遇到A后，立即返回向B点运动，遇到B点后立即返回向A点运动，如此往返，直到B追上A时，C立即停止运动．若点C一直以20单位长度/秒的速度匀速运动，那么点C从开始到停止运动，运动的路程是多少单位长度．例4:已知数轴上两点A、B对应的数分别为-1、3，点P为数轴上一动点，其对应的数为x．（1）若点P到点A，点B的距离相等，求点P对应的数；（2）数轴上是否存在点P，使点P到点A、点B的距离之和为6？若存在，请求出x的值；若不存在，说明理由；（3）点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以6个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间，求当点A与点B重合时，点P所经过的总路程是多少？例5数轴上两个质点A、B所对应的数为-8、4，A、B两点各自以一定的速度在上运动，且A点的运动速度为2个单位/秒．（1）点A、B两点同时出发相向而行，在原点处相遇，求B点的运动速度；（2）A、B两点以（1）中的速度同时出发，向数轴正方向运动，几秒钟时两者相距6个单位长度；（3）A、B两点以（1）中的速度同时出发，向数轴负方向运动，与此同时，C点从原点出发作同方向的运动，且在运动过程中，始终有CB：CA=1：2，若干秒钟后，C停留在-10处，求此时B点的位置？例6:在数轴上，点A表示的数是-30，点B表示的数是170．（1）求A、B中点所表示的数．（2）一只电子青蛙m，从点B出发，以4个单位每秒的速度向左运动，同时另一只电子青蛙n，从A点出发以6个单位每秒的速度向右运动，假设它们在C点处相遇，求C点所表示的数．（3）两只电子青蛙在C点处相遇后，继续向原来运动的方向运动，当电子青蛙m处在A 点处时，问电子青蛙n处在什么位置？（4）如果电子青蛙m从B点处出发向右运动的同时，电子青蛙n也向右运动，假设它们在D点处相遇，求D点所表示的数例7、已知数轴上有A、B、C三点，分别代表- 24，- 10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒。

七年级上册数学动点问题压轴题

七年级上册数学动点问题压轴题一、数轴上的动点问题。

1. 已知数轴上A、B两点对应的数分别为 1、3，点P为数轴上一动点，其对应的数为x。

（1）若点P到点A、点B的距离相等，求点P对应的数。

解析：因为点P到点A、点B的距离相等，所以PA = PB。

根据数轴上两点间的距离公式d=| a b|（d为两点间距离，a、b为两点对应的数），则| x-(-1)|=| x 3|，即| x + 1|=| x-3|。

当x≥3时，x + 1=x 3，方程无解。

当-1时，x + 1=-(x 3)，x+1=-x + 3，2x=2，解得x = 1。

当x≤-1时，-(x + 1)=-(x 3)，方程无解。

所以点P对应的数为1。

（2）数轴上是否存在点P，使PA+PB = 5？若存在，请求出x的值；若不存在，请说明理由。

解析：根据距离公式PA=| x+1|，PB=| x 3|，则| x + 1|+| x-3| = 5。

当x≥3时，x + 1+x 3=5，2x-2 = 5，2x=7，解得x=(7)/(2)。

当-1时，x + 1-(x 3)=5，x + 1-x + 3=5，4 = 5，方程无解。

当x≤-1时，-(x + 1)-(x 3)=5，-x-1-x + 3 = 5，-2x+2 = 5，-2x=3，解得x=-(3)/(2)。

所以存在点P，x=(7)/(2)或x =-(3)/(2)。

2. 点A在数轴上对应的数为 2，点B对应的数为1，点P在数轴上对应的数为x。

（1）若点P到点A、点B的距离之和为5，求x的值。

解析：由题意得| x-(-2)|+| x 1|=5，即| x + 2|+| x-1| = 5。

当x≥1时，x + 2+x 1=5，2x+1 = 5，2x = 4，解得x = 2。

当-2时，x + 2-(x 1)=5，x + 2-x + 1=5，3 = 5，方程无解。

当x≤-2时，-(x + 2)-(x 1)=5，-x-2-x + 1 = 5，-2x-1 = 5，-2x = 6，解得x=-3。

7年级动点题10道

7年级动点题10道一、数轴上的动点问题。

1. 已知数轴上点A表示的数为 -2，点B表示的数为4，点P从点A出发，以每秒2个单位长度的速度沿数轴向右运动，同时点Q从点B出发，以每秒1个单位长度的速度沿数轴向左运动，设运动时间为t秒。

- 当t = 1时，求点P和点Q所表示的数。

- 求经过多少秒，点P与点Q相遇？- 求经过多少秒，点P与点Q之间的距离为2个单位长度？解析：- 点P从 - 2出发，速度为每秒2个单位长度，当t = 1时，点P表示的数为-2 + 2×1=0；点Q从4出发，速度为每秒1个单位长度，当t = 1时，点Q表示的数为4-1×1 = 3。

- 设经过t秒点P与点Q相遇。

点P向右运动的路程为2t，点Q向左运动的路程为t，相遇时2t + t=4 - (-2)，即3t = 6，解得t = 2秒。

- 分两种情况：- 相遇前相距2个单位长度：2t+t+2 = 4-(-2)，3t+2 = 6，3t = 4，解得t=(4)/(3)秒。

- 相遇后相距2个单位长度：2t + t-2=4 - (-2)，3t-2 = 6，3t = 8，解得t=(8)/(3)秒。

2. 数轴上点A对应的数为 -1，点B对应的数为3，点P为数轴上一动点，其对应的数为x。

- 若点P到点A、点B的距离相等，求点P对应的数。

- 数轴上是否存在点P，使点P到点A、点B的距离之和为5？若存在，求出x的值；若不存在，请说明理由。

- 当点P以每分钟1个单位长度的速度从原点向左运动时，点A以每分钟5个单位长度的速度向左运动，点B以每分钟20个单位长度的速度向左运动，问几分钟时点P到点A、点B的距离相等？解析：- 因为点P到点A、点B的距离相等，所以x=(-1 + 3)/(2)=1。

- 存在。

当点P在点A左侧时，-1 - x+3 - x = 5，-2x+2 = 5，-2x = 3，解得x =-(3)/(2)；当点P在点B右侧时，x - (-1)+x - 3 = 5，2x - 2 = 5，2x = 7，解得x=(7)/(2)。

七年级动点问题20道含答案

七年级动点问题20道含答案一、七年级动点问题20道1. 函数$y=3cos\frac{3\pi x}{4}$的图像称作：(A.余弦曲线)2. 斜率等于负一，斜截式为$y=7x-5$的直线称作：(B.负斜率直线)3. 求函数$f(x)=x^3-7x+2$在$x=2$处取得最大值：(D.8)4. 直线$y=mx+b$中，m 为：(A.斜率)5. 闭合曲线$\frac{x^2}{4}+\frac{y^2}{9}=1$在$x$=4处的坐标是：(C. $(4,\frac{3}{2})$)6. 函数$f(x)=2x^{2}-3$的最小值是：(B. -3)7. 函数$f(x)=\frac{x^2}{2}+1$的图像是：(A.抛物线)8. 函数$f(x)=2x+5$的大致图象是：(B.直线)9. 三维坐标中，z 轴表示的为：(C.高度)10. 绘制抛物线需要：(A.二个点)11. 点$A(-1,2)$绕原点旋转$90^{\circ}$后，其新坐标是：(B. $(2,-1)$)12. 子弹以15米/秒的速度射出，它从出射点到返回出射点所需要的时间为：(B.2秒)13. 平面内的向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角为30°，且$|\overrightarrow{a}|=3$，$|\overrightarrow{b}|=4$，则$\overrightarrow{a}\cdot\overrightarrow{b}$ 为：(D.6)14. 直线$y=2/3x-3$的斜率为：(B. 2/3)15. 一个三角形的两个锐角都为$60^{\circ}$，则这个三角形是：(D.等腰三角形)16. 半径为4的圆的面积为：(B.50.27公分平方）17. 在正方形ABCD中，点P到边AB的距离是4，A点到点P的垂直平分线的距离为：(D. 2)18. 圆$x^{2}+y^{2}+8x+2y-13=0$的圆心坐标是：(C. (-4, -1))19. $f(x)=-2x^2+4$的最小值是：(A. 0)20. 角A,B,C构成的夹角是60度，AB=5,BC=7，AC=：(B. 8)二、七年级动点文章今天，我们就来一起练习一下关于七年级动点的知识吧！首先，对于函数问题，函数$y=3cos\frac{3\pi x}{4}$的图像应当称作余弦曲线。

初中数学动点题型汇总

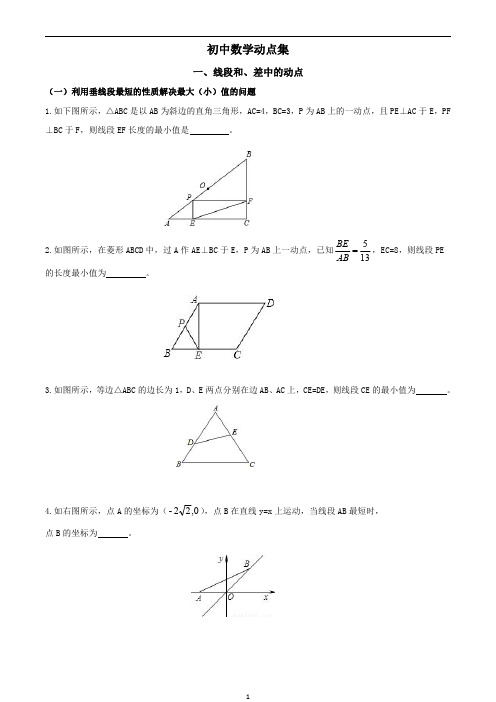
初中数学动点集一、线段和、差中的动点（一）利用垂线段最短的性质解决最大（小）值的问题1.如下图所示，△ABC 是以AB 为斜边的直角三角形，AC=4，BC=3，P 为AB 上的一动点，且PE⊥AC 于E，PF ⊥BC 于F，则线段EF 长度的最小值是。

2.如图所示，在菱形ABCD 中，过A 作AE⊥BC 于E，P 为AB 上一动点，已知135 AB BE ，EC=8，则线段PE 的长度最小值为。

3.如图所示，等边△ABC 的边长为1，D、E 两点分别在边AB、AC 上，CE=DE，则线段CE 的最小值为。

4.如右图所示，点A 的坐标为（0,22-），点B 在直线y=x 上运动，当线段AB 最短时，点B 的坐标为。

5.在平面直角坐标系xoy中，直线y=2x+m与y轴交于点A，与直线y=-x+4交于点B（3，n），p为直线y=-x+4上一动点。

（1）求m，n的值（2）当线段AP最短时，求点p的坐标。

2。

6.已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=30试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的值最短，则此时AM+NB=。

（二）利用三点共线的特征解决最大（小）值的问题1.如图所示，四边形ABCD是正方形，边长是4，E是BC上一点，且BE=1，P是对角线AC上任意一点，则PE+PB的最小值是。

2.如图所示，点P是边长为1的菱形ABCD对角线AC上的一个动点，M、N分别是AB，BC边上的中点，PM+PN 的最小值是。

3.如图所示，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是。

4.如图1所示，F，E分别是正方形ABCD的边CD、DA上两个动点（不与C、D、A重合），满足DF=AE。

直线BE、AF相交于点G，则有BE=AF，BE⊥AF；如图2所示，F，E分别是正方形ABCD的边CD、DA延长线上的两个动点（不与D、A重合），依然有BE=AF，BE⊥AF；若在上述的图1与图2中，正方形ABCD的边长为4，随着动点F、E的移动，线段DG的长也随之变化。

初中动点问题题目汇总情况

一.选择题1.（2015湖南邵阳第9题3分）如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t的函数关系的图象是（）2.（2015湖北荆州第9题3分）如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从B 点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（）A B C．D．3．（2015•甘肃武威,第10题3分）如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P与点B、C都不重合），现将△PCD沿直线PD折叠，使点C落到点F处；过点P作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（）4．（2015•四川资阳,第8题3分）如图4，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动，设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是5. （2015•四川省内江市，第11题，3分）如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（）A．B．2C． 2D．6. （2015•山东威海，第11题3分）如图，已知△ABC为等边三角形，AB=2，点D为边AB上一点，过点D作DE∥AC，交BC于E点；过E点作EF⊥DE，交AB的延长线于F点．设AD=x，△DEF的面积为y，则能大致反映y与x函数关系的图象是（）7.（2015山东省德州市，11，3分）如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：①OA=OD;②AD⊥EF;③当∠A=90°时，四边形AEDF是正方形；④AE2+DF2=AF2+DE2.其中正确的是（）A. ②③B. ②④C. ①③④D.②③④二.解答题1. （2015•四川甘孜、阿坝，第28题12分）如图，已知抛物线y=ax2﹣5ax+2（a≠0）与y轴交于点C，与x轴交于点A（1，0）和点B．（1）求抛物线的解析式；（2）求直线BC的解析式；（3）若点N是抛物线上的动点，过点N作NH⊥x轴，垂足为H，以B，N，H为顶点的三角形是否能够与△OBC相似？若能，请求出所有符合条件的点N的坐标；若不能，请说明理由．2. （2015•山东威海，第25题12分）已知：抛物线l1：y=﹣x2+bx+3交x轴于点A，B，（点A在点B的左侧），交y轴于点C，其对称轴为x=1，抛物线l2经过点A，与x轴的另一个交点为E（5，0），交y轴于点D（0，﹣）．（1）求抛物线l2的函数表达式；（2）P为直线x=1上一动点，连接PA，PC，当PA=PC时，求点P的坐标；（3）M为抛物线l2上一动点，过点M作直线MN∥y轴，交抛物线l1于点N，求点M自点A运动至点E的过程中，线段MN长度的最大值．3.（2015•山东日照，第22题14分）如图，抛物线y=x2+mx+n与直线y=﹣x+3交于A，B两点，交x轴与D，C两点，连接AC，BC，已知A（0，3），C（3，0）．（Ⅰ）求抛物线的解析式和tan∠BAC的值；（Ⅱ）在（Ⅰ）条件下：（1）P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ACB相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．（2）设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE 以每秒一个单位速度运动到E点，再沿线段EA以每秒个单位的速度运动到A后停止，当点E的坐标是多少时，点M在整个运动中用时最少？4.（2015•山东聊城,第25题12分）如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：（1）求点N 的坐标（用含x 的代数式表示）；（2）设△OMN 的面积是S ，求S 与x 之间的函数表达式；当x 为何值时，S 有最大值？最大值是多少？（3）在两个动点运动过程中，是否存在某一时刻，使△OMN 是直角三角形？若存在，求出x 的值；若不存在，请说明理由．5．(2015·深圳，第22题分)如图1，水平放置一个三角板和一个量角器，三角板的边AB 和量角器的直径DE 在一条直线上，,3,6cm OD cm BC AB ===开始的时候BD =1cm ,现在三角板以2cm /s 的速度向右移动。