初中数学动点问题归纳
初中动点问题的方法归纳

初中动点问题的方法归纳动点问题是初中生学习数学时常遇到的难题之一。
这类问题需要学生掌握一定的解题方法和技巧才能够解决。
本文将从动点问题的基本概念、解题思路和常见解题方法等方面进行详细的归纳和总结,希望能够帮助学生更好地掌握动点问题的解题技巧。
一、动点问题的基本概念动点问题是数学中的一个重要课题,在初中数学中占据着重要的地位。
动点问题通常是指以点的运动规律为基础,通过分析和推理,确定动点在一定条件下的运动轨迹或者位置。
动点问题涉及到数学中的线性代数、平面几何等多个知识领域,对学生的逻辑思维和解决问题的能力提出了较高的要求。
动点问题的基本概念可以概括为以下几个方面:1.动点的定义:动点是指在一定条件下,按照一定的规律进行运动的点。
动点的轨迹、速度等都是动点问题的研究对象。
2.动点的运动规律:动点在其运动过程中会遵循一定的规律,这种规律可以是直线运动、曲线运动、周期性运动等。
了解动点的运动规律是解决动点问题的基础。
3.动点问题的应用:动点问题在生活和工作中有着广泛的应用,如汽车在高速公路上行驶的轨迹、射击运动中子弹的轨迹等,都可以通过动点问题进行模拟和分析。
二、动点问题的解题思路解动点问题需要遵循一定的思维逻辑和解题方法,下面将对解题思路进行详细的介绍:1.熟悉动点的运动规律:在解动点问题之前,首先需要了解动点所遵循的运动规律。
这包括动点的速度、加速度、运动轨迹等相关信息。
只有了解了动点的运动规律,才能够有针对性地解决动点问题。
2.建立数学模型:解动点问题需要建立适当的数学模型,根据动点的运动规律和条件进行建模。
这包括建立坐标系、确定参照物、建立方程等步骤,通过数学模型能够更清晰地描述动点的运动状态。
3.运用数学知识进行推理:在建立数学模型之后,需要通过数学知识进行推理和分析。
这包括运用几何知识、代数知识、函数知识等进行推导和计算,找出动点在不同条件下的位置和轨迹。
4.检验和求解:在进行推理之后,需要对所得的结果进行检验和求解,验证计算结果的正确性,并对结果进行解释和讨论,这样才能够得出准确的结论。
初三数学动点问题归类及解题技巧

初三数学动点问题归类及解题技巧初三数学学科是学生学习的重要科目之一,数学知识的掌握对学生的数学素养和综合能力提高有着非常重要的作用。
其中,解题技巧和问题分类是学生学习数学的关键点之一。
以下将从初三数学动点问题的归类和解题技巧展开讨论。
一、问题归类初三数学动点问题主要包括以下几种类型:1.几何问题:主要涉及到点、线、面等几何图形的性质和运动规律,如点的坐标、直线的方程、圆的性质等。
2.图像问题:主要是通过图像呈现的运动问题,要求学生根据图像进行分析和解答,比如速度图、位移图、加速度图等。
3.速度问题:主要是针对运动物体的速度和位移等概念展开的问题,要求学生掌握速度的定义和相关计算方法。
4.运动方程问题:主要是要求学生建立物体运动的数学模型,并求解相关问题,如撞击问题、相遇问题等。
5.加速度问题:主要是针对物体加速度的概念和计算方法进行考察,要求学生对加速度的定义和公式进行灵活运用。
6.综合问题:综合了以上几种类型的数学问题,要求学生在综合运用各种知识和方法的基础上解答问题。
以上这些类型的动点问题,对学生的数学能力和解题技巧有着很高的要求,需要学生通过不断的练习和思考,逐渐提高自己的解题能力。
二、解题技巧初三数学动点问题的解题技巧主要包括以下几点:1.充分理解问题:在解题前,要先充分理解问题的意思和要求,明确问题中涉及到的数学概念和知识点,了解问题的背景和条件。
2.建立数学模型:对于涉及到物体运动的问题,要根据问题的要求建立数学模型,明确物体的运动规律和相关参数,建立方程或不等式。
3.运用相关知识和公式:根据问题的情况,灵活运用速度、加速度、位移等物理量的定义和相关公式进行计算,注意在计算过程中要完整标明单位。
4.图像分析:对于图像问题,要细致分析图像的特点和变化规律,结合数学知识对图像进行解释和分析,从图像中得出相关信息。
5.综合能力:对于综合问题,要能够综合运用各种知识和方法,进行综合分析和推理,完成问题的解答。
八年级数学动点题型归纳

八年级数学动点题型归纳一、动点与三角形相关题型1. 动点在三角形边上运动求线段长度或周长题目:在等腰三角形公式中,公式,公式,点公式从点公式出发沿公式向点公式运动,速度为每秒公式个单位长度,设运动时间为公式秒。
当公式时,求公式的长度。
解析:过点公式作公式于点公式。
因为公式,等腰三角形三线合一,所以公式。
在公式中,根据勾股定理公式。
当公式时,公式,则公式。
在公式中,根据勾股定理公式。
2. 动点运动过程中三角形面积的变化题目:在公式中,公式,公式,公式,点公式从点公式出发,沿公式向点公式以每秒公式个单位长度的速度运动,同时点公式从点公式出发,沿公式向点公式以每秒公式个单位长度的速度运动,设运动时间为公式秒公式,求公式的面积公式与公式的函数关系式。
解析:已知公式,则公式,公式。
根据三角形面积公式公式,对于公式,底为公式,高为公式。
所以公式。
二、动点与四边形相关题型1. 动点在四边形边上运动判断四边形形状题目:在矩形公式中,公式,公式,点公式从点公式出发沿公式向点公式运动,速度为每秒公式个单位长度,点公式从点公式出发沿公式向点公式运动,速度为每秒公式个单位长度,设运动时间为公式秒。
当公式时,四边形公式是什么四边形?解析:当公式时,公式,公式。
因为四边形公式是矩形,所以公式,公式。
则公式,公式。
在四边形公式中,公式(因为公式),公式,公式(此时公式运动到公式点),公式。
因为公式且公式,所以四边形公式是梯形。
2. 动点运动过程中四边形面积的变化题目:在平行四边形公式中,公式,公式,公式,点公式从点公式出发沿公式向点公式运动,速度为每秒公式个单位长度,点公式从点公式出发沿公式向点公式运动,速度为每秒公式个单位长度,设运动时间为公式秒。
求四边形公式的面积公式与公式的函数关系式。
解析:四边形公式的面积公式。
过点公式作公式于点公式,在公式中,公式,公式,则公式,公式。
所以公式。
因为公式,则公式。
公式。
所以公式。
三、动点与函数图象相关题型1. 根据动点运动情况确定函数图象题目:如图,在边长为公式的正方形公式中,点公式以每秒公式个单位长度的速度从点公式出发,沿公式的路径运动,到点公式停止。
初一动点问题专题

初一动点问题专题动点问题是初一学生学习数学时经常遇到的难题,也是他们在数学学习中的一个难点。
动点问题涉及到的知识点较多,包括速度、时间、距离等,要求学生在解题时综合运用多种数学知识。
本文将结合初一学生的学习特点和解题心得,为大家详细讲解初一动点问题。
一、动点问题的基本概念1、动点问题的概念动点问题指的是一个或多个点在动。
在数学中,我们常常要解决某个点在运动中的位置、速度、时间等问题,这就是动点问题。
在解决动点问题时,常常需要利用速度和时间的关系来确定距离或者位置。
2、常见的动点问题类型在初一数学教学中,动点问题是比较常见的一个问题类型。
常见的动点问题有:两点同时运动、两点交替运动等。
下面我们将结合具体的例子来详细介绍这些类型的动点问题。
二、两点同时运动的问题两点同时运动的问题是初一学生比较容易遇到的一个问题类型。
这类问题的解题步骤一般包括:确定关系式,列方程,解方程,找答案等。
下面我们通过一个例题来详细介绍这类问题的解题方法。
例题:甲、乙两地相距150千米,甲乙两车同时出发相向而行,甲车每小时行60千米,乙车每小时行40千米,问几小时能相遇?解:假设相遇时,甲车行驶了x小时,乙车行驶了y小时。
则根据距离=速度*时间得出60x + 40y = 150 (1)又根据x+y=?得出60x + 60y = 150 (2)将两个方程相减得出20y=0y=3则x=2所以相遇时,甲车行驶了2小时,乙车行驶了3小时。
答:2小时。
三、两点交替运动的问题另一类常见的动点问题是两点交替运动的问题。
这类问题的解题步骤一般包括:列方程,解方程,找答案等。
下面我们通过一个例题来详细介绍这类问题的解题方法。
例题:两列火车从两地同时开出,两地相距150千米,一列火车以50千米/小时的速度开往另一地,另一列火车以40千米/小时的速度开往另一地,问几小时两列火车相遇?解:假设相遇时,快车行驶了x小时,慢车行驶了y小时。
则根据距离=速度*时间得出50x+40y=150 (1)又根据x+y=?得出50x+50y=150 (2)将两个方程相减得出10y=0y=3则x=0所以相遇时,快车行驶了0小时,慢车行驶了3小时。
完整版初中数学动点问题归纳

动点问题题型方法归纳动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、三角形边上动点3x??6y?P、QO BA、点出发,两点,动点年齐齐哈尔市)直线同时从与坐标轴分别交于20091、(4yQ OAA 1沿线段个单同时到达点,运动停止.点运动,速度为每秒BO ABP→运动.位长度,点→沿路线B、A两点的坐标;1)直接写出(Ptt OPQ△Q SS之间的面积为的运动时间为与秒,(2)设点,求出xQOA 的函数关系式;48?SQ、O、P MP的求出点为顶点的平行四边形的第四个顶点的坐标,并直接写出以点(3)当时,5坐标.,6)(0)B0解:1、A(8,2S=t<3时,2、当0<t S=3/8(8-t)t<t<8时,当3 B所有时间分段分类;)问按点提示:第(2P到拐点探究第四点构成平行四边形时按已知线段身份不,O、P、Q第(3)问是分类讨论:已知三定点为边。
然后为对角线、OQ为边、OQ为对角线,③OP同分类-----①OP为边、OQ为边,②OP 画出各类的图形,根据图形性质求顶点坐标。
年衡阳市)2、(2009,是⊙O的直径,弦BC=2cm如图,AB o.∠ABC=60 的直径;1)求⊙O(与⊙O相切;延长线上一点,连结ABCD,当BD长为多少时,CD(2)若D是点出发沿的速度从BAB方向运动,同时动点F以1cm/s的速度从(3)若动点E以2cm/sA点出发沿着t)?t?2)(t(s0为直角三角形.为何值时,△BEF方向运动,设运动时间为BCEF,连结,当CC CF FE ABABADOEB O O1页共11 第页)3图()2图()1图(.注意:第(3)问按直角位置分类讨论0)a??33(y?a(x?1)2),0(?2A D,经过点如图,重庆綦江)已知抛物线抛物线的顶点为,3、(2009xx CO BCOMADOM∥BD.过于点作射线轴正半轴上,,.过顶点连结平行于在轴的直线交射线1)求该抛物线的解析式;(O)st(OMPP.问运动,设点运动的时间为出发,以每秒(2)若动点1从点个长度单位的速度沿射线tDAOP为何值时,四边形分别为平行四边形?直角梯形?等腰梯形?当M yDCQ OOBOC?B个长度同时出发,分别以每秒,动点和点3()若和动点1分别从点BOOC运动,当其中一个点停止运动时另一个点也随个长度单位的速度沿和单位和2Ptt BCPQPQ)(s四边形,之停止运动.设它们的运动的时间为连接为何值时,,当AQOxB PQ的面积最小?并求出最小值及此时的长.注意:发现并充分运用特殊角∠DAB=60°BCPQ 的面积最小。
初一数学动点知识点

初一数学动点知识点
在初一数学中,动点是一个重要的知识点,特别是在平面几何中。
以下是关于动点的一些基本概念和知识点:
1. 动点的定义:在平面几何中,动点通常是指在平面内可以自由移动的点。
这些点可以沿着不同的路径和速度移动,形成各种轨迹和图形。
2. 动点的轨迹:当一个动点按照一定的规律移动时,它所经过的路径被称为轨迹。
在平面几何中,动点的轨迹可以是直线、圆、抛物线、椭圆等。
3. 速度和加速度:在描述动点的运动时,速度和加速度是非常重要的概念。
速度表示动点在单位时间内移动的距离,而加速度表示速度的变化率,即单位时间内速度的增量。
4. 直线的动点问题:在直线上的动点问题通常涉及到距离、速度和时间的关系。
这类问题通常需要利用距离公式、速度公式等来解决。
5. 圆上的动点问题:在圆上的动点问题通常涉及到半径、角度、弦长等概念。
这类问题通常需要利用圆的性质、三角函数的性质等来解决。
6. 动点的应用:动点在实际生活中有广泛的应用,如物理中的运动问题、工程中的机械运动、生物学中的细胞分裂等。
总的来说,动点是平面几何中的一个重要知识点,通过研究动点的运动轨迹、速度和加速度等概念,可以深入了解平面几何的基本原理和应用。
中考动点问题经典题型归类总结附答案
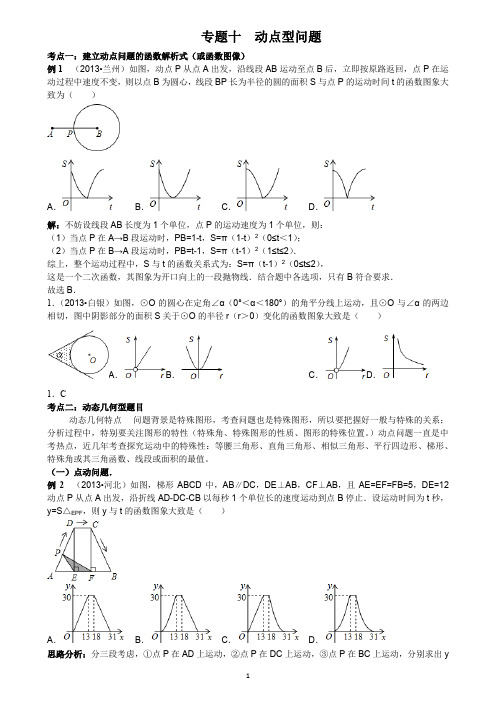
专题十动点型问题考点一:建立动点问题的函数解析式(或函数图像)例1 (2013•兰州)如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为()A.B.C.D.解:不妨设线段AB长度为1个单位,点P的运动速度为1个单位,则:(1)当点P在A→B段运动时,PB=1-t,S=π(1-t)2(0≤t<1);(2)当点P在B→A段运动时,PB=t-1,S=π(t-1)2(1≤t≤2).综上,整个运动过程中,S与t的函数关系式为:S=π(t-1)2(0≤t≤2),这是一个二次函数,其图象为开口向上的一段抛物线.结合题中各选项,只有B符合要求.故选B.1.(2013•白银)如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是()A.B.C.D.1.C考点二:动态几何型题目动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
(一)点动问题.例2 (2013•河北)如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是()A.B.C.D.思路分析:分三段考虑,①点P在AD上运动,②点P在DC上运动,③点P在BC上运动,分别求出y与t 的函数表达式,继而可得出函数图象. 解:在Rt △ADE 中,AD=2213AE DE +=,在Rt △CFB 中,BC=2213BF CF +=,①点P 在AD 上运动:对应训练2.(2013•北京)如图,点P 是以O 为圆心,AB 为直径的半圆上的动点,AB=2.设弦AP 的长为x ,△APO 的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )A .B .C .D .2.A(二)线动问题例3 (2013•荆门)如右图所示,已知等腰梯形ABCD ,AD ∥BC ,若动直线l 垂直于BC ,且向右平移,设扫过的阴影部分的面积为S ,BP 为x ,则S 关于x 的函数图象大致是( )A.B.C.D.解:①当直线l经过BA段时,阴影部分的面积越来越大,并且增大的速度越来越快;②直线l经过DC段时,阴影部分的面积越来越大,并且增大的速度保持不变;③直线l经过DC段时,阴影部分的面积越来越大,并且增大的速度越来越小;结合选项可得,A选项的图象符合.故选A.对应训练3.(2013•永州)如图所示,在矩形ABCD中,垂直于对角线BD的直线l,从点B开始沿着线段BD匀速平移到D.设直线l被矩形所截线段EF的长度为y,运动时间为t,则y关于t的函数的大致图象是()A.B.C.D.3.A(三)面动问题例4 (2013•牡丹江)如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s与t的大致图象应为()A.B.C.D.解:根据题意,设小正方形运动的速度为V,分三个阶段;①小正方形向右未完全穿入大正方形,S=2×2-Vt×1=4-Vt,②小正方形穿入大正方形但未穿出大正方形,S=2×2-1×1=3,③小正方形穿出大正方形,S=Vt×1,分析选项可得,A符合;故选A.对应训练4.(2013•衡阳)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为()A.B.C.D.4.A究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.(4)△QMN 为等腰三角形的情形有两种,需要分类讨论,避免漏解.解:(1)∵C (7,4),AB ∥CD ,∴D (0,4).∵sin ∠DAB=22, ∴∠DAB=45°,∴OA=OD=4,∴A (-4,0).设直线l 的解析式为:y=kx+b ,则有4-40b k b =⎧⎨+=⎩, 解得:k=1,b=4,∴y=x+4.∴点A 坐标为(-4,0),直线l 的解析式为:y=x+4.(2)在点P 、Q 运动的过程中:①当0<t≤1时,如答图1所示:过点C 作CF ⊥x 轴于点F ,则CF=4,BF=3,由勾股定理得BC=5.过点Q 作QE ⊥x 轴于点E ,则BE=BQ•cos ∠CBF=5t•35=3t . ∴PE=PB -BE=(14-2t )-3t=14-5t ,S=12PM•PE=12×2t×(14-5t )=-5t 2+14t ; ②当1<t≤2时,如答图2所示:过点C、Q分别作x轴的垂线,垂足分别为F,E,则CQ=5t-5,PE=AF-AP-EF=11-2t-(5t-5)=16-7t,S=12PM•PE=12×2t×(16-7t)=-7t2+16t;③当点M与点Q相遇时,DM+CQ=CD=7,即(2t-4)+(5t-5)=7,解得t=167.当2<t<167时,如答图3所示:MQ=CD-DM-CQ=7-(2t-4)-(5t-5)=16-7t,S=12PM•MQ=12×4×(16-7t)=-14t+32.(3)①当0<t≤1时,S=-5t2+14t=-5(t-75)2+495,∵a=-5<0,抛物线开口向下,对称轴为直线t=75,∴当0<t≤1时,S随t的增大而增大,∴当t=1时,S有最大值,最大值为9;②当1<t≤2时,S=-7t2+16t=-7(t-87)2+647,∵a=-7<0,抛物线开口向下,对称轴为直线t=87,∴当t=87时,S有最大值,最大值为647;③当2<t<167时,S=-14t+32∵k=-14<0,∴S随t的增大而减小.又∵当t=2时,S=4;当t=167时,S=0,∴0<S<4.综上所述,当t=87时,S有最大值,最大值为647.(4)△QMN为等腰三角形,有两种情形:①如答图4所示,点M在线段CD上,MQ=CD-DM-CQ=7-(2t-4)-(5t-5)=16-7t,MN=DM=2t-4,由MN=MQ,得16-7t=2t-4,解得t=209;②如答图5所示,当点M运动到C点,同时当Q刚好运动至终点D,此时△QMN为等腰三角形,t=125.故当t=209或t=125时,△QMN为等腰三角形.对应训练5.(2013•长春)如图①,在▱ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B-A-D-A 运动,沿B-A运动时的速度为每秒13个单位长度,沿A-D-A运动时的速度为每秒8个单位长度.点Q从点B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q 两点同时停止运动.设点P的运动时间为t(秒).连结PQ.(1)当点P沿A-D-A运动时,求AP的长(用含t的代数式表示).(2)连结AQ,在点P沿B-A-D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B-A-D运动过程中,当线段PQ 扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.5.解:(1)当点P沿A-D运动时,AP=8(t-1)=8t-8.当0<t<1时,如图①.作过点Q作QE⊥AB于点E.S△ABQ=12AB•QE=12BQ×12,4当0<t≤1时,如图③.∵S △BPM =S △BQM ,∴PM=QM .∵AB ∥QR ,∴∠PBM=∠QRM ,∠BPM=∠MQR ,在△BPM 和△RQM 中PBM QRMBPM MQR PM QM∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BPM ≌△RQM .∴BP=RQ ,∵RQ=AB ,∴BP=AB∴13t=13,解得:t=1当1<t≤83时,如图④.∵BR 平分阴影部分面积,∴P 与点R 重合.34∵S△ABR=S△QBR,∴S△ABR<S四边形BQPR.∴BR不能把四边形ABQP分成面积相等的两部分.综上所述,当t=1或83时,线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分.(4)如图⑥,当P在A-D之间或D-A之间时,C′D′在BC上方且C′D′∥BC时,∴∠C′OQ=∠OQC.∵△C′OQ≌△COQ,∴∠C′OQ=∠COQ,∴∠CQO=∠COQ,∴QC=OC,∴50-5t=50-8(t-1)+13,或50-5t=8(t-1)-50+13,解得:t=7或t=95 13.当P在A-D之间或D-A之间,C′D′在BC下方且C′D′∥BC时,如图⑦.同理由菱形的性质可以得出:OD=PD,∴50-5t+13=8(t-1)-50,解得:t=121 13.∴当t=7,t=9513,t=12113时,点C、D关于直线PQ的对称点分别为C′、D′,且C′D′∥BC.中考真题演练一、选择题1.(2013•新疆)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E 以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为()A.2B.2.5或3.5C.3.5或4.5D.2或3.5或4.51.D2.(2013•安徽)图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是()A.当x=3时,EC<EMB.当y=9时,EC>EMC.当x增大时,EC•CF的值增大D.当y增大时,BE•DF的值不变2.D3.(2013•盘锦)如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为()A.B.C.D.3.B4.(2013•龙岩)如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是()A.2B.3C.4D.54.B5.(2013•武汉)如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是.516、如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②四边形CDFE不可能为正方形,③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是()A、①②③B、①④⑤(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.6.解:(1)∵A(8,0),B(0,6),8.(2013•宜昌)半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,⊙O与l相切于点F,DC在l上.(1)过点B作的一条切线BE,E为切点.①填空:如图1,当点A在⊙O上时,∠EBA的度数是;②如图2,当E,A,D三点在同一直线上时,求线段OA的长;(2)以正方形ABCD的边AD与OF重合的位置为初始位置,向左移动正方形(图3),至边BC与OF 重合时结束移动,M,N分别是边BC,AD与⊙O的公共点,求扇形MON的面积的范围.7.解:(1)①∵半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧,当点A在⊙O如图,过O 点作OK ⊥MN 于K ,∴∠MON=2∠NOK ,MN=2NK ,在Rt △ONK 中,sin ∠NOK=2NK NK ON =, ∴∠NOK 随NK 的增大而增大,∴∠MON 随MN 的增大而增大,∴当MN 最大时∠MON 最大,当MN 最小时∠MON 最小,①当N ,M ,A 分别与D ,B ,O 重合时,MN 最大,MN=BD ,∠MON=∠BOD=90°,S 扇形MON 最大=π(cm 2),②当MN=DC=2时,MN 最小,∴ON=MN=OM ,∴∠NOM=60°,S 扇形MON 最小=23π(cm 2), ∴23π≤S 扇形MON ≤π. 故答案为:30°.9.(2013•重庆)已知:如图①,在平行四边形ABCD 中,AB=12,BC=6,AD ⊥BD .以AD 为斜边在平8.解:(1)∵四边形ABCD是平行四边形,∴AD=BC=6.在Rt△ADE中,AD=6,∠EAD=30°,∴AE=AD•cos30°=33,DE=AD•sin30°=3,∴△AED的周长为:6+33+3=9+33.(2)在△AED向右平移的过程中:(I)当0≤t≤1.5时,如答图1所示,此时重叠部分为△D0NK.∵DD0=2t,∴ND0=DD0•sin30°=t,NK=ND0•tan30°=3t,∴S=S△D0NK=12ND0•NK=12t•3t=32t2;(II)当1.5<t≤4.5时,如答图2所示,此时重叠部分为四边形D0E0KN.∵AA0=2t,∴A0B=AB-AA0=12-2t,∴A0N=12A0B=6-t,NK=A0N•tan30°=33(6-t).∴S=S四边形D0E0KN=S△ADE-S△A0NK=12×3×33-12×(6-t)×33(6-t)=-36t2+23t-332;(III)当4.5<t≤6时,如答图3所示,此时重叠部分为五边形D0IJKN.∵AA 0=2t,∴A0B=AB-AA0=12-2t=D0C,∴A0N=12A0B=6-t,D0N=6-(6-t)=t,BN=A0B•cos30°=3(6-t);易知CI=BJ=A0B=D0C=12-2t,∴BI=BC-CI=2t-6,S=S梯形BND0I-S△BKJ=12[t+(2t-6)]• 3(6-t)-12•(12-2t)•33(12-2t)=-1336t2+203t-423.综上所述,S与t之间的函数关系式为:S=2223(0 1.5)2333-23-(1.5 4.5)62133-203-423(4.56)6t tS t t tt t t⎧≤≤⎪⎪⎪⎪=+<≤⎨⎪⎪+<≤⎪⎪⎩.(3)存在α,使△BPQ为等腰三角形.理由如下:经探究,得△BPQ∽△B1QC,故当△BPQ为等腰三角形时,△B1QC也为等腰三角形.(I)当QB=QP时(如答图4),则QB1=QC,∴∠B1CQ=∠B1=30°,即∠BCB1=30°,∴α=30°;(II)当BQ=BP时,则B1Q=B1C,若点Q在线段B1E1的延长线上时(如答图5),∵∠B1=30°,∴∠B1CQ=∠B1QC=75°,即∠BCB1=75°,∴α=75°.10.(2013•吉林)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点D、E、F分别是边AB、(2)在点P 从点F 运动到点D 的过程中,某一时刻,点P 落在MQ 上,求此时BQ 的长度;(3)当点P 在线段FD 上运动时,求y 与x 之间的函数关系式.11.解:(1)当点P 运动到点F 时,∵F 为AC 的中点,AC=6cm ,∴AF=FC=3cm ,∵P 和Q 的运动速度都是1cm/s ,∴BQ=AF=3cm ,∴CQ=8cm -3cm=5cm ,故答案为:5.(2)设在点P 从点F 运动到点D 的过程中,点P 落在MQ 上,如图1,则t+t -3=8,t=112, BQ 的长度为112×1=112(cm );(3)∵D 、E 、F 分别是AB 、BC 、AC 的中点,∴DE=12AC=12×6=3, DF=12BC=12×8=4, ∵MQ ⊥BC ,∴∠BQM=∠C=90°,∵∠QBM=∠CBA ,∴△MBQ ∽△ABC ,∴BQ MQ BC AC=, ∴86x MQ =,MQ=34x,分为三种情况:①当3≤x<4时,重叠部分图形为平行四边形,如图2,y=PN•PD=34x(7-x)即y=-34x2+214x;②当4≤x<112时,重叠部分为矩形,如图3,y=3[(8-X)-(X-3))]即y=-6x+33;③当112≤x≤7时,重叠部分图形为矩形,如图4,y=3[(x-3)-(8-x)]即y=6x-33.213.解:(1)如图,2如图2,由(1)知:抛物线的对称轴l为x=4,因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小∵B(6,0),C(0,2)(3)如图3,连接ME ,∵CE 是⊙M 的切线∴ME ⊥CE ,∠CEM=90°由题意,得OC=ME=2,∠ODC=∠MDE ∵在△COD 与△MED 中COA DEMODC MD EOC ME∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△COD ≌△MED (AAS ),∴OD=DE ,DC=DM设OD=x 则CD=DM=OM -OD=4-x 则RT △COD 中,OD 2+OC 2=CD 2, ∴x 2+22=(4-x )2∴x=32,∴D (32,0)设直线CE 的解析式为y=kx+b ∵直线CE 过C (0,2),D (32,0)两点,则3022k b b ⎧+=⎪⎨⎪=⎩,解得:432k b ⎧=-⎪⎨⎪=⎩。
七年级下册数学动点问题解题技巧

七年级下册数学动点问题解题技巧一、动点问题解题技巧概述。
1. 分析动点的运动轨迹。
- 明确动点是在直线(如数轴、坐标轴上的直线)上运动,还是在平面图形(如三角形、四边形的边或内部)中运动。
例如,在数轴上的动点,其位置可以用一个数来表示,而动点在平面直角坐标系中的坐标则需要用一对数(x,y)来表示。
2. 用含时间t(或其他变量)的代数式表示相关线段的长度。
- 若动点在数轴上,设动点的初始位置为a,速度为v,运动时间为t,则经过t时间后动点的位置为a + vt(当向右运动时v为正,向左运动时v为负),两点间的距离可以根据它们在数轴上的坐标相减的绝对值来表示。
- 在平面直角坐标系中,如果动点P(x,y)从点A(x_1,y_1)出发,沿x轴方向速度为v_x,沿y轴方向速度为v_y,运动时间为t,则x = x_1+v_xt,y=y_1 + v_yt。
对于线段长度,可以利用两点间距离公式d=√((x_2 - x_1)^2+(y_2 - y_1)^2),将坐标用含t 的式子代入来表示线段长度。
3. 根据题目中的等量关系列方程求解。
- 常见的等量关系有:线段相等、面积相等、三角形相似对应边成比例等。
例如,若两个三角形相似,根据相似三角形对应边成比例的性质列出方程,然后求解方程得到关于t(或其他变量)的值。
二、题目及解析。
1. 已知数轴上A、B两点对应的数分别为 - 1和3,点P为数轴上一动点,其对应的数为x。
- 若点P到点A、点B的距离相等,求点P对应的数x。
- 解析:因为点P到点A、点B的距离相等,所以| x - (-1)|=| x - 3|,即| x + 1|=| x - 3|。
当x+1=x - 3时,方程无解;当x + 1=-(x - 3)时,x+1=-x + 3,2x=2,解得x = 1。
- 若点P在点A、点B之间,且PA+PB = 4,求点P对应的数x。
- 解析:因为点P在A、B之间,PA=| x+1|=x + 1,PB=| x - 3|=3 - x,由PA+PB = 4可得x + 1+3 - x=4,恒成立,所以-1中的任意数都满足条件。
七年级动点问题大全

七年级动点问题大全(一)例1:如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b 满足|a+2|+(b+3a)2=0(1)求A、B两点之间的距离;(2)若在数轴上存在一点C,且AC=2BC,求C点表示的数;(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),①分别表示甲、乙两小球到原点的距离(用t表示);②求甲、乙两小球到原点的距离相等时经历的时间.例2:如图,有一数轴原点为O,点A所对应的数是-12,点A沿数轴匀速平移经过原点到达点B.(1)如果OA=OB,那么点B所对应的数是什么?(2)从点A到达点B所用时间是3秒,求该点的运动速度.(3)在(2)的条件下,从点A沿数轴匀速平移经过点K到达点C,所用时间是9秒,且KC=KA,分别求点K和点C所对应的数。
例3动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.例4:已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.(1)若点P到点A,点B的距离相等,求点P对应的数;(2)数轴上是否存在点P,使点P到点A、点B的距离之和为6?若存在,请求出x的值;若不存在,说明理由;(3)点A、点B分别以2个单位长度/分、1个单位长度/分的速度向右运动,同时点P以6个单位长度/分的速度从O点向左运动.当遇到A时,点P立即以同样的速度向右运动,并不停地往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?例5数轴上两个质点A、B所对应的数为-8、4,A、B两点各自以一定的速度在上运动,且A 点的运动速度为2个单位/秒.(1)点A、B两点同时出发相向而行,在原点处相遇,求B点的运动速度;(2)A、B两点以(1)中的速度同时出发,向数轴正方向运动,几秒钟时两者相距6个单位长度;(3)A、B两点以(1)中的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,且在运动过程中,始终有CB:CA=1:2,若干秒钟后,C停留在-10处,求此时B点的位置?例6:在数轴上,点A表示的数是-30,点B表示的数是170.(1)求A、B中点所表示的数.(2)一只电子青蛙m,从点B出发,以4个单位每秒的速度向左运动,同时另一只电子青蛙n,从A点出发以6个单位每秒的速度向右运动,假设它们在C点处相遇,求C点所表示的数.(3)两只电子青蛙在C点处相遇后,继续向原来运动的方向运动,当电子青蛙m处在A点处时,问电子青蛙n处在什么位置?(4)如果电子青蛙m从B点处出发向右运动的同时,电子青蛙n也向右运动,假设它们在D点处相遇,求D点所表示的数例7、已知数轴上有A、B、C三点,分别代表 - 24,- 10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒。
初中数学动点问题大全

初中数学动点问题大全动点问题一直是中考热点题型,近几年考察探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数值、线段或面积的最值问题等,下面就此问题的常见题型作简单介绍。
题型一动点形成的面积问题1.面积公式:三角形面积用12S ah =来表示,利用未知数的代数式来表示底和高。
2.面积比等于相似比的平方:面积无法用底和高表示时,利用相似三角形的面积比等于相似比的平方来求解,只需要知道相似比和另一个三角形面积即可表示。
3.相似三角形:当面积公式和面积比等于相似比的平方不能有效解题时,利用相似三角形的比例关系求解。
角度1:利用公式法解决动点面积问题例题1:在平面直角坐标系xOy 中,抛物线2y x bx c =-++经过点30A (,)和23B (,).过点A 的直线与y 轴的负半轴相交于点C ,且1tan 3CAO ∠=.(1)求这条抛物线的表达式及对称轴;(2)连接AB 、BC ,求ABC ∠的正切值;(3)若点D 在x 轴下方的对称轴上,当ABC ADC S S ∆∆=时,求点D 的坐标.变式1:如图,在平面直角坐标系xOy 中,已知点A 的坐标为(,3)a (其中4a >),射线O 与反比例函数12y x =的图像交于点P ,点B 、C 分别在函数12y x=的图像上,且//AB x 轴,//AC y 轴.(1)当点P 横坐标为6,求直线AO 的表达式;(2)联结BO ,当AB BO =时,求点A 坐标;(3)联结BP 、CP ,试猜想:ABP ACP S S ∆∆的值是否随a 的变化而变化?如果不变,求出ABP ACP S S ∆∆的值;如果变化,请说明理由.O x y (备用图)O xy解析:(1)∵反比例函数12y x=的图像经过横坐标为6的点P ,∴点P 的坐标为(6,2).设直线AO 的表达式为y kx =(0k ≠).将点P (6,2)代入y kx =,解得13k =.∴所求反比例函数的解析式为13y x =.(2)∵AB //x 轴,∴点B 纵坐标为3,将3y =代入12y x=,得4x =.∴B 坐标为(4,3).∵AB =BO ,∴224(40)(30)a -=-+-9a =.∴点A 坐标为(9,3).(3)不变.延长AB 交y 轴于点D ,延长AC 交x 轴于点E ,∴32ADO AEO S S a ∆∆==.∵点C 坐标为(a ,12a ).∴6CEO S ∆=,同理6BDO S ∆=,∴ADO BDO AEO CEO S S S S ∆∆∆∆-=-,即ABO ACO S S ∆∆=.∵△ABP 与△ABO 同高,∴ABP ABO S AP S AO ∆∆=.同理ACP ACO S AP S AO ∆∆=.∴1ABP ACP S S ∆∆=.即当a 变化时,ABP ACPS S ∆∆的值不变,且恒为1变式2:如图,在直角坐标系中,一条抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(3,0)B ,(0,4)C ,点A 在x 轴的负半轴上,4OC OA =;(1)求这条抛物线的解析式,并求出它的顶点坐标;(2)联结AC 、BC ,点P 是x 轴正半轴上一个动点,过点P 作//PM BC 交射线AC 于点M ,联结CP ,若CPM ∆的面积为2,则请求出点P 的坐标;解析:(1)设这条抛物线的解析式为2(0)y ax bx c a =++≠它的顶点坐标为16(1,)3(2)过点P 作PH AC ⊥,垂足为H .∵P 点在x 轴的正半轴上,∴设0P x (,).∵A )0,1(-,∴1PA x =+.∵在Rt AOC ∆中,222OA OC AC +=;又∵14OA OC ==,∴17AC =90sin 117PH PH PHA CAO AP x ∠=︒∴∠===+ 17PH =//BP CM PM BC AB AC ∴= ;300B P x (,),(,)1点P 在点B 的左侧时,3BP x =-,∴3417x -=17(3)4x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)12217x -=解得110x .P =∴(,)2点P 在点B 的右侧时,3BP x =-,∴3417x -=17(3)x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)122417x -=解得11x =+,21x =-(不合题意,舍去)∴P(1+0).综上所述,P 的坐标为(1,0)或(1+0)角度2:利用面积比等于相似比的平方解决动点面积问题例题2:如图,已知在梯形ABCD 中,//AD BC ,5AB DC ==,4AD =.M 、N 分别是边AD 、BC 上的任意一点,联结AN 、DN .点E 、F 分别在线段AN 、DN 上,且//ME DN ,//MF AN ,联结EF .(1)如图1,如果//EF BC ,求EF 的长;(2)如果四边形MENF 的面积是ADN ∆的面积的38,求AM 的长;解析:(1)∵AD //BC ,EF //BC ,∴EF //A D .又∵ME //DN ,∴四边形EF DM 是平行四边形.∴EF =DM .同理可证,EF =AM .∴AM =DM .∵AD =4,∴122EF AM AD ===.(2)∵38ADN MENF S S ∆=四边形,∴58AME DMF ADN S S S ∆∆∆+=.即得58AME DMF ADN ADN S S S S ∆∆∆∆+=.∵ME //DN ,∴△AME ∽△AN D .∴22AME ADN S AM S AD∆∆=.同理可证,△DM F ∽△DN A .即得22DMF ADN S DM S AD ∆∆=.设AM =x ,则4DM AD AM x =-=-.∴22(4)516168x x -+=.即得2430x x -+=.解得11x =,23x =.∴AM 的长为1或3.A B CD M N EF (图1)AB C D M N E F变式3:已知直线1l 、2l ,12//l l ,点A 是1l 上的点,B 、C 是2l 上的点,AC BC ⊥,60ABC ∠=︒,4AB =,O 是AB 的中点,D 是CB 延长线上的点,将DOC ∆沿直线CO 翻折,点D 与'D 重合.(1)如图1,当点'D 落在直线1l 上时,求DB 的长;(2)延长DO 交1l 于点E ,直线'OD 分别交1l 、2l 于点M 、N .①如图2,当点E 在线段AM 上时,设x AE =,y DN =,求y 关于x 的函数解析式及其定义域;②若DON ∆的面积为323时,求AE 的长.解析:变式4:如图1,在梯形ABCD 中,//AD BC ,对角线BC AC ⊥,4AD =cm ,︒=∠45D ,3=BC cm .(1)求B ∠cos 的值;(2)点E 为BC 延长线上的动点,点F 在线段CD 上(点F 与点C 不重合),且满足ADE AFC ∠=∠,如图2,设x BE =,y DF =,求y 关于x 的函数解析式,并写出函数的定义域;(3)点E 为射线BC 上的动点,点F 在射线CD 上,仍然满足ADE AFC ∠=∠,当AFD ∆的面积为2cm 2时,求BE 的长.解析:(1)∵//AD BC ,∴ACB DAC ∠=∠.∵AC BC ⊥,∴90ACB ∠=︒.∴90DAC ∠=︒.∵45D ∠=︒,∴45ACD ∠=︒.∴AD AC =.∵4AD =,∴4AC =.∵3=BC ,∴5AB ==.∴3cos 5BC B AB ∠==.(2)∵//AD BC ,∴ADF DCE ∠=∠.∵AFC FDA FAD ∠=∠+∠,ADE FDA EDC ∠=∠+∠,又AFC ADE ∠=∠,∴FAD EDC ∠=∠.∴ADF DCE ∆~∆.∴AD DF DC CE =.在Rt ADC ∆中,222AC AD DC +=,又4==AC AD ,∴24=DC .∵x BE =,∴3-=x CE .y DF =,∴3244-=x y .22322-=x y .定义域为113<<x .(3)当点E 在BC 的延长线上,由(2)可得:ADF DCE ∆~∆,∴2(DC AD S S DCE ADF =∆∆.∵2AFD S ∆=,4=AD ,24=DC ,∴4=∆DCE S .∵AC CE S DCE ⨯⨯=∆21,∴44)3(21=⨯-⨯BE ,∴5BE =.当点E 在线段BC 上,同理可得:44)3(21=⨯-⨯BE .∴1BE =.所以BE 的长为5或1.角度3:利用锐角三角比法解决动点面积问题例题3:已知在平面直角坐标系xoy (如图)中,抛物线212y x bx c =++经过点(4,0)A 、点(0,4)C -,点B 与点A 关于这条抛物线的对称轴对称;(1)用配方法求这条抛物线的顶点坐标;(2)联结AC 、BC ,求ACB ∠的正弦值;(3)点P 是这条抛物线上的一个动点,设点P 的横坐标为(0)m m >,过点P 作y 轴的垂线PQ ,垂足为Q ,如果QPO BCO ∠=∠,求m 的值;解析:变式5:已知在平面直角坐标系xoy 中,抛物线2(0)y ax bx c a =++>与x 轴相交于(1,0),(3,0)A B -两点,对称轴l 与x 轴相交于点C ,顶点为点D ,且ADC ∠的正切值为12.(1)求顶点D 的坐标;(2)求抛物线的表达式;(3)F 点是抛物线上的一点,且位于第一象限,联结AF ,若FAC ADC ∠=∠,求F 点的坐标.解析:(1)∵抛物线与x 轴相交于()1,0A -,()3,0B 两点,∴对称轴l :直线1x =,2AC =∵90ACD ∠=︒,1tan 2ADC ∠=,∴4CD =,∵0a >,∴()1,4D -(2)设()214y a x =--将1,0x y =-=代入上式,得,1a =所以,这条抛物线的表达为223y x x =--(3)过点F 作FH x ⊥轴,垂足为点H设()2,23F x x x --,∵FAC ADC ∠=∠,∴tan tan FAC ADC ∠=∠,∵1tan 2ADC ∠=,∴1tan 2FH FAC AH ∠==∵223FH x x =--,1AH x =+,∴223112x x x --=+解得172x =,21x =-(舍),∴79,24F ⎛⎫ ⎪⎝⎭巩固1:如图,在直角坐标系xOy 中,抛物线c ax ax y +-=22与x 轴的正半轴相交于点A 、与y 轴的正半轴相交于点B ,它的对称轴与x 轴相交于点C ,且OBC OAB ∠=∠,3AC =.(1)求此抛物线的表达式;(2)如果点D 在此抛物线上,DF OA ⊥,垂足为F ,DF 与线段AB 相交于点G ,且2:3:=∆∆AFG ADG S S ,求点D 的坐标.解析:(1)∵抛物线c ax ax y +-=22的对称轴为直线12=--=a a x ,∴OC =1,OA =OC +AC =4,∴点A (4,0).∵∠OBC =∠OAB ,∴tan ∠OAB =tan ∠OBC ,∴OBOC OA OB =,∴OB OB 14=,∴OB =2,∴点B (0,2),∴⎩⎨⎧+-==,8160,2c a a c ∴⎪⎩⎪⎨⎧=-=.2,41c a ∴此抛物线的表达式为221412++-=x x y .(2)由2:3:=∆∆AFG ADG S S 得DG :FG =3:2,DF :FG =5:2,设m OF =,得m AF -=4,221412++-=m m DF ,由FG //OB ,得OA AF OB FG =,∴24m FG -=,∴2:524:)22141(2=-++-m m m ,∴01272=+-m m ,∴4,321==m m (不符合题意,舍去),∴点D 的坐标是(3,45)巩固2:如图,已知ABC ∆与BDE ∆都是等边三角形,点D 在边AC 上(不与A 、C 重合),DE 与AB 相交于点F .(1)求证:BCD DAF ∆∆∽;(2)若1BC =,设CD x =,AF y =;①求y 关于x 的函数解析式及定义域;②当x 为何值时,79BEF BCD S S ∆∆=?(1)证明:∵ABC ∆与BDE ∆都是等边三角形,∴60A C BDE ∠=∠=∠=︒A C BO yx∵ADF BDE C DBC ∠+∠=∠+∠,∴ADF DBC ∠=∠,∴BCD ∆∽DAF∆(2)∵BCD ∆∽DAF ∆,∴BC CD AD AF=∵1BC =,设CD x =,AF y =,∴11x x y=-,∴()201y x x x =-<<(3)解法一:∵ABC ∆与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∴BE BF BC BD=,∵BE BD =,1BC =,∴2BE BF =∵EBF ∆∽CBD ∆,79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==,∴279BE BF ==,∴29AF =∴229x x -=,解得1221,33x x ==,∴当13x =或23时,79BEF BCD S S ∆∆=解法二:∵△ABC 与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∵79BEF BCD S S ∆∆=,∴2279BEF BCDS BE S BC ∆∆==∵1BC =,BE BD =,∴279BD =过点B 作BH AC ⊥于点H ,∵60C ∠=︒,∴BH =16DH =,12CH =当点D 在线段CH 上时,111263CD CH DH =-=-=当点D 在线段CH 的延长线上时,112263CD CH DH =+=+=综上所述,当13x =或23时,79BEF BCD S S ∆∆=.巩固3:在矩形ABCD 中,4AB =,6AD =,点P 是射线DA 上一动点,将三角板直角顶点重合于点P ,三角板两直角边中的一边始终经过点C ,另一直角边交射线BA 于点E .(1)判断EAP ∆与PDC ∆一定相似吗?请证明你的结论;(2)设PD x =,AE y =,求y 与x 的函数关系式,并写出它的定义域;(3)是否存在这样的点P ,是EAP ∆周长等于PDC ∆周长的2倍?若存在,请求出PD 的长度;若不存在,请简要说明理由.解析:(1)△EAP ∽△PDC①当P 在AD 边上时,如图(1):∵矩形ABCD ,==90D A ∠∠ ,∴1+2=90∠∠据题意=90CPE ∠ ∴3+2=90∠∠ ,∴1=3∠∠,∴△EAP ∽△PDC②当P 在AD 边上时,如图(2):同理可得△EAP ∽△PDC(2)若点P 在边AD 上,据题意:PD x =6PA x =-4DC =AE y =又∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴22613442x x y x x -==-+()06x <<若点P 在边DA 延长线上时,据题意PD x =,则6PA x =-,4DC =,AE y =,∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴()2664x x y x -=>(3)假如存在这样的点P ,使△EAP 周长等于PDC ∆的2倍①若点P 在边AD 上∵△EAP ∽△PDC ∴():6:4EAP PDC C C x =- ,∴()6:42x -=,∴2x =-不合题意舍去;②若点P 在边DA 延长线上,同理得()6:42x -=,∴14x =综上所述:存在这样的点P 满足题意,此时14PD =巩固4:如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C .(1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M 的坐标.解析:(1)∵抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C ∴44201640c a b c a b c =-⎧⎪-+=⎨⎪++=⎩解得方程组的解为1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴这个抛物线的解析式为:2142y x x =--顶点为9(1,)2-(2)如图:取OA 的中点,记为点N ∵OA =OC =4,∠AOC =90°∴∠ACB =45°∵点N 是OA 的中点∴ON =2又∵OB =2∴OB =ON又∵∠BON =90°∴∠ONB =45°∴∠ACB =∠ONB∵∠OMB +∠OAB =∠ACB ∠NBA +∠OAB =∠ONB ∴∠OMB =∠NBA1°当点M 在点N 的上方时,记为M 1∵∠BAN =∠M 1AB ,∠NBA =∠OM 1B ,∴△ABN ∽△AM 1B ∴1AN AB AB AM =又∵AN =2,AB =∴110AM =又∵A (0,—4)∴1(0,6)M 2°当点M 在点N 的下方时,记为M 2,点M 1与点M 2关于x 轴对称,∴2(0,6)M -综上所述,点M 的坐标为(0,6)或(0,6)-题型二动点形成的相切问题1.直线和圆相切:圆心到直线距离等于半径构造直角三角形,利用三角比、勾股定理等来表示圆心到直线距离及半径,建立等量关系2.圆和圆相切:两圆半径和等于圆心距.利用平行线分线段成比例、勾股定理、三角比、相似等表示相关线段,建立等量关系角度4:直线与圆相切问题例题4:如图,在ABC ∆中,10,12,AB AC BC ===点E F 、分别在边BC AC 、上(点F 不与点A 、C 重合)//EF AB .把ABC ∆沿直线EF 翻折,点C 与点D 重合,设FC x =.(1)求B ∠的余切值;(2)当点D 在ABC ∆的外部时,DE DF 、分别交AB 于M 、N ,若MN y =,求y 关于x 的函数关系式并写出定义域;(3)(下列所有问题只要直接写出结果即可)以E 为圆心、BE 长为半径的E 与边AC 1没有公共点时,求x 的取值范围.2一个公共点时,求x 的取值范围.3两个公共点时,求x 的取值范围.AE CB FA B D GC EF变式6:已知:矩形ABCD 中,过点B 作BG ⊥AC 交AC 于点E ,分别交射线AD 于F 点、交射线CD 于G 点,BC =6.(1)当点F 为AD 中点时,求AB 的长;(2)联结AG ,设AFG AB x S y ∆==,,求y 关于x 的函数关系式及自变量x 的取值范围;(3)是否存在x 的值,使以D 为圆心的圆与BC 、BG 都相切?若存在,求出x 的值;若不存在,请说明理由.解析:(1)∵点F 为AD 中点,且AD =BC =6,∴AF =3∵矩形ABCD 中,∠ABC =90°,BG ⊥AC 于点E ,∴∠ABE +∠EBC =90°,∠AC ∠EBC =90°∴∠ABE =∠ACB ,∴△ABF ∽△BCF ,∴AB AF BC AB =∴AB =23(2)由(1)可得△ABF ∽△BCF ∴AB AF BC AB =∵AB =x ,BC =6∴AF =62x ;同理可得:CG =x36①当F 点在线段AD 上时DG =CG -CD =x x x x 23636-=-∴S ⊿AFG =1236213x x CG AF -=⋅。
初中数学动点问题总结

初二动点问题1.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB 边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?分析:(1)四边形PQCD为平行四边形时PD=CQ.(2)四边形PQCD为等腰梯形时QC-PD=2CE.(3)四边形PQCD为直角梯形时QC-PD=EC.所有的关系式都可用含有t的方程来表示,即此题只要解三个方程即可.解答:解:(1)∵四边形PQCD平行为四边形∴PD=CQ∴24-t=3t解得:t=6即当t=6时,四边形PQCD平行为四边形.(2)过D作DE⊥BC于E则四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即3t-(24-t)=4解得:t=7(s)即当t=7(s)时,四边形PQCD为等腰梯形.(3)由题意知:QC-PD=EC时,四边形PQCD为直角梯形即3t-(24-t)=2解得:t=6.5(s)即当t=6.5(s)时,四边形PQCD为直角梯形.点评:此题主要考查了平行四边形、等腰梯形,直角梯形的判定,难易程度适中.2.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.分析:(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的性质解答.解答:解:(1)∵CE平分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理,OC=OF,∴OE=OF.(2)当点O运动到AC中点处时,四边形AECF是矩形.如图AO=CO,EO=FO,∴四边形AECF为平行四边形,∵CE平分∠ACB,∴∠ACE= ∠ACB,同理,∠ACF= ∠ACG,∴∠ECF=∠ACE+∠ACF= (∠ACB+∠ACG)= ×180°=90°,∴四边形AECF是矩形.(3)△ABC是直角三角形∵四边形AECF是正方形,∴AC⊥EN,故∠AOM=90°,∵MN∥BC,∴∠BCA=∠AOM,∴∠BCA=90°,∴△ABC是直角三角形.本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.3.如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A 作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,(2)CB、CN已知,根据勾股定理可求CA=5,即可表示CM;四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;(3)可先根据QN平分△ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t的值.然后根据得出的t的值,求出△MNC的面积,即可判断出△MNC的面积是否为△ABC 面积的一半,由此可得出是否存在符合条件的t值.(4)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:①当MP=MC时,那么PC=2NC,据此可求出t的值.②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.综上所述可得出符合条件的t的值.解答:解:(1)∵AQ=3-t∴CN=4-(3-t)=1+t在Rt△ABC中,AC2=AB2+BC2=32+42∴AC=5在Rt△MNC中,cos∠NCM= = ,CM= .(2)由于四边形PCDQ构成平行四边形∴PC=QD,即4-t=t(3)如果射线QN将△ABC的周长平分,则有:MN+NC=AM+BN+AB即:(1+t)+1+t= (3+4+5)解得:t= (5分)而MN= NC= (1+t)∴S△MNC= (1+t)2= (1+t)2当t= 时,S△MNC=(1+t)2= ≠×4×3∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分.(4)①当MP=MC时(如图1)则有:NP=NC即PC=2NC∴4-t=2(1+t)解得:t=②当CM=CP时(如图2)则有:(1+t)=4-t解得:t=③当PM=PC时(如图3)则有:在Rt△MNP中,PM2=MN2+PN2而MN= NC= (1+t)PN=NC-PC=(1+t)-(4-t)=2t-3∴[ (1+t)]2+(2t-3)2=(4-t)2解得:t1= ,t2=-1(舍去)∴当t= ,t= ,t= 时,△PMC为等腰三角形点评:此题繁杂,难度中等,考查平行四边形性质及等腰三角形性质.考查学生分类讨论和数形结合的数学思想方法.4.如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形;(2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形;(3)以P,Q,M,N为顶点的四边形能否为等腰梯形?如果能,求x的值;如果不能,请说明理由.分析:以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形的必须条件是点P、N重合且点Q、M不重合,此时AP+ND=AD即2x+x2=20cm,BQ+MC ≠BC即x+3x≠20cm;或者点Q、M重合且点P、N不重合,此时AP+ND≠AD即2x+x2≠20cm,BQ+MC=BC即x+3x=20cm.所以可以根据这两种情况来求解x的值.以P,Q,M,N为顶点的四边形是平行四边形的话,因为由第一问可知点Q只能在点M的左侧.当点P在点N的左侧时,AP=MC,BQ=ND;当点P在点N的右侧时,AN=MC,BQ=PD.所以可以根据这些条件列出方程关系式.如果以P,Q,M,N为顶点的四边形为等腰梯形,则必须使得AP+ND≠AD即2x+x2≠20cm,BQ+MC≠BC即x+3x≠20cm,AP=ND即2x=x2,BQ=MC即x=3x,x≠0.这些条件不能同时满足,所以不能成为等腰梯形.解答:解:(1)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形.①当点P与点N重合时,由x2+2x=20,得x1= -1,x2=- -1(舍去).因为BQ+CM=x+3x=4(-1)<20,此时点Q与点M不重合.所以x= -1符合题意.②当点Q与点M重合时,由x+3x=20,得x=5.此时DN=x2=25>20,不符合题意.故点Q与点M不能重合.所以所求x的值为-1.(2)由(1)知,点Q只能在点M的左侧,①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2),解得x1=0(舍去),x2=2.当x=2时四边形PQMN是平行四边形.②当点P在点N的右侧时,由20-(x+3x)=(2x+x2)-20,解得x1=-10(舍去),x2=4.当x=4时四边形NQMP是平行四边形.所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.(3)过点Q,M分别作AD的垂线,垂足分别为点E,F.由于2x>x,所以点E一定在点P的左侧.若以P,Q,M,N为顶点的四边形是等腰梯形,则点F一定在点N的右侧,且PE=NF,即2x-x=x2-3x.解得x1=0(舍去),x2=4.由于当x=4时,以P,Q,M,N为顶点的四边形是平行四边形,所以以P,Q,M,N为顶点的四边形不能为等腰梯形.点评:本题考查到三角形、平行四边形、等腰梯形等图形的边的特点.5.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M 从点A开始,沿边AD向点D运动,速度为1cm/s;点N从点C开始,沿边CB向点B运动,速度为2cm/s、点M、N分别从点A、C出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.(1)当t为何值时,四边形MNCD是平行四边形?(2)当t为何值时,四边形MNCD是等腰梯形?分析:(1)根据平行四边形的性质,对边相等,求得t值;(2)根据等腰梯形的性质,下底减去上底等于12,求解即可.解答:解:(1)∵MD∥NC,当MD=NC,即15-t=2t,t=5时,四边形MNCD是平行四边形;(2)作DE⊥BC,垂足为E,则CE=21-15=6,当CN-MD=12时,即2t-(15-t)=12,t=9时,四边形MNCD是等腰梯形点评:考查了等腰梯形和平行四边形的性质,动点问题是中考的重点内容.6.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P 从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,设运动时间为t(s).(1)设△BPQ的面积为S,求S与t之间的函数关系;(2)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?分析:(1)若过点P作PM⊥BC于M,则四边形PDCM为矩形,得出PM=DC=12,由QB=16-t,可知:s= PM×QB=96-6t;(2)本题应分三种情况进行讨论,①若PQ=BQ,在Rt△PQM中,由PQ2=PM2+MQ2,PQ=QB,将各数据代入,可将时间t求出;②若BP=BQ,在Rt△PMB中,由PB2=BM2+PM2,BP=BQ,将数据代入,可将时间t求出;③若PB=PQ,PB2=PM2+BM2,PB=PQ,将数据代入,可将时间t求出.解答:解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.∴PM=DC=12,∵QB=16-t,∴s= •QB•PM= (16-t)×12=96-6t(0≤t≤).(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16-t)2,解得;②若BP=BQ,在Rt△PMB中,PB2=(16-2t)2+122,由PB2=BQ2得(16-2t)2+122=(16-t)2,此方程无解,∴BP≠PQ.③若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122得,t2=16(不合题意,舍去).综上所述,当或时,以B、P、Q为顶点的三角形是等腰三角形.点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.7.直线y=- 34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 485时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.分析:(1)分别令y=0,x=0,即可求出A、B的坐标;(2))因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O到A 的时间是8秒,点P的速度是2,从而可求出,当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA 上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得 PD=48-6t5,利用S= 12OQ×PD,即可求出答案;(3)令S= 485,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.解答:解:(1)y=0,x=0,求得A(8,0)B(0,6),(2)∵OA=8,OB=6,∴AB=10.∵点Q由O到A的时间是 81=8(秒),∴点P的速度是 6+108=2(单位长度/秒).当P在线段OB上运动(或O≤t≤3)时,OQ=t,OP=2t,S=t2.当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,如图,做PD⊥OA于点D,由 PDBO=APAB,得PD= 48-6t5.∴S= 12OQ•PD=- 35t2+245t.(3)当S= 485时,∵ 485>12×3×6∴点P在AB上当S= 485时,- 35t2+245t= 485∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8AD= 82-(245)2= 325∴OD=8- 325= 85∴P( 85, 245)M1( 285, 245),M2(- 125, 245),M3( 125,- 245)点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.。
初中数学动点问题归纳

…………………………动点问题题型方法归纳动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、三角形边上动点3x???6yP、QO B、A点出发,与坐标轴分别交于、(2009年齐齐哈尔市)直线同时从两点,动点14yQ OAA个单点,运动停止.点运动,速度为每秒沿线段1同时到达BO APB沿路线→→运动.位长度,点B、A(1)直接写出两点的坐标;Ptt OPQ△SQS的运动时间为,求出秒,2)设点之间与的面积为(xQOA 的函数关系式;48?SQP、O、MP的(3)当的坐标,并直接写出以点为顶点的平行四边形的第四个顶点时,求出点5坐标.6)B(0,(8,0)解:1、A2S=t3时,<t<2、当0 /8(8-t)t8时,S=3 当3<t<所有时间分段分类;P到拐点B)问按点提示:第(2探究第四点构成平行四边形时按已知线段身份不同,、Q第(3)问是分类讨论:已知三定点O、P为边。
然后画出各类OQ为对角线,③OP为对角线、OQ为边,②OP为边、OQ分类-----①OP为边、的图形,根据图形性质求顶点坐标。
年衡阳市)(20092、,的直径,弦BC=2cm如图,AB是⊙O o.∠ABC=60 的直径;)求⊙O(1 O相切;BD长为多少时,CD与⊙延长线上一点,连结(2)若D是ABCD,当点出发沿的速度从BF以1cm/s的速度从E以2cm/sA点出发沿着AB方向运动,同时动点(3)若动点t)t?2)(t(s0?BC方向运动,设运动时间为为直角三角形.为何值时,△BEF,连结EF,当C C CFFE A BABAD OEOO B)图(3)图(2图(1)3)问按直角位置分类讨论注意:第(0)?3(?3a??ya(x1)2),02A(?D,经过点,已知抛物线如图,2009(、3重庆綦江)抛物线的顶点为(((((((.…………………………xx CO BCOMAD∥OMBD.连结轴的直线交射线过在作射线于点,.过顶点轴正半轴上,平行于(1)求该抛物线的解析式;Ot(s)OMPP.问出发,以每秒1个长度单位的速度沿射线运动的时间为(2)若动点运动,设点从点tDAOP分别为平行四边形?直角梯形?等腰梯形?当为何值时,四边形M yDCOQ OB?OCB个长度同时出发,分别以每秒分别从点,动点1和动点(3)若和点BOOC运动,当其中一个点停止运动时另一个点也随和单位和2个长度单位的速度沿Ptt BCPQPQs)(四边形当,之停止运动.设它们的运动的时间为连接为何值时,,AQOxB PQ的面积最小?并求出最小值及此时的长.°注意:发现并充分运用特殊角∠DAB=60 的面积最小。
初中数学动点问题归纳

初中数学动点问题归纳动点问题是数学中常见的问题类型之一,它涉及到点在一定规律下的运动轨迹及相关的计算。
在初中数学学习过程中,学生们大多会接触到动点问题,并掌握解决此类问题的方法和技巧。
本文将对初中数学动点问题进行归纳总结,帮助初中学生更好地理解和解决这类问题。
1. 直线运动问题直线运动问题是最基本的动点问题之一。
在这类问题中,点按照直线路径运动,常涉及到时间、距离和速度的关系。
解决直线运动问题时,可以使用速度等于位移除以时间的公式来计算,即 v = s/t。
例子1:小明从家里骑自行车到学校,全程15公里,用时1小时。
求小明的平均速度。
解析:根据公式,平均速度 v = s/t = 15/1 = 15 km/h例子2:小红开车从A市到B市,全程200公里,平均时速60km/h。
求小红从A市到B市的行驶时间。
解析:根据公式,时间 t = s/v = 200/60 = 3.33 小时≈ 3小时20分2. 圆周运动问题圆周运动问题中,点按照圆形轨迹运动。
这类问题通常涉及到半径、圆周长和角度的计算与关系。
解决圆周运动问题时,需要掌握圆周长的计算公式,即 c = 2πr,其中 r 为半径。
例子1:一个半径为5米的圆,它的周长是多少?解析:根据公式,周长c = 2πr = 2 × 3.14 × 5 ≈ 31.4米例子2:一辆汽车在圆形赛道上行驶,赛道半径为100米,驾驶员开车一圈需要用时50秒。
求汽车的平均速度。
解析:首先计算圆周长c = 2πr = 2 × 3.14 × 100 = 628米然后计算平均速度v = c/t = 628/50 ≈ 12.56 m/s3. 直角三角形运动问题直角三角形运动问题是指点在直角三角形内运动,涉及到时间、速度和直角三角形边长的关系。
解决直角三角形运动问题时,可以利用勾股定理或三角函数来计算相关的未知量。
例子1:一个直角三角形的两条边长分别为3米和4米,角度为90度。
初中数学动点问题

关于动点问题的总结 “动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静关键:动中求静.数学思想:分类思想 函数思想 方程思想 数形结合思想 转化思想函数揭示了运动变化过程中量与量之间的变化规律,和动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,一、应用勾股定理建立函数解析式例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,H MN G P O AB图1于是线段GO 、GP 、GH 中,有长度保持不变的线段,这条线段是GH=32NH=2132⋅OP=2. (2)在Rt △POH 中,22236x PH OP OH -=-=, ∴2362121x OH MH -==.在Rt △MPH 中,.∴y =GP=32MP=233631x + (0<x <6).(3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意.②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2(2006年·山东)如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y .(1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式;(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.A EDC B图2解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°,∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴ACBD CE AB =, ∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90. 当=-2αβ︒90时,函数解析式x y 1=成立.例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长.解:(1)连结OD.根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP.A 3(2)3(1)又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54x AD =, ∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x y x 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时,①若EP 交线段CB 的延长线于点F,如图3(1),则CF=4. ∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE,∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE.∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2.类似①,可得CF=CE.∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6.三、应用求图形面积的方法建立函数关系式例4(2004年·上海)如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .A B C O H(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ).(2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形,(特殊角、特殊图形的性质、图形的特殊位置。
七年级动点问题的重要知识点

七年级动点问题的重要知识点动点问题是初中数学中的一个重要知识点,涉及到数学的基础概念和计算方法。
在七年级学习动点问题时,需要掌握以下几个重要知识点。
一、点的坐标在笛卡尔直角坐标系中,每个点都有唯一的坐标表示。
坐标是由两个数值组成的有序数对,表示点在平面直角坐标系中的位置。
第一个数值表示点在x轴上的位置,第二个数值表示点在y轴上的位置。
坐标的顺序是(x, y)。
二、点的对称点的对称分为x轴对称、y轴对称和原点对称。
对称轴是指将坐标系平面分割成两个相等的部分的轴线。
点可以在对称轴上对称,即对称后的点和原点之间的距离保持不变。
关于对称的概念掌握后,则可以用来解决很多动点问题中的计算问题。
三、直线直线是数学中常见的图形,由无数个点组合形成。
在直角坐标系中,可以用一条线段上的两个点的坐标表达一条直线,也可以用一般式方程和斜率方程来表示。
四、方程方程是数学中用来描述两个量之间相互关系的式子。
在动点问题中,常用方程来描述点的运动轨迹。
五、线性函数线性函数是数学中常见的函数类型,由常数项和一次项组成。
在七年级中,学生已经学习了线性函数的基础知识,如斜率、截距等。
六、圆圆是一个几何形状,由一个点到平面上所有其他点的距离相等。
在平面直角坐标系中,可以用圆心和半径来表示一个圆。
圆的方程一般由(x-a)²+(y-b)²=r²表示,其中a和b分别是圆心在x轴和y轴上的坐标,r是圆的半径。
七、角角是数学中一个重要的概念,它表示两个射线的夹角。
角可以表示为度数或弧度单位。
以上是七年级动点问题的重要知识点。
通过掌握这些基础概念和计算方法,可以帮助学生正确解决数学动点问题中的计算问题。
八年级数学上动点知识点

八年级数学上动点知识点动点是数学中一个很重要的概念,在我们的生活和工作中都有广泛的应用。
掌握好动点的知识点可以让我们更好地解决实际问题,因此,在这篇文章中,我将为大家介绍八年级数学上动点的一些基本知识点和应用技巧。
一、动点的定义动点是指在一个几何图形中,点随着某个规律运动的过程中所经过的所有位置构成的集合。
例如,在一条直线上,取定一个点A作为起点,另外再取定一点P作为运动的点。
当点P随着某个规律从起点A向右移动时,它所经过的所有位置所构成的集合,就是一个动点。
二、动点的性质1、动点的位置一般是用函数的形式进行表达的。
例如,在上面的例子中,我们可以用点P沿着坐标轴运动的函数来表示它的位置:P(x,t)=A+(x(t),0),其中x(t)为随时间而改变的位置函数。
2、动点可以是连续的,也可以是不连续的。
例如,当一个物体做匀速直线运动时,它所经过的所有位置构成的集合就是一个连续的动点。
而当一个物体做非匀速运动时,它所经过的所有位置可能是不连续的动点。
3、动点的运动轨迹可以是一个简单的曲线,也可以是由多个曲线段组成的复杂曲线。
例如,在一个圆周上,取定一点作为动点,在圆周上做匀速圆周运动,它所经过的所有位置构成的集合,就是一个简单曲线的动点。
而当一个物体沿着曲线运动时,它所经过的所有位置就构成了一个复杂曲线的动点。
三、动点的应用1、在动点问题中,我们需要确定动点的位置,并计算它在某个特定时间的位置。
例如,在一条公路上,一辆汽车开始沿着公路匀速行驶,它的起点是公路的起点,而它以每小时60公里的速度向前行驶。
如果在2小时后,我们希望知道汽车此时的位置,我们可以用动点的计算方法来求出汽车现在所在的位置。
2、利用动点的概念,我们可以解决一些几何问题。
例如,在一个公平的赛道上,两个人以相同的速度开始奔跑。
假设他们的起点不同,我们希望知道他们在比赛中谁会先到达终点。
我们可以利用动点的方法来解决这个问题。
四、动点问题的解法1、根据实际情况确定动点的位置。
初中数学专题复习(动点问题)

初中数学专题复习(动点问题)一.一次函数动点问题1.(2020•南宁)如图1,在平面直角坐标系中,直线l1:y=x+1与直线l2:x=﹣2相交于点D,点A是直线l2上的动点,过点A作AB⊥l1于点B,点C的坐标为(0,3),连接AC,BC.设点A的纵坐标为t,△ABC的面积为s.(1)当t=2时,请直接写出点B的坐标;(2)s关于t的函数解析式为s=,其图象如图2所示,结合图1、2的信息,求出a与b的值;(3)在l2上是否存在点A,使得△ABC是直角三角形?若存在,请求出此时点A的坐标和△ABC的面积;若不存在,请说明理由.解:(1)如图1,连接AG,当t=2时,A(﹣2,2),设B(x,x+1),在y=x+1中,当x=0时,y=1,∴G(0,1),∵AB⊥l1,∴∠ABG=90°,∴AB2+BG2=AG2,即(x+2)2+(x+1﹣2)2+x2+(x+1﹣1)2=(﹣2)2+(2﹣1)2,解得:x1=0(舍),x2=﹣,∴B(﹣,);(2)如图2可知:当t=7时,s=4,把(7,4)代入s=中得:+7b﹣=4,解得:b=﹣1,如图3,过B作BH∥y轴,交AC于H,由(1)知:当t=2时,A(﹣2,2),B(﹣,),∵C(0,3),设AC的解析式为:y=kx+n,则,解得,∴AC的解析式为:y=x+3,∴H(﹣,),∴BH=﹣=,∴s===,把(2,)代入s=a(t+1)(t﹣5)得:a(2+1)(2﹣5)=,解得:a=﹣;(3)存在,设B(x,x+1),分两种情况:①当∠CAB=90°时,如图4,∵AB⊥l1,∴AC∥l1,∵l1:y=x+1,C(0,3),∴AC:y=x+3,∴A(﹣2,1),∵D(﹣2,﹣1),在Rt△ABD中,AB2+BD2=AD2,即(x+2)2+(x+1﹣1)2+(x+2)2+(x+1+1)2=22,解得:x1=﹣1,x2=﹣2(舍),∴B(﹣1,0),即B在x轴上,∴AB==,AC==2,∴S△ABC===2;②当∠ACB=90°时,如图5,∵∠ABD=90°,∠ADB=45°,∴△ABD是等腰直角三角形,∴AB=BD,∵A(﹣2,t),D(﹣2,﹣1),∴(x+2)2+(x+1﹣t)2=(x+2)2+(x+1+1)2,(x+1﹣t)2=(x+2)2,x+1﹣t=x+2或x+1﹣t=﹣x﹣2,解得:t=﹣1(舍)或t=2x+3,Rt△ACB中,AC2+BC2=AB2,即(﹣2)2+(t﹣3)2+x2+(x+1﹣3)2=(x+2)2+(x+1﹣t)2,把t=2x+3代入得:x2﹣3x=0,解得:x=0或3,当x=3时,如图5,则t=2×3+3=9,∴A(﹣2,9),B(3,4),∴AC==2,BC==,∴S△ABC===10;当x=0时,如图6,此时,A(﹣2,3),AC=2,BC=2,∴S△ABC===2.2.(2020•中山区二模)在平面直角坐标系中,直线y=x+3与x轴、y轴分别交于点B、A,动点C以每秒2个单位长度的速度从点B向终点O运动,过点C作∠BCD=∠ABO,交直线AB于点D.设∠BDC=α°,将CD 绕点C顺时针旋转α°得到线段CE,连接DE.设四边形BCED与△ABO的重叠部分面积为S(平方单位),S >0,点C的运动时间为t秒.(1)求AB的长;(2)求证:四边形BCED是平行四边形;(3)求S与t的函数关系式,并直接写出自变量取值范围.解:(1)∵直线与x轴、y轴分.别交于点B、A,∴A(0,3),B(﹣6,0).∴OA=3,OB=6.∴.(2)证明:∵∠DBC=∠DCB,∴DB=DC.由旋转知CD=CE,∠BDC=∠DCE.∴BD∥CE,BD=CE.∴四边形ABCD是平行四边形.(3)∵直线与x轴、y轴分别交于点B、A,∴A(0,3),B(﹣6,0).∴.如图1,过点D作DH⊥BC于点H,∵BD=CD,∴.∴.∴当0<t≤2时,;如图2,当2<t≤3时,∵,∴.∵DE∥OB,∴∠ADE=∠ABC.∴.∴.∴DM=6﹣t.∴EM=2t﹣(6﹣t)=3t﹣6.∵四边形ABCD是平行四边形,∴∠ABC=∠E.∴.∴.∴.∴.综上所述,.3.(2020•铁西区二模)如图,在平面直角坐标系中,直线y1=kx+b与x轴交于点A(4,0),与y轴交于点B (0,3),点C是直线y2=﹣x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.(1)求直线y1=kx+b的函数表达式;(2)当BC∥x轴时,求BD的长;(3)点E在线段OA上,OE=OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.解:(1)把A(4,0),B(0,3)代入y1=kx+b,得到,解得:,∴y1=﹣x+3.(2)∵BC∥x轴,∴点C的纵坐标为3,当y=3时,3=﹣x+5,解得x=,∴C(,3),∵CD⊥AB,∴直线CD的解析式为y=x+,由,解得,∴D(,),∴BD==.(3)如图,当∠BCD=∠BEO时,过点A作AM⊥AB交BC的延长线于M,点M作MN⊥x轴于N.∵OB=3,OE=OA=,∴tan∠BEO==2,∵CD⊥AB,AM⊥AB,∴CD∥AM,∴∠AMB=∠BCD=∠BEO,∴tan∠AMB==2,∵AB===5,∴AM=AB=,∵∠AOB=∠ANM=∠BAM=90°,∴∠BAO+∠ABO=90°,∠BAO+∠MAN=90°,∴∠MAN=∠ABO,∴△ABO∽△MAN,∴==,∴==,∴AN=,MN=2,∴M(,2),∴直线BM的解析式为y=﹣x+3,由,解得x=,∴点C的横坐标为,当∠CBD=∠BEO时,同法可得点C的横坐标为.4.(2020•大东区二模)如图,Rt△OAB的直角边OA在x轴上,边OB在y轴上,A的坐标为(6,0),B的坐标为(0,3),在第一象限有一点C的坐标为(3,4).(1)求直线AB的函数表达式;(2)P是x轴上一动点,点P在运动过程中,是否存在某个位置,使得∠PBO=∠BOC?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)若动点P在x轴上从点(﹣6,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.请直接写出当t为何值时,在直线l上存在点M,在直线AB上存在点Q.使得以OC 为一边,O,C,M,Q为顶点的四边形为菱形.解:(1)设直线AB的解析式为y=kx+b(k≠0),∵点A(6,0),B(0,3)在直线AB上,∴,∴,∴直线AB的解析式为y=﹣x+3;(2)如图1,当点P在x轴负半轴上时,∵点C(3,4),∴直线OC的解析式为y=x,∵∠PBO=∠BOC,∴BP∥CO,∵B(0,3),∴直线BP的解析式为y=x+3,令y=0,则x+3=0,∴x=﹣,∴P(﹣,0),当点P在x轴正半轴上时,由对称性知,P'(,0),即点P的坐标为(﹣,0)或(,0);(3)如图3,由(1)知,直线AB的解析式为y=﹣x+3,∵C(3,4),∴OC=5,设Q(m,﹣m+3),①以OC与CQ为邻边时,CQ=OC=5,∴CQ==5,∴m=﹣2或m=6,∴Q1(﹣2,4),Q3(6,0),∵点C(3,4)向左平移3﹣(﹣2)=5个单位到点Q,∵(﹣2,4),∴点O也向左平移5个单位得到点M1(﹣5,0),∴t=﹣5﹣(﹣6)=1,∵点C(3,4)向右平移6﹣3=3个单位,再向下平移4﹣0=4个单位到点Q3,∴点O也向右平移3个单位,再向下平移4个单位得到点M3(3,﹣4),∴t=3﹣(﹣6)=9,②以OC与OQ为邻边时,OQ=OC=5,∴=5,∴m=或m=,∴Q2(,),Q4(,),∵点O向左平移个单位,再向上平移个单位到点Q2(,),∴点C(3,4)也向左平移个单位,再向上平移个单位到点M2(,),∴t=﹣(﹣6)=,∵点O向右平移个单位,再向上个单位到Q4,∴点C(3,4)也向右平移个单位,再向上平移个单位到点M4(,),∴t=﹣(﹣6)=,即t的值为1或9或或.5.(2020•沈河区二模)如图1,在平面直角坐标系中,点A的坐标是(﹣1,0),点B(2,3),点C(3,).(1)求直线AB的解析式;(2)点P(m,0)是x轴上的一个动点,过点P作直线PM∥y轴,交直线AB于点M,交直线BC于点N(P,M,N三点中任意两点都不重合),当MN=MP时,求点M的坐标;(3)如图2,取点D(4,0),动点E在射线BC上,连接DE,另一动点P从点D出发,沿线段DE以每秒1个单位的速度运动到点E,再沿线段EB以每秒个单位的速度运动到终点B,当点E的坐标是多少时,点P 在整个运动过程中用时最少?请直接写出此时点E的坐标.解:(1)设直线AB的解析式为y=kx+b,∵点A的坐标是(﹣1,0),点B(2,3),∴,解得:,∴直线AB的解析式为y=x+1;(2)∵点B(2,3),点C(3,),∴直线BC的解析式为y=﹣x+4,∵点P(m,0),PM∥y轴,交直线AB于点M,交直线BC于点N,∴M(m,m+1),N(m,﹣m+4),∵MN=MP,∴m+1=(﹣m+4)﹣(m+1),解得:m=,∴M(,);(3)如图2中,作BT∥AD,过点E作EK⊥BT于K.设直线BC交x轴于J.∵直线BC的解析式为y=﹣x+4,∴tan∠BJO=,∵BT∥OJ,∴∠BJO=∠TBJ,∴tan∠TBJ=tan∠BJO=,∴=,设EK=m,BK=2m,则BE=m,∴EK=BE,∵点P在整个运动过程中的运动时间t=+=DE+BE=DE+EK,∴当D,E,K共线,DE+EK的值最小,此时DE=DJ=2,EK=BK=1,∴点P在整个运动过程中的运动时间的最小值为2+1=3秒,此时E(4,2).二.反比例函数动点问题6.(2020•五华县模拟)如图,点A是双曲线y=在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=﹣(x<0).解:连接OC,作CD⊥x轴于D,AE⊥x轴于E,如图,设A点坐标为(a,),∵A点、B点是正比例函数图象与双曲线y=的交点,∴点A与点B关于原点对称,∴OA=OB∵△ABC为等腰直角三角形,∴OC=OA,OC⊥OA,∴∠DOC+∠AOE=90°,∵∠DOC+∠DCO=90°,∴∠DCO=∠AOE,∵在△COD和△OAE中∴△COD≌△OAE(AAS),∴OD=AE=,CD=OE=a,∴C点坐标为(﹣,a),∵﹣•a=﹣4,∴点C在反比例函数y=﹣图象上.故答案为y=﹣(x<0).7.(2020•金华二模)如图,反比例函数y=(x>0),点A(a,0)是x轴上的动点.B(0,4),以AB为边在AB右侧作正方形ABCD.(1)当a=4时,判断点D是否在反比例函数图象上?请说明理由;(2)当点D落在反比例函数y=(x>0)图象上时,求a的值;(3)在(2)的条件下,沿水平方向平移正方形,使正方形的一个顶点落在反比例函数图象上时,求点A的平移距离.解:(1)如图1,过点D作DE⊥x轴于E,∴∠AED=90°=∠BOA,∵a=4,∴A(4,0),∴OA=4,∵B(0,4),∴OB=4,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∴∠OAB+∠DAE=90°,∵∠AOB=90°,∴∠OAB+∠OBA=90°,∴∠OBA=EAD,∴△AOB≌△DEA(AAS),∴DE=OA=a=4,AE=OB=4,∴OE=OA+AE=8,∴D(8,4),当x=8时,y=≠4,∴点D不在反比例函数y=(x>0)的图象上;(2)由(1)知,△AOB≌△DEA(AAS),∴DE=OA=a,AE=OB=4,∴OE=OA+AE=a+4,∴D(a+4,a),∵点D落在反比例函数y=(x>0)图象上,∴a(a+4)=5,∴a=﹣5或a=1,∵点D在双曲线上,∴a>0,即a=1;(3)∵点B(0,4),当y=4时,x=,∴正方形ABCD向右平移个单位,∴点A向右平移个单位,即点A的平移距离为.同(2)的方法得,C(4,5),当y=5时,x==1,而4﹣1=3,∴正方形ABCD向左平移3个单位,∴点A向左平移3个单位,即点A的平移距离为3.即点A的平移距离为3或.8.(2020•历下区三模)如图,正比例函数y=kx与反比例函数y=(m≠0)的图象交于A、B两点,点A的坐标为(1,2),点C为反比例函数图象第一象限上的一动点,连接OC、AC、BC.(1)求正比例函数与反比例函数的表达式;(2)作AD⊥y轴于点D,CE⊥x轴于点E,且OA=OC时,求直线BC的函数表达式;(3)当△AOC是以OA为直角边的直角三角形时,求点C的坐标.解:(1)将点A的坐标分别代入y=kx和y=并解得:k=2,m=2,故正比例函数与反比例函数的表达式分别为:y=2x,y=①;(2)∵反比例函数的图象关于原点成中心对称,故点B(﹣1,﹣2),∵反比例函数的图象关于直线y=x对称且OA=OC,∴点A、C关于直线y=x对称,过点C(2,1),设直线BC的表达式为:y=tx+s,则,解得,故直线BC的表达式为:y=x﹣1;(3)如下图,延长AC交x、y轴于点M、N,直线AB的表达式为:y=2x,则tan∠AOC=2,当△AOC是以OA为直角边的直角三角形时,即∠OAC=90°,则tan∠ANO=,故设直线AC的表达式为:y=﹣x+r,将点A的坐标代入上式并解得:r=,故直线AC的表达式为:y=﹣x+②,联立①②并解得:x=1(舍去)或4,故点C(4,).9.(2021•禹州市一模)如图,在平面直角坐标系xOy中,菱形ABCD的顶点B的坐标为(1,0),顶点C的坐标为(4,2),对角线AC∥x轴,边AB所在直线y1=ax+b与反比例函数y2=(k<0)的图象交于A,E 两点.(1)求y1和y2的函数解析式;(2)当y1>y2时,求x的取值范围;(3)点P是x轴上一动点,当△PAC是以AC为斜边的直角三角形时,请直接写出点P的坐标.解:(1)连接BD,∵四边形ABCD为菱形,AC∥x轴,由图形的对称性知,点A、C关于BD对称,则点A的坐标为(﹣2,2),将点A、B的坐标代入直线的表达式得,解得,故y1=﹣x+①;将点A的坐标代入反比例函数表达式得:2=,解得k=﹣4,则y2=﹣②;(2)联立①②得:﹣x+=﹣,解得x=﹣2(舍去)或3,则点E(3,),观察函数图象知,当y1>y2时,则x的取值范围为x<﹣2或0<x<3;(3)设点P的坐标为(x,0),由点P、A、C的坐标得:AC2=(4+2)2=36,PA2=(x+2)2+4,PC2=(x﹣4)2+4,由题意得:AC2=PA2+PC2,即36=(x+2)2+4+(x﹣4)2+4,解得x=1±,故点P的坐标为(1+,0)或(1﹣,0).10.(2020•岳麓区校级模拟)直线y=﹣x+2a(常数a>0)和双曲线y=(k>0,x>0)的图象有且只有一个交点B.(1)求点B的坐标(用含a的式子表示);(2)如图1,一次函数y=﹣x+2a与x轴交于点A,点P是线段OA上的动点,点Q在反比例函数图象上,且满足∠BPO=∠QPA.①若a=1时,点P在移动过程中,求BP+PQ的最小值;②如图2,设PQ与线段AB的交点为M,若OM⊥BP,试求的值.解:(1)由消去x得到,x2﹣2ax+k=0,由题意△=0,∴4a2﹣4k=0,∴k=a2,解方程组得到,,∴B(a,a).(2)①如图1中,作过B关于OA的对称点B′,连接QB′交OA于P,此时∠BPO=∠QPA,设Q(m,),∵B(1,1),B′(1,﹣1),∴PB+PQ=PB′+PQ=B′Q====,∵1>0,∴当m﹣=1时,PB+PQ的值最小,最小值为.②过点B作BH⊥OA于H交OM于J,设OM交PB于K.由题意,B(a,a),A(2a,0),∴OH=BH=AH=2a,∵OM⊥PB,BH⊥OA,∴∠OHJ=∠BKJ=90°,∵∠OJH=∠BJK,∴∠HOJ=∠HBP,∵∠OHJ=∠BHP=90°,OH=BH,∴△OHJ≌△BHP(ASA),∴OJ=PB,JH=PH,∠OJH=∠BPH,AP=BJ,∵∠AHB=90°,HB=HA,∴∠PAM=∠JBM=45°,∵∠BPH=∠APM,∠OJH=∠BJM,∴∠BJM=∠APM,∴△BJM≌△APM(ASA),∴JM=PM,∴OM﹣PB=OJ+JM﹣BP=JM=PM,∴=1.三.二次函数动点问题11.(2020•广西)如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,已知B(3,0),C(0,﹣3),连接BC,点P是抛物线上的一个动点,点N是对称轴上的一个动点.(1)求该抛物线的函数解析式.(2)当△PAB的面积为8时,求点P的坐标.(3)若点P在直线BC的下方,当点P到直线BC的距离最大时,在抛物线上是否存在点Q,使得以点P,C,N,Q为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.解:(1)∵抛物线y=x2+bx+c经过点B(3,0),C(0,﹣3),∴,解得:,∴抛物线的解析式为y=x2﹣2x﹣3;(2)∵抛物线y=x2﹣2x﹣3与x轴交于A,B两点,∴0=x2﹣2x﹣3,∴x1=﹣1,x2=3,∴点A(﹣1,0),∴AB=4,设点P(p,p2﹣2p﹣3),∵△PAB的面积为8,∴×4×|p2﹣2p﹣3|=8,∴p2﹣2p﹣3=4或p2﹣2p﹣3=﹣4,∴p1=2+1,p2=﹣2+1,p3=1,∴点P坐标为(2+1,4)或(﹣2+1,4)或(1,﹣4);(3)如图1,过点P作PE⊥x轴,交BC于E,∵点B(3,0),C(0,﹣3),∴直线BC的解析式为y=x﹣3,设点P(a,a2﹣2a﹣3),则点E(a,a﹣3),∴PE=a﹣3﹣(a2﹣2a﹣3)=﹣a2+3a,∴S△BCP=×(﹣a2+3a)×3=﹣(a﹣)2+,∴当a=时,S△BCP有最大值,即点P到直线BC的距离最大,此时点P(,﹣),设点N(1,n),点Q(m,m2﹣2m﹣3),若CP为边,CN为边时,则CQ与NP互相平分,∴,∴m=,∴点Q(,﹣),若CP为边,CQ为边时,则CN与PQ互相平分,∴=,∴m=﹣,∴点Q(﹣,﹣),若CP为对角线,则CP与NQ互相平分,∴,∴m=,∴点Q(,﹣),综上所述:点Q坐标为(,﹣)或(﹣,﹣)或(,﹣).12.(2020•兰州)如图,二次函数y=x2+bx+c的图象过点A(4,﹣4),B(﹣2,m),交y轴于点C(0,﹣4).直线BO与抛物线相交于另一点D,连接AB,AD,点E是线段AB上的一动点,过点E作EF∥BD交AD于点F.(1)求二次函数y=x2+bx+c的表达式;(2)判断△ABD的形状,并说明理由;(3)在点E的运动过程中,直线BD上存在一点G,使得四边形AFGE为矩形,请判断此时AG与BD的数量关系,并求出点E的坐标;(4)点H是抛物线的顶点,在(3)的条件下,点P是平面内使得∠EPF=90°的点,在抛物线的对称轴上,是否存在点Q,使得△HPQ是以∠PQH为直角的等腰直角三角形,若存在,直接写出符合条件的所有点Q的坐标;若不存在,请说明理由.解:(1)∵二次函数y=x2+bx+c的图象过点A(4,﹣4),点C(0,﹣4),∴,解得,∴二次函数的解析式为y=x2﹣x﹣4.(2)△ABD是直角三角形,理由:∵B(﹣2,m)在y=x2﹣x﹣4,∴B(﹣2,﹣1),∴直线OB的解析式为y=x,由,解得(即点B)或,∴D(8,4),∵A(4,﹣4),∴AB==3,AD==4,BD==5,∴BD2=AB2+AD2,∴∠BAD=90°,∴△ABD是直角三角形.(3)结论AG=BD.理由:如图1中,连接AG,交EF于H.∵四边形AEGF是矩形,∴AH=HG,EH=FH,∵EF∥BD,∴==1,∴AE=BE,∴E(1,﹣),∵==,EH=FH,∴BG=GD,∵∠BAD=90°,∴AG=BD.(4)如图2中,设EF的中点为K,P(x,y),连接PK.∵E(1,﹣),F(6,0),∴K(,﹣),EF==,∵∠EPF=90°,∴点P在以EF为直径的⊙K上运动,∵△PQH是等腰直角三角形,∠PQH=90°,∴∠QHP=45°,∵抛物线的顶点H(2,﹣5),∴直线PH的解析式为y=x﹣7,∵PK=EF,∴(x﹣)2+(y+)2=()2,(y+7﹣)2+(y+)2=()2,解得y=﹣4或﹣,∴Q(2,﹣4)或(2,﹣).13.(2020•阜新)如图,二次函数y=x2+bx+c的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C.点P(m,0)是x轴上的一动点,PM⊥x轴,交直线AC于点M,交抛物线于点N.(1)求这个二次函数的表达式;(2)①若点P仅在线段AO上运动,如图,求线段MN的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.解:(1)把A(﹣3,0),B(1,0)代入y=x2+bx+c中,得,解得,∴y=x2+2x﹣3.(2)①设直线AC的表达式为y=kx+b,把A(﹣3,0),C(0,﹣3)代入y=kx+b′.得,解得,∴y=﹣x﹣3,∵点P(m,0)是x轴上的一动点,且PM⊥x轴.∴M(m,﹣m﹣3),N(m,m2+2m﹣3),∴MN=(﹣m﹣3)﹣(m2+2m﹣3)=﹣m2﹣3m=﹣(m+)2+,∵a=﹣1<0,∴此函数有最大值.又∵点P在线段OA上运动,且﹣3<﹣<0,∴当m=﹣时,MN有最大值.②如图2﹣1中,当点M在线段AC上,MN=MC,四边形MNQC是菱形时.∵MN=﹣m2﹣3m,MC=﹣m,∴﹣m2﹣3m=﹣m,解得m=﹣3+或0(舍弃)∴MN=3﹣2,∴CQ=MN=3﹣2,∴OQ=3+1,∴Q(0,﹣3﹣1).如图2﹣2中,当MC是菱形的对角线时,四边形MNCQ是正方形,此时CN=MN=CQ=2,可得Q(0,﹣1).如图2﹣3中,当点M在CA延长线上时,MN=CM,四边形MNQC是菱形时,则有,m2+3m=﹣m,解得m=﹣3﹣或0(舍弃),∴MN=CQ=3+2,∴OQ=CQ﹣OC=3﹣1,∴Q(0,3﹣1).当点P在y轴的右侧时,显然MN>CM,此时满足条件的菱形不存在.综上所述,满足条件的点Q的坐标为(0,﹣3﹣1)或(0,﹣1)或(0,3﹣1).14.(2020•盘锦)如图1,直线y=x﹣4与x轴交于点B,与y轴交于点A,抛物线y=﹣x2+bx+c经过点B和点C(0,4),△ABO沿射线AB方向以每秒个单位长度的速度平移,平移后的三角形记为△DEF(点A,B,O的对应点分别为点D,E,F),平移时间为t(0<t<4)秒,射线DF交x轴于点G,交抛物线于点M,连接ME.(1)求抛物线的解析式;(2)当tan∠EMF=时,请直接写出t的值;(3)如图2,点N在抛物线上,点N的横坐标是点M的横坐标的,连接OM,NF,OM与NF相交于点P,当NP=FP时,求t的值.解:(1)∵直线y=x﹣4与x轴交于点B,与y轴交于点A,∴B(4,0),A(0,﹣4),把B(4,0),C(0,4)代入y=﹣x2+bx+c得到,解得,∴抛物线的解析式为y=﹣x2+x+4.(2)如图1中,当点M在线段DF的上方时,由题意得,D(t,t﹣4),则M(t,﹣t2+t+4),∴DM=﹣t2+8,在Rt△MEF中,tan∠EMF===,∴MF=3,∵DF=EF=4,∴DM=7,∴﹣t2+8=7,∴t=或﹣(舍弃).当点F在点M上方时,可得DM=1,即﹣t2+8=1,∴t=或﹣(舍弃),综上所述,t的值为或.(3)如图2中,过点N作NT∥y轴于T.由题意得D(t,t﹣4),则M(t,﹣t2+t+4),N(t,﹣t2+t+4),T(t,﹣t2+t+2),F(t,t)∵NT∥FM,∴∠PNT=∠PFM,∵∠NPT=∠MPF,PN=PF,∴△NPT≌△FPM(ASA),∴NT=MF,∴﹣t2+t+4﹣(﹣t2+t+2)=﹣t2+t+4﹣t,解得t=或﹣(舍弃),∴t的值为.15.(2020•德阳)如图1,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A,B.与y轴交于点C.连接AC,BC.已知△ABC的面积为2.(1)求抛物线的解析式;(2)平行于x轴的直线与抛物线从左到右依次交于P,Q两点.过P,Q向x轴作垂线,垂足分别为G,H.若四边形PGHQ为正方形,求正方形的边长;(3)如图2,平行于y轴的直线交抛物线于点M,交x轴于点N(2,0).点D是抛物线上A,M之间的一动点,且点D不与A,M重合,连接DB交MN于点E.连接AD并延长交MN于点F.在点D运动过程中,3NE+NF 是否为定值?若是,求出这个定值;若不是,请说明理由.解:(1)如图1,y=ax2﹣2ax﹣3a=a(x2﹣2x﹣3)=a(x﹣3)(x+1),∴A(﹣1,0),B(3,0),∴AB=4,∵△ABC的面积为2,即,∴,∴OC=1,∴C(0,1),将C(0,1)代入y=ax2﹣2ax﹣3a,得:﹣3a=1,∴a=﹣,∴该二次函数的解析式为y=﹣x2+x+1;(2)分两种情况:①当PQ在x轴的上方时,如图2,设点P的纵坐标为m,当y=m时,﹣x2+x+1=m,解得:x1=1+,x2=1﹣,∴点P的坐标为(1﹣,m),点Q的坐标为(1+,m),∴点G的坐标为(1﹣,0),点H的坐标为(1+,0),∵矩形PGHQ为正方形,∴1+﹣(1﹣)=m,解得:m1=﹣6﹣2(舍),m2=﹣6+2;②当PQ在x轴的下方时,m<0,同理可得m=﹣6﹣2;∴当四边形PGHQ为正方形时,边长为6+2或2﹣6;(3)如图3,设点D(n,﹣n2+n+1),延长BD交y轴于K,∵A(﹣1,0),设AD的解析式为:y=kx+b,则,解得:,∴AD的解析式为:y=(﹣)x﹣,当x=2时,y=﹣n+2﹣n+1=﹣n+3,∴F(2,3﹣n),∴FN=3﹣n,同理得直线BD的解析式为:y=(﹣)x+n+1,∴K(0,n+1),∴OK=n+1,∵N(2,0),B(3,0),∴,∵EN∥OK,∴,∴OK=3EN,∴3EN+FN=OK+FN=n+1+3﹣n=4,∴在点D运动过程中,3NE+NF为定值4.。
(完整版)初中数学动点问题归纳

BB动点问题题型方法归纳动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、三角形边上动点1、(2009年齐齐哈尔市)直线364y x =-+与坐标轴分别交于A B 、两点,动点P Q 、同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单 位长度,点P 沿路线O →B →A 运动. (1)直接写出A B 、两点的坐标;(2)设点Q 的运动时间为t 秒,OPQ △的面积为S ,求出S 与t 之间 的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标.解:1、A (8,0) B (0,6)2、当0<t <3时,S=t2当3<t <8时,S=3/8(8-t)t提示:第(2)问按点P 到拐点B 所有时间分段分类;第(3)问是分类讨论:已知三定点O 、P 、Q ,探究第四点构成平行四边形时按已知线段身份不同分类-----①OP 为边、OQ 为边,②OP 为边、OQ 为对角线,③OP 为对角线、OQ 为边。
然后画出各类的图形,根据图形性质求顶点坐标。
2、(2009年衡阳市)如图,AB 是⊙O 的直径,弦BC=2cm , ∠ABC=60º.(1)求⊙O 的直径;(2)若D 是AB 延长线上一点,连结CD ,当BD 长为多少时,CD 与⊙O 相切;(3)若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动,同时动点F 以1cm/s 的速度从B 点出发沿BC 方向运动,设运动时间为)20)((<<t s t ,连结EF ,当t 为何值时,△BEF 为直角三角形.注意:第(3)问按直角位置分类讨论3、(2009重庆綦江)如图,已知抛物线(1)20)y a x a =-+≠经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1单位和2个长度单位的速度沿OC 和BO 之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长. 注意:发现并充分运用特殊角∠DAB=60°当△OPQ 面积最大时,四边形BCPQ 的面积最小。
初中动点问题的方法归纳

初中动点问题的方法归纳初中动点问题是指在空间移动的过程中,需要确定一个或多个点的位置。
这种问题需要运用几何知识和分析能力来解决。
下面将对初中动点问题的方法进行归纳。
一、直线运动问题直线运动是最简单的动点问题之一,常见的例子包括匀速直线运动和匀变速直线运动。
1.匀速直线运动问题的解法:假设动点的速度为v,则可以根据速度和时间的关系确定动点在某个时刻t的位置:距离=速度×时间。
例如,问题描述为“某动点从A点出发,以60km/h的速度匀速向B点行进,已行进2小时,请问此时该动点距离A点多远?”解法:距离=速度×时间= 60km/h × 2h = 120km。
2.匀变速直线运动问题的解法:如果动点的速度随着时间的变化而变化,可以应用速度-时间图像或速度-时间关系的知识来解决问题。
例如,问题描述为“一辆汽车以10m/s^2的加速度匀加速,在10s 内的位移是多少?”解法:根据匀变速运动中的公式s = (初速度+末速度) ×时间/ 2,代入已知条件初速度为0,加速度为10m/s^2,时间为10s,计算得到位移为(0 + 10) × 10 / 2 = 50m。
二、曲线运动问题1.匀速圆周运动问题的解法:当动点以恒定速度绕固定的圆周运动时,可以应用圆的性质来解决问题。
例如,问题描述为“一个半径为5cm的圆正好需要6秒完成一周,求圆周的长度。
”解法:根据圆的性质,圆周长= 2π ×半径= 2π × 5cm =10πcm ≈ 31.4cm。
2.曲线运动问题的解法:在一些特殊的曲线运动问题中,可以利用对称性、角度关系和距离比例等方法来解决。
例如,问题描述为“一个人从A点出发,按其速度向直线BC行进,当经过点B时,BC边所形成的角度是90°,请问此时人到底B点的距离是BC边长的多少?”解法:利用角度关系,已知∠B = 90°,可以得出AB与BC互补,所以AB : BC = 1 : 1,即人到B点的距离等于BC边长的一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xA O QP B y 动点问题题型方法归纳动态几何特点问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、三角形边上动点1、(2009年齐齐哈尔市)直线364y x =-+与坐标轴分别交于A B 、两点,动点P Q 、同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿路线O →B →A 运动. (1)直接写出A B 、两点的坐标;(2)设点Q 的运动时间为t 秒,OPQ △的面积为S ,求出S 与t 之间 的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标. 解:1、A (8,0) B (0,6) 2、当0<t <3时,2当3<t <8时,3/8(8)t图AB CO E F ABCOD 图 ABO EFC 图提示:第(2)问按点P 到拐点B 所有时间分段分类;第(3)问是分类讨论:已知三定点O 、P 、Q ,探究第四点构成平行四边形时按已知线段身份不同分类①为边、为边,②为边、为对角线,③为对角线、为边。
然后画出各类的图形,根据图形性质求顶点坐标。
2、(2009年衡阳市) 如图,是⊙O 的直径,弦2, ∠60º.(1)求⊙O 的直径;(2)若D 是延长线上一点,连结,当长为多少时,与⊙O 相切; (3)若动点E 以2的速度从A 点出发沿着方向运动,同时动点F 以1的速度从B 点出发沿方向运动,设运动时间为)20)((<<t s t ,连结,当t 为何值时,△为直角三角形.注意:第(3)问按直角位置分类讨论3、(2009重庆綦江)如图,已知抛物线(1)233(0)y a x a =-+≠经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射xy MC D PQ O AB PQA BCD线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.注意:发现并充分运用特殊角∠60°当△面积最大时,四边形的面积最小。
二、 特殊四边形边上动点4、(2009年吉林省)如图所示,菱形ABCD 的边长为6厘米,60B ∠=°.从初始时刻开始,点P 、Q 同时从A 点出发,点P 以1厘米/秒的速度沿A C B→→的方向运动,点Q 以2厘米/秒的速度沿A B C D →→→的方向运动,当点Q 运动到D 点时,P 、Q 两点同时停止运动,设P 、Q 运动的时间为x 秒时,APQ △和线与ABC △重叠部分....的面积为y 平方厘米(这里规定:点段是面积为O 的三角形),解答下列问题:(1)点P 、Q 从出发到相遇所用时间是 秒; (2)点P 、Q 从开始运动到停止的过程中,当APQ △是等边三角形时x 的值是 秒;OM BH A C xy 图OM BH A C xy 图(3)求y 与x 之间的函数关系式.提示:第(3)问按点Q 到拐点时间B 、C 所有时间分段分类 ; 提醒 高相等的两个三角形面积比等于底边的比 。
5、(2009年哈尔滨)如图1,在平面直角坐标系中,点O 是坐标原点,四边形是菱形,点A 的坐标为(3-,4),点C 在x 轴的正半轴上,直线交y 轴于点M ,边交y 轴于点H . (1)求直线的解析式;(2)连接,如图2,动点P 从点A 出发,沿折线方向以2个单位/秒的速度向终点C 匀速运动,设△的面积为S (0S ≠),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);(3)在(2)的条件下,当 t 为何值时,∠与∠互为余角,并求此时直线与直线所夹锐角的正切值.注意:第(2)问按点P 到拐点B 所用时间分段分类;第(3)问发现∠90°,∠与∠互余,画出点P 运动过程中, ∠∠的两种情况,求出t 值。
利用⊥,再求与夹角正切值.6、(2009年温州)如图,在平面直角坐标系中,点A(3,0),B(33,2),C (0,2).动点D 以每秒1个单位的速度从点0出发沿向终点C 运动,同时动点E 以每秒2个单位的速度从点A 出发沿向终点B 运动.过点E 作上,交于点F ,连结、.设运动时间为t 秒. (1)求∠的度数; (2)当t 为何值时,∥; (3)设四边形的面积为S . ①求S 关于t 的函数关系式; ②若一抛物线2经过动点E ,当S<23时,求m 的取值范围(写出答案即可).注意:发现特殊性,∥7、(07黄冈)已知:如图,在平面直角坐标系中,四边形是菱形,且 ∠60°,点B 的坐标是(0,83),点P 从点C开始以每秒1个单位长度的速度在线段上向点B 移动,同时,点Q 从点O 开始以每秒a (1≤a ≤3)个单位长度的速度沿射线方向移动,设(08)t t <≤秒后,直线交于点D. (1)求∠的度数及线段的长;(2)求经过A ,B ,C 三点的抛物线的解析式; (3)当43,33a OD ==时,求t 的值及此时直线的解析式;(4)当a 为何值时,以O ,P ,Q ,D 为顶点的三角形与OAB ∆相似?当a 为何值时,以O ,P ,Q ,D 为顶点的三角形与OAB ∆不相似?请给出你的结论,B ACD P OQ xy并加以证明.8、(08黄冈)已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P 从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒. (1)求直线BC 的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的27? (3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围; (4)当动点P 在线段AB 上移动时,能否在线段OA 上找到一点Q ,使四边形CQPD 为矩形?请求出此时动点P 的坐标;若不能,请说明理由.9、(09年黄冈市)如图,在平面直角坐标系中,抛物线21410189y x x =--与x 轴的交点为点A,与y 轴的交点为点B . 过点B 作x 轴的平行线,交抛物线于点C ,连结.现有两动点分别从两点同时出发,点P 以每秒4个单位的速度沿向终点A 移动,点Q 以每秒1个单位的速度沿向点B 移动,点P 停止运动时,点Q 也同时停止运动,线段相交于点D ,过点DA B DC O PxyA B DC Oxy(此题备y C N P作∥,交于点E ,射线交x 轴于点F .设动点移动的时间为t (单位:秒) (1)求三点的坐标和抛物线的顶点的坐标;(2)当t 为何值时,四边形为平行四边形?请写出计算过程;(3)当0<t <92时,△的面积是否总为定值?若是,求出此定值, 若不是,请说明理由;(4)当t 为何值时,△为等腰三角形?请写出解答过程. 提示:第(3)问用相似比的代换,得(定值)。
第(4)问按哪两边相等分类讨论 ①,②,③. 三、 直线上动点8、(2009年湖南长沙)如图,二次函数2y ax bx c =++(0a ≠)的图象与x 轴交于A B 、两点,与y 轴相交于点C .连结AC BC A C 、,、两点的坐标分别为(30)A -,、(03)C ,,且当4x =-和2x =时二次函数的函数值y 相等.(1)求实数a b c ,,的值;(2)若点M N 、同时从B 点出发,均以每秒1个单位长度的速度分别沿BA BC 、边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t 秒时,连结MN ,将BMN △沿MN 翻折,B 点恰好落在AC 边上的P 处,求t 的值及点P 的坐标;(3)在(2)的条件下,二次函数图象的对称轴上是否存在点Q ,使得以B N Q ,,为项点的三角形与ABC △相似?如果存在,请求出点Q 的坐标;如果不存在,请说明理由.提示:第(2)问发现特殊角∠30°,∠60° 特殊图形四边形为菱形;第(3)问注意到△为直角三角形后,按直角位置对应分类;先画出与△相似的△ ,再判断是否在对称轴上。
9、(2009眉山)如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
⑴求该抛物线的解析式;⑵动点P 在x 轴上移动,当△是直角三角形时,求点P 的坐标P 。
⑶在抛物线的对称轴上找一点M ,使||AM MC -的值最大,求出点M 的坐标。
提示:第(2)问按直角位置分类讨论后画出图形①P 为直角顶点为斜边时,以为直径画圆与x 轴交点即为所求点P ,②A 为直角顶点时,过点A 作垂线交x 轴于点P ,③E 为直角顶点时,作法同②;第(3)问,三角形两边之差小于第三边,那么等于第三边时差值最大。
10、(2009年兰州)如图①,正方形 中,点A 、B 的坐标分别为(0,10),(8,4), 点C 在第一象限.动点P 在正方形 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴正半轴上运动,当P 点到达D 点时,两点同时停止运动,设运动的时间为t 秒.(1)当P 点在边上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图②所示,请写出点Q 开始运动时的坐标及点P 运动速度; (2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△的面积最大,并求此时P 点的坐标; (4)如果点P 、Q 保持原速度不变,当点P 沿A →B →C →D 匀速运动时,与能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由. 注意:第(4)问按点P 分别在、、边上分类讨论;求t 值时,灵活运用等腰三角形“三线合一”。
