随机波浪谱
随机波浪理论

波高的分布
一、按高。我国和苏联常用。
波高的分布
二、部分大波的平均波高 H P
H P 将波高整个系列按大小顺序排列,从大波算起,其中最大
的P部分的平均值,称为P部分大波的平均波高。 美国、日本比较常用。
波高的分布
三、有效波高 H S
H S 当P=1/3时,1/3大波平均波高接近于目测的波高,通
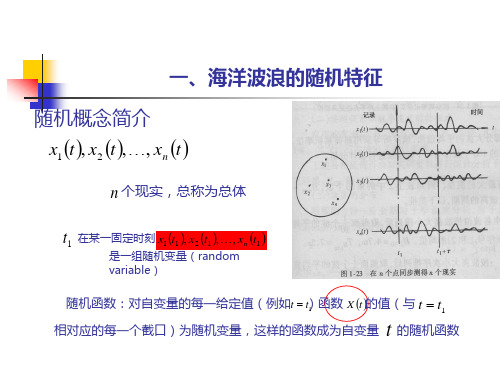
随机函数及其统计特征值
概率密度函数:
概率分布函数:
几种重要的概率分布:
均匀分布:
高斯分布:
x x 2 1 p x exp 2 2 x 2 x
瑞利分布:
海浪要素的统计特征 波面高度的分布 平稳海况下的海浪视为平稳 的各态历经的随机过程,波 动可以认为是无限多个振幅 不等、频率不等、初相位随 机,并沿与x轴成不同角度 的方向传播的简单余弦波的 叠加。这种方式最早由 Longuet-Higgins提出:
确定设计波浪要素
选择波浪理论
波浪力计算
特征波法
设计波浪要素: 是指在某一确定的重现期、某一特征波所对应的波 高和周期;包括两个方面: 1 )设计波浪的重现期;2 )设计特征波; 比如:设计波高采用50年一遇、波列累积概率为1 %的波高H1%,设计波周期采用平均周期T; “50年一遇”即是重现期,是指在多年期间可能 出现某一特征波高的平均时间间隔。 注:不能认为具有TR年重现期的波高HR 将在每 TR年出现一次,也不能预测它将在何时出现。
常称为有效波高。 在造船界又称为有义波高。 其数值相当于波列累积概率为13.5%的波高。
☞ 随机波浪的谱特性
研究波浪可以从两方面入手: 外在表现:概率分布 内部结构:谱特性——谱分析 频谱:海浪能量相对于波浪 频率的分布; 方向谱:海浪能量相对于波 浪频率和船舶方向的分布; 谱分析:阐明海浪的能量相 对于波浪频率、传播方向或 其他独立变量的分布规律, 建立其函数关系。
二维随机波浪中畸形波的数值模拟

二维随机波浪中畸形波的数值模拟畸形波是一种在没有预警的情况下突然发生,并迅速消失的灾害性事件。
由r畸形波会给海洋建筑物和船只带來巨大威胁,畸形波受到人们越來越多的重视。
以往的研丸主要集中在畸形波的生成机制,而在工程中我们更加关心的是畸形波的发生概率和如何预报。
本文采用四阶非线性薛定渭方程模拟了二维JONSWAP谱情况下畸形波的生成。
为了探讨波浪参数对畸形波的影响,模拟实验分成了多组初始波浪参数不同的工况。
首先分析了深水不稳定波列的演化过程。
畸形波从形成到消失的演化过程即调制一反调制的过程:调制过程中,畸形波位置处能最发生汇聚,波高升高,其附近的波高减小:反调制过程中,畸形波位置处波幅减小,直至畸形波的特征消失,其他位置处波高增大。
然后本文探讨了峰度、有效波高、偏度值和波浪谱的演化过程以及JONSWAP谱参数对它们的影响。
结果表明:Benjamin-Feir指数(BFI)是判断波列不稳定调制是否发生的重要参数:峰度值的空间演化曲线和畸形波生成概率曲线趋势一致,峰度值可以预测畸形波生成概率的大小。
在随机波浪场中,谱宽较窄和有效波高较小吋,畸形波较容易发生。
有效波高和偏度值在波浪传播过程中基本无变化,偏度的大小与初始波陡有关。
波浪之间的非线性作用导致主频处的能最向高频和低频部分传递,因此在波浪传播过程中谱峰高度下降,频谱变宽。
在讨论了前面一系列问题的基础上,我们分析了Benjamin-Feir不稳定性与深水畸形波的内在联系和畸形波的发生机制。
畸形波的生成与波浪二阶非线性和束缚波关系很小,畸形波的生成主要是四波共振造成的,也就是Benjamin-Feir 不稳定性。
最后对模拟实验波高进行了统计分析。
结果表明:对于BFI<1.0的情况, 模拟波高分布与瑞利分布基本一致:而对于BFI>il.O的情况,由于发生了不稳定调制,瑞利分布只在演化初期与模拟波高分布相吻合,在其他位置处瑞利分布会低估大波发生的概率,畸形波发生概率比瑞利分布预测的大一个数童级以上。
第七章 随机波浪

H 1 = 2ξ
3
a
1 3
H 1 = 4.00ቤተ መጻሕፍቲ ባይዱσ
3
• 保证率:波幅超过某给定值的可能值所占的百分率。
•
ξ a > ξ a1 的保证率:
F (ξ a1 ) =
∫
∞
a1
p (ξ a )d ξ a
• 波幅满足Rayleigh分布
∫
ξa1
0
p(ξ a )d ξ a = ∫
ξa1
0
• 保证率 ξ a1 ( − ξ 2 a 1 ) /( 2 σ 2 ) ( − ξ 2 a 1 ) /( 2 σ 2 ) F (ξ a1 ) = 1 − ∫ p (ξ a )d ξ a = 1 − (1 − e )=e
概率分布
• Rayleigh分布 概率密度 概率分布
• 4 数学期望(平均值)
• 5 方差(偏离程度)
三 不规则波描述
• 不规则性描述: 给定时间或位置 波高出现频率分布 • 平稳随机过程 随机过程是时间的函数 (1)样集的每一记录在统计上相当于 其它记录。 (2)样集在任一瞬间的所有统计特征 等于在足够长时间间隔内单一 记录的所有统计特征 长期观测分析表明,海浪记录在时间充分长时,都具有相同的分布规律。
方向谱
• 斜入射规则波表达式
ξ ( x, y, t ) = a cos(kx cos θ − ky sin θ − ωt )
• Fourier级数展开:
ξ ( x, y, t ) = ∑ ξ n cos(kn x cos θ + kn y sin θ − ωnt + ε n )
n= n =1 ∞
• 相应的谱密度函数为:
7-2 不规则波的表达
随机波浪谱

Jonswap 谱:峰形参数a σσ=(当m ωω≤时),b σσ=(当m ωω>时),因此该谱共有五个参量,它们都随各个谱而变化。
对于平均的JONSWAP 谱:3.3γ=0.07a σ= 0.09b σ= 0.615 1.080.615 1.0883.7220 4.515.403(/)s U kX H m s --==⨯⨯=22/9.82201000/15.4039087.368X gX U ==⨯⨯=0.330.3322(/)()22(9.8/15.403)9087.3640.69145(/)m g u X rad s ω--==⨯⨯= 0.220.220.076()0.0769087.3680.0102319X α--==⨯=在m ωω≤时,2222222exp[()/(2)]24524exp[(0.69145)/(0.070.69145)]5exp[426.85695(0.69145)]5415()exp[()]4150.691450.01023199.8exp[()] 3.3410.285730.9827exp() 3.3m m m S g ωωσωωωωωαγωωωωωω----⨯--=-=⨯-⨯=-⨯在m ωω>时,2222222exp[()/(2)]24524exp[(0.69145)/(0.090.69145)]5exp[258.22211(0.69145)]5415()exp[()]4150.691450.01023199.8exp[()] 3.3410.285730.9827exp() 3.3m m m S g ωωσωωωωωαγωωωωωω----⨯--=-=⨯-⨯=-⨯ 22exp[426.85695(0.69145)]54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()10.285730.9827exp() 3.3mm S ωωωωωωωωωωω----⎧-⨯≤⎪⎪=⎨⎪-⨯>⎪⎩P-M 谱:450.78()exp[ 1.25()]m S ωωωω=- 其中谱峰频率1.253/0.59067(/)m rad s ω===45540.780.590670.780.15216()exp[ 1.25()]exp()S ωωωωω=-=-TMA 谱:()()()J S f S f kh =Φ322tanh tanh ()tanh tanh 12/sinh 2kh kh kh kh kh kh kh kh khΦ==+-+ 波数k 由色散关系2tanh gk kh ω=确定, 由()()S f df S d ωω=可知,()()/()/2()()/2J S S f df d S f S f kh ωωππ===Φ则()()/2()J J J S f S d df S ωωπω==()()/()/2()()/2()()J J S S f df d S f S f kh S kh ωωππω===Φ=Φ22exp[426.85695(0.69145)]54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()()10.285730.9827exp() 3.3()mmkh S kh ωωωωωωωωωωω----⎧-⨯⨯Φ≤⎪⎪=⎨⎪-⨯⨯Φ>⎪⎩取上述JONSWAP 波浪谱为靶谱22exp[426.85695(0.69145)]54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()10.285730.9827exp() 3.3mm S ωωωωωωωωωωω----⎧-⨯≤⎪⎪=⎨⎪-⨯>⎪⎩海浪的波面:~1())Mi i i t t ηωε==+i ε为第i 个组成波的初相位 ,此处取在(0,2π)范围内取均布的随机数;取^1()/2i i i ωωω-=+,0.5t s ∆=,采用M=200,取频率上限H ω为4倍谱峰频率;(i ω为区间端点频率)440.69145 2.7658(/)H m rad s ωω==⨯=/ 2.7658/2000.013829(/)H M rad s ωω∆===采用^1()/2i i i ωωω-=+计算时,模拟的所得的波浪将以周期为2/πω∆重复出现,除非ω∆足够小,否则与实际的波浪情况不符。
随机波浪理论简介
0
0 S
d
2 m0
方向谱
x, y,t an coskn x cosn kn y sinn nt n n1
S ,
1 2
an2
S , S G ,
G ,
方向分布函数
方向函数意义
S
S
,
d
S , S G ,
G , d
1
/ 2 G , d 1
/ 2
en
1 2
gan2
全部组成波的总能量:
E
n1
1 2
gan2
波浪谱
n
n1
n1
1
2
2
0 an cos nt n d 0
2
2 n
n
n1
n1
2
n2
n1
n1
1
2
2 0
an2
cos2
nt
n
d
n1
12an2
2
S
n1
12an2SΒιβλιοθήκη 2 S d0
波频谱对原点的零阶矩: m0
Rayleigh:
f
a
a
2
exp
a2
2
2
波面坐标的均方差
平均振幅
a af ada 0
2
H 2a, H 2a
f
H
2
H H2
exp
4
H H
2
平均波高表示的波高的 理论概率分布函数
波高累积频率及与平均波高关系
波高累积频率函数:
F
H
exp
H
2
4 H
H1% 2.42 H
1.522 0.245P 0.00292P2
波浪谱频率范围

波浪谱频率范围
波浪谱是描述海洋波浪形状和频率的数学模型,其频率范围是指波浪谱的离散程度。
波浪谱的频率范围可以从 0.1 Hz 到 10 Hz,具体取决于波浪的形态和来源。
在海洋工程中,波浪谱频率范围对于设计和分析波浪谱模型非常重要。
波浪谱的频率范围可以用于确定波浪的波长、频率和速度,进而分析波浪的来源、形态和运动方式。
在波浪谱频率范围的研究过程中,需要考虑到波浪谱的离散程度。
波浪谱的离散程度是指波浪谱中各个频率成分的占比,通常使用百分比来表示。
波浪谱的频率范围越广,各个频率成分的占比越均匀,但是在某些情况下,波浪谱的频率范围可能会发生明显的变化。
波浪谱的频率范围还可以用于确定海洋波浪的形态和来源。
在海洋波浪的研究中,通常使用波浪谱分析来识别波浪的形态和来源。
例如,在识别波浪形态时,可以使用波浪谱的频率范围和振幅范围来确定波浪的波长、形状和振幅大小。
在确定波浪来源时,可以使用波浪谱的频率范围和波形特征来分析波浪的来源方向和方式。
波浪谱的频率范围在波浪谱研究中扮演着重要的角色,可以用于确定波浪形态和来源,也可以用于设计波浪谱模型和分析波浪谱数据。
概率论中波浪号的含义

概率论中波浪号的含义
概率论是一门研究随机事件的概率以及其规律的学科。
在研究过程中,我们经常会遇
到一些符号,其中最常见的就是波浪号(~)。
它在概率论中有着特殊的含义,下面我们就来详细解释一下。
波浪号在概率论中有两种不同的用法:
1. 表示概率分布
在概率论中,波浪号常常用来表示概率分布,即某个随机变量的取值所对应的概率。
例如,我们可以用X~N(μ,σ^2)来表示一个正态分布的随机变量X,其中μ表示期望,
σ^2表示方差。
这个符号的含义是,X的分布服从均值为μ,方差为σ^2的正态分布。
类似地,我们还可以用P~(A)来表示事件A发生的概率,其中P表示概率分布。
这个符号的含义是,事件A的概率为P(A)。
2. 表示近似相等
除了表示概率分布外,波浪号还可以用来表示近似相等的关系。
具体来说,如果我们
说x~y,那么它的含义是x约等于y。
用波浪号表示近似相等的原因是,在概率论中,我们经常需要处理连续变量而不是离
散的值。
因此,我们不可能精确地计算出某个随机事件的概率,只能通过近似的方式来得
到一个范围。
这时,我们就可以用波浪号来表示这种近似的关系。
例如,我们可以说“X~N(0,1)时,P(|X|<1)约等于0.68”。
这个语句的含义是,当X
满足均值为0,方差为1的正态分布时,|X|小于1的概率大约为0.68。
总结:
在概率论中,波浪号具有两种不同的含义。
一种是用来表示某个随机事件的概率分布,另一种则是用来表示近似相等的关系。
弄清这些用法,对我们在概率论中的理解非常重
要。
水平运动模拟器复演随机海浪谱实验

水平运动模拟器复演随机海浪谱实验薛米安;邢建建;苑晓丽;陈奕超;罗铆钧【摘要】A horizontal movement simulator is designed in this study.The random motion displacements generated by broad band B spectrum and narrow band J spectrum are studied experimentally by using a horizontal movement simulator.Statistical characteristics such as themaximum/minimum displacement and standard deviation of random motion displacement generated by ocean wave spectrum and determinate coefficient between corresponding measured power spectrum density and theoretical spectrum are analyzed by varying significant wave height and peak period.The determinate coefficient between measured power spectrum density and theoretical spectrum of B spectrum is greater than that of J spectrum,which is mainly affected by peak period for J spectrum.The standard deviation of the random motion displacement and the variance of power spectrum density of J spectrum are also found to be greater than that of B spectrum. The result indicates that it is difficult to generate random motion displacement exactly by a horizontal movement simulator for more highly dispersed J spectrum compared with broad band Bretschneider spectrum.%设计了一种水平随机运动模拟器,并基于模型实验研究了该水平运动模拟器复演宽频带Bretschneider谱(B谱)与窄频带JONSWAP谱(J 谱)所生成随机运动位移的能力及其关键影响因素.通过改变谱峰周期和有效波高讨论了两种海浪谱所生成水平随机运动位移的极值及与随机运动位移相应的频谱密度特征,确定了谱峰周期及有效波高对水平运动模拟器冲程的影响规律.基于实测频谱密度与理论谱之间的拟合优度,发现该模拟器对宽频带的B谱具有较高的复演精度,而对能量分布相对集中的窄频带J谱的复演精度相对较低,并且发现谱峰周期是影响J谱实测谱与理论谱拟合优度的主要因素,同时由J谱生成的随机运动位移的标准差及相应频域中能谱密度的方差均大于B谱,表明J谱相对B谱而言是一种高离散度的谱型,在运动模拟器中很难被精确复演为随机运动位移.【期刊名称】《振动、测试与诊断》【年(卷),期】2019(039)002【总页数】8页(P346-352,446)【关键词】运动模拟器;宽频带谱;窄频带谱;统计特征;快速傅里叶变换【作者】薛米安;邢建建;苑晓丽;陈奕超;罗铆钧【作者单位】河海大学海岸灾害及防护教育部重点实验室, 南京, 210098;河海大学港口海岸与近海工程学院, 南京, 210098;河海大学港口海岸与近海工程学院, 南京, 210098;河海大学理学院, 南京, 210098;河海大学港口海岸与近海工程学院, 南京, 210098;河海大学港口海岸与近海工程学院, 南京, 210098【正文语种】中文【中图分类】TH115;TB534+.2引言海洋工程结构物如浮式生产储卸油系统(floating production storage and offloading,简称FPSO)、半潜式平台、大型液货船等主力海洋工程装备,长期遭受着风浪流等复杂动载荷的作用,尤其是在波浪作用下常常会引起上述结构物的剧烈运动。
随机波浪及工程应用第一章

F 1 2 0 ei0t F ei0t 2 0
若0 0
F 1 2 F k 2 k
F b cos 0t
b F{e it eit } 2
S (f) (m2 s)
理 论 谱 实 测 谱
0.00300
0.00200
0.00100
0.00000 0 0.4 0.8
f (Hz)
1.2
1.6
Longuet-Higgins (1957) 建议的谱宽参数
mrf f r S f df
0
mr S d
r 0
用单侧谱表示:
Sxx Rxx
x(t)是实数
0
1
0
Rxx cos( )d
S xx cos( )d
自相关函数特性: Rxx 0 D x t 0 S xx d m0 谱密度函数积分面积等于随机过程的方差
Chapter 2 随机过程的谱分析
2.1 谱密度函数
•平稳的各态历经的随机过程可以用一个样本来代替整体。 •随机的时间过程可以认为是由很多不同频率的简谐波叠 加而成。 •各个简谐波 (波浪:能量)相对于组成波频率的分布 随机过程的频域特性 谱分析 随机过程的时域 频谱
随机过程:以波浪为例
波浪的能量正比于波高的平方gH2/8 {x2(t)}正比于随机过程X(t)的能量
x(t)是实数
S xx
Rxx S xx ei d
1 S 2
xx
海浪谱

描述海浪内部能量相对于频率和方向的分布。
为研究海浪的重要概念。
通常假定海浪由许多随机的正弧波叠加而成。
不同频率的组成波具有不同的振幅,从而具有不同的能量。
设有圆频率ω的函数S(ω),在ω至(ω+ω)的间隔内,海浪各组成波的能量与S(ω)ω成比例,则S(ω)表示这些组成波的能量大小,它代表能量对频率的分布,故称为海浪的频谱或能谱。
同样,设有一个包含组成波的圆频率ω和波向θ的函数S(ω,θ),且在ω至(ω+ω)和θ至(θ+ω)的间隔内,各组成波的能量和S(ω,θ)ωθ成比例,则S(ω,θ)代表能量对ω和θ的分布,称为海浪的方向谱。
将组成波的圆频率换为波数,可得到波数谱;将ω换为2π(频率为周期的倒),得到以表示的频谱S()数。
以上各种谱统称为海浪谱。
海浪谱不仅表明海浪内部由哪些组成波构成,还能给出海浪的外部特征。
比如,理论上可由谱计算各种特征波高和平均周期,利用这些特征量连同波高与周期的概率密度分布,可推算海浪外观上由哪些高低长短不同的波所构成。
若已知海浪的谱,海浪的内外结构都可得到描述,因此谱是非常有用的概念。
事实上,海浪的研究(包括许多应用问题),大多和谱有关。
频谱在海浪谱中,风浪频谱得到最广泛的研究,因为它的应用最广,也最易于得到。
但尚无基于严格理论的风浪频谱。
已提出的经验的或半经验的频谱很多,大多数用[245-1]的乘积来表达。
通常p为5~7,q为2~4,在正量A和B之内。
除了数值常数外,还包含风要素(如风速、风时和风区)或浪要素(如特征波高和周期)作为参量,故谱的形状随风的状态或对应的浪的状态而变化。
上述两项的乘积代表的谱,在ω=0处为0,在0附近的值很小,ω增加时,它骤然增大至一个峰值,然后随频率的增大而迅速减小,在ω→∞ 时趋于0。
这表明谱的频率范围在理论上虽为0~∞,但其显著部分却集中在谱峰附近。
海面上存在的许多波,其显著部分的周期范围很小,恰和理论结果相对应。
随着风速的增大,谱曲线下面的面积(从而风浪的总能量或波高)增大,峰沿低频率方向推移,表明风浪显著部分的周期增大。
随机波浪谱

Jonswap 谱:联合北海波浪项目峰形参数a σσ=(当m ωω≤时),b σσ=(当m ωω>时),因此该谱共有五个参量,它们都随各个谱而变化。
对于平均的JONSWAP 谱:3.3γ=0.07a σ= 0.09b σ=0.615 1.080.615 1.0883.7220 4.515.403(/)s U kX H m s --==⨯⨯=22/9.82201000/15.4039087.368X gX U ==⨯⨯=0.330.3322(/)()22(9.8/15.403)9087.3640.69145(/)m g u X rad s ω--==⨯⨯=0.220.220.076()0.0769087.3680.0102319X α--==⨯=在m ωω≤时,2222222exp[()/(2)]24524exp[(0.69145)/(0.070.69145)]5exp[426.85695(0.69145)]5415()exp[()]4150.691450.01023199.8exp[()] 3.3410.285730.9827exp() 3.3m m m S g ωωσωωωωωαγωωωωωω----⨯--=-=⨯-⨯=-⨯在 m ωω>时,2222222exp[()/(2)]24524exp[(0.69145)/(0.090.69145)]5exp[258.22211(0.69145)]5415()exp[()]4150.691450.01023199.8exp[()] 3.3410.285730.9827exp() 3.3m m m S g ωωσωωωωωαγωωωωωω----⨯--=-=⨯-⨯=-⨯22exp[426.85695(0.69145)]54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()10.285730.9827exp() 3.3mm S ωωωωωωωωωωω----⎧-⨯≤⎪⎪=⎨⎪-⨯>⎪⎩P-M 谱:又称ITTC 谱450.78()exp[ 1.25()]m S ωωωω=- 其中谱峰频率0.59067(/)m rad s ω===45540.780.590670.780.15216()exp[ 1.25()]exp()S ωωωωω=-=-TMA 谱:()()()J S f S f kh =Φg322tanh tanh ()tanh tanh 12/sinh 2kh khkh kh kh kh kh kh khΦ==+-+ 波数k 由色散关系2tanh gk kh ω=确定, 由()()S f df S d ωω=可知,()()/()/2()()/2J S S f df d S f S f kh ωωππ===Φg则()()/2()J J J S f S d df S ωωπω==()()/()/2()()/2()()J J S S f df d S f S f kh S kh ωωππω===Φ=Φg g22exp[426.85695(0.69145)]54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()()10.285730.9827exp() 3.3()mmkh S kh ωωωωωωωωωωω----⎧-⨯⨯Φ≤⎪⎪=⎨⎪-⨯⨯Φ>⎪⎩取上述JONSWAP 波浪谱为靶谱22exp[426.85695(0.69145)]54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()10.285730.9827exp() 3.3mm S ωωωωωωωωωωω----⎧-⨯≤⎪⎪=⎨⎪-⨯>⎪⎩海浪的波面:~1())Mi i i t t ηωε==+i ε为第i 个组成波的初相位 ,此处取在(0,2π)范围内取均布的随机数;取^1()/2i i i ωωω-=+,0.5t s ∆=,采用M=200,取频率上限H ω为4倍谱峰频率;(i ω为区间端点频率)440.69145 2.7658(/)H m rad s ωω==⨯=/ 2.7658/2000.013829(/)H M rad s ωω∆===采用^1()/2i i i ωωω-=+计算时,模拟的所得的波浪将以周期为2/πω∆重复出现,除非ω∆足够小,否则与实际的波浪情况不符。
随机波浪的模拟1

随机波数值模拟方法1 概述研究海浪及其对工程的作用有三种途径:一是现场观测研究;二是在实验室内进行模拟研究;三是理论分析研究。
由于海浪的复杂多变性,加上现场环境恶劣,进行现场观测需花费大量的人力物力;理论研究目前也有较大的局限性,特别是对于不规则波浪,很多问题有赖于室内的模拟研究。
模拟研究的方法可分为两大类。
开始是在水槽或水池内利用风或造波机进行物理模拟,亦即进行波浪模型试验。
在人们的精心设计下,可以把负责的现象分解为多个简单的模型,然后再把成果综合起来。
过去已取得了大量的研究成果,目前仍是主要的研究方法之一。
随着电子计算机的发展和普及,海浪的数值模拟得到迅速的发展,它具有经济方便等优点,日益受到人们的重视和广泛的应用。
天然海浪是很复杂的,人们对它的认识和研究过程是由简到繁,由浅入深,及即由单向规则波—斜向规则波—单向不规则波—多向不规则波。
2 不规则波浪的数值模拟—模拟频谱单向不规则波浪的数值模拟方法,大多建立在线性波浪理论的基础上。
本文主要介绍利用线性叠加法和线性过滤法进行二维不规则波的模拟。
2.1 线性波浪叠加法在工程中,如果已经得到了特征波的波参数如有效波高H s、周期T 等参数,如何得到一列不规则波面时间历程呢?一般通过模拟靶谱法来完成。
将有效波高H s、周期T 等参数代入某波浪频谱形式中,得到的海浪谱即为靶谱。
现在要模拟某波面不规则波面时间历程,使得模拟的波谱同靶谱一致。
平稳海况下的海浪可视为平稳的具有各态历经性的随机过程,波动可以看作无限多个振幅不等、频率不等、初相位随机的简谐余弦波叠加而成,即Mt a i cos k i x i t i (1i 1式中,t 为波动水面相对于静水面的瞬时高度;a i 为第i 个组成波的振幅;k i, i为第i个组成波的波数和圆频率;k i 2 L i , i 2 T iL ,T 分别为波长、周期;x,t 分别表示位置和时间,通常固定位置,可取x=0;i 为第i 个组成波的初位相,此处取在(0,2 π)范围内均布的随机数。
随机海浪的数值仿真与频谱分析_许景波

2010, 46 (36)
Computer Engineering and Applications 计算机工程与应用
随机海浪的数值仿真与频谱分析
2 许景波 1, , 边信黔 3, 付明玉 3 2 XU Jing-bo1, , BIAN Xin-qian3, FU Ming-yu3
1.哈尔滨工程大学 控制科学与工程博士后流动站, 哈尔滨 150001 2.哈尔滨理工大学 测控技术与通信工程学院, 哈尔滨 150080 3.哈尔滨工程大学 自动化学院, 哈尔滨 150001 1.Postdoctoral Research Station of Control Science & Engineering, Harbin Engineering University, Harbin 150001, China 2.College of Measure-control Technology & Communication Engineering, Harbin University of Science and Technology, Harbin 150080, China 3.Automation College, Harbin Engineering University, Harbin 150001, China E-mail: hitxjb@ XU Jing-bo, BIAN Xin-qian, FU Ming-yu.Simulation and spectral analysis of random sea puter Engineering and Applications, 2010, 46 (36) : 226-229. Abstract: This paper deals with the method of simulating sea wave for decreasing its disturbance in the watercraft navigating.Firstly the ITTC two-parameter spectrum is selected as the power spectrum of sea wave.Secondly the selected power spectrum is aivided by energy inpart, and the frequency of harmonic wave is determined by calculating the mass center of each section.All harmonic waves are synthesized on the basis of the Longuest-Higgins model in time domain.Finally, the simulation algorithm based on energy in part is presented and the simulated sea wave with time and space is determined.The simulation accuracy arrives at 1.6% compared with the ideal wave frequency spectrum by the spectral analysis of the simulated sea wave in Welch.That testifies the validity of this method and provides the vessel motion parameters filtering with reliable exciting signals. Key words:sea wave simulation; energy in part; spectral estimation 摘 要: 针对船舶航行抑制海浪干扰的需要, 研究了海浪波形的建立方法。选取 ITTC 双参数谱作为海浪谱, 通过能量等分法对
随机波浪谱

Jonswap 谱:联合北海波浪项目 峰形参数 a (当 m 时), b(当都随各个谱而变化。
对于平均的 JONSWAP 谱:3.30.615 1.08 0.615 1.08 U kX 0.615 H s 1.08 83.7 220 0.615 4.51.08 15.403( m / s)X gX /U 29.8 220 1000 /15.403 29087.368m22(g/u)(X) 0.3322 (9.8/15.403) 9087.364 0.330.69145(rad / s)0.22 0.22 0.076( X ) 0.220.076 9087.368 0.220.0102319在m 时,S( ) g 2 15 exp[ 5( m )4] exp[ (m )2/(2 22m )]42 1 5 0.69145 4 exp[ ( 0.69145)2/(0.0720.691452)]0.0102319 9.82 5 exp[ ( )4] 3.3exp[ ( 0.69145) /(0.07 0.69145 )] 540.9827 15 exp( 0.2854 73 ) 3.3exp[ 426.85695( 0.69145)2]在 m 时,S( )g 2 15 exp[ 5( m )4] exp[ ( m )2/(2 22m )]5421 5 0.69145 4 exp[ ( 0.69145)2/(0.0920.691452)] 0.0102319 9.8 5exp[ ( ) ] 3.341 0.28573 exp[ 258.22211( 0.69145)2]0.9827 5 exp( 4 ) 3.3exp[ 258.22211( 0.69145) ]S( )0.9827 15 exp( 0.28573)4)3.3exp[ 426.85695( 0.69145)2]0.9827 15 exp( 0.28573)4)3.3exp[ 258.22211( 0.69145)2]P-M 谱:又称 ITTC 谱1.253/ H s 1.253/ 4.5 0.59067(rad /s)0.07b0.09S( )0.758exp[ 1.25( m)4]m 时),因此该谱共有五个参量,它们其中谱峰频率S( ) S( f )df /d则 S J ( f ) S J ( )dS( ) S( f )df /dS J (f )g (kh)/2)S J (f )g (kh)/ 20.78 0.59067 4 S( ) 5 exp[ 1.25( )4]0.78 0.152165 exp( 4 )TMA 谱: S( f ) S J ( f)g (kh) (kh) 3tanh 3 kh 2 tanh kh kh kh tanh 2 kh2tanh 2kh 1 2kh/sinh2kh波数 k 由色散关系 2 gk tanh kh 确定, 由 S( f )df S( )d 可知,S( ) 0.9827 15exp(0.9827 15exp(0.28573) 3.3exp[ 0.28573) 3.3exp[ 426.85695(258.22211(20.69145) 2 ]0.69145)2](kh) (kh)取上述 JONSWAP 波浪谱为靶谱S(f)/2 /df 2 S J (S( f)/2S J ( )g (kh)1海浪的波面:M ^ ~(t) 2S ( i ) i cos( i t i ) i1^取i ( i1 i)/2, t 0.5s ,采用 M=200 ,取频率上限 H 为4倍谱峰频率;( i 为区间端点频率)H4 m 4 0.69145 2.7658(rad / s)H/M 2.7658/ 200 0.013829( rad /s)^采用 i ( i 1 i ) / 2计算时,模拟的所得的波浪将以周期为 2 / 重复出现,除非 足够小, 否则与实际的波浪情况不符。
波浪谱密度函数数值分析

大连理工大学硕士学位论文波浪谱密度函数数值分析姓名赫亮申请学位级别硕士专业船舶与海洋结构物设计制造指导教师王言英20050617大连理工大学硕士学位论文摘要本文针对欧洲北海的一次为期六天的风暴中定点测得的波浪海面瞬时升高数据样本应用快速傅立叶变换方法分析计算得到相应的能量谱密度函数靶谱。
根据北海删平台对于一次风暴的观测记录进行了对经验谱公式谱的谱峰升高因子和峰频控制因子进行了修正。
结果表明谱矩。
随参变量和峰频∞随互×∞变化显著当互×国时脚。
与∞的预报值同实测分析结果符合得令人满意。
应当指出所测的波浪记录的平均过零周期和谱的零阶矩相差很大不属于同一海况这与观测条件是在一次风暴中测得结果的相符。
通过对个子样给出的有义波高和某一时段的统计值与实际根据计算得到的有义波高和这一时段的统计值进行比较发现两者符合得尚好。
传统的风浪谱估计方法法假定在所取时间滞后数乘机之外其协方差函数为零在周期图中假定所取数据长度为一完整周期。
其谱估计实际为频谱和窗函数的乘积。
本文重点进行了最大熵法风浪谱估计和传统谱估计方法的分析比较讨论了最大熵法的原理。
结果表明最大熵法优于传统方法如快速付立叶交换方法最大熵法避免了一些不切实际的假设不需要使用窗函数减少了谱泄漏提高了谱估计精度。
对于北海风浪采用赤池定阶法和经验定阶法相结合的办法确定最小的阶数。
同时最大熵对已有的时间序列的信息量保持最大当样本容量较小时也能得到较好的谱估计结果。
为风浪谱估计又提供了一种有效的方法。
关键词风浪谱谱快速付立叶法最大熵法波浪谱密度函数数值分析国 五脚正国 乱’ ’’黜吼’℃ 假’’七 飞 Ⅱ独创性说明作者郑重声明本硕士学位瓯论文是我个人在导师指导下进行的研究工作及取得研究成果。
尽我所知除了文中特别加以标注和致谢的地方外论文中不包含其他人已经发表或撰写的研究成果也不包含为获得大连理工大学或者其他单位的学位或证书所使用过的材料。
与我一同工作的同志对本研究所做的贡献均己在论文中做了明确的说明并表示了谢意。
随机波浪及工程应用第二章

Covz t , t ' Covx t , t ' Cov y t , t ' Covxy t , t ' Covxy t ' , t
Covxy t , t ' Cov yx t ' , t
mz t mx t my t
x的自相关函 数
17
Cov x t1 , x t2 E x t1 mx t1 x t2 mx t2
Cov x t1 , x t2 E x t1 x t2 mx t1 mx t2
随机过程是随机变量系的推广,是时间的函数,其 统计特征随时间变化
均值(数学期望):
mx t E X t xf x dx
是每个时间截口的随机 变量的分布中心,平 均函数,非随机的
方差(variance):
Dx t D X t
各态历经性的数学条件: Et x1 t Et x2 t Et xi t Et x1 t x1 t Et x2 t x2 t =E t x i t xi t =
6
课程的主要内容:
随机波浪理论的基础 海浪的统计特征(外部特征) 海浪谱(内部特征) 不规则波波浪的模拟和变形 不规则波对工程建筑物的作用
7
Chapter 1 随机过程
1.1 随机过程的基本概念
确定性过程: 可以预先知道其变化过程
自然界中的 两种变化过程
波浪力学第六章 随机波浪和随机波浪力

系
Prob [x < x(t ) < x + ∆x ] p ( x) = lim ∆x ∆x → 0
dx
Xm众值
x
海 洋 工 程 波 浪 力 学
概率分布函数
P ( x) = Prob [x(t ) ≤ x ] = ∫ p ( x)dx
x −∞
p(x)
超值累积概率分布函数
F ( x) = Prob [x(t ) ≥ x ] = ∫ p ( x)dx
中 国 海 洋 大 学 海 洋 工 程 系
6.1 随机波浪的统计特性
6.1.4 谱密度函数
一. 谱密度函数
1 傅立叶积分公式 x (t ) = 2π
傅立叶变换
海 洋 工 程 波 浪 力 学
∫ [∫
−∞
∞
∞
−∞
x(t ) exp(− iωt )dt ] exp(iωt )dω
G (ω ) = ∫ x(t ) exp(− iωt )dt
R (t1 , t1 + τ ) = R (τ )
1 M [ x(t1 )] = lim N →∞ N 1 R (t1 , t1 + τ ) = lim N →∞ N
N
∑ x (t )
k =1 k 1 k 1
N
∑ x (t ) ⋅ x (t
k =1 k 1
+τ )
王 树 青
第六章 随机波浪及随机波浪力
x ∞
x
x
p (x )
王 树 青
= 1 − P( x)
x
x
第六章 随机波浪及随机波浪力
中 国 海 洋 大 学 海 洋 工 程 系
6.1 随机波浪的统计特性
在随机波浪中波浪和波浪载荷的分布

应用举例12(随机变量的函数和可靠性分析)在随机波浪中波浪和波浪载荷的分布海洋表面和波浪高度的分布在暴风雨时海平面的提升可以用正态(或者高斯)随机函数充分地描述。
也就是说,在一般的时间和地点,海平面的提升可以用平均海平面提升的正态分布很好的近似。
考虑到由正态随机函数理论推导出瑞利型波浪高度H 的分布,其累积密度函数这里参数H S 叫做特征波浪高度,它是在一般点海平面提升的标准差的4倍。
在公式1中的H 其均值为0.627H S ,方差为0.328H S 。
图1中的曲线(a )描绘了正态变量X=2H/H S的瑞利概率密度。
我们感兴趣的是H 的分布的上尾,因为较大的波浪会对舰船近海结构和海事活动带来威胁。
在一场暴风雨中波浪最大高度公式1中F H (h)是在海况下带有参数H S 任意被选波浪高度小于h 的概率。
考虑有1000个波浪(这个波浪数代表了有效持续时间为3小时且平均波浪时间为10秒的暴风雨)的暴风雨,并假定这些波浪高度独立同分布。
那么经历暴风雨时最大波浪高度的分布,即H 1000为:X 1000= 2H 1000/H S 的概率密度函数如图1中曲线(b )所示。
对于1000个波浪,最可能的最大大波浪载荷关心的不仅仅是波浪高度分布,还有对所关注的结构由此产生高度为1.868H S 。
最大波浪高度的分布对暴风雨持续时间不是非常敏感。
比如,对于2000个波浪的暴风雨,最可能的最大高度为1.958H S ,见图1曲线(c ),它表明X 2000=2H 2000/H S 的概率密度函数。
经历单一暴风雨的最对于工程设计和安全核查,所的载荷的分布。
高度为h 的波浪作用于固定平台载荷为q 的简化模型为这里C 为接近于2的常量。
因此,如果h 0表示设计波浪高度,q 0表示相应的设计应力,则q 和h 的关系为如果q 和h 的关系是单调递增,波浪高度H 和载荷Q 的的分布有如下关系利用公式1或者2中F H的分布,可以得到由1或1000个波浪和海洋特征波浪高度为H S 的最大载荷的分布。
随机海浪谱的物理模型与海洋结构波浪动力可靠度分析的开题报告

随机海浪谱的物理模型与海洋结构波浪动力可靠度分析的开题报告一、选题背景海洋结构工程作为工程结构学中的一个分支,主要聚焦于海洋环境中的结构响应、海洋工程设施的建设和维护等方面。
对于海洋结构工程的设计和施工,其波浪动力研究至关重要。
其中,随机海浪谱的物理模型与海洋结构波浪动力可靠度分析成为前沿热点研究方向。
二、研究目的与意义本研究将探索随机海浪谱的物理模型与海洋结构波浪动力可靠度分析之间的关系。
在此基础上,我们将实现以下目标:1. 对随机海浪谱的物理模型进行研究,包括概率分布、统计特性等方面的探索与分析。
2. 基于离散波数谱的方法,对随机海浪谱进行数值模拟,验证物理模型的准确性。
3. 利用开发的随机海浪谱的物理模型和数值模拟方法,对海洋结构波浪动力进行可靠度分析,评估其安全性和可靠性。
4. 建立一套完整的随机海浪谱的物理模型和海洋结构波浪动力可靠度分析方法,为实际海洋工程项目提供技术支持及指导。
三、研究内容与技术路线1. 研究随机海浪谱的物理模型,建立随机海浪谱的概率分布函数、统计特性指标等定量分析方法。
2. 基于离散波数谱的方法,开发随机海浪谱数值模拟程序。
3. 对海洋结构波浪动力进行可靠度分析,包括建立结构响应数值模型和进行现场试验等。
4. 建立一套完整的随机海浪谱的物理模型和海洋结构波浪动力可靠度分析方法,并将其应用于实际海洋工程项目。
四、存在的问题及解决途径1. 随机海浪谱的物理模型的可靠性和准确性问题。
解决途径是通过与现场观测、大规模试验的结果进行对比,进行模型验证和优化。
2. 数值模拟结果与实际情况的误差较大。
解决途径是优化模型参数,提高模拟方法的准确性。
3. 可靠度分析结果的精度和可靠性需要进一步提高。
解决途径是引入更加精细的模型和数据,并进行多次模拟验证,提高结果的可信度。
五、预期成果和创新点1. 研究出一套完整的随机海浪谱的物理模型和海洋结构波浪动力可靠度分析方法,成为海洋结构工程领域的重要技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Jonswap 谱:联合北海波浪项目
峰形参数a σσ=(当m ωω≤时),b σσ=(当m ωω>时),因此该谱共有五个参量,它们都随各个谱而变化。
对于平均的JONSWAP 谱:
3.3γ=
0.07a σ= 0.09b σ=
0.615 1.080.615 1.0883.7220 4.515.403(/)s U kX H m s --==⨯⨯=
22/9.82201000/15.4039087.368X gX U ==⨯⨯=
0.330.3322(/)()22(9.8/15.403)9087.3640.69145(/)m g u X rad s ω--==⨯⨯=
0.220.220.076()0.0769087.3680.0102319X α--==⨯=
在m ωω≤时,
2222222exp[()/(2)]2
4524
exp[(0.69145)/(0.070.69145)]5exp[426.85695(0.69145)]
54
1
5()exp[()]4150.691450.01023199.8exp[()] 3.3410.285730.9827exp() 3.3m m m S g ωωσωωωωωαγ
ωω
ωω
ωω
----⨯--=-=⨯-⨯=-⨯
在 m ωω>时,
2222222exp[()/(2)]
2
4524
exp[(0.69145)/(0.090.69145)]5exp[258.22211(0.69145)]
54
1
5()exp[()]4150.691450.01023199.8exp[()] 3.3410.285730.9827exp() 3.3m m m S g ωωσωωωωωαγωω
ωω
ωω
----⨯--=-=⨯-⨯=-⨯
22
exp[426.85695(0.69145)]
54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()10.285730.9827exp() 3.3m
m S ωωωωωωωωωωω----⎧-⨯≤⎪⎪=⎨⎪-⨯>⎪⎩
P-M 谱:又称ITTC 谱
4
5
0.78
()exp[ 1.25(
)]m S ωωωω
=
- 其中谱峰频率
0.59067(/)m rad s ω===
45
5
4
0.78
0.59067
0.78
0.15216
()exp[ 1.25(
)]exp()S ωωω
ωω=
-=
-
TMA 谱:
()()()J S f S f kh =Φg
322
tanh tanh ()tanh tanh 12/sinh 2kh kh
kh kh kh kh kh kh kh
Φ==+-+ 波数k 由色散关系2
tanh gk kh ω=确定, 由()()S f df S d ωω=可知,
()()/()/2()()/2J S S f df d S f S f kh ωωππ===Φg
则()()/2()J J J S f S d df S ωωπω==
()()/()/2()()/2()()J J S S f df d S f S f kh S kh ωωππω===Φ=Φg g
22exp[426.85695(0.69145)]
54exp[258.22211(0.69145)]54
10.285730.9827exp() 3.3()()10.285730.9827exp() 3.3()m
m
kh S kh ωωωωωωωωωωω----⎧-⨯⨯Φ≤⎪⎪=⎨⎪-⨯⨯Φ>⎪⎩
取上述JONSWAP 波浪谱为靶谱
22
exp[426.85695(0.69145)]
54exp[258.22211(0.69145)]5410.285730.9827exp() 3.3()10.285730.9827exp() 3.3m
m S ωωωωωωωωωωω----⎧-⨯≤⎪⎪=⎨⎪-⨯>⎪⎩
海浪的波面:
~
1
())M
i i i t t ηωε==+
i ε为第i 个组成波的初相位 ,此处取在(0,2π)范围内取均布的随机数;
取^
1()/2i i i ωωω-=+,0.5t s ∆=,采用M=200,取频率上限H ω为4倍谱峰频率;(i ω为区间端点频率)
440.69145 2.7658(/)H m rad s ωω==⨯=
/ 2.7658/2000.013829(/)H M rad s ωω∆===
采用^
1()/2i i i ωωω-=+计算时,模拟的所得的波浪将以周期为2/πω∆重复出现,除非ω∆足够小,否则与实际的波浪情况不符。
因此在各区间内部随机的选取频率作为该区间的代表
频率;
由上述参数可以模拟出需要的波面,由下述公式可以得到自相关函数;
1
1
()()()N n
n n R t t
t t N ννηνην
-=∆=
+∆-∑
,0,1,2,...,t m τνν=∆=
此处N=2200,m=100
这样便得到()R τ的1m +个值,它们等间隔地分布着,并分别位于0,,2,...,t t m t τ=∆∆∆; 有下述公式可以估算谱初值:
2
2
()cos ()cos(2)m t
m
n n
n
L R d R t f t t τ
ντωττνπνπ
π∆===
=∆∆∆∑∑ 此处采用的频率间隔为1
/2N f f m m t
∆==
∆ 1
2n n f n f m t
=∆=
∆代入上式得:
1
1
211[(0)()cos ()cos ]
220,1,2,...,m n n L R R t R m t n m n m
νπννππ-==+∆+∆=∑
1
220.06283182n n n f n m t
ωππ
===∆
采用哈明(Hamming)窗对初值谱进行光滑处理,得到光滑谱;
对模拟实现的波面进行统计分析可知, 统计波高共150个 最大波高为6.42089 其对应的周期为8.5
1/10大波波高为5.122027 其对应的周期为8.366667 1/3大波波高为4.201093
其对应的周期为8.32 平均波高为2.677328 其对应的平均周期为7.31
模拟实现的谱的一阶谱矩m 0
=1.16832
1/303.89s H H m == 02.48H m =
由线性波浪理论可得:
cos()A kx t ηω=-
cosh ()cosh ()
cos()sinh sinh k z d k z d u A kx t kd kd ω
ωηω
++=-= sinh ()sinh ()
sin()tan()
sinh sinh k z d k z d v A kx t kx t kd kd
ωωηωω++=-=- 在水深20d m =,0x =,3z m =-处水质点的速度为: °°1
11
cosh ()cosh17(,)cos()cos()sinh sinh 20m N
i i i i i i i i i i
i i i i k z d k u z t a t a t k d k ωωεωωε==+=+=+∑∑ °°111
sinh ()sinh17(,)sin()sin()sinh sinh 20m N
i i
i i i i i i i i
i i i i k z d k v z t a t a t k d k ωωεωωε==+=+=+∑∑ 把谱分成m 1=200份,取
µ2()i i i
a S ηηωω=∆ 频率划分的方法采用等分频率的方法,其具体方法和°i ωµi
ω及i ε的选取方法同上,由此可以得到速度过程线(下图为速度过程线的一段);
由速度过程线可以得到自相关函数以及速度谱:
1
1
()()()
N
n n
n
R t u t t u t
N
ν
νν
ν
-
=
∆=+∆
-
∑
,0,1,2,...,
t m
τνν
=∆=
此处N=2200,m=100
这样便得到()
Rτ的1
m+个值,它们等间隔地分布着,并分别位于0,,2,...,
t t m t
τ=∆∆∆;有下述公式可以估算谱初值:
00
22
()cos()cos(2)
m t m
n n n
L R d R t f t t
τν
τωττνπν
ππ
∆
==
==∆∆∆
∑∑
同上采用哈明(Hamming)窗对初值谱进行光滑处理,得到光滑谱;。
