多重均衡
第二讲多重纳什均衡.ppt

香精包子的思考
香精包子——其他包子企业如何做?
参与人根据其共同观测到的信号选择行动。
•
博弈论第三章
4,4 -8,-2 -2,-8 -2,-2
17
第三节多重纳什均衡的选择标准
五、抗共谋均衡 (一)案例:是否采用新技术
厂商1
厂商2 新技术 旧技术 新技术 2,2,2 5,0,5 旧技术 0,5,5 1,1,10 厂商3:新技术 厂商2 新技术 旧技术 新技术 5,5,3 10,1,1 旧技术 1,10,1 2,2,2 厂商3:旧技术
(一)案例:计算机产品的兼容性
企业C
3.5
英
寸
盘
5.25英寸盘
3.5英寸盘
企业A
8,8 2,3
3,2 6,6
5.25英寸盘
•
博弈论第三章
4
第三节 多重纳什均衡的选择标准
一、帕累托优势标准:得益最大
(二)帕累托优势标准
按照支付大小筛选纳什均衡
(3.5英寸盘,3.5英寸盘)
8,8 2,3
二、风险优势标准:风险更小
(三)纳什均衡的选择标准:风险优势标准
比较不同纳什均衡之间的风险状况,风险小的纳什均衡 优先
帕累托标准还是风险标准? 1.人会犯错误; 2.大多数人是风险厌恶者。 帕累托标准:理论 风险优势标准:实践
• 博弈论第三章
9,9 8,0
0,8 7,7
12
第三节多重纳什均衡的选择标准
(二)分析:偏离损失比较法
2.乙:单独偏离均衡的损失 (1)偏离“作弊”:9-8=1
甲坚守
(2)偏离“不作弊”:7-0=7
9,9 8,0
多重均衡
博弈论与行为经济学章平pzhng@反应函数法乙正面q 反面1-q1-1甲正面p-11-11反面1-p1-1期望支付函数混合策略均衡eg1混合策略均衡eg1混合策略均衡eg1多重纳什均衡及甄别•标准一:帕累托占优猎鹿博弈Stag Hunt Game两个猎人以狩猎为生,主要有两种猎物——鹿和兔子,两人一起猎鹿,才能猎获一只鹿,如果单枪匹马,只能打到4只兔。
乙猎鹿打兔104甲猎鹿10004打兔44帕累托改进•就是一项政策能够至少有利于一个人,而不会对任何其他人造成损害。
所谓“帕累托最优”就是上述一切帕累托改进的机会都用尽了,再要对任何一个人有所改善,就不得不损害另外一些人。
•帕累托最优的想法是从多目标数学规划得到的。
•比如城市交通,除了政府办的公共交通,私人也能办小公交,和大公交竞争;•在医疗系统除了原有的低收费的系统,另外开辟了专家挂号,收费高一些;•学校有公立的,也有了私立的。
•股票市场也有双轨制,原有的股票是非流通股,新股票可以自由买卖,是流通股。
•新人新办法、老人老办法也是双轨制。
•这些措施大大地缓解了改革中可能有的矛盾,谁的利益都没有受损。
•房地产市场是一步取消了福利分房,没有经过双轨制就建立了房地产市场。
标准二:风险占优乙左右98甲上9007下87偏离损失比较法两害相权取其轻帕累托占优与风险占优的关系•对参与人的基本假定存在差异:帕累托占优适用于符合完全理性假定的参与人风险占优适用于判断搭档(对手)会犯错误,不信任;判断对手很可能是风险厌恶型的参与人。
基本原则:“在怕累托标准和风险标准之间,理论给帕累托占优以优先权,而风险占优只有在参与人面临不知道选哪个均衡好的不确定性时,才变得重要。
当一个均衡符合帕累托占优时,参与人一定选择这个均衡,不确定性也就不存在了。
”谢林的《冲突的策略》•其中一个例子:你和其他参与人均从下面一组数中选择一个数,并画上圈:7,100,13,261,99,666。
如果你们选择相同则赢利越多。
金融市场多重均衡模型研究

金融市场多重均衡模型研究摘要:金融市场作为一个复杂而又具有高度耦合性的系统,其内部的交互和变化关系一直是研究的热点之一。
多重均衡模型作为一种有助于解释市场现象的重要理论框架,被广泛应用于金融市场的研究中。
本文旨在对金融市场多重均衡模型进行深入的探讨和研究,并分析其应用价值和潜在问题。
引言:在金融市场中,投资者的行为和市场的状态常常呈现多样性和复杂性。
传统的均衡经济学模型难以解释这种多样性和复杂性,因此,研究人员开始使用多重均衡模型来更好地描述和解释金融市场中的现象。
一、多重均衡模型的发展历程:多重均衡模型的研究可以追溯到20世纪60年代的“柏兰德晃动”模型。
这一模型认为,市场参与者可能在不同的预期下作出不同的决策,从而导致市场出现多个均衡。
随后,学者们逐渐提出了一系列关于多重均衡的理论模型,如“信息板”和“羊群效应”模型,进一步丰富了对多重均衡的认识。
二、多重均衡模型的基本原理和机制:多重均衡模型的基本原理是,在金融市场中存在多个可能的均衡状态,这些均衡可以由市场参与者的预期和行为所决定。
不同的市场参与者会根据自身的信息和预期做出不同的决策,这些决策将进一步影响其他参与者的预期和行为,从而形成多个均衡状态。
三、多重均衡模型的应用案例:多重均衡模型在金融市场的研究中具有广泛的应用价值。
例如,在股票市场中,多重均衡模型可以帮助解释股价波动、市场崩盘和投资者的羊群行为。
在外汇市场中,多重均衡模型可以用来分析汇率的波动和投资者对外汇市场的预期。
此外,多重均衡模型还可以用于研究货币政策的效果和金融危机的演化机制。
四、多重均衡模型的潜在问题:虽然多重均衡模型在金融市场的研究中有着广泛的应用,但也存在一些潜在问题。
首先,多重均衡模型的参数估计和验证难度较大,需要大量的数据和复杂的数学方法。
其次,多重均衡模型往往假设市场参与者具有理性和信息对称性,这与现实市场存在的不完全理性和信息不对称相悖。
因此,在将多重均衡模型应用于实际问题时,需要进行适当的修正和拓展。
F-博弈论专题--纳什均衡多重性精选PPT

中国
欧 盟 求助
救助 (1500,300)
不救 (-200,-100)
等待 (2000,-200)
(0,0)
讨论分析:
1、温州民间借贷问题:政府如何出手? (1)出手600亿;(2)不管;(3)? 2、郑州市担保公司——扭曲的学习效应
温州市金融综合改革试验区,位于中国浙 江省,由国务院决定设立。 年3月28日, 国务院常务会议决定设立温州市金融综合 改革试验区,批准实施《浙江省温州市金 融综合改革试验区总体方案》,引导民间
在“性别战”博弈中,存在两个纯战略Nash均 衡——(F,F)和(B,B)以及一个混合战略Nash均 衡 ((3 , 1),(1 , 3)) 。
44 44
事实上,在对“性别战”博弈进行建模的过程 中,除了保留上图所示的要素(即参与人、战略 和支付)以外,其它与“性别战”博弈有关的所 有信息,如夫妻双方的生活习俗、他们所遵循 的文化传统等等,都被我们抛弃在模型之外。
博
弈U
方 1
D
博弈方2
L
R
9, 9 8, 0
0, 8 7, 7
风险上策均衡(D,R)
猎人2
鹿
兔子
猎 人
鹿
1 兔子
5, 5 3, 0
0, 3 3, 3
猎鹿博弈 风险上策均衡(兔子,兔子)
三、聚点(焦点)均衡
一对青年夫妻决定周末出去娱乐,可供他们娱乐的项目有或者去观看足球比赛(用表示F),或者观看芭蕾演出(用表示B)。 (2000,-200) (十)加强社会信用体系建设。
引导民间资金依法设立创业 企业、股权 企业及相关 管理机构。 (三)发展专业资产管理机构。 事实上,在对“性别战”博弈进行建模的过程中,除了保留上图所示的要素(即参与人、战略和支付)以外,其它与“性别战”博弈有关
开放经济中人力资本与经济增长的多重均衡——模型及中国的经验研究

文章 编 号 :0 02 7 (0 6 0 .170 10 .4 2 2 0 )60 3 .4
Y: 经 济 中 人 力 资 本 与 经 济 增 长 的 多 重 均 衡 i 放
— —
模 型 及 中 国的 经 验 研 究
祝 树金 ’许 和 连 , 明 勇 , 赖
( 南 大 学 经 济 与 贸 易学 院 , 南 长 沙 湖 湖
lb rtme t rd c h ia o d ra un lt u n c ptli h d c t n s co . eg v r me tn ol ttX S a o i O po u e t e f lg o so c ruaeh ma a i n t ee u a o e tr n e a i o en n my c l c S e e
Z HU h — n ,XU — a S uj i Hel n,LAIMig y n i n —o g
( o eeo cn mi n rd . n n Unv C a gh . u a 4 7 . hn ) C l g f o o e a dT a e Hu a i 。 h n s a H n n 0 9 C ia l E s 1 0 A src : ep p rpe e t a p n eo o cv rin o u a r wt d b t tTh a e rs ns n o e c n mi e s fL c sgo h mO d.wh r ea e tcn f ey al a ehs a o ee t g n a r l l c t i h e o
维普资讯
第3 3卷
第 6期
湖
南 大 学 学 报 (自 然 科 学 版 )
Vo . 3. . 1 3 No 6 De .2 0 0 6 c
多重均衡博弈理论

多重均衡博弈理论关键词:金融危机多重均衡博弈经济基本面用θ表示,θ∈[0,1],θ越大表示经济基本面越好。
维持固定汇率对于政府的好处为常数b,维持固定汇率的成本用连续可导函数c(θ,α)表示,α为总投资者中参加投机攻击者的比率,显然,c为θ的减函数和α的增函数,即偏导数c'θ<0,c'α>0。
面对投机攻击,当维护固定汇率的好处大于其成本时,政府维持固定汇率,当维护固定汇率的好处小于其成本时政府则放弃固定汇率。
每个投资者进行投机攻击的成本为t,t为0到1之间的正数,如果投机攻击使得政府放弃固定汇率时,投机攻击者可从货币贬值中得到好处1,如果政府继续维持固定汇率,那么投机攻击者将一无所获。
因此,投资者不进行攻击时的收益为0,而进行投机攻击并且获得成功时的收益为1-t,进行投机攻击失败时的收益为-t。
此外,假设当c(0,0)>b时,表示在经济基本面最差时,即使没有人进行投机攻击,政府也不能维持固定汇率;当 c (1,1)<b时,表示如果在经济基本面很好时,即使所有的投资者都进行投机攻击,政府也能维持固定汇率。
所以根据函数c的性质,必定存在θ,使c(θ,0)=b,以及θ,使c(θ,1)=b,因此:当θ∈[0,θ]时,不管是否存在投机攻击,政府维护固定汇率的成本超过收益,政府不会维持固定汇率;当θ∈[θ,1]时,不管是否存在投机攻击,政府维护固定汇率的成本小于收益,政府就会维持固定汇率;当θ∈[θ,θ]时,经济基本面处于所谓的“多重均衡区域”,政府是否维持固定汇率依赖于投机攻击者的比率。
金融危机的多重均衡博弈金融危机的产生与传导往往是由本国公众、本国政府、投机者甚至外国公众、外国政府、国际组织等多方参与者参加的多方非对称信息动态博弈过程。
在进行博弈均衡分析前有几个基本假设:当θ∈[θ,θ]时,经济基本面处于“多重均衡区域”,经济基本面不是太好,也不是很坏;在第一个假设的基础上,对于政府是强势政府还是弱势政府也很难有全面的信息了解;为了分析方便,文中给各博弈方的支付水平赋予了具体的数值,这些数值只表明大小多少关系,并不代表数值本身的四则运算关系。
多重纳什均衡的选择问题

多重纳什均衡的选择问题在博弈论和信息经济学中,我们常常面临一个问题:在存在多种纳什均衡的情况下,如何选择最优的均衡点。
这种选择问题涉及到市场竞争、政府决策、引入新技术等多个领域,在选择最优的策略时需要考虑众多的因素和权衡。
本文将从纳什均衡的定义出发,介绍多重纳什均衡的产生原因及其影响因素,并探讨选择最优均衡点的方法。
1. 纳什均衡的定义纳什均衡是博弈论中的一个重要概念,指的是在博弈中,每个参与者选择最优策略的状态。
具体地说,如果对于每个参与者的策略选择,其他参与者的策略都是最优的,那么这种状态就是纳什均衡。
例如,在一个两人博弈中,A和B的策略分别为合作和背叛,如果A选择合作,B 也选择合作,那么这种状态就是一个纳什均衡。
因为在这种情况下,A不会改变他的策略,因为他没有更好的选择了,B也不会改变,因为他的策略也是最优的。
2. 多重纳什均衡的产生原因在现实生活中,很多博弈存在多种纳什均衡的情况。
这种现象主要是因为以下两个原因所致。
2.1 非对称性在博弈中,参与者的利益和策略选择可能存在非对称性。
例如,在一个拍卖中,卖家和买家的目的可能是不同的。
卖家想要卖出商品,而买家则想以最低的价格买到这个商品。
因此,在这种情况下,可能存在多种纳什均衡。
2.2 多站点竞争在多站点竞争中,参与者的收益和策略选择可能会受到其它站点的影响。
例如,在一个城市中,如果只有一家咖啡店,那么这家咖啡店就可以定价较高,因为消费者没有其他选择。
但是,如果有多家咖啡店,则它们之间的定价策略和市场份额就会相互影响,可能存在多种纳什均衡。
3. 选择最优均衡点的方法在存在多重纳什均衡的情况下,如何选择最优的均衡点是一个复杂的问题。
以下是一些常用的方法:3.1 政策干预政府可以通过政策干预来引导市场选择最优的均衡点。
例如,在城市中建造公共场所,例如咖啡厅、购物中心等,以增加市场竞争和选择产品的范围。
3.2 引入新技术引入新技术也可以改变市场竞争的格局,在这个过程中可能会产生新的纳什均衡状态。
《博弈论与信息经济学讲义》第3章多重均衡与制度和文化

交通规则的演变
• 在法国大革命以前,贵族的马车习惯上是靠左行的, 穷人在路上看到富人的马车来了,要站在马路的右边。 因此,靠左行与“特权阶级”相联系,而靠右行被认 为更为“民主”。随着法国大革命,作为一个革命的 象征,规定所有的车都要靠右走。随着拿破仑对欧洲 大陆的征服,拿破仑将法国的规则带给了欧洲,也包 括靠右行驶的规则。当然,在地域上这个规则的转变 也是从西到东逐步完成的。比如说,与靠右行的西班 牙接壤的葡萄牙是在一战之后才转为靠右行,奥地利 是从西到东一个省一个省逐步转变的,匈牙利、捷克 和德国是在二战前才由左行转向右行的。瑞典,一直 到1967年,才通过法律宣布从靠左行改为靠右行。
资源争夺博弈(chicken)
Hawk Dove
Hawk -1,-1 0,10
Dove 10,0 5,5
产权的先占规则
• 人们为什么遵守这个规则? • 人们希望得到别人认可的愿望: • 一旦规则建立,每个人都预期其他人会遵守规则;给定这个预期,
每个人发现遵守规则是自己的利益所在,也希望别人能遵守这个 规则。任何不守规则的行为都会使守规则的人受到损害或者感到 威胁,从而引起后者的愤怒;任何其他人也因此会觉得自己未来 的利益受到威胁,对此种行为表示不满,对受害人表示同情; • 少数人不守规则并不会导致规则的消失; • 但如果规则总是偏向于某一组特定的人群,受到不公正对待的人 并不会蔑视不守规则的人,规则就容易被违反。 • 罗尔斯(Rawls)的正义论
纳什均衡。
1
x1
资源争夺博弈(chicken)
Hawk Dove
Hawk -1,-1 0,10
Dove 10,0 5,5
如何协调?
• 仅仅“理性”是不够的; • FOCAL POINT(PROMINENCE):
第10讲 多重纳什均衡的确定

10.1多重纳什均衡的存在
• • 许多博弈有多个纳什均衡,博弈的可能结局依赖于 的各种信息,如习惯、习俗、法律规章等。 如,在简单的道路行使规则上,在随机行使时的博 弈结构如下:
一旦由权力强制引入一种制度后,就会产生制度本身的自我约束性。而且,在权力的强制力 消失以后,仍可能作为稳定的制度继续运作。即使那些并不是最有效的制度与习惯,也可能 仅仅因为历史上曾由于采用的集团处于支配地位,而渗透到了新加入的人群之中,……
•三人相关均衡博弈
•纳什均衡是(D,r,A),收益为(2,2,2)。
•但显然,这不是一个理想状态。为了获得更高的收益,现设计一个信号装置以 使局中人相关地选择自己的策略。这个信号装置借助于投币来进行,它提供的 信息是:如果是正面,则甲取R,乙取r;而如果是反面,则甲取D,乙取d;丙 则总是取B。这样,借助于这样的信息,甲、乙、丙就可以达成(R,r,B)和(D ,d,B)均衡,从而优化各自的效用。
……习俗和规范可以被解释为提供由价格体制所不 能提供的某些商品而增进经济体制效率的合约”。
•
相关均衡
• 相关均衡是指通过“相关装置”,使局中人获得更 多的信息,从而协调博弈各方的行动。它是 Aumann(1974)首先提出的概念,随后,Myerson 在(1986)作了进一步发展,并发展出了机制设计 理论。 •美餐以后谁去洗碗?
社会制约机制
当前占世界主要地位的发达国家大多崇尚浮士德精神,其基本特征就是以军 事实力为基础实行殖民扩张; 在这种浮士德文明的指导下,世界演化的博 弈矩阵就可表示如下:
假设国际上联合起来对那些实行扩张对抗主义的国家实施惩 罚。如我们假设:存在一个联合国对对抗方处以5 的惩罚, 而补助损失方5 的收益,上面博弈矩阵变为以下形式:
多重纳什均衡课件

例如,在双寡头市场中,两个企业可能采用不同 的混合策略组合,如企业A采用高价和低产的混合 策略,企业B采用低价和高产的混合策略。
此外,如果企业之间采用相同的混合策略组合, 也可能形成多个纳什均衡点。例如,两个企业都 采用高价和低产的混合策略或都采用低价和高产 的混合策略。
04
多重纳什均衡的经济学意义
纳什均衡
在非合作博弈中,如果每个参与者在给定其他参与者策略的 前提下,选择自己的最优策略,那么所有参与者的策略组合 就构成一个纳什均衡。
多重纳什均衡
当存在多个纳什均衡时,这些均衡被称为多重纳什均衡。
多重纳什均衡的存在性条件
博弈的策略空间和参与者的数量
01
当博弈的策略空间和参与者的数量较大时,多重纳什均衡存在
的可能性增加。
博弈的支付函数
02
支付函数的非线性程度和分布情况也会影响多重纳什均衡的存
在性。
博弈的规则和约束条件
03
博弈的规则和约束条件也会对多重纳什均衡的存在性产生影响。
多重纳什均衡的求解方法
直观判断法
对于一些简单的博弈, 可以通过直观判断来找
出多重纳什均衡。
迭代法
通过迭代计算的方法, 可以找出多重纳什均衡。
这种方法通常适用于较 小的博弈。
线性规划法
通过线性规划的方法, 可以找出多重纳什均衡。
这种方法通常适用于较 大的博弈。
概率方法
通过概率方法,可以找 出多重纳什均衡。这种 方法通常适用于具有随
机性的博弈。
03
多重纳什均衡的实例分析
价格竞争中的多重纳什均衡
价格竞争中的多重纳什均衡是指在价格竞争中,企业 之间可能存在多个纳什均衡点,这些均衡点反映了不
金融脆弱性研究中的多重均衡模型

( O I L S I N E E II N) S CA CE C DTO
金 融 脆 弱 性 研 究 中的多 重 均 衡模 型 术
陆 家骝 ,陆
摘
婷
要: 多重均衡模型是论证金融体系脆弱性 的一个重要技术方 法。这个 方法 的思想性 在于颠覆 了市场
均衡惟一性 和最优性 的主流经济学 教条 , 从而可 以解释金融产业或金 融市 场在现实中的系统性 波动和危机 的 发 生。文章通过两个 代表性 多重均衡模 型的考察 , 分别从 内因和外 因的层面表 明 , 场体系 的内在动 力会 自 市
的一 种主要 技 术 方法 —— “ 重均 衡 模 型 ” 多 方法 。
作为 国家 社 会 科 学 基 金 重 点 项 目研 究 的一 个 内
考虑后 一种 可能性 的学理基 础 。第二 个 问题在 逻 辑上 同第一 个 问题 一 致 , 在西 方学 者看来 , 比 但 它
第一个 问题 更 重 要 。这 个 问题 就 是 , 果 放 任 市 如
20 0 8年 以来 , 由世 界 主要 的 资本 主 义 经济 体 引发 的全球 性经 济危 机导致 学术 界对 于 主流 经济 学 的一 些传 统教 条进 行反思 。这 些反 思 主要 聚焦
于两个 基本 问题 。第 一个 问题 同西方 国家 过去 二 三十年 间极 力 推 动 的经 济 全球 化 过程 相 关 , 即放 任市场 力量 , 实行 自由贸易 和 自由投 资政 策 , 界 世 最终会 是一 个 平衡 发 展 的 、 国都 能 发挥 其 竞 争 各
自 T=1 的储 存加 上他 在 T=2时 的所 得 , c 时 即 + c 。这样 , 人 们 可 公 开 观 察 到 的 变 量 c 就 而
多重均衡与优化博弈智能(二)

D
D C
C P
D
D
C
P
T S R R
-5
-5
0 -10
S T
C -10
0 -1 -1
T>R>P>S, 2R>T+S
3、帕累托最优均衡与纳什均衡的关系
(3.5’’, 3.5’’) 帕累托优于(5.5’’, 5.5”) 协商可以 帮助协调到一个 帕累托最优均衡
8, 8
3, 2
5.5’’
2, 3
6, 6
• 达成协议有难度,最初的非帕累托均衡可以被锁定(lock-in), 导 致路径依赖(path dependence):结果是整个社会被锁定在现有 的产品(标准)(非帕累托最优)。
交通博弈与交通规则
靠左行 靠右行
靠左行
1,1
-1,-1
靠右行
-1,-1
1,1
1、占优策略与智猪博弈
智猪博弈的其它例子: • “搭便车”现象 • 穷人和富人修路博弈 • 大股东对管理者的监督 • 俗语“天塌下来有大个子顶着”
占优策略和纳什均衡的比较
1. 占优策略:“不管你怎么做,我所做的 都是我能做得最好的。” 2. 纳什均衡:
– “给定你的做法后,我所做的是我能做得 最好的。” – 如果你有占优策略, 你可以使用此策略, 以 不变应万变; – 如果你没有占优策略, 你必须随机应变。在 达到了纳什均衡之后, 所有参与者都没有动 机想再变了。
交通规则的演变
• 在多个纳什均衡之间不存在优劣之分时,偶然事件对选择 具有重要意义; • 从历史上来考察,许多交通规则一开始并不体现为法律, 而是长期演化而来的。在欧洲大陆的早期,道路行走规范 是非常地方化的,有些地方采用靠左走的习惯,有些地方 采用靠右走的习惯,是不统一的。只是随着道路的增加和 地区间交往的扩大,地方性的习惯才逐步演变为区域性的 规范,然后有演变为全国性的规范。但直到19世纪前, 道路规则也仅仅是作为规范而得到遵守,而不是作为交通 法律而得到执行。现在欧洲大陆的靠右走的规则是在法国 兴起的。
1.5 多重纳什均衡及其甄别
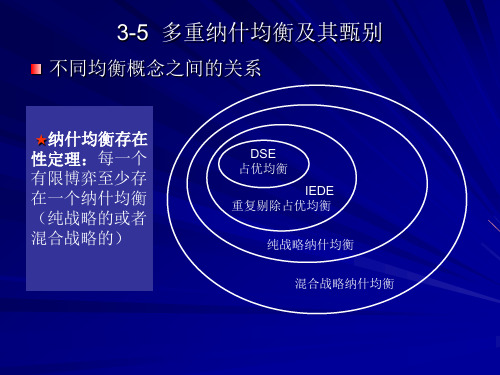
0,0,10 -5,-5,0
-5,-5,0 1,1,-5
乙
矩阵B
U 甲 D
L
R
-2,-2,0 -5,-5,0
-5,-5,0 -1,-1,5
1、上述博弈,如处于均衡(U,L,A),甲、乙共谋有共 上述博弈,如处于均衡(U
谋的激励,会导致结果(D 谋的激励,会导致结果(D,R,A) 纳什均衡的精髓:单独偏离没有好处。 纳什均衡的精髓:单独偏离没有好处。 但共谋偏离,那时均衡及前面介绍的方法就无法解决了。这 就需要抗共谋均衡的思想 就需要抗共谋均衡的思想。 抗共谋均衡的思想。 2、抗共谋均衡:与一般纳什均衡的区别,主要是在没有单 抗共谋均衡: 独偏离的激励的基础上,进一步引入了没有集体偏离的激 励的要求。即一个策略组合之所以成为抗共谋均衡,不仅 要求局中人在这个策略组合下没有单独偏离的激励,而且 也要求他们没有合伙集体偏离的激励。
(四)聚点均衡
在现实生活中,局中人可能会使用某些被博弈模型抽 象掉的信息来达到一个均衡,这些信息往往跟社会文化习 惯、局中人过去博弈的历史和经历有关。这就是聚点均衡 惯、局中人过去博弈的历史和经历有关。这就是聚点均衡 的思想。 对于一些即不存在帕累托优势,又不存在风险优势的 博弈,人们往往利用聚点均衡的思想来指导人们的行动。 如:交通靠左靠右问题;打电话续 接问题;看足球还是芭蕾舞;
L U 甲 D
R
5,1
4,4 图5
0,0 1,5
更为重要的是,奥蒙证明,如果每一个人收到不同的但 相关的信号,每个人都可以得到更高的期望效应。设想 两人同意由第三人通过掷骰子的办法决定每个人的选择, 如果1点或2点出现,A选择U;如果3 如果1点或2点出现,A选择U;如果3—6点出现,A选择 点出现,A D。B的情况相反:如果1—4点出现,B选择L,如果5—6 的情况相反:如果1 点出现,B选择L,如果5 点出现,B选择R 点出现,B选择R。假定第三方只告诉每个参与人选择什 么行动,而不透露什么点出现,。这样,当A被告诉D 么行动,而不透露什么点出现,。这样,当A被告诉D时, 他只知道3 他只知道3—6中的一个出现了,但并不知道是哪一个; 特别地他不知道B 特别地他不知道B被告诉选择什么。所以我们说每个人收 到的信号是相关的但不同的。下面我们说明上述规则是 一个纳什均衡。
多重平衡体系-概述说明以及解释

多重平衡体系-概述说明以及解释1.引言1.1 概述概述:多重平衡体系是一个复杂而关键的概念,它在许多领域和系统中起着重要的作用。
简而言之,多重平衡体系是指一个系统中存在着多个互相依赖、相互作用的平衡因素或平衡机制。
这些平衡因素相互制约、相互影响,一起维持着系统的稳定和平衡状态。
在自然界和人类社会中,多重平衡体系无处不在。
例如,生态系统就是一个具有多重平衡体系的典型例子。
在生态系统中,各种物种之间存在着复杂的相互依赖关系,如食物链、物种间的竞争关系等。
这些平衡因素共同维持着生态系统的稳定性和多样性。
另一个例子是经济系统中的供需平衡。
在市场经济中,供求关系是市场价格形成和资源配置的基础。
供给和需求的平衡对于维持市场稳定和经济发展至关重要。
当供求关系失衡时,市场会出现价格波动和资源错配,从而影响整个经济系统的稳定性。
多重平衡体系的特点是相互制约和相互影响。
不同的平衡因素之间存在着相互制约的关系,任何一个因素的改变都可能对其他因素产生连锁反应。
因此,维持多重平衡体系的稳定需要全面考虑各种因素之间的相互关系,并采取相应的调节和控制措施。
综上所述,多重平衡体系是一个重要而复杂的概念,在自然界和人类社会中发挥着重要的作用。
了解和研究多重平衡体系的定义和特点,有助于我们更好地理解和应对各种系统和问题,实现稳定和可持续发展。
在接下来的章节中,我们将详细探讨多重平衡体系的定义和特点,并总结其重要性和未来发展前景。
1.2 文章结构:本篇文章将按照以下结构进行展开。
第一部分是引言,概述整篇文章的背景和内容,并对多重平衡体系进行简要介绍。
在引言中,我们将提到多重平衡体系的重要性以及本文的目的。
第二部分是正文,将详细探讨多重平衡体系的定义和特点。
在2.1节中,我们将对多重平衡体系的定义进行解释和阐述,包括其在不同领域中的应用和意义。
在2.2节中,我们将深入探讨多重平衡体系的特点,涵盖其在自然环境、经济发展和社会组织等方面的表现和作用。
第二讲多重纳什均衡

➢(一)案例:串通作弊博弈
➢
逆天的帕 累托优势
学生乙
➢
标准 作弊 不作弊
➢
作弊
➢学生甲
➢
不作弊
9,9 8,0
0,8 7,7
第三节多重纳什均衡的选择标准
➢二、风险优势标准:风险更小 ➢(二)分析:偏离损失比较法 ➢1.甲:单独偏离均衡的损失 ➢(1)偏离“作弊”:9-8=1 ➢(2)偏离“不作弊”:7-0=7
的均衡。 ➢ 2.标准
➢根据社会文化习惯、博弈历史等信息达到均衡 ➢ 3.实质
➢规律性 ➢强调文化与环境的作用
新婚夫妻的家务分担博弈 ; 教室中的座位分配博弈。
第三节多重纳什均衡的选择标准
➢四、相关均衡
➢(一)案例:“地域连坐”下的产品 质量博弈
➢
企业乙
➢
好产品 差产品
➢
好产品 4,4
➢企业甲 ➢
2019年7月17日博弈论第三章第二讲多重纳什均衡第三节多重纳什均衡的选择标准2019年7月17日博弈论第三章第二讲多重纳什均衡35英寸盘525英寸盘525英寸盘883223662019年7月17日博弈论第三章第二讲多重纳什均衡3535883223662019年7月17日博弈论第三章第二讲多重纳什均衡2019年7月17日博弈论第三章第二讲多重纳什均衡99088077累托优势标准2019年7月17日博弈论第三章第二讲多重纳什均衡70799088077乙坚守2019年7月17日博弈论第三章第二讲多重纳什均衡70799088077甲坚守2019年7月17日博弈论第三章第二讲多重纳什均衡10990880772019年7月17日博弈论第三章第二讲多重纳什均衡11990880772019年7月17日博弈论第三章第二讲多重纳什均衡1299088077帕累托标准还是风险标准
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
博弈论与行为经济学章平
pzhng@
反应函数法
乙
正面q 反面1-q
1-1甲
正面p-11
-11反面1-p1-1
期望支付函数
混合策略均衡eg1
混合策略均衡eg1
混合策略均衡eg1
多重纳什均衡及甄别
•标准一:帕累托占优
猎鹿博弈Stag Hunt Game
两个猎人以狩猎为生,主要有两种
猎物——鹿和兔子,两人一起猎鹿,才能猎获一只鹿,如果单枪匹马,只能打到4只兔。
乙
猎鹿打兔104
甲猎鹿100
04打兔44
帕累托改进
•就是一项政策能够至少有利于一个人,而不会对任何其他人造成损害。
所谓“帕累托最优”就是上述一切帕累托改进的机会都用尽了,再要对任何一个人有所改善,就不得不损害另外一些人。
•帕累托最优的想法是从多目标数学规划得到的。
•比如城市交通,除了政府办的公共交通,私人也能办小公交,和大公交竞争;•在医疗系统除了原有的低收费的系统,另外开辟了专家挂号,收费高一些;
•学校有公立的,也有了私立的。
•股票市场也有双轨制,原有的股票是非流通股,新股票可以自由买卖,是流通股。
•新人新办法、老人老办法也是双轨制。
•这些措施大大地缓解了改革中可能有的矛盾,谁的利益都没有受损。
•房地产市场是一步取消了福利分房,没有经过双轨制就建立了房地产市场。
标准二:风险占优
乙左右98甲
上
9007下87偏离损失比较法两害相权取其轻
帕累托占优与风险占优的关系
•对参与人的基本假定存在差异:
帕累托占优适用于
符合完全理性假定的参与人
风险占优适用于
判断搭档(对手)会犯错误,不信任;
判断对手很可能是风险厌恶型的参与人。
基本原则:“在怕累托标准和风险标准之间,理论给帕累托占优以优先权,而风险占优只有在参与人面临不知道选哪个均衡好的不确定性时,才变得重要。
当一个均衡符合帕累托占优时,参与人一定选择这个均衡,不确定性也就不存在了。
”
谢林的《冲突的策略》
•其中一个例子:你和其他参与人均从下面
一组数中选择一个数,并画上圈:7,100,13,261,99,666。
如果你们选择相同则
赢利越多。
•你会选择哪个数呢?
谢林发现选7是最常见的策略;
但在一群比较贪婪的人群中,666也有可能成为聚点。
聚点均衡focal point equilibrium
Schelling, 1960
现实生活中,参与人可能会使用某些被博弈模型抽象掉的信息来达到一个均衡,这些信息往往跟社会文化习惯、参与人过去知识传统、博弈的历史和经历有关。
共同知识
情侣博弈?
靠左还是靠右行驶?
课堂实验
•Q1: 设想在没有事先交流的情况下,必须在
深圳选择一个地点与另一个人会面。
请问你选择在哪里与之会面?
•Q2:设想在没有事先交流的情况下,必须
在深圳大学选择一个地点与另一个同学会面。
请问你选择在哪里与之会面?
Q 1Q 2深圳大学世界之窗
海岸城地王大厦
地王大厦购物公园深大西门
文山湖深大正门图书馆新西南西门
桂庙文科楼科技楼
Q1
Q1选择地点选择人数深大25
世界之窗14万象城7地王大厦
311问题1
Q2
Q2选择地点选择人数文山湖11深大正门11图书馆10新图书馆8新西南5
科技楼4文科楼4西门311问题2
09问题1
09问题2
为什么?
•如果让我选:“脚踏实地”
•是因为选课同学中大一新生占了多数?还是本来我的感觉就是错误的?
•MEETING POINT
•柏林6.17大道的柏林世界杯球迷乐园,乐园中轴的6.17大道的中心,市政当局设立了一个MEETING POINT
如果博弈重复多次,则过去的历史常常就规定了聚点之所在
•学院每到周一下午就会开会,大家在会议室的座位本来是不固定的,但是每学期第一次会议大家所坐的位置,基本上会在这个学期都是他坐的位置,因为每次开会时大家就会习惯性地坐到上次坐过的位置,这种座位配置也如同产生了聚点一样。
•新婚夫妻的家务分担博弈也是如此,在婚姻初期谁做家务做得多,那就意味着可能这一辈子他/她都会做更多的家务,这也是一个聚点。
•在理论上一个博弈中可能有多个纳什均衡点,这时在现实生活中,行为人往往利用在理论上省略掉的那些信息,找到一个大家都感兴趣的点,这个点往往成为现实世界中博弈的最终解。
•当参与人之间没有正式的信息交流时,他们存在于其中的
“环境”往往可以提供某种暗
示,使得参与人不约而同地选
择与各自条件相称的策略(聚
点),从而达到均衡。
•——这个点之所以成为“聚点”,是因为博弈各方的文化和经验
使他们相信这个点是大家都容
易想到的、习惯选择的点。
•经济学研究的一个规范过程:
•假设——理论——模型——验证:证明or证伪•哪个是聚点?为什么是它?
•参与人的文化生活背景(城乡家庭)、以往经历(大一新生刚入学/经常上课地点/用餐地点;教师一般都在脚踏实地坐校车)、兴趣点(吃的地方、等车的地方)、年龄。
相关均衡correlated equilibrium
Aumann, 1974
乙左
右
1
甲上
5
4
5
下
4
1
参与人通过大家都能观测到的共同信号(拥有的共同知识)来选择行动,并由此确定了博弈结果。
规则:甲先到,则走甲上乙左均衡;乙先到,则走甲下乙右均衡。
•《圣经》上所罗门王的故事
•两个女人抱着一个男婴来到所罗门王跟前,要求他评判到底谁是真的母亲。
•所罗门王见她们争执不下,便喝令侍卫拿一把剑来,要把孩子劈成两半,一个母亲一半。
这时其中一个女人说:“大王,不要杀死孩子。
把孩子给她吧,我不和她争了”。
•所罗门王听了却说:“这个女人才是真的母亲,把孩子给她。
”
应用
•把竞相投标一项工程的两个企业,看作是两个“母亲”,其中一个实力可靠,另一个企业只是想夺标以后转包给他人,赚取差价利益。
模型把实力可靠的企业看做孩子的真母亲,把只是想夺标转包的企业,看作是假母亲,讨论如何做机制设计,甄别真伪信息。
•相关均衡中按照约定信号的行动和策略选择,必须是在信号出现的情况下对每个博弈参与人都有利的行动和策略选择。
标准二:风险占优
乙左右98甲
上
9007下87偏离损失比较法两害相权取其轻
帕累托占优与风险占优
•对参与人的基本假定存在差异:
帕累托占优适用于
符合完全理性假定的参与人
风险占优适用于:判断搭档(对手)会犯错误,不信任;判断对手很可能是风险厌恶型的参与人。
基本原则:“在怕累托标准和风险标准之间,理论给帕累托占优以优先权,而风险占优只有在参与人面临不知道选哪个均衡好的不确定性时,才变得重要。
当一个均衡符合帕累托占优时,参与人一定选择这个均衡,不确定性也就不存在了。
”
美国每天降生的婴儿数周末比平时少30-40%。
即便是顺产的孩子,周日出生的也比周三或周四出生的少35%
Gans&Leigh文章:周末出生的婴儿较少,广为人知,因为产科医生希望和亲友共度周末。
4月1日(愚人节)和2月29日出生的婴儿也较少,因为父母认为这些日子不吉利。
他们在研究,当父母和产科医生偏好的出生日期有冲突时,哪方的影响力大。
•美国情人节出生的婴儿比其他时候显着地多,而万圣节出生的婴儿比其他时候显着地少。
他们解释为情人节是正面的符号而万圣节是负面的象征,所以父母希望子女出生在情人节而非万圣节,并由此推断女性可能能控制自然生产的时间。
